Informative prior on structural equation modelling with non-homogenous error structure

Oladapo A. Olalude; Bernard O. Muse; Oluwayemisi O. Alaba

doi:10.12688/f1000research.108886.1

Home Browse Informative prior on structural equation modelling with non-homogenous...

ALL Metrics

-

Views

-

Downloads

Get PDF

Get XML

Export

▬

✚

Research Article

Informative prior on structural equation modelling with non-homogenous error structure

[version 1; peer review: 1 approved, 1 approved with reservations]

Oladapo A. Olalude ¹, Bernard O. Muse², Oluwayemisi O. Alaba¹

PUBLISHED 04 May 2022

Author details Author details

¹ Department of Statistics, University of Ibadan, Ibadan, Oyo State, +234, Nigeria
² Department of Mathematics and Statistics, Rufus Giwa Polytechnic, Owo, Ondo State, Nigeria

Oladapo A. Olalude
Roles: Data Curation, Methodology

Bernard O. Muse
Roles: Validation

Oluwayemisi O. Alaba
Roles: Resources, Supervision

OPEN PEER REVIEW

REVIEWER STATUS

Abstract

Introduction: This study investigates the impact of informative prior on Bayesian structural equation model (BSEM) with heteroscedastic error structure. A major drawback of homogeneous error structure is that, in most studies the underlying assumption of equal variance across observation is often unrealistic, hence the need to consider the non-homogenous error structure.
Methods: Updating appropriate informative prior, four different forms of heteroscedastic error structures were considered at sample sizes 50, 100, 200 and 500.
Results: The results show that both posterior predictive probability (PPP) and log likelihood are influenced by the sample size and the prior information, hence the model with the linear form of error structure is the best.
Conclusions: The study has been able to address sufficiently the problem of heteroscedasticity of known form using four different heteroscedastic conditions, the linear form outperformed other forms of heteroscedastic error structure thus can accommodate any form of data that violates the homogenous variance assumption by updating appropriate informative prior. Thus, this approach provides an alternative approach to the existing classical method which depends solely on the sample information.

Keywords

Bayesian SEM, Latent Variable, Observed Variable, Heteroscedastic error structure, Predictive Performance

Corresponding author: Oladapo A. Olalude

Competing interests: No competing interests were disclosed.

Grant information: The author(s) declared that no grants were involved in supporting this work.

Copyright: © 2022 Olalude OA et al. This is an open access article distributed under the terms of the Creative Commons Attribution License, which permits unrestricted use, distribution, and reproduction in any medium, provided the original work is properly cited.

How to cite: Olalude OA, Muse BO and Alaba OO. Informative prior on structural equation modelling with non-homogenous error structure [version 1; peer review: 1 approved, 1 approved with reservations]. F1000Research 2022, 11:494 (https://doi.org/10.12688/f1000research.108886.1) First published: 04 May 2022, 11:494 (https://doi.org/10.12688/f1000research.108886.1) Latest published: 20 Sep 2022, 11:494 (https://doi.org/10.12688/f1000research.108886.2)

Introduction

Bayesian structural equation modeling (BSEM) analyses the relationship between the observed, unobserved, and latent variables within the Bayesian context.¹⁴^,¹⁶^,²¹^,²⁴ The data visualization can be done by path diagram. In Bayesian inference, $θ$ is random, which depicts the level of uncertainty about the true value of $θ$ because both the observed data $y$ and the parameters $θ$ are assumed random. The joint probability of the parameters and the data as functions of the conditional distribution of the data given the parameters, and the prior distribution of the parameters can be modelled. More formally,

(1)

p (θ |Y) \propto p (θ) p (Y |θ)

where

P(θ|y) is the posterior distribution

P(θ) is the prior distribution

P(y|θ) is the likelihood function

The un-normalized posterior distribution when expressed in terms of the unknown parameters θ for fixed values of $y$ , this term is the likelihood L(θ|y). Thus, can be rewritten as:

(2)

p (θ |Y) \propto p (θ) L (θ |y)

Studies abound on classical methods and Bayesian methods with a focus on homogeneous variance.⁸^,¹⁹^,²²^,²⁵ This study explores the BSEM using different forms of heteroscedastic error structure.

Methods

Bayesian estimation of structural equation models (SEM)

This section develops a Gibbs sampler to estimate SEM with reflective measurement indicators.¹^,¹¹^,¹² The Bayesian estimation is illustrated by considering a SEM that is equivalent to the mostly used model. A SEM is composed of a measurement equation (3) and a structural equation (4)⁹:

(3)

y_{i} = Λ ω_{i} + ε_{i}

(4)

η_{i} = Π η_{i} + Γ ξ_{i} + δ_{i}

where

i ϵ \{1 \dots n\}

It is assumed that measurement errors are uncorrelated with $ω$ and $δ$ , residuals are uncorrelated with $ω$ and the variables are distributed as follows:

(5)

ε_{i} \sim N (0, Ψ_{ε})

(6)

δ_{i} \sim N (0, Ψ_{δ})

(7)

ω_{i} \sim N (0, Σ_{ω})

$\forall_{i} ϵ \{1 \dots n\}$ , where $Ψ_{ε}$ and $Ψ_{δ}$ are diagonal matrices. The covariance matrix of $ω$ is derived based on the SEM:

(8)

Σ_{ω} = [\begin{matrix} E ({ηη}^{T}) & E ({ξη}^{T}) \\ E ({ηξ}^{T}) & E ({ξξ}^{T}) \end{matrix}]

(9)

Σ_{ω} = [\begin{matrix} Π_{0}^{- 1} ({ΓΦΓ}^{T} + Ψ_{δ}) Π_{0}^{- T} & Π_{0}^{- 1} ΓΦ \\ {ΦΓ}^{T} Π_{0}^{- T} & Φ \end{matrix}]

(10)

{ηη}^{T} = (Π_{0}^{- 1} Γ ξ + Π_{0}^{- 1} δ) {(Π_{0}^{- 1} Γ ξ + Π_{0}^{- 1} δ)}^{T} = Π_{0}^{- 1} ({Γ ξξ}^{T} Γ^{T} + {δδ}^{T}) Π_{0}^{- T} + Π_{0}^{- 1} ({Γ ξδ}^{T} + {δξ}^{T} Γ^{T}) Π_{0}^{- T} E ({ηη}^{T}) = Π_{0}^{- 1} ({ΓΦΓ}^{T} + Ψ_{δ}) Π_{0}^{- T} {ηξ}^{T} = (Π_{0}^{- 1} Γ ξ + Π_{0}^{- 1} δ) ξ^{T} E ({ηξ}^{T}) = Π_{0}^{- 1} Γ

Prior distributions

In order to enable Gibbs sampling from full conditional posterior distributions, natural conjugate prior distributions for the unknown parameters are considered.²⁵ Let $ψ_{εκ}$ be the kth diagonal element of $Ψ_{ε}$ , $ψ_{δι}$ be the $l$ th diagonal element of $Ψ_{δ}, Λ_{κ}^{T}$ be the kth row of $Λ$ and $M_{ι}^{T}$ be the lth row of M,

(11)

ψ_{εk}^{- 1} \sim Gamma (α_{0 εk}, β_{0 εk})

(12)

[Λ_{k}| ψ_{εk}^{- 1}] \sim N (Λ_{0 k}, ψ_{εk}, H_{0 Λ k})

(13)

ψ_{δi}^{- 1} \sim Gamma (α_{0 δi}, β_{0 δi})

(14)

[M_{i}| ψ_{δi}^{- 1}] \sim N (M_{0 i}, ψ_{δi}, H_{0 Mi})

(15)

Φ \sim IW [v_{0}, V_{0}]

with

κ ϵ \{1 \dots p\}

and

ι ϵ \{1 \dots q 1\}

Derivations of conditional distributions

The joint posterior of all unknown parameters is proportional to the likelihood times the prior,

(16)

p (Λ, Ψ_{ε}, Ω, M, Ψ_{δ}, Φ, Y) \propto p (Y| Λ| Ψ_{ε}| Ω| M| Ψ_{δ}| Φ) * p (Λ, Λ_{ε}, Ω, M, Ψ_{δ}, Φ)

Given Y and $Ω$ , $Λ$ and $Ψ_{ε}$ are independent from $Σ_{ω}$ . Draws of $Ω$ , can cause estimation of $Λ$ and $Ψ_{ε}$ as a simple regression model. Thus, sampling from the posterior distribution of $Λ$ and $Ψ_{ε}$ without reference to $Σ_{ω} .$ The same holds for inference with regard to M, $Φ$ and $Ψ_{δ}$ , which are independent from Y given $Ω$ .

Heteroscedastic error structures

The heteroscedastic error structure with different functional form of error variance under consideration are double logarithmic form, linear form, linear-inverse form and linear-absolute form as expressed in equation 17, 18, 19 and 20, respectively.

(17)

σ^{2} = ln σ^{2} = λ_{o}^{*} + λ_{i}^{*} ln γ_{i}^{*} + vi

(18)

σ^{2} = | ε_{i}^{*} ε_{i}^{*'} | = {(λ_{i}^{*} + λ_{2}^{*} γ_{i}^{*} + νi)}^{2}

(19)

σ^{2} = | ε_{i}^{*} ε_{i}^{*'} | = {(λ_{i}^{*} + λ_{2}^{*} \sqrt{γ_{i}^{*}} + νi)}^{2}

(20)

σ^{2} = | ε_{i}^{*} ε_{i}^{*'} | = {(λ_{i}^{*} + λ_{2}^{*}| γ_{i}^{*}| + νi)}^{2}

Each of the functional forms of heteroscedastic error structure will be incorporated into the modified model. The variance matrix for disturbance vector is given as

(21)

\sum = (ε_{i}^{*} ε_{j}^{*'}) = ({σ_{λ}^{2}}_{i}^{*}, i = j)

(22)

Ω = [\begin{array}{l} σ^{2} λ_{i}^{*} & 0 & \dots & 0 \\ 0 & σ^{2} λ_{2}^{*} & \dots & 0 \\ ⋮ & 0 & \dots & 0 \\ 0 & 0 & \dots & σ^{2} λ_{n}^{*} \end{array}]

The posterior distribution

The posterior density is the product of the likelihood and the prior distribution chosen²^,¹³

(23)

(P (λ^{*}, h), Ω | y^{*}) αp (y^{*}| λ^{*}| h| Ω) p (λ^{*}) p (h) p (Ω)

(24)

p (P (λ^{*}, h), Ω, y^{*}) = h \frac{N}{2} (exp [- \frac{h}{2} {(γ^{*} - λ^{*})}^{'} (γ^{*} - λ^{*} γ^{*})]) \times h \frac{N + v - k}{2} exp [- \frac{hv}{2 s^{- 2}}] \times p (Ω) \times exp [- \frac{1}{2} {(λ^{*} - λ_{0}^{*})}^{'}] \underline{V^{- 1}} (λ^{*} - λ_{0}^{*})

(25)

P (λ^{*}, h, Ω, y^{*}) = h \frac{N}{2} | Ω | \frac{1}{2} exp [- \frac{h}{2} (y^{*} - λ^{*} γ) Ω^{- 1} (y^{*} - λ^{*} γ)] \times exp [- \frac{\underline{v^{- 1}}}{2} ({\underline{λ}}^{*} - λ_{0}^{*}) \underline{V^{- 1}} ({\underline{λ}}^{*} - λ_{0}^{*})] \times n^{- 1 (α + 1)} exp (\frac{- β}{h}) \times {|Ω^{*}|}^{- 1 (β_{0} + k + 1) / 2} e^{- tr (R_{0}^{- 1} β_{0}^{- 1}) / 2}

Since the full posterior distribution is intractable; a Markov chain Monte Carlo (MCMC) simulation method of Gibbs sampling is employed.²⁵ This involves the use of marginal posterior distribution.

(26)

λ = λ_{0}^{*} = {(γ' Ω^{- 1} γ)}^{- 1} γ' Ω^{- 1} γ = {(γ^{*'} γ)}^{- 1} γ^{*'} γ^{*}

S^{2} = \frac{(γ^{*} - γ^{*} λ_{0}) (γ^{*} - γ^{*} λ_{0})}{\underline{V}}

Also

\underline{{Vs}^{2}} + (λ^{*} - {\hat{λ}}_{0})' {γ_{i}}^{*}^{'} {γ_{i}}^{*} (λ^{*} - {\hat{λ}}_{0}) = (γ^{*} - {γ_{i}}^{*} λ^{*})' (γ^{*} - {γ_{i}}^{*} λ^{*})

(27)

p ({γ_{i}}^{*}| γ_{i}| σ^{2}) = \frac{h^{v + k / 2}}{(2 π) \frac{N}{2}} exp (- \frac{h}{2} (\underline{v} S^{2} + (λ^{*} - {\hat{λ}}_{0})' {γ_{i}}^{'} {γ_{i}}^{*} (λ^{*} - {\hat{λ}}_{0}))

\underline{v} = N - K and N = \underline{v} + K

Consider an informative prior created by set.

\underline{v^{- 1}} j = (\frac{1}{c^{k} j}) γ_{j}^{*} γ_{j}^{*}

And letting c $\to 0 for j = 1, 2$

The posterior distribution of $λ^{*}$ conditional on $γ^{*}$ , h, $Ω$ is given by:

(28)

p (λ^{*}| γ^{*}| h| Ω) α h^{\frac{N}{2}} exp (- \frac{h}{2} (γ^{*} - λ^{*} γ^{*})' Ω^{- 1} (γ^{*} - λ^{*} γ^{*}) + (λ^{*} - λ_{0}^{*})' \underline{V^{- 1}} (γ^{*} - λ_{0}^{*}) \times exp [- \frac{h}{2 (Ω)} (γ_{i}^{*} - λ^{*} γ_{i}^{*})' (γ_{i}^{*} - λ^{*} γ_{i}^{*}) + \frac{(λ^{*} - λ_{0}^{*})' (λ^{*} - λ_{0}^{*})}{\underline{v}}]

Solving the exponential part of the above equation, we will have:

(γ_{i}^{*} - λ^{*} γ_{i}^{*})' (γ_{i}^{*} - λ^{*} γ_{i}^{*}) = {(γ^{*})}^{2} + {(λ^{*} γ^{*})}^{2} - 2 y_{i}^{*} λ^{*} γ^{*} and (γ^{*} - λ_{0}^{*})' (λ^{*} - λ_{0}^{*}) = {(λ^{*})}^{2} + ({(λ_{0}^{*})}^{2} - 2 λ^{*} λ_{0}^{*})

Therefore,

= exp [- \frac{h}{2 (Ω)} \sum_{i = 1}^{N} y_{i}^{*^{2}} + {(λ^{*} γ^{*})}^{2} - 2 y_{i}^{*} λ^{*} γ_{i}^{*} + {\frac{(λ^{*} - λ_{0}^{*})}{\underline{v}}}^{2}]

The additional term not involving $λ^{*}$ is factored out to give:

(29)

= exp [- \frac{λ^{* 2}}{2 \underline{v^{2}}} + \frac{λ^{* 2} λ_{0}^{*}}{\underline{v^{2}}} + \frac{λ^{*} {ny}^{*}}{Ω σ^{2}} - \frac{n λ^{* 2}}{2 Ω σ^{2}}]

Factorization in terms of $λ^{*}$ , the term in the exponential becomes:

= - \frac{λ^{* 2}}{σ^{2}} + \frac{2 {λλ}_{*}^{*}}{2 {σ_{*}}^{2}}

σ_{*}^{2} = {(\frac{1}{\underline{v}} + \frac{n}{Ω σ^{2}})}^{- 1} and λ_{*}^{*} = σ_{*}^{2} (\frac{λ_{0}^{2}}{\underline{v}} + \frac{{ny}^{*}}{Ω σ^{2}})

So, the posterior density of $λ^{*}$ conditioned on other parameter h, $Ω$ , y^∗ is a multivariate normal with mean $λ^{*}$ and variance $σ_{*}^{2}$ .

That is,

p (λ^{*}| h| Ω| y^{*}) \sim N (λ_{*}^{*}, σ_{*}^{2})

The posterior distribution of h conditional on $λ^{*}$ , $Ω$ , $y^{*}$ is given by:

(30)

P (λ^{*}| h| Ω| γ^{*}) α h \frac{N}{2} exp [- \frac{h}{2} (γ^{*} - λ^{*} γ^{*})' Ω^{- 1} (γ^{*} - λ^{*} γ^{*}) \times h \frac{N + v - k}{2} exp (- \frac{hv}{2 S^{2}})] = h \frac{N + v - k}{2} exp (- \frac{h}{2 Ω}) \sum_{i}^{N} (y_{i}^{2 *} + n {(λ^{*} γ^{*})}^{2} - 2 y^{*} n λ^{*} γ^{*} - [\frac{hv}{2 s^{2}}])

The posterior distribution of Ω^*, conditional on y^*, λ^*, h, is given by:

(31)

P (Ω| y^{*}| λ^{*}| h) α P (Ω) \times h \frac{N}{2} exp [- \frac{h}{2} (y^{*} - λ^{*} γ^{*})' Ω^{- 1} (y^{*} - λ^{*} γ^{*})]

(32)

P (Ω| y^{*}| λ^{*}| h) α h \frac{N}{2} exp [- \frac{h}{2} (y^{*} - λ^{*} γ^{*})' Ω^{- 1} (y^{*} - λ^{*} γ^{*})] \times {| Ω^{*} |}^{- (β_{0} + k + 1) / 2} exp tr (R_{0}^{- 1} β_{0}^{- 1}) / 2

The Gibbs sampler

The Gibbs sampling procedure used in this study involves generation of sequence of draws from the conditional posterior distribution of each parameter.²^,²²^,²⁵

Gibbs sampling procedure

(i) Chose a starting or initial value, $ϕ^{(0)}$ for $s = 1, 2, \dots, S$
(ii) Take a random draw, $ϕ_{1}^{x}$ from the full conditional, $p (ϕ_{(1)}| y| ϕ_{(1)}^{(x - 1)})$
(iii) Take a random draw, $ϕ_{2}^{x}$ from the full conditional, $p (ϕ_{(2)}| y| ϕ_{(1)}^{(x)})$ using the updated values of $ϕ_{1}^{x}$
(iv) Repeat until M draws are obtained, each being a vector of $ϕ^{(x)}$
(v) Perform the Burn-in by dropping the first $S_{(0)}$ of these draws to eliminate the effect of $ϕ_{0}$ , the remaining $S_{1}$ draws are then averaged to obtain the estimate of the posterior $E [g (ϕ) / y]$ .

The right-hand side of (15) is proportional to the density function of an inverse Wishart distribution

Then,

(33)

P (Φ| Y| Ω) \sim {IW}_{q} [({ΩΩ}^{T} R_{0}^{- 1}), n + ρ_{0}]

Design of simulation

• At different functional forms of³ heteroscedastic error structure with changes in sample size of 50, 100, 200 and 500. Hyper-parameter will be arbitrarily chosen for the simulation using Gibbs sampler an MCMC method.⁶^,²²
• The R code can be accessed via the Extended data.²⁶
• Factor loading and error precision followed multivariate normal and inverse gamma distributions respectively to assess the prior sensitivity.²¹
• The criteria that will be used to assess the performance of the posterior simulation technique are the posterior estimates.

In order to evaluate the Bayesian model fit, we used the posterior predictive probability (PPP) procedure.⁴^,⁵^,⁷^,²⁴

(34)

PPP = P (f (y, \hat{λ} i) < f (y^{rep}, {\hat{λ}}_{i}) \equiv \frac{1}{m} \sum_{i = 1}^{m} δ_{i}

After achieving convergence (after j iterations). $({\hat{λ}}^{* (j + 1)}, λ^{(j + 1)}, Ω^{(j + 1)})$ can be regarded as observation from p(λ*, Ω|y) collect $[(λ^{* (t)}, Ω^{* (t)}) t = j + 1, . \dots, + T]$ for statistical inference.

(35)

\hat{λ} = T^{- 1} \sum_{t = 1}^{T} λ^{(t)}, \hat{Ω} = T^{- 1} \sum_{t = 1}^{T} Ω^{(t)}

gives Bayesian estimates of parameter and the latent variables.¹⁰^,¹⁷^,²³

Results and discussion

The section presents the discussion of analysis of results; performances of the estimators across the parameters for the different forms of heteroscedasticity, performances of Bayesian posterior simulation and analytical methods in the presence of heteroscedasticity via consideration of four (4) different forms of heteroscedastic error structures over four sample sizes of 50, 100, 200 and 500.

Performance of the estimators at heteroscedasticity condition

This gives the results for the latent and observed variables at various sample sizes for the four heteroscedastic error conditions considered.

Comparison of latent variable estimates at different sample sizes under the heteroscedasticity condition

Using the assumed values for the estimates which are $λ_{1}$ = 2.0, $λ_{2}$ = 3.0 and precision = 15.0.

The covariance matrix of ω was derived to be $E \cdot ηξT = \prod_{0}^{- 1} Γ$ with M at fixed values (0 or 1). The Bayesian estimates of SEM using the independent normal-gamma priors were derived for the two classes of SEM. Hyper-parameter was arbitrarily chosen for the simulation using Gibbs sampler a Markov chain Monte Carlo (MCMC) method since the joint posterior density does not have a tractable form. For the double logarithmic form, at 95% credible interval, when n=50, Posterior Mean, PM, and Precision, PR (2.011, 2.435, and 13.202), Posterior Standard Deviation PSD (0.035, 0.033, and 0.223) and when n=100, PM, and PR (2.022, 2.528, and 13.70), PSD (0.023, 0.025, and 0.251), when n=200, PM, and PR (2.052, 2.611, and 14.4), PSD (0.017, 0.018, and 0.255), when n=500, PM, and PR (2.010, 2.801, and 14.7), PSD (0.031, 0.021, and 0.258).

For the linear form, when n=50, PM, and PR (1.845, 2.779, and 13.95), PSD (0.240, 0.242, and 0.235). When n=100, PM, and PR (1.861, 2.811, and 14.22), PSD (0.328, 0.226, and 0.325), when n= 200, PM, and PR (1.956, 2.921, and 14.72), PSD (0.219, 0.217, and 0.212), and when n=500, PM, and PR (2.120, 3.122, and 14.95), PSD (0.211, 0.311, and 0.114).

For the linear-inverse form when n=50, PM, and PR (1.882, 2.742, and 14.95), PSD (0.040, 0.028, and 0.291). When n=100, PM, and PR (1.972, 2.835, and 14.65), PSD (0.024, 0.023, and 0.229). When n=200, PM, and PR (1.988, 2.901, and 14.45), PSD (0.017, 0.016, and 0.109), and when n=500, PM, and PR (2.021, 3.003, and 14.21), PSD (0.011, 0.015, and 0.105).

For the linear-absolute form, when n=50, PM, and PR (2.036, 2.824, and 14.500), PSD (0.032, 0.034, and 0.122), When n=100, PM, and PR (1.908, 2.903, and 13.92), PSD (0.022, 0.026, and 0.234). When n=200, PM, and PR (1.893, 2.809, and 13.85), PSD (0.017, 0.023, and 0.311), and when n=500, PM, and PR (1.806, 2.788, and 13.55), PSD (0.031, 0.035, and 0.433).

Examining different forms of heteroscedastic error structures in Bayesian structural equation modeling using informative priors, rather than assuming homogenous variance which is often a statistical fallacy in many studies. We compare the models’ posterior means and standard deviations in Tables 1, 2, 3 and 4. The differences are unlikely to impact substantive conclusions, but two of them are noteworthy.

Table 1. Double logarithmic form on latent variable and observed variable estimates.

Sample sizes	Latent variables	Posterior Mean (PM)	Posterior Standard Deviation (PSD)	Credible Interval (CI)		Measured variables	Estimate	Standard Deviation
n=50	$λ_{1}$	2.011	0.035	1.959	2.062	x₁	0.045	0.023
	$λ_{2}$	2.435	0.033	2.384	2.485	x₂	0.038	0.023
	Precision (PR)	13.202	0.223	13.071	13.332	x₂	0.038	0.023
n=100	$λ_{1}$	2.022	0.023	1.979	2.064	x₁	0.053	0.008
	$λ_{2}$	2.528	0.025	2.484	2.571	x₂	0.037	0.024
	Precision	13.700	0.251	13.561	13.838	x₂	0.037	0.024
N=200	$λ_{1}$	2.052	0.017	2.015	2.088	x₁	0.006	0.045
	$λ_{2}$	2.611	0.018	2.573	2.648	x₂	0.048	0.020
	Precision	14.4	0.255	14.260	14.539	x₂	0.048	0.020
N=500	$λ_{1}$	2.010	0.031	1.961	2.058	x₁	0.040	0.028
	$λ_{2}$	2.801	0.021	2.760	2.841	x₂	0.018	0.004
	Precision	14.7	0.258	14.559	14.840	x₂	0.018	0.004

Table 2. Linear form on latent variable and observed variable estimates.

Sample sizes	Latent variables	Posterior Mean (PM)	Posterior Standard Deviation (PSD)	Credible Interval (CI)		Measured variables	Estimate	Standard Deviation
n=50	$λ_{1}$	1.845	0.240	1.709	1.981	x₁	0.078	0.017
	$λ_{2}$	2.779	0.242	2.643	2.915	x₂	0.055	0.036
	Precision	13.950	0.235	13.816	14.844	x₂	0.055	0.036
n=100	$λ_{1}$	1.861	0.328	1.702	2.0197	x₁	0.079	0.012
	$λ_{2}$	2.811	0.226	2.679	2.943	x₂	0.036	0.028
	Precision	14.220	0.325	14.062	14.378	x₂	0.036	0.028
N=200	$λ_{1}$	1.956	0.219	1.826	2.086	x₁	0.071	0.008
	$λ_{2}$	2.921	0.217	2.792	3.050	x₂	0.047	0.016
	Precision	14.72	0.212	14.542	14.898	x₂	0.047	0.016
N=500	$λ_{1}$	2.120	0.211	1.993	2.247	x₁	0.052	0.022
	$λ_{2}$	3.122	0.311	2.967	3.277	x₂	0.059	0.010
	Precision	14.95	0.114	14.857	15.044	x₂	0.059	0.010

Table 3. Linear inverse form on latent variable and observed variable estimates.

Sample sizes	Latent variables	Posterior Mean (PM)	Posterior Standard Deviation (PSD)	Credible Interval (CI)		Measured variables	Estimate	Standard Deviation
n=50	$λ_{1}$	1.882	0.043	1.827	1.937	x₁	0.075	0.020
	$λ_{2}$	2.742	0.028	2.696	2.788	x₂	0.023	0.017
	Precision	14.95	0.291	14.801	15.099	x₂	0.023	0.017
n=100	$λ_{1}$	1.972	0.024	1.929	2.015	x₁	0.055	0.010
	$λ_{2}$	2.835	0.023	2.793	2.877	x₂	0.031	0.021
	Precision	14.65	0.229	14.317	14.583	x₂	0.031	0.021
N=200	$λ_{1}$	1.988	0.017	1.826	2.102	x₁	0.054	0.006
	$λ_{2}$	2.901	0.016	2.790	3.012	x₂	0.032	0.024
	Precision	14.45	0.109	14.358	14.541	x₂	0.032	0.024
N=500	$λ_{1}$	2.021	0.011	1.992	2.050	x₁	0.052	0.015
	$λ_{2}$	3.003	0.015	2.969	3.037	x₂	0.050	0.022
	Precision	14.210	0.105	14.120	14.300	x₂	0.050	0.022

Table 4. Linear absolute form on latent variable and observed variable estimates.

Sample sizes	Latent variables	Posterior Mean (PM)	Posterior Standard Deviation (PSD)	Credible Interval (CI)		Measured variables	Estimate	Standard Deviation
n=50	$λ_{1}$	2.036	0.032	1.986	2.086	x₁	0.043	0.018
	$λ_{2}$	2.824	0.034	2.773	2.875	x₂	0.027	0.022
	Precision	14.500	0.122	14.403	14.597	x₂	0.027	0.022
n=100	$λ_{1}$	1.908	0.022	1.867	1.949	x₁	0.047	0.017
	$λ_{2}$	2.903	0.026	2.858	2.948	x₂	0.043	0.025
	Precision	13.92	0.234	13.786	14.054	x₂	0.043	0.025
N=200	$λ_{1}$	1.893	0.017	1.857	1.929	x₁	0.054	0.017
	$λ_{2}$	2.809	0.023	2.767	2.851	x₂	0.041	0.024
	Precision	13.85	0.311	13.696	14.005	x₂	0.041	0.024
N=500	$λ_{1}$	1.806	0.031	1.757	1.855	x₁	0.048	0.019
	$λ_{2}$	2.788	0.035	2.736	2.840	x₂	0.044	0.022
	Precision	13.55	0.433	13.367	13.732	x₂	0.044	0.022

First, the posterior means of the loadings ( $λ_{1}$ and $λ_{2}$ ) are somewhat smaller under different heteroscedastic condition with the informative priors as observed in Tables 6 and 7. Second, the factor variance $γ^{*}$ is larger under our model with informative priors, likely because the informative prior placed more density on larger values of the posterior standard deviation. An evaluation of the model fit was based on the values of PPP as shown in Table 5 and it was observed that the linear form is the best with minimum PPP value as sample size increases. It was also revealed by the downward slope of the model as the sample size increases from 50 to 500 shown in Figure 1b when compared with Figure 1a, 2a and 2b.

Table 5. Comparison at varying sample sizes of different heteroscedastic form.

Sample size	Double logarithmic		Linear		Linear inverse		Linear absolute
Sample size	LogLik	PPP	LogLik	PPP	LogLik	PPP	LogLik	PPP
N=50	-17.577	0.538	-17.309	0.501	-19.701	0.567	-20.065	0.560
N=100	-24.324	0.543	-43.058	0.523	-16.214	0.544	-19.777	0.544
N=200	-29.427	0.541	-44.935	0.545	-15.305	0.540	-19.547	0.532
N=500	-35.510	0.482	-60.920	0.570	-14.494	0.531	-18.171	0.506

Table 6. Latent variable estimates at different sample sizes under the double-logarithmic and linear forms.

Sample size	Latent variables	Double logarithmic				Linear
Sample size	Latent variables	Posterior Mean (PM)	Posterior Standard Deviation (PSD)	Credible Interval (CI)		Posterior Mean (PM)	Posterior Standard Deviation (PSD)	Credible Interval (CI)
N=50	$λ_{1}$	2.001	0.231	1.868	2.134	2.110	0.230	1.977	2.243
N=50	$λ_{2}$	2.283	0.538	2.080	2.486	2.554	0.201	2.430	2.678
N=100	$λ_{1}$	2.021	0.312	1.866	2.176	2.020	0.123	1.923	2.117
N=100	$λ_{2}$	2.478	0.562	2.270	2.686	2.601	0.356	2.436	2.766
N=200	$λ_{1}$	2.032	0.432	1.850	2.214	2.011	0.174	1.895	2.127
N=200	$λ_{2}$	2.770	0.832	2.517	3.023	2.705	0.456	2.518	2.892
N=500	$λ_{1}$	2.100	0.445	1.915	2.285	2.005	0.253	1.866	2.144
N=500	$λ_{2}$	2.888	1.564	2.541	3.234	3.102	0.575	2.892	3.312

Table 7. Latent variable estimates at different sample sizes under the linear-inverse and linear absolute forms.

Sample size	Latent variables	Linear-inverse				Linear-absolute
Sample size	Latent variables	Posterior Mean (PM)	Posterior Standard Deviation (PSD)	Credible Interval (CI)		Posterior Mean (PM)	Posterior Standard Deviation (PSD)	Credible Interval (CI)
N=50	$λ_{1}$	2.101	0.352	1.937	2.265	1.732	0.311	1.577	1.887
N=50	$λ_{2}$	2.637	0.528	2.436	2.838	2.582	0.583	2.370	2.794
N=100	$λ_{1}$	1.982	0.421	1.802	2.162	1.810	0.252	1.671	1.949
N=100	$λ_{2}$	2.754	0.192	2.633	2.875	2.634	0.375	2.464	2.804
N=200	$λ_{1}$	1.975	0.476	1.784	2.166	1.820	0.211	1.696	1.947
N=200	$λ_{2}$	2.814	0.901	2.551	3.077	2.723	0.766	2.480	2.966
N=500	$λ_{1}$	2.111	0.488	1.917	2.305	1.920	0.145	1.815	2.026
N=500	$λ_{2}$	3.073	1.102	2.782	3.364	2.902	0.331	2.743	3.062

Figure 1. Plot of log likelihood and posterior predictive probability (PPP) at various sample sizes under (a) the double logarithmic form and (b) the linear form.

Figure 2. Plot of log likelihood and posterior predictive distribution (PPP) at various sample sizes under (a) the linear-inverse form (b) the linear-absolute form.

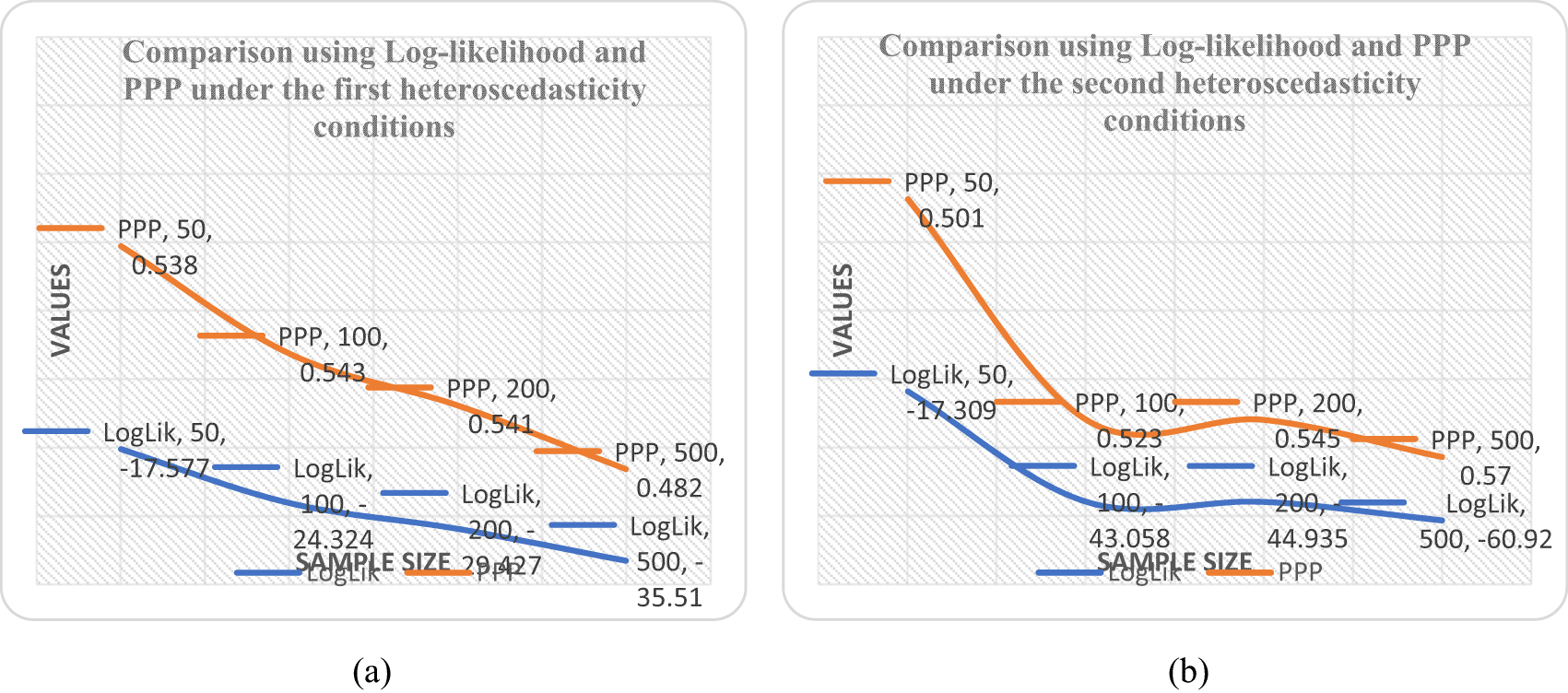
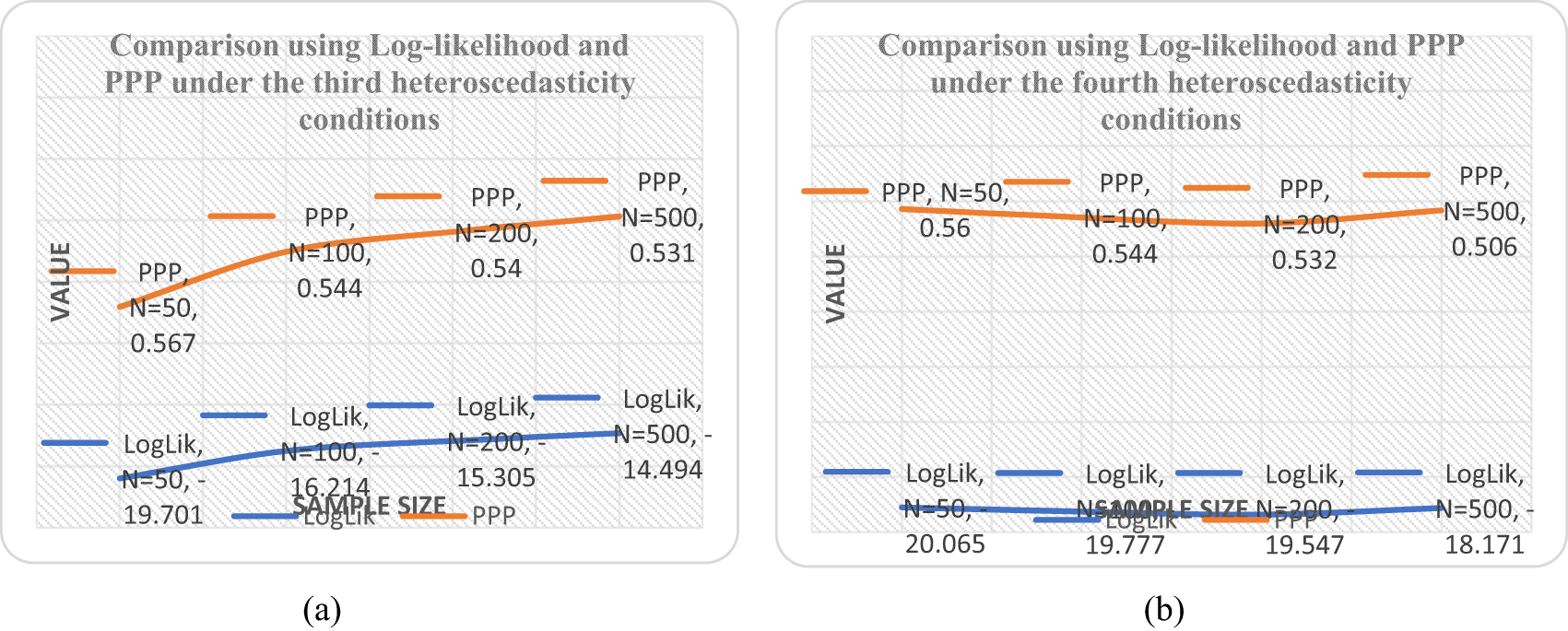
Considering an improvement to maximum likelihood method, in Bayesian estimations, parameters are considered as random with informative prior distribution also known as the conjugate family of the posterior, once the data is simulated/collected, it is combined with prior distribution using Bayes theorem, next posterior distribution is calculated reflecting the prior knowledge and simulated data.¹⁴^,¹⁵^,²¹ Joint posterior distribution is summarized using MCMC simulation techniques in terms of lower dimensional summary statistics as posterior mean and posterior standard deviations.⁵^,²⁵ We observe that the structural and measurement equation obtained from this study are adequate and in general we could accept the proposed model.

Conclusion

In this research, the derived Bayesian estimators of a structural equation model in the presence of different forms of heteroscedastic error structures validated accurate statistical inference. The study has also been able to address sufficiently the problem of heteroscedasticity of known form using four different heteroscedastic conditions for both linear and quadratic forms, and it has also successfully modified the homogenous error structure to heteroscedastic error structure in Bayesian structural equation model.²⁰ The linear form outperformed other forms of heteroscedastic error structure thus can accommodate any form of data that violates the homogenous variance assumption by updating appropriate informative prior.¹⁶^,¹⁸ Thus, this approach provides an alternative approach to the existing classical method which depends solely on the sample information.

Data availability

Underlying data

All data underlying the results are available as part of the article and no additional source data are required.

Extended data

Figshare: RCODE BSEM.docx. https://doi.org/10.6084/m9.figshare.19299851.²⁶

Data are available under the terms of the Creative Commons Zero “No rights reserved” data waiver (CC0 1.0 Public domain dedication).

References

1. Anderson JC, Gerbing DW: Some methods for respecifying measurement models to obtain unidimensional construct measurement. Journal of Marketing Research . 1982; 19(4): 453–460. Publisher Full Text
2. Ansari A, Jedidi K: Bayesian Factor Analysis for Multilevel Binary Observations. Psychometrika . 2000; 65(4): 475–496. Publisher Full Text
3. Ansari A, Jedidi K, Dube L: Heterogeneous factor analysis models: A Bayesian approach. Psychometrika . 2002; 67(1): 49–77. Publisher Full Text
4. Asparouhov T, Muthén BO: Bayesian analysis of latent variable models using Mplus. 2010. www.statmodel.com/download/BayesAdvantages18.pdf.
5. Bansal S: A new Gibbs sampling-based Bayesian model updating approach using modal data from multiple setups. International Journal for Uncertainty Quantification. 2015; 5(4): 361–374. Publisher Full Text
6. Bellman R: Dynamic programming and Lagrange multipliers.Proceedings of the National Academy of Sciences of the United States of America.1956; 42(10), 767–769. Publisher Full Text | PubMed Abstract | Free Full Text
7. Bentler PM: Comparative Fit Indexes in Structural Models. Psychological Bulletin . 1990; 107(2): 238–246. PubMed Abstract | Publisher Full Text
8. Das S, Chen M-H, Kim S, et al.: A Bayesian Structural Equations Model for Multilevel Data with Missing Responses and Missing Covariates.2008 ; vol 3, Number 1, pp. 197–224
9. Depaoli S: Measurement and structural model class separation in mixture CFA: ML/EM versus MCMC. Structural Equation Modeling . 2012; 19: 178–203. Publisher Full Text
10. Dunson DB: Bayesian Latent Variable Models for Clustered Mixed Outcomes.Journal of the Royal Statistical Society, Series B, 2000; 62: 355–366. Publisher Full Text
11. Hancock GR, Mueller RO: Structural equation modeling: A second course. Information Age Publishing, Inc.; 2006.
12. Kaplan D, Depaoli S: Bayesian statistical methods. In T. D. Little (Ed.).Oxford handbook of quantitative methods.Oxford: Oxford University Press; 2013 (pp. 407–437).
13. Kass RE, Raftery AE: Bayes Factors. Journal of the American Statistical Association . 1995; 90: 773–795. Publisher Full Text
14. Lee: Structural Equation Modeling: A Bayesian approach. New York: John Wiley & Sons, Ltd.; 2007.
15. Lee S, Song X: Maximum Likelihood Analysis of a General Latent Variable Model with Hierarchically Mixed Data. Biometrics . 2003; 60: 624–636.
16. Lee SY, Shi JQ: Bayesian analysis of structural equation model with fixed covariates. Structural Equation Modeling . 2000; 7: 411–430. Publisher Full Text
17. Mauricio G, Jorgensen TD: Adapting Fit Indices for Bayesian Structural Equation Modeling. Comparison to Maximum Likelihood Journal of Psychological Methods . 2019; 25(1): 46–70. Publisher Full Text
18. Meghan K. Cain1 and Zhang Z: Fit for a Bayesian: An Evaluation of PPP and DIC for Structural Equation Modeling2018; 26: 39–50. Publisher Full Text
19. Oberski DL, Satorra A: Measurement error models with uncertainty about the error variance. Structural Equation Modeling . 2013; 20(3): 409–428. Publisher Full Text
20. Olsson UH, Foss T, Troye SV, et al.: The performance of ML, GLS, and WLS estimation in SEM under conditions of misspecification and non-normality. Structural Equation Modeling . 2000, 2000; 7: 557–595.
21. Palomo J, Dunson DB, Bollen K: Bayesian structural equation modeling. Handbook of Computing and Statistics with Application . 2007; 1: 163–188. Publisher Full Text
22. Scheines R, Hoijtink H, Boomsma A: Bayesian estimation and testing of structural equation models. Psychometrika . 1999; 64: 37–52. Publisher Full Text
23. Spiegelhalter DJ, et al.: Bayesian measures of model complexity and fit. Journal of Royal Statistical Society B. 2002; 64(4): 583–639.
24. Van Erp S, Mulder J, Oberski DL: Prior sensitivity analysis in default Bayesian structural equation modeling. Psychological Methods . 2018; 23(2): 363–388. PubMed Abstract | Publisher Full Text
25. Yanuar F, Ibrahim K, Abdul AJ: Bayesian structural equation modeling for the health index. Journal of Applied Statistics . 2013; 40(6): 1254–1269. Publisher Full Text
26. Olalude O, Alaba OO, Muse O, et al.: RCODE BSEM.docx, Tables and the figures.figshare. Dataset. 2022. Publisher Full Text

Comments on this article Comments (0)

Version 2

VERSION 2 PUBLISHED 04 May 2022

Author details Author details

¹ Department of Statistics, University of Ibadan, Ibadan, Oyo State, +234, Nigeria
² Department of Mathematics and Statistics, Rufus Giwa Polytechnic, Owo, Ondo State, Nigeria

Oladapo A. Olalude
Roles: Data Curation, Methodology

Bernard O. Muse
Roles: Validation

Oluwayemisi O. Alaba
Roles: Resources, Supervision

Competing interests

No competing interests were disclosed.

Grant information

The author(s) declared that no grants were involved in supporting this work.

Article Versions (2)

version 2

Revised

Published: 20 Sep 2022, 11:494

https://doi.org/10.12688/f1000research.108886.2

version 1

Published: 04 May 2022, 11:494

https://doi.org/10.12688/f1000research.108886.1

Copyright

© 2022 Olalude OA et al. This is an open access article distributed under the terms of the Creative Commons Attribution License, which permits unrestricted use, distribution, and reproduction in any medium, provided the original work is properly cited.

Download

Export To

metrics

	Views	Downloads
F1000Research	-	-
PubMed Central Data from PMC are received and updated monthly.	-	-

Citations

0

SEE MORE DETAILS

CITE

how to cite this article

Olalude OA, Muse BO and Alaba OO. Informative prior on structural equation modelling with non-homogenous error structure [version 1; peer review: 1 approved, 1 approved with reservations]. F1000Research 2022, 11:494 (https://doi.org/10.12688/f1000research.108886.1)

NOTE: If applicable, it is important to ensure the information in square brackets after the title is included in all citations of this article.

track

receive updates on this article

Track an article to receive email alerts on any updates to this article.

Open Peer Review

Version 1

VERSION 1

PUBLISHED 04 May 2022

Views

14

Reviewer Report 26 Jul 2022

Mohamed R. Abonazel, Department of Applied Statistics and Econometrics, Faculty of Graduate Studies for Statistical Research, Cairo University, Giza, Egypt

Approved with Reservations

https://doi.org/10.5256/f1000research.120326.r136840

This paper investigated the impact of informative prior on Bayesian structural equation model with heteroscedastic error structure. Four different forms of heteroscedastic error structures were considered. The suggested Bayesian approach provides an alternative approach to the existing classical method which ... Continue reading

This paper investigated the impact of informative prior on Bayesian structural equation model with heteroscedastic error structure. Four different forms of heteroscedastic error structures were considered. The suggested Bayesian approach provides an alternative approach to the existing classical method which depends solely on the sample information. The results indicate that the suggested Bayesian estimation method is more efficient than the existing classical method.

In my opinion, the paper offers a good contribution. So, I recommend accepting this paper, but after making the following modifications to improve the manuscript:

I think the title of the paper needs improvement. I suggest the following title: “Bayesian estimation of structural equation modelling with non-homogenous error structure”.
In the “abstract” section, the findings or research results should be introduced briefly in the abstract.
In the “introduction” section, the introduction did not contain enough background information. Also discuss the similar work that has been done in this area to give a detailed view of this work. The authors should add more papers related to the Bayesian estimation of structural equation modelling.
In the “methods” section, the authors should define each symbol given in each equation.
In the “conclusion” section, the limitation and future research directions should be mentioned.

Is the work clearly and accurately presented and does it cite the current literature?

Partly
Is the study design appropriate and is the work technically sound?

Yes
Are sufficient details of methods and analysis provided to allow replication by others?

Yes
If applicable, is the statistical analysis and its interpretation appropriate?

Yes
Are all the source data underlying the results available to ensure full reproducibility?

Yes
Are the conclusions drawn adequately supported by the results?

Yes

Competing Interests: No competing interests were disclosed.

Reviewer Expertise: Applied statistics, Econometric models.

I confirm that I have read this submission and believe that I have an appropriate level of expertise to confirm that it is of an acceptable scientific standard, however I have significant reservations, as outlined above.

CITE

Report a concern

Respond or Comment

Views

12

Reviewer Report 12 Jul 2022

Adenike Oluwafunmilola Olubiyi, Department of Statistics, Ekiti State University, Ado Ekiti, Nigeria

Approved

https://doi.org/10.5256/f1000research.120326.r140694

ABSTRACT

In this paper, the research team investigates the impact of informative prior on Bayesian Structural equation model (BSEM) with heteroscedastic error structure.
The drawback of homogeneous error structure was addressed

ABSTRACT

In this paper, the research team investigates the impact of informative prior on Bayesian Structural equation model (BSEM) with heteroscedastic error structure.
The drawback of homogeneous error structure was addressed by considering the non-homogenous error structure.

General Comment under this section: the researcher can add their findings

INTRODUCTION

Bayesian structural equation modelling (BSEM) analyses the relationship between the observed, unobserved and latent variables within the Bayesian context
The likelihood is the un-normalized posterior distribution when expressed in terms of the unknown parameters θ for fixed values of y.
The study explores the BSEM using different forms of heteroscedastic error structure.
Other studies abound on classical methods and Bayesian methods with focus on homogeneous variance.^8,19,22,25

General Comment under this section: The Introductory part was well presented and detailed with relevant citation, even though the researchers can still explore more.

Methods

Gibbs sampler was developed to estimate SEM with reflective measurement indictors.^1,11,12
The SEM equation used is composed of a measurement equation and a structural equation.⁹
To enable Gibbs sampling from full conditioner posterior distributions, natural conjugate prior distributions for the unknown parameters were considered.
The heteroscedastic error structure with different functional form of error variance under consideration are double logarithm form, linear form, linear-inverse form and linear-absolute form as expresses in equation 17,18,19 and 20.
Markov Chain Monte Carlo (MCMC) Simulation method of Gibbs Sampling was employed.

SIMULATION

At different functional forms of³ heteroscedastic error structure with changes in sample size of 50,100,200 and 500. Hyper-parameter was arbitrarily chosen for the simulation using Gibbs sampler an MCMC method.
To assess the prior sensitivity, factor loading and error precision followed multivariate normal and inverse gamma distributions respectively.
The posterior estimate is used to assess the performance of the posterior simulation technique.
In order to evaluate the Bayesian Model fit, the researcher used the posterior predictive probability (PPP) procedure.^4,5,7,24

General Comment under this section: The methods were well presented and the simulation study well organized.

RESULTS

This gives the results for the latent and observed variables at various sample sizes for the four heteroscedastic error conditions considered using the assumed values for the estimates which are λ₁ = 2.0, λ₂ = 3.0 and precision 15.0.
The posterior means of loadings λ₁and λ₂ are somewhat smaller under different heteroscedastic condition with the informative priors.
It was observed that the linear form is the best with minimum PPP value as sample size increases.
It was also revealed by the downward slope of the model as the sample size increases from 50 500.
It was observed that the structural and measurement equation obtained from this study are adequate and in general could be accepted for the proposed model.

General comment under this section: The obtained results in this section indicate the correct performances with increased sample sizes and the incorporation of informative priors.

CONCLUSION

The study has been able to address sufficiently the problem of heteroscedasticity of known form using four different heteroscedasticity of known form using four different heteroscedastic conditions for both linear and quadratic forms.
It has also successfully modified the homogenous error structure to heteroscedastic error structure in Bayesian structural equation model.
Thus, the approach provides an alternative approach to the existing classical method which depends solely on sample information.

General comment: this section flows with the contents of the paper and is well presented.
The manuscript is well written and followed the format of the Journal and has substance; the manuscript can be approved.

Is the work clearly and accurately presented and does it cite the current literature?

Yes
Is the study design appropriate and is the work technically sound?

Yes
Are sufficient details of methods and analysis provided to allow replication by others?

Yes
If applicable, is the statistical analysis and its interpretation appropriate?

Yes
Are all the source data underlying the results available to ensure full reproducibility?

Yes
Are the conclusions drawn adequately supported by the results?

Yes

References

1. Ansari A, Jedidi K: Bayesian factor analysis for multilevel binary observations. Psychometrika. 2000; 65 (4): 475-496 Publisher Full Text
2. Anderson J, Gerbing D: Some Methods for Respecifying Measurement Models to Obtain Unidimensional Construct Measurement. Journal of Marketing Research. 1982; 19 (4). Publisher Full Text
3. Bellman R: DYNAMIC PROGRAMMING AND LAGRANGE MULTIPLIERS.Proc Natl Acad Sci U S A. 1956; 42 (10): 767-9 PubMed Abstract | Publisher Full Text

Competing Interests: No competing interests were disclosed.

Reviewer Expertise: Environmental Statistics and Econometric

I confirm that I have read this submission and believe that I have an appropriate level of expertise to confirm that it is of an acceptable scientific standard.

CITE

Report a concern

Respond or Comment

Comments on this article Comments (0)

Version 2

VERSION 2 PUBLISHED 04 May 2022

Open Peer Review

Reviewer Status

Reviewer Reports

	Invited Reviewers
	1	2
Version 2 (revision) 20 Sep 22		read
Version 1 04 May 22	read	read

Adenike Oluwafunmilola Olubiyi, Ekiti State University, Ado Ekiti, Nigeria
Mohamed R. Abonazel, Cairo University, Giza, Egypt

Comments on this article

All Comments(0)

Add a comment

Sign up for content alerts

Browse by related subjects

Back to all reports

Reviewer Report

4 Views

27 Sep 2022 | for Version 2

Mohamed R. Abonazel, Department of Applied Statistics and Econometrics, Faculty of Graduate Studies for Statistical Research, Cairo University, Giza, Egypt

4 Views Cite this report Responses(0)

Approved

I am happy with the corrections in the revised paper. It was improved. So, the current version of this manuscript is suitable for indexing. Good luck.

Competing Interests

No competing interests were disclosed.

Reviewer Expertise

Econometrics, R Programming, Panel Data, Time Series, Computational Statistics, Data Analysis, R Statistical Packages, Statistical Modeling, Nonparametric Models, Robust Regression.

I confirm that I have read this submission and believe that I have an appropriate level of expertise to confirm that it is of an acceptable scientific standard.

Respond to this report

Responses (0)

Back to all reports

Reviewer Report

14 Views

26 Jul 2022 | for Version 1

Mohamed R. Abonazel, Department of Applied Statistics and Econometrics, Faculty of Graduate Studies for Statistical Research, Cairo University, Giza, Egypt

14 Views Cite this report Responses(0)

Approved With Reservations

This paper investigated the impact of informative prior on Bayesian structural equation model with heteroscedastic error structure. Four different forms of heteroscedastic error structures were considered. The suggested Bayesian approach provides an alternative approach to the existing classical method which depends solely on the sample information. The results indicate that the suggested Bayesian estimation method is more efficient than the existing classical method.

In my opinion, the paper offers a good contribution. So, I recommend accepting this paper, but after making the following modifications to improve the manuscript:

I think the title of the paper needs improvement. I suggest the following title: “Bayesian estimation of structural equation modelling with non-homogenous error structure”.
In the “abstract” section, the findings or research results should be introduced briefly in the abstract.
In the “introduction” section, the introduction did not contain enough background information. Also discuss the similar work that has been done in this area to give a detailed view of this work. The authors should add more papers related to the Bayesian estimation of structural equation modelling.
In the “methods” section, the authors should define each symbol given in each equation.
In the “conclusion” section, the limitation and future research directions should be mentioned.

Is the work clearly and accurately presented and does it cite the current literature?

Partly
Is the study design appropriate and is the work technically sound?

Yes
Are sufficient details of methods and analysis provided to allow replication by others?

Yes
If applicable, is the statistical analysis and its interpretation appropriate?

Yes
Are all the source data underlying the results available to ensure full reproducibility?

Yes
Are the conclusions drawn adequately supported by the results?

Yes

Competing Interests

No competing interests were disclosed.

Reviewer Expertise

Applied statistics, Econometric models.

I confirm that I have read this submission and believe that I have an appropriate level of expertise to confirm that it is of an acceptable scientific standard, however I have significant reservations, as outlined above.

Respond to this report

Responses (0)

Back to all reports

Reviewer Report

12 Views

12 Jul 2022 | for Version 1

Adenike Oluwafunmilola Olubiyi, Department of Statistics, Ekiti State University, Ado Ekiti, Nigeria

12 Views Cite this report Responses(0)

Approved

ABSTRACT

In this paper, the research team investigates the impact of informative prior on Bayesian Structural equation model (BSEM) with heteroscedastic error structure.
The drawback of homogeneous error structure was addressed by considering the non-homogenous error structure.

General Comment under this section: the researcher can add their findings

INTRODUCTION

Bayesian structural equation modelling (BSEM) analyses the relationship between the observed, unobserved and latent variables within the Bayesian context
The likelihood is the un-normalized posterior distribution when expressed in terms of the unknown parameters θ for fixed values of y.
The study explores the BSEM using different forms of heteroscedastic error structure.
Other studies abound on classical methods and Bayesian methods with focus on homogeneous variance.^8,19,22,25

General Comment under this section: The Introductory part was well presented and detailed with relevant citation, even though the researchers can still explore more.

Methods

Gibbs sampler was developed to estimate SEM with reflective measurement indictors.^1,11,12
The SEM equation used is composed of a measurement equation and a structural equation.⁹
To enable Gibbs sampling from full conditioner posterior distributions, natural conjugate prior distributions for the unknown parameters were considered.
The heteroscedastic error structure with different functional form of error variance under consideration are double logarithm form, linear form, linear-inverse form and linear-absolute form as expresses in equation 17,18,19 and 20.
Markov Chain Monte Carlo (MCMC) Simulation method of Gibbs Sampling was employed.

SIMULATION

At different functional forms of³ heteroscedastic error structure with changes in sample size of 50,100,200 and 500. Hyper-parameter was arbitrarily chosen for the simulation using Gibbs sampler an MCMC method.
To assess the prior sensitivity, factor loading and error precision followed multivariate normal and inverse gamma distributions respectively.
The posterior estimate is used to assess the performance of the posterior simulation technique.
In order to evaluate the Bayesian Model fit, the researcher used the posterior predictive probability (PPP) procedure.^4,5,7,24

General Comment under this section: The methods were well presented and the simulation study well organized.

RESULTS

This gives the results for the latent and observed variables at various sample sizes for the four heteroscedastic error conditions considered using the assumed values for the estimates which are λ₁ = 2.0, λ₂ = 3.0 and precision 15.0.
The posterior means of loadings λ₁and λ₂ are somewhat smaller under different heteroscedastic condition with the informative priors.
It was observed that the linear form is the best with minimum PPP value as sample size increases.
It was also revealed by the downward slope of the model as the sample size increases from 50 500.
It was observed that the structural and measurement equation obtained from this study are adequate and in general could be accepted for the proposed model.

General comment under this section: The obtained results in this section indicate the correct performances with increased sample sizes and the incorporation of informative priors.

CONCLUSION

The study has been able to address sufficiently the problem of heteroscedasticity of known form using four different heteroscedasticity of known form using four different heteroscedastic conditions for both linear and quadratic forms.
It has also successfully modified the homogenous error structure to heteroscedastic error structure in Bayesian structural equation model.
Thus, the approach provides an alternative approach to the existing classical method which depends solely on sample information.

General comment: this section flows with the contents of the paper and is well presented.
The manuscript is well written and followed the format of the Journal and has substance; the manuscript can be approved.

Is the work clearly and accurately presented and does it cite the current literature?

Yes
Is the study design appropriate and is the work technically sound?

Yes
Are sufficient details of methods and analysis provided to allow replication by others?

Yes
If applicable, is the statistical analysis and its interpretation appropriate?

Yes
Are all the source data underlying the results available to ensure full reproducibility?

Yes
Are the conclusions drawn adequately supported by the results?

Yes

References

1. Ansari A, Jedidi K: Bayesian factor analysis for multilevel binary observations. Psychometrika. 2000; 65 (4): 475-496 Publisher Full Text
2. Anderson J, Gerbing D: Some Methods for Respecifying Measurement Models to Obtain Unidimensional Construct Measurement. Journal of Marketing Research. 1982; 19 (4). Publisher Full Text
3. Bellman R: DYNAMIC PROGRAMMING AND LAGRANGE MULTIPLIERS.Proc Natl Acad Sci U S A. 1956; 42 (10): 767-9 PubMed Abstract | Publisher Full Text

Competing Interests

No competing interests were disclosed.

Reviewer Expertise

Environmental Statistics and Econometric

I confirm that I have read this submission and believe that I have an appropriate level of expertise to confirm that it is of an acceptable scientific standard.

Respond to this report

Responses (0)

[1] 1. Anderson JC, Gerbing DW: Some methods for respecifying measurement models to obtain unidimensional construct measurement. Journal of Marketing Research . 1982; 19(4): 453–460. Publisher Full Text

[2] 2. Ansari A, Jedidi K: Bayesian Factor Analysis for Multilevel Binary Observations. Psychometrika . 2000; 65(4): 475–496. Publisher Full Text

[3] 3. Ansari A, Jedidi K, Dube L: Heterogeneous factor analysis models: A Bayesian approach. Psychometrika . 2002; 67(1): 49–77. Publisher Full Text

[4] 4. Asparouhov T, Muthén BO: Bayesian analysis of latent variable models using Mplus. 2010. www.statmodel.com/download/BayesAdvantages18.pdf.

[5] 5. Bansal S: A new Gibbs sampling-based Bayesian model updating approach using modal data from multiple setups. International Journal for Uncertainty Quantification. 2015; 5(4): 361–374. Publisher Full Text

[6] 6. Bellman R: Dynamic programming and Lagrange multipliers.Proceedings of the National Academy of Sciences of the United States of America.1956; 42(10), 767–769. Publisher Full Text | PubMed Abstract | Free Full Text

[7] 7. Bentler PM: Comparative Fit Indexes in Structural Models. Psychological Bulletin . 1990; 107(2): 238–246. PubMed Abstract | Publisher Full Text

[8] 8. Das S, Chen M-H, Kim S, et al.: A Bayesian Structural Equations Model for Multilevel Data with Missing Responses and Missing Covariates.2008 ; vol 3, Number 1, pp. 197–224

[9] 9. Depaoli S: Measurement and structural model class separation in mixture CFA: ML/EM versus MCMC. Structural Equation Modeling . 2012; 19: 178–203. Publisher Full Text

[10] 10. Dunson DB: Bayesian Latent Variable Models for Clustered Mixed Outcomes.Journal of the Royal Statistical Society, Series B, 2000; 62: 355–366. Publisher Full Text

[11] 11. Hancock GR, Mueller RO: Structural equation modeling: A second course. Information Age Publishing, Inc.; 2006.

[12] 12. Kaplan D, Depaoli S: Bayesian statistical methods. In T. D. Little (Ed.).Oxford handbook of quantitative methods.Oxford: Oxford University Press; 2013 (pp. 407–437).

[13] 13. Kass RE, Raftery AE: Bayes Factors. Journal of the American Statistical Association . 1995; 90: 773–795. Publisher Full Text

[14] 14. Lee: Structural Equation Modeling: A Bayesian approach. New York: John Wiley & Sons, Ltd.; 2007.

[15] 15. Lee S, Song X: Maximum Likelihood Analysis of a General Latent Variable Model with Hierarchically Mixed Data. Biometrics . 2003; 60: 624–636.

[16] 16. Lee SY, Shi JQ: Bayesian analysis of structural equation model with fixed covariates. Structural Equation Modeling . 2000; 7: 411–430. Publisher Full Text

[17] 17. Mauricio G, Jorgensen TD: Adapting Fit Indices for Bayesian Structural Equation Modeling. Comparison to Maximum Likelihood Journal of Psychological Methods . 2019; 25(1): 46–70. Publisher Full Text

[18] 18. Meghan K. Cain1 and Zhang Z: Fit for a Bayesian: An Evaluation of PPP and DIC for Structural Equation Modeling2018; 26: 39–50. Publisher Full Text

[19] 19. Oberski DL, Satorra A: Measurement error models with uncertainty about the error variance. Structural Equation Modeling . 2013; 20(3): 409–428. Publisher Full Text

[20] 20. Olsson UH, Foss T, Troye SV, et al.: The performance of ML, GLS, and WLS estimation in SEM under conditions of misspecification and non-normality. Structural Equation Modeling . 2000, 2000; 7: 557–595.

[21] 21. Palomo J, Dunson DB, Bollen K: Bayesian structural equation modeling. Handbook of Computing and Statistics with Application . 2007; 1: 163–188. Publisher Full Text

[22] 22. Scheines R, Hoijtink H, Boomsma A: Bayesian estimation and testing of structural equation models. Psychometrika . 1999; 64: 37–52. Publisher Full Text

[23] 23. Spiegelhalter DJ, et al.: Bayesian measures of model complexity and fit. Journal of Royal Statistical Society B. 2002; 64(4): 583–639.

[24] 24. Van Erp S, Mulder J, Oberski DL: Prior sensitivity analysis in default Bayesian structural equation modeling. Psychological Methods . 2018; 23(2): 363–388. PubMed Abstract | Publisher Full Text

[25] 25. Yanuar F, Ibrahim K, Abdul AJ: Bayesian structural equation modeling for the health index. Journal of Applied Statistics . 2013; 40(6): 1254–1269. Publisher Full Text

[26] 26. Olalude O, Alaba OO, Muse O, et al.: RCODE BSEM.docx, Tables and the figures.figshare. Dataset. 2022. Publisher Full Text

Informative prior on structural equation modelling with non-homogenous error structure

Abstract

Keywords

Introduction

(1)

(2)

Methods

Bayesian estimation of structural equation models (SEM)

(3)

(4)

(5)

(6)

(7)

(8)

(9)

(10)

Prior distributions

(11)

(12)

(13)

(14)

(15)

Derivations of conditional distributions

(16)

Heteroscedastic error structures

(17)

(18)

(19)

(20)

(21)

(22)

The posterior distribution

(23)

(24)

(25)

(26)

(27)

(28)

(29)

(30)

(31)

(32)

The Gibbs sampler

Gibbs sampling procedure

(33)

Design of simulation

(34)

(35)

Results and discussion

Performance of the estimators at heteroscedasticity condition

Comparison of latent variable estimates at different sample sizes under the heteroscedasticity condition

Table 1. Double logarithmic form on latent variable and observed variable estimates.

Table 2. Linear form on latent variable and observed variable estimates.

Table 3. Linear inverse form on latent variable and observed variable estimates.

Table 4. Linear absolute form on latent variable and observed variable estimates.

Table 5. Comparison at varying sample sizes of different heteroscedastic form.

Table 6. Latent variable estimates at different sample sizes under the double-logarithmic and linear forms.

Table 7. Latent variable estimates at different sample sizes under the linear-inverse and linear absolute forms.

Figure 1. Plot of log likelihood and posterior predictive probability (PPP) at various sample sizes under (a) the double logarithmic form and (b) the linear form.

Figure 2. Plot of log likelihood and posterior predictive distribution (PPP) at various sample sizes under (a) the linear-inverse form (b) the linear-absolute form.

Conclusion

Data availability

Underlying data

Extended data

References

Comments on this article Comments (0)

Open Peer Review

Comments on this article Comments (0)

Open Peer Review

Reviewer Status

Reviewer Reports

Comments on this article

Browse by related subjects

Competing Interests Policy

Stay Updated