Keywords
Developmental Gene Regulatory Networks, Cis-Regulatory Elements, Heterogeneous Graph Representation Learning, Deep Graph Auto-encoders
This article is included in the Bioinformatics gateway.
Developmental Gene Regulatory Networks, Cis-Regulatory Elements, Heterogeneous Graph Representation Learning, Deep Graph Auto-encoders
Gene regulatory networks drive gene expression during cell development. Studying the regulatory networks’ effects on gene expression has become an essential topic in evolutionary developmental biology. Recently, a wide range of temporal high-throughput experiments has become available for both normal development and disease-related investigations.1–3 For example, the ENCODE consortium has provided comprehensive fetal development datasets for 12 tissues in mice from the E10.5 stage to the birth time P0.1 These datasets include both gene expression data and major transcriptional and epigenetic features. Some of the latter come from ATAC-seq experiments that measure chromatin accessibility, whole-genome shotgun bisulfite sequencing experiments measuring DNA methylation, and histone modifications.1 Similar datasets, though in lesser amount, exist to study aging (see a recent review by Pagiatakis et al.2). Cancer, instead, is among the diseases with the largest amount of available gene regulatory datasets (see a recent review by Zboril et al.3).
Gene expression regulation occurs via non-coding segments, also known as cis-regulatory elements (CRE).4 Associating CREs to the genes they regulate is the key to deciphering temporal dynamic changes through development. As CREs and genes are distinct entities located on different genome coordinates, a concurrent study of these has been challenging. Many methods have been developed to study genes and CREs separately through development in the last years. Infinite Gaussian Process Mixture Model5 and Convolutional Neural Networks6 are among the most successful methods to find temporal clusters of either genes or CREs. Generally, high-throughput datasets are highly clusterable, and even conventional clustering methods like K-Means clustering can also generate satisfactory results when used for a single source dataset (i.e. genes or CREs). However, combining or aligning the clusters across data sources is still a major challenge.
Insights about developmental regulatory networks are typically gained by the application of Multiview learning7 to align single-cell RNA sequencing (scRNA-seq) and single-cell ATAC sequencing (scATAC-seq).8,9 Such methods permit the classification of different cells through the combination of various high-throughput experiments made over the same cell population.10,11 The Seurat method,12 for example, makes different reduced dimension representations of single-cell gene expression and CREs data. Such a method uses Canonical Correlation Analysis to place multiple datasets on a common latent space with reduced dimension and anchor a population of cells across different modality datasets. Other methods rely on stronger prior knowledge about cell alignment to anchor multiple modalities. This is the case of the Multi-Omics Factor Analysis v2 (MOFA+), a statistical framework for the comprehensive and scalable integration of single-cell multi-modal data.13 More recently, multi-modal dataset alignment methods have been developed based on state-of-the-art deep learning techniques.14,15 MAGAN,16 for example, successfully aligned scRNA-seq and scATAC-seq datasets using Generative Adversarial Networks (GAN). Yang et al.,17 used deep auto-encoders to map multiple data modalities of a population of cells to a common latent space. They used prior knowledge and adversarial learning to drive the correct alignment of data. Comprehensive surveys on multi-modal or multi-view learning applied to multi-omics datasets can be found in.8,18
The works mentioned above explore gene expression regulatory mechanisms by combining multiple views of the same cell population. This work investigates gene regulatory networks by clustering two diverse entity types together: We sought to group CREs with their correspondent regulated genes. In this sense, we performed a heterogeneous network clustering task. Heterogeneous data interaction was also modelled by Huang et al.19 for predicting transcription factor interactions with their target genes. Wang20 and Zhou21 instead, modelled gene-disease interactions trough a heterogenous-network model. Other recent problems solved through heterogeneous graph-based models include Gene Ontology Representation Learning,22 Gene prioritization for rare diseases23 and drug repurposing.24 The main novelty of this work is the introduction of a model for regulatory networks discovery which is based on the concept of “Heterogeneous Graphs”.25 We modelled a graph containing two classes of nodes: genes and their potential regulatory elements, now on termed as candidate-CREs (cCRE), and multiple types of relations or edges between nodes. One such relation type is the similarity between temporal gene expression profiles. Another relation type is the similarity between temporal cCREs activity patterns. Finally, we introduced a third edge type: the base-pair distance between genes and cCREs in the genome. Having defined such relations, we propose the usage of graph representation learning (graph RL) to group genes and cCREs as a function of the probability of the existence of gene regulation mechanisms between them.
To this end, we extended a state-of-the-art graph RL algorithm presented in Ref. 26 to make it capable of learning representations of heterogeneous graphs and applied it to the ENCODE heart dataset in Ref. 1. We used open chromatin regions from ATAC-seq as cCREs. Besides ATAC-seq, we used H3K27ac and H3K27me3 histone marks, well-known markers of enhancer activity, and polycomb repression. Our framework produced a relation type between genes and cCREs which is aware of both same-class pattern similarities and base-pair proximities between elements of different classes. Moreover, through the usage of the adaptive neighbors model presented in Ref. 26 we produced a “clustering-friendly” embedding where we could straightforwardly perform clustering. The resulting clusters contained both genes and cCREs and tended to identify possible regulatory mechanisms. We demonstrated this claim by evaluating such clusters’ semantic power with external expert criteria. We concluded that the proposed methodology is able to learn suitable combinations of multiple entity relations to form a unique relation under a graph that resembles a gene regulatory network. Our framework is called DeepReGraph, because it is a Deep learning-based algorithm for identification of gene expression Regulatory mechanisms through heterogeneous Graph RL. Our full code, the pre-processed datasets used, and the values used for all the parameters and hyperparameters used in our experiment are online available at our repository[1].
To demonstrate DeepReGraph’s ability to cluster genes and cCREs simultaneously, we applied this method to a mouse heart fetal developmental dataset from the ENCODE project.1 Gene expression and cCRE activities were time-series formatted. We used three well-characterized epigenetic markers: ATAC-seq, H3K27ac, and H3K27me3 measurements as features of cCRE temporal activities. We aimed to create a low-dimensional and clustered representation of the whole dataset, where clusters represent candidate gene-expression regulatory mechanisms (GERM). In other words, we aimed to create clusters containing both genes and cCREs, with the working hypothesis that cCRES on a cluster are plausibly regulating the expression of the genes in the same cluster. Moreover, genes on the same GERM cluster should have similar gene expression profiles, and cCREs should have similar activity profiles. Lastly, the base-pair distances between genes and cCREs on the same cluster should be relatively small with respect to distances between elements in different clusters. We validated heterogeneous clusters of genes and cCRES to study how gene regulatory networks (GRN) drive changes in gene expression during mouse heart fetal development. To validate gene expression clusters, we performed enrichment analysis of biological process gene ontology terms using the ClusterProfiler bioconductor package.27 To validate the cCRE clusters, we looked for the Enriched Homer Motifs.28
Data pre-processing was done in two stages. Firstly, gene expression and cCRE datasets were normalized across temporal data. The second stage included filtering-out temporal profiles where the correlation across replicates or the variance across time was below some pre-defined thresholds. We explain the pre-processing stages in greater detail below.
We firstly downloaded the gene expression values, called peaks, and bam files of ATAC-seq, H3K27ac, and H3K27me3 from the ENCODE database1 (mice heart fetal tissue). We used logFPKM values of gene expression throughout this paper. To detect cCRE regions, we re-centered ATAC-seq called peaks across time points and replicates using the bioconductor DiffBind package.29 To determine chromatin accessibility in each cCRE region, we took regions of 500 nucleotides long (250 nucleotides on each side from the center of cCREs). We recorded binding intensities for each replicate of each time point separately by using the bioconductor Rsubread package.30 We counted H3K27ac and H3K27me3 marks for cCREs in the same manner, but used regions 3000 nucleotides long instead (1500 nucleotides each side from the center of cCREs). We took the median value of non-peak regions in each experiment separately to remove background counts from real intensity counts. Then, we subtracted these median values from the intensities of each experiment separately. We used logRPKM values of denoised counts across replicates and time points. Removing the background noise caused the distribution of each experiment to resemble a Gaussian distribution.
At the end of this process, we had two replicas of gene expression time-series profiles for a set of genes and two replicas of cCRE activity time-series for each activity marker over a set of cCREs. We then proceeded to filter out invalid genes and cCREs based on two criteria. The first group of filters we applied to this data were proposed in Ref. 31. For each gene, we measured the correlation of the gene expression profiles of both replicates and discarded every gene whose replicate had a negative correlation value. We did the same with the cCREs for each activity marker profile. If only one activity marker had a negative correlation between replicates, the cCRE was discarded. We also discarded every element (gene or cCRE) where two consecutive time probes had an absolute ratio greater than 2.
We also discarded low-expressed genes and low activity-characterized cCREs.32 We computed the mean gene expression value for each gene and discarded every gene whose mean expression value was under the 0.8 percentile of such mean value distribution. We did the same with cCREs: we computed the mean activity value for each activity marker and discarded every cCRE where the mean value was below a minimum percentile threshold. Such thresholds were 0.8 for ATAC-seq and 0.7 for H3K27ac and H3K27me3. Lastly, for gene expression and each activity marker dataset, we created a 3-rd degree polynomial regression to estimate the variance of each time series as a function of its mean value. We discarded all the elements where the actual variance was below the predicted variance. Our pre-processed and cleaned data consisted of 607 genes and 5239 cCREs from the mouse heart dataset. This dataset is available online on our public repository. Our objective was to shed light on regulatory mechanisms among genes and cCREs. Having cleaned our dataset, modeling it as a heterogeneous graph is the strategy we used to combine all the data and learn a new relation type between elements that gives information about gene expression regulation. We explain the graph modelling in the next paragraph.
Many industrial data are represented in a graph, as multiple entities with quantifiable relationships between them. Nowadays, graph modelisation is widely used in bioinformatics.33 One strategy to extract added-value from graphs is the use of graph RL algorithms. Graph RL has been widely studied by the research community over the past few years years.25,34–36 Graph RL algorithms seek to map the information of a graph on a reduced-dimension latent space where the geometrical distances between elements in such space resemble the relations in the original graph. In other words, graph RL, also referred to as “graph embedding”, consists in finding a reduced dimensional representation of the nodes of a graph while conserving most of the semantic information of such a graph.37,38
A graph can be homogeneous if it has a unique type of node and a unique type of relation defined between them, or heterogeneous, if it introduces multiple edge and node types. We argue that regulatory networks during embryonic development can also benefit from being modelled as a heterogeneous graph. Reduced-dimension representations of such a graph could contain multiple types of information that, if well combined, could semantically express regulatory mechanisms of gene expression.
We defined a heterogeneous graph and described it as , where is the set of nodes, is the set of edges and is the set containing all the node types and edge types. The set of node types consists of genes and cCREs, and is denoted by . Each gene in the dataset is characterized by a gene expression time-series profile that will be encoded in a vector denoted by . Note that the length of coincides with the number of time-points considered in the gene expression data. The vectors can be concatenated as rows to form the feature matrix represented in red in panel A of Figure 1.

Our framework combines multiple temporal enhancer activity markers with temporal gene expression data and base-pair distances to build a heterogeneous graph of genes and cis-regulatory elements (CRE). The proposed framework then applies an adapted version of AdaGAE26 to find a low-dimensional, easy-to-cluster embedding representation of data through an iterative optimisation process. In the final embedding produced by our method, the spatial distribution of genes and cCREs resembles candidate gene-expression regulatory Mechanisms.
Every candidate cis-regulatory element, instead, will be denoted as and will be characterized by activity time-series profiles, that will be encoded in corresponding vectors denoted as . The time-points under which gene expression and cCRE activity values are available are the same. In this work, . Specifically, we considered the ATAC-seq, H3K27ac, and H3K27me3 activity time-series profiles for each cCRE, but one could include more cCRE activity markers in the set of features. Note that the vectors can be concatenated as rows to form the matrices represented in blue in panel A of Figure 1.
Each node of our graph was associated to one or multiple feature vectors that can be seen as points on a multi-dimensional feature space. The set of feature-spaces defined for the nodes in is denoted as where is the gene expression feature space and are the feature spaces of the cCRE activity data. Each one of these feature spaces will be referred to as original feature space, and the vectors as original feature vectors from now on. Note that such vectors correspond to the rows of the matrices in panel A of Figure 1. It is well-known that the probability of the existence of a regulatory mechanism between a gene and a cis-regulatory element is inversely proportional to the base-pair distance between them.39 For this reason, in our work, we used another data source, called the Link Matrix, that gives us information about the base-pair distance between genes and cCREs. We represented such a matrix in panel C of Figure 1. Interaction between cCREs and genes is generally possible in the range of 1 Mega base-pair.40 Consequently, we considered only distances lower than base-pairs. For practical purposes, we scaled the base-pair distance values in the interval to define a scaled base-pair distance function, :
Given the scaled distance function, we created a base-pair proximity relationship using a parametric transformation:
The interaction between CREs and the genes they regulate is complex. Some CRE markers are correlated with gene expression and some others are anti-correlated.41 This correlation or anti-correlation is governed by the mechanism that a specific marker affects the gene expression. For example, chromatin should be opened prior to the gene expression. Therefore, chromatin accessibility is commonly directly correlated with gene expression. H3K27ac is also directly correlated with gene expression, as this epigenetic modification happens in active transcription regions. On the other hand, H3K27me3 shows epigenetic modifications that happen at polycomb repressed regions, and are consequently inversely correlated with the expression of the corresponding regulated genes. We needed to capture the relevance of these and other temporal covariances between gene expression and the correspondent regulatory elements’ activity markers.
To this end, we created a joining score, , as a function of the temporal slopes of gene expression and cCRE activity time-series:
We computed a trend-aware score multiplying (1) and (2) for each gene-cCRE pair in our graph:
We represented the computation of Equation (3) in panel D of Figure 1. Having defined the trend-aware score, we could differentiate between any pair of genes, and , when these were equally proximal to any cCRE but had gene expression vectors with different temporal trends. In this case, the original base-pair proximity score in (1) assigned the same value to the association and . Notice that the trend-aware score in (2), instead, distinguishes the most plausible association of with respect to the alternatives and as a function of the temporal slopes of the gene expressions elements. In our experiment, we found the best results setting and in Equation (2).
The set of edge types in the graph is denoted as . As explained before, indicates the trend-aware base-pair proximity relationship explained above; stands for the gene expression profile similarity between genes, and , , …, are the relationships that express the different cCRE activity time-series similarities. We aimed to combine all edge types in to find a unique multi-semantic edge type that resembled gene expression regulation mechanisms. The process of combining edge types is represented in panel E of Figure 1 and is explained later in this section. To perform the combination of all edge types in , we modelled the data as a heterogeneous graph and designed a graph RL algorithm capable of extracting such a dependency between elements using prior biological knowledge and the data available. We explain the graph RL algorithm we used to fulfil our objective in the next paragraph.
Graph RL algorithms aim at finding a matrix: that contains information about every feature-space in . In our case, we used a graph RL algorithm to find a unique feature space for the nodes of that comprises most of the information encoded by the feature spaces contained in . The rows of correspond to a new set of feature vectors for each node in . Each row of is called an “embedding vector” and is a reduced-dimension representation of the whole set of original feature vectors of a given node.37,34 The embedding vectors are “multi-semantic” in that they contain information from every feature space in . The dimension of embedding vectors, , is generally lower with respect to the dimension of the original feature spaces. The embedding matrix is represented in panel F of Figure 1.
Graph RL is also referred to as “graph embedding”. Giving a node , and a specific edge-type , the neighborhood of in is denoted as and corresponds to the set of nodes that are connected to by -type edges. We denote with instead the set containing every neighborhood of :
The heterogeneous graph embedding process can be represented by an encoding function that takes in input a node and its neighborhood set, , and returns a new representation for that node:
One of the most common methodologies for implementing (4) is the encoder-decoder paradigm.25 This paradigm also models an auxiliary decoding function. Considering a homogeneous graph, i.e. a graph with a unique node feature space , the encoder function in (4) takes as input original feature vectors of , and outputs the corresponding embedding vectors:
The decoding function, instead, takes as input a pair of node embeddings produced by the encoder, e.g. and , and outputs a real number. Such a number is the prediction of the value of a pre-defined pair-wise relationship between and :
The encoding and decoding functions should minimize a reconstruction loss of the form:
A convenient framework that implements the encoding-decoding paradigm is the deep graph auto-encoder (deep GAE).42 In this framework, (4) was implemented through a graph neural network (GNN), an artificial neural network that takes the original feature vectors and the adjacency matrix of as input and produces the node embedding vectors. GNNs are non-linear parametric functions, and after a pre-defined initialization schema, the parameters of these functions can be optimized to minimize (6) through gradient descent.
In this work, we proposed the use of the basic GNN model presented in Ref. 25. In a homogeneous graph context, the basic GNN takes as input the node feature matrix and a pre-defined graph adjacency matrix denoted by , and performs non-linear parametric operations with this information to produce . In matrix notation, the operations made by the basic GNN model can be represented as follows:
We defined a parametric “architecture” for the encoding function using (7), but still needed to define and , to drive the optimization of the parameters of to minimize (6). The initialization of these matrices can follow multiple strategies. For example, in the neural message passing framework,43 given a homogeneous graph context, one generally constructs stacking the original feature vectors as the rows of such a matrix. However, it is not the only valid strategy. In our heterogeneous graph context, we decided to initialize as the identity matrix because we had multiple original feature matrices. We were confident to use the identity matrix to initialize because we carefully initialized the adjacency matrix combining the information of every relationship type in our graph, as we will explain in the next paragraph.
Finally, the similarity measure that the decoder is meant to predict needs to be specified to implement (5). In this paper, we proposed the use of the decoding similarity function proposed by Ref. 26 to converge into a clustering-friendly embedding, i.e., an embedding with dense and easily identifiable clusters. In the next paragraph, we give a brief explanation of the algorithm in,26 which performs graph RL on a single-feature space. For a more detailed exposition of the work of Xuelong et al., the reader is referred to the original paper.26
In this work, we proposed the use of AdaGAE,26 which is a state-of-the-art method for RL and clustering through graph modelling of a dataset. The whole AdaGAE algorithm is wrapped in a gray rectangle in Figure 1. This algorithm is defined in a homogeneous data context. In other words, given a unique original feature matrix , the objective was to produce a low-dimensional embedding matrix where . Authors in26 used a deep GAE to embed high-dimensional datasets in a graph-like, low-dimensional format. Xuelong et al. generated a sparse graph as a function of the Euclidean distances between the original feature vectors using a k-nearest neighbors44 (k-NN) model.
The main novelty of AdaGAE is the adaptiveness in the sparsity parameter . The graph auto-encoder is, in fact, iteratively optimized with respect to various objective functions like (6), and each objective function is constructed using a different sparsity parameter. With a custom decoding function, such a dynamic model leads to a sparse graph. In other words, they produce a clustering-friendly embedding of the original data.
In other words, at each iteration, , a sparse and weighted graph is generated. In this graph, the nodes correspond to the samples of the original dataset. Instead, the weights of the edges are inversely proportional to the Euclidean distances between the original feature vectors. Specifically, at iteration , a graph is generated in which the weight of the link between nodes and is denoted as and is a function of a sparsity parameter :
Notice that, in (8), the parameter might have a different value at each iteration. Such a parameter induces the sparsity of the generated graph: for each node , only up to elements will have a non-zero weighted link with that node. Thus, at each iteration , AdaGAE generates a -sparse graph. Notice also that the function (8) is a discrete probability density function (PDF):
where a different PDF is defined for each single node in the dataset. Thus, at each iteration , AdaGAE generates a probability distribution family :where each PDF in contains information about the weights of the links between one node and the rest of the nodes in the graph. Authors in Ref. 26 proposed to re-initialize the adjacency matrix of the auto-encoder at each iteration using the family . In other words, at each iteration , AdaGAE stacks the different distributions to form .The embedding matrix produced by AdaGAE was iteratively optimized. We denoted with the embedding matrix after iteration . The embedding vector of node after iteration , instead, coincides with the -th row of and is denoted as . At each iteration, AdaGAE proposes to implement the decoding function in (5) as a function of the embeddings of the previous iteration:
At each iteration , AdaGAE proposes to use the Kullback-Leibler divergence (KL-divergence)45 of with respect to to implement (6). Explicitly, the reconstruction loss that AdaGAE seeks to minimize is the following:
Xuelong et al. relied on the graph convolutional network (GCN) model46 to implement the encoder of their deep GAE. However, in this paper, we used a simpler GNN model, as explained in the previous paragraph. We represented the iterative computation of (8) and (9) and the iterative optimization of (10) in panel E of Figure 1.
Notice that the main dynamic criterion that causes the objective functions to change is the sparsity parameter . However, the sparsity is not the only thing that changes from iteration to iteration: In the first iteration, the distribution family is generated through (8) using the Euclidean distances between the original feature vectors. After the first iteration, instead, the distribution family is generated using (8) as a function of the Euclidean distances between the embedding vectors of the embedding matrix. By doing so, AdaGAE considers high-order neighborhoods of each node to construct the final embedding matrix. In other words, AdaGAE is said to “exploit the high-level information” present in the data.
Different embeddings for various iterations are plotted in panel G of Figure 1. In those plots, one can see the embedding of a small set of genes and cCREs extracted from the original mouse heart dataset. Large points represent genes, while cCREs are the small points. Point colors, instead, correspond to single-modality or homogeneous cluster assignments, i.e., cluster assignments of genes and cCREs, taking into account their corresponding feature spaces separately. Note that the embedding turns more cluster-friendly at each iteration. In other words, the density and separation of clusters are increased at each iteration, and clusters can be caught visually in the final embedding in panel H of Figure 1. In AdaGAE, the sparsity parameter initialization, , the increment of this parameter from iteration to iteration, , and the number of iterations, , regulate the number of clusters in the final embedding. In our experiment, we tested various parameter configurations and found eight significant GERM clusters with , , .
Notice that the original work of Xuelong et al. defined (8) as a function of the Euclidean distances over a unique feature space. We extended the AdaGAE framework to deal with multiple node feature spaces. In particular, at each iteration , we combined the Euclidean distances of multiple node feature spaces - the gene expression and the cCRE activity time-series - to generate a unique distance function that is given to (8) to generate . In the next paragraph, we explain how we combined the feature spaces to adapt AdaGAE to heterogeneous graph RL.
As explained previously, we modelled the whole set of gene expression and cCRE-activity data as a heterogeneous graph. We proposed to extend the work in Ref. 26 to heterogeneous graph RL. We ran the same process described in the previous paragraph, with some differences. The first difference was the construction of the reference distance function to feed to (8). At each iteration , we combined the Euclidean distances defined in each one of the original feature spaces to form a unique distance function that generated the sparse distribution family .
Recall that is the set of feature spaces defined, where is the gene-expression feature space and are the cCRE activity feature spaces, for example ATAC-seq, H3k27ac, aH3k27me3, etc. At each iteration , for each feature space , we computed the Euclidean distances between the original feature vectors in , scaled these distances into the interval , and denoted them with . Notice that the Euclidean distances between the original feature vectors were only defined between same-class elements: The Euclidean distances in the gene-expression feature space , were defined between genes, and the distances in , only between cCREs. Consequently, we set the distance between different-class elements to the maximum value, i.e., 1, for each feature space. Finally, we create a custom linear combination of these distance functions to form a unique distance function :
At the beginning of the -th iteration, the Euclidean distances between the embedding vectors of are denoted by . We combined such information with defined in (11), to generate the unified distance function, as follows:
In (13), is the fixed parametric importance weight of the Euclidean distances in . Notice that, in (12), allows to exploit the high-level information in the data and helps to reduce the loss of information with respect to the original feature spaces at each iteration.
At each iteration , we computed using (12). This computation is represented in panel E of Figure 1. We then used and the corresponding sparsity parameter to compute a connectivity distribution family using (8). Notice that this distribution family was generated using only the same-class relation types in . In other words, we only used the node feature spaces in to create . We needed to add the trend-aware base-pair proximity relationship defined in (3) to compute the definitive distribution family that takes into account all information we have:
After computing , we computed using (9), and optimized the embedding matrix , minimizing a reconstruction loss of the form (6). AdaGAE proposed the use of (10) to implement the reconstruction loss. In this paper, however, we propose to extend such a loss function to better separate elements that are distant in the original feature spaces, as explained in the next paragraph.
The minimization of (10) has the same effect of an attractive force that tends to collapse points in the embedding space, reducing the distances between and proportionally to . When considering a single node , such an objective function could lead to errors in the manipulation of the position of the most distant neighbors of such node.47 Inspired by Ref. 48, in this work, we added a regularization term that acts as a repulsive force. Such a repulsive force tends to increase proportionally to the inverse of . In other words, we pushed elements away from each other proportionally to their distance in (12). To create this force, we added the KL-divergence of with respect to to (10).
Notice that the union of the attractive and repulsive force is equivalent to the minimization of the binary cross-entropy of with respect to as defined in Ref. 48. Lastly, we added parametric importance weights to the attractive and repulsive force components and constructed our final objective function:
We iteratively optimized the parameters of our GNN-based encoder. At each iteration, we minimized (15) with a different set of parameters. After running the optimization for a predefined number of iterations, we processed to a clustering-friendly embedding where the clusters reflect plausible gene regulatory networks. We then ran k-means clustering on the embedding to find plausible gene expression regulatory mechanisms. This clusterization is represented in panel H of Figure 1.
DeepReGraph performs the co-clustering of genes and cCREs together. Consequentially, resulting clusters are heterogeneous in the class of elements they might contain. DeepReGraph helped us identify eight co-clusters when applied to developmental fetal mouse heart datasets. We assessed the quality of gene expression and cCREs clusters from a computational point of view. We also analyzed these clusters from a biological perspective as described below.
We employed a principle component analysis (PCA) to visualize the cCRE clusters on dimension reduced plots as shown in panel A of Figure 2. This figure highlights a clear separation of clusters on , , and which explains the 57% variability in the cCRE datasets. We also performed k-means clustering using . Panel B of Figure 2 shows a confusion matrix that compares cCRE clusters from DeepReGraph with the uni-modal clustering produced with k-means clustering. It is clear from this confusion matrix that the result of the multi-modal clustering of DeepReGraph was highly similar to the uni-modal clustering one. This similarity indicates that DeepReGraph clustering does take into account the same-class pattern similarities when defining clusters. We also visualized the PCA plot of gene expression data in panel C of Figure 2. PC0 by itself explains 76% of the variability in gene expression. Basically, gene expression has two distinct patterns throughout mouse fetal heart tissue development: genes with increasing expression and genes with decreasing expression. Interestingly, these two major patterns have been divided into sub-patterns based on the cCRE clusters that plausibly drive their regulation.
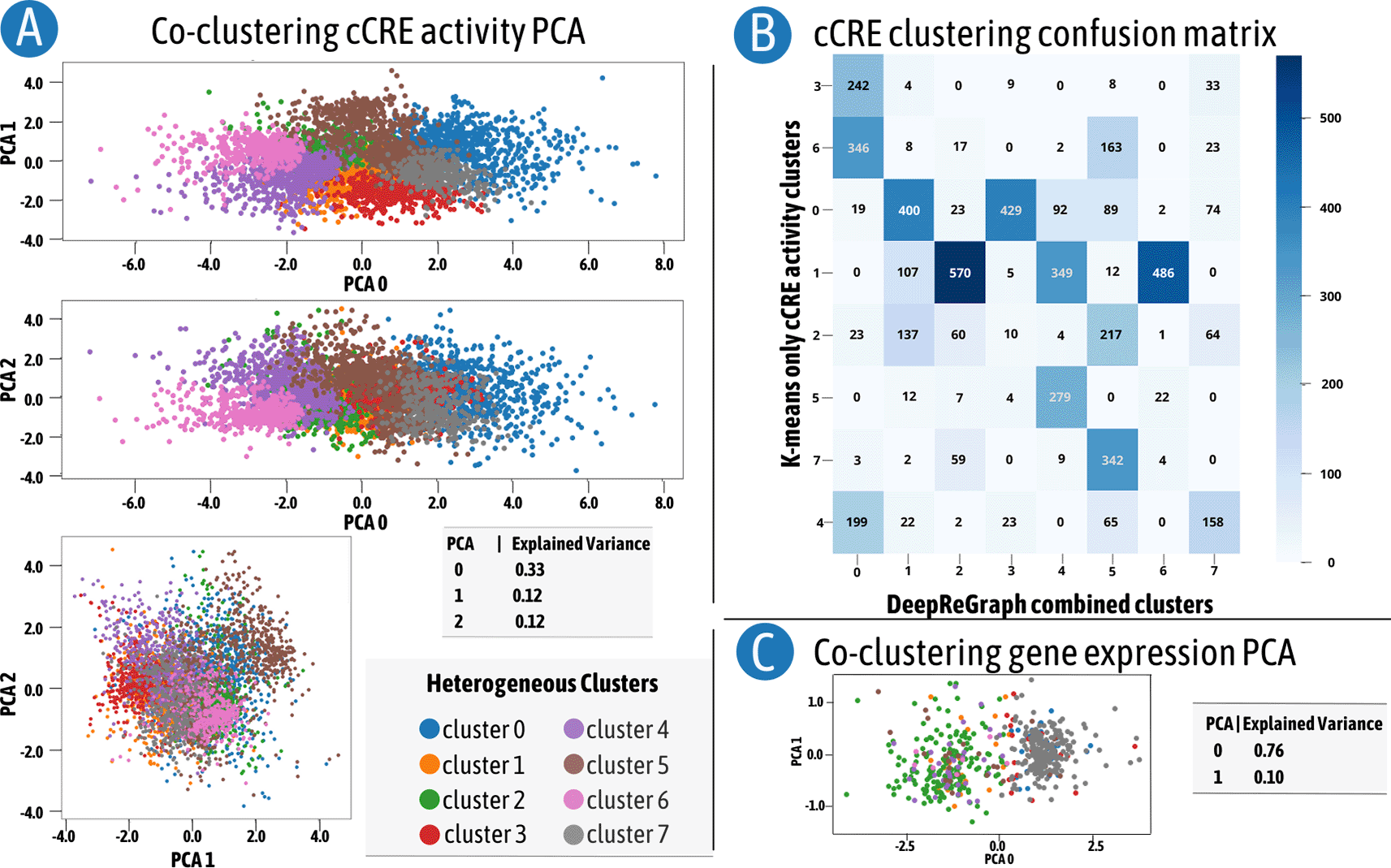
A) Principal component analysis (PCA) reduced dimension of candidate cis-regulatory elements (cCRE) profiles colored by the correspondent DeepReGraph cluster. B) Intersection between only-cCRE agglomerative clustering and cCRE extracted from DeepReGraph heterogeneous clusters. C) PCA reduced dimension of gene expression profiles colored by the corresponding DeepReGraph cluster.
The clustered patterns produced by DeepReGraph are presented in Figure 3. In this figure, the y-axis contains the mean-centered values for gene expression in the left-most column, while mean-centered CRE features are in the last three columns. The mean value reduction process mentioned was done as follows: given a time-series vector , with a mean value , the mean-reduced vector is . The x-axes of the plots instead correspond to the considered time-points of mouse fetal heart development. Notice that each cluster contains a set of genes and cCREs. The area between the first and 0.75 quantile is colored for each trend plot, to help visualize the trend of each cluster.
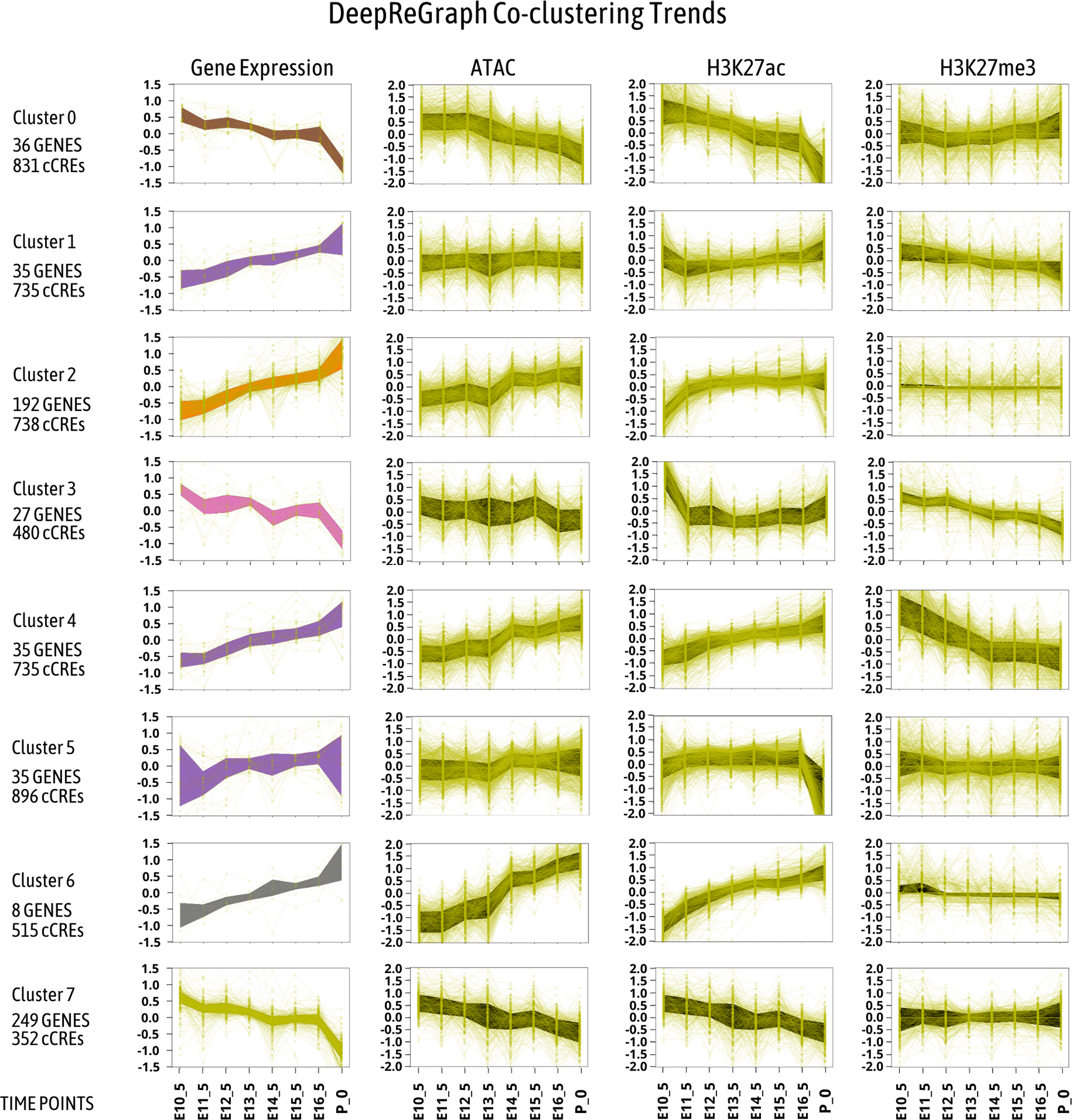
The first column of plots contains gene expression time profiles, and the rest of the columns contain enhancer activity time profiles. The space between the first and third quartile for each plot was colored to better show the trend.
We investigated the enriched function of gene expression clusters and enriched transcription factor binding site motifs of cCRE clusters to decipher the general signature of mouse fetal heart development. Figure 4 summarizes these enrichment analysis. It clearly shows that all gene expression clusters have clear functional annotation and all cCRE clusters entail clear transcription factor binding site motifs.

In general, expression of genes related to cell proliferation functions decrease during mouse fetal development, while expression of genes related to heart functions increase.4 However, if we look at the enriched terms for the detected gene expression clusters in panel A of Figure 3, and the pattern of gene expression the cCREs that drive them in Figure 3, we can observe that the story is not so simple. Two of the largest gene expression clusters are cluster2 (192 genes) which represents the heart functional genes (enriched for heart contraction function), and cluster7 (249 genes) which represents the cell proliferation genes. The smaller gene expression clusters have more specific enriched functions. Considering the other gene expression clusters down-regulated during development, cluster0 was more enriched for DNA replication, while cluster3 was enriched for non-heart developmental processes. Similarly, the smaller gene expression clusters up-regulated during development gained specific functional enrichment: cluster1 was enriched in metabolic processes to generate energy for the heart to function. Cluster4 was enriched for ventricular cardiac muscle cell membrane repolarization, and cluster6 was enriched for heart contraction. Cluster5 contained genes enriched for regulation of muscle system process. Here, co-clustering of gene expression and cCREs enabled us to derive smaller and more specific clusters. Otherwise, as it is clear from Figure 2 panel C, the smaller clusters of gene expression with more focused functions could not be deduced from gene expression alone.
Multi-modal clustering can also describe how cCREs can drive gene expression during development. First, smaller gene expression clusters gained more cCREs per genes, as Figure 3 shows. Secondly, cCREs with different epigenetic patterns have been linked to similar pattern of gene expression, as can be seen also in Figure 3. For example, in the major cluster with up-regulated genes during development, i.e. cluster2, the trends of ATAC-seq and H3K27ac increased as expected. Similarly, for cluster7 which entails a large set of down-regulated genes throughout development, the trend of ATAC-seq and H3K27ac decreased. However, the H3K27me3 pattern for both cluster2 and cluster7 showed no changes in Figure 3. We can observe polycomb removal events in cluster1, cluster3, and cluster4 as H3K27me3 levels decreased in these clusters.
Multi-modal clustering can further clarify how gene expression changes through development, as cCRE clusters exhibited clearly enriched motifs in panel B of Figure 4. These enriched motifs can prioritize the candidate transcription factors which drive the development. For example, the MEF2 motif was enriched in the clusters related to up-regulated genes. The only exception was cluster1, for which the AP1 motif was enriched. We can assume that a MEF2 binding transcription factor, and more probably MEF2C, was the major transcription factor which caused the increase in gene expression values. Other binding site motifs were been enriched for the clusters entailing temporally up-regulated genes in Figure 4 panel B. Interestingly, these motifs were highly cluster-specific. A similar dynamic was seen for clusters with temporally decreased gene expression. Although zinc finger motifs were enriched in these clusters, the GATA motif was only enriched in cluster0 and the basic helix-loop-helix (BHLH), nuclear receptor motifs are only enriched in cluster3.
This study introduced a novel method called DeepReGraph to perform multi-modal clustering of gene expression and cCREs. DeepReGraph allows a cluster-friendly embedding, where clusters contain genes and CREs and tend to identify gene regulation mechanisms. Interestingly, the results of multi-modal clusters derived by DeepReGraph for cCRES were highly similar to the uni-modal clustering using k-means. However, DeepReGraph generated gene expression clusters that could not be derived by using gene expression data alone. Such a result might be expected if we consider cCRE and gene expression changes in a “cause and effect” manner. cCREs are part of the regulatory network and are among the driving causes of alternation in gene expression. Therefore, we can expect cCRE uni-modal clustering to be similar to co-clustering gene expression and cCREs together. However, gene expression is controlled by cCREs. In mouse fetal heart development, we have shown that similar gene expression (similar effect) can be divided into different clusters based on the controlling cCREs. This result shows the added values of the multi-modal clustering method to understand the signature of development.
Developmental regulatory networks can be straightforwardly modelled as heterogeneous graphs. The main reason for such a claim is because they are made of two distinct classes of elements (genes and CREs) whose interaction tends to be highly correlated with multiple features like gene expression, base-pair distance, and cCRE activity. Modelling such regulatory networks as heterogeneous graphs is key to using graph RL algorithms to converge to low-dimensional embeddings for such systems. The spatial distribution of nodes in the embedding might resemble complex relationships between nodes.
We undertook the challenge of converging to an embedding where gene expression regulation mechanisms are easily identifiable. To do so, we created our own heterogeneous graph RL algorithm by carefully designing an extension of AdaGAE.26 First, we designed a dynamic combination schema of multiple node feature spaces to create a unique node feature space. This unification was a necessary step to adapt AdaGAE to a heterogeneous graph scenario. We also created a repulsive force by extending the loss function in Ref. 26. This repulsive force has proven essential to separate elements with different gene expression or activity trends. Third, we introduce a trend-aware regularization of the base-pair distance relationship between nodes. This regularization proved essential to produce more compact clusters. The resulting schema is responsible for producing a clustering-friendly embedding space that sheds light on regulatory mechanisms.
In this work, we extended the algorithm presented in Ref. 26 to produce an algorithm capable of embedding a heterogeneous graph into a low-dimensional, easy-to-cluster embedding. Other approaches to heterogeneous graph embedding that we could further investigate exist34; for example, the relational graph convolutional networks (RGCN).49 Such a model implies a greater number of parameters; various parameter-sharing approaches have been proposed, some of them making use of the attention mechanism.50,51 We could further investigate attention-based prioritization of nodes and relationships for learning embeddings.52 If we consider the production of a unified embedding of heterogeneous data as a first step, we could conceive other offline clustering algorithms. The clustering-friendly embedding we present resembles a differentiable version of agglomerative clustering. However, other algorithms like the ones in Refs. 53,54 use a differential expectation-maximization schema, where a distance-to-centroid loss is minimized to reach final embedding with compact clusters. Consequently, the use of different deep clustering approaches should be further investigated.
Regulatory networks and gene regulation are dynamic processes. Therefore, temporal datasets can potentially describe them better than static ones. However, initial efforts to associate regulatory networks and chromatin states to the gene expression were made based on limited data. ChromHMM55 is the most used method to assign states of the chromatin to genes. However, with the advent of large temporal datasets like ENCODE, which we used in this paper, it is possible to move beyond a static view of regulatory networks and gene expression. This study used chromatin accessibility, H3K27ac, and H3K27me3, three well-known epigenetic markers with a well-characterized effect on gene expression. This framework can be further expanded to other epigenetic markers. Such an expansion could have two main advantages. The first advantage is the potential improvement of clustering quality. The second consists in better deciphering the combinatorial trends of epigenetic changes and their effects on gene expression dynamics.
Source code, Data and Interactive Notebook available at: https://github.com/QwertyJacob/DeepReGraph. Archived source code, data and notebook at time of publication: https://doi.org/10.5281/zenodo.6416055
Data are available under the terms of the Apache License, Version 2.0
The authors wish to thank Prof. L. Casasús and Dr. Raúl P. Caulier for their valuable insights.
| Views | Downloads | |
|---|---|---|
| F1000Research | - | - |
|
PubMed Central
Data from PMC are received and updated monthly.
|
- | - |
Is the rationale for developing the new method (or application) clearly explained?
Yes
Is the description of the method technically sound?
Yes
Are sufficient details provided to allow replication of the method development and its use by others?
Partly
If any results are presented, are all the source data underlying the results available to ensure full reproducibility?
Partly
Are the conclusions about the method and its performance adequately supported by the findings presented in the article?
Partly
Competing Interests: No competing interests were disclosed.
Reviewer Expertise: Bioinformatics, Single-cell Expression, Spatial Transcriptomics
Is the rationale for developing the new method (or application) clearly explained?
Partly
Is the description of the method technically sound?
Yes
Are sufficient details provided to allow replication of the method development and its use by others?
Yes
If any results are presented, are all the source data underlying the results available to ensure full reproducibility?
Yes
Are the conclusions about the method and its performance adequately supported by the findings presented in the article?
Yes
Competing Interests: No competing interests were disclosed.
Reviewer Expertise: Epigenetics
Alongside their report, reviewers assign a status to the article:
| Invited Reviewers | ||
|---|---|---|
| 1 | 2 | |
|
Version 1 13 May 22 |
read | read |
Provide sufficient details of any financial or non-financial competing interests to enable users to assess whether your comments might lead a reasonable person to question your impartiality. Consider the following examples, but note that this is not an exhaustive list:
Sign up for content alerts and receive a weekly or monthly email with all newly published articles
Already registered? Sign in
The email address should be the one you originally registered with F1000.
You registered with F1000 via Google, so we cannot reset your password.
To sign in, please click here.
If you still need help with your Google account password, please click here.
You registered with F1000 via Facebook, so we cannot reset your password.
To sign in, please click here.
If you still need help with your Facebook account password, please click here.
If your email address is registered with us, we will email you instructions to reset your password.
If you think you should have received this email but it has not arrived, please check your spam filters and/or contact for further assistance.
Comments on this article Comments (0)