Remote sensing and machine learning for yield prediction of lowland paddy crops

Lala Septem Riza; Afina Hadaina Yudianita; Eki Nugraha; Lili Somantri; Imas Sukaesih Sitanggang; Khyrina Airin Fariza Abu Samah; Shah Nazir

doi:10.12688/f1000research.110608.1

Home Browse Remote sensing and machine learning for yield prediction of lowland...

ALL Metrics

-

Views

-

Downloads

Get PDF

Get XML

Export

▬

✚

Research Article

Remote sensing and machine learning for yield prediction of lowland paddy crops

[version 1; peer review: 1 approved, 1 not approved]

Lala Septem Riza ¹, Afina Hadaina Yudianita¹, Eki Nugraha¹, [...] Lili Somantri², Imas Sukaesih Sitanggang³, Khyrina Airin Fariza Abu Samah⁴, Shah Nazir⁵

Lala Septem Riza ¹, Afina Hadaina Yudianita¹, [...] Eki Nugraha¹, Lili Somantri², Imas Sukaesih Sitanggang³, Khyrina Airin Fariza Abu Samah⁴, Shah Nazir⁵

PUBLISHED 21 Jun 2022

Author details Author details

¹ Department of Computer Science Education, Universitas Pendidikan Indonesia, Bandung, 40154, Indonesia
² Department of Geography Education, Universitas Pendidikan Indonesia, Bandung, 40154, Indonesia
³ Department of Computer Science, IPB University, Bogor, 16680, Indonesia
⁴ Faculty of Computer and Mathematical Sciences, Universiti Teknologi Mara Cawangan Melaka Kampus Jasin Melaka, Melaka, 75450, Malaysia
⁵ Department of Computer Science, University of Swabi, Swabi, 23561, Pakistan

Lala Septem Riza
Roles: Conceptualization, Methodology, Supervision, Writing – Original Draft Preparation, Writing – Review & Editing

Afina Hadaina Yudianita
Roles: Data Curation, Software

Eki Nugraha
Roles: Project Administration, Resources, Supervision, Visualization

Lili Somantri
Roles: Data Curation, Methodology, Resources, Validation

Imas Sukaesih Sitanggang
Roles: Conceptualization, Methodology, Writing – Original Draft Preparation, Writing – Review & Editing

Khyrina Airin Fariza Abu Samah
Roles: Formal Analysis, Validation, Writing – Original Draft Preparation, Writing – Review & Editing

Shah Nazir
Roles: Software, Supervision, Writing – Original Draft Preparation, Writing – Review & Editing

OPEN PEER REVIEW

REVIEWER STATUS

This article is included in the Agriculture, Food and Nutrition gateway.

This article is included in the Machine learning: life sciences collection.

Abstract

Background: Paddy is one of the crops with the largest production worldwide, after corn and wheat. In Indonesia, paddy crops play a role as one of the main boosters of national economic growth based on their contribution to Indonesia's gross domestic product (GDP). Therefore, it is imperative to do research aimed at predicting the yield of paddy crops.
Methods: This research exploits the technology of remote sensing and machine learning methods (i.e. Gradient Boosting Regressor) to predict the yield of lowland paddy crops. Remote sensing with a Landsat 8 satellite was used to obtain the input data in the form of the vegetation index (i.e. NDVI) value, surface temperature, and total pixels of the observed area. Afterward, the input data was arranged into training data by combining paddy yield data and the paddy harvest period.
Results: The obtained training data was modelled to predict the yield of paddy crops using a Gradient Boosting Regressor. The results obtained from experiments conducted in Bandung, Indonesia, showed the scenario with the best parameter combination is an estimator of 2000, a learning rate of 0.001, minimum samples split of 2, and a maximum depth of 4, which has RMSE of 9766.72.
Conclusions: This research succeeded in designing a computational model to predict the yield of lowland paddy crops by involving remote sensing and Gradient Boosting Regressor.

Keywords

remote sensing, NDVI, Landsat 8 satellite, Gradient Boosting Regressor, machine learning, agriculture, crop yield, Geographic information systems (GIS)

Corresponding author: Lala Septem Riza

Competing interests: No competing interests were disclosed.

Grant information: The author(s) declared that no grants were involved in supporting this work.

Copyright: © 2022 Septem Riza L et al. This is an open access article distributed under the terms of the Creative Commons Attribution License, which permits unrestricted use, distribution, and reproduction in any medium, provided the original work is properly cited.

How to cite: Septem Riza L, Yudianita AH, Nugraha E et al. Remote sensing and machine learning for yield prediction of lowland paddy crops [version 1; peer review: 1 approved, 1 not approved]. F1000Research 2022, 11:682 (https://doi.org/10.12688/f1000research.110608.1) First published: 21 Jun 2022, 11:682 (https://doi.org/10.12688/f1000research.110608.1) Latest published: 21 Jun 2022, 11:682 (https://doi.org/10.12688/f1000research.110608.1)

Introduction

Agriculture is a term that is used broadly to describe the various aspects and origin of plant and animal foodstuffs and plant growth. This term exists in a framework consisting of three environments, i.e. the biophysical environment, socio-political environment, and economic and technological environment (Yunlong and Smit, 1994). Agriculture plays an important role in a country, both developed and developing countries. However, not all countries have the same agricultural technology, and the differences are seen in developed and developing countries. For example, according to the United States Department of Agriculture, corn yields in the US in 2020 were around 4.3 t/ha. Meanwhile, corn yields in Ethiopia have only increased from 0.9 to 3.5 t/ha since 1960 (Petersen, 2018). In Indonesia, corn yields increased by about 4.52% from 2014 to 2015 (BPS-Statistics Indonesia, 2015). Farmers in developing countries don’t have financial and educational resources available compared to farmers in developed countries, in general. Therefore, yield prediction in developing countries is imperative as the crop yields are more susceptible to droughts and other dangerous issues (Petersen, 2018).

There are a few agriculture-related research methods that have been used to predict crop yields. Petersen (2018) predicted the yield of corn, soybean, and sorghum –two to four months before its harvest time. He utilized remote sensing technology from MODIS satellite imagery to obtain the relationship between a few vegetation indices and crop yields using a machine learning method (i.e. multivariate regression). Shiu and Chuang (2019) predicted the yield of rice paddy using SPOT-7 satellite imagery to obtain the vegetation index of rice paddy. They used a machine learning method (i.e. support vector regression) to predict the yield of rice paddy. Pantazi et al. (2016) also used a machine learning method (i.e. artificial neural network) and satellite imagery to predict the yield of wheat. Ahmad et al. (2010) estimated soil moisture using TRRM satellite imagery using machine learning methods (i.e. support vector machine and artificial neural network). Maas (1988), utilized Landsat satellite imagery to estimate the yield of sorghum grain.

The following research shows that crop vegetation indices have a linear relationship with yield. These researchers used machine learning methods called linear regression. Bartlett et al. (1989) utilized satellite imagery to estimate solar radiation and carbon dioxide exchange of a grass canopy. Du Plessis (1999) obtained a linear relationship between a vegetation index and rainfall using NOAA AVHRR satellite imagery. Irsan et al. (2019) predicted corn yield from a few types of vegetation indices extracted from Sentinel 2A satellite imagery. Zhang et al. (2019) predicted rice paddy productivity from a vegetation index extracted from Landsat 8 satellite imagery and Sari et al. (2013) utilized Landsat 8 satellite imagery to estimate rice paddy yield.

Currently, remote sensing technology can be used to detect the phenomenon of food plant vegetation because satellite imagery is easily accessible to anyone (Maas, 1988). Useful data such as vegetation indices and the earth’s surface temperature can be generated from satellite imagery. Vegetation indices describe how healthy the crop is (Zhang et al., 2019), and surface temperature is one of the external factors that affect crop growth (Bartlett et al., 1989). This research utilized Landsat 8 satellite imagery to obtain a vegetation index (i.e. NDVI) and surface temperature. The relationship between remote sensing data and crop yields was obtained using Gradient Boosting Regressor machine learning methods as Gradient Boosting Regressor is a linear method that uses boosting techniques to produce a powerful and robust model in predicting crop yields (Friedman, 2001).

Methods

In this research, we built a computational model in several stages to predict the yield of lowland paddy crops, which is illustrated in Figure 1. This workflow diagram is described in detail in the following section.

Figure 1. Research procedure.

Data collection using remote sensing

The first stage in the workflow diagram was remote sensing data gathering and processing using ENVI remote sensing software version 5.3 or other software that has the ability to process Landsat 8 satellite data, such as the open-access alternatives: QGIS (RRID:SCR_018507), Orfeo ToolBox, and GRASS GIS, which can provide equivalent functions. Landsat 8 (L8) satellite imagery were downloaded from the EarthExplorer website with the following criteria: 1) dataset using satellite Landsat 8 OLI/TIRS C1 Level-1; 2) coordinate on Bandung (Lat: -6.9455, Lon: 107.6138); 3) date from May 21, 2013 to December 5, 2015. The specific location that was studied included four different sub-districts in Bandung, which were Cikancung, Ciparay, Majalaya, and Paseh. Landsat 8 (L8) satellite imagery data was processed to obtain the Normalized Difference Vegetation Index (NDVI) and the earth’s surface temperature value. Lowland rice yield data was obtained from reports published by BPS-Statistics Indonesia of Bandung (see Data availability).

An Indonesian topographical map was used to determine the boundaries of the paddy field area in Bandung. This can be downloaded through the Indonesia Geospatial Portal. All relevant data can be found in Riza et al. (2022a).

Before the satellite imagery data was processed, the data was resized and divided into subsets so that the data size was not too large. Large data sizes caused slow processing and consumed a lot of storage on the computer. Resizing and sub setting of data were performed using Region of Interest (ROI) files created based on the topographical map. Satellite imagery data was cleaned if pixels were considered as clouds and shadows using the Quality channel in L8 imagery. The pixels that were considered disrupting were greater than 2800 on the Quality L8 band (Landsat Missions | U.S. Geological Survey (usgs.gov)). The pixels that were processed were pixels with a value below 2800. Satellite imagery data needed to be calibrated and corrected so that the image was free from disturbances caused by the atmosphere. An example of this is the absorption of red light by ozone gas in the atmosphere that distorts the reflectance value in the imagery so that it cannot represent the phenomenon of vegetation (Tanre et al., 1992).

Not every pixel in the imagery could be involved in the process of obtaining NDVI and the earth’s surface temperature value due to the disturbances of the clouds and shadows. Clouds and shadows cause variations in the number of pixels in various locations every day. Therefore, sampling techniques were required. The number of samples can be obtained by the Cochran formula (Cochran, 2007) as follows:

(1)

n_{0} = \frac{Z^{2} pq}{e^{2}}

Where:

$n_{0} =$ number of samples

$Z =$ Z value depends on confidence level

$p =$ percentage picking a choice (0.5 used for sample size needed)

q = 1 - p

$e =$ confidence interval

For a finite population number, there are adjustments to the formula as follows:

(2)

n = \frac{n_{0}}{1 + \frac{(n_{0} - 1)}{N}}

Where:

$n =$ number of samples

$N =$ number of populations

The sampling technique used was stratified random sampling that is already available in the ENVI software. ENVI will automatically stratum the total pixels and determine which pixels will be sampled.

The NDVI vegetation index is a transformation of the combination of the red and near-infrared band (Ikasari et al., 2016) that is formulated as follows:

(3)

NDVI = \frac{NIR - Red}{NIR + Red}

Where:

NIR = reflectance of near infrared

Red = reflectance of red

Near infrared contributes to light reflected by leaf structures, while the red band contributes to light absorbed by leaf structures (Jensen, 1996). In ENVI, NDVI calculations can be obtained automatically based on the type of satellite imagery using the NDVI tool.

The temperature of the earth’s surface is one of the external factors that can affect the growth of paddy crops. Cold temperatures will cause rice seedlings to grow slower than warmer temperatures (Vergara, 1992). In the L8 imagery, the temperature of the earth’s surface can be obtained by performing a brightness temperature calibration on the thermal band of the satellite imagery.

Data pre-processing

The second stage in the workflow is the data pre-processing stage. This stage consists of three stages, which are the one-hot encoding process, adjusting the array of input data, and data standardization. One-hot encoding is an approach to convert categorical features into a more suitable format as input in a machine learning model (Zheng and Casari, 2018). Gradient Boosting Regressor model as a regression model requires input data in numerical form. The categorical features of remote sensing data used in this study were the harvest period or harvest sub round features.

Adjusting the input data array converts the data from Pandas DataFrame into a NumPy array. This conversion is intended so that the data can be processed using various mathematical operation functions available in the NumPy library version 1.19.1 (RRID:SCR_008633) in Python (Python Programming Language, RRID:SCR_008394).

Data standardization aims to change each feature in the input data so it has the same value range, which is between 0 and 1. With standardization, each feature has the same opportunity to influence the computational model. Standardization was done using Z-score standardization (Zill et al., 2011) which is formulated as follows:

(4)

z = \frac{x - μ}{s}

Where:

$z =$ standardized samples

$x =$ samples

$μ =$ mean of samples

Gradient Boosting Regressor

The Gradient Boosting algorithm uses the boosting technique to the Gradient Descent method, both for classification and regression problems (Bishop, 2006). The model built with the Gradient Boosting Regressor algorithm (Friedman, 2001) can be seen in Table 1.

Table 1. Gradient Boosting Regressor algorithm.

Algorithm 1 Gradient Boosting Regressor

Input: Data

D = {\{(x_{i}, y_{i})\}}_{i = 1}^{n}

Derivative of the loss function

L (y_{i}, γ)

Output: Output function

F_{m} (x)

Initialization:
1: Constant value

F_{0} (x) = \binom{argmin}{γ} \sum_{i = 1}^{n} L (y_{i}, γ)

LOOP process
2: for

m = 1

to

M

do
3:

r_{im} = - {[\frac{\partial}{\partial F (x_{i})} L (y_{i}, F (x_{i}))]}_{F (x) = F_{m - 1} (x)}

for

i = 1, . ., n

4: Build a regression tree that predicts

r_{im}

and create terminal regions for

j = 1, \dots, J_{m}

5: Calculate

γ_{jm} = \binom{argmin}{γ} \sum_{x_{i} \in R_{jm}} L (y_{i}, F_{m - 1} (x_{i}) + γ)

for

j = 1, \dots, J_{m}

6: Update

F_{m} (x) = F_{m - 1} (x) + ν \sum_{j = 1}^{J_{m}} γ_{m} I (x \in R_{jm})

7: end for

The training process begins with an input consisting of input data and loss function derivatives. The loss function that can be used in this model is the square loss function (Friedman, 2001) which is formulated as follows:

(5)

L (y_{i}, F (x)) = \frac{1}{2} {(y_{i} - F (x))}^{2}

Constant value initialization is done by calculating the optimal value that can minimize the loss function. After the constant value has been initialized, calculate the $r_{im}$ (pseudo residual) for each row of data. Once $r_{im}$ is obtained, create a Regression Tree that predicts $r_{im}$ . Calculate $γ_{jm}$ (output value) for each leaf in the Regression Tree. Update the output function $F_{m} (x)$ every time the Regression Tree is built.

The Regression Tree (James et al., 2013) model as a weak learner in Gradient Boosting Regression can be seen from the algorithm in Table 2.

Table 2. Regression Tree algorithm.

Algorithm 2 Regression Tree

Input: Data

D = {\{(x_{i}, y_{i})\}}_{i = 1}^{n}

Output: Tree in array form
Initialization:
LOOP process
1: for

i

in feature do
2: unique values = unique values in feature

i

LOOP process
3:    for threshold in unique values do
4: calculate metric
5: feature index = threshold
6:    end for
7:    take the best metric results after looping
8: end for
9: Compare the metrics for each feature
10: Select a feature with the best metric to become a node
11: Split data on the node based on the selected threshold
12: Repeat process 1-11 for the next node

The metric used for the data splitting process in the Regression Tree used in this study is variance reduction (Loh, 2011), which involves the variance value for the total data and two splitting results based on the threshold. Model testing is done by tracing each Regression Tree that has been created. The learning rate is involved in the leaf value obtained in each tree to obtain the prediction result. The prediction results at the testing stage are the output of this research workflow. The source code of this computational model can be found in Riza et al. (2022b).

Experimental study

We conducted experiments based on the workflow diagram that was built. This section describes the experimental study in constructing a computational model to predict the yield of lowland paddy crops.

Data collection

Figure 2 is a map of Bandung as a research area and the zone of interest is in white. Pixels that interfered with image data (clouds and shadows) were removed using the Quality channel on the Landsat 8 (L8) image data. The Region of Interest (ROI) was created based on disrupting pixels. Figure 3 shows the ROI file of the cloud pixels and its shadow in green.

Figure 2. Map of Sub-district of Bandung: Ciparay, Majalaya, Paseh, Cikancung (Map data ©2020).

Figure 3. Removing pixels of clouds and shadows.

After the imagery data was clean of disturbing pixels, the next step was to perform radiometric calibration and atmospheric correction. The differences in the image before and after being calibrated and corrected are not visible to the human eye. Nevertheless, the difference can be seen in the reflectance value that changes at each stage as in Table 3. After the data was calibrated and corrected, the pixel value was adjusted to obtain the accurate reflectance value by dividing 10,000 by all pixels.

Table 3. The difference in reflectance value.

No.	Imagery data	Reflectance value
No.	Imagery data	Red band	Green band	Blue band
1	Raw data (before calibrated and corrected)	7013	7658	8162
2	Radiometrically calibrated	1,950518	3,054464	3,943182
3	Atmospherically corrected	374	407	173
4	Surface reflectance	0,037400	0,040700	0,017300

The sampling process on ENVI was done using the Generate Random Sample Tool Using Ground Truth ROIs by creating an ROI file specifically for the paddy crop area to be sampled. ROI files can be created in the Band Threshold to ROI tool by marking all pixels. After the ROI file was available, the next step was to determine the required sample size using the Cochran formula (Cochran, 2007). The sampling technique used in ENVI was stratified random sampling. Figure 4 shows the appearance of the sample pixel dots on the L8 imagery data.

Figure 4. ENVI stratified random sampling results.

NDVI vegetation index was calculated after the imagery data was calibrated and corrected. Calculations were done by the NDVI tool in ENVI by selecting the type of OLI sensor (Landsat 8) with the red channel band (number four) and the near-infrared channel band (number five). Figure 5 is the difference in the appearance of the image before and after being transformed into NDVI. The image on the right is the result of adding a colour slice so that the difference between high NDVI values and low NDVI values can be seen properly.

Figure 5. The difference in imagery data before and after NDVI calculation.

After the NDVI was obtained within a predetermined period, the next step was to plot the NDVI value into a parabolic graph. It represents one harvest season for the paddy crop. The NDVI value taken from one harvest season is the biggest.

The temperature of the earth’s surface can be obtained by performing the Brightness Temperature radiometric calibration on the thermal band of the L8 satellite imagery. After calibration, the pixel values in the image represent Kelvin units. To convert Kelvin to Celsius, we can use the Band Math tool and enter the formula below:

(6)

C = K - 273.15

After the satellite imagery data was processed using ENVI, the next step was to combine the remote sensing data with the yield of lowland paddy crop reported by BPS-Statistics Indonesia. The report from BPS-Statistics Indonesia is a report for each district per year in one file. The data available in each report file is the yield of lowland paddy crop and the area of planted paddy crop for each village. Data downloaded from BPS-Statistics Indonesia is required to obtain the percentage of paddy crop yield in each period.

Table 4 is the input data as a result of combining remote sensing data with lowland paddy yield reported for several different harvest seasons. The NDVI column, total pixels, and temperature are data obtained from remote sensing data collection, while the period column, planted area, and paddy crop yield are data obtained from the BPS-Statistics Indonesia.

Table 4. Data input for the computational model.

No.	NDVI	Total pixels	Periods	Temperature (°C)	Planted area (Ha)	Paddy crop yield (Quintal)
1	0,80	9826	P2	21,93	1564,22	37631,20
2	0,32	9917	P3	24,84	1564,22	25969,59
3	0,67	8494	P1	12,59	2147,86	56457,23
4	0,81	9908	P2	19,24	2147,86	57275,23
5	0,34	8362	P3	29,05	2147,86	43573,85
6	0,77	9590	P1	19,35	2197,85	70171,86
7	0,71	9923	P2	24,76	2197,85	63204,94
8	0,30	9499	P3	35,67	2197,85	39929,85
9	0,74	2403	P2	20,34	642,30	11032,54
10	0,40	3633	P3	23,66	642,30	7613,64
….	…	…	…	…	…	…
263	0,67	2314	P1	15,88	295,08	7274,47
264	0,78	2369	P2	20,92	295,08	7379,87
265	0,83	2273	P1	19,78	498,72	79616,38
266	0,76	2402	P2	24,00	498,72	71711,76
267	0,31	2344	P3	33,22	498,72	45068,10

The total pixels (population) are included in Table 4, but the sample size is not. This is because the total pixels already represent the sample value itself. In Table 4 there is also a period column that indicates the period or sub round for taking NDVI values. P1 indicates January – April, P2 indicates May – August, and P3 indicates September – October. This period column represents the date of the image data used to obtain the NDVI value. The column for the planted area is in hectares and the column for production is in quintal units, obtained from reports on food crop yield in Bandung.

Experimental scenarios

Remote sensing and loss function data were required to build the computational model. In doing so, the model also required several parameters, e.g. the number of Regression Trees to be created (estimators), learning rate, the maximum value of the Regression Tree depth (maximum depth), and the minimum amount of data obtained by a node in the Regression Tree for data splitting.

Scenarios were performed to compare the accuracy and speed of computations. In the scenario of comparing the accuracy, the root mean squared error (RMSE) was used to evaluate the experimental results. RMSE is the standard deviation for the residual or the resulting predictive error. RMSE shows how much residual dispersion occurs (Barnston, 1992). RMSE is formulated as follows:

(7)

{RMSE}_{fo} = \sqrt{\frac{\sum_{i = 1}^{N} {(z_{fi} - z_{fo})}^{2}}{N}}

Where:

$f =$ index of predicted data

$o =$ index of observed data

$z_{fi} =$ predicted data

$z_{fo} =$ observed data

$N =$ number of samples

All parameters may influence the RMSE value in the scenario of comparing the accuracy. The larger the size and number of regression trees built, the greater the opportunity for the model to study the data. The greater the learning rate value used, the shrinkage of the predicted results for each Regression Tree will also be greater. Therefore, all of the parameters in the RMSE value testing scenario were involved.

The computation speed of the Gradient Boosting Regressor algorithm depends on the number and size of the Regression Tree being built. Therefore, the computation speed can be influenced by several parameters, e.g. estimators, minimum samples split, and maximum depth.

Results and discussion

The output of the program is a file in the comma-separated value (CSV) format which contains data on the prediction of lowland paddy crop yield based on the data input at the beginning of the program. Table 5 is the output of the program displayed in the CSV file with an estimator parameter of 2000, a learning rate of 0,001, a maximum depth tree of 4, and minimum samples split of 2. The scatter plot and RMSE value are shown in Figure 6.

Table 5. The program output of the computational model.

No	NDVI	Total pixels	Period	Temp (°C)	Planted area (Ha)	Observed yield (Quintal)	Predicted yield (Quintal)
1	0.77	1254	P1	20.29	173.00	4659.18	2872.55
2	0.81	1651	P2	18.88	378.94	8636.56	13164.07
3	0.40	1583	P3	14.10	439.62	39729.64	37428.55
4	0.47	2554	P3	26.62	378.94	6570.52	5298.32
5	0.76	1683	P2	17.06	166.58	4166.11	2344.01
6	0.66	2495	P1	15.04	224.11	5216.04	3923.12
7	0.49	1952	P3	22.73	757.69	14370.35	10113.23
8	0.62	2142	P1	15.14	206.93	2483.34	3313.89
9	0.67	521	P3	14.68	503.70	7292.73	7531.71
10	0.75	3835	P1	20.30	621.91	19940.92	12599.95
…	…	…	…	…	…	…	…
40	0.49	1191	P3	30.49	62.70	1257.73	232.94
41	0.82	1129	P1	19.97	679.55	108480.69	77685.62
42	0.50	1474	P1	15.85	165.30	3922.42	2582.48
43	0.66	3717	P2	20.38	692.34	12930.94	11611.03
44	0.44	629	P3	19.82	230.36	4208.17	2425.74
45	0.56	3892	P2	26.19	520.00	12505.56	8721.51
46	0.43	341	P3	32.07	164.15	2155.24	1529.38
47	0.77	9590	P1	19.35	2197.85	70171.86	45331.60
48	0.55	3907	P1	6.08	607.77	16043.90	9806.82
49	0.45	3851	P3	26.84	881.96	12774.78	12327.67
50	0.64	3251	P2	25.52	783.42	14353.61	11718.58
51	0.32	928	P3	19.73	101.79	2004.92	1032.32
52	0.54	1286	P3	24.97	166.85	2699.95	1528.98
53	0.77	1100	P2	18.7	144.13	2222.70	1629.13

Figure 6. Scatter plot from observed and predicted paddy crop yield.

To test the effect of parameters on the RMSE value, a model was built based on several scenarios. The scenario in Table 6 is a combination of various parameters. The parameter estimator was tested at the values of 200, 500, 1000, 1500, and 2000. The learning rate parameters were tested at values of 0.1, 0.01, and 0.001. The minimum parameters of samples split were tested at values 2 and 10. The maximum depth parameters were tested at values 4, 6, and 8.

Table 6. Experimental results for testing the RMSE of the computational model.

No.	Estimator	Learning rate	Min. samples split	Max. depth	RMSE
1	200	0.100	2	4	10386.23
2	200	0.010	2	4	9775.79
3	200	0.001	2	4	15312.73
4	200	0.100	2	6	11322.44
5	200	0.010	2	6	10311.56
6	200	0.001	2	6	14852.49
7	200	0.100	2	8	11494.76
8	200	0.010	2	8	10285.11
9	200	0.001	2	8	14818.50
10	200	0.100	10	4	10521.17
…	…	…	…	…	…
72	1500	0.001	10	8	10352.90
73	2000	0.100	2	4	10387.34
74	2000	0.010	2	4	10345.43
75	2000	0.001	2	4	9766.72
76	2000	0.100	2	6	11322.49
77	2000	0.010	2	6	11371.27
78	2000	0.001	2	6	10302.96
79	2000	0.100	2	8	11494.76
80	2000	0.010	2	8	11495.74
81	2000	0.001	2	8	10277.60
82	2000	0.100	10	4	10538.33
83	2000	0.010	10	4	10180.24
84	2000	0.001	10	4	10568.62
85	2000	0.100	10	6	11773.43
86	2000	0.010	10	6	11756.63
87	2000	0.001	10	6	10330.89
88	2000	0.100	10	8	11908.48
89	2000	0.010	10	8	12387.41
90	2000	0.001	10	8	10571.03

From Table 6, we could see that the value of scenario number 75 produces the best RMSE value. From this experiment, the scenario with the best parameter combination is an estimator of 2000, a learning rate of 0.001, minimum samples split of 2, and a maximum depth of 4.

Figure 7 contains graphs showing the average RMSE value for each estimator, learning rate, minimum samples split, and maximum depth. The RMSE value tends to be constant in the estimator with a value of 1000 to 2000. The value of the estimator with the best RMSE was 1500. The value of the learning rate with the best RMSE was 0.01. The minimum value of samples split with the best RMSE was 2. The maximum depth value with the best RMSE was 4.

Figure 7. Plot between estimators, learning rate, minimum sample slit, and maximum depth against RMSE.

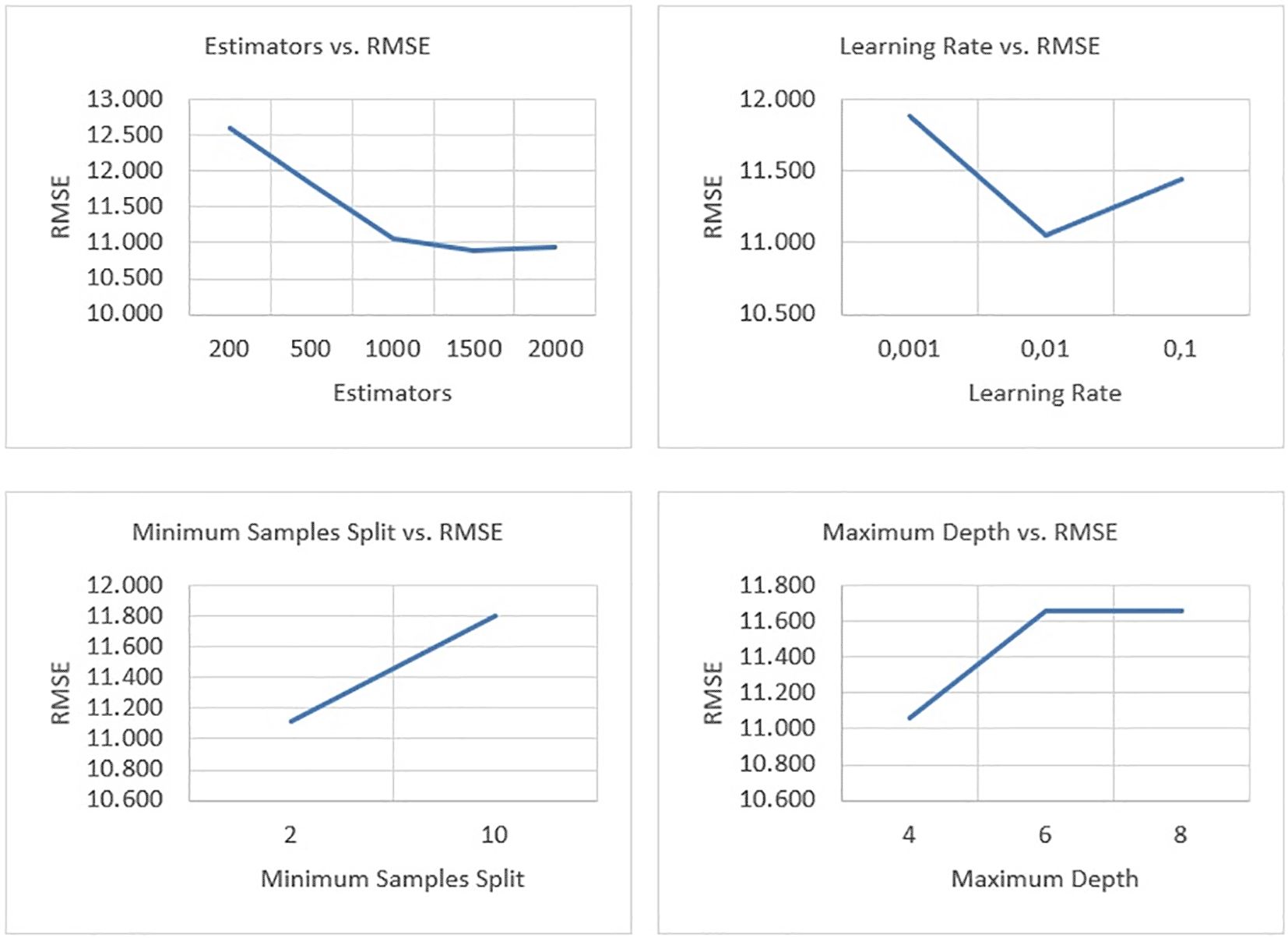
According to the experiments, it can be seen that the developed application was able to predict crop yields with reasonable accuracy. This result can be compared with research conducted by Petersen (2018). This study predicts production 2-4 months before harvest time based on MODIS satellite imagery. The model was created and validated using satellite imagery of Illinois, United States of America by calculating the linear fit between production and vegetation index. The model is made by looking for a linear regression relationship between the average vegetation index and the vegetation index anomaly with production. The model made is able to predict the production of corn, soybeans, and sorghum, respectively, the median error is 5.7%, 5.8%, and 22%. The next model is applied in several countries on the African continent by making predictions for 2-4 months before harvest time. The result is that the prediction has an error of less than 5%.

Conclusions

After performing some experiments, we came to several conclusions that were in line with the research objectives as follows: (i) This research succeeded in conducting a regression analysis between the NDVI vegetation index and rice production using the Gradient Boosting Regressor algorithm with five main stages. The stages are remote sensing data collecting, data preprocessing, data standardization, model training, and model testing; (ii) This research succeeded in designing a computational model to identify the yield of lowland paddy crops based on the regression relationship in the Gradient Boosting Regressor algorithm between the vegetation index and its yield; and (iii) This study conducted 90 experiments divided into two main scenarios. From the results and discussions, the authors conclude that the estimator parameters, learning rate, minimum samples split, and maximum depth used have different contributions to the accuracy and speed of computation in the computational model to predict the yield of lowland paddy crops.

Data availability

Underlying data

Open Science Framework: Underlying data for ‘Remote sensing and machine learning for yield prediction of lowland paddy crops’, https://doi.org/10.17605/OSF.IO/P9CY3 (Riza et al., 2022a).

This project contains the following underlying data:

• Data NDVI with ENVI.zip: Data containing vegetation index (i.e., NDVI)
• Data Portal Geospasial Indonesia.zip: The Indonesian topographical map was used to determine the boundaries of the paddy field area in Bandung.
• Dataset Final.xlsx

Data are available under the terms of the Creative Commons Zero “No rights reserved” data waiver (CC0 1.0 Public domain dedication).

Landsat 8 (L8) satellite imagery were downloaded from the EarthExplorer website. An Indonesian topographical map was used to determine the boundaries of the paddy field area in Bandung and is available from the Indonesia Geospatial Portal). Lowland rice yield data was obtained from reports published by BPS-Statistics Indonesia of Bandung:

• Ciparay City: Ciparay, 2013; Ciparay, 2014; Ciparay, 2015.
• Cikancung City:: Cikancung, 2013; Cikancung, 2014; Cikancung, 2015.
• Paseh City: Paseh, 2013; Paseh, 2014; Paseh, 2015.
• Majalaya City: Majalaya, 2013; Majalaya, 2014.

Software availability

Source code available from: https://github.com/lala-s-riza/Remote-sensing-and-machine-learning-for-yield-prediction-of-lowland-paddy-crops.git

Archived source code at time of publication: https://doi.org/10.5281/zenodo.6459715 (Riza et al., 2022b).

License: GNU General Public License (GPL-2.0)

References

Ahmad S, Kalra A, Stephen H: Estimating soil moisture using remote sensing data: A machine learning approach. Adv. Water Resour. 2010; 33(1): 69–80. Publisher Full Text
Ariza AA: Machine Learning and Big Data Techniques for Satellite-Based Rice Phenology Monitoring. The University of Manchester;2019.
Barnston AG: Correspondence among the correlation, RMSE, and Heidke forecast verification measures; refinement of the Heidke score. Weather Forecast. 1992; 7(4): 699–709. Publisher Full Text
Bartlett DS, Whiting GJ, Hartman JM: Use of vegetation indices to estimate indices to estimate intercepted solar radiation and net carbon dioxide exchange of a grass canopy. Remote Sens. Environ. 1989; 30(2): 115–128. Publisher Full Text
Bishop CM: Pattern recognition and machine learning. Springer;2006.
BPS-Statistics Indonesia: Production of Food Crops. Jakarta:CV. Tapasuma Ratu Agung;2015.
Cochran WG: Sampling techniques. John Wiley & Sons;2007.
Du Plessis WP: Linear regression relationships between NDVI, vegetation and rainfall in Etosha National Park, Namibia. J. Arid Environ. 1999; 42(4): 235–260. Publisher Full Text
Friedman JH: Greedy function approximation: a gradient boosting machine. Ann. Stat. 2001; 29: 1189–1232.
Ikasari IH, Ayumi V, Fanany MI, et al.: Multiple regularizations deep learning for paddy growth stages classification from LANDSAT-8. International Conference on Advanced Computer Science and Information Systems (ICACSIS). 2016; 2016: 512–517.
Irsan LM, Murti SH, Widayani P: Estimasi Produksi Jagung (Zea Mays L.) dengan Menggunakan Citra Sentinel 2A Di Sebagian Wilayah Kabupaten Jeneponto Provinsi Sulawesi Selatan. Jurnal Teknosains. 2019; 8(2): 93–104. Publisher Full Text
James G, Witten D, Hastie T, et al.: An introduction to statistical learning. New York:springer;2013.
Jensen JR: Introductory digital image processing: a remote sensing perspective. Prentice-Hall Inc.;1996.
Loh WY: Classification and regression trees. Wiley Interdisciplinary Reviews: Data Mining and Knowledge Discovery;2011.
Maas SJ: Using satellite data to improve model estimates of crop yield. Agron. J. 1988; 80(4): 655–662. Publisher Full Text
Pantazi XE, Moshou D, Alexandridis T, et al.: Wheat yield prediction using machine learning and advanced sensing techniques. Comput. Electron. Agric. 2016; 121: 57–65. Publisher Full Text
Petersen LK: Real-time prediction of crop yields from MODIS relative vegetation health: A continent-wide analysis of Africa. Remote Sens. 2018; 10(11): 1–31.
Riza LS, Yudianita AH, Nugraha E, et al.: Remote sensing and machine learning for yield prediction of lowland paddy crops. Dataset. 2022a. Publisher Full Text
Riza LS, Yudianita AH, Nugraha E, et al.: Remote sensing and machine learning for yield prediction of lowland paddy crops. Source Code.2022b. Publisher Full Text
Sari DK, Ismullah IH, Sulasdi WN, et al.: Estimation of water consumption of lowland rice in tropical area based on heterogeneous cropping calendar using remote sensing technology. Procedia Environ. Sci. 2013; 17: 298–307. Publisher Full Text
Shiu YS, Chuang YC: Yield Estimation of Paddy Rice Based on Satellite Imagery: Comparison of Global and Local Regression Models. Remote Sens. 2019; 11(2): 1–18.
Tanre D, Holben BN, Kaufman YJ: Atmospheric correction algorithm for NOAA-AVHRR products: theory and application. IEEE Trans. Geosci. Remote Sens. 1992; 30(2): 231–248. Publisher Full Text
Vergara BS: A farmer’s primer on growing rice. Int. Rice Res. Inst.;1992.
Yunlong C, Smit B: Sustainability in agriculture: a general review. Agric. Ecosyst. Environ. 1994; 49(3): 299–307. Publisher Full Text
Zhang K, Ge X, Shen P, et al.: Predicting rice grain yield based on dynamic changes in vegetation indexes during early to mid-growth stages. Remote Sens. 2019; 11(4): 1–24.
Zheng A, Casari A: Feature engineering for machine learning: principles and techniques for data scientists. O’Reilly Media, Inc.;2018.
Zill D, Wright WS, Cullen MR: Advanced engineering mathematics. Jones & Bartlett Learning;2011.

Comments on this article Comments (0)

Version 1

VERSION 1 PUBLISHED 21 Jun 2022

Author details Author details

¹ Department of Computer Science Education, Universitas Pendidikan Indonesia, Bandung, 40154, Indonesia
² Department of Geography Education, Universitas Pendidikan Indonesia, Bandung, 40154, Indonesia
³ Department of Computer Science, IPB University, Bogor, 16680, Indonesia
⁴ Faculty of Computer and Mathematical Sciences, Universiti Teknologi Mara Cawangan Melaka Kampus Jasin Melaka, Melaka, 75450, Malaysia
⁵ Department of Computer Science, University of Swabi, Swabi, 23561, Pakistan

Lala Septem Riza
Roles: Conceptualization, Methodology, Supervision, Writing – Original Draft Preparation, Writing – Review & Editing

Afina Hadaina Yudianita
Roles: Data Curation, Software

Eki Nugraha
Roles: Project Administration, Resources, Supervision, Visualization

Lili Somantri
Roles: Data Curation, Methodology, Resources, Validation

Imas Sukaesih Sitanggang
Roles: Conceptualization, Methodology, Writing – Original Draft Preparation, Writing – Review & Editing

Khyrina Airin Fariza Abu Samah
Roles: Formal Analysis, Validation, Writing – Original Draft Preparation, Writing – Review & Editing

Shah Nazir
Roles: Software, Supervision, Writing – Original Draft Preparation, Writing – Review & Editing

Competing interests

No competing interests were disclosed.

Grant information

The author(s) declared that no grants were involved in supporting this work.

Article Versions (1)

version 1

Published: 21 Jun 2022, 11:682

https://doi.org/10.12688/f1000research.110608.1

Copyright

© 2022 Septem Riza L et al. This is an open access article distributed under the terms of the Creative Commons Attribution License, which permits unrestricted use, distribution, and reproduction in any medium, provided the original work is properly cited.

Download

Export To

metrics

	Views	Downloads
F1000Research	-	-
PubMed Central Data from PMC are received and updated monthly.	-	-

Citations

0

SEE MORE DETAILS

CITE

how to cite this article

Septem Riza L, Yudianita AH, Nugraha E et al. Remote sensing and machine learning for yield prediction of lowland paddy crops [version 1; peer review: 1 approved, 1 not approved]. F1000Research 2022, 11:682 (https://doi.org/10.12688/f1000research.110608.1)

NOTE: If applicable, it is important to ensure the information in square brackets after the title is included in all citations of this article.

track

receive updates on this article

Track an article to receive email alerts on any updates to this article.

Open Peer Review

Version 1

VERSION 1

PUBLISHED 21 Jun 2022

Views

5

Reviewer Report 02 Apr 2024

Attila Nagy, Faculty of Agricultural and Food Science and Environmental Management, University of Debrecen, Debrecen, Hungary

Not Approved

https://doi.org/10.5256/f1000research.122233.r253183

The manuscript describes the use of one type of ML for paddy crop yield prediction using Landsat 8. The topic has broad importance, but due to several issues and discrepancies I recommend to reject this manuscript.
My detailed reasons:
... Continue reading

The manuscript describes the use of one type of ML for paddy crop yield prediction using Landsat 8. The topic has broad importance, but due to several issues and discrepancies I recommend to reject this manuscript.
My detailed reasons:
Overall, it looks more a thesis than a scientific paper, sounds like a student book in some parts, especially in the introduction (e.g. first rows of the introduction. Linear regression itself is no ML method.
English has to be improved significantly, it is hard to read the text fluently
Lack of references throughout the text, and not using the original references (e.g. in the case of NDVI).
There is not a word about the aim, motivation of the study in the introduction.
There is no explanation why Landsat 8 (out of several potentials) was used.
There is no explanation why only one ML model (out of several potentials) was used, and why that specific one.
The method requires restructuring and rewriting in general. Study site should be the first chapter, then data, data collection, followed by method.
Listed several softwares, but not stating (or stating later) which one is used in data processing. But the used algorithms, GIS solutions are not adequately explained.
Figure 2 is not informative.
Interpretation of the data is not acceptable. Authors should discuss about the results (it is totally missing and inadequate) There are only set of tables, with no proper assessments. It is not enough to state “shown in figure x”.

Is the work clearly and accurately presented and does it cite the current literature?

No
Is the study design appropriate and is the work technically sound?

No
Are sufficient details of methods and analysis provided to allow replication by others?

Partly
If applicable, is the statistical analysis and its interpretation appropriate?

No
Are all the source data underlying the results available to ensure full reproducibility?

Yes
Are the conclusions drawn adequately supported by the results?

Partly

Competing Interests: No competing interests were disclosed.

Reviewer Expertise: remote sensing, GIS, yield prediction, water management

I confirm that I have read this submission and believe that I have an appropriate level of expertise to state that I do not consider it to be of an acceptable scientific standard, for reasons outlined above.

CITE

Report a concern

Respond or Comment

Views

13

Reviewer Report 01 Aug 2022

Daniel Peralta, Department of Information Technology, Ghent University– imec, Ghent, Belgium

Approved

https://doi.org/10.5256/f1000research.122233.r143635

The paper analyzes a dataset of satellite images to predict the yield of crop production. This research is valuable and sound. Furthermore, the dataset used has been published by the authors, which adds a lot of value to this research ... Continue reading

The paper analyzes a dataset of satellite images to predict the yield of crop production. This research is valuable and sound. Furthermore, the dataset used has been published by the authors, which adds a lot of value to this research . Therefore, I recommend to Approve this article.

I have a few comments about aspects that could be further clarified:

I miss a paragraph in the introduction that would summarize the contribution of this paper.
Further details about data pre-processing e.g. the data was resized and divided into subsets, but what size? How many subsets?
Include a table with the input features that were used.
How was the data split into training/test?
Include a table comparing the results of this paper with those in the literature.
There is one point in Figure 6 that appears to be badly predicted, while the rest of the dataset has very good predictions. I wonder if it would be possible to explain why?

Is the work clearly and accurately presented and does it cite the current literature?

Yes
Is the study design appropriate and is the work technically sound?

Yes
Are sufficient details of methods and analysis provided to allow replication by others?

Partly
If applicable, is the statistical analysis and its interpretation appropriate?

Yes
Are all the source data underlying the results available to ensure full reproducibility?

Yes
Are the conclusions drawn adequately supported by the results?

Yes

Competing Interests: No competing interests were disclosed.

Reviewer Expertise: Machine learning

I confirm that I have read this submission and believe that I have an appropriate level of expertise to confirm that it is of an acceptable scientific standard.

CITE

Report a concern

Respond or Comment

Comments on this article Comments (0)

Version 1

VERSION 1 PUBLISHED 21 Jun 2022

Open Peer Review

Reviewer Status

Reviewer Reports

	Invited Reviewers
	1	2
Version 1 21 Jun 22	read	read

Daniel Peralta, Ghent University– imec, Ghent, Belgium
Attila Nagy, University of Debrecen, Debrecen, Hungary

Comments on this article

All Comments(0)

Add a comment

Sign up for content alerts

Browse by related subjects

Back to all reports

Reviewer Report

5 Views

02 Apr 2024 | for Version 1

Attila Nagy, Faculty of Agricultural and Food Science and Environmental Management, University of Debrecen, Debrecen, Hungary

5 Views Cite this report Responses(0)

Not Approved

The manuscript describes the use of one type of ML for paddy crop yield prediction using Landsat 8. The topic has broad importance, but due to several issues and discrepancies I recommend to reject this manuscript.
My detailed reasons:
Overall, it looks more a thesis than a scientific paper, sounds like a student book in some parts, especially in the introduction (e.g. first rows of the introduction. Linear regression itself is no ML method.
English has to be improved significantly, it is hard to read the text fluently
Lack of references throughout the text, and not using the original references (e.g. in the case of NDVI).
There is not a word about the aim, motivation of the study in the introduction.
There is no explanation why Landsat 8 (out of several potentials) was used.
There is no explanation why only one ML model (out of several potentials) was used, and why that specific one.
The method requires restructuring and rewriting in general. Study site should be the first chapter, then data, data collection, followed by method.
Listed several softwares, but not stating (or stating later) which one is used in data processing. But the used algorithms, GIS solutions are not adequately explained.
Figure 2 is not informative.
Interpretation of the data is not acceptable. Authors should discuss about the results (it is totally missing and inadequate) There are only set of tables, with no proper assessments. It is not enough to state “shown in figure x”.

Is the work clearly and accurately presented and does it cite the current literature?

No
Is the study design appropriate and is the work technically sound?

No
Are sufficient details of methods and analysis provided to allow replication by others?

Partly
If applicable, is the statistical analysis and its interpretation appropriate?

No
Are all the source data underlying the results available to ensure full reproducibility?

Yes
Are the conclusions drawn adequately supported by the results?

Partly

Competing Interests

No competing interests were disclosed.

Reviewer Expertise

remote sensing, GIS, yield prediction, water management

I confirm that I have read this submission and believe that I have an appropriate level of expertise to state that I do not consider it to be of an acceptable scientific standard, for reasons outlined above.

Respond to this report

Responses (0)

Back to all reports

Reviewer Report

13 Views

01 Aug 2022 | for Version 1

Daniel Peralta, Department of Information Technology, Ghent University– imec, Ghent, Belgium

13 Views Cite this report Responses(0)

Approved

The paper analyzes a dataset of satellite images to predict the yield of crop production. This research is valuable and sound. Furthermore, the dataset used has been published by the authors, which adds a lot of value to this research . Therefore, I recommend to Approve this article.

I have a few comments about aspects that could be further clarified:

I miss a paragraph in the introduction that would summarize the contribution of this paper.
Further details about data pre-processing e.g. the data was resized and divided into subsets, but what size? How many subsets?
Include a table with the input features that were used.
How was the data split into training/test?
Include a table comparing the results of this paper with those in the literature.
There is one point in Figure 6 that appears to be badly predicted, while the rest of the dataset has very good predictions. I wonder if it would be possible to explain why?

Is the work clearly and accurately presented and does it cite the current literature?

Yes
Is the study design appropriate and is the work technically sound?

Yes
Are sufficient details of methods and analysis provided to allow replication by others?

Partly
If applicable, is the statistical analysis and its interpretation appropriate?

Yes
Are all the source data underlying the results available to ensure full reproducibility?

Yes
Are the conclusions drawn adequately supported by the results?

Yes

Competing Interests

No competing interests were disclosed.

Reviewer Expertise

Machine learning

I confirm that I have read this submission and believe that I have an appropriate level of expertise to confirm that it is of an acceptable scientific standard.

Respond to this report

Responses (0)

[1] Ahmad S, Kalra A, Stephen H: Estimating soil moisture using remote sensing data: A machine learning approach. Adv. Water Resour. 2010; 33(1): 69–80. Publisher Full Text

[2] Ariza AA: Machine Learning and Big Data Techniques for Satellite-Based Rice Phenology Monitoring. The University of Manchester;2019.

[3] Barnston AG: Correspondence among the correlation, RMSE, and Heidke forecast verification measures; refinement of the Heidke score. Weather Forecast. 1992; 7(4): 699–709. Publisher Full Text

[4] Bartlett DS, Whiting GJ, Hartman JM: Use of vegetation indices to estimate indices to estimate intercepted solar radiation and net carbon dioxide exchange of a grass canopy. Remote Sens. Environ. 1989; 30(2): 115–128. Publisher Full Text

[5] Bishop CM: Pattern recognition and machine learning. Springer;2006.

[6] BPS-Statistics Indonesia: Production of Food Crops. Jakarta:CV. Tapasuma Ratu Agung;2015.

[7] Cochran WG: Sampling techniques. John Wiley & Sons;2007.

[8] Du Plessis WP: Linear regression relationships between NDVI, vegetation and rainfall in Etosha National Park, Namibia. J. Arid Environ. 1999; 42(4): 235–260. Publisher Full Text

[9] Friedman JH: Greedy function approximation: a gradient boosting machine. Ann. Stat. 2001; 29: 1189–1232.

[10] Ikasari IH, Ayumi V, Fanany MI, et al.: Multiple regularizations deep learning for paddy growth stages classification from LANDSAT-8. International Conference on Advanced Computer Science and Information Systems (ICACSIS). 2016; 2016: 512–517.

[11] Irsan LM, Murti SH, Widayani P: Estimasi Produksi Jagung (Zea Mays L.) dengan Menggunakan Citra Sentinel 2A Di Sebagian Wilayah Kabupaten Jeneponto Provinsi Sulawesi Selatan. Jurnal Teknosains. 2019; 8(2): 93–104. Publisher Full Text

[12] James G, Witten D, Hastie T, et al.: An introduction to statistical learning. New York:springer;2013.

[13] Jensen JR: Introductory digital image processing: a remote sensing perspective. Prentice-Hall Inc.;1996.

[14] Loh WY: Classification and regression trees. Wiley Interdisciplinary Reviews: Data Mining and Knowledge Discovery;2011.

[15] Maas SJ: Using satellite data to improve model estimates of crop yield. Agron. J. 1988; 80(4): 655–662. Publisher Full Text

[16] Pantazi XE, Moshou D, Alexandridis T, et al.: Wheat yield prediction using machine learning and advanced sensing techniques. Comput. Electron. Agric. 2016; 121: 57–65. Publisher Full Text

[17] Petersen LK: Real-time prediction of crop yields from MODIS relative vegetation health: A continent-wide analysis of Africa. Remote Sens. 2018; 10(11): 1–31.

[18] Riza LS, Yudianita AH, Nugraha E, et al.: Remote sensing and machine learning for yield prediction of lowland paddy crops. Dataset. 2022a. Publisher Full Text

[19] Riza LS, Yudianita AH, Nugraha E, et al.: Remote sensing and machine learning for yield prediction of lowland paddy crops. Source Code.2022b. Publisher Full Text

[20] Sari DK, Ismullah IH, Sulasdi WN, et al.: Estimation of water consumption of lowland rice in tropical area based on heterogeneous cropping calendar using remote sensing technology. Procedia Environ. Sci. 2013; 17: 298–307. Publisher Full Text

[21] Shiu YS, Chuang YC: Yield Estimation of Paddy Rice Based on Satellite Imagery: Comparison of Global and Local Regression Models. Remote Sens. 2019; 11(2): 1–18.

[22] Tanre D, Holben BN, Kaufman YJ: Atmospheric correction algorithm for NOAA-AVHRR products: theory and application. IEEE Trans. Geosci. Remote Sens. 1992; 30(2): 231–248. Publisher Full Text

[23] Vergara BS: A farmer’s primer on growing rice. Int. Rice Res. Inst.;1992.

[24] Yunlong C, Smit B: Sustainability in agriculture: a general review. Agric. Ecosyst. Environ. 1994; 49(3): 299–307. Publisher Full Text

[25] Zhang K, Ge X, Shen P, et al.: Predicting rice grain yield based on dynamic changes in vegetation indexes during early to mid-growth stages. Remote Sens. 2019; 11(4): 1–24.

[26] Zheng A, Casari A: Feature engineering for machine learning: principles and techniques for data scientists. O’Reilly Media, Inc.;2018.

[27] Zill D, Wright WS, Cullen MR: Advanced engineering mathematics. Jones & Bartlett Learning;2011.

Remote sensing and machine learning for yield prediction of lowland paddy crops

Abstract

Keywords

Introduction

Methods

Figure 1. Research procedure.

Data collection using remote sensing

(1)

(2)

(3)

Data pre-processing

(4)

Gradient Boosting Regressor

Table 1. Gradient Boosting Regressor algorithm.

(5)

Table 2. Regression Tree algorithm.

Experimental study

Data collection

Figure 2. Map of Sub-district of Bandung: Ciparay, Majalaya, Paseh, Cikancung (Map data ©2020).

Figure 3. Removing pixels of clouds and shadows.

Table 3. The difference in reflectance value.

Figure 4. ENVI stratified random sampling results.

Figure 5. The difference in imagery data before and after NDVI calculation.

(6)

Table 4. Data input for the computational model.

Experimental scenarios

(7)

Results and discussion

Table 5. The program output of the computational model.

Figure 6. Scatter plot from observed and predicted paddy crop yield.

Table 6. Experimental results for testing the RMSE of the computational model.

Figure 7. Plot between estimators, learning rate, minimum sample slit, and maximum depth against RMSE.

Conclusions

Data availability

Underlying data

Software availability

References

Comments on this article Comments (0)

Open Peer Review

Comments on this article Comments (0)

Open Peer Review

Reviewer Status

Reviewer Reports

Comments on this article

Browse by related subjects

Competing Interests Policy

Stay Updated