Home Browse MRI data harmonization across sites using ComBat enhances classification...
ALL Metrics
-
Views
-
Downloads
Get PDF
Get XML
Cite
Export
Track
▬
✚
Case Study

MRI data harmonization across sites using ComBat enhances classification of meningioma and glioma brain-tumors in dogs: a case study

[version 1; peer review: 2 approved with reservations]
Debmalya Nandy
https://orcid.org/0000-0002-1640-6895
1,2, Xinyi Yang1, Xin Jin1, Lynn Griffin3, Katerina Kechris1,2*, Fuyong Xing1*
Debmalya Nandy
https://orcid.org/0000-0002-1640-6895
1,2, Xinyi Yang1, [...] Xin Jin1, Lynn Griffin3, Katerina Kechris1,2*, Fuyong Xing1*
* Equal contributors
PUBLISHED 07 Jul 2022
Author details Author details
OPEN PEER REVIEW
REVIEWER STATUS

Abstract

Background: Magnetic resonance imaging (MRI) in clinical patients is often evaluated for diagnostic purposes. However, to develop a disease classifier, imaging data can be “noisy”, as in being heterogeneous (e.g., obtained from multiple sites), having significant crossover between normal and pathological processes, being highly imbalanced for the outcome variable (i.e., unequal numbers of cases and controls), or due to a lack of accurate quantitative analysis tools that are transferable, easily usable, and accurate to generate the final image variables for machine learning analyses.

Methods: In this article, we demonstrate the effectiveness of ComBat harmonization of heterogeneous MRI data on dogs’ brains, collected across multiple sites, prior to using them in the random forest (RF) classifier to attempt to differentiate the meningioma and the glioma tumor-types. We consider three image variables generated from each of the brain scans and three clinical covariates – age, sex, and breedtype – for each subject. The scans are generated either at Colorado State University (CSU) or outside CSU. We compare the RF classifier performance in identifying the two tumor types, with and without preprocessing the data with ComBat site-specific harmonization.

Results: The post-ComBat disease classification accuracy measures – sensitivity, specificity, and total accuracy – indicate an overall significant edge in the RF performance compared to their without-ComBat counterparts across different scenarios. Moreover, incorporating both the image variables and the clinical covariates in the RF model results in the highest total accuracy.

Conclusions: Use of MRI data in combination with clinical covariates is more informative than using only clinical covariates in classifying meningioma and glioma brain-tumors in dogs. Moreover, as a preprocessing step for MRI data, we recommend adjusting for the site-specific variability using ComBat harmonization prior to performing downstream analyses, such as disease classification.

Keywords

Brain MRI, Canines, ComBat, Data harmonization, Multiple sites, Meningioma, Glioma, Random forest classification

Corresponding author: Debmalya Nandy
Competing interests: No competing interests were disclosed.
Grant information: Funds provided by the NIH/NCATS Colorado CTSA Grant Number UL1TR002535 supported DN, KK, and FX. These funds were distributed through the Translational Methods Pilot Awards 2020-2021 (Biostatistics / Bioinformatics category) offered by the Colorado Clinical and Translational Sciences Institute (CCTSI) at the University of Colorado Anschutz Medical Campus, Aurora, Colorado. DN and KK were also supported by NIH grant NCI U01CA235488. The contents of this research are the authors’ sole responsibility and do not necessarily represent official NIH views.
The funders had no role in study design, data collection and analysis, decision to publish, or preparation of the manuscript.
Copyright:  © 2022 Nandy D et al. This is an open access article distributed under the terms of the Creative Commons Attribution License, which permits unrestricted use, distribution, and reproduction in any medium, provided the original work is properly cited.
How to cite: Nandy D, Yang X, Jin X et al. MRI data harmonization across sites using ComBat enhances classification of meningioma and glioma brain-tumors in dogs: a case study [version 1; peer review: 2 approved with reservations]. F1000Research 2022, 11:759 (https://doi.org/10.12688/f1000research.117334.1) First published: 07 Jul 2022, 11:759 (https://doi.org/10.12688/f1000research.117334.1) Latest published: 07 Jul 2022, 11:759 (https://doi.org/10.12688/f1000research.117334.1)

Introduction

Magnetic resonance imaging (MRI), a powerful technology to detect abnormalities in human and animal organs,1–9 can be challenging for clinically differential diagnosis.10–14 In omics sciences, data normalization (henceforth, “harmonization”) is a crucial preprocessing step prior to downstream analyses,15–21 mitigating any spurious effects on the scientific conclusions incorporated due to undesired sources of variation, such as batch effects, intrinsic factors within the subjects, and scanning sites. Such harmonization is also essential for MRI data, as the signal intensities in these data are measured in arbitrary units that vary across study-visits and patients.22–25

In this study, we demonstrate the effectiveness of a batch-effect correction tool, ComBat,26 widely used in transcriptomics27,28 but also adopted for radiomics data,29,30 in adjusting for undesirable effects of multiple sites on MRI signal intensities (SIs). We chose ComBat due to its superior performance in removing site-specific unwanted variations from fractional anisotropy and mean diffusivity maps in diffusor tensor MRI.29 In their study, the authors considered only controls, used data that were from two “pure” sites, and implemented a sophisticated image-processing pipeline to generate the tissue outcome labels, which resulted in final measurements on the image variables (voxels) having dimensions in the order of 10,000’s. In our case, however, each subject is diseased (meningioma/glioma) and the data come from two “impure” sites, i.e., the “outside” site consists of multiple non-CSU sites, the data thus potentially being noisy due to heterogeneous MRI scanners/protocols used. Notably, such site-heterogeneity can be commonplace to ensure a sufficient sample size. Additionally, we use only three manually recorded image variables, available for all subjects across the sites. Via the downstream performance of the ensemble machine learning classification tool, random forest31–34 (RF), our study thus aims to demonstrate the utility of ComBat harmonization in a “non-ideal” yet practical scenario.

Methods

Study population and data generation

We use n = 244 subjects (dogs) in our study, belonging to one of the following four subpopulations: 1) glioma, scanned at the Colorado State University – Veterinary Teaching Hospital (CSU-VTH), n = 39; 2) glioma, obtained from a site outside CSU, n = 20; 3) meningioma scanned at the CSU-VTH, n = 106; and 4) meningioma, obtained from a site outside CSU, n = 79. Note that we treat the subjects as coming from only two sites -- CSU and “outside”. However, the “outside” site actually consists of 36 unique sites (Table 1).

Table 1. List of 36 unique sites that we combinedly call the “outside” site.

Advanced Veterinary Care
Animal Emergency & Speciality Center (AESC)
AMI Diamond Hill
The ANIC
Animal Imaging
Animal Neurology & MRI Center
Aspen Valley Hospital
Blackmore
Boulder Road Veterinary Specialists
Brain Med BRN
Canada West vet Specialists
Chicago Veterinary MRI
Chicago Veterinary Emergency & Specialty Center (CVESC)
The Ohio State University (OSU) Veterinary Hospital
Diagnostic Radiology Institute
Esaote S.p.A
GCVNN
University of Utah Imaging & Neurosciences Center (INC)
ISU Vet Teaching Hospital
Michigan State University (MSU)
PPER_S
Rocky Mountain Veterinary Neurology
Tacoma Vet Imaging
Texas A & M Veterinary Teaching Hospital
University of Missouri Veterinary Health Center
VCA Alameda East Veterinary Hospital
VCA North West (NW) Veterinary Specialists
VCA Veterinary Specialists of Northern Colorado (VSNC)
Veterinary Specialty Center Tucson
Veterinary Imaging, LLC
Veterinary Neurology
Veterinary Neurological Center (VNC) Phoenix
Veterinary Speciality Hospital of SanDiego (VSHSD)
Western Orthopedics and Sports Medicine
WestVet
Wheat Ridge Animal Hospital

DN and XY, the two “processors”, generate the data used in the final analyses. DN scans through the conclusion of each patient’s brain MRI diagnostic report stored in the CSU-VTH Philips IntelliSpace PACS (picture archiving and communication system) Radiology software (henceforth referred to as “PACS”) database, labeling the associated brain tumor-type as either “glioma” or “meningioma” based on the radiologist’s/principal interpreter’s conclusion including terms such as “likely”/“most likely”/“most consistent”, etc. Therefore, these binary tumor-type labels are not based on surgical, histopathological evidence and are used as the outcome variable in the downstream RF classification (see the “Statistical analysis” section). Since we do not have access to the diagnostic reports for the subjects from the “outside” site, we consider instead the corresponding ones from the CSU PACS database that are closest to their original exam dates.

For each patient, we only consider the transverse/axial section, T1-weighted, post-contrast scans (typically labeled as “Trans T1 +C”). The processors scan through all the slices within each patient’s respective DICOM file and select up to three representative slices in which the cancerous lesions are most prominently visible (i.e., highest contrast) by naked eye. Note that, among the 244 subjects, we settle with only one suitable slice for seven subjects and two for six subjects (Extended data: Table S1).47 Then, within each chosen slice, two circular regions of interest (ROIs) are drawn encompassing the densest parts visually examined, one each on the lesion and on the “normal” tissue, using the PACS software in-built “drawing” tool. Also note that, as “normal” tissue, we choose facial muscle for seven meningioma subjects and muscle of mastication for the rest (Extended data: Table S2).48 From each of these two ROIs, three statistics for the SIs are noted: mean, standard deviation, and the central point-value. See Figure 1 for an example.

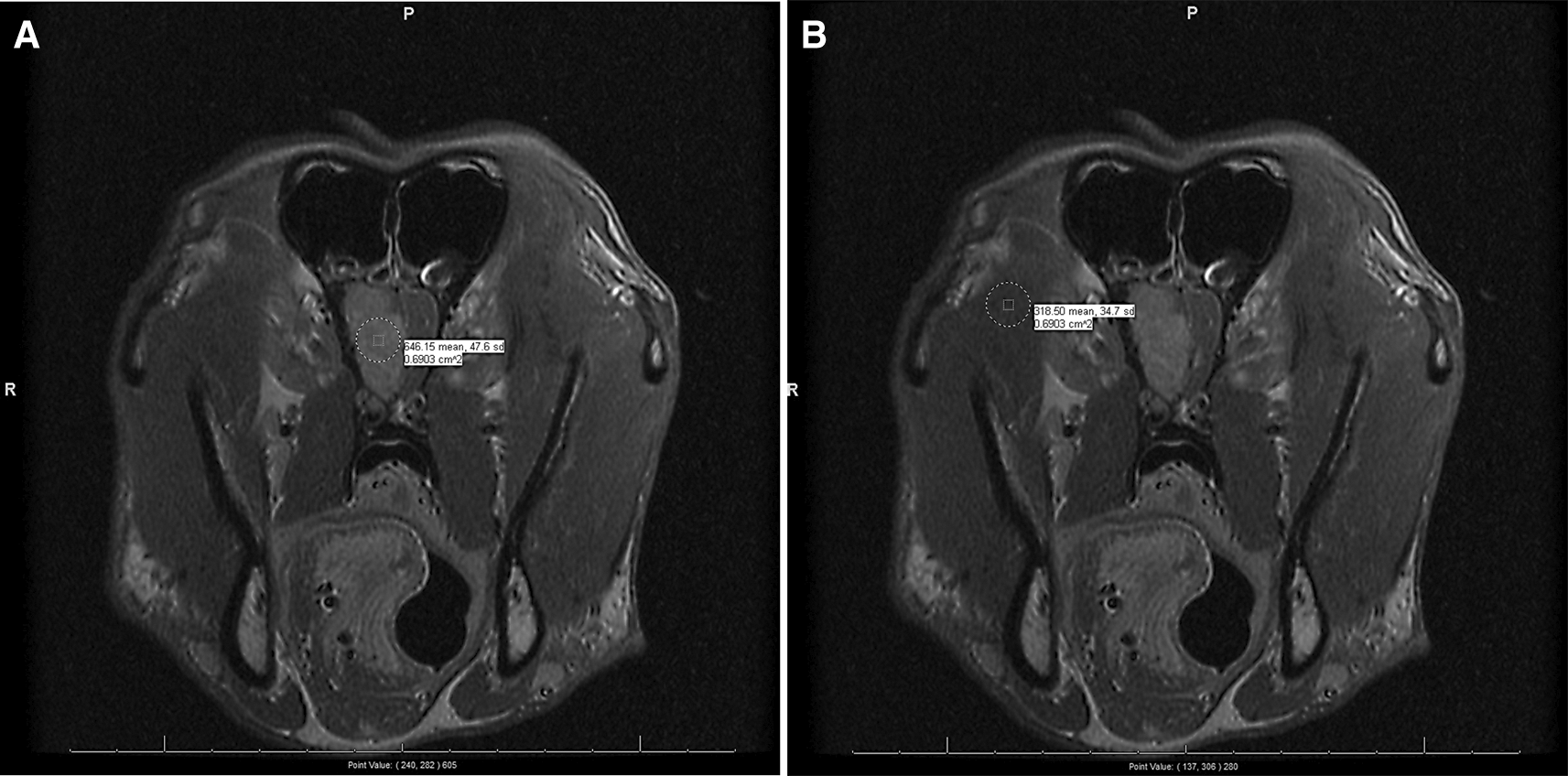
1324e15f-f42a-454b-9e8a-ce08b185d629_figure1.gif

Figure 1. Example of data generation from circular regions of interest (ROIs) – diseased lesion (A) and normal tissue (B) – drawn within the same slice (axial T1-weighted, post-contrast) using the PACS software tools.

This subject (dog) belongs to the “meningioma outside” subpopulation, i.e., its brain MRI is performed at a non-CSU site and diagnosed with meningioma tumor-type. The normal tissue chosen in (B) is muscle of mastication. The means and the standard deviations of the SIs within the two ROIs are indicated beside the circles drawn and the central point-value SIs are indicated at the bottom of the slides, outside of the parentheses.

Besides the three MRI variables, for each patient we also record the following covariates: three clinical – age (in months) at the time of MRI scan, sex (male, female, male castrated, female spade/spayed), and breedtype; six related to MRI scanner – repetition time (TR), echo time (TE), number of excitations (NEX), slice thickness (mm), frequency phase (X x Y), and field-of-view reconstruction (FOV recon; cm); and one technical – processor.

Note that, for the final analysis, we use both sex and breedtype as binary variables: sex (female/male) and breedtype (non-brachycephalic/brachycephalic). Data on frequency phase are used as two independent scanner covariates. Due to the presence of missing data, we eventually omit the “FOV Recon” scanner covariate from the final analysis. Thus, we have three binary covariates – sex, breedtype, and processor, coded as 0/1; the rest are treated as continuous variables. See Table 2 for a summary of all of the final variables used in our analyses.

Table 2. Summary of the three clinical covariates, one technical covariate, six magnetic resonance imaging (MRI) scanner covariates, and three MR curated image variables used in our statistical analyses.

The data are grouped based on the four subpopulations as indicated in the columns. Apart from the three binary covariates – sex, breedtype, and processor – that are coded as 0/1, the rest are treated as continuous variables; each cell-value indicates the range in the top line and the median (median absolute deviation in parentheses) in the bottom line.

Meningioma CSU (n = 106)Meningioma outside (n = 79)Glioma CSU (n = 39)Glioma outside (n = 20)
Clinical covariates
Age (in months)18-204
119.5 (32.617)		53-210
123 (28.169)		16-178
94 (56.339)		38-167
99 (26.687)
Sex (F/M)54/5240/3921/1814/6
Breed-Type (Brachycephalic/Non-brachycephalic)15/917/7215/2410/10
Technical covariate
Processor (DN/XY)54/5239/4020/199/11
MRI scanner covariates
TR300 – 1003
573 (84.757)		350 – 2100
600 (171.982)		400 – 859
566.664 (103.284)		250 – 1310
584.50 (148.26)
TE8-15.62
13.016 (2.988)		3.25 – 26
14.358 (5.400)		7.984-15.048
13 (3.011)		2.92 – 26
11.787 (3.950)
NEX1 – 4
3 (1.483)		1 – 4
2 (1.483)		1 – 4
3 (1.483)		1 – 4
2 (0.741)
Thickness (in mm)2 – 4
3 (1.483)		2 – 5
3 (0.445)		2 – 4
3 (1.483)		2.5 – 5
3 (0)
Frequency Phase 1192 – 320
288 (47.443)		192 – 512
256 (47.443)		256 – 320
288 (47.443)		192 – 512
256 (11.861)
Frequency Phase 2192 – 224
224 (0)		72 – 320
224 (47.443)		192 – 256
224 (0)		144 – 256
195.50 (52.632)
Image variables
μ (adj-mean [SI])0.846-3.138
1.932 (0.262)		1.220-2.953
2.007 (0.380)		1.170-2.704
1.591 (0.310)		1.076-2.860
1.743 (0.378)
μ (adj-SD [SI])0.748-6.832
2.328 (0.840)		0.850-7.497
1.652 (0.610)		0.870-6.912
2.234 (1.438)		0.704-3.882
1.504 (0.550)
μ (adj-cent [SI])0.914-3.220
1.975 (0.327)		1.119-3.436
2.041 (0.399)		1.144-2.739
1.582 (0.297)		1.159-2.985
1.722 (0.370)

Statistical analysis

Preprocessing of the data and final variables

For each of up to three selected slices corresponding to each sample, we first normalize the mean, the standard deviation, and the central point-value of the SIs within the diseased ROI by taking respective ratios to the normal ROI within that same slice (Figure 1). We call these three measures adj-mean (SI), adj-SD (SI), and adj-cent (SI), respectively. Next, for each sample, we compute the means of these adjusted measures across the selected slices. These three summarized measures, respectively referred to as μ (adj-mean (SI)), μ (adj-SD (SI)), and μ (adj-cent (SI)), are used as the final three image variables in the subsequent analyses (Figures S1 and S2).50–55 The intercorrelations among the three continuous image variables and the disease labels (0 = glioma, 1 = meningioma) are shown in Figure S3.56,57 We note that, for both CSU and outside sites μ (adj-mean (SI)) and μ (adj-cent (SI)) are maximally correlated with the disease labels and the correlations among the μ (adj-SD (SI)) and disease labels are negligible. Among the continuous covariates across both sites, while age (in months), μ (adj-mean (SI)), and μ (adj-cent (SI)) resemble a Gaussian distribution, those of others deviate greatly from it (data not shown).

Tumor classification

For the classification of meningioma and glioma brain-tumors (glioma treated as the “positive” class), we apply RF31–34 and evaluate classification performance based on sensitivity, specificity, and total accuracy, benchmarked via “lower” and “upper” bounds (Table 3). Using the same site for training and test sets, we expect better RF classification performance (upper bound) compared to when using different sites (lower bound).

Table 3. Choice of sites for the computation of the “lower” and the “upper” bounds of random forest (RF) classification metrics.

M: Meningioma, G: Glioma. For “lower” bound computations, we use all the samples within the outside site (n = 99, M/G = 79/20) to train the RF model, and randomly subsample n = 38 subjects from the CSU population, ensuring M/G = 19/19 representation, for the test set. For “upper” bound computations, we randomly subsample n = 79 meningioma CSU subjects from the remaining 87 for the training sets and use the same test sets as those used for the lower bounds.

Training set (n = 99, M/G = 79/20)Test set (n = 38, M/G = 19/19)
Lower boundOutsideCSU
Upper boundCSUCSU

For the “lower” bound calculations, we use all the samples within the outside site (n = 99, M/G = 79/20) to train the RF classifier, and randomly subsample n = 38 subjects from the CSU population, ensuring M/G = 19/19 representation, for the test set. Note that, the training set for the lower bound have 4:1 imbalanced class distribution in the outcome, which we adjust for using the Synthetic Minority Oversampling TEchnique (SMOTE),35 using arguments perc.over = 3 and perc.under = 1.45 within the smote() function. The size of a final training set is thus increased to n = 159 (M/G = 79/80). We use the original n = 79 meningioma samples and the n = 80 glioma cases that are generated using SMOTE. Within this training set, we tune the parameters of the RF classifier using 5-fold cross-validation repeated 25 times, and using all possible combinations of predictor variables in the model via the mtry argument in the train() function. For the “upper” bound calculations, we keep the identical test set compositions as in lower bound computations, and form the training set by randomly subsampling n = 79 “meningioma CSU” subjects from the remaining 87. We repeat this exercise of computing lower and upper bounds 75 times, each time with a different training-test split. Finally, we report the medians (and median absolute deviations) of the classification metrics across these 75 random samples; see Table 5 for an example.

Scenarios studied

We investigate the RF classifier performance at the lower and upper bounds for the following scenarios:

  • • [Case 0: one scenario] We examine the effectiveness of using three clinical covariates only in classifying the tumor types. No image, technical, and scanner covariates are used, and therefore, no ComBat harmonization is involved.

  • • [Case 1: four scenarios] We use the three image variables in ComBat. Besides, we either use the three clinical covariates or not in ComBat and in subsequent RF, thus giving rise to four scenarios (a – d; Table 4). We do not use any technical and scanner covariates in ComBat.

Table 4. Schematic table of four scenarios in Case 1 indicating use of the three clinical covariates in the ComBat harmonization and in the random forest (RF) classification model.

ComBat: 3 Clinical covariates
NoYes
Random Forest: 3 Clinical covariatesNoScenario aScenario b
YesScenario dScenario c

To assess the impact of ComBat harmonization on RF classification performance, we conduct nonparametric tests (Wilcoxon’s signed-rank paired one-sided tests with continuity correction) to examine whether a post-ComBat classification metric lower bound is: (1) significantly greater than that for its pre-ComBat counterpart, and (2) significantly lower than the corresponding upper bound (Table 5). Glioma is treated as the “positive” class in classification and, therefore, sensitivity measures the proportion of true glioma cases correctly identified, specificity measures the proportion of true meningioma cases correctly identified, and total accuracy measures the total proportion of true meningioma and glioma cases correctly identified.

Table 5. Random forest (RF) classification median (median absolute deviation in parentheses) sensitivity (“Sens”), specificity (“Spec”), and total accuracies (“Tot Acc”) corresponding to Case 1, scenarios a – d (Table 4).

The medians and median absolute deviations of the classifiation metrics are computed based on 75 repetitions of random training/test splits. Values closer to 1 indicate better performance. For post-ComBat lower bounds: 1) bold indicates significantly greater value (p-value < 0.05, Wilcoxon’s signed-rank paired one-sided test with continuity correction) compared to the corresponding pre-ComBat lower bound; 2) underline indicates corresponding upper bound is not significantly higher. Therefore, bold and underline together indicate the best results using ComBat.

Lower boundUpper bound
Pre-ComBatPost-ComBat Clinical covariates = NOPost-ComBat Clinical covariates = YESNo ComBat
SensSpecTot AccSensSpecTot AccSensSpecTot AccSensSpecTot Acc
Scenario aScenario b
RF Clinical covariates = NO0.474 (0.078)0.684 (0.156)0.605 (0.078)0.579 (0.078)0.737 (0.078)0.658 (0.078)0.632 (0.078)0.737 (0.078)0.658 (0.078)0.526 (0.078)0.789 (0.078)0.658 (0.039)
Scenario dScenario c
RF Clinical covariates = YES0.526 (0.078)0.789 (0.078)0.684 (0.078)0.526 (0.078)0.842 (0.078)0.684 (0.078)0.526 (0.078)0.842 (0.078)0.711 (0.039)0.632 (0.156)0.842 (0.078)0.711 (0.078)

Results

Below we discuss the full set of results for the scenarios in Cases 0 and 1.43–46,50–57 Note that, besides these two cases, we also examine the results of another case (Case 2) in which, alongside the three image variables, we include one technical covariate and six scanner covariates (see the “Study population and data generation” section) in the ComBat step. However, since the essence of these results is mostly similar to that of Case 1, we set them aside as “Extended data” (Extended data: Table S3).49

Using only three clinical covariates in the RF classification model (no ComBat harmonization involved)

Using only the clinical covariates of the subjects in the RF model (Case 0), the lower bound total accuracies are not significantly lower than those for upper bounds: both medians = 57.9%; p-value = 0.332 (Figure 2). The lower bounds of the sensitivity and the specificity measures are also not significantly lower than those for the upper bounds: p-values 0.133 and 0.884 respectively. Thus, the distributions of the age/sex/breed-type between meningioma/glioma subjects do not vary significantly across sites. For example, exact p-values corresponding to the Pearson’s chi-squared tests (with Yates’ continuity correction) on the two 2×2 contingency tables for sex and breed-type distributions across CSU and Outside sites are 0.762 and 0.604, respectively. Also, among all scenarios, RF achieves the lowest medians of total accuracy and sensitivity in this case, which indicates an overall poor predictive strength of using only clinical covariates in the RF model (Figures 2 and 3).

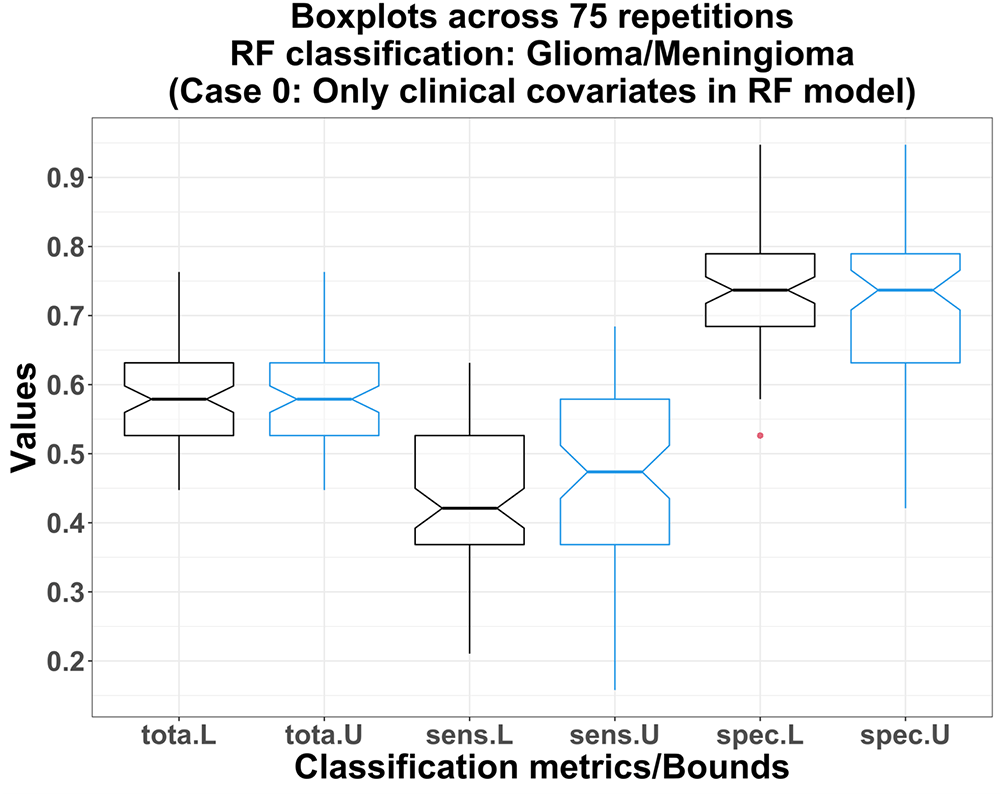
1324e15f-f42a-454b-9e8a-ce08b185d629_figure2.gif

Figure 2. Boxplots of random forest (RF) classification metrics corresponding to Case 0: “tota” = total accuracy, “sens” = sensitivity, and “spec” = specificity.

L, U: lower bound (black) and upper bound (blue) obtained from RF models using only three clinical covariates.

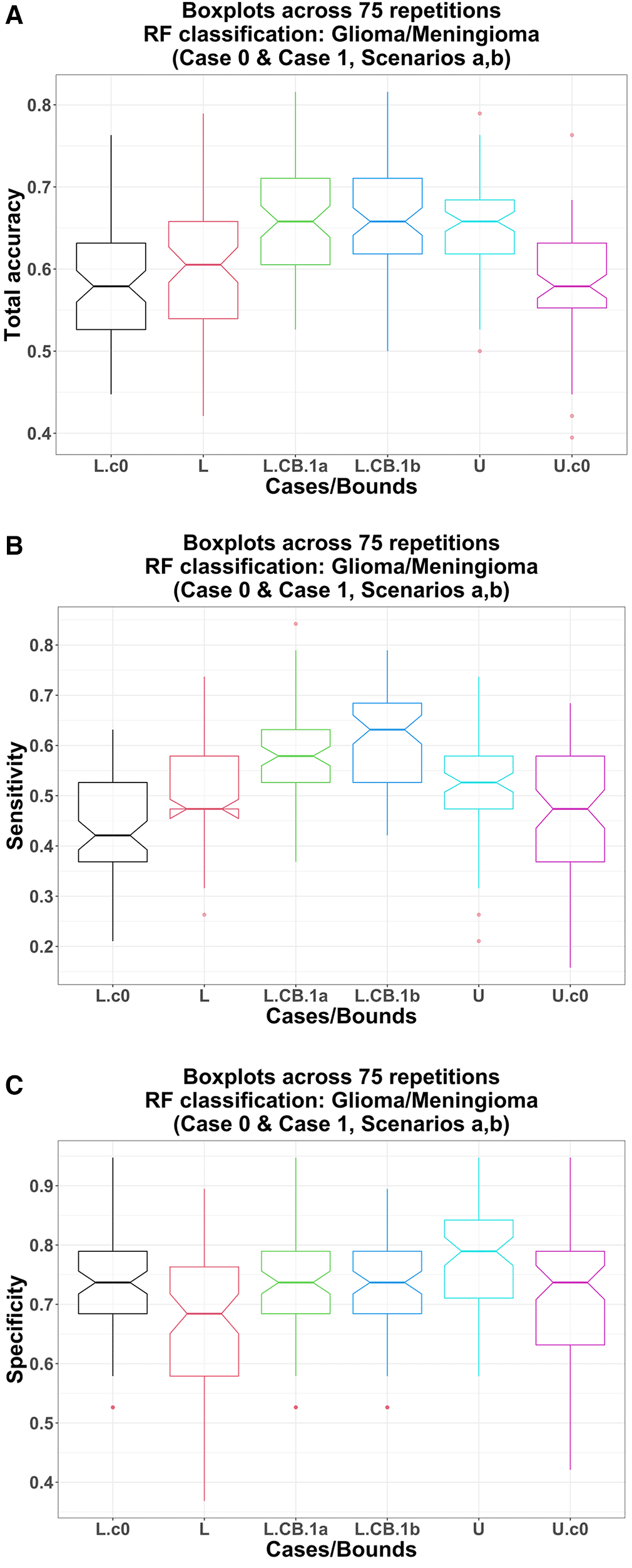
1324e15f-f42a-454b-9e8a-ce08b185d629_figure3.gif

Figure 3. Boxplots of random forest (RF) classification metrics: (A) total accuracy, (B) sensitivity, and (C) specificity, corresponding to Case 0 (“c0”) and Case 1 pre-ComBat and post-ComBat scenarios a (“1a”) and b (“1b”); see Table 4.

L.c0, U.c0: lower bound (black) and upper bound (magenta) obtained from RF models using only three clinical covariates; no ComBat harmonization involved; L, L.CB, U: pre-ComBat lower bound (red), post-ComBat lower bounds (green, 1a; blue, 1b), and upper bound (cyan) obtained from RF models using only three image variables.

Using only three image variables in the RF classification model

Pre-harmonization

Total accuracy: Using only the image variables in the RF model, the lower bound total accuracy (pre-ComBat) does not differ significantly from that using only three clinical covariates (Case 0): medians 60.5% vs. 57.9%; p-value = 0.270. However, the upper bound total accuracy is significantly higher than that in Case 0: medians 65.8% vs. 57.9%; p-value = 4.06 E-07 (Figure 3-A).

Sensitivity: Using only the image variables in the RF model, the lower bound sensitivity (pre-ComBat) is significantly higher than that using only three clinical covariates (Case 0): medians 47.4% vs. 42.1%; p-value = 9.68 E-04. Similarly, the upper bound sensitivity is also significantly higher than that in Case 0: medians 52.6% vs. 47.4%; p-value = 6.58 E-04 (Figure 3-B).

Specificity: Using only the image variables in the RF model, interestingly, the lower bound specificity (pre-ComBat) is significantly lower than that using only three clinical covariates (Case 0): medians 68.4% vs. 73.7%; p-value = 3.31 E-03. However, the upper bound specificity is significantly higher than that in Case 0: medians 78.9% vs. 73.7%; p-value = 5.67 E-05 (Figure 3-C).

Post-harmonization

Total accuracy: Using post-ComBat harmonization (scenarios a, b), the total accuracy lower bounds are significantly higher compared to their pre-ComBat and Case 0 counterparts. For example, post-ComBat with only three image variables (scenario a): (1) vs. pre-ComBat: medians 65.8% vs. 60.5%; p-value = 2.64 E-08 (Table 5, Figure 3-A) and (2) vs. using only the clinical covariates (Case 0): medians 65.8% vs. 57.9%; p-value = 4.98 E-08 (Figure 3-A).

Sensitivity: Using post-ComBat harmonization (scenarios a, b), the sensitivity lower bounds are significantly higher compared to their pre-ComBat and Case 0 counterparts. For example, post-ComBat with only three image variables (scenario a): (1) vs. pre-ComBat: medians 57.9% vs. 47.4%; p-value = 4.33 E-08 (Table 5 and Figure 3-B) and (2) vs. using only the clinical covariates (Case 0): medians 57.9% vs. 42.1%; p-value = 7.88 E-11 (Figure 3-B).

Specificity: Using post-ComBat harmonization (scenarios a, b), the specificity lower bounds are significantly higher compared to their pre-ComBat counterparts. For example, post-ComBat with only three image variables (scenario a) vs. pre-ComBat: medians 73.7% vs. 68.4%; p-value = 1.16 E-03 (Table 5 and Figure 3-C). Interestingly though, these post-ComBat lower bounds are not significantly higher than that using only the clinical covariates (Case 0): all three medians 73.7%; p-values (scenarios a and b vs. Case 0) = 0.347 and 0.359, respectively (Figure 3-C).

These results confirm that using just the three image variables in the RF model, ComBat harmonization enhances the RF classification performance (except for specificity) compared to that in pre-ComBat and when using only the clinical covariates.

Using three image variables and three clinical covariates in the RF classification model

Pre-harmonization

Total accuracy: Using the image variables and the clinical covariates in the RF model, the lower bound total accuracy (pre-ComBat) is significantly higher than that using only three image variables in RF: medians 68.4% vs. 60.5%; p-value = 7.48 E-09. Similarly, the upper bound total accuracy is also significantly higher: medians 71.1% vs. 65.8%; p-value = 3.64 E-07 (Table 5, Figure 4-A).

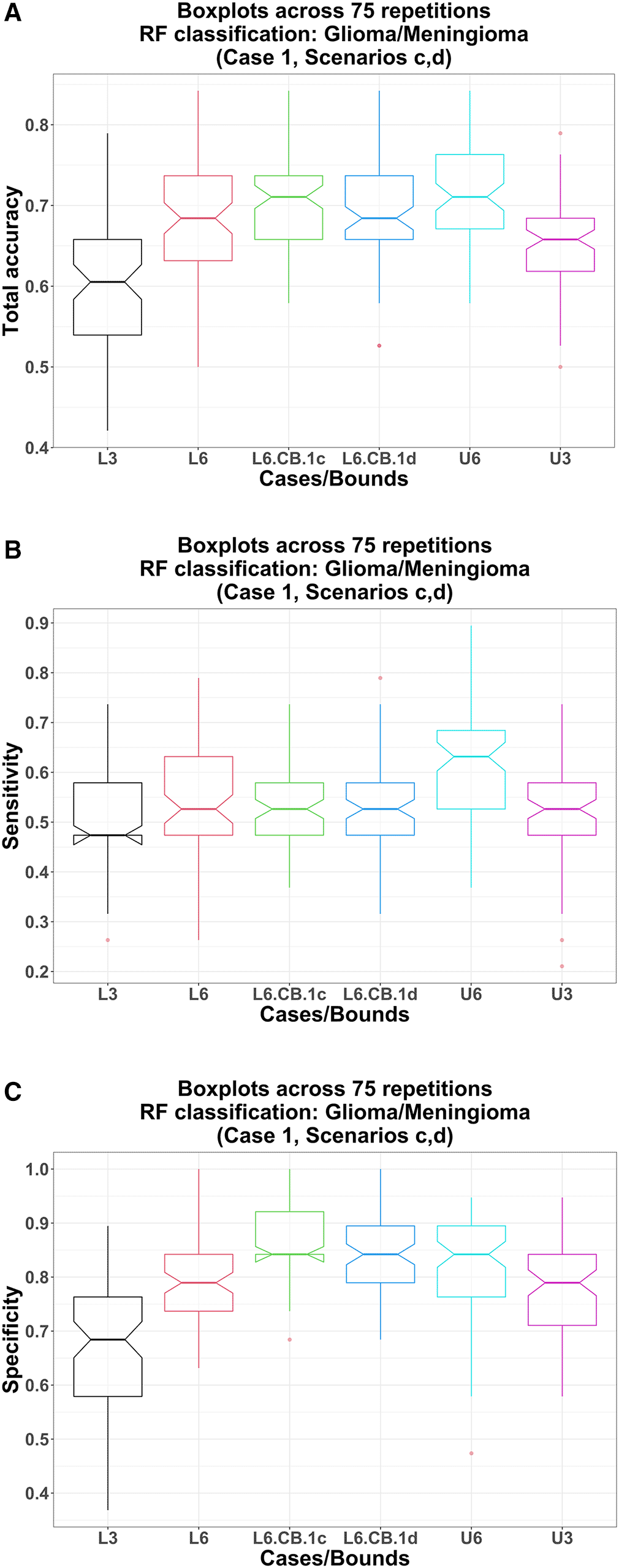
1324e15f-f42a-454b-9e8a-ce08b185d629_figure4.gif

Figure 4. Boxplots of random forest (RF) classification metrics: (A) total accuracy, (B) sensitivity, and (C) specificity, corresponding to Case 1 pre-ComBat (RF model using only the image variables and using both the image variables and the clinical covariates) and post-ComBat scenarios c (“1c”) and d (“1d”); see Table 4.

L3, U3: pre-ComBat lower bound (black) and upper bound (magenta) obtained from RF models using only three image variables; L6, L6.CB, U6: pre-ComBat lower bound (red), post-ComBat lower bounds (green, 1c; blue, 1d), and upper bound (cyan) obtained from RF models using three image variables and three clinical covariates.

Sensitivity: Using the image variables and the clinical covariates in the RF model, the lower bound sensitivity (pre-ComBat) is significantly higher than that using only three image variables in RF: medians 52.6% vs. 47.4%; p-value = 8.77 E-04. Similarly, the upper bound sensitivity is also significantly higher: medians 63.2% vs. 52.6%; p-value = 1.76 E-06 (Table 5, Figure 4-B).

Specificity: Using the image variables and the clinical covariates in the RF model, the lower bound specificity (pre-ComBat) is significantly higher than that using only three image variables in RF: medians 78.9% vs. 68.4%; p-value = 2.33 E-10. Similarly, the upper bound specificity is also significantly higher: medians 84.2% vs. 78.9%; p-value = 2.90 E-03 (Table 5, Figure 4-C).

Post-harmonization

Total accuracy: Using post-ComBat harmonization (scenarios c, d), the total accuracy lower bounds are significantly higher compared to their pre-ComBat and post-ComBat with only image variables in RF counterparts. For example, post-ComBat using three image variables and three clinical covariates (scenario c): (1) vs. pre-ComBat: medians 71.1% vs 68.4%; p-value = 8.80 E-04 and (2) vs. using only image variables in the RF model (scenario b): medians 71.1% vs. 65.8%; p-value = 1.84 E-04. Moreover, comparing between post-ComBat scenarios c and d: medians 71.1% vs 68.4%, p-value = 6.97 E-03 (Table 5, Figure 4-A).

Sensitivity: Using post-ComBat harmonization (scenarios c, d), the sensitivity lower bounds are not significantly higher compared to their pre-ComBat counterparts. For example, post-ComBat using three image variables and three clinical covariates (scenario c) vs. pre-ComBat: both medians 52.6%; p-value = 0.953 (Table 5, Figure 4-B). However, this post-ComBat sensitivity lower bound in scenario c is significantly higher than that using only image variables (scenario d): both medians 52.6%; p-value = 0.0177. Interestingly, post-ComBat sensitivity in scenario c (and d) deteriorates significantly compared to those when not using the clinical covariates in the RF model in scenario b (and scenario a): medians 52.6% vs. 63.2% (52.6% vs. 57.9%); p-value = 2.07 E-05 (6.93 E-05; Table 5).

Specificity: Using post-ComBat harmonization (scenarios c, d), the specificity lower bounds are again significantly higher compared to their pre-ComBat counterparts. For example, post-ComBat specificity lower bound using three image variables and three clinical covariates (scenario c) vs. pre-ComBat: medians 84.2% vs. 78.9%; p-value = 9.44 E-10 (Table 5, Figure 4-C). This post-ComBat specificity lower bound in scenario c is also significantly higher than that using only image variables (scenario d): both medians 84.2%; p-value = 2.69 E-03 (Table 5, Figure 4-C) and compared to those when not using the clinical covariates in the RF model (scenario b): medians 84.2% vs. 73.7%; p-value = 3.05 E-12 (Table 5).

These results confirm that using the image variables and clinical covariates together in the RF model, with or without ComBat harmonization, results in better RF classification performance (except for sensitivity) than using only the image variables. Furthermore, using the image variables as well as the clinical covariates in both ComBat harmonization and the RF model provides the highest total accuracy and specificity across all scenarios.

Discussion

In this case-study, we demonstrate the efficacy of MRI data harmonization using ComBat in enhancing the downstream RF classification performance. Utilizing the clinical covariates along with the image variables both in ComBat and RF (Case 1, scenario c) results in the highest total accuracy. When adjusting for the technical and scanner covariates in ComBat (Case 2), we only notice significant improvements in specificity (correct identification of true meningioma cases; scenarios c, d) compared to when not using them (Case 1; Tables 5 and S3). For both cases, RF achieves the highest specificity with the clinical covariates included in the model, irrespective of including them in ComBat (e.g., maximum median value for Case 1 is 84.2%, scenarios c, d; Table 5). Of all cases and scenarios, RF attains the highest sensitivity (correct identification of true glioma cases) when we include the clinical covariates in ComBat but not in the classification model in Case 1 (maximum median value is 63.2%, scenario b; Table 5).

In summary, we confirm the overall effectiveness of ComBat harmonization in adjusting for the site-specific variability even for our “non-ideal” as a practically feasible, noisy, low-dimensional, manually processed MRI dataset.

Limitations

The highest median total accuracy we obtain is 71.1% (Case 1, scenario c). However, among the 75 repetitions, we do notice up to a maximum of 84.2%. The challenge in attaining any higher total accuracy is mainly poised by low sensitivity, i.e., correct identification of true glioma cases, possibly due to: 1) insufficient predictors – we have used three available, manually generated image variables and three covariates for our analyses; 2) the possible minor mislabeling of the tumor-types or imprecise ROIs because the labels are based on the visual inspection and subjective, expert conclusion of the examining radiologists at the CSU-VTH and not confirmed via surgical histopathology, or because the ROIs in each scan-slice are drawn by two non-radiologists, and hence can possibly incur imprecise diseased/normal ROIs; 3) non-homogeneous sites – ComBat performance can potentially sharpen further with more homogeneous composition of the “outside” site; 4) an imbalanced outcome classes – although we address the severe class imbalance, a more balanced distribution in the original data may enhance RF performance36; and 5) the choice of class imbalance adjustor and classifier – one may choose a different class-imbalance adjustment, such as “over-sampling”,37 or a different classifier, such as logistic regression.38 However, our initial exploration suggests that the SMOTE-RF combination provides better results than those of some other alternatives (data not shown).

Data availability

Underlying data

Figshare: Image and Covariates Data on CSU-Meningioma Subjects. https://doi.org/10.6084/m9.figshare.19497671.v1.43

Figshare: Image and Covariates Data on CSU-Glioma Subjects. https://doi.org/10.6084/m9.figshare.19497683.v1.44

Figshare: Image and Covariates Data on Outside-Meningioma Subjects. https://doi.org/10.6084/m9.figshare.19497686.v1.45

Figshare: Image and Covariates Data on Outside-Glioma Subjects. https://doi.org/10.6084/m9.figshare.19497692.v1.46

Extended data

Figshare: Table S1: Number of Subjects with Less Than Three Image Slices Selected. https://doi.org/10.6084/m9.figshare.19497701.v3.47

Figshare: Table S2: Number of Subjects for Whom Facial Muscle is Used as Normal Tissue. https://doi.org/10.6084/m9.figshare.19497707.v2.48

Figshare: Table S3: Case 2 Full Results. https://doi.org/10.6084/m9.figshare.19498832.49

Figshare: Figure S1-A. https://doi.org/10.6084/m9.figshare.19498934.v1.50

This project contains the following extended data:

  • • New_CSUOut-MeninGlio_boxplot_final_meanSI.png (Boxplots of means [across up to three slices] of normalized mean of signal intensities measured on 244 subjects distributed across four subpopulations).

Figshare: Figure S1-B. https://doi.org/10.6084/m9.figshare.19498937.v1.51

This project contains the following extended data:

  • • New_CSUOut-MeninGlio_boxplot_final_sdSI.png (Boxplots of means [across up to three slices] of normalized standard deviation of signal intensities measured on 244 subjects distributed across four subpopulations).

Figshare: Figure S1-C. https://doi.org/10.6084/m9.figshare.19498940.v1.52

This project contains the following extended data:

  • • New_CSUOut-MeninGlio_boxplot_final_centSI.png (Boxplots of means [across up to three slices] of normalized central point-value of signal intensities measured on 244 subjects distributed across four subpopulations).

Figshare: Figure S2-A. https://doi.org/10.6084/m9.figshare.19498943.v1.53

This project contains the following extended data:

  • • Processors_allGroups_boxplot_final_meanSI.png (Boxplots of means [across up to three slices] of normalized mean of signal intensities measured by two processors [“XY” and “DN”] on 244 subjects distributed across four subpopulations: GC = “Glio-CSU”, MC = “Menin-CSU”, GO = “Glio-Out”, MO = “Menin-Out”).

Figshare: Figure S2-B. https://doi.org/10.6084/m9.figshare.19498946.v1.54

This project contains the following extended data:

  • • Processors_allGroups_boxplot_final_sdSI.png (Boxplots of means [across up to three slices] of normalized standard deviation of signal intensities measured by two processors [“XY” and “DN”] on 244 subjects distributed across four subpopulations: GC = “Glio-CSU”, MC = “Menin-CSU”, GO = “Glio-Out”, MO = “Menin-Out”).

Figshare: Figure S2-C. https://doi.org/10.6084/m9.figshare.19498949.v1.55

This project contains the following extended data:

  • • Processors_allGroups_boxplot_final_centSI.png (Boxplots of means [across up to three slices] of normalized central point-value of signal intensities measured by two processors [“XY” and “DN”] on 244 subjects distributed across four subpopulations: GC = “Glio-CSU”, MC = “Menin-CSU”, GO = “Glio-Out”, MO = “Menin-Out”).

Figshare: Figure S3-A. https://doi.org/10.6084/m9.figshare.19498952.v1.56

This project contains the following extended data:

  • • meninglioCSU_corr_final_3img_dislab.png (Pearson’s correlations among the three image variables and the disease labels [“dis.lab”; meningioma = 1, glioma = 0] within CSU subjects).

Figshare: Figure S3-B. https://doi.org/10.6084/m9.figshare.19498964.v1.57

This project contains the following extended data:

  • • meninglioOut_corr_final_3img_dislab.png (Pearson’s correlations among the three image variables and the disease labels [“dis.lab”; meningioma = 1, glioma = 0] within “Outside” subjects).

Data are available under the terms of the Creative Commons Zero “No rights reserved” data waiver (CC0 1.0 Public domain dedication).

Software availability

Source code available from: https://github.com/KechrisLab/ComBat_dogBrainMRI/tree/MRI

Archived source code at time of publication: https://doi.org/10.5281/zenodo.6632525.58

License: GNU General Public License v3.0

We generated all imaging data using the Philips IntelliSpace PACS Radiology software v4.4 (Philips Healthcare Informatics, Inc, 4100 East Third Avenue, Suite 101, Foster City, CA 94404, USA); license purchased by the CSU-VTH. We performed all of the statistical analyses and generate all of the figures using the R statistical software, version 4.1.0.39 We implemented the ComBat data harmonization using the neuroCombat R software package, which is publicly available in Jean-Philippe Fortin’s GitHub: https://bit.ly/fortin-ComBat-git, and the SMOTE imbalanced class adjustment using the smote() function within the performanceEstimation CRAN package.40 For the RF classifier, we use method = “rf” input argument in the train() function and compute the classification performance evaluation metrics using the confusionMatrix() function, both within the caret CRAN package.41,42 As a freely available alternative to PACS for a DICOM viewer and imaging data generator, we suggest Horos.

Ethical approval

Approval of VCS #2018-162 “Lymphotropic Nanoparticle Enhanced MRI for Diagnosis of Metastatic Disease in Canine Head and Neck Tumors” was obtained by Dr. Lynn Griffin on June 4, 2018, and subsequently on August 8, 2019 (for amendment to increase the approved animal numbers), from the Colorado State University Veterinary Teaching Hospital Clinical Review Board. The Clinical Review Board consists of 14 faculty members (as of August 8, 2019) from the College of Veterinary Medicine and Biomedical Sciences including a standing member of IACUC, the Hospital Director, and the Chair of the Department of Clinical Sciences.

Client consent was obtained from the respective owners of all dogs included in this study to use all obtained images and medical data for the purposes of research. Consent for publication is not applicable.

Acknowledgements

We are grateful to Kevin Kirsch of Colorado State University for providing us generous support on the setup of and access to CSU remote workstation and the Philips IntelliSpace PACS software and promptly clarifying our doubts as and when they appeared. We also thank Debashis Ghosh of Colorado School of Public Health and Natalie Serkova of University of Colorado School of Medicine for providing valuable suggestions and recommendations.

References

  • 1.  Chapter Two: Lifespan Communication Methodology. yesThe Handbook of Lifespan Communication. . DOI: 10.3726/978-1-4539-1367-3/14
  • 2.  Runge VM, et al.: Magnetic Resonance Imaging and Computed Tomography of the Brain-50 Years of Innovation, With a Focus on the Future. Investig. Radiol. 2015; 50: 551–556. PubMed Abstract | Publisher Full Text
  • 3.  Sutton BP, Ouyang C, Karampinos DC, et al.: Current trends and challenges in MRI acquisitions to investigate brain function. Int. J. Psychophysiol. 2009; 73: 33–42. PubMed Abstract | Publisher Full Text
  • 4.  Villanueva-Meyer JE, Mabray MC, Cha S: Current Clinical Brain Tumor Imaging. Neurosurgery. 2017; 81: 397–415. PubMed Abstract | Publisher Full Text
  • 5.  Henson JW, Ulmer S, Harris GJ: Brain tumor imaging in clinical trials. AJNR Am. J. Neuroradiol. 2008; 29: 419–424. PubMed Abstract | Publisher Full Text
  • 6.  Baig MA, Klein JP, Mechtler LL: Imaging of Brain Tumors. Continuum. 2016; 22: 1529–1552. PubMed Abstract
  • 7.  Di Ieva A, Le Reste P-J, Carsin-Nicol B, et al.: Diagnostic Value of Fractal Analysis for the Differentiation of Brain Tumors Using 3-Tesla Magnetic Resonance Susceptibility-Weighted Imaging. Neurosurgery. 2016; 79: 839–846. PubMed Abstract | Publisher Full Text
  • 8.  Jin Y, Peng H, Peng J: Brain Glioma Localization Diagnosis Based on Magnetic Resonance Imaging. World Neurosurg. 2021; 149: 325–332. PubMed Abstract | Publisher Full Text
  • 9.  Maclellan MJ, Ober CP, Feeney DA, et al.: Evaluation of diffusion-weighted magnetic resonance imaging at 3.0 Tesla for differentiation between intracranial neoplastic and noninfectious inflammatory lesions in dogs. J. Am. Vet. Med. Assoc. 2019; 255: 71–77. PubMed Abstract | Publisher Full Text
  • 10.  Zacharaki EI, et al.: Classification of brain tumor type and grade using MRI texture and shape in a machine learning scheme. Magn. Reson. Med. 2009; 62: 1609–1618. Publisher Full Text
  • 11.  Wang KY, Chen MM, Malayil Lincoln CM: Adult Primary Brain Neoplasm, Including 2016 World Health Organization Classification. Neuroimaging Clin. N. Am. 2021; 31: 121–138. PubMed Abstract | Publisher Full Text
  • 12.  Lin NU, et al.: Response assessment criteria for brain metastases: proposal from the RANO group. Lancet Oncol. 2015; 16: e270–e278. PubMed Abstract | Publisher Full Text
  • 13.  Lin NU, et al.: Challenges relating to solid tumour brain metastases in clinical trials, part 1: patient population, response, and progression. A report from the RANO group. Lancet Oncol. 2013; 14: e396–e406. PubMed Abstract | Publisher Full Text
  • 14.  Lin NU, et al.: Challenges relating to solid tumour brain metastases in clinical trials, part 2: neurocognitive, neurological, and quality-of-life outcomes. A report from the RANO group. Lancet Oncol. 2013; 14: e407–e416. Publisher Full Text
  • 15.  Ghandi M, Beer MA: Group normalization for genomic data. PLoS One. 2012; 7: e38695. PubMed Abstract | Publisher Full Text
  • 16.  Müller C, et al.: Removing Batch Effects from Longitudinal Gene Expression – Quantile Normalization Plus ComBat as Best Approach for Microarray Transcriptome Data. PLoS One. 2016; 11: e0156594. PubMed Abstract | Publisher Full Text
  • 17.  Sun Z, et al.: Batch effect correction for genome-wide methylation data with Illumina Infinium platform. BMC Med. Genet. 2011; 4: 84. PubMed Abstract | Publisher Full Text
  • 18.  Liu X, et al.: Normalization Methods for the Analysis of Unbalanced Transcriptome Data: A Review. Front. Bioeng. Biotechnol. 2019; 7. PubMed Abstract | Publisher Full Text
  • 19.  Misra BB: Data normalization strategies in metabolomics: Current challenges, approaches, and tools. Eur. J. Mass Spectrom. 2020; 26: 165–174. PubMed Abstract | Publisher Full Text
  • 20.  Cuevas-Delgado P, Dudzik D, Miguel V, et al.: Data-dependent normalization strategies for untargeted metabolomics—a case study. Anal. Bioanal. Chem. 2020; 412: 6391–6405. Publisher Full Text
  • 21.  Yang Q, et al.: NOREVA: enhanced normalization and evaluation of time-course and multi-class metabolomic data. Nucleic Acids Res. 2020; 48: W436–W448. PubMed Abstract | Publisher Full Text
  • 22.  Reinhold JC, Dewey BE, Carass A, et al.: Evaluating the Impact of Intensity Normalization on MR Image Synthesis. Proc. SPIE Int. Soc. Opt. Eng. 2019; 10949.
  • 23.  Shinohara RT, et al.: Statistical normalization techniques for magnetic resonance imaging. Neuroimage Clin. 2014; 6: 9–19. PubMed Abstract | Publisher Full Text
  • 24.  Carré A, et al.: Standardization of brain MR images across machines and protocols: bridging the gap for MRI-based radiomics. Sci. Rep. 2020; 10: 12340. PubMed Abstract | Publisher Full Text
  • 25.  Mirzaalian H, et al.: Multi-site harmonization of diffusion MRI data in a registration framework. Brain Imaging Behav. 2018; 12: 284–295. PubMed Abstract | Publisher Full Text
  • 26.  Johnson WE, Li C, Rabinovic A: Adjusting batch effects in microarray expression data using empirical Bayes methods. Biostatistics. 2007; 8: 118–127. Publisher Full Text
  • 27.  Conesa A, et al.: A survey of best practices for RNA-seq data analysis. Genome Biol. 2016; 17: 13. PubMed Abstract | Publisher Full Text
  • 28.  Guinney J, et al.: The consensus molecular subtypes of colorectal cancer. Nat. Med. 2015; 21: 1350–1356. Publisher Full Text
  • 29.  Fortin J-P, et al.: Harmonization of multi-site diffusion tensor imaging data. NeuroImage. 2017; 161: 149–170. Publisher Full Text
  • 30.  Fortin J-P, et al.: Harmonization of cortical thickness measurements across scanners and sites. NeuroImage. 2018; 167: 104–120. PubMed Abstract | Publisher Full Text
  • 31.  Liaw A, Matthew W: Classification and Regression by randomForest. R News. 2002; 2: 18–22.
  • 32.  Ho TK: Random decision forests. Proceedings of 3rd International Conference on Document Analysis and Recognition. Publisher Full Text
  • 33.  Ho TK: The random subspace method for constructing decision forests. IEEE Trans. Pattern Anal. Mach. Intell. 1998; 20: 832–844. Publisher Full Text
  • 34.  Hastie T, Tibshirani R, Friedman J: The Elements of Statistical Learning: Data Mining, Inference, and Prediction, Second Edition. Springer Science & Business Media;2009.
  • 35.  Chawla NV, Bowyer KW, Hall LO, et al.: SMOTE: Synthetic Minority Over-sampling Technique. J. Artif. Intell. Res. 2002; 16: 321–357. Publisher Full Text
  • 36.  Tharwat A: Classification assessment methods. Applied Computing and Informatics. 2021; 17: 168–192. Publisher Full Text
  • 37.  Yap BW, et al.: An Application of Oversampling, Undersampling, Bagging and Boosting in Handling Imbalanced Datasets. Lecture Notes in Electrical Engineering. 2014: 13–22. Publisher Full Text
  • 38.  Hosmer DW Jr, Lemeshow S, Sturdivant RX: Applied Logistic Regression. John Wiley & Sons;2013.
  • 39.  R Core Team: R: A Language and Environment for Statistical Computing. 2021.
  • 40.  Torgo L: An Infra-Structure for Performance Estimation and Experimental Comparison of Predictive Models in R. CoRR. 2014; abs/1412.0436.
  • 41.  Kuhn M: caret: Classification and Regression Training. 2021.
  • 42.  Irizarry RA: The caret package. Introduction to Data Science. 2019: 523–528. Publisher Full Text
  • 43.  Nandy D: Image and Covariates Data on CSU-Meningioma Subjects. figshare. [Dataset].2022. Publisher Full Text
  • 44.  Nandy D: Image and Covariates Data on CSU-Glioma Subjects. figshare. [Dataset].2022. Publisher Full Text
  • 45.  Nandy D: Image and Covariates Data on Outside-Meningioma Subjects. figshare. [Dataset].2022. Publisher Full Text
  • 46.  Nandy D: Image and Covariates Data on Outside-Glioma Subjects. figshare. [Dataset].2022. Publisher Full Text
  • 47.  Nandy D: Table S1: Number of Subjects with Less Than Three Image Slices Selected. figshare. [Extended data].2022. Publisher Full Text
  • 48.  Nandy D: Table S2: Number of Subjects for Whom Facial Muscle is Used as Normal Tissue. figshare. [Extended data].2022. Publisher Full Text
  • 49.  Nandy D: Table S3: Case 2 Full Results. figshare. [Extended data].2022. Publisher Full Text
  • 50.  Nandy D: Figure S1-A. figshare. [Extended data].2022. Publisher Full Text
  • 51.  Nandy D: Figure S1-B. figshare. [Extended data].2022. Publisher Full Text
  • 52.  Nandy D: Figure S1-C. figshare. [Extended data].2022. Publisher Full Text
  • 53.  Nandy D: Figure S2-A. figshare. [Extended data].2022. Publisher Full Text
  • 54.  Nandy D: Figure S2-B. figshare. [Extended data].2022. Publisher Full Text
  • 55.  Nandy D: Figure S2-C. figshare. [Extended data].2022. Publisher Full Text
  • 56.  Nandy D: Figure S3-A. figshare. [Extended data].2022. Publisher Full Text
  • 57.  Nandy D: Figure S3-B. figshare. [Extended data].2022. Publisher Full Text
  • 58.  Nandy D: KechrisLab/ComBat_dogBrainMRI: ComBat for Dog-Brain MRI Data Harmonization (MRI). Zenodo. [Software]. 2022. Publisher Full Text

Comments on this article Comments (0)

Version 1
VERSION 1 PUBLISHED 07 Jul 2022
Comment
Author details Author details
Competing interests
Grant information
Article Versions (1)
Copyright
Download
 
Export To
metrics
Views Downloads
F1000Research - -
PubMed Central
Data from PMC are received and updated monthly.
 - -
Citations
SEE MORE DETAILS
CITE
how to cite this article
Nandy D, Yang X, Jin X et al. MRI data harmonization across sites using ComBat enhances classification of meningioma and glioma brain-tumors in dogs: a case study [version 1; peer review: 2 approved with reservations]. F1000Research 2022, 11:759 (https://doi.org/10.12688/f1000research.117334.1)
NOTE: If applicable, it is important to ensure the information in square brackets after the title is included in all citations of this article.
track
receive updates on this article
Track an article to receive email alerts on any updates to this article.

Open Peer Review

Current Reviewer Status: ?
Key to Reviewer Statuses VIEW
ApprovedThe paper is scientifically sound in its current form and only minor, if any, improvements are suggested
Approved with reservations A number of small changes, sometimes more significant revisions are required to address specific details and improve the papers academic merit.
Not approvedFundamental flaws in the paper seriously undermine the findings and conclusions
Version 1
VERSION 1
PUBLISHED 07 Jul 2022
Views
5
Cite
Reviewer Report 28 May 2024
Abbe Crawford, Clinical Science and Services, Royal Veterinary College, North Mymms, Hatfield, UK 
Approved with Reservations
VIEWS 5
https://doi.org/10.5256/f1000research.129171.r276291
This study uses a tool to “normalise”/reduce heterogeneity in MRI data from multiple institutes prior to analysis with a Random Forest classifier.  As a proof of principle this study  provides useful information and has a valuable goal, but evaluation in ... Continue reading
CITE
CITE
HOW TO CITE THIS REPORT
Crawford A. Reviewer Report For: MRI data harmonization across sites using ComBat enhances classification of meningioma and glioma brain-tumors in dogs: a case study [version 1; peer review: 2 approved with reservations]. F1000Research 2022, 11:759 (https://doi.org/10.5256/f1000research.129171.r276291)
The direct URL for this report is:
https://f1000research.com/articles/11-759/v1#referee-response-276291
NOTE: it is important to ensure the information in square brackets after the title is included in all citations of this article.
Report a concern
Views
9
Cite
Reviewer Report 16 Oct 2023
Nick Jeffery, Department of Small Animal Clinical Sciences, Texas A&M University, College Station, TX, USA 
Approved with Reservations
VIEWS 9
https://doi.org/10.5256/f1000research.129171.r207729
General comments

It is an interesting and important idea to apply data normalization to veterinary MR images, so as to be able to accumulate data from many sources. This manuscript does achieve a demonstration of this process ... Continue reading
CITE
CITE
HOW TO CITE THIS REPORT
Jeffery N. Reviewer Report For: MRI data harmonization across sites using ComBat enhances classification of meningioma and glioma brain-tumors in dogs: a case study [version 1; peer review: 2 approved with reservations]. F1000Research 2022, 11:759 (https://doi.org/10.5256/f1000research.129171.r207729)
The direct URL for this report is:
https://f1000research.com/articles/11-759/v1#referee-response-207729
NOTE: it is important to ensure the information in square brackets after the title is included in all citations of this article.
Report a concern

Comments on this article Comments (0)

Version 1
VERSION 1 PUBLISHED 07 Jul 2022
Comment

Open Peer Review

Reviewer Status

Alongside their report, reviewers assign a status to the article:

Approved
The paper is scientifically sound in its current form and only minor, if any, improvements are suggested
Approved with reservations
A number of small changes, sometimes more significant revisions are required to address specific details and improve the papers academic merit.
Not approved
Fundamental flaws in the paper seriously undermine the findings and conclusions

Reviewer Reports

Invited Reviewers
1 2
Version 1
07 Jul 22 		read read
  1. Nick Jeffery, Texas A&M University, College Station, TX, USA
  2. Abbe Crawford, Clinical Science and Services, Royal Veterinary College, North Mymms, Hatfield, UK

Comments on this article

All Comments(0)

Add a comment
Sign up for content alerts

Browse by related subjects

    keyboard_arrow_left Back to all reports
    keyboard_arrow_left Back to all reports
    Alongside their report, reviewers assign a status to the article:
    Approved - the paper is scientifically sound in its current form and only minor, if any, improvements are suggested
    Approved with reservations - A number of small changes, sometimes more significant revisions are required to address specific details and improve the papers academic merit.
    Not approved - fundamental flaws in the paper seriously undermine the findings and conclusions
    Sign In
    If you've forgotten your password, please enter your email address below and we'll send you instructions on how to reset your password.

    The email address should be the one you originally registered with F1000.
    Email address not valid, please try again

    You registered with F1000 via Google, so we cannot reset your password.

    To sign in, please click here.

    If you still need help with your Google account password, please click here.

    You registered with F1000 via Facebook, so we cannot reset your password.

    To sign in, please click here.

    If you still need help with your Facebook account password, please click here.

    Code not correct, please try again
    Email us for further assistance.
    Server error, please try again.