Keywords
exploratory data analysis, visualization, heatmap, consensus clustering, networks, obesity
exploratory data analysis, visualization, heatmap, consensus clustering, networks, obesity
Visualization methods relying on a combination of statistical and interactive techniques are becoming necessary for researchers to efficiently perform quality assessments and glean insights from their data.1 Networks are data structures that are particularly benefiting from such advancements. A network consists of a set of nodes, also called vertices, that are connected to one-another by edges. Networks allow scientists to model and investigate the complexities of structure of the systems they are researching, offering more insight than analyzing their individual components.2 They have been used to model and study various phenomena, from Internet traffic to food webs.
Network data are commonly visualized by node-link diagrams (Figure 1), which consist of plotting the nodes and edges. Variables pertaining to the nodes and edges are also often included in the node-link diagram; the node’s colour may represent a categorical variable, or the thickness of an edge may capture an aspect of the relationship between connected nodes. While this makes it easy to discern some topological qualities of the network,3 such as the number of edges a node shares with the other nodes (the node’s degree) or the interconnectedness of the nodes (the network’s density), this visualization’s utility is limited by the size of the network and the number of variables used to describe its various parts.

The visualization to the left helps observers gain a sense of the structure of the network by emphasizing the most central node. On the other hand, the depiction on the right permits a quick assessment of the network’s connectedness.
As the number of vertices, edges and variables characterizing each increase, the visualization becomes cluttered and difficult to interpret. These issues are compounded when attempting to perform exploratory data analysis (EDA) on network data with multiple components, i.e. a network in which there are groups of nodes that do not share any edges, or many disjoint ego networks, such as personal social networks. Ego networks consist of a central node (the ego) that is implicitly connected to all other nodes in the network (the alters), which can share edges among themselves. Due to the constraint on the size of the node-link diagrams and the amount of information that can be presented, comparisons between many ego networks at once is difficult.
An alternative representation technique that may be more appropriate for such network data is the heatmap. A heatmap is a graphical representation of a two-dimensional matrix4 and is a versatile tool for illustrating multivariate data, as demonstrated with the mtcars dataset (https://stat.ethz.ch/R-manual/R-devel/library/datasets/html/mtcars.html) in Figure 2. Since heatmaps can display large quantities of information in a single figure, it is an ideal tool for presenting multiple ego networks and their variables. Heatmaps rely on two key elements to convey information clearly and efficiently: hierarchical clustering and an appropriate color palette.4 These two elements maximize the pattern recognition potential within the visualization. Additionally, when presented in the appropriate medium (i.e. in a dynamic report), heatmaps can be turned into interactive visualizations using software like heatmaply.5 The interactivity of the heatmap can improve its legibility, and therefore its use as an EDA tool.
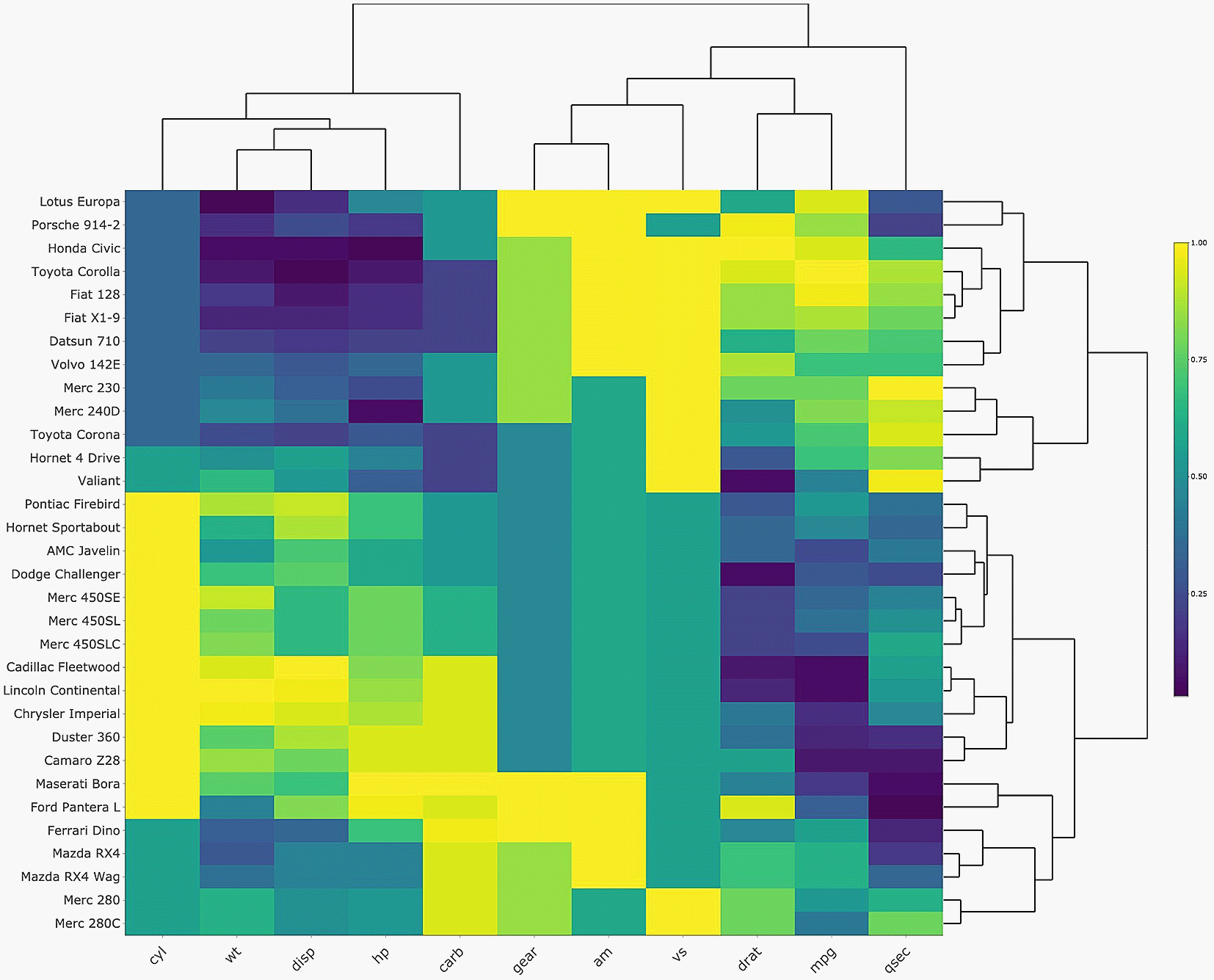
Notice the cluster of compact cars in the top left corner, clearly grouped together by their relatively small engines and weight (top left, dark green-blue rectangles), and by their superior efficiency (top right, light green and yellow rectangles). The most performant cars are grouped together near the center of the y-axis, clustered together due to their larger engines and reduced efficiency.
Although heatmaps offer an efficient way to depict large quantities of data,4 it can be difficult to identify the meaningful patterns in the visualization. Thus, heatmaps’ pattern recognition potential can be augmented by using methods that identify stable patterns under data perturbations. Consensus clustering6 is one such nonparametric method for assessing the stability and stability of patterns identified in a heatmap. More information on consensus clustering is provided in the methods section.
The objective of this analysis was to determine whether the combination of heatmaps and consensus clustering is an effective tool for representing ego network data. Heatmaps are particularly convenient for depicting high-dimensional data, though, to the best of our knowledge, their application in this setting has yet to be studied. Data from a pilot study investigating the influence of adolescent’s social network on their obesity outcomes were used to evaluate this methodology’s performance.
This methodology relies on the application of agglomerative hierarchical clustering (referred throughout the paper as hierarchical clustering), heatmaps and consensus clustering to ego network data. The following paragraphs provide details on their individual implementations, and how they are used in tandem to produce a novel EDA method for this data structure.
Hierarchical clustering is an unsupervised learning method that aims to find clusters of similar items in a data set, where items can be either variables or observations. Numerous methods exist to quantify the similarity among items, like Euclidean distance, correlation or Manhattan distance. At the start of the procedure, each item forms its cluster. These items are then paired with others based on their similarities, forming new clusters.7 Between cluster similarity can be measured by various methods, though the most popular are the single, average and complete linkage methods. For information on these linkage methods, see James et al.7 With each iteration of the algorithm, the number of elements in each cluster increases, the number of individual clusters decreases and, generally, the average similarity among the items in each cluster decreases. The process ends when only a single cluster remains. The result of this procedure is often depicted by a tree, known as a dendrogram (Figures 2 and 3), illustrated on the axes of the heatmaps. The dendrogram can be used to infer the cluster membership of each item by “cutting” the tree at various levels of similarity, which corresponds to the height of the tree. Cutting the tree at higher levels of similarity will produce granular clusters (i.e. many small groups of similar items), whereas lower levels of similarity will produce larger clusters composed of more dissimilar items. Thus, the dendrogram can be cut at the lowest height that produces an a priori specified number of clusters. Selecting the appropriate number of clusters in the data is a challenging task, though, as we will see later, consensus clustering can help in making a reasonable choice. As is customary with methods relying on some notion of distance, the data subjected to hierarchical clustering are often normalized.
An aggregation step must take place prior to the application of hierarchical clustering due to the structure of ego network data. Ego networks can be described by variables pertaining to the ego, the alters, the edges between alters and to the network itself, such as its structural characteristics. Unfortunately, there is no obvious way to apply hierarchical clustering to multilevel data, where the higher level comprises the ego and network variables, and the lower level is composed of the alter and edge variables. To transform the data into a format compatible with hierarchical clustering, the alter and edge variables within each network are summarized by some measure of center. The choice of statistic, such as the mean, median or mode, will depend on the characteristics of the variables being summarized. Once this step is accomplished, the transformed ego network data is ready to undergo hierarchical clustering; each observation consists of an ego network described by variables relating to the ego, the network and measures of centers of the alter and edge variables.
The dendrograms produced by subjecting the transformed ego network data to hierarchical clustering are then used to create the heatmap of the data. The heatmap is comprised of networks across rows and of variables across columns. The cells in the heatmap, represent normalized variable values and, should be colored using a divergent color palette to promote pattern recognition.4
Consensus clustering is then used to identify the number of clusters among the transformed network data’s variables and to quantify the stability of the clusters nonparametrically.6 Consensus clustering repeatedly applies multiple user-defined clustering methods to random subsets of the data and evaluates the frequency with which variables are clustered together over repeated samples. Given a set of n items subjected to some clustering method, the consensus matrix, X, is an n×n matrix where Xi,j corresponds to the fraction of iterations of the algorithm for which items i and j were members of the same cluster. A value near one signifies that items i and j are often clustered together, whereas a value near zero implies that they are rarely grouped together. The resulting consensus matrix is then summarized using the cluster consensus and item consensus statistics,6 which measure within-cluster stability and item-wise stability, respectively.6 Consensus clustering thus identifies stable clusters in the data, further increasing the interpretability of the heatmaps by pinpointing the more meaningful patterns in the visualization. Additionally, Monti et al. use the empirical cumulative density function (ECDF) of the entries in the consensus matrix to identify the appropriate number of stable clusters in the data.6 For example, if hierarchical clustering is used to group the items, consensus clustering can be repeatedly applied such that each iteration of hierarchical clustering specifies a different number of clusters. The ECDFs produced by applying consensus clustering for a range of the number of clusters can then be compared. When the items in the data are perfectly clustered under repetition, i.e. the consensus matrix entries consist of zeros and ones, the ECDF of the consensus clustering is a step function with a single step between zero and one.6 As the clustering becomes less exact, the step transforms into a smooth, monotonically non-decreasing line.6 Sharp changes in the ECDF curves of consecutive consensus clustering procedures can help distinguish the number of stable clusters in the data.6
Consensus clustering is therefore applied to the variables of the transformed ego network data in order to identify the meaningful associations depicted in the heatmap, and to quantify the strengths of these relationships. Hierarchical clustering is used to cluster the random subsets of the data in each iteration. Depending on the goals of the EDA, consensus clustering may also be applied to the ego networks to identify clusters of similar networks.
An open-source R implementation8 (R Project for Statistical Computing, RRID:SCR_001905) of this methodology was developed and is available in the neatmaps package (v2.1.1).9 This software, along with relevant documentation and examples, is available on CRAN and on GitHub at github.com/PhilBoileau/neatmaps.10 This package makes heavy use of two packages: heatmaply (v.1.3.0)5 was used to produce the heatmaps, and ConcencusClusterPlus (v1.36.0)11 was used to implement consensus clustering.
In the realm of public health, social networks have been used to model the spread of non-infectious diseases like obesity.12–14 However, as the obesity epidemic currently affects over a third of the world’s population,15 the development of novel methods to better understand and potentially mitigate its spread are needed. While targeting multiple behaviours like diet and physical activity to reduce body weight is recognized as an effective strategy,16 their benefits may be further augmented through social network-based programs. Though evidence suggests that these interventions may positively impact obesity outcomes, further investigation is required.14 Thus, we applied our novel EDA approach to an ego network data set collected by a pilot study exploring the relationship between adolescent social networks and obesity outcomes.
Data were obtained from a pilot study on the influence of adolescent’s social networks on health outcomes (n = 46) from the Quebec Adipose and Lifestyle Investigation in Youth (QUALITY) cohort (n = 630). QUALITY is an ongoing longitudinal study which investigates the natural history of obesity using a sample of at-risk Caucasian youths in Quebec.17 At-risk youth were defined as children with at least one overweight parent (i.e. body mass index (BMI) over 30 kg/m2 or waist circumference over 102 cm for men and 88 cm for women, based on self-reported height, weight and waist circumference)17 at the start of the study. The pilot aimed to evaluate the data collection processes and to identify patterns that could lead to new research questions for the full-scale study. A complete case analysis of the pilot data was performed (n = 35 ego networks). QUALITY obtained ethics approval (#MP-21-2005-79, 2040) from the Centre Hospitalier Universitaire Sainte-Justine. Parents signed consent forms and children provided assent. This secondary data analysis was approved by the Concordia Research Ethics Board (#300116369).
Each of the pilot study’s participants (egos) was asked to list up to ten people (alters) with whom they felt comfortable discussing important personal matters in the past year. The egos then reported their alters’ demographic characteristics (age, sex), location of alter’s residence with respect to the ego’s, perceived body type, health behaviours (frequency of physical activity, frequency of eating healthy (e.g. avoiding junk food), frequency of undertaking a diet for weight loss, frequency of Internet use), and support (frequency of encouraging ego to be physically active and frequency of performing at least 30 minutes of physical activity with the alter). Egos also reported on relationship characteristics (duration, closeness, importance, frequency of contact, types of interaction [i.e. face to face, phone, email, SMS, social media, video call and other]), location of interactions (home, work, school, hobby, media and other). The mean of these alter variables was computed within each ego network. Each participant was also asked to answer the questions pertaining to their own frequency of physical activity, of healthy eating, of dieting for weight loss, and of Internet use using questionnaires published in the literature18,19 as described in our previous work.20
Other ego data included height and weight (measured via stadiometer and electronic weight scale, respectively),17 fat mass percentage (measured using dual-energy absorptiometry) and body mass index z-scores in accordance with the WHO growth curves accounting for age and sex.21
Each participant (ego) has an associated network consisting of alters (nodes) based on ego-reported friendship or family ties (edges). Based on these ties, certain topological characteristics of each ego network were computed. These metrics were the ego degree, mean alter degree, density, constraint,22 hierarchy,23 effective size and efficiency.24 Additionally, the networks’ homophily indices25 were calculated for each of the following variables: age, gender, perceived body type and frequency of physical activity, of eating healthy, dieting for weight loss and of Internet use.
The EDA method was applied to the QUALITY ego network data using Euclidean distance as a similarity metric and the average linkage method for between-cluster similarity of the network clusters and the variable clusters. The data were normalized by rescaling each variable to have a range between 0 and 1. For variable vector v of length n with values vi for i = 1, …, n, each value vi was standardized as follows:
Thus, hierarchically clustering the variables produces clusters that contain positively linearly-associated variables.26 The consensus clustering step of the method was performed with predefined numbers of clusters ranging from 2 to 10. For each cluster count, 1000 repetitions of the clustering algorithm were performed on a random subset of 80% of the ego networks, as recommended in the documentation of ConcencusClusterPlus (v1.36.0).11
The heatmap of the QUALITY ego network data is shown in Figure 3, efficiently visualizing the 35 ego networks and their 41 variables. Figure 4 illustrates the consensus matrices for the consensus cluster iterations of three, four and five clusters. The ECDFs produced by the consensus clustering are illustrated in Figure 5. The clusters, their contents (along with each items’ item consensus statistic) and the clusters consensus statistic are also presented (Table 1).
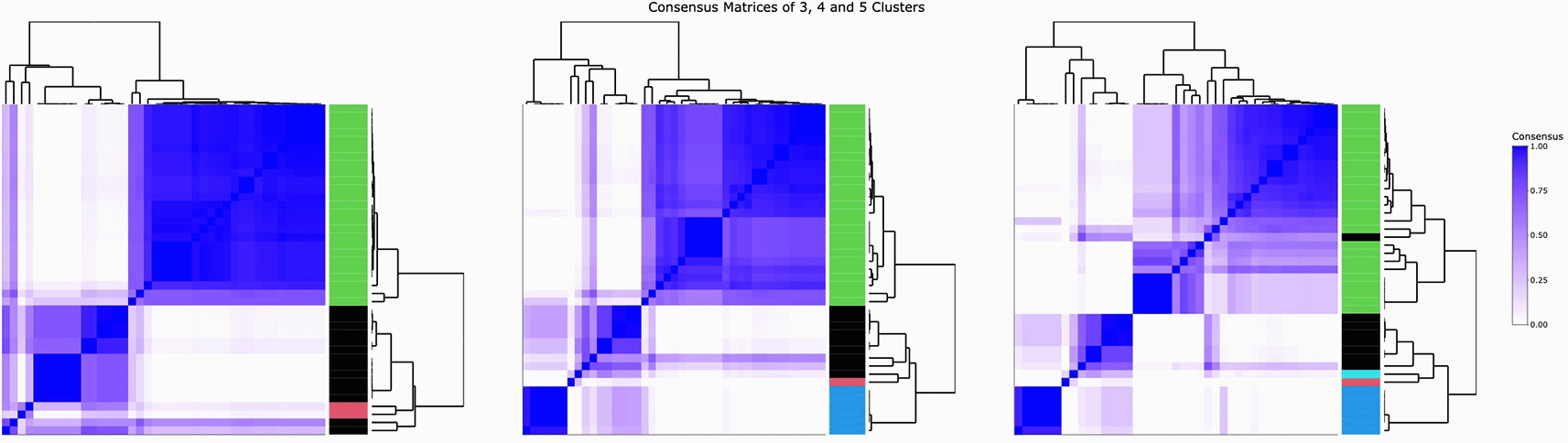
This evidence suggests that four relatively stable clusters are identified in the data.
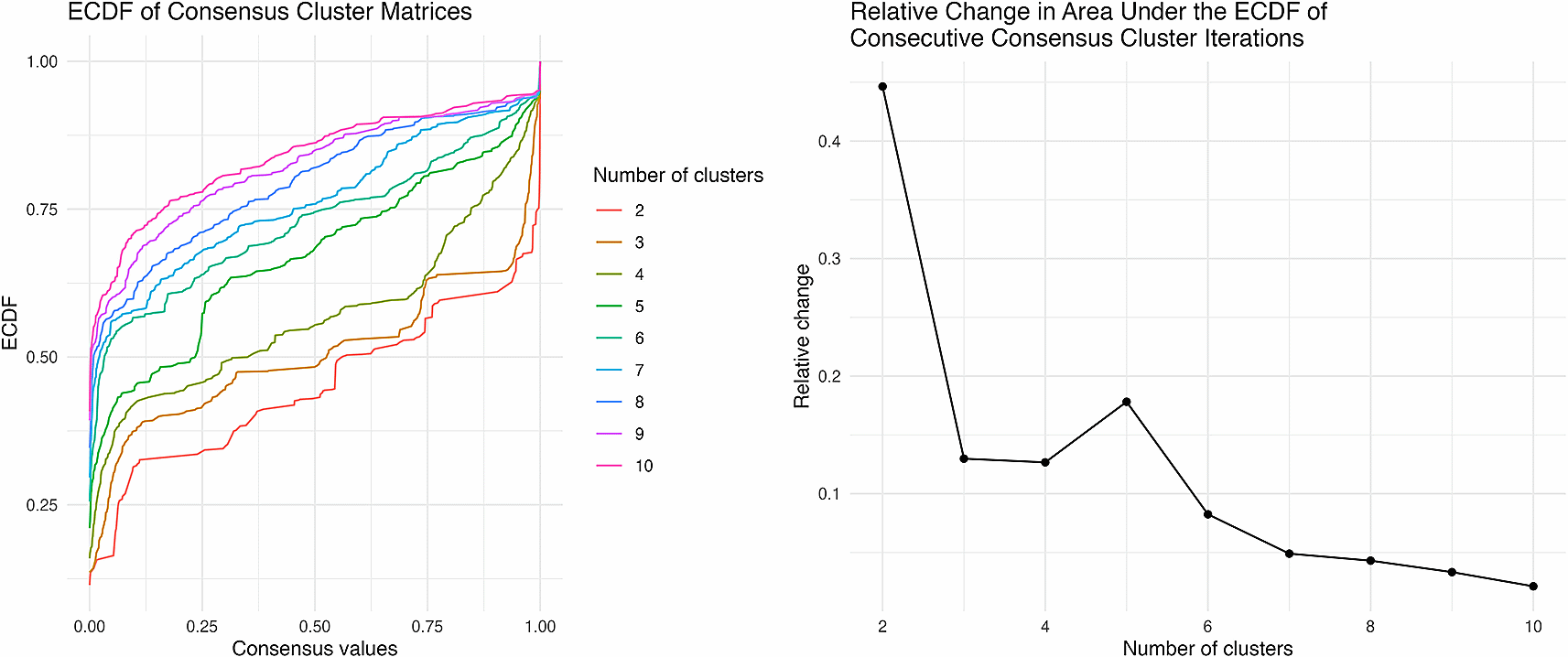
There is a clear change in the distributions of the consensus matrices for four and five clusters, suggesting that there are four clusters among the ego network data variables.
The ECDFs and the consensus matrix suggest that the data contains four stable clusters. Cluster one consists of variables relating to the interconnectivity of the ego networks and the locations of interaction, cluster two consists of the ego’s age, cluster three contains lifestyle variables and obesity outcomes and cluster four is comprised of variables measuring alter importance and diet.
Of the four clusters identified during consensus clustering, cluster four is the most stable with a cluster consensus of m(5) = 0.988 (Table 1). This cluster corresponds to the six rightmost columns in the heatmap (Figure 3). This grouping suggests a positive linear relationship between the dieting habits of the egos and those of their alters, and the mean strength of the relationships in the egos’ networks. However, upon closer inspection of the heatmap, this result may be due to the lack of variability in the distributions of the variables composing the cluster.
Cluster three is also a stable cluster given its cluster consensus value of m(3) = 0.873 (Table 1). This cluster is positioned to the left of the solid blue streak in the center of the heatmap and provides evidence of a positive association between certain lifestyle behaviours and the obesity measures for both the egos and their alters. These results indicate that the frequency of physical activity of the egos and the alters, the frequency with which the alters encourage the ego to be physically active, the homophily of frequency of physical activity, the ego’s and alter’s frequency of healthy eating and the homophily of frequency of healthy eating in the network are potentially related to the egos’ adiposity measures such as BMI z-score, fat mass percentage and perceived body type.
Cluster two consists solely of the ego’s age since it was not found to be strongly associated with any of the other variables. This result is unsurprising given that all egos are approximately the same age. Such a homogeneous variable does not provide any meaningful information, and consensus clustering successfully recognized this.
Although the results of cluster two, three and four are stable, the first cluster identified using cluster consensus is not. Cluster one has a moderate cluster consensus statistic (m(1) = 0.708), implying that its variables are less strongly associated. This cluster is positioned in between the solid blue and red columns on the right side of the heatmap (Figure 3).
Lastly, streaks of a single solid color (blue or red) in Figure 3 indicate that variables comprising these columns exhibit little variability. These variables are, in blue, the ego’s frequency of Internet use for entertainment, number of components, hierarchy, effective size, and, in red, density, proportion of ego interaction with alters at home, and the ego’s dieting frequency.
The heatmap allows analysts to quickly identify potential associations among networks and variables, study the distributions of the variables and assess the quality of the data.
The results of the consensus clustering augment the interpretation of the heatmap by pinpointing the most meaningful clusters in the data and quantifying the associations among the clusters’ variables. The third and fourth clusters identified by this method capture previously studied relationships among the obesity outcomes and lifestyle behaviours of the egos and alters, and the ego network structure. De la Haye et al. previously observed an association between dietary intake and friendship ties among males in school-based social networks.27 Similarly, the fourth cluster identified via consensus clustering identified an association between friendship ties and dieting habits. The third cluster is consistent with the literature on childhood obesity outcomes and lifestyle behaviours within social networks.22–25 Additionally, this method recognized that ego age could not be meaningfully grouped with any other variable, which would not be apparent if the analysis relied solely on hierarchical clustering. The heatmap also permitted the efficient identification of variables which exhibit little variation, indicating to the study investigators that questions associated with these variables should be modified to capture more discerning information on the measures of interest.
Although these results are encouraging, there are some limitations associated with using heatmaps and consensus clustering to explore ego network data. First, this EDA process requires that the data have no missing values, a rare occurrence in empirical research. Although judicious pre-processing and data imputation can remedy the situation, further work must be done to assess the sensitivity of this technique to missingness. Secondly, though consensus clustering can evaluate the quality of the hierarchical clustering, its results are data dependent. Its results should only be taken seriously when the data are a representative sample of the population of interest. Additionally, the data was scaled such that the variables were hierarchically clustered based on the strengths of their linear associations. Other data normalization methods could be used so that the hierarchical clustering targets the non-linear relationships among variables.
We demonstrate that, when applied to ego network data, the combination of heatmaps and consensus clustering successfully identified a number of important relationships that are consistent with literature on social networks and childhood obesity. These results may motivate further research in this field. This was accomplished without the need for substantial expertise using network analysis software; only a few functions from the neatmaps R package (v.2.1.1) were required to perform this analysis. Replication in other ego network data sets is warranted in order to further validate this methodology.
These data were collected by the QUALITY research team, in a small subset of the cohort (35 participants out of the original 630 participants). Data are not provided in an online repository due to ethical considerations regarding confidentiality/privacy concerns for study participants. Data can be made available upon reasonable request sent to the manuscript authors or the QUALITY research team (www.etudequalitystudy.ca).
Software available from: https://github.com/PhilBoileau/neatmaps, https://CRAN.R-project.org/package=neatmaps
Source code available from: https://github.com/PhilBoileau/neatmaps
Archived source code at time of publication: https://doi.org/10.5281/zenodo.645038610
License: MIT
PB, LP and LK conceived the method. TB and MH furnished the data. PB implemented the method, processed the data and performed analyses. LP, LK and TB supervised the work. PB wrote the manuscript with input from all authors. All authors provided critical feedback on the method, analyses and manuscript. All authors read the final version of the manuscript and approved it.
Dr. Marie Lambert (July 1952 – February 2012), a pediatric geneticist and researcher, initiated the QUALITY cohort. Her leadership and devotion to QUALITY will always be remembered and appreciated. Finally, we are grateful to all the families participating in the QUALITY cohort.
Portions of this research were presented at the Quebec Society for lipid, nutrition and metabolism scientific meeting (Magog-Orford, Quebec, February 7–9, 2018), the 5th annual PERFORM Centre conference (Montreal, Quebec, May 17, 2018) and the Canadian Statistics Student Conference (Montreal, Quebec, June 2, 2018). Thank you to all attendees who provided valuable feedback.
| Views | Downloads | |
|---|---|---|
| F1000Research | - | - |
|
PubMed Central
Data from PMC are received and updated monthly.
|
- | - |
Is the rationale for developing the new method (or application) clearly explained?
Partly
Is the description of the method technically sound?
Partly
Are sufficient details provided to allow replication of the method development and its use by others?
Yes
If any results are presented, are all the source data underlying the results available to ensure full reproducibility?
No source data required
Are the conclusions about the method and its performance adequately supported by the findings presented in the article?
Partly
Competing Interests: No competing interests were disclosed.
Reviewer Expertise: Data Visualization, Visual Analytics, Population Count Data Analysis, Geospatial Data Analysis, Analysis of Visualizations, Machine Learning/Deep Learning.
Is the rationale for developing the new method (or application) clearly explained?
Yes
Is the description of the method technically sound?
Yes
Are sufficient details provided to allow replication of the method development and its use by others?
Partly
If any results are presented, are all the source data underlying the results available to ensure full reproducibility?
Partly
Are the conclusions about the method and its performance adequately supported by the findings presented in the article?
Yes
Competing Interests: No competing interests were disclosed.
Reviewer Expertise: infectious disease dynamics, drug resistance, networks, evolutionary dynamics
Alongside their report, reviewers assign a status to the article:
| Invited Reviewers | ||
|---|---|---|
| 1 | 2 | |
|
Version 1 11 Jul 22 |
read | read |
Provide sufficient details of any financial or non-financial competing interests to enable users to assess whether your comments might lead a reasonable person to question your impartiality. Consider the following examples, but note that this is not an exhaustive list:
Sign up for content alerts and receive a weekly or monthly email with all newly published articles
Already registered? Sign in
The email address should be the one you originally registered with F1000.
You registered with F1000 via Google, so we cannot reset your password.
To sign in, please click here.
If you still need help with your Google account password, please click here.
You registered with F1000 via Facebook, so we cannot reset your password.
To sign in, please click here.
If you still need help with your Facebook account password, please click here.
If your email address is registered with us, we will email you instructions to reset your password.
If you think you should have received this email but it has not arrived, please check your spam filters and/or contact for further assistance.
Comments on this article Comments (0)