Estimating the sample size of sham-controlled randomized controlled trials using existing evidence

George C.M. Siontis; Adriani Nikolakopoulou; Romy Sweda; Dimitris Mavridis; Georgia Salanti

doi:10.12688/f1000research.108554.1

Home Browse Estimating the sample size of sham-controlled randomized controlled...

ALL Metrics

Views

Downloads

Get PDF

Get XML

Export

▬

✚

Method Article

Estimating the sample size of sham-controlled randomized controlled trials using existing evidence

[version 1; peer review: 2 approved with reservations]

George C.M. Siontis ¹, Adriani Nikolakopoulou², Romy Sweda¹, Dimitris Mavridis³, Georgia Salanti⁴

George C.M. Siontis ¹, Adriani Nikolakopoulou², [...] Romy Sweda¹, Dimitris Mavridis³, Georgia Salanti⁴

PUBLISHED 24 Jan 2022

Author details Author details

¹ Department of Cardiology, University Hospital of Bern, Bern, Switzerland
² Institute of Medical Biometry and Statistics, University of Freiburg, Freiburg, Germany
³ Department of Primary Education, University of Ioannina, Ioannina, Greece
⁴ Institute of Social and Preventive Medicine (ISPM), University of Bern, Bern, Switzerland

George C.M. Siontis
Roles: Conceptualization, Data Curation, Formal Analysis, Investigation, Methodology, Visualization, Writing – Original Draft Preparation, Writing – Review & Editing

Adriani Nikolakopoulou
Roles: Conceptualization, Data Curation, Formal Analysis, Investigation, Methodology, Visualization, Writing – Original Draft Preparation, Writing – Review & Editing

Romy Sweda
Roles: Data Curation

Dimitris Mavridis
Roles: Conceptualization, Formal Analysis, Supervision, Writing – Review & Editing

Georgia Salanti
Roles: Conceptualization, Formal Analysis, Methodology, Supervision, Visualization, Writing – Original Draft Preparation, Writing – Review & Editing

OPEN PEER REVIEW

REVIEWER STATUS

Abstract

Background: In randomized controlled trials (RCTs), the power is often ‘reverse engineered’ based on the number of participants that can realistically be achieved. An attractive alternative is planning a new trial conditional on the available evidence; a design of particular interest in RCTs that use a sham control arm (sham-RCTs).
Methods: We explore the design of sham-RCTs, the role of sequential meta-analysis and conditional planning in a systematic review of renal sympathetic denervation for patients with arterial hypertension. The main efficacy endpoint was mean change in 24-hour systolic blood pressure. We performed sequential meta-analysis to identify the time point where the null hypothesis would be rejected in a prospective scenario. Evidence-based conditional sample size calculations were performed based on fixed-effect meta-analysis.
Results: In total, six sham-RCTs (981 participants) were identified. The first RCT was considerably larger (535 participants) than those subsequently published (median sample size of 80). All trial sample sizes were calculated assuming an unrealistically large intervention effect which resulted in low power when each study is considered as a stand-alone experiment. Sequential meta-analysis provided firm evidence against the null hypothesis with the synthesis of the first four trials (755 patients, cumulative mean difference -2.75 (95%CI -4.93 to -0.58) favoring the active intervention)). Conditional planning resulted in much larger sample sizes compared to those in the original trials, due to overoptimistic expected effects made by the investigators in individual trials, and potentially a time-effect association.
Conclusions: Sequential meta-analysis of sham-RCTs can reach conclusive findings earlier and hence avoid exposing patients to sham-related risks. Conditional planning of new sham-RCTs poses important challenges as many surgical/minimally invasive procedures improve over time, the intervention effect is expected to increase in new studies and this violates the underlying assumptions. Unless this is accounted for, conditional planning will not improve the design of sham-RCTs.

Keywords

meta-analysis, sequential methods, power calculation, renal sympathetic denervation

Corresponding author: George C.M. Siontis

Competing interests: No competing interests were disclosed.

Grant information: This work was supported by project funding (Grant No. 179158) from the Swiss National Science Foundation (SNSF). AN is supported by a Swiss National Science Foundation (SNSF) personal fellowship (P400PM_186723).

Copyright: © 2022 Siontis GCM et al. This is an open access article distributed under the terms of the Creative Commons Attribution License, which permits unrestricted use, distribution, and reproduction in any medium, provided the original work is properly cited.

How to cite: Siontis GCM, Nikolakopoulou A, Sweda R et al. Estimating the sample size of sham-controlled randomized controlled trials using existing evidence [version 1; peer review: 2 approved with reservations]. F1000Research 2022, 11:85 (https://doi.org/10.12688/f1000research.108554.1) First published: 24 Jan 2022, 11:85 (https://doi.org/10.12688/f1000research.108554.1) Latest published: 07 Nov 2022, 11:85 (https://doi.org/10.12688/f1000research.108554.2)

Introduction

A central decision when designing a randomized-control trial (RCT) is the number of patients that should be enrolled. RCTs including too few participants have been characterized as having limited clinical value and being unethical.¹ However, conducting adequately powered trials often presents practical difficulties and investigators sometimes end up performing ‘reverse engineering’ in their sample size calculations.² Instead of defining the treatment effect that is expected in the particular setting, which along with other parameters will result in the sample size needed, the ‘expected’ treatment effect is derived by the available-based usually on practical and economic considerations-sample size. This practice may result to unrealistically large treatment effects to justify the small number of participants to be enrolled.

Designing a new trial using the existing evidence in the form of meta-analysis has several advantages.²^–⁵ Meta-analysis provides more powerful and precise effect estimates over individual trials which is an important advantage when the necessary means for conducting a large trial of adequate power are not available. Conditional planning of a new trial means that the calculations for the required sample size are not based on the power of the trial as stand-alone experiment but on the power of the resulting meta-analysis of the available evidence. The concept of conditional planning builds upon and combines ideas of meta-analysis and living systematic reviews,⁶^,⁷ which are continuously updated as new data become available over time, and evidence-based sample size calculations²^,³^,⁵ which base the determination of sample size on the existing available evidence.⁸ This typically leads to smaller required sample sizes compared to that obtained using the conventional approach.⁹

Conditional planning of new trials should ideally be placed in a collaborative framework, where investigators of trials on the same topic work together to determine the similarities and differences of their studies and the prospective nature of the meta-analysis. The approach has been recently promoted as a promising route towards expediting drug licensing and inform reimbursement.¹⁰

Minimizing the required sample size is particularly important in specific settings where achieving a large sample size in a trial is challenging. This includes interventions for rare diseases, expensive or very cumbersome interventions, early-phase trials in drug development or when the control intervention poses important health risks and raises ethical concerns. RCTs with sham-controlled interventions (sham-RCTs) feature many of these characteristics and are typically small and underpowered.¹¹^–¹³ This makes the use of conditional planning promising in this context. However, the method makes a series of assumptions. Among others it is assumed that the true underlying effect size (which we assume is unbiasedly estimated by the summary effect) should not change over time. This is rather unlikely to happen in sham-RCTs as the learning curve applies to most surgical/minimally invasive interventions and studies of their efficacy show larger effects over time. Hence, the conditional power approach is both promising and challenging to be applied in this context.

In this paper, we aim to illustrate some of the challenges encountered when sham-RCTs are designed using the conventional approach to calculate the sample size and explore any potential advantages of using existing evidence both in drawing inferences about the differences between the interventions (active versus sham intervention) and when planning a new future study. We included RCTs comparing renal sympathetic denervation to a sham intervention for the control of arterial hypertension in patients with resistant hypertension with or without the combination of different antihypertensive medications. To this aim, we attempt to replicate the sample size calculations as described in individual trials, perform standard and sequential meta-analysis and calculate the sample size that would have been required conditional on the existing evidence in each step of the evidence synthesis.

Methods

Systematic review methods

We performed a systematic literature search (last search in December 2019) limited to English-language articles published in Medline and the Cochrane Central Register of Controlled Trials (CENTRAL) using the terms “randomized (randomised) controlled trial”, “sham”, “renal denervation”, “arterial hypertension”, as subject headings and text words, was conducted by one investigator. The detailed search algorithms can be found as Extended data.⁴³ The reference lists of original studies, review papers, and relevant meta-analyses of the interventions of interest initially identified by the electronic searches were also reviewed in an attempt to identify additional eligible trials. For each eligible sham-RCT, we also retrieved any publicly available study protocol, in which details related to the study design were provided. We excluded trials which were terminated preterm. No further limitations were applied.

The full text reports of relevant trials and their protocols were retrieved, and data on study design, patient and intervention characteristics, the outcome of interest, time to follow-up, and the exact description of the active intervention were extracted. Information about sample size calculations were independently extracted by two investigators in separate using prespecified data extraction forms. Any discrepancies were resolved by consensus after consulting a third investigator.

We extracted from each study the following information about sample size calculations: type I error, type II error or power, assumptions in the control group (standard deviation), the superiority margin (when relevant) for the primary efficacy endpoint, the anticipated treatment effect (mean difference), the recruitment period, randomization ratio, the calculated sample size and the achieved sample size for each arm. Details related to power calculations were retrieved from the main document, supplementary material, and previously published protocols of the trials. The outcome of interest was mean change in 24-hour ambulatory systolic blood pressure (SBP).

Sample size recalculations

We first attempted to replicate the sample size calculations described in individual trials. We hypothesized that the tests were two-sided and the type I error at 5% and power 80% unless different assumptions were stated. All other parameters for the power calculations were adopted as reported in the original articles. Sample size recalculations were performed by using the power command in Stata 15.¹⁴ We also calculated the relative difference between the achieved and initially calculated sample size as (achieved sample size - calculated sample size)/achieved sample size.

Standard and sequential meta-analysis

We performed standard and sequential pairwise meta-analysis for mean differences (MD).¹⁵^,¹⁶ As heterogeneity was low in this setting, we performed fixed effect meta-analyses. The available sham-RCTs were included in the sequential (cumulative) meta-analysis following the chronological order of publication and drawn boundaries calculated using an adaptation of the continuous alpha-spending function.¹⁶^,¹⁷ Crossing a boundary indicates strong evidence against the null hypothesis of equal means between active and sham procedures. We recorded the timepoint when one of the boundaries is crossed; this is the time point that the addition of a published study to the meta-analysis rejects the null hypothesis. We called this timepoint ‘final’ indicating that beyond this timepoint no further research is needed. We calculated the ‘unnecessary’ sample size as the total sample size of studies published after the final timepoint. All analyses were performed in R (version 4.0.2; R-Project for Statistical Computing) using the package meta and self-programmed routines.¹⁸

Conditional planning of trials assuming a prospective meta-analysis

We examine the scenario where the identified studies were a-priori planned and aimed to test the null hypothesis that the mean SBP is the same between active invasive and sham intervention. We calculate the conditional power of meta-analysis to estimate the required sample size in several steps of the analysis. In the sample size calculations, the difference in SBP in the new trial is assumed to be sufficiently similar to the ones observed and included in the meta-analysis. We assume absence of time-effect interaction between effect modifiers and time (i.e. the effect size is the same between early and later studies). We consider the sequential order of the trials until the final timepoint. We start with the first published trial, and we calculate the sample size needed for a second trial which, when added to the first trial their synthesis will lead into a rejection of the null hypothesis using the conditional power method.² Then, we synthesize the data from the first two published trials and we estimate the sample size needed in a third trial using again the conditional power; the difference in SBP in the new trial is assumed to be sufficiently similar the one estimated from the meta-analysis of the first two trials. We continue until the final timepoint. We compare the estimated sample size and the anticipated effect size from the conditional planning approach to those presented in the original papers. Analyses have been performed in Stata 15 using 1,000 simulations. Box 1 summarizes the key aspects in sample size calculations based on the conditional power of a meta-analysis.

Box 1. Key aspects in sample size calculations based on conditional power.

Assumed quantities
Type I error (also known as “false positive”)	The error of rejecting a null hypothesis when it is actually true needs to be defined. It refers to the probability of accepting an alternative hypothesis when the results can be attributed just to chance.
Type II error (also known as “false negative”)	The error of not rejecting a null hypothesis when the alternative hypothesis is true needs to be defined. It refers to the error of failing to accept an alternative hypothesis when you don't have adequate power. It occurs when we are failing to observe a difference when in truth there is one.
Assumed effect size	The effect size to be considered in power calculations for a future trial based on previous experience, or results from previous meta-analysis of existing evidence, or what is considered clinically relevant.
Key assumptions
Lack of association between effect/effect modifiers and time	As in conventional meta-analytic approaches, the assumption that the effect sizes of individual trials are independent should be fulfilled for conditional planning of future trial(s). The true underlying effect size (which we assume is unbiasedly estimated by the summary effect) should not be dependent on time. Similarly, any effect modifiers shall not change over time. Any time-dependent changes in effects would distort the sample size calculations.
Small heterogeneity	The variability of the true treatment effect across trials should be low. Otherwise, even the planning of huge trials will not result in the anticipated conditional power.

Results

Search findings and characteristics of eligible sham-RCTs

In the Online Figure (see Extended data⁴³) we summarize details of the study selection process. Overall, six sham-RCTs (with a total of 981 patients)¹⁹^–²⁷ comparing renal sympathetic denervation (n=585 patients) to a sham-intervention (n=396 patients) were deemed eligible (Table 1). Random allocation was 1:1 in 5 trials²¹^–²⁷ and 2:1 in one¹⁹^,²⁰ of the trials giving more weight to patients randomized to the active intervention. Two of the trials²³^–²⁵ were not prospectively powered; this is because they were designed as small-scale proof-of-concept trials to minimize exposure of patients to an interventional procedure with not previously documented efficacy (based on the findings of SYMPLICITY HTN-3 trial¹⁹^,²⁰). 24-hour ambulatory SBP and daytime ambulatory SBP were the primary endpoints in 4 and 2 trials, respectively. The majority of the trials (5 out of 6) were single-blinded, but outcome assessment was performed in blinded manner in all trials (Table 1). Follow-up period for reported results ranged from 2 up to 6 months. While the sample size in the first trial²⁰ was relatively large (535 participants), the sample sizes of subsequent individual trials ranged from 69 to 146 with a median of 80 participants.

Table 1. Characteristics of sham-RCTs comparing renal denervation to a sham-intervention considered eligible.

Trials	Recruitment period	Year of publication	Random allocation	Blinding/Trial design	Blind outcome evaluation	Follow up (months)	Funding source	Active arm	Primary endpoint (mean change)
SYMPLICITY HTN-3¹⁹^,²⁰	Oct 2011 to May 2013	2014	2:1	Single-blind/superiority	yes	6	Industry-related	RDN	24-hour ambulatory SBP*
Desch S., et al.²¹	Jul 2012 to Jan 2014	2015	1:1	Single-blind/superiority	yes	6	Non-industry related	RDN	24-hour ambulatory SBP
ReSET²²	nd	2016	1:1	Double-blind/not specified	yes	3	Non-industry related	RDN	Daytime ambulatory SBP
SPYRAL HTN-OFF MED²³^,²⁴	Jun 2015 to Jan 2017	2017	1:1	Single-blind/na**	yes	3	Industry-related	RDN	24-hour ambulatory SBP
SPYRAL HTN-ON MED²³^,²⁵	Jul 2015 to Jun 2017	2018	1:1	Single-blind/na**	yes	6	Industry-related	RDN	24-hour ambulatory SBP
RADIANCE-HTN SOLO²⁶^,²⁷	Mar 2016 to Dec 2017	2018	1:1	Single-blind/superiority	yes	2 and 6	Industry-related	Ultrasound renal denervation	Daytime ambulatory SBP

* The trial was also powered for this efficacy endpoint.

** Not prospectively powered. Proof-of-concept trials. There were no powered endpoints in the trials.

Sample size recalculations

Three sham-RCTs were designed to show superiority of renal denervation over sham intervention, two were not prospectively powered, and in one trial the authors do not specify their perspective (Table 2, Box 2). We were able to replicate the sample size calculations in 3 of the trials²¹^,²²^,²⁷ and in 2 of the studies no power analyses were performed.²⁴^,²⁵ In one study¹⁹^,²⁰ the power calculation was made for both the safety and subsequently for the efficacy primary outcome based on historical data and we were not able to replicate these (Table 2, Box 2, Online Table 1 in the Extended data⁴³).

Table 2. Sample size assumptions and conditional sample size calculations.

Trials	Details about sample size calculations as reported in the paper			Achieved sample size (active vs. sham (cumulative total sample size))	Recalculated sample size using the reported details (active vs. sham)	Recalculated sample size using the effect size from the meta-analysis (active vs. sham) **	Conditional planning sample size (active vs. sham) ***	Relative increase between achieved and calculated sample size (%)	Observed mean difference (SE) (mmHg)	Cumulative mean difference based on meta-analysis (mmHg)
Trials	Calculated sample size in (active vs. sham)	Planned power	Anticipated mean difference (standard deviation) (mmHg)*				Conditional planning sample size (active vs. sham) ***		Observed mean difference (SE) (mmHg)	Cumulative mean difference based on meta-analysis (mmHg)
SYMPLICITY HTN-3¹⁹^,²⁰	316 vs. 158	95%	−5 (25)	364 vs. 171 (535)	975 vs. 488****	na	na	11	−1.96 (1.54)	−1.96
Desch S., et al.²¹	29 vs. 29	80%	−6 (8)	35 vs. 36(606)	29 vs. 29	263 vs. 263	1050 vs. 1050	18	−3.50 (2.55)	−2.37
ReSET²²	28 vs. 28	80%	−10 (13)	36 vs. 33 (675)	28 vs. 28	474 vs. 474	260 vs. 260	19	−1.10 (3.53)	−2.22
SPYRAL HTN-OFF MED²³^,²⁴	na	na	na	38 vs. 42 (755)	na	na	250 vs. 250	na	−5.00 (2.51)	−2.75
SPYRAL HTN-ON MED²³^,²⁵	na	na	na	38 vs. 42 (835)	na	na	0	na	−7.40 (2.63)	−3.45
RADIANCE-HTN SOLO²⁶^,²⁷	64 vs. 64	80%	−6 (12)	74 vs. 72 (981)	64 vs. 64	190 vs. 190	0	12	−1.60 (2.04)	−3.08

* Assumed difference (mean and standard deviation) between the two groups of interventions for the respective primary efficacy outcome in each trial.

** Calculated based at each stage on the previous meta-analysis for mean difference, standard deviation of the one considered by the investigators in individual trials and assumed 80% power.

*** Calculated based at each stage on the previous meta-analysis for mean difference, standard deviation of 10 (the minimum observed in any arm) and assumed 80% power.

**** We were not able to recalculate the sample size calculations of the specific trial even after contacting the principal investigator of the trial.

Box 2. Power calculations as reported in individual sham-RCTs.

Trial	Power calculation description
SYMPLICITY HTN-3¹⁹^,²⁰	“ … In agreement with the Food and Drug Administration, the superiority of denervation over the sham procedure was established by a margin of 5 mmHg for the primary efficacy end point and by a margin of 2 mmHg for the secondary efficacy end point. The superiority margin of 5 mmHg for the primary efficacy end point was considered a clinically meaningful blood-pressure reduction on the basis of the observed decreases in cardiovascular morbidity with small reductions in systolic blood pressure (2 to 5 mmHg) with pharmacologic therapy. The detailed power and sample-size calculations have been published previously … ”, “… Regarding the primary effectiveness end point, a reduction in office-based SBP of ≥5 mmHg is considered a clinically meaningful improvement. Specifically, a 5-mm Hg reduction in SBP has been associated with a 14% decrease in stroke, a 9% decline in cardiovascular disease, and 7% reduction in mortality. Assuming a true difference between treatment means of 15mmHg with a 25 mmHg standard deviation of SBP change per group, a sample size of 316 treatment and 158 control subjects provides 95% statistical power to demonstrate a >5-mm Hg difference between treatment groups at a 1-sided alpha level 0.025. …”
Desch S., et al.²¹	“… Sample size was calculated for the between-group comparison with regard to the primary end point. At the time of trial planning, previous data to guide calculation were scarce. The only available randomized trial of RSD in resistant hypertension (Symplicity HTN-2) compared RSD against no-sham control in patients with resistant hypertension and severely elevated BP. ABPM recordings were available for a subgroup of patients: the mean reduction in 24-hour systolic BP at 6 months was 11±15 mmHg in patients assigned to RSD and 3±19 mmHg in control patients (for a net difference of 8 mmHg between groups). For the current trial, we assumed a less pronounced effect of RSD on BP in light of inclusion of patients with only mildly elevated BP. We speculated that RSD would lead to a difference of at least 6 mmHg between groups with regard to the primary end point (75% of the treatment effect observed in Symplicity HTN-2). We assumed a lower SD of systolic BP values based on a more homogeneous population compared with Symplicity HTN-2. Based on data from a previous trial in mildly hypertensive patients, the presumed SD was set at 8 mmHg for both groups. Thus, 29 patients per treatment arm needed to be analyzed to reject the null hypothesis of equal means between the 2 groups to provide a statistical power of 80% (2-sided test, α=0.05). To account for potential dropouts or nonanalyzable ABPM recordings, an additional 20% of patients were randomized in each arm. Sample size was calculated using nQuery Advisor 7.0 (Statistical Solutions, Saugus, MA) …”
ReSET²²	“… The ReSET trial was initiated before the HTN3 trial. Therefore, according to ABPM data from the HTN2 trial and according to our own pilot data, we hypothesized a between-group difference on the primary endpoint of 10mmHg (daytime systolic ABPM after 3 months). Expecting a SD of approximate 13mmHg on ABPM (own data), we calculated a minimum sample size of 28 patients in each group, beta value 0.8 and alpha value 0.05. Analysis was planned according to the intention-to-treat principle (meaning from the time of randomization), and we therefore decided to randomize a total of 70 patients … ”
SPYRAL HTN-OFF MED²³^,²⁴	“… The current proof-of-concept trial was designed in collaboration with, and approved by, the US Food and Drug Administration (FDA) with consideration of the recommendations in the 2014 Scientific Statement by the American Society of Hypertension, which suggested a phase 2-type trial in a small group of patients. The protocol allowed up to 120 patients to be randomly assigned with prospectively planned interim analyses after 40, 60, 80, or 100 patients had completed the 3-month follow-up. The purpose of each interim analysis was to ascertain whether there was an adequate treatment effect with a sufficient reduction in variability of the blood pressure measurements to allow design of a larger, pivotal trial. All patients enrolled after this decision point will be included in the pivotal dataset, as discussed with the FDA, and thus this report represents the primary results of the SPYRAL HTN-OFF MED trial. There were no powered endpoints in the trial. To do a properly powered randomised trial assuming a 5 mmHg SBP reduction with a standard deviation of 12, it was established that 246 patients would be required. Because of the unsatisfactory outcome of the SYMPLICITY HTN-3 trial, we decided to proceed with a smaller, proof-of-concept trial that would minimise exposure of patients to an interventional procedure and provide sufficient evidence to move forward with a larger, powered trial. Statistical analyses were done according to the intention-to-treat principle. …”
SPYRAL HTN-ON MED²³^,²⁵	“… The protocol allowed up to 110 patients to be randomly assigned with prospectively planned interim analyses after 40, 60, and 80 patients completed 3 months follow up, respectively. Because the current study prespecified that patients should be maintained on the same medication regimen through 6 months follow-up, analysis of the 80 patient cohort was then performed to assess the pattern and progression of blood pressure change over time. The purpose of each interim analysis was to confirm the safety of the procedure and determine if the blood pressure lowering effect of renal denervation was sufficient to support design of future trials. There are no powered endpoints in the trial. Statistical analyses were done based on the intention-to-treat principle. …”
RADIANCE-HTN SOLO²⁶^,²⁷	“… Assuming a 6 mmHg difference in change in daytime ambulatory systolic blood pressure at 2 months between the renal denervation and the sham groups,17 a common SD of 12 mmHg, 1:1 randomisation, and a two-sided type 1 error rate of 5%, a sample size of 128 evaluable patients would yield 80% power. To account for up to 10% missing data on the primary endpoint, we planned to randomise a total 146 patients in the study. …”

The achieved sample size was in all cases larger than that calculated and the relative difference was between 11% to 19% (Table 2). The anticipated mean differences used in sample size calculations by the study authors were larger than those which were actually observed in the trials, or in the trials published before (Figure 1). Consequently, each study could not detect any important differences between the active and sham interventions. This can be attributed to the over-optimistic effect considered in the sample size calculations to be able to conform with the available sample of patients for recruitment (‘reverse engineered’ sample size calculation).

Figure 1. Plot of assumed and observed mean differences in each individual trial, and the cumulative mean difference derived at each step of the cumulative meta-analysis using fixed-effect.

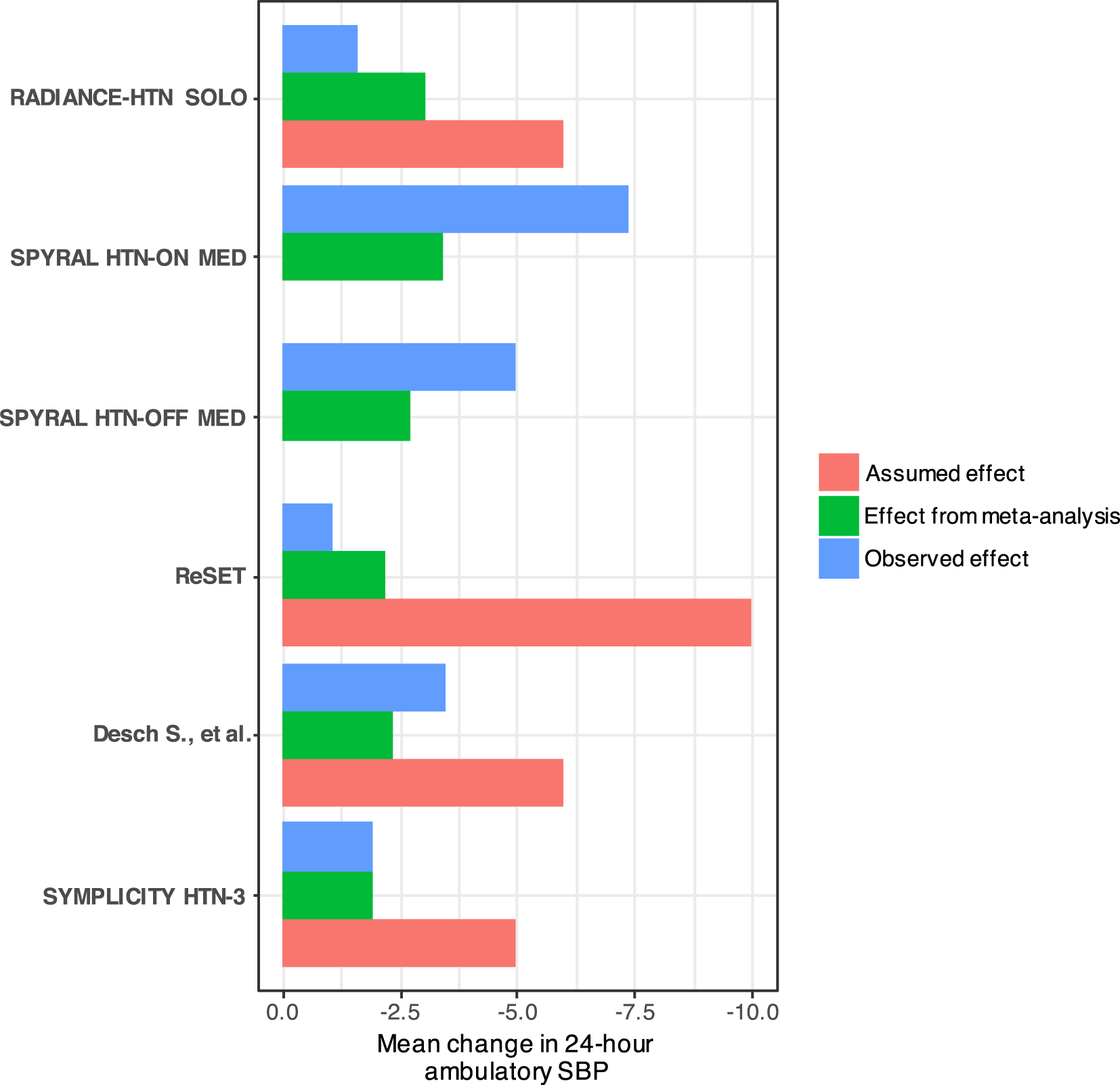
Two of the trials (SPYRAL HTN-OFF MED and SPYRAL HTN-ON MED) were designed as proof-of-concept trials. Therefore, they were not prospectively powered and assumed effects are not provided.

Abbreviation: SBP, systolic blood pressure.

Standard and sequential meta-analysis

The standard meta-analysis forest plot illustrates the individual results of each trial and its contribution (weight) to the summary effect (Figure 2 panel A); the cumulative meta-analysis plot shows how the evidence evolved over time (Figure 2 panel B). Data used are available in Online Table 2 (see underlying data⁴³). The estimated heterogeneity variance was zero. If a meta-analysis was conducted immediately after the publication of the fourth study (when 755 patients had been randomized in total), the summary mean difference favoring the active intervention would have been found to be -2.76 (95%CI -4.93 to -0.59). Even after accounting for the sequential nature of the data accumulation, the addition of the fourth study would provide evidence against the null hypothesis (Figure 3). The final time point is therefore the time of publication of the fourth study (in 2017). The total sample size randomized thereafter (in the fifth and sixth trials) could be considered redundant (226 study participants in total, of which 114 randomized to sham).

Figure 2. Standard (panel A) and cumulative (panel B) fixed-effect meta-analysis of sham-RCTs comparing renal sympathetic denervation to sham intervention for the outcome of mean change from baseline to follow-up in 24-hour ambulatory systolic blood pressure (mmHg).

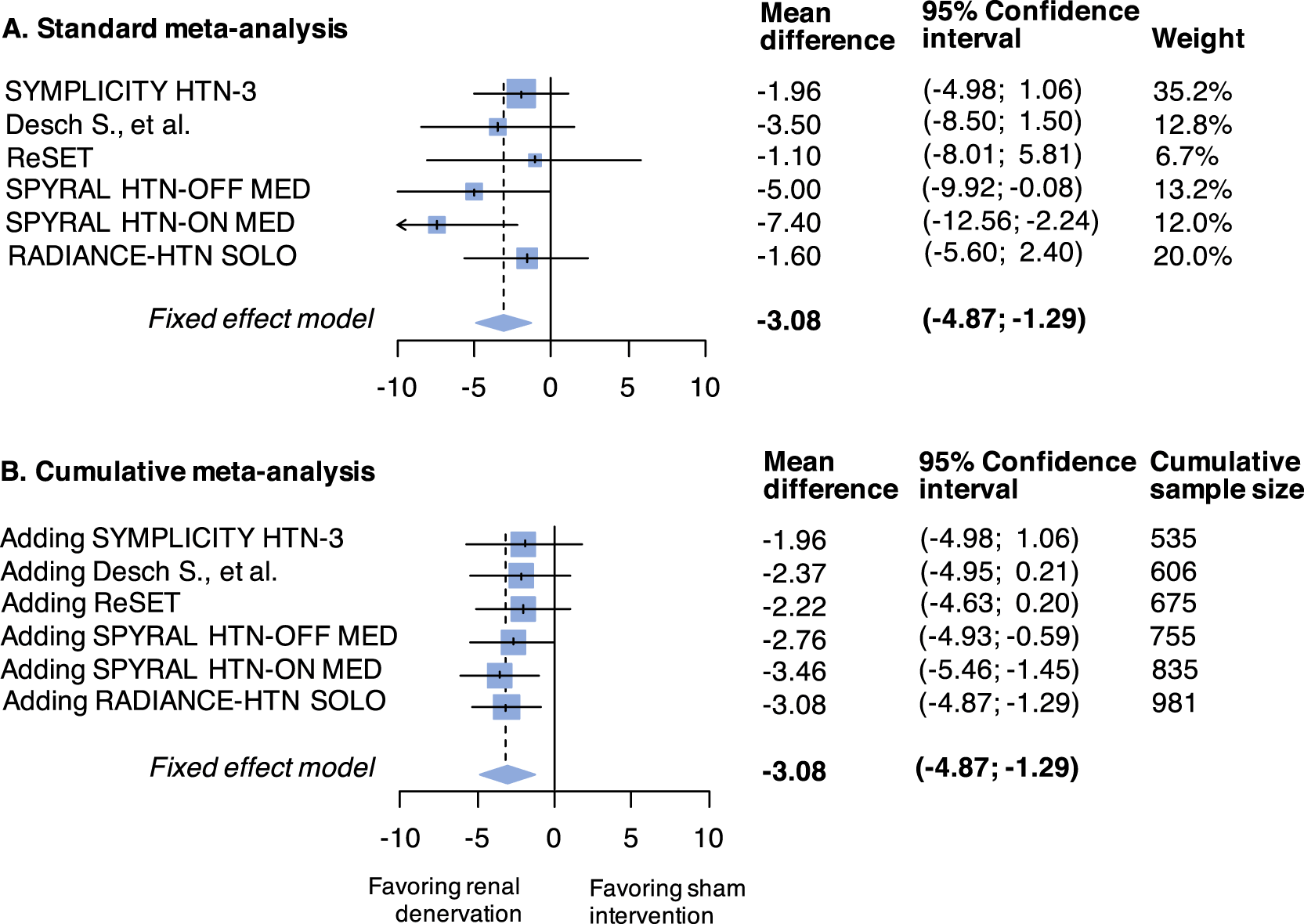
Abbreviation: RCT, randomized controlled trial.

Figure 3. Hypothetical prospectively planned sequential fixed effect meta-analysis framework (type I error=5%, power=90%).

Estimation of the sample size using conditional planning

The sample size of each future study calculated based on conditional power of meta-analysis is presented in Table 2. The summary effect of the meta-analysis after each study was included was much smaller than the anticipated effect used by the authors in their sample size calculations (Figure 2). Consequently, sample size calculations using the meta-analysis mean difference results to substantially larger calculated sample size compared to that calculated by the trialists (Table 2).

The large sample sizes calculated with conditional power compared to that calculated by the trials is explained by the fact that the trialists chose unrealistically large anticipated mean differences. If studies had been planned prospectively, the third study would have needed 260 participants per arm and the synthesis of the first three studies would have been enough to reject the null hypothesis. The total sample size from the three trials would have been 1126 (the achieved sample size from the first two trials and the estimated using conditional power from the third trial), while the total achieved sample size in the published studies is 981. Τhis means that the sample size with conditional planning under this scenario is larger than the total observed in the studies (Figures 1 and 2, Table 2).

Discussion

Critical review of the available evidence in terms of systematic reviews and meta-analyses of RCTs can provide an in-depth summary of available evidence on a specific topic and contribute in the planning of future research agenda in two ways: by identifying gaps in knowledge on which efforts should be focused, and by contributing to the conditional planning of a future trial based on the relevant existing evidence.⁹^,²⁸^–³⁰ For the latter, both, pairwise and network meta-analyses, have been proposed as appropriate tools.³^–⁵^,³¹ Here, in a retrospectively designed scenario of the particular setting of sham-RCTs, we demonstrated how sequential meta-analysis and conditional planning of a future trial can provide an alternative strategy to the practice of conducting many small, underpowered RCTs with unrealistically large assumed expected treatment differences. Through sequential meta-analysis of sham-controlled trials, investigators can achieve conclusive findings earlier than individual small-scale trials and hence avoid exposing patients to sham-related risks. However, as we illustrated in our example, conditional planning of a future sham-RCT poses important challenges, since invasive procedures may improve over time and the intervention effect is expected to increase in new studies which violates the underlying assumptions.

Systematic reviews of sham-RCTs constitute an ideal setting for considering existing evidence when planning new studies as it is even more imperative to prevent exposure of patients to risks related to the sham intervention. The dataset of trials we used, which has been previously extensively synthesized in meta-analyses,¹³ was no exception to the practice of setting large expected differences. The exaggerated power calculations were also reflected by the fact that the achieved sample size was always larger than the calculated. Moreover, individual trials in the early phase resulted in conflicting findings compared to subsequent trials, although statistical heterogeneity was estimated at zero.³² Differences among the trials were attributed to variability in sample sizes, study design (i.e. proof-of-concept trials), blinding of outcomes assessors, patient characteristics, modification of procedural technique and ablation catheters over time, physicians’ experience, medical treatment protocols, and outcome adjudication methods which may yield differences not only among the trials but even in the same trial.¹³^,³² Nevetheless, the resulted sample sizes based on conditional planning were much larger than those used in individual trials. This can be also attributed to the overoptimistic expected effect sizes in individual trials and to a small trend of increase in the intervention effect over time, possibly because of a learning curve effect in performing the specific procedure.

Clinical research is characterized by sequential flow. New studies are built on the knowledge of the previous ones by using either prior information in making the decision to conduct a new trial or meta-analysis of existing evidence to design the subsequent trial. Even though both approaches have been established under different conditions, concerns have been raised regarding potential sources of biases due to the sequential design, particularly when a clinically relevant effect is ignored in sample size calculations.³³ In this scenario, appropriate specification of clinically relevant effects is an important aspect in planning future trials to avoid unrealistic expectations. Along these lines, previous evaluations have shown the appropriateness of conditional planning under different scenarios of inconclusive meta-analysis (confidence interval of the summary effect includes effect sizes with different implications).³

Conditional planning in a frequentist or Bayesian framework can be applied for planning future research agenda.⁴^,⁵^,³⁴^–³⁷ Nowadays, clinical trials are becoming costly and time consuming; whereas consideration of such approaches in planning future trials can potentially overcome obvious challenges (i.e. lower recruitment rates than expected or limited funding sources), better prioritize research agenda and subsequently mitigate the growing problem of wasteful research efforts in the biomedical field.⁹^,³⁰^,³⁸^,³⁹ It is of obvious importance to better design the required future single study or studies, in order to maximize their efficiency and potentially provide the information needed to make informed decisions in clinical effectiveness research. It could be that a small-scale study is needed to confirm previous findings or alternatively new studies may be deemed unnecessary in a scenario where the existing evidence suggests a small effect size which is unlikely to subsequently change. However, particular attention should be paid on the required assumptions of the method before embarking on applying conditional planning of new trials (Box 1).

Limitations

Our evaluation has several limitations. First, we chose an example of relatively limited number of available trials with small sample sizes and special design (sham-RCTs with two of them serving as proof-of-concept studies). Even though our example can be representative of the size of the available sham-RCTs in any medical field, the small number of studies might have resulted in clinical heterogeneity not manifesting in the data as statistical heterogeneity. In a real application, imputing a value for heterogeneity, informed for example by empirical predictive distributions,⁴⁰^,⁴¹ and performing random-effects would be a reasonable model choice. Second, sequential methods have inherited limitations since they have been mainly built on the principal of statistical significance and do not differentiate between clinically relevant and non-relevant effects. Along these lines, the Cochrane Handbook authors underline the methodological limitations that arise from sequential methods.⁴² Third, the applied method of conditional planning is based on aggregated findings of completed trials. However, investigators may need to adapt a trial’s design (i.e. sample size re-calculations) after its launch. These interim findings could potentially provide important insights for the planning of future trials, but available statistical approaches cannot safely consider this information. Finally, we applied a retrospective analysis while aiming to illustrate the process in a hypothetical prospective framework. In an actual application, the process should be planned and undertaken prospectively by a collaborative panel including clinicians, decision makers, methodologists and patient representatives.

Conclusions

Sequential meta-analysis of sham-controlled trials can help answering the research question earlier and avoid unnecessarily exposing patients to sham-related risks. However, conditional planning of new sham-RCTs poses important challenges. As many surgical/minimally invasive procedures improve over time, the intervention effect is expected to increase in new studies and this violates the underlying assumptions. Unless this is accounted for, conditional planning will not improve the design of sham-RCTs.

Data availability

Underlying data

Zenodo: Estimating the sample size of sham-controlled randomized controlled trials using existing evidence. https://doi.org/10.5281/zenodo.5865523.⁴³

This project contains the following underlying data:

- Online Table 2: Mean changes in each group of intervention and the difference between the groups for the efficacy outcome of 24-hour ambulatory systolic blood pressure as given in individual trials

Extended data

Zenodo: Estimating the sample size of sham-controlled randomized controlled trials using existing evidence. https://doi.org/10.5281/zenodo.5865523.⁴³

This project contains the following extended data:

- Online Box 1: Medline and CENTRAL search algorithm
- Online Figure: Study selection flowchart.
- Online Table 1: Sample-size recalculations in individual sham RCTs in Stata.

Data are available under the terms of the Creative Commons Attribution 4.0 International license (CC-BY 4.0).

Rerefences

1. Otte WM, Tijdink JK, Weerheim PL, et al.: Adequate statistical power in clinical trials is associated with the combination of a male first author and a female last author. elife. 2018; 7. PubMed Abstract | Publisher Full Text
2. Sutton AJ, Cooper NJ, Jones DR, et al.: Evidence-based sample size calculations based upon updated meta-analysis. Stat. Med. 2007; 26: 2479–2500. PubMed Abstract | Publisher Full Text
3. Roloff V, Higgins JPT, Sutton AJ: Planning future studies based on the conditional power of a meta-analysis. Stat. Med. 2013; 32: 11–24. PubMed Abstract | Publisher Full Text
4. Nikolakopoulou A, Mavridis D, Salanti G: Using conditional power of network meta-analysis (NMA) to inform the design of future clinical trials. Biom. J. 2014; 56: 973–990. PubMed Abstract | Publisher Full Text
5. Salanti G, Nikolakopoulou A, Sutton AJ, et al.: Planning a future randomized clinical trial based on a network of relevant past trials. Trials. 2018; 19: 365. PubMed Abstract | Publisher Full Text
6. Elliott JH, Turner T, Clavisi O, et al.: Living Systematic Reviews: An Emerging Opportunity to Narrow the Evidence-Practice Gap. PLoS Med. 2014; 11. Publisher Full Text
7. Créquit P, Trinquart L, Yavchitz A, et al.: Wasted research when systematic reviews fail to provide a complete and up-to-date evidence synthesis: The example of lung cancer. BMC Med. 2016; 14: 8. PubMed Abstract | Publisher Full Text
8. Salanti G, Nikolakopoulou A: Actively Living Network Meta-Analysis. Accessed 31 May 2021. Reference Source
9. Chalmers I, Bracken MB, Djulbegovic B, et al.: How to increase value and reduce waste when research priorities are set. Lancet. 2014; 383: 156–165. PubMed Abstract | Publisher Full Text
10. Naci H, Salcher-Konrad M, Kesselheim AS, et al.: Generating comparative evidence on new drugs and devices before approval. Lancet. 2020; 395: 986–997. PubMed Abstract | Publisher Full Text
11. Miller FG, Kaptchuk TJ: Sham procedures and the ethics of clinical trials. J. R. Soc. Med. 2004; 97: 576–578. PubMed Abstract | Publisher Full Text
12. Galpern WR, Corrigan-Curay J, Lang AE, et al.: Sham neurosurgical procedures in clinical trials for neurodegenerative diseases: Scientific and ethical considerations. Lancet Neurol. 2012; 11: 643–650. Publisher Full Text
13. Sardar P, Bhatt DL, Kirtane AJ, et al.: Sham-Controlled Randomized Trials of Catheter-Based Renal Denervation in Patients With Hypertension. J. Am. Coll. Cardiol. 2019; 73: 1633–1642. PubMed Abstract | Publisher Full Text
14. StataCorp.: Stata Statistical Software: Release 15. College Station, TX: StataCorp LLC; 2017.
15. Higgins JPT, Whitehead A, Simmonds M: Sequential methods for random-effects meta-analysis. Stat. Med. 2011; 30: 903–921. PubMed Abstract | Publisher Full Text
16. Nikolakopoulou A, Mavridis D, Egger M, et al.: Continuously updated network meta-analysis and statistical monitoring for timely decision-making. Stat. Methods Med. Res. 2018; 27: 1312–1330. PubMed Abstract | Publisher Full Text
17. Demets DL, Lan KKG: Interim analysis: The alpha spending function approach. Stat. Med. 1994; 13: 1341–1352. PubMed Abstract | Publisher Full Text
18. Balduzzi S, Rücker G, Schwarzer G: How to perform a meta-analysis with R: A practical tutorial. Evid. Based Ment. Health. 2019; 22: 153–160. PubMed Abstract | Publisher Full Text
19. Kandzari DE, Bhatt DL, Sobotka PA, et al.: Catheter-based renal denervation for resistant hypertension: Rationale and design of the SYMPLICITY HTN-3 trial. Clin. Cardiol. 2012; 35: 528–535. PubMed Abstract | Publisher Full Text
20. Bhatt DL, Kandzari DE, O’Neill WW, et al.: A Controlled Trial of Renal Denervation for Resistant Hypertension. N. Engl. J. Med. 2014; 370: 1393–1401. Publisher Full Text
21. Desch S, Okon T, Heinemann D, et al.: Randomized Sham-Controlled Trial of Renal Sympathetic Denervation in Mild Resistant Hypertension. Hypertension. 2015; 65: 1202–1208. PubMed Abstract | Publisher Full Text
22. Mathiassen ON, Vase H, Bech JN, et al.: Renal denervation in treatment-resistant essential hypertension. A randomized, SHAM-controlled, double-blinded 24-h blood pressure-based trial. J. Hypertens. 2016; 34: 1639–1647. PubMed Abstract | Publisher Full Text
23. Kandzari DE, Kario K, Mahfoud F, et al.: The SPYRAL HTN Global Clinical Trial Program: Rationale and design for studies of renal denervation in the absence (SPYRAL HTN OFF-MED) and presence (SPYRAL HTN ON-MED) of antihypertensive medications. Am. Heart J. 2016; 171: 82–91. Publisher Full Text
24. Townsend RR, Mahfoud F, Kandzari DE, et al.: Catheter-based renal denervation in patients with uncontrolled hypertension in the absence of antihypertensive medications (SPYRAL HTN-OFF MED): a randomised, sham-controlled, proof-of-concept trial. Lancet. 2017; 390: 2160–2170. Publisher Full Text
25. Kandzari DE, Böhm M, Mahfoud F, et al.: Effect of renal denervation on blood pressure in the presence of antihypertensive drugs: 6-month efficacy and safety results from the SPYRAL HTN-ON MED proof-of-concept randomised trial. Lancet. 2018; 391: 2346–2355. PubMed Abstract | Publisher Full Text
26. Azizi M, Schmieder RE, Mahfoud F, et al.: Endovascular ultrasound renal denervation to treat hypertension (RADIANCE-HTN SOLO): a multicentre, international, single-blind, randomised, sham-controlled trial. Lancet. 2018; 391: 2335–2345. PubMed Abstract | Publisher Full Text
27. Azizi M, Schmieder RE, Mahfoud F, et al.: Six-Month Results of Treatment-Blinded Medication Titration for Hypertension Control After Randomization to Endovascular Ultrasound Renal Denervation or a Sham Procedure in the RADIANCE-HTN SOLO Trial. Circulation. 2019; 139: 2542–2553. PubMed Abstract | Publisher Full Text
28. Ferreira ML, Herbert RD, Crowther MJ, et al.: When is a further clinical trial justified?. BMJ (Online). 2012; 345. Publisher Full Text
29. Goudie AC, Sutton AJ, Jones DR, et al.: Empirical assessment suggests that existing evidence could be used more fully in designing randomized controlled trials. J. Clin. Epidemiol. 2010; 63: 983–991. PubMed Abstract | Publisher Full Text
30. Ioannidis JPA, Greenland S, Hlatky MA, et al.: Increasing value and reducing waste in research design, conduct, and analysis. Lancet. 2014; 383: 166–175. PubMed Abstract | Publisher Full Text
31. Jones HE, Ades AE, Sutton AJ, et al.: Use of a random effects meta-analysis in the design and analysis of a new clinical trial. Stat. Med. 2018; 37: 4665–4679. PubMed Abstract | Publisher Full Text
32. Pocock SJ, Bakris G, Bhatt DL, et al.: Regression to the Mean in SYMPLICITY HTN-3: Implications for Design and Reporting of Future Trials. J. Am. Coll. Cardiol. 2016; 68: 2016–2025. PubMed Abstract | Publisher Full Text
33. Kulinskaya E, Huggins R, Dogo SH: Sequential biases in accumulating evidence. Res. Synth. Methods. 2016; 7: 294–305. PubMed Abstract | Publisher Full Text | Free Full Text
34. Shohoudi A, Stephens DA, Khairy P: Bayesian adaptive trials for rare cardiovascular conditions. Futur. Cardiol. 2018; 14: 143–150. PubMed Abstract | Publisher Full Text
35. Wason JMS, Trippa L: A comparison of Bayesian adaptive randomization and multi-stage designs for multi-arm clinical trials. Stat. Med. 2014; 33: 2206–2221. PubMed Abstract | Publisher Full Text
36. Bittl JA, He Y: Bayesian Analysis: A Practical Approach to Interpret Clinical Trials and Create Clinical Practice Guidelines. Circ. Cardiovasc. Qual. Outcomes. 2017; 10. PubMed Abstract | Publisher Full Text
37. Berry DA: Introduction to Bayesian methods III: Use and interpretation of Bayesian tools in design and analysis. Clin. Trials. 2005; 2: 295–300. PubMed Abstract | Publisher Full Text
38. Macleod MR, Michie S, Roberts I, et al.: Biomedical research: Increasing value, reducing waste. Lancet. 2014; 383: 101–104. Publisher Full Text
39. Siontis GCM, Sweda R, Windecker S: Cardiovascular clinical trials in the era of a pandemic. J. Am. Heart Assoc. 2020; 9: e018288. PubMed Abstract | Publisher Full Text
40. Turner RM, Davey J, Clarke MJ, et al.: Predicting the extent of heterogeneity in meta-analysis, using empirical data from the Cochrane Database of Systematic Reviews. Int. J. Epidemiol. 2012; 41: 818–827. PubMed Abstract | Publisher Full Text
41. Rhodes KM, Turner RM, Higgins JPT: Predictive distributions were developed for the extent of heterogeneity in meta-analyses of continuous outcome data. J. Clin. Epidemiol. 2015; 68: 52–60. PubMed Abstract | Publisher Full Text
42. Higgins JPT, Thomas J, Chandler J, et al.: Cochrane Handbook for Systematic Reviews of Interventions. 2nd ed.Chichester (UK): John Wiley & Sons; 2019. Publisher Full Text
43. Siontis G, Nikolakopoulou A, Sweda R, et al.: Estimating the sample size of sham-controlled randomized controlled trials using existing evidence.2022. Publisher Full Text

Comments on this article Comments (0)

Version 2

VERSION 2 PUBLISHED 24 Jan 2022

Author details Author details

George C.M. Siontis
Roles: Conceptualization, Data Curation, Formal Analysis, Investigation, Methodology, Visualization, Writing – Original Draft Preparation, Writing – Review & Editing

Adriani Nikolakopoulou
Roles: Conceptualization, Data Curation, Formal Analysis, Investigation, Methodology, Visualization, Writing – Original Draft Preparation, Writing – Review & Editing

Romy Sweda
Roles: Data Curation

Dimitris Mavridis
Roles: Conceptualization, Formal Analysis, Supervision, Writing – Review & Editing

Georgia Salanti
Roles: Conceptualization, Formal Analysis, Methodology, Supervision, Visualization, Writing – Original Draft Preparation, Writing – Review & Editing

Competing interests

No competing interests were disclosed.

Grant information

This work was supported by project funding (Grant No. 179158) from the Swiss National Science Foundation (SNSF). AN is supported by a Swiss National Science Foundation (SNSF) personal fellowship (P400PM_186723).

Article Versions (2)

version 2

Revised

Published: 07 Nov 2022, 11:85

https://doi.org/10.12688/f1000research.108554.2

version 1

Published: 24 Jan 2022, 11:85

https://doi.org/10.12688/f1000research.108554.1

© 2022 Siontis GCM et al. This is an open access article distributed under the terms of the Creative Commons Attribution License, which permits unrestricted use, distribution, and reproduction in any medium, provided the original work is properly cited.

Download

Export To

metrics

	Views	Downloads
F1000Research	-	-
PubMed Central Data from PMC are received and updated monthly.	-	-

Citations

SEE MORE DETAILS

CITE

how to cite this article

Siontis GCM, Nikolakopoulou A, Sweda R et al. Estimating the sample size of sham-controlled randomized controlled trials using existing evidence [version 1; peer review: 2 approved with reservations]. F1000Research 2022, 11:85 (https://doi.org/10.12688/f1000research.108554.1)

NOTE: If applicable, it is important to ensure the information in square brackets after the title is included in all citations of this article.

track

receive updates on this article

Track an article to receive email alerts on any updates to this article.

Open Peer Review

Version 1

VERSION 1

PUBLISHED 24 Jan 2022

Views

Reviewer Report 17 Oct 2022

Waldemar Siemens, Institute for Evidence in Medicine, Medical Center - University of Freiburg, Faculty of Medicine, Freiburg, Germany; Cochrane Germany, Cochrane Germany Foundation, Freiburg, Germany

Approved with Reservations

https://doi.org/10.5256/f1000research.119949.r150812

The authors present an empirical example comparing renal sympathetic denervation to sham intervention and provide data and calculations on power, cumulative meta-analysis, and sequential meta-analysis aiming to present the idea of conditional power. Many important points are well addressed and methodological aspects are well connected to the clinical relevance of the methods. I have some major and minor questions and encourage the authors to comment to improve the manuscript.

Major comments:

Limitations: “performing random-effects would be a reasonable model choice” - Why have you worked with the FE model then?

If conditional power would say that only a “small trial” is needed: Would this be a problem regarding the sampling error? Should trials have a minimum size to avoid sampling error? As the trial gets smaller, the problem of chance increases, or? Could you comment on that and reflect you approach (conditional power)?

This is an empirical example. Could a reasonable simulation study add value? If yes, how could it look like?

Minor comments:

Abstract:

You could add more numeric results in the results of you abstract if appropriate.

Background:

“This typically leads to smaller required sample sizes compared to that obtained using
the conventional approach.” - I wonder if a disadvantage of this approach is that the sampling error increases with a small sample size in a trial. Could you comment on that?

“Among others it is assumed that the true underlying effect size (which we assume is unbiasedly estimated by the summary effect) should not change over time. This is rather unlikely to happen in sham-RCTs as the learning curve applies to most surgical/minimally invasive interventions and studies of their efficacy show larger effects over time. Hence, the conditional power approach is both promising and challenging to be applied in this context.” - Does the fixed-effect (FE) model makes sense in this context? Clinical trials vary in their PICO by nature, which makes it hard to assume the FE model.

“As heterogeneity was low in this setting, we performed fixed effect meta-analyses.” - Shouldn’t that be a choice based on the homogeneity of the trials according to the PICO scheme?

Box 1:

“The variability of the true treatment effect across trials should be low. Otherwise, even the planning of huge trials will not result in the anticipated conditional power.” - This again puts the FE model into question, or? Should the conditional power calculations be based the random-effects model?

Results:

Table 1 / meta-analysis: Is it appropriate to pool “24-hour ambulatory SBP” with “Daytime ambulatory SBP”?

Link for “Online Table 2”: Only “Table 2” is a link and leads to Table 2 in the manuscript, not to Online Table 2. Please check all link in the manuscript.

“heterogeneity variance” (p. 5) - Do you mean the between-study variance Tau^2? Please be more precise.

“The total sample size randomized thereafter (in the fifth and sixth trials) could be considered redundant (226 study participants in total, of which 114 randomized to sham).” - I think this should be one key message of the paper exactly with this wording, i.e., how many patients would not receive sham. It adds weight for a clinically meaningful understanding of the methods presented.

“The large sample sizes calculated with conditional power compared to that calculated by the trials is explained by the fact that the trialists chose unrealistically large anticipated mean differences.” - Sometimes you already interpret your results in the discussion section. Please move the explaining sentences rather to the discussion.

“Figure 3. Hypothetical prospectively planned sequential fixed effect meta-analysis framework (type I error=5%, power=90%).” - I suggest adding more sentences for explaining Figure 3. Not everyone is familiar with sequential meta-analysis so it might be important to help readers understand the idea of it.

Discussion:

Feasibility of large trials when trial authors would consider conditional power.

Stop when rejecting the null hypothesis is defined as the “final time point”, correct? How does this fit to clinical relevance of results? One could argue to stop if a threshold of irrelevance is not anymore included by the 95% CI for example.

Have prediction intervals a role in cumulative meta-analysis and sequential meta-analysis to describe heterogeneity?

Is the R code available? You may add it to zenodo.

“Unless this is accounted for, conditional planning will not improve the design of sham-RCTs.” - Could you explicitly say what you mean by “this” to avoid misunderstandings in the conclusion? Somehow I find it hard to follow, maybe also because you word your statement with a negation. Please consider rewriting it.

Is the rationale for developing the new method (or application) clearly explained?

Yes
Is the description of the method technically sound?

Yes
Are sufficient details provided to allow replication of the method development and its use by others?

Partly
If any results are presented, are all the source data underlying the results available to ensure full reproducibility?

Partly
Are the conclusions about the method and its performance adequately supported by the findings presented in the article?

Yes

Competing Interests: No competing interests were disclosed.

Reviewer Expertise: Meta-research, meta-analysis, living systematic review

I confirm that I have read this submission and believe that I have an appropriate level of expertise to confirm that it is of an acceptable scientific standard, however I have significant reservations, as outlined above.

CITE

Report a concern

Author Response 07 Nov 2022

Georgios Siontis, Department of Cardiology, University Hospital of Bern, Bern, Switzerland

07 Nov 2022

Author Response

We were pleased to receive the comments of the Reviewer. We are grateful for the very insightful comments that helped us to improve our work further. In the revised version ... Continue reading We were pleased to receive the comments of the Reviewer. We are grateful for the very insightful comments that helped us to improve our work further. In the revised version of our manuscript we have addressed all of the suggestions/comments made by the Reviewer. In more detail:

Reviewer 2:

The authors present an empirical example comparing renal sympathetic denervation to sham intervention and provide data and calculations on power, cumulative meta-analysis, and sequential meta-analysis aiming to present the idea of conditional power. Many important points are well addressed and methodological aspects are well connected to the clinical relevance of the methods. I have some major and minor questions and encourage the authors to comment to improve the manuscript.

Reply: Thank you for your feedback.

Major comments:

Limitations: “performing random-effects would be a reasonable model choice” - Why
have you worked with the FE model then?

Reply: We thank the reviewer for this comment. In fact, our intention was to employ a random-effects meta-analysis model. As the between-study variance (r²) estimation was 0, this was equivalent to fixed-effect. We realize that this was not clearly stated, and we thus now have rephrased to clarify our approach. In particular, we write in the ‘Standard and sequential meta-analysis’ section: “We intended to perform random-effects meta-analysis, but as between-study variance (r²) was estimated at 0 in this setting, our calculations are identical to those from a fixed effect meta-analysis.”. We did not change the term “fixed-effect” in the abstract and the figure legends.

An alternative strategy would be to inform heterogeneity from empirical distributions (our references 40 and 41). However, such an approach would be appropriate in a prospective application of sequential meta-analysis and conditional planning, rather than a retrospective application, like the one presented in this paper. This is because in a prospective application, estimation of heterogeneity in the first stages of the reviews would be suboptimal. Moreover, imputing a value for heterogeneity would make results from “conventional” and “evidence-based” sample size calculations non-comparable.

We already wrote in the Discussion: “In a real application, imputing a value for heterogeneity, informed for example by empirical predictive distributions [40, 41], and performing random-effects would be a reasonable model choice”. And we now added: “Such an approach would be less reasonable in a retrospective application of the methods and would mitigate the comparability between conventional and evidence-based sample size calculations.”

If conditional power would say that only a “small trial” is needed: Would this be a problem regarding the sampling error? Should trials have a minimum size to avoid sampling error? As the trial gets smaller, the problem of chance increases, or? Could you comment on that and reflect you approach (conditional power)?

Reply: This is a topic that would benefit from further investigation. On one hand, a small trial should be a desirable outcome of the conditional planning method, on the other hand it would indeed be associated with greater within-study variation. Although this potentially large within-study variation is in theory incorporated in the conditional planning method (saying for example that an addition of such a study would render conclusive the updated meta-analysis effect, which is our goal), it would probably question the requirement of such individual study to be a standalone experiment. We added in the Discussion: “However, conditional planning might in theory result to recommendations of very small trials, which would be associated with great within-study variance and not be standalone experiments. Setting a minimum sample size for a future trial designed using conditional planning would be a potential remedy for such a situation.”.

This is an empirical example. Could a reasonable simulation study add value? If yes, how could it look like?

Reply: We thank the reviewer for this interesting comment. We do believe that a simulation study could contribute on the evaluation of the robustness of the method, and this could be a follow-up project. In such a simulation study, one should construct scenarios reflecting various assumptions being and not being met. We added under “Limitations”: “A comprehensive simulation study would be a more appropriate tool to investigate the performance and robustness of the method under a variety of settings.”

Minor comments:

Abstract:
You could add more numeric results in the results of you abstract if appropriate.

Reply: We have added in the Abstract: “Conditional planning resulted in much larger sample sizes compared to those in the original trials (relative increase between achieved and calculated sample size ranged between 11-19%), …”.

Background:
“This typically leads to smaller required sample sizes compared to that obtained using
the conventional approach.” - I wonder if a disadvantage of this approach is that the sampling error increases with a small sample size in a trial. Could you comment on that?

Reply: Please see our response on your second comment from ‘Major comments’.

“Among others it is assumed that the true underlying effect size (which we assume is unbiasedly estimated by the summary effect) should not change over time. This is rather unlikely to happen in sham-RCTs as the learning curve applies to most surgical/minimally invasive interventions and studies of their efficacy show larger effects over time. Hence, the conditional power approach is both promising and challenging to be applied in this context.” - Does the fixed-effect (FE) model makes sense in this context? Clinical trials vary in their PICO by nature, which makes it hard to assume the FE model.

Reply: Please see our response on your first comment from ‘Major comments’. Our intention was to perform a random-effects meta-analysis, but heterogeneity being 0 ended up to a fixed-effect model.

“As heterogeneity was low in this setting, we performed fixed effect meta-analyses.” - Shouldn’t that be a choice based on the homogeneity of the trials according to the PICO scheme?

Reply: We have now rephrased this sentence to: “We intended to perform random-effects meta-analysis, but as between-study variance (r²) was estimated at 0 in this setting, our calculations are identical to those from a fixed effect meta-analysis.”

Box 1:
“The variability of the true treatment effect across trials should be low. Otherwise, even the planning of huge trials will not result in the anticipated conditional power.” - This again puts the FE model into question, or? Should the conditional power calculations be based the random-effects model?

Reply: Please see our response on your first comment from ‘Major comments’. Furthermore, we acknowledge that heterogeneity might be estimated to be zero due to large within-study variation. We write in the ‘Limitations’ section: “Even though our example can be representative of the size of the available sham-RCTs in any medical field, the small number of studies might have resulted in clinical heterogeneity not manifesting in the data as statistical heterogeneity.”.

Results:
Table 1 / meta-analysis: Is it appropriate to pool “24-hour ambulatory SBP” with “Daytime ambulatory SBP”?

Reply: Thank you for mentioning this. Yes, both measurements are highly consistent in changes of similar magnitude for the patient populations recruited in the individual trials.

Link for “Online Table 2”: Only “Table 2” is a link and leads to Table 2 in the manuscript, not to Online Table 2. Please check all link in the manuscript.

Reply: Done.

“heterogeneity variance” (p. 5) - Do you mean the between-study variance Tau^2? Please be more precise.

Reply: The text has been revised as follows: “The estimated between-study variance (r²) was zero.”.

“The total sample size randomized thereafter (in the fifth and sixth trials) could be considered redundant (226 study participants in total, of which 114 randomized to sham).” - I think this should be one key message of the paper exactly with this wording, i.e., how many patients would not receive sham. It adds weight for a clinically meaningful understanding of the methods presented.

Reply: Thank you for this comment. We now mention in Abstract: “Sequential meta-analysis provided firm evidence against the null hypothesis with the synthesis of the first four trials (755 patients, cumulative mean difference -2.75 (95%CI -4.93 to -0.58) favoring the active intervention)), with the fifth and sixth trial to be considered redundant (226 study participants in total, of which 114 randomized to sham).”

“The large sample sizes calculated with conditional power compared to that calculated by the trials is explained by the fact that the trialists chose unrealistically large anticipated mean differences.” - Sometimes you already interpret your results in the discussion section. Please move the explaining sentences rather to the discussion.

Reply: The above-mentioned sentence has been moved to the Discussion as suggested.

“Figure 3. Hypothetical prospectively planned sequential fixed effect meta-analysis framework (type I error=5%, power=90%).” - I suggest adding more sentences for explaining Figure 3. Not everyone is familiar with sequential meta-analysis so it might be important to help readers understand the idea of it.

Reply: Thank you for pointing this issue. We now mention in Methods: “Meta-analyses of medical interventions may result in false positive or false negative results, due to low statistical power when the required number of randomised participants or trials has not been reached. Under this scenario, trial sequential analysis of a meta-analysis may amend these problems by handling a meta-analysis of several RCTs in an analogous manner to interim analysis of a single RCT.”

Discussion:
Feasibility of large trials when trial authors would consider conditional power.

Reply: We are not sure what the reviewer means with this comment. Is it related to the previous comment about the large within-study variation if small trials are recommended by conditional planning approach? If yes, we refer to our response (and amendments in the paper) on this comment.

Stop when rejecting the null hypothesis is defined as the “final time point”, correct? How does this fit to clinical relevance of results? One could argue to stop if a threshold of irrelevance is not anymore included by the 95% CI for example.

Reply: A limitation of sequential methods lies on them being based on the principles of statistical significance. We write in the ‘Limitations’: “Second, sequential methods have inherited limitations since they have been mainly built on the principal of statistical significance and do not differentiate between clinically relevant and non-relevant effects. Along these lines, the Cochrane Handbook authors underline the methodological limitations that arise from sequential methods [42].»

We could indeed extend the methodology to account for clinically relevant results, but such an approach would require further development and evaluation of its feasibility.

Have prediction intervals a role in cumulative meta-analysis and sequential meta-analysis to describe heterogeneity?

Reply: Yes, prediction intervals fall naturally within the principles of cumulative meta-analysis, although they have not been used in this way. We refer to the Appendix A2 (a short paragraph) of our methodological paper: Nikolakopoulou A, Mavridis D, Egger M, Salanti G. Continuously updated network meta-analysis and statistical monitoring for timely decision-making. Statistical Methods in Medical Research. 2016 Jan.
We do not think that a discussion of the topic would fit in the current paper but please advise if this was the intention of your comment.

Is the R code available? You may add it to zenodo.

Reply: Yes. The R code is available upon request.

“Unless this is accounted for, conditional planning will not improve the design of sham-RCTs.” - Could you explicitly say what you mean by “this” to avoid misunderstandings in the conclusion? Somehow I find it hard to follow, maybe also because you word your statement with a negation. Please consider rewriting it.

Reply: Thank you for your comment. In our conclusive statement, “this” corresponds to the expected increase of the intervention effect in new studies. We have rephrased the conclusive statement as follows: “Unless this expected change is accounted for, conditional planning will not improve the design of sham-RCTs.”
We were pleased to receive the comments of the Reviewer. We are grateful for the very insightful comments that helped us to improve our work further. In the revised version of our manuscript we have addressed all of the suggestions/comments made by the Reviewer. In more detail:

Reviewer 2:

The authors present an empirical example comparing renal sympathetic denervation to sham intervention and provide data and calculations on power, cumulative meta-analysis, and sequential meta-analysis aiming to present the idea of conditional power. Many important points are well addressed and methodological aspects are well connected to the clinical relevance of the methods. I have some major and minor questions and encourage the authors to comment to improve the manuscript.

Reply: Thank you for your feedback.

Major comments:

Limitations: “performing random-effects would be a reasonable model choice” - Why
have you worked with the FE model then?

Reply: We thank the reviewer for this comment. In fact, our intention was to employ a random-effects meta-analysis model. As the between-study variance (r²) estimation was 0, this was equivalent to fixed-effect. We realize that this was not clearly stated, and we thus now have rephrased to clarify our approach. In particular, we write in the ‘Standard and sequential meta-analysis’ section: “We intended to perform random-effects meta-analysis, but as between-study variance (r²) was estimated at 0 in this setting, our calculations are identical to those from a fixed effect meta-analysis.”. We did not change the term “fixed-effect” in the abstract and the figure legends.

An alternative strategy would be to inform heterogeneity from empirical distributions (our references 40 and 41). However, such an approach would be appropriate in a prospective application of sequential meta-analysis and conditional planning, rather than a retrospective application, like the one presented in this paper. This is because in a prospective application, estimation of heterogeneity in the first stages of the reviews would be suboptimal. Moreover, imputing a value for heterogeneity would make results from “conventional” and “evidence-based” sample size calculations non-comparable.

We already wrote in the Discussion: “In a real application, imputing a value for heterogeneity, informed for example by empirical predictive distributions [40, 41], and performing random-effects would be a reasonable model choice”. And we now added: “Such an approach would be less reasonable in a retrospective application of the methods and would mitigate the comparability between conventional and evidence-based sample size calculations.”

If conditional power would say that only a “small trial” is needed: Would this be a problem regarding the sampling error? Should trials have a minimum size to avoid sampling error? As the trial gets smaller, the problem of chance increases, or? Could you comment on that and reflect you approach (conditional power)?

Reply: This is a topic that would benefit from further investigation. On one hand, a small trial should be a desirable outcome of the conditional planning method, on the other hand it would indeed be associated with greater within-study variation. Although this potentially large within-study variation is in theory incorporated in the conditional planning method (saying for example that an addition of such a study would render conclusive the updated meta-analysis effect, which is our goal), it would probably question the requirement of such individual study to be a standalone experiment. We added in the Discussion: “However, conditional planning might in theory result to recommendations of very small trials, which would be associated with great within-study variance and not be standalone experiments. Setting a minimum sample size for a future trial designed using conditional planning would be a potential remedy for such a situation.”.

This is an empirical example. Could a reasonable simulation study add value? If yes, how could it look like?

Reply: We thank the reviewer for this interesting comment. We do believe that a simulation study could contribute on the evaluation of the robustness of the method, and this could be a follow-up project. In such a simulation study, one should construct scenarios reflecting various assumptions being and not being met. We added under “Limitations”: “A comprehensive simulation study would be a more appropriate tool to investigate the performance and robustness of the method under a variety of settings.”

Minor comments:

Abstract:
You could add more numeric results in the results of you abstract if appropriate.

Reply: We have added in the Abstract: “Conditional planning resulted in much larger sample sizes compared to those in the original trials (relative increase between achieved and calculated sample size ranged between 11-19%), …”.

Background:
“This typically leads to smaller required sample sizes compared to that obtained using
the conventional approach.” - I wonder if a disadvantage of this approach is that the sampling error increases with a small sample size in a trial. Could you comment on that?

Reply: Please see our response on your second comment from ‘Major comments’.

“Among others it is assumed that the true underlying effect size (which we assume is unbiasedly estimated by the summary effect) should not change over time. This is rather unlikely to happen in sham-RCTs as the learning curve applies to most surgical/minimally invasive interventions and studies of their efficacy show larger effects over time. Hence, the conditional power approach is both promising and challenging to be applied in this context.” - Does the fixed-effect (FE) model makes sense in this context? Clinical trials vary in their PICO by nature, which makes it hard to assume the FE model.

Reply: Please see our response on your first comment from ‘Major comments’. Our intention was to perform a random-effects meta-analysis, but heterogeneity being 0 ended up to a fixed-effect model.

“As heterogeneity was low in this setting, we performed fixed effect meta-analyses.” - Shouldn’t that be a choice based on the homogeneity of the trials according to the PICO scheme?

Reply: We have now rephrased this sentence to: “We intended to perform random-effects meta-analysis, but as between-study variance (r²) was estimated at 0 in this setting, our calculations are identical to those from a fixed effect meta-analysis.”

Box 1:
“The variability of the true treatment effect across trials should be low. Otherwise, even the planning of huge trials will not result in the anticipated conditional power.” - This again puts the FE model into question, or? Should the conditional power calculations be based the random-effects model?

Reply: Please see our response on your first comment from ‘Major comments’. Furthermore, we acknowledge that heterogeneity might be estimated to be zero due to large within-study variation. We write in the ‘Limitations’ section: “Even though our example can be representative of the size of the available sham-RCTs in any medical field, the small number of studies might have resulted in clinical heterogeneity not manifesting in the data as statistical heterogeneity.”.

Results:
Table 1 / meta-analysis: Is it appropriate to pool “24-hour ambulatory SBP” with “Daytime ambulatory SBP”?

Reply: Thank you for mentioning this. Yes, both measurements are highly consistent in changes of similar magnitude for the patient populations recruited in the individual trials.

Link for “Online Table 2”: Only “Table 2” is a link and leads to Table 2 in the manuscript, not to Online Table 2. Please check all link in the manuscript.

Reply: Done.

“heterogeneity variance” (p. 5) - Do you mean the between-study variance Tau^2? Please be more precise.

Reply: The text has been revised as follows: “The estimated between-study variance (r²) was zero.”.

“The total sample size randomized thereafter (in the fifth and sixth trials) could be considered redundant (226 study participants in total, of which 114 randomized to sham).” - I think this should be one key message of the paper exactly with this wording, i.e., how many patients would not receive sham. It adds weight for a clinically meaningful understanding of the methods presented.

Reply: Thank you for this comment. We now mention in Abstract: “Sequential meta-analysis provided firm evidence against the null hypothesis with the synthesis of the first four trials (755 patients, cumulative mean difference -2.75 (95%CI -4.93 to -0.58) favoring the active intervention)), with the fifth and sixth trial to be considered redundant (226 study participants in total, of which 114 randomized to sham).”

“The large sample sizes calculated with conditional power compared to that calculated by the trials is explained by the fact that the trialists chose unrealistically large anticipated mean differences.” - Sometimes you already interpret your results in the discussion section. Please move the explaining sentences rather to the discussion.

Reply: The above-mentioned sentence has been moved to the Discussion as suggested.

“Figure 3. Hypothetical prospectively planned sequential fixed effect meta-analysis framework (type I error=5%, power=90%).” - I suggest adding more sentences for explaining Figure 3. Not everyone is familiar with sequential meta-analysis so it might be important to help readers understand the idea of it.

Reply: Thank you for pointing this issue. We now mention in Methods: “Meta-analyses of medical interventions may result in false positive or false negative results, due to low statistical power when the required number of randomised participants or trials has not been reached. Under this scenario, trial sequential analysis of a meta-analysis may amend these problems by handling a meta-analysis of several RCTs in an analogous manner to interim analysis of a single RCT.”

Discussion:
Feasibility of large trials when trial authors would consider conditional power.

Reply: We are not sure what the reviewer means with this comment. Is it related to the previous comment about the large within-study variation if small trials are recommended by conditional planning approach? If yes, we refer to our response (and amendments in the paper) on this comment.

Stop when rejecting the null hypothesis is defined as the “final time point”, correct? How does this fit to clinical relevance of results? One could argue to stop if a threshold of irrelevance is not anymore included by the 95% CI for example.

Reply: A limitation of sequential methods lies on them being based on the principles of statistical significance. We write in the ‘Limitations’: “Second, sequential methods have inherited limitations since they have been mainly built on the principal of statistical significance and do not differentiate between clinically relevant and non-relevant effects. Along these lines, the Cochrane Handbook authors underline the methodological limitations that arise from sequential methods [42].»

We could indeed extend the methodology to account for clinically relevant results, but such an approach would require further development and evaluation of its feasibility.

Have prediction intervals a role in cumulative meta-analysis and sequential meta-analysis to describe heterogeneity?

Reply: Yes, prediction intervals fall naturally within the principles of cumulative meta-analysis, although they have not been used in this way. We refer to the Appendix A2 (a short paragraph) of our methodological paper: Nikolakopoulou A, Mavridis D, Egger M, Salanti G. Continuously updated network meta-analysis and statistical monitoring for timely decision-making. Statistical Methods in Medical Research. 2016 Jan.
We do not think that a discussion of the topic would fit in the current paper but please advise if this was the intention of your comment.

Is the R code available? You may add it to zenodo.

Reply: Yes. The R code is available upon request.

“Unless this is accounted for, conditional planning will not improve the design of sham-RCTs.” - Could you explicitly say what you mean by “this” to avoid misunderstandings in the conclusion? Somehow I find it hard to follow, maybe also because you word your statement with a negation. Please consider rewriting it.

Reply: Thank you for your comment. In our conclusive statement, “this” corresponds to the expected increase of the intervention effect in new studies. We have rephrased the conclusive statement as follows: “Unless this expected change is accounted for, conditional planning will not improve the design of sham-RCTs.”
Competing Interests: None Close
Report a concern
Respond or Comment

COMMENTS ON THIS REPORT

Author Response 07 Nov 2022

Georgios Siontis, Department of Cardiology, University Hospital of Bern, Bern, Switzerland

07 Nov 2022

Author Response

We were pleased to receive the comments of the Reviewer. We are grateful for the very insightful comments that helped us to improve our work further. In the revised version ... Continue reading We were pleased to receive the comments of the Reviewer. We are grateful for the very insightful comments that helped us to improve our work further. In the revised version of our manuscript we have addressed all of the suggestions/comments made by the Reviewer. In more detail:

Reviewer 2:

The authors present an empirical example comparing renal sympathetic denervation to sham intervention and provide data and calculations on power, cumulative meta-analysis, and sequential meta-analysis aiming to present the idea of conditional power. Many important points are well addressed and methodological aspects are well connected to the clinical relevance of the methods. I have some major and minor questions and encourage the authors to comment to improve the manuscript.

Reply: Thank you for your feedback.

Major comments:

Limitations: “performing random-effects would be a reasonable model choice” - Why
have you worked with the FE model then?

Reply: We thank the reviewer for this comment. In fact, our intention was to employ a random-effects meta-analysis model. As the between-study variance (r²) estimation was 0, this was equivalent to fixed-effect. We realize that this was not clearly stated, and we thus now have rephrased to clarify our approach. In particular, we write in the ‘Standard and sequential meta-analysis’ section: “We intended to perform random-effects meta-analysis, but as between-study variance (r²) was estimated at 0 in this setting, our calculations are identical to those from a fixed effect meta-analysis.”. We did not change the term “fixed-effect” in the abstract and the figure legends.

An alternative strategy would be to inform heterogeneity from empirical distributions (our references 40 and 41). However, such an approach would be appropriate in a prospective application of sequential meta-analysis and conditional planning, rather than a retrospective application, like the one presented in this paper. This is because in a prospective application, estimation of heterogeneity in the first stages of the reviews would be suboptimal. Moreover, imputing a value for heterogeneity would make results from “conventional” and “evidence-based” sample size calculations non-comparable.

We already wrote in the Discussion: “In a real application, imputing a value for heterogeneity, informed for example by empirical predictive distributions [40, 41], and performing random-effects would be a reasonable model choice”. And we now added: “Such an approach would be less reasonable in a retrospective application of the methods and would mitigate the comparability between conventional and evidence-based sample size calculations.”

If conditional power would say that only a “small trial” is needed: Would this be a problem regarding the sampling error? Should trials have a minimum size to avoid sampling error? As the trial gets smaller, the problem of chance increases, or? Could you comment on that and reflect you approach (conditional power)?

Reply: This is a topic that would benefit from further investigation. On one hand, a small trial should be a desirable outcome of the conditional planning method, on the other hand it would indeed be associated with greater within-study variation. Although this potentially large within-study variation is in theory incorporated in the conditional planning method (saying for example that an addition of such a study would render conclusive the updated meta-analysis effect, which is our goal), it would probably question the requirement of such individual study to be a standalone experiment. We added in the Discussion: “However, conditional planning might in theory result to recommendations of very small trials, which would be associated with great within-study variance and not be standalone experiments. Setting a minimum sample size for a future trial designed using conditional planning would be a potential remedy for such a situation.”.

This is an empirical example. Could a reasonable simulation study add value? If yes, how could it look like?

Reply: We thank the reviewer for this interesting comment. We do believe that a simulation study could contribute on the evaluation of the robustness of the method, and this could be a follow-up project. In such a simulation study, one should construct scenarios reflecting various assumptions being and not being met. We added under “Limitations”: “A comprehensive simulation study would be a more appropriate tool to investigate the performance and robustness of the method under a variety of settings.”

Minor comments:

Abstract:
You could add more numeric results in the results of you abstract if appropriate.

Reply: We have added in the Abstract: “Conditional planning resulted in much larger sample sizes compared to those in the original trials (relative increase between achieved and calculated sample size ranged between 11-19%), …”.

Background:
“This typically leads to smaller required sample sizes compared to that obtained using
the conventional approach.” - I wonder if a disadvantage of this approach is that the sampling error increases with a small sample size in a trial. Could you comment on that?

Reply: Please see our response on your second comment from ‘Major comments’.

“Among others it is assumed that the true underlying effect size (which we assume is unbiasedly estimated by the summary effect) should not change over time. This is rather unlikely to happen in sham-RCTs as the learning curve applies to most surgical/minimally invasive interventions and studies of their efficacy show larger effects over time. Hence, the conditional power approach is both promising and challenging to be applied in this context.” - Does the fixed-effect (FE) model makes sense in this context? Clinical trials vary in their PICO by nature, which makes it hard to assume the FE model.

Reply: Please see our response on your first comment from ‘Major comments’. Our intention was to perform a random-effects meta-analysis, but heterogeneity being 0 ended up to a fixed-effect model.

“As heterogeneity was low in this setting, we performed fixed effect meta-analyses.” - Shouldn’t that be a choice based on the homogeneity of the trials according to the PICO scheme?

Reply: We have now rephrased this sentence to: “We intended to perform random-effects meta-analysis, but as between-study variance (r²) was estimated at 0 in this setting, our calculations are identical to those from a fixed effect meta-analysis.”

Box 1:
“The variability of the true treatment effect across trials should be low. Otherwise, even the planning of huge trials will not result in the anticipated conditional power.” - This again puts the FE model into question, or? Should the conditional power calculations be based the random-effects model?

Reply: Please see our response on your first comment from ‘Major comments’. Furthermore, we acknowledge that heterogeneity might be estimated to be zero due to large within-study variation. We write in the ‘Limitations’ section: “Even though our example can be representative of the size of the available sham-RCTs in any medical field, the small number of studies might have resulted in clinical heterogeneity not manifesting in the data as statistical heterogeneity.”.

Results:
Table 1 / meta-analysis: Is it appropriate to pool “24-hour ambulatory SBP” with “Daytime ambulatory SBP”?

Reply: Thank you for mentioning this. Yes, both measurements are highly consistent in changes of similar magnitude for the patient populations recruited in the individual trials.

Link for “Online Table 2”: Only “Table 2” is a link and leads to Table 2 in the manuscript, not to Online Table 2. Please check all link in the manuscript.

Reply: Done.

“heterogeneity variance” (p. 5) - Do you mean the between-study variance Tau^2? Please be more precise.

Reply: The text has been revised as follows: “The estimated between-study variance (r²) was zero.”.

“The total sample size randomized thereafter (in the fifth and sixth trials) could be considered redundant (226 study participants in total, of which 114 randomized to sham).” - I think this should be one key message of the paper exactly with this wording, i.e., how many patients would not receive sham. It adds weight for a clinically meaningful understanding of the methods presented.

Reply: Thank you for this comment. We now mention in Abstract: “Sequential meta-analysis provided firm evidence against the null hypothesis with the synthesis of the first four trials (755 patients, cumulative mean difference -2.75 (95%CI -4.93 to -0.58) favoring the active intervention)), with the fifth and sixth trial to be considered redundant (226 study participants in total, of which 114 randomized to sham).”

“The large sample sizes calculated with conditional power compared to that calculated by the trials is explained by the fact that the trialists chose unrealistically large anticipated mean differences.” - Sometimes you already interpret your results in the discussion section. Please move the explaining sentences rather to the discussion.

Reply: The above-mentioned sentence has been moved to the Discussion as suggested.

“Figure 3. Hypothetical prospectively planned sequential fixed effect meta-analysis framework (type I error=5%, power=90%).” - I suggest adding more sentences for explaining Figure 3. Not everyone is familiar with sequential meta-analysis so it might be important to help readers understand the idea of it.

Reply: Thank you for pointing this issue. We now mention in Methods: “Meta-analyses of medical interventions may result in false positive or false negative results, due to low statistical power when the required number of randomised participants or trials has not been reached. Under this scenario, trial sequential analysis of a meta-analysis may amend these problems by handling a meta-analysis of several RCTs in an analogous manner to interim analysis of a single RCT.”

Discussion:
Feasibility of large trials when trial authors would consider conditional power.

Reply: We are not sure what the reviewer means with this comment. Is it related to the previous comment about the large within-study variation if small trials are recommended by conditional planning approach? If yes, we refer to our response (and amendments in the paper) on this comment.

Stop when rejecting the null hypothesis is defined as the “final time point”, correct? How does this fit to clinical relevance of results? One could argue to stop if a threshold of irrelevance is not anymore included by the 95% CI for example.

Reply: A limitation of sequential methods lies on them being based on the principles of statistical significance. We write in the ‘Limitations’: “Second, sequential methods have inherited limitations since they have been mainly built on the principal of statistical significance and do not differentiate between clinically relevant and non-relevant effects. Along these lines, the Cochrane Handbook authors underline the methodological limitations that arise from sequential methods [42].»

We could indeed extend the methodology to account for clinically relevant results, but such an approach would require further development and evaluation of its feasibility.

Have prediction intervals a role in cumulative meta-analysis and sequential meta-analysis to describe heterogeneity?

Reply: Yes, prediction intervals fall naturally within the principles of cumulative meta-analysis, although they have not been used in this way. We refer to the Appendix A2 (a short paragraph) of our methodological paper: Nikolakopoulou A, Mavridis D, Egger M, Salanti G. Continuously updated network meta-analysis and statistical monitoring for timely decision-making. Statistical Methods in Medical Research. 2016 Jan.
We do not think that a discussion of the topic would fit in the current paper but please advise if this was the intention of your comment.

Is the R code available? You may add it to zenodo.

Reply: Yes. The R code is available upon request.

“Unless this is accounted for, conditional planning will not improve the design of sham-RCTs.” - Could you explicitly say what you mean by “this” to avoid misunderstandings in the conclusion? Somehow I find it hard to follow, maybe also because you word your statement with a negation. Please consider rewriting it.

Reply: Thank you for your comment. In our conclusive statement, “this” corresponds to the expected increase of the intervention effect in new studies. We have rephrased the conclusive statement as follows: “Unless this expected change is accounted for, conditional planning will not improve the design of sham-RCTs.”
We were pleased to receive the comments of the Reviewer. We are grateful for the very insightful comments that helped us to improve our work further. In the revised version of our manuscript we have addressed all of the suggestions/comments made by the Reviewer. In more detail:

Reviewer 2:

The authors present an empirical example comparing renal sympathetic denervation to sham intervention and provide data and calculations on power, cumulative meta-analysis, and sequential meta-analysis aiming to present the idea of conditional power. Many important points are well addressed and methodological aspects are well connected to the clinical relevance of the methods. I have some major and minor questions and encourage the authors to comment to improve the manuscript.

Reply: Thank you for your feedback.

Major comments:

Limitations: “performing random-effects would be a reasonable model choice” - Why
have you worked with the FE model then?

Reply: We thank the reviewer for this comment. In fact, our intention was to employ a random-effects meta-analysis model. As the between-study variance (r²) estimation was 0, this was equivalent to fixed-effect. We realize that this was not clearly stated, and we thus now have rephrased to clarify our approach. In particular, we write in the ‘Standard and sequential meta-analysis’ section: “We intended to perform random-effects meta-analysis, but as between-study variance (r²) was estimated at 0 in this setting, our calculations are identical to those from a fixed effect meta-analysis.”. We did not change the term “fixed-effect” in the abstract and the figure legends.

An alternative strategy would be to inform heterogeneity from empirical distributions (our references 40 and 41). However, such an approach would be appropriate in a prospective application of sequential meta-analysis and conditional planning, rather than a retrospective application, like the one presented in this paper. This is because in a prospective application, estimation of heterogeneity in the first stages of the reviews would be suboptimal. Moreover, imputing a value for heterogeneity would make results from “conventional” and “evidence-based” sample size calculations non-comparable.

We already wrote in the Discussion: “In a real application, imputing a value for heterogeneity, informed for example by empirical predictive distributions [40, 41], and performing random-effects would be a reasonable model choice”. And we now added: “Such an approach would be less reasonable in a retrospective application of the methods and would mitigate the comparability between conventional and evidence-based sample size calculations.”

If conditional power would say that only a “small trial” is needed: Would this be a problem regarding the sampling error? Should trials have a minimum size to avoid sampling error? As the trial gets smaller, the problem of chance increases, or? Could you comment on that and reflect you approach (conditional power)?

Reply: This is a topic that would benefit from further investigation. On one hand, a small trial should be a desirable outcome of the conditional planning method, on the other hand it would indeed be associated with greater within-study variation. Although this potentially large within-study variation is in theory incorporated in the conditional planning method (saying for example that an addition of such a study would render conclusive the updated meta-analysis effect, which is our goal), it would probably question the requirement of such individual study to be a standalone experiment. We added in the Discussion: “However, conditional planning might in theory result to recommendations of very small trials, which would be associated with great within-study variance and not be standalone experiments. Setting a minimum sample size for a future trial designed using conditional planning would be a potential remedy for such a situation.”.

This is an empirical example. Could a reasonable simulation study add value? If yes, how could it look like?

Reply: We thank the reviewer for this interesting comment. We do believe that a simulation study could contribute on the evaluation of the robustness of the method, and this could be a follow-up project. In such a simulation study, one should construct scenarios reflecting various assumptions being and not being met. We added under “Limitations”: “A comprehensive simulation study would be a more appropriate tool to investigate the performance and robustness of the method under a variety of settings.”

Minor comments:

Abstract:
You could add more numeric results in the results of you abstract if appropriate.

Reply: We have added in the Abstract: “Conditional planning resulted in much larger sample sizes compared to those in the original trials (relative increase between achieved and calculated sample size ranged between 11-19%), …”.

Background:
“This typically leads to smaller required sample sizes compared to that obtained using
the conventional approach.” - I wonder if a disadvantage of this approach is that the sampling error increases with a small sample size in a trial. Could you comment on that?

Reply: Please see our response on your second comment from ‘Major comments’.

“Among others it is assumed that the true underlying effect size (which we assume is unbiasedly estimated by the summary effect) should not change over time. This is rather unlikely to happen in sham-RCTs as the learning curve applies to most surgical/minimally invasive interventions and studies of their efficacy show larger effects over time. Hence, the conditional power approach is both promising and challenging to be applied in this context.” - Does the fixed-effect (FE) model makes sense in this context? Clinical trials vary in their PICO by nature, which makes it hard to assume the FE model.

Reply: Please see our response on your first comment from ‘Major comments’. Our intention was to perform a random-effects meta-analysis, but heterogeneity being 0 ended up to a fixed-effect model.

“As heterogeneity was low in this setting, we performed fixed effect meta-analyses.” - Shouldn’t that be a choice based on the homogeneity of the trials according to the PICO scheme?

Reply: We have now rephrased this sentence to: “We intended to perform random-effects meta-analysis, but as between-study variance (r²) was estimated at 0 in this setting, our calculations are identical to those from a fixed effect meta-analysis.”

Box 1:
“The variability of the true treatment effect across trials should be low. Otherwise, even the planning of huge trials will not result in the anticipated conditional power.” - This again puts the FE model into question, or? Should the conditional power calculations be based the random-effects model?

Reply: Please see our response on your first comment from ‘Major comments’. Furthermore, we acknowledge that heterogeneity might be estimated to be zero due to large within-study variation. We write in the ‘Limitations’ section: “Even though our example can be representative of the size of the available sham-RCTs in any medical field, the small number of studies might have resulted in clinical heterogeneity not manifesting in the data as statistical heterogeneity.”.

Results:
Table 1 / meta-analysis: Is it appropriate to pool “24-hour ambulatory SBP” with “Daytime ambulatory SBP”?

Reply: Thank you for mentioning this. Yes, both measurements are highly consistent in changes of similar magnitude for the patient populations recruited in the individual trials.

Link for “Online Table 2”: Only “Table 2” is a link and leads to Table 2 in the manuscript, not to Online Table 2. Please check all link in the manuscript.

Reply: Done.

“heterogeneity variance” (p. 5) - Do you mean the between-study variance Tau^2? Please be more precise.

Reply: The text has been revised as follows: “The estimated between-study variance (r²) was zero.”.

“The total sample size randomized thereafter (in the fifth and sixth trials) could be considered redundant (226 study participants in total, of which 114 randomized to sham).” - I think this should be one key message of the paper exactly with this wording, i.e., how many patients would not receive sham. It adds weight for a clinically meaningful understanding of the methods presented.

Reply: Thank you for this comment. We now mention in Abstract: “Sequential meta-analysis provided firm evidence against the null hypothesis with the synthesis of the first four trials (755 patients, cumulative mean difference -2.75 (95%CI -4.93 to -0.58) favoring the active intervention)), with the fifth and sixth trial to be considered redundant (226 study participants in total, of which 114 randomized to sham).”

“The large sample sizes calculated with conditional power compared to that calculated by the trials is explained by the fact that the trialists chose unrealistically large anticipated mean differences.” - Sometimes you already interpret your results in the discussion section. Please move the explaining sentences rather to the discussion.

Reply: The above-mentioned sentence has been moved to the Discussion as suggested.

“Figure 3. Hypothetical prospectively planned sequential fixed effect meta-analysis framework (type I error=5%, power=90%).” - I suggest adding more sentences for explaining Figure 3. Not everyone is familiar with sequential meta-analysis so it might be important to help readers understand the idea of it.

Reply: Thank you for pointing this issue. We now mention in Methods: “Meta-analyses of medical interventions may result in false positive or false negative results, due to low statistical power when the required number of randomised participants or trials has not been reached. Under this scenario, trial sequential analysis of a meta-analysis may amend these problems by handling a meta-analysis of several RCTs in an analogous manner to interim analysis of a single RCT.”

Discussion:
Feasibility of large trials when trial authors would consider conditional power.

Reply: We are not sure what the reviewer means with this comment. Is it related to the previous comment about the large within-study variation if small trials are recommended by conditional planning approach? If yes, we refer to our response (and amendments in the paper) on this comment.

Stop when rejecting the null hypothesis is defined as the “final time point”, correct? How does this fit to clinical relevance of results? One could argue to stop if a threshold of irrelevance is not anymore included by the 95% CI for example.

Reply: A limitation of sequential methods lies on them being based on the principles of statistical significance. We write in the ‘Limitations’: “Second, sequential methods have inherited limitations since they have been mainly built on the principal of statistical significance and do not differentiate between clinically relevant and non-relevant effects. Along these lines, the Cochrane Handbook authors underline the methodological limitations that arise from sequential methods [42].»

We could indeed extend the methodology to account for clinically relevant results, but such an approach would require further development and evaluation of its feasibility.

Have prediction intervals a role in cumulative meta-analysis and sequential meta-analysis to describe heterogeneity?

Reply: Yes, prediction intervals fall naturally within the principles of cumulative meta-analysis, although they have not been used in this way. We refer to the Appendix A2 (a short paragraph) of our methodological paper: Nikolakopoulou A, Mavridis D, Egger M, Salanti G. Continuously updated network meta-analysis and statistical monitoring for timely decision-making. Statistical Methods in Medical Research. 2016 Jan.
We do not think that a discussion of the topic would fit in the current paper but please advise if this was the intention of your comment.

Is the R code available? You may add it to zenodo.

Reply: Yes. The R code is available upon request.

“Unless this is accounted for, conditional planning will not improve the design of sham-RCTs.” - Could you explicitly say what you mean by “this” to avoid misunderstandings in the conclusion? Somehow I find it hard to follow, maybe also because you word your statement with a negation. Please consider rewriting it.

Reply: Thank you for your comment. In our conclusive statement, “this” corresponds to the expected increase of the intervention effect in new studies. We have rephrased the conclusive statement as follows: “Unless this expected change is accounted for, conditional planning will not improve the design of sham-RCTs.”
Competing Interests: None Close
Report a concern

Views

Reviewer Report 11 Apr 2022

Thomas Karagiannis, Clinical Research and Evidence-Based Medicine Unit, Second Medical Department, Aristotle University of Thessaloniki, Thessaloniki, Greece; Diabetes Centre, Second Medical Department, Aristotle University of Thessaloniki, Thessaloniki, Greece

Approved with Reservations

https://doi.org/10.5256/f1000research.119949.r129149

I do not have any particular comments on the methodological aspects of the paper as it appears to be methodologically sound.

In my opinion, the most important limitation of this methodological study is that the conditional sample size calculation method, as presented by the authors, is based on the principle of statistical significance (i.e. the treatment effect as produced by a meta-analysis of available trials) and not on the rationale/principle of what value is considered clinically relevant (i.e. a conventional approach in which the anticipated treatment effect of an intervention is based on the minimal clinically important difference). I believe that the authors should emphasize this issue in their discussion; I do realize that they make mention to this limitation in the discussion (Limitations section), but I think it should be further elaborated in the context of clinical/practical implications. For example, one might wonder whether an alternative approach combining elements of both the conventional and the conditional approaches might be more reasonable when designing a new trial, i.e. use the minimal clinically important difference in sample calculation and adjust the planned sample size based on previous similar trials in the sense that the cumulative sample of all available trials (be means of a meta-analysis) would be adequately powered to collectively assess the minimal clinically important effect estimate.

Regardless, I believe that it is noteworthy that this paper highlights various shortcomings/limitations of individual trials when it comes to sample size calculation, such as the use of “reverse engineering” (calculation is based on practical or unspecified considerations resulting in unrealistically large assumed treatment effects which in turn lead to inadequate sample size). I was also interested to see that, based on table 2, the replicated/recalculated sample size (975+488) in SYMPLICITY HTN-3 trial was much larger the sample size originally calculated in the actual trial (316+158), which implicates that sample size calculation in individual studies can still be flawed even when a minimal clinically important difference (not reverse engineering) is used.

Finally, I noticed in Box 2 that SYMPLICITY HTN-2 trial is mentioned. I am wondering why this trial was not included in the pool of studies.

Is the rationale for developing the new method (or application) clearly explained?

Yes
Is the description of the method technically sound?

Yes
Are sufficient details provided to allow replication of the method development and its use by others?

Yes
If any results are presented, are all the source data underlying the results available to ensure full reproducibility?

Yes
Are the conclusions about the method and its performance adequately supported by the findings presented in the article?

Yes

Competing Interests: No competing interests were disclosed.

Reviewer Expertise: Evidence synthesis, Systematic reviews, Diabetes Mellitus

CITE

Report a concern

Author Response 07 Nov 2022

Georgios Siontis, Department of Cardiology, University Hospital of Bern, Bern, Switzerland

07 Nov 2022

Author Response

We were pleased to receive the comments of the Reviewer. We are grateful for the very insightful comments that helped us to improve our work further. In the revised version ... Continue reading We were pleased to receive the comments of the Reviewer. We are grateful for the very insightful comments that helped us to improve our work further. In the revised version of our manuscript we have addressed all of the suggestions/comments made by the reviewer. In more detail:

Reviewer 1:

I do not have any particular comments on the methodological aspects of the paper as it appears to be methodologically sound.

Reply: Thank you for your feedback.

In my opinion, the most important limitation of this methodological study is that the conditional sample size calculation method, as presented by the authors, is based on the principle of statistical significance (i.e. the treatment effect as produced by a meta-analysis of available trials) and not on the rationale/principle of what value is considered clinically relevant (i.e. a conventional approach in which the anticipated treatment effect of an intervention is based on the minimal clinically important difference). I believe that the authors should emphasize this issue in their discussion; I do realize that they make mention to this limitation in the discussion (Limitations section), but I think it should be further elaborated in the context of clinical/practical implications. For example, one might wonder whether an alternative approach combining elements of both the conventional and the conditional approaches might be more reasonable when designing a new trial, i.e. use the minimal clinically important difference in sample calculation and adjust the planned sample size based on previous similar trials in the sense that the cumulative sample of all available trials (be means of a meta-analysis) would be adequately powered to collectively assess the minimal clinically important effect estimate.

Reply: We thank the reviewer for this thought-provoking comment. We certainly agree that methodological developments, along with interpretation of findings in clinical applications, should move away from the principle of statistical significance. We argue, however, that conventional sample size calculations are also based on statistical significance, despite making use of a minimal clinically important difference. What is measured (in conventional sample size calculations) is the expected sample size to detect the minimal clinically important difference as statistically significant. Thus, conditional power used in this paper in fact makes the two approaches comparable.

Alternative evidence-based sample size calculation approaches include planning new studies based on a desired precision of the updated meta-analysis effect. We write in the Discussion: “Along these line, previous evaluations have shown the appropriateness of conditional planning under different scenarios of inconclusive meta-analysis (confidence interval of the summary effect includes effect sizes with different implications) [3].” And we also added: “Further development and establishment of evidence-base sample size calculation approaches that would move away from the principles of statistical significance would be an important step forward in the field.”.

Regardless, I believe that it is noteworthy that this paper highlights various shortcomings/limitations of individual trials when it comes to sample size calculation, such as the use of “reverse engineering” (calculation is based on practical or unspecified considerations resulting in unrealistically large assumed treatment effects which in turn lead to inadequate sample size). I was also interested to see that, based on table 2, the replicated/recalculated sample size (975+488) in SYMPLICITY HTN-3 trial was much larger the sample size originally calculated in the actual trial (316+158), which implicates that sample size calculation in individual studies can still be flawed even when a minimal clinically important difference (not reverse engineering) is used.

Reply: We thank the reviewer for this concrete comment.

Finally, I noticed in Box 2 that SYMPLICITY HTN-2 trial is mentioned. I am wondering why this trial was not included in the pool of studies.

Reply: Thank you for pointing this. Indeed, SYMPLICITY HTN-2 trial was not included in the current analysis because the control arm was “standard of care” and not a sham intervention.
We were pleased to receive the comments of the Reviewer. We are grateful for the very insightful comments that helped us to improve our work further. In the revised version of our manuscript we have addressed all of the suggestions/comments made by the reviewer. In more detail:

Reviewer 1:

I do not have any particular comments on the methodological aspects of the paper as it appears to be methodologically sound.

Reply: Thank you for your feedback.

In my opinion, the most important limitation of this methodological study is that the conditional sample size calculation method, as presented by the authors, is based on the principle of statistical significance (i.e. the treatment effect as produced by a meta-analysis of available trials) and not on the rationale/principle of what value is considered clinically relevant (i.e. a conventional approach in which the anticipated treatment effect of an intervention is based on the minimal clinically important difference). I believe that the authors should emphasize this issue in their discussion; I do realize that they make mention to this limitation in the discussion (Limitations section), but I think it should be further elaborated in the context of clinical/practical implications. For example, one might wonder whether an alternative approach combining elements of both the conventional and the conditional approaches might be more reasonable when designing a new trial, i.e. use the minimal clinically important difference in sample calculation and adjust the planned sample size based on previous similar trials in the sense that the cumulative sample of all available trials (be means of a meta-analysis) would be adequately powered to collectively assess the minimal clinically important effect estimate.

Reply: We thank the reviewer for this thought-provoking comment. We certainly agree that methodological developments, along with interpretation of findings in clinical applications, should move away from the principle of statistical significance. We argue, however, that conventional sample size calculations are also based on statistical significance, despite making use of a minimal clinically important difference. What is measured (in conventional sample size calculations) is the expected sample size to detect the minimal clinically important difference as statistically significant. Thus, conditional power used in this paper in fact makes the two approaches comparable.

Alternative evidence-based sample size calculation approaches include planning new studies based on a desired precision of the updated meta-analysis effect. We write in the Discussion: “Along these line, previous evaluations have shown the appropriateness of conditional planning under different scenarios of inconclusive meta-analysis (confidence interval of the summary effect includes effect sizes with different implications) [3].” And we also added: “Further development and establishment of evidence-base sample size calculation approaches that would move away from the principles of statistical significance would be an important step forward in the field.”.

Regardless, I believe that it is noteworthy that this paper highlights various shortcomings/limitations of individual trials when it comes to sample size calculation, such as the use of “reverse engineering” (calculation is based on practical or unspecified considerations resulting in unrealistically large assumed treatment effects which in turn lead to inadequate sample size). I was also interested to see that, based on table 2, the replicated/recalculated sample size (975+488) in SYMPLICITY HTN-3 trial was much larger the sample size originally calculated in the actual trial (316+158), which implicates that sample size calculation in individual studies can still be flawed even when a minimal clinically important difference (not reverse engineering) is used.

Reply: We thank the reviewer for this concrete comment.

Finally, I noticed in Box 2 that SYMPLICITY HTN-2 trial is mentioned. I am wondering why this trial was not included in the pool of studies.

Reply: Thank you for pointing this. Indeed, SYMPLICITY HTN-2 trial was not included in the current analysis because the control arm was “standard of care” and not a sham intervention.
Competing Interests: None Close
Report a concern
Respond or Comment

COMMENTS ON THIS REPORT

Author Response 07 Nov 2022

Georgios Siontis, Department of Cardiology, University Hospital of Bern, Bern, Switzerland

07 Nov 2022

Author Response

We were pleased to receive the comments of the Reviewer. We are grateful for the very insightful comments that helped us to improve our work further. In the revised version ... Continue reading We were pleased to receive the comments of the Reviewer. We are grateful for the very insightful comments that helped us to improve our work further. In the revised version of our manuscript we have addressed all of the suggestions/comments made by the reviewer. In more detail:

Reviewer 1:

I do not have any particular comments on the methodological aspects of the paper as it appears to be methodologically sound.

Reply: Thank you for your feedback.

In my opinion, the most important limitation of this methodological study is that the conditional sample size calculation method, as presented by the authors, is based on the principle of statistical significance (i.e. the treatment effect as produced by a meta-analysis of available trials) and not on the rationale/principle of what value is considered clinically relevant (i.e. a conventional approach in which the anticipated treatment effect of an intervention is based on the minimal clinically important difference). I believe that the authors should emphasize this issue in their discussion; I do realize that they make mention to this limitation in the discussion (Limitations section), but I think it should be further elaborated in the context of clinical/practical implications. For example, one might wonder whether an alternative approach combining elements of both the conventional and the conditional approaches might be more reasonable when designing a new trial, i.e. use the minimal clinically important difference in sample calculation and adjust the planned sample size based on previous similar trials in the sense that the cumulative sample of all available trials (be means of a meta-analysis) would be adequately powered to collectively assess the minimal clinically important effect estimate.

Reply: We thank the reviewer for this thought-provoking comment. We certainly agree that methodological developments, along with interpretation of findings in clinical applications, should move away from the principle of statistical significance. We argue, however, that conventional sample size calculations are also based on statistical significance, despite making use of a minimal clinically important difference. What is measured (in conventional sample size calculations) is the expected sample size to detect the minimal clinically important difference as statistically significant. Thus, conditional power used in this paper in fact makes the two approaches comparable.

Alternative evidence-based sample size calculation approaches include planning new studies based on a desired precision of the updated meta-analysis effect. We write in the Discussion: “Along these line, previous evaluations have shown the appropriateness of conditional planning under different scenarios of inconclusive meta-analysis (confidence interval of the summary effect includes effect sizes with different implications) [3].” And we also added: “Further development and establishment of evidence-base sample size calculation approaches that would move away from the principles of statistical significance would be an important step forward in the field.”.

Regardless, I believe that it is noteworthy that this paper highlights various shortcomings/limitations of individual trials when it comes to sample size calculation, such as the use of “reverse engineering” (calculation is based on practical or unspecified considerations resulting in unrealistically large assumed treatment effects which in turn lead to inadequate sample size). I was also interested to see that, based on table 2, the replicated/recalculated sample size (975+488) in SYMPLICITY HTN-3 trial was much larger the sample size originally calculated in the actual trial (316+158), which implicates that sample size calculation in individual studies can still be flawed even when a minimal clinically important difference (not reverse engineering) is used.

Reply: We thank the reviewer for this concrete comment.

Finally, I noticed in Box 2 that SYMPLICITY HTN-2 trial is mentioned. I am wondering why this trial was not included in the pool of studies.

Reply: Thank you for pointing this. Indeed, SYMPLICITY HTN-2 trial was not included in the current analysis because the control arm was “standard of care” and not a sham intervention.
We were pleased to receive the comments of the Reviewer. We are grateful for the very insightful comments that helped us to improve our work further. In the revised version of our manuscript we have addressed all of the suggestions/comments made by the reviewer. In more detail:

Reviewer 1:

I do not have any particular comments on the methodological aspects of the paper as it appears to be methodologically sound.

Reply: Thank you for your feedback.

In my opinion, the most important limitation of this methodological study is that the conditional sample size calculation method, as presented by the authors, is based on the principle of statistical significance (i.e. the treatment effect as produced by a meta-analysis of available trials) and not on the rationale/principle of what value is considered clinically relevant (i.e. a conventional approach in which the anticipated treatment effect of an intervention is based on the minimal clinically important difference). I believe that the authors should emphasize this issue in their discussion; I do realize that they make mention to this limitation in the discussion (Limitations section), but I think it should be further elaborated in the context of clinical/practical implications. For example, one might wonder whether an alternative approach combining elements of both the conventional and the conditional approaches might be more reasonable when designing a new trial, i.e. use the minimal clinically important difference in sample calculation and adjust the planned sample size based on previous similar trials in the sense that the cumulative sample of all available trials (be means of a meta-analysis) would be adequately powered to collectively assess the minimal clinically important effect estimate.

Reply: We thank the reviewer for this thought-provoking comment. We certainly agree that methodological developments, along with interpretation of findings in clinical applications, should move away from the principle of statistical significance. We argue, however, that conventional sample size calculations are also based on statistical significance, despite making use of a minimal clinically important difference. What is measured (in conventional sample size calculations) is the expected sample size to detect the minimal clinically important difference as statistically significant. Thus, conditional power used in this paper in fact makes the two approaches comparable.

Alternative evidence-based sample size calculation approaches include planning new studies based on a desired precision of the updated meta-analysis effect. We write in the Discussion: “Along these line, previous evaluations have shown the appropriateness of conditional planning under different scenarios of inconclusive meta-analysis (confidence interval of the summary effect includes effect sizes with different implications) [3].” And we also added: “Further development and establishment of evidence-base sample size calculation approaches that would move away from the principles of statistical significance would be an important step forward in the field.”.

Regardless, I believe that it is noteworthy that this paper highlights various shortcomings/limitations of individual trials when it comes to sample size calculation, such as the use of “reverse engineering” (calculation is based on practical or unspecified considerations resulting in unrealistically large assumed treatment effects which in turn lead to inadequate sample size). I was also interested to see that, based on table 2, the replicated/recalculated sample size (975+488) in SYMPLICITY HTN-3 trial was much larger the sample size originally calculated in the actual trial (316+158), which implicates that sample size calculation in individual studies can still be flawed even when a minimal clinically important difference (not reverse engineering) is used.

Reply: We thank the reviewer for this concrete comment.

Finally, I noticed in Box 2 that SYMPLICITY HTN-2 trial is mentioned. I am wondering why this trial was not included in the pool of studies.

Reply: Thank you for pointing this. Indeed, SYMPLICITY HTN-2 trial was not included in the current analysis because the control arm was “standard of care” and not a sham intervention.
Competing Interests: None Close
Report a concern

Comments on this article Comments (0)

Version 2

VERSION 2 PUBLISHED 24 Jan 2022

Open Peer Review

Reviewer Status

Reviewer Reports

	Invited Reviewers
	1	2
Version 2 (revision) 07 Nov 22	read	read
Version 1 24 Jan 22	read	read

Thomas Karagiannis, Aristotle University of Thessaloniki, Thessaloniki, Greece; Aristotle University of Thessaloniki, Thessaloniki, Greece
Waldemar Siemens, Medical Center - University of Freiburg, Faculty of Medicine, Freiburg, Germany; Cochrane Germany Foundation, Freiburg, Germany

Comments on this article

All Comments(0)

Add a comment

Browse by related subjects

Back to all reports

Reviewer Report

7 Views

16 Nov 2022 | for Version 2

Waldemar Siemens, Institute for Evidence in Medicine, Medical Center - University of Freiburg, Faculty of Medicine, Freiburg, Germany; Cochrane Germany, Cochrane Germany Foundation, Freiburg, Germany

7 Views Cite this report Responses(0)

Approved

The authors revised the paper and addressed all comments thoroughly. Congratulations to this work.

Competing Interests

No competing interests were disclosed.

Reviewer Expertise

Meta-research, meta-analysis, living systematic review

I confirm that I have read this submission and believe that I have an appropriate level of expertise to confirm that it is of an acceptable scientific standard.

Respond to this report

Responses (0)

Back to all reports

Reviewer Report

12 Views

07 Nov 2022 | for Version 2

12 Views Cite this report Responses(0)

Approved

The authors have adequately addressed my comments. I have no more comments to add.

Competing Interests

No competing interests were disclosed.

Reviewer Expertise

Evidence synthesis, Systematic reviews, Diabetes Mellitus

I confirm that I have read this submission and believe that I have an appropriate level of expertise to confirm that it is of an acceptable scientific standard.

Respond to this report

Responses (0)

Back to all reports

Reviewer Report

16 Views

17 Oct 2022 | for Version 1

Waldemar Siemens, Institute for Evidence in Medicine, Medical Center - University of Freiburg, Faculty of Medicine, Freiburg, Germany; Cochrane Germany, Cochrane Germany Foundation, Freiburg, Germany

16 Views Cite this report Responses(1)

Approved With Reservations

Is the rationale for developing the new method (or application) clearly explained?

Yes
Is the description of the method technically sound?

Yes
Are sufficient details provided to allow replication of the method development and its use by others?

Partly
If any results are presented, are all the source data underlying the results available to ensure full reproducibility?

Partly
Are the conclusions about the method and its performance adequately supported by the findings presented in the article?

Yes

Competing Interests

No competing interests were disclosed.

Reviewer Expertise

Meta-research, meta-analysis, living systematic review

Respond to this report

Responses (1)

Author Response

07 Nov 2022

Georgios Siontis, Department of Cardiology, University Hospital of Bern, Bern, Switzerland

We were pleased to receive the comments of the Reviewer. We are grateful for the very insightful comments that helped us to improve our work further. In the revised version of our manuscript we have addressed all of the suggestions/comments made by the Reviewer. In more detail:

Reviewer 2:

The authors present an empirical example comparing renal sympathetic denervation to sham intervention and provide data and calculations on power, cumulative meta-analysis, and sequential meta-analysis aiming to present the idea of conditional power. Many important points are well addressed and methodological aspects are well connected to the clinical relevance of the methods. I have some major and minor questions and encourage the authors to comment to improve the manuscript.

Reply: Thank you for your feedback.

Major comments:

Limitations: “performing random-effects would be a reasonable model choice” - Why
have you worked with the FE model then?

Reply: We thank the reviewer for this comment. In fact, our intention was to employ a random-effects meta-analysis model. As the between-study variance (r²) estimation was 0, this was equivalent to fixed-effect. We realize that this was not clearly stated, and we thus now have rephrased to clarify our approach. In particular, we write in the ‘Standard and sequential meta-analysis’ section: “We intended to perform random-effects meta-analysis, but as between-study variance (r²) was estimated at 0 in this setting, our calculations are identical to those from a fixed effect meta-analysis.”. We did not change the term “fixed-effect” in the abstract and the figure legends.

An alternative strategy would be to inform heterogeneity from empirical distributions (our references 40 and 41). However, such an approach would be appropriate in a prospective application of sequential meta-analysis and conditional planning, rather than a retrospective application, like the one presented in this paper. This is because in a prospective application, estimation of heterogeneity in the first stages of the reviews would be suboptimal. Moreover, imputing a value for heterogeneity would make results from “conventional” and “evidence-based” sample size calculations non-comparable.

We already wrote in the Discussion: “In a real application, imputing a value for heterogeneity, informed for example by empirical predictive distributions [40, 41], and performing random-effects would be a reasonable model choice”. And we now added: “Such an approach would be less reasonable in a retrospective application of the methods and would mitigate the comparability between conventional and evidence-based sample size calculations.”

If conditional power would say that only a “small trial” is needed: Would this be a problem regarding the sampling error? Should trials have a minimum size to avoid sampling error? As the trial gets smaller, the problem of chance increases, or? Could you comment on that and reflect you approach (conditional power)?

Reply: This is a topic that would benefit from further investigation. On one hand, a small trial should be a desirable outcome of the conditional planning method, on the other hand it would indeed be associated with greater within-study variation. Although this potentially large within-study variation is in theory incorporated in the conditional planning method (saying for example that an addition of such a study would render conclusive the updated meta-analysis effect, which is our goal), it would probably question the requirement of such individual study to be a standalone experiment. We added in the Discussion: “However, conditional planning might in theory result to recommendations of very small trials, which would be associated with great within-study variance and not be standalone experiments. Setting a minimum sample size for a future trial designed using conditional planning would be a potential remedy for such a situation.”.

This is an empirical example. Could a reasonable simulation study add value? If yes, how could it look like?

Reply: We thank the reviewer for this interesting comment. We do believe that a simulation study could contribute on the evaluation of the robustness of the method, and this could be a follow-up project. In such a simulation study, one should construct scenarios reflecting various assumptions being and not being met. We added under “Limitations”: “A comprehensive simulation study would be a more appropriate tool to investigate the performance and robustness of the method under a variety of settings.”

Minor comments:

Abstract:
You could add more numeric results in the results of you abstract if appropriate.

Reply: We have added in the Abstract: “Conditional planning resulted in much larger sample sizes compared to those in the original trials (relative increase between achieved and calculated sample size ranged between 11-19%), …”.

Background:
“This typically leads to smaller required sample sizes compared to that obtained using
the conventional approach.” - I wonder if a disadvantage of this approach is that the sampling error increases with a small sample size in a trial. Could you comment on that?

Reply: Please see our response on your second comment from ‘Major comments’.

“Among others it is assumed that the true underlying effect size (which we assume is unbiasedly estimated by the summary effect) should not change over time. This is rather unlikely to happen in sham-RCTs as the learning curve applies to most surgical/minimally invasive interventions and studies of their efficacy show larger effects over time. Hence, the conditional power approach is both promising and challenging to be applied in this context.” - Does the fixed-effect (FE) model makes sense in this context? Clinical trials vary in their PICO by nature, which makes it hard to assume the FE model.

Reply: Please see our response on your first comment from ‘Major comments’. Our intention was to perform a random-effects meta-analysis, but heterogeneity being 0 ended up to a fixed-effect model.

“As heterogeneity was low in this setting, we performed fixed effect meta-analyses.” - Shouldn’t that be a choice based on the homogeneity of the trials according to the PICO scheme?

Reply: We have now rephrased this sentence to: “We intended to perform random-effects meta-analysis, but as between-study variance (r²) was estimated at 0 in this setting, our calculations are identical to those from a fixed effect meta-analysis.”

Box 1:
“The variability of the true treatment effect across trials should be low. Otherwise, even the planning of huge trials will not result in the anticipated conditional power.” - This again puts the FE model into question, or? Should the conditional power calculations be based the random-effects model?

Reply: Please see our response on your first comment from ‘Major comments’. Furthermore, we acknowledge that heterogeneity might be estimated to be zero due to large within-study variation. We write in the ‘Limitations’ section: “Even though our example can be representative of the size of the available sham-RCTs in any medical field, the small number of studies might have resulted in clinical heterogeneity not manifesting in the data as statistical heterogeneity.”.

Results:
Table 1 / meta-analysis: Is it appropriate to pool “24-hour ambulatory SBP” with “Daytime ambulatory SBP”?

Reply: Thank you for mentioning this. Yes, both measurements are highly consistent in changes of similar magnitude for the patient populations recruited in the individual trials.

Link for “Online Table 2”: Only “Table 2” is a link and leads to Table 2 in the manuscript, not to Online Table 2. Please check all link in the manuscript.

Reply: Done.

“heterogeneity variance” (p. 5) - Do you mean the between-study variance Tau^2? Please be more precise.

Reply: The text has been revised as follows: “The estimated between-study variance (r²) was zero.”.

“The total sample size randomized thereafter (in the fifth and sixth trials) could be considered redundant (226 study participants in total, of which 114 randomized to sham).” - I think this should be one key message of the paper exactly with this wording, i.e., how many patients would not receive sham. It adds weight for a clinically meaningful understanding of the methods presented.

Reply: Thank you for this comment. We now mention in Abstract: “Sequential meta-analysis provided firm evidence against the null hypothesis with the synthesis of the first four trials (755 patients, cumulative mean difference -2.75 (95%CI -4.93 to -0.58) favoring the active intervention)), with the fifth and sixth trial to be considered redundant (226 study participants in total, of which 114 randomized to sham).”

“The large sample sizes calculated with conditional power compared to that calculated by the trials is explained by the fact that the trialists chose unrealistically large anticipated mean differences.” - Sometimes you already interpret your results in the discussion section. Please move the explaining sentences rather to the discussion.

Reply: The above-mentioned sentence has been moved to the Discussion as suggested.

“Figure 3. Hypothetical prospectively planned sequential fixed effect meta-analysis framework (type I error=5%, power=90%).” - I suggest adding more sentences for explaining Figure 3. Not everyone is familiar with sequential meta-analysis so it might be important to help readers understand the idea of it.

Reply: Thank you for pointing this issue. We now mention in Methods: “Meta-analyses of medical interventions may result in false positive or false negative results, due to low statistical power when the required number of randomised participants or trials has not been reached. Under this scenario, trial sequential analysis of a meta-analysis may amend these problems by handling a meta-analysis of several RCTs in an analogous manner to interim analysis of a single RCT.”

Discussion:
Feasibility of large trials when trial authors would consider conditional power.

Reply: We are not sure what the reviewer means with this comment. Is it related to the previous comment about the large within-study variation if small trials are recommended by conditional planning approach? If yes, we refer to our response (and amendments in the paper) on this comment.

Stop when rejecting the null hypothesis is defined as the “final time point”, correct? How does this fit to clinical relevance of results? One could argue to stop if a threshold of irrelevance is not anymore included by the 95% CI for example.

Reply: A limitation of sequential methods lies on them being based on the principles of statistical significance. We write in the ‘Limitations’: “Second, sequential methods have inherited limitations since they have been mainly built on the principal of statistical significance and do not differentiate between clinically relevant and non-relevant effects. Along these lines, the Cochrane Handbook authors underline the methodological limitations that arise from sequential methods [42].»

We could indeed extend the methodology to account for clinically relevant results, but such an approach would require further development and evaluation of its feasibility.

Have prediction intervals a role in cumulative meta-analysis and sequential meta-analysis to describe heterogeneity?

Reply: Yes, prediction intervals fall naturally within the principles of cumulative meta-analysis, although they have not been used in this way. We refer to the Appendix A2 (a short paragraph) of our methodological paper: Nikolakopoulou A, Mavridis D, Egger M, Salanti G. Continuously updated network meta-analysis and statistical monitoring for timely decision-making. Statistical Methods in Medical Research. 2016 Jan.
We do not think that a discussion of the topic would fit in the current paper but please advise if this was the intention of your comment.

Is the R code available? You may add it to zenodo.

Reply: Yes. The R code is available upon request.

“Unless this is accounted for, conditional planning will not improve the design of sham-RCTs.” - Could you explicitly say what you mean by “this” to avoid misunderstandings in the conclusion? Somehow I find it hard to follow, maybe also because you word your statement with a negation. Please consider rewriting it.

Reply: Thank you for your comment. In our conclusive statement, “this” corresponds to the expected increase of the intervention effect in new studies. We have rephrased the conclusive statement as follows: “Unless this expected change is accounted for, conditional planning will not improve the design of sham-RCTs.”

View more View less

Competing Interests

None

Back to all reports

Reviewer Report

27 Views

11 Apr 2022 | for Version 1

27 Views Cite this report Responses(1)

Approved With Reservations

Is the rationale for developing the new method (or application) clearly explained?

Yes
Is the description of the method technically sound?

Yes
Are sufficient details provided to allow replication of the method development and its use by others?

Yes
If any results are presented, are all the source data underlying the results available to ensure full reproducibility?

Yes
Are the conclusions about the method and its performance adequately supported by the findings presented in the article?

Yes

Competing Interests

No competing interests were disclosed.

Reviewer Expertise

Evidence synthesis, Systematic reviews, Diabetes Mellitus

Respond to this report

Responses (1)

Author Response

07 Nov 2022

Georgios Siontis, Department of Cardiology, University Hospital of Bern, Bern, Switzerland

View more View less

Competing Interests

None

Alongside their report, reviewers assign a status to the article:

Approved - the paper is scientifically sound in its current form and only minor, if any, improvements are suggested

Approved with reservations - A number of small changes, sometimes more significant revisions are required to address specific details and improve the papers academic merit.

Not approved - fundamental flaws in the paper seriously undermine the findings and conclusions

[1] 1. Otte WM, Tijdink JK, Weerheim PL, et al.: Adequate statistical power in clinical trials is associated with the combination of a male first author and a female last author. elife. 2018; 7. PubMed Abstract | Publisher Full Text

[2] 2. Sutton AJ, Cooper NJ, Jones DR, et al.: Evidence-based sample size calculations based upon updated meta-analysis. Stat. Med. 2007; 26: 2479–2500. PubMed Abstract | Publisher Full Text

[3] 3. Roloff V, Higgins JPT, Sutton AJ: Planning future studies based on the conditional power of a meta-analysis. Stat. Med. 2013; 32: 11–24. PubMed Abstract | Publisher Full Text

[4] 4. Nikolakopoulou A, Mavridis D, Salanti G: Using conditional power of network meta-analysis (NMA) to inform the design of future clinical trials. Biom. J. 2014; 56: 973–990. PubMed Abstract | Publisher Full Text

[5] 5. Salanti G, Nikolakopoulou A, Sutton AJ, et al.: Planning a future randomized clinical trial based on a network of relevant past trials. Trials. 2018; 19: 365. PubMed Abstract | Publisher Full Text

[6] 6. Elliott JH, Turner T, Clavisi O, et al.: Living Systematic Reviews: An Emerging Opportunity to Narrow the Evidence-Practice Gap. PLoS Med. 2014; 11. Publisher Full Text

[7] 7. Créquit P, Trinquart L, Yavchitz A, et al.: Wasted research when systematic reviews fail to provide a complete and up-to-date evidence synthesis: The example of lung cancer. BMC Med. 2016; 14: 8. PubMed Abstract | Publisher Full Text

[8] 8. Salanti G, Nikolakopoulou A: Actively Living Network Meta-Analysis. Accessed 31 May 2021. Reference Source

[9] 9. Chalmers I, Bracken MB, Djulbegovic B, et al.: How to increase value and reduce waste when research priorities are set. Lancet. 2014; 383: 156–165. PubMed Abstract | Publisher Full Text

[10] 10. Naci H, Salcher-Konrad M, Kesselheim AS, et al.: Generating comparative evidence on new drugs and devices before approval. Lancet. 2020; 395: 986–997. PubMed Abstract | Publisher Full Text

[11] 11. Miller FG, Kaptchuk TJ: Sham procedures and the ethics of clinical trials. J. R. Soc. Med. 2004; 97: 576–578. PubMed Abstract | Publisher Full Text

[12] 12. Galpern WR, Corrigan-Curay J, Lang AE, et al.: Sham neurosurgical procedures in clinical trials for neurodegenerative diseases: Scientific and ethical considerations. Lancet Neurol. 2012; 11: 643–650. Publisher Full Text

[13] 13. Sardar P, Bhatt DL, Kirtane AJ, et al.: Sham-Controlled Randomized Trials of Catheter-Based Renal Denervation in Patients With Hypertension. J. Am. Coll. Cardiol. 2019; 73: 1633–1642. PubMed Abstract | Publisher Full Text

[14] 14. StataCorp.: Stata Statistical Software: Release 15. College Station, TX: StataCorp LLC; 2017.

[15] 15. Higgins JPT, Whitehead A, Simmonds M: Sequential methods for random-effects meta-analysis. Stat. Med. 2011; 30: 903–921. PubMed Abstract | Publisher Full Text

[16] 16. Nikolakopoulou A, Mavridis D, Egger M, et al.: Continuously updated network meta-analysis and statistical monitoring for timely decision-making. Stat. Methods Med. Res. 2018; 27: 1312–1330. PubMed Abstract | Publisher Full Text

[17] 17. Demets DL, Lan KKG: Interim analysis: The alpha spending function approach. Stat. Med. 1994; 13: 1341–1352. PubMed Abstract | Publisher Full Text

[18] 18. Balduzzi S, Rücker G, Schwarzer G: How to perform a meta-analysis with R: A practical tutorial. Evid. Based Ment. Health. 2019; 22: 153–160. PubMed Abstract | Publisher Full Text

[19] 19. Kandzari DE, Bhatt DL, Sobotka PA, et al.: Catheter-based renal denervation for resistant hypertension: Rationale and design of the SYMPLICITY HTN-3 trial. Clin. Cardiol. 2012; 35: 528–535. PubMed Abstract | Publisher Full Text

[20] 20. Bhatt DL, Kandzari DE, O’Neill WW, et al.: A Controlled Trial of Renal Denervation for Resistant Hypertension. N. Engl. J. Med. 2014; 370: 1393–1401. Publisher Full Text

[21] 21. Desch S, Okon T, Heinemann D, et al.: Randomized Sham-Controlled Trial of Renal Sympathetic Denervation in Mild Resistant Hypertension. Hypertension. 2015; 65: 1202–1208. PubMed Abstract | Publisher Full Text

[22] 22. Mathiassen ON, Vase H, Bech JN, et al.: Renal denervation in treatment-resistant essential hypertension. A randomized, SHAM-controlled, double-blinded 24-h blood pressure-based trial. J. Hypertens. 2016; 34: 1639–1647. PubMed Abstract | Publisher Full Text

[23] 23. Kandzari DE, Kario K, Mahfoud F, et al.: The SPYRAL HTN Global Clinical Trial Program: Rationale and design for studies of renal denervation in the absence (SPYRAL HTN OFF-MED) and presence (SPYRAL HTN ON-MED) of antihypertensive medications. Am. Heart J. 2016; 171: 82–91. Publisher Full Text

[24] 24. Townsend RR, Mahfoud F, Kandzari DE, et al.: Catheter-based renal denervation in patients with uncontrolled hypertension in the absence of antihypertensive medications (SPYRAL HTN-OFF MED): a randomised, sham-controlled, proof-of-concept trial. Lancet. 2017; 390: 2160–2170. Publisher Full Text

[25] 25. Kandzari DE, Böhm M, Mahfoud F, et al.: Effect of renal denervation on blood pressure in the presence of antihypertensive drugs: 6-month efficacy and safety results from the SPYRAL HTN-ON MED proof-of-concept randomised trial. Lancet. 2018; 391: 2346–2355. PubMed Abstract | Publisher Full Text

[26] 26. Azizi M, Schmieder RE, Mahfoud F, et al.: Endovascular ultrasound renal denervation to treat hypertension (RADIANCE-HTN SOLO): a multicentre, international, single-blind, randomised, sham-controlled trial. Lancet. 2018; 391: 2335–2345. PubMed Abstract | Publisher Full Text

[27] 27. Azizi M, Schmieder RE, Mahfoud F, et al.: Six-Month Results of Treatment-Blinded Medication Titration for Hypertension Control After Randomization to Endovascular Ultrasound Renal Denervation or a Sham Procedure in the RADIANCE-HTN SOLO Trial. Circulation. 2019; 139: 2542–2553. PubMed Abstract | Publisher Full Text

[28] 28. Ferreira ML, Herbert RD, Crowther MJ, et al.: When is a further clinical trial justified?. BMJ (Online). 2012; 345. Publisher Full Text

[29] 29. Goudie AC, Sutton AJ, Jones DR, et al.: Empirical assessment suggests that existing evidence could be used more fully in designing randomized controlled trials. J. Clin. Epidemiol. 2010; 63: 983–991. PubMed Abstract | Publisher Full Text

[30] 30. Ioannidis JPA, Greenland S, Hlatky MA, et al.: Increasing value and reducing waste in research design, conduct, and analysis. Lancet. 2014; 383: 166–175. PubMed Abstract | Publisher Full Text

[31] 31. Jones HE, Ades AE, Sutton AJ, et al.: Use of a random effects meta-analysis in the design and analysis of a new clinical trial. Stat. Med. 2018; 37: 4665–4679. PubMed Abstract | Publisher Full Text

[32] 32. Pocock SJ, Bakris G, Bhatt DL, et al.: Regression to the Mean in SYMPLICITY HTN-3: Implications for Design and Reporting of Future Trials. J. Am. Coll. Cardiol. 2016; 68: 2016–2025. PubMed Abstract | Publisher Full Text

[33] 33. Kulinskaya E, Huggins R, Dogo SH: Sequential biases in accumulating evidence. Res. Synth. Methods. 2016; 7: 294–305. PubMed Abstract | Publisher Full Text | Free Full Text

[34] 34. Shohoudi A, Stephens DA, Khairy P: Bayesian adaptive trials for rare cardiovascular conditions. Futur. Cardiol. 2018; 14: 143–150. PubMed Abstract | Publisher Full Text

[35] 35. Wason JMS, Trippa L: A comparison of Bayesian adaptive randomization and multi-stage designs for multi-arm clinical trials. Stat. Med. 2014; 33: 2206–2221. PubMed Abstract | Publisher Full Text

[36] 36. Bittl JA, He Y: Bayesian Analysis: A Practical Approach to Interpret Clinical Trials and Create Clinical Practice Guidelines. Circ. Cardiovasc. Qual. Outcomes. 2017; 10. PubMed Abstract | Publisher Full Text

[37] 37. Berry DA: Introduction to Bayesian methods III: Use and interpretation of Bayesian tools in design and analysis. Clin. Trials. 2005; 2: 295–300. PubMed Abstract | Publisher Full Text

[38] 38. Macleod MR, Michie S, Roberts I, et al.: Biomedical research: Increasing value, reducing waste. Lancet. 2014; 383: 101–104. Publisher Full Text

[39] 39. Siontis GCM, Sweda R, Windecker S: Cardiovascular clinical trials in the era of a pandemic. J. Am. Heart Assoc. 2020; 9: e018288. PubMed Abstract | Publisher Full Text

[40] 40. Turner RM, Davey J, Clarke MJ, et al.: Predicting the extent of heterogeneity in meta-analysis, using empirical data from the Cochrane Database of Systematic Reviews. Int. J. Epidemiol. 2012; 41: 818–827. PubMed Abstract | Publisher Full Text

[41] 41. Rhodes KM, Turner RM, Higgins JPT: Predictive distributions were developed for the extent of heterogeneity in meta-analyses of continuous outcome data. J. Clin. Epidemiol. 2015; 68: 52–60. PubMed Abstract | Publisher Full Text

[42] 42. Higgins JPT, Thomas J, Chandler J, et al.: Cochrane Handbook for Systematic Reviews of Interventions. 2nd ed.Chichester (UK): John Wiley & Sons; 2019. Publisher Full Text

[43] 43. Siontis G, Nikolakopoulou A, Sweda R, et al.: Estimating the sample size of sham-controlled randomized controlled trials using existing evidence.2022. Publisher Full Text

Estimating the sample size of sham-controlled randomized controlled trials using existing evidence

Abstract

Keywords

Introduction

Methods

Systematic review methods

Sample size recalculations

Standard and sequential meta-analysis

Conditional planning of trials assuming a prospective meta-analysis

Box 1. Key aspects in sample size calculations based on conditional power.

Results

Search findings and characteristics of eligible sham-RCTs

Table 1. Characteristics of sham-RCTs comparing renal denervation to a sham-intervention considered eligible.

Sample size recalculations

Table 2. Sample size assumptions and conditional sample size calculations.

Box 2. Power calculations as reported in individual sham-RCTs.

Figure 1. Plot of assumed and observed mean differences in each individual trial, and the cumulative mean difference derived at each step of the cumulative meta-analysis using fixed-effect.

Standard and sequential meta-analysis

Figure 2. Standard (panel A) and cumulative (panel B) fixed-effect meta-analysis of sham-RCTs comparing renal sympathetic denervation to sham intervention for the outcome of mean change from baseline to follow-up in 24-hour ambulatory systolic blood pressure (mmHg).

Figure 3. Hypothetical prospectively planned sequential fixed effect meta-analysis framework (type I error=5%, power=90%).

Estimation of the sample size using conditional planning

Discussion

Limitations

Conclusions

Data availability

Underlying data

Extended data

Rerefences

Comments on this article Comments (0)

Open Peer Review

Comments on this article Comments (0)

Open Peer Review

Reviewer Status

Reviewer Reports

Comments on this article

Browse by related subjects

Competing Interests Policy

Stay Updated