Quantum data communication protection with the quantum permutation pad block cipher in counter mode and Clifford operators

Michel Barbeau

doi:10.12688/f1000research.140027.1

Home Browse Quantum data communication protection with the quantum permutation...

ALL Metrics

Views

Downloads

Get PDF

Get XML

Export

▬

✚

Research Article

Quantum data communication protection with the quantum permutation pad block cipher in counter mode and Clifford operators

[version 1; peer review: 1 approved]

Michel Barbeau

PUBLISHED 11 Sep 2023

Author details Author details

School of Computer Science, Carleton University, Ottawa, Ontario, K1S5B6, Canada

Michel Barbeau
Roles: Conceptualization, Formal Analysis, Methodology, Writing – Original Draft Preparation, Writing – Review & Editing

OPEN PEER REVIEW

REVIEWER STATUS

This article is included in the Cybersecurity collection.

This article is included in the Quantum Technology collection.

Abstract

Background: This article integrates two cryptographic schemes for quantum data protection. The result achieves authentification, confidentiality, integrity, and replay protection. The authentication, integrity, and replay aspects leverage quantum Clifford operators. Confidentiality of quantum messages is achieved using the quantum permutation pad (QPP) cryptographic scheme.
Methods: Clifford operators and the QPP are combined into a block cipher in counter mode. A shared secret is used to seed a random number generator for the arbitrary selection of Clifford operators and quantum permutations to produce a signature field and perform encryption. An encryption and signature algorithm and a decryption and authentication algorithm are specified to protect quantum messages.
Results: A symmetric key block cipher with authentication is described. The plain text is signed with a sequence of randomly selected Clifford operators. The signed plaintext is encrypted with a sequence of randomly selected permutations. The algorithms are analyzed. As a function of the values selected for the security parameters, there is an unavoidable risk of collision. The probability of block collision
is modelled versus the number of blocks encrypted, for block sizes two, three, four, and five qubits.
Conclusions: The scheme is practical but does not achieve perfect indistinguishability because of the risk of message collision. This is normal and unavoidable when fixed-size fields are assumed to make a scheme practical. The model can be used
to determine the values of the security parameters and the lifetime of session keys to mitigate the risk of information leakage according to the needs of the scheme’s users. The session key can be renewed when a tolerable maximum number of
messages has been sent.

Keywords

Clifford operator, quantum permutation pad, quantum communication, quantum network, security, confidentiality, encryption.

Corresponding author: Michel Barbeau

Competing interests: No competing interests were disclosed.

Grant information: We acknowledge the support of the Natural Sciences and Engineering Research Council of Canada (NSERC). Funding ref RGPIN-2019-06156
The funders had no role in study design, data collection and analysis, decision to publish, or preparation of the manuscript.

Copyright: © 2023 Barbeau M. This is an open access article distributed under the terms of the Creative Commons Attribution License, which permits unrestricted use, distribution, and reproduction in any medium, provided the original work is properly cited.

How to cite: Barbeau M. Quantum data communication protection with the quantum permutation pad block cipher in counter mode and Clifford operators [version 1; peer review: 1 approved]. F1000Research 2023, 12:1123 (https://doi.org/10.12688/f1000research.140027.1) First published: 11 Sep 2023, 12:1123 (https://doi.org/10.12688/f1000research.140027.1) Latest published: 11 Sep 2023, 12:1123 (https://doi.org/10.12688/f1000research.140027.1)

Introduction

Classical communications and networks, such as sonars, cellular networks, and the Internet, use the macroscopic properties of acoustic, electromagnetic, or light waves. In contrast, quantum communications use the microscopic properties of light. For instance, using an appropriate encoding, the quanta of light, called a photon, is used for quantum data communications. Each photon represents a quantum value. Applications of quantum communications include secret communications, quantum networking, and distributed quantum computing. Quantum networks are envisioned for quantum communications across long distances. A quantum network comprises links, repeaters, routers, and terminals. Nodes combine classical memory and quantum bit (qubit) memory. They have classical and quantum computing capabilities. Links are the communication channels, which may be classical or quantum. Applications of quantum networks encompass communications and computation. Quantum communications and networking enable the transfer of quantum states from one location to another. They permit pooling quantum computation resources to solve complex and distributed computing issues.

As with classical data, quantum data is vulnerable to various attacks.¹^–⁶ Quantum data needs to be protected. Fundamental properties are authenticity, confidentiality, integrity, and replay protection.⁷^–⁹ We focus on the authenticity, confidentiality, integrity, and replay protection of quantum messages. An authenticity attack deceives the destination about the trustworthy source of a message.⁷^,⁹ Mitigating the authenticity attack requires a proof of the source identity in a message. Confidentiality protection mitigates the risk of disclosing or leaking information contained in messages. Confidentiality protection is achieved by ciphering plaintext messages. An integrity attack modifies the content of a message. In the quantum setting, this modification on a quantum state $| ϕ ⟩$ takes the form of a unitary transformation $U$ . The state $| ϕ ⟩$ is modified by $U$ . Mitigating this attack requires a modification detection mechanism. In the quantum setting, a replay attack in the classical sense is not possible because of its non-cloning property. However, an adversary can delay the delivery of a message or, when it knows how, can recreate the state. Mitigating this attack requires a mechanism to ensure that a message is new. Classical computing uses a digital signature to address authenticity, integrity, and replay attacks, possibly combined with a nonce field or a timestamp. This signature mechanism cannot be used in the quantum world in the classical sense.⁷ Indeed, generating a digital signature in the classical sense requires reading the message content and generating a corresponding signature value using, for instance, a one-way hash function. Reading the content of a quantum state, i.e., measuring, is destructive. However, in the following, we use the signature concept with the understanding that it is not obtained by calculating a value that involves measuring the content of a quantum message.

The article includes one main result. It presents a quantum data protection scheme that achieves all these properties, acknowledging that, at least in the short term, qubit bandwidth is narrow. Such protection schemes need to be lightweight (few additional qubits are required to implement a security scheme). The solution integrates two existing cryptographic schemes: Clifford-operator based authentication⁹ and quantum permutation pad (QPP).¹⁰ In this context, lightweight means that few additional qubits are required to implement a security scheme. Confidentiality is achieved using quantum permutations while authenticity, integrity, and replay protection are obtained using quantum Clifford operators. While this new protection scheme benefits from the security analyses developed for the two cryptographic schemes that it uses, the article takes the investigation further by combining a collision probability analysis, Clifford-operator-based authentication, the QPP symmetric-key encryption, and the block counter mode to create a quantum data protection scheme.

We review related work and introduce relevant quantum information background. We present and analyze the original quantum data block cipher and authentication scheme.

Related work

The work presented in this article is about protecting quantum data using quantum resources. It is a topic that has received attention in the research literature, as discussed in this section. Work can be categorized into two groups: authentication and confidentiality.

Barnum et al. introduced an authentication scheme for quantum data, considering their specific nature, and defined the concepts of completeness and soundness in this context.⁷ Foundations for cryptographic schemes for authentication have been proposed by Aharonov et al.¹¹ and Broadbent and Wainewright,¹²^,¹³ building on quantum Clifford operators. This work has been used to build an authenticity, integrity, and replay protection scheme for quantum messages by Barbeau et al.,¹⁴^,¹⁵ with demonstrated soundness and completeness, and to analyze attack probability. Other quantum data authentication efforts include the work of Das and Siopsis,¹⁶ building on a position authentication protocol, and Satoh et al.,¹⁷ building on the concept of quantum state tomography.

For confidentiality, asymmetric and symmetric encryption schemes have been proposed by Alagic et al.¹⁸ and St-Jules,¹⁹ using Clifford operators. Efforts have been devoted to adapting the Advanced Encryption Standard (AES)²⁰ to the quantum environment.²¹^–²³ A challenge is the amount of required quantum resources. In the short term, the available quantum computers have low quantities of memory and high error probabilities in comparison to classical computers. New lighter-weight quantum encryption schemes requiring fewer quantum resources have been proposed.²⁴^–²⁶ Kuang and Barbeau introduced a universal symmetric encryption scheme called QPP.¹⁰ The scheme can be used in several ways in classical and quantum environments.

In this article, we propose and analyze a symmetric key encryption scheme for blocks of quantum data. Building on our previous research,⁹^,¹⁰ a general symmetric-key cipher is developed building on QPP in counter mode. Conditions are identified to achieve perfect indistinguishability. Use cases are also identified where perfect indistinguishability is not achieved, but where the probability of collision is low. As emphasized in,¹⁰ the QPP scheme can be considered for both classical data and quantum data. In companion papers, we developed a QPP block cipher scheme in counter mode for classical data adapted specifically for the underwater environment.¹⁴^,¹⁵ For the encryption aspect, this article parallels this work for quantum data for a general quantum networking environment. More related work is cited in the following sections.

Quantum information background

In the quantum computing model, the unit of information is called the quantum bit (qubit). Mathematically, using the Dirac ket notation $| ⟩$ , the Boolean values zero and one are represented, with the matrix-form equivalent, as

(1)

| 0 ⟩ = (\begin{array}{c} 1 \\ 0 \end{array}) and | 1 ⟩ = (\begin{array}{c} 0 \\ 1 \end{array}) .

Ket zero, i.e., $| 0 ⟩$ , and ket one, i.e., $| 1 ⟩$ , are the standard computational basis states. A qubit can be in both states $| 0 ⟩$ and $| 1 ⟩$ at the same time. A qubit is in a continuum of intermediate states. These intermediate states are called a superposition. A superposition is represented as a unit vector in a complex vector space. Let $α$ and $β$ be two complex numbers, with the constraint that [1]

(2)

{|α|}^{2} + {|β|}^{2} = 1

a qubit is represented as the linear superposition

(3)

| ψ ⟩ = α | 0 ⟩ + β | 1 ⟩ .

The term $| ψ ⟩$ reads as ket $ψ$ . The factors $α$ and $β$ are the probability amplitudes associated with each state, i.e., $| 0 ⟩$ and $| 1 ⟩$ . In other words, we do not know in which state a qubit is. According to the probabilistic model of Equation (3), however, the actual measurement of a qubit yields $| 0 ⟩$ , i.e., Boolean value zero, with probability ${|α|}^{2}$ and $| 1 ⟩$ , i.e., Boolean value one, with probability ${|β|}^{2}$ . The matrix format is a convenient alternative equivalent representation of the linear superposition of a qubit:

(4)

α | 0 ⟩ + β | 1 ⟩ \equiv (\begin{array}{c} α \\ β \end{array})

The two coefficients $α$ and $β$ are organized in a one-column, two-row vector. A qubit state that can be written in the form of Equation (4), that is, in the column-vector form, is called a pure state. A qubit is a two-dimensional entity. Using probability amplitude $α$ , the first dimension defines the 0 information component. Using probability amplitude $β$ , the second dimension defines the 1 information component.

Qubits can be composed together. For instance, a two-qubit register consists of a superposition of the four states $| 00 ⟩$ , $| 01 ⟩$ , $| 10 ⟩$ , and $| 11 ⟩$ , i.e., the four possible two-bit binary values. Together with the corresponding probability amplitudes $α$ , $β$ , $γ$ , and $δ$ , the two-qubit linear superposition is

| ψ ⟩ = α | 00 ⟩ + β | 01 ⟩ + γ | 10 ⟩ + δ | 11 ⟩ .

All $α$ , $β$ , $γ$ , and $δ$ are complex numbers with the constraint that ${|α|}^{2} + {|β|}^{2} + {|γ|}^{2} + {|δ|}^{2}$ is equal to one.

In general, a $n$ -qubit quantum register is a $2^{n}$ -term expression of the following form

(5)

| ψ ⟩ = \sum_{i = 0}^{2^{n} - 1} ψ_{i} | i ⟩ \equiv (\begin{array}{c} ψ_{0} \\ ψ_{1} \\ ⋮ \\ ψ_{2^{n} - 1} \end{array})

with the constraint

\sum_{i = 0}^{2^{n} - 1} | ψ_{i} | i ⟩ | = 1 .

The computational basis is the orthogonal basis

(6)

B (n) = \{0 ⟩ 1 ⟩ \dots 2^{n} - 1 ⟩\} .

A $n$ -qubit quantum register is a $2^{n}$ -dimensional entity. The $i$ th dimension, using probability amplitude $ψ_{i}$ , defines the $i$ th information component, with $i = 0, 1, 2, \dots, 2^{n} - 1$ . Both the summation form and equivalent column-vector form are shown. In the summation form, the plus sign is conjunctive, rather than disjunctive. In the quantum-superposition model, all terms in the summation exist simultaneously. One can also appreciate the memory complexity of simulating the quantum computing model with a classical one. A $n$ -qubit register requires the storage of $2^{n}$ probability amplitudes. For instance, the memory complexity of a 10-qubit register is in the order of kilobytes, a 20-qubit register is in the order of megabytes, and a 30-qubit register is in the order of gigabytes.

The $2^{n}$ probability amplitudes are organized in a one-column, $2^{n}$ -row vector in the column-vector form. The ket notation $| ⟩$ reflects the vectorial nature of a qubit or a quantum register. The term ket $ψ$ can be interpreted as a mapping to a column vector of the corresponding probability amplitudes:

(7)

| ψ ⟩ \mapsto (\begin{array}{c} ψ_{0} \\ ψ_{1} \\ ⋮ \\ ψ_{2^{n} - 1} \end{array})

Quantum data block cipher and authentication scheme

We first briefly review the highlights of Clifford-operator-based authentication, QPP encryption, and the block counter mode. Then, we define original source and destination algorithms for authenticated and confidential quantum data communications.

Clifford-operator-based authentication

The following four matrices constitute the Pauli operators:

(8)

I = (\begin{array}{c} 1 & 0 \\ 0 & 1 \end{array}), X = (\begin{array}{c} 0 & 1 \\ 1 & 0 \end{array}), Y = (\begin{array}{c} 0 & - j \\ j & 0 \end{array}), and Z = (\begin{array}{c} 1 & 0 \\ 0 & - 1 \end{array})

Over the $n$ -qubit quantum states, the Pauli matrices $P (n)$ are the set of all $2^{n}$ by $2^{n}$ matrices resulting from tensor products like $P_{1} \otimes P_{2} \otimes \dots \otimes P_{n}$ , where $P_{1}, P_{2}, \dots, P_{n}$ are Pauli operators. The set $P (n)$ has $2^{2 n}$ . Pauli matrices form a group. Hence, they can be interpreted as operators mapping Pauli matrices to Pauli matrices.

The set $P {(n)}^{*}$ contains all the Pauli matrices in $P (n)$ excluding the identity matrix $I^{\otimes n}$ . The set $U (1)$ represents the set of all complex numbers modulo one. That is, $U (1)$ is equal to $\{e^{jθ} : θ \in ℝ\}$ , with $j$ equal to $\sqrt{- 1}$ . The set $U (2^{n})$ represents all the $2^{n}$ by $2^{n}$ unitary matrices. Given a unitary $C$ , its conjugate transpose $C^{†}$ , and a Pauli matrix $P$ , the expression ${CPC}^{†}$ is the conjugation of matrix $P$ by unitary $C$ .

Over the $n$ -qubit quantum states, the set of Clifford operators is defined as

(9)

C (n) = \{C \in U (2^{n}) : P \in P {(n)}^{*} \Rightarrow {CPC}^{†} \in \pm P {(n)}^{*}\} / U (1)

A Clifford operator is a bijection mapping Pauli matrices in $P {(n)}^{*}$ to Pauli matrices in $P {(n)}^{*}$ , through the action of conjugation. The suffix $/ U (1)$ implies that two Clifford operators, different solely because of a factor in $U (1)$ , are considered equivalent. The set $C (n)$ has $2^{n^{2} + 2 n} \prod_{i = 1}^{n} (4^{i} - 1)$ elements. In the following, we refer to it as $| C (n) |$ .

Quantum permutation pad

Let us consider the $n$ -qubit orthonormal computational basis defined in Equation (6). Let $V$ be the vector space where every element of it can be expressed as a linear combination of members of this basis. The elements of the symmetric group $S_{2^{n}}$ are permutations over the set $V$ . The degree of the group $S_{2^{n}}$ is $2^{n}$ . It is of order $2^{n}!$ . This means that there are $2^{n}!$ permutation operators. In the following, we refer to them as $| S_{2^{n}} |$ . Each of them can be represented by a $2^{n}$ by $2^{n}$ matrix $P_{i}$ , where $i = 1, \dots, 2^{n}!$ . Note that every permutation $P_{i}$ is a bijective function from the set $V$ to itself. Furthermore, the inverse of $P_{i}$ , denoted as $P_{i}^{- 1}$ , is also contained in the symmetric group $S_{2^{n}}$ .

A plaintext $M$ is made of $m$ vectors $v_{0}, v_{1}, \dots, v_{m - 1}$ in $V$ . QPP encryption of plaintext $M$ uses a sequence $π$ of $m$ randomly selected permutations corresponding to the list $P_{0}, P_{1}, \dots, P_{m - 1}$ , all selected in group $S_{2^{n}}$ . The sequence $π$ is the encryption key of message $M$ . The encryption of plaintext message $M$ with key $π$ is denoted as $E_{π} (M)$ . It corresponds to the sequence $W$ of vectors $w_{0}, w_{1}, \dots, w_{m - 1}$ where $w_{0} = P_{0} (v_{0}), w_{1} = P_{1} (v_{1}), \dots, w_{m - 1} = P_{m - 1} (v_{m - 1})$ . Conversely, the decryption of $W$ , encrypted with key $π$ , is denoted as $D_{π} (W)$ . It corresponds to the sequence of vectors $P_{0}^{- 1} (w_{0})$ , $P_{1}^{- 1} (w_{1}), \dots, P_{m - 1}^{- 1} (w_{m - 1})$ .

Definition 1

(Shannon perfect secrecy). For any pair of plaintexts $M_{1}$ and $M_{2}$ , when ciphertext $W$ is equally likely to be the encryption of $M_{1}$ or $M_{2}$ , the corresponding cryptographic scheme is perfectly secure.

Theorem 1

The QPP cryptographic scheme is perfectly secure.

Proofs can be found in Refs. 10 and 14. The proofs establish that the probabilities are identical for all messages. The statement of Theorem 1 is theoretical because it requires very long keys. In the following, we use the QPP practically. This property is not maintained.

The implementation of QPP for quantum data has been investigated by Kuang and Perepechaenko.²⁷^–²⁹ They proposed solutions to several quantum implementation issues, while the open problem of dispatching quantum permutations - that is, the selection of the applied permutations in a quantum circuit - is highlighted. The security of block sizes ( $n$ ) two, three, four, and five is analyzed for the number of different permutations in a session required to achieve 256-bit of entropy, to mitigate the risk of breaking keys by the Grover’s algorithm.³⁰^–³² It is highlighted that a 256-bit size yields a brute force search space of $2^{256}$ keys. In the sequel, we take the security analysis one step further. As highlighted by Bellare and Rogaway, making the plaintext hard to recover from ciphertext is not enough to declare a cryptographic scheme secure.³³ Indeed, information may leak just by observing patterns in traffic. In the next section, we analyze the probability of collisions, which is a cause of information leakage.

Block counter mode

The concept of block counter mode has been examined in detail by Bellare and Rogaway.³³ We summarize the main facts.

There are four main block modes, namely the electronic code book (ECB), cipher-block chaining (CBC) with a random initialization vector (IV), counter-based version of CBC (CBCC), and counter (CTR). The block modes are compared in Table 1. An important criterion is the risk of information leakage, which is significant for both the ECB and CBC with random IV modes. We use the CTR mode because of the low risk of information leakage.

Table 1. Block modes.

Mode	Leak risk
ECB	significant
CBC with IV	significant
CBCC	low
CTR	low

Encryption and signature algorithm

The symmetric key block cipher with authentication is described hereafter. Let $m$ and $n$ be non-null positive integers. A quantum plaintext message consists of $m$ quantum blocks $w_{0}, w_{1}, \dots, w_{m - 1}$ . Each block consists of $n$ qubits. An additional $ℓ$ qubits are added to every block for a signature field; $ℓ$ is a non-null positive integer.

There are two participants: a message source and a message destination. They share the following security parameters: i) block size ( $n$ ), ii) number of blocks in a message ( $m$ ), iii) length of the signature field ( $ℓ$ ), iv) a set $C$ of $d_{1}$ Clifford operators randomly selected in $C (n + ℓ)$ , and v) a set $P$ of $d_{2}$ permutations randomly selected in $S_{2^{n + ℓ}}$ . $d_{1}$ and $d_{2}$ are non-null positive integers. The source and destination share two secret arbitrary long sequences of random numbers $s$ , modulo $d_{1}$ , and $r$ , modulo $d_{2}$ . The sequence $s$ and set $C$ , and the sequence $r$ and set $P$ can be interpreted as the session authentication and encryption keys shared between the source and destination.

Before transmission, the source signs and encrypts each message. On the source side, there is a static variable $i$ . It is initialized to zero. After the completion of the encryption of a message, the new value of the static variable $i$ is incremented by $m$ units.

The plaintext is signed with a sequence of $m$ randomly selected Clifford operators:

(10)

π = C_{s (i)}, C_{s (i + 1)}, \dots, C_{s (i + m - 1)}

All operators are in the set $C$ . The selection of Clifford operators is determined by the sequence of random numbers $s$ . The message signing key is the sequence of Clifford operators $π$ .

Following the signature procedure, the signed plaintext is encrypted with a sequence of $m$ randomly selected permutations:

(11)

ρ = P_{r (i)}, P_{r (i + 1)}, \dots, P_{r (i + m - 1)}

All permutations are in the set $P$ . The selection of permutations is determined by the sequence of random numbers $r$ . The message encryption key is the sequence of permutations $ρ$ .

The expression

(12)

P_{r (j)} C_{s (j)} w_{j} | j mod ℓ ⟩, with j = i, i + 1, \dots, i + m - 1

represents the quantum block

w_{j}

suffixed with the signature quantum state

| j mod ℓ ⟩

ℓ

qubits in state

j mod ℓ

. The Clifford operator

C_{s (j)}

is applied, then the permutation

P_{r (j)}

is applied. The encryption of the plaintext message is the quantum ciphertext resulting from the following tensor product:

(13)

C = \otimes_{j = i}^{i + m - 1} P_{r (j)} C_{s (j)} w_{j} | j mod ℓ ⟩

The quantum ciphertext $C$ and the value of classical variable $i$ are sent together to the destination.

Note that the term signature is used but not in the classical sense. A classical message signature is calculated by reading the payload of a message. For quantum data, reading the payload to calculate a signature is not feasible because the measurement of the payload qubits would destroy their states.

It is assumed that the plaintext is random and unbiased. A diffusion phase before encryption, on the source side, and an assembly phase after decryption, on the destination side, can be added to remove statistical bias in ciphertext. See Ref. 27 for a circuit design which does that using CNOT gates.

Building the set $C$ of Clifford operators involves the random selection of $d_{1}$ integers in the range one to $| C (n + ℓ) |$ and mapping these integers to Clifford operators. Koenig and Smolin have published a $O (n^{3})$ algorithm for doing this mapping while van den Berg³⁴ proposed a $O (n^{2})$ algorithm. Barbeau et al.⁹ investigated this aspect for message key purposes.

Decryption and authentication algorithm

The destination receives a quantum ciphertext $C$ and a classical value $i$ . For the purposes of replay protection, the destination ensures that the value of $i$ is new. The ciphertext $C$ consists of $m$ blocks of $n + ℓ$ qubits $ω_{j}$ , $j = i, \dots, i + m - 1$ . The decryption of a block with index $j$ consists of the following product:

(14)

X_{j} = C_{s (j)}^{†} P_{r (j)}^{- 1} ω_{j}

$C_{s (j)}^{†}$ is the conjugate transpose of Clifford operator $C_{s (j)}$ . The product $C_{s (j)}^{†} C_{s (j)}$ is an identity. $P_{r (j)}^{- 1}$ is the inverse permutation of $P_{r (j)}$ . The product $P_{r (j)}^{- 1} P_{r (j)}$ is also an identity. Assuming that a received message is intact, we have:

(15)

X_{j} = C_{s (j)}^{†} P_{r (j)}^{- 1} ω_{j} = C_{s (j)}^{†} P_{r (j)}^{- 1} P_{r (j)} C_{s (j)} w_{j} | j mod ℓ ⟩ = C_{s (j)}^{†} C_{s (j)} w_{j} | j mod ℓ ⟩ = w_{j} | j mod ℓ ⟩

The original content is restored. To confirm that a verification is performed, measuring the qubits from positions $n$ to $n + ℓ - 1$ of every block, testing equality with the corresponding block number $j$ , and taking the logical conjunction of the results:

(16)

v = \land_{j = i}^{i + m - 1} (X_{j} [n, n + ℓ - 1] = (j mod ℓ))

The result is the Boolean value $v$ . When it evaluates to one, the message is accepted and the resulting plaintext is

(17)

X_{i} [0, n - 1], X_{i + 1} [0, n - 1], \dots, X_{i + m - 1} [0, n - 1] .

Otherwise, the ciphertext $C$ is rejected.

The message verification key is the sequence of conjugate transposes $C_{s (i)}^{†}, C_{s (i + 1)}^{†}, \dots, C_{s (i + m - 1)}^{†}$ , which can easily be derived given $π$ . Verification of the condition of Equation (16) is interpreted as a proof of ownership of the authentication key $π$ by the message source and a validation of integrity. The value of the signature suffix aims to make every message unique, for replay protection. However, there is a risk of collision according to the selected security parameters. The collision probability is further investigated in the next section. The message decryption key is the sequence of inverse permutations $P_{r (i)}^{- 1}, P_{r (i + 1)}^{- 1}, \dots, P_{r (i + m - 1)}^{- 1}$ , also easily derived given $ρ$ . It is a symmetric key that both the source and destination must share.

Collision probability

As a function of the values selected for the security parameters, $d_{1}$ , $d_{2}$ , $ℓ$ , $m$ , and $n$ , there is a risk of collision, i.e., a repeated message value is signed and encrypted the same way.

Definition 2

(Collision). A collision arises when a reoccurring message consisting of $m$ quantum blocks, each of them representing a $n$ -qubit state, is re-numbered with the same sequence of integers $i, i + 1, \dots, i + m - 1$ , modulo $ℓ$ , re-resigned with the same sequence of Clifford operators $C_{0}, C_{1}, \dots, C_{m - 1}$ , chosen in the group $C (n + ℓ)$ , and re-encrypted with the same sequence of permutations $P_{0}, P_{1}, \dots, P_{m - 1}$ , chosen in the symmetric group $S_{2^{n + ℓ}}$ . The same numbering, Clifford operators, and permutations are picked twice to sign and encrypt a repeating message content.

The smaller the collision probability, the better, because collisions leak information. They make it possible to identify traffic patterns, which can eventually lead to breaking encryption schemes. For the analysis, let us assume that a quantum block state is a single member of the orthonormal basis, i.e., no superposition. A message consists of $m$ column vectors in the basis $B (n)$ . It is assumed that all members of the basis are equally probable. It is also assumed that, for a message, all block numbering sequences of $m$ integers module $ℓ$ are equally probable. These assumptions are reasonable, particularly when diffusion before encryption and assembly after decryption are done.

There are $2^{m (n + ℓ)} d_{1}^{m} d_{2}^{m}$ unique combinations consisting of a message of $m$ blocks of $n$ qubits, a numbering sequence of $ℓ$ -bit integers, a sequence of $m$ Clifford operators chosen among a set of $d_{1}$ available operators, and a sequence of $m$ permutations chosen among a set of $d_{2}$ available permutations. When over $2^{m (n + ℓ)} d_{1}^{m} d_{2}^{m}$ messages are authenticated and encrypted with the same session key, at least one collision has occurred. We calculate the collision probability when less than $\sqrt{2^{m (n + ℓ)} d_{1}^{m} d_{2}^{m}}$ messages have been encrypted with the same session key. Note that collisions are unavoidable with finite-length fields, determined in this case by the security parameters.

Theorem 2

Let $i$ be the number of messages consisting of $m$ quantum states in $B (n)$ authenticated using $m$ Clifford operators, chosen in subset $C$ , included in $C (n + ℓ)$ , of $d_{1}$ Clifford operators, and encrypted with $m$ permutations, chosen in subset $P$ , included in $S_{2^{n + ℓ}}$ , of $d_{2}$ permutations. $ℓ$ is the number of signature qubits allocated for each block. Let $i$ be greater than zero and less than equal to $imax = \sqrt{2^{m (n + ℓ)} d_{1}^{m} d_{2}^{m}}$ . When $i$ messages have been encrypted, the probability that at least one collision has occurred, denoted as $K (d_{1}, d_{2}, ℓ, m, n, i)$ , is at least $cmin = 0.6 \cdot \frac{i (i - 1)}{2^{m (n + ℓ) + 1} d_{1}^{m} d_{2}^{m}}$ but not greater than $cmax = \frac{i (i - 1)}{2^{m (n + ℓ) + 1} d_{1}^{m} d_{2}^{m}}$ .

Proof.

Let us assume that all messages are equally probable, that the choice of Clifford operators and permutations is uniform, and that probabilities are independent across messages.

Lower bound. The absence of collision after encrypting $i$ messages is represented as the event $e_{i}$ . The event corresponds to a condition where $i$ messages have been authenticated and encrypted. When no collision has occurred after the authentication and encryption of $i$ messages, it means that among the available $2^{m (n + ℓ)} d_{1}^{m} d_{2}^{m}$ combinations of message value, numbering sequence, Clifford operator sequence, and permutation sequence, solely $2^{m (n + ℓ)} d_{1}^{m} d_{2}^{m} - i$ combinations have not been used. Therefore, the probability of no collision when the $i + 1$ -th message is signed and encrypted is

Pr [e_{i + 1}| e_{i}] = \frac{2^{m (n + ℓ)} d_{1}^{m} d_{2}^{m} - i}{2^{m (n + ℓ)} d_{1}^{m} d_{2}^{m}} = 1 - \frac{i}{2^{m (n + ℓ)} d_{1}^{m} d_{2}^{m}}

It follows that the probability of the absence of collision after the completion of the signature and encryption of $i$ messages is

(18)

\begin{array}{l} 1 - K (d_{1}, d_{2}, ℓ, m, m, i) \\ = Pr [e_{i}] \\ = Pr [e_{i}| e_{i - 1}] \cdot Pr [e_{i}] \\ = \dots \\ = \prod_{k = 1}^{i - 1} Pr [e_{k + 1}| e_{k}] \\ = \prod_{k = 1}^{i - 1} (1 - \frac{k}{2^{m (n + ℓ)} d_{1}^{m} d_{2}^{m}}) \end{array}

Leveraging the inequality $1 - x \leq e^{- x} \leq x$ , with $0 \leq x \leq 1$ , the fact $0 \leq \frac{k}{2^{m (n + ℓ)} d_{1}^{m} d_{2}^{m}} \leq 1$ , and the equality $\sum_{k = 1}^{i - 1} k = \frac{i (i - 1)}{2}$ , the product of Equation (18) is less than equal to

(19)

\prod_{k = 1}^{i - 1} e^{\frac{k}{2^{m (n + ℓ)} d_{1}^{m} d_{2}^{m}}} = e^{\frac{i (i - 1)}{2^{m (n + ℓ) + 1} d_{1}^{m} d_{2}^{m}}}

which implies that

(20)

K (d_{1}, d_{2}, ℓ, m, n, i) \geq 1 - e^{\frac{i (i - 1)}{2^{m (n + ℓ) + 1} d_{1}^{m} d_{2}^{m}}} .

Leveraging the inequality $(1 - e^{x}) \geq (1 - 1 / e) x$ , Equation (20) is greater than

(1 - \frac{1}{e}) \cdot \frac{i (i - 1)}{2^{m (n + ℓ) + 1} d_{1}^{m} d_{2}^{m}} \geq 0.6 \cdot \frac{i (i - 1)}{2^{m (n + ℓ) + 1} d_{1}^{m} d_{2}^{m}} .

Hence, we obtain that

K (d_{1}, d_{2}, ℓ, m, n, i) \geq 0.6 \cdot \frac{i (i - 1)}{2^{m (n + ℓ) + 1} d_{1}^{m} d_{2}^{m}} .

Upper bound. Let the event $f_{i}$ denote a collision resulting from the $i$ th block encryption. The probability of $f_{i}$ is

Pr [f_{i}] = \frac{i - 1}{2^{m (n + ℓ)} d_{1}^{m} d_{2}^{m}} .

Due to the existence of $2^{m (n + ℓ)} d_{1}^{m} d_{2}^{m}$ of unique triples comprising a message, a Clifford operator, and a permutation, we obtain that

(21)

\begin{array}{l} K (d_{1}, d_{2}, m, n, i) = Pr [f_{0} \lor f_{1} \lor \dots \lor f_{i - 1}] \\ \leq Pr [f_{0}] + Pr [f_{1}] + \dots + Pr [f_{i - 1}] \\ \leq \frac{1}{2^{m (n + ℓ)}} [\frac{0}{d_{1}^{m} d_{2}^{m}} + \frac{1}{d_{1}^{m} d_{2}^{m}} + \dots \frac{i - 1}{d_{1}^{m} d_{2}^{m}}] \\ = \frac{i (i - 1)}{2^{m (n + ℓ) + 1} d_{1}^{m} d_{2}^{m}} \end{array}

□

Remark 1

The collision probability approaches the value of one-half by growing the block size ( $n$ ) and number of blocks in a message ( $m$ ). It is upper bounded by the value one-half because the weight of the subtrahend one is progressively diminishing, in the numerator $i (i - 1)$ , with $i$ reaching $imax$ .

Figure 1 plots the collision probability $K (d_{1}, d_{2}, ℓ, 1, n, i)$ ( $y$ -axis) versus the number of transmitted messages $i$ ( $x$ -axis), from one to $imax$ . The message size ( $m$ ) is one. There are curves for two-, three-, four-, and five-qubit QPP ( $n$ ). The corresponding numbers of gates are 56, 17, six, and three. As mentioned in Remark 1, in the analysis, the maximum collision probability is one-half (or $10^{- 0.3}$ on the logarithmic $y$ -axis) when the number of encrypted blocks $i$ is equal to $imax$ . Of course, when $i$ is greater than equal to $2^{m (n + ℓ)} d_{1}^{m} d_{2}^{m}$ , the probability is one. From this perspective, i.e., from the block-key point of view, the collision probability is noticeably high for a low number of encrypted blocks.

Figure 1. Probability of block collision versus the number of blocks ( $i$ ) encrypted, for block sizes ( $n$ ) two, three, four, and five qubits.

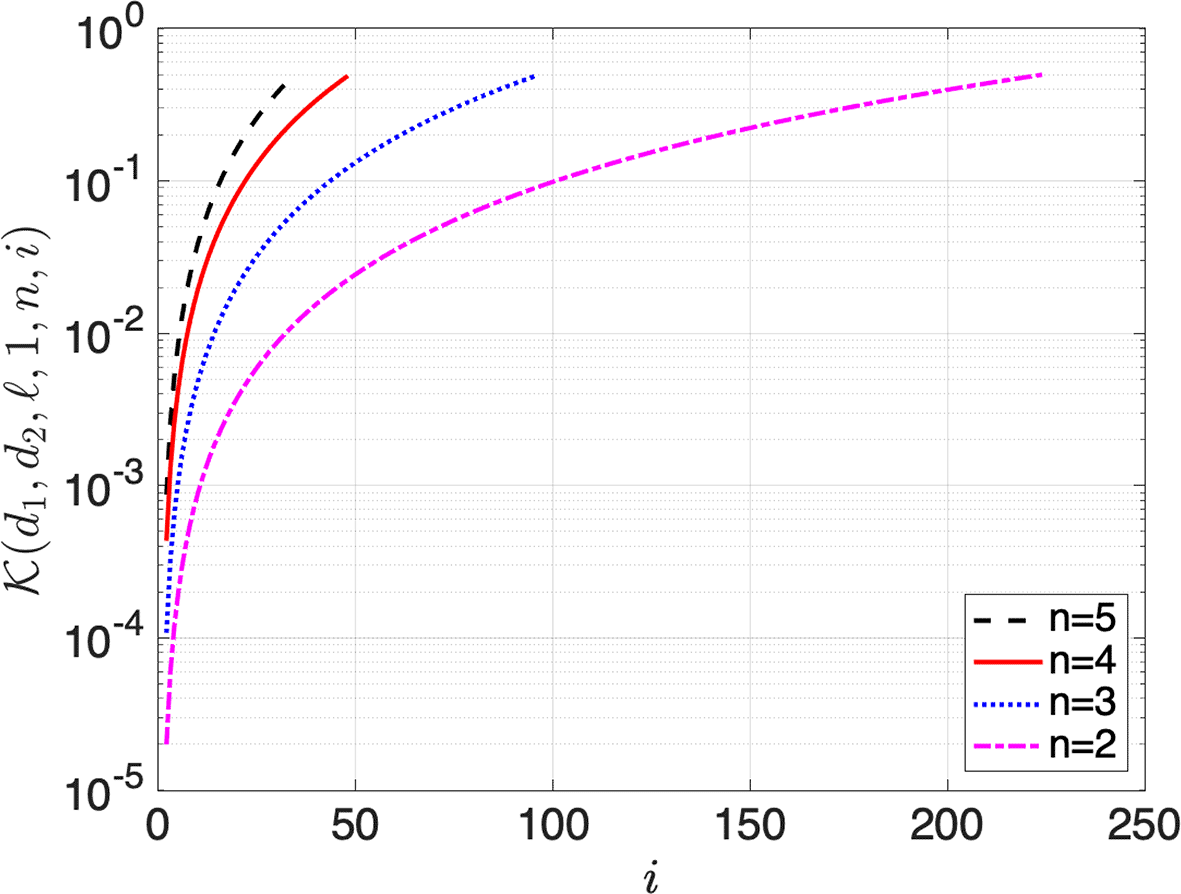
Figure 2 presents the message-key point of view. The $x$ -axis corresponds to the block size ( $n$ ), while the $y$ -axis represents the value of $imax$ as a function of the number of blocks in a message ( $m$ ) and the block size ( $n$ ). Again, as noted in Remark 1, in the analysis, the collision probability approaches value one-half as the number of blocks in a message ( $m$ ) and the block size ( $n$ ) grow and $i$ approaches $imax$ . Figure 2 plots values for $imax$ (Theorem 2) for block sizes two, three, four, and five and message sizes one, two, four, and eight. $imax$ is a parameter to consider when conducting a risk assessment and determining the maximum number of messages that can be sent before renewing a session key.

Figure 2. Value of imax (see Theorem 2) according to the block size ( $n$ ) and message size ( $m$ ).

Security parameters $d_{1}$ and $d_{2}$ , selected according to the block size, are as suggested by Kuang and Perepechaenko.²⁷ $ℓ$ is equal to two.

Conclusion

An authentication and encryption scheme for quantum messages consisting of blocks of qubits has been presented. The scheme is simple and considers the scarcity of qubits for the upcoming first-generation quantum Internet. The authentication and verification key consists of a sequence of quantum Clifford operators. The encryption and decryption key is made of a sequence of quantum permutations. The scheme uses the block counter mode. Integrity and replay protection are also provided. For authentication, the source provides proof of ownership of the authentication key to the destination. Validation of integrity and replay protection rely on testing the consistency of the signature field of every block. The scheme is practical but does not achieve perfect indistinguishability because of the risk of message collision. This is normal and unavoidable when fixed-size fields are assumed to make a scheme practical. The message collision probability has been analytically determined. The model can be used to determine the values of the security parameters and the lifetime of session keys to mitigate the risk of information leakage according to the needs of the scheme’s users.

Data and software availability

Zenodo. Quantum Data Communication Protection with the Quantum Permutation Pad Block Cipher in Counter Mode and Clifford Operators https://doi.org/10.5281/zenodo.8246914.

This project contains the following underlying data:

• QPPCTRC.mlx (The data and Matlab scripts used to produce the plots presented in this article

Data are available under the terms of the Creative Commons Attribution 4.0 International license (CC-BY 4.0).

References

1. National Security Agency - Central Security Service: Quantum Key Distribution (QKD) and Quantum Cryptography (QC). accessed: August 26, 2023. Reference Source
2. Vakhitov A, Makarov V, Hjelme DR: Large pulse attack as a method of conventional optical eavesdropping in quantum cryptography. J. Mod. Opt. 2001; 48(13): 2023–2038. Publisher Full Text
3. Makarov V, Hjelme DR: Faked states attack on quantum cryptosystems. J. Mod. Opt. 2005; 52(5): 691–705. Publisher Full Text
4. Ferenczi A, Grangier P, Grosshans F: Calibration attack and defense in continuous variable quantum key distribution. International Quantum Electronics Conference. Optica Publishing Group; 2007; page IC_13.
5. Zhao Y, Fung C-HF, Qi B, et al.: Quantum hacking: Experimental demonstration of time-shift attack against practical quantum-key-distribution systems. Phys. Rev. A. 2008; 78(4): 042333. Publisher Full Text
6. Scarani V, Kurtsiefer C: The black paper of quantum cryptography: real implementation problems. Theor. Comput. Sci. 2014; 560: 27–32. Publisher Full Text
7. Barnum H, Crépeau C, Gottesman D, et al.: Authentication of quantum messages. The 43rd Annual IEEE Symposium on Foundations of Computer Science, 2002. Proceedings. IEEE; 2002; pp. 449–458.
8. Schuknecht C: Quantum Private Broadcasting. Université d’Ottawa/University of Ottawa; 2021. PhD thesis.
9. Barbeau M, Kranakis E, Perez N: Authenticity, Integrity, and Replay Protection in Quantum Data Communications and Networking. ACM Transactions on Quantum Computing. 2022; 3(2): 1–22. Publisher Full Text
10. Kuang R, Barbeau M: Quantum Permutation Pad for Universal Quantum-Safe Cryptography. Quantum Inf. Process. 2022; 21(6): 211. Publisher Full Text
11. Aharonov D, Ben-Or M, Eban UME: Interactive proofs for quantum computations. Proceedings of Innovations of Computer Science. New York, NY: ACM; 2010; pp. 453–469.
12. Wainewright E: Efficient simulation for quantum message authentication. Ottawa, ON, Canada: Faculty of Graduate and Postdoctoral Studies, University of Ottawa; 2016. Master’s thesis.
13. Broadbent A, Wainewright E: Efficient simulation for quantum message authentication. International Conference on Information Theoretic Security. Heidelberg: Springer; 2016; pp. 72–91.
14. Barbeau M: Cryptographic Schemes for Secret Long-Distance Underwater Communications. J. Commun. 2023. to appear. Publisher Full Text
15. Barbeau M: Confidential Underwater Communications Using Quantum Permutation Pad in Counter Mode. Proceedings of 12th International Conference on Communications, Circuits, and Systems (ICCCAS), Singapore. 2023.
16. Das S, Siopsis G: Practically secure quantum position verification. New J. Phys. June 2021; 23(6): 063069. 1367-2630. Publisher Full Text
17. Satoh T, Nagayama S, Oka T, et al.: The network impact of hijacking a quantum repeater. Quantum Science and Technology. 2018; 3(3): 034008. Publisher Full Text
18. Alagic G, Broadbent A, Fefferman B, et al.: Computational security of quantum encryption. International Conference on Information Theoretic Security. Heidelberg: Springer; 2016; pp. 47–71.
19. St-Jules M: Secure quantum encryption. Ottawa, ON, Canada: School of Graduate Studies and Research, University of Ottawa; November 2016. Master’s thesis.
20. National Institute of Standards and Technology: Advanced Encryption Standard (AES). accessed: June 23, 2023. Reference Source
21. Langenberg B, Pham H, Steinwandt R: Reducing the cost of implementing the advanced encryption standard as a quantum circuit. IEEE Transactions on Quantum Engineering. 2020; 1: 1–12. Publisher Full Text
22. Wang Z-G, Wei S-J, Long G-L: A quantum circuit design of AES requiring fewer quantum qubits and gate operations. Front. Phys. 2022; 17(4): 41501. Publisher Full Text
23. Zou J, Wei Z, Sun S, et al.: Quantum circuit implementations of AES with fewer qubits. Advances in Cryptology–ASIACRYPT 2020: 26th International Conference on the Theory and Application of Cryptology and Information Security, Daejeon, South Korea, December 7–11, 2020, Proceedings, Part II 26. Springer; 2020; pp. 697–726.
24. Jang K, Song G, Kim H, et al.: Efficient implementation of PRESENT and GIFT on quantum computers. Appl. Sci. 2021; 11(11): 4776. Publisher Full Text
25. Baksi A, Jang K, Song G, et al.: Quantum implementation and resource estimates for RECTANGLE and KNOT. Quantum Inf. Process. 2021; 20: 1–24. Publisher Full Text
26. Zixuan H, Kais S: A quantum encryption design featuring confusion, diffusion, and mode of operation. Sci. Rep. 2021; 11(1): 23774. Publisher Full Text
27. Kuang R, Perepechaenko M: Quantum encryption with quantum permutation pad in IBMQ systems. EPJ Quantum Technol. 2022; 9(1): 26. Publisher Full Text
28. Kuang R, Perepechaenko M: Quantum encryption and decryption in IBMQ systems using quantum permutation pad. J. Commun. 2022; 17(12): 972–978. Publisher Full Text
29. Perepechaenko M, Kuang R: Quantum encryption of superposition states with quantum permutation pad in IBM quantum computers. EPJ Quantum Technol. 2023; 10(1): 7. Publisher Full Text
30. Grover LK: A fast quantum mechanical algorithm for database search. Proceedings of the Twenty-eighth Annual ACM Symposium on Theory of Computing. 1996; pp. 212–219.
31. Mashatan A, Heintzman D: The complex path to quantum resistance. Commun. ACM. 2021; 64(9): 46–53. Publisher Full Text
32. Bernstein DJ, Lange T: Post-quantum cryptography. Nature. 2017; 549(7671): 188–194. Publisher Full Text
33. Bellare M, Rogaway P: Introduction to modern cryptography. accessed: June 23, 2023. Reference Source
34. Van Den E: A simple method for sampling random Clifford operators. 2021 IEEE International Conference on Quantum Computing and Engineering (QCE). IEEE; 2021; pp. 54–59.

Footnotes

1 Let $α = x + jy$ be a complex number, $| α |$ yields the absolute value (also called modulus or magnitude) of the complex number, that is, $\sqrt{x^{2} + y^{2}}$ .

Comments on this article Comments (0)

Version 1

VERSION 1 PUBLISHED 11 Sep 2023

Author details Author details

School of Computer Science, Carleton University, Ottawa, Ontario, K1S5B6, Canada

Michel Barbeau
Roles: Conceptualization, Formal Analysis, Methodology, Writing – Original Draft Preparation, Writing – Review & Editing

Competing interests

No competing interests were disclosed.

Grant information

We acknowledge the support of the Natural Sciences and Engineering Research Council of Canada (NSERC). Funding ref RGPIN-2019-06156
The funders had no role in study design, data collection and analysis, decision to publish, or preparation of the manuscript.

Article Versions (1)

version 1

Published: 11 Sep 2023, 12:1123

https://doi.org/10.12688/f1000research.140027.1

© 2023 Barbeau M. This is an open access article distributed under the terms of the Creative Commons Attribution License, which permits unrestricted use, distribution, and reproduction in any medium, provided the original work is properly cited.

Download

Export To

metrics

	Views	Downloads
F1000Research	-	-
PubMed Central Data from PMC are received and updated monthly.	-	-

Citations

SEE MORE DETAILS

CITE

how to cite this article

Barbeau M. Quantum data communication protection with the quantum permutation pad block cipher in counter mode and Clifford operators [version 1; peer review: 1 approved]. F1000Research 2023, 12:1123 (https://doi.org/10.12688/f1000research.140027.1)

NOTE: If applicable, it is important to ensure the information in square brackets after the title is included in all citations of this article.

track

receive updates on this article

Track an article to receive email alerts on any updates to this article.

Open Peer Review

Version 1

VERSION 1

PUBLISHED 11 Sep 2023

Views

Reviewer Report 23 Jan 2024

Cherry Mangla, CN Infometic Inc, Edmonton, Alberta, Canada

Approved

https://doi.org/10.5256/f1000research.153354.r230252

This article plays a crucial role in the world of cybersecurity and quantum computing, and I fully agree with what the author is saying. The author points out that because of some problems with quantum mechanics, many cybersecurity plans hit roadblocks or never get off the ground. I agree that we need more research like this to push forward in both quantum computing and cybersecurity.

However, I think the author could explain the proposed plan in more detail. It seems like the author has a background in this area, so a bit more explanation would help. A deeper dive into the plan's ins and outs, including how it works, what it found, and what it could mean, would make the research more thorough. This would not only make the research more trustworthy but also contribute more to what we already know in this field.

In simple terms, the connection between quantum computing and cybersecurity is important, and this article is a part of that connection. By calling for more attention and refinement of the proposed plan, we create a space for continued growth and new ideas in both these fields.

Is the work clearly and accurately presented and does it cite the current literature?

Yes
Is the study design appropriate and is the work technically sound?

Yes
Are sufficient details of methods and analysis provided to allow replication by others?

Yes
If applicable, is the statistical analysis and its interpretation appropriate?

I cannot comment. A qualified statistician is required.
Are all the source data underlying the results available to ensure full reproducibility?

Yes
Are the conclusions drawn adequately supported by the results?

Yes

Competing Interests: No competing interests were disclosed.

Reviewer Expertise: Quantum communication and cybersecuirty schemes

I confirm that I have read this submission and believe that I have an appropriate level of expertise to confirm that it is of an acceptable scientific standard.

CITE

Report a concern

Author Response 22 Mar 2024

Michel Barbeau, School of Computer Science, Carleton University, Ottawa, K1S5B6, Canada

22 Mar 2024

Author Response

Thanks for your report! I will address your feedback.
Competing Interests: No competing interests were disclosed.
Thanks for your report! I will address your feedback.
Thanks for your report! I will address your feedback.
Competing Interests: No competing interests were disclosed. Close
Report a concern
Respond or Comment

COMMENTS ON THIS REPORT

Author Response 22 Mar 2024

Michel Barbeau, School of Computer Science, Carleton University, Ottawa, K1S5B6, Canada

22 Mar 2024

Author Response

Thanks for your report! I will address your feedback.
Competing Interests: No competing interests were disclosed.
Thanks for your report! I will address your feedback.
Thanks for your report! I will address your feedback.
Competing Interests: No competing interests were disclosed. Close
Report a concern

Comments on this article Comments (0)

Version 1

VERSION 1 PUBLISHED 11 Sep 2023

Open Peer Review

Reviewer Status

Reviewer Reports

	Invited Reviewers
	1
Version 1 11 Sep 23	read

Cherry Mangla, CN Infometic Inc, Edmonton, Canada

Comments on this article

All Comments(0)

Add a comment

Browse by related subjects

Back to all reports

Reviewer Report

13 Views

23 Jan 2024 | for Version 1

Cherry Mangla, CN Infometic Inc, Edmonton, Alberta, Canada

13 Views Cite this report Responses(1)

Approved

Is the work clearly and accurately presented and does it cite the current literature?

Yes
Is the study design appropriate and is the work technically sound?

Yes
Are sufficient details of methods and analysis provided to allow replication by others?

Yes
If applicable, is the statistical analysis and its interpretation appropriate?

I cannot comment. A qualified statistician is required.
Are all the source data underlying the results available to ensure full reproducibility?

Yes
Are the conclusions drawn adequately supported by the results?

Yes

Competing Interests

No competing interests were disclosed.

Reviewer Expertise

Quantum communication and cybersecuirty schemes

I confirm that I have read this submission and believe that I have an appropriate level of expertise to confirm that it is of an acceptable scientific standard.

Respond to this report

Responses (1)

Alongside their report, reviewers assign a status to the article:

Approved - the paper is scientifically sound in its current form and only minor, if any, improvements are suggested

Approved with reservations - A number of small changes, sometimes more significant revisions are required to address specific details and improve the papers academic merit.

Not approved - fundamental flaws in the paper seriously undermine the findings and conclusions

[1] 1. National Security Agency - Central Security Service: Quantum Key Distribution (QKD) and Quantum Cryptography (QC). accessed: August 26, 2023. Reference Source

[2] 2. Vakhitov A, Makarov V, Hjelme DR: Large pulse attack as a method of conventional optical eavesdropping in quantum cryptography. J. Mod. Opt. 2001; 48(13): 2023–2038. Publisher Full Text

[3] 3. Makarov V, Hjelme DR: Faked states attack on quantum cryptosystems. J. Mod. Opt. 2005; 52(5): 691–705. Publisher Full Text

[4] 4. Ferenczi A, Grangier P, Grosshans F: Calibration attack and defense in continuous variable quantum key distribution. International Quantum Electronics Conference. Optica Publishing Group; 2007; page IC_13.

[5] 5. Zhao Y, Fung C-HF, Qi B, et al.: Quantum hacking: Experimental demonstration of time-shift attack against practical quantum-key-distribution systems. Phys. Rev. A. 2008; 78(4): 042333. Publisher Full Text

[6] 6. Scarani V, Kurtsiefer C: The black paper of quantum cryptography: real implementation problems. Theor. Comput. Sci. 2014; 560: 27–32. Publisher Full Text

[7] 7. Barnum H, Crépeau C, Gottesman D, et al.: Authentication of quantum messages. The 43rd Annual IEEE Symposium on Foundations of Computer Science, 2002. Proceedings. IEEE; 2002; pp. 449–458.

[8] 8. Schuknecht C: Quantum Private Broadcasting. Université d’Ottawa/University of Ottawa; 2021. PhD thesis.

[9] 9. Barbeau M, Kranakis E, Perez N: Authenticity, Integrity, and Replay Protection in Quantum Data Communications and Networking. ACM Transactions on Quantum Computing. 2022; 3(2): 1–22. Publisher Full Text

[10] 10. Kuang R, Barbeau M: Quantum Permutation Pad for Universal Quantum-Safe Cryptography. Quantum Inf. Process. 2022; 21(6): 211. Publisher Full Text

[11] 11. Aharonov D, Ben-Or M, Eban UME: Interactive proofs for quantum computations. Proceedings of Innovations of Computer Science. New York, NY: ACM; 2010; pp. 453–469.

[12] 12. Wainewright E: Efficient simulation for quantum message authentication. Ottawa, ON, Canada: Faculty of Graduate and Postdoctoral Studies, University of Ottawa; 2016. Master’s thesis.

[13] 13. Broadbent A, Wainewright E: Efficient simulation for quantum message authentication. International Conference on Information Theoretic Security. Heidelberg: Springer; 2016; pp. 72–91.

[14] 14. Barbeau M: Cryptographic Schemes for Secret Long-Distance Underwater Communications. J. Commun. 2023. to appear. Publisher Full Text

[15] 15. Barbeau M: Confidential Underwater Communications Using Quantum Permutation Pad in Counter Mode. Proceedings of 12th International Conference on Communications, Circuits, and Systems (ICCCAS), Singapore. 2023.

[16] 16. Das S, Siopsis G: Practically secure quantum position verification. New J. Phys. June 2021; 23(6): 063069. 1367-2630. Publisher Full Text

[17] 17. Satoh T, Nagayama S, Oka T, et al.: The network impact of hijacking a quantum repeater. Quantum Science and Technology. 2018; 3(3): 034008. Publisher Full Text

[18] 18. Alagic G, Broadbent A, Fefferman B, et al.: Computational security of quantum encryption. International Conference on Information Theoretic Security. Heidelberg: Springer; 2016; pp. 47–71.

[19] 19. St-Jules M: Secure quantum encryption. Ottawa, ON, Canada: School of Graduate Studies and Research, University of Ottawa; November 2016. Master’s thesis.

[20] 20. National Institute of Standards and Technology: Advanced Encryption Standard (AES). accessed: June 23, 2023. Reference Source

[21] 21. Langenberg B, Pham H, Steinwandt R: Reducing the cost of implementing the advanced encryption standard as a quantum circuit. IEEE Transactions on Quantum Engineering. 2020; 1: 1–12. Publisher Full Text

[22] 22. Wang Z-G, Wei S-J, Long G-L: A quantum circuit design of AES requiring fewer quantum qubits and gate operations. Front. Phys. 2022; 17(4): 41501. Publisher Full Text

[23] 23. Zou J, Wei Z, Sun S, et al.: Quantum circuit implementations of AES with fewer qubits. Advances in Cryptology–ASIACRYPT 2020: 26th International Conference on the Theory and Application of Cryptology and Information Security, Daejeon, South Korea, December 7–11, 2020, Proceedings, Part II 26. Springer; 2020; pp. 697–726.

[24] 24. Jang K, Song G, Kim H, et al.: Efficient implementation of PRESENT and GIFT on quantum computers. Appl. Sci. 2021; 11(11): 4776. Publisher Full Text

[25] 25. Baksi A, Jang K, Song G, et al.: Quantum implementation and resource estimates for RECTANGLE and KNOT. Quantum Inf. Process. 2021; 20: 1–24. Publisher Full Text

[26] 26. Zixuan H, Kais S: A quantum encryption design featuring confusion, diffusion, and mode of operation. Sci. Rep. 2021; 11(1): 23774. Publisher Full Text

[27] 27. Kuang R, Perepechaenko M: Quantum encryption with quantum permutation pad in IBMQ systems. EPJ Quantum Technol. 2022; 9(1): 26. Publisher Full Text

[28] 28. Kuang R, Perepechaenko M: Quantum encryption and decryption in IBMQ systems using quantum permutation pad. J. Commun. 2022; 17(12): 972–978. Publisher Full Text

[29] 29. Perepechaenko M, Kuang R: Quantum encryption of superposition states with quantum permutation pad in IBM quantum computers. EPJ Quantum Technol. 2023; 10(1): 7. Publisher Full Text

[30] 30. Grover LK: A fast quantum mechanical algorithm for database search. Proceedings of the Twenty-eighth Annual ACM Symposium on Theory of Computing. 1996; pp. 212–219.

[31] 31. Mashatan A, Heintzman D: The complex path to quantum resistance. Commun. ACM. 2021; 64(9): 46–53. Publisher Full Text

[32] 32. Bernstein DJ, Lange T: Post-quantum cryptography. Nature. 2017; 549(7671): 188–194. Publisher Full Text

[33] 33. Bellare M, Rogaway P: Introduction to modern cryptography. accessed: June 23, 2023. Reference Source

[34] 34. Van Den E: A simple method for sampling random Clifford operators. 2021 IEEE International Conference on Quantum Computing and Engineering (QCE). IEEE; 2021; pp. 54–59.

Quantum data communication protection with the quantum permutation pad block cipher in counter mode and Clifford operators

Abstract

Keywords

Introduction

Related work

Quantum information background

(1)

(2)

(3)

(4)

(5)

(6)

(7)

Quantum data block cipher and authentication scheme

Clifford-operator-based authentication

(8)

(9)

Quantum permutation pad

Definition 1

Theorem 1

Block counter mode

Table 1. Block modes.

Encryption and signature algorithm

(10)

(11)

(12)

(13)

Decryption and authentication algorithm

(14)

(15)

(16)

(17)

Collision probability

Definition 2

Theorem 2

Proof.

(18)

(19)

(20)

(21)

Remark 1

Figure 1. Probability of block collision versus the number of blocks (i) encrypted, for block sizes (n) two, three, four, and five qubits.

Figure 2. Value of imax (see Theorem 2) according to the block size (n) and message size (m).

Conclusion

Data and software availability

References

Footnotes

Comments on this article Comments (0)

Open Peer Review

Comments on this article Comments (0)

Open Peer Review

Reviewer Status

Reviewer Reports

Comments on this article

Browse by related subjects

Competing Interests Policy

Stay Updated

Figure 1. Probability of block collision versus the number of blocks ( $i$ ) encrypted, for block sizes ( $n$ ) two, three, four, and five qubits.

Figure 2. Value of imax (see Theorem 2) according to the block size ( $n$ ) and message size ( $m$ ).