Analytical approach to piezoelectric model synthesis with the use of Cauer’s method for system design

Jacek Harazin; Andrzej Wróbel

doi:10.12688/f1000research.140943.1

Home Browse Analytical approach to piezoelectric model synthesis with the use...

ALL Metrics

Views

Downloads

Get PDF

Get XML

Export

▬

✚

Research Article

Analytical approach to piezoelectric model synthesis with the use of Cauer’s method for system design

[version 1; peer review: 2 approved with reservations]

Jacek Harazin ¹, Andrzej Wróbel¹

PUBLISHED 05 Oct 2023

Author details Author details

¹ Faculty of Mechanical Engineering, Politechnika Slaska, Gliwice, Silesian Voivodeship, 44-100, Poland

Jacek Harazin
Roles: Data Curation, Formal Analysis, Funding Acquisition, Investigation, Methodology, Software, Visualization, Writing – Original Draft Preparation

Andrzej Wróbel
Roles: Conceptualization, Project Administration, Resources, Supervision, Validation, Writing – Review & Editing

OPEN PEER REVIEW

REVIEWER STATUS

Abstract

Background: Piezoceramic materials have unique property which enables direct and bilateral conversion between mechanical and electrical energy. This ability facilitates significant miniaturisation of technology and opens many opportunities in design of new actuators and energy harvesters. Mathematical modelling of piezoelectric modules is notoriously hard due to complex constitutive equations defining mechanical and electrical energy conversion.
Methods: The article presents research on a new synthesis method based on the Cauer’s method for electrical and mechanical system design. Mechanical damping is introduced with the use of Rayleigh’s approximation. A discrete electromechanical model is formed based on the Mason’s piezoelectric model. As an additional element of the research, a non-standard model analysis method using edge graphs and structural numbers is employed to investigate potential reductions in computational requirements for model analysis.
Results: The electromechanical model analysis has shown an error of 5% in relation to the resonance target. The calculated peak in magnitude of displacement at the resonant frequency was well above the capability of a 3.5mm thick piezoelectric plate. The proposed non-standard method of analysis gave identical results in terms of obtained resonance frequencies. The calculated magnitude of vibrations was varying by 50 – 58%.
Conclusions: The synthesis method presented in this paper allows an approximation of piezoelectric parameters of a real system based on the created mathematical model. Currently this method is subject to a considerable error in the determined vibration amplitudes of the system, but it allows a coarse approximation of the parameters while having a very limited number of input data. The additional method of analysis based on structural numbers offers a promising alternative to matrix calculations but requires a more thorough investigation of the computational power required to determine whether it can compete with existing algorithms.

Keywords

piezoelectricity, mathematical model, synthesis

Corresponding author: Jacek Harazin

Competing interests: No competing interests were disclosed.

Grant information: The article was financed from the subvention for maintenance and development of research potential of young scientists of the Silesian University of Technology.
The funders had no role in study design, data collection and analysis, decision to publish, or preparation of the manuscript.

Copyright: © 2023 Harazin J and Wróbel A. This is an open access article distributed under the terms of the Creative Commons Attribution License, which permits unrestricted use, distribution, and reproduction in any medium, provided the original work is properly cited.

How to cite: Harazin J and Wróbel A. Analytical approach to piezoelectric model synthesis with the use of Cauer’s method for system design [version 1; peer review: 2 approved with reservations]. F1000Research 2023, 12:1273 (https://doi.org/10.12688/f1000research.140943.1) First published: 05 Oct 2023, 12:1273 (https://doi.org/10.12688/f1000research.140943.1) Latest published: 06 Sep 2024, 12:1273 (https://doi.org/10.12688/f1000research.140943.3)

Introduction

One of the purposes of mathematical modelling in case of physics is to give a clear and systemic picture of relations and energy flow between elements of a system. Physicists use mathematical modelling to describe phenomena and problem solve the mechanics of a wide variety of systems.¹ Mathematical synthesis supported by previous empirical analysis of underlying phenomena helps in creating models which describe real behaviour of materials and components with mathematical correlations. Deep understanding gained by thorough analysis can be later used in development of highly sophisticated systems that are used for precise control of various system variables.² Systems that precisely control room temperature or humidity, systems responsible for engine control and its smooth acceleration or deceleration or systems used for active vibration cancellation are only few of the examples.³^–⁶ Polynomial equations are great mathematical tools for approximation and interpolation of numerous phenomena which is why they are commonly used in mathematical modelling.⁷^–⁹^,¹⁰ Laplacian and Lagrangian algebra rely on polynomial and exponential equations to systemically represent components of force and energy having influence on successive derivatives of displacement or charge. Polynomial equations are among the main set of tools in control theory²^,⁷^–⁹^,¹¹^–¹⁶ and were used during the development of signal filters composed of RLC (R – resistor, L – coil, C – capacitor) components.¹⁷^,¹⁸

Wilhelm Cauer was among the pioneers of electrical model synthesis, creating algorithms based on transfer function polynomials, defining large range of electrical systems by using mathematical decomposition. Cauer synthesis¹⁷^,¹⁸ relies on decomposing transfer function polynomials into continued fractions. The set of coefficients of a continued fraction represents values defining each system component properties (like impedance or capacitance). This procedure allows any transfer function of a complex system to be broken down into a series of components represented by a lumped model. Moreover, because of existing analogies between electrical and mechanical elements, this method can be applied to both electrical and mechanical models.⁷^–⁹^,¹¹ Piezoelectric materials exhibit properties that can be described with a combination of interactions between both electrical and mechanical components.¹⁹ A set of constitutive equations for piezoelectricity¹² has been established to describe electromechanical coupling for simple and inverse piezoelectric effect. Because of the complex set of dimensional relations, described by tensors, mathematical modelling of piezoelectric components is being focused mainly on the analytical aspect of this phenomenon. Researchers largely focus on modelling simple piezoelectric components with lumped models¹³^,¹⁴ and matrix tensor equations²⁰ or try to approach the problem using FEM (finite element method) analysis.²¹ There are also analytical methods that can be labelled as “non-classical” which rely on AI (artificial intelligence) algorithms or graphical representations of the system like “edge graphs”. Many of the developed models are used on a case-by-case basis where system variables defining piezoelectric behaviour are fully or partially known or they are being empirically determined.¹⁵^,²¹^–²⁷ There is a small research gap when it comes to the subject of a full piezoelectric system synthesis where majority of the initial parameters are unknown. This article tries to focus on the development of a new method for piezoelectric system synthesis where the only initial information comes in the form of established resonant and anti-resonant frequencies. The algorithm based on Cauer synthesis method is used to construct an initial discrete mechanical model which serves as the base for piezoelectric model synthesis. Mechanical damping is introduced to the model with the help of Rayleigh’s method.²⁸ The transition between purely mechanical model and a discrete electromechanical model of the piezoelectric plate is done with the combination of Mason’s model and analogies between mechanical and electrical components. There are many unknown piezoelectric parameters which have to be determined in this process. To solve this problem, authors have chosen an approach where most of the parameters are being approximated by using the obtained mechanical properties of an already synthesized system and a set of equations derived from the constitutive equations of piezoelectricity.

Part of this article has been devoted to a study on the potential reductions in computational requirements for model analysis that might be possible when using edge graphs.⁷^,⁸^,¹¹^,²⁹ Some methods based on edge graphs bare close naming resemblance like the ones used in¹⁵^,²² which may cause confusion. As a matter of clarification, this article is focusing on the method using edge graphs in combination with structural number algebra. Structural numbers visually resemble matrix calculation as each structural number construct consist of rows and columns of numbers. The number of rows and columns, however, is tightly connected to the shape of an edge graph which a given structural number relates to. Each node in an edge graph and all its connections are represented by a single structural number vector (e.g.,|1 2 3 4|for a node connecting four edges numbered from 1 to 4). A structural number is then created by multiplying such node vectors by themselves according to structural number algebra. Arithmetic and logic operations based on structural number algebra were described in depth by professor Stanisław Bellert in his book.²⁹ More details can also be found in previous article published by authors.³⁰ The article also directly relates to adaptations of this method used by other researchers for analysis and synthesis of various systems.²^,¹¹^,¹⁶

Methods

Mechanical model synthesis

The synthesis process begins with a selection of predetermined resonant and anti-resonant frequencies. The set of frequencies may be freely defined according to future applications or may result from a vibration spectral analysis of the object of interest. In this method, the identified set of frequencies is the only input information. It is used to generate a transfer function polynomial, which can later be transformed into a chain fraction equation. Cauer’s algorithm mentioned in Refs. 8 and 11 was used to create four different types of mechanical models depending on the allocation of coefficients in the chosen transfer function polynomial. Depending on the polynomial, the cascade model resulting from the chain fractioning process can be constrained on one end or not constrained at all. Additionally, the model can be excited by either a kinetic or dynamic force. A combination of those factors creates four different types of models with their own transfer functions (detailed examples of each type and associated transfer function structures are given in Refs. 8 and 11). The model chosen for the purposes of this article is a cascade model with one of its ends constrained and which is being excited by the dynamic force. The choice is motivated by the close resemblance of such a model to a fixed piezoelectric stack, where individual plates can be described as successive stages of the model. According to the models proposed in Refs. 8 and 11, a hypothetical transfer function for an infinite degree cascade model constrained on one end and excited with a dynamic force takes the factorial form:

(1)

T (s) = H \frac{(s^{2} + ω_{1}^{2}) (s^{2} + ω_{3}^{2}) \dots (s^{2} + ω_{n - 2}^{2}) (s^{2} + ω_{n}^{2})}{s (s^{2} + ω_{2}^{2}) (s^{2} + ω_{4}^{2}) \dots (s^{2} + ω_{n - 1}^{2})},

where:

T(s) – response of a system,

H – response amplification factor,

ω – consecutive frequencies (even are resonant and odd are anti-resonant),

s – Laplacian variable.

The factorial form is transformed into a standard polynomial form to define the coefficients for successive powers of the equation:

(2)

T (s) = H \frac{a_{i} s^{n} + a_{i - 1} s^{n - 2} + \dots + a_{1} s^{2} + a_{0}}{b_{i} s^{n - 1} + b_{i - 1} s^{n - 3} + \dots + b_{1} s},

where:

a_i – numerator coefficients,

b_i – denominator coefficients.

After the initial calculation of the polynomial coefficients, the transfer function is converted into a continued fraction by using the Cauer’s method in its first form.¹⁷ The method involves breaking down a polynomial into a chain fraction using simple mathematical operations. The first form of Cauer synthesis is implemented by dividing the coefficient of the greatest power of a numerator by the coefficient of the greatest power of a denominator. The resulting fraction is being multiplied by the denominator and subtracted from the polynomial function, leaving the rest, which is then inverted. This process is repeated until all powers of the transfer function are reduced:

(3)

I_{p}^{1} = \frac{a_{i} s^{n}}{b_{i} s^{n - 1}} = \frac{a_{i}}{b_{i}} s,

(4)

R_{p}^{1} = \frac{a_{i} s^{n} + a_{i - 1} s^{n - 2} + \dots + a_{1} s^{2} + a_{0}}{b_{i} s^{n - 1} + b_{i - 1} s^{n - 3} + \dots + b_{1} s} - I_{p}^{1},

(5)

R_{p}^{j + 1} = \frac{1}{R_{p}^{j}} - I_{p}^{j + 1},

where:

$I_{p}^{i}$ – fraction extracted by division of parameters next to the highest power “s”,

$R_{p}^{i}$ – rest of the original polynomial after subtraction.

A continued fraction resulting from the process can be used to determine the values of discrete component parameters in the synthesized system:

(6)

\frac{T (s)}{H} = I_{p}^{1} ∙ s + \frac{1}{I_{p}^{2} ∙ s + \dots + \frac{1}{I_{p}^{n - 1} ∙ s + I_{p}^{n} ∙ s}} .

Obtained values can be used in either mechanical or electrical cascade systems which gives this method a high degree of flexibility. An example of an infinite stage mechanical system resulting from the calculations have been shown in Figure 1.

Figure 1. A mechanical cascade system composed of an infinite number of stages composed of mass “m” and spring “c” pairs, synthesized from the transfer function polynomial with the Cauer’s method.

The newly obtained mechanical model consists of springs and inertial components which can be used to determine the stiffness and mass/density of the piezoelectric material. Damping elements can be added to the model to account for energy dissipation which is an inherent property of piezoelectric materials. The mechanical quality factor is often used to indicate piezoelectric mechanical damping ability. The factor is inversely proportional to the amount of damping generated by the material and can be derived from Rayleigh’s method.²⁸^,³¹ However, damping introduces complex derivatives into the equations of motion for any mechanical or electrical system. Every system can be considered under the case of subcritical, critical, and over-critical damping. Depending on the strength of damping elements, a system can be in a state of damped oscillations (subcritical damping) or the oscillations may stop immediately after the harmonic excitation disappears (critical damping), they do not occur (over-critical damping). Because of that, there are three separate integral solutions that describe each case respectively. A resonance (additive interference of harmonic oscillations) occurs only under the case of subcritical damping. In order to limit the range of possible solutions, it was assumed that all models would only be considered under subcritical damping, thus eliminating cases where vibrations cannot resonate. The decision was made because the project was focused on piezoelectric applications where vibration generation was their main purpose. Another assumption limited the range of solutions to those with a Rayleigh damping coefficient related to stiffness. According to literature,²⁴ most cases of piezoelectric damping are restricted to damping with respect to element stiffness only. The two assumptions simplify the term for the damping coefficient. Based on the obtained equations, it is then possible to determine the damping parameters for each stage in relation to the spring stiffness:

(7)

β < \frac{2}{ω_{1} + ω_{n}},

(8)

b_{i} = β c_{i},

where:

$β$ – stiffness damping coefficient,

$b_{i}$ – damping value,

$c_{i}$ – spring stiffness.

To verify the model in its current state, an intermediate electromotive force was also added at each stage. Its role was to simulate the actuation of piezoelectric plates by an electrical stimulus, similar to.¹⁵^,²⁵ The electromotive force acts as a simplified force generated by the electromechanical coupling used to describe the conversion of energy conversion between the mechanical and electrical part of a piezoelectric plate. The mechanical model with added damping and electromotive forces is shown in Figure 2.

Figure 2. A discrete cascade mechanical model with added damping elements.

The model masses are marked with “m” symbols, springs with “c” symbols, dampers with “b” symbols and electromotive forces with “G” symbols. The displacement of each mass was marked with “x”.

Mechanical model verification

The synthesized model had to be verified after the addition of new damping elements and additional forces. An analysis of the model response was carried out in terms of its magnitude along the frequency axis. Two analysis methods were used to verify the existing mechanical model. The classical matrix method served as a reference for an additional method using structural numbers.²^,¹¹^,¹⁶^,²⁹ The use of a second method is considered as part of the ongoing research³⁰ aimed at evaluating the accuracy and computational load of structural numbers in comparison to the matrix calculation. Current state of the algorithm based on structural numbers should still not be considered as final as there are more improvements to be made in terms of its compatibility with computation software. Starting with the classical method, a set of equations of motion was created to describe relations between parts of the model. To avoid overcomplicating the example, only two degrees of freedom were considered. The equations of motion for a two-stage model derived from the Lagrangian equations were as follows:

(9)

\{\begin{cases} G_{1} = m_{1} {\ddot{x}}_{1} + b_{1} ({\dot{x}}_{1} - {\dot{x}}_{2}) + c_{1} (x_{1} - x_{2}) \\ G_{2} = m_{2} {\ddot{x}}_{2} - b_{1} ({\dot{x}}_{1} - {\dot{x}}_{2}) + b_{2} {\dot{x}}_{2} - c_{1} (x_{1} - x_{2}) + c_{2} x_{2} \end{cases} .

Under the assumption into account, that the system is only considered in the case of subcritical damping, an integral of a second-order differential equation³² for the variable displacement x can be described by the equation:

(10)

\{\begin{cases} x_{1} = A_{11} sinωt + A_{12} cosωt \\ x_{2} = A_{21} sinωt + A_{22} cosωt \end{cases},

where:

$A_{i 1}$ – real part of the i^th element amplitude response,

$A_{i 2}$ – imaginary part of the i^th element amplitude response.

Combining (9) with (10) and separating the components with sine and cosine coefficients, then reordering the equations by combining all the coefficients standing next to consecutive amplitudes, yields a coefficient matrix:

(11)

[\begin{matrix} k_{1} - m_{1} ω^{2} & - b_{1} ω & - k_{1} & b_{1} ω \\ b_{1} ω & k_{1} - m_{1} ω^{2} & - b_{1} ω & - k_{1} \\ - k_{1} & b_{1} ω & - m_{2} ω^{2} + k_{1} + k_{2} & - b_{1} ω - b_{2} ω \\ - b_{1} ω & - k_{1} & b_{1} ω + b_{2} ω & - m_{2} ω^{2} + k_{1} + k_{2} \end{matrix}] .

Based on the obtained coefficient matrix (11) and a vector of actuating forces, a vector of amplitudes can be calculated. To obtain absolute displacement, the sine and cosine coefficient must be combined using Pythagoreans’ theorem:

(12)

\begin{array}{l} A_{1} = \sqrt{{(A_{11})}^{2} + {(A_{12})}^{2}} \\ A_{2} = \sqrt{{(A_{21})}^{2} + {(A_{22})}^{2}} \end{array}

To calculate phase-shift of each stage along the frequency spectrum, a tangent between the real and imaginary component of displacement can be calculated:

(13)

\begin{array}{l} φ_{1} = atan \frac{A_{11}}{A_{12}} \\ φ_{2} = atan \frac{A_{21}}{A_{22}} \end{array} .

The set of derived equations (12,13) allows the amplitude response and phase shifts to be determined for any cascade system built using standard discrete elements representing model inertia, stiffness, and damping. Calculations are relatively quick and easy when considering systems with a small number of degrees of freedom. However, calculations become much more complex and computationally intensive for systems with a large number of degrees of freedom. This is an effect of the number of elements being multiplied in the determinant of a matrix. The numbers get big really fast because of the accumulation of the powers when all the matrix components are being combined. This problem prompted the search for alternative solutions for rapid analysis of more complex systems.

One of the alternatives to matrix calculations is being developed by the researchers at the Silesian University of Technology.²^,⁷^,⁸^,¹¹^,¹⁶^,²⁹ The non-classical method of system analysis involves the use graphs and structural numbers to illustrate relations between forces in a system. The structural number method offers an alternative solution for deriving equations of motion by using a graphical representation of relations in the system. Each edge of the graph corresponds to a single discrete relation between two elements of a system, represented by nodes. All the edges and nodes in the graph are assigned numbers called “structural numbers”. These numbers form structures similar to matrices based on edge connections with nearby nodes. Using the algebra of structural numbers, it is then possible to derive a system of equations similar to equations of motion. A detailed description of this method in the context of solving mechanical cascade systems without damping was presented in Ref. 30. The structural number algebra is an entirely separate method of performing mathematical operations and therefore requires extensive explanation. It is strongly recommended to consult the book of the original author of this method²⁹ for the details on its usage.

In the context of this article, several necessary changes had to be introduced to account for damping elements in the model. The basic method does not allow a simple decomposition of the sine and cosine coefficients when damping is present in the system. A standard approach includes resolving the equations with motion derivatives replaced with Laplacian transform. The issue arises when the final equation obtained with structural number algebra is turned back into its derivative form. When motion derivatives are replaced with the integral solution for sub critically damped motion as in (10), the equation becomes extremely tangled. To overcome this problem, an intermediate method has been developed, which realises the mentioned decomposition of sine and cosine components (10) prior to the application of the structural number algebra, Effectively, that means that the entire graph of relations was duplicated, separating the edges corresponding to sine and cosine coefficients. Each case is then being calculated separately until the last step. Both resulting graphs are shown in Figure 3.

Figure 3. Graph of the cascade model where: a) shows the sine coefficients b) shows the cosine coefficients.

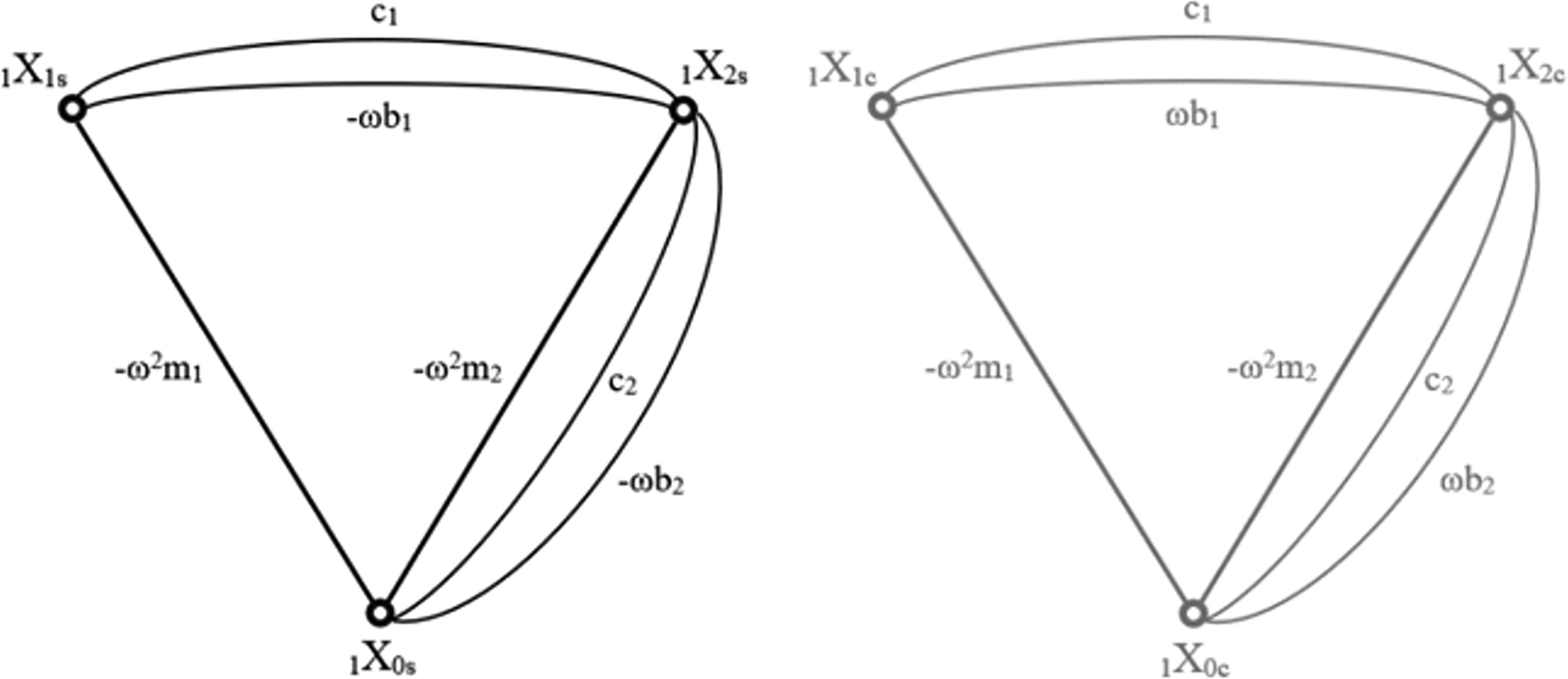
The nodes of each graph represent the degrees of freedom of the model they are describing. Each edge corresponds to forces acting between each degree and is being described by the formula of elements creating each force. “ω” is the frequency, “m” is the mass of each element, “c” corresponds to spring loads and “b” to damping.

The structural numbers of both graphs are synonymous, the only difference being the opposite sign in the first derivatives of the sine and cosine function, which relate to the damping coefficients. As with the matrix method, the sine graph corresponds to the real part of the calculation and the cosine part to the imaginary part. This time, in order to obtain absolute values of the displacements, the merging (similar to (12)) has to be performed for the whole structural number and all the simultaneity functions.¹¹^,²⁹^,³⁰ The amplitude response of each stage can be calculated by solving the equations:

(14)

A_{11} = |\frac{(\binom{Sim}{z} (\frac{\partial D (ω)}{\partial [1]}) G_{11})}{\partial D (ω)} + \frac{(\binom{Sim}{z} (\frac{\partial D (ω)}{\partial [2]}; \frac{\partial D (ω)}{\partial [1]}) G_{21})}{\partial D (ω)}|,

(15)

A_{1} = \sqrt{{(A_{11})}^{2} + {(A_{12})}^{2}},

(16)

D (ω) = \sqrt{D_{s} {(ω)}^{2} + D_{c} {(ω)}^{2}},

where:

$D_{s} (ω)$ – structural number for the sine graph,

$D_{c} (ω)$ – structural number for the cosine graph,

$A_{ij}$ – amplitude calculated with simultaneity function.

The process of obtaining the necessary structural numbers to derive equations (14–16) and the meaning of a simultaneity function has been explained in more detail in.²⁹^,³⁰ The computer algorithm which was later used for this purpose is described in detail under the section dedicated to the algorithm testing.

Electromechanical model synthesis

The synthesized mechanical model serves as a basis for the construction of a combined electromechanical model of a piezoelectric system. Constitutive equations and analogy between mechanical and electrical components were used to derive parameters of the piezoelectric model.¹⁴^,¹⁹^,²⁴^,²⁵ The electromechanical coupling coefficient for piezoelectric coupling perpendicular to the plate surface was determined based on resonant, anti-resonant frequency pairs:

(17)

k_{33}^{2} = \frac{\frac{π}{2}}{1 + \frac{∆ f}{f_{r}}} tan \frac{\frac{π}{2} + \frac{∆ f}{f_{r}}}{1 + \frac{∆ f}{f_{r}}}, ∆ f = f_{a} - f_{r},

where:

$k_{33}$ – electromechanical coupling factor in the 3-3 direction,

$f_{a}$ – anti-resonant frequency of a given stage,

$f_{r}$ – resonant frequency of a given stage.

A broader term defining electromechanical coupling for a general case, called an effective coupling coefficient was used to approximate the capacity of piezoelectric plates³³:

(18)

\frac{k_{eff}^{2}}{1 - k_{eff}^{2}} = \frac{∆ f^{2}}{f_{r}^{2}},

(19)

C_{p} = \frac{k_{eff} C_{m}}{1 - k_{eff}},

(20)

C_{m} = \frac{1}{c_{m}},

where:

$k_{eff}$ – effective electromechanical coupling factor,

$C_{p}$ – plate capacitance,

$C_{m}$ – equivalent capacitance from mechanical stiffness,

$c_{m}$ – mechanical stiffness of a lumped piezoelectric model.

Another property of a piezoelectric material frequently mentioned in specifications is the mechanical quality factor. This property describes the amount of energy that is being lost during dynamic operation of a piezoelectric plate. It corresponds to mechanical losses in a system. An approximate value of a mechanical quality factor can be calculated using the equation derived from the established Rayleigh’s method:

(21)

Q_{m} = \frac{1}{βω} .

Electrical permittivity can be also approximated if piezoelectric capacitance is known by using an equation:

(22)

ε_{33}^{T} = \frac{C_{p} h}{A},

where:

$ε_{33}^{T}$ – electrical permittivity of a piezoelectric material in 3-3 direction under constant stress,

$h$ – plate thickness,

$A$ – plate cross section field.

Lastly, based on the lumped stiffness of the mechanical model, a piezoelectric material stiffness can be obtained using Hooke’s law:

(23)

c_{33}^{E} = c_{m} \frac{h}{A},

where:

$c_{33}^{E}$ – piezoelectric stiffness in 3-3 direction under constant electrical field.

Piezoelectric discrete model verification

To analyse piezoelectric response with calculated parameters, a discrete electromechanical model was created based on the Butterworth-Van Dyke model and other lumped piezoelectric models available in the literature.¹³^–¹⁵^,³⁴ The basic form of constitutive equations for piezoelectric effect in a 33 mode was used:

(24)

\{\begin{matrix} D_{3} = ε_{33}^{T} E_{3} + d_{33} T_{3} \\ S_{3} = d_{33} E_{3} + s_{33}^{E} T_{3} \end{matrix},

where:

$D_{3}$ – electric displacement field,

$S_{3}$ – mechanical strain,

$E_{3}$ – electric field,

$T_{3}$ – mechanical stress,

$d_{33}$ – piezoelectric charge constant,

$s_{33}^{E}$ – mechanical compliance constant (inverse of mechanical stiffness constant).

The equation (24) was modified using Hooke’s law and by converting equations for underlying variables:

(25)

E_{3} = \frac{U_{p}}{h},

where:

U_{p}

– voltage across the piezoelectric plate thickness,

(26)

D_{3} = \frac{Q_{p}}{A},

where:

Q_{p}

– charge across the piezoelectric plate surface.

By combining the constitutive equations with (25,26) and plugging the equations of motion for the initial mechanical model (9) into the mechanical input of the electromechanical system, a lumped piezoelectric model was created. Relations inside a single piezoelectric plate are described by a system of equations:

(27)

\{\begin{matrix} m \ddot{x} + b \dot{x} + c_{m} x = - c_{m} d_{33} U_{p} + F \\ U_{0} C_{p} = x c_{m} d_{33} + U_{p} ε_{33}^{T} \frac{A}{h} (1 - k_{33}^{2}) \end{matrix},

where:

$F$ – external force applied to a piezoelectric plate,

$U_{0}$ – external voltage applied to a piezoelectric plate,

$m$ – lumped piezoelectric mass,

$b$ – lumped piezoelectric damping,

$c_{m}$ – lumped piezoelectric stiffness,

$U_{p}$ – lumped piezoelectric capacitance,

The discrete piezoelectric model has been shown in Figure 4. Inputs and outputs were extracted from (27) by grouping parameters and converting the equation into a Laplace form. The resulting matrix was used to create an algorithm for piezoelectric model analysis:

(28)

[\begin{matrix} X (s) \\ U_{p} (s) \end{matrix}] ∙ [\begin{matrix} m s^{2} + bs + c_{m} & c_{m} d_{33} \\ c_{m} d_{33} & ε_{33}^{T} \frac{A}{h} (1 - k_{33}^{2}) \end{matrix}] = [\begin{matrix} F \\ U_{0} C_{p} \end{matrix}] .

Figure 4. Discrete piezoelectric model composed of mechanical lumped model combined by a transformer with an electrical network.

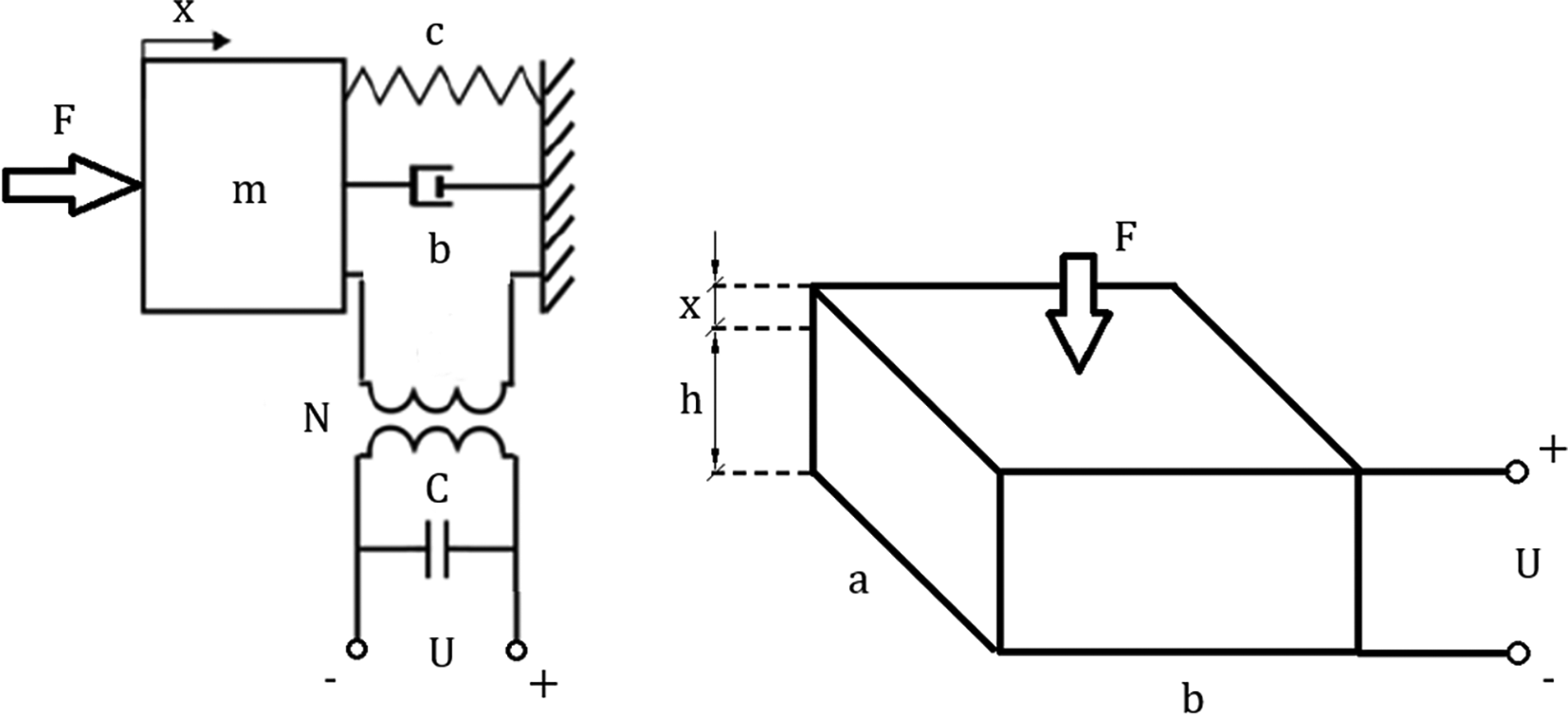
“F” represents an external force, “c” is the mechanical stiffness, “b” corresponds to damping, “N” is the electromechanical coupling, “C” is the electrical capacitance of the piezoelement and “U” represents the voltage exciting the circuit. “a,b,h” correspond to geometric dimensions of the piezoelectric element, while “x” represents the displacement.

The top left coefficient of the coefficient matrix (28) refers to purely mechanical transformations within the piezoelectric plate. Top right and bottom left coefficients refer to the electromechanical coupling. The bottom right coefficient refers to purely electrical transformations. The matrix can be easily expanded by adding more stages to the model as well as it can be calculated using the matrix method mentioned in (10).

Algorithm testing

A series of computer programs were prepared to test the accuracy and computational load of used algorithms. All the programs were written using mathematical software called MATLAB in version R2019b (RRID:SCR_001622). The code was prepared using basic functions offered by the standard MATLAB suite.

The polynomial equation was created using “for” loops which added consecutive elements to its product form, depending on the number of frequencies given as an input. The MATLAB software operates interchangeably between the product form and exponential form of polynomials, so the conversion was done automatically. The Cauer synthesis was realised with basic program loops which continuously calculated the remainders of the polynomial function, as was explained with equations (3,4,5). Based on the order of elements in the resulting chain fraction, consecutive parameters in form of spring loads and masses were extracted from the equation in each iteration of the loop.

The analysis method using matrix calculations was realised by first creating the equations of motion (9) depending on the number of masses given as an input. The displacement was described using a substitute parameter “X” which then was replaced in bulk with derivatives of the sine cosine integral (10) by using MATLAB function “subs”. Next, the equations were transformed into a matrix form and solved with the inbuilt MATLAB solver. The input vector of external forces was used to manipulate the output amplitudes of the matrix formula.

The structural number method was constructed from ground up, using vector transformation operations inside MATLAB. The structural numbers were represented by matrices consisting of simple numbers corresponding to numbered graph edges. Each number was bound to a set of equations representing forces acting inside the system. The method of assigning numbers to equations was explained in.³⁰ The structural number was formed by adding vectors (each vector consists of numbers corresponding to edges connected to a single graph vertex). The process was done using inbuilt MATLAB function called “combvec”. After that, several sorting operations were done in a loop to eliminate any repeats in the matrix representing the graph structural number. Further steps done to determine all simultaneity functions were also done by appropriately sorting and pruning the structural number matrix to create each structural number operation. To obtain final equations from the graph algebra, an intermediate step was introduced, which replaced each number with the equation that was bound to it. The step was also done using the “subs” function.

The eletromechanical system analysis was an extended matrix algorithm that was based on the equation (27). No new functions were introduced to make the algorithms and every step was made in analogy to the matrix method used to analyse purely mechanical systems.

The code has been saved in a proprietary MATLAB format “.mlx” and placed in repositories of Mendeley Data site.³⁵^,³⁶ The code placed in the repository³⁵ contains algorithms used for the synthesis of mechanical systems and their comparison through the matrix and structural number methods. The repository³⁶ contains the algorithm used to synthesise and analyse a full eletromechanical model, simulating the real behaviour of a piezoelectric module. MATLAB is using an open standard for their file formats, so it is possible to open files using standard Windows tools. For reproduction purposes a user has to convert the extension of the file format into “.zip” and open its contents through the “.xml” file stored inside the package. It must be noted however, that the precision and calculation times may vary, depending on the type of software used to reproduce the results and even on the hardware used to process the computation tasks. It is also necessary to note that some of the code may have to be rewritten because of the use of MATLAB specific syntax that may be different in other software. For the sake of consistency and repeatability, all calculations were done on a single computer with a Ryzen 7 2700X processor and a 4 × 8 GB kit of DDR4 CL16 RAM clocked at 3000 Mhz.

Algorithms used to compare the precision and computation time of both matrix and structural number methods were published in an on-line repository.³⁵ To compare the precision of both algorithms the chosen input data consisted of a collection of resonant (41 kHz and 55 kHz) and anti-resonant (47 kHz) frequencies. The frequencies were chosen arbitrarily based around a rough estimation of piezoelectric elements resonating at the lower spectrum of the possible range of resonating piezoelectric modules. The necessary system component parameters were calculated using the synthesis algorithm. The damping ratio was left at 100% and the scaling factor H was set to a value of 0.01. The dynamical forces were set to 1N of harmonic force with a cosine wave on both degrees of freedom. The program named “comparison”³⁵ was used to compare the precision of both algorithms and produce the resulting graphs and calculate deviations for the extrema.

A simple test was also carried out to check how computationally demanding are both methods in comparison to each other. For that purpose, two programs called “Matrix_method” and “Structural_number_method” were written in MATLAB R2019b. Both algorithms were written with a fixed set of model parameters and a fixed set of equations. To avoid long computation times, parameters were chosen for a two-degree system resonating at frequencies of 10 rad/s and 22 rad/s with an antiresonant frequency of 17 rad/s. The computation time was measured for both methods using the inbuilt MATLAB timer function “tic/toc”. The timer measured seconds that the program took to form the equation and calculate the amplitudes in both cases. Each program was run 10 times with the exact same settings and all calculation time measurements were noted down with an average time derived additionally. Before each run, all the variables generated in the previous runs were cleared to avoid any potential changes in computation speed because of reusing the stored results.

For the analysis of the electromechanical system, model with a single degree of freedom was chosen. The resonant frequency was 590kHz and the scaling factor H was set to 0.0025. The damping factor β was calculated from an existing mechanical quality factor Q_m of 83 using equation (7) which was inversed. The remaining input parameters such as plate dimensions, plate stiffness and capacitance were either taken from an existing piezoelectric material specification or derived using the known physical properties (17-26) (http://www.steminc.com/piezo/PZ_property.asp). All parameters used in the case of this article are also contained in the program called “analysis_piezoelectric_system” in the on-line repository.³⁶

Results

A comparison of the efficiency and accuracy of the two methods was done with the comparing program. A two-stage mechanical system with two resonant frequencies of 41kHz and 55kHz (257611rad/s and 345575rad/s respectively) was used for the comparison. The graphs in Figure 5 show the displacement amplitudes for both degrees of freedom of the considered case, obtained by matrix calculation and structural numbers.

Figure 5. Model response calculated for a) first vibrating mass, and b) second vibrating mass.

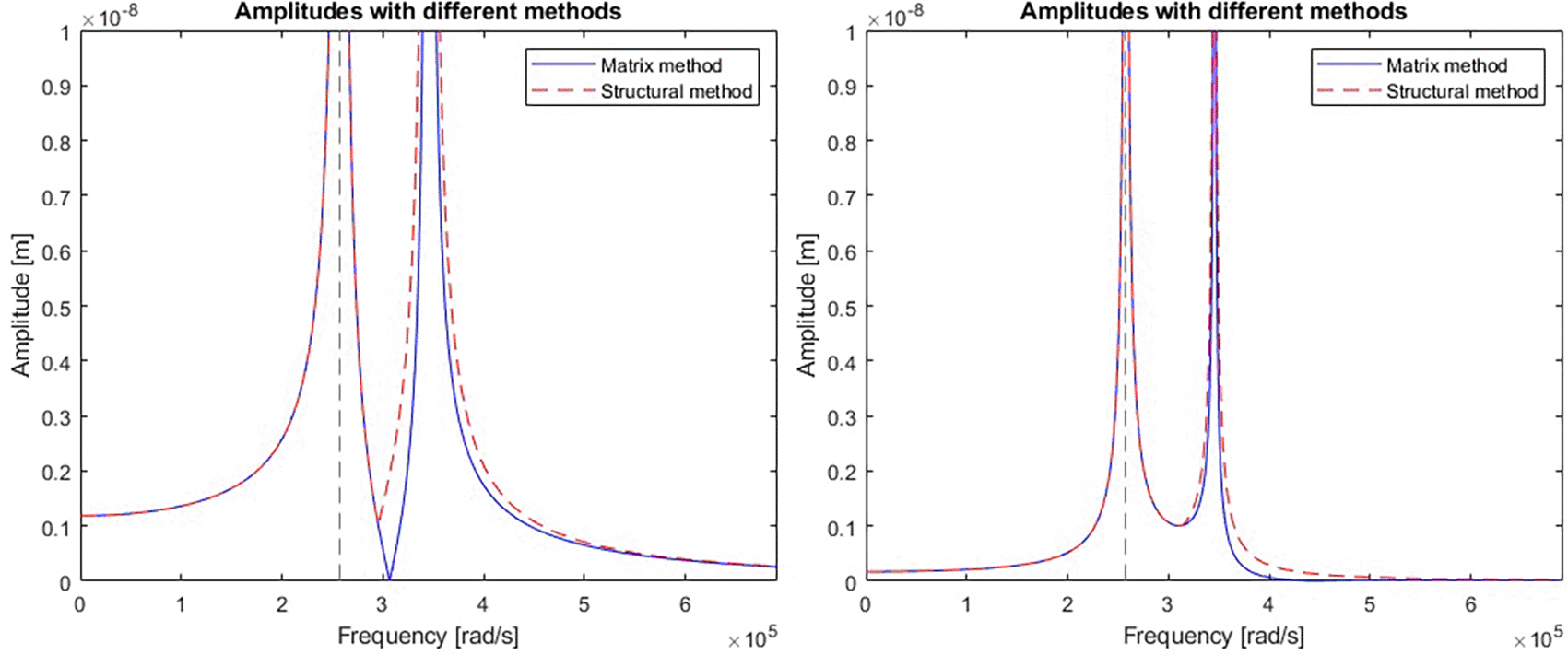
Blue line represents a response calculated with matrix method; red line represents the response calculated with structural number algebra.

It is clear that there are some differences between the results obtained by the two methods. To gain a better understanding, derivatives were taken from the model response equations to calculate the local extremes obtained by both functions. Table 1 gives a direct and relative comparison between the frequencies obtained with both functions. Table 2 gives the calculated values of the displacement amplitude for each characteristic frequency.

Table 1. Comparison of frequencies between model responses obtained with both methods.

	Matrix method	Structural numbers	Indirect difference
1^st stage	257611 rad/s	257611 rad/s	0%
1^st stage	345575 rad/s	345575 rad/s	0%
2^nd stage	257611 rad/s	257611 rad/s	0%
2^nd stage	345575 rad/s	345575 rad/s	0%

Table 2. Comparison of amplitude responses obtained with both methods on the nodes.

	Matrix method	Structural numbers	Direct difference	Indirect difference
1^st stage	0.0101 mm	0.0101 mm	0 mm	0%
1^st stage	0.0017 mm	0.0027 mm	0.001 mm	58.82%
2^nd stage	0.0033 mm	0.0033 mm	0 mm	0%
2^nd stage	0.0004 mm	0.0006 mm	0.0002 mm	50%

The nodal frequencies match perfectly, but there are significant differences in the amplitudes obtained around the second resonant frequency of the system in both stages. The alternative method using structural numbers is sufficient if the priority is only to check the nodal frequencies. However, when it comes to accuracy in terms of amplitude response, this method is subject to considerable error.

Another problem with the structural number method is that the authors were unable to establish the equations necessary to calculate the phase shifts in the system’s response.

Table 3 shows the computation time and an average time from all measurements done on both algorithms based on matrix and structural number methods.³⁵ The test showed that matrix method took an average of 13.972 s to calculate the amplitude response of a two-stage system. The alternative method took only 8.637 s on average, which is 38% faster than the classical method.

Table 3. Computation time for both methods used to analyse a simple mechanical system.

Trial	Matrix method	Structural numbers
1	12.815 s	7.531 s
2	12.824 s	7.649 s
3	12.761 s	7.577 s
4	12.759 s	7.546 s
5	13.099 s	7.563 s
6	12.905 s	7.578 s
7	12.839 s	7.626 s
8	13.162 s	7.574 s
9	13.080 s	7.570 s
10	13.088 s	7.627 s
Average	12.933 s	7.584 s

The discrete electromechanical model³⁶ was verified on a system simulating the behaviour of a single piezoelectric plate with specifications very close to the real ones taken from (http://www.steminc.com/piezo/PZ_property.asp). The plate had to vibrate at a resonance frequency of 590kHz (3707079rad/s). Mechanical parameters of the plate were determined with the Cauer synthesis method. Piezoelectric plate dimensions were taken from (https://www.steminc.com/PZT/EN/piezoelectric-plate-45x45x35mm-55-khz). Resulting graph of an amplitude response for piezoelectric plate displacement and voltage were shown in Figure 6.

Figure 6. Model response calculated for a) displacement curve, and b) voltage curve along the frequency axis.

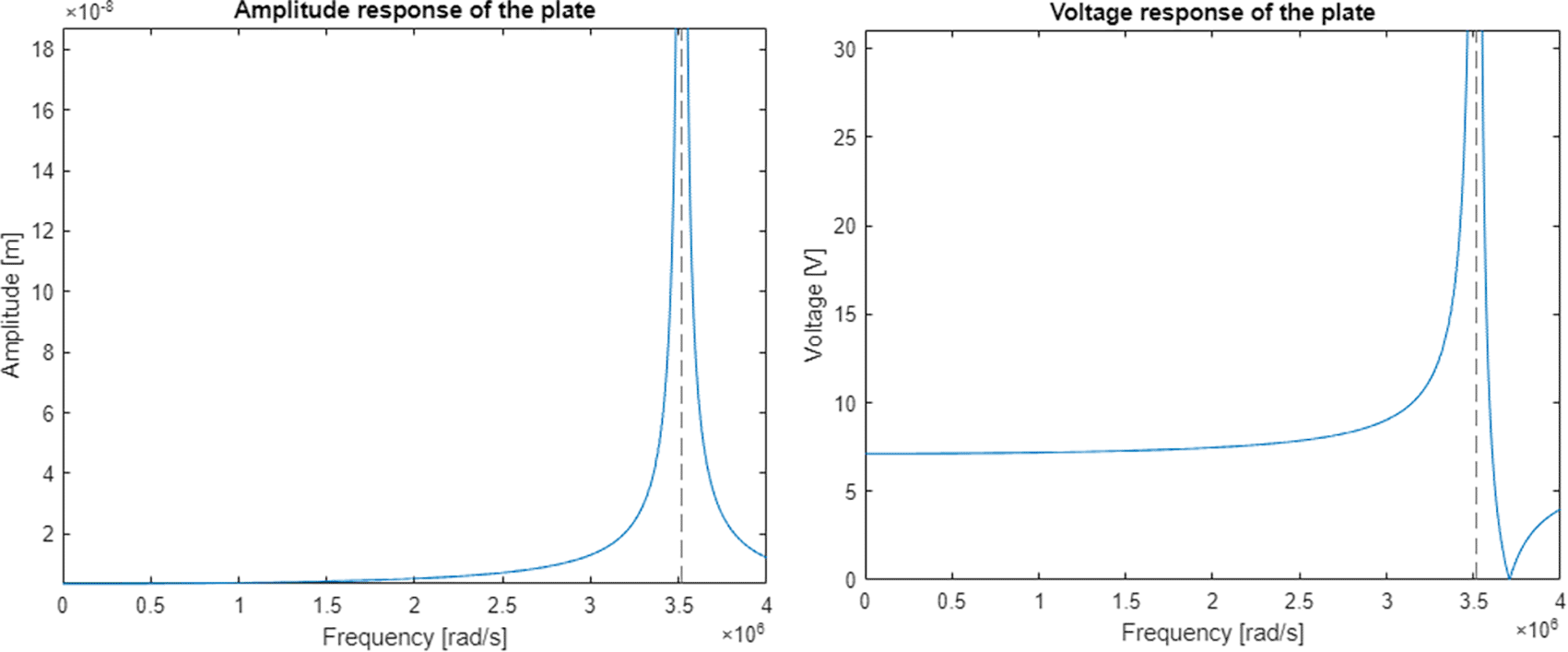
The model had a resonance near the frequency of 560 kHz (3516624 rad/s) which gives an error of 5% in relation to the resonance target. The calculated magnitude of displacement at the resonant frequency is 2.6 mm which is well above the capability of a 3.5 mm thick piezoelectric plate. The voltage shows a significant increase in piezoelectric voltage in the resonant region and a complete reduction near the frequency of 590 kHz which was supposed to be the original resonant frequency.

Conclusions

The aim of this work was to demonstrate a method that allows a piezoelectric model to be synthesized using only on a set of resonant/anti-resonant frequencies as the input data. The paper has shown that combining Cauer’s method of synthesis for mechanical or electrical networks with Rayleigh’s damping approximation and a variant of the Van Dyke-Butterworth model can yield a discrete electromechanical cascade model which parameters can be approximated to simulate the behaviour of a real piezoelectric component. This method differs from most other methods found in the literature¹³^–¹⁵^,¹⁹^,²⁴ in that it focuses on developing a new set of possible solutions based on a very limited information, rather than trying to break down a specific case under consideration. The ultimate goal of this method, which is under constant development, is to provide the ability to synthesize piezoelectric systems capable of resonating in a defined range of frequencies required for a target solution. An example application of such a method could be an attempt to scale up the active vibration cancellation technology to dampen vibrations generated by motors and engines. This technology is currently used in many audio solutions and new, larger piezoelectric resonators could be used for more industrial oriented projects. This method offers the possibility of constructing a piezoelectric stack of plates which have different material properties or geometrical sizes to create multiple resonant frequencies within a single module.

The method presented in this article relies heavily on mechanical model synthesis in its initial stage. In order to proceed with confidence, it was necessary to verify the mechanical model before using it in later stages of the work. However, for more complex systems the classical matrix calculation creates a significant computational load, which has the effect of significantly extending the computation time. An additional set goal was to develop an alternative method for mechanical system analysis using graphs and structural numbers. The presented alternative solution gave promising results in terms of computation time. The accuracy of calculated characteristic frequencies between the standard matrix method and the proposed alternative using structural numbers was on par in terms of calculated peaks near resonant frequencies. However, the calculated amplitudes differed significantly from those calculated using the matrix method, used as a reference. The issue was tested on different models and the inconsistency of calculated responses was random. In its current state the algorithm can be useful for verifying only the resonant frequencies of a model. This method definitely needs further fine-tuning and testing to correct the errors in the amplitudes obtained and to further verify the advantages indicated.

The final verification of the piezoelectric model has shown a small deviation from the target resonant frequency. An initial hypothesis is that this error could be corrected by applying a correction factor to the input frequency. A bigger set of tests on the algorithm has to be conducted to verify it. Another problem highlighted was the calculated amplitude response for the resonant frequency which was several orders of magnitude greater than the expected value of displacement for a plate of given thickness. The cause of this problem is currently unknown. It is suspected that the problem may be due to an error in the algorithm, or it may be caused by differences between the real piezoelectric parameters for a plate that is vibrating at its resonant frequency and its specification which is measured for a frequency of 1kHz. It is clear that this model needs more tests before it can be considered acceptably accurate. The reference plate specification (more information here) also didn’t contain enough data to reliably compare the results obtained from the model analysis. Only a rough comparison of material properties could be conducted. The data of specific plates such as their exact resonant or anti-resonant frequencies was sometimes missing as well as information about their intended mode of vibration (longitudinal, thickness wise) and related coupling factors. It is necessary to plan a series of empirical tests to obtain reference data more reliably for model validation.

Data availability

Source data

Reference data for the specific piezoelectric module has been sourced from a piezoelectric materials vendor: https://www.steminc.com/PZT/EN/piezoelectric-plate-45x45x35mm-55-khz.

A list of detailed material properties used for algorithms and the electromechanical model analysis was taken from: http://www.steminc.com/piezo/PZ_property.asp.

Underlying data

Mendeley Data: Model algorithms. https://doi.org/10.17632/gdt8yr9m3d.4 ³⁵

This project contains the following data:

- Comp_time_test.xlsx
- Comparison_value_set.mat

Mendeley Data: Piezoelectric electromechanical model (first iteration), https://doi.org/10.17632/pydnfmkfdk.3 ³⁶

This project contains the following underlying data:

- electromech_model.mat

Data are available under the terms of the Creative Commons Zero “No rights reserved” data waiver (CC0 1.0 Public domain dedication).

Software availability

Model algorithms

Source code available from:

Archived source code available from: https://doi.org/10.17632/gdt8yr9m3d.4 ³⁵

License: CC0 1.0

Piezoelectric electromechanical model

Source code available from:

Archived source code available from: https://doi.org/10.17632/pydnfmkfdk.3 ³⁶

License: CC0 1.0

References

1. Palmgren E, Rasa T: Modelling Roles of Mathematics in Physics. Sci. Educ. 2022. Publisher Full Text
2. Buchacz A, Wróbel A: Modelowanie i badanie wpływu zjawiska piezoelektrycznego na charakterystyki układu mechanicznego. Gliwice: Wydawnictwo Politechniki Śląskiej; 2010.
3. Brownjohn J, Pavic A: Vibration control of ultra-sensitive facilities. Proceedings of the Institution of Civil Engineers - Structures and Buildings. 2006; 159: 295–306. Publisher Full Text
4. Zhang Y, Yan T, Xu X, et al.: Room temperature and humidity decoupling control of common variable air volume air-conditioning system based on bilinear characteristics. Energy and Built Environment. 2023; 4: 354–367. Publisher Full Text
5. Fundamentals of Automotive and Engine Technology: Standard Drives, Hybrid Drives, Brakes, Safety Systems. Springer Fachmedien Wiesbaden; 2014.
6. Bai R, Tong S, Karimi HR: Modeling and Backstepping Control of the Electronic Throttle System. Math. Probl. Eng. 2013; 2013: 1–6. Publisher Full Text
7. Buchacz A, Dymarek A, Dzitkowski T: Synthesis of discrete, continuous and discrete continuous vibrating systems represent-ed by graphs. Sixth International Scientific and Engineering Conference - Machine-Building and Technosphere on the Border of the XXI Century. 1999; 3: 243–245.
8. Buchacz A, Żurek K: Modelowanie i badanie wpływu zjawiska piezoelektrycznego na charakterystyki układu mechanicznego. Wydawnictwo Politechniki Śląskiej. 2010.
9. Smith M: Synthesis of mechanical networks: the inerter. IEEE Trans. Automat. Contr. 2002; 47: 1648–1662. Publisher Full Text
10. Phillips GM: Interpolation and Approximation by Polynomials. Springer-Verlag; 2003. Publisher Full Text
11. Białas K, Buchacz A, Dzitkowski T: Synteza drgających aktywnych układów mechanicznych z tłumieniem w ujęciu grafów biegunowych i liczb strukturalnych. Wydawnictwo Politechniki Śląskiej. 2010.
12. IEEE: Standard on Piezoelectricity. ANSI/IEEE; 1988.
13. Adriaens H, Koning W, Banning R: Modelling piezoelectric actuators. IEEE ASME Trans. Mechatron. 2000; 5: 331–341. Publisher Full Text
14. Goldfarb M, Celanovic N: Modelling piezoelectric stack actuators for control of micromanipulation. IEEE Control. Syst. 1997; 17: 69–79. Publisher Full Text
15. Wang S-H, Tsai M-C: Dynamic modelling of thickness-mode piezoelectric transducer using the block diagram approach. Ultrasonics. 2011; 51: 617–624. PubMed Abstract | Publisher Full Text
16. Wróbel A: Classical and non-classical research methods and experimental studies of piezoelectric plates. Gliwice: Wydawnictwo Politechniki Śląskiej; 2018.
17. Cauer W: Ideale Transformatoren und lineare Transformationen. Elektrische Nachrichtentechnik (ENT). 1932; 9: 157–174.
18. Cauer W: Theorie der linearen Wechselstromschaltungen. Berlin: Akademie-Verlag; 1960; vol. 2. .
19. Richter B, Twiefel J, Wallaschek J: Piezoelectric Equivalent Circuit Models.Priya S, Inman DJ, editors. Energy Harvesting Technologies. Boston, MA: Springer; 2009. Publisher Full Text
20. Soluch W, et al.: Wstęp do piezoelektryki. Warszawa: Wydawnictwo Komunikacji i Łączności; 1980.
21. Lahmer T, Kaltenbacher M, Kaltenbacher B, et al.: FEM-based determination of real and complex elastic, dielectric, and piezoelectric moduli in piezoceramic materials. IEEE Trans. Ultrason. Ferroelectr. Freq. Control. 2008; 55(2): 465–475. PubMed Abstract | Publisher Full Text
22. Goldstein A: Self-Tuning multimodal piezoelectric shunt damping. J. Braz. Soc. Mech. Sci. Eng. 2011; 33: 428–436. Publisher Full Text
23. Batra R, Dell’isola F, Vidoli S, et al.: Multimode vibration suppression with passive two-terminal distributed network incorporating piezoceramic transducers. Int. J. Solids Struct. 2005; 42: 3115–3132. Publisher Full Text
24. San Miguel J, Buiochi F, Adamowski J: Numerical modelling of a circular piezoelectric ultrasonic transducer radiating in water. ABCM Symposium Series in Mechatronics. 2000; 2: 458–464.
25. Yamaoka S, Ohnishi K: Reaction force estimation of piezoelectric actuator by charge observation. IEEE International Conference on Mechatronics (ICM). Vicenza, Italy IEEE Xplore. 2013. Publisher Full Text
26. Delibas B, Arockiarajan A, Seemann W: Rate dependent properties of perovskite type tetragonal piezoelectric materials using micromechanical model. Int. J. Solids Struct. 2006; 43: 697–712. Publisher Full Text
27. Gan J, Zhang X: A review of nonlinear hysteresis modelling and control of piezoelectric actuators. AIP Adv. 2019; 9(4): 040702. Publisher Full Text
28. Nakamura N: Extended Rayleigh Damping Model. Front. Built Environ. 2016; 2. Publisher Full Text
29. Bellert S, Woźniacki H: Analiza I synteza układów elektrycznych metodą liczb strukturalnych. Warszawa: WNT; 1968.
30. Harazin J, Wróbel A: Research on a cascade model synthesis with the use of classical and non-classical methods in the context of new piezoelectric stack applications. Int. J. Mech. Sci. 2021; 12: 959–969. Publisher Full Text
31. Adamowski JC, Nader G, Silva ECN: Effective Damping Value of Piezoelectric Transducer Determined by Experimental Techniques and Numerical Analysis. ABCM Symposium Series in Mechatronics. 2004; 1: 271–279.
32. Giergiel J: Tłumienie drgań mechanicznych. Kraków: Wydawnictwo Akademii Górniczo-Hutniczej; 1984.
33. Trindade M, Benjeddou A: Effective Electromechanical Coupling Coefficients of Piezoelectric Adaptive Structures: Critical Evaluation and Optimization. Mech. Adv. Mater. Struct. 2009; 16: 210–223. Publisher Full Text
34. Buchacz A, Płaczek M: Modelowanie i badanie jednowymiarowych drgających układów mechatronicznych. Gliwice: Wydawnictwo Politechniki Śląskiej; 2011.
35. Harazin J: Model algorithms. Mendeley Data. 2022. Publisher Full Text
36. Harazin J: Piezoelectric electromechanical model (first iteration). Mendeley Data. 2023. Publisher Full Text

Comments on this article Comments (0)

Version 3

VERSION 3 PUBLISHED 05 Oct 2023

Author details Author details

¹ Faculty of Mechanical Engineering, Politechnika Slaska, Gliwice, Silesian Voivodeship, 44-100, Poland

Jacek Harazin
Roles: Data Curation, Formal Analysis, Funding Acquisition, Investigation, Methodology, Software, Visualization, Writing – Original Draft Preparation

Andrzej Wróbel
Roles: Conceptualization, Project Administration, Resources, Supervision, Validation, Writing – Review & Editing

Competing interests

No competing interests were disclosed.

Grant information

The article was financed from the subvention for maintenance and development of research potential of young scientists of the Silesian University of Technology.
The funders had no role in study design, data collection and analysis, decision to publish, or preparation of the manuscript.

Article Versions (3)

version 3

Revised

Published: 06 Sep 2024, 12:1273

https://doi.org/10.12688/f1000research.140943.3

version 2

Revised

Published: 02 Apr 2024, 12:1273

https://doi.org/10.12688/f1000research.140943.2

version 1

Published: 05 Oct 2023, 12:1273

https://doi.org/10.12688/f1000research.140943.1

© 2023 Harazin J and Wróbel A. This is an open access article distributed under the terms of the Creative Commons Attribution License, which permits unrestricted use, distribution, and reproduction in any medium, provided the original work is properly cited.

Download

Export To

metrics

	Views	Downloads
F1000Research	-	-
PubMed Central Data from PMC are received and updated monthly.	-	-

Citations

SEE MORE DETAILS

CITE

how to cite this article

Harazin J and Wróbel A. Analytical approach to piezoelectric model synthesis with the use of Cauer’s method for system design [version 1; peer review: 2 approved with reservations]. F1000Research 2023, 12:1273 (https://doi.org/10.12688/f1000research.140943.1)

NOTE: If applicable, it is important to ensure the information in square brackets after the title is included in all citations of this article.

track

receive updates on this article

Track an article to receive email alerts on any updates to this article.

Open Peer Review

Version 1

VERSION 1

PUBLISHED 05 Oct 2023

Views

Reviewer Report 29 Nov 2023

Saurabh K. Yadav, Institute of Infrastructure Technology Research and Management, Ahmedabad, Gujarat, India

Approved with Reservations

https://doi.org/10.5256/f1000research.154351.r222666

The manuscript proposes a new approach for parameter estimation of piezoelectric structures based on the Cauer’s method, and compares its computational performance with the traditional matrix method. The authors claim that their method can synthesize a piezoelectric model using only a set of resonant and anti-resonant frequencies as the input data, and approximate the piezoelectric parameters using the synthesized mechanical model and some physical equations. The authors also use a non-classical method based on structural numbers and edge graphs to analyze the mechanical model and reduce the computational load. The manuscript is well-written and organized, and the mathematical derivations are clear and rigorous. However, I have some concerns and suggestions that need to be addressed before the manuscript can be accepted for publication.

The main merit and novelty of the manuscript are not clearly stated in the abstract, introduction and conclusion. The authors should highlight how their method differs from the existing methods in the literature, and what are the advantages and limitations of their method.
The authors use a single piezoelectric plate as an example to verify their electromechanical model. However, the results show that the model has a significant error in the resonant frequency and the displacement amplitude. The authors should explain the sources of this error and how it can be reduced or corrected. Moreover, the authors should test their model on more realistic and complex piezoelectric structures, such as stacks, rings, beams, etc., and compare their results with experimental data or other numerical methods.
The authors compare the computational performance of their method with the matrix method using a two-degree system. However, this is not a fair comparison, as the matrix method can handle systems with any number of degrees of freedom, while the structural number method is limited by the complexity of the edge graph. The authors should compare the computational performance of both methods on systems with different numbers of degrees of freedom, and use more appropriate metrics, such as the number of floating point operations, the memory usage, the accuracy, etc.
The authors use some references that are published in non-English languages, such as Refs. 8, 11 and 29. The authors should provide English translations of these references, or use more accessible sources that are published in English. The authors should also update their literature review with some recent works on piezoelectric modelling and parameter estimation.

Is the work clearly and accurately presented and does it cite the current literature?

Yes
Is the study design appropriate and is the work technically sound?

Yes
Are sufficient details of methods and analysis provided to allow replication by others?

Yes
If applicable, is the statistical analysis and its interpretation appropriate?

Yes
Are all the source data underlying the results available to ensure full reproducibility?

Yes
Are the conclusions drawn adequately supported by the results?

Yes

Competing Interests: No competing interests were disclosed.

Reviewer Expertise: Mathematical modelling

I confirm that I have read this submission and believe that I have an appropriate level of expertise to confirm that it is of an acceptable scientific standard, however I have significant reservations, as outlined above.

CITE

Report a concern

Author Response 13 Apr 2024

Jacek Harazin, Faculty of Mechanical Engineering, Politechnika Slaska, Gliwice, 44-100, Poland

13 Apr 2024

Author Response

Thank you for the critical review. I would also like to apologise for a long break before my reply. I have prepared several corrections to the article regarding your review ... Continue reading Thank you for the critical review. I would also like to apologise for a long break before my reply. I have prepared several corrections to the article regarding your review and they will be published with the new version. I've also tried to address your concerns directly:

1. Let me repeat my answer to the second reviewer here, as it addresses the same concerns. The article showcases a new method to synthesize cascading electromechanical models using the Cauer method coupled with Van Dyke-Butterworth models to represent piezoelectric stacks with clumped mechanical and electrical components. Each of those methods have been already used by researchers but i have found no literature on the particular approach presented in this article. The novelty revolves around the general approach to synthesis with very limited input information. Most researchers focus on specific applications where piezoelectric parameters and the analysed structure is largely known or predetermined experimentally. Here, only the frequencies are known and there is an infinite number of possible models that could realise those predetermined resonant frequencies. Coupled with further steps presented in the article, this method offers a possibility to design piezoelectric stacks with different material properties or geometric dimensions, capable of resonating in predetermined frequencies.
The limitation of this method is that it can only be used to synthesize models composed of components connected in series. So far, it can only be used to synthesise specific piezoelectric plate configuraions, where each component in a stack is responsible exclusively for a single resonant frequency set as the input. I have modified the article to better reflect those statements.

2. Following up from my response to the second reviever, I agree and i can already attest that the method is currently being verified empirically. The synthesis method has been verified already with three real piezoelectric stacks with different geometrical dimensions which has shown some discrepancy between model results and real plate behaviour. The source of those differences was traced back to how some of the piezoelectric parameters are determined in the factory (under 1kHz wave stimulation) versus plate properties in the resonance proximity. It has to be noted as well, that this method relies on a lumped representation of an otherwise continous system. The main issue of this approach is that the lumped parameters are approximations of the real parameters and an electromechanical model currently can't perfectly match the behavior of a piezoelectric plate, where the interactions and their magnitude changes between the layers of a single piezoelement. There are also boundaries between piezoelectric elements, made with adhesives and isolating layers, which also introduce many hidden variables in the real model behaviour. The presented method is still in its infancy and requires more testing and refinement. I would like to provide a consice report on the empirical results in a follow up article though, as including all the information about the procedure and test stand would make this article very bloated.

3. I was made aware that a comparison of calculation time used exclusively is a bad metric for algorithm complexity. I have tried looking for more literature on the matter and added more references to the article. Given my abilities and available resources, i have prepared a second study which focused more on the memory criterion. I've used the available Matlab evaluation modules to estimate the average RAM usage between both algorithms on a variety of models, along with a comparison between the average time it took both algorithms to complete. New suite of tests has uncovered more information about the structural number algorithm optimisation and shed some light on its shortcomings. I have modified the manusript to showcase the second study. I am aware that this method may also not be the best way to evaluate algorithm complexity and only presents a rough estimation and i will try to consult a specialist on the topic with an intent of providing some collaboration with more indepth information about algorithm complexity of the proposed method.

4. I have provided additional literature references to publications of the authors involved in the development of the structural number method where they descibe mentioned models in english. I hope that will provide the necessary background which was lacking previously.

I hope that my response provides an exhaustive explanation to the issues raised.

Best Regards,
Thank you for the critical review. I would also like to apologise for a long break before my reply. I have prepared several corrections to the article regarding your review and they will be published with the new version. I've also tried to address your concerns directly:

1. Let me repeat my answer to the second reviewer here, as it addresses the same concerns. The article showcases a new method to synthesize cascading electromechanical models using the Cauer method coupled with Van Dyke-Butterworth models to represent piezoelectric stacks with clumped mechanical and electrical components. Each of those methods have been already used by researchers but i have found no literature on the particular approach presented in this article. The novelty revolves around the general approach to synthesis with very limited input information. Most researchers focus on specific applications where piezoelectric parameters and the analysed structure is largely known or predetermined experimentally. Here, only the frequencies are known and there is an infinite number of possible models that could realise those predetermined resonant frequencies. Coupled with further steps presented in the article, this method offers a possibility to design piezoelectric stacks with different material properties or geometric dimensions, capable of resonating in predetermined frequencies.
The limitation of this method is that it can only be used to synthesize models composed of components connected in series. So far, it can only be used to synthesise specific piezoelectric plate configuraions, where each component in a stack is responsible exclusively for a single resonant frequency set as the input. I have modified the article to better reflect those statements.

2. Following up from my response to the second reviever, I agree and i can already attest that the method is currently being verified empirically. The synthesis method has been verified already with three real piezoelectric stacks with different geometrical dimensions which has shown some discrepancy between model results and real plate behaviour. The source of those differences was traced back to how some of the piezoelectric parameters are determined in the factory (under 1kHz wave stimulation) versus plate properties in the resonance proximity. It has to be noted as well, that this method relies on a lumped representation of an otherwise continous system. The main issue of this approach is that the lumped parameters are approximations of the real parameters and an electromechanical model currently can't perfectly match the behavior of a piezoelectric plate, where the interactions and their magnitude changes between the layers of a single piezoelement. There are also boundaries between piezoelectric elements, made with adhesives and isolating layers, which also introduce many hidden variables in the real model behaviour. The presented method is still in its infancy and requires more testing and refinement. I would like to provide a consice report on the empirical results in a follow up article though, as including all the information about the procedure and test stand would make this article very bloated.

3. I was made aware that a comparison of calculation time used exclusively is a bad metric for algorithm complexity. I have tried looking for more literature on the matter and added more references to the article. Given my abilities and available resources, i have prepared a second study which focused more on the memory criterion. I've used the available Matlab evaluation modules to estimate the average RAM usage between both algorithms on a variety of models, along with a comparison between the average time it took both algorithms to complete. New suite of tests has uncovered more information about the structural number algorithm optimisation and shed some light on its shortcomings. I have modified the manusript to showcase the second study. I am aware that this method may also not be the best way to evaluate algorithm complexity and only presents a rough estimation and i will try to consult a specialist on the topic with an intent of providing some collaboration with more indepth information about algorithm complexity of the proposed method.

4. I have provided additional literature references to publications of the authors involved in the development of the structural number method where they descibe mentioned models in english. I hope that will provide the necessary background which was lacking previously.

I hope that my response provides an exhaustive explanation to the issues raised.

Best Regards,
Competing Interests: No competing interests were disclosed. Close
Report a concern
Respond or Comment

COMMENTS ON THIS REPORT

Author Response 13 Apr 2024

Jacek Harazin, Faculty of Mechanical Engineering, Politechnika Slaska, Gliwice, 44-100, Poland

13 Apr 2024

Author Response

Thank you for the critical review. I would also like to apologise for a long break before my reply. I have prepared several corrections to the article regarding your review ... Continue reading Thank you for the critical review. I would also like to apologise for a long break before my reply. I have prepared several corrections to the article regarding your review and they will be published with the new version. I've also tried to address your concerns directly:

1. Let me repeat my answer to the second reviewer here, as it addresses the same concerns. The article showcases a new method to synthesize cascading electromechanical models using the Cauer method coupled with Van Dyke-Butterworth models to represent piezoelectric stacks with clumped mechanical and electrical components. Each of those methods have been already used by researchers but i have found no literature on the particular approach presented in this article. The novelty revolves around the general approach to synthesis with very limited input information. Most researchers focus on specific applications where piezoelectric parameters and the analysed structure is largely known or predetermined experimentally. Here, only the frequencies are known and there is an infinite number of possible models that could realise those predetermined resonant frequencies. Coupled with further steps presented in the article, this method offers a possibility to design piezoelectric stacks with different material properties or geometric dimensions, capable of resonating in predetermined frequencies.
The limitation of this method is that it can only be used to synthesize models composed of components connected in series. So far, it can only be used to synthesise specific piezoelectric plate configuraions, where each component in a stack is responsible exclusively for a single resonant frequency set as the input. I have modified the article to better reflect those statements.

2. Following up from my response to the second reviever, I agree and i can already attest that the method is currently being verified empirically. The synthesis method has been verified already with three real piezoelectric stacks with different geometrical dimensions which has shown some discrepancy between model results and real plate behaviour. The source of those differences was traced back to how some of the piezoelectric parameters are determined in the factory (under 1kHz wave stimulation) versus plate properties in the resonance proximity. It has to be noted as well, that this method relies on a lumped representation of an otherwise continous system. The main issue of this approach is that the lumped parameters are approximations of the real parameters and an electromechanical model currently can't perfectly match the behavior of a piezoelectric plate, where the interactions and their magnitude changes between the layers of a single piezoelement. There are also boundaries between piezoelectric elements, made with adhesives and isolating layers, which also introduce many hidden variables in the real model behaviour. The presented method is still in its infancy and requires more testing and refinement. I would like to provide a consice report on the empirical results in a follow up article though, as including all the information about the procedure and test stand would make this article very bloated.

3. I was made aware that a comparison of calculation time used exclusively is a bad metric for algorithm complexity. I have tried looking for more literature on the matter and added more references to the article. Given my abilities and available resources, i have prepared a second study which focused more on the memory criterion. I've used the available Matlab evaluation modules to estimate the average RAM usage between both algorithms on a variety of models, along with a comparison between the average time it took both algorithms to complete. New suite of tests has uncovered more information about the structural number algorithm optimisation and shed some light on its shortcomings. I have modified the manusript to showcase the second study. I am aware that this method may also not be the best way to evaluate algorithm complexity and only presents a rough estimation and i will try to consult a specialist on the topic with an intent of providing some collaboration with more indepth information about algorithm complexity of the proposed method.

4. I have provided additional literature references to publications of the authors involved in the development of the structural number method where they descibe mentioned models in english. I hope that will provide the necessary background which was lacking previously.

I hope that my response provides an exhaustive explanation to the issues raised.

Best Regards,
Thank you for the critical review. I would also like to apologise for a long break before my reply. I have prepared several corrections to the article regarding your review and they will be published with the new version. I've also tried to address your concerns directly:

1. Let me repeat my answer to the second reviewer here, as it addresses the same concerns. The article showcases a new method to synthesize cascading electromechanical models using the Cauer method coupled with Van Dyke-Butterworth models to represent piezoelectric stacks with clumped mechanical and electrical components. Each of those methods have been already used by researchers but i have found no literature on the particular approach presented in this article. The novelty revolves around the general approach to synthesis with very limited input information. Most researchers focus on specific applications where piezoelectric parameters and the analysed structure is largely known or predetermined experimentally. Here, only the frequencies are known and there is an infinite number of possible models that could realise those predetermined resonant frequencies. Coupled with further steps presented in the article, this method offers a possibility to design piezoelectric stacks with different material properties or geometric dimensions, capable of resonating in predetermined frequencies.
The limitation of this method is that it can only be used to synthesize models composed of components connected in series. So far, it can only be used to synthesise specific piezoelectric plate configuraions, where each component in a stack is responsible exclusively for a single resonant frequency set as the input. I have modified the article to better reflect those statements.

2. Following up from my response to the second reviever, I agree and i can already attest that the method is currently being verified empirically. The synthesis method has been verified already with three real piezoelectric stacks with different geometrical dimensions which has shown some discrepancy between model results and real plate behaviour. The source of those differences was traced back to how some of the piezoelectric parameters are determined in the factory (under 1kHz wave stimulation) versus plate properties in the resonance proximity. It has to be noted as well, that this method relies on a lumped representation of an otherwise continous system. The main issue of this approach is that the lumped parameters are approximations of the real parameters and an electromechanical model currently can't perfectly match the behavior of a piezoelectric plate, where the interactions and their magnitude changes between the layers of a single piezoelement. There are also boundaries between piezoelectric elements, made with adhesives and isolating layers, which also introduce many hidden variables in the real model behaviour. The presented method is still in its infancy and requires more testing and refinement. I would like to provide a consice report on the empirical results in a follow up article though, as including all the information about the procedure and test stand would make this article very bloated.

3. I was made aware that a comparison of calculation time used exclusively is a bad metric for algorithm complexity. I have tried looking for more literature on the matter and added more references to the article. Given my abilities and available resources, i have prepared a second study which focused more on the memory criterion. I've used the available Matlab evaluation modules to estimate the average RAM usage between both algorithms on a variety of models, along with a comparison between the average time it took both algorithms to complete. New suite of tests has uncovered more information about the structural number algorithm optimisation and shed some light on its shortcomings. I have modified the manusript to showcase the second study. I am aware that this method may also not be the best way to evaluate algorithm complexity and only presents a rough estimation and i will try to consult a specialist on the topic with an intent of providing some collaboration with more indepth information about algorithm complexity of the proposed method.

4. I have provided additional literature references to publications of the authors involved in the development of the structural number method where they descibe mentioned models in english. I hope that will provide the necessary background which was lacking previously.

I hope that my response provides an exhaustive explanation to the issues raised.

Best Regards,
Competing Interests: No competing interests were disclosed. Close
Report a concern

Views

Reviewer Report 29 Nov 2023

Guangtao Lu, Wuhan University of Science and Technology, Wuhan, Hubei, China

Approved with Reservations

https://doi.org/10.5256/f1000research.154351.r222661

This manuscript proposed a new approach for parameter estimation of piezoelectric structures based on the Cauer’s method, and its computational performance is compared with the traditional method. However, in my opinion, some concerns need to be addressed more clearly before ... Continue reading

What’s the main merit of the manuscript? It should be clearly addressed in the abstract, introduction and conclusion.
To compare the computational performance of the new model, the model response and computation time are compared with the matrix method. What are the errors of these two models? The two frequencies of the new model are compared with the ones of matrix method. Are the results of the matrix method accurate? What are the actual frequencies?

It is the same during the amplitude comparison. Moreover, to compare the computational performance of the algorithm, there are many metrics, such as time cost, the number of floating points (FLOPs) multiple adds (MAdds), and so on. In addition, what is the meaning of only decreasing the computation time?
Page 4: “A combination of those factors creates four different types of models…” It refers to Refs. 8 and 11. However, Refs. 8 and 11 are published in non-English. Therefore, the details of the four models are suggested to be introduced in the manuscript.
Experimental results: the results should be further analyzed.

Is the work clearly and accurately presented and does it cite the current literature?

Yes
Is the study design appropriate and is the work technically sound?

Partly
Are sufficient details of methods and analysis provided to allow replication by others?

Partly
If applicable, is the statistical analysis and its interpretation appropriate?

Not applicable
Are all the source data underlying the results available to ensure full reproducibility?

Yes
Are the conclusions drawn adequately supported by the results?

Yes

Competing Interests: No competing interests were disclosed.

Reviewer Expertise: Structural health monitoring by uisng lamb waves

CITE

Report a concern

Author Response 13 Apr 2024

Jacek Harazin, Faculty of Mechanical Engineering, Politechnika Slaska, Gliwice, 44-100, Poland

13 Apr 2024

Author Response

Thank you very much for the critical review and Your suggestions regarding the article clarity. I would also like to apologise for a long break before my reply. I have ... Continue reading Thank you very much for the critical review and Your suggestions regarding the article clarity. I would also like to apologise for a long break before my reply. I have prepared several corrections to the article regarding your review and they will be published with the new version. I've also tried to address your querries to the best of my ability:

1. The article showcases a new method to synthesize cascading electromechanical models using the Cauer method coupled with Van Dyke-Butterworth models to represent piezoelectric stacks with clumped mechanical and electrical components. Each of those methods have been already used by researchers but i have found no literature on the particular approach presented in this article. The novelty revolves around the general approach to synthesis with very limited input information. Most researchers focus on specific applications where piezoelectric parameters and the analysed structure is largely known or predetermined experimentally. Here, only the frequencies are known and there is an infinite number of possible models that could realise those predetermined resonant frequencies. Coupled with further steps presented in the article, this method offers a possibility to design piezoelectric stacks with different material properties or geometric dimensions, capable of resonating in predetermined frequencies.

2. The predetermined frequencies and amplitudes were chosen arbitrarily and do not reflect any real piezoelectric system. A comparison between both analysis methods was done on the same model synthesized with the Cauer method. The matrix method was considered as a reference method because its a known and established way to calculate model response. The structural number method was compared against it and it was a pure comparison between two analytical methods.
I was also made aware that a comparison of calculation time used exclusively is a bad metric for algorithm complexity. I have tried looking for more literature on the matter and added more references to the article. Given my abilities and available resources, i have prepared a second study which focused more on the memory criterion. I've used the available Matlab evaluation modules to estimate the average RAM usage between both algorithms on a variety of models, along with a comparison between the average time it took both algorithms to complete. I am aware that this method may also not be the best way to evaluate algorithm complexity and only presents a rough estimation. I will need to consult a specialist on that matter and conduct more tests but that would probably go beyond the scope of this article and should be contained in a separate paper focused only on the comparison between both methods.

3. I have provided additional literature references to publications of the authors involved in the development of the structural number method where they descibe mentioned models in english. I hope that will provide the necessary background which was lacking previously.

4. I agree and i can already attest that the method is currently being verified empirically. The synthesis method has been verified already with three real piezoelectric stacks with different geometrical dimensions which has shown some discrepancy between model results and real plate behaviour. The source of those differences was traced back to how some of the piezoelectric parameters are determined in the factory (under 1kHz wave stimulation) versus plate properties in the resonance proximity. However, i would like to envelope the empirical analysis, along with all the necessary test procedures and the test stand description in a second article, serving as the continuation for this study.

I hope that i have provide an exhaustive explanation to the issues raised.

Best Regards,
Thank you very much for the critical review and Your suggestions regarding the article clarity. I would also like to apologise for a long break before my reply. I have prepared several corrections to the article regarding your review and they will be published with the new version. I've also tried to address your querries to the best of my ability:

1. The article showcases a new method to synthesize cascading electromechanical models using the Cauer method coupled with Van Dyke-Butterworth models to represent piezoelectric stacks with clumped mechanical and electrical components. Each of those methods have been already used by researchers but i have found no literature on the particular approach presented in this article. The novelty revolves around the general approach to synthesis with very limited input information. Most researchers focus on specific applications where piezoelectric parameters and the analysed structure is largely known or predetermined experimentally. Here, only the frequencies are known and there is an infinite number of possible models that could realise those predetermined resonant frequencies. Coupled with further steps presented in the article, this method offers a possibility to design piezoelectric stacks with different material properties or geometric dimensions, capable of resonating in predetermined frequencies.

2. The predetermined frequencies and amplitudes were chosen arbitrarily and do not reflect any real piezoelectric system. A comparison between both analysis methods was done on the same model synthesized with the Cauer method. The matrix method was considered as a reference method because its a known and established way to calculate model response. The structural number method was compared against it and it was a pure comparison between two analytical methods.
I was also made aware that a comparison of calculation time used exclusively is a bad metric for algorithm complexity. I have tried looking for more literature on the matter and added more references to the article. Given my abilities and available resources, i have prepared a second study which focused more on the memory criterion. I've used the available Matlab evaluation modules to estimate the average RAM usage between both algorithms on a variety of models, along with a comparison between the average time it took both algorithms to complete. I am aware that this method may also not be the best way to evaluate algorithm complexity and only presents a rough estimation. I will need to consult a specialist on that matter and conduct more tests but that would probably go beyond the scope of this article and should be contained in a separate paper focused only on the comparison between both methods.

3. I have provided additional literature references to publications of the authors involved in the development of the structural number method where they descibe mentioned models in english. I hope that will provide the necessary background which was lacking previously.

4. I agree and i can already attest that the method is currently being verified empirically. The synthesis method has been verified already with three real piezoelectric stacks with different geometrical dimensions which has shown some discrepancy between model results and real plate behaviour. The source of those differences was traced back to how some of the piezoelectric parameters are determined in the factory (under 1kHz wave stimulation) versus plate properties in the resonance proximity. However, i would like to envelope the empirical analysis, along with all the necessary test procedures and the test stand description in a second article, serving as the continuation for this study.

I hope that i have provide an exhaustive explanation to the issues raised.

Best Regards,
Competing Interests: No competing interests were disclosed. Close
Report a concern
Respond or Comment

COMMENTS ON THIS REPORT

Author Response 13 Apr 2024

Jacek Harazin, Faculty of Mechanical Engineering, Politechnika Slaska, Gliwice, 44-100, Poland

13 Apr 2024

Author Response

Thank you very much for the critical review and Your suggestions regarding the article clarity. I would also like to apologise for a long break before my reply. I have ... Continue reading Thank you very much for the critical review and Your suggestions regarding the article clarity. I would also like to apologise for a long break before my reply. I have prepared several corrections to the article regarding your review and they will be published with the new version. I've also tried to address your querries to the best of my ability:

1. The article showcases a new method to synthesize cascading electromechanical models using the Cauer method coupled with Van Dyke-Butterworth models to represent piezoelectric stacks with clumped mechanical and electrical components. Each of those methods have been already used by researchers but i have found no literature on the particular approach presented in this article. The novelty revolves around the general approach to synthesis with very limited input information. Most researchers focus on specific applications where piezoelectric parameters and the analysed structure is largely known or predetermined experimentally. Here, only the frequencies are known and there is an infinite number of possible models that could realise those predetermined resonant frequencies. Coupled with further steps presented in the article, this method offers a possibility to design piezoelectric stacks with different material properties or geometric dimensions, capable of resonating in predetermined frequencies.

2. The predetermined frequencies and amplitudes were chosen arbitrarily and do not reflect any real piezoelectric system. A comparison between both analysis methods was done on the same model synthesized with the Cauer method. The matrix method was considered as a reference method because its a known and established way to calculate model response. The structural number method was compared against it and it was a pure comparison between two analytical methods.
I was also made aware that a comparison of calculation time used exclusively is a bad metric for algorithm complexity. I have tried looking for more literature on the matter and added more references to the article. Given my abilities and available resources, i have prepared a second study which focused more on the memory criterion. I've used the available Matlab evaluation modules to estimate the average RAM usage between both algorithms on a variety of models, along with a comparison between the average time it took both algorithms to complete. I am aware that this method may also not be the best way to evaluate algorithm complexity and only presents a rough estimation. I will need to consult a specialist on that matter and conduct more tests but that would probably go beyond the scope of this article and should be contained in a separate paper focused only on the comparison between both methods.

3. I have provided additional literature references to publications of the authors involved in the development of the structural number method where they descibe mentioned models in english. I hope that will provide the necessary background which was lacking previously.

4. I agree and i can already attest that the method is currently being verified empirically. The synthesis method has been verified already with three real piezoelectric stacks with different geometrical dimensions which has shown some discrepancy between model results and real plate behaviour. The source of those differences was traced back to how some of the piezoelectric parameters are determined in the factory (under 1kHz wave stimulation) versus plate properties in the resonance proximity. However, i would like to envelope the empirical analysis, along with all the necessary test procedures and the test stand description in a second article, serving as the continuation for this study.

I hope that i have provide an exhaustive explanation to the issues raised.

Best Regards,
Thank you very much for the critical review and Your suggestions regarding the article clarity. I would also like to apologise for a long break before my reply. I have prepared several corrections to the article regarding your review and they will be published with the new version. I've also tried to address your querries to the best of my ability:

1. The article showcases a new method to synthesize cascading electromechanical models using the Cauer method coupled with Van Dyke-Butterworth models to represent piezoelectric stacks with clumped mechanical and electrical components. Each of those methods have been already used by researchers but i have found no literature on the particular approach presented in this article. The novelty revolves around the general approach to synthesis with very limited input information. Most researchers focus on specific applications where piezoelectric parameters and the analysed structure is largely known or predetermined experimentally. Here, only the frequencies are known and there is an infinite number of possible models that could realise those predetermined resonant frequencies. Coupled with further steps presented in the article, this method offers a possibility to design piezoelectric stacks with different material properties or geometric dimensions, capable of resonating in predetermined frequencies.

2. The predetermined frequencies and amplitudes were chosen arbitrarily and do not reflect any real piezoelectric system. A comparison between both analysis methods was done on the same model synthesized with the Cauer method. The matrix method was considered as a reference method because its a known and established way to calculate model response. The structural number method was compared against it and it was a pure comparison between two analytical methods.
I was also made aware that a comparison of calculation time used exclusively is a bad metric for algorithm complexity. I have tried looking for more literature on the matter and added more references to the article. Given my abilities and available resources, i have prepared a second study which focused more on the memory criterion. I've used the available Matlab evaluation modules to estimate the average RAM usage between both algorithms on a variety of models, along with a comparison between the average time it took both algorithms to complete. I am aware that this method may also not be the best way to evaluate algorithm complexity and only presents a rough estimation. I will need to consult a specialist on that matter and conduct more tests but that would probably go beyond the scope of this article and should be contained in a separate paper focused only on the comparison between both methods.

3. I have provided additional literature references to publications of the authors involved in the development of the structural number method where they descibe mentioned models in english. I hope that will provide the necessary background which was lacking previously.

4. I agree and i can already attest that the method is currently being verified empirically. The synthesis method has been verified already with three real piezoelectric stacks with different geometrical dimensions which has shown some discrepancy between model results and real plate behaviour. The source of those differences was traced back to how some of the piezoelectric parameters are determined in the factory (under 1kHz wave stimulation) versus plate properties in the resonance proximity. However, i would like to envelope the empirical analysis, along with all the necessary test procedures and the test stand description in a second article, serving as the continuation for this study.

I hope that i have provide an exhaustive explanation to the issues raised.

Best Regards,
Competing Interests: No competing interests were disclosed. Close
Report a concern

Comments on this article Comments (0)

Version 3

VERSION 3 PUBLISHED 05 Oct 2023

Open Peer Review

Reviewer Status

Reviewer Reports

	Invited Reviewers
	1	2	3	4
Version 3 (revision) 06 Sep 24	read		read
Version 2 (revision) 02 Apr 24	read		read	read
Version 1 05 Oct 23	read	read

Guangtao Lu, Wuhan University of Science and Technology, Wuhan, China
Saurabh K. Yadav, Institute of Infrastructure Technology Research and Management, Ahmedabad, India
Pedro M. Ferreira, Universidade Nova de Lisboa, Lisbon, Portugal
Zine Ghemari, University Mohamed Boudiaf,, M’sila,, Algeria

Comments on this article

All Comments(0)

Add a comment

Browse by related subjects

Back to all reports

Reviewer Report

5 Views

09 Sep 2024 | for Version 3

Pedro M. Ferreira, Universidade Nova de Lisboa, Lisbon, Lisbon, Portugal

5 Views Cite this report Responses(0)

Approved

All the comments have been taken into account, the manuscript is in a position to be approved.

Competing Interests

No competing interests were disclosed.

Reviewer Expertise

Piezoelectric Composites, Piezoelectric Behaviour, Advanced Materials, Smart Materials

I confirm that I have read this submission and believe that I have an appropriate level of expertise to confirm that it is of an acceptable scientific standard.

Respond to this report

Responses (0)

Back to all reports

Reviewer Report

8 Views

09 Sep 2024 | for Version 3

Guangtao Lu, Wuhan University of Science and Technology, Wuhan, Hubei, China

8 Views Cite this report Responses(0)

Approved

The manuscript has been greatly improved, and the authors have responsed to all the main concerns. As the authors replied to comments, they are still trying their best to further investigate and solve some main concerns the two reviewers point out. Of course, I am looking forward to your newest study.

Competing Interests

No competing interests were disclosed.

Reviewer Expertise

Structural health monitoring by uisng lamb waves

I confirm that I have read this submission and believe that I have an appropriate level of expertise to confirm that it is of an acceptable scientific standard.

Respond to this report

Responses (0)

Back to all reports

Reviewer Report

3 Views

13 Sep 2024 | for Version 2

Zine Ghemari, University Mohamed Boudiaf,, M’sila,, Algeria

3 Views Cite this report Responses(0)

Approved With Reservations

The synthesis method described in this paper enables the creation of piezoelectric cascade models using limited information in the form of characteristic frequencies. At present, this method provides a rough approximation of the actual piezoelectric parameters with a limited number of inputs. An alternative analysis method based on structural numbers shows promise compared to matrix calculations, but it needs further investigation to assess the computational power required to determine its competitiveness with current algorithms.
The authors should revise this article according to the following comments:
1- do you show the economic profit of this work?
2- Add recent work on piezoelectricity such as:
- Improvement of the piezoelectric sensor by the progress of the measurement accuracy." IEEE International Conference on Smart Materials and Spectroscopy (SMS’2018), Yassmine Hammamet (Tunisia).
- Improvement of the vibration analysis technique by optimizing the parameters of the piezoelectric accelerometer
- Extraction of the relative sensitivity model and improvement of the piezoelectric accelerometer performances
- Mechanical resonator sensor characteristics development for precise vibratory analysis
3-Correct any spelling mistakes

Is the work clearly and accurately presented and does it cite the current literature?

Yes
Is the study design appropriate and is the work technically sound?

Yes
Are sufficient details of methods and analysis provided to allow replication by others?

Yes
If applicable, is the statistical analysis and its interpretation appropriate?

Not applicable
Are all the source data underlying the results available to ensure full reproducibility?

Yes
Are the conclusions drawn adequately supported by the results?

Yes

Competing Interests

No competing interests were disclosed.

Reviewer Expertise

Maintenance, Piezoelectricity, Sensors

Respond to this report

Responses (0)

Back to all reports

Reviewer Report

16 Views

28 Aug 2024 | for Version 2

Guangtao Lu, Wuhan University of Science and Technology, Wuhan, Hubei, China

16 Views Cite this report Responses(1)

Approved With Reservations

Thank the authors for their response and detailed revisions. The current version has been greatly improved, and however there are still some concerns that need be addressed. Moreover, impressed by the innovative effort.

If the name of the proposed method is included in the title, the novelty of this manuscript will be more easily got by the readers.
Figure 3: what do these symbols, ₁X_0s, ₁X_1s and so on, stand for?
The material type and some key parameters of PZT should be clearly addressed instead of just putting a website link.
The resolution of the figures is low and their quality should be further improved.
Table 2 and 5: how to confirm the accuracy of the data?
Based on the results, the proposed method can be used to analyze the characteristics of piezoelectric systems accurately. However, the computation cost is much larger than the traditional method. Therefore, what is the merit or advantage of this method?

Competing Interests

No competing interests were disclosed.

Reviewer Expertise

Structural health monitoring by uisng lamb waves

Respond to this report

Responses (1)

Author Response

10 Sep 2024

Jacek Harazin, Faculty of Mechanical Engineering, Politechnika Slaska, Gliwice, 44-100, Poland

Thank You for another insightful review. Unfortunately I have already sent a new version of the article prior to receiving your comments on version 2 so any possible amendments will have to be placed in another version of the article if necessary. I will try to address the issues point by point, as previously.

The aim of this article’s title was to focus the attention of the reader on the aspect of piezoelectric model synthesis, with the main “tool” being the Cauer’s method. The presented analysis method using structural numbers was placed within the article as it was necessary to provide means to validate the synthesis method. The research on the alternative using structural numbers was done in parallel and there were plans initially, to also use structural numbers for the synthesis itself, hence this method ended up being part of the article. I realise the outcome of that idea is not ideal and the title may be somewhat ambiguous but at the same time the title is not too concise already and I’m afraid I would only make it worse by trying to fix this issue.
₁X₀and ₁X₁are nodes of the graph of relations. Each node represents the displacement of any object being part of a physical model. So, if we had an example of a model with two moving masses, a graph of such model would contain three nodes. The ₁X₀node is special in that it represents any relations of a model with anything we consider being “outside” of the model’s scope. In the case of this article, the ₁X₀node represents one of the fixed ends of the model, where the last spring and damper are attached. The first number symbolizes an entire isolated system with its own relations. So, if we had two models working in parallel, the first one would have “1” at the front, and the second one would have “2”. The second number is used to number nodes within each system.
I agree that putting just the link to the used material catalogue might have introduced unnecessary ambiguity into the article. I did a mistake of not properly disclosing that I chose the SM411 material to test the model response which would have made it slightly better. If You consider this a major issue with the article, then I will try to prepare another version with clearly disclosed information about the used material.
I will try to improve the quality of figures in the next version if necessary.
The entire code used to perform the study and obtain the data in tables 2 and 5 was placed in an online repository (Mendeley data) under the reference 42. The algorithm is written in such a way that it should automatically collect all the data and print the amplitude responses with both studied methods. The only caveat is that the algorithm was written using the proprietary Matlab code format, so it is recommended that the algorithm is used with Matlab r2019b to ensure the same results.
The method of system analysis presented in the article has a markedly different approach to the way in which the relationships occurring within the analysed system are represented.
The response equations of the system are obtained based on transformations on structural numbers, which are in principle less complex than matrix equations. This led the authors to believe that the algorithmisation of this method would allow the response to be calculated with less computing power than in the case of the matrix method. Unfortunately, this could not be proved in the article. However, it is not clear whether the inferior performance of the method obtained from calculations performed in Matlab is directly due to the shortcomings of the method itself, or whether it is the result of poor optimisation of the code itself, or even of the environment, which is optimised for the well-known matrix method. Therefore authors assumed that it is still worth sharing the results and the method may have potential, however more work is necessary to determine the cause of worse performance.

Thank you again for your time spent on preparing your review. I hope my answers have cleared at least some of the issues raised. I will be eagerly waiting for any further responses.

Best regards,

View more View less

Competing Interests

No competing interests were disclosed.

Back to all reports

Reviewer Report

17 Views

09 Aug 2024 | for Version 2

Pedro M. Ferreira, Universidade Nova de Lisboa, Lisbon, Lisbon, Portugal

17 Views Cite this report Responses(1)

Approved With Reservations

The manuscript presents a novel approach to synthesizing piezoelectric systems, starting with only known resonant and anti-resonant frequencies. This method offers a broader perspective on system modelling utilizing an algorithm based on the Cauer synthesis method, an initial discrete mechanical model is constructed, forming the foundation for piezoelectric model synthesis. The manuscript is well-composed and systematically organized. However, there are a few concerns and suggestions that should be addressed before it can be accepted for indexing. In my view, these issues require more detailed clarification before the manuscript can be considered for indexing.

The introduction to the present literature review is poor, particularly in the following excerpt: "Researchers largely focus on modelling simple piezoelectric components with lumped models and matrix tensor equations or try to approach the problem using FEM (finite element method) analysis." There are several models that could be referenced in the introduction, such as Eshelby-Type Models, Micromechanics-based models, or Asymptotic Homogenization-Based Models, which are widely used to model the behaviour of piezoelectric composites. Additionally, this excerpt needs to be supported with more current references. Keywords that could help in finding up-to-date references include: "Piezoelectric composites, Electro-mechanical properties, Analytical models, Numerical models."
In the last paragraph of the introduction, the excerpt “The number of rows and columns, however, is tightly connected to the shape of an edge graph which a given structural number relates to,” is very unclear. It should be rewritten for better clarity and explained in more detail.
The author compares the computation time and memory usage of parameterized algorithms, highlighting a significant increase in both when using the structural number method compared to the classical matrix method (as shown in Table 4). The authors should clarify why the calculation time and memory usage of the modified algorithms increase so dramatically as the number of degrees of freedom in the analysed systems rises.
The conclusion is overly long and needs to be more concise, with an emphasis on the limitations of the authors' analytical approach. For better clarity, consider presenting the main conclusions and limitations as bullet points.

Is the work clearly and accurately presented and does it cite the current literature?

Partly
Is the study design appropriate and is the work technically sound?

Yes
Are sufficient details of methods and analysis provided to allow replication by others?

Yes
If applicable, is the statistical analysis and its interpretation appropriate?

Not applicable
Are all the source data underlying the results available to ensure full reproducibility?

Yes
Are the conclusions drawn adequately supported by the results?

Partly

Competing Interests

No competing interests were disclosed.

Reviewer Expertise

Piezoelectric Composites, Piezoelectric Behaviour, Advanced Materials, Smart Materials

Respond to this report

Responses (1)

Author Response

06 Sep 2024

Jacek Harazin, Faculty of Mechanical Engineering, Politechnika Slaska, Gliwice, 44-100, Poland

Thank You for your insightful review. In line with Your remarks, I have rewritten most of the introductory section of the article, adding more up-to-date literature references and including links to the numerical methods mentioned in the review. I also rewrote the research gap statement to make it more readable. The conclusion section has also been revised. Below I have included corresponding point by point responses to the various comments made in the review.

1. After rereading the introduction section, I must agree that it was too vague and contained too much information that could be considered irrelevant in the scope of the article. To amend that, I have completely rewritten most of this section, while also adding mentions and new references to current works (2020-2023) related with Eshelby-Type/micromechanical models. I must admit that I was so focused on the mathematical synthesis aspect in the context of piezoelectric models that I didn’t encounter works on models mentioned in your review. Thank You for bringing this issue up because that also helped me in finding new potential paths to expand my research in the future.

2. I have decided to extend the explanation with a graphical clue in form of a new figure 1, which shows an example of a graph, from which a new structural number is being created. The example of a structural number has also been placed under new equation 1. I think that a simple figure might provide much more insight than my extensive explanations, while also conserving more space. In hindsight, I should have provided a descriptive figure in the first place.

3. I agree that this issue was left with a vague explanation. It was already pointed out that the conclusions were overly long and realising that I was trying to make the explanation concise. Unfortunately, I made it too vague instead. I have tried to amend this by adding more detailed explanation in the conclusions. To summarize the explanation, the uncovered issue may be due to the structure of the written code for the method based on structural number algebra. It was made using closed loops which were combined with quite complicated substitution operations and complex algebraic representations of each graph edge. Combined, these three elements could contribute to the perceived great increase in both computation time and RAM requirement. The matrix method was largely an unmodified module readily available as an integral part of the Matlab software which may have been the reason for its much better performance. The new method had to be written from ground up which probably left a lot of the performance on the table due to my lack of programming skill and also the inability to better access program’s memory and CPU handling operations.

4. Most of the conclusions section was reworked according to raised issues. I have tried to form several bullet points to streamline the thought process and make the text more accessible to readers. I wasn’t able to put the entire section in a set of bullet points, but I made an attempt to better separate the conclusions from both experiments described in the article to avoid confusion. I hope that will satisfy the requirements.

View more View less

Competing Interests

No competing interests were disclosed.

Back to all reports

Reviewer Report

21 Views

29 Nov 2023 | for Version 1

Saurabh K. Yadav, Institute of Infrastructure Technology Research and Management, Ahmedabad, Gujarat, India

21 Views Cite this report Responses(1)

Approved With Reservations

The main merit and novelty of the manuscript are not clearly stated in the abstract, introduction and conclusion. The authors should highlight how their method differs from the existing methods in the literature, and what are the advantages and limitations of their method.
The authors use a single piezoelectric plate as an example to verify their electromechanical model. However, the results show that the model has a significant error in the resonant frequency and the displacement amplitude. The authors should explain the sources of this error and how it can be reduced or corrected. Moreover, the authors should test their model on more realistic and complex piezoelectric structures, such as stacks, rings, beams, etc., and compare their results with experimental data or other numerical methods.
The authors compare the computational performance of their method with the matrix method using a two-degree system. However, this is not a fair comparison, as the matrix method can handle systems with any number of degrees of freedom, while the structural number method is limited by the complexity of the edge graph. The authors should compare the computational performance of both methods on systems with different numbers of degrees of freedom, and use more appropriate metrics, such as the number of floating point operations, the memory usage, the accuracy, etc.
The authors use some references that are published in non-English languages, such as Refs. 8, 11 and 29. The authors should provide English translations of these references, or use more accessible sources that are published in English. The authors should also update their literature review with some recent works on piezoelectric modelling and parameter estimation.

Is the work clearly and accurately presented and does it cite the current literature?

Yes
Is the study design appropriate and is the work technically sound?

Yes
Are sufficient details of methods and analysis provided to allow replication by others?

Yes
If applicable, is the statistical analysis and its interpretation appropriate?

Yes
Are all the source data underlying the results available to ensure full reproducibility?

Yes
Are the conclusions drawn adequately supported by the results?

Yes

Competing Interests

No competing interests were disclosed.

Reviewer Expertise

Mathematical modelling

Respond to this report

Responses (1)

Author Response

13 Apr 2024

Jacek Harazin, Faculty of Mechanical Engineering, Politechnika Slaska, Gliwice, 44-100, Poland

Thank you for the critical review. I would also like to apologise for a long break before my reply. I have prepared several corrections to the article regarding your review and they will be published with the new version. I've also tried to address your concerns directly:

1. Let me repeat my answer to the second reviewer here, as it addresses the same concerns. The article showcases a new method to synthesize cascading electromechanical models using the Cauer method coupled with Van Dyke-Butterworth models to represent piezoelectric stacks with clumped mechanical and electrical components. Each of those methods have been already used by researchers but i have found no literature on the particular approach presented in this article. The novelty revolves around the general approach to synthesis with very limited input information. Most researchers focus on specific applications where piezoelectric parameters and the analysed structure is largely known or predetermined experimentally. Here, only the frequencies are known and there is an infinite number of possible models that could realise those predetermined resonant frequencies. Coupled with further steps presented in the article, this method offers a possibility to design piezoelectric stacks with different material properties or geometric dimensions, capable of resonating in predetermined frequencies.
The limitation of this method is that it can only be used to synthesize models composed of components connected in series. So far, it can only be used to synthesise specific piezoelectric plate configuraions, where each component in a stack is responsible exclusively for a single resonant frequency set as the input. I have modified the article to better reflect those statements.

2. Following up from my response to the second reviever, I agree and i can already attest that the method is currently being verified empirically. The synthesis method has been verified already with three real piezoelectric stacks with different geometrical dimensions which has shown some discrepancy between model results and real plate behaviour. The source of those differences was traced back to how some of the piezoelectric parameters are determined in the factory (under 1kHz wave stimulation) versus plate properties in the resonance proximity. It has to be noted as well, that this method relies on a lumped representation of an otherwise continous system. The main issue of this approach is that the lumped parameters are approximations of the real parameters and an electromechanical model currently can't perfectly match the behavior of a piezoelectric plate, where the interactions and their magnitude changes between the layers of a single piezoelement. There are also boundaries between piezoelectric elements, made with adhesives and isolating layers, which also introduce many hidden variables in the real model behaviour. The presented method is still in its infancy and requires more testing and refinement. I would like to provide a consice report on the empirical results in a follow up article though, as including all the information about the procedure and test stand would make this article very bloated.

3. I was made aware that a comparison of calculation time used exclusively is a bad metric for algorithm complexity. I have tried looking for more literature on the matter and added more references to the article. Given my abilities and available resources, i have prepared a second study which focused more on the memory criterion. I've used the available Matlab evaluation modules to estimate the average RAM usage between both algorithms on a variety of models, along with a comparison between the average time it took both algorithms to complete. New suite of tests has uncovered more information about the structural number algorithm optimisation and shed some light on its shortcomings. I have modified the manusript to showcase the second study. I am aware that this method may also not be the best way to evaluate algorithm complexity and only presents a rough estimation and i will try to consult a specialist on the topic with an intent of providing some collaboration with more indepth information about algorithm complexity of the proposed method.

4. I have provided additional literature references to publications of the authors involved in the development of the structural number method where they descibe mentioned models in english. I hope that will provide the necessary background which was lacking previously.

I hope that my response provides an exhaustive explanation to the issues raised.

Best Regards,

View more View less

Competing Interests

No competing interests were disclosed.

Back to all reports

Reviewer Report

31 Views

29 Nov 2023 | for Version 1

Guangtao Lu, Wuhan University of Science and Technology, Wuhan, Hubei, China

31 Views Cite this report Responses(1)

Approved With Reservations

What’s the main merit of the manuscript? It should be clearly addressed in the abstract, introduction and conclusion.
To compare the computational performance of the new model, the model response and computation time are compared with the matrix method. What are the errors of these two models? The two frequencies of the new model are compared with the ones of matrix method. Are the results of the matrix method accurate? What are the actual frequencies?

It is the same during the amplitude comparison. Moreover, to compare the computational performance of the algorithm, there are many metrics, such as time cost, the number of floating points (FLOPs) multiple adds (MAdds), and so on. In addition, what is the meaning of only decreasing the computation time?
Page 4: “A combination of those factors creates four different types of models…” It refers to Refs. 8 and 11. However, Refs. 8 and 11 are published in non-English. Therefore, the details of the four models are suggested to be introduced in the manuscript.
Experimental results: the results should be further analyzed.

Is the work clearly and accurately presented and does it cite the current literature?

Yes
Is the study design appropriate and is the work technically sound?

Partly
Are sufficient details of methods and analysis provided to allow replication by others?

Partly
If applicable, is the statistical analysis and its interpretation appropriate?

Not applicable
Are all the source data underlying the results available to ensure full reproducibility?

Yes
Are the conclusions drawn adequately supported by the results?

Yes

Competing Interests

No competing interests were disclosed.

Reviewer Expertise

Structural health monitoring by uisng lamb waves

Respond to this report

Responses (1)

Author Response

13 Apr 2024

Jacek Harazin, Faculty of Mechanical Engineering, Politechnika Slaska, Gliwice, 44-100, Poland

Thank you very much for the critical review and Your suggestions regarding the article clarity. I would also like to apologise for a long break before my reply. I have prepared several corrections to the article regarding your review and they will be published with the new version. I've also tried to address your querries to the best of my ability:

1. The article showcases a new method to synthesize cascading electromechanical models using the Cauer method coupled with Van Dyke-Butterworth models to represent piezoelectric stacks with clumped mechanical and electrical components. Each of those methods have been already used by researchers but i have found no literature on the particular approach presented in this article. The novelty revolves around the general approach to synthesis with very limited input information. Most researchers focus on specific applications where piezoelectric parameters and the analysed structure is largely known or predetermined experimentally. Here, only the frequencies are known and there is an infinite number of possible models that could realise those predetermined resonant frequencies. Coupled with further steps presented in the article, this method offers a possibility to design piezoelectric stacks with different material properties or geometric dimensions, capable of resonating in predetermined frequencies.

2. The predetermined frequencies and amplitudes were chosen arbitrarily and do not reflect any real piezoelectric system. A comparison between both analysis methods was done on the same model synthesized with the Cauer method. The matrix method was considered as a reference method because its a known and established way to calculate model response. The structural number method was compared against it and it was a pure comparison between two analytical methods.
I was also made aware that a comparison of calculation time used exclusively is a bad metric for algorithm complexity. I have tried looking for more literature on the matter and added more references to the article. Given my abilities and available resources, i have prepared a second study which focused more on the memory criterion. I've used the available Matlab evaluation modules to estimate the average RAM usage between both algorithms on a variety of models, along with a comparison between the average time it took both algorithms to complete. I am aware that this method may also not be the best way to evaluate algorithm complexity and only presents a rough estimation. I will need to consult a specialist on that matter and conduct more tests but that would probably go beyond the scope of this article and should be contained in a separate paper focused only on the comparison between both methods.

3. I have provided additional literature references to publications of the authors involved in the development of the structural number method where they descibe mentioned models in english. I hope that will provide the necessary background which was lacking previously.

4. I agree and i can already attest that the method is currently being verified empirically. The synthesis method has been verified already with three real piezoelectric stacks with different geometrical dimensions which has shown some discrepancy between model results and real plate behaviour. The source of those differences was traced back to how some of the piezoelectric parameters are determined in the factory (under 1kHz wave stimulation) versus plate properties in the resonance proximity. However, i would like to envelope the empirical analysis, along with all the necessary test procedures and the test stand description in a second article, serving as the continuation for this study.

I hope that i have provide an exhaustive explanation to the issues raised.

Best Regards,

View more View less

Competing Interests

No competing interests were disclosed.

Alongside their report, reviewers assign a status to the article:

Approved - the paper is scientifically sound in its current form and only minor, if any, improvements are suggested

Approved with reservations - A number of small changes, sometimes more significant revisions are required to address specific details and improve the papers academic merit.

Not approved - fundamental flaws in the paper seriously undermine the findings and conclusions

[1] 1. Palmgren E, Rasa T: Modelling Roles of Mathematics in Physics. Sci. Educ. 2022. Publisher Full Text

[2] 2. Buchacz A, Wróbel A: Modelowanie i badanie wpływu zjawiska piezoelektrycznego na charakterystyki układu mechanicznego. Gliwice: Wydawnictwo Politechniki Śląskiej; 2010.

[3] 3. Brownjohn J, Pavic A: Vibration control of ultra-sensitive facilities. Proceedings of the Institution of Civil Engineers - Structures and Buildings. 2006; 159: 295–306. Publisher Full Text

[4] 4. Zhang Y, Yan T, Xu X, et al.: Room temperature and humidity decoupling control of common variable air volume air-conditioning system based on bilinear characteristics. Energy and Built Environment. 2023; 4: 354–367. Publisher Full Text

[5] 5. Fundamentals of Automotive and Engine Technology: Standard Drives, Hybrid Drives, Brakes, Safety Systems. Springer Fachmedien Wiesbaden; 2014.

[6] 6. Bai R, Tong S, Karimi HR: Modeling and Backstepping Control of the Electronic Throttle System. Math. Probl. Eng. 2013; 2013: 1–6. Publisher Full Text

[7] 7. Buchacz A, Dymarek A, Dzitkowski T: Synthesis of discrete, continuous and discrete continuous vibrating systems represent-ed by graphs. Sixth International Scientific and Engineering Conference - Machine-Building and Technosphere on the Border of the XXI Century. 1999; 3: 243–245.

[8] 8. Buchacz A, Żurek K: Modelowanie i badanie wpływu zjawiska piezoelektrycznego na charakterystyki układu mechanicznego. Wydawnictwo Politechniki Śląskiej. 2010.

[9] 9. Smith M: Synthesis of mechanical networks: the inerter. IEEE Trans. Automat. Contr. 2002; 47: 1648–1662. Publisher Full Text

[10] 10. Phillips GM: Interpolation and Approximation by Polynomials. Springer-Verlag; 2003. Publisher Full Text

[11] 11. Białas K, Buchacz A, Dzitkowski T: Synteza drgających aktywnych układów mechanicznych z tłumieniem w ujęciu grafów biegunowych i liczb strukturalnych. Wydawnictwo Politechniki Śląskiej. 2010.

[12] 12. IEEE: Standard on Piezoelectricity. ANSI/IEEE; 1988.

[13] 13. Adriaens H, Koning W, Banning R: Modelling piezoelectric actuators. IEEE ASME Trans. Mechatron. 2000; 5: 331–341. Publisher Full Text

[14] 14. Goldfarb M, Celanovic N: Modelling piezoelectric stack actuators for control of micromanipulation. IEEE Control. Syst. 1997; 17: 69–79. Publisher Full Text

[15] 15. Wang S-H, Tsai M-C: Dynamic modelling of thickness-mode piezoelectric transducer using the block diagram approach. Ultrasonics. 2011; 51: 617–624. PubMed Abstract | Publisher Full Text

[16] 16. Wróbel A: Classical and non-classical research methods and experimental studies of piezoelectric plates. Gliwice: Wydawnictwo Politechniki Śląskiej; 2018.

[17] 17. Cauer W: Ideale Transformatoren und lineare Transformationen. Elektrische Nachrichtentechnik (ENT). 1932; 9: 157–174.

[18] 18. Cauer W: Theorie der linearen Wechselstromschaltungen. Berlin: Akademie-Verlag; 1960; vol. 2. .

[19] 19. Richter B, Twiefel J, Wallaschek J: Piezoelectric Equivalent Circuit Models.Priya S, Inman DJ, editors. Energy Harvesting Technologies. Boston, MA: Springer; 2009. Publisher Full Text

[20] 20. Soluch W, et al.: Wstęp do piezoelektryki. Warszawa: Wydawnictwo Komunikacji i Łączności; 1980.

[21] 21. Lahmer T, Kaltenbacher M, Kaltenbacher B, et al.: FEM-based determination of real and complex elastic, dielectric, and piezoelectric moduli in piezoceramic materials. IEEE Trans. Ultrason. Ferroelectr. Freq. Control. 2008; 55(2): 465–475. PubMed Abstract | Publisher Full Text

[22] 22. Goldstein A: Self-Tuning multimodal piezoelectric shunt damping. J. Braz. Soc. Mech. Sci. Eng. 2011; 33: 428–436. Publisher Full Text

[23] 23. Batra R, Dell’isola F, Vidoli S, et al.: Multimode vibration suppression with passive two-terminal distributed network incorporating piezoceramic transducers. Int. J. Solids Struct. 2005; 42: 3115–3132. Publisher Full Text

[24] 24. San Miguel J, Buiochi F, Adamowski J: Numerical modelling of a circular piezoelectric ultrasonic transducer radiating in water. ABCM Symposium Series in Mechatronics. 2000; 2: 458–464.

[25] 25. Yamaoka S, Ohnishi K: Reaction force estimation of piezoelectric actuator by charge observation. IEEE International Conference on Mechatronics (ICM). Vicenza, Italy IEEE Xplore. 2013. Publisher Full Text

[26] 26. Delibas B, Arockiarajan A, Seemann W: Rate dependent properties of perovskite type tetragonal piezoelectric materials using micromechanical model. Int. J. Solids Struct. 2006; 43: 697–712. Publisher Full Text

[27] 27. Gan J, Zhang X: A review of nonlinear hysteresis modelling and control of piezoelectric actuators. AIP Adv. 2019; 9(4): 040702. Publisher Full Text

[28] 28. Nakamura N: Extended Rayleigh Damping Model. Front. Built Environ. 2016; 2. Publisher Full Text

[29] 29. Bellert S, Woźniacki H: Analiza I synteza układów elektrycznych metodą liczb strukturalnych. Warszawa: WNT; 1968.

[30] 30. Harazin J, Wróbel A: Research on a cascade model synthesis with the use of classical and non-classical methods in the context of new piezoelectric stack applications. Int. J. Mech. Sci. 2021; 12: 959–969. Publisher Full Text

[31] 31. Adamowski JC, Nader G, Silva ECN: Effective Damping Value of Piezoelectric Transducer Determined by Experimental Techniques and Numerical Analysis. ABCM Symposium Series in Mechatronics. 2004; 1: 271–279.

[32] 32. Giergiel J: Tłumienie drgań mechanicznych. Kraków: Wydawnictwo Akademii Górniczo-Hutniczej; 1984.

[33] 33. Trindade M, Benjeddou A: Effective Electromechanical Coupling Coefficients of Piezoelectric Adaptive Structures: Critical Evaluation and Optimization. Mech. Adv. Mater. Struct. 2009; 16: 210–223. Publisher Full Text

[34] 34. Buchacz A, Płaczek M: Modelowanie i badanie jednowymiarowych drgających układów mechatronicznych. Gliwice: Wydawnictwo Politechniki Śląskiej; 2011.

[35] 35. Harazin J: Model algorithms. Mendeley Data. 2022. Publisher Full Text

[36] 36. Harazin J: Piezoelectric electromechanical model (first iteration). Mendeley Data. 2023. Publisher Full Text

Analytical approach to piezoelectric model synthesis with the use of Cauer’s method for system design

Abstract

Keywords

Introduction

Methods

Mechanical model synthesis

(1)

(2)

(3)

(4)

(5)

(6)

Figure 1. A mechanical cascade system composed of an infinite number of stages composed of mass “m” and spring “c” pairs, synthesized from the transfer function polynomial with the Cauer’s method.

(7)

(8)

Figure 2. A discrete cascade mechanical model with added damping elements.

Mechanical model verification

(9)

(10)

(11)

(12)

(13)

Figure 3. Graph of the cascade model where: a) shows the sine coefficients b) shows the cosine coefficients.

(14)

(15)

(16)

Electromechanical model synthesis

(17)

(18)

(19)

(20)

(21)

(22)

(23)

Piezoelectric discrete model verification

(24)

(25)

(26)

(27)

(28)

Figure 4. Discrete piezoelectric model composed of mechanical lumped model combined by a transformer with an electrical network.

Algorithm testing

Results

Figure 5. Model response calculated for a) first vibrating mass, and b) second vibrating mass.

Table 1. Comparison of frequencies between model responses obtained with both methods.

Table 2. Comparison of amplitude responses obtained with both methods on the nodes.

Table 3. Computation time for both methods used to analyse a simple mechanical system.

Figure 6. Model response calculated for a) displacement curve, and b) voltage curve along the frequency axis.

Conclusions

Data availability

Source data

Underlying data

Software availability

Model algorithms

References

Comments on this article Comments (0)

Open Peer Review

Comments on this article Comments (0)

Open Peer Review

Reviewer Status

Reviewer Reports

Comments on this article

Browse by related subjects

Competing Interests Policy

Stay Updated