Benchmarking graph representation learning algorithms&nbsp;for detecting modules in molecular networks

Zhiwei Song; Brittany Baur; Sushmita Roy

doi:10.12688/f1000research.134526.1

Home Browse Benchmarking graph representation learning algorithmsfor detecting...

ALL Metrics

-

Views

-

Downloads

Get PDF

Get XML

Export

▬

✚

Research Article

Benchmarking graph representation learning algorithms for detecting modules in molecular networks

[version 1; peer review: 1 approved, 1 approved with reservations]

Zhiwei Song^1,2, Brittany Baur¹, Sushmita Roy ^1,3

PUBLISHED 07 Aug 2023

Author details Author details

¹ Wisconsin Institutes for Discovery, Madison, Wisconsin, 53715, USA
² Department of Computer Science, University of Wisconsin-Madison, Madison, Wisconsin, 53715, USA
³ Department of Biostatistics and Medical Informatics, University of Wisconsin-Madison, Madison, Wisconsin, 53715, USA

Zhiwei Song
Roles: Formal Analysis, Investigation, Software, Visualization, Writing – Original Draft Preparation

Brittany Baur
Roles: Data Curation, Writing – Review & Editing

Sushmita Roy
Roles: Conceptualization, Methodology, Project Administration, Supervision, Validation, Writing – Review & Editing

OPEN PEER REVIEW

REVIEWER STATUS

This article is included in the Bioinformatics gateway.

This article is included in the Machine Learning in Genomics collection.

Abstract

Background: A common task in molecular network analysis is the detection of community structures or modules. Such modules are frequently associated with shared biological functions and are often disrupted in disease. Detection of community structure entails clustering nodes in the graph, and many algorithms apply a clustering algorithm on an input node embedding. Graph representation learning offers a powerful framework to learn node embeddings to perform various downstream tasks such as clustering. Deep embedding methods based on graph neural networks can have substantially better performance on machine learning tasks on graphs, including module detection; however, existing studies have focused on social and citation networks. It is currently unclear if deep embedding methods offer any advantage over shallow embedding methods for detecting modules in molecular networks.
Methods: Here, we investigated deep and shallow graph representation learning algorithms on synthetic and real cell-type specific gene interaction networks to detect gene modules and identify pathways affected by sequence nucleotide polymorphisms. We used multiple criteria to assess the quality of the clusters based on connectivity as well as overrepresentation of biological processes.
Results: On synthetic networks, deep embedding based on a variational graph autoencoder had superior performance as measured by modularity metrics, followed closely by shallow methods, node2vec and Graph Laplacian embedding. However, the performance of the deep methods worsens when the overall connectivity between clusters increases. On real molecular networks, deep embedding methods did not have a clear advantage and the performance depended upon the properties of the graph and the metrics.
Conclusions: Deep graph representation learning algorithms for module detection-based tasks can be beneficial for some biological networks, but the performance depends upon the metrics and graph properties. Across different network types, Graph Laplacian embedding followed by node2vec are the best performing algorithms.

Keywords

network biology, module detection, graph clustering, graph representation learning, node embedding, graph neural network, machine learning

Corresponding author: Sushmita Roy

Competing interests: No competing interests were disclosed.

Grant information: This work is supported by NHGRI R01 grant #R01- HG010045-01 and James McDonnell Foundation Grant #3194-133-349500-4-AAB5159.

Copyright: © 2023 Song Z et al. This is an open access article distributed under the terms of the Creative Commons Attribution License, which permits unrestricted use, distribution, and reproduction in any medium, provided the original work is properly cited.

How to cite: Song Z, Baur B and Roy S. Benchmarking graph representation learning algorithms for detecting modules in molecular networks [version 1; peer review: 1 approved, 1 approved with reservations]. F1000Research 2023, 12:941 (https://doi.org/10.12688/f1000research.134526.1) First published: 07 Aug 2023, 12:941 (https://doi.org/10.12688/f1000research.134526.1) Latest published: 07 Aug 2023, 12:941 (https://doi.org/10.12688/f1000research.134526.1)

Introduction

Graphs provide ubiquitous powerful representations of interacting components in many complex systems.¹ In molecular biology, graphs are used to represent interactions between molecular components; for example, protein-protein interactions represent interactions between proteins, while gene regulatory networks describe interactions between transcription factor proteins and genes. A common property of graphs of complex systems, including molecular networks, is the presence of community structures or modules, defined by groups of densely interacting nodes. In protein-protein interaction networks, such modules often correspond to key biological processes needed for cells to accomplish different tasks.² Disruptions to module connectivity have been implicated in many diseases.¹ Therefore, the accurate detection of these modules is an important problem in the analysis of molecular networks.³ Graph representation learning (GRL),⁴ which aims to embed graph nodes in a $d$ -dimensional space (Figure 1), offers a powerful framework for performing machine learning tasks on graphs, including clustering.⁵ Both deep and shallow graph representation algorithms exist; however, deep representation learning methods have been designed and tested on non-biological networks such as social networks, citation networks and recommendation systems⁶^–⁹ or only tested on link prediction and node classification tasks.¹⁰ It is unclear if deep graph representation learning methods are beneficial for module detection of molecular networks.

Figure 1. Graph representation learning (GRL) for module detection on graphs.

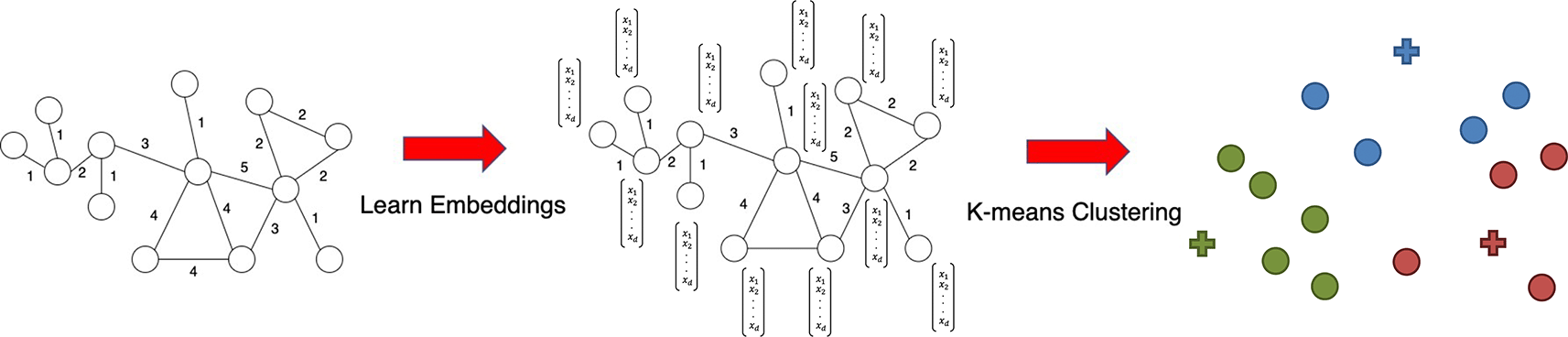
A GRL algorithm converts graph structure into node embeddings denoted as vectors for each node. A standard clustering method, such as K-means clustering, can be applied to embeddings to obtain group clusters.

To address this need, we benchmarked several state-of-the-art shallow and deep learning GRL frameworks for the task of module detection on both real molecular networks and synthetic benchmark networks. Our benchmark included three shallow GRL methods: Graph Laplacian embedding,¹¹ DeepWalk,¹² and node2vec¹³ and two deep GRL algorithms: Variational Graph Auto-Encoder (VGAE)⁷ and GraphSAGE.¹⁴ We evaluated the methods on one simulated and three real world molecular network datasets. Two of the three real network datasets captured the impact of single nucleotide polymorphisms (SNPs) identified from genome wide association studies (GWAS). We used multiple clustering metrics to evaluate the quality of the inferred clusters including modularity index, silhouette index, adjusted mutual information index (when cluster labels were available) and enrichment of gene ontology processes for modules inferred on the molecular networks. Our results show that on simulated benchmarks, deep GRL methods offered some advantages over shallow methods, however, on real networks we did not see a clear advantage of deep GRL methods over shallow GRL methods for detecting modules in biological networks.

Methods

Datasets

We applied five different representation learning algorithms to simulated and cell type-specific gene interactions that we previously generated.¹⁵

Lancichinetti-Fortunato-Radicchi (LFR) benchmark graphs

We evaluated all the algorithms on a synthetic network based on the LFR graph generator. We chose to use LFR benchmark graphs¹⁶ as they can support larger graphs and capture the distribution of node degree and community sizes of real-world networks, which often follow the power law distribution. We used the graph generator to obtain weighted undirected graphs with ground-truth non-overlapping communities.

The LFR benchmark has a number of parameters: ( $N$ , $K$ , $γ$ , $β$ , $μ$ , $k_{\min}$ , $k_{\max}$ , $s_{\min}$ , $s_{\max}$ ). $N$ is the number of nodes in the whole graph, $K$ is the average degree of nodes, $γ$ is the exponent value for the power-law distribution of node degrees, $β$ is the exponent value for the power-law distribution of community sizes, and $μ$ is the mixing the parameter controlling the percentage of the degree of each node interconnecting from its own community to another community. When the mixing parameter is low, there is a higher chance for an edge to stay within one community; while when it is high, there will be more interconnected edges between two communities than edges with two ends in the same community. The last four parameters $k_{\min}$ , $k_{\max}$ , $s_{\min}$ , $s_{\max}$ are the lower and upper bounds of node degree and community size when constructing synthetic networks.

By setting different parameters in the LFR package, we can generate networks of different topological properties and compare various node embedding techniques. Based on the statistics of the 55 cell-type specific networks, we set the number of nodes $N = 1000$ , the average degree of nodes $K = [10, 25, 50, 100]$ , the exponent for degree distribution $γ = 2$ , the exponent for community size distribution $β = 1$ , and the mixing parameter $μ = [0.1, 0.5]$ . We left the bounds of node degree and community size as default. For each parameter setting, we generated five sets of weighted synthetic networks. Since some of our GRL algorithms take unweighted graphs, we derived unweighted graphs by keeping edges with weights higher than the average weight. In total, there are eight groups of synthetic network datasets for each parameter setting with five networks each in total (Tables 1 and 2).

Table 1. Network characteristics on Lancichinetti-Fortunato-Radicchi (LFR) benchmark graph.

The unweighted networks comprise edges with weights larger or equal to the average edge weights in weighted ones.

	# of nodes	# of edges	# of nodes in unweighted graphs	# of edges in unweighted graphs
$α = 0.1$
k = 10	1000	9754.8	733.2	4368.4
k = 25	1000	25468.4	867.4	11338.4
k = 50	1000	49685.2	903.4	22863.2
k = 100	1000	99511.2	965.4	47397.6
$α = 0.5$
k = 10	1000	9766.4	988.6	4806.4
k = 25	1000	25436.8	970.0	12257.6
k = 50	1000	49759.2	996.6	24617.6
k = 100	1000	99896.4	997.6	49694.4

Table 2. The number of communities when constructing eight groups of synthetic network datasets with five networks each in total.

These values can be used to compare with the optimal k value detected when applying K-Means in each algorithm.

$α = 0.1$	Average # of node communities	$α = 0.5$	Average # of node communities
k = 10	88.8	k = 10	96.6
k = 25	34.6	k = 25	33.6
k = 50	18	k = 50	18.6
k = 100	9.2	k = 100	9.4

Cell-type specific networks

The cell-type specific networks consist of 55 gene networks capturing protein-protein and transcription factor (TF) gene regulatory interactions in different cell types that were generated to link regulatory single nucleotide polymorphisms (SNPs) to genes from Baur et al.¹⁵ The cell types represent major cell and tissue types studied by the NIH Roadmap Epigenomics Project.¹⁷ To create these networks we obtained the protein-protein interactions from the STRING database,¹⁸ RRID:SCR_005223. The protein-protein network is not cell type specific and combined it with cell type-specific TF-gene regulatory interactions. The regulatory interactions were defined in a cell-type specific manner and included both promoter-proximal and distal regulatory interactions. To create the cell-type specific regulatory networks, we downloaded Roadmap DNase I data from NIH Roadmap Epigenomics Project for each cell type and sequence-specific motifs for transcription factors from JASPAR,¹⁹ RRID:SCR_003030. Accessible motif instances were identified by intersecting motif instances with DNase I peaks on gene promoters and distal regions that exhibited long-range interactions with genes.¹⁵ The proximal TF-target regulatory network captures interactions between TFs and gene promoters exhibiting a significant and accessible motif instance. The distal regulatory network captures the interactions between TFs and genes, where the TF’s motif instance is on a region that interacts with the gene. The proximal and distal regulatory networks and the protein-protein interaction networks were merged by concatenating edges into one unweighted network per cell type. The statistics of these networks are described in Table 3.

Table 3. The network characteristics of 55 cell-type specific networks and phenotype-specific networks, including the average of nodes, the average of edges, and the average density of networks.

Density is calculated by dividing the maximum number of edges in a full network by the number of edges. The values presented in the table are in mean (std) format.

Dataset	Type	# of nodes	# of edges	Density
Undiffused networks	Unweighted	15241(2961)	416296.36(241399.39)	0.32%(0.06%)
ASD diffused networks	Weighted	1358.45(129.95)	923257.05(178044.45)	99.15%(1.86%)
	Unweighted	1352.91(134.91)	83692.14(29989.69)	8.77%(0.89%)
CAD diffused networks	Weighted	1675.31(101.16)	704642.32(83412.50)	50.06%(0.004%)
	Unweighted	1636.8(112.65)	68578.29(17438.98)	5.02%(0.79%)

Phenotype-specific diffused networks

We used the cell-type specific networks to identify parts of the network that were most affected by SNPs identified in different genome-wide association studies (GWAS,¹⁵). We refer to these as phenotype-specific networks. Briefly, for each of the 55 cell types, we scored genes in each network based on their propensity to interact with a non-coding SNP as assessed by the strength of the interaction between the region harboring a SNP and a gene promoter. The higher the score, the greater the strength of interaction between a gene and a region with the SNP. After assigning the node scores in the gene network, a two-step diffusion process was applied to first obtain scores for all other genes in the network using a regularized Laplacian kernel,²⁰ followed by a second diffusion using a heat kernel to diffuse the signal among all genes. The output is a weighted adjacency matrix format where diagonal elements are node scores and off-diagonal elements are diffused edge weights. Since each cell type has a different network, we end up with 55 different nearly fully connected, weighted networks for each phenotype. We created these networks for SNPs from two phenotypes: Autism Spectrum Disorder (ASD) and Coronary Artery Disease (CAD). The statistics of these networks are described in Table 3.

Graph representation learning algorithms

Graph Laplacian embedding

The Graph Laplacian is a key operator for a given graph that has a large number of applications ranging from spectral clustering¹¹ to using the Laplacian to smooth clusters on the graph.²¹^–²³ The normalized Graph Laplacian can be used to produce node embeddings as well and is computed as:

(1)

L_{normalized} = I - D^{- \frac{1}{2}} {AD}^{- \frac{1}{2}}

Here $I$ is the identity matrix and $D$ is the degree matrix obtained by summing the edge weights associated with each node and adding the average degree to the diagonal of the degree matrix. The addition of the average degree transformation was shown to be useful for real-world graphs with non-uniform degree distributions.²⁴ Next, we compute eigenvectors associated with the $k$ smallest eigenvalues of the normalized Graph Laplacian matrix. Each node is then represented by corresponding entries in these $k$ eigenvectors to produce a $k$ -dimensional embedding of the node.

DeepWalk

The DeepWalk¹² algorithm is based on random walks, which uses the skip-gram model²⁵ to learn a node representation. We note that the authors of DeepWalk refer to this algorithm as a deep learning algorithm; however, we use the classification provided by Hamilton et al.,⁶ which considers DeepWalk as a shallow representation learning algorithm. In DeepWalk, each node’s representation is obtained from a set of random walks of a fixed window size on the graph starting from that node. For each node $v$ , the algorithm tries to find the embedding of node $v$ that maximizes the log-likelihood of neighbors observed in the random walk. This yields the optimization objective function that maximizes $Pr (u_{k}| Φ (v))$ , where $ϕ (v)$ , the embedding of node $v$ and $u_{k}$ is a neighbor node. Naively optimizing this objective is computationally prohibitive, so DeepWalk uses a hierarchical softmax function where the neighbor nodes are stored as leaves on a binary tree and the above probability can be calculated by the product of the probability of observing nodes on the path from the root ( $v_{j}$ ):

(2)

Pr (u_{k}| Φ (v_{j})) = \prod_{l = 1}^{⌈log V⌉} Pr (b_{l}| Φ (v_{j}))

where

b_{1}, b_{2}, \dots, b_{⌈log V⌉}

is a sequence of tree nodes on the path and the maximum number of nodes equals the maximum depth of the binary tree,

⌈log V⌉

. As in the skip-gram model, the parameters of the probability distribution are learned by a stochastic gradient descent algorithm. The hyperparameters for the DeepWalk algorithm are num-walks (the number of random walks from each node), walk-length (length of one walk from each node), window-size (window size of the skip-gram model), and embedding space dimension. We set num-walks to the default of 10 walks per node and walk-length to the default value of 80 nodes. We used the default settings for all the parameters with the exception of the embedding space dimension, which we set to

[64, 128, 256]

(Table 4).

Table 4. The optimal hyper-parameter setting used in the comparison of different algorithms for the simulated and real biological networks.

Dataset	Methods	Embedding dimension	Other parameters
Synthetic networks	DeepWalk	128
	node2vec	128	p = 1, q = 2
	GraphSAGE	[256,256]
	VGAE	[128,128]
Undiffused networks	DeepWalk	64
	node2vec	128	p = 0.5, q = 1
	GraphSAGE	[64,64]
	VGAE	[256,256]
ASD diffused networks	DeepWalk	64
	node2vec	256	p = 1, q = 2
	GraphSAGE	[256,256]
	VGAE	[128,128]
CAD diffused networks	DeepWalk	64
	node2vec	256	p = 1, q = 2
	GraphSAGE	[256,256]
	VGAE	[64,64]

As Deepwalk accepts unweighted graphs as input, we converted the fully connected weighted graph to an unweighted graph by keeping edges with the highest weights. Briefly, we computed the mean value of all edge weights in a network and used it as a threshold to remove the edges with weights lower than the threshold. Edges that remained in the graph were set to a weight of 1. After this step the networks for Autism Spectrum Disorder, the average node number reduces from 1358.45 to 1352.91 and the average edge number in the graphs reduces from 1,846,514.09 to 167,384.27 (approximately 1/10 of the edges in the original weighted networks), Table 3.

node2vec

Similar to the DeepWalk algorithm, node2vec¹³ also uses random walks and the skip-gram model on the graph to obtain node embeddings. However, in node2vec, biased random walks are used to better capture the node’s neighborhood information and are controlled by two parameters, $p$ and $q$ . The parameter $p$ controls the probability of revisiting a node right after moving away from it, while $q$ specifies the probability of visiting a node’s 1-hop neighbors.⁶ These parameters can be set to make the random walk behave more like a Breadth First Search algorithm (high $p$ ) versus Depth First Search (DFS, low $p$ ). As in DeepWalk, the embedding of a node is learned based on the probability of the neighbor set. This probability distribution is estimated efficiently by making the assumption that the probability of observing one node in a neighborhood is independent of another one and that a node $u$ and its neighbor nodes should have a symmetric effect on each other’s feature space. Let $N_{s} (v)$ denote the set of neighbors of $v$ and $ϕ (v)$ denote the embedding of node $v$ . The independence assumption allows the probability of the neighbor set to be written as:

(3)

Pr (N_{s} (v)| ϕ (v)) = \sum_{u_{k} \in N_{s} (u)} Pr (u_{k}| ϕ (v))

The probability of node pairs is defined as a softmax function. We define the likelihood of node pairs as a softmax function of:

(4)

Pr (u_{k}| ϕ (v)) = \frac{exp (ϕ (u_{k}) \cdot ϕ (v))}{\sum_{u_{k} \in V} exp (ϕ (v) \cdot ϕ (u_{k}))}

node2vec implements negative sampling strategies when optimizing the likelihood function and updating the node’s embedding features. This improves computation efficiency and becomes more scalable compared to the DeepWalk algorithm. We explored a range of $p$ and $q$ values to explore neighborhoods using a more BFS or DFS algorithm. In addition to the default setting of $p = q = 1$ , we also applied $p$ , $q$ with values $(p, q) \in \{(1, 2), (1, 0.5), (2, 1), (0.5, 1)\}$ . In order to facilitate the comparison between various settings of $p$ and $q$ parameters, we used the default embedding dimension proposed in the algorithm implementation. The difference in performance under various $p$ and $q$ values is minor across all values of $k$ , the number of clusters (Underlying data: Supplementary Figure 1²⁶^,²⁷). However, under the silhouette index, the default setting ( $p = 1, q = 1$ ) always achieves top performance except when $k = 70$ . For consistency with DeepWalk, we set the embedding space dimension to be $d \in \{64, 128, 256\}$ (Table 4).

GraphSAGE

The GraphSAGE framework generalizes an inductive Graph Convolutional Network (GCN) framework and estimates a function with learnable parameters that can generate node embeddings based on the node attributes and the attributes of its neighboring nodes.¹⁴ The function in turn is a deep neural network where each layer makes use of aggregation and propagation of information from a node’s neighborhood. Given a learned function, GraphSAGE uses a forward algorithm to generate node embeddings, that consist of message passing and aggregation functions. In the message-passing step, each node retrieves its neighboring nodes’ current embedding and passes it through an aggregation function. This is denoted as

(5)

h_{v}^{(l)} = {AGG}^{(l)} (\{m_{u}^{(l)}, u \in N (v)\}), m_{u}^{(l)} = W^{(l)} h_{u}^{(l - 1)}

where

h_{v}^{(l)}

refers to the embedding of node

v

at layer

l

,

m_{u}^{(l)}

refers to the message passed from node

v

’s neighbor node

u

, and

N (v)

refers to node

v

’s 1-hop neighboring nodes. To train the GraphSAGE parameters, a loss function that captures the graph topology is defined. In particular, for each node, positive and negative links are generated via negative sampling and the parameters of the embedding function are learned via stochastic gradient descent.

The hyperparameters of GraphSAGE include the number of hidden layers and the dimension of each layer. We set the number of layers to 2 as recommended by⁶ and constrain the number of units in both the hidden and output layers to be $d \in \{64, 128, 256\}$ (Table 4). The objective function is optimized with batch gradient descent with a batch size of 256 and step size of 0.005. We also implement the negative sampling strategy by uniformly randomly selecting a target node to create an equal amount of negative links compared to positive ones. We use the mean aggregator function in the message passing step. As in the case of Deepwalk, we gave GraphSAGE unweighted versions of the phenotype-specific networks.

Variational graph auto-encoders (VGAE)

Graph auto-encoders (GAE)⁷ are commonly used unsupervised graph representation learning algorithms. They can be implemented either with or without node features. GAEs typically contain an encoder, which is often a Graph Convolutional Network (GCN)⁸ and a decoder, which uses inner products to predict edge presence. The loss function is based on the difference between the original adjacency matrix and the reconstructed one. Variational graph auto-encoder (VGAE)⁷ is an extension of GAEs that uses variational inference of model features. It assumes a prior distribution and encodes the node embeddings into a latent space via a GCN. In addition to the GAE loss function, its loss function minimizes the KL divergence between feature distributions and the standard normal distribution.

When training the VGAE model, we set the number of layers to two so that it is consistent with GraphSAGE and the input node feature matrix as an identity matrix. The hidden layers and embedding space dimensions are also set to be $\{(64, 64), (128, 128), (256, 256)\}$ (Table 4). The size of the embedding space does not significantly impact VGAE’s performance as assessed on the cell-type specific networks (Underlying data: Supplementary Figure 2²⁶^,²⁷). Since the encoder of VGAE, GCN, is also based on the aggregation of node embeddings from their neighbors, under similar reasoning as GraphSAGE, VGAE was applied to unweighted versions of the phenotype-specific graphs.

Defining clusters from learned representations

To define cell clusters we applied the K-means clustering algorithm to the node embeddings obtained from each GRL algorithm. We set the number of clusters, $k$ , to vary from 10 to 100 with a step size of 10. To uniformly compare across algorithms, we had to pick a single $k$ that was optimal for all algorithms. To this end, we obtained the $k$ value for each method on each cell line that achieves the highest value based on the clustering evaluation metrics defined below. Then we select the mode value among all $k$ values to be and use the clustering results from this $k$ to compare across algorithms on different real and simulated networks. The optimal $k$ values for the simulated dataset was $k = 30$ , for the cell type-specific networks was $k = 50$ , and was $k = 10$ for both phenotype-specific networks. For selected cell lines, we additionally visualized the modularity and silhouette scores for each algorithm as a function of $k$ (Underlying data: Supplementary Figures: 3–8²⁶^,²⁷). These values for individual cell lines are provided in Underlying data: Supplementary Tables 1–6.²⁶^,²⁷

Evaluation metrics

For the synthetic networks, we used three metrics to evaluate the quality of our clusters from each of the learned embeddings. Two of these, Modularity and Silhouette Index do not require any additional information to evaluate the quality of clusters. The third metric is Adjusted Mutual Information (AMI), which is used when there are ground truth labels for each cluster. AMI and Silhouette Index are widely used to assess the results from any clustering algorithm. Modularity is used specifically for graph clustering algorithms. All three metrics were used for the simulated networks, while SI and Modularity were used for the real networks.

Modularity

Modularity, proposed by Newman and Girvan,²⁸ is the most widely used evaluation metric for the assessment on detected community structure. It represents the difference between the fraction of edges within one community and the fraction of edges in an equivalent network whose edges are randomly connected. Let $i$ denote the cluster $i$ , $C_{i}$ denotes the nodes in cluster $i$ , and $E$ denotes the set of edges. Modularity is defined as follows:

(6)

Q = \sum_{i = q}^{k} (e_{ii} - a_{i}^{2})

where

(7)

e_{ii} = \frac{| \{(u, v) : u \in C_{i}, v \in C_{i}, (u, v) \in E\} |}{| E |}

and

(8)

a_{i} = \frac{| \{(u, v) : u \in C_{i}, (u, v) \in E\} |}{| E |}

Here $e_{ii}$ captures the proportion of edges within nodes of cluster $i$ and $a_{i}$ is the expected number of edges for members in cluster $i$ . The modularity score ranges from -1 to 1, with more positive values indicating greater community structure.

Silhouette Index

Silhouette Index²⁹ measures how close a node is to its own cluster compared to its closest neighbor cluster and scores each node based on this schema. Each node’s overall average silhouette score is treated as a measurement of cluster quality. It is defined as:

(9)

S (G) = mean (\frac{b (i) - a (i)}{max \{a (i), b (i)\}}), \forall i \in V

where

a (i)

is the mean distance between node

i

and all other nodes within the same cluster,

b (i)

is the mean distance from node

i

to all nodes in the nearest cluster, and

V

is the node set of the graph. The silhouette score ranges from -1 to 1 with a maximum of 1 corresponding to best cluster assignments.

Adjusted Mutual Information Index (AMI)

The mutual information (MI) score is a similarity measurement between two sets of clusterings, $U$ and $V$ defined as:

(10)

MI (U, V) = \sum_{i = 1}^{| U |} \sum_{j = 1}^{| V |} \frac{| U_{i} \cap V_{j} |}{N} log \frac{N | U_{i} \cap V_{j} |}{| U_{i} ‖ V_{j} |}

where

U_{i}

is the cluster

i

in

U

and

V_{j}

is the cluster

j

in

V

.

| U_{i} |

represents the number of nodes in cluster

i

in

U

and

| V_{j} |

is the number of nodes in cluster

j

in

V

.

N

is the total number of nodes in the graph. The AMI score is the adjustment of the MI score so that cluster assignments with larger clusters do not have biased higher scores. The AMI score ranges from 0 to 1 with the best score at 1.

Gene ontology enrichment analysis

To interpret the clusters identified on the cell-type and phenotype-specific networks, we used GO enrichment analysis (Release 106).³⁰^–³² GO enrichment analysis was done using a Hypergeometric test with FDR correction. We set the threshold of q-value to be $10^{- 5}$ to define enriched terms. As GO enrichment can provide a large number of overlapping terms, we developed additional summary metrics to evaluate the GO enrichment: (a) the number of clusters enriched with any term, (b) the number of terms enriched in any cluster, (c) the distribution of the number of clusters a term is enriched in. This analysis was focused on the $k$ =50 results to obtain the greatest resolution of the clusters, while being optimal for most methods. Finally, we used terms that were deemed specific to a cell line (defined as enriched in a small number of clusters), to bicluster the cell lines and the terms using Non-negative matrix factorization (NMF).³³ We first filtered out the GO terms that are enriched in more than 20% of the cell lines and created a GO term count matrix, where the row of the matrix is a GO term and the column represents the 55 cell lines. The entry of the matrix is the number of times a term is enriched in the corresponding cell line (maxed at the number of clusters). This matrix was factorized with NMF to group GO terms into distinct term categories and cell lines into different categories with 10 factors. This enabled us to associate groups of terms with groups of cell lines. We reordered the GO terms and cell lines based on the group assignments and visualized the count matrix as heatmaps (Underlying data: Supplementary Figure 10 to Supplementary Figure 12²⁶^,²⁷). The code for doing the NMF-based ontology summarization is available at.²⁶

Results

We compared our three shallow (DeepWalk, node2vec, Graph Laplacian) and two deep (GraphSAGE, VGAE) GRL methods on simulated networks with known ground truth and real cell type-specific molecular networks.

Deep graph representation learning methods offer some advantages over shallow representation learning on synthetic benchmarks

We first evaluated the different methods on the synthetic graphs from the LFR benchmark using three metrics, Modularity, AMI and Silhouette Index. The synthetic graphs were generated by setting the mixing parameter, $α$ which controls the connectivity between clusters, to 0.1 or 0.5 (Methods). When $α = 0.1$ , 10 percent of edges connected to each node link to another node in a different cluster and the remaining edges stay in the node’s cluster. Thus $α = 0.1$ is easier to cluster compared to $α = 0.5$ which has more inter-cluster edges. For $α = 0.1$ , Graph Laplacian and node2vec embeddings performed overall the best for both modularity index (Figure 2A), followed closely by VGAE. VGAE achieved the highest score under silhouette index and AMI (Figure 2B & 2C). GraphSAGE outperformed others when evaluated by the modularity score, but had a relatively low score when considering the other metrics. This suggests that GraphSAGE is able to recover community structure better than other methods, even though the low dimensional embeddings of nodes within a cluster may not be as coherent as the other methods. These results also demonstrate the utility of assessing results using multiple metrics which can provide complementary information (e.g., modularity for GraphSAGE results). Deepwalk had the worst performance compared to other methods. Overall, VGAE, node2vec, and Graph Laplacian embedding had higher performance compared to GraphSAGE and Deepwalk.

Figure 2. Comparison of deep and shallow graph representation learning methods on simulated networks.

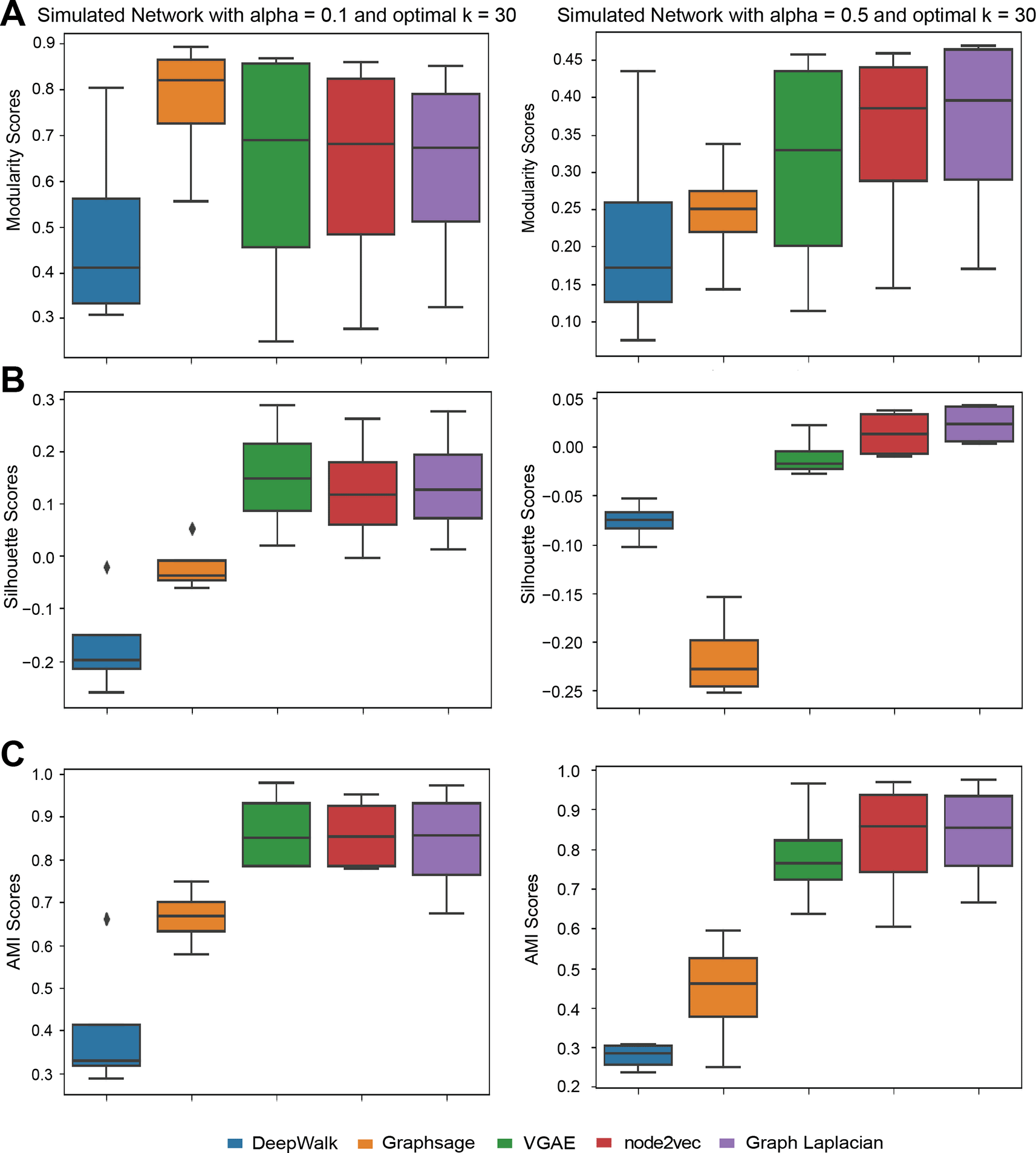
(A) The modularity scores with alpha = 0.1 and 0.5. (B) The Silhouette Index scores with alpha = 0.1 and 0.5. (C) The AMI scores with alpha = 0.1 and 0.5. Each algorithm is applied to simulated networks with the node degree [10, 25, 50, 100] and their scores form distributions that are summarized into box plots. For each data set, the optimal $k$ is chosen based on the overall performance of all algorithms.

For $α = 0.5$ , which is more challenging from a clustering point of view, GraphSAGE and VGAE significantly dropped in performance under all three metrics. However, node2vec and Graph Laplacian were still robust for these graphs. GraphSAGE and Deepwalk were the two poorest-performing methods when aggregating the different metrics.

Deep GRL methods do not offer significant benefits over shallow methods for defining modules on gene networks

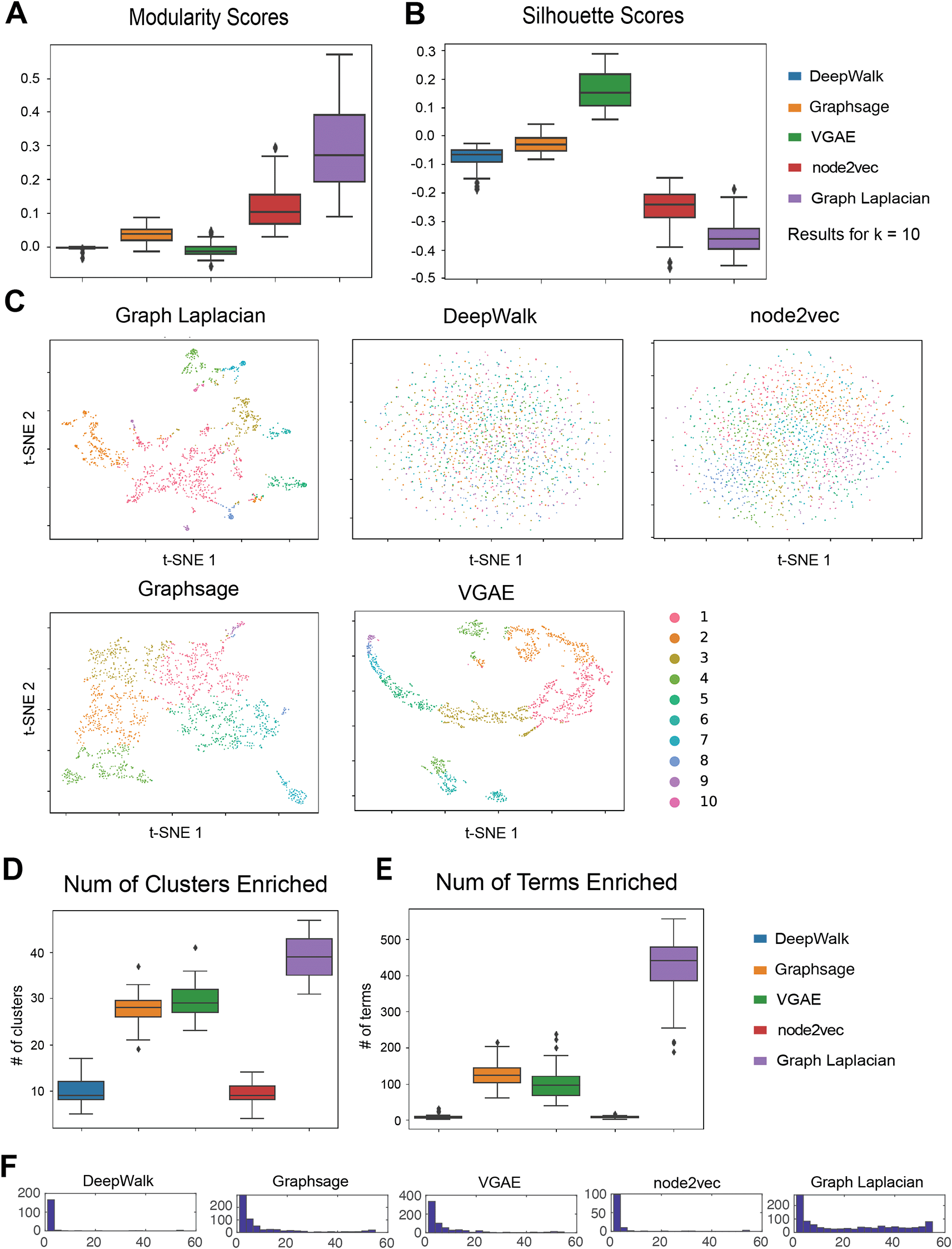
We next evaluated our five GRL methods for their ability to retrieve gene modules from 55 cell type-specific networks (Methods). These cell types corresponded to diverse cell lines and tissue types that were studied by the ENCODE ROADMAP consortium project.¹⁷ We first evaluated the quality of the modules based on Silhouette Index and Modularity, which did not require ground truth labels. The evaluation metrics were computed for each $k$ (number of clusters), to determine the best number of clusters for each algorithm for each cell line (Underlying data: Supplementary Table 1²⁶^,²⁷). To compare across algorithms, we used $k = 50$ as this was the best across all cell lines and methods when using either modularity or SI. Furthermore, the choice of $k$ did not substantially affect the relative performance of algorithms (Underlying data: Supplementary Figure 3²⁶^,²⁷). Based on both modularity and SI for $k = 50$ , DeepWalk performed the best, followed by Graph Laplacian (Figure 3A & 3B). Node2vec had a better performance under the modularity index but achieved a worse silhouette score. The deep GRL method VGAE had a better SI score than node2vec, but was outperformed on modularity by node2vec. GraphSAGE had the worst performance using both metrics. Overall, DeepWalk and Graph Laplacian embedding had a consistently high performance using both metrics. Deep GRL methods had poor performance for Modularity, but we saw better silhouette scores for the VGAE algorithm.

Figure 3. Comparison of deep and shallow graph representation learning methods on 55 cell type-specific networks.

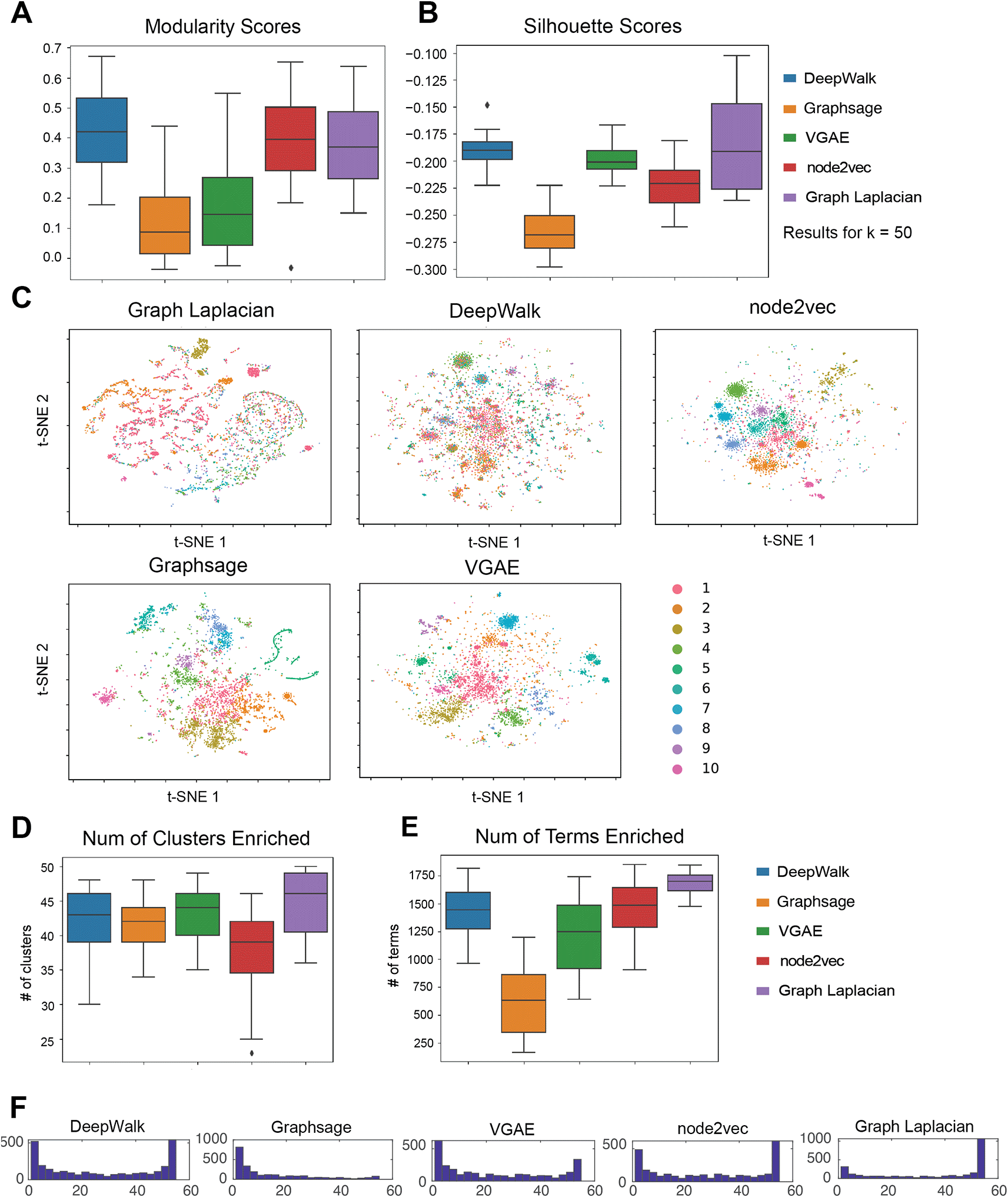
(A) The distribution of modularity across 55 cell-type specific networks. Each algorithm is applied to 55 cell line networks and their scores form distributions that are summarized into box plots. For each data set, the optimal $k$ is chosen based on the overall performance of all algorithms. (B) The distribution of Silhouette Index scores across the 55 cell type-specific networks. As in Modularity, we picked the $k$ that was best for each cell line. In general, Modularity and Silhouette Index picked a similar $k$ . (C) tSNE visualizations of the embeddings learned by each method. The colors correspond to the different clusters. The colors are matched across methods so that the largest cluster is shown as cluster ID 1, followed by cluster 2, etc. (D) Number of clusters enriched with a GO term in 55 cell line networks. (E) Number of terms enriched in any cluster in 55 cell line networks. (F) Distribution of the number of cell lines a term is enriched in any cluster.

To further examine the inferred clusters, we used tSNE³⁴ to visualize the node embedding of genes for each method in a two-dimensional space (Figure 3C) and color the nodes based on their cluster membership. To be consistent with the above analysis, we selected cluster assignments with $k$ = 50 and plotted the 10 largest clusters. We selected the heart cell line since it had the highest Modularity across methods. For all methods, there was a clear visual separation between the members of each cluster (different colors). The tSNE visualization also showed that the Graph Laplacian embedding tended to identify less uniform-sized clusters, with two large clusters (2922-1448 genes) in comparison to the other methods.

We next interpreted the cluster assignments by performing GO enrichment analysis. Across 55 cell-type specific networks, we counted the number of clusters (out of a total of 50) that are enriched for a GO process term (Figure 3D). Across all methods, the majority of the clusters were enriched, with Graph Laplacian producing the largest number of enriched clusters across cell lines followed by DeepWalk and VGAE. Node2vec had the lowest average number of enriched clusters. This indicates that Graph Laplacian, DeepWalk and VGAE obtained the most biologically meaningful clusters for these networks. We next counted the total number of terms enriched in any cluster for each of the methods (Figure 3E). Across the 55 cell lines, we found that Graph Laplacian had the greatest number of terms on average, which was followed by node2vec and DeepWalk. Here, GraphSAGE had significantly fewer terms compared to any of the methods. We aimed to assess the overall specificity of the clusters for the GO terms by examining the distribution of the number of clusters a term is enriched in. We expect this distribution to be bimodal, with some general terms to be enriched in many clusters, while more specialized terms would be enriched in fewer clusters (Figure 3F). Here DeepWalk, VGAE and node2vec exhibited the clearest bimodal distributions. Graph Laplacian embedding tended to identify more generic terms (inferred in many clusters) and relatively fewer cluster-specific terms compared to other methods. In contrast, GraphSAGE had the opposite behavior with most terms enriched in a smaller number of clusters. In parallel, we examined the distribution of the number of cell lines a term was enriched in each of the GRL methods. Most methods with the exception of GraphSAGE exhibited a bimodal distribution, with most terms either being enriched in many of the cell lines ( $>$ 50) or few cell lines ( $<$ 4). Graph Laplacian was unique in that most of the terms were shared across cell lines. Finally, we used the specific GO terms for each method (defined by biclustering cell lines and the enriched GO terms using non-negative matrix factorization (Underlying data: Supplementary Figure 10,²⁶^,²⁷ Methods). Both DeepWalk and VGAE grouped the fetal cells separately, providing more skewed cell line clusters, while the other methods provided more uniform groups of cell lines and their corresponding terms. The association of the GO terms with cell line clusters was consistent with the role of the cell lines for these methods. For example, in Graph Laplacian, we identified the immune cell lines associated with immune function, and developmental processes were associated with the embryonic stem cell lines. Taken together, these results show that shallow representation learning methods are able to recover biologically meaningful groupings of cell lines.

Deep GRL methods for network-based interpretation of GWAS phenotypes

Network-based approaches offer a powerful framework for interpreting sequence variants identified from GWAS by identifying pathways that might be jointly perturbed by a set of sequence variants.³⁵^,³⁶ A common theme of these approaches is to map a set of sequence variants onto a network and interpret these variants based on subnetworks connected by these variants. As another application of GRL, we examined how the embedding affects the results for network-based GWAS interpretation. To this end, we considered two phenotypes, Autism Spectrum Disorder (ASD) and Coronary Artery Disease (CAD), which are among the most well-studied phenotypes in the NHGRI catalog.³⁷ We focused specifically on non-coding variants, which are more challenging to interpret as they are often far away from genes. We used heat diffusion kernel to first construct weighted graphs for each phenotype (Methods), and then applied each GRL method to obtain an embedding followed by k-means clustering (Figure 4, Figure 5). Because GraphSAGE and DeepWalk require unweighted graphs, we first removed edges with weights less than the average edge weight per cell line and then gave the remaining edges as an unweighted graph as input to GraphSAGE and DeepWalk. For the VGAE algorithm, the encoder was based on Graph Convolutional Network that learns each node’s embeddings from its neighborhood. Since both ASD and CAD phenotype-specific networks were nearly fully-connected, this can produce noisy embeddings. Thus, we applied VGAE on the unweighted graphs as well.

Figure 4. Comparison of deep and shallow GRL methods for ASD phenotype-specific networks.

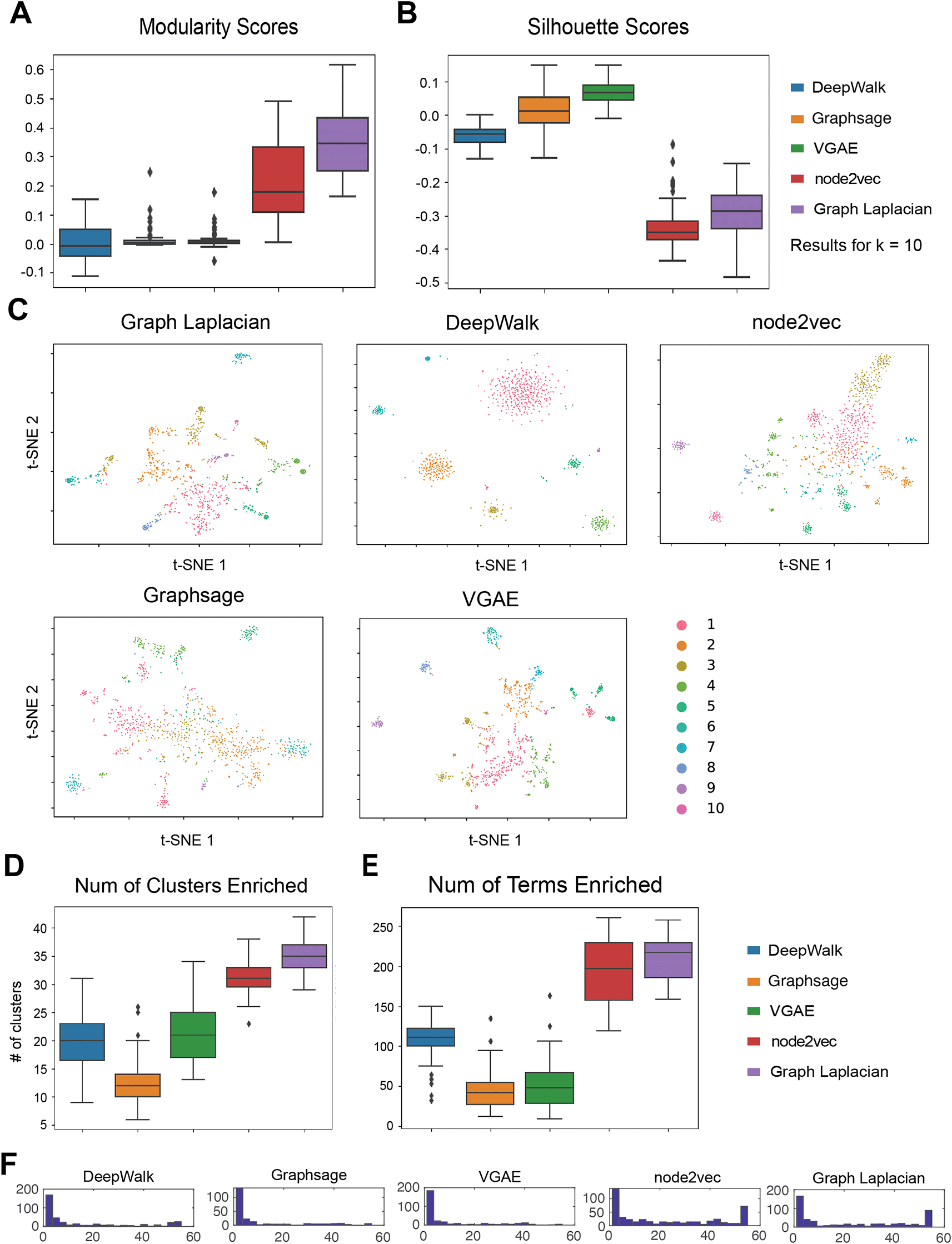
(A) The distribution of modularity across 55 cell line networks obtained with ASD. Each algorithm is applied to 55 cell line networks and the scores are summarized in a box plot. Shown are the results for $k = 10$ , which was chosen as the optimal $k$ based on the overall performance of all algorithms. (B) The distribution of silhouette scores across the 55 networks when using $k = 10$ clusters. (C) tSNE visualizations of the embeddings learned by each method. The colors correspond to the different clusters. The order of cluster numbers matches the decreasing order of cluster sizes. (D) Number of clusters enriched with a GO term in 55 cell line networks. (E) Number of terms enriched in any cluster of the 55 cell line networks. (F) Distribution of the number of cell lines a term is enriched in any cluster.

Figure 5. Comparison of deep and shallow graph representation learning methods on CAD phenotype-specific networks.

(A) The distribution of modularity across 55 cell line networks obtained with CAD. Each algorithm is applied to 55 cell line networks and the scores are summarized in a box plot. Shown are the results for $k = 10$ , which was chosen as the optimal $k$ based on the overall performance of all algorithms. (B) The distribution of silhouette scores across the 55 CAD phenotype-specific networks when using $k = 10$ clusters. (C) tSNE visualizations of the embeddings learned by each method. The colors correspond to different clusters. The order of cluster numbers matches the decreasing order of cluster sizes. (D) Number of clusters enriched with a GO term in 55 cell line networks. (E) Number of terms enriched in any cluster in 55 cell line networks. (F) Distribution of the number of cell lines a term is enriched in any cluster.

As in the analysis of the cell-type specific networks, we chose the optimal $k$ value based on the mode of the Modularity and Silhouette Index values across 55 cell lines and all 5 methods (Underlying data: Supplementary Table 3–6,²⁶^,²⁷). The optimal $k$ under these two metrics was 10. Based on the modularity metric, the top-performing method was Graph Laplacian followed by node2vec for the ASD phenotype network (Figure 4A). However, with the Silhouette Index, Graph Laplacian and node2vec had the worst performance (Figure 4B). Here, VGAE exhibited the best performance followed by GraphSAGE and node2vec. VGAE, GraphSAGE and DeepWalk accepted undirected weighted graphs and the opposite behavior of these algorithms for modularity and Silhouette Index could be due to that. These results demonstrate the benefit of deep learning frameworks for embedding graphs for GWAS analysis. We also visualized the clusters obtained for ASD phenotype networks in the heart cell line with t-SNE plots (Figure 4C). For all algorithms, the clustering structure was visually discernible with genes in the same cluster being positioned close together.

We next evaluated the different GRL methods based on GO enrichment of the inferred clusters. Here we considered $k = 50$ to have a sufficient granularity of the clusters to capture specific biological processes. We examined the distribution of the number of clusters enriched with a GO process as well as the number of GO process terms that were enriched across the 55 cell lines. Graph Laplacian embedding produced the highest number of clusters enriched with biological functions, followed by node2vec (Figure 4D). DeepWalk and VGAE had a similar average number of clusters enriched and GraphSAGE had the fewest. GraphLaplacian and node2vec were equally good when considering the number of terms followed by DeepWalk (Figure 4E). Both GraphSAGE and VGAE had the fewest number of GO terms. Finally, we examined the distribution of the number of clusters for each term (Figure 4F). Only Graph Laplacian and node2vec exhibited a bimodal distribution, meaning that they can discover both generic and specific term GO terms. As we did previously, we selected the most specific terms (defined by their enrichment in any cluster of 20% of the cell lines) and applied NMF to find cell line and term clusters (Underlying data: Supplementary Figure 11²⁶^,²⁷). Graph Laplacian and node2vec exhibited the clearest block diagonal structure with groups of cell lines associated with groups of GO terms. Several of these groupings were biologically meaningful, for example, the association of muscle and cardiac functions with a cell line cluster with heart (Graph Laplacian) and immune response associated with cd14 primary cells (node2vec).

We performed a similar analysis for the CAD phenotype network as well (Figure 5). We observed similar trends for the relative algorithm performance when using Modularity and Silhouette Index, with methods using undirected graphs exhibiting a higher Silhouette Index compared to methods using the weighted graphs (Graph Laplacian and node2vec) and an opposite trend when using Modularity (Figure 5A & 5B). Visualization of the tSNE plots for the heart cell line showed that while Graph Laplacian, GraphSAGE and VGAE retrieved layouts that were consistent with the clustering, DeepWalk and node2vec visualization were noisy (Figure 5C). A similar noisy layout was observed for other cell lines as well suggesting that the CAD networks were noisier than the ASD networks (Underlying data: Supplementary Figure 9²⁶^,²⁷). Based on the number of enriched clusters and terms enriched, Graph Laplacian performed best, followed by VGAE and GraphSAGE (Figure 5D). The low enrichment of the DeepWalk and node2vec algorithms is consistent with the lack of clustering structure in the tSNE results. The histogram of term specificity exhibited a bimodal distribution only with the GraphLaplacian embedding (Figure 5E); however, all three methods (Graph Laplacian, VGAE and GraphSAGE) produced well-separated cell line and biological process groups (Underlying data: Supplementary Figure 12²⁶^,²⁷).

Overall, our comparison of the GRL methods for the GWAS interpretation task showed that Graph Laplacian provided the most robust embedding under all metrics. Furthermore, the performance of the methods depended upon the metric and phenotype and deep GRL methods were less prone to noisy diffusion-based graphs compared to random-walk based methods (node2vec, DeepWalk).

Discussion

Graph representation learning (GRL) has emerged as a powerful paradigm for applying machine learning algorithms on graphs. More recent deep graph representation learning algorithms have shown improved performance on numerous graph machine learning problems such as node classification and link prediction. Given the modular organization of molecular networks such as protein-protein and regulatory networks, a natural question is whether deep GRL methods have an advantage for detecting modules or clusters on graphs over shallow GRL methods. In this paper, we performed a comprehensive benchmarking study on synthetic networks and real molecular networks capturing protein-protein and regulatory interactions. On real networks, we considered two types of applications: detection of gene modules from cell type-specific networks and detection of candidate pathways affected by single nucleotide polymorphisms identified in GWAS. We observed some benefits of deep GRL algorithms on simulated networks as well as in situations where the graph may be noisy.

Our experiments on simulated networks were helpful because of the availability of ground truth and a controlled experimental setting. In particular, the mixing parameter of 0.1, which results in sharper boundaries across clusters, all but DeepWalk perform well using Modularity. However, for a more challenging cluster structure, GraphSAGE dropped in performance. Between VGAE and GraphSAGE, which are both deep methods, VGAE was consistently better. It is likely that GraphSAGE is better for graphs where node attributes provide complementary information to the graph structure. When the networks are sparse, VGAE achieved equally good performance as node2vec and Graph Laplacian embeddings. However, shallow methods consistently outperformed deep learning frameworks for denser graphs where modules are harder to detect. Our experiments showed that deep GRL methods such as VGAE can outperform other algorithms but this depends upon the structure of the graph and the specific metric.

On real molecular networks, the relative performance of the algorithms depended upon the task. When defining gene modules across 55 cell line/type-specific networks, shallow GRL methods consistently outperformed both VGAE and GraphSAGE when using Modularity. However, when using the Silhouette Index, VGAE was comparable to shallow methods but GraphSAGE remained worse. Interestingly, despite low silhouette scores, all methods generated well-clustered tSNE visualizations and identified clusters that were enriched for gene ontology processes. When considering the task of GWAS interpretation, we found both GraphSAGE and VGAE and the shallow method, DeepWalk, to produce better silhouette scores, but this trend was reversed when using modularity. This observation was reproducible for the second phenotype as well. All three algorithms accepted filtered undirected graphs as input, while GraphLaplacian and node2vec accepted nearly fully connected weighted graphs. The pre-processing of graphs before providing them as input to graph embedding algorithms could be a major determinant of an algorithm’s performance. When compared to the ASD phenotype-specific graphs, we found DeepWalk and node2vec to produce noisy tSNE visualizations, which could be due to the greater noise in this graph and the susceptibility of random walk methods to noisy graphs. This was consistent with the relatively lower modularity score of node2vec compared to Graph Laplacian as well as a smaller number of enriched terms for these methods. Finally, across all network types, tasks and metrics, we found Graph Laplacian to provide consistently good embeddings, though it was not necessarily the best for some conditions. The only potential limitation of the Graph Laplacian is to infer unbalanced gene clusters for the cell-type specific networks. A direction of future work would be to consider alternative pre-processing of the graph or additional regularization to obtain more uniformly-sized clusters.

Our study compared select deep GRL and shallow GRL algorithms on graphs that did not have any node attributes. One direction of future work is to expand the type of graphs to those with node attributes and accordingly increase the class of algorithms to be compared. Another direction of future work is to detect dynamic gene modules, for which there are shallow³⁸ and deep learning algorithms.³⁹

Conclusions

In conclusion, our benchmarking study shows that the performance of different embedding methods depends on the metrics used as well as network characteristics, such as sparsity and edge weight distribution. Deep GRL algorithms are not necessarily advantageous over shallow methods for module detection and this depends upon the algorithm, the type of graph and the specific module-based task. Between the two deep GRL algorithms, we found the VGAE algorithm to offer superior performance. Comparing across different graph types and module metrics, Graph Laplacian provided consistently robust and high-quality embeddings suggesting that it could be a good baseline algorithm to compare for newly developed representation learning algorithms.

Data availability

Underlying data

Zenodo: Underlying data for’Benchmarking graph representation learning algorithms for detecting modules in molecular networks’, https://doi.org/10.5281/zenodo.7876238 ²⁷

This project contains the following underlying data:

• Cell Type Specific Networks.zip This includes all the cell type specific networks from the 55 cell lines.
• ASD Phenotype Networks.zip This includes all the cell type-specific weighted networks, where the weights correspond to the output of diffusing signals on the graph using SNPs associated with ASD.
• CAD Phenotype Networks.zip This includes all the cell type-specific weighted networks, where the weights correspond to the output of diffusing signals on the graph using SNPs associated with CAD.
• Simulated Networks.zip This includes all the simulated networks used to evaluate the performance of different methods.

Data are available under the terms of the Creative Commons Attribution 4.0 International license (CC-BY 4.0)

Software availability

Source code and experiment results available from: https://github.com/Roy-lab/graph-representation-learning.git

Archived source code and results at time of publication: Roy-lab/graph-representation-learning: v1.3 https://doi.org/10.5281/zenodo.8101884 ²⁶

License: MIT License

Acknowledgements

We would like to thank Sara Knaack and Junha Shin for assistance with the generation and visualization of Gene Ontology enrichments.

References

1. Barabási A-L, Oltvai ZN: Network biology: understanding the cell’s functional organization. Nat. Rev. Genet. February 2004; 5(2): 101–113. Number: 2 Publisher: Nature Publishing Group. Publisher Full Text
2. Das S, Chakrabarti S: Classification and prediction of protein-protein interaction interface using machine learning algorithm. Sci. Rep. January 2021; 11(1): 1761. Number: 1 Publisher: Nature Publishing Group. PubMed Abstract | Publisher Full Text | Free Full Text
3. Mitra K, Carvunis A-R, Ramesh SK, et al.: Integrative approaches for finding modular structure in biological networks. Nat. Rev. Genet. October 2013; 14(10): 719–732. Number: 10 Publisher: Nature Publishing Group. PubMed Abstract | Publisher Full Text | Free Full Text
4. Zhang D, Yin J, Zhu X, et al.: Network Representation Learning: A Survey. Technical Report arXiv:1801.05852, arXiv, July 2018. arXiv:1801.05852 [cs, stat] type: article.
5. Muzio G, O’Bray L, Borgwardt K: Biological network analysis with deep learning. Brief. Bioinform. March 2021; 22(2): 1515–1530. PubMed Abstract | Publisher Full Text | Free Full Text
6. Hamilton WL, Ying R, Leskovec J: Representation Learning on Graphs: Methods and Applications. Technical Report arXiv:1709.05584, arXiv, arXiv:1709.05584 [cs] type: article. April 2018.
7. Kipf TN, Welling M: Variational Graph Auto-Encoders, arXiv:1611.07308 [cs, stat].November 2016.
8. Kipf TN, Welling M: Semi-Supervised Classification with Graph Convolutional Networks, arXiv:1609.02907 [cs, stat].February 2017.
9. Wang D, Peng C, Zhu W: Structural Deep Network Embedding. Proceedings of the 22nd ACM SIGKDD International Conference on Knowledge Discovery and Data Mining, KDD’16. Association for Computing Machinery; 2016; pp. 1225–1234.
10. Yue X, Wang Z, Huang J, et al.: Graph embedding on biomedical networks: methods, applications and evaluations. Bioinformatics. February 2020; 36(4): 1241–1251. PubMed Abstract | Publisher Full Text | Free Full Text
11. Ng A, Jordan M, Weiss Y: On Spectral Clustering: Analysis and an algorithm. Advances in Neural Information Processing Systems. MIT Press; 2001; volume 14. .
12. Perozzi B, Al-Rfou R, Skiena S: DeepWalk: Online Learning of Social Representations. Proceedings of the 20th ACM SIGKDD international conference on Knowledge discovery and data mining. August 2014; pp. 701–710. arXiv:1403.6652 [cs].
13. Grover A, Leskovec J: node2vec: Scalable Feature Learning for Networks. Technical Report arXiv:1607.00653, arXiv, arXiv:1607.00653 [cs, stat] type: article.July 2016.
14. Hamilton WL, Ying R, Leskovec J: Inductive Representation Learning on Large Graphs, arXiv:1706.02216 [cs, stat].September 2018.
15. Baur B, Schreiber J, Shin J, et al.: Leveraging epigenomes and three-dimensional genome organization for interpreting regulatory variation.August 2021; pp. 2021.08.29.458098. Section: New Results.
16. Lancichinetti A, Fortunato S, Radicchi F: Benchmark graphs for testing community detection algorithms. Phys. Rev. E. October 2008; 78(4): 046110. arXiv:0805.4770 [physics]. PubMed Abstract | Publisher Full Text
17. Kundaje A, Meuleman W, Ernst J, et al.: Siebenthall, Nicholas A. Sinnott-Arms. Integrative analysis of 111 reference human epigenomes. Nature. February 2015; 518(7539): 317–330. Number: 7539 Publisher: Nature Publishing Group. PubMed Abstract | Publisher Full Text | Free Full Text
18. von Mering C , Huynen M, Jaeggi D, et al.: STRING: a database of predicted functional associations between proteins. Nucleic Acids Res. January 2003; 31(1): 258–261. PubMed Abstract | Publisher Full Text | Free Full Text
19. Khan A, Fornes O, Stigliani A, et al.: JASPAR 2018: update of the open-access database of transcription factor binding profiles and its web framework. Nucleic Acids Res. January 2018; 46(D1): D260–D266. PubMed Abstract | Publisher Full Text | Free Full Text
20. Smola AJ, Kondor R: Kernels and Regularization on Graphs.Schölkopf B, Warmuth MK, editors. Learning Theory and Kernel Machines, Lecture Notes in Computer Science. Berlin, Heidelberg: Springer; 2003; pp. 144–158.
21. Lee D-I, Roy S: GRiNCH: simultaneous smoothing and detection of topological units of genome organization from sparse chromatin contact count matrices with matrix factorization. Genome Biol. May 2021; 22(1): 164. PubMed Abstract | Publisher Full Text | Free Full Text
22. Gligorijević V, Malod-Dognin N, Pržulj N: Fuse: multiple network alignment via data fusion. Bioinformatics. April 2016; 32(8): 1195–1203. Publisher Full Text
23. Deng C, He X, Han J, et al.: Graph Regularized Nonnegative Matrix Factorization for Data Representation. IEEE Trans. Pattern Anal. Mach. Intell. August 2011; 33(8): 1548–1560. Conference Name: IEEE Transactions on Pattern Analysis and Machine Intelligence. PubMed Abstract | Publisher Full Text
24. Rohe K, Chatterjee S, Bin Y: Spectral clustering and the high-dimensional stochastic blockmodel. Ann. Stat. August 2011; 39(4). arXiv:1007.1684 [math, stat]. Publisher Full Text
25. Mikolov T, Chen K, Corrado G, et al.: Efficient Estimation of Word Representations in Vector Space, arXiv:1301.3781 [cs].September 2013.
26. Song Z, Baur B, Roy S: Source code and supplementary materials. [Software].2023. Publisher Full Text
27. Song Z, Baur B, Roy S: Benchmarking graph representation learning algorithms for detecting modules in molecular networks. [Dataset]. 2023. Publisher Full Text
28. Newman MEJ: Modularity and community structure in networks. Proc. Natl. Acad. Sci. June 2006; 103(23): 8577–8582. Publisher: Proceedings of the National Academy of Sciences. PubMed Abstract | Publisher Full Text | Free Full Text
29. Rousseeuw PJ: Silhouettes: A graphical aid to the interpretation and validation of cluster analysis. J. Comput. Appl. Math. November 1987; 20: 53–65. Publisher Full Text
30. Ashburner M, Ball CA, Blake JA, et al.: Gene Ontology: tool for the unification of biology. Nat. Genet. May 2000; 25(1): 25–29. PubMed Abstract | Publisher Full Text | Free Full Text
31. Gene Ontology Consortium: The Gene Ontology resource: enriching a GOld mine. Nucleic Acids Res. January 2021; 49(D1): D325–D334. PubMed Abstract | Publisher Full Text | Free Full Text
32. Cunningham F, Allen JE, Allen J, et al.: Ensembl 2022. Nucleic Acids Res. January 2022; 50(D1): D988–D995. PubMed Abstract | Publisher Full Text | Free Full Text
33. Lee D, Sebastian Seung H: Algorithms for Non-negative Matrix Factorization. Advances in Neural Information Processing Systems. MIT Press; 2000; volume 13. .
34. van der Maaten L , Hinton G: Visualizing Data using t-SNE. J. Mach. Learn. Res. 2008; 9(86): 2579–2605.
35. Barrio-Hernandez I, Schwartzentruber J, Shrivastava A, et al.: Network expansion of genetic associations defines a pleiotropy map of human cell biology. Nat. Genet. March 2023; 55(3): 389–398. Number: 3 Publisher: Nature Publishing Group. PubMed Abstract | Publisher Full Text | Free Full Text
36. Jia P, Zhao Z: Network-assisted analysis to prioritize GWAS results: principles, methods and perspectives. Hum. Genet. February 2014; 133(2): 125–138. PubMed Abstract | Publisher Full Text | Free Full Text
37. Sollis E, Mosaku A, Abid A, et al.: The NHGRI-EBI GWAS Catalog: knowledgebase and deposition resource. Nucleic Acids Res. January 2023; 51(D1): D977–D985. PubMed Abstract | Publisher Full Text | Free Full Text
38. Lee C, Wilkinson DJ: A review of stochastic block models and extensions for graph clustering. Appl. Netw. Sci. December 2019; 4(1): 1–50. Number: 1 Publisher: SpringerOpen. Publisher Full Text
39. Kazemi SM, Goel R, Jain K, et al.: Representation Learning for Dynamic Graphs: A Survey, arXiv:1905.11485 [cs, stat].April 2020.

Comments on this article Comments (0)

Version 1

VERSION 1 PUBLISHED 07 Aug 2023

Author details Author details

¹ Wisconsin Institutes for Discovery, Madison, Wisconsin, 53715, USA
² Department of Computer Science, University of Wisconsin-Madison, Madison, Wisconsin, 53715, USA
³ Department of Biostatistics and Medical Informatics, University of Wisconsin-Madison, Madison, Wisconsin, 53715, USA

Zhiwei Song
Roles: Formal Analysis, Investigation, Software, Visualization, Writing – Original Draft Preparation

Brittany Baur
Roles: Data Curation, Writing – Review & Editing

Sushmita Roy
Roles: Conceptualization, Methodology, Project Administration, Supervision, Validation, Writing – Review & Editing

Competing interests

No competing interests were disclosed.

Grant information

This work is supported by NHGRI R01 grant #R01- HG010045-01 and James McDonnell Foundation Grant #3194-133-349500-4-AAB5159.

Article Versions (1)

version 1

Published: 07 Aug 2023, 12:941

https://doi.org/10.12688/f1000research.134526.1

Copyright

© 2023 Song Z et al. This is an open access article distributed under the terms of the Creative Commons Attribution License, which permits unrestricted use, distribution, and reproduction in any medium, provided the original work is properly cited.

Download

Export To

metrics

	Views	Downloads
F1000Research	-	-
PubMed Central Data from PMC are received and updated monthly.	-	-

Citations

0

SEE MORE DETAILS

CITE

how to cite this article

Song Z, Baur B and Roy S. Benchmarking graph representation learning algorithms for detecting modules in molecular networks [version 1; peer review: 1 approved, 1 approved with reservations]. F1000Research 2023, 12:941 (https://doi.org/10.12688/f1000research.134526.1)

NOTE: If applicable, it is important to ensure the information in square brackets after the title is included in all citations of this article.

track

receive updates on this article

Track an article to receive email alerts on any updates to this article.

Open Peer Review

Version 1

VERSION 1

PUBLISHED 07 Aug 2023

Views

10

Reviewer Report 21 Sep 2023

Renming Liu, Michigan State University, East Lansing, Michigan, USA

Approved

https://doi.org/10.5256/f1000research.147588.r201156

This paper conducted a systematic study to compare two classes of approaches, shallow network embeddings, and graph neural network-based methods, for their usage in aiding the analysis of molecular networks, such as finding modules related to particular diseases or biological ... Continue reading

This paper conducted a systematic study to compare two classes of approaches, shallow network embeddings, and graph neural network-based methods, for their usage in aiding the analysis of molecular networks, such as finding modules related to particular diseases or biological processes. The authors used well-developed graph embedding methods, including graph Laplacian eigenmaps, deepwalk, node2vec, GraphSAGE, and VGAE. After conducting systematic module detection evaluations using both synthetic and real molecular networks, the authors suggest that shallow graph embedding techniques, particularly the graph Laplacian eigenmaps, perform well in finding modular structures in the networks. GNNs, on the other hand, do not always provide benefits over shallow embedding methods despite their complexities.

Overall, the paper is well written, and the claims made are well aligned with the results presented. However, I have a few questions and suggestions for the authors.

Phenotype-specific diffused network construction: what is the purpose of the two-step diffusion process using regularized Laplacian and heat kernels? Could the authors provide some context or justification for this particular choice of processing instead of just using one diffusion kernel? Does this have any effect on the downstream evaluation?
The link prediction function used for GraphSAGE, and similarly VGAE, is unclear. Particularly, the authors mentioned that “for each noe, positive and negative links are generated via negative sampling and the parameters of the embedding function are learned via stochastic gradient descent”, but how the predictions for and edge is made from the model is unclear.
In equation (6), what is “q” in the summation? Should it be “1” instead?
The first results section title could be more specific. Deep GRL methods provide advantages in what general settings?
It would be beneficial to delve into a detailed discussion regarding the seemingly conflicting results observed in Fig 4.A and Fig.A, particularly concerning the disparities in rankings between VGAE and node2vec across the two metrics - modularity and SI. What are the potential reasons behind these discrepancies and the implications that future studies should consider?
For the network diffusion-based analysis, the authors applied a sparsifying threshold using the mean edge weight. This processing step seems to be one of the most crucial data processing for the embedding methods. Have the authors tried other thresholds besides the default edge weight and see if the overall major conclusion changes? The authors also mentioned that deep GRL methods perform less well when the networks are dense and noisy. Could increasing the sparsifying threshold be one of the solutions to further improve the GRL results and make them more on par with shallow embedding methods?
According to the methods section, the GRL embeddings are trained by predicting the presence of edges in the network. Is the edge weight information also being used during the training process in the case of weighted graphs?

Is the work clearly and accurately presented and does it cite the current literature?

Yes
Is the study design appropriate and is the work technically sound?

Yes
Are sufficient details of methods and analysis provided to allow replication by others?

Partly
If applicable, is the statistical analysis and its interpretation appropriate?

Yes
Are all the source data underlying the results available to ensure full reproducibility?

Yes
Are the conclusions drawn adequately supported by the results?

Yes

Competing Interests: No competing interests were disclosed.

Reviewer Expertise: Computational Biology, Network Biology, Graph Representation Learning, Single Cell Analysis

I confirm that I have read this submission and believe that I have an appropriate level of expertise to confirm that it is of an acceptable scientific standard.

CITE

Report a concern

Respond or Comment

Views

18

Reviewer Report 20 Sep 2023

Claude Pasquier, UNS CNRS, Universite Cote d'Azur, Sophia-Antipolis, Provence-Alpes-Côte d'Azur, France

Nina Singlan, I3S, Universite Cote d'Azur, Sophia-Antipolis, Provence-Alpes-Côte d'Azur, France

Approved with Reservations

https://doi.org/10.5256/f1000research.147588.r201155

This article "Benchmarking graph representation learning algorithms for detecting modules in molecular networks" investigates deep and shallow graph representation learning algorithms for gene module detection in molecular networks. The authors compare 5 graph representation learning (GRL) techniques on 4 different ... Continue reading

This article "Benchmarking graph representation learning algorithms for detecting modules in molecular networks" investigates deep and shallow graph representation learning algorithms for gene module detection in molecular networks. The authors compare 5 graph representation learning (GRL) techniques on 4 different datasets, 1 synthetic and 3 real biological networks. The GRL techniques are divided into two categories, shallow and deep, containing 3 and 2 state-of-the-art methods respectively. The authors report that, while deep methods, especially Variational Graph Auto-Encoder (VGAE), perform well on synthetic networks, their performance varies on real networks, depending on the graph's characteristics and evaluation metrics. Shallow methods like Graph Laplacian embedding and node2vec often outperform deep methods in identifying gene modules. The paper concludes that the choice between deep and shallow graph representation learning methods for module detection tasks in biological networks depends on various factors, including the graph's structure and the evaluation metrics used.

The novelty of the article lies in the fact that the authors have specifically tackled the performance evaluation of graph representation learning techniques on biological networks, which is particularly interesting and differs from many other existing studies which focus on social and citation networks. Although the article provides valuable information on the comparison of deep and shallow graph representation learning methods for module detection we have identified some potential limitations or weaknesses of the study.

Major comments

1. One significant issue with this paper is its heavy reliance on K-Means clustering as the sole evaluation metric for graph embeddings. The authors benchmark various graph representation learning algorithms and draw conclusions about embedding quality based on K-Means performance. However, it is well-known that clustering methods can be highly dataset-dependent, as is the choice of embedding method. As shown in Woma & Ngo (2019)¹, the quality of clustering depends on both the embedding and clustering methods. The paper cannot assert, as it does, that examining K-Means results is a comprehensive measure of embedding quality. The authors should consider testing other clustering methods and discussing the results.

2. Another important concern is the use by the authors of a network generator that preserves a certain community structure. Although the topology of the generated graphs may resemble social graphs to some extent, it is by no means certain that they accurately represent real biological networks. Some studies show that biological networks constitute a special case with very specific characteristics, particularly in the way the communities are formed (Gutiérrez-Bunster et al. 2014)². This could perhaps explain why the results obtained on artificial and real biological graphs are different. It would be beneficial to discuss how this choice of synthetic data generation relates to the characteristics of real biological networks.

3. Following on from the previous remark, it is regrettable that the metrics used are classic clustering metrics. Since the interest of this work is to compare LRM methods with graphs that have different properties from the graphs generally used in the literature, wouldn't it make sense to judge them with different metrics?

4. The title of the article suggests that the authors are carrying out a study evaluating the performance of graph representation learning methods on molecular networks, but they focus their study on cell-type-specific networks. Although these networks are important in molecular biology, they do not cover the full diversity of biological networks, and the results may not be generalizable to other types of molecular networks. Here again, the article would benefit from addressing the limitations of the comparative analyses carried out and the difficulties of generalizing them.

5. The authors tested different methods on artificial networks generated with Lancichinetti-Fortunato-Radicchi (LFR) graph generator, setting the number of nodes to 1000, the average degree of nodes K = 10, 25, 50 and 100, the exponent for degree distribution γ = 2, the exponent for community size distribution β = 1, and the mixing parameter μ = 0.1 and 0.5. So there are 8 different networks, listed in Table 1. Next, clustering results are presented for α (μ? see minor comments) equals to 0.1 and 0.5 (figure 2). It seems that the results obtained for each value of k have been averaged. This does not give a detailed view of the results for the different configurations. Since the authors present 8 test datasets, they should give the results for each one. If this is due to space constraints, they could include the detailed results as supplemental data.

6. The authors are testing the methods on artificial networks of 1000 nodes, which is small for a biological network. The authors should add benchmarks on larger networks and discuss the performances of the algorithms.

7. The description of the cell-type specific networks and phenotype-specific diffused networks is unclear. It is not evident whether the creation of these networks is part of the work described in this paper or if it was performed in the paper of Baur et al. The paper should clarify this point.

8. The paper evaluates a relatively small set of deep and shallow graph representation learning algorithms. There are numerous other algorithms available in this field, and the selection may not represent the full spectrum of possibilities. The authors should either include a wider range of algorithms or explain how the selected algorithms are representative of existing methods.

9. The evaluation using GO enrichment involves counting enriched terms but doesn't consider group size, which can impact the results. In the article, there's no data on the size of the clusters obtained; could the authors go into a little more detail, mentioning the size of the clusters and their distribution?

10. Furthermore, the metrics used to indicate the relevance of clusters according to their GO annotation (the number of clusters enriched with a GO term, the number of terms enriched in any cluster and the distribution of the number of clusters in which a term is enriched) do not seem enough in our view. The authors need to provide a more detailed biological analysis.

Minor comments

1. The paper introduces the concepts of deep and shallow embedding quite late, on page 5, with a reference to Hamilton et al. This crucial terminology and distinction should be introduced earlier in the paper to enhance reader comprehension.

2. The mixing parameter is referred to as μ on pages 3 and 4, similar to the notation used in Lancichinetti et al. However, it appears to be identified as α in the rest of the paper, including the tables. This inconsistency should be rectified for clarity.

3. The variable k is first used to describe the average degree of the nodes before becoming the number of clusters used by the K-Means algorithm. This dual use of k can lead to confusion and should be clarified.

4. This sentence doesn't seem to be well constructed: "The protein-protein network is not cell type specific and combined it with cell type-specific TF-gene regulatory interactions."

5. The objective function is optimized with batch gradient descent with a batch size of 256 and step size of 0.005. => The objective function is optimized with batch gradient descent with a batch size of 256 and a step size of 0.005.

6. This yields the optimization objective function that maximizes Pr(uk∣∣Φ(v)), where ϕ(v), the embedding of node v and uk is a neighbor node => This yields the optimization objective function that maximizes Pr(uk∣∣Φ(v)), where ϕ(v) is the embedding of node v and uk is a neighbor node

7. Zenodo: Underlying data for’Benchmarking [...]. => Zenodo: Underlying data for ’Benchmarking [...].

Is the work clearly and accurately presented and does it cite the current literature?

Yes
Is the study design appropriate and is the work technically sound?

Partly
Are sufficient details of methods and analysis provided to allow replication by others?

Yes
If applicable, is the statistical analysis and its interpretation appropriate?

Yes
Are all the source data underlying the results available to ensure full reproducibility?

Yes
Are the conclusions drawn adequately supported by the results?

Yes

References

1. Woma J, Ngo K: Comparisons of Community Detection Algorithms in the YouTube Network. CS 224W: Machine Learning with Graphs, Stanford University. 2019. Reference Source
2. Gutiérrez-Bunster T, Stege U, Thomo A, Taylor J: How do biological networks differ from social networks? (an experimental study). 2014 IEEE/ACM International Conference on Advances in Social Networks Analysis and Mining (ASONAM 2014), Beijing, China. 2014. 744-751 Publisher Full Text | Reference Source

Competing Interests: No competing interests were disclosed.

Reviewer Expertise: Computer science, computational biology

We confirm that we have read this submission and believe that we have an appropriate level of expertise to confirm that it is of an acceptable scientific standard, however we have significant reservations, as outlined above.

CITE

Report a concern

Respond or Comment

Comments on this article Comments (0)

Version 1

VERSION 1 PUBLISHED 07 Aug 2023

Open Peer Review

Reviewer Status

Reviewer Reports

	Invited Reviewers
	1	2
Version 1 07 Aug 23	read	read

Claude Pasquier, Universite Cote d'Azur, Sophia-Antipolis, France

Nina Singlan, Universite Cote d'Azur, Sophia-Antipolis, France
Renming Liu, Michigan State University, East Lansing, USA

Comments on this article

All Comments(0)

Add a comment

Sign up for content alerts

Browse by related subjects

Back to all reports

Reviewer Report

10 Views

21 Sep 2023 | for Version 1

Renming Liu, Michigan State University, East Lansing, Michigan, USA

10 Views Cite this report Responses(0)

Approved

This paper conducted a systematic study to compare two classes of approaches, shallow network embeddings, and graph neural network-based methods, for their usage in aiding the analysis of molecular networks, such as finding modules related to particular diseases or biological processes. The authors used well-developed graph embedding methods, including graph Laplacian eigenmaps, deepwalk, node2vec, GraphSAGE, and VGAE. After conducting systematic module detection evaluations using both synthetic and real molecular networks, the authors suggest that shallow graph embedding techniques, particularly the graph Laplacian eigenmaps, perform well in finding modular structures in the networks. GNNs, on the other hand, do not always provide benefits over shallow embedding methods despite their complexities.

Overall, the paper is well written, and the claims made are well aligned with the results presented. However, I have a few questions and suggestions for the authors.

Phenotype-specific diffused network construction: what is the purpose of the two-step diffusion process using regularized Laplacian and heat kernels? Could the authors provide some context or justification for this particular choice of processing instead of just using one diffusion kernel? Does this have any effect on the downstream evaluation?
The link prediction function used for GraphSAGE, and similarly VGAE, is unclear. Particularly, the authors mentioned that “for each noe, positive and negative links are generated via negative sampling and the parameters of the embedding function are learned via stochastic gradient descent”, but how the predictions for and edge is made from the model is unclear.
In equation (6), what is “q” in the summation? Should it be “1” instead?
The first results section title could be more specific. Deep GRL methods provide advantages in what general settings?
It would be beneficial to delve into a detailed discussion regarding the seemingly conflicting results observed in Fig 4.A and Fig.A, particularly concerning the disparities in rankings between VGAE and node2vec across the two metrics - modularity and SI. What are the potential reasons behind these discrepancies and the implications that future studies should consider?
For the network diffusion-based analysis, the authors applied a sparsifying threshold using the mean edge weight. This processing step seems to be one of the most crucial data processing for the embedding methods. Have the authors tried other thresholds besides the default edge weight and see if the overall major conclusion changes? The authors also mentioned that deep GRL methods perform less well when the networks are dense and noisy. Could increasing the sparsifying threshold be one of the solutions to further improve the GRL results and make them more on par with shallow embedding methods?
According to the methods section, the GRL embeddings are trained by predicting the presence of edges in the network. Is the edge weight information also being used during the training process in the case of weighted graphs?

Is the work clearly and accurately presented and does it cite the current literature?

Yes
Is the study design appropriate and is the work technically sound?

Yes
Are sufficient details of methods and analysis provided to allow replication by others?

Partly
If applicable, is the statistical analysis and its interpretation appropriate?

Yes
Are all the source data underlying the results available to ensure full reproducibility?

Yes
Are the conclusions drawn adequately supported by the results?

Yes

Competing Interests

No competing interests were disclosed.

Reviewer Expertise

Computational Biology, Network Biology, Graph Representation Learning, Single Cell Analysis

I confirm that I have read this submission and believe that I have an appropriate level of expertise to confirm that it is of an acceptable scientific standard.

Respond to this report

Responses (0)

Back to all reports

Reviewer Report

18 Views

20 Sep 2023 | for Version 1

Claude Pasquier, UNS CNRS, Universite Cote d'Azur, Sophia-Antipolis, Provence-Alpes-Côte d'Azur, France

Nina Singlan, I3S, Universite Cote d'Azur, Sophia-Antipolis, Provence-Alpes-Côte d'Azur, France

18 Views Cite this report Responses(0)

Approved With Reservations

This article "Benchmarking graph representation learning algorithms for detecting modules in molecular networks" investigates deep and shallow graph representation learning algorithms for gene module detection in molecular networks. The authors compare 5 graph representation learning (GRL) techniques on 4 different datasets, 1 synthetic and 3 real biological networks. The GRL techniques are divided into two categories, shallow and deep, containing 3 and 2 state-of-the-art methods respectively. The authors report that, while deep methods, especially Variational Graph Auto-Encoder (VGAE), perform well on synthetic networks, their performance varies on real networks, depending on the graph's characteristics and evaluation metrics. Shallow methods like Graph Laplacian embedding and node2vec often outperform deep methods in identifying gene modules. The paper concludes that the choice between deep and shallow graph representation learning methods for module detection tasks in biological networks depends on various factors, including the graph's structure and the evaluation metrics used.

The novelty of the article lies in the fact that the authors have specifically tackled the performance evaluation of graph representation learning techniques on biological networks, which is particularly interesting and differs from many other existing studies which focus on social and citation networks. Although the article provides valuable information on the comparison of deep and shallow graph representation learning methods for module detection we have identified some potential limitations or weaknesses of the study.

Major comments

1. One significant issue with this paper is its heavy reliance on K-Means clustering as the sole evaluation metric for graph embeddings. The authors benchmark various graph representation learning algorithms and draw conclusions about embedding quality based on K-Means performance. However, it is well-known that clustering methods can be highly dataset-dependent, as is the choice of embedding method. As shown in Woma & Ngo (2019)¹, the quality of clustering depends on both the embedding and clustering methods. The paper cannot assert, as it does, that examining K-Means results is a comprehensive measure of embedding quality. The authors should consider testing other clustering methods and discussing the results.

2. Another important concern is the use by the authors of a network generator that preserves a certain community structure. Although the topology of the generated graphs may resemble social graphs to some extent, it is by no means certain that they accurately represent real biological networks. Some studies show that biological networks constitute a special case with very specific characteristics, particularly in the way the communities are formed (Gutiérrez-Bunster et al. 2014)². This could perhaps explain why the results obtained on artificial and real biological graphs are different. It would be beneficial to discuss how this choice of synthetic data generation relates to the characteristics of real biological networks.

3. Following on from the previous remark, it is regrettable that the metrics used are classic clustering metrics. Since the interest of this work is to compare LRM methods with graphs that have different properties from the graphs generally used in the literature, wouldn't it make sense to judge them with different metrics?

4. The title of the article suggests that the authors are carrying out a study evaluating the performance of graph representation learning methods on molecular networks, but they focus their study on cell-type-specific networks. Although these networks are important in molecular biology, they do not cover the full diversity of biological networks, and the results may not be generalizable to other types of molecular networks. Here again, the article would benefit from addressing the limitations of the comparative analyses carried out and the difficulties of generalizing them.

5. The authors tested different methods on artificial networks generated with Lancichinetti-Fortunato-Radicchi (LFR) graph generator, setting the number of nodes to 1000, the average degree of nodes K = 10, 25, 50 and 100, the exponent for degree distribution γ = 2, the exponent for community size distribution β = 1, and the mixing parameter μ = 0.1 and 0.5. So there are 8 different networks, listed in Table 1. Next, clustering results are presented for α (μ? see minor comments) equals to 0.1 and 0.5 (figure 2). It seems that the results obtained for each value of k have been averaged. This does not give a detailed view of the results for the different configurations. Since the authors present 8 test datasets, they should give the results for each one. If this is due to space constraints, they could include the detailed results as supplemental data.

6. The authors are testing the methods on artificial networks of 1000 nodes, which is small for a biological network. The authors should add benchmarks on larger networks and discuss the performances of the algorithms.

7. The description of the cell-type specific networks and phenotype-specific diffused networks is unclear. It is not evident whether the creation of these networks is part of the work described in this paper or if it was performed in the paper of Baur et al. The paper should clarify this point.

8. The paper evaluates a relatively small set of deep and shallow graph representation learning algorithms. There are numerous other algorithms available in this field, and the selection may not represent the full spectrum of possibilities. The authors should either include a wider range of algorithms or explain how the selected algorithms are representative of existing methods.

9. The evaluation using GO enrichment involves counting enriched terms but doesn't consider group size, which can impact the results. In the article, there's no data on the size of the clusters obtained; could the authors go into a little more detail, mentioning the size of the clusters and their distribution?

10. Furthermore, the metrics used to indicate the relevance of clusters according to their GO annotation (the number of clusters enriched with a GO term, the number of terms enriched in any cluster and the distribution of the number of clusters in which a term is enriched) do not seem enough in our view. The authors need to provide a more detailed biological analysis.

Minor comments

1. The paper introduces the concepts of deep and shallow embedding quite late, on page 5, with a reference to Hamilton et al. This crucial terminology and distinction should be introduced earlier in the paper to enhance reader comprehension.

2. The mixing parameter is referred to as μ on pages 3 and 4, similar to the notation used in Lancichinetti et al. However, it appears to be identified as α in the rest of the paper, including the tables. This inconsistency should be rectified for clarity.

3. The variable k is first used to describe the average degree of the nodes before becoming the number of clusters used by the K-Means algorithm. This dual use of k can lead to confusion and should be clarified.

4. This sentence doesn't seem to be well constructed: "The protein-protein network is not cell type specific and combined it with cell type-specific TF-gene regulatory interactions."

5. The objective function is optimized with batch gradient descent with a batch size of 256 and step size of 0.005. => The objective function is optimized with batch gradient descent with a batch size of 256 and a step size of 0.005.

6. This yields the optimization objective function that maximizes Pr(uk∣∣Φ(v)), where ϕ(v), the embedding of node v and uk is a neighbor node => This yields the optimization objective function that maximizes Pr(uk∣∣Φ(v)), where ϕ(v) is the embedding of node v and uk is a neighbor node

7. Zenodo: Underlying data for’Benchmarking [...]. => Zenodo: Underlying data for ’Benchmarking [...].

Is the work clearly and accurately presented and does it cite the current literature?

Yes
Is the study design appropriate and is the work technically sound?

Partly
Are sufficient details of methods and analysis provided to allow replication by others?

Yes
If applicable, is the statistical analysis and its interpretation appropriate?

Yes
Are all the source data underlying the results available to ensure full reproducibility?

Yes
Are the conclusions drawn adequately supported by the results?

Yes

References

1. Woma J, Ngo K: Comparisons of Community Detection Algorithms in the YouTube Network. CS 224W: Machine Learning with Graphs, Stanford University. 2019. Reference Source
2. Gutiérrez-Bunster T, Stege U, Thomo A, Taylor J: How do biological networks differ from social networks? (an experimental study). 2014 IEEE/ACM International Conference on Advances in Social Networks Analysis and Mining (ASONAM 2014), Beijing, China. 2014. 744-751 Publisher Full Text | Reference Source

Competing Interests

No competing interests were disclosed.

Reviewer Expertise

Computer science, computational biology

We confirm that we have read this submission and believe that we have an appropriate level of expertise to confirm that it is of an acceptable scientific standard, however we have significant reservations, as outlined above.

Respond to this report

Responses (0)

[1] 1. Barabási A-L, Oltvai ZN: Network biology: understanding the cell’s functional organization. Nat. Rev. Genet. February 2004; 5(2): 101–113. Number: 2 Publisher: Nature Publishing Group. Publisher Full Text

[2] 2. Das S, Chakrabarti S: Classification and prediction of protein-protein interaction interface using machine learning algorithm. Sci. Rep. January 2021; 11(1): 1761. Number: 1 Publisher: Nature Publishing Group. PubMed Abstract | Publisher Full Text | Free Full Text

[3] 3. Mitra K, Carvunis A-R, Ramesh SK, et al.: Integrative approaches for finding modular structure in biological networks. Nat. Rev. Genet. October 2013; 14(10): 719–732. Number: 10 Publisher: Nature Publishing Group. PubMed Abstract | Publisher Full Text | Free Full Text

[4] 4. Zhang D, Yin J, Zhu X, et al.: Network Representation Learning: A Survey. Technical Report arXiv:1801.05852, arXiv, July 2018. arXiv:1801.05852 [cs, stat] type: article.

[5] 5. Muzio G, O’Bray L, Borgwardt K: Biological network analysis with deep learning. Brief. Bioinform. March 2021; 22(2): 1515–1530. PubMed Abstract | Publisher Full Text | Free Full Text

[6] 6. Hamilton WL, Ying R, Leskovec J: Representation Learning on Graphs: Methods and Applications. Technical Report arXiv:1709.05584, arXiv, arXiv:1709.05584 [cs] type: article. April 2018.

[7] 7. Kipf TN, Welling M: Variational Graph Auto-Encoders, arXiv:1611.07308 [cs, stat].November 2016.

[8] 8. Kipf TN, Welling M: Semi-Supervised Classification with Graph Convolutional Networks, arXiv:1609.02907 [cs, stat].February 2017.

[9] 9. Wang D, Peng C, Zhu W: Structural Deep Network Embedding. Proceedings of the 22nd ACM SIGKDD International Conference on Knowledge Discovery and Data Mining, KDD’16. Association for Computing Machinery; 2016; pp. 1225–1234.

[10] 10. Yue X, Wang Z, Huang J, et al.: Graph embedding on biomedical networks: methods, applications and evaluations. Bioinformatics. February 2020; 36(4): 1241–1251. PubMed Abstract | Publisher Full Text | Free Full Text

[11] 11. Ng A, Jordan M, Weiss Y: On Spectral Clustering: Analysis and an algorithm. Advances in Neural Information Processing Systems. MIT Press; 2001; volume 14. .

[12] 12. Perozzi B, Al-Rfou R, Skiena S: DeepWalk: Online Learning of Social Representations. Proceedings of the 20th ACM SIGKDD international conference on Knowledge discovery and data mining. August 2014; pp. 701–710. arXiv:1403.6652 [cs].

[13] 13. Grover A, Leskovec J: node2vec: Scalable Feature Learning for Networks. Technical Report arXiv:1607.00653, arXiv, arXiv:1607.00653 [cs, stat] type: article.July 2016.

[14] 14. Hamilton WL, Ying R, Leskovec J: Inductive Representation Learning on Large Graphs, arXiv:1706.02216 [cs, stat].September 2018.

[15] 15. Baur B, Schreiber J, Shin J, et al.: Leveraging epigenomes and three-dimensional genome organization for interpreting regulatory variation.August 2021; pp. 2021.08.29.458098. Section: New Results.

[16] 16. Lancichinetti A, Fortunato S, Radicchi F: Benchmark graphs for testing community detection algorithms. Phys. Rev. E. October 2008; 78(4): 046110. arXiv:0805.4770 [physics]. PubMed Abstract | Publisher Full Text

[17] 17. Kundaje A, Meuleman W, Ernst J, et al.: Siebenthall, Nicholas A. Sinnott-Arms. Integrative analysis of 111 reference human epigenomes. Nature. February 2015; 518(7539): 317–330. Number: 7539 Publisher: Nature Publishing Group. PubMed Abstract | Publisher Full Text | Free Full Text

[18] 18. von Mering C , Huynen M, Jaeggi D, et al.: STRING: a database of predicted functional associations between proteins. Nucleic Acids Res. January 2003; 31(1): 258–261. PubMed Abstract | Publisher Full Text | Free Full Text

[19] 19. Khan A, Fornes O, Stigliani A, et al.: JASPAR 2018: update of the open-access database of transcription factor binding profiles and its web framework. Nucleic Acids Res. January 2018; 46(D1): D260–D266. PubMed Abstract | Publisher Full Text | Free Full Text

[20] 20. Smola AJ, Kondor R: Kernels and Regularization on Graphs.Schölkopf B, Warmuth MK, editors. Learning Theory and Kernel Machines, Lecture Notes in Computer Science. Berlin, Heidelberg: Springer; 2003; pp. 144–158.

[21] 21. Lee D-I, Roy S: GRiNCH: simultaneous smoothing and detection of topological units of genome organization from sparse chromatin contact count matrices with matrix factorization. Genome Biol. May 2021; 22(1): 164. PubMed Abstract | Publisher Full Text | Free Full Text

[22] 22. Gligorijević V, Malod-Dognin N, Pržulj N: Fuse: multiple network alignment via data fusion. Bioinformatics. April 2016; 32(8): 1195–1203. Publisher Full Text

[23] 23. Deng C, He X, Han J, et al.: Graph Regularized Nonnegative Matrix Factorization for Data Representation. IEEE Trans. Pattern Anal. Mach. Intell. August 2011; 33(8): 1548–1560. Conference Name: IEEE Transactions on Pattern Analysis and Machine Intelligence. PubMed Abstract | Publisher Full Text

[24] 24. Rohe K, Chatterjee S, Bin Y: Spectral clustering and the high-dimensional stochastic blockmodel. Ann. Stat. August 2011; 39(4). arXiv:1007.1684 [math, stat]. Publisher Full Text

[25] 25. Mikolov T, Chen K, Corrado G, et al.: Efficient Estimation of Word Representations in Vector Space, arXiv:1301.3781 [cs].September 2013.

[26] 26. Song Z, Baur B, Roy S: Source code and supplementary materials. [Software].2023. Publisher Full Text

[27] 27. Song Z, Baur B, Roy S: Benchmarking graph representation learning algorithms for detecting modules in molecular networks. [Dataset]. 2023. Publisher Full Text

[28] 28. Newman MEJ: Modularity and community structure in networks. Proc. Natl. Acad. Sci. June 2006; 103(23): 8577–8582. Publisher: Proceedings of the National Academy of Sciences. PubMed Abstract | Publisher Full Text | Free Full Text

[29] 29. Rousseeuw PJ: Silhouettes: A graphical aid to the interpretation and validation of cluster analysis. J. Comput. Appl. Math. November 1987; 20: 53–65. Publisher Full Text

[30] 30. Ashburner M, Ball CA, Blake JA, et al.: Gene Ontology: tool for the unification of biology. Nat. Genet. May 2000; 25(1): 25–29. PubMed Abstract | Publisher Full Text | Free Full Text

[31] 31. Gene Ontology Consortium: The Gene Ontology resource: enriching a GOld mine. Nucleic Acids Res. January 2021; 49(D1): D325–D334. PubMed Abstract | Publisher Full Text | Free Full Text

[32] 32. Cunningham F, Allen JE, Allen J, et al.: Ensembl 2022. Nucleic Acids Res. January 2022; 50(D1): D988–D995. PubMed Abstract | Publisher Full Text | Free Full Text

[33] 33. Lee D, Sebastian Seung H: Algorithms for Non-negative Matrix Factorization. Advances in Neural Information Processing Systems. MIT Press; 2000; volume 13. .

[34] 34. van der Maaten L , Hinton G: Visualizing Data using t-SNE. J. Mach. Learn. Res. 2008; 9(86): 2579–2605.

[35] 35. Barrio-Hernandez I, Schwartzentruber J, Shrivastava A, et al.: Network expansion of genetic associations defines a pleiotropy map of human cell biology. Nat. Genet. March 2023; 55(3): 389–398. Number: 3 Publisher: Nature Publishing Group. PubMed Abstract | Publisher Full Text | Free Full Text

[36] 36. Jia P, Zhao Z: Network-assisted analysis to prioritize GWAS results: principles, methods and perspectives. Hum. Genet. February 2014; 133(2): 125–138. PubMed Abstract | Publisher Full Text | Free Full Text

[37] 37. Sollis E, Mosaku A, Abid A, et al.: The NHGRI-EBI GWAS Catalog: knowledgebase and deposition resource. Nucleic Acids Res. January 2023; 51(D1): D977–D985. PubMed Abstract | Publisher Full Text | Free Full Text

[38] 38. Lee C, Wilkinson DJ: A review of stochastic block models and extensions for graph clustering. Appl. Netw. Sci. December 2019; 4(1): 1–50. Number: 1 Publisher: SpringerOpen. Publisher Full Text

[39] 39. Kazemi SM, Goel R, Jain K, et al.: Representation Learning for Dynamic Graphs: A Survey, arXiv:1905.11485 [cs, stat].April 2020.

Benchmarking graph representation learning algorithms for detecting modules in molecular networks

Abstract

Keywords

Introduction

Figure 1. Graph representation learning (GRL) for module detection on graphs.

Methods

Datasets

Table 1. Network characteristics on Lancichinetti-Fortunato-Radicchi (LFR) benchmark graph.

Table 2. The number of communities when constructing eight groups of synthetic network datasets with five networks each in total.

Table 3. The network characteristics of 55 cell-type specific networks and phenotype-specific networks, including the average of nodes, the average of edges, and the average density of networks.

Graph representation learning algorithms

(1)

(2)

Table 4. The optimal hyper-parameter setting used in the comparison of different algorithms for the simulated and real biological networks.

(3)

(4)

(5)

Defining clusters from learned representations

Evaluation metrics

(6)

(7)

(8)

(9)

(10)

Gene ontology enrichment analysis

Results

Deep graph representation learning methods offer some advantages over shallow representation learning on synthetic benchmarks

Figure 2. Comparison of deep and shallow graph representation learning methods on simulated networks.

Deep GRL methods do not offer significant benefits over shallow methods for defining modules on gene networks

Figure 3. Comparison of deep and shallow graph representation learning methods on 55 cell type-specific networks.

Deep GRL methods for network-based interpretation of GWAS phenotypes

Figure 4. Comparison of deep and shallow GRL methods for ASD phenotype-specific networks.

Figure 5. Comparison of deep and shallow graph representation learning methods on CAD phenotype-specific networks.

Discussion

Conclusions

Data availability

Underlying data

Software availability

Acknowledgements

References

Comments on this article Comments (0)

Open Peer Review

Comments on this article Comments (0)

Open Peer Review

Reviewer Status

Reviewer Reports

Comments on this article

Browse by related subjects

Competing Interests Policy

Stay Updated