Keywords
Fiscal Sustainability, Nonlinear Granger Causality, Regime Changes, Kalman Filter, Markov Switching Model, SADC, Extra Trees Regressor
This study aims to evaluate the changes in the sustainability of fiscal policies in South Africa and selected Southern African Development Community (SADC) countries by employing the Kalman filter and Markov switching model and further overcome the limitations of previous studies by considering the impact of previously neglected variables.
The paper utilizes regression analysis, the Kalman filter, and the Markov switching model. By analysing GDP data for SADC countries, regime shifts are estimated, and fiscal sustainability is evaluated. To enhance numerical adaptation, a random walk state space model is incorporated into the conventional Kalman filter.
This study significantly contributes to academia and the field of economics in South Africa by addressing previous research limitations on fiscal policy sustainability. It incorporates previously omitted variables and employs advanced estimation techniques, such as the random walk-based Kalman filter and Markov switching model, to provide a comprehensive understanding of fiscal sustainability in South Africa and selected SADC countries. The findings offer valuable recommendations for policymakers and government authorities, including the necessity of fiscal consolidation to reduce debt, adherence to specified borrowing ratios, and reforms to increase savings and overall fiscal sustainability in the SADC region.
The random walk-based Kalman filter exhibits superior numerical adaptation compared to the conventional approach. An analysis of normalized financial impacts reveals significant variations in fiscal sustainability among SADC countries and different GDP categories. Countries with higher GDPs generally exhibit greater financial sustainability, while those with lower GDPs face more challenges in this regard.
Advanced estimation techniques like the random walk-based Kalman filter and Markov switching model offer critical insights into fiscal sustainability in South Africa and the broader SADC region. They further provide a more accurate and comprehensive analysis, revealing significant variations in fiscal stability across different GDP categories.
Fiscal Sustainability, Nonlinear Granger Causality, Regime Changes, Kalman Filter, Markov Switching Model, SADC, Extra Trees Regressor
For years, the global economy has been facing a crisis, and the burden of debt has continued to increase. Nandelenga (2021) suggests that in certain macroeconomic conditions, monetary and fiscal actions may create more problems than they solve. Recent financial crises, along with the impact of the COVID-19 pandemic on South Africa and other SADC countries, have once again highlighted the importance of fiscal policy for policymakers and academics (Nandelenga, 2021). Insufficient fiscal management can raise doubts about the appropriateness of fiscal policy (Pierre and Creel, 2016). Economists argue that as debt, debt distress, and the need for debt relief become more prevalent, fiscal policy authorities are forced to relinquish policy discretion and breach policy norms (Mickiewicz, 2021). These conditions are becoming increasingly common as individuals face financial difficulties and seek relief from their debt burdens.
De Rugy and Salmon (2022) defines fiscal sustainability as the government’s ability to remain solvent without resorting to tax hikes, expenditure cuts, or deficit monetization. Fiscal sustainability is a crucial component of an economy and, in turn, sustainable economic development. Following the financial crisis, South Africa’s public debt increased significantly due to the implementation of large-scale expenditure programs to support the economy (Nzimande and Ngalawa, 2019). In the third quarter of 2019, public debt accounted for 61.5% of the country’s gross domestic product (GDP).
The global economic recession of 2008–2009 exerted pressure on many economies worldwide, including South Africa. Government debt and fiscal deficits increased as monetary policy failed to stimulate and sustain economic growth. Output growth experienced a significant decline from 2008 (3.6%) to 2009 (-1.7%) (International Monetary Fund (IMF), 2017). A recovery was observed in 2010 with a growth rate of 2.9%, only to decline again by 1.2% in 2015. During the years following the global financial crisis, South Africa’s primary balance positions declined by -3.1% in 2009 and -2.7% in 2010. The primary deficit trend persisted from 2010 to 2017, albeit gradually narrowing from 2.8% in 2010 to -0.6% in 2017. South Africa’s debt-to-GDP ratio significantly increased from 22.2% in the fourth quarter of 2008 to 46% in the third quarter of 2016. From the fourth quarter of 2011 until the third quarter of 2016, the country’s economic situation remained weak, with an average primary balance ratio of -1.3% (South African Reserve Bank, 2017). The slow pace of economic growth placed significant pressure on public finances, necessitating fiscal consolidation to stabilize public debt and reduce fiscal deficits. Despite the worsening financial situation, reduced economic growth, and inadequate regulation, South Africa’s financial sector maintained good financial management, fiscal policy credibility, and transparency in its budgetary systems (Calitz et al., 2016). The government demonstrated fiscal credibility by increasing the primary surplus and reducing the primary deficit as a response to the growing public debt. South Africa’s monetary policy measures for managing fiscal debt and deficits rely on strict adherence to financial management mechanisms and the national budget process.
Numerous studies examining the sustainability of fiscal policy in South Africa have predominantly used linear approaches that assume linear relationships between fiscal variables (Ganyaupfu, 2019; Ganyaupfu and Robinson, 2019; Phiri, 2019; Ndlovu, 2021; Sanusi, 2020; Sanusi, Eita et al., 2021; Plaatjies, 2022). However, based on empirical studies conducted globally in other countries and regions.
There is substantial evidence that fiscal relationships are nonlinear, as demonstrated by Nganga et al. (2018). Despite the limited number of studies conducted by Phiri (2019) and Woldu (2020) using nonlinear methods in South Africa, these studies did not consider the impact of temporary government spending or the public spending gap, as highlighted by Bui (2019), which could have implications for fiscal policy sustainability. Additionally, past studies on fiscal policy sustainability in South Africa did not adequately account for the role of monetary policy instruments in a nonlinear manner, despite partially capturing the effect of monetary policy in a linear approach using the vector error correction model (VECM) (Ganyaupfu, 2019; Ganyaupfu & Robinson, 2019). Addressing these research gaps is the objective of this study.
One of the employed methods is the Kalman filter estimation strategy, introduced by Kalman (2020). Time-varying models have been widely utilized in numerous studies as effective approaches to evaluating fiscal policy. The initial application of the model involved smooth transition error correction, as proposed by Cipollini (2001) and McMillan (2005). Another model used in this research is threshold regression, which assesses fiscal sustainability. Arestis et al. (2004) employed this model in their case study to examine the fiscal sustainability of selected South African countries and the USA. This study focuses on evaluating the fiscal sustainability of the South African economy compared to other SADC states. The argument put forth is that the existing evidence is insufficient, as most studies adopt a time-invariant approach to monetary policy, resulting in portraying the results as long-term averages. However, ideological economic theory contradicts this notion by considering fiscal sustainability as something that can either maintain solvency or fail over decades (Pierre and Creel, 2016). Different political regimes may have varying monetary and fiscal policies driven by distinct goals. Therefore, employing a method that accounts for factors subject to temporal changes is a better strategy than averaging fiscal response function variables across the entire cohort (De Rugy and Salmon, 2022). In this study, a dynamic approach was employed using a governmental model of fiscal policy to examine fiscal policy and sustainability. This technique demonstrates that the overall situation varies. It is important to note that among the examined nations, Angola, Botswana, and Malawi meet the formal criterion for fiscal sustainability, while Mozambique has a poorly recorded fiscal policy history. On the other hand, Zimbabwe and Namibia lack long-term stability and have experienced exponential increases in debt.
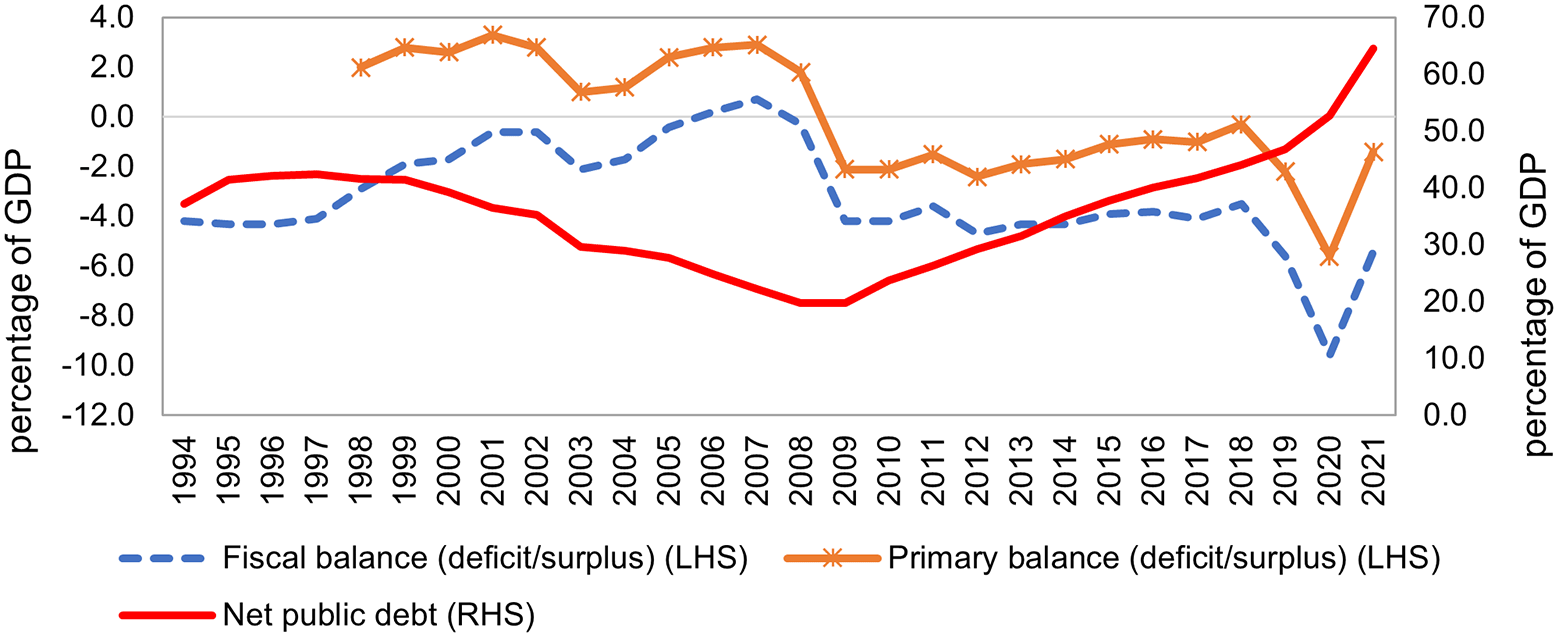
Between 2009 and 2021, South Africa grappled with continual deficits in both its fiscal and primary balance-to-output ratios. Examining Figure 1, it becomes evident that throughout this timeframe, the primary deficit ratio exhibited fluctuations, hitting its lowest point of -5.6% (intensified by the advent of the global COVID-19 pandemic) and its zenith of -0.3% in 2018. Similarly, the fiscal deficit ratio oscillated between -9.6% in 2020 and -3.5% in 2018. Despite the challenges posed by the deterioration in both fiscal and primary balances, the proportion of net public debt to output embarked on an unbroken upward journey, escalating from 19.8% in 2009 to 64.6% in 2021. These persistent fiscal trends in South Africa give rise to substantial and enduring risks concerning the nation’s fiscal well-being and longevity. See Małgorzata & Krzysztof (2020) for the impact of COVID in other countries.
This section offers a comprehensive review of the empirical literature concerning fiscal policy sustainability. In Section 2.2, the chapter introduces the definition of fiscal policy sustainability, followed by an exploration of the key approaches to analysing fiscal sustainability in Section 2.3. The conceptual framework is discussed in Section 2.4, while the empirical literature is examined in Section 2.5.
Numerous studies in the field of public finance management provide different definitions of fiscal policy sustainability based on various metrics or indicators that assess fiscal policy performance (Bui, 2019; Ganyaupfu, 2019). These definitions are formulated based on different economic theories and relevant schools of thought for specific macroeconomic framework designs (Ramos-Herrera & Prats, 2020). Some earlier studies emphasize these aspects (Nxumalo & Hlophe, 2018; Beqiraj et al., 2018; Feld et al., 2020; Ramos-Herrera & Prats, 2020).
Chalk and Hemming (2000) define fiscal sustainability as a condition where public debt either remains stable or increases without posing risks to the solvency of public finances. They highlight the importance of distinguishing between gross public debt and net public debt, as well as variations in these indicators. Despite the view that gross debt may misrepresent the government’s fiscal sustainability position, most empirical analyses in developing economies still use gross debt instead of net debt (Chalk & Hemming, 2000).
The primary reason behind this supposition is that governments usually have financial assets that can be quickly liquidated to repay public debt. Gross debt is calculated as the total stock of the government’s outstanding financial liabilities, often measured at market value (Hemming, 1999; Chalk & Hemming, 2000). Therefore, careful consideration is necessary when deciding whether to use gross debt or net debt.
Pradhan (2019) highlights two primary approaches for analysing fiscal policy sustainability: Domar’s approach and the solvency approach.
2.3.1 Domar’s approach
Domar’s (1944) approach involves calculating the primary balance-to-output ratio (z t) necessary to stabilize the current debt-to-output ratio (d t) at a particular level, along with a specific growth-interest rate difference. The cost of government borrowing (r) and the rate of growth in national production (n) are set exogenously and independently of fiscal policy administration. Domar’s approach can be represented algebraically as follows:
d = D/GDP (government debt-to-output ratio), ge = G/GDP (government non-interest expenditure-to-output ratio), rr = RR/GDP (government revenue-to-output ratio), z = Z/GDP (government primary balance-to-output ratio or z = ge - rr), (inflation), (real output growth rate), n (annual nominal growth rate, n = +), D/D = r (annual growth rate of D excluding off-budget government obligations and fiscal deficits).
When the budgetary deficit or surplus is zero, the debt can rise at a rate equal to the interest charged on the debt. In this case, the dynamic government or public debt (d) equation can be formulated in three different forms:
If the primary balance-to-GDP ratio is not zero, equation (2.1) can be expressed as:
Alternatively, equation (2.2) can be expressed as:
When the monetization of government deficits (seigniorage, denoted by s) as a percentage of GDP is integrated into equation (2.2), it becomes:
The condition for debt ratio stabilization requires d to be equal to or less than zero
Setting equation (2.2) equal to zero, the stabilizing value of d becomes:
From the above computations, two conditions can ensure debt stabilization:
1. If (+) > r, the debt-to-output ratio can decrease over time, and fiscal policy sustainability may not be at risk when the primary deficit-to-output ratio is constant. Alternatively, if the primary deficit grows, the debt ratio can still be stabilized by a growth rate of nominal output exceeding the interest rate.
2. If (+) r, equation (2.2) implies that d can be reduced over time if z + d (r - -) < 0. This suggests that generating reasonable levels of the primary surplus is crucial to lessening the burden of accumulated public debt. When monetization of fiscal deficits occurs, both z and r > (+) may be useful for government stabilization and fiscal solvency.
To empirically operationalize Domar’s method of public debt, information on the cost of borrowing (r), real national output growth rate (), inflation rate (), and primary balance (z) is necessary. These variables can be used to calculate the stabilizing public debt ratio (d*) based on equation (2.6). According to Domar’s approach, the interest rate-growth differential (r + n) plays a crucial role in exerting either downward or upward pressure on the public borrowing ratio, depending on whether r > n or r n (Pradhan, 2019).
2.3.2 Method
Solvency method
The solvency method, sometimes referred to as the present value budget constraint (PVBC), is based on the intertemporal budget constraint (IBC) of the national government (Pradhan, 2019). This method considers a fiscal policy sustainable if the government can repay all its existing commitments by generating future primary surpluses. In an economically efficient environment, fiscal policy is sustainable when the discounted value of future primary surpluses is at least equal to the stock of public debt (Buiter & Patel, 1992; Pradhan, 2019).
The theoretical foundation for the solvency approach is established using the following equations:
Factoring in the nominal output growth rate at period t in equation (2.8) yields:
The solvency condition is satisfied when the present value budget constraint is met.
Equation (2.10) implies that the government’s total debt must be supported by future expected positive primary balances in present value terms. The government’s fiscal reaction follows a Markov switching rule, represented by equation (2.11), where E represents the episode-switching factor indicating the reaction outcome of the public debt ratio on the primary surplus ratio based on fiscal regimes (2.11). A sustainable episode is denoted by E, and an unsustainable episode is denoted by E’.
The sustainability of fiscal policy has been extensively examined in various countries and regions worldwide, employing diverse fiscal variables and estimation methods. Studies commonly utilize time-series data on a quarterly or annual basis for individual countries and panel data for regions, employing linear or nonlinear estimation methods (Gopalratnam et al., 2017). It is worth noting that the majority of empirical studies on fiscal sustainability have predominantly focused on developed and emerging countries and regions, with fewer studies conducted in developing countries. The distribution of these empirical studies is discussed in a disaggregated manner, beginning with a global perspective (Table 1), followed by the African continent (Table 2), regional analysis (Southern African Development Community, SADC) (Table 3), and finally, at the country level, specifically South Africa (Table 4).
| Study | Country/region | Sample period | Methodology | Result(s) |
|---|---|---|---|---|
| Afonso & Coelho (2022) | Eurozone states | 1995–2020 | Panel cointegration | Sustainable |
| Aldama & Creel (2019) | USA | 1940–2016 | Markov switching | Sustainable |
| Aldama & Creel (2020) | France | 1965–2013 | Markov-switching | Sustainable |
| Akar (2019) | Turkey | 2001–2018 | FM-OLS | Unsustainable |
| Ikhsan & Virananda (2021) | Indonesia | 1976–2019 | ARDL | Sustainable |
| Beqiraj, Fedeli & Forte (2018) | OECD countries | 1991–2015 | Mean group regression: EC | Unsustainable |
| Bui (2019) | Asia | 1999–2017 | CCEMG | Unsustainable |
| Khadan (2019) | Caribbean countries | 1991–2017 | Panel IV-FE, Pooled OLS, MG, PMG, LSDV | Sustainable |
| Phiri (2019) | BRICS countries | 1980–2016: Brazil 1999–2016: Russia 1974–2016: India 1982–2016: China 1972–2015: SA | Nonlinear unit root tests (FFF) | Sustainable: Brazil Sustainable: Russia Unsustainable: India Unsustainable: China Sustainable: SA |
| Ramos-Herrera & Prats (2020) | European countries | 2000–2019 | Panel ARDL | Unsustainable (long-run) and Sustainable (short-run period) |
| Study | Country/region | Sample period | Methodology | Result(s) |
|---|---|---|---|---|
| Nganga, Chevallier & Ndiritu (2018) | Kenya, and East African countries | 1963–2014 | Markov switching, ANN and SETAR | Sustainable and unsustainable states |
| Otonne, A. & Oyenuga (2019) | Nigeria | 2005: Q1 – 2016: Q4 | Modified ADF test, cointegration tests | Unsustainable |
| Nyambe & Matundu (2020) | Namibia | 1980–2019 | VECM, and ARDL | Sustainable |
| Nyambe & Kaulihowa (2020) | Zambia | 1990–2017 | OLS regressions | Unsustainable |
| Study | Country/region | Sample period | Methodology | Result(s) |
|---|---|---|---|---|
| Nxumalo & Hlope (2018) | Swaziland | 1980–2015 | DOLS, VECM | Unsustainable |
| Ndlovu (2021) | Swaziland | 1960–2017 | OLS | Sustainable |
| Mackiewicz (2021) | Nine southern African nations | 1960–2020 | Time-varying | Mixed |
| Study | Country/region | Sample period | Methodology | Result(s) |
|---|---|---|---|---|
| Ganyaupfu (2019) | South Africa | 1997: Q4 – 2016: Q3 | VECM | Sustainable |
| Ganyaupfu & Robinson (2019) | South Africa | 1994: Q4 – 2016: Q2 | VECM | Sustainable |
| Phiri (2019) | South Africa | 1960: Q1 – 2016: Q2 | MTAR model | Weak sustainability |
| Woldu (2020) | South Africa | 1960: Q – 2019: Q | Markov switching model | Sustainable |
| Ndlovu (2021) | South Africa | 1960–2017 | OLS | Sustainable |
| Sanusi, Eita & Meyer (2021) | South Africa | 2009: M1 –2019: M12 | Bayesian VAR | Unsustainable |
2.4.1 Global literature on fiscal sustainability
In this section, we delve into the empirical literature examining regime changes and fiscal sustainability across various countries on a global scale. Table 1 below offers a comprehensive summary of the research conducted on sampled periods of fiscal sustainability worldwide. The table provides information on the researchers involved, the countries and states (regions) studied, the sampled periods, the methodology employed, and the key findings about fiscal sustainability.
Several studies have examined the sustainability of fiscal policy across different countries and regions, providing valuable insights into the relationship between public debt and primary balance. Beqiraj et al. (2018) focused on OECD countries from 1991 to 2015 and found significant negative effects of public debt on the primary balance, indicating unsustainable public finances.
Aldama and Creel (2016, 2019) investigated fiscal policy sustainability in the USA from 1940 to 2016, using the Markov switching rule. Although the government periodically stabilized its public debt, the study revealed that reactions towards debt stabilization were limited over the entire period. Nevertheless, the study concluded that tight contractions in policy were sufficient to ensure long-term debt sustainability.
Akar (2019) analysed fiscal sustainability in Turkey from 2001 to 2018 and found significant negative effects of public debt on the primary balance. The study employed the fully modified ordinary least squares (FM-OLS) method and threshold models to estimate the long-run nonlinear fiscal reaction, suggesting that Turkey’s fiscal policy was unsustainable during the sample period.
Bui (2019) examined the fiscal sustainability of 22 Asian developing countries from 1999 to 2017 and found evidence of unsustainable fiscal policies. The study employed the common correlated effects mean group (CCEMG) estimator to estimate the fiscal reaction function.
Aldama and Creel (2020) studied fiscal sustainability regimes in France from 1965 to 2013. By employing the Markov-switching rule and integrating exogenous variables such as temporary government spending, the output gap, and the financial crisis as dummy variables, the study concluded that France’s fiscal policy adhered to the No-Ponzi game rule, indicating sustainability.
Khadan (2019) analysed the fiscal sustainability of 10 Caribbean countries from 1991 to 2017, employing various estimators such as panel instrumental variable (IV), fixed effects (FE), pooled ordinary least squares (POLS), mean group (MG), pooled mean group (PMG), and least squares dummy variable (LSDV). The results indicated that these countries’ fiscal policies satisfied the intertemporal budget constraint condition, signifying sustainability.
Phiri (2019) assessed the sustainability of fiscal policies in BRICS countries, analysing data for specific periods for each country. The results indicated that fiscal policies in Brazil, Russia, and South Africa were sustainable, while those in India and China were deemed unsustainable.
Ramos-Herrera and Prats (2020) examined fiscal sustainability in a panel of 20 European countries from 2000 to 2019, employing the panel auto-regressive distributed lag (ARDL) model. The study concluded that while public debt had a significant and positive impact on the government’s primary balance ratio in the short run, it had the opposite effect in the long run, suggesting sustainability in the short term but unsustainability in the long term.
Ikhsan and Virananda (2021) analysed the sustainability of fiscal policy in Indonesia from 1976 to 2019 and found a significant positive reaction of the primary surplus ratio to an increase in the public debt ratio in both the short and long run. This indicates the presence of a sustainable fiscal policy in the country.
Afonso and Coelho (2022) investigated the sustainability of public finances in 19 Eurozone nations from 1995 to 2020. Their findings, based on panel cointegration, indicated that the public finances of these countries were consistent with the Ricardian condition, thereby suggesting the sustainability of public finances.
These studies provide valuable insights into the sustainability of fiscal policies in various countries and regions, shedding light on the interplay between public debt, primary balance, and long-term sustainability.
Nganga et al. (2018) conducted a study to investigate fiscal policy regime changes in Kenya, comparing them with selected East African nations using nonlinear Granger causalities. The analysis utilized annual data from 1963 to 2014 and employed the Markov switching model, the artificial neural networks (ANN) model, and the self-exciting threshold autoregressive (SETAR) model. The results from the Markov switching estimates revealed the presence of sustainable and unsustainable regimes in Kenya’s fiscal policy, each lasting an average of four years and exerting dominance. However, the fiscal policy in Kenya was classified as procyclical as the non-Ponzi game condition was weakly held. Sensitivity tests based on regime analysis indicated that the presence of an unsustainable regime, lasting approximately as long as the sustainable regime, posed a threat to the long-term sustainability of fiscal policy in Kenya.
In another study, Otonne and Oyenuga (2019) assessed the sustainability of Nigeria’s fiscal policy using monthly data covering the period from 2005: Q1 to 2016: Q4. The findings derived from various tests such as the modified augmented Dicky-Fuller (ADF) test, Engle-Granger cointegration test, Bounds cointegration test, and Johansen cointegration test all indicated that the trends in the government’s tax revenue and spending exhibited a continuous divergence beyond acceptable bounds (Johansen, 1988). As a result, it was concluded that Nigeria’s fiscal policy did not satisfy the intertemporal budget constraint conditions, indicating its unsustainability during the respective sample period.
The fiscal sustainability of SADC countries is summarised in Table 2 while the log transformation of the same dataset is summarised in Table 3. Log transformation helps in normalizing data that is skewed, especially when the data has a long tail. This makes the distribution more symmetric and closer to a normal distribution, which is a common assumption for many statistical analyses and models (see Table 6).
2.4.2 SADC regional literature on fiscal sustainability (excluding South Africa)
This section explores the empirical literature on regime changes and fiscal sustainability across various countries in the South African Development Community (SADC) Region, excluding South Africa. Table 4 offers a summary of the research conducted on sampled periods of fiscal sustainability within the SADC Region. The table includes information on the researchers, the countries and states (regions) studied, the sampled period, the methodology employed, and the findings related to fiscal sustainability.
Nxumalo and Hlophe (2018) analysed the sustainability of fiscal policy in Swaziland, using data from 1980 to 2015. The study examined variables such as public debt, primary balance, and tax gap as output ratios. Findings obtained through dynamic ordinary least squares (DOLS) and vector error correction model (VECM) estimations indicate that Swaziland’s fiscal policy was deemed unsustainable.
In a study by Mackiewicz (2021), the sustainability of fiscal policy in nine southern African nations belonging to the Southern African Development Community (SADC) block was analysed using data from 1960 to 2020. The countries included in the study were Angola, Botswana, Eswatini, Lesotho, Namibia, Malawi, South Africa, Zambia, and Zimbabwe. Results from the time-varying approach revealed mixed outcomes for different countries. Namibia and Zimbabwe were found to have violated the solvency condition in their fiscal reaction functions, indicating unsustainable fiscal policies. On the other hand, Angola, Botswana, and Malawi exhibited sustainable fiscal policies. In the cases of South Africa, Eswatini, and Zambia, the solvency condition was fulfilled, but explosive public debt paths raised concerns about the long-term ability of these governments to manage public debt growth effectively.
Ndlovu (2021) estimated a fiscal policy reaction function for Swaziland, as well as other countries in the Southern African Customs Union (SACU) block, using annual data from 1960 to 2017. The dependent variable in the reaction function was government expenditure, while the independent variables included lagged public debt, lagged government expenditure, and output. The ordinary least squares (OLS) method was employed for the estimation. The results indicated that Swaziland’s government spending adjusted to its public debt levels, suggesting that the fiscal policy in the country was sustainable.
2.4.3 South African literature on fiscal sustainability
This section presents empirical literature on regime changes and fiscal sustainability surveyed South Africa.
Table 4 below provides a summary of research carried out on sampled periods of fiscal sustainability in South Africa. It presents the researcher, the country/state (region) studied, the sampled period, the methodology used and the findings on fiscal sustainability.
Literature has examined fiscal sustainability in South Africa, with studies conducted by Ganyaupfu (2014) and Ganyaupfu & Robinson (2019) using sample data from 1994: Q4 to 2016: Q2. The results of the fiscal reaction function, estimated through the vector error correction model (VECM), provide strong evidence that South Africa’s fiscal policy was sustainable. However, Phiri (2019) conducted an analysis using sample data from 1960: Q1 to 2016: Q2 and employed the MTAR model, which indicated that the country’s fiscal policy was weakly sustainable.
Sanusi et al. (2021) examined the impact of government expenditure shocks on tax revenue and total public debt in South Africa from 2009:M1 to 2019:M12, utilizing the Bayesian VAR. The results from the impulse response analysis demonstrated that a shock in government spending led to a deterioration in tax revenue and an increase in total public debt, suggesting an unsustainable fiscal policy during the respective sample period.
Woldu (2022) empirically assessed the sustainability of South Africa’s fiscal policy using quarterly data from 1960: Q1 to 2019: Q3. The fiscal reaction function tested the response of the budget deficit ratio to changes in the total government debt-to-output ratio, employing the Markov switching dynamic regression (MSDR) model. The empirical results indicated that South Africa’s fiscal policy aligned with the intertemporal budget conditions, satisfying the no-Ponzi game condition. This confirmed that the policy was indeed sustainable, with a longer duration compared to the unsustainable regime.
Existing studies on the sustainability of fiscal policy in South Africa have predominantly employed linear approaches, assuming linear relationships between fiscal variables. Studies conducted by Ganyaupfu (2019), Ganyaupfu & Robinson (2019), Phiri (2019), Ndlovu (2021), and Sanusi et al. (2021) fall into this category. However, evidence from studies conducted in other countries and regions globally, such as Nganga et al. (2018), Mackiewicz (2021), and Aldama & Creel (2019, 2020), suggests that fiscal relationships are nonlinear. In addition, previous studies in South Africa did not account for the impact of temporary government spending or the public spending gap, as highlighted by Bui (2019), which could have implications for fiscal policy sustainability. Furthermore, the role of monetary policy instruments has not been adequately addressed in a nonlinear manner, despite being partially captured in a linear approach by Ganyaupfu (2019) and Ganyaupfu & Robinson (2019) using the VECM. Addressing these research gaps is the objective of this study.
This research obtained data from a set of methods by contacting quantitative analyses. Because the ability to maintain fiscal stability is not typically a quality that would remain constant over several decades, it was necessary to put more emphasis on the set of methods that would make it possible for fiscal authorities to behave in a way that would make sustainability an untenable rather than a perpetual characteristic. One of the methods used is the Kalman Filter estimation strategy. Many studies have been using time-varying models as effective methods for evaluating fiscal policy. The model used was initially applied by Cipollini (2000) and it involved smooth transition error correction (McMillan, 2005). The second model was a threshold regression that is used to assess fiscal sustainability and had been applied by Arestis et al. (2004) in their case study to examine the fiscal sustainability of the selected South African countries and the U.S.
The application of Kalman filters is a widely used strategy for addressing cost estimation models with time-varying parameters. This technique, developed by Swerling (1959) and Kalman (1960), has found applications in various fields, including time-series econometrics, route planning, global positioning, fault detection, and machine learning (Kalman, 1960). It provides a flexible framework for modelling complex time-series data, allowing for the inclusion of multiple latent random variables and time-varying statistical metrics.
The Kalman filter estimation strategy is based on a state space model consisting of two equations: a measurement equation and a state equation. The measurement equation describes the relationship between the observed variables ( and ) and the unobserved state variables (). The state equation captures the dynamics of the unobserved state variables a_1,…, a_n. In this paper, we represent this dynamic model, considering parameters that change over time, using the following measurement and state equations:
Here, a is a constant parameter, and B and H are matrices containing the parameters in the measurement and state equations, respectively. is a column vector of observations of the dependent variable, and is the column vector of independent variables. _t is a vector of unobservable variables that influence the dependent variable. Additionally, w_t represents a vector of disturbance terms in the measurement equation, and v_t is the disturbance term or error term in the state equation. The function represents the matrix of valued functions; az_t represents a vector of valued functions; and represents a matrix of elements that are functions of independent variables, .
Before estimating equations (Afonso & Coelho, 2022) and (Akar, 2019), it is important to consider the possibility of parameter instability in the variable of interest. This can be achieved by conducting the Hansen (1992) test, which tests the null hypothesis of parameter stability. After performing this test, the time-varying parameters of the relationship between fiscal sustainability and regime switching, taking into account other control variables, can be specified as follows:
In equation (2.12), FS represents the dependent variable, fiscal sustainability, which refers to the government’s ability to meet its financial obligations on time. It is measured by the ratio of surplus to national output (GDP). RS represents the independent variable, Regime Switching, which is measured by the ratio of net borrowing or net lending to GDP. X represents the control variables included in the model, which have an impact on the dependent variable, fiscal sustainability. These control variables may include the public debt ratio, the government revenue ratio, the government expenditure ratio, and the output gap. is the error term, encompassing all other factors that are not explicitly accounted for in the model but influence the dependent variable.
Autoregression is one classical model of forecasting based on time series data (Granger and Anderson, 1978; Granger and Terasvirta, 1993; Yao et al., 2000; Stelzer, 2008; Malgorzata and Echaust, 2020). It refers to a regression model based on itself (“auto”). It takes p number of time steps before the one to be forecast and fits a regression model based on that. Or, in other words, predict the current value based on the previous values. Time steps before the one to be forecasted are referred to as lags, so one could also say, predict the current value based on p lags. The number of lags is called the order of the model.
The autoregressive model is represented as follows:
When selecting the Markov switching model, we performed estimations using different states and included covariates such as lagged GDP. Additionally, we estimated the autoregressive Markov switching model. Based on diagnostic test results and a lower information criterion for the MDSR compared to the autoregressive model, we determined that the dynamic model is appropriate. This model allows for rapid adjustment after the Markov process changes state and is suitable for high-frequency data, such as our estimation data.
To specify the process in state sss at time ttt, we can write the MSDR model as:
We assume that the Markov chain s is ergodic, with transition probabilities between states defined as:
The set of six parameters (two transition probabilities, two trends, and two volatility parameters) is estimated using an expectation-maximization algorithm. Due to the rapid increase in the number of parameters with more states amd relatively small smaple size, we tested a minimum of two states, which seems appropriate. We report robust standard errors to correct for the heteroscedasticity in herent in high-frequency data.
The classificaiton state of states is largely subjective and can be inferred from state-dependent observations. Thus, the two identified states can be classified as “fiancial sustainability” and “non financial sustainability. These names distinguish the regimes aof sustainability in selected SADC Region countries and do no indicate relative sustainability levels compared to ther countries.
Finally, given the estimated transition probabilities, we compute the expected duration duration in each of the two states using the following equation:
After fitting the MSDR model, we use the estimated parameters to predict the evolution of the states over time.
Due to the global economic recession of 2008-2009, many economies in the world faces pressure, and South Africa is no exception. There was an increase in government debt and fiscal deficits as monetary policy failed to spur and maintain economic growth. There was a marked decrease in output growth from 2008 (3.6%) to 2009 (-1.7%) (International Monetary Fund (IMF), 2017). However, a recovery was witnessed in 2010, when a 2.9% growth rate was recorded, only for it to plummet again in 2015 by 1.2%. In the last quarter of the years following the global financial crisis, South Africa’s primary balance positions recorded declines of -3.1% in 2009 and -2.7% in 2010.
The primary deficit trend persisted over the period from 2010 to 2017, even though it gradually narrowed from -2.8% in 2010 to -0.6% in 2017. Since the fourth quarter of 2008, South Africa’s debt-to-GDP ratio has significantly increased from 22.2% to 46% in the third quarter of 2016. From the fourth quarter of 2011 up to the third quarter of 2016, the country’s economic situation remained weak, with an average of -1.3% primary balance ratio being recorded (South African Reserve Bank (2017)). There was concerted pressure on public finances due to the slow pace of economic growth, which meant that there was a need for fiscal consolidation to steady the public debt and reduce fiscal deficits. Regardless of the worsening of the financial situation and reduced economic growth, the country’s financial sector continued to maintain good financial management, fiscal policy credibility, and transparency in its budgetary systems despite the lack of financial regulation (Calitz, Siebrits, & Stuart, 2016). The government maintained fiscal credibility by increasing the primary surplus and reducing the primary deficit as a solution to the increasing public debt. South Africa’s monetary policy measures to manage the fiscal debt and deficits are hinged on strict adherence to financial management mechanisms and the national budget process.
From the start of the 2012/13 financial year, an expenditure limit was introduced so that medium-term expenditures were changed from baselines to numerical targets (Stuart & Dhlamini, 2015). In 2014, a Fiscal Risk Committee was formed by the National Treasury so that it could accelerate the attainment of financial targets (Stuart & Dhlamini, 2015). The 2016 Medium Term Budget Policy Statement (MTBPS) Fisk Risk Statement highlights that South Africa has several institutional strengths that contribute to the promotion of fiscal sustainability, which includes the Public Finance Management Act (PFMA), transparent budget processes reinforced by the Medium Term Expenditure Framework (MTEF), reduced debt financing of liquid long-term debt from domestic currency and domestic bond markets, and deep risks.
The primary premise of this research is that SADC countries will have long-term budgetary sustainability. However, the analysis concludes that, on average, SADC countries are severely indebted despite maintaining fiscal sustainability.
We test this hypothesis using yearly time series data on GDP and government debt (as a percentage of GDP) from the World Bank Development Indicators of 2022 and the International Monetary Fund (IMF) for a 50-year timeframe (1971–2021). To carry out our investigation, we used yearly time series data. The data collection included information from nine SADC member nations. The countries and data intervals were selected based on the data’s availability.
The observations are weighed against the study objectives and hypotheses, which seek to quantify regime transitions and fiscal sustainability in South Africa by comparing nonlinear Granger causalities across a variety of SADC nations. A fixed regression analysis,
A Markov random walk with a focus on South Africa and experiential results connected to the Kalman filter for all SADC countries make up the three aspects of our investigations.
R statistical software (R Core team 2024) has been used since it is frequently regarded as ideal for investigations using time series data because it offers descriptive statistics and inferential techniques.
It also explores some of Python’s efficient and elegant features, which make it a great fit for a range of statistical computing applications. The purpose of this research is to demonstrate how state space models in Kalman filters may be expressed and forecasted using the Python program (Python, 2024). The IMF and World Bank have easy access to the countries’ GDP statistics. With the certainty that the information is accurate, current, and reliable, data was gathered from the World Bank and IMF with the cooperation of the organizations.
The dataset used for all our experiments is presented in Table 5. For the sake of space, only a sample of 9 instances out of a total of 401 is presented. For the full dataset the reader is referred to Mbaye et al., (2018) [Global Debt Database (imf.org)]. For the GDP data the reader is referred to Feenstra et al., (2015) [ Penn World Table version 10.01 - Groningen Growth and Development Centre - GGDC (dataverse.nl)].
The time-series extrapolation model is expanded using auto-regression analysis to add independent variables other than time. Another benefit of regression is its capacity to detect outliers or anomalies in the dataset. Only linear or nonlinear links between two variables may be studied using other approaches, such as correlational rather than time. Another benefit of regression is its capacity to detect outliers or anomalies in the dataset. Only linear or nonlinear links between two variables may be studied using other approaches, such as correlation. This job makes use of nineteen regressors against six performance metrics. Mean absolute error (MAE), mean squared error (MSE), root mean squared error (RMSE), correlation coefficient (R2), root mean squared logarithmic error (RMSLE), and mean absolute percentage error (MAPE) are the six performance measurements.
4.1.1 Experimental results (Markov AutoRegression- based model Analysis)
This section presents empirical literature on regime changes and fiscal sustainability surveyed South Africa.
Overall, the extra tree regressor was shown to be the most robust technique across most performance evaluation measures, demonstrating that these techniques are an effective strategy when dealing with financial sustainability using GDP as an indicator. The worst performance is by the passive aggressive regressor, and this is across all the six performance measures. In terms of computation, the dummy regressor proved to be the least costly (Table 7). Two more boosting-based regressor techniques (gradient and extreme gradient) achieve good results. The Bayesian ridge performs better than the passive-aggressive regressor.
This function trains all models in the model library and scores them using k-fold cross-validation for metric evaluation. To ensure robustness, the experiments were repeated 10 times, and the results were averaged for a comprehensive comparison. The primary goal of this comparison was to assess the effectiveness of the Markov switching approach in evaluating fiscal sustainability, with the extra tree regressor achieving superior accuracy rates. Table 8 highlights the cross-validation impact of the top-performing evaluation model developed using machine learning and feature-selection algorithms. The extra trees regressor model generally performs better across most performance measures without cross-validation folds, except for MAPE, where it has the lowest error at the 8th fold. Additionally, the model shows the least standard deviation for mean-squared error, indicating consistent performance.
The residuals were used to assess the model’s performance and ability to fit the data (Figures 1 and 2). The residuals do not appear to be spread equally over the expected value range. As a result, the correlation coefficient is rather small. This might be attributed to the partial erasure of traits that were previously governed by individual countries or the SADC Region. As a result, various assessment indicators were researched.
Figure 3 shows that the year appears to be the most important factor in predicting the financial sustainability of the SADC members analysed. The second most significant component is the real GDP.
The feature importance plot (Figure 4) provides a visual representation of the relative significance of each feature in a machine learning model. By assessing the importance of individual features, we can gain insights into which variables have the most substantial impact on the model’s predictions. The plot highlights the features that contribute most significantly to the predictive power of the model. Year shows the highest importance score, which suggests that Year has a strong influence on the model’s predictions. The least most important feature is the country Botswana.
The Kalman filter is a powerful tool used in time series analysis and control systems to estimate the state of a dynamic system from a series of incomplete and noisy measurements. In the context of this study on fiscal sustainability in South Africa and selected SADC countries, the Kalman filter is applied to assess the stability and predict future states of fiscal indicators.
The time-series extrapolation model is expanded using auto-regression analysis to add independent variables other than time. Another benefit of regression is its capacity to detect outliers or anomalies in the dataset. Only linear or nonlinear links between two variables may be studied using other approaches, such as correlational rather than time. Another benefit of regression is its capacity to detect outliers or anomalies in the dataset. Only linear or nonlinear links between two variables may be studied using other approaches, such as correlation. This job makes use of nineteen regressors against six performance metrics. Mean absolute error (MAE), mean squared error (MSE), root mean squared error (RMSE), correlation coefficient (R2), root mean squared logarithmic error (RMSLE), and mean absolute percentage error (MAPE) are the six performance measurements.
The Kalman filter
Important things to remember: the KF (Kalman filter) assumes linear dynamics for the true state xk with k ∈ N, and Normally distributed errors.
The first equation is the process equation for the true state, where Fk is the state transition function (or matrix), and wk is the process noise with covariance Qk.
The second equation is the measurement equation, where zk is the measurement of the true state xk. The term Hk is the measurement function (or matrix), and vk is the measurement noise with covariance Rk.
The Kalman filter overview is given in Figure 5.
Table 9 provides descriptive statistics for the variables of interest. Each SADC country has 50 observations for each variable. However, for some countries, the observations are less than 50 because of the missing observations in some years, especially for the Government Debt to GDP Ratio (gov debt GDP ratio). Among the selected SADC countries, on average, the out gap is highest in Angola (0.243), followed by South Africa (0.196).
Exploring the realm of government debt concerning GDP, a distinct trajectory unfolds over the last fifty years. Throughout this extended timeframe, Angola has consistently maintained its position as the most indebted SADC nation, with an average government debt-to-GDP ratio of 73%. Following closely, Lesotho demonstrates a debt-to-GDP ratio of 55%. Among this ensemble of eight SADC countries, Botswana distinctly stands out with the lowest average debt over the past half-century, registering an impressive 19%.
Shifting the lens to a broader perspective encompassing the last five decades, a salient pattern emerges among the consortium of eight designated SADC nations. It’s worth noting that only Angola and South Africa have exhibited an unwavering positive output gap, signifying that their realized economic output has consistently exceeded their potential. This distinct feature sets these economies apart as robust performers due to their sustained capability to function above their potential capacities.
Conversely, the remaining countries within this group have consistently operated below their potential output over the same fifty-year period. Among these nations manifesting negative output gaps, Namibia consistently reports the lowest figure at -0.115, followed successively by Botswana at -0.102, Zambia at -0.072, Lesotho at -0.066, Zimbabwe at -0.055, and lastly, Malawi at -0.029. In summation, Angola emerges as the most proficient at consistently exceeding its potential output, while Malawi consistently ranks as the least effective in harnessing its potential, especially in comparison to the other chosen SADC countries scrutinized in this study.
Figure 5 shows the time series of the output gap of eight selected SADC countries from 1970–2021. Between 1970 and 1980, only Angola and South Africa had a positive output. Between 1980 and 2009, these countries had a negative output gap. From 2009 to 2021, Angola went back to the positive output gap. The majority of the countries (Botswana, Lesotho, Malawi, Namibia, Zambia, and Zimbabwe) that had a negative output gap before 1980 achieved a positive output gap in current years except for Lesotho and Namibia.
The patterns in the ratio of government debt to GDP for a selection of SADC countries are depicted in Figure 6. A comparison with other nations reveals that Zambia had the lowest GDP between 1970 and the late 1990s. From the late 1990s to the early 2000s, Zambia’s GDP ratio surged significantly, reaching a peak of over 200% in 2000. Starting in 2000, Zambia’s debt began a gradual decline until 2005. Across all countries, the GDP-debt ratios have been on an upward trajectory. Among these, Angola showcases the highest debt ratio, while Botswana exhibits the lowest.
The time series data (1970–2019) has been organized as outlined in the provided spreadsheet. Using the Hodrick-Prescott Filter in Python, the policy variable of interest and the gap in output variables have been calculated. This gap is derived as the difference between the logarithm of real GDP and potential real GDP.
The application of the Kalman Filter to assess financial sustainability provides a dynamic and adaptive framework for understanding the fiscal health of a country. This technique allows for real-time estimation and prediction of key economic indicators, which are crucial for assessing financial sustainability. A graphic representation of the results from the Kalman filter, estimated from equations (Afonso & Coelho, 2022) and (Akar, 2019), is presented in Figure 7. This figure portrays the Kalman outcomes for the aggregate of eight selected SADC countries during the period 1970–2019. In the graph, the blue line signifies the outcomes from the measurement equation (equation 1), while the red line represents the results from the state equation.
The x-axis of the graph represents the number of predictions for the output gap during the study period. It’s evident that the filtered series of the output gap in the selected SADC countries consistently aligns with the observed values of the output gap. Furthermore, the Kalman filter tends to project ahead. In simpler terms, although the trends of the filtered and observed data are largely similar, the filter often anticipates the fiscal sustainability observed. Notably, the predictions between the 50th and 150th data points offer a more accurate reflection of the observed values. Overall, the predictions generated by the Kalman filter offer enhanced insight into the fiscal sustainability dynamics of the eight selected SADC countries.
This section presents empirical literature on regime changes and fiscal sustainability surveyed South Africa.
The global economic recession of 2008–2009 didn’t spare South Africa, much like many other economies worldwide. The aftermath saw a surge in government debt and fiscal deficits, revealing the limitations of monetary policy in stimulating and sustaining economic growth. Notably, output growth underwent a stark transformation, dropping from 3.6% in 2008 to a significant decline of -1.7% in 2009, according to the International Monetary Fund (IMF, 2017). A glimpse of recovery emerged in 2010, when growth reached 2.9%, only to take a subsequent hit, plummeting to -1.2% in 2015. Importantly, the immediate aftermath of the global financial crisis triggered substantial fluctuations in South Africa’s primary balance positions—a contraction of -3.1% in 2009 followed by -2.7% in 2010.
This pattern of a persistent primary deficit extended from 2010 to 2017, albeit with a gradual narrowing from -2.8% in 2010 to -0.6% in 2017. Throughout this period, the primary deficit remained a consistent concern. Interestingly, the debt-to-GDP ratio embarked on an upward trajectory in the fourth quarter of 2008, soaring from a baseline of 22.2% to a significant 46% by the third quarter of 2016. From Q4 2011 to Q3 2016, South Africa grappled with a sustained period of economic fragility, characterized by an average primary balance ratio of -1.3%, as reported by the South African Reserve Bank (2017). This prolonged economic sluggishness put immense pressure on public finances, necessitating the implementation of fiscal consolidation to mitigate escalating public debt and curb fiscal deficits.
Even amidst the prevailing financial adversity and economic deceleration, South Africa’s financial sector demonstrated remarkable resilience by upholding sound financial management practices, credible fiscal policies, and transparent budgetary systems. Notably, this commendable financial prudence was maintained even in the absence of stringent financial regulation, as indicated by Calitz, Siebrits, and Stuart (2013). Responding to the mounting public debt, the government adopted measures to uphold fiscal credibility. This was achieved through strategic enhancements to the primary surplus and concerted efforts to rein in the primary deficit. Intriguingly, South Africa’s monetary policy strategies for managing fiscal debt and deficits revolved around a steadfast commitment to financial management mechanisms and the national budgetary process.
Commencing with the 2012/13 fiscal year, South Africa introduced an expenditure ceiling to transition medium-term expenditures from baselines to numerical targets, as noted by Stuart & Dhlamini (2015). Notably, in 2014, the National Treasury took a pivotal step by establishing a Fiscal Risk Committee to expedite the achievement of critical financial targets. Highlighting the nation’s institutional strengths contributing to fiscal sustainability, the 2016 Medium Term Budget Policy Statement (MTBPS) Fiscal Risk Statement emphasized crucial elements, including the Public Finance Management Act (PFMA), a transparent budgetary process fortified by the Medium-Term Expenditure Framework (MTEF), and strategic management of debt financing from domestic sources, including the domestic bond market.
In the context of this analysis, the examination utilized time-series quarterly data spanning the period 1998q3–2018q1 for both the primary balance-to-GDP ratio (B/Y) and the net debt-to-GDP ratio (D/Y). These critical data sets were sourced from the South African Reserve Bank (SARB, 2018), while GDP growth data was acquired from the International Monetary Fund (IMF, 2018). These invaluable datasets formed the basis for computing the output gap using the Hodrick-Prescott filter. Notably, the trends in the primary balance ratio and net public debt ratio were also succinctly depicted in Figure 1.
The net public debt ratio, which compares a country’s total public debt to its GDP, is a vital measure of fiscal health and debt sustainability (Figure 8). During the sample period 1998q1 to 2018q1, the public debt ratio constantly declined from 47.3% in 1998q3 to 21.6% in 2008q2 and continually increased to 47.3% in 2017q3. The primary balance ratio varied between -6.0% in 2012q3 and 7.3% in 1999q1. A rising net public debt ratio indicates that debt is growing faster than the economy, which could signal potential difficulties in managing and repaying debt in the future while a falling debt ratio suggests that the economy is growing at a pace that outstrips debt accumulation, indicating a healthier fiscal position.
Fiscal processes usually transition over time with discreet changes in fiscal policy outcomes. Transitions are bounded over a finite set of latent states according to the Markov process. The processes evolve differently in each episode while the time of transition from one state to another, and durations among transitions across regimes follow a random process. Since the data used were of low frequency and quarterly, the Markov-switching autoregressive method was used to estimate the transition probabilities and the durations of the persistence of each fiscal regime. The model was used on the basis that it accommodates gradual adjustments or smoother changes by modelling transition probabilities as an autoregressive process.
In line with the Markov switching rule, fiscal policy in each time-period t is subject to two regimes defined by. The regime can be either passive (Recardian) or active (non-Recardian). Fiscal policy is deemed passive if the primary balance remains sensitive to variations in debt levels. Conversely, fiscal policy is deemed active if the primary balance ratio is insensitive to changes in the debt levels. The estimated fiscal reaction function was expressed based on the Markov-switching rule to measure the response of the primary balance ratio to changes in the initial debt ratio defined by equation (3.1)
4.4.1 Experimental Results (Markov Random Walk)
The variables of the data set were as follows: country, year, government debt to GDP ratio, RGDP, lnRGDP, and output gap. The country is a category variable, whereas the rest are numeric. The variable lnRGDP looks to be an RGDP logarithm. Based on the analysis of the target variable (output_gap), this research will ignore the modified logarithm variable and an auto-regression analysis is best suited for this data (Table 5).
Within Table 10, a nuanced portrait of fiscal sustainability unfolds, casting a spotlight on South Africa’s adept navigation of a two-state Markov-switching fiscal rule. Beneath the surface, two distinct fiscal regimes emerge, each distinguished by its unique response mechanism linking the primary balance ratio to the ebbs and flows of the debt ratio. In the canvas of the examined period, regime 1 commands our attention, revealing an intriguing correlation: a mere 1% escalation in the initial debt ratio manifests in a notable elevation of nearly 0.5 percentage points in the primary balance ratio. This resolute positive reaction unveils a fiscal landscape characterized by sustainability, where elevated primary balances assume the role of sentinels, curbing the expansion of public debt. Moreover, within this realm, the luminous presence of a positively significant output gap coefficient underscores a harmonious interplay between propitious output gap levels and heightened primary balance ratios. This orchestrated symphony aligns seamlessly with earlier scholarly endeavours such as Ganyaupfu (2019) and Ganyaupfu & Robinson (2019), effectively endorsing the country’s fiscal policy as an astute guardian against the tides of business cycles. This strategic counteraction stands as a bulwark, staunchly guarding against the tide of debt accumulation.
Navigating into regime 2, a distinct narrative unfolds. Here, the coefficient governing the initial debt takes on a converse persona, descending into the realm of negativity while bearing immense consequence. The narrative is crystal clear: a mere 1% escalation in the initial debt ratio precipitates a noticeable erosion of 0.6 percentage points in the primary balance ratio. This sobering shift delineates an unsustainable fiscal trajectory, where a waning in primary balances unfurls a path toward heightened net public debt expansion. However, this regime’s output gap coefficient, though positive, grapples with insignificance. This phenomenon signifies a subdued fiscal counter-cyclicality in the presence of the business cycle’s undulating rhythms, presenting a departure from the vigour observed in the previous regime.
As we delve into the realm of transition probabilities, a captivating tapestry of insights unfurls. The probability of fiscal policy adopting a passive posture (Recardian) in period t-1 and seamlessly transitioning into a sustained stance in period t resonates at approximately 0.85. In parallel, the intriguing panorama of fiscal policy transitioning from an active posture (non-Recardian) in period t-1 and seamlessly sustaining its unsustainable trajectory into the parallel period t commands a probability of approximately 0.67. A panoramic perspective of transitions paints a vivid tableau: the likelihood of fiscal policy transitioning from a sustainable regime to an unsustainable one, though less frequent, materializes at a probability of 0.15, while the inverse odyssey—a shift from an unsustainable regime to one that boasts sustainability—graces the stage with a probability of 0.33.
The overarching goal of this study was to quantify regime changes in South Africa’s fiscal sustainability in comparison to other SADC nations. A quantitative research approach was employed to test theories and evaluate independent variables using regression analysis, the Markov switching model, and the Kalman filter with GDP data from selected SADC nations. The results indicate that extra tree regressors outperform other predictors of financial sustainability. Numerical adaptation analysis reveals that the random walk-based Kalman filter performs better than the standard Kalman filter. The analysis of adjusted financial impacts shows significant disparities among SADC nations and GDP divisions. High-GDP SADC nations appear to have achieved fiscal sustainability, while the opposite holds as well.
The findings highlight that South Africa’s debt stock will continue to dominate the primary balance, emphasizing the need for the government to limit borrowing within prescribed revenue-to-revenue and debt-to-output ratios. Furthermore, the government should implement additional measures to promote higher savings and overall budgetary sustainability. This research recommends that nations and officials adopt sound fiscal policies to achieve credible, countercyclical, and long-term fiscal incentives for sustainable growth in the SADC region. Markov regime switching, the Kalman filter, and the random walk-based Kalman filter can be used to analyse the correlation between sovereign debt and the budget deficit and assess the sustainability of current trajectories.
The research aimed to assess the impact of systemic changes on South Africa’s fiscal sustainability relative to other SADC nations. A quantitative methodology and various econometric and statistical computational tools, including regression analysis, the Markov switching model, and the Kalman filter were employed to analyse GDP data for specified SADC states. The findings reveal that supplementary tree regressors are effective in correlating with financial sustainability, and the random walk-based Kalman filter exhibits superior numerical adaptation compared to the conventional Kalman filter.
The research provides valuable insights into regime changes in fiscal sustainability in South Africa and other SADC states using various economic and statistical modelling approaches. The results underscore the importance of solid fiscal policies and institutional effectiveness, particularly in minimizing government borrowing, to generate long-term fiscal incentives and equitable growth. Policymakers are encouraged to explore the use of extra tree regressors and the random walk-based Kalman filter for more robust fiscal sustainability forecasts.
Various additional disciplines can contribute to and expand the existing knowledge base on the subject in the future. One notable avenue is investigating the long-term sustainability of linear structures in various applications, as this is a crucial consideration in calculations. Regression analysis, the Kalman filter, and the Markov switching model, as used in this study, can be employed for such investigations. Additionally, exploring neglected components in previous studies can provide a more comprehensive understanding of the factors influencing fiscal sustainability.
Future investigations can utilize a Kalman filter-based model or a Markov switching methodology to forecast regime changes in budgetary practices within South Africa and other SADC nations by considering specific contextual scenarios. Nonlinear Granger causality calculations can also be employed to examine the relationship between fiscal sustainability and other macroeconomic variables.
Furthermore, future research could explore measures to curb illicit financial flows, enhance the governance of public finances, and implement proactive fiscal policies to maintain economic equilibrium and mitigate pro-cyclical fiscal policy challenges. These efforts would help prevent the accumulation of unsustainable debt and reduce the need for future debt-restructuring obligations.
The data on public debt was sourced from the Global Debt database provided by the IMF at https://www.imf.org (See Mbaye et al., 2018) [Global Debt Database (imf.org)].
For the GDP data the reader is referred to Feenstra et al., (2015) [ Penn World Table version 10.01 - Groningen Growth and Development Centre - GGDC (dataverse.nl)].
The authors would like to express their heartfelt appreciation to Stellenbosch University’s Faculty of Economic and Management Sciences for their significant institutional assistance during this research study. The author wishes to express his gratitude to Stellenbosch University Business School for enabling his MPhil thesis. Finally, the authors would like to thank the editor and anonymous reviewers for their time and informative criticism during the review process. Their contributions have been critical to improving the quality and rigour of this manuscript.
The authors would also like to thank the Southern African Development Community (SADC), the International Monetary Fund (IMF), the World Bank, and the South African Reserve Bank for their assistance in obtaining the required data.
| Views | Downloads | |
|---|---|---|
| F1000Research | - | - |
|
PubMed Central
Data from PMC are received and updated monthly.
|
- | - |
Provide sufficient details of any financial or non-financial competing interests to enable users to assess whether your comments might lead a reasonable person to question your impartiality. Consider the following examples, but note that this is not an exhaustive list:
Sign up for content alerts and receive a weekly or monthly email with all newly published articles
Already registered? Sign in
The email address should be the one you originally registered with F1000.
You registered with F1000 via Google, so we cannot reset your password.
To sign in, please click here.
If you still need help with your Google account password, please click here.
You registered with F1000 via Facebook, so we cannot reset your password.
To sign in, please click here.
If you still need help with your Facebook account password, please click here.
If your email address is registered with us, we will email you instructions to reset your password.
If you think you should have received this email but it has not arrived, please check your spam filters and/or contact for further assistance.
Comments on this article Comments (0)