Keywords
Aparc label; combination test; false discovery rate; mass-univariate linear model; program comprehension
We are considering the statistical analysis of functional magnetic resonance imaging (fMRI) data. As demonstrated in previous work, grouping voxels into regions (of interest) and carrying out a multiple test for signal detection on the basis of these regions typically leads to a higher sensitivity when compared with voxel-wise multiple testing approaches.
In the case of a multi-subject study, we propose to define the regions for each subject separately based on their individual brain anatomy, represented, e.g., by regional labels. The aggregation of the subject-specific evidence for the presence of signals in the different regions is then performed by means of a combination function for p-values. We validate the proposed methodology with simulated data and apply it to real fMRI data of a hypothesis-driven approach towards identifying brain regions involved in understanding software code.
The results of our simulated data show that our proposed method demonstrated significantly higher power in detecting true activation. Testing our method on real fMRI data, we found that our approach yields overlapping results with a two-stage approach for which two independent experiments are needed, one for defining the regions and one for actual signal detection.
In this paper, we overall demonstrate that our method of utilizing anatomical information is a candidate to provide a more sensitive analysis of fMRI data.
Aparc label; combination test; false discovery rate; mass-univariate linear model; program comprehension
Signal detection in high-dimensional data is a major topic of modern statistics. Typically, structural information like, for instance, (the degree of ) sparsity of the signal is necessary for its detectability and/or (consistent) estimability; see, e.g., Figure 1 in Refs. 13, 47, Chapter 7 in Ref. 50, as well as references therein.
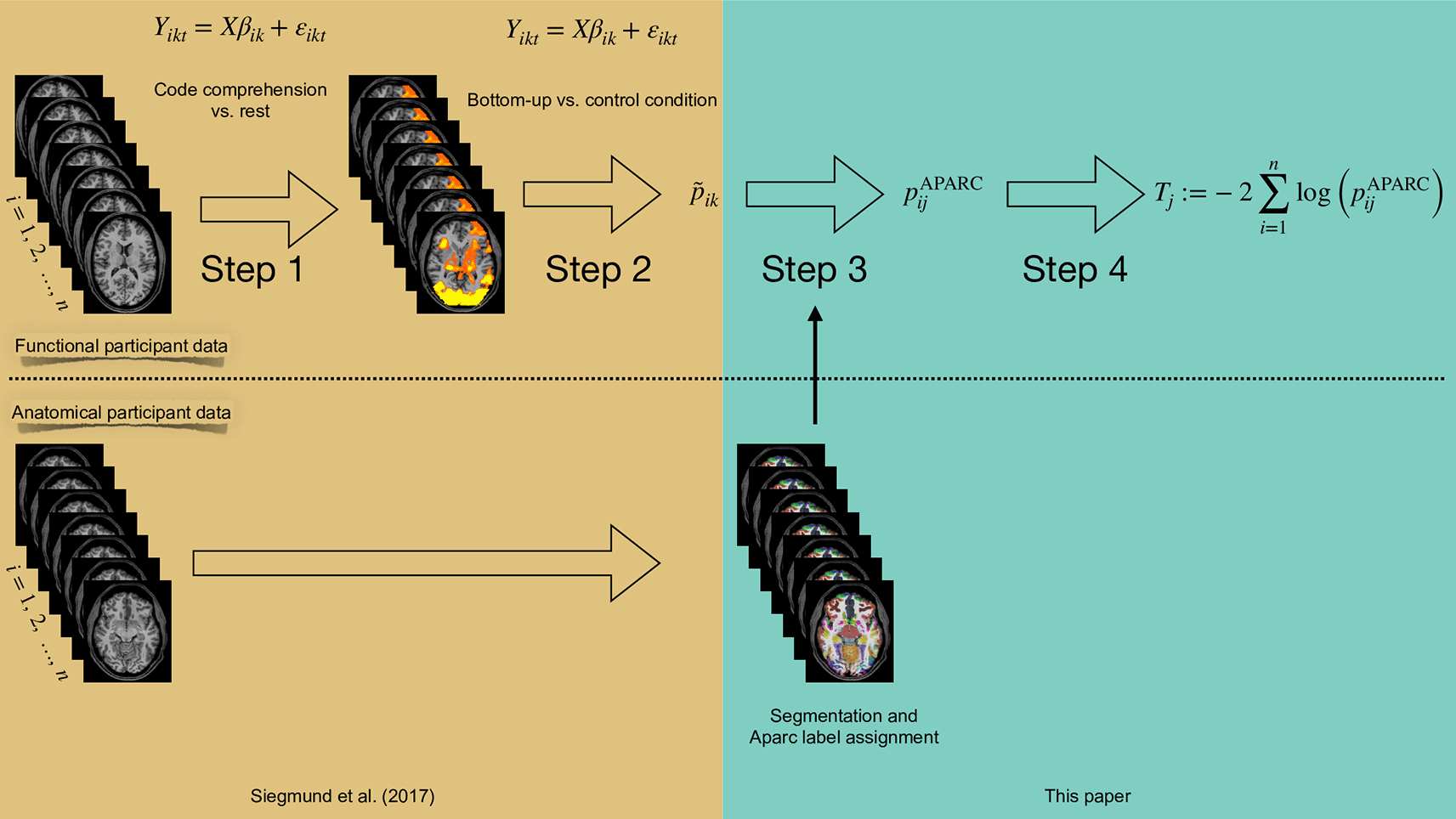
The box in Harvest Gold indicates analysis steps that have already been performed in Siegmund et al.43 The box in Monte Carlo indicates the processing steps proposed in this paper.
Especially in the context of functional magnetic resonance imaging (fMRI), another type of structural information is localization. The primary units of fMRI measurement are volume units (voxels) of the human brain. Localization means that scattered, spread-out signals (in single voxels or very small groups of voxels) are prone to be artifacts. Instead, topologically contiguous signals forming larger groups of voxels are much more plausible; see Refs. 19, 28. This information rules out certain patterns of the signal structure a priori, and can hence be exploited to increase the statistical power for signal detection; see, among many others.40 There are different possibilities to define or find such regions: (i) One may refer to an atlas of the brain, like the Brodmann atlas (see Ref. 7) and aggregate data within the regions given by this atlas. This has been the strategy in Ref. 40. (ii) One may find the regions (of interest) in a data-driven manner, e.g., by a cluster analysis. This has been proposed, among others, in Ref. 26. However, as emphasized for instance in Ref. 4, it is important that this data-driven definition of regions is “based on information outside the data that we set out to analyze”, meaning that the dataset used for defining the regions should be (stochastically) independent of the dataset which is used for signal detection, to avoid selection biases. (iii) One may choose a statistical methodology which ensures statistically valid conclusions even for regions which are selected in a post-hoc manner after having seen the actual study data. This can be achieved by simultaneous inference methods which guarantee that any possible selection event is accounted for; see, e.g., Ref. 38 and references therein.
All of the three aforementioned strategies have their assets and their drawbacks: Strategy (i) is inexpensive and easy to implement, but the regions taken from the atlas may not be optimally aligned with the specific task at hand, and differences in the individual brain anatomies of the study participants may complicate its application. For a statistical approach to the alignment of fMRI data, see, e.g. Ref. 2 and the references therein. Strategy (ii) is costly (two independent experiments are needed), but is supposed to yield a more accurate definition of the regions (of interest). Strategy (iii) avoids both the (potentially suboptimal) a priori definition of regions and the need for an additional independent experiment. However, the issue of multiple testing (see, e.g., Refs. 12, 14) becomes much more severe if simultaneity over all possible selection events has to be guaranteed, and the selection of the regions is not based on a clear-cut (statistical) criterion, but on the expert judgment of the study data. Therefore, it is hard to compare the results of Strategy (iii) with those of Strategies (i) and (ii).
Strategy (ii) has been followed in two studies (published in Refs. 42, 43) in which programmers comprehended program code (see Table 1 for details). In the first study (see Ref. 42), participants were asked to understand short program code snippets, such as shown in Listing 1. The program code did not contain any useful identifier names, which induces bottom-up comprehension (cf. Ref. 37). In this first study, the bottom-up comprehension task was contrasted with a syntax task, in which participants were presented with similar program code snippets, but only had to focus on syntax errors (e.g., missing semicolon). This control condition was intended to reveal only brain activation that is necessary for programmers to comprehend program code in-depth. As an additional control condition, the experiment included phases of rest in between the comprehension and syntax conditions.
| Study 1; see Ref. 42 | Study 2; see Ref. 43 | |
|---|---|---|
| Participant sessions | 16 | 14 |
| Trials | 12 | 30 |
| Conditions | Bottom-up program comprehension, control (syntax), rest | Top-down program comprehension, Bottom-up program comprehension, control (syntax), rest |
| Scans | 900 | 900 |

The snippet uses non-meaningful identifiers to induce bottom-up comprehension. Participants needed to figure out the output of this snippet “5”.
The second study (see Ref. 43) was a follow-up study that also differentiated the program-comprehension task into more nuanced conditions. One aim was to differentiate between bottom-up comprehension and top-down comprehension (cf. Ref. 9) which was induced by varying the meaningfulness of identifier names and by prior training to provide participants with the necessary knowledge. As in the previous study, the syntax task served as a control condition. Another research question addressed the goal of confirming the activated brain areas from the first study. To this end, the second study built on the regions identified in the first study, thus following Strategy (ii). Both studies were approved by the ethics board of the University of Magdeburg (Application: 87/14).
In the present work, we propose a new strategy and apply it to the data from Ref. 43 without using the knowledge about cortical regions relevant for understanding software code and identified in Ref. 42: We first utilize structural information from the individual’s brain scans. Here, we use an automatic parcellation of the brain into anatomical labels, which assign the voxels of an individual to pre-defined anatomic regions. This step of data analysis provides us with a significance evaluation (in terms of a p-value) for the presence of signals in anatomically defined regions for every study participant separately. By this, the method incorporates the rationale, that functional activation is also spatially connected28 and is thus able to gain more sensitivity without using the “localizer” data of the first study. Then, in a second step, we combine for each of these regions the p-values of all voxels within that region from all study participants using an appropriate combination function, and we evaluate the significance of the whole region by means of the resulting combined p-value. As we will demonstrate by means of the concrete example from the field of programming language comprehension, this new strategy can be similarly powerful as Strategy (ii) described above, while avoiding the sequence of two separate fMRI studies where the data of the first is used for definition of suitable regions for the second. In fact, our present methodology will not at all rely on the data from the first study42 that had been performed and utilized at that time by the authors of Ref. 43, while achieving similar results. Thus, it can enable researchers to spare precious measurement time.
In general, statistical analyses that are more advanced than voxel-wise regression analyses increase in popularity; see, e.g., Ref. 34 for a recent approach. Another alternative approach to analyze fMRI data is multi-voxel pattern analysis (MVPA) introduced by Haxby and colleagues, see Ref. 22 and the multiple papers cited therein. MVPA predicts stimulus event categories from the relative changes in activation across a set of voxels. Such a set of voxels is extracted in the first by a feature selection analysis. The second step partitions the data into a training set and a testing set entered into a pattern classification algorithm. From a statistical point of view this requires a sufficiently large number of comparable events. In the experiments described in Ref. 42 the events are code snippets that must be read and understood within 60 seconds to enable a certain complexity of software code and were thus limited in number to fit into the duration of a typical fMRI session of about 45 minutes. Such limited number of events may pose difficulties for MVPA cross-validation. Such low number of rather long events is, however, sufficient for general linear model (GLM) analyses of block design experiments that typically yield strong detection power (albeit low discrimination power).
Moreover, as functional activation is spatially distributed over several voxels rather than focused in single ones, cluster-based inferences have become rather standard (cf. Ref. 28). This is implemented and used in all major software package. However, a recent discussion in Ref. 15 revealed their flaws in practical situations. Furthermore, cluster-based inference requires simulation according to the smoothness of the data at hand.
In fact, the majority of fMRI studies like our studies from Refs. 42, 43 still use GLM-based analyses which require corrections for multiple comparisons. The experiments were constructed such that perceptual and cognitive processes necessary but not specific for understanding software code were controlled by specific test conditions, either requiring to read the same code but with a different task or controlling for attentional demands. Thus, it was a classical hypothesis-driven design, which is widely used in the literature, especially to unravel complex cognitive processing. Besides that, understanding software code is a highly idiosyncratic process and therefore identification of brain activity using control conditions within individual subjects is possibly more feasible as a first step towards identifying the most relevant brain areas involved in such a complex cognitive process. Thus, our method can serve as a valuable alternative using spatial aggregation while still being fast and easy to implement.
The rest of the paper is structured as follows. In Section 2, we describe our proposed statistical methodology. Section 3 describes conducted computer simulations comparing three different methods of fMRI data analysis. Section 4 is devoted to the detailed description of our re-analysis of the fMRI data from Ref. 43, and the results of this re-analysis are presented in Section 4.3. We conclude with a discussion in Section 5.
In this section, we describe our statistical model for fMRI data as well as the proposed data analysis workflow for detecting brain regions which are significantly associated with a certain cognitive task.
Let Yixt denote the observed data from a functional MRI experiment at voxel and time for the -th subject. Here, we adopt the common view (cf. Section 5.4 in Ref. 28) of a mass-univariate linear model
The SPM then forms a random -field (cf. Ref. 53) with an inherent multiple comparison problem due to the large number of local hypotheses. One common strategy is to define local p-values at each voxel and for each subject based on the local values of the random -field and to control the family-wise error rate (FWER) using accordingly adjusted thresholds; cf. Ref. 54. However, this is known to be a very conservative approach with respect to the detectability of significant brain signals in the outlined framework. In contrast, approaches related to the control of the false discovery rate (FDR) can handle the multiple comparison problem, e.g., by the procedure proposed in. Ref. 6.
Neuroanatomic research has found that the human brain can be parcellated into different sub-regions based on structural similarities. One of the earliest atlases is the Brodmann atlas (see7) which is based on the cytoarchitectural organization of the brain. The Brodmann Areas have been schematically transferred to a template brain, the so-called Talairach-Atlas (see Ref. 46) which is commonly used in fMRI studies to report the location of significant grand average activation, as used in Refs. 42, 43. For the analysis of these data in the current paper, we chose the Harvard-Oxford brain atlas (cf. Refs. 10, 31) that provides a parcellation based on gross anatomical landmarks and delivers an Aparc label for each voxel of each individual brain space. However, any other brain parcellation to define regional labels could be used with our methodology.
As outlined in the introduction, we re-used fMRI data from a program code comprehension task first analyzed in Ref. 43 and performed a new analysis comprising the four steps outlined below. The experiment used two different levels of software program code comprehension stimuli, henceforth denote as bottom-up and top-down comprehension, to infer on the related cognitive processes. In our strategy, we combined the methods from Ref. 43 (steps 1 and 2) and Ref. 40 (step 3). Furthermore, we implemented our new methodological contribution of combining the evidence for activation of a given brain region across the subjects (step 4). For the first two steps, we conducted, for each subject, a random-effects linear model analysis as described above for deriving voxel-wise p-values.
Step 1: Program comprehension versus rest
In the first step, we contrasted (for each participant separately) the comprehension of program code (cf. Ref. 43) to the rest condition. This identifies brain areas with a positive deflection of the BOLD response. Furthermore, in order to account for the multiple comparison problem, we performed the Benjamini-Hochberg test (see Ref. 6) for FDR control. Only those voxels which have been declared significant by this procedure were considered in step 2. This methodology is justified by the fact that the FDR is an established screening criterion for high-dimensional multiple test problems.
Step 2: Bottom-up comprehension versus control condition
In this step, we contrasted (again, for each participant separately) one type of program comprehension: bottom-up comprehension. Bottom-up comprehension is induced when program code provides no semantic cues and programmers need to comprehend each line separately and then integrate the information in a slow, tedious process. For the significant voxels from the first step, we applied in a second step the same multiple test to the contrast of bottom-up comprehension against the control condition (syntax task) on the restricted set of voxels. As a result of this step, we get for each participant and for each considered voxel a p-value .
Step 3: Regional p-values for every participant
This step builds upon the methodology from Ref. 40, and it delivers for each participant and for each anatomical (regional) label a (confirmatory) significance evaluation with respect to the contrast specified in step 2. Hence, the evidence from all voxels of participant i in the brain region labeled by is combined in this step of data analysis.
To this end, let be a tuning parameter with values in the interval [0, 1] (i.e. in per cent) and let be the number of voxels contained in the brain region labeled by region label . To keep the notation feasible, we implicitly assume here that for each participant the same number of voxels belong to the brain region labeled by . We consider the null hypothesis of no relevant differential activation of the region labeled by for participant during the two tasks mentioned in step 2, together with its two-sided alternative hypothesis . We call the “regional null hypothesis” for the brain region labeled by for participant . We formalize as a so-called partial conjunction hypothesis (see40 and the references therein for a formal mathematical description), meaning that we consider the differential activation in region for participant relevant, if it contains at least significant voxels. For testing we calculate the “regional p-value” , given by
In order to achieve family-wise error rate (FWER) control, we have to choose the tuning parameter smaller than or equal to , where is the number of regional labels. Choosing corresponds to the so-called Bonferroni multiplicity correction. The choice of is discussed further in Appendix S1 of Ref. 40.
Step 4: Combined regional hypothesis tests by Fisher’s method
In this final step, we combine for each regional label the regional p-values calculated in step 3 over all participants . In order to do this, we apply the so-called Fisher method to combine p-values. Namely, the Fisher test statistic for region is given by
Under independence of the data with respect to the participants, is asymptotically -distributed (chi squared) with degrees of freedom under the null. The latter independence assumption is justified, because the participants have been included in the study independently from each other.
Finally, we can reject the (over all participants combined) regional hypothesis (i.e., the respective partial conjunction hypothesis, but now with respect to the population, not with respect to a single participant) if and only if Fisher’s test statistic is larger than the (1-ακ)-quantile of the -distribution with degrees of freedom, where the tuning parameter has been introduced in step 3. This parameter addresses the multiplicity of the test problem with respect to the regional labels which are simultaneously under consideration.
In order to compare the performance of three different methods for fMRI data analysis in a controlled framework, we have carried out computer simulations.
We have simulated a dataset with eleven subjects (referring to the index and corresponding to the group size in the real dataset below), a spatial grid of size voxels (referring to the index ), and 195 time points (scans, referring to the index ). We have assumed that the 8,000 voxels are grouped into eight anatomical regions of size each, and that these regions are correctly annotated for all eleven subjects. Two alternating stimuli in an ON-OFF block task design with a total of six ON blocks of a duration of 15 scans have been used for the temporal signal: In a circular area in one of the predefined anatomical regions the signal of one stimulus was twice as high as the signal by the other stimulus mimicking a signal contrast. In a corresponding area in a second anatomical region the signal was created with no difference between the stimuli. The datasets with first order autocorrelated Rician noise have been created using the R package neuRosim51; p-values for Contrast 1 (ON of either stimulus versus rest) and Contrast 2 (one stimulus versus the other) where determined using the R package fmri45. This simulation setup has been run 500 times.
For the statistical analysis of the simulated data, we have considered three different methods.
• Voxel-wise: On the basis of voxel-wise -scores (aggregated over all eleven participants) and the resulting p-values for Contrast 1, voxels have been screened by applying the Benjamini-Hochberg method at level . For the screened voxels only, -scores (again aggregated over all eleven participants) and the resulting p-values for Contrast 2 have been computed. A region has been declared significantly activated, if the number of Contrast 2 p-values below in that region has been larger than , with denoting the number of screened voxels in region and , meaning that we considered a region to be relevantly activated if at least 10 out of the 1,000 voxels in that region are statistically significantly activated under the stimulus. The rejection threshold accounts for the (reduced) multiplicity resulting from the pre-selection by means of Contrast 1.
• Cluster-wise: Activation is typically spatially spread over multiple voxels. In fact, single isolated voxels are mostly considered as spurious rather than activated; see Ref. 28. Thus, we also analyzed the simulated datasets and the two contrasts with cluster-based thresholds: At the given significance level the value of the test statistic at a voxel must exceed some threshold and it has to belong to a cluster of at least s connected voxel. Thresholds can be pre-determined by simulations. To determine p-values we used the R package fmri45, where the method is implemented.
• Region-wise (this paper): Our proposed method from Section 2, again with FDR level 0.05, , and in Step 4.
We have assessed the type I and the type II error behavior of the three methods described in the previous subsection by calculating (for each of the three methods) the proportion of simulation runs in which any region without true activation has been declared significantly activated (type I error component) as well as the proportion of simulation runs in which the one region with true activation has not been declared significantly activated (type II error component). Table 2 summarizes the results of our computer simulations.
The estimated type I error refers to the proportion of simulation runs in which any region without true activation has been declared significantly activated. The estimated type II error refers to the proportion of simulation runs in which the one region with true activation has not been declared significantly activated.
| Voxel-wise | Cluster-wise | Region-wise (this paper) | |
|---|---|---|---|
| Estimated type I error | 0% | 0% | 0.8% |
| Estimated type II error | 24.6% | 0% | 0% |
From Table 2 it becomes apparent that all three methods are capable of protecting reliably against type I errors under our data-generating model. However, the power of the proposed method appears to be considerably larger than that of the voxel-wise method. Namely, during our 500 simulation runs, our new method as well as the cluster-wise method always detected the truly activated region, while the voxel-wise method detected it only in 367 out of the 500 runs.
We re-used the data from Ref. 43 and compared our results with those obtained by additionally utilizing42 as pre-study in the sense of Strategy (ii) outlined in the introduction.
In the two previous studies mentioned before, Siegmund et al. used similar analysis processes. They used BrainVoyager™ QX 2.8.4[1]. The anatomical scans were transformed into the Talairach brain to account for differences in brain size; cf. Ref. 46. They preprocessed the functional data of both studies with a standard pipeline of: 3-D motion correction, slice-scan-time correction, and temporal filtering. In addition, they applied a spatial smoothing with a Gaussian filter (FWHM = 4 mm).
In the first study42, the random-effects GLM revealed five brain areas (BAs 6, 21, 40, 44, 47) with significant activation with the contrast Bottom-Up Comprehension versus Control condition, i.e. syntax task. In the second study, the same contrast revealed no significant areas anymore, likely due to the reduced statistical power of five instead of twelve bottom-up comprehension tasks per session. Thus, the authors ran a regions-of-interest analysis restricted to the identified activation clusters of the first study on the data of the second study. This resulted in a significantly stronger activation for Bottom-Up Comprehension versus Syntax in BAs 21, 40, and 44.
In Figure 1, we illustrate the overall process for the re-analysis of the data from Ref. 43. For our re-analysis, we exported the already pre-processed data from the second study. We did not use the data of the first study as our method does not need prior definitions of regions of interest. We used BrainVoyager to access the data from Siegmund et al. We exported the statistical values (i.e., t-scores, p-values) of the obtained brain activation on a voxel basis for each participant. The voxel resolution is the same BrainVoyager uses, i.e., a 1 mm interpolated resolution.
In addition, we used FreeSurfer to segment and parcellate the brain of each participant based on their anatomical scan; cf. Refs. 17, 18. We used the Destrieux’ cortical atlas to assign Aparc labels on an individual participant basis (see Ref. 11) as a suitable region definition. Next, we used Nipype (see Refs. 16, 21) to convert Freesurfer labels to a BrainVoyager-readable format.
Our last step annotated the exported functional data with the individual anatomical labels for each participant. We removed all functional voxels for coordinates that had no assigned Aparc label, which typically are voxels that are not considered gray matter.
Figure 2 displays the six brain regions which have been declared as significant (at FWER level ) associated with the task at hand by our described methodology. There is an overlap with the results obtained by Ref. 43 in which they utilized prior knowledge, but also some differences which we discuss in the following in their nuances. We visualize the confirmed network of brain activation from Siegmund et al. in Figure 3 and our identified network of significantly activated Aparc labels in Figure 4. Figure 3 and Figure 4 show overlapping results with regard to the Brodmann area 21 that covers the middle and inferior temporal gyrus (separated by the inferior temporal sulcus). However, we observed differences regarding smaller brain regions. We compare Siegmund’s replication efforts to our results in Section 5.1.

In each row, each point corresponds to the Aparc p-value of one study participant i, where the index j refers to the area indicated by the code at the beginning of the row.
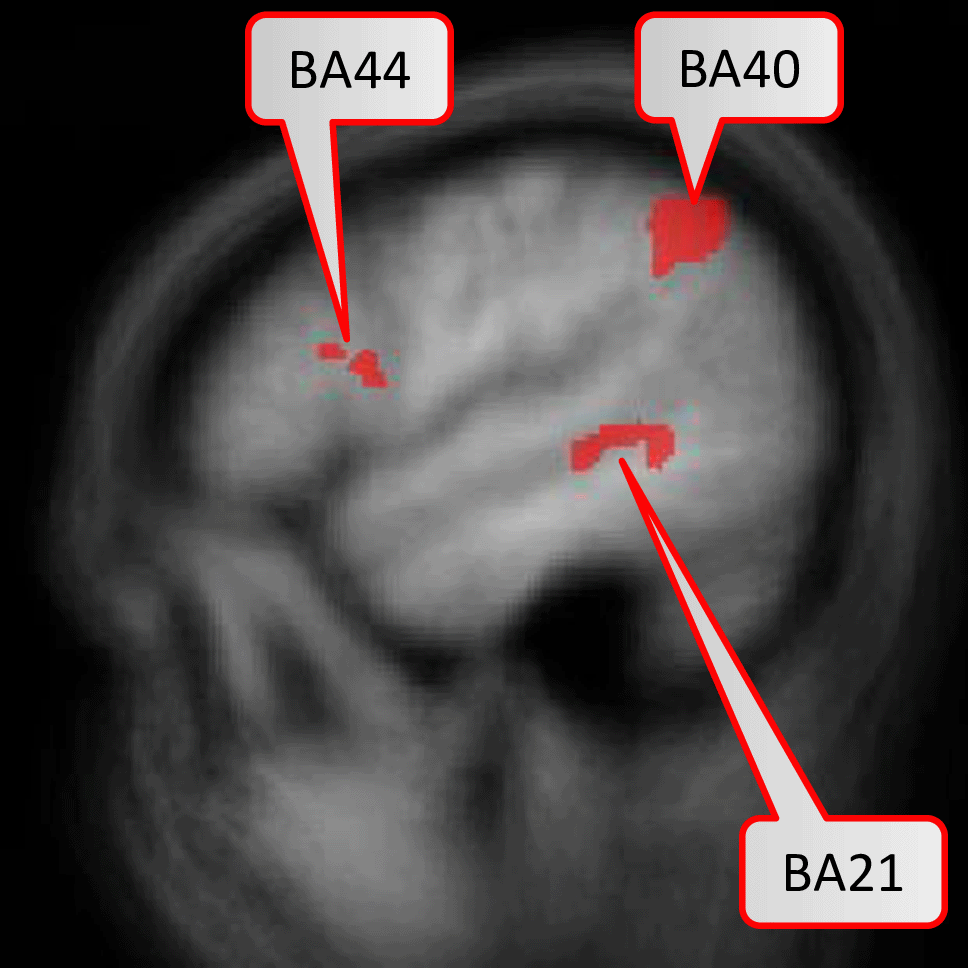

Activation are particularly in the middle and inferior temporal lobe.
Our method found three Aparc labels in the inferior and middle temporal gyrus in the left hemisphere. Siegmund et al. found their largest and most robust activation cluster in BA21 of the left hemisphere, which covers several gyri in the temporal lobe. These left temporal gyri are often associated with semantic processing of natural language, which is typically left-lateralized for right-handed participants. In the context of programming, the activation is believed to be responsible for extracting the meaning of individual identifiers and symbols during program comprehension. We found two further Aparc labels bilaterally in the inferior temporal gyrus and the anterior collateral sulci, which are both in the temporal lobe as well.
For each of these six regions indexed by , we display all subject-specific regional p-values }, where is the number of study participants. For each considered in Figure 2, it can clearly be observed that not a single extreme outlier (one very small p-value corresponding to one individual subject) is responsible for the statistical significance with respect to the combination test statistic but that the combined information contributed by all subjects supports our statistical conclusions. Regional p-values can occur, if none of the voxels belonging to region has been selected in Steps 1 and 2 described before for a certain subject . By construction of this essentially means that the “effective sample size” for such a region is reduced, while the number of degrees of freedom for the null distribution of remains unchanged.
This paper introduces a new strategy to analyze fMRI data and demonstrates its performance by drawing a comparison to two studies by Siegmund et al. In their second study, they investigated a new research question which was based on a design with reduced statistical power regarding the network of brain areas activated during bottom-up program comprehension. Only by using prior knowledge of the location of identified clusters from the first study and conducting a regions-of-interest analysis with increased statistical power, they were able to exceed standard thresholds of statistical significance but restricted to the subset of areas identified in the first study.
Research that similarly aims to detect small differences between cognitive processes with state-of-the-art methods would need to increase statistical power, e.g. by conducting two studies: first, to identify the network of brain areas involved in the overarching cognitive process, and second, to identify differential effects within the activated brain areas. The method of utilizing anatomically predefined regions of interest as determined in each individual brain is a candidate for a more sensitive analysis as compared to statistical testing of single voxels with identical coordinates of a template brain. This is possibly due to allowing more flexibility with respect to the exact anatomical location of functional units across different brains. Our example of using ROIs from the Harvard-Oxford atlas can easily be replaced in future applications by brain parcellation schemes that are based on more refined anatomical and/or functional databases. We demonstrated by simulations that our method can accurately detect signals based on region aggregation and outperforms standard mass-univariate approach while achieving a similar performance as cluster-based inferences without the need to define thresholds based on data smoothness via simulations. Further, we demonstrated that our method can find significantly activated brain areas without relying on prior knowledge on a real fMRI dataset. Moreover, additional brain areas were identified which have been described in two fMRI studies of programmers and interpreted as being involved in visuo-spatial processing. One study investigated manipulating data structures, which share similarities to spatial rotation (see Ref. 25) and one writing program code (see Ref. 27). Since the study by Siegmund et al. (2014) was the first study on program comprehension they used a rather small FDR corrected significance level ( as compared to the more common ). Possibly this is one reason why the two areas identified by the current approach were not identified there and as a consequence could not emerge in Siegmund et al. (2017). Thus, our current approach seems valuable in cases where new research questions are explored and little to no prior work is available and which would require careful statistical hypothesis testing to initially minimize false positives.
However, inferior frontal gyrus (BA 44) and inferior parietal lobule (with BA 40), shown to be significant in Siegmund et al., were not significant with our method. Therefore, we exemplarily investigated this difference with the activation cluster in BA 40. In Figure 5, we display a histogram of p-values for the (statistically significant) Aparc label in the middle temporal gyrus, in which a majority of the participants contribute with small p-values. In contrast, in Figure 6, we display a histogram of p-values for the inferior parietal lobule. Across the entire group, we also observe an accumulation of very small p-values, but only three of eleven participants contribute to this. Unlike the regions-of-interest analysis done by Siegmund et al., our method relying on combining Aparc p-values by Fisher’s method does not reject hypotheses with such a p-value distribution.
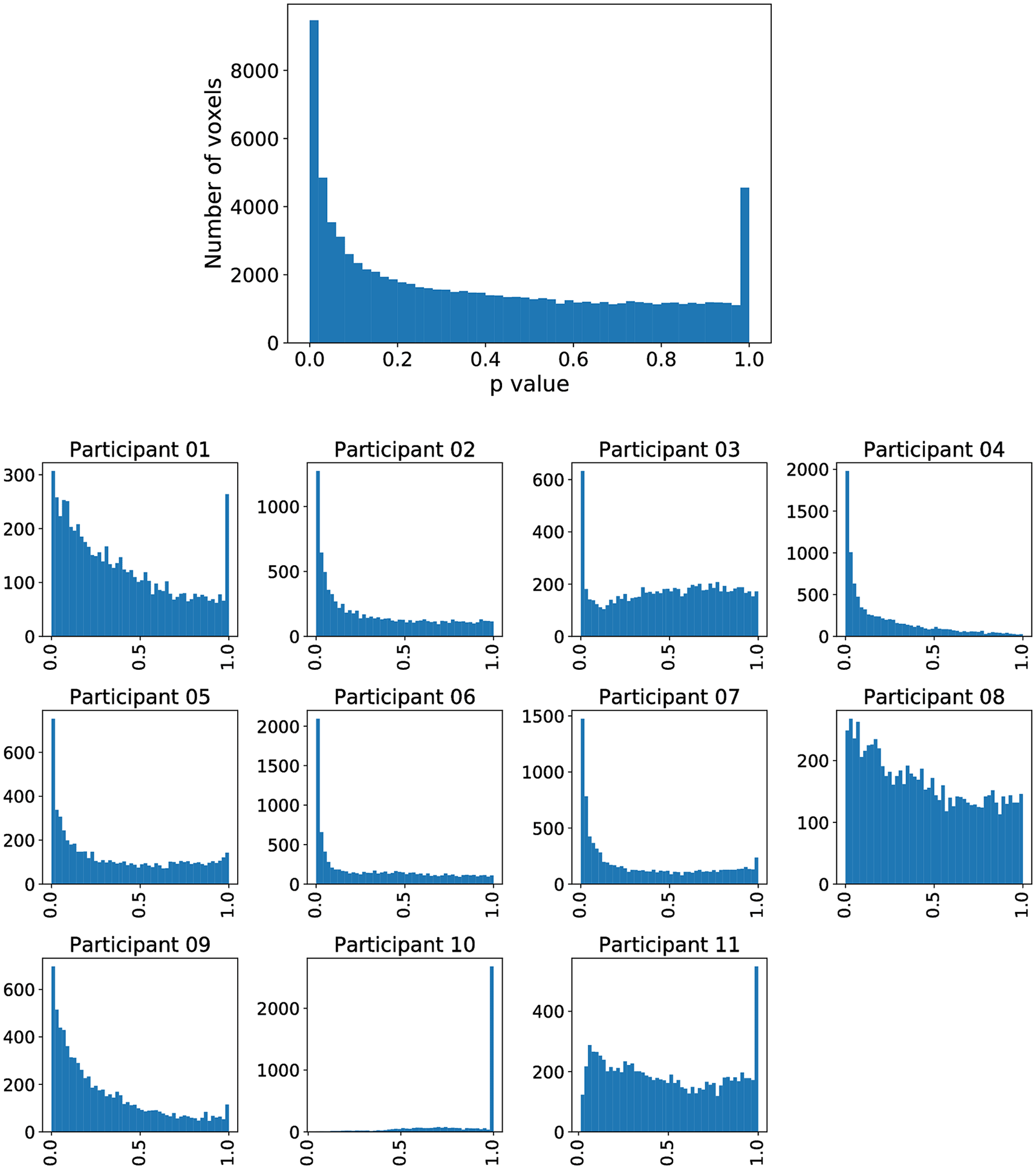
The plot without a heading is across all participants, while the eleven plots with headings show the distribution across individual participants. The majority of participants is contributing to the significance.
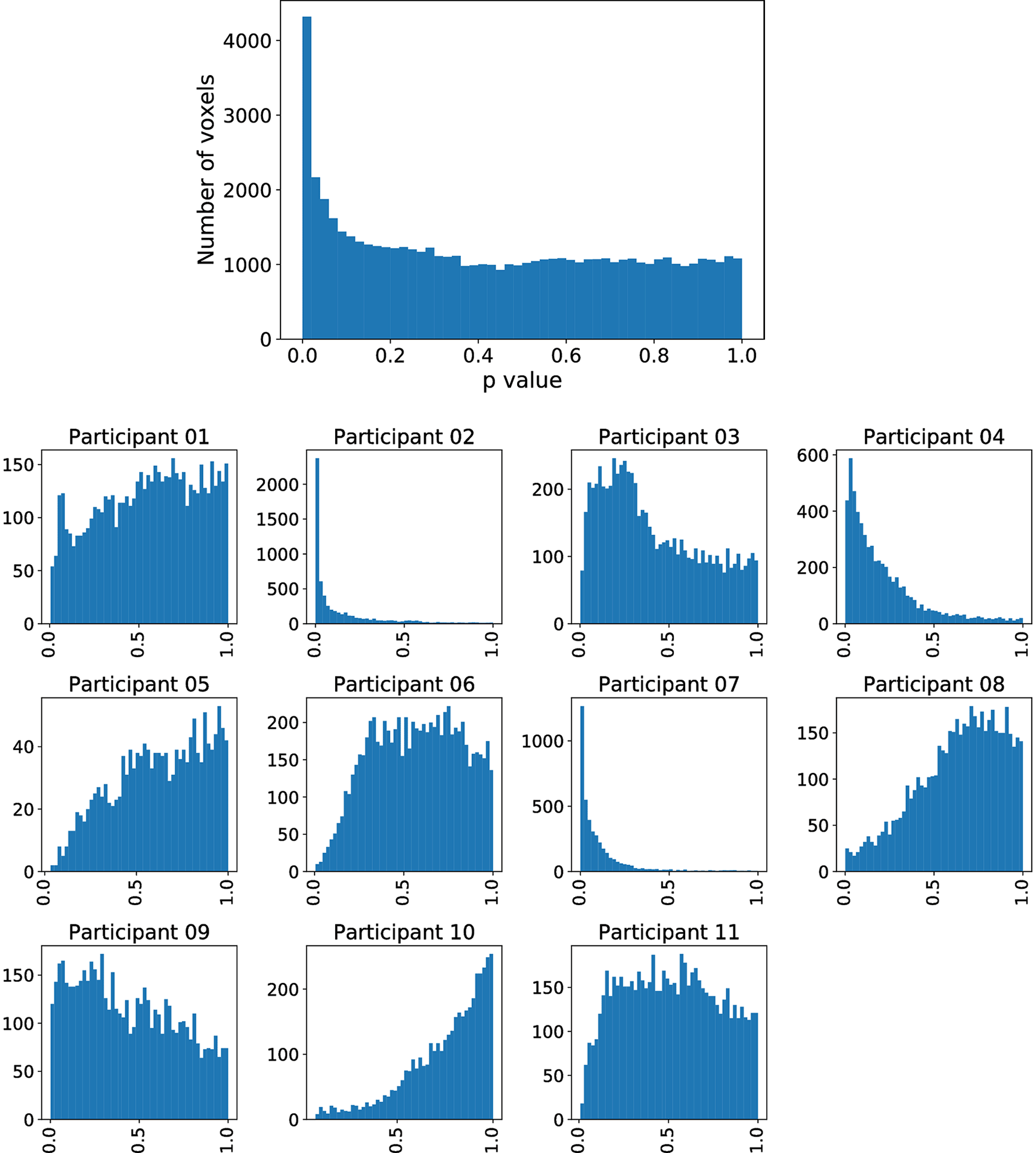
The plot without the heading is across all participants, while the eleven plots with headings show the distribution across individual participants. While there are many small p- values, only a few participants contribute these small values.
By transforming the Aparc labels into the Talairach space, we observed that the voxels included in the activation cluster of BA 40 do not perfectly align with the Aparc label that should cover this brain area, i.e. the inferior angular gyrus of the parietal lobe. Table 4 shows that the overlap to the activation cluster in BA40 is less than 50% and that only around 5% of its voxels are assigned to an Aparc label at all. In contrast, Table 3 shows that at least 75% of the voxels of the BA 21 cluster are aligned to Aparc labels of which two are significant with our method. Thus, a small activation cluster within a large anatomical region may get lost with our approach. We further discuss this potential drawback of the used anatomical segmentation and possible remedies in Section 5.3.
Only a subset of these voxels is assigned to Aparc labels. However, the assigned Aparc labels are larger and only a smaller section overlaps with the activation cluster. Aparc labels in bold are evaluated as significant. Only Aparc labels with at least 75 overlapping voxels are included.
Only a subset of these voxels is assigned to Aparc labels. However, the assigned Aparc labels are larger and only a smaller section overlaps with the activation cluster. No Aparc label is evaluated as significant. Only Aparc labels with at least 75 overlapping voxels are included.
From the methodological point of view, our main contribution consists in a novel way how to combine evidence: Instead of aggregating single voxel data over all participants by mapping them to a standard brain template, we define subject-specific regions and combine the evidence on the level of these regions by means of a combination function. This is a generic methodological approach which is not restricted to the specific study setup of Siegmund et al., but can be applied to essentially any fMRI study design, involving an arbitrary number of contrasts.
Furthermore, also the (final) combination step of our proposed approach is generic in the sense that instead of the Fisher combination function any other (appropriate) combination function for p-values may be used. Recently, there has been a renewed interest in p-value combination methods; see, e.g., Ref. 52 (with discussion), Ref. 48, and Ref. 49.
Under the multiple testing framework, testing of grouped null hypotheses with (potential) application in fMRI is an active research topic. In Ref. 23 as well as in Ref. 4, clustering techniques were employed to define regions of interest, and the authors incorporated the heterogeneous cluster sizes in a weighting scheme for the linear step-up test from Ref. 6. In the same vein, the authors of Ref. 24 as well as Ref. 56 made use of the different proportions of true null hypotheses in each of the groups in their proposed weighting. A Bayesian variant of this idea has been derived in Ref. 30. Hierarchical methods, which exclude groups without strong evidence for the presence of signals in several stages of data analysis, have been worked out by several researchers; see, e. g., Refs. 3, 40 and 55. However, these methods rely on combining the subject-specific data on the voxel level, which is a standard technique as mentioned, for instance, in Section 5 of Ref. 29 Also on the basis of (combined) voxel data, a hierarchical independent component analysis for the comparison of brain functional networks has been proposed in Ref. 41. To the best of our knowledge, our proposed method to define subject-specific regions by means of regional labels and to combine the resulting subject-specific regional p-values by means of a combination function is a novel idea.
It is worth mentioning that both our proposed methodology and the methods from previous literature that we are considering in our comparisons make certain assumptions about the data: First, a linear relationship between the features encoded in the design matrix and the response is assumed. Thus, non-linear effects cannot (fully) be captured by models of the type (1). Second, Gaussianity of error terms is assumed, implying symmetry and light tails, among other things. It can be of interest to validate or to test these assumptions for a concrete dataset at hand. However, since this aspect is not the main focus of our present work, we defer such investigations to future research. In particular, modeling the data that we have re-analyzed in this work with different model assumptions would diminish the comparability of our data analysis results with the results from previous analyses. One simple (numerical) robustness analysis regarding the Gaussianity assumption can be performed by simulating data with a different error distribution and comparing the results with the results presented here. To this end, the source code which is available as supplementary material for this article may be helpful for practical implementation.
Instead of utilizing a single voxel GLM group analysis in common brain templates, we used a parcellation of the brain for each individual participant into regional labels, here Aparc labels, before aggregation into the group analysis. This procedure provides more labels than a traditional Brodmann atlas. Still, some of the regions are very large and thus presumably contain several functional areas. There is ongoing research to subdivide the brain based on cytoarchitectonic details, e.g. the Jülich-Brain (see Ref. 1). This will provide more detailed parcellation schemes in the future and that could easily be integrated into our proposed method. Another refinement could be to use functionally defined brain regions for our presented methodology. A study that implements functional localizers could identify participant-specific functional maps of the brain for well-defined standardized tasks (e.g., see Ref. 33). Then, in the analysis, our presented methodology can aggregate across all participant-specific brains with less imprecision than traditional methods. We would like to note that such functional localizers are currently restricted to research areas that include brain regions with specific functional specialization; cf. Refs. 20 and 39. The studies we presented in this paper are concerned with a rather complex cognitive task. Moreover, understanding program code is highly individual since different programmers rely on different comprehension strategies based on their preferences, domain knowledge, and experience (e.g., Refs. 8, 9 and 44).
Weierstrass Institute for Applied Analysis and Stochastics publication server: Utilizing anatomical information for signal detection in functional magnetic resonance imaging - Data. https://doi.org/10.20347/wias.data.9.36
This project contains the underlying data:
Data are available under the terms of the Creative Commons Attribution 4.0 International license (CC-BY 4.0).
Source code available from: https://github.com/ktabelow/HierarchicalFMRI/
Archived software available from: https://zenodo.org/records/17097938
License: GNU General Public License v3.0
We thank André Neumann for collaborating with us on a previous version of this article (available as preprint32) and Jörg Stadler for his technical support in data processing with Nipype and FreeSurfer.
| Views | Downloads | |
|---|---|---|
| F1000Research | - | - |
|
PubMed Central
Data from PMC are received and updated monthly.
|
- | - |
Is the work clearly and accurately presented and does it cite the current literature?
Yes
Is the study design appropriate and is the work technically sound?
Partly
Are sufficient details of methods and analysis provided to allow replication by others?
Yes
If applicable, is the statistical analysis and its interpretation appropriate?
Partly
Are all the source data underlying the results available to ensure full reproducibility?
Yes
Are the conclusions drawn adequately supported by the results?
Partly
Competing Interests: No competing interests were disclosed.
Reviewer Expertise: Biostatistics, high-dimensional data analysis, voxel-level multiple comparison, multi-view data analysis
Is the work clearly and accurately presented and does it cite the current literature?
Partly
Is the study design appropriate and is the work technically sound?
Partly
Are sufficient details of methods and analysis provided to allow replication by others?
Partly
If applicable, is the statistical analysis and its interpretation appropriate?
Partly
Are all the source data underlying the results available to ensure full reproducibility?
Yes
Are the conclusions drawn adequately supported by the results?
Partly
Competing Interests: No competing interests were disclosed.
Reviewer Expertise: Statistical methods for neuroimaging; computational methods for neuroimaging; computer science and applied mathematics (Cravo)
Is the work clearly and accurately presented and does it cite the current literature?
Partly
Is the study design appropriate and is the work technically sound?
Yes
Are sufficient details of methods and analysis provided to allow replication by others?
Partly
If applicable, is the statistical analysis and its interpretation appropriate?
I cannot comment. A qualified statistician is required.
Are all the source data underlying the results available to ensure full reproducibility?
Yes
Are the conclusions drawn adequately supported by the results?
Yes
Competing Interests: No competing interests were disclosed.
Reviewer Expertise: clinical neuroradiology, functional neuroimaging (methods and applied research)
Alongside their report, reviewers assign a status to the article:
| Invited Reviewers | |||
|---|---|---|---|
| 1 | 2 | 3 | |
|
Version 1 01 Oct 25 |
read | read | read |
Provide sufficient details of any financial or non-financial competing interests to enable users to assess whether your comments might lead a reasonable person to question your impartiality. Consider the following examples, but note that this is not an exhaustive list:
Sign up for content alerts and receive a weekly or monthly email with all newly published articles
Already registered? Sign in
The email address should be the one you originally registered with F1000.
You registered with F1000 via Google, so we cannot reset your password.
To sign in, please click here.
If you still need help with your Google account password, please click here.
You registered with F1000 via Facebook, so we cannot reset your password.
To sign in, please click here.
If you still need help with your Facebook account password, please click here.
If your email address is registered with us, we will email you instructions to reset your password.
If you think you should have received this email but it has not arrived, please check your spam filters and/or contact for further assistance.
Comments on this article Comments (0)