Keywords
photon, mass-speed relation, classical mass, inertial mass, gravitational mass, relativistic mass, moving mass, observed mass, observational mass
The theory of Observational Relativity (OR), as a new theory in human-developed physics, has revealed the essence of the relativistic effects of Einstein theory of relativity, and moreover, has generalized and unified Newton’s classical mechanics and Einstein’s relativity theory. However, the original intention of OR research is not to establish the theory of OR, but to give photons a little rest mass. According to Einstein special relativity, an object of matter moving in inertial spacetime has two types of mass: the rest mass; the moving mass. However, Einstein claimed that photons had no the rest mass. In fact, the moving mass depends on observation and is not objectively real. So, photons would have no mass if they had no the rest mass.
According to the materialist view of nature, the natural world is a world of matter, and all matter or material particles, including photons, have the objectively intrinsic mass. Naturally, the objectively real mass must be independent of observation. OR serial report 1 has elucidate the theoretical validity and empirical basis of OR. Now, OR serial report 2 will report the logical consequence of OR: photons have the rest mass.
The theory of Inertial OR (IOR) has theoretically proved that photons possess the rest mass; the theory of Gravitational OR (GOR) has theoretically calculated and predicted that the rest mass of a photon with the frequency f is mo = hf/c 2.
The logical consequence that photons has the rest mass are in line with the materialist view of nature: all matter or material particles must possess the objectively real mass; an object of matter, whether it is a massive star or a tiny photon, must possess the rest mass of its own if it exists objectively; otherwise, it does not exist.
photon, mass-speed relation, classical mass, inertial mass, gravitational mass, relativistic mass, moving mass, observed mass, observational mass
OR serial report 11 has reported a new theory in physics: Observational Relativity (OR).2–5
The theory of OR has discovered that the human perception of the objective world relies on observation and is restricted by observation. All spacetime models and theoretical systems in human-developed physics must be branded with observation: the Galilean transformation and Newtonian mechanics are the products of idealized observation with the idealized agent OA∞; the Lorentz transformation and Einstein theory of relativity, both special and general, are the products of optical observation with the optical observation agent OA(c).
Galileo and Newton represent the objective and real physical world; whereas Einstein presents to us only the optical image of the physical world.
Unexpectedly, the theory of OR has generalized and unified the two great theoretical systems of human-developed physics, Newton’s classical mechanics and Einstein’s relativity theory, in the same theoretical system under the same axiom system. The theory of OR has had significant discoveries, revealing the root and essence of the relativistic effects of spacetime and matter motion: all relativistic effects are observational effects and apparent phenomena; the speed of light is not really invariant, and spacetime is not really curved.
OR serial report 2 will report another important discovery of the theory of OR: the rest mass of photons is not zero.
The theory of OR was not designed or manufactured; it was just an accident.
Revealing the essence of relativistic effects and unifying Newton’s classical mechanics and Einstein’s relativity theory was not the original intention of OR.
Initially, the theory of OR only attempted to give photons a small amount of rest mass.
The issue of photon mass is a major one in physics.
The author believes that a physicist should first and foremost be a materialist: the natural world is a world of matter, and mass characterizes the objective existence of matter; all matter or material particles, including photons, must possess objective and real intrinsic mass. The objective mass must be independent of observation, and the real mass must exhibit both real inertial effects and real gravitational effects.
Human-developed physics should embrace the dialectical materialist view of nature: everything in the natural world is the contradictory unity; the two sides of the contradiction are both mutually independent and interdependent, and can be transformed into each other under certain conditions.
In a sense, Einstein’s theory of relativity, both the special6 and the general,7 provides an excellent interpretation of the Dialectics of Nature and the Dialectical Materialist View of Nature.
Matter is the contradictory unity of mass and energy. According to Mach8 and Einstein,9,10 everything in the natural world is relative. In Einstein’s theory of relativity, mass and energy are relative and can be transformed into each other: mass is energy; energy is mass.
However, the Hypothesis of the invariance of light speed, as the most basic logical premise of Einstein relativity theory, leads to two specious arguments:
(1) The speed of light is the ultimate speed in the universe, and it cannot be surpassed;
(2) Photons have no rest mass.
Subconsciously, people believe that the objective and real mass of matter or material particles is, and can only be, the rest mass. The absence of rest mass in photons is tantamount to the assertion that photons have no mass. With no mass, what could the energy of photons rely on for existence? The existence of matter with only energy and no mass cannot be reconciled with the dialectical materialist view of nature.
Thus, providing photons with a small amount of rest mass became the original intention of OR research.
Driven by their inherent views on nature, great physicists such as Feynman,11 de Broglie,12,13 and Schrödinger14,15 did not believe that photons have no rest mass and ever spared no time and effort in attempting to determine the rest mass of photons by observations or experiments. Till this day, many experimental physicists still attempt to find the rest mass of photons through observations and experiments. They hope to find out the rest mass of photons outside the moving mass of photons. Proca even prepared an amendment scheme for Maxwell’s electromagnetic equations to account for the presence of massive photons.16 However, all efforts to determine the rest mass of photons have been futile, leaving only a series of upper limits on the rest mass of photons that continuously approaches zero.17–19 In 2014, the Particle Data Group (PDG) recommended an upper limit of 1.5 × 10−54 kg for the rest mass of photons.20
Unlike determining the rest mass of photons through observations or experiments, the author of OR attempts to theoretically assign a small rest mass to photons and establish a theoretical model of the expected photon mass (EPM).
However, the theoretical model of EPM has unexpectedly evolved into the theory of OR.
The theory of OR goes beyond the original intention and expectation, not only obtaining the rest mass of photons but also establishing the entire theoretical system of OR,2–5 generalizing and unifying Newton’s classical mechanics, and Einstein’s relativity theory.1 Moreover, it establishes the basic theoretical framework for the theory of observational quantum (see Chapter 6 of the 1st volume IOR of OR Monograph2–5), generalizing Planck’s quantum mechanics and de Broglie’s matter-wave theory and moving towards the unification of relativity theory and quantum theory.21
The theory of OR2–5 lists the problem of photon mass as one of the 15 big puzzles in modern physics, involving two fundamental questions:
The 1st volume of OR monograph, Inertial Observational Relativity (IOR), theoretically proves that photons, like all material particles, possess the objective and real mass, that is, the so-called rest mass mo; the 2nd volume of OR monograph, Gravitational Observational Relativity (GOR), theoretically proves that the theoretical value of the rest mass of a photon with frequency f is mo = hf/c2.
OR serial report 11 has elucidated the logical and theoretical correctness of OR as well as the empirical basis and empirical evidence of OR.
OR serial report 2 focuses on interpreting BP-02: The Problem of Photon Mass, one of the 15 big puzzles in modern physics listed by the theory of OR.
The matter is the objective existence and physical reality of the natural world. The mass is the quantity of matter contained in a material object or a material system.
Excluding electromagnetic radiation, gravitational radiation, and other mass adsorption or mass dissipation, the mass of a matter system should be conserved.
According to the theory of OR, a material object or system, whether it is a massive star or a tiny photon, must possess its own intrinsic mass if it exists objectively; otherwise, it does not exist. This is in line with dialectical materialist views of matter and nature.
So, what views on matter and mass did Newton and Einstein hold respectively?
The concept of mass originated from Newton.
In his book The Mathematical Principles of Natural Philosophy, Newton wrote22: “The quantity of matter is that measure of it which arises from its density and from its density and volume conjointly.”
This passage can be roughly understood as:
The mass of matter makes the material object present both inertial effects and gravitational effects.
In Newtonian mechanics, the inertial and gravitational effects of mass are clear and unambiguous. Newton’s second law, F = ma, embodies the inertial effect of mass m, and Newton’s law of universal gravitation, F = GMm/r2, embodies the gravitational effect of mass m.
The existence of gravitational interaction is objective.
A balance can be used to measure the weight of an apple on the surface of the earth, which is related to the gravitational force of the earth or the gravitational interaction between the earth and the apple but not to whether the spacetime around the earth is curved.
However, Newton seemed unsure whether the mass that embodied the inertial effect and the mass that embodied the gravitational effect were the same. Thus, Newton proposed the concepts of inertial mass mI and gravitational mass mG.
Regarding the materiality of light, there have been two doctrines in history: the corpuscular theory of light and the wave theory of light. It was Newton who proposed the corpuscular theory of light. As early as 1675, Newton put forward the hypothesis that light is composed of tiny particles of matter.23
However, Newton was unable to determine the volume V and density d of a photon; therefore, he was unable to calculate the mass m of a photon based on his own definition.
According to the theory of OR, Newtonian mechanics is the theory of the idealized observation agent OA∞. For ease of distinction, we agree to use the following symbols.
Einstein’s view of mass seems to differ from Newton’s. In his theory of relativity, Einstein did not explicitly adopt the concepts of inertial mass mI and gravitational mass mG but introduced two new mass concepts: the rest mass mo and the moving mass m.
2.2.1 Einstein’s Relativistic Mass
According to the mass-speed relation in Einstein theory of special relativity:
A material object P, as the observed object, possesses both its rest mass mo and moving mass m, in which m = m(v) is relativistic, involving the speed v of the observed object P relative to the observer O.
Therefore, which, mo or m, represents the objective and real mass of the observed material object P? Or, which one, mo or m, has the objectively real inertial and gravitational effects? In Einstein’s theory of relativity, the inertial and gravitational effects of mass are relativistic and ambiguous rather than clear.
People often mistakenly think that, in Einstein’s theory of relativity, inertial mass and gravitational mass are the same. In fact, Einstein’s relativistic mass also distinguishes between inertial mass and gravitational mass, involving the relativistic mass-speed relation, mass-energy formula, gravitational field equation, gravitational motion equation, and even the Planck equation.
According to the theory of OR, Einstein relativity theory is that of the optical observation agent OA(c). For ease of distinction, we agree to use the following symbols.
(1) mo: the rest mass (independent of observation);
(2) m(c) = mI(c): Einstein’s moving mass or Einstein’s inertial mass;
(3) mG(c): Einstein’s gravitational mass.
Here, m(c) or mI(c) and mG(c) are all the relativistic masses observed by the optical agent OA(c), contain observational effects and apparent phenomena, and are not entirely objective or real.
2.2.2 Einstein’s Photon Mass
According to Einstein relativity theory, a photon, as a material particle, should possess both the rest mass mo and moving mass m. However, Einstein’s photons seem quite peculiar: they only have the moving mass and no the rest mass.
The Rest Mass of Photons: m o = 0
According to Einstein’s mass–speed relation (Eq. (1)), if the speed v of the observed object P reaches the speed of light c, either its rest mass mo becomes infinitely small or its moving mass m becomes infinitely large.
A physical quantity of infinity contradicts the principle of physical observability; no observation agent can observe it. Therefore, Einstein could only set the rest mass of photons to zero: mo = 0.
In fact, the physical quantity of infinitesimal also contradicts the principle of physical observability: the physical quantity of infinitesimal QP implies that the physical quantity 1/ QP is infinitely large; either the observed object P does not exist, or the physical or material effects of P represented by QP do not exist.
The Moving Mass of Photons: m = hf/c 2
Einstein’s theory of relativity alone cannot determine the moving mass m of a photon. Therefore, Einstein had to resort to the Planck equation E = hf, although the Planck equation was originally merely a hypothesis and did not belong to the theoretical system of Einstein relativity theory.
According to Einstein’s theory of special relativity, since a photon has no rest mass (mo = 0), it naturally has no rest energy: Eo = moc2 = 0. Therefore, the kinetic energy of a photon is K = E − Eo = E = mc2. The energy E = hf in Planck’s hypothesis of energy quanta is the kinetic energy of photons. Thus, using the Planck equation, Einstein obtained the relativistic moving mass of photons as m = hf/c2.
The moving mass of photons obtained in this manner is not only used in the inertial-motion model of photons, but also in the gravitational-interaction model of photons.
2.2.3 Hawking Singularity
Our reason and logic dictate that the mass of material object P at a specific moment should be deterministic and unique. However, according to Einstein’s relativistic mass-speed relation (Eq. (1)), the mass of P not only expands but also depends on observation.
As depicted in Figure 1, for an apple resting on the surface of the earth, its mass observed by the relatively stationary observer Oo is the rest mass mo of the apple; however, its mass observed by the relatively moving observers O′ and O ″ are its moving masses, which are greater than the rest mass: m(v ″) > m(v′) > mo—the higher the speed of the observer relative to the apple, the greater the moving mass of the apple. Therefore, different observers, such as the stationary observer Oo, train observer O′ and plane observer O ″, have different masses of the apple.
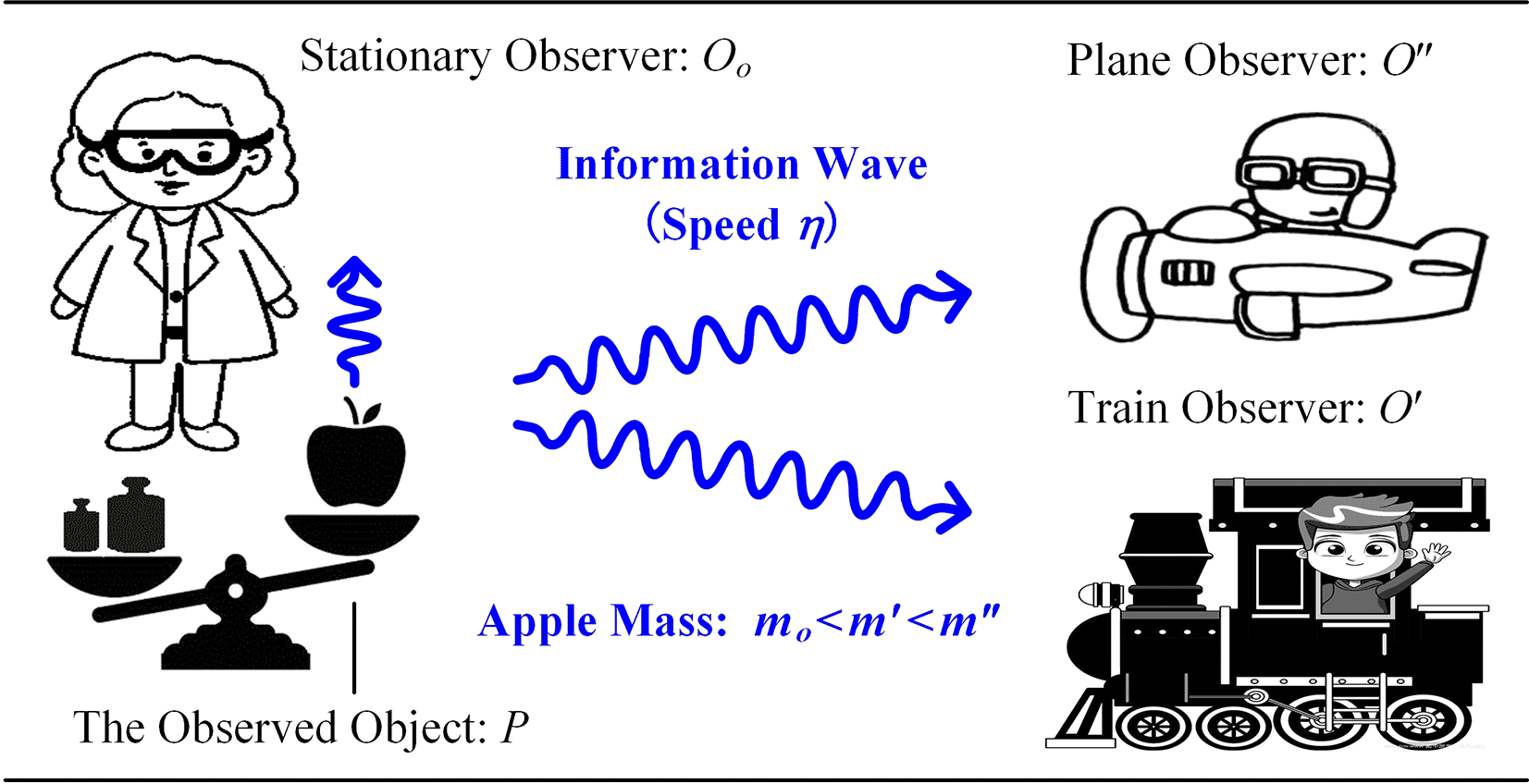
Annotations: (1) Observed object P: an apple; (2) Stationary observer Oo: a balance or an observer stationary relative to P; (3) Observer O′: a train driver; (4) Observer O ″: a plane driver; (5) mo: the rest mass of the apple; (6) m′ and m ″: the moving masses of the apple observed by O′ and O ″, respectively.
This means that Einstein’s relativistic mass relies on or depends on observation and observers and is not entirely objective and real.
The theory of OR has clarified that the rest mass mo is the objective and real mass of matter, possessing objectively real inertial and gravitational effects. Removing the rest mass mo, the remaining part Δm = m − mo of Einstein’s relativistic moving mass m is purely an observational effect of the optical agent OA(c), rather than the objectively real physical existence, and naturally, has no objectively real inertial and gravitational effects.
Therefore, the null rest mass of photons implies that they have no objectively real mass. This would signify that photons would have no objectively real momentum and energy, and thus, photons would no longer be the objectively physical existence.
The reason for the formation of such a paradox lies in Hawking Singularity.
There is a singularity in the mass-speed relation of Einstein special relativity: Hawking Singularity. The theory of OR also has Hawking Singularity.
The theory of OR has discovered that light and photons play a special role in Einstein’s theory of relativity. Einstein’s theory of relativity, both special and general, is a theory of optical observation armed with the optical agent OA(c). OA(c) adopts light as the observation medium; therefore, its information wave is light, and its informons are photons.
Therefore, in Einstein’s theory of relativity, the physical quantities of light and photons, including the speed of light and the mass of photons, are all located at the singularities of the theoretical model.
Based on the mass-speed relation of his special relativity, Einstein deduced that the rest mass mo of photons is zero, and precisely, the speed of light v = c falls at the singularity of the mass-speed relation m = mo/√(1 − v2/c2).
In A Brief History of Time, Hawking wrote24: “Mathematics cannot really handle infinite numbers. At singularity, the theory itself breaks down or fails.”
It can be seen that the rest mass of a photon is not truly zero, but only means that Einstein’s mass-speed relation fails at Hawking Singularity (v = c).
The singularities in all theoretical models of Einstein relativity theory are rooted in Einstein’s hypothesis of the invariance of light speed and are characterized by the Lorentz factor in the Lorentz transformation: γ = 1/√(1 − v2/c2), where the singularity v = c can be referred to as the Lorentz singularity. Similarly, there is the general Lorentz transformation in the theory of OR, in which the general Lorentz factor is Γ = 1/√(1 − v2/η2) and the singularity v = η can be referred to as the general Lorentz singularity.
Both the Lorentz singularity and general Lorentz singularity are referred to as the Hawking singularity in this article and even in the theory of OR.
Originally, the author of OR believed in Einstein’s theory of relativity, believing that the universe possesses the invariant and unsurpassable speed. However, based on the dialectical materialist view of nature, the author of OR cannot accept Einstein’s assertion that photons have no rest mass.
Therefore, the author attempted to establish a theoretical model of the expected photon mass (EPM) that can confer the rest mass on photons.
Unexpectedly, however, the theoretical model of the EPM has evolved into the theory of OR.
The so-called ultimate speed of the universe refers to the speed that cannot be surpassed.
In 1905, based on the Michelson-Morley experiment, Einstein proposed the principle of the invariance of light speed, theoretically derived the Lorentz transformation, and finally established his theory of special relativity6 and his theory of general relativity.7
The hypothesis of the invariance of light speed is the fundamental and indispensable logical premise of Einstein relativity theory, both special and general.
The hypothesis of invariance of light speed implies that the speed of light is the ultimate speed of the universe, which cannot be surpassed by any other form of matter motion in the universe.
The author of OR once even believed that the ultimate speed of the universe is not only unsurpassable but also inaccessible or unattainable by all forms of matter motion in the universe, including light or photons.
Perhaps the ultimate speed of the universe should be defined with Λ as follows:
The Ultimate Speed of the Universe: The speed |v| → Λ (< + ∞) at which the frequency f of the matter wave of a moving object P converges to infinity is referred to as the ultimate speed of the universe.
To maintain the feasibility of logical deduction, Definition 3.1 does not limit the speed of matter motion to reach Λ. However, although the frequency of light waves is very high, it is still finite. Therefore, the speed of light may be less than the ultimate speed Λ of the universe, defined in Definition 3.1: c < Λ. In this case, the mass-speed relation m = mo/ √(1 − v2/c2) in Einstein’s theory of special relativity can be rewritten as
This is the EPM model envisioned by the author.
If the moving mass m of photons and the ultimate speed Λ of the universe can be determined, the rest mass mo of photons can theoretically be calculated as follows:
;
then the rest mass mo of photons would no longer be zero.
Definition 3.1 has two direct logical consequences.
Observational Limit Speed Λ : The observed speed v of any moving object P cannot exceed the ultimate speed Λ of the universe; that is, ∀v|v| ≤ Λ.
Ultimate Speed Invariance: Relative to all inertial observers, the ultimate speed Λ of the universe is the same or invariant.
According to the theoretical model of the EPM (Eq. (2)), the ultimate speed Λ of the universe should be greater than the speed of light c in vacuum; otherwise, photons would still be unable to acquire the rest mass.
So, what exactly is the ultimate speed Λ?
The author of OR originally thought that the invariant speed, that is, the ultimate speed of the universe, is Λ defined by Definition 3.1 rather than the speed of light c. Based on this idea, the author embarked on establishing an axiom system, in the hope of being able to deduce a spacetime transformation relation for the theoretical model of EPM that confer the rest mass on photons.
Compared to Newtonian mechanics and Einstein relativity theory, the EPM model and the theory of OR have more basic logical premises and axiom system1–5:
(I) The Principle of Physical Observability
(II) The Conditions of Wave-Particle Duality
(III) The Definition of Time
(IV) The Principle of GOR Equivalence
(V) The Principle of GOR Covariance
As stated by the theory of OR,1–5 in the axiom system of OR, only the definition of OR time serves as an indispensable logical premise for the theory of OR, including IOR and GOR.
Time is the most basic physical quantity in physics. In a sense, the definition of OR time can be regarded as the first principle or the most basic logical premise.
In the axiom system of OR, the principle of physical observability and the conditions of wave-particle duality serve as auxiliary logical premises for the theory of IOR. To deduce the theory of GOR based on IOR, there are two additional auxiliary logical premises in the axiom system of OR: the principle of GOR equivalence, and the principle of GOR covariance.
The logical deduction of the EPM model and the spacetime transformation of OR requires a physical quantity, whose physical significance is very clear1: the speed of the spacetime information of the observed object P relative to the observer O, denoted as η.
The theoretical derivation has led to an intriguing logical consequence2–5: Λ = η!
Λ = η suggests that the so-called ultimate speed of the universe is actually only the speed η at which the information on the observed object P is transmitted, depending on the observation medium that is employed in the observation by observer O.
Thus, the theory of OR has discovered that all theoretical systems in human-developed physics are linked to specific observation media or observation systems and must be branded with observation. Human perception of the objective world relies on observation and is restricted by observation. This has led to the formation of the concepts of Observation Agent and Observational Locality in the theory of OR.
This implies that the relativistic physical quantities of the observed object P, including the relativistic moving mass of P, are physical quantities observed by a specific observation agent OA(η) (η < ∞), restricted by the observational locality of OA(η) (η < ∞), and are not completely objective and real.
3.3.1 Observation Agent: OA(η)
Theoretically, all forms of matter motion or matter waves can serve as observation media to transmit the information on the observed object P to the observer O.
The theory of OR establishes an important concept: Observational Agent.
Observation Agent: The observation agent OA(η) or observation system (P, M(η),O) employs the observation medium M(η) to transmit the information about the observed object P for the observer O at a speed η; the matter wave M(η) that transmits information is referred to as the information wave of OA(η), and the matter particles constituting the information wave of OA(η) are referred to as the informons of OA(η).
The concept of Informon originates from Železnikar, referring to the material particles that load and transmit information.25
Theoretically, the information wave of the general observation agent OA(η) (0 < η < ∞; η → ∞) can be any form of matter motion, and the informons of OA(η) can be any material particles, even a rock. Naturally, the information-wave speed η of OA(η) can theoretically have any value.
In particular, OA∞ (η → ∞) represents Galileo and Newton’s idealized observation agent, and OA(c) (η → c) represents Einstein’s optical observation agent.
The theory of OR is the theory of the general observational agent OA(η) (0 < η < ∞; η → ∞), which is the complete theory in Hawking’s sense, so Newton’s classical mechanics and Einstein’s relativity theory are merely two partial theories of OR.1
3.3.2 Observational Locality: ∀OA(η) η < ∞
In modern physics, the principle of locality plays an important role.26,27 The principle of observational locality can be expressed as a corollary of the locality principle.
The Principle of Observational Locality (POL)2–5: According to the principle of locality, the information-wave speed η of a realistic observation agent OA(η) must be finite or limited (η < ∞); it takes time for the information wave of OA(η) to cross space.
All observation agents with which mankind perceives the objective world, such as the human eye and ear, have the observational locality.
The theory of OR has discovered that all relativistic effects or phenomena, including time dilation and length contraction, the relativity of simultaneity, the null rest mass of photons, spacetime curvature, and even the invariance of light speed, are observational effects and apparent phenomena rather than objective and real physical realities, the root and essence of which lie in the observational locality of human observation agents.
Theoretically, all forms of matter motion or matter waves, not just light or electromagnetic interaction, can serve as observation media or information waves to transmit the information about observed objects for observers, and the information-wave speed (the transmission speed of observed information) η of the observation agent OA(η) can be any speed, not just the speed of light c.
Λ = η leads to an important theorem in the theory of OR --
The Invariance of Information-Wave Speeds: ∀u∈(−η, η) η ⊕ u = η. 1–5
The theorem of the invariance of information-wave speeds states that if observers employ an specific observation agent OA(η) to perceive or observe the objective world, owing to the observational locality (η < ∞) of OA(η), the information-wave speed η of OA(η) becomes the ultimate speed Λ of the observers. Therefore, from the perspective of the observers, the information-wave speed η of OA(η) is invariant relative to the observers or OA(η), and cannot be surpassed by the speeds of observed objects.
This implies that the universe does not truly possess ultimate or unsurpassable speed. The speed of light is not invariant. The invariance of light speed is merely a special case of the invariance of information-wave speeds, and it is valid only if observers observe the physical world through light or electromagnetic waves.
Einstein’s theory of relativity, both special and general, has existed for over 100 years. People still do not understand why the speed of light is invariant. However, readers must understand the invariance of information-wave speeds.
As stated in OR serial report 1,1 the invariance of information-wave speeds is not only a product of logic and theory, but also has empirical basis and empirical evidence, supported by observations and experiments. In the Michelson-Morley experiment, the invariance of light speed is only a phenomenon, whereas the invariance of the information-wave speeds is the essence. As empirical evidence, the Michelson-Morley experiment does not support Einstein’s invariance of light speed, but supports the invariance of information-wave speeds.
OR serial report 11 has elucidated how to deduce the theory of OR based on the invariance of information-wave speeds, including IOR and GOR.
Based on the axiom system of OR, starting from the definition of time, to the invariance of the time-frequency ratio, to Λ = η, to the invariance of information-wave speeds, and ultimately, the author’s original intention of EPM has evolved into the theory of OR.
The theory of OR has achieved and surpassed the original intention of EPM.
The theory of OR has revealed the root and essence of the relativistic effects in Einstein’s theory of relativity: all relativistic effects or relativistic phenomena, including inertial and gravitational, are observational effects and apparent phenomena caused by the observational locality (c < ∞) of Einstein’s optical agent OA(c).
Einstein’s assertion that photons have no rest mass is limited from the perspective of optical observation, and its root also lies in the observation locality (c < ∞) of the optical observation agent OA(c).
OR serial report 2 only discusses photon-mass issue.
The theory of OR suggests that the rest mass of photons is not zero.
As the author of OR wishes, the theory of IOR theoretically proves that photons, like all other material particles, have their own rest mass: mo > 0, and the theory of GOR predicts that the rest mass of a photon with frequency f is mo = hf/c2.
Photon-mass problem 1: Does a photon have its own rest mass?
The answer of the theory of IOR is affirmative.
The theory of Inertial Observational Relativity (IOR) has generalized and unified Newton’s inertial mechanics and Einstein’s special relativity.1
According to the theory of OR, the rest mass is exactly the objectively real mass of matter; all material particles, including photons, have their own rest mass (see Chapter 5 of the 1st volume IOR of OR monograph2–5).
The theory of IOR is a theory of inertial motion for the general observation agent OA(η) (0 < η<∞; η → ∞), in which the IOR factor Γ(η, v) = 1/√(1 − v2/η2) is the characteristic physical quantity of IOR, characterizing the relativistic effects of the inertial spacetime and inertial motion observed by OA(η).
If v < η, the IOR relativistic factor Γ(η, v) can be decomposed into the Galilean factor Γ∞ and the observational-effect factor ΔΓ(η, v) in term of Taylor series:
The theory of IOR theoretically derives the IOR mass-speed relation of inertial spacetime related to the IOR factor Γ(η, v) for the general observation agent OA(η) (0 < η < ∞; η → ∞):
Similar to Einstein’s mass-speed relation (Eq. (1)), the IOR mass-speed relation (Eq. (4)) is also relativistic, relying on the relative speed v between the observer O and the observed object P. Therefore, the moving mass m of P is also a relativistic mass: m = m(v).
However, the IOR mass-speed relation indicates that, in essence, the moving mass m = m(η) of the observed object P depends on observation, on the observation agent OA(η), and on the information-wave speed η of OA(η). The lower the η value, the more significant the relativistic effects exhibited by P. Therefore, the theory of OR refers to the relativistic mass m as the observed mass, that is, the mass observed by the observation agent OA(η).
The theory of IOR is the theory of the general observation agent OA(η). For ease of distinction, we agree to use the following symbols.
According to the IOR mass-speed relation, the IOR moving mass m = m(η) is the observed mass with the general observation agent OA(η), depending on observation: for the same observed object P, different observation agents have different observed masses. This suggests that the IOR moving mass m = m(η) contains the observational effects and apparent phenomena caused by the observational locality (η < ∞) of the observation agent OA(η) and is not completely objective and real, but only a sort of mass in the sense of observation.
Similar to Einstein’s mass-speed relation (Eq. (1)), the IOR mass-speed relation (Eq. (4)) also has Hawking Singularity: v = η. Following Einstein’s logic, we should set the rest mass of the informons for all observation agents to zero.
This paradox stems from Einstein’s misconception of Hawking Singularity (v = c) in his mass-speed relation. This does not mean that the rest mass of the informons of the observation agent OA(η) (including the photons of OA(c)) is really zero. This only means that, in Hawking’s words, the IOR mass-speed relation fails at Hawking Singularity (v = η), and that, restricted by the observational locality (η < ∞) of OA(η), the speed v observed by OA(η) cannot reach the information-wave speed η of OA(η): v < η.
If v < η, the IOR moving mass m(η, v) or inertial mass mI(η, v) can be decomposed in term of Taylor series (Eq. (3)) of Γ(η, v) as follows:
Given the relative v between the observer O and the observed object P, the higher the information-wave speed η of OA(η), the smaller the apparent mass Δm(η, v) becomes, and the closer the IOR observed mass m(η, v) is to the objective and real rest mass mo of P.
The observed mass m(η, v) in the IOR mass-speed relation has generalized and unified Einstein’s relativistic moving mass m(c) and Newton’s classical inertial mass m∞ = m I∞. Now, from the broad perspective of the general observation agent OA(η) (0 < η < ∞; η → ∞), we reexamine Einstein’s relativistic moving mass and Newton’s classical inertial mass.
In fact, Einstein’s moving mass m(c, v) or inertial mass mI(c, v) is merely a special case of the IOR observed mass, that is, the mass m = m(c) (η = c) observed with the optical agent OA(c).
If η → c, then OA(η) → OA(c) and the IOR mass-speed relation strictly converges to the mass-speed relation of Einstein special relativity:
Einstein’s optical agent OA(c) has the observational locality: c<∞, the observational-effect factor ΔΓ(c, v) > 0, and the apparent mass ∆m(c, v) > 0. Therefore, Einstein’s moving mass m(c, v) contains the observational effects of OA(c) rather than the completely objective and real mass of the observed object P.
Owing to the observational locality (c < ∞) of the optical agent OA(c), we cannot employ OA(c) to measure or determine the mass of the observed object P if P reaches or exceeds the speed of light c.
Einstein’s assertion that the rest mass of photons is zero roots from Hawking Singularity v = c in the mass-speed relation of the optical agent OA(c). This does not mean that the rest mass of photons is really zero, but merely that the mass-speed relation of OA(c) fails at the Hawking Singularity v = c: OA(c) cannot determine the mass of photons (just as you cannot lift yourself up).
If we aspire to measure the objective and real rest mass of photons, we must be equipped with a superluminal observation agent OA(η) (η > c).
Newton’s classical mass m∞ or inertial mass m I∞ is also a special case of the IOR observed mass, that is, the observed mass m = m(∞) (η → ∞) with the idealized agent OA∞.
The information-wave speed of OA∞ is idealized as infinitely large: η → ∞, with no observational locality, it takes no time for the information wave of OA∞ to cross space. Therefore, the idealized agent OA∞ might be regarded as the God’s eye: Galileo-Newtonian inertial mechanics represents the objective and real inertial spacetime; its classical mass m∞ or inertial mass m I∞ is the objective and real moving mass or inertial mass of the observed object P.
According to the definition of the IOR moving mass, as the observed physical quantity of the idealized agent OA∞, Newton’s inertial mass m I∞ should be the IOR observed mass m∞ = m(∞) when η → ∞
Equation (7) has enlightening implications1:
There is no idealized observation agent OA∞ in the objective world: OA∞ could only exist in human reason.
For a realistic observation agent OA(η) (0 < η < ∞), the IOR mass-speed relation (Eq. (4)) also has Hawking Singularity: v = η, where the speed v of the informons of OA(η) coincides with Hawking Singularity: v = η. Theoretically, any material particle can serve as an informon of OA(η). Of course, this does not imply that it has no rest mass, but that the IOR mass-speed relation fails at the Hawking Singularity v = η.
According to the IOR mass-speed relation, for any material object P being observed, regardless of how fast its speed v is, the idealized agent OA∞ or an observation agent OA(η) (η > v) can tell us that P definitely possesses the objective and real rest mass mo of its own:
Thus, the theory of IOR theoretically proves that all matter or material particles, including photons and even gravitons, possess their own objective and real rest mass, exhibiting objective and real inertial effects.
This logical consequence conforms to the dialectical materialist view of nature.
If we can be equipped with a superluminal observation agent OA(η) (η > c), we can measure and determine the objectively real rest mass mo of a photon (v = c):
Photon-mass problem 2: How much does a photon weigh?
According to the theory of IOR, only the rest mass is the intrinsic and objectively real mass of matter; photons, like all other material particles, possess their own rest mass, and the objectively real inertial effect of a photon is just the physical effect generated by its own rest mass.
However, the theory of IOR remains uncertain as to how much a single photon weighs.
The task of calculating the theoretical value of the rest mass of photons is left to the theory of Gravitational Observational Relativity (GOR).
The theory of GOR has generalized and unified Newton’s theory of universal gravitation and Einstein’s theory of general relativity.1 According to the theory of GOR, the rest mass of matter not only has the objectively inertial effects, but also the objectively gravitational effects.
It is based on the gravitational effects of photons that the theory of GOR theoretically calculates and predicts the theoretical value of the rest mass mo of a photon with frequency f: mo = m = hf/c2 (see Chapter 18 of the 2nd volume GOR of OR monograph2–5).
The theory of GOR is a theory of gravitational interaction for the general observation agent OA(η) (0 < η < ∞; η → ∞), in which the GOR factor Γ(η, v,χ) = 1/√(1 − v2/η2 + 2χ/η2) is the characteristic physical quantity of GOR, characterizing the relativistic effects of the material object P in gravitational spacetime observed by OA(η).
If α < η (α2 = v2 − 2χ), the GOR relativistic factor Γ(η, v,χ) can be decomposed into the Galilean factor Γ∞ and the observational-effect factor ΔΓ(η, v,χ) in term of Taylor series:
The theory of GOR theoretically derives the GOR mass-speed relation of gravitational spacetime related to the GOR factor Γ(η, v,χ) for the general observation agent OA(η) (0 < η < ∞; η → ∞):
The GOR mass-speed relation indicates that, in essence, the relativistic mass m of P depends on the observation agent OA(η) and on the information-wave speed η of OA(η): m = m(η). The lower the η value, the more significant the relativistic effects exhibited by P. Therefore, the relativistic mass m(η, v,χ) of OR gravitational spacetime is also the mass observed with the general observation agent OA(η).
If α < η (α2 = v2 − 2χ), then the GOR observed mass m(η, v,χ) can be decomposed into the objectively real rest mass mo and the purely apparent mass Δm(η, v,χ) in term of Taylor series (Eq. (10)) of Γ(η, v,χ):
Given the moving speed v of the observed object P and the Newtonian gravitational potential χ where P is located, the higher the information-wave speed η of OA(η), the smaller the apparent mass Δm(η, v,χ) and the closer the GOR observed mass m(η, v,χ) is to the objectively real rest mass mo of P.
The GOR mass-speed relation (Eq. (11)) generalizes the IOR mass-speed relation (Eq. (4)). The GOR observed mass m (η, v,χ) generalizes the IOR observed mass m(η, v).
Similar to the theory of IOR, the mass in the theory of GOR as a theory of gravitation for the general observation agent OA(η) (0 < η < ∞; η → ∞) is also the observational mass observed by OA(η), or called the GOR observed mass, which may not necessarily be completely objective and true.
However, unlike the theory of IOR, the mass in the theory of GOR not only has inertial effects but also gravitational effects. It is worth noting that, with the realistic observation agent OA(η) (0 < η < ∞), the observed inertial mass and the observed gravitational mass are different.
Therefore, the concepts of inertial mass and gravitational mass, which originated in Newton, truly acquire their existence value and significance in the theory of GOR.
5.2.1 GOR Inertial Mass and Gravitational Mass: Observed by OA(η)
Newton thought that matter might have inertial mass and gravitational mass: inertial mass embodied the inertial effects of matter; gravitational mass embodied the gravitational effects of matter.
Einstein introduced the concepts of moving mass and rest mass in his relativity theory. However, Einstein never explicitly used the concept of gravitational mass. It is thought that the gravitational mass and inertial mass are equal in Einstein’s theory of relativity. In fact, it is also necessary for Einstein relativity theory to distinguish between inertial mass and gravitational mass.
Based on the GOR mass-speed relation (Eq. (11)), the theory of GOR defines two concepts of the observed mass for the general observation agent OA(η) as follows.
The Inertial Mass Observed by OA(η):
The Gravitational Mass Observed by OA(η):
The GOR definitions (Eqs. (13-14)) on the observed mass clarifies the concepts of inertial mass and gravitational mass in the theory of OR. Note that the concept of inertial mass in the theory of GOR (Eq. (13)) is equivalent to the concept of moving mass in the theory of IOR (Eq. (4)).
It is noteworthy that the inertial mass mI(η) = m(η,v,0) (Eq. (13)) of the observed object P in the theory of GOR gravitational spacetime is generally not equivalent to the gravitational mass mG(η) = mG(η,0,χ) (Eq. (14)) of P: mG(η) ≠ mI(η).
In particular, the GOR observed inertial mass (Eq. (13)) has generalized and unified the relativistic inertial mass of Einstein’s optical agent OA(c) and the classical inertial mass of Newton’s idealized agent OA∞; the GOR observed gravitational mass (Eq. (14)) has generalized and unified the relativistic gravitational mass of Einstein’s optical agent OA(c) and the classical gravitational mass under Newton’s idealized agent OA∞.
Therefore, in the theory of OR, the GOR mass (Eq. (12)) observed by the general observation agent OA(η) ((0 < η < ∞; η → ∞) has generalized and unified the relativistic mass of Einstein’s optical agent OA(c) and the classical mass of Newton’s idealized agent OA∞.
5.2.2 Einstein’s Inertial Mass and Gravitational Mass: Observed by OA(c)
Einstein’s theory of relativity is also required to distinguish between the inertial mass mI(c, v,0) and gravitational mass mG(c,0,χ). In fact, the relativistic mass in Einstein general relativity is merely a special case of the GOR observed mass, that is, the observational mass observed by the optical agent OA(c).
As the mass observed by the general observation agent OA(η), the GOR observed mass naturally generalizes the mass observed by the optical agent OA(c) in Einstein general relativity.
If η → c, then OA(η) → OA(c) and the GOR inertial mass mI(η) = m(η,v,0) (Eq. (13)) observed by OA(η) strictly converges to the inertial mass mI(c) = m(c,v,0) observed with the optical observation agent OA(c) in Einstein general relativity:
If η → c, then OA(η) → OA(c) and the GOR gravitational mass mG(η) = m(η,0,χ) (式(14)) observed by OA(η) strictly converges to the gravitational mass mG(c) = m(c,0,χ) observed with the optical agent OA(c) in Einstein general relativity:
Because of the observational locality of the optical agent OA(c): c < ∞, both the inertial mass mI(c) = m(c,v,0) and the gravitational mass mG(c) = m(c,0,χ) in Einstein’s general relativity contain the observational effects of OA(c) and are not completely objective and real.
People, including physicists, often mistakenly thought that in Einstein’s theory of relativity, inertial mass was equal to gravitational mass and frequently incorrectly employed Einstein’s relativistic moving mass as gravitational mass in the theoretical models of gravitational interaction.
In Einstein’s theory of general relativity, the moving mass or inertial mass mI(c) = m(c,v,0) (Eq. (15)) is not equal to the gravitational mass mG(c) = m(c,0,χ) (Eq. (16)): mG(c) ≠ mI(c).
5.2.3 Newton’s Inertial Mass and Gravitational Mass: Observed by OA ∞
In Eq. (7) of IOR theory, m∞ represents only the idealized observed mass in inertial spacetime and does not signify Newton’s classical mass. As the observed mass of the idealized observation agent OA∞, Newton’s classical mass m∞ should be the idealized observed mass m∞ = m(∞) in the GOR mass-speed relation (Eq. (11)) if the information-wave speed η of the observed agent OA(η) is idealized as infinity (η → ∞):
Significantly, Eq (17) indicates that Newton’s classical mass m∞ is exactly the objective and real rest mass mo of matter or matter particles.
Newton’s classical inertial mass mI(∞, v,0) and classical gravitational mass mG(∞,0,χ) are also special cases of the GOR observed mass, that is, the observed mass with the idealized observation agent OA∞.
As the mass observed with the general observation agent OA(η), the GOR observed mass naturally generalizes the mass observed with the idealized observation agent OA∞, that is, Newton’s classical mass.
If η → ∞, then OA(η) → OA∞ and the GOR inertial mass mI(η) = m(η,v,0) (Eq. (13)) observed by OA(η) strictly converges to the inertial mass m I∞ = m(∞,v,0) observed with the idealized agent OA∞ in Newton’s classical mechanics as follows:
If η → ∞, then OA(η) → OA∞ and the GOR gravitational mass mG(η) = m(η,0,χ) (Eq. (14)) observed by OA(η) strictly converges to the gravitational mass m G∞ = m(∞,0,χ) observed with the idealized agent OA∞ in Newton’s classical mechanics as follows:
Just like Eq. (7), Eqs. (17-19) have enlightening implications1:
(1) Newton’s classical mass m∞, inertial mass m I∞, and gravitational mass m G∞ are all equivalent to the objective and real rest mass mo of matter or matter particles:
(2) The idealized agent OA∞ has no the observational locality (η → ∞); therefore, Newton’s classical mass m∞ represents the objective and real mass of matter or material particles, presenting both the objectively real inertial effects and gravitational effects of matter.
(3) There is no need to distinguish between the inertial mass m I∞ and gravitational mass m G∞ for the objectively real mass of matter.
Similar to the theory of IOR, the energy in the theory of GOR as a theory of gravitation for the general observation agent OA(η) (0 < η < ∞; η → ∞) is also the observational energy observed by OA(η) or called the GOR observed energy, which may not necessarily be completely objective and true.
However, unlike the theory of IOR, the energy of matter or material particles in the theory of GOR not only has kinetic energy but also potential energy.
5.3.1 GOR Kinetic Energy and Potential Energy: Observed by OA(η)
According to the principle of GOR relativity or GOR covariance, all observers are equal or have equal rights, and all observation agents are equal or have equal rights.2–5 Thus, the laws of physics have the same form or corresponding relationship of isomorphic consistency for different observers and for different observation agents.
Therefore, in the gravitational spacetime observed by the general observation agent OA(η), the observed object P, similar to that observed by the idealized agent OA∞, has both the kinetic energy K(η), potential energy V(η), and total energy H (η), following the principle of energy conservation: H(η) = K(η) + V(η).
Based on the GOR mass-speed relation (Eq. (11)), the theory of GOR defines two concepts of observed energy for the general observation agent OA(η) as follows.
The Kinetic Energy Observed by OA(η):
The Potential Energy Observed by OA(η):
Then, the total energy of the observed object P in the GOR gravitational spacetime is
The GOR observed kinetic energy (Eq. (21)) has generalized and unified the relativistic kinetic energy of Einstein’s optical agent OA(c) and the classical kinetic energy of Newton’s idealized agent OA∞; the GOR observed gravitational mass (Eq. (22)) has generalized and unified the relativistic potential energy of Einstein’s optical agent OA(c) and the classical potential energy of Newton’s idealized agent OA∞.
Therefore, the GOR energy-conservation formula (Eq. (23)) have generalized and unified Einstein’s relativistic energy-conservation formula and Newton’s classical energy-conservation formula.
5.3.2 Einstein’s Kinetic Energy and Potential Energy: Observed by OA(c)
In Einstein’s theory of general relativity, the energy of matter or material particles is observed with the optical observation agent OA(c), and is a special case of the GOR observed energy.
If η → c, then OA(η) → OA(c) and the GOR kinetic energy K(η) (Eq. (21)) observed by OA(η) strictly converges to the kinetic energy K(c) observed with the optical agent OA(c) in Einstein’s general relativity:
If η → c, then OA(η) → OA(c) and the GOR potential energy V(η) (Eq. (22)) observed by OA(η) strictly converges to the potential energy V(c) observed with the optical agent OA(c) in Einstein’s general relativity:
Naturally, if η → c, the total energy (Eq. (23)) H(η) of the object P in gravitational spacetime observed with the general observation agent OA(η) strictly converges to Einstein’s relativistic total energy, that is, the total energy H(c) observed with the optical agent OA(c):
5.3.3 Newton’s Kinetic Energy and Potential Energy: Observed by OA ∞
The energy of matter or material particles in Newton’s theory of universal gravitation is observed with the idealized observation agent OA∞ and is also a special case of the GOR observed energy.
If η → ∞, then OA(η) → OA∞ and the GOR kinetic energy K(η) (Eq. (21)) observed by OA(η) strictly converges to the kinetic energy K∞ observed with the idealized agent OA∞ in Newton’s gravitational theory:
Equation (27) is exactly Newton’s classical kinetic energy formula: K∞=m∞v2/2.
If η → ∞, then OA(η) → OA∞ and the GOR potential energy V(η) (Eq. (22)) observed by OA(η) strictly converges to the potential energy V∞ observed with the idealized agent OA∞ in Newton’s gravitational theory:
Equation (28) is exactly Newton’s classical potential-energy formula: V∞ = −GMm∞/r.
Naturally, if η → ∞, the total energy (Eq. (23)) H(η) of the object P in gravitational spacetime observed with the general observation agent OA(η) strictly converges to Newton’s classic total energy, that is, the total energy H∞ = H(∞) observed with the idealized agent OA∞:
However, as the matter energy from the perspective of the idealized observational agent OA∞ (God’s eye), Newton’s inertial mass and gravitational mass are not that in the observational sense, but the objective and real energy of matter or matter particles.
Before formally establishing his theory of general relativity, Einstein predicted, based on the principle of equivalence, that light in a gravitational field would be curved and exhibit gravitational redshift. This is Einstein’s famous predictions of the gravitational deflection and redshift of light.
Newton’s theory of universal gravitation can also predict the gravitational deflection and redshift of light.
In gravitational fields, all matter or material particles, not just light or photons, may exhibit gravitational deflection and gravitational redshift. Of course, they may also exhibit gravitational blueshift.
In terms of gravitational redshift, if a material object moves in a gravitational field, its energy should follow the principle of energy conservation: its kinetic energy and potential energy constantly change or transform, but the total energy is conserved. Gravitational redshift means the decrease of the object’s kinetic energy; the gravitational blueshift means the increase of the object’s kinetic energy.
5.4.1 Einstein’s Gravitational Redshift of Light
The gravitational redshift or blueshift of light refers to that, in gravitational spacetime, the frequency of light or photons changes with the variation of gravitational potential: the decrease of light frequency, that is, redshift, means the decrease of the kinetic energy of photons; the increase of light frequency, that is, blueshift, means the increase of the kinetic energy of photons.
Einstein’s theory of gravitational redshift of light is the product of his theory of general relativity. Considering the motion scene of light or photons in the spherically-symmetric gravitational spacetime depicted in Figure 2, Einstein’s gravitational-redshift formula for light can be deduced based on the principle of equivalence and the effect of potential clock28:
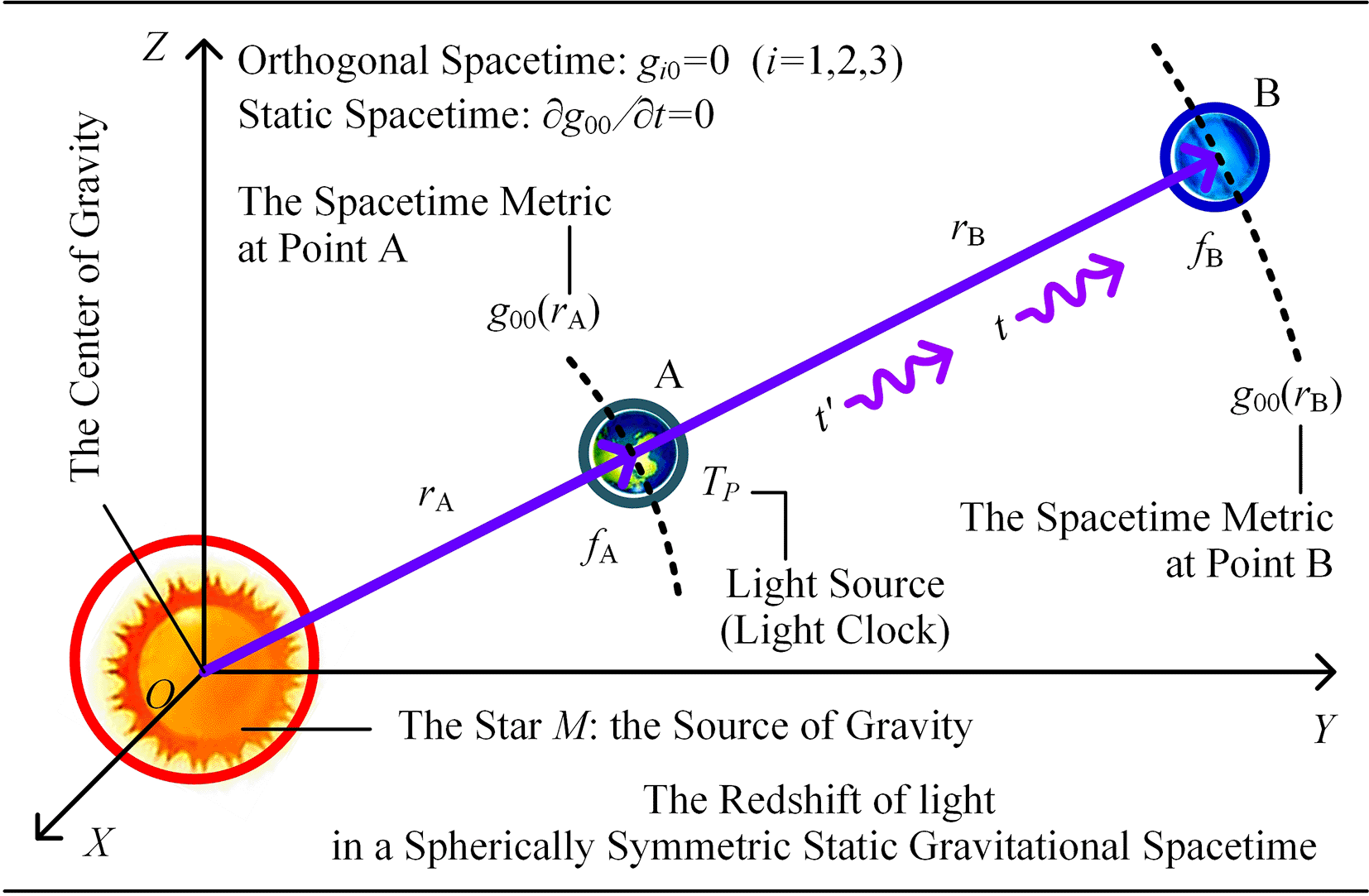
Annotations: The star M is the gravitational source and center of spherically-symmetric gravitational spacetime. The light source (light clock) TP stationary at the point A in the gravitational spacetime of M emits a light signal with the frequency fA towards the distant point B. The observer stationary at the point B receives the light signal with the frequency fB. According to Einstein's principle of equivalence and Einstein's theory of general relativity, fB<fA: the optical signal while propagating in gravitational spacetime exhibits gravitational redshift phenomenon.
The simplest and most feasible way to test or verify Einstein’s prediction for the gravitational redshift of light is for the observers on Earth to observe the solar spectrum originating from the sun.
Let rA be the radius RS of the sun and rB be the distance RS + DSE between the sun and the earth, where DSE >> RS. Then, based on Einstein’s gravitational-redshift formula (Eq. (30)), the gravitational redshift of the solar spectrum can be calculated theoretically as follows:
Adam (1959)29 provided the actual observed value of the redshift in the solar spectrum: Z = −2×10−6. Blamont and Roddier (1961)30 and Brault (1963)31 provided more accurate observed value: Z = −2.12 × 10−6, which is consistent with Einstein’s prediction within the accuracy range of 5%.
The actual observation and spectral analysis of the sun seem to support Einstein’s prediction of the gravitational redshift of light, based on his general relativity.
The scenario of observing the solar spectrum by the observers on Earth can be approximately idealized as the scenario of observing the solar spectrum by the observers in the free spacetime SF: rB → ∞, g00(c, rB) → 1; rA = RS, g00(c, rA) = 1 − 2GMS/RSc2.
5.4.2 Pseudo Newtonian Gravitational Redshift of Light
Newton’s theory of the gravitational redshift of light should naturally be the product of Newtonian mechanics, without the need for the principle of equivalence or the effect of potential clock.
Just as people expect to see the difference in the predictions of the gravitational deflection of light between Einstein and Newton, they also expect to see the difference in the predictions of the gravitational redshift of light between Einstein and Newton.
Unlike gravitational deflection, however, Einstein’s theory of gravitational redshift of light seems to lose the challenge and competition from Newtonian mechanics. Newton’s prediction of the gravitational redshift of light seems to be the same as Einstein’s: they lack observational distinguishability.
To predict the gravitational redshift of light based on Newtonian mechanics, it is necessary to first determine the inertial and gravitational masses of photons. However, in Newtonian mechanics, the mass of photons is uncertain or unknown.
At present, the so-called Newtonian gravitational-redshift formula of light28 takes Einstein’s relativistic mass m as Newton’s classical inertial mass m I∞ and gravitational mass m G∞ and borrows the Einstein formula E = mc2 belonging to Einstein relativity theory and the Planck equation E = hf belonging to quantum mechanics:
By comparing the pseudo Newtonian gravitational-redshift formula (Eq. (32)) and Einstein’s gravitational-redshift formula (Eq. (31)), it can be seen that they are highly approximate and extremely difficult to distinguish in observation.
Accordingly, people think that Einstein’s theory of general relativity and Newton’s theory of universal gravitation are consistent in terms of the gravitational redshift of light.
5.4.3 Newton’s Gravitational Redshift of Light
In fact, Eq. (32) is not truly the gravitational redshift of light based on Newtonian mechanics but a mixture of Newton’s mechanics, Einstein’s relativity theory, and even Planck’s quantum theory, which can be called the pseudo Newtonian gravitational-redshift formula of light.
Completely based on Newtonian mechanics, the theory of OR has derived the true Newtonian gravitational-redshift formula of light and has incorporated it into the theoretical system of GOR.
The essence of the gravitational redshift of light is the transformation of the kinetic and potential energy of photons, following the principle of energy conservation. Therefore, the definition and deduction of the gravitational redshift of light should be based on the perspective of energy or the idea of energy conservation rather than the principle of equivalence or the effect of potential clock.
Based on the idea of energy transformation and the principle of energy conservation, and according to the mass formula (Eq. (20)), and energy formulae (Eqs. (27-29)) of GOR theory, Newton’s gravitational redshift of light can be defined as follows:
Thus, continuing to derive from the definition of Newtonian gravitational redshift of light (Eq. (33)), the true gravitational redshift equation of Newtonian light can be obtained:
Thus, based on the definition of Newtonian gravitational redshift of light (Eq. (33)), the true Newtonian gravitational-redshift formula of light can be obtained as follows:
Considering the scenario where an observer armed with the idealized agent OA∞ on Earth or in the free spacetime SF observes the solar spectrum: M = MS, rA = RS, rB → ∞, and then the Newtonian-gravitational formula (Eq. (34)) of light is reduced to
It can be seen that the gravitational redshift ZN of light based on Newtonian mechanics is twice that of Einstein’s gravitational redshift ZE: ZN = 2ZE, which is not equal to Einstein’s theoretical prediction.
This is in line with the logic of OR: different observational agents, Newton’s idealized agent OA∞ and Einstein’s optical agent OA(c), should have observed different gravitational redshifts of light.
Later, we will verify the validity of the true Newtonian gravitational-redshift formula (Eq. (34)) of light.
5.4.4 GOR Gravitational Redshift of Light
As stated in Section 5.3.3, the essence of the gravitational redshift of light is the transformation of the kinetic and potential energy of photons, following the principle of energy conservation.
Based on the idea of energy transformation and the principle of energy conservation, and according to the GOR mass formulae (Eqs. (13-14)), and energy formulae (Eqs. (21-23)), the gravitational redshift of light observed by the general observation agent OA(η) (η ≥ c) can be defined as
Thus, based on Eqs. (21-23), from the definition in Eq. (36) of the gravitational redshift of light observed by the general observation agent OA(η) (η ≥ c), one can derive the GOR gravitational-redshift formula of light:
Later, we will verify the validity of the GOR gravitational-redshift formula (Eq. (37)) of light.
The theory of IOR has proven that photons, like all other material particles, possess their own rest masses. However, the theory of IOR fails to theoretically calculate the rest mass or weight of photons.
Now, the GOR gravitational-redshift formulae (Eqs. (36-37)) of light provides important information about the rest mass of photons.
If η → c, then the ZGOR in Eq. (37) observed by OA(η) (η ≥ c) is reduced to the gravitational redshift of light observed by the optical agent OA(c), that is, Einstein’s gravitational redshift ZE of light, where the kinetic energy of a photon in absolute vacuum (the free spacetime SF) observed by OA(c) is KFη = KF(c) = mc2.
For the gravitational-redshift scene of light depicted in Figure 2, according to the GOR gravitational-redshift formula (Eq. (37)) of light, this should hold true in the observation of Einstein’s optical agent OA(c):
It is worth noting that in Eq. (38), mo represents the objectively true rest mass of the photon, whereas m = m(c) represents Einstein’s relativistic moving mass of the photon, that is, the mass observed by the optical agent OA(c).
Consider the scenario where an observer in the free spacetime SF observes the solar spectrum through OA(c): M = MS, rA = RS, g00(c, rA) = 1 − 2GMS/RSc2; rB → ∞, g00(c, rB) = 1 − 2GMS/rBc2 → 1. Then Eq. (38) is reduced to
Compare Eq. (31) and Eq. (39):
Equation (39) is the gravitational redshift formula of the solar spectrum for OA(c) with Z = ΔK/K defined based on the GOR energy-shift theory; whereas Eq. (31) is based on Einstein’s theory of general relativity, which defines the gravitational redshift of light with Z = Δf/f based on the frequency-shift theory.
The theoretical predicted value ZE = −2.12 × 10−6 of the gravitational redshift of the solar spectrum based on Eq. (31) has been validated through observations and experiments with the optical agent.29–31
Considering the equivalence between the energy-shift definition of Z = ΔK/K and the frequency-shift definition of Z = Δf/f for the gravitational redshift of light, and that, under the optical agent OA(c), the kinetic energy of a photon with frequency f is E = mc2 = hf, it holds true from Eq. (31) and Eq. (39) that
It turns out that, in Einstein’s relativity theory of the observation optical agent OA(c), the rest mass mo of photons is exactly the relativistic moving mass m = m(c); thus, mo is not really zero: mo = m > 0.
Perhaps we are now able to understand why experimental physicists fail to find the rest mass of photons after experiencing countless hardships.
By substituting mo = m into Eq. (38), it can be seen that the GOR gravitational redshift ZGOR or ZOA(η) (Eq. (37)) of light in the case of ZOA(c) is exactly Einstein’s gravitational redshift ZE (Eq. (30)) of light:
This suggests that the GOR gravitational-redshift formula (Eq. (37)) of light has generalized Einstein’s gravitational-redshift formula (Eq. (30)) of light: as η → c, ZGOR in Eq. (37) is strictly reduced to Einstein’s gravitational redshift ZE in Eq. (30).
In particular, the GOR gravitational-redshift formula (Eq. (37)) of light has also generalized the true Newtonian gravitational-redshift formula (Eq. (34)) of light: as η → ∞, K F∞ = m∞c2/2 = moc2/2, ZGOR in Eq. (37) is strictly reduced to Newton’s gravitational redshift ZN of light in Eq. (34):
Thus, the GOR gravitational-redshift theory of light has generalized and unified Einstein’s gravitational-redshift theory of light and Newton’s gravitational-redshift theory of light. This confirms the logical consistency and theoretical validity of the GOR gravitational-redshift formula of light, and also confirms the validity of Newton’s gravitational-redshift formula (Eq. (34)), which is based on the energy-shift definition of ZN = ΔK∞/K∞.
Meanwhile, from one aspect, this confirms the correctness of the theoretical value of the rest mass of photons predicted by the theory of GOR: mo = m∞ = m = m(c).
Based on the GOR theoretical prediction value in Eq. (40), photons of different frequencies have different rest masses or objectively real masses, and the rest mass mo of a photon with frequency f is mo = hf/c2.
The recommended values of physical constants:
Light speed c = 2.99792458 × 108 m/s
Planck constant h = 6.62607015 × 10 -34 J·s
The rest mass of a visible red photons with the frequency of f = 4.5 × 1014 Hz is
And the rest mass of a gamma photon with frequency f = 1020 Hz can reach
Now, the task of measuring and determining the rest mass of photons by observations and experiments is left to experimental physicists.
It should be pointed out that both Einstein’s theory of relativity and the theory of OR imply an important idealized assumption in the concept of rest mass: the rest mass mo of a material object or a matter system is static or time-invariant, that is,
Actually, all material objects or matter systems constantly radiate gravitons and gravitational waves outward and interact with external gravitons and gravitational waves at all times. According to the theory of OR, all material particles, including gravitons, have the objectively true rest mass. Therefore, the mass of any material body must be time-variant: mo = m(t).
According to the theory of OR, Einstein’s relativistic mass contains observational effects and apparent phenomena that are not completely objective and real; the objective and real mass of matter or material particles should be Newton’s classical mass, that is, Einstein’s rest mass, which has the objectively real inertial and gravitational effects.
The theory of IOR has proven that photons, like all other matter particles, possess their own rest mass. The theory of GOR has further proven that the rest mass of photons, like all other matter particles, is both the inertial mass and gravitational mass, possessing not only inertial effects but also gravitational effects.
In particular, the theory of GOR predicts that the theoretical value of the objective and real rest mass of a photon with frequency f is mo = m∞ = m = m(c) = hf/c2.
So, what does it mean for photons to have rest mass?
The theory of OR supports the materialist view of nature: the natural world is the world of matter, a material object, or a matter system, regardless of whether a massive star or a tiny photon must have the mass of its own if it objectively exists; otherwise, it does not exist. According to the theory of OR, the objectively real mass of matter is the rest mass, that is, Newton’s classical mass rather than Einstein’s relativistic mass.
As early as 1756, Mikhail Lomonosov proposed the law of the conservation of matter or mass32: the mass of matter is conserved. This law links the existence and mass of matter, and even makes them equivalent.
The widely accepted law of conservation of energy and Lomonosov’s law of the conservation of mass can be regarded as the most important dual principle in the objectively physical world.
As clarified by the theory of OR, Lomonosov’s and Newton’s views on energy and mass are correct: the energy of matter and the mass of matter are independent of each other: mass is mass; energy is energy. The mass of matter is conserved; and the energy of matter is conserved, too. Therefore, Einstein’s mass energy E = mc2 is not the objectively physical existence.
Mankind needs to re-understand Lomonosov’s law of the conservation of matter or mass.
The theory of OR has clarified that all matter or material particles have the objectively real mass, that is, Newton’s classical mass and Einstein’s rest mass. This suggests that all matter or matter particles, regardless of celestial bodies, photons, or gravitons, are mass quanta rather than energy quanta.
The fact that photons possess the rest mass confirms the conclusion of the theory of OR: there are no energy quanta with no mass in the objectively physical world.
In 1900, Planck theoretically derived the Planck formula for blackbody radiation based on his energy-quantum hypothesis, which was highly consistent with blackbody radiation experiments and is known as Planck’s law.33
However, the most important thing is not Planck’s law itself, but the hypothetical logical premise: E = hf, which suggests that the energy of light is discrete rather than continuous, which laid the first foundation stone for quantum theory and marked the birth of quantum mechanics.34,35
However, Planck himself did not seem to enjoy the quantization of light energy. In traditional beliefs, the energy of matter or material particles should be continuous rather than discrete. Planck had no choice but to construct the hypothesis E = hf of energy quanta. In order to theoretically derive the blackbody-radiation formula, Planck had to employ the energy-quantum hypothesis as his logical premise.
The theory of OR states that photons have the rest mass. This suggests that photons are mass quanta and not energy quanta with no mass. Thus, both the momentum and energy of photons are the physical effects of the rest mass of photons.
The theory of OR has elucidated2–5: quantum mechanics based on the Planck hypothesis E = hf of energy quanta is also a partial theory in Hawking’s words,24 belonging to the optical agent OA(c). Similar to relativistic effects, quantum effects are also observational effects, where photons act as the informons of OA(c) and perturb the objects observed by OA(c).
Actually, in Planck’s blackbody radiation experiment, the object observed by Planck was light, and the observation medium that transmitted the information about the observed object to Planck was also light. Photons, as mass quanta with the rest mass, act as informons for the optical agent OA(c), representing the highest resolution of the optical agent OA(c). Naturally, the minimum scale for measuring energy using OA(c) must be the energy ε = hf of a single photon.
Therefore, the quantization of energy measured with the optical agent OA(c) is natural and inevitable. Continuous energy measurement can only occur in idealized observation scenarios of the idealized observation agent OA∞.
Thus, Mr. Planck would not have had to worry about his hypothesis of energy quanta and quantization of photon energy. What truly cannot be accepted by our reason is the non-discrete continuity of mass and energy.
It should be pointed out that the fact that photons have the rest mass indicates that the quantum effects in quantum mechanics based on the Planck equation E = hf are, in essence, not the physical effects of photons as energy quanta, but the physical effects of photons as mass quanta.
In essence, the quantum effects observed in the microphysical world are due to the quantization of matter mass, rather than the quantization of matter energy.
In the history of human-developed physics, there have always been two doctrines about the materiality of light: Newton’s Corpuscular Theory of Light (1675)23 and Huygens’ wave theory of light (1678).36
Nowadays, it is widely accepted that light or photons possess wave-particle duality: a photon itself is a wave; in other words, a single photon has the properties of a wave. De Broglie further extended the wave-particle duality of light or photons to all matter: a single particle of matter is a wave, that is, de Broglie wave.37–39
In fact, there is no such thing as de Broglie wave in the objectively physical world. As the theory of OR has clarified,2–5 de Broglie wave is actually just the information wave of the optical observation agent OA(c), which loads and carries information about the observed object P, including its mass, momentum, and energy.
The doctrine of the wave-particle duality of light confuses the two different forms of photons and light waves and confuses the individual behavior of a single photon as an individual and the collective behavior of light as a group of photons.
According to the theory of OR, photons, like all other material particles, have the rest mass. This fact tells us that Newton’s corpuscular theory of light is correct23: light is composed of microscopic material particles, which we now call photons; all material particles, including photons, obey the same laws and rules of physics.
Of course, this does not mean that Huygens’ wave theory of light is incorrect.
Newton’s corpuscular theory of light describes the material composition of light, and Huygens’ wave theory of light describes the wave characteristics of light.
Particles are particles, waves are waves.
A material particle, as a physical entity, is the smallest or most fundamental unit of a specific matter, and a wave is a group of material particles that exhibits the behavioral characteristics of waves.
Newton stated that light is composed of microscopic material particles: countless photons form light, converging into an ocean of light or photons, similar to countless H2O molecules from water, lakes, rivers, and seas.
Huygens stated that light, as a group of photons, exhibits wave effects. Huygens’ wave theory of light systematically elaborates the wave nature of light, including the reflection and refraction phenomena of light.
We are familiar with the story of Einstein and light: photons have no mass; therefore, the speed of light is invariant, and photons can never stop.
So, does light or photons really never stop?
Waves, such as light waves, sound waves, water waves, gravitational waves, and all matter waves, seem to have a certain mechanism that can maintain their intrinsic speeds. This unique mechanism of maintaining speed is the collective or aggregate effect exhibited by numerous material particles converging into waves. The material particles of a matter wave move with the wave. As the kinetic energy of material particles decreases, the frequency of the wave decreases, so that the intrinsic speed of the wave remains unchanged. As the kinetic energy of material particles increases, the frequency of the wave increases, so that the intrinsic speed of the wave remains unchanged.
However, it is difficult for a single particle to possess such a mechanism to maintain speed.
The physical properties of matter waves require the frequency f and wavelength λ as their characteristic physical quantities. However, our reason indicates that it is difficult for an isolated matter particle or photon in the free spacetime or absolute vacuum to exhibit the physical properties of waves and to describe its physical effects with frequency f and wavelength λ.
We repeatedly emphasize that photons possess the rest mass and are, in essence, mass quanta rather than energy quanta. Therefore, the momentum p and kinetic energy K of an isolated photon depend on its rest mass mo: in the free spacetime observed by the idealized agent OA∞, p = moc and K = moc2/2 (we temporarily regard c as the initial speed of photons emitted in absolute vacuum). As an isolated photon moves in the universe that is not an absolute vacuum, like a bullet moving in Earth’s atmosphere, its momentum and kinetic energy will inevitably gradually decay. The photon cannot be expected to abandon some mass to maintain its intrinsic speed. The only result is that, like the bullet, the photon must be slower and slower and finally stop.
Actually, neither photons nor light waves are what Einstein imagined: they cannot fly forever. The unique mechanism of maintaining the speed of light as a group of photons must be relative: the decrease of the kinetic energy of photons must lead to the redshift of light frequency, which implies the decrease of the total energy of light. This is the essence of Hubble’s Cosmological Redshift. When the total energy of light is consumed to a certain extent, the speeds of light and photons must not be maintained, so that light and photons must stop in the end.
The mass of matter, that is, the quantity of matter contained in a matter object or a matter system, is a sign of whether matter objectively exists or not: matter must have mass if it objectively exists; otherwise, it would have not existed.
There are two types of important physical effects of matter mass: the inertial and the gravitational. According to the theory of OR, the objective and real mass of matter is Newton’s classical mass, that is, Einstein’s rest mass but not Einstein’s relativistic mass. The objectively real inertial and gravitational effects are rooted in Newton’s classical mass.
Photons, as Newton said,23 are the microscopic particles of matter called Corpuscles that obey the same laws of physics as all other particles of matter. This is because photons possess the rest mass that, like all other particles of matter, exhibits real inertial and gravitational effects.
The fact that photons objectively exhibit real inertial and gravitational effects confirms the logical conclusion of OR: photons have the objectively real rest mass.
6.4.1 The Mass of Photons and the Inertial Effects of Photons
The inertia effect of photons is evident.
The fact that photons have mass and the fact that photons has inertia effect can be mutually confirmed.
The quantum effect of light or photons is a type of inertial effect of light or photons: photons with the rest mass move at the speed of light c, and therefore, they have momentum and kinetic energy. As they act as the informons of the optical agent OA(c), they must perturb the observed object P, causing P to exhibit quantum effects.
Conversely, the quantum effects of the observed object P caused by the informons (photons) of the optical agent OA(c) confirm that photons possess the objectively real mass, that is, the rest mass.
The Compton effect is an example of the quantum and inertial effects of light or photons.
In the 1920s, Compton discovered the photon-scattering effect.40 If X-rays enter certain substances, the photons collide with the electrons in the atoms of the substances and scatter. The scattered photons become softer, their wavelengths exhibit redshift, and the amount of redshift is related to the scattering angle θ. Such a scattering phenomenon does not seem to conform to Newton’s classical laws of momentum conservation and energy conservation but conforms to Einstein’s relativistic laws of momentum conservation and energy conservation.
It is based on Einstein special relativity as well as the Planck equation E = hf and de Broglie relation p = h/λ that Compton derived the photon-scattering formula that conforms to observations and experiments:
The basic idea behind the logical deduction of Compton’s photon-scattering formula (Eq. (46)) is that the photon-electron system in photon-scattering experiments follows Einstein’s relativistic laws of momentum and energy conservation.
Accordingly, Compton was awarded the 1927 Nobel Prize in Physics.
The Compton effect has become important empirical evidence supporting Einstein’s theory of special relativity. In essence, however, the Compton effect does not support Einstein’s theory of special relativity but supports the theory of IOR.
In fact, similar to Planck’s blackbody-radiation experiment, the observation agent of Compton’s photon-scattering experiment is also the optical agent OA(c): the object observed by Compton is light and photons, and the observation medium that transmits the information about the observed object for Compton is also light and photons. Naturally, the photon-scattering effects presented by OA(c) should be more in line with Einstein’s theory of relativity than the theory of optical observation. However, as the theory of OR repeatedly emphasizes, this does not mean that Einstein is more correct than Newton.
If we could be equipped with the idealized observation agent OA∞, we would observe the photon-scattering effects that conform to Newton’s classical laws of momentum conservation and energy conservation.
For the general observation agent OA(η) (c ≤ η < ∞; η → ∞), the redshift Δλ of the photon-scattering wavelength can be equivalently defined by the momentum p(η) and kinetic energy K(η) observed by OA(η), based on the principle of general correspondence,1 the photon-scattering formula (Eq. (46)) for the optical agent OA(c) can be transformed into the photon-scattering formula for the general observation agent OA(η):
In a photon-scattering experiment, once OA(η) observes the momentum pI(η) and kinetic energy KI(η) of the incident photons as well as the momentum pS(η) and kinetic energy KS(η) of the scattered photons, the photon-scattering angle θ observed by OA(η) can be calculated using the photon-scattering formula (Eq. (47)).
As η→c, the photon-scattering formula (Eq. (47) for the general observation agent OA(η) strictly converges to the Compton photon-scattering formula (Eq. (46)) for the optical agent OA(c):
As η → ∞, the photon-scattering formula (Eq. (47)) for the general observation agent OA(η) strictly converges to the Newtonian photon-scattering formula for the idealized agent OA∞:
If we had the idealized observation agent OA∞, we could observe Newton’s classical momentum p I∞ and classical kinetic energy K I∞ of incident photons as well as Newton’s classical momentum p S∞ and classical kinetic energy K S∞ of scattered photons. Then, we can calculate the Newtonian scattering angle θ of photons observed by the idealized agent OA∞ based on Eq. (49).
Similar to all formulas in the theory of OR, the OR photon-scattering formula (Eq. (47)) for the general observation agent OA(η) has generalized and unified the photon-scattering formula (Eq. (46) or (48)) for Einstein’s optical agent OA(c), and the photon-scattering formula (Eq. (49)) for Newton’s idealized agent OA∞.
Thus, the photon-scattering formula (Eq. (47)) for the general observation agent OA(η) (η ≥ c) in the theory of OR can be called the general Compton formula.
It should be noted that the Compton formula (Eq. (46)) and the general Compton formula (Eq. (47)) are that for light rather than for a single photon and may not necessarily conform to the experimental scene of an isolated photon.
Similar to the Compton formula, the basic idea behind the logical deduction of the general Compton formula is that the photon-electron system in the photon-scattering experiment follows the principles of momentum and energy conservation for the general observation agent OA(η) (η ≥ c).
According to the theory of OR, the objectively real momentum or kinetic energy of matter particles are actually the inertial effects generated by the rest mass of matter particles. The logical deductions of the Compton formula and the general Compton formula indicate that photons have real inertial effects.
This confirms the logical conclusion of OR from one aspect: photons have the rest mass.
6.4.2 The Mass of Photons and the Gravitational Effects of Photons
The gravitational effect of photons is also evident.
The fact that photons have mass and that photons have gravitational effects can also be mutually confirmed.
According to the theory of OR, the rest mass mo of matter or material particles is exactly Newton’s classical mass m∞, which is Newton’s classical inertial mass m I∞ and Newton’s classical gravitational mass m G∞: mo = m∞ = m I∞ = m G∞. Therefore, the rest mass of matter, including the rest mass of photons, not only has inertial effects but also gravitational effects.
Both the gravitational redshift and gravitational deflection of light are the objectively real gravitational effects generated by the rest mass of photons: a photon with the rest mass mo = m∞, in a gravitational field, not only has the kinetic energy K∞ = m∞c2/2 but also the potential energy V∞ = −GMm∞/r. The gravitational redshift and deflection of light were verified by observations and experiments. Moreover, as clarified by the theory of OR, if we had the idealized observation agent OA∞, we could observe the gravitational redshift and deflection of light that must conform to Newton’s theory of universal gravitation.
This suggests that photons in a gravitational field obey Newton’s law of universal gravitation and Newton’s law of energy conservation: the total energy of classical kinetic and classical potential energy of a material object in gravitational spacetime is conserved. As Newton speculated, photons as particles of matter obey the same laws of physics as all other material particles.
The gravitational redshift and deflection of light confirm that photons have the rest mass.
Therefore, photons, as mass quanta, are inevitably subject to gravitational forces; in other words, like all material objects or matter particles, photons must interact gravitationally with all matter.
Spacetime Curvature or Gravitational Interaction?
Originally, according to Newton’s law of universal gravitation, gravity was one of the four fundamental interactions in the physical world, that is, a force. After the birth of Einstein general relativity, however, gravitational interactions were geometrically transformed into the effects of spacetime curvature: matter makes spacetime curved; the curved spacetime makes matter move.
Therefore, the rotation of the earth around the sun is no longer due to the gravitational interaction between the sun and earth but due to the spacetime curvature around the sun.
However, it is worth considering that we can feel the gravity of the earth, but we cannot feel the curvature of spacetime around the earth. We can attribute the deflection of the solar eclipse starlight to the curvature of spacetime around the sun, but we cannot attribute the redshift of the solar spectrum to the curvature of spacetime around the sun.
The theory of OR has clarified that the speed of light is not really invariant and spacetime is not really curved. The effects of spacetime curvature, such as the invariance of light speed, are not the objectively physical reality, but rather observational effects and apparent phenomena caused by the observational locality (c < ∞) of Einstein’s optical agent OA(c).
The theory of OR has proven that the objectively real spacetime must not be curved.
Therefore, we have reasons to believe that, regardless of the gravitational redshift of light or the gravitational deflection of light, it is caused by the gravitational effect of photon mass, or in other words, by the gravitational interaction between the gravitational fields of photons and the gravitational fields of celestial bodies.
It should be pointed out that the photon mass that generates gravitational effects here is not Einstein’s relativistic mass but Newton’s classical mass, that is, the objectively real rest mass of photons.
The Mass of Photons and the Gravitational Redshift of Light
The gravitational redshift of light cannot be explained with the curvature of spacetime.
According to the theory of GOR, for the gravitational redshift of light, the decay of the frequency of light is merely a phenomenon, whereas the essence is the decay of the kinetic energy of light or photons, which is a gravitational effect caused by the rest mass of photons. In a gravitational field, photons with the rest mass not only have kinetic energy, but also potential energy. Based on the principle of energy conservation, as photons move in the gravitational field, the total energy of photons is conserved, the kinetic energy and potential energy of photons continuously transform: the kinetic energy either decreases or increases, resulting in a redshift or blueshift in the frequency of light waves.
The fact that light exhibits redshift or blueshift in gravitational fields suggests that photons have the rest mass. Thus, the GOR gravitational-redshift formula of light and the redshift phenomenon of solar spectra provide the information about the rest mass of photons.
It is based on the GOR gravitational-redshift formula of light that the theory of OR calculates and predicts the theoretical value of the rest mass of a photon with the frequency f: mo = m∞ = m(c) = hf/c2.
The Mass of Photons and the Gravitational Deflection of Light
The gravitational deflection of light is Einstein’s most famous prediction based on his general relativity.
In 1919, a team led by Eddington observed a solar eclipse on the island of Príncipe in West Africa and determined the gravitational-deflection angle δ of starlight passing over the surface of the sun: δ = 1.61″ ± 0.40″, verifying Einstein’s theoretical prediction of gravitational deflection of starlight: δE = 1.75″.
In fact, Newton’s theory of universal gravitation can also predict the gravitational deflection of starlight. However, Newton’s starlight deflection angle δN is only half of Einstein’s starlight deflection angle δE: δN = δE/2 = 0.875″.
The conclusion of Edington’s observation of solar eclipse starlight tends to support Einstein’s theory of general relativity rather than Newton’s theory of universal gravitation. However, just as the theory of OR repeatedly emphasizes, this does not mean that Einstein’s theory of general relativity is more correct than Newton’s theory of universal gravitation.
Edington’s observation of solar eclipse starlight employed the optical agent OA(c) and, naturally, should be more in line with or inclined to support Einstein’s theory of general relativity. As the theory of OR repeatedly emphasizes, if we had the idealized agent OA∞, we would observe the objectively real deflection of solar-eclipse starlight that must be more in line with Newton’s theory of universal gravitation.
After the solar-eclipse observation of the 1919, Eddington wrote a poem to express his insights:
“Oh, leave the wise our measures to collate
One thing at least is certain, light also has weight
One thing is certain and the rest debate
Light rays, when near the Sun, do not go straight.”
Eddington’s insights are rational and discreet.
In Eddington’s view, his solar eclipse observation could be very certain that “light also has weight”. Eddington conveyed two important messages:
(1) Light or photons have weight, and Eddington’s concept of “Weight” seems to be more in line with Newton’s gravitational mass;
(2) The deflection of starlight is due to the weight of light or photons, that is, due to gravity rather than spacetime curvature.
Eddington’s understanding of the mass or weight of light or photons is simple and plain, in which the concepts of Weight and Gravitational Mass should be equivalent, in line with the logical conclusion of OR that photons have the objectively real rest mass.
Therefore, why did experimental physicists after Eddington turn a blind eye to the obvious weight of photons, which is presented in the gravitational deflection of solar-eclipse starlight?
As mentioned earlier, many physicists, including the great Feynman, de Broglie, and Schrödinger,11–15 subconsciously refuse to accept Einstein’s judgment that photons have no rest mass. Both in the past and at present, many experimental physicists have been attempting to determine the rest mass of photons through observations and experiments.17–19 However, all the attempts failed, leaving only a string of upper bounds of the rest mass of photons that gradually approaches zero.
The upper limit of 1.5 × 10−54 kg of the rest mass of photons, which was provided by the PDG20 in 2014, is already very close to Einstein’s speculation based on his mass-speed relation: photons have no rest mass.
Since the gravitational effects of light, including the gravitational redshift and deflection of light, are caused by the rest mass of photons rather than spacetime curvature, since the inertial effects of light suggest that photons have the inertial mass and the gravitational effect of light suggests that photons have the gravitational mass, since the theory of OR has proven that photons have the objectively real rest mass like all other matter particles, since the theory of OR has theoretically predicted the rest mass of photons to be mo = m∞ = m I∞ = m G∞ = hf/c2, why have experimental physicists, after countless hardships, been unable to find the rest mass of photons?
Physicists have developed many methods to determine the rest mass of photons. According to Proca’s massive-photon correction scheme for Maxwell’s electromagnetic equations,16 if a photon has the rest mass, there would be corresponding physical effects and, by examining these possible physical effects, the rest mass of photons might be determined: the test of the dispersion effect of light speed in vacuum, the test of Coulomb’s inverse square law, the test of Ampere’s loop law, the test of Schrödinger’s external field, and the test of interstellar-magnetohydrodynamic effects.
As discussed earlier, light, similar to other matter waves, has a unique mechanism for maintaining its intrinsic speed. Therefore, we may not be able to observe or measure the dispersion effect of light. However, this is not related to the rest mass of photons.
Why have they failed to find the rest mass of photons?
Firstly, photons could not lift themselves up.
Experimental physicists have not realized that the observation agent they employ to observe or measure the rest mass of photons is the optical agent OA(c). According to the theory of OR, owing to the observational locality (c < ∞) and observational perturbation-effect (h > 0) of OA(c), the information wave (light wave) and informons (photons) of OA(c) cannot determine the mass of photons themselves.
Second, physicists turn a blind eye to the rest mass of photons that is immediately in front of them.
The Compton effect, gravitational deflection of light, and gravitational redshift of light have presented the objective and real mass of photons in front of experimental physicists.
The theory of OR states that the relativistic moving mass m of photons in Einstein’s theory of special relativity is, in fact, the rest mass mo of photons. Experimental physicists regard Einstein’s photon moving mass as the objective and real mass of photons and then try to find the rest mass mo of photons beyond the so-called moving mass m of photons. This is tantamount to turning a blind eye to the objective and real rest mass of photons in front of them.
Physicists’ understanding of the rest mass of photons might be described in the verses of an ancient Chinese poet: “They failed to see the true face of Mount Lu, but only because they were right in Mount Lu.”
Perhaps the theoretical prediction of OR for the rest mass of photons can help experimental physicists measure and determine the rest mass of photons through observations and experiments.
As a new theory in human-developed physics, the theory of Observational Relativity (OR), both IOR and GOR, has brought us new discoveries and insights. OR serial report 1 reported the significant discoveries of OR: the speed of light is not really invariant; spacetime is not really curved. This article, OR serial report 2, has reported another significant discovery of OR: the rest mass of photons is not zero.
The original intention of OR was to explore the objective and real mass of photons.
The theory of Inertial Observational Relativity (IOR) has theoretically proven that photons, like all other particles of matter, have the objectively real mass, that is, Einstein’s rest mass mo, Newton’s classical mass m∞, Newton’s inertial mass m I∞ and Newton’s gravitational mass m G∞: mo = m∞ = m I∞ = m G∞.
The theory of Gravitational Observational Relativity (GOR) has theoretically calculated and predicted the rest mass of photons: mo = m∞ = m(c) = hf/c2, which is based on the gravitational redshift effect of photons and the observation of solar spectra.
According to the theory of OR, only the rest mass is the objectively real mass of matter. The fact that photons possess the objective and real rest mass is in line with the dialectical materialist view of nature: a matter system, whether a massive star or a tiny photon, if it objectively exists, must have the rest mass of its own; otherwise, it must not exist objectively.
According to the theory of OR, both Einstein’s relativistic effects and Planck’s quantum effects are the observational effects of the optical agent OA(c), and not completely objective and real. Owing to the observational locality (c < ∞) and perturbation effects (h < 0), the optical agent OA(c) cannot measure the mass of photons themselves. Einstein’s speculation that the rest mass of a photon is zero from the mass-speed relation of his special relativity does not conform to the objectively physical reality, but only means that his relativity theory fails at Hawking Singularity (v = c).
Light and photons play a special role in modern physics: the information wave of the optical agent OA(c) is light, and the informons of OA(c) are photons.
The relativity theory established by Einstein and the quantum theory that Planck laid its basis are the most important theoretical foundation of modern physics. Thus, modern physics, such as Einstein’s relativity theory and Planck’s quantum theory, is also a product of the optical observation agent OA(c). As the theory of optical observation, modern physics does not represent the objectively physical world, which is valid or effective only for the optical agent OA(c).
Naturally, the doctrine of the null rest mass of photons as the product of OA(c) does not conform to the objectively physical existence and reality.
The Swedish physicist Alfvén, a Nobel Prize winner, ever in his book Cosmology: Myth or Science bluntly criticized the scientific superstition that has spread after Einstein relativity theory.41 In Alfvén’s view, science is becoming increasingly like a myth and contrary to common sense. The mission of science seems no longer to discover natural laws and explore scientific truths, but to manufacture scientific superstitions and create scientific myths.
Now, the theory of OR has cleared the photons’ name: photons possess the objectively real mass; photons are mass quanta, not energy quanta. There are no energy quanta with no mass in the objectively physical world.
Thus, mankind needs to re-examine his physics, the relativistic effects of light and the quantum effects of light, Einstein’s relativity theory and Planck’s quantum theory, and modern physics belonging to the optical observation agent OA(c).
Mankind needs to reshape his views of matter and mass, and to reshape his view of nature.
| Views | Downloads | |
|---|---|---|
| F1000Research | - | - |
|
PubMed Central
Data from PMC are received and updated monthly.
|
- | - |
Is the work clearly and accurately presented and does it cite the current literature?
Yes
Is the study design appropriate and is the work technically sound?
Yes
Are sufficient details of methods and analysis provided to allow replication by others?
Yes
If applicable, is the statistical analysis and its interpretation appropriate?
Yes
Are all the source data underlying the results available to ensure full reproducibility?
Yes
Are the conclusions drawn adequately supported by the results?
Yes
References
1. Vegt W: Enhancing precision in electromagnetic force density modulation using LASER control. Journal of Laser Applications. 2025; 37 (1). Publisher Full TextCompeting Interests: No competing interests were disclosed.
Reviewer Expertise: General Relativity, QLT (Quantum Light Theory)
Alongside their report, reviewers assign a status to the article:
| Invited Reviewers | |
|---|---|
| 1 | |
|
Version 1 12 Nov 25 |
read |
Provide sufficient details of any financial or non-financial competing interests to enable users to assess whether your comments might lead a reasonable person to question your impartiality. Consider the following examples, but note that this is not an exhaustive list:
Sign up for content alerts and receive a weekly or monthly email with all newly published articles
Already registered? Sign in
The email address should be the one you originally registered with F1000.
You registered with F1000 via Google, so we cannot reset your password.
To sign in, please click here.
If you still need help with your Google account password, please click here.
You registered with F1000 via Facebook, so we cannot reset your password.
To sign in, please click here.
If you still need help with your Facebook account password, please click here.
If your email address is registered with us, we will email you instructions to reset your password.
If you think you should have received this email but it has not arrived, please check your spam filters and/or contact for further assistance.
Comments on this article Comments (0)