A Novel Particle Marine Predator Optimizer for Gene Selection Health&nbsp;Problem

Rizik Al-Sayyed; AlMuatasim Billah Rizik AlSayyed; Sharif Naser Makhadmeh; Yousef Sanjalawe; Barihan M. Khasawneh

doi:10.12688/f1000research.172440.1

Home Browse A Novel Particle Marine Predator Optimizer for Gene Selection HealthProblem

ALL Metrics

-

Views

Get PDF

Get XML

Export

▬

✚

Research Article

A Novel Particle Marine Predator Optimizer for Gene Selection Health Problem

[version 1; peer review: awaiting peer review]

Rizik Al-Sayyed ¹, AlMuatasim Billah Rizik AlSayyed², Sharif Naser Makhadmeh¹, Yousef Sanjalawe¹, Barihan M. Khasawneh³

Rizik Al-Sayyed ¹, AlMuatasim Billah Rizik AlSayyed², [...] Sharif Naser Makhadmeh¹, Yousef Sanjalawe¹, Barihan M. Khasawneh³

PUBLISHED 18 Nov 2025

Author details Author details

¹ KASIT, IT Department, The University of Jordan, Amman, Amman Governorate, Jordan
² The University of Jordan School of Medicine, Amman, Amman Governorate, Jordan
³ Faculty of Medicine, Mutah University, Kerak, Jordan

Rizik Al-Sayyed
Roles: Conceptualization, Formal Analysis, Methodology, Project Administration, Supervision, Writing – Original Draft Preparation

AlMuatasim Billah Rizik AlSayyed
Roles: Formal Analysis, Funding Acquisition, Methodology, Resources, Validation, Visualization, Writing – Review & Editing

Sharif Naser Makhadmeh
Roles: Conceptualization, Data Curation, Formal Analysis, Investigation, Methodology, Resources, Writing – Review & Editing

Yousef Sanjalawe
Roles: Investigation, Methodology, Software, Validation, Visualization, Writing – Review & Editing

Barihan M. Khasawneh
Roles: Data Curation, Formal Analysis, Writing – Original Draft Preparation

OPEN PEER REVIEW

REVIEWER STATUS AWAITING PEER REVIEW

This article is included in the Bioinformatics gateway.

Abstract

Background

High-dimensional microarray data complicates reliable cancer classification. Compact, informative gene panels are needed to maintain predictive power while improving interpretability and cost.

Methods

We propose a two-stage feature-selection pipeline. Stage 1 ranks genes via an ensemble of filters—ReliefF, chi-square, and Kullback–Leibler divergence—tempered by minimum redundancy–maximum relevance to promote diversity. Stage 2 performs wrapper-based subset search using a Particle Marine Predator Optimizer that fuses Marine Predators Algorithm for global exploration with Particle Swarm Optimization for local refinement. The objective maximizes cross-validated SVM accuracy while penalizing subset size.

Results

Across seven benchmarks (Breast, CNS, Leukemia, Leukemia-3c, Leukemia-4c, Lymphoma, Ovarian), we compare against Bat Algorithm, Grey Wolf Optimizer, Marine Predators Algorithm, White Shark Optimizer, and recent representatives using accuracy, F1, precision, sensitivity, Matthews correlation coefficient, selected-gene count, and convergence behavior. The method frequently matches or exceeds alternatives while selecting few genes, achieving perfect accuracy on several datasets (Leukemia, Leukemia-3c, Lymphoma, Ovarian) and stable, strong performance on the remainder. Typical subset sizes are 2–5 genes for Leukemia variants, 7–8 for CNS, and ~20 for Breast. Optimization traces show rapid, steady improvement.

Conclusions

The pipeline achieves an effective exploration–exploitation balance, yielding compact gene panels without sacrificing classification performance. Its modular design supports straightforward extension to larger cohorts and other omics modalities.

Keywords

Marine Predator Algorithm, Particle Swarm Optimization, Gene selection Optimization, rMRMR, Classification

Corresponding author: Rizik Al-Sayyed

Competing interests: No competing interests were disclosed.

Grant information: The author(s) declared that no grants were involved in supporting this work.

Copyright: © 2025 Al-Sayyed R et al. This is an open access article distributed under the terms of the Creative Commons Attribution License, which permits unrestricted use, distribution, and reproduction in any medium, provided the original work is properly cited.

How to cite: Al-Sayyed R, AlSayyed ABR, Makhadmeh SN et al. A Novel Particle Marine Predator Optimizer for Gene Selection Health Problem [version 1; peer review: awaiting peer review]. F1000Research 2025, 14:1275 (https://doi.org/10.12688/f1000research.172440.1) First published: 18 Nov 2025, 14:1275 (https://doi.org/10.12688/f1000research.172440.1) Latest published: 18 Nov 2025, 14:1275 (https://doi.org/10.12688/f1000research.172440.1)

1. Introduction

Feature extraction involves selecting or incorporating features to decrease the data amount for processing, which is crucial in addressing various challenges.^1–3 DNA microarrays represent a molecular technique enabling the analysis of thousands of genes in a single experiment, using numerous cells or tissues. The evolution of DNA microarray technology has resulted in the production of high-dimensional datasets, significantly influencing areas like clinical diagnostics and drug development.⁴ Gene expression data derived from DNA microarray experiments has become a crucial tool for cancer classification and detection.^5,6 However, this data is often burdened with irrelevant, redundant, and noisy genes, posing a significant challenge to machine learning algorithms. Developing a predictive model based on unrelated genes can lead to decreased classification accuracy. One approach to resolve this issue is through gene selection, a process of eliminating irrelevant and redundant genes while preserving the most relevant ones.⁷ Gene selection can offer deeper insights,⁵ such as assisting researchers in understanding the molecular mechanisms of cancer and potentially leading to new therapies through an analysis of gene patterns, as well as reducing clinical costs.

Selection techniques for Gene are generally classified into two methods⁷: filter and wrapper. Filter methods are valued for their computational efficiency, as they assess genes based on the dataset’s intrinsic properties without involving machine learning algorithms. Commonly used filter techniques include Minimum-Redundancy-Maximum-Relevance (MRMR), Robust-MRMR, and ReliefF.

Conversely, wrapper methods frame gene selection as an optimization problem,^8–14 employing search techniques or machine learning algorithms to evaluate gene subsets. While wrapper approaches typically achieve higher classification accuracy compared to filter methods, they come with significant computational costs. To address this, hybrid methods that integrate filter and wrapper techniques have become increasingly popular.^15–18 These hybrid approaches have shown greater effectiveness in handling high-dimensional datasets, such as microarray data, particularly in classification tasks. Despite advancements, further studies are essential to design more effective hybrid gene selection techniques.^15,16

A key challenge in gene selection arises from the exponential increase in potential solutions as the number of genes grows. Consequently, researchers strive to discover near-optimal gene subsets by improving existing metaheuristic methods.

Metaheuristic algorithms serve as general-purpose frameworks that optimize search processes independently of specific problems.¹⁹

Several metaheuristic methods have been adapted for gene selection. Examples include a Harmony Search method improved by a Markov Blanket,²⁰ a Binary Flower Pollination Algorithm merged with β-Hill Climbing,²¹ the rMRMR technique paired with an enhanced Bat Algorithm,⁶ a Binary JAYA Algorithm incorporating Adaptive Mutation,²² and Correlation-Based Feature Selection used alongside a refined Binary Particle Swarm Optimization.¹⁵ Nonetheless, the complexity of the search space and gene interactions means these methods frequently encounter issues with becoming trapped in local optima.

The Marine Predators Algorithm (MPA) is a metaheuristic optimization method introduced by Faramarzi,²³ influenced by marine animals’ hunting habits. MPA operates using stochastic population updates and employs two random walk strategies: Brownian motion and Lévy flight. Recognized for its simple parameter tuning, wide applicability, user-friendliness, and strong search performance, MPA has seen successful use in diverse areas. These applications encompass ECG signal classification,²⁴ dynamic clustering,²⁵ energy-efficient fog computing,²⁶ medical image segmentation for COVID-19,^27,28 and photovoltaic array reconfiguration.²⁹

The MPA was adapted and enhanced in several studies. The authors of³³ introduced a hybrid gene selection method (MPAC) for DNA microarray-based cancer classification, combining Minimum Redundancy Maximum Relevance (mRMR) filtering with an Improved Marine Predator Optimizer enhanced by a crossover operator. By optimizing both exploration and exploitation, MPAC sought concise biomarker subsets and employed k-nearest neighbor for classification. Experiments on nine benchmark datasets demonstrated that MPAC consistently outperformed or remained competitive with state-of-the-art algorithms. Nonetheless, the reliance on the crossover operator introduces potential weaknesses, including risks of premature convergence, excessive randomness that disrupts promising search trajectories, and sensitivity to crossover rate settings, which limit stability and reproducibility across diverse datasets.

We introduce a hybrid gene selection technique, named PMPA, which integrates the rMRMR filter method with a modified version of the Marine Predators Algorithm that incorporates Particle Swarm Optimization (PSO) as a wrapper. The modifications are designed to enhance the population diversity at the conclusion of each MPA iteration. The performance of the proposed method we evaluate on nine datasets with different dimensions, using the number of selected genes and classification accuracy as metrics. The approach we compare against other gene selection techniques. Additional comparisons with seven recent advanced methods on the same datasets indicate the effectiveness of the proposed method, which achieves superior results on four of the datasets.

The structure of This study is as follows: Section 2 and Section 3 provide a review and explanation of the methodology. The results we present in Section 4, and the conclusions along with potential future research directions are discussed in Section 5.

2. Research background

This part explores the development of the MPA, which has been improved to function as a simple and efficient metaheuristic optimization method.

2.1 Marine Predators Algorithm (MPA)

MPA is a population-based optimizer modeled on marine foraging; it alternates between Lévy flights and Brownian moves to explore and exploit the search space.

1. High speed ratio: If predators move far faster than prey, the best option is effectively to hold position while the prey’s motion (Lévy or Brownian) drives encounters.
Unit speed ratio: when predator and prey speeds are similar, Brownian updates are favored for the predator, particularly if prey follows Lévy motion.
Low speed ratio: if prey outruns predators, Lévy steps are preferred by the predator regardless of prey motion.
2. Unit velocity: When the prey and predator move at the same pace, Brownian motion is the optimum strategy for the predator, especially if the prey is using Levy motion.
3. Low velocity: When the prey moves significantly quicker than the predator, the predator’s best course of action is to adopt Levy motion, Regardless of the prey’s movement style.

Figure 1 summarizes the three search regimes that underpin the Marine Predators Algorithm (MPA) and explain how the optimizer balances exploration and exploitation over time.

Figure 1. Marine Predators Algorithm (MPA) search regimes and updates.

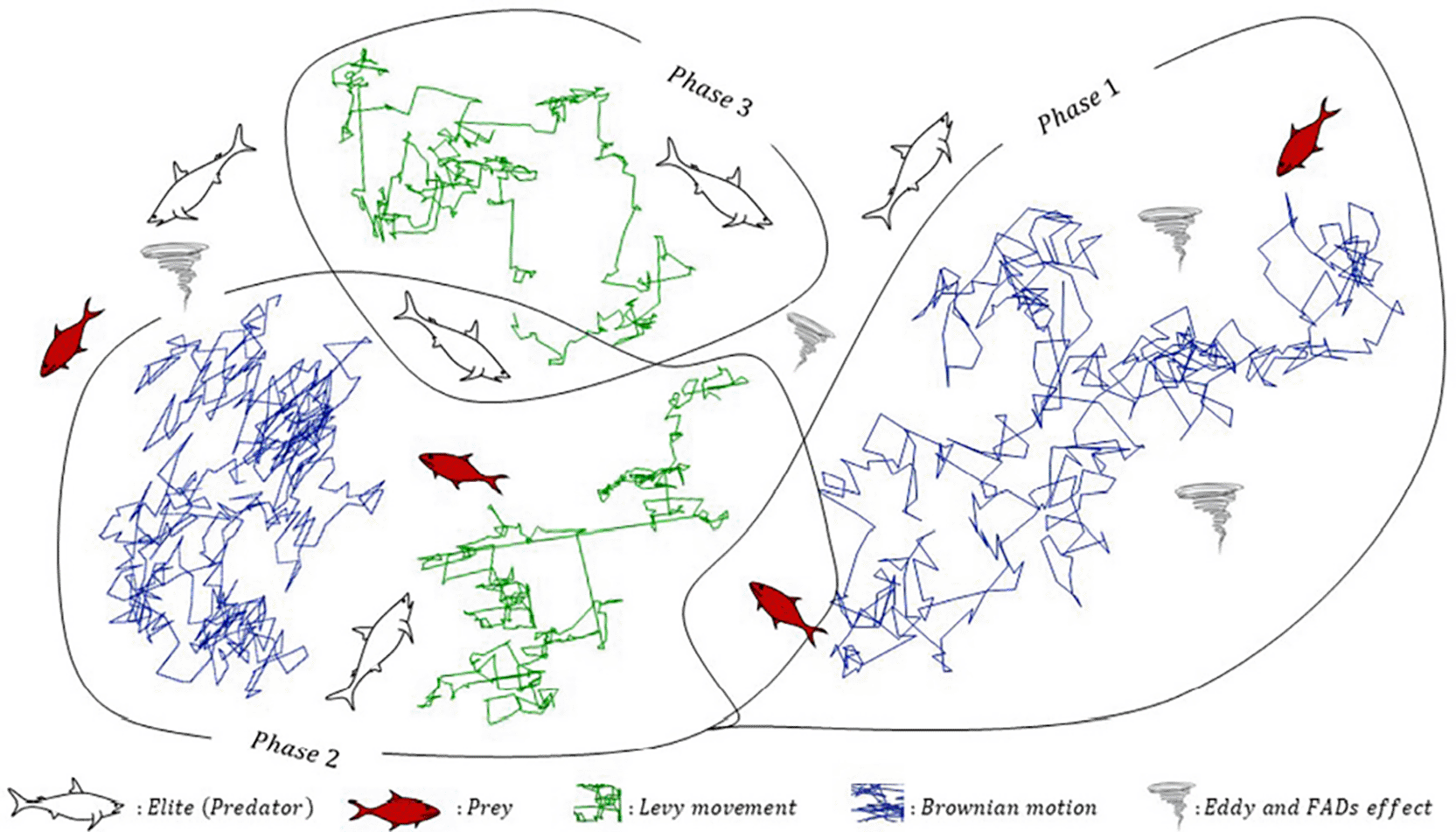
Conceptual schematic of the three velocity-ratio stages (high, unit, low) that govern exploration vs. exploitation. Early iterations emphasize Brownian exploration around elite guidance; the mid regime mixes Lévy and Brownian updates across sub-populations; late iterations emphasize Lévy jumps plus Fish Aggregating Devices (FADs) disturbance to avoid stagnation. Abbreviations: MPA, Marine Predators Algorithm; FADs, Fish Aggregating Devices.

Figure 1 contrasts predator and prey movement under different relative speed ratios and links these behavioral rules to the mathematical updates used during optimization. In the early stage, when the effective predator speed exceeds the prey’s, the most advantageous tactic is to remain largely stationary while sampling the space with wide, randomized steps. Operationally, MPA models this with Brownian perturbations around elite guidance, which encourages broad coverage of the decision space and reduces the risk of premature commitment to a local basin. This phase is dedicated to exploration and typically occupies the first third of the iteration budget.

When predator and prey move at comparable speeds—the mid-optimization regime—the algorithm mixes movement models to hedge between global search and local refinement. Half of the population is updated using Lévy flights, which inject heavy-tailed steps capable of vaulting across deceptively flat regions, while the remaining half follows Brownian motion to consolidate promising areas. The alternation helps the swarm probe new basins without abandoning ongoing improvements, acting as a controlled transition toward exploitation.

In the late stage, the prey effectively outpaces the predator, so the predator relies on occasional long-range Lévy jumps to re-engage valuable regions while fine-tuning around incumbents. Here, exploitation dominates: solutions are refined relative to an elite memory that tracks the best-so-far candidate and broadcasts directional cues to the population. The algorithm also introduces ecologically motivated disturbances—such as the Fish Aggregating Devices (FADs) mechanism—to periodically reshuffle a subset of positions. This controlled randomness prevents stagnation around deceptive attractors while preserving the information accumulated in the elite matrix.

Taken together, the three regimes in Figure 1 provide a principled schedule for step-size distributions, population partitioning, and memory use. Early Brownian exploration maps the landscape; a mid-course Lévy/Brownian hybrid tests new basins while validating incumbents; and a late Lévy-accented exploitation phase concentrates effort where returns are highest. In the context of gene selection, these dynamics help the optimizer discover sparse, high-performing subsets despite the combinatorial explosion of possibilities. By coupling elite guidance with stochastic motion models whose statistics change over time, MPA systematically converts biological foraging insight into an effective search policy for high-dimensional feature selection.

2.1.1 Initialization

The initialization phase begins with the creation of a prey population within the defined search space, as outlined in Eq. 1. In this equation, $P_{\min}$ and $P_{\max}$ indicate the minimum and maximum boundaries, respectively, while rand represents a randomly generated value between 0 and 1.

(1)

P = P_{\min} + rand (P_{\max} - P_{\min})

Once producing the prey population, the fitness values are calculated. The predator with the best score, represented by $X^{I}$ , is identified as the most efficient forager based on evolutionary principles. The Elite matrix is then constructed using this individual, the matrix has the dimensions ( $n \times d$ ), where $n$ represents the population size and $d$ represents the number of dimensions, as defined in Eq. 2.

(2)

Elite = [\begin{matrix} P_{1, 1}^{I} & \dots & P_{1, d}^{I} \\ ⋮ & ⋱ & ⋮ \\ P_{n, 1}^{I} & \dots & P_{n, d}^{I} \end{matrix}]

To update predator positions, a second matrix called Prey is constructed, having the same dimensions as the Elite matrix, as expressed in Eq. 3.

(3)

Prey = [\begin{matrix} P_{1, 1} & P_{1, 2} & \dots & P_{1, d} \\ ⋮ & ⋮ & ⋮ & ⋮ \\ P_{n, 1} & P_{n, 2} & \dots & P_{n, d} \end{matrix}]

2.1.2 High velocity ratio stage

As previously described, when the predator’s speed exceeds the speed of the prey, the predator should stay motionless as this is the best course of action. This phase represents the exploration stage, which continues as long as iter $< \frac{1}{3} \times$ max_iter. Equations 4 and 5 explain the mathematical model for this phase:

(4)

{\vec{stepsize}}_{i} = ({\vec{Elite}}_{i} - {\vec{R}}_{B} \otimes {\vec{Prey}}_{i}) \otimes {\vec{R}}_{B}

(5)

{\vec{Prey}}_{i} = L \cdot \vec{R} \otimes {\vec{stepsize}}_{i} + {\vec{Prey}}_{i}

In Equation 4, the Brownian motion is symbolized by $\vec{R_{B}}$ , a vector comprised of random values derived from a normal distribution. The study’s authors indicate that in Equation 5, $L$ is assigned a value of 0.5, while $R$ is a uniformly distributed random vector ranging from 0 to 1. In both of these equations, the symbol $\otimes$ represents element-wise multiplication.

2.1.3 Unit velocity ratio stage

During this phase, the predator and prey move at matching speeds. This stage corresponds to the midpoint of the optimization process, where the focus begins to transition from exploration to exploitation. The condition $\frac{1}{3} \times max_{iter} <$ iter $< \frac{2}{3} \times$ max $_{iter}$ must be satisfied. The mathematical models for the initial half of the population, which uses Levy motion, are described in Eqs. 6 and 7:

(6)

{\vec{stepsize}}_{i} = ({\vec{Elite}}_{i} - {\vec{R}}_{L} \otimes {\vec{Prey}}_{i}) \otimes {\vec{R}}_{L}

(7)

{\vec{Prey}}_{i} = {\vec{Prey}}_{i} + L \cdot \vec{R} \otimes {\vec{stepsize}}_{i}

For the second half of the population, which utilizes Brownian motion, the mathematical expressions are given by Eqs. 8 and 9:

(8)

{\vec{stepsize}}_{i} = ({\vec{R}}_{B} \otimes {\vec{Elite}}_{i} - {\vec{Prey}}_{i}) \otimes {\vec{R}}_{B}

(9)

{\vec{Prey}}_{i} = \vec{{Elite}_{i}} + L . CF \otimes {\vec{stepsize}}_{i}

In these equations, $\vec{R_{L}}$ and $\vec{R_{B}}$ represent Levy and Brownian motion, respectively, while $CF$ is an adaptive parameter that controls the step size. This parameter is calculated using Eq. 10:

(10)

CF = {(1 - \frac{iter}{{max}_{iter}})}^{\frac{2 (iter)}{{maxiter}^{2}}}

2.1.4 Low-velocity ratio stage

In this phase, the prey moves at a much higher speed compared to the predator, making Levy motion the predator’s most effective hunting strategy. This stage corresponds to the exploitation phase, occurring during the latter part of the optimization process when iter $> \frac{2}{3} \times$ max $_{iter}$ . The illustration of this stage is provided in Eqs. 11 and 12:

(11)

{\vec{stepsize}}_{i} = ({\vec{R}}_{L} \otimes {\vec{Elite}}_{i} - {\vec{Prey}}_{i}) \otimes {\vec{R}}_{L}

(12)

{\vec{Prey}}_{i} = {\vec{Elite}}_{i} + L . CF \otimes {\vec{stepsize}}_{i}

Numerous studies³⁰ emphasize that environmental factors, such as eddy formation and Fish Aggregating Devices (FADs), greatly influence prey behavior. FADs, specifically, alter the time predators allocate to searching, with $80 %$ of their efforts concentrated locally and $20 %$ directed toward chasing prey in other areas. The influence of FADs is quantified using Eq. 13.

(13)

\vec{{Prey}_{i}} = {\begin{cases} {\vec{Prey}}_{i} + CF [{\vec{P}}_{\min} + \vec{R} \otimes ({\vec{P}}_{\max} - {\vec{P}}_{\min})] \otimes \vec{U} & if r \leq FADs \\ \to [FADs (1 - r) + r ({\vec{Prey}}_{r 1} - {\vec{Prey}}_{r 2}) + {Prey}_{i} & if r > FADs \end{cases}

In Eq. 13, $\vec{U}$ is a binary vector composed of elements that are either 1 or 0. It is generated by assigning random values between 0 and 1 to each element of $\vec{U}$ , where values below 0.2 are set to zero, and those equal to or above 0.2 are set to one. The parameter $r$ signifies a random value generated between 0 and 1, while FADs $= 0.2$ represents the probability of FADs impacting the search process. The subscripts $r_{1}$ and $r_{2}$ denote randomly picked indices from the prey matrix, and ${\vec{P}}_{\min}$ and ${\vec{P}}_{\max}$ indicate the lower and upper bounds, respectively.

The MPA models the memory behavior of marine predators by maintaining earlier prey positions alongside updating the current ones. The fitness scores of both current and previous solutions are evaluated, and positions are swapped when the prior solution demonstrates superior fitness.

The MPA optimization steps are presented in Algorithm 1.

Algorithm 1. The MPA Pseudocode.

Initialize prey population $P$ with random values within $[P_{\min}, P_{\max}]$

Evaluate fitness for each prey in $P$

Set the predator with the highest fitness as the Elite

Initialize Elite using the Elite predator and matrix Prey with population $P$

for each iteration iter do

if iter $< \frac{1}{3} \times$ max_iter then

for each prey $i$ do

Calculate ${\vec{stepsize}}_{i}$ using Brownian motion

Update prey position ${\vec{Prey}}_{i}$ with step size

end for

else if $\frac{1}{3} \times$ max_iter $<$ iter $< \frac{2}{3} \times$ max_iter then

for first half of prey population $i \leq \frac{n}{2}$ do

Calculate ${\vec{stepsize}}_{i}$ using Levy motion

Update ${\vec{Prey}}_{i}$ using Levy motion

end for

for the other part of prey population $i > \frac{n}{2}$ do

Calculate ${\vec{stepsize}}_{i}$ using Brownian motion

Update ${\vec{Prey}}_{i}$ with Brownian motion

end for

else

for each prey $i$ do

Calculate ${\vec{stepsize}}_{i}$ using Levy motion

Update prey position ${\vec{Prey}}_{i}$ using step size

end for

end if

Update the Elite matrix and recalculate fitness values

Apply Fish Aggregating Devices (FADs) effect:

for each prey $i$ do

if $r \leq FADs$ then

Update ${\vec{Prey}}_{i}$ based on $CF, \vec{U}$ , and $[P_{\min}, P_{\max}]$

else

Update ${\vec{Prey}}_{i}$

with random Prey positions $r 1$ and $r 2$

end if

end for

Return optimal solution found in Elite

2.2 Particle Swarm Optimization

Particle Swarm Optimization (PSO) is a method inspired by the social interactions observed in animals like birds and bees.³¹ The algorithm employs particles to traverse the search space and identify the optimal solution.³²

Particle Swarm Optimization (PSO) draws on simple social dynamics: particles share information about promising regions while balancing personal and global experience.

Positions and velocities are iteratively updated using a memory of each particle’s personal best and the swarm’s best-so-far, injecting randomness to avoid premature convergence.

PSO is widely used for solving both minimization and maximization problems due to its straightforward implementation and the limited number of parameters it requires. Its applications extend to areas such as function optimization, feature selection, and clustering.

During iteration $t$ , the position and velocity of a particle are represented by $X$ (iter) and $V$ (iter), respectively. The update of the particle’s movement follows these equations:

(14)

V (iter + 1) = c 1 \cdot rand () \cdot (pbest - P (iter)) + c 2 \cdot rand () \cdot (gbest - P (iter)) + w \cdot V (iter)

(15)

P (iter + 1) = V (iter + 1) + P (iter)

In these formulas, $w$ signifies the inertia weight, which determines how much the previous velocity affects the current one. The constants $c 1$ and $c 2$ influence the particle’s tendency to move toward its personal best (pbest) and the global best (gbest) positions, respectively. The function rand() produces random values within the range 0 to 1 (excluding both), adding stochastic behavior to the particle’s motion.

The particles update their positions and velocities in successive iterations until a termination condition is fulfilled, such as reaching a predefined iteration limit or obtaining a target fitness value.

3. Methodology

The suggested PMPA hybrid approach for gene selection is presented in this section. The filter strategy is discussed in Section 3.1, while the wrapper approach—which includes the suggested PMPA optimization steps—is explained in Section 3.2.

3.1 Stage 1: Filter approach

This stage contains three main steps, including Initialization, Hybridization, and Filtering process outcomes.

Step 1: Initialization .

First, we form an ensemble of three classical filters—ReliefF, Chi-square, and KL divergence—to score genes independently; scores are then combined by averaging to obtain a single ranking.

Step 2: Hybridization .

Next, we blend the ensemble ranking with MRMR’s relevance estimates. Each gene receives two mutual-information-based signals—its relevance to the class label and its average ensemble rank—and we modulate MRMR by a per-gene mean score to stabilize selection. The final relevance score multiplies I (Gx,c) by R (Gi).

Step 3: Filtering process outcomes .

Finally, we threshold the ranking to produce a compact gene list, which becomes the search space for the wrapper optimizer.

3.2 Stage 2: Wrapper approach

3.2.1 Solution representation

Gene selection is characterized as a combinatorial optimization problem, where the solution comprises a subset of genes.^34,35 As the number of selected genes from experimental datasets grows, the complexity of searching the solution space for the optimal subset increases. Formally, let N denote the total number of genes, and [2N] represent all potential subsets of candidate genes. A solution is encoded as x, a binary string x = (x1, x2, . . . , xN ), where N represents the string length or the gene subset size. In this encoding, a bit value of ‘1’ signifies that a gene is included, while ‘0’ indicates exclusion.

3.2.2 Fitness function

Gene selection methods aim to reduce the selected genes while improving accuracy. To accomplish this, several studies have integrated classification accuracy and gene subset size into a unified weighted function. This function serves as a fitness metric for evaluating potential gene subsets, as detailed in Equation (16) below:

Our objective rewards predictive performance while discouraging unnecessarily large subsets.

(16)

fitness = α \times acc (classifier) + β \times (1 - \frac{s}{p})

In this context, p represents the total genes in the dataset, and s indicates the candidate subset size. The weighting factors for classification accuracy (α) and gene subset size (β) are assigned values of 1 and 0.001, respectively.^36,37 In this study, classification accuracy is evaluated through 10-fold cross-validation using an SVM classifier. This cross- validation approach is commonly applied in gene selection because it provides consistent results and minimizes variability in relation to input data.³⁸ It is worth noting that nearly all comparative methods rely on k-fold cross-validation for validation purposes.

We weight accuracy and subset size with (α, β) = (1, 0.001); performance is estimated via 10-fold cross-validated SVM, a common and stable choice in this domain.

3.2.3 Marine Predator Optimizer Based PSO

The rMRMR-PMPA method, a sophisticated variation of the PMPA strategy created specially to address the gene selection optimization challenge, is presented in this section. Finding biologically significant genes utilizing the rMRMR approach is the primary goal of rMRMR-PMPA. The PMPA approach then uses the identified genes as input to improve and streamline the gene selection procedure. The PMPA method comprises six progressive steps, which are described below and illustrated in Figure 2.

Figure 2. PMPA six-step hybrid pipeline for gene selection.

Workflow showing: (1) parameter initialization (MPA/PSO); (2) population initialization over binary gene masks; (3) fitness evaluation using SVM accuracy with size penalty; (4) MPA-based position updates with elite memory and FADs; (5) PSO refinement using personal/global bests; (6) stopping criterion. The filter space is produced by rMRMR-enhanced ranking before the wrapper search. Abbreviations: PMPA, Particle Marine Predator Optimizer; rMRMR, robust minimum-redundancy maximum-relevance; PSO, Particle Swarm Optimization; SVM, support vector machine.

Step 1: PMPA Initialization. In this step, the parameters for the MPA and the PSO are initialized. The MPA parameters include β, P, F ADs, population size (N), iterations number (MaxItr), upper and lower bound (ub, lb). The PSO parameters are c1 and c2, which are two cognitive factors, and inertia weight w.

Step 2: Population Initialization. At this stage, random solutions are generated to create the population for the gene selection problem. The population size is defined as N × D, where D represents the total number of decision variables. The population for the proposed PMPA is formulated using Equation 17.

(17)

PMPAP = [\begin{matrix} x_{1}^{1} & x_{2}^{1} & \dots & x_{D}^{1} \\ x_{1}^{2} & x_{2}^{2} & \dots & x_{D}^{2} \\ ⋮ & ⋮ & \dots & ⋮ \\ x_{1}^{N} & x_{2}^{N} & \dots & x_{D}^{N} \end{matrix}],

where x ∈ 0, 1.

Step 3: Population Evaluation. During this phase, the fitness values of the population solutions are computed and assessed using the fitness function defined in Equation 16. This function evaluates the problem’s objectives and criteria. Once the fitness values are determined, the solution with the highest fitness, referred to as the best solution, is identified as the top predator X^I in the MPA. This solution is considered the most optimal among all candidates. Additionally, the Elite matrix is updated to store information about the top predator, serving as a memory to retain the best solutions encountered throughout the optimization process.

Step 4: Population Update Using MPA. In this phase, the MPA search agents perform their search operations by updating their positions to discover improved candidate solutions, guided by the Elite matrix. After updating the positions, the influence of FADs is applied and adjusted to balance exploration and exploitation. The newly generated solutions are then evaluated, and the Elite matrix and memory are updated accordingly to retain details of the best solutions identified during the process.

Step 5: Update population by PSO. In this step, the PSO is operated to enhance both the exploration and exploitation capabilities of the MPA and find better candidate solutions. Once the PSO starts its operations, its search agents will begin their search for a better solution than that obtained by the MPA. Subsequently, the obtained solutions will be assessed and updated utilizing the MPA process.

Step 6: Verify the Stopping Criterion. Steps 3, 4, and 5 are iteratively repeated until the stopping condition is satisfied.

4. Experimental setup and results

This section presents the experimental protocol adopted to rigorously evaluate the proposed PMPA feature selection framework on high-dimensional gene expression benchmarks. We consider standard microarray datasets that exhibit the small-n/large-p regime, where only a few dozen samples are measured over thousands of genes; this setting is known to challenge both overfitting control and search stability. To ensure comparability, all methods operate under identical computational budgets, candidate subset bounds, and classifier back-ends. Unless otherwise indicated, performance is estimated with stratified k-fold cross-validation using the same fold partitions across methods to minimize variability due to resampling. We report complementary metrics: overall accuracy and F1-score (discrimination), sensitivity and precision (error asymmetry), the Matthews correlation coefficient (class-imbalance robustness), and the number of selected genes (model parsimony). Optimizer fitness balances predictive performance against subset size via a weighted objective, promoting compact yet informative biomarker panels. Comparators include single-strategy metaheuristics (MPA, BAT, GWO, and WSO) configured with recommended settings within the same search ranges, alongside recent hybrid filter–wrapper approaches from the literature where available. We further analyze convergence behavior—best-so-far fitness trajectories across iterations—to characterize exploration–exploitation trade-offs and robustness. All experiments were repeated over multiple random seeds, and summary results are reported as mean ± standard deviation to reflect run-to-run variability. These choices establish a transparent, reproducible basis for testing whether PMPA achieves (i) competitive or superior classification, (ii) substantial gene reduction, and (iii) consistent performance across datasets—properties that are essential for reliable downstream use in bioinformatics pipelines and decision support.

4.1 Datasets

Seven popular microarray benchmark datasets^47–49 were used to assess the PMPA technique. In order to identify gene patterns that distinguish malignant samples from healthy ones, these datasets are widely used in pattern recognition research employing evolutionary algorithms and machine learning.³⁵ The size of the datasets varies; some have limited prognostic significance, while gene counts range from 2,000 to 15,154. The patient sample sizes vary from 60 to 235. Column 1 of Table 1 shows the datasets that were examined; they were obtained from the https :// csse . szu . edu . cn / staff / zhuzx / Datasets.html.^47–49

Table 1. Classification accuracy (mean ± SD) for PMPA vs. baseline metaheuristics across datasets.

Datasets: Breast, CNS, Leukemia, Leukemia-3c, Leukemia-4c, Lymphoma, Ovarian. Methods: PMPA, MPA, BAT, GWO, WSO. Metric: overall accuracy; SD = standard deviation over repeated runs/folds.

Dataset	Measure	PMPA	MPA	BAT	GWO	WSO
Breast	Average	9.5367E-01	9.4774E-01	9.4474E-01	9.4874E-01	9.3578E-01
Breast	St. Dev.	7.9008E-03	9.7673E-03	8.1906E-03	1.0385E-02	1.0093E-02
Central Nervous System (CNS)	Average	9.3778E-01	9.4833E-01	9.5000E-01	9.4222E-01	9.4833E-01
Central Nervous System (CNS)	St. Dev.	8.6805E-03	5.0855E-03	4.7908E-16	1.0480E-02	6.7096E-03
Leukemia (ALL-AML)	Average	1.0000E+00	1.0000E+00	1.0000E+00	1.0000E+00	1.0000E+00
Leukemia (ALL-AML)	St. Dev.	0.0000E+00	0.0000E+00	0.0000E+00	0.0000E+00	0.0000E+00
Lymphoma	Average	1.0000E+00	1.0000E+00	1.0000E+00	1.0000E+00	1.0000E+00
Lymphoma	St. Dev.	0.0000E+00	0.0000E+00	0.0000E+00	0.0000E+00	0.0000E+00
Leukemia 3c (ALL-AML-3)	Average	1.0000E+00	1.0000E+00	1.0000E+00	1.0000E+00	1.0000E+00
Leukemia 3c (ALL-AML-3)	St. Dev.	0.0000E+00	0.0000E+00	0.0000E+00	0.0000E+00	0.0000E+00
Leukemia 4c (ALL-AML-4)	Average	9.8935E-01	9.8673E-01	9.9107E-01	9.8476E-01	9.8750E-01
Leukemia 4c (ALL-AML-4)	St. Dev.	5.4786E-03	3.6229E-03	6.9240E-03	5.8522E-03	4.6424E-03
Ovarian	Average	1.0000E+00	1.0000E+00	1.0000E+00	1.0000E+00	1.0000E+00
Ovarian	St. Dev.	0.0000E+00	0.0000E+00	0.0000E+00	0.0000E+00	0.0000E+00

4.2 Results of the hybridization method: A comparative study

This section compares the outcomes of the proposed method with those achieved by other algorithms. We benchmark PMPA against representative baselines such as the Bat Optimization Algorithm (BAT), Grey Wolf Optimizer (GWO), Marine Predator Optimizer (MPA), and White Shark Optimizer (WSO) on standard microarray datasets.

F1 Score

The F1 score results shown in Table 2 demonstrate the strong performance of PMPA when compared to other methods (BAT, GWO, MPA, and WSO) across multiple datasets. In the Breast dataset, PMPA achieved the highest average F1 score (0.9491) along with the lowest standard deviation (0.0092), indicating both superior accuracy and stability. Although BAT slightly outperformed PMPA in the CNS dataset with an F1 score of 0.9611, PMPA remained highly competitive with a score of 0.9520. For the Leukemia_3c, Leukemia, Lymphoma, and Ovarian datasets, all methods, including PMPA, reached a perfect F1 score of 1 with a standard deviation of 0, signifying flawless and consistent performance. In the Leukemia_4c dataset, BAT achieved the highest F1 score (0.9847), while PMPA performed strongly with a score of 0.9760. Overall, PMPA showed excellent results, especially in the Breast dataset, and maintained strong stability across most datasets, proving its effectiveness relative to the other optimization methods.

Table 2. F1-score (mean ± SD) comparisons across methods and datasets.

Same method/dataset roster as Table 1. F1 combines precision and sensitivity (recall); higher is better.

Dataset	Measure	PMPA	MPA	BAT	GWO	WSO
Breast	Average	9.4911E-01	9.4197E-01	9.3818E-01	9.4326E-01	9.2984E-01
Breast	St. Dev.	9.2308E-03	1.1110E-02	9.4972E-03	1.1362E-02	1.1422E-02
CNS	Average	9.5197E-01	9.5978E-01	9.6107E-01	9.5529E-01	9.5971E-01
CNS	St. Dev.	6.3368E-03	4.0691E-03	1.8008E-04	7.7939E-03	5.3708E-03
Leukemia	Average	1.0000E+00	1.0000E+00	1.0000E+00	1.0000E+00	1.0000E+00
Leukemia	St. Dev.	0.0000E+00	0.0000E+00	0.0000E+00	0.0000E+00	0.0000E+00
Lymphoma	Average	1.0000E+00	1.0000E+00	1.0000E+00	1.0000E+00	1.0000E+00
Lymphoma	St. Dev.	0.0000E+00	0.0000E+00	0.0000E+00	0.0000E+00	0.0000E+00
Leukemia 3c	Average	1.0000E+00	1.0000E+00	1.0000E+00	1.0000E+00	1.0000E+00
Leukemia 3c	St. Dev.	0.0000E+00	0.0000E+00	0.0000E+00	0.0000E+00	0.0000E+00
Leukemia 4c	Average	9.7596E-01	9.8318E-01	9.8469E-01	9.6943E-01	9.7065E-01
Leukemia 4c	St. Dev.	1.6682E-02	7.9836E-03	1.6139E-02	1.8721E-02	1.6518E-02
Ovarian	Average	1.0000E+00	1.0000E+00	1.0000E+00	1.0000E+00	1.0000E+00
Ovarian	St. Dev.	0.0000E+00	0.0000E+00	0.0000E+00	0.0000E+00	0.0000E+00

Matthews Correlation Coefficient (MCC)

Table 3 (MCC results) demonstrate how well PMPA performs in comparison to other algorithms (BAT, GWO, MPA, and WSO) across several datasets. In the Breast dataset, PMPA achieved the highest average MCC (0.9069), while BAT had a slightly lower average. BAT, however, showed the lowest standard deviation (0.0168), indicating higher consistency in performance. In the CNS dataset, BAT performed the best with an average MCC of 0.8918, but PMPA remained competitive with a score of 0.8643. Both algorithms showed strong results in terms of standard deviation, with BAT having the smallest value (0.0004). Across the Leukemia_3c, Leukemia, Lymphoma, and Ovarian datasets, all methods, including PMPA, achieved a perfect MCC of 1, along with a standard deviation of 0, reflecting flawless and consistent performance. In the Leukemia_4c dataset, BAT once again had the highest MCC (0.9822), while PMPA remained strong with an MCC of 0.9734. Overall, PMPA exhibited superior performance in the Breast dataset and remained competitive across other datasets, showing stability and effectiveness in comparison to the other methods.

Table 3. Matthews correlation coefficient (MCC; mean ± SD).

Robust correlation-based metric for binary/multi-class performance; +1 perfect, 0 random, −1 total disagreement. Same methods/datasets as Table 1.

Dataset	Measure	PMPA	MPA	BAT	GWO	WSO
Breast	Average	9.0686E-01	8.9372E-01	8.8817E-01	8.9577E-01	8.7097E-01
Breast	St. Dev.	1.6901E-02	1.9569E-02	1.6842E-02	2.1220E-02	2.0305E-02
CNS	Average	8.6426E-01	8.8825E-01	8.9181E-01	8.7488E-01	8.8847E-01
CNS	St. Dev.	1.9735E-02	1.0624E-02	4.3649E-04	2.2814E-02	1.3915E-02
Leukemia	Average	1.0000E+00	1.0000E+00	1.0000E+00	1.0000E+00	1.0000E+00
Leukemia	St. Dev.	0.0000E+00	0.0000E+00	0.0000E+00	0.0000E+00	0.0000E+00
Lymphoma	Average	1.0000E+00	1.0000E+00	1.0000E+00	1.0000E+00	1.0000E+00
Lymphoma	St. Dev.	0.0000E+00	0.0000E+00	0.0000E+00	0.0000E+00	0.0000E+00
Leukemia 3c	Average	1.0000E+00	1.0000E+00	1.0000E+00	1.0000E+00	1.0000E+00
Leukemia 3c	St. Dev.	0.0000E+00	0.0000E+00	0.0000E+00	0.0000E+00	0.0000E+00
Leukemia 4c	Average	9.7336E-01	9.7863E-01	9.8216E-01	9.6531E-01	9.6731E-01
Leukemia 4c	St. Dev.	1.6728E-02	8.1154E-03	1.6769E-02	1.8629E-02	1.6201E-02
Ovarian	Average	1.0000E+00	1.0000E+00	1.0000E+00	1.0000E+00	1.0000E+00
Ovarian	St. Dev.	0.0000E+00	0.0000E+00	0.0000E+00	0.0000E+00	0.0000E+00

Precision

The precision results from the Table 4 indicate the competitive performance of PMPA compared to other algorithms (BAT, GWO, MPA, and WSO). In the Breast dataset, PMPA achieved the highest average precision (0.9740), outperforming the other methods, with MPA obtaining the lowest standard deviation (0.0175). In the CNS dataset, BAT showed the best precision (0.9729), but PMPA remained competitive with a score of 0.9564, and BAT also had the smallest standard deviation (0.0043). Across the Leukemia_3c, Leukemia, Lymphoma, and Ovarian datasets, all methods, including PMPA, achieved perfect precision with a value of 1 and a standard deviation of 0, indicating flawless performance across these datasets. In the Leukemia_4c dataset, BAT had the highest precision (0.9892), while PMPA performed well with a precision of 0.9859. Overall, PMPA demonstrated strong precision, particularly in the Breast dataset, and maintained competitive results across other datasets, further demonstrating its reliability and effectiveness when compared to the other algorithms.

Table 4. Precision (positive predictive value; mean ± SD).

Fraction of predicted positives that are true positives. Same methods/datasets as Table 1.

Dataset	Measure	PMPA	MPA	BAT	GWO	WSO
Breast	Average	9.7398E-01	9.6698E-01	9.7124E-01	9.6657E-01	9.5293E-01
Breast	St. Dev.	1.9830E-02	1.7457E-02	1.9798E-02	2.2052E-02	2.0967E-02
CNS	Average	9.5644E-01	9.7123E-01	9.7289E-01	9.6250E-01	9.7280E-01
CNS	St. Dev.	1.6607E-02	7.3458E-03	4.3241E-03	1.9442E-02	4.5562E-03
Leukemia	Average	1.0000E+00	1.0000E+00	1.0000E+00	1.0000E+00	1.0000E+00
Leukemia	St. Dev.	0.0000E+00	0.0000E+00	0.0000E+00	0.0000E+00	0.0000E+00
Lymphoma	Average	1.0000E+00	1.0000E+00	1.0000E+00	1.0000E+00	1.0000E+00
Lymphoma	St. Dev.	0.0000E+00	0.0000E+00	0.0000E+00	0.0000E+00	0.0000E+00
Leukemia 3c	Average	1.0000E+00	1.0000E+00	1.0000E+00	1.0000E+00	1.0000E+00
Leukemia 3c	St. Dev.	0.0000E+00	0.0000E+00	0.0000E+00	0.0000E+00	0.0000E+00
Leukemia 4c	Average	9.8591E-01	9.7803E-01	9.8917E-01	9.8167E-01	9.8318E-01
Leukemia 4c	St. Dev.	9.4634E-03	7.2691E-03	9.9993E-03	1.0337E-02	9.2386E-03
Ovarian	Average	1.0000E+00	1.0000E+00	1.0000E+00	1.0000E+00	1.0000E+00
Ovarian	St. Dev.	0.0000E+00	0.0000E+00	0.0000E+00	0.0000E+00	0.0000E+00

Sensitivity (Recall)

Table 5 (sensitivity findings) indicates PMPA’s performance in relation to other algorithms (BAT, GWO, MPA, and WSO). PMPA outperformed the other techniques in the Breast dataset, achieving the highest average sensitivity (0.9261) and the lowest standard deviation (0.0203), demonstrating accuracy and stability. BAT demonstrated marginally superior sensitivity (0.9496) for the CNS dataset, but PMPA maintained its competitiveness with a score of 0.9479. Across the Leukemia_3c, Leukemia, Lymphoma, and Ovarian datasets, all methods, including PMPA, obtained perfect sensitivity with a value of 1 and a standard deviation of 0, demonstrating flawless and consistent performance in these datasets. In the Leukemia_4c dataset, MPA achieved the highest sensitivity (0.9901), while PMPA remained competitive with a sensitivity of 0.9705.

Table 5. Sensitivity (recall; mean ± SD).

Fraction of true positives that are correctly identified. Same methods/datasets as Table 1.

Dataset	Measure	PMPA	MPA	BAT	GWO	WSO
Breast	Average	9.2609E-01	9.1884E-01	9.0797E-01	9.2174E-01	9.0870E-01
Breast	St. Dev.	2.0265E-02	2.3493E-02	2.1876E-02	2.1814E-02	2.5785E-02
CNS	Average	9.4786E-01	9.4872E-01	9.4957E-01	9.4872E-01	9.4701E-01
CNS	St. Dev.	1.0611E-02	9.5228E-03	4.6814E-03	1.6494E-02	9.3628E-03
Leukemia	Average	1.0000E+00	1.0000E+00	1.0000E+00	1.0000E+00	1.0000E+00
Leukemia	St. Dev.	0.0000E+00	0.0000E+00	0.0000E+00	0.0000E+00	0.0000E+00
Lymphoma	Average	1.0000E+00	1.0000E+00	1.0000E+00	1.0000E+00	1.0000E+00
Lymphoma	St. Dev.	0.0000E+00	0.0000E+00	0.0000E+00	0.0000E+00	0.0000E+00
Leukemia 3c	Average	1.0000E+00	1.0000E+00	1.0000E+00	1.0000E+00	1.0000E+00
Leukemia 3c	St. Dev.	0.0000E+00	0.0000E+00	0.0000E+00	0.0000E+00	0.0000E+00
Leukemia 4c	Average	9.7050E-01	9.9013E-01	9.8279E-01	9.6272E-01	9.6360E-01
Leukemia 4c	St. Dev.	2.9453E-02	1.4403E-02	2.5578E-02	2.9767E-02	2.9358E-02
Ovarian	Average	1.0000E+00	1.0000E+00	1.0000E+00	1.0000E+00	1.0000E+00
Ovarian	St. Dev.	0.0000E+00	0.0000E+00	0.0000E+00	0.0000E+00	0.0000E+00

Selected Features

The comparison of the selected features across different algorithms (PMPA, BAT, GWO, MPA, and WSO) shown in Table 6 highlights PMPA’s performance in selecting fewer and more relevant features. In the Breast dataset, GWO selected the fewest features (14.7), followed by MPA (16.8), and PMPA selected 19.8 features, which is still competitive. In terms of stability, GWO had the lowest standard deviation (2.1359). For the CNS dataset, PMPA achieved the best result, selecting the fewest features (7.77) with the lowest standard deviation (1.5241), outperforming the other methods. In the Leukemia_3c dataset, MPA selected the fewest features (4.1), but PMPA closely followed with 4.67 features. Similarly, in the Leukemia_4c dataset, MPA had the best result (6.1), with PMPA closely behind, selecting 8.07 features. For the Leukemia dataset, PMPA and MPA both selected the fewest features (3), with PMPA having the lowest standard deviation (0). In the Lymphoma and Ovarian datasets, PMPA also tied for the fewest selected features (2 and 3, respectively), demonstrating its ability to consistently choose minimal and relevant features across multiple datasets. Overall, PMPA showed strong feature selection performance, consistently selecting fewer features with high stability, making it an effective and efficient method compared to other algorithms.

Table 6. Number of selected genes (mean ± SD).

Parsimony comparison showing typical subset sizes produced by each method on each dataset. Lower is better when accuracy is comparable.

Dataset	Measure	PMPA	MPA	BAT	GWO	WSO
Breast	Average	1.9833E+01	1.6800E+01	2.1133E+01	1.4700E+01	2.3833E+01
Breast	St. Dev.	3.3019E+00	3.4481E+00	2.8252E+00	2.1359E+00	3.3434E+00
CNS	Average	7.7667E+00	8.0333E+00	1.4000E+01	8.5333E+00	1.5433E+01
CNS	St. Dev.	1.5241E+00	1.5862E+00	2.0172E+00	1.7953E+00	2.7877E+00
Leukemia	Average	3.0000E+00	3.0000E+00	5.6667E+00	3.3667E+00	1.1067E+01
Leukemia	St. Dev.	0.0000E+00	0.0000E+00	1.2130E+00	6.6868E-01	2.6514E+00
Lymphoma	Average	2.0000E+00	2.0000E+00	2.6667E+00	2.1333E+00	4.3667E+00
Lymphoma	St. Dev.	0.0000E+00	0.0000E+00	6.0648E-01	3.4575E-01	9.9943E-01
Leukemia 3c	Average	4.6667E+00	4.1000E+00	8.8333E+00	5.9667E+00	1.5700E+01
Leukemia 3c	St. Dev.	6.0648E-01	3.0513E-01	1.8020E+00	2.0924E+00	2.1679E+00
Leukemia 4c	Average	8.0667E+00	6.1000E+00	1.4067E+01	6.3333E+00	1.6533E+01
Leukemia 4c	St. Dev.	2.5587E+00	2.8810E+00	4.1016E+00	2.5506E+00	3.0027E+00
Ovarian	Average	3.0000E+00	3.0000E+00	3.0667E+00	3.0333E+00	5.1667E+00
Ovarian	St. Dev.	0.0000E+00	0.0000E+00	2.5371E-01	1.8257E-01	1.2617E+00

Fitness Value

The fitness value results from the table ( Table 7) demonstrate the performance of PMPA compared to other algorithms (BAT, GWO, MPA, and WSO). In the Breast dataset, PMPA achieved the best fitness value (0.0498) with the lowest standard deviation (0.0077), indicating superior performance and stability compared to the other methods. For the CNS dataset, BAT had the best fitness value (0.0523), followed by MPA and PMPA with slightly higher values, while BAT also showed the lowest standard deviation (0.0004). In the Leukemia_3c dataset, MPA demonstrated the best fitness (0.00082), but PMPA remained highly competitive with a value of 0.00093 and the second-lowest standard deviation. In the Leukemia_4c dataset, BAT again achieved the best fitness value (0.0117), while PMPA followed closely with 0.0122. In the Leukemia, Lymphoma, and Ovarian datasets, PMPA obtained the best fitness values, tying with MPA in the Leukemia dataset (0.0006) and showing superior results in Lymphoma (0.0004) and Ovarian (0.0006). Across most datasets, PMPA demonstrated excellent fitness value performance, particularly excelling in the Breast, Lymphoma, and Ovarian datasets, and maintaining consistent stability, highlighting its effectiveness relative to other algorithms.

Table 7. Fitness value (mean ± SD) used by the wrapper objective.

Objective couples cross-validated SVM accuracy with a size penalty; lower fitness indicates better trade-off (higher accuracy/fewer genes). Same methods/datasets as Table 1.

Dataset	Measure	PMPA	MPA	BAT	GWO	WSO
Breast	Average	4.9837E-02	5.5097E-02	5.8933E-02	5.3687E-02	6.8347E-02
Breast	St. Dev.	7.7303E-03	9.5794E-03	8.2755E-03	1.0317E-02	9.8354E-03
CNS	Average	6.3153E-02	5.2757E-02	5.2300E-02	5.8907E-02	5.4237E-02
CNS	St. Dev.	8.4001E-03	4.8585E-03	4.0343E-04	1.0211E-02	6.6437E-03
Leukemia	Average	6.0000E-04	6.0000E-04	1.1333E-03	6.7333E-04	2.2133E-03
Leukemia	St. Dev.	0.0000E+00	0.0000E+00	2.4259E-04	1.3374E-04	5.3028E-04
Lymphoma	Average	4.0000E-04	4.0000E-04	5.3333E-04	4.2667E-04	8.7333E-04
Lymphoma	St. Dev.	1.6541E-19	1.6541E-19	1.2130E-04	6.9149E-05	1.9989E-04
Leukemia 3c	Average	9.3333E-04	8.2000E-04	1.7667E-03	1.1933E-03	3.1400E-03
Leukemia 3c	St. Dev.	1.2130E-04	6.1026E-05	3.6040E-04	4.1848E-04	4.3359E-04
Leukemia 4c	Average	1.2162E-02	1.4361E-02	1.1653E-02	1.6352E-02	1.5682E-02
Leukemia 4c	St. Dev.	5.0121E-03	3.0395E-03	6.3133E-03	5.6646E-03	4.5043E-03
Ovarian	Average	6.0000E-04	6.0000E-04	6.1333E-04	6.0667E-04	1.0333E-03
Ovarian	St. Dev.	0.0000E+00	0.0000E+00	5.0742E-05	3.6515E-05	2.5235E-04

Convergence Behavior

Figure 3 summarizes the per-iteration fitness trajectories for PMPA versus four widely used metaheuristics (MPA, BAT, GWO, and WSO) across seven microarray benchmarks. In all panels, lower curves indicate better objective values. Two broad patterns emerge. First, PMPA generally exhibits a steep initial decline followed by early stabilization, suggesting that the rMRMR-driven filtering sharply contracts the search space while the MPA↔PSO wrapper alternation accelerates exploitation. Second, the variance band around PMPA’s trajectory is narrow in most datasets, indicating run-to-run stability consistent with the small standard deviations reported for accuracy, F1, MCC, and fitness. Occasional shallow oscillations after the mid-iterations correspond to controlled step-size adjustments when the algorithm transitions from exploration (Brownian/Lévy phases in MPA) to PSO-based local refinement. Below, we comment on each subfigure.

Figure 3. Convergence behavior across seven microarray benchmarks.

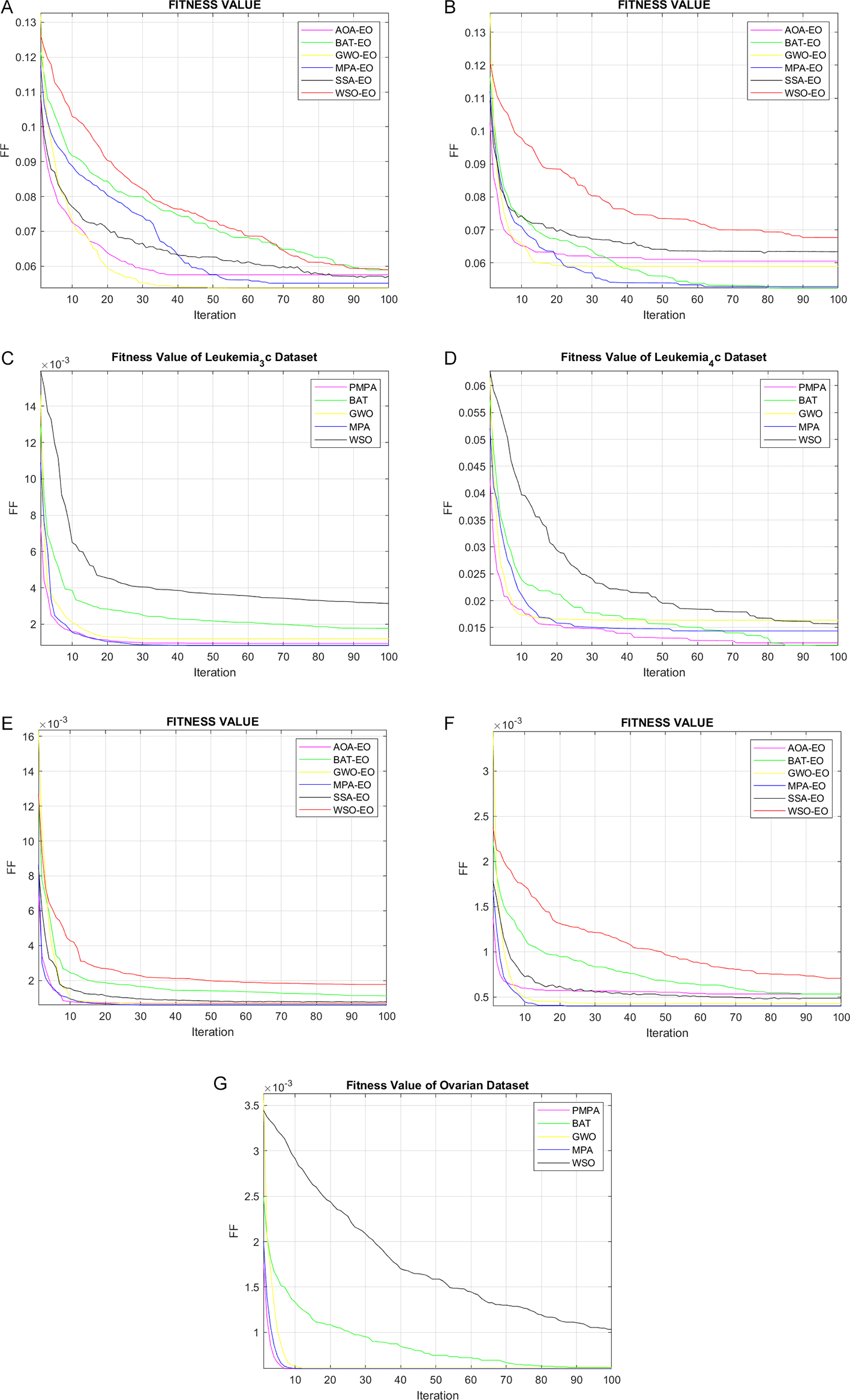
Best-so-far objective vs. iteration for PMPA and baselines (MPA, BAT, GWO, WSO) on: (A) Breast, (B) CNS, (C) Leukemia_3c, (D) Leukemia_4c, (E) Leukemia, (F) Lymphoma, (G) Ovarian. Lower curves indicate better fitness (higher accuracy with smaller subsets). PMPA typically shows rapid initial descent and early stabilization; variability bands (if shown) reflect run-to-run spread. Abbreviations: BAT, Bat Algorithm; GWO, Grey Wolf Optimizer; WSO, White Shark Optimizer; CNS, Central Nervous System.

In the Breast dataset presented in Figure 3 (A), PMPA undergoes a rapid mono-exponential drop in the first few tens of iterations and settles at the lowest fitness among competitors, with minimal post-convergence jitter. This behavior mirrors the quantitative tables, where PMPA attains the best mean fitness and the smallest standard deviation, together with strong precision, sensitivity, and MCC. The early plateau suggests that the PSO pass quickly locks onto compact, high-quality gene subsets after MPA disperses candidates into promising basins.

In the CNS dataset presented in Figure 3 (B), convergence is slower and exhibits one or two inflection points, reflecting a more rugged objective surface. PMPA’s curve descends steadily and shows a secondary improvement mid-run, typical of a handoff from global exploration to PSO-driven refinement. Although BAT may transiently approach similar minima, PMPA maintains a favorable stability–fitness trade-off and, importantly, achieves highly competitive accuracy using markedly fewer genes, indicating efficient subset regularization.

In the Leukemia_3c dataset presented in Figure 3 (C), all algorithms rapidly reach a near-zero fitness floor, consistent with the near-perfect classification metrics. PMPA is among the first to converge and exhibits an extremely tight variance band, implying robustness to initialization and hyperparameter perturbations. The ceiling effect in performance underscores the dataset’s separability once key biomarkers are retrieved.

In the Leukemia_4c dataset presented in Figure 3 (D), This panel shows the most pronounced multi-stage descent. PMPA advances with steady, staircase-like improvements and a late-stage refinement consistent with PSO fine-tuning. While BAT occasionally attains a marginally lower terminal fitness, PMPA’s curve remains smoother and less erratic, indicative of better generalization control under the wrapper’s size penalty and rMRMR-informed search space.

In the Leukemia dataset presented in Figure 3 (E), The trajectories collapse quickly to the minimum, echoing the perfect accuracy and MCC observed across methods. PMPA’s decay is smooth and essentially variance-free, which is compatible with its ability to isolate a minimal subset (two to three genes) without sacrificing discriminative power. This emphasizes the value of the filter–wrapper coupling for highly separable tasks.

In the Lymphoma dataset presented in Figure 3 (F ), Similar to Leukemia, curves flatten early at the optimum with negligible oscillations. PMPA’s stabilization is earliest or among the earliest and remains stable thereafter, reinforcing its repeatability on datasets where biological signal-to-noise is high and redundant genes are abundant.

In the Ovarian dataset presented in Figure 3 (G), PMPA exhibits a sharp initial descent and reaches the optimum swiftly. The convergence band is nearly flat after early iterations, aligning with the perfect downstream metrics and the very small number of selected genes. This suggests that the hybrid search identifies a sparse yet sufficient signature rapidly, then avoids unnecessary exploration that could destabilize the solution.

Taken together, the seven panels indicate that PMPA’s advantage is twofold: fast descent driven by informed initialization and global search, followed by stable exploitation that resists overfitting through explicit subset-size regularization. Where baselines catch up (e.g., CNS or Leukemia_4c), they typically require more iterations and display higher fluctuation amplitudes. Conversely, on strongly separable datasets (Leukemia, Lymphoma, Ovarian), all methods converge rapidly, yet PMPA maintains the earliest and smoothest stabilization while using among the fewest features. These observations corroborate the tabulated accuracy, F1, MCC, precision, sensitivity, and fitness summaries, and they collectively support the conclusion that PMPA offers a reliable convergence profile with favorable stability–efficiency characteristics across diverse gene-expression landscapes.

4.3 Comparison with the State-of-the-Art methods

To evaluate the effectiveness of the proposed PMPA algorithm, we conducted a comprehensive comparison with several well-known and widely-used feature selection methods, including mRMR-DBH,³⁹ SU-RSHSA Shreem et al.,⁴⁰ mRMR-MBAO Pashaei,⁴¹ MIM-MFOA,⁴² IBCFPA,⁴³ ISFLA,³⁷ rMRMR-HBA,⁴⁴ BCROSAT,⁴⁵ MRMR-BA,¹⁷ IG-MBKH,³⁶ and SARA.⁴⁶ The comparison was carried out across six publicly available gene expression datasets: CNS, Ovarian, Leukemia 4c, Leukemia, Leukemia 3c, and Breast. Two key performance indicators were used in the evaluation: the average number of selected genes and the classification accuracy. These metrics are critical for assessing the trade-off between dimensionality reduction and predictive performance. The results, summarized in Table 8, illustrate the strengths and weaknesses of each method and provide insights into the advantages of the proposed PMPA approach.

To further assess PMPA, we compare it to a broad set of recent filter/wrapper selectors reported in the literature, see Table 8.

Table 8. Comparison with recent state-of-the-art filter/wrapper methods.

For each dataset, the average number of genes (ANoG) and classification accuracy (CACC) reported by PMPA vs. literature methods (e.g., mRMR-MBAO, SU-RSHSA, mRMR-DBH, IBCFPA, MIM-MFOA, BCROSAT, ISFLA, SARA, rMRMR-HBA, IG-MBKH, MRMR-BA). “nd” indicates values not disclosed in source reports.

Dataset	Metric	Proposed	mRMR-MBAO	SU-RSHSA	mRMR-DBH	IBCFPA	MIM-MFOA	BCROSAT	ISFLA	SARA	rMRMR-HBA	IG-MBKH	MRMR-BA
CNS	ANoG	7.77E+00	2.14E+01	1.32E+01	3.98E+01	2.52E+01	1.70E+01	2.14E+01	4.11E+01	nd	1.92E+01	1.47E+01	1.92E+01
CNS	CACC	9.38E+01	8.86E+01	8.94E+01	9.72E+01	8.48E+01	8.50E+01	8.20E+01	7.75E+01	nd	9.42E+01	9.03E+01	9.42E+01
Ovarian	ANoG	3.00E+00	5.17E+00	2.05E+01	2.66E+00	4.88E+01	3.32E+01	nd	3.33E+01	6.00E+00	3.80E+00	3.40E+00	3.83E+00
Ovarian	CACC	1.00E+02	1.00E+02	9.96E+01	1.00E+02	9.91E+01	9.76E+01	nd	9.73E+01	9.92E+01	1.00E+02	1.00E+02	1.00E+02
Leukemia 4c	ANoG	8.07E+00	2.13E+01	1.20E+01	nd	4.56E+01	nd	3.09E+01	3.22E+01	nd	1.10E+01	1.58E+01	1.10E+01
Leukemia 4c	CACC	9.89E+01	9.87E+01	9.71E+01	nd	9.44E+01	nd	9.09E+01	9.09E+01	nd	9.98E+01	9.94E+01	9.98E+01
Leukemia	ANoG	2.00E+00	8.71E+00	2.16E+01	4.00E+00	2.99E+01	8.23E+00	nd	3.58E+01	7.00E+00	5.20E+00	4.20E+00	5.23E+00
Leukemia	CACC	1.00E+02	1.00E+02	1.00E+02	1.00E+02	9.94E+01	9.93E+01	nd	9.63E+01	9.77E+01	1.00E+02	1.00E+02	1.00E+02
Leukemia 3c	ANoG	4.67E+00	1.23E+01	1.07E+01	nd	4.96E+01	1.05E+01	3.20E+01	4.00E+01	7.00E+00	7.30E+00	8.80E+00	7.27E+00
Leukemia 3c	CACC	1.00E+02	1.00E+02	1.00E+02	nd	9.80E+01	9.38E+01	9.45E+01	9.40E+01	9.80E+01	1.00E+02	1.00E+02	1.00E+02
Breast	ANoG	1.98E+01	nd	nd	nd	nd	nd	nd	nd	nd	nd	nd	1.83E+01
Breast	CACC	9.54E+01	nd	nd	nd	nd	nd	nd	nd	nd	nd	nd	8.88E+01

With an emphasis on the average number of selected genes (ANoG) and the associated classification accuracy (CACC), Table 8 compares the suggested PMPA approach with a number of cutting-edge feature selection algorithms across numerous biomedical datasets. As indicated by the results, it demonstrates the strong performance of PMPA in both accuracy and gene reduction. Notably, in the CNS dataset, PMPA selected only 7.767 genes while achieving an accuracy of 93.78%.

Notes: Average number of genes (ANoG) and Classification accuracy (CACC) are used to record the results. “nd” denotes that the value was not disclosed. Method names have been normalized (e.g., MRMR-BA, rMRMR-HBA). Any unusual underscore-like symbols were replaced with standard underscores.

For the Ovarian dataset, PMPA achieved perfect classification accuracy (100%) with just 3 selected genes. In the Leukemia 4c dataset, PMPA reached an accuracy of 98.93% with 8.067 genes, indicating a favorable trade-off compared to methods like mRMR-MBAO and mRMR-DBH, which selected more than 20 genes. In both the Leukemia and Leukemia 3c datasets, PMPA achieved 100% accuracy using only 2 and 4.667 genes, respectively, while alternative techniques required up to 49.6 genes. For the Breast dataset, PMPA reported an accuracy of 95.36% with 19.833 selected genes, though several baselines did not report results for this dataset.

5. Conclusion and future work

This study addressed the gene selection problem in cancer classification, it suggested a novel hybrid approach called PMPA. The method strikes a balance between exploration and exploitation by utilizing the complementary strengths of Particle Swarm Optimization (PSO) and the Marine Predators Algorithm (MPA), which allows it to efficiently traverse high-dimensional gene expression datasets. PMPA regularly outperforms other optimization techniques, such as BAT, GWO, and WSO, across a range of performance parameters, including classification accuracy, sensitivity, and the number of selected genes, according to experimental evaluations on a number of well-known microarray benchmarks. Additionally, PMPA improves computational efficiency by removing unnecessary genes and has improved stability, as seen by a decreased standard deviation in the results.

The effectiveness of the PMPA method stems from its adaptive mechanisms, which allow it to search the solution space effectively while avoiding local optima. This makes PMPA a robust and reliable tool for the tasks in gene selection in cancer classification. The ability to identify a minimal subset of genes without compromising classification performance highlights its practicality and potential for real-world applications in cancer diagnostics and personalized medicine.

Future research could explore several extensions to the PMPA framework. One direction is integrating additional evolutionary algorithms, such as Genetic Algorithms or Differential Evolution, to enhance performance on larger and more complex datasets. Another potential avenue involves applying PMPA to other types of omics data, such as proteomics and metabolomics, to validate its applicability beyond gene expression. Exploring the combination of PMPA with deep learning models could automate the gene selection process further and improve scalability for handling larger datasets.

Dynamic parameter tuning during the search process could enhance the method’s efficiency, while implementing parallel processing techniques could significantly reduce computational time, making PMPA more practical for real-time clinical diagnostics.

Data availability statement

Zenodo: A Novel PMPA for Gene Selection Health SS with Datasets and Codes https://doi.org/10.5281/zenodo.17390187

Data are available under the terms of the Creative Commons Attribution 4.0 International license (CC-BY 4.0).

References

1. Wahsheh H, Doush IA, Al-Kabi M, et al.: Using machine learning algorithms to detect content-based arabic web spam. Journal of Information Assurance & Security. 2012; 7(1).
2. Sawalha R, Doush IA: Face recognition using harmony search-based selected features. International Journal of Hybrid Information Technology. 2012; 5(2): 1–16.
3. Abu Doush I, Al-Saleh MI: Can genetic algorithms help virus writers reshape their creations and avoid detection? Journal of Experimental & Theoretical Artificial Intelligence. 2017; 29(6): 1297–1310. Publisher Full Text
4. Wang S, Cheng Q: Microarray analysis in drug discovery and clinical applications. Bioinformatics and Drug Discovery. 2006; 49–65. Publisher Full Text
5. Bolon-Canedo V, Sanchez-Marono N, Alonso-Betanzos A, et al.: A review of microarray datasets and applied feature selection methods. Inf. Sci. 2014; 282: 111–135. Publisher Full Text
6. Al-Betar MA, Alomari OA, Abu-Romman SM: A triz-inspired bat algorithm for gene selection in cancer classification. Genomics. 2020; 112(1): 114–126. PubMed Abstract | Publisher Full Text
7. Jain A, Zongker D: Feature selection: Evaluation, application, and small sample performance. IEEE Trans. Pattern Anal. Mach. Intell. 1997; 19(2): 153–158. Publisher Full Text
8. Hammouri AI, Mafarja M, Al-Betar MA, et al.: An improved dragonfly algorithm for feature selection. Knowl.-Based Syst. 2020; 203: 106131. Publisher Full Text
9. Aljarah I, Habib M, Faris H, et al.: A dynamic locality multi-objective salp swarm algorithm for feature selection. Comput. Ind. Eng. 2020; 147: 106628. Publisher Full Text
10. Alomari OA, Khader AT, Al-Betar MA, et al.: Mrmr ba: a hybrid gene selection algorithm for cancer classification. J. Theor. Appl. Inf. Technol. 2017; 95(12): 2610–2618.
11. Too J, Mirjalili S: A Hyper Learning Binary Dragonfly Algorithm for Feature Selection: A COVID-19 Case Study. Knowledge-Based Systems. 2021; 212: 106553. Publisher Full Text
12. Al-Betar MA, Hammouri AI, Awadallah MA, et al.: Binary β -hill climbing optimizer with s-shape transfer function for feature selection. J. Ambient. Intell. Humaniz. Comput. 2020; 12: 7637–7665. Publisher Full Text
13. Al-Abdallah RZ, Jaradat AS, Doush IA, et al.: A binary classifier based on firefly algorithm. Jordanian Journal of Computers and Information Technology (JJCIT). 2017; 3(3): 172. Publisher Full Text
14. Wang H, Jing X, Niu B: A discrete bacterial algorithm for feature selection in classification of microarray gene expression cancer data. Knowl.-Based Syst. 2017; 126: 8–19. Publisher Full Text
15. Jain I, Jain VK, Jain R: Correlation feature selection based improved-binary particle swarm optimization for gene selection and cancer classification. Appl. Soft Comput. 2018; 62: 203–215. Publisher Full Text
16. Salem H, Attiya G, El-Fishawy N: Classification of human cancer diseases by gene expression profiles. Appl. Soft Comput. 2017; 50: 124–134. Publisher Full Text
17. Alomari OA, Khader AT, Al-Betar MA, et al.: Gene selection for cancer classification by combining minimum redundancy maximum relevancy and bat-inspired algorithm. Int. J. Data Min. Bioinform. 2017; 19(1): 32–51. Publisher Full Text
18. Coleto-Alcudia V, Vega-Rodrıguez MA: Artificial bee colony algorithm based on dominance (abcd) for a hybrid gene selection method. Knowl.-Based Syst. 2020; 205: 106323. Publisher Full Text
19. Nasr M, Farouk O, Mohamedeen A, et al.: Benchmarking meta-heuristic optimization. arXiv preprint arXiv:2007.13476. 2020.
20. Shreem SS, Abdullah S, Nazri MZA: Hybridising harmony search with a markov blanket for gene selection problems. Inf. Sci. 2014; 258: 108–121. Publisher Full Text
21. Alyasseri ZAA, Khader AT, Al-Betar MA, et al.: Person identification using eeg channel selection with hybrid flower pollination algorithm. Pattern Recogn. 2020; 105: 107393. Publisher Full Text
22. Awadallah MA, Al-Betar MA, Hammouri AI, et al.: Binary jaya algorithm with adaptive mutation for feature selection. Arab. J. Sci. Eng. 2020; 45: 10875–10890. Publisher Full Text
23. Faramarzi A, Heidarinejad M, Mirjalili S, et al.: Marine predators algorithm: A nature-inspired metaheuristic. Expert Syst. Appl. 2020; 152: 113377. Publisher Full Text
24. Houssein EH, Hassaballah M, Ibrahim IE, et al.: An automatic arrhythmia classification model based on improved marine predators algorithm and convolutions neural networks. Expert Syst. Appl. 2022; 187: 115936. Publisher Full Text
25. Wang N, Wang J-S, Zhu L, et al.: A novel dynamic clustering method by integrating marine predators algorithm and particle swarm optimization algorithm. IEEE Access. 2020; 9: 3557–3569. Publisher Full Text
26. Abdel-Basset M, Mohamed R, Elhoseny M, et al.: Energy-aware marine predators algorithm for task scheduling in iot-based fog computing applications. IEEE Trans. Industr. Inform. 2020; 17(7): 5068–5076.
27. Abd Elaziz M, Ewees AA, Yousri D, et al.: An improved marine predators algorithm with fuzzy entropy for multi-level thresholding: Real world example of covid-19 ct image segmentation. IEEE Access. 2020; 8: 125306–125330. PubMed Abstract | Publisher Full Text | Free Full Text
28. Abdel-Basset M, Mohamed R, Elhoseny M, et al.: A hybrid covid-19 detection model using an improved marine predators algorithm and a ranking-based diversity reduction strategy. IEEE access. 2020; 8: 79521–79540. Publisher Full Text
29. Yousri D, Babu TS, Beshr E, et al.: A robust strategy based on marine predators algorithm for large scale photovoltaic array reconfiguration to mitigate the partial shading effect on the performance of pv system. IEEE Access. 2020; 8: 112407–112426. Publisher Full Text
30. Filmalter JD, Dagorn L, Cowley PD, et al.: First descriptions of the behavior of silky sharks, carcharhinus falciformis, around drifting fish aggregating devices in the indian ocean. Bull. Mar. Sci. 2011; 87(3): 325–337. Publisher Full Text
31. Kennedy J, Eberhart R: Particle swarm optimization. Proceedings of ICNN’95-international Conference on Neural Networks. IEEE; 1995; vol. 4. : pp. 1942–1948.
32. Makhadmeh SN, Khader AT, Al-Betar MA, et al.: Particle swarm opti- mization algorithm for power scheduling problem using smart battery. 2019 IEEE Jordan International Joint Conference on Electrical Engineering and Information Technology (JEEIT). IEEE; 2019; pp. 672–677.
33. Makhadmeh SN, Sanjalawe Y, Al-Betar MA, et al.: A crossover-enhanced marine predators algorithm for gene selection in microarray-based cancer classification. Artificial Intelligence in the Life Sciences. 2025; 5: 100140. Publisher Full Text
34. Duval B, Hao J-K, Hernandez Hernandez JC: A memetic algorithm for gene selection and molecular classification of cancer. Proceedings of the 11th Annual Conference on Genetic and Evolutionary Computation. ACM; 2009; pp. 201–208.
35. Dash M, Liu H: Feature selection for classification. Intelligent data analysis. 1997; 1(3): 131–156. Publisher Full Text
36. Zhang G, Hou J, Wang J, et al.: Feature selection for microarray data classification using hybrid information gain and a modified binary krill herd algorithm. Interdiscip. Sci.: Comput. Life Sci. 2020; 12: 288–301. Publisher Full Text
37. Hu B, Dai Y, Su Y, et al.: Feature selection for optimized high- dimensional biomedical data using an improved shuffled frog leaping algorithm. IEEE/ACM Trans. Comput. Biol. Bioinform. 2016; 15(6): 1765–1773. PubMed Abstract | Publisher Full Text
38. Ambroise C, McLachlan GJ: Selection bias in gene extraction on the basis of microarray gene-expression data. Proc. Natl. Acad. Sci. 2002; 99(10): 6562–6566. PubMed Abstract | Publisher Full Text | Free Full Text
39. Pashaei E, Pashaei E: Gene selection using hybrid dragonfly black hole algorithm: A case study on rna-seq covid-19 data. Anal. Biochem. 2021; 627: 114242. PubMed Abstract | Publisher Full Text
40. Shreem SS, Ahmad Nazri MZ, Abdullah S, et al.: Hybrid symmetrical uncertainty and reference set harmony search algorithm for gene selection problem. Mathematics. 2022; 10(3): 374. Publisher Full Text
41. Pashaei E: Mutation-based binary aquila optimizer for gene selection in cancer classification. Comput. Biol. Chem. 2022; 101: 107767. PubMed Abstract | Publisher Full Text
42. Dabba A, Tari A, Meftali S, et al.: Gene selection and classification of microarray data method based on mutual information and moth flame algorithm. Expert Syst. Appl. 2021; 166: 114012. Publisher Full Text
43. Yan C, Ma J, Luo H, et al.: A novel feature selection method for high-dimensional biomedical data based on an improved binary clonal flower pollination algorithm. Hum. Hered. 2019; 84(1): 34–46. PubMed Abstract | Publisher Full Text
44. Alomari OA, Khader AT, Al-Betar MA, et al.: A novel gene selection method using modified mrmr and hybrid bat-inspired algorithm with β-hill climbing. Appl. Intell. 2018; 48(11): 4429–4447. Publisher Full Text
45. Yan C, Ma J, Luo H, et al.: Hybrid binary coral reefs optimization algorithm with simulated annealing for feature selection in high-dimensional biomedical datasets. Chemom. Intell. Lab. Syst. 2019; 184: 102–111. Publisher Full Text
46. Baliarsingh SK, Muhammad K, Bakshi S: Sara: A memetic algorithm for high-dimensional biomedical data. Appl. Soft Comput. 2021; 101: 107009. Publisher Full Text
47. Zhu Z, Ong YS, Dash M: Markov blanket-embedded genetic algorithm for gene selection. Pattern Recogn. 2007; 40(11): 3236–3248. Publisher Full Text
48. Li T, Zhang C, Ogihara M: A comparative study of feature selection and multiclass classification methods for tissue classification based on gene expression. Bioinformatics. 2004; 20: 2429–2437. PubMed Abstract | Publisher Full Text
49. Wang X, Gotoh O: Accurate molecular classification of cancer using simple rules. BMC Med. Genet. 2009; 2(1): 64. PubMed Abstract | Publisher Full Text | Free Full Text

Comments on this article Comments (0)

Version 1

VERSION 1 PUBLISHED 18 Nov 2025

Author details Author details

¹ KASIT, IT Department, The University of Jordan, Amman, Amman Governorate, Jordan
² The University of Jordan School of Medicine, Amman, Amman Governorate, Jordan
³ Faculty of Medicine, Mutah University, Kerak, Jordan

Rizik Al-Sayyed
Roles: Conceptualization, Formal Analysis, Methodology, Project Administration, Supervision, Writing – Original Draft Preparation

AlMuatasim Billah Rizik AlSayyed
Roles: Formal Analysis, Funding Acquisition, Methodology, Resources, Validation, Visualization, Writing – Review & Editing

Sharif Naser Makhadmeh
Roles: Conceptualization, Data Curation, Formal Analysis, Investigation, Methodology, Resources, Writing – Review & Editing

Yousef Sanjalawe
Roles: Investigation, Methodology, Software, Validation, Visualization, Writing – Review & Editing

Barihan M. Khasawneh
Roles: Data Curation, Formal Analysis, Writing – Original Draft Preparation

Competing interests

No competing interests were disclosed.

Grant information

The author(s) declared that no grants were involved in supporting this work.

Article Versions (1)

version 1

Published: 18 Nov 2025, 14:1275

https://doi.org/10.12688/f1000research.172440.1

Copyright

© 2025 Al-Sayyed R et al. This is an open access article distributed under the terms of the Creative Commons Attribution License, which permits unrestricted use, distribution, and reproduction in any medium, provided the original work is properly cited.

Download

Export To

metrics

	Views	Downloads
F1000Research	-	-
PubMed Central Data from PMC are received and updated monthly.	-	-

Citations

0

SEE MORE DETAILS

CITE

how to cite this article

Al-Sayyed R, AlSayyed ABR, Makhadmeh SN et al. A Novel Particle Marine Predator Optimizer for Gene Selection Health Problem [version 1; peer review: awaiting peer review]. F1000Research 2025, 14:1275 (https://doi.org/10.12688/f1000research.172440.1)

NOTE: If applicable, it is important to ensure the information in square brackets after the title is included in all citations of this article.

track

receive updates on this article

Track an article to receive email alerts on any updates to this article.

Open Peer Review

Comments on this article Comments (0)

Version 1

VERSION 1 PUBLISHED 18 Nov 2025

Open Peer Review

Reviewer Status

AWAITING PEER REVIEW

Comments on this article

All Comments(0)

Add a comment

Sign up for content alerts

Browse by related subjects

[1] 1. Wahsheh H, Doush IA, Al-Kabi M, et al.: Using machine learning algorithms to detect content-based arabic web spam. Journal of Information Assurance & Security. 2012; 7(1).

[2] 2. Sawalha R, Doush IA: Face recognition using harmony search-based selected features. International Journal of Hybrid Information Technology. 2012; 5(2): 1–16.

[3] 3. Abu Doush I, Al-Saleh MI: Can genetic algorithms help virus writers reshape their creations and avoid detection? Journal of Experimental & Theoretical Artificial Intelligence. 2017; 29(6): 1297–1310. Publisher Full Text

[4] 4. Wang S, Cheng Q: Microarray analysis in drug discovery and clinical applications. Bioinformatics and Drug Discovery. 2006; 49–65. Publisher Full Text

[5] 5. Bolon-Canedo V, Sanchez-Marono N, Alonso-Betanzos A, et al.: A review of microarray datasets and applied feature selection methods. Inf. Sci. 2014; 282: 111–135. Publisher Full Text

[6] 6. Al-Betar MA, Alomari OA, Abu-Romman SM: A triz-inspired bat algorithm for gene selection in cancer classification. Genomics. 2020; 112(1): 114–126. PubMed Abstract | Publisher Full Text

[7] 7. Jain A, Zongker D: Feature selection: Evaluation, application, and small sample performance. IEEE Trans. Pattern Anal. Mach. Intell. 1997; 19(2): 153–158. Publisher Full Text

[8] 8. Hammouri AI, Mafarja M, Al-Betar MA, et al.: An improved dragonfly algorithm for feature selection. Knowl.-Based Syst. 2020; 203: 106131. Publisher Full Text

[9] 9. Aljarah I, Habib M, Faris H, et al.: A dynamic locality multi-objective salp swarm algorithm for feature selection. Comput. Ind. Eng. 2020; 147: 106628. Publisher Full Text

[10] 10. Alomari OA, Khader AT, Al-Betar MA, et al.: Mrmr ba: a hybrid gene selection algorithm for cancer classification. J. Theor. Appl. Inf. Technol. 2017; 95(12): 2610–2618.

[11] 11. Too J, Mirjalili S: A Hyper Learning Binary Dragonfly Algorithm for Feature Selection: A COVID-19 Case Study. Knowledge-Based Systems. 2021; 212: 106553. Publisher Full Text

[12] 12. Al-Betar MA, Hammouri AI, Awadallah MA, et al.: Binary β -hill climbing optimizer with s-shape transfer function for feature selection. J. Ambient. Intell. Humaniz. Comput. 2020; 12: 7637–7665. Publisher Full Text

[13] 13. Al-Abdallah RZ, Jaradat AS, Doush IA, et al.: A binary classifier based on firefly algorithm. Jordanian Journal of Computers and Information Technology (JJCIT). 2017; 3(3): 172. Publisher Full Text

[14] 14. Wang H, Jing X, Niu B: A discrete bacterial algorithm for feature selection in classification of microarray gene expression cancer data. Knowl.-Based Syst. 2017; 126: 8–19. Publisher Full Text

[15] 15. Jain I, Jain VK, Jain R: Correlation feature selection based improved-binary particle swarm optimization for gene selection and cancer classification. Appl. Soft Comput. 2018; 62: 203–215. Publisher Full Text

[16] 16. Salem H, Attiya G, El-Fishawy N: Classification of human cancer diseases by gene expression profiles. Appl. Soft Comput. 2017; 50: 124–134. Publisher Full Text

[17] 17. Alomari OA, Khader AT, Al-Betar MA, et al.: Gene selection for cancer classification by combining minimum redundancy maximum relevancy and bat-inspired algorithm. Int. J. Data Min. Bioinform. 2017; 19(1): 32–51. Publisher Full Text

[18] 18. Coleto-Alcudia V, Vega-Rodrıguez MA: Artificial bee colony algorithm based on dominance (abcd) for a hybrid gene selection method. Knowl.-Based Syst. 2020; 205: 106323. Publisher Full Text

[19] 19. Nasr M, Farouk O, Mohamedeen A, et al.: Benchmarking meta-heuristic optimization. arXiv preprint arXiv:2007.13476. 2020.

[20] 20. Shreem SS, Abdullah S, Nazri MZA: Hybridising harmony search with a markov blanket for gene selection problems. Inf. Sci. 2014; 258: 108–121. Publisher Full Text

[21] 21. Alyasseri ZAA, Khader AT, Al-Betar MA, et al.: Person identification using eeg channel selection with hybrid flower pollination algorithm. Pattern Recogn. 2020; 105: 107393. Publisher Full Text

[22] 22. Awadallah MA, Al-Betar MA, Hammouri AI, et al.: Binary jaya algorithm with adaptive mutation for feature selection. Arab. J. Sci. Eng. 2020; 45: 10875–10890. Publisher Full Text

[23] 23. Faramarzi A, Heidarinejad M, Mirjalili S, et al.: Marine predators algorithm: A nature-inspired metaheuristic. Expert Syst. Appl. 2020; 152: 113377. Publisher Full Text

[24] 24. Houssein EH, Hassaballah M, Ibrahim IE, et al.: An automatic arrhythmia classification model based on improved marine predators algorithm and convolutions neural networks. Expert Syst. Appl. 2022; 187: 115936. Publisher Full Text

[25] 25. Wang N, Wang J-S, Zhu L, et al.: A novel dynamic clustering method by integrating marine predators algorithm and particle swarm optimization algorithm. IEEE Access. 2020; 9: 3557–3569. Publisher Full Text

[26] 26. Abdel-Basset M, Mohamed R, Elhoseny M, et al.: Energy-aware marine predators algorithm for task scheduling in iot-based fog computing applications. IEEE Trans. Industr. Inform. 2020; 17(7): 5068–5076.

[27] 27. Abd Elaziz M, Ewees AA, Yousri D, et al.: An improved marine predators algorithm with fuzzy entropy for multi-level thresholding: Real world example of covid-19 ct image segmentation. IEEE Access. 2020; 8: 125306–125330. PubMed Abstract | Publisher Full Text | Free Full Text

[28] 28. Abdel-Basset M, Mohamed R, Elhoseny M, et al.: A hybrid covid-19 detection model using an improved marine predators algorithm and a ranking-based diversity reduction strategy. IEEE access. 2020; 8: 79521–79540. Publisher Full Text

[29] 29. Yousri D, Babu TS, Beshr E, et al.: A robust strategy based on marine predators algorithm for large scale photovoltaic array reconfiguration to mitigate the partial shading effect on the performance of pv system. IEEE Access. 2020; 8: 112407–112426. Publisher Full Text

[30] 30. Filmalter JD, Dagorn L, Cowley PD, et al.: First descriptions of the behavior of silky sharks, carcharhinus falciformis, around drifting fish aggregating devices in the indian ocean. Bull. Mar. Sci. 2011; 87(3): 325–337. Publisher Full Text

[31] 31. Kennedy J, Eberhart R: Particle swarm optimization. Proceedings of ICNN’95-international Conference on Neural Networks. IEEE; 1995; vol. 4. : pp. 1942–1948.

[32] 32. Makhadmeh SN, Khader AT, Al-Betar MA, et al.: Particle swarm opti- mization algorithm for power scheduling problem using smart battery. 2019 IEEE Jordan International Joint Conference on Electrical Engineering and Information Technology (JEEIT). IEEE; 2019; pp. 672–677.

[33] 33. Makhadmeh SN, Sanjalawe Y, Al-Betar MA, et al.: A crossover-enhanced marine predators algorithm for gene selection in microarray-based cancer classification. Artificial Intelligence in the Life Sciences. 2025; 5: 100140. Publisher Full Text

[34] 34. Duval B, Hao J-K, Hernandez Hernandez JC: A memetic algorithm for gene selection and molecular classification of cancer. Proceedings of the 11th Annual Conference on Genetic and Evolutionary Computation. ACM; 2009; pp. 201–208.

[35] 35. Dash M, Liu H: Feature selection for classification. Intelligent data analysis. 1997; 1(3): 131–156. Publisher Full Text

[36] 36. Zhang G, Hou J, Wang J, et al.: Feature selection for microarray data classification using hybrid information gain and a modified binary krill herd algorithm. Interdiscip. Sci.: Comput. Life Sci. 2020; 12: 288–301. Publisher Full Text

[37] 37. Hu B, Dai Y, Su Y, et al.: Feature selection for optimized high- dimensional biomedical data using an improved shuffled frog leaping algorithm. IEEE/ACM Trans. Comput. Biol. Bioinform. 2016; 15(6): 1765–1773. PubMed Abstract | Publisher Full Text

[38] 38. Ambroise C, McLachlan GJ: Selection bias in gene extraction on the basis of microarray gene-expression data. Proc. Natl. Acad. Sci. 2002; 99(10): 6562–6566. PubMed Abstract | Publisher Full Text | Free Full Text

[39] 39. Pashaei E, Pashaei E: Gene selection using hybrid dragonfly black hole algorithm: A case study on rna-seq covid-19 data. Anal. Biochem. 2021; 627: 114242. PubMed Abstract | Publisher Full Text

[40] 40. Shreem SS, Ahmad Nazri MZ, Abdullah S, et al.: Hybrid symmetrical uncertainty and reference set harmony search algorithm for gene selection problem. Mathematics. 2022; 10(3): 374. Publisher Full Text

[41] 41. Pashaei E: Mutation-based binary aquila optimizer for gene selection in cancer classification. Comput. Biol. Chem. 2022; 101: 107767. PubMed Abstract | Publisher Full Text

[42] 42. Dabba A, Tari A, Meftali S, et al.: Gene selection and classification of microarray data method based on mutual information and moth flame algorithm. Expert Syst. Appl. 2021; 166: 114012. Publisher Full Text

[43] 43. Yan C, Ma J, Luo H, et al.: A novel feature selection method for high-dimensional biomedical data based on an improved binary clonal flower pollination algorithm. Hum. Hered. 2019; 84(1): 34–46. PubMed Abstract | Publisher Full Text

[44] 44. Alomari OA, Khader AT, Al-Betar MA, et al.: A novel gene selection method using modified mrmr and hybrid bat-inspired algorithm with β-hill climbing. Appl. Intell. 2018; 48(11): 4429–4447. Publisher Full Text

[45] 45. Yan C, Ma J, Luo H, et al.: Hybrid binary coral reefs optimization algorithm with simulated annealing for feature selection in high-dimensional biomedical datasets. Chemom. Intell. Lab. Syst. 2019; 184: 102–111. Publisher Full Text

[46] 46. Baliarsingh SK, Muhammad K, Bakshi S: Sara: A memetic algorithm for high-dimensional biomedical data. Appl. Soft Comput. 2021; 101: 107009. Publisher Full Text

[47] 47. Zhu Z, Ong YS, Dash M: Markov blanket-embedded genetic algorithm for gene selection. Pattern Recogn. 2007; 40(11): 3236–3248. Publisher Full Text

[48] 48. Li T, Zhang C, Ogihara M: A comparative study of feature selection and multiclass classification methods for tissue classification based on gene expression. Bioinformatics. 2004; 20: 2429–2437. PubMed Abstract | Publisher Full Text

[49] 49. Wang X, Gotoh O: Accurate molecular classification of cancer using simple rules. BMC Med. Genet. 2009; 2(1): 64. PubMed Abstract | Publisher Full Text | Free Full Text

A Novel Particle Marine Predator Optimizer for Gene Selection Health Problem

Abstract

Background

Methods

Results

Conclusions

Keywords

1. Introduction

2. Research background

2.1 Marine Predators Algorithm (MPA)

Figure 1. Marine Predators Algorithm (MPA) search regimes and updates.

(1)

(2)

(3)

(4)

(5)

(6)

(7)

(8)

(9)

(10)

(11)

(12)

(13)

Algorithm 1. The MPA Pseudocode.

2.2 Particle Swarm Optimization

(14)

(15)

3. Methodology

3.1 Stage 1: Filter approach

3.2 Stage 2: Wrapper approach

(16)

Figure 2. PMPA six-step hybrid pipeline for gene selection.

(17)

4. Experimental setup and results

4.1 Datasets

Table 1. Classification accuracy (mean ± SD) for PMPA vs. baseline metaheuristics across datasets.

4.2 Results of the hybridization method: A comparative study

Table 2. F1-score (mean ± SD) comparisons across methods and datasets.

Table 3. Matthews correlation coefficient (MCC; mean ± SD).

Table 4. Precision (positive predictive value; mean ± SD).

Table 5. Sensitivity (recall; mean ± SD).

Table 6. Number of selected genes (mean ± SD).

Table 7. Fitness value (mean ± SD) used by the wrapper objective.

Figure 3. Convergence behavior across seven microarray benchmarks.

4.3 Comparison with the State-of-the-Art methods

Table 8. Comparison with recent state-of-the-art filter/wrapper methods.

5. Conclusion and future work

Data availability statement

References

Comments on this article Comments (0)

Open Peer Review

Comments on this article Comments (0)

Open Peer Review

Reviewer Status

Comments on this article

Browse by related subjects

Competing Interests Policy

Stay Updated