Regarding the Novel IDNAII Distribution: Mathematical and Statistical Characteristics

Abbas Najim; Iden Hassan Hussein

doi:10.12688/f1000research.173663.1

Home Browse Regarding the Novel IDNAII Distribution: Mathematical and Statistical...

ALL Metrics

-

Views

-

Downloads

Get PDF

Get XML

Export

▬

✚

Research Article

Regarding the Novel IDNAII Distribution: Mathematical and Statistical Characteristics

[version 1; peer review: awaiting peer review]

Abbas Najim ¹, Iden Hassan Hussein²

PUBLISHED 24 Dec 2025

Author details Author details

¹ Department of Mathematics, University of Baghdad College of Education for Pure Science Ibn Al-Haitham, Baghdad, Baghdad Governorate, 10053, Iraq
² Department of Mathematics, University of Baghdad Al-Jaderyia Campus College of Science, Baghdad, Baghdad Governorate, 10070, Iraq

Abbas Najim
Roles: Conceptualization, Formal Analysis, Methodology, Software, Validation, Visualization, Writing – Original Draft Preparation, Writing – Review & Editing

Iden Hassan Hussein
Roles: Conceptualization, Formal Analysis, Methodology, Project Administration, Supervision, Writing – Original Draft Preparation, Writing – Review & Editing

OPEN PEER REVIEW

REVIEWER STATUS AWAITING PEER REVIEW

This article is included in the Fallujah Multidisciplinary Science and Innovation gateway.

Abstract

Over the last decade, there has been an increased range of probability distributions in statistical and reliability literature aimed at enhancing standard models. This trend reflects a greater understanding of empirical integrity, flexibility, and adaptability in modeling income distributions, reliability, and lifetime statistics. To provide greater flexibility and general distributions, this study employs a technique that generates the T−R{Y} family distributions. It might be employed to agree with particular forms of data distributions, including the significantly left, right, thin, or heavy-tailed distributions, or for creating new distributions that are very flexible and adaptive. These results in an individual belonging to a new sub-family called the IDNAII distribution, which is also referred to as the Lomax–Weibull {Exponential} distribution. The main statistical and mathematical aspects of the new family distribution are examined. A variety of estimation approaches, including the maximum likelihood method (MLE), method of moments (MOM), least squares method (LS), and shrinkage method (SH), will be introduced to estimate the parameters of the new class distribution. Simulation tools have been created to evaluate the effectiveness of estimation approaches. The study’s findings indicate that the shrinkage estimation approach exceeded the others regarding bias and mean squared error criterion. On the contrary, a real-world dataset application has been demonstrated and the examination of the real dataset showed that the new class distribution fit the data better than the particular classical and moderate distributions, as indicated by several types of information criteria.

Keywords

Transformed-transformer family, Quantile function, Statistical properties, Estimation methods, Monte Carlo simulation, Real data application and Goodness-of-Fit.

Corresponding author: Abbas Najim

Competing interests: No competing interests were disclosed.

Grant information: The author(s) declared that no grants were involved in supporting this work.

Copyright: © 2025 Najim A and Hassan Hussein I. This is an open access article distributed under the terms of the Creative Commons Attribution License, which permits unrestricted use, distribution, and reproduction in any medium, provided the original work is properly cited.

How to cite: Najim A and Hassan Hussein I. Regarding the Novel IDNAII Distribution: Mathematical and Statistical Characteristics [version 1; peer review: awaiting peer review]. F1000Research 2025, 14:1442 (https://doi.org/10.12688/f1000research.173663.1) First published: 24 Dec 2025, 14:1442 (https://doi.org/10.12688/f1000research.173663.1) Latest published: 24 Dec 2025, 14:1442 (https://doi.org/10.12688/f1000research.173663.1)

1. Introduction

In contrast to other facets of life, statistical modeling is important, particularly in probability theory, which is frequently applied to find variation and draw conclusions from observable data. Over the past few decades, a number of novel generalized distributions have been developed and gained importance. The idea that these distributions had more parameters served as the main foundation for their development. Many expansions of traditional statistical models are being used to model the data in every aspect of life.

The majority of new distributions are made using contemporary methods, even though researchers are currently examining methods that have been utilized to build new distributions since 1980; see for example Refs. 1-10.

One of the more recent methods used in this study is the transformed-transformer methodology, which was developed by Alzaatreh et al.¹¹ A novel class of distribution functions was obtained by transforming an extra variable through (-∞, ∞) using the density and distribution functions of a random variable X with r(x) and R(x), respectively.

(1)

G (x) = \int_{c}^{Z (F (x))} r (t) dt = R {Z (F (X))}

Anywhere Z(F(X)) belong to [c,d] is monotone increasing, $Z ́ (F (X))$ less than infinity, $lim_{x \to - \infty} Z (F (X)) = c$ in addition to $lim_{x \to \infty} Z (F (X)) = d$ , besides the following matching pdf

(2)

g (x) = \overset{´}{Z} (F (X)) r {Z (F (X))}

Numerous research have employed the transformed-transformer approach; for example, Refs. 12-14. Aljarrah et al.¹⁵ developed a novel family of distributions by substituting the quantile function of extra r. v. Y in relations of F (x) for the function Z (F (x)). This resulted in the T-X{Y} distribution class.

(3)

G (x) = \int_{c}^{Q_{Y} (F (x))} r (t) dt = R {Q_{Y} (F (X))}

When F(x) equal to λ and p(y) greater than 0 for all y in neighborhood of Q_y (λ), such that 0 < λ< 1, this implies that $\overset{´}{Q}$ _Y (λ) less than infinity and it is equivalent to P[Q_y (λ)]⁻¹.

Consequently, the correlated pdf of G(x) is

(4)

g (x) = \frac{f (x)}{p {Q_{Y} (F (x))}} . r [Q_{Y} (F (x))]

Assume T, R, and Y are random variables having the quantile functions: Q_T (p), Q_R (p) and Q_Y (p); suppose that their distribution functions are F_T (x), F_R (x) and F_Y (x), and their corresponding densities which is represented for instance f_T (x), f_R (x) and f_Y(x) respectively, through T, Y∈[c, d], besides R∈[e, f] for -∞ < c < d < ∞ and -∞ < e < f < ∞.

Following that, the new class’s distribution function is shown as

(5)

F_{X} (x) = \int_{c}^{Q_{Y} (F_{R} (x))} f_{T} (t) dt = F_{T} {Q_{Y} (F_{R} (x))}

With the corresponding PDF as

(6)

f_{X} (x) = f_{R} (x) . {\overset{´}{Q}}_{Y} (F_{R} (x)) . f_{T} {Q_{Y} (F_{R} (x))} = f_{R} (x) f_{T} (Q_{Y} (F_{R} (x))) / f_{Y} (Q_{Y} (F_{R} (x))) .

In 2021, Ibeh et al.¹⁶; introduce new Weibull–Exponential {Rayleigh} distribution based the idea of T-X{Y} family distribution.

The Transformed-Transformer (T-X) Family approach is a modern statistical strategy that offers a flexible framework for generating new probability distributions beyond the limitations of conventional models, utilizing the quantile function as its foundation. This method enables the generation of customized statistical models through the combination of the quantile function of a generating distribution with the cumulative distribution function (CDF) of a base distribution, allowing precise control over shape characteristics such as smoothness, kurtosis, and tail behavior. Its significance arises from its ability to accurately represent non-standard data, provide direct control over the resulting distribution’s shape, and facilitate risk analysis and simulation. This methodology is an effective instrument for scholars and applied statisticians, having demonstrated efficacy across diverse fields, including industrial engineering, medical statistics, financial modeling, and environmental sciences.

In various applied fields, particularly in healthcare and finance, data infrequently follows to the assumptions of fundamental probability models such as the Gaussian (Normal) distribution. Empirical data regularly exhibits skewness, heavy tails, and sometimes multimodal characteristics, interpretation conventional parametric models less effective. In healthcare, variables such as hospital length of stay or blood glucose levels are sometimes markedly skewed: most patients fall within a typical range, whilst a minority exhibit extreme values. In finance, asset returns and market fluctuations exhibit fat-tailed behavior, indicating that significant profits or losses occur more frequently than predicted by Gaussian models. Such deviations from the norm necessitate more adaptable probabilistic modeling techniques capable of managing these complexities while providing precise evaluations of uncertainty. The integration of modified distributions, transformed-transformer family using quantile functions, provides a robust and flexible approach to analyzing complex real-world data.

This paper aims to present and examine the key statistical and mathematical properties of the IDNAII distribution, a novel sub-family of the Lomax–Weibull {Exponential} distribution. Method of estimation will be introduced to estimate the parameters of the new class distribution. Simulation tools have been created to evaluate the effectiveness of estimation approaches. A real-world dataset application has been demonstrated, and the examination to fit the real dataset of the new class distribution with the particular specific distributions, using several types of information criteria will be made.

This article’s additional parts are arranged as follows. The construct of IDNAII distribution, also known as the Lomax–Weibull {Exponential} distribution, is introduced in Subsection 2-1. In Subsection 2-2, most of the aspects of the distribution are presented and analyzed. Parameter estimate techniques for the $IDNAII$ distribution are introduced in Subsection 2-3. The simulation study and comparison estimators are shown in Subsection 2-4. The application of the real data set is shown in Subsection 2-5. The results are displayed in Section 3. Discussions of the results are exhibited in Section 4. The paper’s summary and conclusions are given in Section 5.

2. Methods

2-1 Constructing a new IDNAII distribution

Assume a random variable T with the Lomax distribution, including shape parameter (λ), in addition to cdf, pdf and quantile function which are provided as

(7)

F_{T} (x; λ) = 1 - {(1 + X)}^{- λ}, f_{T} (x; λ) = λ {(1 + X)}^{- (λ + 1)} and Q_{T} (p) = [{(1 - P)}^{- 1 / λ} - 1]

Where λ > 0, x > 0 and 0 < P < 1.

Similarly, let a random variable R follows the Weibull distribution with one shape parameter α. The distribution function, probability density function, and the quantile function of R are provided as

(8)

F_{R} (x; α) = 1 - exp (- x^{α}), f_{R} (x; α) = α x^{α - 1} exp (- x^{α}) and Q_{R} (p) = {- ln (1 - p)}^{1 / α}

Where α > 0, x > 0 and 0 < P < 1.

Furthermore, the cdf, pdf, and quantile function are given as follows if a random variable Y follows the exponential distribution with the scale parameter β.

(9)

F_{Y} (x) = 1 - exp (- x / β), f_{Y} (x) = (1 / β) exp (- x / β) and Q_{Y} (p) = - β ln (1 - p), where β > 0, x > 0 and 0 < P < 1 .

Equation (8), together with Equation (9), gives us

Q_{Y} (F_{R} (x)) = - β ln (1 - (1 - exp (- x^{α}))) = {βX}^{α}

Accordingly, using Equation (7), we get

F_{T} (Q_{Y} (F_{R} (x))) = 1 - {(1 + {βX}^{α})}^{- λ}

Consequently, the cdf of the IDNAII distribution or Lomax–Weibull{exponential} distribution is given by

(10)

F_{IDNAII} (x; α, β, λ) = 1 - {(1 + β X^{α})}^{- λ}

Therefore, we obtain from Equation (7)

(11)

f_{T} (Q_{Y} (F_{R} (x))) = λ {(1 + {βX}^{α})}^{- (λ + 1)}

Afterwards, from Equation (9), we acquired

(12)

\begin{array}{c} f_{Y} (Q_{Y} (F_{R} (x))) = (1 / β) exp (- {βX}^{α} / β) \\ f_{Y} (Q_{Y} (F_{R} (x))) = (1 / β) exp (- X^{α}) \end{array}

Upon modifying Equation (6) using the previously mentioned equations, the relevant IDNAII distribution pdf is generated as

f_{X} (x) = f_{R} (x) . {\overset{´}{Q}}_{Y} (F_{R} (x)) . f_{T} {Q_{Y} (F_{R} (x))} = f_{R} (x) f_{T} (Q_{Y} (F_{R} (x))) / f_{Y} (Q_{Y} (F_{R} (x))) .

f_{X} (x) = f_{IDNAII} (x) = [α x^{α - 1} exp (- x^{α})] [λ {(1 + β X^{α})}^{- (λ + 1)}] / [(1 / β) exp (- X^{α})],

Consequently,

(13)

f_{IDNAII} (x; α, β, λ) = (αβλ) x^{α - 1} {(1 + {βX}^{α})}^{- (λ + 1)}

We deduce that the cdf and pdf of the new class IDNAII distribution with three parameters (α,β,λ) are given by Equations (10) and (13) respectively.

Furthermore, the reliability function for the IDNAII distribution will be determined using Equation (10).

(14)

R_{IDNAII} (x; α, β, λ) = {(1 + {βx}^{α})}^{- λ} for x > 0 and α, β, λ > 0

2-2 The IDNAII distribution’s characteristics

Moreover, this section provides a number of fundamental statistical and mathematical characteristics of the IDNAII distribution, like the following:

2-2-1 Additional IDNAII distribution probability functions

Together with the three functions discussed before in Equations (10), (13), and (14), we present the majority of the probability functions in this section.

a- Hazard function of IDNAII distribution h_IDNAII(x;α,β,λ)
(15)
$\begin{array}{l} h_{IDNAII} (x; α, β, λ) = f (x; α, β, λ) / R (x; α, β, λ) for x > 0 and α, β, λ > 0 \\ h_{IDNAII} (x; α, β, λ) = (αβλ) (x^{α - 1}) / (1 + β X^{α}) for x > 0 and α, β, λ > 0 \end{array}$
b- Cumulative hazard function of IDNAII distribution H_IDNAII (x;α,β,λ)
(16)
$H_{IDNAII} (x; α, β, λ) = λ Ln (1 + {βX}^{α}) for x > 0 and α, β, λ > 0$
c- Reverse Hazard Function of IDNAII distribution Ф_IDNAII (x;α,β,λ)
(17)
$\begin{array}{l} Ф_{IDNAII} (x; α, β, λ) = f (x; α, β, λ) / F (x; α, β, λ) \\ Ф_{IDNAII} (x; α, β, λ) = [(αβλ) x^{α - 1} {(1 + β X^{α})}^{- (λ + 1)}] / [1 - {(1 + β X^{α})}^{- λ}], for x > 0 and α, β, λ > 0 \end{array}$
d- Odd Function of IDNAII distribution ʘ _IDNA (x;α,β,λ)
(18)
$\begin{array}{l} Θ_{IDNA} (x; α, β, λ) = F (x; α, β, λ) / R (x; α, β, λ) \\ Θ_{IDNA} (x; α, β, λ) = {(1 + β X^{α})}^{λ} - 1, for x > 0 and α, β, λ > 0 \end{array}$

2-2-2 The quntial function of IDNAII distribution

The $q$ ^th quantile function of the IDNAII distribution may be found as

(19)

\begin{array}{l} F (x) = 1 - {(1 + β X^{α})}^{- λ} = q; (0 < q < 1) \to {(1 + β X^{α})}^{- λ} = 1 - q \\ x_{q} = {[{(1 - q)}^{- 1 / λ} - 1] / β}^{1 / α} \end{array}

The median (x_med) of the IDNAII distribution can therefore be determined with the setting q = 0.5 as

(20)

x_{med} = {[2^{1 / λ} - 1] / β}^{1 / α}

2-2-3 The Mode of IDNAII distribution

The following formula may be used to determine the IDNAII distribution’s mode:

From Equation (13);

f (x; α, β, λ) = (αβλ) x^{α - 1} {(1 + β X^{α})}^{- (λ + 1)}

Ln f (x; α, β, λ) = ln (αβλ) + (α - 1) ln x - (λ + 1) ln (1 + β X^{α})

\frac{∂Ln f (x; α, β, λ)}{∂x} = \frac{(α - 1)}{x} - (λ + 1) \frac{(αβ x^{α - 1})}{(1 + β x^{α})} = 0

(α - 1) (1 + β X^{α}) = (λ + 1) (αβ x^{α})

Put

β x^{α} = y \to x = {(\frac{y}{β})}^{\frac{1}{α}} \to (α - 1) (1 + \frac{1}{y}) = α (λ + 1) \to (1 + \frac{1}{y}) = \frac{α (λ + 1)}{(α - 1)}

(α - 1) (1 + \frac{1}{y}) = α (λ + 1) \to (1 + \frac{1}{y}) = \frac{α (λ + 1)}{(α - 1)}

y = \frac{(α - 1)}{α (λ + 1) - (α - 1)} \to β x^{α} = \frac{(α - 1)}{α (λ + 1) - (α - 1)} \to x^{α} = \frac{(α - 1)}{β [α (λ + 1) - (α - 1)]}

Hence,

(21)

x_{mode} = {[\frac{(α - 1)}{β (α λ + 1]}]}^{\frac{1}{α}}

2-2-4 Limit of the pdf and cdf of IDNAII distribution

a- The Limit of pdf $f (x; α; β; λ)$
- 1-
  (22)
  $\begin{array}{l} lim_{x \to 0} f (x; α; β; λ) = lim_{x \to 0} (αβλ) x^{α - 1} {(1 + β x^{α})}^{- (λ + 1)} = (αβλ) lim_{x \to 0} x^{α - 1} {(1 + αβ X^{2})}^{- (λ + 1)} \\ lim_{x \to 0} f (x; α; β; λ) = (αβλ) * 0^{*} 1 \\ \to lim_{x \to 0} f (x; α; β; λ) = 0 . \end{array}$
- 2-
  (23)
  $\begin{array}{l} lim_{x \to \infty} f (x; α; β; λ) = lim_{x \to \infty} (αβλ) x^{α - 1} {(1 + αβ x^{α})}^{- (λ + 1)} = (αβλ) lim_{x \to \infty} \frac{x^{α - 1}}{{(1 + β x^{α})}^{(λ + 1)}} \\ = (αβλ) lim_{x \to \infty} \frac{\frac{x^{α - 1}}{{(x^{α})}^{(λ + 1)}}}{\frac{{(1 + β x^{α})}^{(λ + 1)}}{{(x^{α})}^{(λ + 1)}}} = (αβλ) lim_{x \to \infty} \frac{{(\frac{1}{x})}^{αλ + 1}}{{(\frac{1}{x^{α}} + β)}^{(λ + 1)}} \\ = (αβλ) \frac{\frac{1}{\infty}}{{(\frac{1}{\infty} + β)}^{(λ + 1)}} = (αβλ) \frac{0}{{(β)}^{(λ + 1)}} = 0 \\ \to {lim}_{x \to \infty} f (x; α; β; λ) = 0 . \end{array}$
b- The Limit of cdf $F (x; α; β; λ)$
- 1-
  (24)
  $\begin{array}{l} lim_{x \to 0} F (x; α; β; λ) = lim_{x \to 0} [1 - {(1 + β x^{α})}^{- λ}] = 1 - {(1 + 0)}^{- λ} = 0 \\ lim_{x \to 0} F (x; α; β; λ) = 0 . \end{array}$
- 2-
  (25)
  $\begin{array}{l} lim_{x \to \infty} F (x; α; β; λ) = lim_{x \to \infty} [1 - {(1 + β x^{α})}^{- λ}] \\ = lim_{x \to \infty} [1 - \frac{1}{{(1 + β x^{α})}^{λ}}] = 1 - \frac{1}{\infty} = 1 - 0 = 1 \\ \to lim_{x \to \infty} F (x; α; β; λ) = 1 . \end{array}$

2-2-5 Moments

The IDNAII distribution’s $r$ ^th moments regarding origin and mean are shown in this section.

a- The $r$ ^th moments about origin
$\begin{array}{l} E (x^{r}) = \int_{0}^{\infty} x^{r} (αβλ) x^{α - 1} {(1 + β x^{α})}^{- (λ + 1)} dx \\ = (αβλ) \int_{0}^{\infty} x^{r + α + 1} {(1 + β x^{α})}^{- (λ + 1)} dx \end{array}$
Put $y = β x^{α} \to^{0} < y < \infty \to x = {(\frac{y}{β})}^{\frac{1}{α}} \to dx = {(\frac{1}{β})}^{\frac{1}{α}} (\frac{1}{α}) {(y)}^{\frac{1}{α} - 1}$
(26)
$\begin{array}{l} E (x^{r}) = λ {(β)}^{\frac{- r}{α}} \int_{0}^{\infty} y^{\frac{r}{α}} {(1 + y)}^{- (λ + 1)} dy \\ = {(β)}^{\frac{- r}{α}} \int_{0}^{\infty} y^{(\frac{r}{α} + 1) - 1} {(1 + y)}^{- (\frac{r}{α} + 1) - [- (\frac{r}{α} + 1) + (λ + 1)]} dy \\ = λ {(β)}^{\frac{- r}{2}} \int_{0}^{\infty} y^{(\frac{r}{α} + 1) - 1} {(1 + y)}^{- (\frac{r}{α} + 1) - (λ - \frac{r}{α})} dy \\ = λ {(β)}^{\frac{- r}{2}} . B (\frac{r}{α} + 1, λ - \frac{r}{α}), B (., .) refer to Beta type II distribution \\ = λ {(β)}^{\frac{- r}{α}} \frac{Γ (\frac{r}{α} + 1) Γ (λ - \frac{r}{α})}{Γ (λ + 1)} \\ E (X^{r}) = \frac{{(\frac{1}{β})}^{\frac{r}{α}} (\frac{r}{α}) Γ (\frac{r}{α}) Γ (λ - \frac{r}{α})}{Γ (λ)} \end{array}$
b- The r^th moments about mean μ
$\begin{array}{l} E {(X - μ)}^{r} = \int_{0}^{\infty} {(x - μ)}^{r} f (x; \underline{ϑ}) dx, \underline{ϑ} = (α, β, λ) \\ = \int_{0}^{\infty} \sum_{i = 0}^{r} (\begin{array}{c} r \\ i \end{array}) {(- 1)}^{i} μ^{i} (X^{r - i}) f (x; \underline{ϑ}) dx \\ = \sum_{i = 0}^{r} (\begin{array}{c} r \\ i \end{array}) {(- 1)}^{i} μ^{i} \int_{0}^{\infty} (X^{r - i}) f (x; \underline{ϑ}) dx \\ = \sum_{i = 0}^{r} (\begin{array}{c} r \\ i \end{array}) {(- 1)}^{i} μ^{i} E (X^{r - i}), \end{array}$
Using Equation (26)
(27)
$E {(X - μ)}^{r} = \frac{\sum_{i = 0}^{r} (\binom{r}{i}) {(- 1)}^{i} μ^{i} {(\frac{1}{β})}^{\frac{r - i}{α}} (\frac{r - i}{α}) Γ (\frac{r - i}{α}) Γ (λ - \frac{r - i}{α})}{Γ (λ)}$

2-2-6 Moment generating function M_X(t)

An easy way to define the IDNAII distribution’s moment generating function (MGF) is as

M_{X} (t) = E (e^{tx}) = \int_{0}^{\infty} e^{tx} f (x; \underline{ϑ}) dx \to M_{X} (t) = \int_{0}^{\infty} \sum_{i = 0}^{\infty} \frac{{(tx)}^{i}}{i!} f (x; \underline{ϑ}) dx

M_X(t) = $\sum_{i = 0}^{\infty} \frac{t^{i}}{i!} \int_{0}^{\infty} x^{i}$ $f (x; \underline{ϑ}) dx$ $\to$ M_X(t) = $\sum_{i = 0}^{\infty} \frac{t^{i}}{i!}$ E ( $x^{i})$ , from Equation (26) above we get

(28)

M_{X} (t) = \sum_{i = 0}^{\infty} \frac{(\frac{t^{i}}{i!}) {(\frac{1}{β})}^{\frac{i}{α}} (\frac{i}{α}) Γ (\frac{i}{α}) Γ (λ - \frac{i}{α})}{Γ (λ)}

2-2-7 Characteristic function Ф_X(t)

One may determine the IDNAII distribution’s characteristic function as

\begin{array}{l} Ф_{X} (t) = E (e^{itx}), i = \sqrt{- 1} \\ = \int_{0}^{\infty} e^{itx} f (x; \underline{ϑ}) dx \to Ф_{X} (t) = \int_{0}^{\infty} \sum_{r = 0}^{\infty} \frac{{(itx)}^{r}}{r!} f (x; \underline{ϑ}) dx \end{array}

Ф_{X} (t) = \sum_{r = 0}^{\infty} \frac{{(it)}^{r}}{r!} \int_{0}^{\infty} x^{r} f (x; \underline{ϑ}) dx \to ΦX (t) = \sum_{r = 0}^{\infty} \frac{{(it)}^{r}}{r!} E (x^{r}),

from Equation (26) above we get

(29)

Φ_{X} (t) = \sum_{r = 0}^{\infty} \frac{(\frac{{(it)}^{r}}{r!}) {(\frac{1}{β})}^{\frac{r}{α}} (\frac{r}{α}) Γ (\frac{r}{α}) Γ (λ - \frac{r}{α})}{Γ (λ)}

2-2-8 Factorial generating function Ʒ_X(t)

The following formula may be used to get the IDNAII distribution’s factorial generating function:

Ʒ_{X} (t) = E (t^{x}) \to ƷX (t) = \int_{0}^{\infty} t^{x} f (x; \underline{ϑ}) dx \to Ʒ_{X} (t) = \int_{0}^{\infty} e^{xlnt} f (x; \underline{ϑ}) dx

Ʒ_{X} (t) = \int_{0}^{\infty} \sum_{r = 0}^{\infty} \frac{{(xlnt)}^{r}}{r!} f (x; \underline{ϑ}) dx \to Ʒ_{X} (t) = \sum_{r = 0}^{\infty} \frac{{(lnt)}^{r}}{r!} \int_{0}^{\infty} x^{r} f (x; \underline{ϑ}) dx

Ʒ_X(t) = $\sum_{r = 0}^{\infty} \frac{{(lnt)}^{r}}{r!} E (x^{r})$ , from Equation (26) above we get

(30)

Ʒ_{X} (t) = \sum_{r = 0}^{\infty} \frac{(\frac{{(lnt)}^{r}}{r!}) {(\frac{1}{β})}^{\frac{r}{α}} (\frac{r}{α}) Γ (\frac{r}{α}) Γ (λ - \frac{r}{α})}{Γ (λ)}

2-2-9 Coefficients

We arrive to the following conclusions based on the preceding subsection 2-2-5 (a) and (b). The coefficients of Skewness, Kurtosis, and Variation for the IDNAII distribution are shown below.

a- Coefficient of Skewness (C.S.)
The definition of the skewness coefficient (C.S.) is follows
$C . S . = {E {(X - μ)}^{3} / {[E {(X - μ)}^{2}]}^{3 / 2}}$
Thus, skewness coefficient for the IDNAII distribution will be
(31)
$C . S . = {\begin{cases} [\sum_{i = 0}^{3} (\begin{array}{c} 3 \\ i \end{array}) {(- 1)}^{i} μ^{i} {(\frac{1}{β})}^{\frac{3 - i}{α}} (\frac{3 - i}{α}) Γ (\frac{3 - i}{α}) Γ (λ - \frac{3 - i}{α}) / Γ (λ)] / \\ {[\sum_{i = 0}^{2} (\begin{array}{c} 2 \\ i \end{array}) {(- 1)}^{i} μ^{i} {(\frac{1}{β})}^{\frac{2 - i}{α}} (\frac{2 - i}{α}) Γ (\frac{2 - i}{α}) Γ (λ - \frac{2 - i}{α}) / Γ (λ)]}^{3 / 2} \end{cases}}$
b- Coefficient of Kurtosis (C.K.)
The Kurtosis coefficient (C.K.) is defined as follows.
$C . K . = {E {(X - μ)}^{4} / {[E {(X - μ)}^{2}]}^{2}}$
Thus, Kurtosis coefficient for the IDNAII distribution will be
(32)
$C . K . = {\begin{cases} [\sum_{i = 0}^{4} (\begin{array}{c} 4 \\ i \end{array}) {(- 1)}^{i} μ^{i} {(\frac{1}{β})}^{\frac{4 - i}{α}} (\frac{4 - i}{α}) Γ (\frac{4 - i}{α}) Γ (λ - \frac{4 - i}{α}) / Γ (λ)] / \\ {[\sum_{i = 0}^{2} (\begin{array}{c} 2 \\ i \end{array}) {(- 1)}^{i} μ^{i} {(\frac{1}{β})}^{\frac{2 - i}{α}} (\frac{2 - i}{α}) Γ (\frac{2 - i}{α}) Γ (λ - \frac{2 - i}{α}) / Γ (λ)]}^{2} \end{cases}} .$
c- Coefficient of Variation (C.V.)
The Variation coefficient (C.V.) is defined as follows.
$C . V . = {{[E {(X - μ)}^{2}]}^{1 / 2} / E (X)}$
Consequently, the IDNAII distribution’s variation coefficient will be
(33)
$C . V . = {{[\sum_{i = 0}^{2} (\binom{2}{i}) {(- 1)}^{i} μ^{i} {(\frac{1}{β})}^{\frac{2 - i}{α}} (\frac{2 - i}{α}) Γ (\frac{2 - i}{α}) Γ (λ - \frac{2 - i}{α}) / Γ (λ)]}^{1 / 2} / [{(\frac{1}{β})}^{\frac{1}{α}} (\frac{1}{α}) Γ (\frac{1}{α}) Γ (λ - \frac{1}{α}) / Γ (λ)]} .$

2-2-10 Probability density functions of order statistic (O.S.)

Assuming a random sample x₁,x₂,…,x_n of size $n$ taken from the IDANII distribution having cdf F(x; $\underline{ϑ}$ ) and pdf f(x; $\underline{ϑ}$ ), where $\underline{ϑ}$ =(α,β,λ). Let y₁< y₂ <… < y_n denote to order statistic for this sample. Then the probability density function of y_r (r =1, 2,…, n) can be obtained by the following:

f (y_{r}) = (\frac{1}{B (r; n - r + 1)}) = f (x; \underline{ϑ}) {[F (x)]}^{r - 1} {[1 - F (x)]}^{n - r},

for (1 < r < n), hence we get

a-
(34)
$\begin{array}{l} f (y_{r}) = (\frac{1}{B (r; n - r + 1)}) (αβλ) ({y_{r}}^{α - 1}) {(1 + β {y_{r}}^{α})}^{- (λ + 1)} {[1 - {(1 + β y_{r}^{α})}^{- λ}]}^{r - 1} {[{(1 + β y_{r}^{α})}^{- λ}]}^{n - r} \\ = (\frac{1}{B (r; n - r + 1)}) (αβλ) ({y_{r}}^{α - 1}) {(1 + β {y_{r}}^{α})}^{- λ - 1 - nλ + rλ} \sum_{i = 0}^{r - 1} (\begin{array}{c} r - 1 \\ i \end{array}) {(- 1)}^{i} {(1 + β y_{r}^{α})}^{- iλ} \\ f (y_{r}) = (\frac{1}{B (r; n - r + 1)}) (αβλ) ({y_{r}}^{α - 1}) \sum_{i = 0}^{r - 1} (\begin{array}{c} r - 1 \\ i \end{array}) {(- 1)}^{i} {(1 + β y_{r}^{α})}^{- [(1 + n + i - r) λ + 1}, for (1 < r < n) . \end{array}$
b-
(35)
$\begin{array}{l} f (y_{1}) = n f (x; \underline{ϑ}) {[1 - F (x)]}^{n - 1} \\ = n (αβλ) ({y_{r}}^{α - 1}) {(1 + β {y_{1}}^{α})}^{- (λ + 1)} {[{(1 + β y_{1}^{α})}^{- λ}]}^{n - 1} \\ f (y_{1}) = nαβλ y_{1} {(1 + β {y_{1}}^{α})}^{- (n λ + 1)} \end{array}$

According to this, y₁~IDNAII (α,β,nλ)
c-
(36)
$\begin{array}{l} f (y_{n}) = n f (x; \underline{ϑ}) {[F (x)]}^{n - 1} \\ = n (αβλ) ({y_{n}}^{α - 1}) {(1 + β {y_{n}}^{α})}^{- (λ + 1)} {[{(1 + β y_{n}^{α})}^{- λ}]}^{n - 1} \\ = n (αβλ) ({y_{n}}^{α - 1}) {(1 + β {y_{n}}^{α})}^{- (λ + 1)} \sum_{i = 0}^{n - 1} (\begin{array}{c} n - 1 \\ i \end{array}) {(- 1)}^{i} {(1 + β {y_{n}}^{α})}^{- iλ} \\ = nαβλ {y_{n}}^{α - 1} \sum_{i = 0}^{n - 1} (\begin{array}{c} n - 1 \\ i \end{array}) {(- 1)}^{i} {(1 + β {y_{n}}^{α})}^{- [(1 + i) λ + 1]} \end{array}$

2-2-11 Cumulative distribution functions of order statistic (O.S.)

This section presents the order statistic’s cumulative distribution.

The common formula for the cdf of order statistic is

(37)

F_{i} (t) = \sum_{k = i}^{n} (\binom{n}{k}) {[F (t)]}^{k} {[1 - F (t)]}^{n - k}

Consequently,

\begin{matrix} F (y_{r}) = \sum_{j = r}^{n} (\binom{n}{j}) [1 - {(1 + β y_{r}^{α})}^{- λ}] j {[{(1 + β y_{r}^{α})}^{- λ}]}^{n - j} \\ = \sum_{j = r}^{n} (\binom{n}{j}) {(1 + β y_{r}^{α})}^{- λ (n - j)} \sum_{i = 0}^{j} (\binom{j}{i}) {(- 1)}^{i} {[{(1 + β y_{r}^{α})}^{- λ}]}^{i} \\ \begin{matrix} = \sum_{j = r}^{n} \sum_{i = 0}^{j} (\binom{n}{j}) (\binom{j}{i}) {(- 1)}^{i} {(1 + β y_{r}^{α})}^{- λ (n - j + i)} \\ = \sum_{j = r}^{n} \sum_{i = 0}^{j} (\binom{n}{j}) (\binom{j}{i}) {(- 1)}^{i} \sum_{k = 0}^{\infty} {(- 1)}^{k} (\binom{λ (n - j + i) + k - 1}{k}) {(β y_{r}^{α})}^{k} \end{matrix} \end{matrix}

Hence, the cumulative distribution function of r^th order statistic will be

(38)

F (y_{r}) = \sum_{k = 0}^{\infty} \sum_{J = r}^{n} \sum_{i = 0}^{j} (\binom{n}{j}) (\binom{j}{i}) (\binom{λ (n - j + i) + k - 1}{k}) {(- 1)}^{i + k} {({βy}_{r}^{α})}^{k}, {βy}_{r}^{α} < 1

2-2-12 Mean time to failure (death); MTTF

In this section, we introduce the mean time to failure (death)

\begin{matrix} MTTF = \int_{0}^{\infty} R (x; \underline{ϑ}) dx; R (x; \underline{ϑ}) = {(1 + β x^{α})}^{- λ} refer to reliability function of IDNAII distribution \\ = \int_{0}^{\infty} {(1 + β x 2)}^{- λ} dx \end{matrix}

Put y= βx^α $\to$ 0 $< y < \infty \to$ x= ${(\frac{y}{β})}^{\frac{1}{α}} \to$ dx= ${(\frac{1}{β})}^{\frac{1}{α}} (\frac{1}{α})$ ${(y)}^{\frac{1}{α} - 1}$

(39)

\begin{array}{l} MTTF = {(\frac{1}{β})}^{\frac{1}{α}} (\frac{1}{α}) \int_{0}^{\infty} {(1 + y)}^{- λ} {(y)}^{\frac{1}{α} - 1} dy \\ = {(\frac{1}{β})}^{\frac{1}{α}} (\frac{1}{α}) \int_{0}^{\infty} {(y)}^{\frac{1}{α} - 1} {(1 + y)}^{- λ} dy \\ = {(\frac{1}{β})}^{\frac{1}{α}} (\frac{1}{α}) \int_{0}^{\infty} {(y)}^{\frac{1}{α} - 1} {(1 + y)}^{\frac{- 1}{α} - (λ - \frac{1}{α})} dy \\ = {(\frac{1}{β})}^{\frac{1}{α}} (\frac{1}{α}) B (\frac{1}{α}, λ - \frac{1}{α}), B (., .) refer to Beta type II distribution \\ = \frac{{(\frac{1}{β})}^{\frac{1}{α}} (\frac{1}{α}) Γ (\frac{1}{α}) Γ (λ - \frac{1}{α})}{Γ (λ)} \end{array}

2-2-13 The Average failure rate (AFR)

a- The Average failure rate over time (0, t)
(40)
$AFR (0, t) = L (t) = \frac{H (t)}{t} = \frac{λ Ln (1 + β t^{α})}{t}$
b- The Average failure rate over time ( $t_{1}$ , $t_{2}$ )
(41)
$AFR (t_{1}, t_{2}) = \frac{λ [Ln (1 + β t_{2}^{α}) - Ln (1 + β t_{1}^{α})]}{t_{2} - t_{1}}$

2-2-14 Self-reproducing property

Let y₁< y₂ <… < y_n denote to order statistic for the sample x₁,x₂,…,x_n of size n drawn from IDNAII distribution having cdf as well as pdf defined in Equations (10) and (13).

Using Equation (35) in property 2-2-10, the pdf of y₁ is, f (y₁) = nαβλ y₁ ^α-1 (1+ β y₁ ^α)^{- (n λ+1))}

It is clear that y₁ follows IDNAII distribution with the parameters (α,β,nλ). As a result, the self-reproducing property is satisfied by the IDNAII distribution.

2-2-15 Entropies

Entropy functions are fundamental concepts in information theory and statistics, as they offer precise estimates of uncertainty inside probability distributions. We present several uncertainty measurements, such as Shannon and Rényi entropies, that may be employed to measure the total amount of data in the system.

a- Shannon entropy of IDNAII distribution SH_X

Shannon’s entropy has been used in many technical fields, such as physics and economics. Shannon entropy quantifies the anticipated information content of a random variable and is extensively utilized in statistics to characterize variability, inform model selection, and underpin information-theoretic criteria like the Akaike Information Criterion (AIC).

According to Shannon’s 1948 formulation, the entropy of a random variable X with density function f(x) is defined as follows¹⁷;

η_{x} = E {- ln [f (X)]} .

The Shannon entropy for T-R{Y} family distribution was defined as follows¹⁶;

{SH}_{T - R {Y}} = {SH}_{T} + E (ln (f_{Y} (T))) - E ((ln (f_{R} (X))) .

Additionally, as was previously indicated; T~ Lomax (λ); R~ Weibull (α) and Y~ Exponential (β).

Where, the Shannon entropy of T is known as

(42)

{SH}_{T} = 1 / λ + ln (1 / λ) + 1

ln (f_{Y} (T)) = ln (1 / β) - (T / β) \to E (ln (f_{Y} (T))) = ln (1 / β) - (1 / β) µ_{T}

ln (f_{R} (X)) = ln (α) + (α - 1) ln (x) - x^{α} \to E ((ln (f_{R} (X))) = ln (α) + (α - 1) E (ln (x)) - E (X^{α}), E (X^{α}) = 1

\begin{array}{l} E (ln (x)) = \int_{0}^{\infty} ln (x) (α x^{α - 1} e^{- x^{α}}) dx \\ = α \int_{0}^{\infty} x^{α - 1} e^{- x^{α}} ln (x) dx \end{array}

Recall; $\int_{0}^{\infty} x^{m}$ $e^{- s x^{b}}$ ln (x) dx = $\frac{Γ (a)}{b^{2} s^{a}}$ [ ψ(a)- ln(s)]¹⁸;

\begin{matrix} E (ln (x)) = α \frac{Γ (1)}{α^{2} . 1} [(ψ (1) - ln (1)] \\ = \frac{1}{α} ψ (1) \end{matrix}

Hence, Shannon entropy of IDNAII distribution will be as follow:

(43)

{SH}_{X} = [\frac{1}{λ} + ln (\frac{1}{λ}) + 1] + [ln (\frac{1}{β}) - (\frac{1}{β}) μ_{T}] - [ln (α) + (1 - \frac{1}{α}) ψ (1) - 1]

Everywhere, μ_T refer to the mean of the random variable T.

b- Rényi entropy of IDNAII distribution RE _θ

The Rényi entropy is an extension of Shannon’s formulation that modifies the relative importance of uncommon and frequent occurrences by adding a parameter. This generalization makes it possible to characterize distributions more freely and has been useful in fields including anomaly detection, clustering, robust estimation, and hypothesis testing.

The measure of uncertainty of a random variable X follows IDNAII distribution is determined by its entropy. The Rényi entropy is defined as follows¹⁹;

{RE}_{θ} = (\frac{1}{1 - θ}) Ln {\int_{0}^{\infty} {[f (x; α; β; λ)]}^{θ}} dx .

Consequently, The Rényi entropy of IDNAII distribution will be as follows

f_{IDNAII} (x; α, β, λ) = (αβλ) x^{α - 1} {(1 + {βx}^{α})}^{- (λ + 1)}

\int_{0}^{\infty} {[f (x; α; β; λ)]}^{θ} dx = {(α βλ)}^{θ} \int_{0}^{\infty} x^{(α - 1) θ} {(1 + β X^{α})}^{- θ (λ + 1)} dx

Put

\begin{matrix} y = βxα \to 0 < y < \infty \to x = {(\frac{y}{β})}^{\frac{1}{α}} \to dx = {(\frac{1}{β})}^{\frac{1}{α}} (\frac{1}{α}) {(y)}^{\frac{1}{α} - 1} dy \\ \int_{0}^{\infty} {[f (x; α; β; λ)]}^{θ} dx = {(α βλ)}^{θ} \int_{0}^{\infty} {(\frac{y}{β})}^{\frac{θ (α - 1)}{α}} {(1 + y)}^{- θ (λ + 1)} {(\frac{1}{β})}^{\frac{1}{α}} (\frac{1}{α}) {(y)}^{\frac{1}{α} - 1} dy \\ \begin{matrix} = {(α βλ)}^{θ} (\frac{1}{α}) {(\frac{1}{β})}^{\frac{θ (α - 1)}{α}} {(\frac{1}{β})}^{\frac{1}{α}} \int_{0}^{\infty} y^{\frac{θ (α - 1) + 1}{α} - 1} {(1 + y)}^{- θ (λ + 1)} dy \\ = {(α βλ)}^{θ} (\frac{1}{α}) {(\frac{1}{β})}^{\frac{θ (α - 1) + 1}{α}} \int_{0}^{\infty} y^{\frac{θ (α - 1) + 1}{α} - 1} {(1 + y)}^{- \frac{θ (α - 1) + 1}{α} - [- \frac{θ (α - 1) + 1}{α} + θ (λ + 1)]} dy \\ = {(α βλ)}^{θ} (\frac{1}{α}) {(\frac{1}{β})}^{\frac{θ (α - 1) + 1}{α}} B (\frac{θ (α - 1) + 1}{α} -, - \frac{θ (α - 1) + 1}{α} + θ (λ + 1)), \end{matrix} \end{matrix}

Consequently, The Rényi entropy IDNAII distribution will be as follows

(44)

\begin{array}{l} {RE}_{θ} = (\frac{1}{1 - θ}) {Ln [{(αβλ)}^{θ} (\frac{1}{α}) {(\frac{1}{β})}^{\frac{θ (α - 1) + 1}{α}} B (\frac{θ (α - 1) + 1}{α} -, - \frac{θ (α - 1) + 1}{α} + θ (λ + 1))]} \\ {RE}_{θ} = (\frac{1}{1 - θ}) {θ Ln (αβλ) - (θ - \frac{θ}{α} + \frac{1}{α}) Ln β - Lnα + Ln [B ((θ - \frac{θ}{α} + \frac{1}{α}, θ (λ + 1) - (θ - \frac{θ}{α} + \frac{1}{α}))]} \end{array}

2-3 Parameter estimation methods for IDNAII (α, β, λ) distribution

2-3-1 Maximum Likelihood Estimator (MLE)

The Maximum Likelihood estimation methodology is particularly notable due to its invariance property, distinguishing it from other methods. We investigate the application of the maximum likelihood method to estimate the unknown parameters of the IDNAII (α, β, λ) distribution.

Let x₁, x₂, …, x_n denote the observed values of a random sample of size n from the IDNAII (α, β, λ) distribution.

The probability density function of the IDNAII (α, β, λ) distribution is as follows:

f (x; α, β, λ) = (αβλ) x^{\propto - 1} {(1 + β x^{\propto})}^{- (λ - 1)}; x > 0, α, β, λ > 0

The likelihood function for the vector $ϑ$ = (α, β, λ) of parameters can be written as:

L (x_{i}; α, β, λ) = \prod_{i = 1}^{n} f (x; α, β, λ) = {(αβ λ)}^{n} \prod_{i = 1}^{n} x_{i}^{\propto - 1} \prod_{i = 1}^{n} {(1 + β {x_{i}}^{α})}^{- (λ + 1)}

The log likelihood function is going to be

LnL (x_{i}; α, β, λ) = nLnα + nLnβ + nLnλ + (\propto - 1) \sum_{i = 1}^{n} Ln x_{i} - (λ + 1) \sum_{i = 1}^{n} Ln (1 + β {x_{i}}^{α})

The log likelihood function with respect to α, β, and λ is derived as follows:

(45)

\frac{∂LnL (x_{i}; α, β, λ)}{∂α} = \frac{n}{\propto} - \sum_{i = 1}^{n} {lnx}_{i} - (λ + 1) \sum_{i = 1}^{n} \frac{β x_{i}^{\propto} {lnx}_{i}}{(1 + β x_{i}^{\propto})}

(46)

\frac{∂LnL (x_{i}; α, β, λ)}{∂β} = \frac{n}{β} - (λ + 1) \sum_{i = 1}^{n} \frac{x_{i}^{α}}{(1 + β x_{i}^{α})}

(47)

\frac{∂LnL (x_{i}; α, β, λ)}{∂λ} = \frac{n}{λ} - \sum_{i = 1}^{n} ln (1 + β x_{i}^{α})

By setting the aforementioned nonlinear equations to zero and employing the Newton-Raphson approach, the maximum likelihood estimates for the three parameters $\hat{α}$ , $\hat{β}$ and $\hat{λ}$ were obtained.

2-3-2 Moment Method Estimator (MOM)

The moment method, proposed by Pearson in 1894, was among the earliest techniques employed to estimate population parameters. Let x₁, x₂, …, x_n represent the observed values of a random sample of size n drawn from the IDNAII (α, β, λ) distribution. From the features of the IDNAII distribution in Equation (26), the non-central moment of order $r$ is

E (x^{r}) = {(β)}^{- \frac{r}{α}} Γ (1 + \frac{r}{α}) \frac{Γ (λ - \frac{r}{α})}{Γ (λ)}

In this technique, the k^th population moments E ( $x^{k})$ ) are equated with the k^th sample moment $\frac{\sum_{i = 1}^{n} x_{i}^{k}}{n}$ , for $k = 1, 2, 3$ .

We derive three equations as follows

(48)

\frac{{(\frac{1}{β})}^{\frac{1}{α}} Γ (1 + \frac{1}{α}) Γ (λ - \frac{1}{α})}{Γ (λ)} = \frac{\sum_{i = 1}^{n} x_{i}}{n}

(49)

\frac{{(\frac{1}{β})}^{\frac{2}{α}} Γ (1 + \frac{2}{α}) Γ (λ - \frac{2}{α})}{Γ (λ)} = \frac{\sum_{i = 1}^{n} x_{i}^{2}}{n}

(50)

\frac{{(\frac{1}{β})}^{\frac{3}{α}} Γ (1 + \frac{3}{α}) Γ (λ - \frac{3}{α})}{Γ (λ)} = \frac{\sum_{i = 1}^{n} x_{i}^{3}}{n}

Utilize the Newton-Raphson method to resolve the aforementioned three nonlinear equations, resulting in the moment estimates for the parameters $\hat{α}$ , $\hat{β}$ and $\hat{λ} .$

2-3-3 Least Squared Estimator (LS)

This subsection addresses the estimator of the Least Squares approach. This approach is utilized for numerous mathematical and engineering applications. The primary objective of this strategy is to reduce the sum of squared errors between the observed values and the expected value.

To estimate the three parameters (α, β, λ) of the IDNAII distribution using the specified least squares approach, let x₁, x₂, …, x_n represent the observed values of a random sample of size n from the IDNAII (α, β, λ) distribution, and

(51)

S = \sum_{i = 1}^{n} [F (x_{i}) - E (F (x_{i}))]^{2}

Where, $F (x_{i})$ refers to the CDF of $IDNAII (α, β, λ)$ distribution which is defined as follows:

\begin{array}{l} F (x; α, β, λ) = 1 - {(1 + β x^{α})}^{- λ} for x > 0 and α, β, λ > 0 \\ And, E (F (x_{i})) = P_{i}, P_{i} = \frac{i}{n + 1}, i = 1, 2, ., n . \end{array}

Derive S w.r.t. $α, β and λ$ , we obtained the following three nonlinear equations respectively

(52)

\frac{∂S}{∂α} = 2βλ \sum_{i = 1}^{n} {(1 - p_{i}) x_{i}^{α} ln x_{i} {(1 + β x_{i}^{α})}^{- (λ + 1)} - x_{i}^{α} ln x_{i} {(1 + β x_{i}^{α})}^{- (2 λ + 1)}}

(53)

\frac{∂S}{∂β} = 2λ \sum_{i = 1}^{n} {(1 - p_{i}) x_{i}^{α} {(1 + β x_{i}^{α})}^{- (λ + 1)} - x_{i}^{α} {(1 + β x_{i}^{α})}^{- (2 λ + 1)}}

(54)

\frac{∂S}{∂λ} = 2 \sum_{i = 1}^{n} {(1 - p_{i}) {(1 + β x_{i}^{α})}^{- λ} ln (1 + β x_{i}^{α}) - {(1 + β x_{i}^{α})}^{- 2 λ} ln (1 + β x_{i}^{α})}

By equating the above-mentioned nonlinear equations to zero and employing the Newton-Raphson approach, the Least Squares estimates for the three parameters $\hat{α}$ , $\hat{β}$ and $\hat{λ}$ will be achieved.

2-3-4 Shrinkage Estimator (SH)

In 1968, Thompson introduced the concept of reducing the traditional estimator $\hat{α}$ (MLE) of the parameter α to prior knowledge α₀, obtained from prior experiments or the author’s experiences, by utilizing a shrinkage weight factor ∅( $\hat{α}$ ̂), where 0 ≤ ∅( $\hat{α}$ ̂) ≤ 1. The result is a linear combination of the classical estimator, Maximum Likelihood Estimation (MLE), and the previous estimate, α₀. Thompson states, “We are estimating α and believe that α₀ closely approximates the true value of α, or we are afraid that α₀ may be near the true value of α, and we fail to employ α₀.” The shrinkage estimator of α, denoted as ${\hat{α}}_{Sh}$ , is defined as follows:

(55)

{\hat{α}}_{Sh} = \emptyset ({\hat{α}}_{mle}) {\hat{α}}_{mle} + (1 - \emptyset ({\hat{α}}_{mle})) α_{0} .

Utilizing the maximum likelihood estimator ${\hat{α}}_{mle}$ as a conventional estimator alongside the prior information (initial value or prior estimate) of $α$ in Equation (55) above. Where $\emptyset (\hat{α})$ denote the shrinkage weight factor as we mentioned above such that 0 $\leq \emptyset (\hat{α}) \leq$ 1, which may be a function of ${\hat{α}}_{mle}$ , a function of sample size ( $n$ ), a constant or can be found by minimizing the mean square error of ${\hat{α}}_{mle}$ . Thus, the shrinkage estimators of the three parameter $s of$ IDNAII distribution will be as follows:

(56)

{\hat{α}}_{Sh} = \emptyset ({\hat{α}}_{mle}) {\hat{α}}_{mle} + (1 - \emptyset ({\hat{α}}_{mle})) α_{0} .

(57)

{\hat{β}}_{Sh} = \emptyset ({\hat{β}}_{mle}) {\hat{β}}_{mle} + (1 - \emptyset ({\hat{β}}_{mle})) β_{0} .

(58)

{\hat{λ}}_{Sh} = \emptyset ({\hat{λ}}_{mle}) {\hat{λ}}_{mle} + (1 - \emptyset ({\hat{λ}}_{mle})) λ_{0} .

Where, $\emptyset ({\hat{θ}}_{mle})$ refer to modified Thompson type shrinkage weight factor by minimizing the mean squared error of ${\hat{θ}}_{mle}$ as follows²⁰:

\emptyset ({\hat{θ}}_{mle}) = \frac{{({\hat{θ}}_{mle} - θ_{0})}^{2}}{{({\hat{θ}}_{mle} - θ_{0})}^{2} + var ({\hat{θ}}_{mle})} (0.1), for θ = (α, β, λ);

2-4 Comparison of estimators via Monte Carlo simulation

The simulation study will be conducted to demonstrate the behaviour of estimators regarding parameters through four proposed estimating methods, followed by a comparison of outcomes utilizing two statistical criteria: bias and mean squared error (MSE). The simulation training is conducted 1000 times in order to gather independent samples of different sizes.

2-4-1 Generating random variables

Let U be a random variable uniformly distributed over the interval (0,1). The data for the IDNAII distribution can be produced with the inverse transformation method for the cumulative distribution function (CDF), where if²¹:

F (x_{i}; α, β, λ) = 1 - {(1 + β {x_{i}}^{α})}^{- λ} \to U_{i} = 1 - {(1 + β {x_{i}}^{α})}^{- λ}

Then $x_{i}$ = $F {(x_{i}; α, β, λ)}^{- 1} =$ { [ (1- $U_{i}$ )^-1/λ -1] / β }^{1/ α}

2-4-2 Simulation study

The Monte Carlo simulation program built with MATLAB 2022 includes the following steps for comparing consistency estimators:

1. Random samples x₁, x₂, …, x_n, of sizes $n$ , where $n$ = 10, 20, 50, 100, are produced from the IDNAII distribution in subsection 2-4-1.
2. The actual parameter values for four cases (α, β, λ) are considered in Table 1.
3. The Bias for all suggested estimators for the parameters was calculated as follows, utilizing L=1000 duplicates, which showed in Tables 2-5.
(59)
$Bias = \frac{1}{L} \sum_{i = 1}^{L} | {\hat{ϑ}}_{i} - ϑ |, ϑ = (α, β, λ)$
4. The MSE for all proposed estimators w.r.t. parameters was calculated as below using L=1000 duplicates: as demonstrated in Tables 6-9.
(60)
$MSE = \frac{1}{L} \sum_{i = 1}^{L} {({\hat{ϑ}}_{i} - ϑ)}^{2} .$

Table 1. Four cases of real parameters.

Case	α	β	λ
1	1.0	2.5	3.0
2	2.0	3.0	1.6
3	1.5	2.0	2.5
4	3.5	1.0	1.7

Table 2. Shown Bias for $\hat{\propto}$ , $\hat{β}$ and $\hat{λ}$ w.r.t. case 1.

		∝=1.0 β=2.5 λ= 3.0
n	Bias	MLE	MOM	LS	SH	Best
10	Bias $\hat{\propto}$	0.2553	0.0076	0.0139	0.0030	SH
	Bias $\hat{β}$	0.1002	0.0211	0.0592	0.0022	SH
	Bias $\hat{λ}$	0.9963	0.0044	0.0406	0.0027	SH
20	Bias $\hat{\propto}$	0.2520	0.0079	0.0129	0.0090	SH
	Bias $\hat{β}$	0.1825	0.0243	0.1280	0.0023	SH
	Bias $\hat{λ}$	0.9775	0.0088	0.0936	0.0027	SH
50	Bias $\hat{\propto}$	0.2282	0.0082	0.0112	0.0090	SH
	Bias $\hat{β}$	0.1659	0.0235	0.1374	0.0023	SH
	Bias $\hat{λ}$	0.9111	0.0231	0.1056	0.0027	SH
100	Bias $\hat{\propto}$	0.2905	0.0081	0.0112	0.0090	SH
	Bias $\hat{β}$	0.1148	0.0232	0.2024	0.0023	SH
	Bias $\hat{λ}$	0.9461	0.0229	0.1539	0.0027	SH

Table 3. Shown Bias for $\hat{\propto}$ , $\hat{β}$ and $\hat{λ}$ w.r.t. case 2.

		∝=2.0 β=3.0 λ= 1.6
n	Bias	MLE	MOM	LS	SH	Best
10	Bias $\hat{\propto}$	0.9120	0.0181	0.0080	0.0018	SH
	Bias $\hat{β}$	0.8944	0.0283	0.0675	0.0027	SH
	Bias $\hat{λ}$	0.9142	0.0063	0.0243	0.0014	SH
20	Bias $\hat{\propto}$	0.5332	0.0184	0.0085	0.00180	SH
	Bias $\hat{β}$	0.4220	0.0294	0.1016	0.00270	SH
	Bias $\hat{λ}$	0.5933	0.0475	0.0555	0.00144	SH
50	Bias $\hat{\propto}$	0.8782	0.0183	0.0108	0.0180	SH
	Bias $\hat{β}$	0.3708	0.0285	0.2441	0.0027	SH
	Bias $\hat{λ}$	0.5337	0.0111	0.1061	0.0014	SH
100	Bias $\hat{\propto}$	0.0053	0.0184	0.0106	0.0018	SH
	Bias $\hat{β}$	0.0079	0.0287	0.1605	0.0027	SH
	Bias $\hat{λ}$	0.1662	0.0117	0.0985	0.0014	SH

Table 4. Shown Bias for $\hat{\propto}$ , $\hat{β}$ and $\hat{λ}$ w.r.t. case 3.

		∝=1.5 β=2.0 λ= 2.5
n	Bias	MLE	MOM	LS	SH	Best
10	Bias $\hat{\propto}$	0.9143	0.0132	0.0065	0.0013	SH
	Bias $\hat{β}$	0.7960	0.0196	0.1260	0.0018	SH
	Bias $\hat{λ}$	0.8236	0.0091	0.0956	0.0023	SH
20	Bias $\hat{\propto}$	0.7979	0.0132	0.0071	0.0014	SH
	Bias $\hat{β}$	0.3780	0.0193	0.0929	0.0018	SH
	Bias $\hat{λ}$	0.4401	0.0044	0.0601	0.0022	SH
50	Bias $\hat{\propto}$	0.2862	0.0132	0.0065	0.0014	SH
	Bias $\hat{β}$	0.2888	0.0194	0.0849	0.0018	SH
	Bias $\hat{λ}$	0.7805	0.0122	0.0568	0.0022	SH
100	Bias $\hat{\propto}$	0.0046	0.0132	0.0053	0.0013	SH
	Bias $\hat{β}$	0.0192	0.0186	0.2053	0.0018	SH
	Bias $\hat{λ}$	0.1782	0.0200	0.1497	0.0023	SH

Table 5. shown Bias for $\hat{\propto}$ , $\hat{β}$ and $\hat{λ}$ w.r.t case4.

		∝=3.5 β=1.0 λ=1.7
n	Bias	MLE	MOM	LS	SH	Best I
10	Bias $\hat{\propto}$	0.0050	0.0086	0.0172	2.4000e-04	SH
	Bias $\hat{β}$	0.0013	0.0011	0.0096	9.0000e-05	SH
	Bias $\hat{λ}$	0.1011	0.0125	0.2885	1.6000e-04	SH
20	Bias $\hat{\propto}$	0.0024	6.8900e-04	0.0603	2.4000e-04	SH
	Bias $\hat{β}$	1.3200e-04	0.0025	0.0265	9.0000e-05	SH
	Bias $\hat{λ}$	0.0393	0.0095	0.3106	1.6000e-04	SH
50	Bias $\hat{\propto}$	0.0024	0.0039	0.0862	2.4000e-04	SH
	Bias $\hat{β}$	4.0200e-04	1.0800e-04	0.0376	9.0000e-05	SH
	Bias $\hat{λ}$	0.0048	0.0076	0.2539	1.6000e-04	SH
100	Bias $\hat{\propto}$	0.0021	0.0037	0.0952	2.4000e-04	SH
	Bias $\hat{β}$	6.9400e-04	3.0900e-04	0.0320	9.0000e-05	SH
	Bias $\hat{λ}$	0.0022	0.0059	0.2663	1.6000e-04	SH

Table 6. Shown the MSE for $\hat{\propto}$ , $\hat{β}$ and $\hat{λ}$ based on case1.

		∝=2.0 β=3.0 λ= 1.6
n	Mse	MLE	MOM	LS	SH	Best
10	Mse $\hat{\propto}$	0.5658	0.0364	0.2304	0.0036	SH
	Mse $\hat{β}$	0.1152	0.0888	0.2549	0.0081	SH
	Mse $\hat{λ}$	0.1522	0.0314	1.1160	0.0023	SH
20	Mse $\hat{\propto}$	0.0306	0.0363	0.1980	0.0036	SH
	Mse $\hat{β}$	0.0807	0.0869	2.0101	0.0081	SH
	Mse $\hat{λ}$	0.0177	0.5562	2.3991	0.0023	SH
50	Mse $\hat{\propto}$	0.4196	0.0363	0.0924	0.0036	SH
	Mse $\hat{β}$	0.5382	0.0848	2.8979	0.0081	SH
	Mse $\hat{λ}$	0.5960	0.0367	3.3316	0.0023	SH
100	Mse $\hat{\propto}$	0.4662	0.0362	0.0951	0.0036	SH
	Mse $\hat{β}$	0.5877	0.0841	2.7563	0.0081	SH
	Mse $\hat{λ}$	0.4807	0.0316	3.3061	0.0023	SH

Table 7. Shown the MSE for $\hat{\propto}$ , $\hat{β}$ and $\hat{λ}$ based on case 2.

		∝=1.0 β=2.5 λ= 3.0
n	Mse	MLE	MOM	LS	SH	Best
10	Mse $\hat{\propto}$	0.1780	0.0113	0.0435	0.0090	SH
	Mse $\hat{β}$	0.1637	0.1656	0.6498	0.0056	SH
	Mse $\hat{λ}$	0.1627	0.8348	0.2181	0.0081	SH
20	Mse $\hat{\propto}$	0.1707	0.0103	0.0926	0.0090	SH
	Mse $\hat{β}$	0.0265	0.0599	0.5323	0.0056	SH
	Mse $\hat{λ}$	0.0245	0.8024	0.2775	0.0081	SH
50	Mse $\hat{\propto}$	0.7338	0.0097	0.0806	0.0090	SH
	Mse $\hat{β}$	0.9400	0.0593	0.0711	0.0056	SH
	Mse $\hat{λ}$	0.9955	0.1136	0.3770	0.0081	SH
100	Mse $\hat{\propto}$	0.5039	0.0098	0.0736	0.0090	SH
	Mse $\hat{β}$	0.6577	0.0590	0 .8601	0.0056	SH
	Mse $\hat{λ}$	0.8730	0.1087	0 .7719	0.0081	SH

Table 8. Shown the MSE for $\hat{\propto}$ , $\hat{β}$ and $\hat{λ}$ based on case 3.

		∝=3.5 β=1.0 λ=1.7
n	Mse	MLE	MOM	LS	SH	Best
10	Mse $\hat{\propto}$	0.0622	0.0557	4.4276	1.2000e-05	SH
	Mse $\hat{β}$	0.0056	0.0057	0.4522	1.0000e-06	SH
	Mse $\hat{λ}$	0.6143	0.0226	13.1175	3.0000e-06	SH
20	Mse $\hat{\propto}$	0.0337	0.1454	5.5851	1.2000e-05	SH
	Mse $\hat{β}$	0.0026	0.0071	0.4931	1.0000e-06	SH
	Mse $\hat{λ}$	0.9234	0.0184	15.9498	3.0000e-06	SH
50	Mse $\hat{\propto}$	0.0148	0.0514	9.6574	1.2000e-05	SH
	Mse $\hat{β}$	0.0011	0.0031	0.7899	1.0000e-06	SH
	Mse $\hat{λ}$	0.1211	0.0117	8.9392	3.0000e-06	SH
100	Mse $\hat{\propto}$	0.0063	0.0259	9.8537	1.2000e-05	SH
	Mse $\hat{β}$	0.0007	0.0173	0.7082	1.0000e-06	SH
	Mse $\hat{λ}$	0.0102	0.0069	11.0680	3.0000e-06	SH

Table 9. Shown the MSE for $\hat{\propto}$ , $\hat{β}$ and $\hat{λ}$ based on case4.

		∝=1.5 β=2.0 λ= 2.5
n	Mse	MLE	MOM	LS	SH	Best
10	Mse $\hat{\propto}$	0.8765	0.0205	0.0854	0.0020	SH
	Mse $\hat{β}$	0.2734	0.0386	0.2527	0.0036	SH
	Mse $\hat{λ}$	0.2800	0.2952	0.2546	0.0056	SH
20	Mse $\hat{\propto}$	0.0482	0.0204	0.0695	0.0020	SH
	Mse $\hat{β}$	0.1322	0.0384	0.2673	0.0036	SH
	Mse $\hat{λ}$	0.1740	0.8185	0.8097	0.0056	SH
50	Mse $\hat{\propto}$	0.9459	0.0204	0.0746	0.0020	SH
	Mse $\hat{β}$	0.5050	0.0381	0.6722	0.0036	SH
	Mse $\hat{λ}$	0.9689	0.2213	0.8629	0.0056	SH
100	Mse $\hat{\propto}$	0.1796	0.0204	0.0908	0.0020	SH
	Mse $\hat{β}$	0.4177	0.0371	0.2493	0.0036	SH
	Mse $\hat{λ}$	0.7377	0.0674	2.3007	0.0056	SH

2-5 Application of real dataset

This section does an analysis based on a real dataset. The dataset illustrates the period of time between failures for a repairable item obtained from Refs. 16 and 22. IDNAII appears to be a very competitive model for this data compared to the Lomax distribution, Weibull-Exponential distribution (WED),²³ Weibull-Rayleigh distribution (WRD),²⁴ and Exponential-Rayleigh distribution (ERD),²⁵ each with their associated probability density functions (PDFs). The data set and its descriptive statistics are shown respectively in Tables 10 and 11.

To verify that IDNAII distribution is suitable model for the data set, a minus two times of negative log-likelihood value, Akaike information criteria (AIC), Bayesian information criteria (BIC), corrected Akaike information criterion (AICC), Hannan-Quinn information criterion (HQIC), consistent Akaike information criterion (CAIC) and Kolmogorov-Smirnov K-S distance with P-values are used and shown in Table 12, where:

(61)

\begin{matrix} {AIC = 2 k - 2 logl, BIC = klog (n) - 2 logl, AICC = AIC + (2 k (k + 1)) / (n - k - 1), \\ HQIC = - 2 logl + 2 klog (log (n)), CAIC = - 2 logl + 2 kn / (n - k - 1}, \end{matrix}

Where logl denotes the log-likelihood at MLEs, k is the number of parameters, and n is a sample size.

The empirical cdf and estimated cdf of IDNAII and the other distributions as well as the histogram of K-S and P-value are respectively presented in Figures 3 and 4.

3. Results

This section presents the research findings.

3-1 Particular instances of the novel IDNAII distribution

The PDF of the suggested IDNAII distribution in (13) leads to the following conclusions.

(i) The IDNAII (α,β,λ) distribution follows the Lomax distribution with one parameter λ for the random variable y = βX ^α or Beta prime distribution with parameter 1 and λ.
(ii) When the random variable Z = X ^α, then the IDNAII (α,β,λ) distribution is interpreted to Lomax distribution with two parameters (β,λ).
(iii) When the random variable V = 1+ βx^α then the IDNAII (α,β,λ) distribution reduce to power function distribution with one parameter λ, for V > 1.

3-2 Figures of probability functions of IDNAII distribution

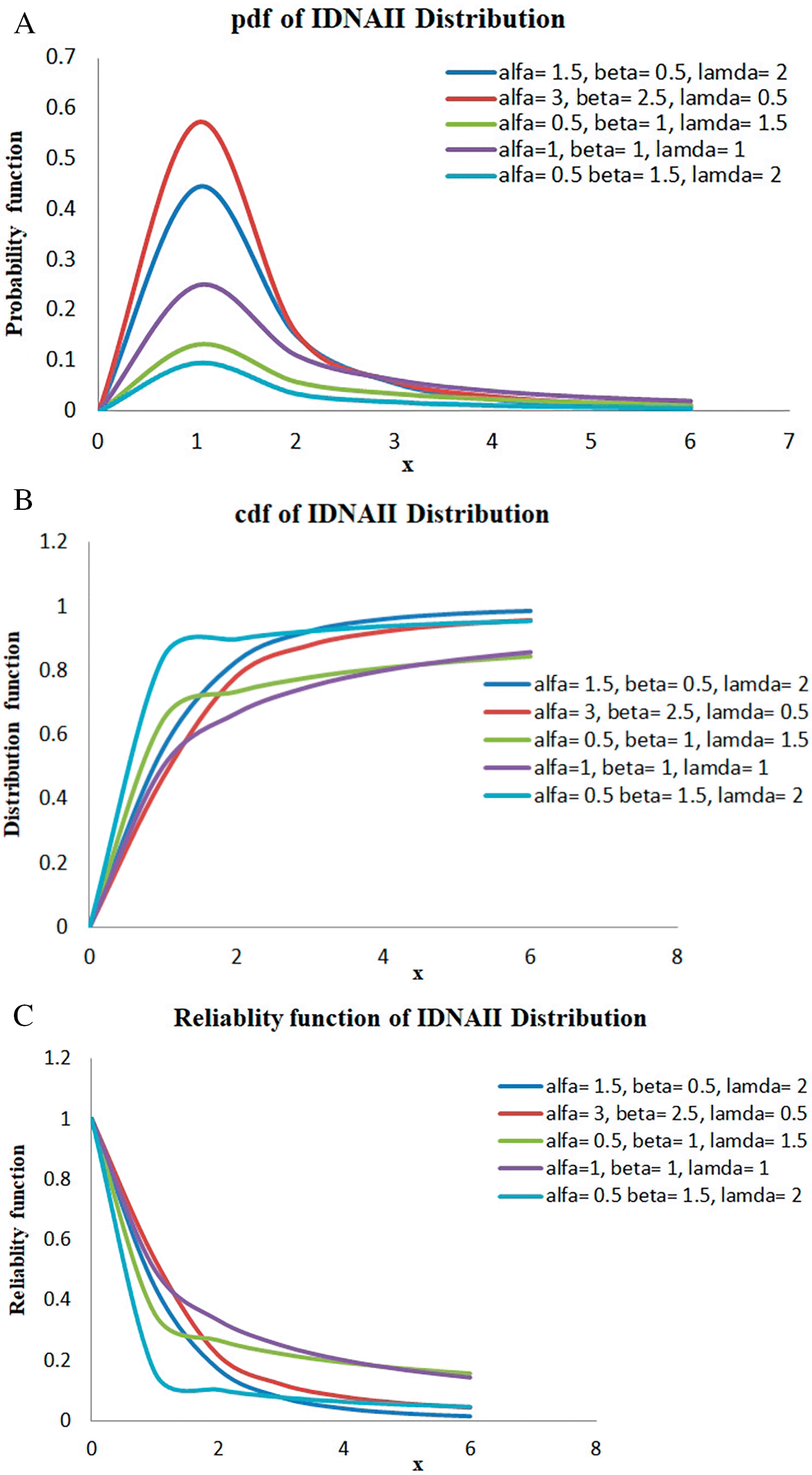
The graphs of the probability density function, cumulative distribution function, and reliability function for the IDNAII distribution for particular parameter values are shown in Figure 1 with the following details.

Figure 1(A) shows that the graph of the probability density functions for the IDNAII distribution with certain parameter values.

Figure 1(B) shows the cumulative distribution function graph for the IDNAII distribution with certain parameter values.

The graph in Figure 1(C) shows the Reliability function for the IDNAII distribution with certain parameter values.

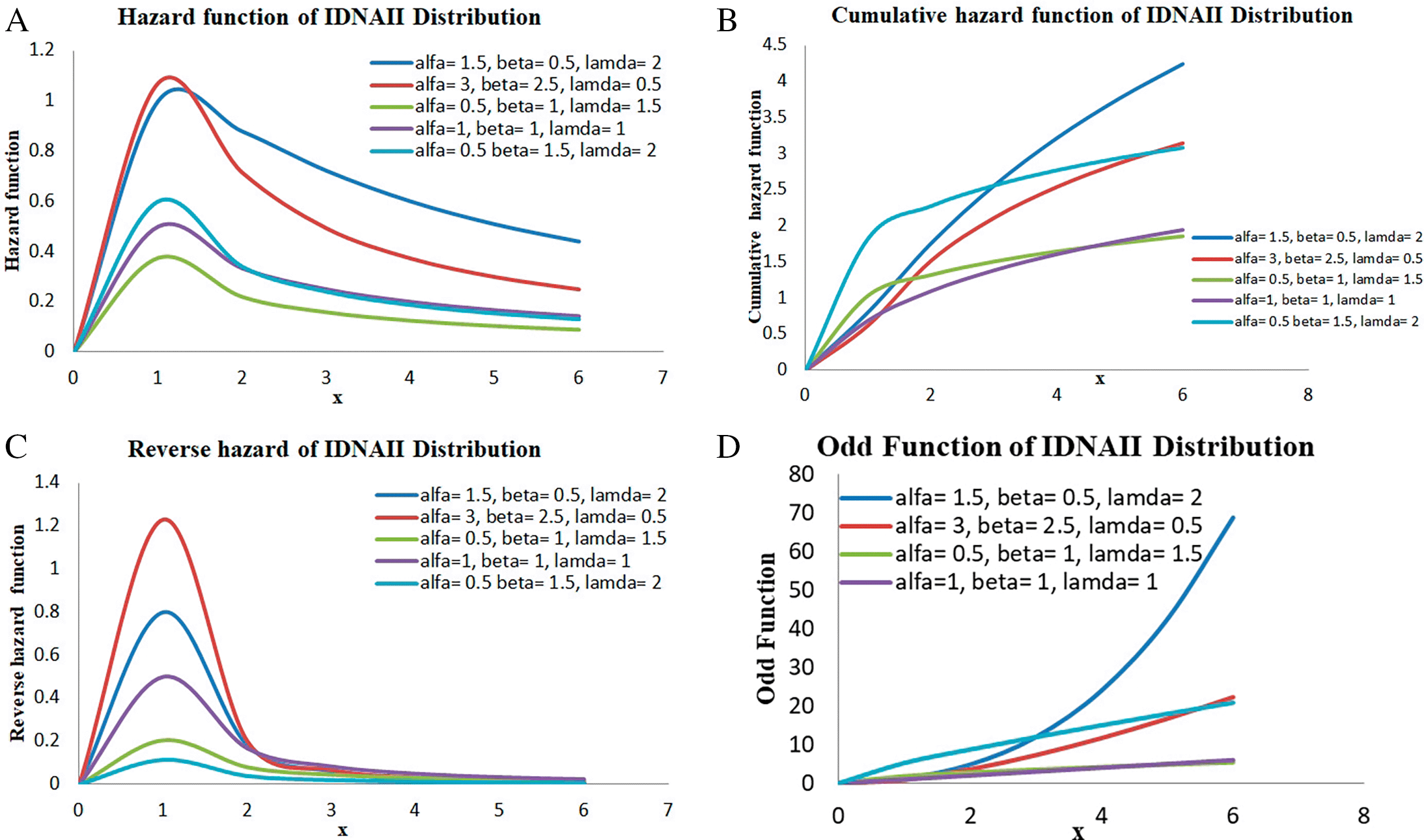
The graph in Figure 2(A) displays the hazard function for the IDNAII distribution for a range of parameter values.

Figure 2(B) shows the graph of cumulative hazard function of the IDNAII distribution.

The graph in Figure 2(C) illustrates the graph for the reverse hazard function with influenced by parameters α, β, and λ.

Figure 2(D) displays the graph for odd function with certain parameter values.

The empirical cdf and estimated cdf of IDNAII and the other specific distributions as well as the histogram of K-S and P-value are respectively presented in Figures 3 and 4. It shows how well a model fits by comparing the empirical cumulative distribution function (CDF) of a dataset with many fitted CDFs from theoretical models and the p-values and Kolmogorov-Smirnov (K-S) statistics for five fitted distributions side by side.

3-3 Tables of Bias, MSE, dataset, and parameter estimations utilizing different information criteria

The suggested real parameters are shown in Table 1, and the Bias computations for the proposed estimators are detailed in Tables 2 to 5. The Mean Squared Error calculations for the proposed estimators are presented in Tables 6 to 9. Tables 10 and 11 present the dataset and its corresponding descriptive statistics, respectively. Table 12 presents the information criterion and estimation parameters for each fitted distribution.

4. Discussions

This section discusses the findings from the study in the following manner.

4-1 A brief overview of the recommended new model

Since the proposed distribution is so adaptable, it can be used as a model for a wide range of data types, particularly containing skewed, kurtosis, or otherwise non-symmetrical data. It is more beneficial for studies of inequality and reliability because of its structural flexibility, which enables it to represent a variety of real world behaviors. Additionally, the distribution provides a coherent framework for statistical modeling by generalizing many well-known classical models and including them as particular cases.

4-2 Overview figures

This work introduces an innovative probability distribution that enhances statistical modeling, demonstrating adaptability and a solid mathematical foundation. It captures important statistical properties like skewness, kurtosis, and multimodality. The model’s validity is backed up by a rigorous derivation of its probability functions and a full graphical analysis, which shows that it can accurately represent a wide range of real-world data formats.

Figure 1(A) shows that the graph of the probability density functions for the IDNAII distribution with certain parameter values. The density of the IDNAI distribution might be symmetric, adjacent symmetric, right-skewed, or bimodal.

Figure 1(B) shows the cumulative distribution function graph for the IDNAII distribution with certain parameter values. This graph shows that the cumulative distribution function of the IDNAII distribution is a function that does not decrease.

The graph in Figure 1(C) shows the Reliability function for the IDNAII distribution with certain parameter values. This graph shows that the reliability function of IDNAII distribution is a non-increasing function, which is what most people already know.

The graph Figure 2(A) displays the hazard function for the IDNAII distribution for a range of parameter values. The graphs display varying failure rate patterns, with sharper increases for larger λ values, such as the curve for α= 0.5, β= 1.5, and λ= 2. It is an excellent option for flexible reliability modeling because of this behavior, which demonstrates that the model is flexible to changes in parameters and may capture growing risk over time.

Figure 2(B) shows the graph of cumulative hazard function of the IDNAII distribution. This graph shows how it may be used in survival analysis and reliability theory by showing the overall failure risk up to time x. It demonstrates that when x increases, the cumulative danger escalates, conforming to standard survival model expectations. When λ is larger, the cumulative hazard is higher, which means the failure rates are higher. When α and β are removed, the curves are flatter, which means the risk increase is lower. The graphic shows how the properties of the IDNAII distribution change based on different dependability scenarios.

The graph in Figure 2(C) illustrates the variations in the reverse hazard function with increasing x, influenced by parameters α, β, and λ. A higher λ value (cyan curve, λ = 2) results in a steeper curve, indicating a higher likelihood of late failures and more pronounced tail behavior. In contrast, curves with lower λ values (red and blue curves, λ = 0.5) exhibit slower growth, reflecting lighter tails and more concentrated failure times. This function is crucial for reliability modeling, as it depicts distribution behavior in later life stages and highlights the sensitivity of reverse hazard to parameter changes, demonstrating the flexibility and controllability of the IDNAII model towards its conclusion.

Figure 2(D) illustrates that the odd function displays rapid growth with increasing x, especially with larger values of α.β and λ. Specifically, functions with λ = 1 show a significantly faster expansion rate compared to those with λ = 0.5, indicating a stronger influence on the upper range of x and pronounced tail behavior. This function is valuable for comparing configurations and understanding the impact of each parameter on the distribution’s shape, serving as an effective tool for evaluating the model’s adaptability and sensitivity to parameter variations.

Figures 3 shows how well a models fits by comparing the empirical cumulative distribution function (CDF) of a dataset with many fitted CDFs from theoretical models.

Figure 4 shows the p-values and Kolmogorov-Smirnov (K-S) statistics for five fitted distributions side by side.

Figure 1. pdf (A), cdf (B) and reliability function (C) for IDNAII distribution according to different values of α,β and λ.

Figure 2. Displays Hazard function (A), cumulative hazard function (B), reverse hazard function (C), and odd function of IDNAII distribution for various values of α,β and λ.

Figure 3. Empirical, fitted IDNAII, Lomax, WED, WRD and EDR.

Figure 4. Histogram for K-S and P-value of IDNAII, Lomax,WED, WRD and ERD for the time between failures.

4-3 Overview tables

4-3-1 Bias and Mean Squared Error (MSE) tables

Utilize summary statistics, specifically Tables 2-9 of Bias and Mean Squared Error (MSE) of proposed estimators for the parameters. It is particularly beneficial for assisting in the selection of an appropriate estimator in simulation tables to analyze the results.

Based on the mentioned Tables, bias and mean squared error (MSE), were ascertain:

1. Bias:
Distinctly demonstrated the patterns seen across the four scenarios according to Tables 2-5:
The SH method consistently demonstrated the lowest bias, regardless of sample size. MOM and MLE demonstrated differing levels of bias performance. The LS demonstrated amplified bias especially due to the estimation of λ.
2. Mean Squared Error (MSE):
Employing all methods over all four scenarios, SH had the lowest mean squared error overall across all parameter settings, according to Tables 6-9 of the estimators of parameters. MLE and MOM came next, but they weren’t consistent across cases. LS aren’t very effective, especially in the estimation of λ and in rare cases of β.

4-3-2 Data set tables

The data set and its descriptive statistics are shown respectively in Tables 10 and 11. The dataset illustrates the period of time between failures for a repairable item obtained from Refs. 16 and 22.

4-3-3 Parameter estimation and information criterion table

Table 12 indicates that the IDNAII exhibits lower values for -2Logl, AIC, BIC, AICC, HQIC, CAIC, and K-S distance compared to the other distributions, along with accurate P-values correspondingly. This suggests that the IDNAII may be selected as the most effective model for the proposed real dataset.

Table 10. The time between failures for a repairable item.

1.43	0.11	0.71	0.77	2.63	1.49	3.46	2.46	0.59	0.74
1.23	0.94	4.36	0.40	1.74	4.73	2.23	0.45	0.70	1.06
1.46	0.30	1.82	2.37	0.63	1.23	1.24	1.97	1.86	1.17

Table 11. Descriptive statistics of dataset.

Min	Max	Mean	Median	Mode	Std. Dev.	Skewness	Kurtosis	Sample size
0.11	4.73	1.5427	1.2350	1.2300	1.1277	1.2955	4.3192	30

Table 12. Parameter estimates according to various criteria.

No.	Distribution	Estimated parameters	-2LogL	AIC	BIC	HQIC	CAIC	AICC	KS_Stat	P_Value
1	IDNAII	α=3.7, β=1.3, λ=0.8	82.123	87.123	91.457	88.789	93.235	87.123	0.1200	0.4200
2	Lomax	α =241797927.272, λ =373036339.617	86.0108	90.0108	92.8131	90.9073	90.4552	90.4552	0.1845	0.2290
3	WED	α=2.5825, β=1.2113, λ =0.2079	81.1868	87.1869	91.9380	88.2550	94.9490	87.9369	0.0749	0.7630
4	WRD	α=8.1794, β=0.6989, λ=0.0320	80.0808	87.1869	91.9370	88.2600	94.9380	87.9370	0.0811	0.9800
5	ERD	β=238.8614, λ=63.3332	85.9780	89.9780	94.7290	90.0460	97.7300	90.7280	0.1899	0.2020

5. Conclusion

The Transformed-Transformer (T-X) Family method, grounded on the quantile function, serves as a robust mathematical framework for constructing tailored probability distributions. This method integrates the quantile function of a generating distribution with the cumulative distribution function (CDF) of a base distribution, so providing direct control over essential distributional attributes such as skewness, kurtosis, tail behavior (left or right), tail heaviness (heavy or light), and bimodality. Its versatility has been demonstrated across various domains, including environmental sciences, medical statistics, financial modeling, and reliability analysis, making it a valuable tool in modern applied statistics. The suggested family demonstrates various statistical and mathematical characteristics, covering probability density functions, moments, reliability functions, cumulative hazard functions, entropy measures, order statistics, and more aspects. The IDNAII distribution is a specific member of this family of distributions. We utilized various methods to estimate parameters for IDNAII, subsequently employing Monte Carlo simulation to assess their efficacy. The findings demonstrated that the shrinkage technique outperformed the other methods when evaluated from a bias viewpoint and regarding mean squared error. The proposed distribution was applied to empirical data, and a comparison shown that it exceeded existing models according to goodness-of-fit measurements, including the Akaike Information Criterion (AIC) and the Bayesian Information Criterion (BIC), and others.

AI disclosure statement

The authors independently generated all scientific components of this research, including mathematical and statistical derivations, statistical analyses, and findings, without the assistance of AI technologies. The Microsoft Copilot (October 2025 edition) was utilized solely to enhance linguistic clarity, formatting, and structural organization in accordance with open scientific and academic publishing norms.

Data and software availability

This study neither generates nor analyzes any novel data. The data employed was obtained from the published article:

Ibeh GC, Ekpenyoung EJ, Anyiam K, John C: The Weibull-exponential {Rayleigh} Distribution: Theory and Applications. Earthline Journal of Mathematical Sciences, 2021; Volume 6, Issue 1, Pages 65-86. Available at: https://earthlinepublishers.com/index.php/ejms/article/view/289/225

Furthermore, the volume: Murthy DNP, Xie M, Jiang R: Weibull Models. John Wiley & Sons, New Jersey, 2004.

The datasets used in that study were applied here to evaluate the effectiveness of the proposed IDNAII distribution. All data were obtained from publicly available sources and used solely for comparative modeling purposes.

Extended data

Figshare: Supplementary Files.

Figshare. Figures and tables of IDNAII distribution. https://doi.org/10.6084/m9.figshare.30508448.v4²⁶

Figshare. Matlab code -fit data –IDNAII distribution. https://doi.org/10.6084/m9.figshare.30685514.v1²⁷

Figshare. Methodological Note on Data Usage. https://doi.org/10.6084/m9.figshare.30685583²⁷

Data are available under the terms of the Creative Commons Attribution 4.0 International license (CC-BY 4.0).

Acknowledgements

The authors appreciate the anonymous reviewers for their constructive feedback that enhanced the quality of this work. The authors would like to acknowledge the support provided by the University of Al-Fallujah Conference, which kindly covered the article processing charges for the publishing of this work.

References

1. Al-Hussaini EK, Abdel-Hamid AH: Generation of distribution functions: A survey. J Stat Appl Probab. 2018; 7(1): 91–103. Publisher Full Text
2. Mohammed MJ, Hussein IH: Some estimation methods for new mixture distribution with simulation and application. IOP Conf Ser Mater Sci Eng. 2019; 571: 012014. Publisher Full Text
3. Mohammed MJ, Hussein IH: Study of new mixture distribution. ARPN J Eng Appl Sci. 2019; 14(20): 7566–7573. Publisher Full Text
4. Shallan RN, Alkanani IH: Statistical properties of generalized exponential Rayleigh distribution. Palest J Math. 2023; 12(Special Issue I): 46–58.
5. Noaman AA, Suhad AA, Mohammed KH: Constructing a new mixed probability distribution with fuzzy reliability estimation. Period Eng Nat Sci. 2020; 8(2): 590–601. Publisher Full Text
6. Lamyaa KH, Rasheed HA, Iden HH: A class of exponential Rayleigh distribution and new modified weighted exponential Rayleigh distribution with statistical properties. Ibn Al-Haitham J Pure Appl Sci. 2023; 6(2): 390–406.
7. Shakir GH, Iden HH: Study of new exponential-Weibull distribution about children with leukemia. AIP Conf Proc. 2024; 3036(1): 040030.
8. Kalaf BA, Batah FS, AbdulNabi AI: Right truncated Shankar distribution and its properties. Ibn Al-Haitham J Pure Appl Sci. 2025; 38(1): 493–499.
9. Abdul-Ameer NJ, Bayda KA: A new hybrid algorithm based on the firefly algorithm and cuckoo search to estimate survival analysis of truncated inverse Gompertz distribution. Iraqi J Sci. 2024; 65(2): 891–906.
10. Hameed BA, Salman AN, Kalaf BA: On estimation of in cased inverse Kumaraswamy distribution. Iraqi J Sci. 2020; 61(4): 845–853. Publisher Full Text
11. Alzaatreh A, Lee C, Famoye F: A new method for generating families of continuous distributions. Metron. 2013; 71(1): 63–79. Publisher Full Text
12. Alzaatreh A, Famoye F, Lee C: Weibull-Pareto distribution and its applications. Commun Stat Theory Methods. 2013; 42(9): 1673–1691. Publisher Full Text
13. Al-Aqtash R, Lee C, Famoye F: Gumbel-Weibull distribution: Properties and applications. J Mod Appl Stat Methods. 2014; 13(2): 201–225. Publisher Full Text
14. Osatohanmwen P, Oyegue FO, Ogbonmwan SM: A new member from the T-X family of distributions: The Gumbel-Burr XII distribution and its properties. Sankhya A. 2019; 81: 298–322. Publisher Full Text
15. Aljarrah MA, Lee C, Famoye F: On generating T-X family of distributions using quantile functions. J Stat Distrib Appl. 2014; 1: 1–17. Publisher Full Text
16. Ibeh GC, Ekpenyoung EJ, Anyiam K, et al.: The Weibull-exponential Rayleigh distribution: Theory and applications. Earthline J Math Sci. 2021; 6(1): 65–86. Publisher Full Text
17. Shannon CE: A mathematical theory of communication. Bell Syst Tech J. 1948; 27(3): 379–423. Publisher Full Text
18. Moll VH: The integrals in Gradshteyn and Ryzhik. Part 3: Combinations of logarithms and exponentials. Sci Ser A Math Sci (N.S.). 2007; 15(1): 31–36.
19. Rényi A: On measures of entropy and information. Proc Fourth Berkeley Symp Math Stat Probab. 1961; 1: 547–561.
20. Thompson JR: Some shrinkage techniques for estimating the mean. J Am Stat Assoc. 1968; 63(321): 113–122. Publisher Full Text
21. Rubinstein RY: Simulation and the Monte Carlo Method. Book review. Technometrics. 1982; 24(2): 167–168.
22. Murthy DNP, Xie M, Jiang R: Weibull Models. New Jersey: John Wiley & Sons; 2004.
23. Oguntunde P, Balogun OS, Okagbue HI, et al.: The Weibull-exponential distribution: Its properties and application. J Appl Sci. 2015; 15(11): 1305–1311. Publisher Full Text
24. Merovci F, Elbatal I: Weibull Rayleigh distribution: Theory and applications. Appl Math Inf Sci. 2015; 9(4): 2127–2137.
25. Fatima K, Ahmad SP: Statistical properties of exponential Rayleigh distribution and its application to medical sciences and engineering. Int Conf Recent Innovations Sci Agric Eng Manag. Bathinda, India: Guru Kashi Univ; 2017; 491–506.
26. Najim A: Figures and tables of IDNAII distribution. figshare. Figure. 2025. Publisher Full Text
27. Najim A: Matlab code -fit data -IDNAII. figshare. Software. 2025. Publisher Full Text

Comments on this article Comments (0)

Version 1

VERSION 1 PUBLISHED 24 Dec 2025

Author details Author details

¹ Department of Mathematics, University of Baghdad College of Education for Pure Science Ibn Al-Haitham, Baghdad, Baghdad Governorate, 10053, Iraq
² Department of Mathematics, University of Baghdad Al-Jaderyia Campus College of Science, Baghdad, Baghdad Governorate, 10070, Iraq

Abbas Najim
Roles: Conceptualization, Formal Analysis, Methodology, Software, Validation, Visualization, Writing – Original Draft Preparation, Writing – Review & Editing

Iden Hassan Hussein
Roles: Conceptualization, Formal Analysis, Methodology, Project Administration, Supervision, Writing – Original Draft Preparation, Writing – Review & Editing

Competing interests

No competing interests were disclosed.

Grant information

The author(s) declared that no grants were involved in supporting this work.

Article Versions (1)

version 1

Published: 24 Dec 2025, 14:1442

https://doi.org/10.12688/f1000research.173663.1

Copyright

© 2025 Najim A and Hassan Hussein I. This is an open access article distributed under the terms of the Creative Commons Attribution License, which permits unrestricted use, distribution, and reproduction in any medium, provided the original work is properly cited.

Download

Export To

metrics

	Views	Downloads
F1000Research	-	-
PubMed Central Data from PMC are received and updated monthly.	-	-

Citations

0

SEE MORE DETAILS

CITE

how to cite this article

Najim A and Hassan Hussein I. Regarding the Novel IDNAII Distribution: Mathematical and Statistical Characteristics [version 1; peer review: awaiting peer review]. F1000Research 2025, 14:1442 (https://doi.org/10.12688/f1000research.173663.1)

NOTE: If applicable, it is important to ensure the information in square brackets after the title is included in all citations of this article.

track

receive updates on this article

Track an article to receive email alerts on any updates to this article.

Open Peer Review

Comments on this article Comments (0)

Version 1

VERSION 1 PUBLISHED 24 Dec 2025

Open Peer Review

Reviewer Status

AWAITING PEER REVIEW

Comments on this article

All Comments(0)

Add a comment

Sign up for content alerts

Browse by related subjects

[1] 1. Al-Hussaini EK, Abdel-Hamid AH: Generation of distribution functions: A survey. J Stat Appl Probab. 2018; 7(1): 91–103. Publisher Full Text

[2] 2. Mohammed MJ, Hussein IH: Some estimation methods for new mixture distribution with simulation and application. IOP Conf Ser Mater Sci Eng. 2019; 571: 012014. Publisher Full Text

[3] 3. Mohammed MJ, Hussein IH: Study of new mixture distribution. ARPN J Eng Appl Sci. 2019; 14(20): 7566–7573. Publisher Full Text

[4] 4. Shallan RN, Alkanani IH: Statistical properties of generalized exponential Rayleigh distribution. Palest J Math. 2023; 12(Special Issue I): 46–58.

[5] 5. Noaman AA, Suhad AA, Mohammed KH: Constructing a new mixed probability distribution with fuzzy reliability estimation. Period Eng Nat Sci. 2020; 8(2): 590–601. Publisher Full Text

[6] 6. Lamyaa KH, Rasheed HA, Iden HH: A class of exponential Rayleigh distribution and new modified weighted exponential Rayleigh distribution with statistical properties. Ibn Al-Haitham J Pure Appl Sci. 2023; 6(2): 390–406.

[7] 7. Shakir GH, Iden HH: Study of new exponential-Weibull distribution about children with leukemia. AIP Conf Proc. 2024; 3036(1): 040030.

[8] 8. Kalaf BA, Batah FS, AbdulNabi AI: Right truncated Shankar distribution and its properties. Ibn Al-Haitham J Pure Appl Sci. 2025; 38(1): 493–499.

[9] 9. Abdul-Ameer NJ, Bayda KA: A new hybrid algorithm based on the firefly algorithm and cuckoo search to estimate survival analysis of truncated inverse Gompertz distribution. Iraqi J Sci. 2024; 65(2): 891–906.

[10] 10. Hameed BA, Salman AN, Kalaf BA: On estimation of in cased inverse Kumaraswamy distribution. Iraqi J Sci. 2020; 61(4): 845–853. Publisher Full Text

[11] 11. Alzaatreh A, Lee C, Famoye F: A new method for generating families of continuous distributions. Metron. 2013; 71(1): 63–79. Publisher Full Text

[12] 12. Alzaatreh A, Famoye F, Lee C: Weibull-Pareto distribution and its applications. Commun Stat Theory Methods. 2013; 42(9): 1673–1691. Publisher Full Text

[13] 13. Al-Aqtash R, Lee C, Famoye F: Gumbel-Weibull distribution: Properties and applications. J Mod Appl Stat Methods. 2014; 13(2): 201–225. Publisher Full Text

[14] 14. Osatohanmwen P, Oyegue FO, Ogbonmwan SM: A new member from the T-X family of distributions: The Gumbel-Burr XII distribution and its properties. Sankhya A. 2019; 81: 298–322. Publisher Full Text

[15] 15. Aljarrah MA, Lee C, Famoye F: On generating T-X family of distributions using quantile functions. J Stat Distrib Appl. 2014; 1: 1–17. Publisher Full Text

[16] 16. Ibeh GC, Ekpenyoung EJ, Anyiam K, et al.: The Weibull-exponential Rayleigh distribution: Theory and applications. Earthline J Math Sci. 2021; 6(1): 65–86. Publisher Full Text

[17] 17. Shannon CE: A mathematical theory of communication. Bell Syst Tech J. 1948; 27(3): 379–423. Publisher Full Text

[18] 18. Moll VH: The integrals in Gradshteyn and Ryzhik. Part 3: Combinations of logarithms and exponentials. Sci Ser A Math Sci (N.S.). 2007; 15(1): 31–36.

[19] 19. Rényi A: On measures of entropy and information. Proc Fourth Berkeley Symp Math Stat Probab. 1961; 1: 547–561.

[20] 20. Thompson JR: Some shrinkage techniques for estimating the mean. J Am Stat Assoc. 1968; 63(321): 113–122. Publisher Full Text

[21] 21. Rubinstein RY: Simulation and the Monte Carlo Method. Book review. Technometrics. 1982; 24(2): 167–168.

[22] 22. Murthy DNP, Xie M, Jiang R: Weibull Models. New Jersey: John Wiley & Sons; 2004.

[23] 23. Oguntunde P, Balogun OS, Okagbue HI, et al.: The Weibull-exponential distribution: Its properties and application. J Appl Sci. 2015; 15(11): 1305–1311. Publisher Full Text

[24] 24. Merovci F, Elbatal I: Weibull Rayleigh distribution: Theory and applications. Appl Math Inf Sci. 2015; 9(4): 2127–2137.

[25] 25. Fatima K, Ahmad SP: Statistical properties of exponential Rayleigh distribution and its application to medical sciences and engineering. Int Conf Recent Innovations Sci Agric Eng Manag. Bathinda, India: Guru Kashi Univ; 2017; 491–506.

[26] 26. Najim A: Figures and tables of IDNAII distribution. figshare. Figure. 2025. Publisher Full Text

[27] 27. Najim A: Matlab code -fit data -IDNAII. figshare. Software. 2025. Publisher Full Text

Regarding the Novel IDNAII Distribution: Mathematical and Statistical Characteristics

Abstract

Keywords

1. Introduction

(1)

(2)

(3)

(4)

(5)

(6)

2. Methods

2-1 Constructing a new IDNAII distribution

(7)

(8)

(9)

(10)

(11)

(12)

(13)

(14)

2-2 The IDNAII distribution’s characteristics

(15)

(16)

(17)

(18)

(19)

(20)

(21)

(22)

(23)

(24)

(25)

(26)

(27)

(28)

(29)

(30)

(31)

(32)

(33)

(34)

(35)

(36)

(37)

(38)

(39)

(40)

(41)

(42)

(43)

(44)

2-3 Parameter estimation methods for IDNAII (α, β, λ) distribution

(45)

(46)

(47)

(48)

(49)

(50)

(51)

(52)

(53)

(54)

(55)

(56)

(57)

(58)

2-4 Comparison of estimators via Monte Carlo simulation

(59)

(60)

Table 1. Four cases of real parameters.

Table 2. Shown Bias for ∝̂ , β̂ and λ̂ w.r.t. case 1.

Table 3. Shown Bias for ∝̂ , β̂ and λ̂ w.r.t. case 2.

Table 4. Shown Bias for ∝̂ , β̂ and λ̂ w.r.t. case 3.

Table 5. shown Bias for ∝̂ , β̂ and λ̂ w.r.t case4.

Table 6. Shown the MSE for ∝̂ , β̂ and λ̂ based on case1.

Table 7. Shown the MSE for ∝̂ , β̂ and λ̂ based on case 2.

Table 8. Shown the MSE for ∝̂ , β̂ and λ̂ based on case 3.

Table 9. Shown the MSE for ∝̂ , β̂ and λ̂ based on case4.

2-5 Application of real dataset

(61)

Table 2. Shown Bias for $\hat{\propto}$ , $\hat{β}$ and $\hat{λ}$ w.r.t. case 1.

Table 3. Shown Bias for $\hat{\propto}$ , $\hat{β}$ and $\hat{λ}$ w.r.t. case 2.

Table 4. Shown Bias for $\hat{\propto}$ , $\hat{β}$ and $\hat{λ}$ w.r.t. case 3.

Table 5. shown Bias for $\hat{\propto}$ , $\hat{β}$ and $\hat{λ}$ w.r.t case4.

Table 6. Shown the MSE for $\hat{\propto}$ , $\hat{β}$ and $\hat{λ}$ based on case1.

Table 7. Shown the MSE for $\hat{\propto}$ , $\hat{β}$ and $\hat{λ}$ based on case 2.

Table 8. Shown the MSE for $\hat{\propto}$ , $\hat{β}$ and $\hat{λ}$ based on case 3.

Table 9. Shown the MSE for $\hat{\propto}$ , $\hat{β}$ and $\hat{λ}$ based on case4.