The Theory of Observational Relativity Serial Report 3: Einstein's Prediction of Gravitational Waves is an Error

2.1 Einstein’s gravitational scene and field equation

Newton’s law of universal gravitation represents Newton’s gravitational theory; Einstein’s gravitational-field equation represents Einstein’s gravitational theory. Their gravitational scenes are similar.

Newton set the scene of universal gravitation as (M, m) where two matter particles M and m separated by r in space interact with each other due to the gravity F:

This is Newton’s law of universal gravitation, where χ is the Newton gravitational potential.

If M (>>m) is regarded as the gravitational source and center, then Newton’s gravitational scene is a static spherically-symmetric gravitational spacetime: on the surface of a sphere centered around M, the Newtonian gravitational potential χ is the same everywhere. Thus, Newton’s law of universal gravitation can be expressed with the Poisson equation:

Einstein’s gravitational scene (M, m) (M >> m), like Newton’s gravitational scene, is also a static spherically-symmetric gravitational spacetime, and conforms to the interpretation by the Poisson equation for Newton’s law of universal gravitation.

Originally, Einstein envisioned that his general relativity should have two basic equations: the gravitational-field equation, specifying how spacetime is curved; the gravitational-motion equation, specifying how matter moves in curved spacetime.

In the static spherically-symmetric gravitational scene (M, m) (M >> m), Einstein deduced his field equation and motion equation.

Einstein’s Gravitational-Field Equation⁸:

Einstein’s Gravitational-Motion Equation⁸:

Later, Einstein et al.¹⁶ and Fock¹⁷ successively proved that the field equation (Eq. (3)) and the motion equation (Eq. (4)) are equivalent.

Of course, this does not negate the value and significance of the coexistence of the field equation and the motion equation. The calibration of the coefficient κ_E in Einstein field equation needs both of them.

2.2 Einstein’s linearization way: Weak-field approximation

After the establishment of the gravitational-field equation (Eq. (3)) in form, the important issue Einstein faced was how to calibrate the gravitational coefficient κ_E in it.

In order to calibrate the coefficient κ_E, Einstein needed to match his field equation with Newton’s law of universal gravitation in the form of Poisson equation. However, Poisson equation is a linear partial differential equation, and Einstein field equation is nonlinear. It is difficult for Einstein to match his field equation with Poisson equation, and moreover, to solve and calibrate his field equation.

Thus, Einstein conceived a linearization way, that is, the logical way of weak-field approximation.

Einstein envisioned that the curved spacetime of a weak gravitational field should tend to be flat, so that his field equation could be linearized in a weak gravitational field, and the metric g_μν(c) of curved spacetime could be decomposed into the flat metric η_μν = diag(+1,−1,−1,−1) (i.e., Minkowski metric) and a curved metric h_μν(c) (|h_μν(c)| << |η_μν|). Thus, the gravitational-field and gravitational-motion equations could be linearized by weak-field approximation and matched with Newton’s law of universal gravitation in the form of Poisson equation, thereby calibrating the gravitational coefficients κ_E. Moreover, in this way, the linearized field and motion equations are easy to solve.

Actually, Einstein’s logical way of weak-field approximation includes five hypotheses:

The logical way of weak-field approximation is a type of linearization theory developed by Einstein specifically for his theory of general relativity. The linearization of field or motion equation can be referred to as weak-field linearization, and the calibration of the gravitational coefficients κ_E can be referred to as weak-field calibration.

2.3 The weak-field calibration of Einstein’s gravitational coefficient

There is no direct corresponding relationship between Einstein field equation and Newton’s law of universal-gravitation. Therefore, Einstein had to connect the two through weak-field approximation, so that he could calibrate the gravitational coefficient κ_E in his field equation.

Weak-Field Linearization of Motion Equation:

Einstein’s gravitational-motion equation (Eq. (4)) describes the motion trajectory of the observed object in the 4d curved spacetime of gravitational field, a geodesic line, which is connected to the connection Γ^μ_αβ, and the connection Γ^μ_αβ is connected to the metric g_μν.

Under the hypotheses of weak field, the curved 4d geodesic line is approximately linearized and split into 1d time and the straight line in 3d Euclidean space:

By comparing Newton’s law of universal gravitation (Eq. (1)) and the straight line in Einstein’s motion equation (Eq. (5)) of weak-field linearization, it can be obtained that

In this way, the curved metric 00-element h₀₀ in weak gravitational field is linked to the Newtonian gravitational potential χ: h₀₀~χ.

Weak-Field Linearization of Field Equation:

Einstein’s gravitational-field equation (Eq. (3)) describes the relationship between the curvature R_μν(c) of 4d gravitational spacetime and the energy-momentum tensor T_μν(c) of matter.

Under the hypotheses of weak field, Einstein field equation (Eq. (3)) can be approximated as the following linearized relation:

Thus, the field equation (Eq. (7)) reduces to

In this way, the curved metric 00-element h₀₀ in weak gravitational field is linked to the gravitational coefficient κ_E of Einstein field equation (Eq. (3)): h₀₀~κ_E.

Weak-Field Calibration of the Gravitational Coefficient κ _E :

Substituting h₀₀ in Eq. (6) into Eq. (8), it can be obtained that

By comparing Eq. (9) with the Poisson-equation form of Newton’s universal-gravitation law (Eq. (2)), the gravitational coefficient κ_E of Einstein field equation can be calibrated as

In a sense, the calibration of the coefficient κ_E in Einstein gravitational-field equation represents the establishment of Einstein’s theory of general relativity.

2.4 The weak-field delayed solution of Einstein field equation

Newton’s law of universal gravitation brought significant discoveries to human being’s physics: there exists gravitational interaction between matter and matter.

So, what about Einstein’s gravitational-field equation?

Answering this question requires solving Einstein’s gravitational-field equation.

The left-hand end of Einstein field equation (Eq. (3)) is usually defined or labeled as the tensor G_μν(c), known as the Einstein tensor. Then, Einstein field equation can be succinctly written as

Based on Einstein’s logic of weak-field approximation, under the conditions of weak field, g_μν(c) ≈ η_μν, R(c) ≈ □h(c)/2, and R_μν(c) ≈ □h_μν(c)/2. Thus, the tensor of metric perturbation can be defined as

As shown in Eq. (6), in the weak-field case of g_μν(c) = η_μν + h_μν(c) (|h_μν| << |η_μν|), the curved metric h_μν(c) represents the Newtonian gravitational potential χ and is a small quantity. The so-called metric perturbation h^~_μν(c) means that the flat spacetime represented by the Minkowski metric η_μν is slightly perturbed by the Newtonian gravitational potential χ, resulting in ripples.

Thus, under the conditions of weak-field approximation, the Einstein tensor G_μν(c) can be defined by the tensor h^~_μν(c) of metric perturbation, and Einstein field equation (Eq. (11)) can be expressed by h^~_μν(c) as

Einstein’s gravitational-field equation (Eq. (13)) of weak-field linearization that satisfies the coordinate condition of Eq. (14) has the following solution:

This is the delayed integral formula of Einstein’s gravitational-field equation.

It is puzzling that, on the one hand, Einstein geometrized the gravitational effect, believing that gravitational spacetime is curved and denying the objective existence of gravity or gravitational radiation; on the other hand, the delayed solution of Einstein field equation suggests that there exists gravity or gravitational radiation in the physical world.

Einstein believed that the energy-momentum tensor T_μν(t−d/c, x′ⁱ,c) in Eq. (15) represents the gravitational source, while t−d/c represents the time delay of the gravitational interaction from x′ⁱ to xⁱ.

Thus, Einstein decided that the speed of gravitational radiation is the speed of light c.

At this point, the speed of gravitational radiation seemed to have been identified, however, the concept of Gravitational Wave had not yet been formed.

2.5 Einstein’s wave equation and gravitational waves

Under the conditions of weak-field approximation, the energy-momentum tensor T_μν(c) as the gravitational source tends to zero: T_μν(c) ≈ 0; the weak-field linearized gravitational-field equation (Eq. (13)) is reduced to the vacuum form of field equation: $\square$ h^~_μν(c) ≈ 0. According to the definitions of the d’ Alembert operator “□” and the Laplace operator “∇²” of the optical observation agent OA(c) (see Chapter 5 of the 1^st IOR volume in Observational Relativity^1–4), it holds true that

This is Einstein’s wave equation.

Hendry observed¹⁵: “This is a crucial outcome.”

Equation (16) is exactly the mathematical form of a wave, a typical wave equation, where the metric-perturbation tensor h^~_μν(c) is the wave function, and c is the wave speed of h^~_μν(c). From Eq. (6) and Eq. (12), h^~_μν(c), like the curved metric h_μν(c), is linked to the Newtonian gravitational potential χ=−GM/r. Accordingly, Einstein decided that h^~_μν(c) must be the wave of gravitational radiation, and could be called a gravitational wave; moreover, gravitational waves must propagate at the speed of light c.

Thus, Einstein’s concept of Gravitational Wave and Einstein’s prediction of gravitational waves were born.

Afterwards, analogous to the quantization of electromagnetic waves, gravitational waves are quantized; analogous to the concept of photon as the mediator of electromagnetic interaction, physics introduces the concept of Graviton as the mediator of gravitational interaction. According to Einstein’s theory of special relativity, a matter particle moving at the speed of light must have no rest mass. Thus, the graviton is set as a type of elementary particle of spin 2 with no rest mass.

However, as stated in OR Serial Report 2, all matter particles have the rest mass of their own. Both photons and gravitons must possess their objective and real rest mass.

The theory of OR does not doubt the objective existence of gravitational waves and gravitons.

Later, we will deduce the GOR wave equation of the general observation agent OA(η), and then, will clarify that the wave in Einstein’s wave equation is not a gravitational wave, but the information wave of the optical agent OA(c), that is, light or an electromagnetic wave.

3.1 Early gravitational-wave detection

The objective existence of gravity and gravitational radiation should have been evident.

We can all feel the effect of the earth’s gravity on our bodies. The gravitational radiation or gravitational waves from the moon and sun continuously make waves in the earth’s oceans, causing the tides to rise and fall. When we use a balance to measure the weight of an apple, we have more reason than LIGO to claim: “We have detected the gravitational wave!” However, it does not come from deep space, but from our own planet, not related with the so-called binary black-hole systems and their mergers.

This is more real than LIGO’s detection!

However, for physicists, detecting gravitational waves seems to be a highly challenging task and tedious scholastic philosophy.

Our ears can perceive sound waves; our eyes can perceive light waves. The sonar invented by mankind has greatly expanded the observation frequency band of sound waves, including underwater sound; the radar invented by mankind has greatly expanded the observation frequency band of electromagnetic waves, including long waves far beyond infrared and short waves far beyond ultraviolet. However, we cannot hear or see gravitational waves; we lack instruments and equipment for observing or detecting gravitational waves.

After Einstein’s prediction of gravitational waves in 1916, physicists had failed to come up with a specific scheme for detecting gravitational waves for forty years. Until 1955, British physicist Pirani proposed that gravitational waves could be detected by testing the change in distance between two small-mass objects.¹⁸ Based on Einstein’s theory of general relativity, Pirani proved that, if gravitational waves passed between two objects, the distance between the two objects would change.

Inspired by Pirani, Weber designed and manufactured a resonant bar, called Weber bar.¹⁹ In 1968, Weber announced that his resonant bar had detected gravitational waves.^20,21 However, numerous repeated experiments imitating Weber bar afterwards failed to detect gravitational waves. The conclusion was that the Weber bar was too short and its sensitivity is not sufficient to detect gravitational waves.

It should be pointed out that, in fact, the principle design of LIGO’s gravitational-wave detector has also follow and adopt Pirani’s scheme.

3.2 LIGO detector: Principle scheme

The mission of LIGO is to detect gravitational radiation or gravitational waves, verifying Einstein’s prediction of gravitational waves.

The prototype of LIGO was created by Professor Wesis of the Massachusetts Institute of Technology.

In the 1970s, Wesis designed a laser interferometer for detecting gravitational waves, similar to the Michelson interferometer²² that was used by Michelson and Morley in 1887 to detect the ether. Although the Michelson-Morley experiment did not detect the ether, it led to the establishment of the principle of the invariance of light speed, and finally, to the establishment of Einstein’s theory of relativity, both the special and the general.

The basic structure of the LIGO detection system is depicted in Figure 1(a), and its basic principle is rooted from Pirani’s theory¹⁸: gravitational waves sweeping over two small-mass objects can cause a change in the spatial distance between the two objects.

Figure 1. LIGO Detector: Architecture and Principle.

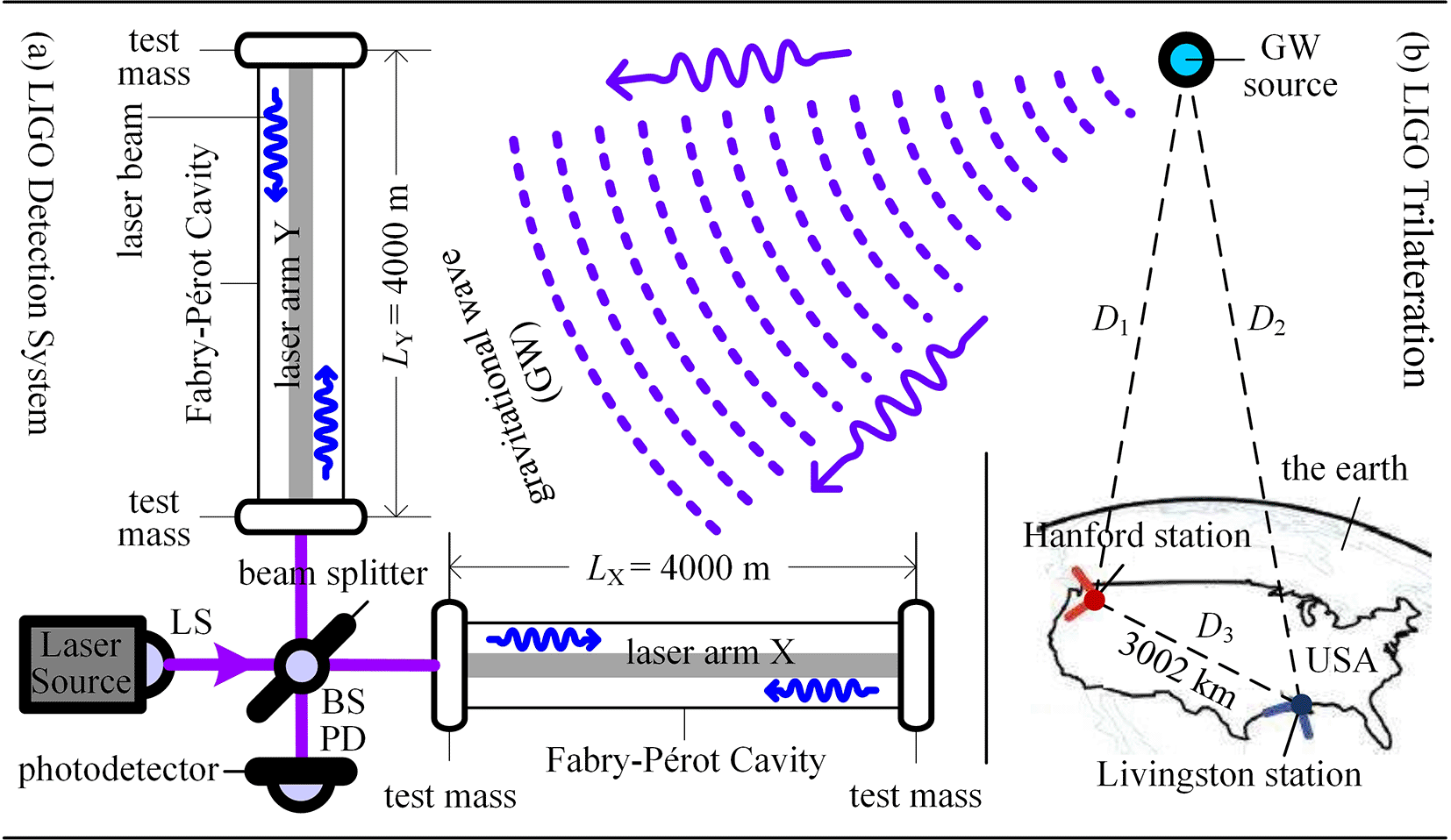
Annotation (a) LIGO Detection System. (1) LS: Laser source, emitting monochromatic laser with stable frequency; (2) BS: Beam splitter, splitting the laser into two beams, one entering the X-arm and the other entering the Y-arm (X and Y perpendicular to each other); (3) F-P vacuum resonant cavity with the test mass TM at each ends: The laser travels back and forth between the tow TMs, and the equivalent length of a laser arm can reach 1.12×10⁶ m; (4) Laser interference: the two laser beams return to BS to interfere with each other; (5) PD: Photodetector, recording laser interference fringes and triggering the LIGO detector.

Annotation (b) LIGO Trilateration. LIGO built two base stations, Hanford station and Livingston station in the United States, attempting to determine the direction and distance of gravitational-wave sources based on trilateration method, and then determine the speed of gravitational waves.

In fact, the basic principle of Weber bar¹⁹ was also rooted in Pirani’s theory. But Weber bars were too short, and the physical effect of its stretching and contracting were too limited to sense or detect gravitational waves sweeping over Weber bars.

In terms of system structure, the LIGO detector is an imitation of the Michelson interferometer: the core consists of two perpendicular laser arms (X and Y), that is, the Fabry-Pérot vacuum resonant cavities, each with a length of L = 4000 m and two test-mass bodies (TM) at the both ends. Laser can travel back and forth between the two TMs in an F-P vacuum cavity multiple times, with an equivalent arm length of 1.12 × 10⁶ m, which is 5 × 10⁵ times that of a Weber bar. Therefore, the sensitivity of LIGO system in detecting matter waves, including gravitational waves, is much higher than that of a Weber bar.

In terms of work process, the LIGO detector is also an imitation of the Michelson interferometers: the laser source (LS) emits a monochromatic laser beam with stable frequency, which is split into two beams of equal intensity by the beam splitter (BS), one entering the X-arm and the other entering the Y-arm. Two laser beams travel 1.12 × 10⁶ m in their respective F-P vacuum cavities, and then return to the beam splitter (BS).

According to Einstein’s theory of general relativity and Pirani’s theory, when gravitational radiation or gravitational waves asymmetrically sweep over the LIGO detector, the stretching and contracting rates of the X and Y-arms are different, so as to result in the optical-path difference between the two laser beams and generate interference fringes. In this way, LIGO’s photodetector PD can record relevant information about gravitational radiation or gravitational waves.

This is the basic principle of the LIGO detector.

In 1991, Massachusetts Institute of Technology and California Institute of Technology, with support from the National Science Foundation, officially began joint construction of the LIGO detection system. As depicted in Figure 1(b), in order to determine the direction and distance of the gravitational-wave sources and to measure the speed of gravitational waves based on trilateration method, LIGO constructed two base stations: the Hanford station located in Washington State, USA, and the Livingston station located in Louisiana, USA, with a distance of about 3002 km and an optical path of about 10ms.

LIGO was completed at the end of 1999. Perhaps, due to the failure to detect gravitational waves after its completion, LIGO underwent an upgrade from 2005 to 2007, called Advanced LIGO. Afterwards, LIGO developed into an international scientific alliance of detecting gravitational waves, that is, LIGO Scientific Collaboration (LSC). In 2007, the Virgo station built by the European Gravitational Wave Observatory was connected to LIGO’s Hanford and Livingston stations for parallel operation. Gradually, almost all observatories around the world have participated in LSC’s activities of detecting gravitational waves, conducting the so-called all-round multi messenger detection of gravitational waves.

It should be pointed out that LIGO and Pirani’s detection schemes of gravitational waves based on Einstein’s theory of general relativity have theoretical flaws. As clarified by the theory of OR,^1–4 Einstein’s theory of relativity does not represent the objective physical reality, and Einstein’s theory of general relativity does not represent the objective gravitational interaction.

According to the theory of OR, spacetime, whether gravitational or inertial, neither stretches nor bends. Therefore, the X and Y-arms of LIGO detectors never stretch or contract. However, the invasion of matter or matter waves including electromagnetic and gravitational must produce corresponding physical effects. Once matter or matter waves asymmetrically invades LIGO’s F-P vacuum cavities must result in a speed difference and an equivalent optical-path difference between the laser beams in the X and Y-arms, leaving non-strictly speaking or unstable laser interference patterns on LIGO’s photodetector PD, such as amplitude modulated signals, optical beat frequency, and transient superposition phenomena.

In fact, any matter or matter waves invading the F-P vacuum cavities of LIGO detector must cause varying degrees of changes in the speeds of the laser beams in the F-P vacuum cavities. Therefore, LIGO is more like a detector for all matter systems or matter waves, rather than a detector only for gravitational waves.

3.3 LIGO’s detecting targets: Binary black holes

To detect gravitational waves, LIGIO needs gravitational-wave sources as the detecting targets.

According to Newton’s law of universal gravitation, all matter particles or matter systems attract each other. So, any material object, including the sun, earth, moon, an apple, or even a photon, is a source of gravitational radiation or gravitational waves, and can be employed as LIGO’s detecting target.

An apple is of a small mass and cannot compare to a massive celestial body; however, it can get close enough to the LIGO detector. According to the inverse square law of universal gravitation, in theory, if an apple is close enough to the LIGO detector, the gravitational wave radiated by the apple may be sufficient to trigger the LIGO detector. How about a train close enough to be parallel to LIGO’s X-arm? Can the gravitational wave radiated by the train trigger the LIGO detector? Why cannot the gravitational waves radiated by the earth, the closest celestial body to the LIGO detector, trigger the LIGO detector? The moon is the closest celestial body to the earth; the sun is the closest star to the earth. Why can the gravitational waves radiated by the moon and sun be sensed by the earth’s oceans, making waves in the oceans but failing to trigger the LIGO detector?

Of course, LIGO must have conducted extensive calculations to decide LIGO’s detecting targets.

It seems that, from the beginning, LIGO has been targeting binary black-hole systems as its detecting targets, hoping that they can erupt strong enough gravitational waves when they merge.

This story should start with the little green men.²³

LIGO’s physicists believe that detecting gravitational radiation or gravitational waves requires massive celestial bodies as the sources of gravitational waves.

Heaven bless LIGO. The development of radio astronomy has broadened the horizons of mankind. Armed with a radio telescope, in 1967, Bell discovered the first pulsar^23,24: PSR1919+21; in 1974, Hulse and Taylor discovered the first binary pulsar^25,26: PSR1913+16.

Pulsars are considered to be high-speed spinning neutron stars with a material density second only to black holes. A binary pulsar is a binary star system in which a pulsar and a companion star orbit each other. If the companion star is also a pulsar, it is called a double pulsar.

It was soon claimed that,^27–29 according to Einstein’s theory of general relativity, pulsar stars would lose their energy due to gravitational radiation, causing their orbits to spiral approach and the pulse period to gradually shorten. For this reason, Professor Taylor has been observing PSR1913 + 16 for decades.³⁰ It is said that Taylor’s observations are consistent with theoretical predictions, with a difference of only 0.4%.

So, physicists further speculate that binary pulsars will eventually merge, explode violently, and erupt high-energy gravitational waves outward.

However, binary pulsars seem not ideal enough: they are too far away from the earth, and their gravitational-radiation intensity decays according to the inverse square law of distance, which cannot necessarily trigger the LIGO detector. Thus, LIGO had to pray to black holes, transform binary pulsars into binary black holes and even double black holes, and point LIGO’s detecting targets towards the mergers of binary black hole systems.^31,32

The issues worth thinking about are:

3.4 LIGO’s discovering gravitational waves

On Feb. 11, 2016, LIGO officially announced that,¹¹ at 5:51 Eastern Time on Sep. 14, 2015, the LIGO detector detected a gravitational wave for the first time, denoted as GW150914. LIGO is convinced that GW150914 is the product of the merge of a double black hole in deep space that LIGO anticipated.

From GW150914’s triggering the LIGO detector to LIGO’s officially announcing the discovery, LIGO experienced 150 days of silence. So, what was LIGO doing during these 150 days?

Optical telescopes represent optical astronomy; radio telescopes represent radio astronomy. Some physicists believe that the LIGO detector has opened up gravitational wave astronomy.³³ However, as shown in Figure 2, unlike optical astronomy which allows intuitively visual observation with the eye, LIGO detectors are similar to radio telescopes and radio astronomy: half listening, half guessing; half believing and half doubting, seemingly right but in fact wrong.

Figure 2. GW150914: Half Listening and Half Guessing.

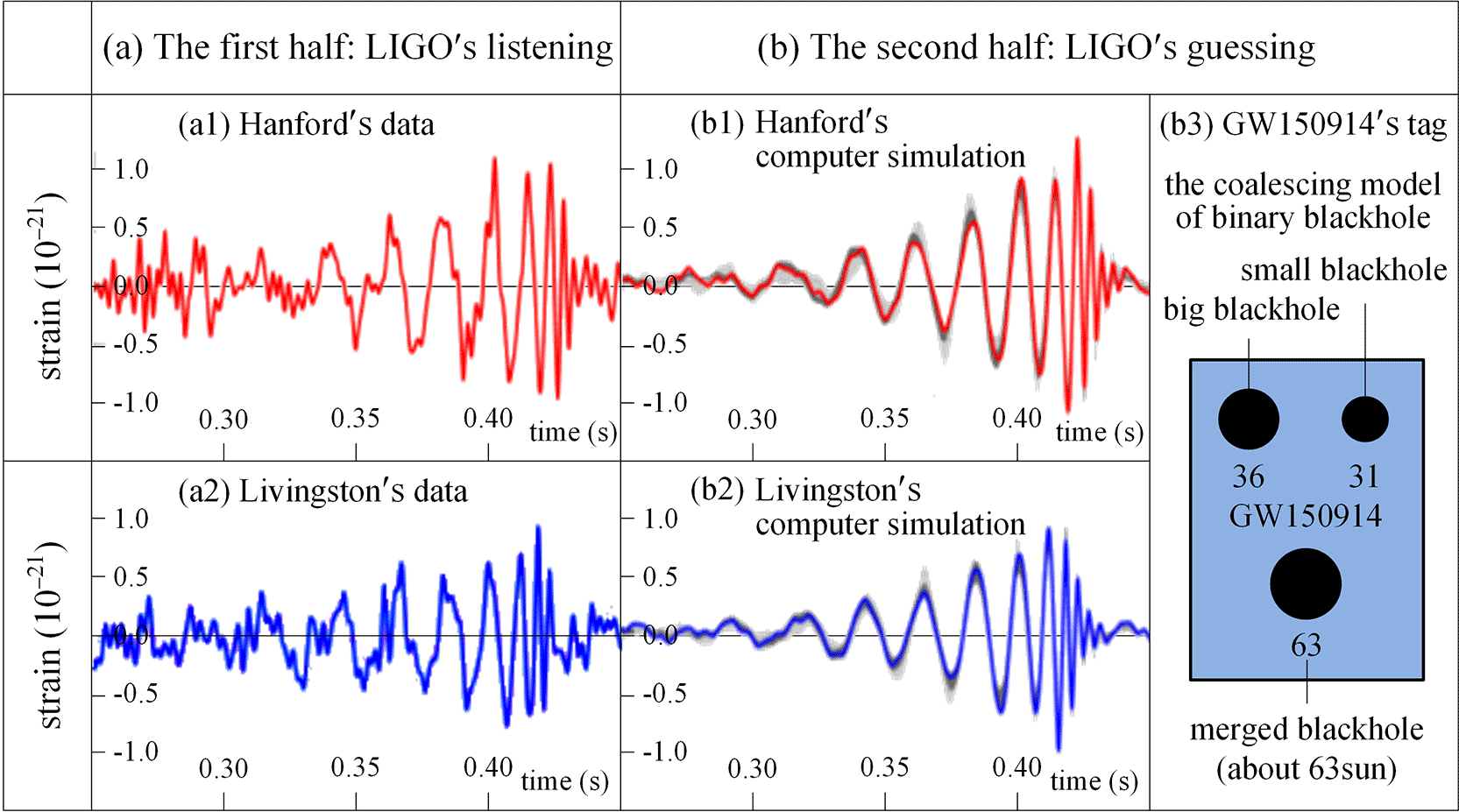
Annotation (a) The First Half: LIGO's Listening. All the objective and real observation data that LIGO can provide: (a1) the observation data of Hanford station; (a2) the observation data of Livingston station.

Annotation (b) The Second Half: LIGO's Guessing. Constructing the dynamics model of binary star systems based on Einstein's theory of relativity, guessing the source of the gravitational wave GW150914 based on LIGO's listening, and matching the suitable star system based on computer simulation: (b1) the computer-simulation data based on Hanford's listening; (b2) the computer-simulation data based on Livingston's listening; (b3) the successfully matched double black hole of GW150914.

LIGO's Evidence: The computer-simulation data matches well with the interference pattern on PD.

As depicted in Figure 2^34,35: Figure 2(a) is LIGO’s Listening; Figure 2(b) is LIGO’s Guessing.

What LIGO does during the 150-day silence period is to guess: What does the interference pattern presented on LIGO’s photodetector PD represent?

It seems certain that LIGO’s Hanford and Livingston based stations did hear a bird chirp on Sep. 14, 2015.^36,37 However, LIGO was not sure what the bird GW150914 was, where it was, and how far away it was from the earth.

There are too many unknowns in the universe for mankind. The interference pattern presented on LIGO’s photodetector PD could have had an infinite number of solutions. However, LIGO has always aimed its detection targets at binary black-hole celestial bodies. Therefore, physicists have constructed the evolutionary model of binary star systems based on Einstein’s theory of relativity, developed numerical relativity, and employed numerical-calculation method and virtual-reality technology to deduce the evolution of binary stars or binary black holes on LIGO’s supercomputers.

It can be imagined that there must be countless binary star or black-hole models stored in LIGO’s supercomputer: just like the example depicted in Figure 2, there is always a model that is suitable for the trigger signal GW150914 or another GWxxxxxx. LIGO can debug and match their binary star or black-hole models based on the observational data or signals of triggering the LIGO detector. Such high-dimensional models naturally have sufficient parameters for debugging. This is very similar to the ringtoss game on street corners: the interference fringes or patterns leaving on the photodetector PD and triggering the LIGO detector are the rings and the binary star or black-hole models are the dolls.

GW150914 shown in Figure 2, as the first so-called gravitational wave detected by LIGO, took 150 days and eventually, was tossed at or matched a binary black-hole model that is located about 13 billion light-years away from the earth, with a primary star of about 36 suns and a secondary star of about 31 suns. The mass of the merged black hole is about 63 suns, and the radiated energy is about 4 suns.

So far, LIGO has announced that it has detected over 500 cases of gravitational waves. LIGO believes that these gravitational waves all originated from the mergers of binary stars or black holes: the vast majority being double black holes, a few binary black holes, a very few binary neutron stars, and one or two uncertain.

The theory of OR has clarified that the energy and mass of matter are independent of each other; Einstein formula E = mc² is only an integral constant of the kinetic-energy integral formula of the observed object m, and is not the objective and real energy of matter (see Chapter 5 of the 1^st volume IOR in Observational Relativity^1–4). Therefore, it is incorrect that LIGO transforms the erupted mass of a binary star or black hole into the erupted energy based on Einstein’s so-called mass-energy relation E = mc², let along that of gravitational waves.

It should be pointed out that the merger of a binary star or black hole must erupt not only energy but also mass, and that the erupted energy can take various forms, including electromagnetic radiation, not necessarily just gravitational waves.

3.5 The speed of LIGO’s So-Called gravitational waves

According to the delayed integral formula (Eq. (15)) and wave equation (Eq. (16)) of Einstein’s metric- perturbation tensor h^~_μν(c) (Eq. (12)), if Einstein’s wave equation were indeed a gravitational-wave equation, then the speed of gravitational radiation or gravitational waves must be the speed of light c.

Calculating or predicting the speed of gravitational waves theoretically is one thing, whereas measuring the speed of gravitational waves through observation and experiment is quite another.

Mankind has invented controllable sources of electromagnetic radiation and mastered the technology of measuring the speed of electromagnetic radiation and light. However, mankind has no controllable source of gravitational radiation, and experimental physicists have no idea how to measure the speed of gravitational radiation or gravitational waves.

LIGO claims to have detected gravitational waves, and the ocean has also done. But neither LIGO nor the ocean can determine the speed of gravitational radiation or gravitational waves.

Originally, LIGO attempted to use trilateration method to determine the speed of gravitational waves. For this purpose, LIGO established Hanford and Livingston base stations. However, due to various factors such as difficulty in locating gravitational wave sources and difficulty in calibrating the clocks of the two base stations, the trilateration method is not effective as expected.

Then, LIGO turned to the so-called Electromagnetic Counterparts of gravitational waves.^38–40 On Aug. 17, 2017, the LIGO and Virgo detectors detected the first merger event of binary neutron star: GW170817. Afterwards, in just 1.7 seconds, the Fermi Gamma-Ray Burst Monitor and the International Gamma Ray Astrophysics Laboratory detected a gamma-ray burst GRB170817A coming from the same celestial region as GW170817.^41,42 In the following weeks, observatories around the world successively reported that they had detected electromagnetic matter or waves with different frequencies or bands sweeping over the earth that appeared to be from the same celestial region as GW170817.

Accordingly, LIGO believes that,⁴² since the gravitational wave GW170817 is throughout the entire journey accompanied by the electromagnetic wave GRB170817A, the speed of gravitational waves must be the speed of light in vacuum.

LIGO selected GW170817 and GRB170817A as samples for calibrating the speed of gravitational waves⁴²: the luminosity distance between the binary neutron star and the earth is D_L = 26 Mpc, approximately 85 million light-years; GW170817 is a gravitational wave with the speed κ; GRB170817A is an electromagnetic wave with the speed v_EM = c. The relative difference between the gravitational-wave speed κ and the electromagnetic-wave speed v_EM is defined as Δv/v_EM ≈ Δt/T, where Δv = κ−v_EM, Δt = T−T_G, T = D/v_EM was the travel time of GRB170817A, and T_G was the travel time of GW170817. If the peak signal of GW170817 and the first gamma photon of GRB170817A departed simultaneously, then Δt ≈ 1.74 ± 0.05s, κ > v_EM, and Δv/v_EM may take the upper-limit value; if GRB170817A departed 10 seconds later than GW170817, then Δt ≈ 1.74−10 = −8.26 s, κ < v_EM, Δv/v_EM may take the lower-limit value.

Thus, the relative difference Δv/v_EM satisfies the following inequality⁴²:

This suggests that the gravitational-wave speed κ is precisely equivalent to the speed of light c.

However, it is worth thinking that, if the speed of gravitational waves were the speed of light, could gravitational waves still escape from black holes, or could black holes still gravitationally interact with the external world?

In 2017, Weiss, Barish and Thorne, the main members of the LIGO team, were awarded the Nobel Prize in Physics for their contributions to gravitational-wave detection. At this point, LIGO seemed to have achieved great success, and the sacred and inviolable status of Einstein’s relativity theory seemed to have further been consolidated.

So, what exactly did the LIGO detector detect? Is the speed of gravitational waves really the speed of light? Such issues will be discussed in Sec. 7 and Sec. 8.

4.1 The observation agents of OR: Information waves and informons

Observation is to sense or perceive the objectively physical world and obtain the information about observed objects. The information of observed objects must be transmitted by a certain observation medium at a certain speed from observed objects to observers, so that observers can perceive observed objects.

Observation Agent is the most important concept in theory of OR, which the concepts of Information Wave and Informon are related to.

Železnikar ever employed Informon to refer to an information entity and analogized it with an electron.⁴³

In theory, all forms of matter motion, not just light or photons, can serve as observation media to transmit observed information for observers; in particular, the speed η of the information wave of M(η) or OA(η) transmitting observed information can be any value: 0 < η < ∞; η→∞.

The ear is the human acoustic agent OA(v_S) (η = v_S ≈ 340 m/s); the eye is the human optical agent OA(c) (η = c). In the theory of OR, OA(η) (0 < η < ∞; η→∞) is referred to as the General Observation Agent.

In the objectively physical world, the speeds of all matter-motion forms are finite or limited. Therefore, all observation agents that mankind can employ must have the observational locality (∀OA(η) η < ∞): its speed η of information wave is limited. In other words, mankind’s perception and cognition of the objective world do not represent the objectively physical reality.

All theoretical systems or spacetime models of human being’s physics, including Galilean doctrine, Newtonian mechanics, and Einstein’s theory of relativity, have the specific observational agents of their own.

4.2 Newton’s OA_∞ and Einstein’s OA(c)

Newton and Einstein did not realize that their theories were linked to specific observation agents.

The theory of OR has clarified that Einstein’s theory of relativity, both the special and the general, is the theory of optical observation with the observation agent OA(c), which has the observational locality (η = c < ∞). Therefore, Einstein’s theory of relativity only presents us with an optical image of the physical world, and does not represent the objectively physical world.

Galilean doctrine and Newtonian mechanics are the theories of idealized observation with the idealized observation agent OA_∞; the speed η of the information wave of OA_∞ is idealized to infinity: η→∞, and therefore, OA_∞ has no the observational locality. So, the Galilean transformation and the Galilean law of speed addition, as well as, Newton’s inertial mechanics and Newton’s theory of universal gravitation, present us with the true portrayal of the objectively physical world.

As clarified in OR Serial Report 1: as the theory of the general observation agent OA(η) (0 < η < ∞; η→∞), the theory of OR has generalized and unified Newtonian mechanics and Einstein relativity theory. As η→c, the OR inertial-spacetime transformation strictly converges to the Lorentz transformation, the theory of IOR is strictly reduced to Einstein’s theory of special relativity, and the theory of GOR is strictly reduced to Einstein’s theory of general relativity. As η→∞, the OR inertial spacetime transformation strictly converges to the Galilean transformation, the theory of IOR is strictly reduced to Newton’s inertial mechanics, and the theory of GOR is strictly reduced to Newton’s theory of universal gravitation. So, the theory of OR is isomorphically consistent to both Newtonian mechanics and Einstein relativity theory. This, from one aspect, confirms the logical consistency and theoretical correctness of the theory of OR.

In this way, readers must be able to understand that the general observation agent OA(η) (0 < η < ∞; η→∞) plays an extremely important role in the theory of OR. The core of the observation agent OA(η) is the observation medium M(η), or the information wave transmitting observed information at a certain speed η that is an important physical quantity: the information-wave speed η of OA(η).

So, do the theoretical systems of human being’s physics, including Newtonian mechanics and Einstein relativity theory, really have information waves that transmit observed information in observed spacetime?

4.3 IOR information waves: To transmit inertial-spacetime information

The concept of Information Wave originated from the inertial theory of OR, i.e., the theory of IOR, which is that of the general observational agent OA(η) (0 < η < ∞; η→∞).

Based on the definition of OR time, the IOR relativistic factor Γ(η) = dt/dτ of the general observation agent OA(η) in inertial spacetime has obtained two forms:

This reflects the observational wave-particle duality of matter motion in inertial spacetime.

According to the theory of IOR, in the sense of wave-particle duality, as a matter particle, the observed object P in inertial spacetime observed by OA(η) should have its kinetic energy K(η) = E(η)−E_o(η) = (m(η)−m_o)η² and momentum p(η) = m(η)v; as a matter wave, the observed object P should have its phase speed v_p and group speed v_g, in addition to its particle speed v as a matter particle.

Combining the particle-like form Γ = m(η)/m_o with the wave-like form Γ = f(η)/f_o of the IOR relativistic factor Γ(η) = dt/dτ, the theory of IOR has derived the relations of the matter waves observed by OA(η) (see Chapter 6 of the 1^st volume IOR in Observational Relativity^1–4):

Equation (18) suggests that the IOR matter waves, the so-called general de Broglie waves, depend on observation, depend on the observation agent OA(η) (0 < η < ∞), depend on the speed η of the information wave of OA(η), and therefore, they are not the objectively existing matter waves, but the information wave of OA(η), the speed of which should naturally be the speed η of the information wave of OA(η). Indeed, according to the IOR matter-wave relations (Eq. (18)), if an informon of OA(η) serves as the observed object P, then the particle speed of P as a particle is v = η, the group speed v_g of P as a wave is v_g = v = η, and the phase speed v_p of P as a wave is v_p = η²/v_g = η.

It is important to point out that E(η), p(η) and v in the IOR relations of general de Broglie waves do not represent P itself, but the observed information loaded or carried by the information wave (a Carrier Wave, CW) of OA(η), that is, the information about the energy, momentum, and speed of the observed object P.

In particular, if η→c, then Eq. (18) is strictly reduced to the relations of de Broglie matter wave:

In this way, the theory of IOR has revealed the essence of de Broglie wave: de Broglie’s matter waves are not the inherent or objectively existing matter waves, but a special case of the IOR information waves, that is, the information wave of the optical agent OA(c) in inertial spacetime.

The IOR matter-wave relations (Eq. (18)) proves that there are indeed information waves in the inertial spacetime of IOR that transmit observed information.

4.4 GOR information waves: To transmit gravitational-spacetime information

The gravitational theory of OR, i.e., the theory of GOR, which is also that of the general observational agent OA(η) (0 < η < ∞; η→∞). Like in the inertial spacetime of IOR, there are also information waves in the gravitational spacetime of GOR that transmit observed information.

Based on his logic of weak-field approximation, Einstein derived a wave equation from his gravitational-field equation (Eq. (16)), in which the wave travels at the speed c of light in vacuum. Since the wave function h^~_μν is characterized by the Newtonian gravitational potential χ and the light speed c, Einstein believed that the metric-perturbation tensor h^~_μν represents gravitational waves, and that the speed of gravitational waves is equivalent to the speed of light c.

This is Einstein’s prediction of gravitational waves.

However, the theory of OR has discovered that, just as de Broglie wave is not the objectively existing matter wave but the information wave of OA(η) transmitting observed information in the inertial spacetime of IOR, Einstein’s wave is not the objectively existing gravitational wave but the information wave of OA(η) transmitting observed information in the gravitational spacetime of GOR, the physical quantity χ in Einstein’s wave function h^~_μν(c) does not represent the gravitational wave radiated by a matter system, but the information about gravitational spacetime loaded and carried by the information wave of the optical agent OA(c). So, the wave speed c in Einstein’s wave function h^~_μν(c) is not the speed of gravitational radiation or gravitational waves, but the speed of the information wave of the optical agent OA(c).

This article (OR serial report 3) will analogize the logic of Einstein’s general relativity and the definition of Einstein’s metric-perturbation tensor h^~_μν(c), derive the delayed solution and wave equation of the GOR metric-perturbation tensor h^~_μν(η), and reveal the quiddity of Einstein’s prediction of gravitational waves.

5.1 GOR gravitational scene and gravitational-field equation

Just as Einstein field equation represent Einstein’s theory of general relativity, the GOR gravitational-field equation represents the theory of GOR.

The gravitational scene (M, m) (M >> m) of GOR is the same as Einstein’s gravitational scene (M, m) (M >> m), similar to Newton’s gravitational scene, also a static spherically-symmetric gravitational spacetime, which conforms to the interpretation for Newton’s law of universal gravitation with Poisson equation.

In the scene of static spherically-symmetric gravitational spacetime, based on the three principles of GOR: (1) the principle of GOR equivalence, (2) the principle of GOR covariance, and (3) the principle of the invariance of information-wave speeds, analogizing the logic of Einstein general relativity, the theory of GOR has deduced the GOR gravitational-field and gravitational-motion equations (see Chapter 14 of the 2^nd volume GOR in Observational Relativity^1–4).

The GOR Gravitational-Field Equation:

The GOR Gravitational-Motion Equation:

5.2 GOR linearization way: Idealized convergence

After the establishment of the GOR gravitational-field equation (Eq. (20)) in form, the important issue the theory of OR faces is how to calibrate the gravitational coefficient κ_GOR in it.

In order to calibrate the gravitational coefficient κ_GOR, just like what Einstein did, the theory of GOR also needs to correspond the GOR field equation (Eq. (20)) with Newton’s law of universal gravitation in the Poisson-equation form (Eq. (2)).

There is no direct corresponding relationship between Einstein field equation and Poisson equation. Therefore, Einstein had to resort to the logical way of weak-field approximation.

However, unlike Einstein’s theory of general relativity, as a gravitational theory of the general observation agent OA(η) (0 < η < ∞; η→∞), the GOR field equation not only can strictly correspond to Einstein field equation as η→c, but also can strictly correspond to Newton’s field equation (i.e., the Poisson-equation form of Newton’s law of universal gravitation) as η→∞.

The theory of GOR has proven an important theorem: The Theorem of Cartesian Spacetime: h _μν ( η )→0 as η →∞.^1–4

According to the theorem of Cartesian spacetime, in the case of the idealized agent OA_∞ (η→∞), the curved metric h_μν(η) of gravitational spacetime is zero. This suggests that the objective and real gravitational spacetime is flat, not curved. The so-called spacetime curvature is only a sort of observational effect and apparent phenomenon, caused by the observational locality (η < ∞) of the observation agent OA(η).

Therefore, the correspondence between the GOR gravitational-field equation and Newton’s law of universal gravitation or Poisson equation does not require the logical way of weak-field approximation, but only the logical way of idealized convergence.

The GOR Idealized Convergence^1–4: If the information-wave speed η of the observation agent OA(η) is sufficiently fast, then the gravitational spacetime observed by OA(η) tends to be flat, and it holds true that

It can be proved that,^1–4 based on the GOR logic of idealized convergence, the five conditions in Einstein’s logic of weak-field approximation that are listed in Sec. 2.2 all hold true.

In this way, the correspondence between the GOR field equation and Newton’s law of universal gravitation or Poisson equation, as well as, the calibration of the GOR gravitational coefficient κ_GOR, are no longer in approximate sense, but in the strict sense of logic.

5.3 The idealized linearization of GOR gravitational-motion equation

The GOR gravitational-motion equation describes the motion trajectory of the observed object P in the 4d curved spacetime of gravitational field, a geodesic line, which is connected to the connection Γ^μ_αβ(η) observed by OA(η), and the connection Γ^μ_αβ(η) is connected to the metric g_μν(η) observed by OA(η).

Under the condition of GOR idealized convergence: η is large enough or η→∞, the GOR motion equation (Eq. 21) is strictly reduced to Newton’s law of universal gravitation (Eq. (1)),^1–4 the curved 4d geodesic line observed by OA(η) is strictly linearized and split into 1d time and the 3d straight line in Euclidean space:

By comparing Newton’s law of universal gravitation (Eq. (1)) and the straight line in the GOR motion equation (Eq. (23)) of idealized linearization, it can be obtained that

In this way, the curved metric 00-element h₀₀(η) in the gravitational field observed by OA(η) is linked to the Newtonian gravitational potential χ: h₀₀(η)~χ.

5.4 The idealized linearization of GOR gravitational-field equation

The GOR gravitational-field equation describes the relationship between the curvature R_μν(η) of 4d gravitational spacetime observed by OA(η) and the energy-momentum tensor T_μν(η) of matter systems.

Under the condition of GOR idealized convergence: η is large enough or η→∞, the GOR field equation (Eq. 20) is strictly reduced to Newton’s law of universal gravitation in the Poisson-equation forms (Eq. (2)),^1–4 and strictly linearized as

Thus, the GOR motion equation (Eq. (20)) reduces to

In this way, the curved metric 00-element h₀₀(η) in the gravitational field observed by OA(η) is linked to the gravitational coefficient κ_GOR in the GOR field equation (Eq. (20)): h₀₀(η)~κ_GOR.

5.5 The idealized calibration of the GOR gravitational coefficient κ_GOR

Based on the GOR logical way of idealized convergence, under the condition of idealized convergence, the GOR field and motion equations form the strict corresponding relationship with Newton’s law of universal gravitation: the GOR gravitational-motion equation under OA(η) strictly corresponds to Newton’s law of universal gravitation of OA_∞ in the form of distance inverse-square law; the gravitational-field equation under OA(η) strictly corresponds to Newton’s law of universal gravitation of OA_∞ in the form of Poisson equation.

Substituting h_μν(η) in Eq. (24) into Eq. (26), it can be obtained that

By comparing Eq. (27) with the Poisson-equation form of Newton’s universal-gravitation law (Eq. (2)), the gravitational coefficient κ_GOR in the GOR field equation can be calibrated as

The calibration of gravitational coefficient κ_GOR in the GOR field equation represents the establishment of GOR field equation or even the theory of GOR.

6.1 The delayed solution of the GOR field equation

Following Einstein’s logic (see Sec. 2.4), the left-hand end of the GOR field equation (Eq. (20)) can be defined or labeled as the general Einstein tensor G_μν(η). Then, the GOR field equation can be succinctly written as

Based on the GOR logic way of idealized convergence, under the condition of GOR idealized convergence: η is large enough or η→∞, it holds true for g_μν(η) = η_μν,, R(η) = □h(η)/2, and R_μν(η) = □h_μν(η)/2; thus, the tensor of metric perturbation observed by the general observation agent OA(η) (0 < η < ∞; η→∞) can be defined as

According to Eqs. (24) and (30), the tensor h^~_μν of metric perturbation observed by OA(η) is characterized by the information-wave speed η and Newtonian gravitational potential χ: h^~_μν = h^~_μν(χ,η).

Thus, under the condition of GOR idealized convergence: η is large enough or η→∞, the general Einstein tensor G_μν(η) can be defined by the tensor h^~_μν(χ, η) of metric perturbation observed by OA(η), and the GOR gravitational-field equation (Eq. (29)) can be expressed by h^~_μν(χ, η) as

The GOR linearized gravitational-field equation (Eq. (31)) that satisfies the coordinate condition of Eq. (32) has the following solution:

This is the delayed integral formula of GOR gravitation field equation.

Naturally, the t−d/η in the delayed solution (Eq. (33)) of GOR field equation represents a delay in the time of a certain physical process. However, it is not a delay in energy, but a delay in information; it is not a delay in gravitational radiation or gravitational interaction, but a delay in the transmission of observed information, that is, the delay in the transmission of the information wave of the observation agent OA(η).

A detailed interpretation of the delayed solution (Eq. (33)) of the GOR field equation is left in Sec. 7.

6.2 GOR wave equation

Based on the GOR logic way of idealized convergence, under the condition of GOR idealized convergence: η is large enough or η→∞, the energy-momentum tensor T_μν(η) as the gravitational source M tends to zero: T_μν(η) →0, and the GOR linearized gravitational-field equation (Eq. (31)) is reduced to the vacuum form of field equation: $\square$ h_μν(η)→0. According to the definitions of the general d’ Alembert operator “□” and Laplace operator “∇²” of the general observation agent OA OA(η) (see Chapter 5 of the 1^st volume IOR in Observational Relativity^1–4), it holds true that

This is the GOR wave equation.

Equation (34) is exactly the mathematical form of waves: a typical wave equation, where the tensor of metric perturbation tensor h^~_μν(χ, η) is the wave function, and the wave speed η is exactly the speed of the information wave of OA(η), that is, the speed of the observation medium M(η) transmitting observed information, depending on the observation agent OA(η).

Obviously, the wave function h^~_μν(χ, η) in the GOR wave equation cannot be interpreted as a gravitational wave as Einstein did, but can only be interpreted as the information wave of the general observation agent OA(η) (0<η<∞;η→∞) transmitting the observed information in gravitational spacetime.

Perhaps, you have now begun to understand the true meaning of Einstein’s wave equation (Eq. (16)).

The detailed interpretation for the GOR wave equation is left in Sec. 7.

7.1 GOR delayed integral formula: Is it the delay of energy or information?

The delayed integral formula (Eq. (33)) indicates that it takes time for information to cross space.

Locality, or the principle of locality, plays an important role in modern physics. However, the issue of locality that physicists are concerned with seems to only involve the locality of energy or matter interactions. Newton and Einstein both believed that there is no action at a distance in the universe. Of course, this does not mean that the transmission speed of energy or information cannot exceed the speed of light.

Physicists, including Newton and Einstein, seem to be indifferent to the locality of information and its impact on the theories or spacetime models of physics.

In fact, the principle of locality suggests that it takes time for both energy and information to cross space. The physical world has the locality not only in the transmission of energy but also in the transmission of information.

7.1.1 The principle of observational locality and the delayed information waves

In order to clarify the locality of observed information in transmission in the physical world, the theory of OR specifically expresses the observational locality as a principle.

The Principle of Observational Locality (POL)^1–5: According to the principle of locality, for any realistic observation agent OA(η), the speed η of its information wave must be finite or limited -- it takes time for the information wave of OA(η) to cross space.

The principle of observational locality indicates that all objectively existing observation agents must have the observational locality: ∀OA(η) η<∞.

Mankind’s perception or observation of the objective world is restricted by the observational locality: as a bird flies across the sky, while you hear its chirping it is no longer in the place where it was chirping, when you see its image it is no longer in the place where it was flying.

The delay t−d/η in the delayed solution of the GOR field equation (Eq. (33)) must represent the delay of some physical process in gravitational spacetime: either the delay of energy or the delay of information.

According to Eq. (33), the time delay t−d/η depends on observation, on the observation agent OA(η), and on the speed η of the information wave of OA(η), that is, the speed at which OA(η) transmits the observed information. Different observation agents may have different information-wave speeds, and therefore, may have different delays of observed information.

So, the time delay t−d/η in the delayed solution (Eq. 33) of GOR field equation must be the delay of the information observed by the observation agent OA(η) (η < ∞), rather than the delay of the energy or gravitational interaction of gravitational source M. The energy-momentum tensor T_μν(η) in the delayed integral formation (Eq. (33)) of GOR field equation is not the gravitational radiation itself, but rather the information about the gravitational spacetime observed by OA(η), loaded and carried by the information wave (Carrier Wave) of OA(η).

The delayed integral formula (Eq. (33)) of GOR field equation reflects the observational locality of the observation agent OA(η), which confirms the principle of observational locality.

7.1.2 Einstein’s Information wave: The speed is naturally the speed of light

Einstein’s theory of relativity is that of optical observation with the optical observation agent OA(c), whose information wave is naturally light or an electromagnetic wave, and whose information-wave speed is naturally the speed of light: η = c. The speed of light is finite or limited: c < ∞, and therefore, the optical agent OA(c) has the observational locality.

The time delay t−d/c in the delayed integral formula of Einstein field equation reflects the observational locality (c<∞) of the optical agent OA(c).

In fact, the delayed solution of the Einstein field equation (Eq. (15)) is just a special case of the delayed solution of the GOR field equation (Eq. (33)): if η→c, then

Actually, the delayed solution of Einstein field equation supports the theory of GOR, which indicates that Einstein’s theory of general relativity is indeed that of optical observation with the observation agent OA(c), and that there is indeed the information wave in the gravitational spacetime observed by OA(c) that transmits observed information at the speed of light c.

It is thus clear that the time delay t−d/c in the delayed integral formula of Einstein field equation is not the time delay of gravitational radiation from the gravitational source M, but the time delay of the information wave of the optical agent OA(c), and in particular, the physical quantity c in the time delay t- d/c does not mean the speed of gravitational radiation or gravitational waves is the speed of light, but the speed of the information wave (i.e., light or an electromagnetic wave) of OA(c).

7.1.3 Newton’s information wave: The speed is idealized as infinite

Newton’s theory of universal gravitation is that of idealized observation with the idealized observation agent OA_∞, whose information-wave speed is idealized as infinite: η→∞. Therefore, the idealized agent OA_∞ has no the observational locality: if η→∞, then

This is consistent with OR’s interpretations for Newtonian mechanics: Newtonian mechanics is indeed the theory of idealized observation, with no the observational locality, with no the time delay of observed information, representing the objective and real physical world.

7.2 GOR wave equation: Is it a gravitational wave or an information wave?

The GOR wave equation (Eq. (34)) indicates that

7.2.1 Interpreting the GOR wave equation

The wave function h^~_μν = h^~_μν(χ,η) in the GOR wave equation (Eq. (34)) has two important characteristic physical quantities: the Newtonian gravitational potential χ; the information-wave speed η of the observation agent OA(η). Although it involves the Newtonian gravitational potential χ, the wave function h^~_μν(χ, η) cannot be interpreted as a gravitational wave. In fact, the physical quantity χ in the GOR wave equation is not the gravitational potential radiated by the gravitational source M, but the information about gravitational spacetime loaded and carried by the information wave h^~_μν(χ, η) of the observation agent OA(η).

According to Eq. (34), for the wave h^~_μν(χ, η) in the GOR wave equation, the wave speed η is the information-wave speed of the general observation agent OA(η) (0 < η < ∞; η→∞): different observation agents have different information-wave speeds.

Therefore, the wave function h^~_μν(χ, η) in the GOR wave equation (Eq. (34)) is not the gravitational wave radiated by the gravitational source M, but the information wave of the general observation OA(η) (0 < η < ∞; η→∞) transmitting observed information.

So, the GOR wave equation (Eq. (34)) must be the GOR Information-Wave Equation.

Like all the relations in the theory of OR, the GOR information-wave equation (Eq. (34)) not only generalizes Einstein’s wave equation (Eq. (16)) but also generalizes Newton’s wave equation.

Einstein’s wave equation (Eq. (16)) is actually a vacuum form of the weak-field approximation of Einstein field equation. If η→c, then the GOR information-wave equation strictly converges to Einstein’s wave equation:

It is thus clear that the Einstein’s wave equation is just a special case of the GOR information-wave equation (Eq. (34), that is, the information-wave equation of the optical agent OA(c).

The Newton wave equation is in fact the vacuum form of Poisson equation of Newton’s universal-gravitation law of: ∇²χ = 0, that is, the Laplace equation. If η→∞, then the GOR information-wave equation strictly converges to Newton’s wave equation:

So, no matter the wave of Einstein’s field equation or the wave of Newton’s field equation is only a special case of the GOR information waves.

7.2.2 A historic mistake

The GOR information-wave equation indicates that Einstein’s prediction of gravitational waves was an error.

As stated earlier, the theory of OR does not doubt the objective existence of gravitational waves. In the theory of OR, Gravitational Wave and Gravitational Radiation are the same or equivalent concept.

However, as the theory of OR has already clarified, whether it is the GOR wave function h^~_μν(χ, η) or Einstein’s wave function h^~_μν(χ, c), the Newtonian gravitational potential χ in it is not the gravitational potential radiated by the gravitational source M, but the information about gravitational spacetime, loaded and carried by the information wave of a certain observation agent OA(η) (0 < η < ∞; η→∞), and therefore, the GOR wave function h^~_μν(χ, η), including Einstein’s wave function h^~_μν(χ, c), is not the gravitational wave radiated by the gravitational source M, but the information wave of OA(η) such as the optical agent OA(c). Einstein’s wave h^~_μν(χ, c) is exactly the information wave of the optical agent OA(c).

In particular, in the GOR wave function h^~_μν(χ, η) and Einstein’s wave function h^~_μν(χ, c), both the physical quantities η and c do not represent the speed of gravitational waves, but the speeds of information waves of OA(η) and OA(c), respectively.

The theory of OR has clarified (see Chapter 12 of the 2^nd volume GOR in Observational Relativity^1–4): In fact, Newton’s theory of universal gravitation, Einstein’s theory of general relativity, and even the theory of GOR, all connote an important idealized assumption: gravitation interaction is a sort of action at a distance. They all do not have any prior information about the speed of gravitational radiation or gravitational waves. Therefore, logically speaking, Einstein was unable to calculate or predict the speed of gravitational radiation or gravitational waves based on his theory of general relativity.

It is worth noting that, in his theory of general relativity, in order to calibrate the gravitational coefficient κ_E of his field equation, Einstein had to correspond his field equation with the Poisson-equation form of Newton’s law of universal gravitation. This suggests that Einstein’s theory of general relativity, like Newton’s theory of universal gravitation, also implies the assumption that gravitational interaction is a sort of action at a distance.

As a form of objective matter interaction, the speed of gravitational radiation or gravitational waves must depend neither on the speeds of information waves of observation agents, nor on the strength of gravitation.

As the information wave h^~_μν(χ, η) of the general observation agent OA(η) (0 < η < ∞; η→∞), it transmits observed information at the speed η of the information-wave of OA(η), which is consistent with the conclusions of the GOR delayed integral formula (Eq. (33)) and the GOR wave equation (Eq. (34)). In particular, when the observation agent OA(η) is the optical agent OA(c) (η = c), the speed of the information wave of OA(c) is naturally the speed of light c, which is consistent with the conclusions of Einstein’s delayed integral formula (Eq. (15)) and Einstein’s wave equation (Eq. (16)).

In the theory of GOR, the wave function h^~_μν(χ, η) in the GOR information-wave equation (Eq. (34)) is in fact the information wave of the general observation agent OA(η) (0 < η < ∞; η→∞), a Carrier Wave that loads and carries the information (χ) of gravitational interaction, is modulated by the Newtonian gravitational potential χ, and transmits the observed information about gravitational spacetime at the speed η of the information wave of OA(η).

The GOR information-wave equation (Eq. (34)) suggests that there exists a wave in the gravitational spacetime observed by a certain observation agent OA(η): h^~_μν(χ, η), that is, the information wave of OA(η) transmitting observed information at the information-wave speed η of OA(η). Naturally, different observation agents have different information waves with different speeds, which may not necessarily be light with the speed of light. Einstein’s wave equation (Eq. (16)) is just a special case of the GOR information-wave equation (Eq. (34)), that is, the case of the optical agent OA(c).

It is thus clear that, as a special case of the GOR information-wave equation (Eq. (34)), Einstein’s so-called gravitational wave h^~_μν(χ, c) predicted based on the wave equation (Eq. (16)) is not a gravitational wave radiated by the gravitational source M, but the information wave of the optical agent OA(c), that is, light or an electromagnetic wave with its inherent speed c.

Einstein mistakenly through that the information wave of the optical agent OA(c) was a gravitational wave, which led Einstein to the wrong conclusion that the speed of gravitational waves is equivalent to the speed of light.

This is the quiddity of Einstein’s so-called prediction of gravitational waves.

8.1 Reinterpreting the principle of LIGO detector

The theory of OR has clarified that, regardless of matter motion or distribution in spacetime, time never dilates, space never stretch or contract, and spacetime never bend. Thus, the principles and schemes of LIGO detecting gravitational waves based on Einstein’s theory of general relativity⁸ and Pirani’s theory of spatial stretching and contracting¹⁸ have lost their theoretical bases.

So, the principle of LIGO detector needs to be reinterpreted as follows.

The principle of LIGO Detector: Although spacetime is never curved, time never dilates, and space never stretch or contract, the LIGO detector with the laser interferometer can detect the speed perturbation of laser in LIGO’s X and Y-arms, so that it can detect whether there is matter or matter waves, including electromagnetic matter and gravitational waves, asymmetrically invading the F-P vacuum cavities of the X and Y-arms.

This suggests that it is not because gravitational waves cause the X and Y-arms to stretch or contract but because matter or matter waves asymmetrically invade the F-P vacuum cavities and asymmetrically change the speeds of laser in the X and Y-arms that the LIGO detector is triggered.

As stated in Sec. 3.2, LIGO is in fact a detector of all things: once matter or a matter wave disturbs LIGO’s X and Y-arms and invades the F-P vacuum cavities, it must change the speeds of laser in the F-P cavities. Different matter waves, different matter densities, different moving speeds and directions, must cause different degrees of changes in the speeds of laser. If matter or a matter wave asymmetrically disturbs LIGO’s X and Y-arms of and invades the F-P vacuum cavities, then it must cause the speed of laser in the X-arm to be different from that in the Y-arm. Therefore, the two laser beams must have an equivalent optical-path difference, interfere with each other, and trigger the LIGO detector.

Consider an extreme example: Supposing the X-arm was filled with water, then the laser speed in the F-P cavity of X-arm would no longer be the speed c = 3×10⁸ m/s of light in vacuum, but the speed v = 2.25×10⁸ m/s of light in water. Thus, the two laser beams in the X and Y-arms would have an equivalent optical-path difference due to their different speeds and interfere with each other, so that the LIGO detector would be triggered.

Of course, LIGO will never allow water to invade LIGO’s F-P vacuum cavities.

So, can electromagnetic matter or electromagnetic waves, for example, the gamma-ray burst GRB170817A, invade LIGO’s F-P vacuum cavities?

There are many doubts in LIGO’s detection of gravitational waves.

8.2 LIGO doubt 1: On the mass of binary black holes and the energy of gravitational waves

As stated in Sec. 3.3, LIGO has been targeting binary black holes from the beginning, hoping that their merging will erupt gravitational waves with enormous energy. LIGO believes that only if a massive binary black-hole system merges can it erupt gravitational waves with enough energy to trigger the LIGO detector.

So, every signal that triggers the LIGO detector is labeled as the name of Gravitational Wave by LIGO and must be matched with a massive binary star or black hole. However, the binary black holes and their mergers are just LIGO’s conjecture and imagination, having theoretical flaws and lacking empirical basis.

As stated in Sec. 3.4, there are too many unknowns in nature for mankind; every signal that triggers the LIGO detector must have an infinite number of possible solutions. However, LIGO places all its hopes on binary black holes. As depicted in Figure 2, with computer simulation and virtual reality, by debugging the model with high-dimensional parameters, every signal or chirp heard by the LIGO detector can always match a binary star or black-hole model in LIGO’s supercomputer, and the probability of successful matching a binary star model is much higher than that of the ringtoss game on street corners.

Taking GW150914 as an example (see Figure 2): According to LIGO’s computer simulation, GW150914 originated from a merger event of a binary black-hole system. The primary-star mass is about 36 suns, the secondary-star mass about 31 suns, and the merged black hole about 63 suns, losing mass about 4 suns and radiating energy about 4 suns. Here, LIGO’s calculation of mass and energy must be based on the Einstein mass-energy relation E=mc², which transforms the losing mass into radiating energy in the form of gravitational waves.

The theory of OR has clarified (see Chapter 5 of the 1^st volume IOR in Observational Relativity^1–4): Mass and energy are independent of each other -- mass cannot be transformed into energy. The E in Einstein formula E=mc² is not the objectively real energy of matter. Both LIGO’s binary black-hole models based on Einstein’s theory of relativity and LIGO’s gravitational-wave energy calculated based on Einstein formula E=mc² cannot represent the objectively physical reality.

Even if binary black-hole systems really exist and eventually they will merge, their mass cannot be transformed into energy. The energy they erupt is either the energy of protons and neutrons originally confined within the atomic nucleus, like nuclear explosions, or the energy of quarks originally confined within protons or neutrons.

It can be imagined that, if a binary star system merges, it must erupt matter with massive mass and enormous energy outward, rather than only energy. It may possibly lead to the formation of new celestial bodies and even a new solar system, rather than only gravitational waves.

Therefore, even if the binary black-hole systems that LIGO expects do exist, the gravitational waves they can contribute to LIGO are also extremely limited.

8.3 LIGO doubt 2: On the distance of binary black holes and the speed of gravitational waves

In fact, whether LIGO can detect gravitational radiation or gravitational waves largely depends on the distance between the gravitational source and the LIGO detector. A matter object, even if its mass is very small, may possibly trigger the LIGO detector if it can disturb at close quarters and invade LIGO’s F-P vacuum cavities.

In LIGO’s binary black-hole models built on Einstein’s theory of relativity, the distance d between a binary black hole and the earth must be one of the most important model parameters in addition to the mass M and energy E of the binary black hole.

But what does LIGO rely on to determine the distance d of a binary black-hole system?

The distances in LIGO’s binary black-hole models are measured in light-years. So, why does not LIGO measure them in gravitational-wave years?

This involves two issues:

Take GW150914 as an example. LIGO determined that GW150914 is a gravitational wave originated from a binary black-hole merger about 1.3 billion light-years away from the earth. If the speed κ of gravitational waves is the speed c of light, then it needs to take 1.3 billion years for GW150914 to travel in the universe to reach the earth. However, according to Laplace’s calculation⁴⁴: κ>7× 10⁶c, it needs to take 186 years for GW150914 to reach the earth; according to Flandern’s calculation⁴⁵: κ=2×10¹⁰c, it only needs to take 24 days for GW150914 to reach the earth. If so, the event of GW150914’s binary black-hole merger should occur on Aug. 21, 2015, rather than 1.3 billion years ago.

Actually, the key issue in verifying Einstein’s prediction of gravitational waves is whether the speed of gravitational waves is equivalent to the speed of light predicted by Einstein, rather than whether gravitational waves exist objectively. The rise and fall of tides in the earth’s oceans have already verified the objective existence of gravity and gravitational radiation.

LIGO should have measured the speed of gravitational waves by physical experiments in a strictly empirical sense, just as mankind ever measured the speed of light, to verify Einstein’s assertion that the speed κ of gravitational waves is equivalent to the speed c of light, so as to verify Einstein’s prediction of gravitational waves. However, the LIGO detector does not have the function to measure the speed of gravitational radiation or gravitational waves. On the contrary, based on Einstein’s prediction of gravitational waves, LIGO directly has set the gravitational-wave speed κ as the light speed c in its computer models. LIGO’s mission seems not to verify Einstein’s prediction of gravitational waves, but to verify the existence of binary black-hole systems in the universe based on Einstein’s theory of relativity and prediction of gravitational waves.

As repeatedly emphasized by the theory of OR, Einstein’s theory of relativity is only an optical image of the objectively physical world, not the objectively physical reality. In this way, LIGO can neither verify the objective existence of binary black-hole systems, nor verify Einstein’s prediction of gravitational waves.

8.4 LIGO doubt 3: On the trigger conditions of the LIGO detector

As stated in 8.1, LIGO is a detector of all things: once a matter object or matter wave invades the F-P vacuum cavities of LIGO, it may trigger the LIGO detector.

Then whatever invaded the F-P cavities of LIGO’s laser interferometer and triggered the LIGO detector?

There are two possible scenarios:

Anyway, the matter density of electromagnetic waves must be much higher than that of gravitational waves.

Therefore, if electromagnetic waves can invade LIGO’s F-P vacuum cavities, then it must be the electromagnetic waves that triggered the LIGO detector. If electromagnetic waves cannot penetrate LIGO’s F-P vacuum cavities, then gravitational waves would become the second option for triggering the LIGO detector.

According to Newton’s law of universal gravitation, all matter systems are attracted to each other.

Thus, all matter objects, including electromagnetic matter and binary black holes, have their own gravitational fields and radiate gravity or gravitational waves. Beyond doubt, the gravitational waves both radiated by electromagnetic matter and erupted by binary black holes can penetrate and invade LIGO’s F-P vacuum cavities, changing the speeds of laser in the F-P vacuum cavities, so that the two laser beams in the X and Y-arms can present an equivalent optical-path difference, interfere with each other, and trigger the LIGO detector.

However, in order to trigger the LIGO detector, the gravitational field or gravitational radiation of a matter object must meet two conditions:

A binary black-hole system in deep space has a massive mass, yet is located billions of light-years away from the earth; an electromagnetic-matter system sweeping over the surface of the earth has a very small mass, yet can disturb the LIGO detector at close quarters or even zero distance. Suppose that there is a gravitational wave originated from a binary black-hole merger in deep space and is a gravitational field radiated by an electromagnetic-matter system sweeping over the earth. Which is more in line with the conditions of triggering the LIGO detector?

Can gravitational waves erupted by binary black holes trigger the LIGO system?

8.5 Why cannot LIGO’s gravitational waves make waves in the earth’s oceans?

As stated earlier, the earth’s oceans itself is a gravitational-wave observatory that can detect gravitational radiation or gravitational waves coming from celestial bodies: the oceans present tidal phenomena due to the induction of gravitational radiation or gravitational waves coming from the moon and sun. According to Newton’s law of universal gravitation, the tide generating force F_T induced by a unit mass of matter or seawater on the earth’s surface is proportional to the mass M of the gravitational source and inversely proportional to the cube of the distance d of the gravitational source:

The LIGO detector, like the earth’s oceans, is a matter system on the surface of the earth.

Equation (39) indicates that, as the gravitational-wave detectors on the surface of the earth, both the oceans and LIGO detector are restricted by the inverse cube law of the distance d of the gravitational source. Whether gravitational radiation can trigger the LIGO detector largely depends on the distance d between the gravitational source and the LIGO detector.

The mass of the sun is 27.112 million times that of the moon; the distance between the sun and the earth is 390.6 times that between the moon and the earth. According to Eq. (39): the equivalent acceleration of solar tidal force a_T = 5.05×10⁻⁷ m/s²; the equivalent acceleration of lunar tidal force is a_T = 1.10×10⁻⁶ m/s², which is 2.18 times that of the sun. Therefore, the lunar tidal force on the earth’s oceans is greater than the solar tidal force on the earth’s oceans. The sun needs to at least double its mass to reach the lever of lunar tide force.

According to the principle of LIGO detector interpreted in Sec. 8.1 and the trigger conditions of LIGO detector stated in Sec. 8.4, triggering the LIGO detector requires not only the gravitational source to be close enough to the LIGO detector, but also the gravitational wave radiated by the gravitational source to asymmetrically pass through the X and Y-arms of the LIGO detector.

The gravitational waves radiated by the moon and sun are spherical waves that approximate plane waves as the radiation distance increases, uniformly and symmetrically sweeping over the X and Y-arms of the LIGO detector. Therefore, although the gravity or gravitational waves radiated by the moon and sun can make waves in the earth’s oceans, they cannot trigger the LIGO detector.

Like the moon and the sun, the gravitational waves erupted by binary black holes when they merge are also spherical waves that approximate plane waves as they reach the earth, uniformly and symmetrically sweeping over the X and Y-arms of the LIGO detector, which does not meet the trigger condition of asymmetrically disturbing the LIGO detector as stated in Sec. 8.4 and cannot trigger the LIGO detector.

What we need to pay special attention to and think about is why the so-called gravitational waves that had triggered the LIGO detector failed to make waves in the earth’s oceans like the gravitational waves radiated by the moon and the sun? The answer can only be that either there are no LIGO’s so-called binary stars and black holes, or the gravitational waves erupted by binary stars and black-hole mergers do not have sufficient tide generating force as shown in Eq. (39).

Everything seems to be reminding us that LIGO’s all trigger signals, including GW150914, are not the gravitational waves from binary star or black-hole mergers.

Actually, LIGO is not certain whether binary stars or binary black holes really exist. Even if they do exist, LIGO is not certain whether they will merge. Even if they merge, LIGO is not certain how much energy they can erupt. Even if the energy can be calculated theoretically, LIGO is also not certain how much of the energy belongs to gravitational radiation or gravitational waves.

8.6 Why do LIGO’s gravitational waves move at the speed of light?

As stated in Sec. 7.1.2 and Sec. 7.2.2, the reason why Einstein predicted that the speed of gravitational waves is the speed of light is because Einstein mistakenly regarded the information wave of the optical agent OA(c), that is, light or an electromagnetic wave, as a gravitational wave.

So, why is the speed of LIGO’s gravitational waves is also the speed of light as predicted by Einstein?

Actually, LIGO does not have the way and function of measuring or determining the speed of gravitational waves. Without doubt, the measurement or determination of the speed of gravitational waves is much more difficult than that of the speed of light.

Mankind has long mastered the technology of measuring the speed of light. However, mankind has not yet had a feasible way or solution for measuring or determining the speed of gravitational waves. This fact suggests that gravitational waves must be much faster than light.

The theory of OR^1–5 has already clarified that the speed of light is not really insurmountable.

In 1805, Pierre-Simon Laplace concluded through theoretical calculations that the speed of gravitational radiation is greater than 7×10⁶c.⁴⁴ American physicist Flandern believed that the speed of gravitational radiation is much higher than the speed of light, otherwise the galaxies in the universe would lose their existing stable structure; in 1998, Flandern concluded through theoretical calculations that the speed of gravitational radiation is 2×10¹⁰c.⁴⁵

Intuition and common sense tell that Laplace and Flandern’s calculations and predictions are reasonable. Otherwise, it is difficult to imagine how light can gravitationally interact with other matter.

A black hole is black because photons or light are not fast enough to escape from it. However, no matter how black a black hole is, gravitons or gravitational waves are not bound by it. Otherwise, black holes would not be able to attract and engulf external matter, and binary black holes would not exist, let alone their merges.

Imagine a massive black hole: According to existing theory of black holes, no matter how massive its mass is, it can still radiate its gravitons or gravitational waves outward so as to gravitationally interact with external matter systems. This suggests that gravitational radiation or gravitational waves have a speed much greater than the speed of light, as predicted and calculated by Laplace and Flandern.^44,45 In this regard, it is reasonable that Newton’s law of universal gravitation ignores the locality of gravitational interaction.

So, why does LIGO claim that the gravitational waves it detected, just as Einstein’s prediction of gravitational waves, travels at the speed of light?

At the beginning, LIGO attempted to determine the speed of gravitational waves based on the trilateration method as depicted in Figure 3(b). Hanford and Livingston base stations are 3002 km apart, with an optical path of 10 ms. The first signal GW150914 triggering the LIGO detector took 7 ms to travel from Hanford to Livingston, roughly within the range of light speed, which seems to be consistent with Einstein’s prediction. However, LIGO was not satisfied with this result, for it is not precise enough.

Figure 3. Why were LIGO's Gravitational Waves Always Accompanied by EPCs?.

Annotation (a) LIGO's Gravitational Waves were Accompanied by Electromagnetic Matter. Whenever LIGO detected a GWxxxxxx signal, it would always be found that there were some electromagnetic-particle clumps (EPCs) before and after it, which are known as electromagnetic counterparts, such as gamma-ray bursts and X-rays; naturally, EPCs move at the speed of light. In fact, LIGO's every GWxxxxxx signal must be one of these so-called electromagnetic counterparts.

Annotation (b) EPCs and Their Gravitational Fields Swept at the Speed of Light over Hanford and Livingston Stations. As matter systems, EPCs have the gravitational fields of their own moving together with EPCs. It is not that gravitational waves moved at the speed of light, but that EPCs and their gravitational fields moved at the speed of light sweeping over Hanford and Livingston Stations.

Annotation (c) EPCs or Their Gravitational Fields Invades F-P Vacuum Cavities. If EPCs or their gravitational fields asymmetrically invades the F-P vacuum cavities of LIGO's X and Y-arms, then the LIGO detector may be triggered. However, this does not mean that LIGO detects the gravitational waves comes from the binary star or black-hole mergers in distant deep space.

Afterwards, in the so-called multi-messenger detection of gravitational waves joint with all observatories around the world, LIGO discovered that whenever it detected a GWxxxxxx signal, there would always be electromagnetic-particle clumps (EPSs), such as gamma rays and X-rays, appeared before and after it, as depicted in Figure 3(a). LIGO believes that these electromagnetic-particle clumps come from the same celestial region as the GWxxxxxx and have been accompanying the GWxxxxxx from the binary star or black-hole merger until reaching the earth. Therefore, LIGO refers to these clumps of electromagnetic particles as the Electromagnetic Counterparts of the GWxxxxxx.

LIGO believes that, since the gravitational-wave GW xxxxxx and its electromagnetic counterparts departed from distant deep space at the same time and reached the earth at the same time, the speed of gravitational waves must be the same as the speed of light in vacuum.

As stated in Sec. 3.5, LIGO selected GW170817 and the gamma-ray burst GRB170817A as the samples to calibrate the speed of gravitational waves.^41,42 Based on the departure and arrival time differences between GW170817 and GRB170817A, LIGO determined that, as shown in Eq. (17), the speed κ of gravitational waves accurately equal to the speed c of light in vacuum.

However, it is LIGO’s arguments and conclusions about the speed of gravitational waves that reveal the quiddity of LIGO’s so-called gravitational waves: they are not gravitational waves; they are electromagnetic waves.

In fact, LIGO’s every trigger signal GWxxxxxx must be one of the so-called electromagnetic counterparts of the GWxxxxxx.

8.7 What exactly did LIGO detect?

As stated in Sec. 3.2 and Sec. 8.1, LIGO is not a pure gravitational-wave detector, but a detector for all things: once matter objects or matter waves, including electromagnetic waves and gravitational waves, asymmetrically invade the F-P vacuum cavities of LIGO’s X and Y-arms, it may trigger the LIGO detector. The higher the density of matter, the greater the probability of LIGO system being triggered.

As stated in Secs. 8.2-8.5, even if binary stars or black holes do exist in the universe, the gravitational waves erupted by their mergers, like the gravity radiated by the moon and sun, cannot also trigger the LIGO detector. As clarified based on the GOR information-wave equation (Eq. (34)) in Sec. 7, Einstein’s prediction of gravitational waves is an error -- Einstein mistakenly thought that the information wave of the optical agent OA(c) was a gravitational wave, and therefore, mistakenly thought that the speed of gravitational waves was equivalent to the speed of light. As stated in Sec. 8.6, the speed of gravitational waves must be much higher than the speed of light as Laplace⁴⁴ and Flandern⁴⁵ calculated and predicted theoretically.

So, what exactly is the matter or matter systems that triggered the LIGO detector? And, why do LIGO’s so-called gravitational waves also move at the speed of light, as Einstein’s prediction?

Originally, the author of OR thought that electromagnetic matter could not penetrate and invade LIGO’s F-P vacuum cavities, and therefore, a GWxxxxxx signal that triggered the LIGO detector could only be the gravitational field of an electromagnetic-particle clump (EPC) which is referred to by LIGO as an electromagnetic counterpart of GWxxxxxx. Although an electromagnetic-particle clump has extremely small mass and weak gravitational field, it can asymmetrically sweep over the LIGO detector at close quarters or even zero distance, so that its gravitational field may trigger the LIGO detector.

However, according to the information provided by the AI model DeepSeek, LIGO’s F-P vacuum cavities is made of stainless-steel material with a thickness of about 3 mm. Therefore, high-energy electromagnetic radiation, such as gamma-ray bursts, can definitely penetrate and invade LIGO’s F-P vacuum cavities. According to the interpretation of LIGO’s principle in Sec. 8.1, gamma-ray bursts, such as GRB170817A that is regarded as an electromagnetic counterpart of GW170817, have higher density of matter, and are more like to trigger the LIGO detector than their own gravitational fields or gravitational waves. As depicted in Figure 3(c), gamma rays and even X-rays can asymmetrically disturb LIGO’s X and Y-arms and invade the F-P vacuum cavities, which must change the speeds of laser in the F-P cavities, so that the two laser beams in LIGO’s X and Y-arms present an equivalent optical-path difference and interfere with each other, leaving interference patterns on the LIGO photodetector PD and triggering the LIGO detector.

In fact, LIGO’s so-called electromagnetic counterparts of gravitational waves, such as the gamma-ray burst GRB170814A, not only can trigger radio telescopes, but also can trigger the LIGO detector.

It can be asserted that the so-called gravitational wave GW150914, and even every GWxxxxxx signal that triggers the LIGO detector, represents an electromagnetic-particle clump (EPC) which swept over the earth’s surface and invaded LIGO’s F-P vacuum cavities, rather than a gravitational wave originated from a binary star or black-hole merger in deep space.

Now, we know why LIGO’s so-called gravitational waves were moving at the speed of light.

In order to cater to Einstein’s prediction of gravitational waves, LIGO mistakenly thought that the GWxxxxxx signals triggering the LIGO detector represented gravitational waves originated from binary star or black-hole mergers and mistakenly thought that the speed of gravitational waves was the speed of light.

This is the quiddity of LIGO’s so-called detection of gravitational waves.

The events that electromagnetic matter sweeps over the earth is extremely common. However, binary stars or black holes, and their mergers, are just imaginations.