Statistical Properties of Second Iteration of Logistic Map

Mahmood A. Shamran; Saad Naji; Ghasaq Haitham Shakir; Iden Hassan

doi:10.12688/f1000research.172880.1

Home Browse Statistical Properties of Second Iteration of Logistic Map

ALL Metrics

-

Views

-

Downloads

Get PDF

Get XML

Export

▬

✚

Research Article

Statistical Properties of Second Iteration of Logistic Map

[version 1; peer review: awaiting peer review]

Mahmood A. Shamran¹, Saad Naji¹, Ghasaq Haitham Shakir ², Iden Hassan¹

PUBLISHED 30 Dec 2025

Author details Author details

¹ mathematics, University of Baghdad, Baghdad, Baghdad Governorate, Iraq
² mathematics, Ministry of Education, Baghdad, Baghdad Governorate, Iraq

Mahmood A. Shamran
Roles: Conceptualization, Data Curation, Formal Analysis, Software, Validation, Writing – Original Draft Preparation, Writing – Review & Editing

Saad Naji
Roles: Conceptualization, Formal Analysis, Investigation, Methodology, Validation, Writing – Original Draft Preparation, Writing – Review & Editing

Ghasaq Haitham Shakir
Roles: Data Curation, Software, Writing – Original Draft Preparation, Writing – Review & Editing

Iden Hassan
Roles: Conceptualization, Formal Analysis, Funding Acquisition, Methodology, Resources, Validation, Visualization

OPEN PEER REVIEW

REVIEWER STATUS AWAITING PEER REVIEW

This article is included in the Fallujah Multidisciplinary Science and Innovation gateway.

Abstract

This paper introduces a novel non-classical probability distribution, termed the Logistic Map distribution, which is constructed by transforming a polynomial function derived from the second iteration of the logistic map. The logistic map a well-known discrete-time dynamical system has been extensively employed in diverse scientific domains, including population dynamics (to model bounded growth under environmental constraints), physics (to study nonlinear dynamics and deterministic chaos), and economics (to represent complex, nonlinear patterns in financial and economic time series).

The proposed distribution is fully characterized by two parameters: a scale parameter and a shape parameter, with the constraint ensuring the non-negativity and integrability of the density. Within this valid parameter space, we rigorously derive and establish a comprehensive suite of statistical properties. These include the probability density function, cumulative distribution function, reliability (survival) function, and hazard (failure rate) function. Furthermore, we obtain analytical expressions for key descriptive measures such as the mode and median, as well as for higher-order characteristics including the moment generating function, factorial moment generating function, and characteristic function. The proposed distribution most closely application field in materials science specifically, the statistical modeling of particle or grain size distributions in industrial powder processing, metallurgy, and pharmaceutical manufacturing.

The primary objective of this study is to formalize a new family of probability distributions grounded in the mathematical framework of dynamical systems, specifically leveraging the logistic function commonly encountered in differential and difference equations. By doing so, we bridge concepts from nonlinear dynamics and classical statistical theory. The secondary aim is to conduct a thorough investigation of the distribution’s mathematical structure and statistical behavior, thereby establishing its potential utility for modeling bounded, non-negative random phenomena in applied fields such as reliability engineering, survival analysis, and environmental statistics.

Keywords

Cumulative Function, Hazard Function, Logistic function, Median, Mode, Probability Density Function, Reliability Function.

Corresponding authors: Mahmood A. Shamran, Ghasaq Haitham Shakir

Competing interests: No competing interests were disclosed.

Grant information: The author(s) declared that no grants were involved in supporting this work.

Copyright: © 2025 A. Shamran M et al. This is an open access article distributed under the terms of the Creative Commons Attribution License, which permits unrestricted use, distribution, and reproduction in any medium, provided the original work is properly cited.

How to cite: A. Shamran M, Naji S, Haitham Shakir G and Hassan I. Statistical Properties of Second Iteration of Logistic Map [version 1; peer review: awaiting peer review]. F1000Research 2025, 14:1469 (https://doi.org/10.12688/f1000research.172880.1) First published: 30 Dec 2025, 14:1469 (https://doi.org/10.12688/f1000research.172880.1) Latest published: 30 Dec 2025, 14:1469 (https://doi.org/10.12688/f1000research.172880.1)

1. Introduction

One of the well-known functions that used in studying the differential equations or dynamical systems in biology, ecology epidemic, economic, etc. is the logistic functions and its iterator.¹

The first mathematical study the logistic function were Verhulst a Belgian mathematician, considered one of the first to study logistic growth where in (1838) used the Logistic Map in the law of population growth,² James Yorke an American mathematician, studied the map of logistics, chaos (1975) and Robert Mayer, an Australian ecologist, studied logistic mapping and its applications in ecology (1976). Mitchell Feigenbaum, an American physicist, studied the chaotic behavior of logistic models (1978).

This logistic equation can exhibit chaotic or periodic behavior, and the Poincaré map can be used to study this behavior and identify critical points and chaotic regions. By applying the Poincaré map, which implies that the pendulum's behavior is demonstrated by the difference equations,³ to logistic equations, one can gain deeper insights into the dynamical behavior of these systems and understand how they change with varying parameters.

The aim of this research is to find a new distribution based on a function used in differential equations, which is the logistic function, and to study the statistical properties of this distribution. In the next section, fall details of the logistic function will be given:

Any statistical distribution must satisfy and approximate all the statistical concepts, such as pdf, cdf, reliability function,¹ hazard function,⁴ mode,⁵ median, moment generating function (MGF),⁶ factorial moment-generating function (FMGF), characteristic function,⁷ coefficient of variation (C.V), coefficient of kurtosis (C.K)⁸ …etc.

The study is divided into five sections: the second one, “Basic Definitions,” is followed by the “structure of building the logistic distribution” in section three, is followed by “results and discussion” in section four, and “conclusion” rounds off the study in section five.

2. Structure of building the logistic distribution

Logistic map is a first-order difference equation discovered which by mathematical biologist Robert May. It's defined by the equation: $Q_{μ} (x) = μx (1 - \frac{x}{k})$ , where x is any population of nth generation, $μ$ ≥ 0 the intrinsic growth rate and k is the carrying capacity.

This model is commonly used in the study of biological populations, including genetics (change in gene frequency), epidemiology (proportion of infected population), economics (relationship between commodity quantity and price), and social sciences.

An item that works well at first, but after a period of time it breaks down. Although it can be repaired, after repair it works less efficiently than before. That is, the item goes through a repeated cycle of failure and repair, but with efficiency that decreases with each repetition as shown in Figures 1 and 2. This type of behavior can be classified under the second iteration of the logistic function and can be written as:

\begin{array}{l} Q_{μ}^{[2]} (x) = μ Q_{μ} (x) [1 - Q_{μ} (x)] \\ Q_{μ}^{[2]} (x) = μ [μx (1 - \frac{x}{k})] [1 - \frac{μx (1 - \frac{x}{k})}{k}] \end{array}

Figure 1. logistic map system where $μ = 2, k = 1$ .

Figure 2. Different dynamical behaviors observed in the logistic map system when k = 10 with μ = 2 and μ = 4.

When we integral the second iteration of the logistic function $Q_{μ}^{[2]} (x)$ for lower value zero and upper value k to determine A's value, let presume:

\begin{array}{l} A = \int_{0}^{k} Q_{μ}^{[2]} (x) dx = \int_{0}^{k} μ [μx (1 - \frac{x}{k})] [1 - \frac{μx (1 - \frac{x}{k})}{k}] dx \\ A = \frac{(5 - μ) μ^{2} k^{2}}{30} \end{array}

Now, it well be transferred to differential equation (the second iteration of the logistic function) to the statistical distribution.

2.1 Probability density function (PDF ) for logistic map distribution

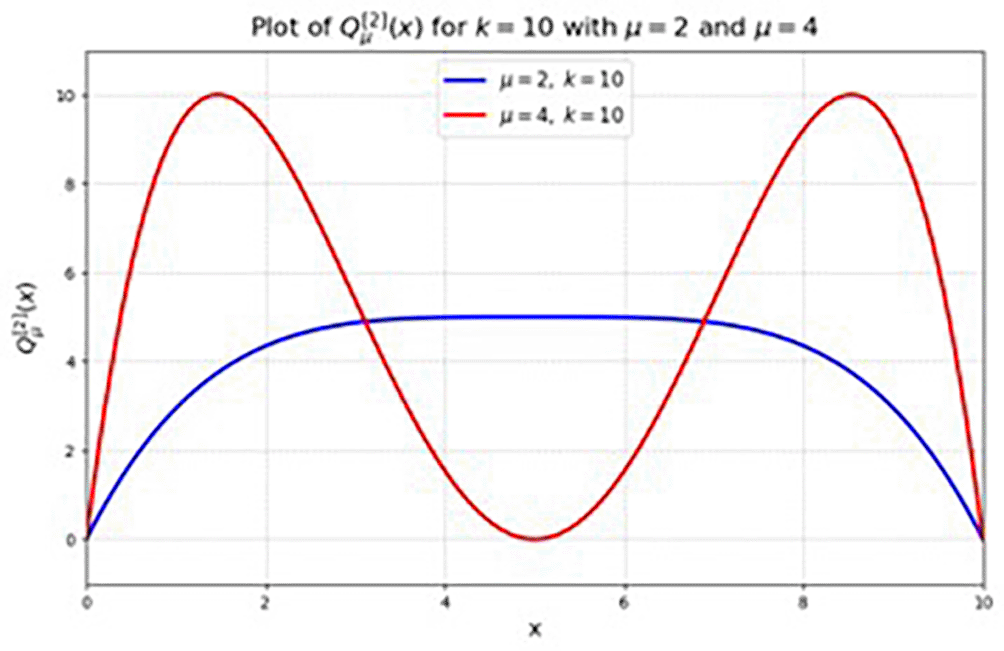
The function $f_{μ, k} (x; μ, k)$ is obtained by multiplying the function $Q_{μ}^{[2]} (x) by \frac{1}{A}$ in order to obtain the probability density function for logistic map distribution, as shown in Figure 3 the form:

(1)

\begin{array}{l} f_{μ, k} (x; μ, k) = {\begin{cases} \frac{1}{A} Q_{μ}^{[2]} (x), x \in (0, k) \\ 0, \frac{O}{W} \end{cases} \\ f_{μk} (x; μ, k) = {\begin{cases} \frac{30 x (x - k) (μx (x - k) + k^{2}))}{(k^{5} (μ - 5))}, x \in (0, k) \\ 0, \frac{O}{W} \end{cases} \end{array}

Lemma 1:

$f_{μk} (x; μ, k)$ is a pdf

Proof:

\begin{array}{l} \int_{all x} f (x) dx = 1 \\ \int_{0}^{k} \frac{30 x (x - k) (μx (x - k) + k^{2})}{k^{5} (μ - 5)} dx = 1 \\ [\frac{x^{2} (6 μ x^{3} - 15 kμ x^{2} + 10 k^{2} (μ + 1) x - 15 k^{3})}{k^{5} (μ - 5)}] \begin{matrix} k \\ 0 \end{matrix} = \frac{k^{5} (μ - 5)}{k^{5} (μ - 5)} = 1 \end{array}

Figure 3. The probability density function logistic map distribution.

2.2 Cumulative Distribution Function (CDF ) for logistic map distribution

Lemma 2:

Let x be a continuous non-negative random variable (r.v.). The Cumulative Distribution Function (CDF) of x is given by the following equation $F_{μk} (x; μ, k)$ as in Figure 4

F_{μk} (x; μ, k) = \frac{x^{2} (μx (6 x^{2} - 15 kx + 10 k^{2}) + 10 k^{2} x - 15 k^{3})}{k^{5} (μ - 5)}

Proof:

F (x) = \int_{0}^{x} f (u) du

\begin{array}{l} F (x) = \int_{0}^{x} \frac{30 u (1 - \frac{u}{k}) (1 - \frac{μu (1 - \frac{u}{k})}{k})}{k^{2} (5 - μ)} du \\ = \int_{- \infty}^{x} (- \frac{30 μ u^{4}}{k^{5} (5 - μ)} + \frac{60 μ u^{3}}{k^{4} (5 - μ)} - \frac{30 μ u^{2}}{k^{3} (5 - μ)} - \frac{30 μ u^{2}}{k^{2} (5 - μ)} + \frac{30 μu}{k^{2} (5 - μ)}) du \\ = [- \frac{6 μ u^{5}}{k^{5} (5 - μ)} + \frac{15 μ u^{4}}{k^{4} (5 - μ)} - \frac{10 (k^{2} μ + k^{2}) u^{3}}{k^{5} (5 - μ)} + \frac{15 u^{2}}{k^{2} (5 - μ)}] |_{x}^{0} \\ = - \frac{(6 x^{5} - 15 k x^{4} + 10 k^{2} x^{3}) μ + 10 k^{2} x^{3} - 15 k^{3} x^{2}}{k^{5} (5 - μ)} \\ = \frac{x^{2} (x (6 x^{2} - 15 kx + 10 k^{2}) μ + 10 k^{2} x - 15 k^{3})}{k^{5} (μ - 5)} \end{array}

Then $F_{μk} (x; μ, k) = \frac{x^{2} (μx (6 x^{2} - 15 kx + 10 k^{2}) + 10 k^{2} x - 15 k^{3})}{k^{5} (μ - 5)}$

Figure 4. The Cumulative Distribution Function (CDF ) for logistic map distribution.

2.3 Reliability function for logistic map distribution

Lemma 3:

Assuming that x is a continuous non-negative random variable following a Logistic map distribution, the reliability function as in Figure 5 of x is given by:

R_{μk} (x) = 1 - \frac{x^{2} (μx (6 x^{2} - 15 kx + 10 k^{2}) + 10 k^{2} x - 15 k^{3})}{k^{5} (μ - 5)}

Proof:

\begin{array}{l} R_{μk} (x) = 1 - F_{μ} (x) \\ = 1 - \frac{x^{2} (μx (6 x^{2} - 15 kx + 10 k^{2}) + 10 k^{2} x - 15 k^{3})}{k^{5} (μ - 5)} \end{array}

Figure 5. The Reliability function for logistic map distribution.

2.4 Hazard rate function for logistic map distribution

Lemma 4:

The hazard function for x is as follows, assuming that x is a continuous positive r.v. distributed with logistic map distribution as in Figure 6:

h_{μk} (x) = \frac{(30 x (x - k) (μx (x - k) + k^{2}))}{(k^{5} (μ - 5) - x^{2} (μx (6 x^{2} - 15 kx + 10 k^{2}) + 10 k^{2} x - 15 k^{3}))}

Proof:

\begin{array}{l} h_{μk} (x) = \frac{f_{μk} (x)}{R_{μk (x)}} \\ = \frac{\frac{(30 x (x - k) (μx (x - k) + k^{2}))}{(k^{5} (μ - 5))}}{1 - \frac{x^{2} (μx (6 x^{2} - 15 kx + 10 k^{2}) + 10 k^{2} x - 15 k^{3})}{k^{5} (μ - 5)}} \\ = \frac{(30 x (x - k) (μx (x - k) + k^{2}))}{(k^{5} (μ - 5)) (1 - \frac{x^{2} (μx (6 x^{2} - 15 kx + 10 k^{2}) + 10 k^{2} x - 15 k^{3})}{k^{5} (μ - 5)})} \\ = \frac{(30 x (x - k) (μx (x - k) + k^{2}))}{(k^{5} (μ - 5) - x^{2} (μx (6 x^{2} - 15 kx + 10 k^{2}) + 10 k^{2} x - 15 k^{3}))} \end{array}

Figure 6. The Hazard function for logistic map distribution.

3. Results and Discussion

This section aims to present a novel logistic map distribution for a discrete dynamical system that is specified by second iteration of the logistic function.

3.1 Mode

Lemma 5:

The mode of $f (x)$ is $x = \frac{2 μk + \sqrt{μk (μk - 3)}}{3 μ}$

Proof:

f_{μk} (x; μ, k) = \frac{(30 x (x - k) (μx (x - k) + k^{2}))}{(k^{5} (μ - 5))}, x \in (0, k)

f_{μk}^{'} (x; μ, k) = \frac{30 (4 μ x^{3} - 6 kμ x^{2} + (2 k^{2} μ + 2 k^{2}) x - k^{3})}{k^{5} (μ - 5)}

For the random variable X, the density function's first derivative equals zero $(f_{μk}^{'} (x) = 0)$ we discover:

(2)

\frac{30 (4 μ x^{3} - 6 kμ x^{2} + (2 k^{2} μ + 2 k^{2}) x - k^{3})}{k^{5} (μ - 5)} = 0,

Both sides are multiplied by $\frac{30}{k^{5} (5 - μ)}$ the following equation is obtained:

4 μ x^{3} - 6 kμ x^{2} + (2 k^{2} μ + 2 k^{2}) x - k^{3} = 0

Since this equation is a polynomial of degrees 3, we obtain:

x_{c} = \frac{k}{2}, \frac{k \sqrt{μ^{2} - 2 μ} + kμ}{2 μ}, - \frac{k \sqrt{μ^{2} - 2 μ} - kμ}{2 μ}

There are many roots for Equation (2), as observed in the shape of the density function Equation (1). So, if $x = x_{c}$ is a root of Equation (2), this root's depends on the second derivative of the equation. That means if the second derivative of the root is less than zero, then the point or the root is a local maximum. Or if the second derivative of the root is greater than zero, then it is a minimum point.

(3)

f''_{μk} (x; μ, k) = \frac{60 (6 μ x^{2} - 6 kμx + k^{2} μ + k^{2})}{k^{5} (μ - 5)}

The value of $x_{c_{1}} = \frac{k}{2}$ is compensated for in Equation (3), we obtain:

{f^{''}}_{μk} (x_{c_{1}}; μ, k) = \frac{60 (k^{2} - \frac{k^{2} μ}{2})}{k^{5} (μ - 5)} > 0

When the value of $x_{c_{2}} = \frac{2 μk + \sqrt{μk (μk - 3)}}{3 μ}$ is compensated for in Equation (3), we obtain:

{f^{''}}_{μk} (x_{c_{2}}; μ, k) = \frac{60 μ (3 μ (μ (μ^{2} - μ - 1) + (μ - 1) \sqrt{(μ - 2) μ} (μ + 1) + 1) + 1)}{k^{3} (μ - 5)} > 0

{f^{''}}_{μk} (x_{c_{2}}; μ, k) = - \frac{60 μ (3 μ (μ (μ^{2} - μ - 1) + (μ - 1) \sqrt{(μ - 2) μ} (μ + 1) - 1) - 1)}{k^{3} (μ - 5)} < 0

Then, the mode is $(\frac{2 μk + \sqrt{μk (μk - 3)}}{3 μ})$

3.2 Median

Lemma 6:

Let x be a continuous non-negative r.v. distributed according to the logistic map distribution, then the median of x is derived as in the form⁹:

Proof:

\begin{array}{l} F (x) = \int_{o}^{x} f (u) du = \frac{1}{2} \\ \frac{x^{2} (μx (6 x^{2} - 15 kx + 10 k^{2}) + 10 k^{2} x - 15 k^{3})}{k^{5} (μ - 5)} = \frac{1}{2} \\ 2 x^{2} (μx (6 x^{2} - 15 kx + 10 k^{2}) + 10 k^{2} x - 15 k^{3}) = k^{5} (μ - 5) \\ 2 x^{2} (μx (6 x^{2} - 15 kx + 10 k^{2}) + 10 k^{2} x - 15 k^{3}) - k^{5} (μ - 5) = 0 \\ x_{1} = \frac{k}{2} \\ x_{2} = \frac{k}{2} + \frac{\sqrt{\frac{2 k^{2} (\sqrt{5} \sqrt{- μ^{2} + 4 μ + 5} - 2 (2 μ + 5))}{3 μ} + 3 k^{2}}}{2} \\ x_{2} = \frac{k}{2} - \frac{\sqrt{\frac{2 k^{2} (\sqrt{5} \sqrt{- μ^{2} + 4 μ + 5} - 2 (2 μ + 5))}{3 μ} + 3 k^{2}}}{2} \\ x_{3} = \frac{k}{2} + \frac{\sqrt{\frac{- 2 k^{2} (\sqrt{5} \sqrt{- μ^{2} + 4 μ + 5} + 2 (2 μ + 5))}{3 μ} + 3 k^{2}}}{2} \\ x_{3} = \frac{k}{2} - \frac{\sqrt{\frac{- 2 k^{2} (\sqrt{5} \sqrt{- μ^{2} + 4 μ + 5} + 2 (2 μ + 5))}{3 μ} + 3 k^{2}}}{2} \end{array}

Since $\frac{- 2 k^{2} (\sqrt{5} \sqrt{- μ^{2} + 4 μ + 5} + 2 (2 μ + 5))}{3 μ} > 0 and \frac{2 k^{2} (\sqrt{5} \sqrt{- μ^{2} + 4 μ + 5} - 2 (2 μ + 5))}{3 μ} > 0$ because $μ \in (0, 4), k > 2$

3.3 The r^th moment

Lemma 7:

The r^th moment function for x is as follows, assuming that x is a positive r.v. distributed as the logistic map distribution⁹: $E (x^{r}) = \frac{30 k^{r} ((2 r + 4) μ - r^{2} - 9 r - 20)}{(r^{4} + 14 r^{3} + 71 r^{2} + 154 r + 120) (μ - 5)}$

Proof:

\begin{array}{l} E (x^{r}) = \int_{all x} x^{r} f_{μk} (x; μ, k) dx \\ E (x^{r}) = \int_{0}^{k} x^{r} \frac{30 x (x - k) (μx (x - k) + k^{2}))}{(k^{5} (μ - 5))} dx \\ E (x^{r}) = \int_{0}^{k} (\frac{30 μ x^{r + 4}}{k^{5} (5 - μ)} - \frac{60 μ x^{r + 3}}{k^{4} (5 - μ)} + \frac{30 μ x^{r + 2}}{k^{3} (5 - μ)} + \frac{30 x^{r + 2}}{k^{3} (5 - μ)} - \frac{30 x^{r} + 1}{k^{2} (5 - μ)}) dx \\ E (x^{r}) = \frac{30 k^{r} ((2 r + 4) μ - r^{2} - 9 r - 20)}{(r^{4} + 14 r^{3} + 71 r^{2} + 154 r + 120) (μ - 5)} \end{array}

If r = 1,2 is substituted in the r^th moment function, Lemma 7 may be used to obtain the mean and variance for the logistic map distribution.

E (x) = \frac{k (6 μ - 30)}{12 (μ - 5)}

And if r = 2 we obtain:

E (x^{2}) = \frac{k^{2} (8 μ - 42)}{28 (5 - μ)}

Now find var( x) so we can get it through: $var (x) = E (x^{2}) - {[E (x)]}^{2}$

\begin{array}{l} var (x) = \frac{k^{2} (8 μ - 42)}{28 (5 - μ)} - {[\frac{k (6 μ - 30)}{12 (μ - 5)}]}^{2} \\ var (x) = \frac{k^{2} (8 μ - 42)}{28 (5 - μ)} - \frac{k^{2} {(6 μ - 30)}^{2}}{144 {(μ - 5)}^{2}} \\ var (x) = \frac{k^{2} (μ - 7)}{28 (5 - μ)} \end{array}

3.4 Moment generating function (MGF )

Lemma 8:

The Moment generating function (MGF) for x is given by, assuming that x is a positive r.v. distributed according to the logistic map distribution¹⁰:

M_{x} (t) = \frac{30 ((2 k^{2} t^{2} - 12 kt + 24) e^{kt} - 2 k^{2} t^{2} - 12 kt - 24) μ + (2 k^{2} t^{2} - k^{3} t^{3}) e^{kt} - k^{3} t^{3} - 2 k^{2} t^{2}}{k^{5} t^{5} (μ - 5)}

Proof:

\begin{array}{l} M_{x} (t) = E (e^{tx}) = \int_{all x} e^{tx} f_{μk} (x; μ, k) dx \\ M_{x} (t) = E (e^{tx}) = \int_{0}^{k} \frac{30 x (x - k) (μx (x - k) + k^{2})) e^{tx}}{(k^{5} (μ - 5))} dx \\ = \frac{30}{(k^{5} (μ - 5))} \int_{0}^{k} 30 x (x - k) (μx (x - k) + k^{2})) e^{tx} dx \\ = \frac{30 ((2 k^{2} t^{2} - 12 kt + 24) e^{kt} - 2 k^{2} t^{2} - 12 kt - 24) μ + (2 k^{2} t^{2} - k^{3} t^{3}) e^{kt} - k^{3} t^{3} - 2 k^{2} t^{2}}{k^{5} t^{5} (μ - 5)} \end{array}

3.5 Characteristic function

Lemma 9:

Let X be r.v. with density function $f_{EW} (x; λ, α)$ , the expected value of $e^{itx}$ is defined to be characteristic function of X. where $i = \sqrt{- 1}$ and tis a real number.

\begin{array}{l} Ф_{x} (it) = E (e^{itx}) = \int_{all x} e^{itx} f_{μk} (x; μ, k) dx \\ Ф_{x} (it) = E (e^{itx}) = \int_{0}^{k} \frac{30 x (x - k) (μx (x - k) + k^{2})) e^{itx}}{(k^{5} (μ - 5))} dx \\ Ф_{x} (it) = E (e^{itx}) = \frac{30}{(k^{5} (μ - 5))} \int_{0}^{k} 30 x (x - k) (μx (x - k) + k^{2})) e^{itx} dx \\ = \frac{[\begin{array}{l} - 30 (i t^{4} μ x^{4} - 2 t^{3} (ikt + 2) μ x^{3} + t^{2} (i k^{2} t^{2} μ + 6 ktμ - 12 iμ + i k^{2} t^{2}) x^{2} - t (2 (kt (kt - 6 i) - 12) μ \\ + k^{2} t^{2} (ikt + 2)) x - 2 (kt (ikt + 6) - 12 i) μ + k^{3} t^{3} - 2 i k^{2} t^{2}) e^{itx} \end{array}]}{k^{5} t^{5} (μ - 5)} |_{0}^{k} \\ = \frac{30 ((2 i k^{2} t^{2} - 12 kt - 24 i) e^{ikt} - 2 i k^{2} t^{2} - 12 kt + 24 i) μ + (k^{3} t^{3} + 2 i k^{2} t^{2}) e^{ikt} + k^{3} t^{3} - 2 i k^{2} t^{2}}{k^{5} t^{5} (μ - 5)} \end{array}

3.6 Factorial moment generating function (FMGF )

Lemma 10:

Let x be a non-negative continuous r.v. has the logistic map distribution then the Factorial moments generating function of x is in the form:

G_{x} (t) = \frac{30 ((2 k^{2} {(lnt)}^{2} - 12 k (lnt) + 24) e^{klnt} - 2 k^{2} {(lnt)}^{2} - 12 k (lnt) - 24) μ + (2 k^{2} {(lnt)}^{2} - k^{3} {(lnt)}^{3}) e^{klnt} - k^{3} {(ln)}^{3} - 2 k^{2} {(lnt)}^{2}}{k^{5} {(lnt)}^{5} (μ - 5)}

Proof:

G_{x} (t) = E (t^{x}) = E (e^{{lnt}^{x}}) = E (e^{xlnt}) = Ϻ_{x} (ln t)

That’s mean found relationship between a (mgf ) and (Fmgf ) where $M_{x} (t) = Ϻ_{x} (ln t)$ From Lemma 8 we obtain:

Ϻ_{x} (lnt) = \frac{30 ((2 k^{2} {(lnt)}^{2} - 12 k (lnt) + 24) e^{klnt} - 2 k^{2} {(lnt)}^{2} - 12 k (lnt) - 24) μ + (2 k^{2} {(lnt)}^{2} - k^{3} {(lnt)}^{3}) e^{klnt} - k^{3} {(ln)}^{3} - 2 k^{2} {(lnt)}^{2}}{k^{5} {(lnt)}^{5} (μ - 5)}

3.7 Coefficient of Variation (C.V)

Lemma 11:

Let x be a non-negative continuous r.v. has the logistic map distribution then the Coefficient of Variation of x is in the form⁷: $C . V = \frac{6 \sqrt{(μ - 7)} (μ - 5)}{\sqrt{7} \sqrt{(5 - μ)} (6 μ - 30)}$

Proof:

The Coefficient of Variation is given by: $C . V = \frac{σ}{M}$

M = E (x) = \frac{k (6 μ - 30)}{12 (μ - 5)}

var (x) = σ^{2} (x) = \frac{k^{2} (μ - 7)}{28 (5 - μ)}

σ (x) = \frac{k \sqrt{(μ - 7)}}{\sqrt{28 (5 - μ)}}

C . V = \frac{σ}{M} = \frac{k \sqrt{(μ - 7)}}{\sqrt{28 (5 - μ)}} \times \frac{12 (μ - 5)}{k (6 μ - 30)}

C . V = \frac{6 \sqrt{(μ - 7)} (μ - 5)}{\sqrt{7} \sqrt{(5 - μ)} (6 μ - 30)}

3.8 Coefficient of Skewness (C.S)

Lemma 12:

Let x be a non-negative continuous r.v. has the logistic map distribution then The Coefficient of Skewness of x is in the form:

C . S = \frac{12 \sqrt{7} {(5 - μ)}^{\frac{3}{2}} (4 μ - 21)}{{(μ - 7)}^{\frac{3}{2}} (μ - 5)}

Proof:

The Coefficient of Skewness is given by: $C . S = \frac{M_{3}}{σ^{3}}$

\begin{matrix} M_{3} = E {(x - M)}^{3} = E {(x - \frac{k (6 μ - 30)}{12 (μ - 5)})}^{3} \\ = E (x^{3}) - 3 (\frac{k (6 μ - 30)}{12 (μ - 5)}) E (x^{2}) + 3 {(\frac{k (6 μ - 30)}{12 (μ - 5)})}^{2} E (x) - {(\frac{k (6 μ - 30)}{12 (μ - 5)})}^{3} \end{matrix}

If r = 3 is substituted in the r^th moment function, Lemma 7 may be used to obtain the $E (x^{3})$ .

E (x^{3}) = \frac{k^{3} (10 μ - 56)}{56 (μ - 5)}

Then

\begin{array}{l} M_{3} = E {(x - M)}^{3} = \frac{k^{3} (10 μ - 56)}{56 (μ - 5)} - 3 (\frac{k (6 μ - 30)}{12 (μ - 5)}) (\frac{k^{2} (8 μ - 42)}{28 (5 - μ)}) + 3 {(\frac{k (6 μ - 30)}{12 (μ - 5)})}^{2} (\frac{k (6 μ - 30)}{12 (μ - 5)}) - {(\frac{k (6 μ - 30)}{12 (μ - 5)})}^{3} \\ = \frac{k^{3} (10 μ - 56)}{56 (μ - 5)} - 3 (\frac{k (6 μ - 30)}{12 (μ - 5)}) (\frac{k^{2} (8 μ - 42)}{28 (5 - μ)}) + 3 {(\frac{k (6 μ - 30)}{12 (μ - 5)})}^{3} - {(\frac{k (6 μ - 30)}{12 (μ - 5)})}^{3} \\ = \frac{k^{3} (10 μ - 56)}{56 (μ - 5)} - 3 (\frac{k (6 μ - 30)}{12 (μ - 5)}) (\frac{k^{2} (8 μ - 42)}{28 (5 - μ)}) + 2 {(\frac{k (6 μ - 30)}{12 (μ - 5)})}^{3} \\ = \frac{k^{3} {(6 μ - 30)}^{3}}{864 {(μ - 5)}^{3}} + \frac{k^{3} (10 μ - 56)}{56 (μ - 5)} - \frac{k^{3} (6 μ - 30) (8 μ - 42)}{112 (5 - μ) (μ - 5)} \end{array}

M_{3} = \frac{3 k^{3} (4 μ - 21)}{14 (μ - 5)}

var (x) = σ^{2} (x) = \frac{k^{2} (μ - 7)}{28 (5 - μ)}

σ (x) = {(\frac{k^{2} (μ - 7)}{28 (5 - μ)})}^{\frac{1}{2}}

σ^{3} (x) = \frac{k^{3} {(μ - 7)}^{\frac{3}{2}}}{{(28 (5 - μ))}^{\frac{3}{2}}}

\begin{matrix} C . S = \frac{M_{3}}{σ^{3}} = \frac{3 k^{3} (4 μ - 21)}{(14 (μ - 5))} \times \frac{{(28 (5 - μ))}^{\frac{3}{2}}}{(k^{3} {(μ - 7)}^{\frac{3}{2}})} \\ = \frac{12 \sqrt{7} {(5 - μ)}^{\frac{3}{2}} (4 μ - 21)}{{(μ - 7)}^{\frac{3}{2}} (μ - 5)} \end{matrix}

3.9 The r^th central moment about mean

Lemma 13:

Let x be a non-negative continuous r.v. has the logistic map distribution then The r^th central moment about mean of x is in the form:

E {(x - M)}^{r} = \frac{30 {(1 - M)}^{r}}{(k^{5} (μ - 5))} [\frac{k^{j + 5} ((2 j + 4) μ - j^{2} - 9 j - 20)}{j^{4} + 14 j^{3} + 71 j^{2} + 154 j + 120}]

Proof:

The r^th central moment about mean is given by: -

E {(x - M)}^{r} = \int_{all x} {(x - M)}^{r} f_{μk} (x; μ, k) dx

E {(x - M)}^{r} = \int_{0}^{k} {(x - M)}^{r} [\frac{30 x (x - k) (μx (x - k) + k^{2}))}{(k^{5} (μ - 5))}] dx

E {(x - M)}^{r} = \int_{0}^{k} (x + (- M)) [\frac{30 x (x - k) (μx (x - k) + k^{2}))}{(k^{5} (μ - 5))}] dx

Recall that:

{(a + b)}^{n} = \sum_{j = 0}^{n} C_{j}^{n} a^{j} b^{n - j}

{(x - M)}^{r} = \sum_{j = 0}^{r} C_{j}^{r} x^{j} {(- M)}^{r - j}, And M = E (x)

E {(x - M)}^{r} = \int_{0}^{k} \frac{30 \sum_{j = 0}^{r} C_{j}^{r} x^{j} {(- M)}^{r - j}}{(k^{5} (μ - 5))} [x (x - k) (μx (x - k) + k^{2}))] dx

E {(x - M)}^{r} = \int_{0}^{k} \frac{30 \sum_{j = 0}^{r} C_{j}^{r} {(- M)}^{r - j}}{(k^{5} (μ - 5))} [x^{j + 1} (x - k) (μx (x - k) + k^{2}))] dx

E {(x - M)}^{r} = \frac{30 \sum_{j = 0}^{r} C_{j}^{r} {(- M)}^{r - j}}{(k^{5} (μ - 5))} [μ \int_{0}^{k} x^{j + 4} dx - 2 kμ \int_{0}^{k} x^{j + 3} dx + (k^{2} μ + k^{2}) \int_{0}^{k} x^{j + 2} dx - k^{3} \int_{0}^{k} x^{j + 1} dx]

E {(x - M)}^{r} = \frac{30 \sum_{j = 0}^{r} C_{j}^{r} {(- M)}^{r - j}}{(k^{5} (μ - 5))} {[\frac{μ x^{j + 5}}{j + 5} - \frac{2 kμ x^{j + 4}}{j + 4} + \frac{k^{2} μ x^{j + 3}}{j + 3} + \frac{k^{2} x^{j + 3}}{j + 3} - \frac{k^{3} x^{j + 2}}{j + 2}] |}_{0}^{k}

E {(x - M)}^{r} = \frac{30 \sum_{j = 0}^{r} C_{j}^{r} {(- M)}^{r - j}}{(k^{5} (μ - 5))} [\frac{k^{j + 5} ((2 j + 4) μ - j^{2} - 9 j - 20)}{j^{4} + 14 j^{3} + 71 j^{2} + 154 j + 120}]

E {(x - M)}^{r} = \frac{30 {(1 - M)}^{r}}{(k^{5} (μ - 5))} [\frac{k^{j + 5} ((2 j + 4) μ - j^{2} - 9 j - 20)}{j^{4} + 14 j^{3} + 71 j^{2} + 154 j + 120}]

4. Maximum likelihood estimation method (MLEM)

This method is one of the most important and most used method for estimating parameters for all distribution.¹¹ The idea of this method is to find the estimate parameters for any distribution which maximize the likelihood function.¹²

Suppose that $x_{1}, x_{2}, \dots, x_{n}$ are (i.i.d) random variable with joint pdf $f (x_{i}; μ, k)$ .

The likelihood function for two parameters for logistic map distribution

\begin{array}{l} L (μ, k; x_{1}, x_{2}, \dots, x_{n}) = \prod_{i = 1}^{n} f (x_{i}; μ, k) \\ = \prod_{i = 1}^{n} \frac{30 x_{i} (x_{i} - k) (μ x_{i} (x_{i} - k) + k^{2}))}{(k^{5} (μ - 5))} \\ = {(\frac{30}{(k^{5} (μ - 5))})}^{n} \prod_{i = 1}^{n} (x_{i} (x_{i} - k) (μ x_{i} (x_{i} - k) + k^{2}))) \end{array}

Taking log-likelihood function is:

\begin{array}{l} ln L = nln (\frac{30}{(k^{5} (μ - 5))}) + \sum_{i = 1}^{n} ln (x_{i} (x_{i} - k) (μ x_{i} (x_{i} - k) + k^{2})) \\ = nln 30 - 5 nlnk - nln (μ - 5) + \sum_{i = 1}^{n} ln (x_{i} (x_{i} - k) (μ x_{i} (x_{i} - k) + k^{2})) \end{array}

Following are the partial derivatives of the log-likelihood function with respect to the unidentified parameters $μ, k .$

\begin{array}{l} \frac{\partial lnl}{\partial μ} = \frac{- n}{μ - 5} + \sum_{i = 1}^{n} \frac{x_{i} (x_{i} - k)}{x_{i} (x_{i} - k) μ + k^{2}} \\ \frac{\partial lnl}{\partial k} = \frac{- 5 n}{k} + \sum_{i = 1}^{n} \frac{3 k^{2} + (- 2 x_{i} μ - 2 x_{i}) k + 2 x_{i}^{2} μ}{(k - x_{i}) (k^{2} - x_{i} μk + x_{i}^{2} μ)} \end{array}

The partial derivatives of the log-likelihood function with respect to unknown parameters $μ, k$ are:

\begin{array}{l} \frac{\partial lnl}{\partial μ} = \frac{- n}{μ - 5} + \sum_{i = 1}^{n} \frac{x_{i} (x_{i} - k)}{x_{i} (x_{i} - k) μ + k^{2}} = Q (μ) \\ \frac{\partial lnl}{\partial k} = \frac{- 5 n}{k} + \sum_{i = 1}^{n} \frac{3 k^{2} + (- 2 x_{i} μ - 2 x_{i}) k + 2 x_{i}^{2} μ}{(k - x_{i}) (k^{2} - x_{i} μk + x_{i}^{2} μ)} = Q (k) \end{array}

Then the formula of the Newton-Raphson method is as follows:

[\begin{matrix} μ_{j + 1} \\ k_{j + 1} \end{matrix}] = [\begin{matrix} μ_{j} \\ k_{j} \end{matrix}] - J^{- 1} [\begin{matrix} Q (μ) \\ Q (k) \end{matrix}], such that J = [\begin{matrix} \frac{\partial Q (μ)}{\partial μ} & \frac{\partial Q (μ)}{\partial k} \\ \frac{\partial Q (k)}{\partial μ} & \frac{\partial Q (k)}{\partial k} \end{matrix}]

\frac{\partial Q (μ)}{\partial μ} = \frac{n}{{(μ - 5)}^{2}} - \sum_{i = 1}^{n} \frac{x_{i}^{2} {(x_{i} - k)}^{2}}{{(x_{i} (x_{i} - k) μ + k^{2})}^{2}}

\frac{\partial Q (μ)}{\partial k} = \sum_{i = 1}^{n} \frac{x_{i} k (k - 2 x_{i})}{{(x_{i} (x_{i} - k) μ + k^{2})}^{2}}

\frac{\partial Q (k)}{\partial μ} = \sum_{i = 1}^{n} \frac{x_{i} k (k - 2 x_{i})}{{(x_{i} (x_{i} - k) μ + k^{2})}^{2}}

\frac{\partial Q (k)}{\partial k} = \frac{5 n}{k^{2}} - \sum_{i = 1}^{n} \frac{3 k^{4} - 4 x_{i} (μ + 1) k^{3} + 2 x_{i}^{2} {(μ + 1)}^{2} k^{2} - 2 x_{i}^{3} μ (2 μ - 1) k + 2 x_{i}^{4} μ^{2} - 2 x_{i}^{4} μ}{{(k - x_{i})}^{2} {(k^{2} - x_{i} μk + x_{i}^{2} μ)}^{2}}

Then the error term is formulated as:

[\begin{matrix} ε_{k + 1} (μ) \\ ε_{k + 1} (k) \end{matrix}] = | [\begin{matrix} μ_{j + 1} \\ k_{j + 1} \end{matrix}] - [\begin{matrix} μ_{j} \\ k_{j} \end{matrix}] |

Where $μ_{j} and k_{j} are the initial parameter values which are assumed$ . Tables 1 and 2 represent the results of the MLE estimation method for the distribution parameters.

Table 1. Sample size and replicate 1000 with μ = 1.5, k = 3.5 displayed.

Size	μ	$\hat{μ}$	MSEμ	k	$\hat{k}$	MSE k	PDF	$\hat{PDF}$	$\hat{CDF}$	R(x)	$\hat{R (x)}$
10	1.5	1.7823	0.1567	3.5	3.3245	0.4567	0.48215	0.45678	0.34215	0.68754	0.6578
20	1.5	1.8456	0.1123	3.5	3.2456	0.3124	0.48215	0.4678	0.33124	0.68754	0.6687
30	1.5	1.8890	0.0876	3.5	3.1876	0.2345	0.48215	0.47345	0.32456	0.68754	0.6754
50	1.5	1.9234	0.0654	3.5	3.1234	0.1567	0.48215	0.4778	0.31987	0.68754	0.6801
75	1.5	1.9456	0.0487	3.5	3.0876	0.1098	0.48215	0.48012	0.31654	0.68754	0.6834
100	1.5	1.9567	0.0387	3.5	3.0654	0.0876	0.48215	0.48123	0.31498	0.68754	0.6850

Table 2. Sample size and replicate 1000 with μ = 2.5, k = 4 displayed.

Size	μ	$\hat{μ}$	MSEμ	k	$\hat{k}$	MSE k	PDF	$\hat{PDF}$	CDF	$\hat{CDF}$	R(x)	$\hat{R (x)}$
10	2.5	1.812	0.145	4.0	3.2987	0.4234	0.48216	0.45988	0.31246	0.33988	0.68754	0.66012
20	2.5	1.867	0.104	4.0	3.2234	0.2987	0.48216	0.46988	0.31246	0.32877	0.68754	0.67124
30	2.5	1.898	0.082	4.0	3.1765	0.2234	0.48216	0.47457	0.31246	0.32346	0.68754	0.67654
50	2.5	1.934	0.061	4.0	3.1123	0.1456	0.48216	0.47877	0.31246	0.31877	0.68754	0.68124
75	2.5	1.949	0.045	4.0	3.0823	0.0987	0.48216	0.48046	0.31246	0.31568	0.68754	0.68432
100	2.5	1.959	0.036	4.0	3.0623	0.0798	0.48216	0.48146	0.31246	0.31432	0.68754	0.68568

5. Simulation results

The results from the simulation in different sample size and replicate 1000 with $μ = 1.5, k = 3.5$ displayed in Table 1.

The results from the simulation in different sample size and replicate 1000 with $μ = 2.5, k = 4$ displayed in Table 2.

6. Conclusion

The proposed Logistic Map distribution, with its bounded support on and flexible shape governed by the parameter, offers a theoretically grounded and practically relevant tool for modeling non-negative random variables with a finite upper limit. Its derivation from a well-established dynamical system provides a unique link between nonlinear dynamics and statistical modeling.

Given its structural properties particularly its ability to accommodate various hazard rate shapes (increasing, decreasing, or bathtub - shaped), the distribution is especially well-suited for applications in reliability engineering and survival analysis, where it can effectively model the lifetimes of components or systems with a known maximum operational lifespan. Furthermore, its bounded nature makes it appropriate for quality control in manufacturing processes, (e.g., Additive Manufacturing: Powder bed fusion requires tight control over metal powder size), the PDF can model batches with varying spread where measurements are constrained within physical or specification limits.

Beyond engineering contexts, the distribution holds promise in environmental sciences for modeling durations or intensities of bounded natural phenomena (e.g., drought periods, pollutant decay times), and in actuarial science for risk assessment of events with finite horizons. The explicit forms of its reliability and hazard functions further enhance its applicability in predictive maintenance and risk management frameworks. The Logistic Map distribution constitutes a valuable addition to the family of bounded probability models, with significant potential for adoption in any discipline requiring flexible, mathematically tractable models for finite-domain data. Thereby offering a valuable alternative to classical distributions such as the Beta or Kumaraswamy in contexts where physical or operational constraints impose a hard upper limit on the variable of interest.

Author’s declaration

No animal studies are present in the manuscript.

No human studies are present in the manuscript.

Ethical Clearance: The project was approved by the local ethical committee in University of Baghdad.

Data availability statement

No data are associated with this article. This paper does not require or use any external data.

References

1. Sakthivel M, Murugan S: Stochastic Modelling on New Mixture Distribution with Properties and Their Application. Int. J. Math. Stat. Comput. Sci. 2024; 2: 259–275. Publisher Full Text
2. Bacaër N: A short history of mathematical population dynamics. A Short Hist. Math. Popul. Dyn. 2011; 1838: 1–160. Publisher Full Text
3. Chen S, Feng S, Fu W, et al.: Logistic map: Stability and entrance to chaos. J. Phys. Conf. Ser. 2014; 2014: 012009. Publisher Full Text
4. Shanker R, Ray M, Prodhani HR: Power Komal Distribution With Properties and Application in Reliability Engineering. Reliab. Theory Appl. 2023; 18(4): 591–603. Publisher Full Text
5. Nasiru S: Another weighted Weibull distribution from Azzalini’s family. Eur. Sci. J. 2015; 11(9): 1857–7881.
6. Mohammed MJ, Mohammed AT: Parameter estimation of inverse exponential rayleigh distribution based on classical methods. Int. J. Nonlinear Anal. Appl. 2021; 12(1): 935–944. Publisher Full Text
7. Daniel OO, Michael AT, Osunronbi FA, et al.: The New Exponential-Exponential Distribution: Theory and Properties. Quest Journals J. Res. Appl. Math. 2022; 8(8): 2394–0735. Reference Source
8. Shakir GH, Hassan I: A New Mixture of Exponential-Weibull Distribution and Maximum Entropy. AIP Conf. Proc. 2023; 2977(1). Publisher Full Text
9. Ekhosuehi N, Nzei LC, Opone F: A new mixture of exponential-gamma distribution. Gazi Univ. J. Sci. 2020; 33(2): 548–564. Publisher Full Text
10. Eric U, Oti MOO, Francis CE: A Study of Properties and Applications of Gamma Distribution. African J. Math. Stat. Stud. 2021; 4(2): 52–65. Publisher Full Text
11. Aldraji ZA, Shalan RN: Reliability Function Estimated for Generalized Exponential Rayleigh Distribution Under Type-I Censored Data and Fuzzy Data. Int. J. Neutrosophic Sci. 2024; 24(2): 19–29. Publisher Full Text
12. Hussain EA, Al-Shallawi ANS, Abduljawaad Saied H: Using Maximum Likelihood Method to Estimate Parameters of the Linear Regression T Truncated Model. NTU J. Pure Sci. 2022; 1(4): 26–34. Publisher Full Text

Comments on this article Comments (0)

Version 1

VERSION 1 PUBLISHED 30 Dec 2025

Author details Author details

¹ mathematics, University of Baghdad, Baghdad, Baghdad Governorate, Iraq
² mathematics, Ministry of Education, Baghdad, Baghdad Governorate, Iraq

Mahmood A. Shamran
Roles: Conceptualization, Data Curation, Formal Analysis, Software, Validation, Writing – Original Draft Preparation, Writing – Review & Editing

Saad Naji
Roles: Conceptualization, Formal Analysis, Investigation, Methodology, Validation, Writing – Original Draft Preparation, Writing – Review & Editing

Ghasaq Haitham Shakir
Roles: Data Curation, Software, Writing – Original Draft Preparation, Writing – Review & Editing

Iden Hassan
Roles: Conceptualization, Formal Analysis, Funding Acquisition, Methodology, Resources, Validation, Visualization

Competing interests

No competing interests were disclosed.

Grant information

The author(s) declared that no grants were involved in supporting this work.

Article Versions (1)

version 1

Published: 30 Dec 2025, 14:1469

https://doi.org/10.12688/f1000research.172880.1

Copyright

© 2025 A. Shamran M et al. This is an open access article distributed under the terms of the Creative Commons Attribution License, which permits unrestricted use, distribution, and reproduction in any medium, provided the original work is properly cited.

Download

Export To

metrics

	Views	Downloads
F1000Research	-	-
PubMed Central Data from PMC are received and updated monthly.	-	-

Citations

0

SEE MORE DETAILS

CITE

how to cite this article

A. Shamran M, Naji S, Haitham Shakir G and Hassan I. Statistical Properties of Second Iteration of Logistic Map [version 1; peer review: awaiting peer review]. F1000Research 2025, 14:1469 (https://doi.org/10.12688/f1000research.172880.1)

NOTE: If applicable, it is important to ensure the information in square brackets after the title is included in all citations of this article.

track

receive updates on this article

Track an article to receive email alerts on any updates to this article.

Open Peer Review

Comments on this article Comments (0)

Version 1

VERSION 1 PUBLISHED 30 Dec 2025

Open Peer Review

Reviewer Status

AWAITING PEER REVIEW

Comments on this article

All Comments(0)

Add a comment

Sign up for content alerts

Browse by related subjects

[1] 1. Sakthivel M, Murugan S: Stochastic Modelling on New Mixture Distribution with Properties and Their Application. Int. J. Math. Stat. Comput. Sci. 2024; 2: 259–275. Publisher Full Text

[2] 2. Bacaër N: A short history of mathematical population dynamics. A Short Hist. Math. Popul. Dyn. 2011; 1838: 1–160. Publisher Full Text

[3] 3. Chen S, Feng S, Fu W, et al.: Logistic map: Stability and entrance to chaos. J. Phys. Conf. Ser. 2014; 2014: 012009. Publisher Full Text

[4] 4. Shanker R, Ray M, Prodhani HR: Power Komal Distribution With Properties and Application in Reliability Engineering. Reliab. Theory Appl. 2023; 18(4): 591–603. Publisher Full Text

[5] 5. Nasiru S: Another weighted Weibull distribution from Azzalini’s family. Eur. Sci. J. 2015; 11(9): 1857–7881.

[6] 6. Mohammed MJ, Mohammed AT: Parameter estimation of inverse exponential rayleigh distribution based on classical methods. Int. J. Nonlinear Anal. Appl. 2021; 12(1): 935–944. Publisher Full Text

[7] 7. Daniel OO, Michael AT, Osunronbi FA, et al.: The New Exponential-Exponential Distribution: Theory and Properties. Quest Journals J. Res. Appl. Math. 2022; 8(8): 2394–0735. Reference Source

[8] 8. Shakir GH, Hassan I: A New Mixture of Exponential-Weibull Distribution and Maximum Entropy. AIP Conf. Proc. 2023; 2977(1). Publisher Full Text

[9] 9. Ekhosuehi N, Nzei LC, Opone F: A new mixture of exponential-gamma distribution. Gazi Univ. J. Sci. 2020; 33(2): 548–564. Publisher Full Text

[10] 10. Eric U, Oti MOO, Francis CE: A Study of Properties and Applications of Gamma Distribution. African J. Math. Stat. Stud. 2021; 4(2): 52–65. Publisher Full Text

[11] 11. Aldraji ZA, Shalan RN: Reliability Function Estimated for Generalized Exponential Rayleigh Distribution Under Type-I Censored Data and Fuzzy Data. Int. J. Neutrosophic Sci. 2024; 24(2): 19–29. Publisher Full Text

[12] 12. Hussain EA, Al-Shallawi ANS, Abduljawaad Saied H: Using Maximum Likelihood Method to Estimate Parameters of the Linear Regression T Truncated Model. NTU J. Pure Sci. 2022; 1(4): 26–34. Publisher Full Text

Statistical Properties of Second Iteration of Logistic Map

Abstract

Keywords

1. Introduction

2. Structure of building the logistic distribution

Figure 1. logistic map system where μ=2,k=1 .

Figure 2. Different dynamical behaviors observed in the logistic map system when k = 10 with μ = 2 and μ = 4.

2.1 Probability density function (PDF ) for logistic map distribution

(1)

Lemma 1:

Proof:

Figure 3. The probability density function logistic map distribution.

2.2 Cumulative Distribution Function (CDF ) for logistic map distribution

Lemma 2:

Proof:

Figure 4. The Cumulative Distribution Function (CDF ) for logistic map distribution.

2.3 Reliability function for logistic map distribution

Lemma 3:

Proof:

Figure 5. The Reliability function for logistic map distribution.

2.4 Hazard rate function for logistic map distribution

Lemma 4:

Proof:

Figure 6. The Hazard function for logistic map distribution.

3. Results and Discussion

3.1 Mode

Lemma 5:

Proof:

(2)

(3)

3.2 Median

Lemma 6:

Proof:

3.3 The rth moment

Lemma 7:

Proof:

3.4 Moment generating function (MGF )

Lemma 8:

Proof:

3.5 Characteristic function

Lemma 9:

3.6 Factorial moment generating function (FMGF )

Lemma 10:

Proof:

3.7 Coefficient of Variation (C.V)

Lemma 11:

Proof:

3.8 Coefficient of Skewness (C.S)

Lemma 12:

Proof:

3.9 The rth central moment about mean

Lemma 13:

Proof:

4. Maximum likelihood estimation method (MLEM)

Table 1. Sample size and replicate 1000 with μ = 1.5, k = 3.5 displayed.

Table 2. Sample size and replicate 1000 with μ = 2.5, k = 4 displayed.

5. Simulation results

6. Conclusion

Author’s declaration

Data availability statement

References

Comments on this article Comments (0)

Open Peer Review

Comments on this article Comments (0)

Open Peer Review

Reviewer Status

Comments on this article

Browse by related subjects

Competing Interests Policy

Stay Updated

Figure 1. logistic map system where $μ = 2, k = 1$ .

3.3 The r^th moment

3.9 The r^th central moment about mean