Assessing nonlinearities in the GFP random mutagenesis landscape using the Power Transform

Dmitry A. Petrov; Dmitry N. Ivankov

doi:10.12688/f1000research.175373.1

Home Browse Assessing nonlinearities in the GFP random mutagenesis landscape using...

ALL Metrics

-

Views

-

Downloads

Get PDF

Get XML

Export

▬

✚

Research Article

Assessing nonlinearities in the GFP random mutagenesis landscape using the Power Transform

[version 1; peer review: awaiting peer review]

Dmitry A. Petrov¹, Dmitry N. Ivankov ¹

PUBLISHED 31 Dec 2025

Author details Author details

¹ Center for Molecular and Cellular Biology, Skolkovo Institute of Science and Technology, Moscow, 121205, Russian Federation

Dmitry A. Petrov
Roles: Formal Analysis, Investigation, Methodology, Software, Validation, Visualization, Writing – Original Draft Preparation

Dmitry N. Ivankov
Roles: Conceptualization, Data Curation, Funding Acquisition, Project Administration, Resources, Supervision, Writing – Original Draft Preparation, Writing – Review & Editing

OPEN PEER REVIEW

REVIEWER STATUS AWAITING PEER REVIEW

This article is included in the Genomics and Genetics gateway.

Abstract

Abstract*

Background

Epistasis, a non-additive contribution of mutations to fitness, complicates genotype-to-phenotype prediction and is often confounded by nonlinearities in phenotype measurements. The Power Transform method, particularly Box-Cox, has been used to reduce epistasis in small, combinatorially complete datasets by linearizing phenotypic scales. However, its applicability to large landscapes, especially those generated by (quasi-)random mutagenesis, remains unclear.

Methods

Here, we apply both Box-Cox and Yeo-Johnson Power Transforms to the extensively characterized green fluorescent protein (GFP) fitness landscape, which contains hundreds of thousands of two- and three-dimensional combinatorially complete datasets.

Results

When applied to individual hypercubes, Box-Cox reduces pairwise epistasis by 19.4% on average, whereas Yeo-Johnson – despite accommodating negative values – slightly increases epistasis (by 4.45%). Moreover, in a notable fraction of hypercubes, both methods increase the magnitude of epistatic coefficients, indicating that Power Transform does not universally reduce nonlinearity at the local scale. In contrast, applying Yeo-Johnson to the largest connected component of the GFP landscape (20,872 genotypes) successfully reduces both pairwise (by 3.86%) and third-order epistasis (by 11.6%), with the majority of coefficients decreasing in magnitude.

Conclusions

Our results demonstrate that Power Transform can be extended to large, real-world landscapes generated by random mutagenesis, but only when applied to connected sublandscapes. Our findings highlight a critical distinction between global and local linearization and caution against assuming that Power Transform always diminishes epistasis.

Keywords

Epistasis, combinatorially complete dataset, hypercube, fitness landscape, nonlinearity, power transform, Box-Cox, Yeo-Johnson

Corresponding author: Dmitry N. Ivankov

Competing interests: No competing interests were disclosed.

Grant information: The research was funded by the Russian Science Foundation, grant No. 25-14-00491, https://rscf.ru/project/25-14-00491/
The funders had no role in study design, data collection and analysis, decision to publish, or preparation of the manuscript.

Copyright: © 2025 Petrov DA and Ivankov DN. This is an open access article distributed under the terms of the Creative Commons Attribution License, which permits unrestricted use, distribution, and reproduction in any medium, provided the original work is properly cited.

How to cite: Petrov DA and Ivankov DN. Assessing nonlinearities in the GFP random mutagenesis landscape using the Power Transform [version 1; peer review: awaiting peer review]. F1000Research 2025, 14:1478 (https://doi.org/10.12688/f1000research.175373.1) First published: 31 Dec 2025, 14:1478 (https://doi.org/10.12688/f1000research.175373.1) Latest published: 31 Dec 2025, 14:1478 (https://doi.org/10.12688/f1000research.175373.1)

Introduction

Epistasis, the dependence of a mutation’s effect on its genetic background, represents a major obstacle to predicting fitness and phenotype from genotype (Cordell, 2002; Phillips, 2008; Moore, Williams, 2009; Poelwijk et al., 2019; Verhoeven et al., 2010; de Visser et al., 2011; Weinreich et al., 2013; Ivankov et al., 2014; MacKay, 2014; Sailer, Harms, 2017; Zhou et al., 2022; Johnson et al., 2023). Therefore, uncovering the patterns that govern epistasis is essential for achieving accurate phenotype and fitness predictions. Experimental data to investigate such patterns can be obtained by measuring how fitness and/or phenotype change in response to specific genetic alterations (Poelwijk et al., 2019; de Visser et al., 2009; Hall et al., 2010; Khan et al., 2011; Olson et al., 2014; Anderson et al., 2015; Sarkisyan et al., 2016; Pokusaeva et al., 2019; Johnston et al., 2024). Because fitness is often more challenging to measure than phenotype, researchers frequently use phenotypic measurements as a proxy for fitness (Olson et al., 2014; Sarkisyan et al., 2016). In this work, we treat fitness as a specific type of phenotype and use the terms “fitness” and “phenotype” interchangeably.

Epistatic coefficients can be calculated from so-called combinatorially complete datasets (Weinreich et al., 2013). In such datasets, for a chosen set of L sites (e.g., protein positions), each site has two possible alleles (e.g., wild-type or mutant), and all 2^L possible genotypes have been experimentally assayed. If we assign a binary axis to each mutation (0 – no mutation, 1 – mutation present), this dataset forms an L-dimensional hypercube in sequence space (in this work, we use terms “combinatorially complete dataset” and “hypercube” interchangeably). Several studies have deliberately generated such combinatorially complete datasets (Poelwijk et al., 2019; de Visser et al., 2009; Hall et al., 2010; Khan et al., 2011; Olson et al., 2014; Anderson et al., 2015; Johnston et al., 2024). Alternatively, mutant libraries can be created using (quasi-)random mutagenesis approaches (Sarkisyan et al., 2016; Pokusaeva et al., 2019). In the resulting phenotype-genotype maps, epistatic coefficients can still be computed provided one identifies embedded combinatorially complete datasets. All such datasets can be efficiently found using the HypercubeME algorithm (Esteban et al., 2019).

The standard methods for quantifying epistasis assume that the phenotypic effects of individual mutations combine additively (Fisher, 1919; Cheverud, Routman, 1995; Phillips, 2008; Weinreich et al., 2013; MacKay, 2014; Poelwijk et al., 2016). However, if mutations instead interact multiplicatively – or through any other nonlinear relationship – the additive model will infer apparent epistasis even in the absence of true interaction between mutations (Sailer, Harms, 2017). Consequently, any nonlinear transformation of the phenotype will alter the amount of detected epistasis. When analyzing empirical landscapes, it remains unclear how much of the observed epistasis stems from such nonlinearity versus genuine interactions between mutations. This raises a critical question for each landscape under study: what amount of epistasis would be detected if we minimize, as far as possible, the contribution from nonlinearity?

In 2017, Sailer and Harms utilized the Power Transform method with the Box-Cox transformation, to remove nonlinearities from epistatic landscapes (Sailer, Harms, 2017). They analyzed seven small combinatorially complete datasets, each comprising five to six loci (i.e., consisting of 2⁵ = 32 or 2⁶ = 64 genotypes) (de Visser et al., 2009; Hall et al., 2010; Khan et al., 2011; Weinreich et al., 2013; Anderson et al., 2015). Sailer and Harms clearly demonstrated that five of these seven datasets still exhibited higher-order epistasis even after applying the Power Transform to correct for nonlinearity (Sailer, Harms, 2017). Thus, applying the Power Transform to individual combinatorially complete datasets offers significant promise for reducing epistasis caused by nonlinear scaling. The next logical step is to extend this approach to entire fitness landscapes – particularly those generated by (quasi-)random mutagenesis (Sarkisyan et al., 2016; Pokusaeva et al., 2019).

In this study, we explore the application of the Power Transform to an entire landscape using the example of the classic landscape of green fluorescence protein (GFP) obtained via random mutagenesis (Sarkisyan et al., 2016), which contains numerous two- and three-dimensional hypercubes (i.e., combinatorially complete datasets of size 2² = 4 and 2³ = 8). When we apply the Box-Cox-based (Box, Cox, 1964) Power Transform (as in Sailer, Harms, 2017) to individual hypercubes, pairwise epistatic coefficients decrease on average by 19.4%, and third-order coefficients decrease by 1.30%. Surprisingly, however, when we use the more flexible Yeo-Johnson transformation instead, epistatic coefficients increase on average – by 4.45% for pairwise epistasis and by 0.43% for third-order epistasis.

Applying the Power Transform to the entire landscape proved feasible only when the landscape is connected. Using the Yeo-Johnson (Yeo, Johnson, 2000) transformation (the Box-Cox transformation failed due to its restrictions), we applied the Power Transform to the largest connected sub-landscape of GFP, which comprises 20,872 genotypes. In this case, the average pairwise epistatic coefficient decreased by 3.86%, and the third-order coefficient decreased by 11.5%.

Our results demonstrate the presence of higher-order epistasis in the GFP landscape both before and after the application of the Power Transform method, supporting earlier conclusions about the importance of higher-order epistasis in empirical fitness landscapes (Weinreich et al., 2013; Sailer, Harms, 2017). Our findings also reveal that the effectiveness of nonlinearity removal in individual hypercubes depends critically on the choice of transformation – Box-Cox (Box, Cox, 1964) versus Yeo-Johnson (Yeo, Johnson, 2000). Most importantly, we demonstrate that the Yeo-Johnson-based Power Transform can be applied to any large landscape – provided it is connected.

Methods

Identification of combinatorially complete datasets

In the GFP landscape (Sarkisyan et al., 2016), we found 408,673 two-dimensional and 1,446 three-dimensional combinatorially complete datasets using the HypercubeME algorithm (Esteban et al., 2019).

Power transform with box-cox transformation

The approach considered by Sailer and Harms to reduce nonlinearities in fitness landscapes (Sailer, Harms, 2017) uses the Power Transform method with a modification of the Box-Cox power transformation (Box, Cox, 1964). For each single mutation present in the landscape, the averaged effect across all genetic contexts is computed, and then, based on these effects, an additive phenotype is calculated for each genotype (Sailer, Harms, 2017). The stepwise approach is as follows (Sailer, Harms, 2017):

1. Compute approximations of additive phenotypes:

(1)

{\hat{P}}_{add, i} = \sum_{j = 1}^{j \leq L} ⟨ ∆ P_{j} ⟩ x_{i, j},

where ⟨ΔP_j⟩ is the average effect of mutation j across all backgrounds calculated from the measured phenotypes P_obs, x_i,j is an index that encodes whether or not mutation j is present in genotype i, and L is the number of sites.

2. Fit a nonlinear least squares regression of observed phenotypes vs. approximations of additive phenotypes:

(2)

{\vec{P}}_{obs} = \frac{{({\hat{\vec{P}}}_{add} + A)}^{λ} - 1}{λ {(GM)}^{λ - 1}} + B,

where A and B are translation constants, GM is the geometric mean of

({\hat{\vec{P}}}_{add} + A)

, and λ is a scaling parameter.

3. Apply the inverse transformation to the observed phenotypes using the fitted parameters, thereby linearizing observed phenotypes:

(3)

P_{obs, linear} = {[\hat{λ} {(GM)}^{λ - 1} (P_{obs} - \hat{B}) + 1]}^{1 / \hat{λ}} - \hat{A}

When we attempted to use the original code from (Sailer, Harms, 2017) on test combinatorially complete datasets of 4 and 8 genotypes, the program crashed in more than half of the cases. To investigate this issue, we implemented our own version following the equations in (Sailer, Harms, 2017). We wrote the implementation in Python 3, using the NumPy, SciPy, and scikit-learn libraries.

Specifically, we first computed additive phenotypes as defined in Eq. 1. Then, to obtain an initial guess for the Box-Cox parameter λ, we applied the power_transform function from scikit-learn library to the observed versus additive phenotype data. Using this initial guess, we performed a refined fit of the nonlinear model (Eq. 2) using scipy.optimize.curve_fit function. Our implementation succeeded in a higher fraction of cases than the implementation from (Sailer, Harms, 2017). Therefore, we used our implementation for all subsequent analyses involving the Box-Cox-based Power Transform.

All Python scripts are available at https://github.com/ivankovlab/power_transform.

Power transform with Yeo-Johnson transformation

Note that the Box-Cox-based (Box, Cox, 1964) Power Transform cannot be applied when either the observed or additive phenotypes take non-positive values. Although measured phenotypes in the GFP landscape are strictly positive, computed additive phenotypes can occasionally become zero or negative during analysis, which makes the Box-Cox transformation (Box, Cox, 1964) inapplicable. To address this limitation, we adopted an alternative formulation of the Power Transform based on the Yeo-Johnson transformation (Yeo, Johnson, 2000), which can accommodate non-positive values:

(4)

P_{obs} = \frac{1}{{(GM)}^{λ - 1}} {\begin{matrix} \frac{{(P_{add} + A + 1)}^{λ} - 1}{λ} if P_{add} + A \geq 0, λ \neq 0 \\ ln (P_{add} + A + 1) if P_{add} + A \geq 0, λ = 0 \\ - \frac{{(- (P_{add} + A) + 1)}^{2 - λ} - 1}{2 - λ} if P_{add} + A < 0, λ \neq 2 \\ - ln (- (P_{add} + A) + 1) if P_{add} + A < 0, λ = 2 \end{matrix} + B

We fit this model to our data; the inverse transformation looks as follows:

(5)

P_{obs, linear} = - A + {\begin{matrix} {(λW + 1)}^{\frac{1}{λ}} - 1 if W \geq 0, λ \neq 0 \\ exp (W) - 1 if W \geq 0, λ = 0 \\ 1 - {(1 - (2 - λ) W)}^{\frac{1}{2 - λ}} if W < 0, λ \neq 2 \\ 1 - exp (- W) if W < 0, λ = 2 \end{matrix},

where

W = (P_{obs} - B) {(GM)}^{λ - 1}

.

Set of combinatorially complete datasets

To enable a comparison between the Box-Cox (Box, Cox, 1964) and Yeo-Johnson (Yeo, Johnson, 2000) transformations, we restricted our analysis to hypercubes for which both methods succeeded (i.e., produced valid results without errors). Of the 408,673 two-dimensional hypercubes, both transformations succeeded for 403,162 hypercubes. For all 1,446 three-dimensional hypercubes, both methods succeeded without failure.

Identification of connected components

We identified connected components of the landscape in two stages: (1) constructing from genotypes with measured phenotypes a connectivity graph in sequence space and (2) detecting connected components in the graph. We represented each genotype as a node and connected two nodes by an edge if Hamming distance between them equaled 1 (i.e., genotypes differed at exactly one amino acid position).

To avoid the O(N ²) complexity of pairwise comparison (where N is the number of genotypes), we generated instead all possible single-mutation neighbors for each genotype – considering the twenty standard amino acids plus the position encoded by a stop codon (overall 21 symbols) – and checked whether each neighbor existed in the landscape. This changed the complexity to O(N·M·K), where M is the number of variable positions and K = 21. We then applied a standard breadth-first search algorithm to identify connected components (Bundy, Wallen, 1984).

We found that the experimental GFP landscape contains only one large connected component with more than two genotypes, comprising 20,872 genotypes.

Calculation of epistatic coefficients

We calculated epistatic coefficients according to the Walsh-Hadamard matrix (Weinreich et al., 2013; Poelwijk et al., 2016):

(6)

\bar{ε} = VH \bar{y},

where

\bar{y}

is the vector of phenotypes within a combinatorially complete landscape,

\bar{ε}

is the vector of background-averaged epistatic terms;

H

is the operator for background-averaged epistasis, defined recursively as:

(7)

H_{n + 1} = (\begin{matrix} H_{n} & H_{n} \\ H_{n} & - H_{n} \end{matrix}), H_{0} = 1;

the recursive definition for the weighting matrix $V$ is

(8)

V_{n + 1} = (\begin{matrix} \frac{1}{2} V_{n} & 0 \\ 0 & - V_{n} \end{matrix}), V_{0} = 1 .

Following Weinreich et al. (2013), we quantified the total amount of epistasis as:

(9)

E = \sqrt{\frac{\sum_{i = 1}^{N} {ε_{i}}^{2}}{N}},

where

ε_{i}

are the epistatic coefficients of the highest order present in each hypercube, and

N

is the number of the hypercubes embedded in the full landscape.

Statistical comparison of distributions

To assess whether Power Transform significantly altered distribution of epistatic coefficients, we performed nonparametric statistical tests. We used two-sided Mann-Whitney U test to compare the full distributions of epistatic coefficients before and after transformation, and one-sided Mann-Whitney U test to compare the distributions of their absolute values.

Estimating uncertainty in epistatic coefficients

We did not find a way to incorporate measurement error in the Power Transform method. Therefore, to estimate the uncertainty in average value of epistatic coefficients resulting from measurement error in GFP fluorescence, we performed ten runs of the Power Transform for each transformation (both Box-Cox and Yeo-Johnson), using phenotype values randomly generated according to their experimentally determined value and standard deviation. As the standard deviation for any GFP variant, we took value of ± 0.1 estimated from 3642 wild-type GFP measurements (Sarkisyan et al., 2016). For each epistatic coefficient, we calculated its standard deviation across these runs, took the average of these standard deviations over all epistatic coefficients $\bar{σ}$ , and divided it by the square root of the number $n$ of epistatic coefficients to get the estimate of uncertainty $σ_{X}$ in average value of epistatic coefficients:

(10)

σ_{X} = \frac{\bar{σ}}{\sqrt{n}} .

Results

Dataset

To investigate and illustrate the capabilities and potential of the Power Transform for experimental fitness landscapes, especially those generated by (quasi-)random mutagenesis, we focused on a single, yet extensively characterized, classic landscape of green fluorescence protein (GFP) (Sarkisyan et al., 2016). That study resulted in 1,817 single mutations across 233 positions in GFP, either individually or in combinations (up to mutants carrying fifteen single mutations), yielding fluorescence measurements for 51,715 missense variants from the neighborhood of wild-type GFP (Sarkisyan et al., 2016).

The GFP landscape is nonlinear; its nonlinearity is largely of a “threshold” nature (Tawfik, 2010; Sarkisyan et al., 2016). Protein stability is the most likely factor underlying both this nonlinearity and the overwhelming majority of observed uni-dimensional epistasis.

The GFP landscape contains 408,673 two-dimensional hypercubes and 1,446 three-dimensional hypercubes (see Materials and Methods). The availability of three-dimensional hypercubes is particularly valuable, as it enables robust detection of higher-order epistasis – in our case, third-order epistasis.

Application of power transform to individual combinatorially complete datasets

To assess how the amount of epistasis changes after applying the Power Transform, we computed epistatic coefficients before any transformation and after applying the Power Transform with either Box-Cox or Yeo-Johnson variant. It should be noted that, among all 408,673 two-dimensional hypercubes, both the Box-Cox and Yeo-Johnson versions succeeded for a common subset of 403,162 hypercubes; therefore, we report all subsequent calculations and results only for this group.

Before any transformation of the phenotypes, the average epistasis (calculated as the root-mean-square of all epistatic coefficients) was 0.6741 ± 0.0002 for pairwise epistasis and 0.460 ± 0.003 for third-order epistasis. The corresponding distributions are shown in Figure 1A (pairwise) and Figure 2A (third-order).

Figure 1. Distribution of pairwise epistatic coefficients computed (A) before Power Transform, (B) after the Box-Cox-based Power Transform, and (C) after the Yeo-Johnson-based Power Transform.

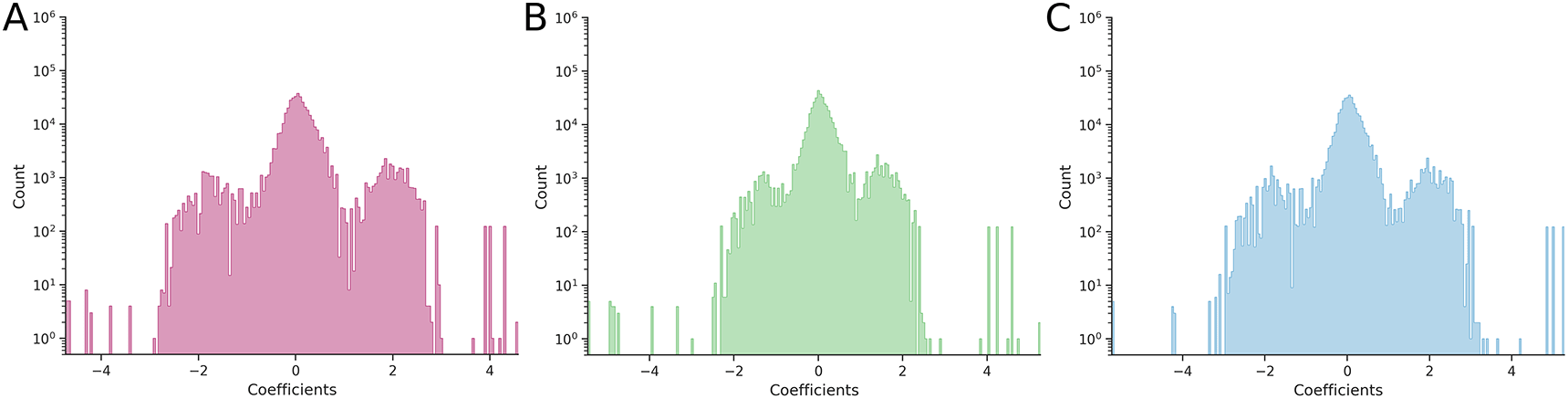
In both (B) and (C) cases, the Power Transform was applied separately to individual two-dimensional combinatorially complete datasets.

Figure 2. Distribution of third-order epistatic coefficients computed (A) before Power Transform, (B) after the Box-Cox-based Power Transform, and (C) after the Yeo-Johnson-based Power Transform.

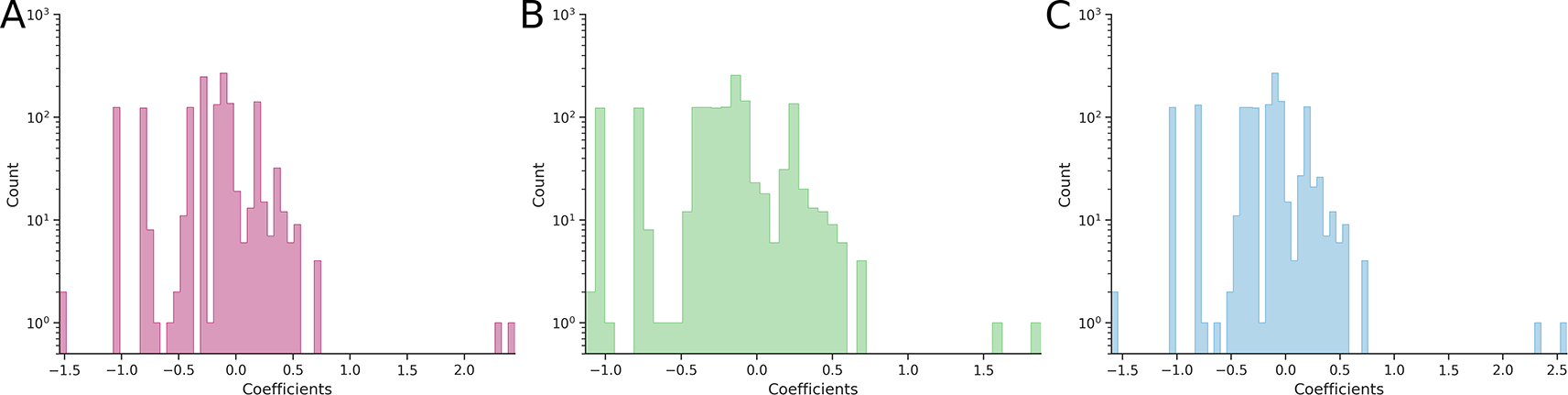
In both (B) and (C) cases, the Power Transform was applied separately to individual three-dimensional combinatorially complete datasets.

We then applied the Power Transform method, expecting that the distributions of epistatic coefficients would become narrower and that the average epistatic coefficients would decrease in absolute value, as the Power Transform should remove “excessive” nonlinearity, thereby reducing the magnitude of epistatic coefficients.

Application of the Box-Cox-based Power Transform to each hypercube individually confirmed our expectations: the average epistatic coefficient decreased to 0.5432 ± 0.0002 (a 19.4% reduction compared to the reference value) for two-dimensional hypercubes and to 0.454 ± 0.003 (a 1.30% reduction) for three-dimensional hypercubes. Comparison of the pairwise epistasis distributions (Figures 1A and 1B) showed a statistically significant narrowing (p = 6.38·10⁻⁹), whereas comparison of third-order epistatic coefficient distributions (Figures 2A and 2B) showed no significant effect (p = 0.178).

In contrast, application of the Yeo-Johnson-based Power Transform led to a slight increase in epistasis: the average coefficient rose to 0.7040 ± 0.0002 (a 4.45% increase) for two-dimensional hypercubes and to 0.462 ± 0.003 (a 0.43% increase) for three-dimensional hypercubes. The corresponding changes in distributions were not statistically significant: p = 0.415 for pairwise coefficients (Figure 1A and 1C) and p = 0.998 for third-order coefficients (Figures 2A and 2C).

From the distribution of third-order epistatic coefficients, we observe that higher-order epistasis – in this case, third-order – is clearly present both in the original data and after applying the Power Transform (Figures 2B and 2C), confirming the results reported in (Sailer, Harms, 2017).

Changes in epistatic coefficients

A narrowing or widening of the entire distribution does not necessarily imply that every coefficient decreased or increased in magnitude, although this is generally expected. To examine this, we calculated the differences in the absolute values of epistatic coefficients for each combinatorially complete dataset. Distributions of these differences are shown in Figure 3 (for two-dimensional hypercubes) and Figure 4 (for three-dimensional hypercubes).

Figure 3. Distribution of changes in absolute values of second-order epistatic coefficients (A) after application of the Box-Cox-based Power Transform, (B) after application of the Yeo-Johnson-based Power Transform.

Figure 4. Distribution of changes in absolute values of third-order epistatic coefficients (A) after application of the Box-Cox-based Power Transform, (B) after application of the Yeo-Johnson-based Power Transform.

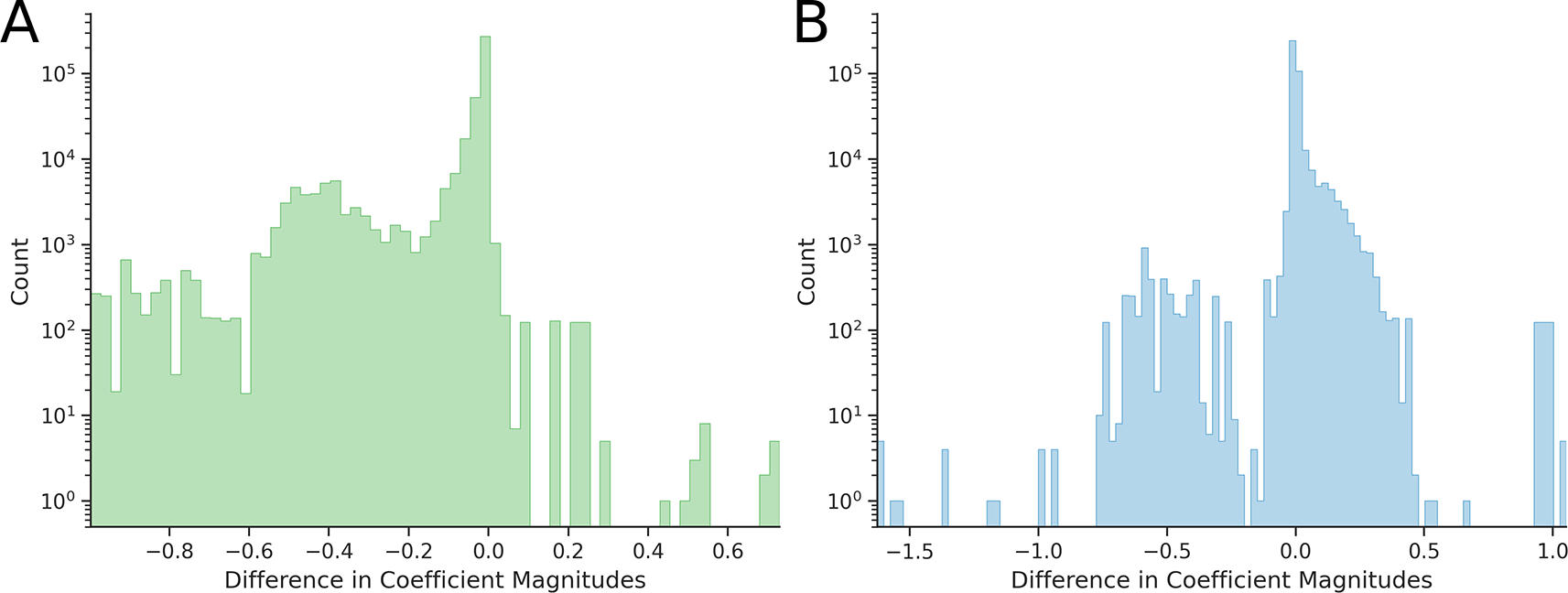
If the magnitudes of the epistatic coefficients decrease – i.e., move closer to zero – then the differences (post-transform minus pre-transform) should be negative. However, we observe hypercubes, both two-dimensional (Figure 3) and three-dimensional (Figure 4), for which the difference is positive, indicating that the absolute values of epistatic coefficients increased after applying the Power Transform. Such cases occur with both the Box-Cox and Yeo-Johnson transformations. A comparison of Figures 3A and 3B, as well as Figures 4A and 4B, shows that the Yeo-Johnson method results in significantly higher number of these cases for both two-dimensional and three-dimensional hypercubes.

Overall, for the Box-Cox-based Power Transform, the absolute values of 12,799 second-order coefficients and 941 third-order coefficients increased; for the Yeo-Johnson method, 254,215 second-order coefficients and 650 third-order coefficients increased. Thus, the Power Transform does not always reduce the magnitude of epistatic coefficients. Within our framework, we interpret this as evidence that the Power Transform does not reduce nonlinearity for some hypercubes.

Application of power transform to the whole landscape

Beyond applying the Power Transform to individual hypercubes, it is desirable to apply it to entire landscapes. However, when attempting this on the GFP landscape, we found that, for landscapes generated by random mutagenesis, the Power Transform generally fails. It appears that, for the Power Transform to function, the landscape must satisfy the following condition: for any single mutation present in the dataset, there must exist at least one pair of genotypes that differ only at that site while being identical at all others.

It can be shown that this condition is satisfied if the landscape represents a connected component – specifically, if for every genotype in the component, there exists at least one other genotype at Hamming distance 1.

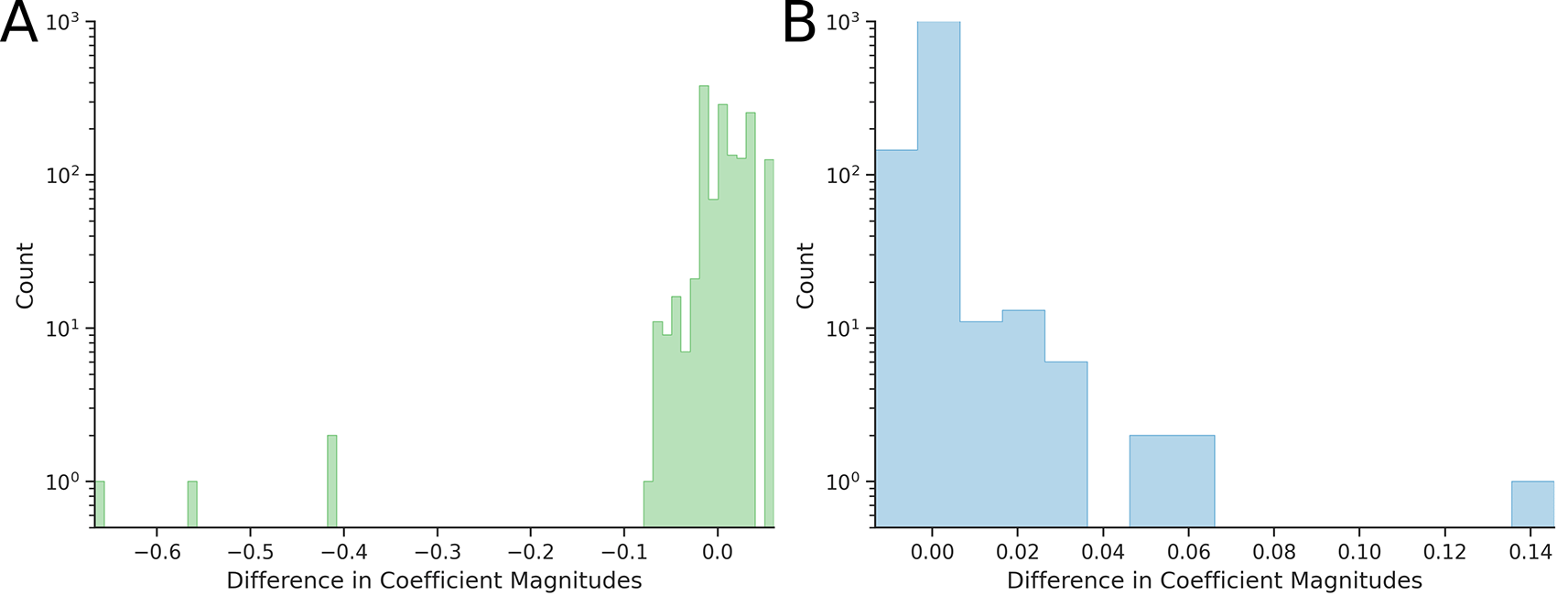
We partitioned the GFP landscape into connected components as described in Materials and Methods. We found that the experimental GFP landscape contains only one large connected component, consisting of 20,872 genotypes. We applied the Yeo-Johnson-based Power Transform to this component and computed epistatic coefficients for all embedded hypercubes (two- and three-dimensional), but using phenotype values linearized accross the entire component. The distributions of epistatic coefficients and the differences in their absolute values, are presented in Figure 5.

Figure 5. Distribution of epistatic coefficients (A) of the second order, (B) of the third order, and changes in absolute values of coefficients (C) of the second order, (D) of the third order after application of Yeo-Johnson-based Power Transform across the entire largest connected component of the GFP landscape.

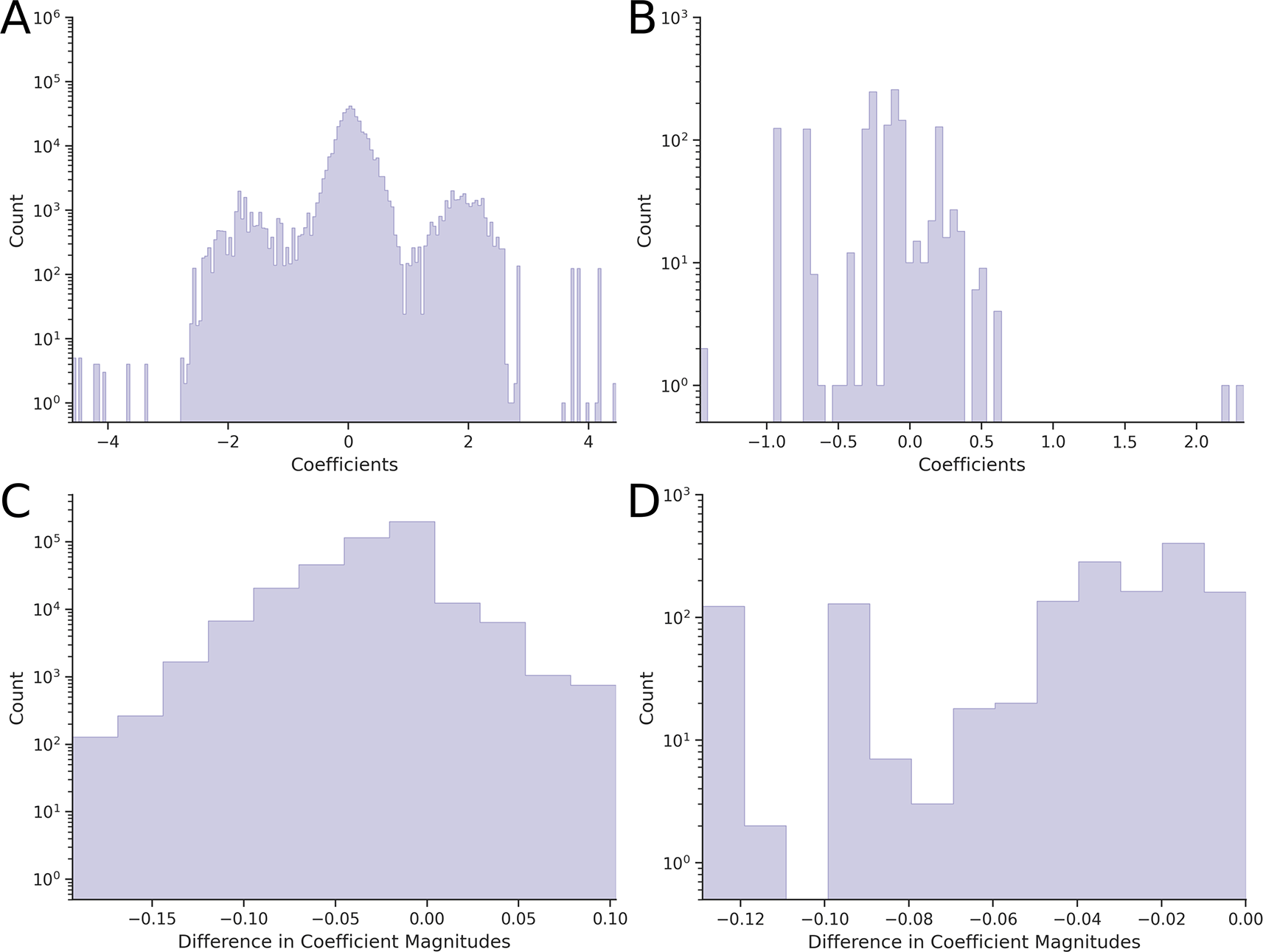
The average epistasis for two- and three-dimensional hypercubes was 0.648 and 0.152, respectively – corresponds to reductions of 3.86% and 11.6% compared to initial reference values.

As shown in Figures 5C and 5D, the majority of two-dimensional epistatic coefficients (note the logarithmic scale on the vertical axis) and all three-dimensional decreased in magnitude after applying the Yeo-Johnson-based Power Transform to the largest connected component. However, in a subset of two-dimensional cases, the absolute value of the epistatic coefficient increased for 6.3% of hypercubes (25,491 out of 403,162).

Discussion

In this work, we introduced and validated a conceptual framework for applying the Power Transform method to large fitness landscapes, including those generated by (quasi-)random mutagenesis. The approach involves partitioning the landscape into connected components and applying a Yeo-Johnson-based Power Transform to each component individually. While the Box-Cox-based Power Transform was found to be more effective on individual hypercubes, it is less universally applicable because it cannot accommodate non-positive values – not only in the observed phenotypes but also in their linearized counterparts. In large landscapes, such as the well-studied GFP landscape (which spans up to 15 mutational steps), non-positive linearized values are highly probable, rendering Box-Cox version of Power Transform inapplicable.

We demonstrated our concept on the canonical GFP landscape obtained via random mutagenesis (Sarkisyan et al., 2016). The only large connected sublandscape amenable to Power Transform comprised 20,872 genotypes. After applying the Yeo-Johnson-based Power Transform, pairwise epistasis decreased by 3.86%, and third-order epistasis by 11.6%.

The original GFP study reported a sigmoidal relationship between the logarithm of fluorescence and a proxy for fitness potential – namely, protein stability (see Figure 5 of (Sarkisyan et al., 2016)). This nonlinearity arises because two mildly destabilizing mutations, when combined, may push the protein beyond its stability threshold, preventing proper folding, chromophore formation, and thus, being fluorescent. This sigmoidal behavior was also captured by a neural network. The trimodal distribution of pairwise epistatic coefficients (Figure 1A) is a direct consequence of this sigmoidal landscape, reflecting three distinct scenarios:

(1) Distinct negative epistasis (left peak, ≈ –2): A stable reference genotype (00) and its single mutants (01, 10) fluoresce, so the double mutant (11) is expected to fluoresce as well. If, however, the double mutant falls beyond the sigmoidal stability threshold and fails to fluoresce, the observed-expected difference yields a distinct negative epistatic coefficient.
(2) Distinct positive epistasis (right peak, ≈ +2): A destabilized reference genotype (00) and its single mutants (01, 10) do not fluoresce, so the double mutant (11) is expected to remain dark. If stabilizing mutations shift the double mutant 11 left of the stability threshold, enabling fluorescence, the epistatic coefficient becomes definitely positive.
(3) Near-zero epistasis (central peak): It occurs when fluorescence changes (nearly) expectedly. For example, when all four genotypes (00, 01, 10, 11) either fluoresce or are dark, or when 00 and 01 are bright while 10 and 11 are dark, yielding negligible epistasis.

Comparing Box-Cox and Yeo-Johnson transformations on individual hypercubes from GFP data reveals a counterintuitive result: Box-Cox achieves better linearization than Yeo-Johnson, despite the latter’s ability to handle both positive and non-positive values and its broader functional scope. One might expect Yeo-Johnson transformation – as more generally applicable – to perform equally well or better than Box-Cox version. However, we did not investigate why Box-Cox outperforms Yeo-Johnson in local contexts of individual hypercubes.

This observation might hint to a critical distinction: optimizing the Power Transform parameters does not necessarily maximize linearization. In other words, “best Power Transform” and “best linearization” are not synonymous. Indeed, for both methods, we observed cases where the transform increased epistatic coefficients, further indicating that Power Transform application does not guarantee reduced nonlinearity.

Surprisingly, Yeo-Johnson-based Power Transform reduced epistasis across the full landscape but, on average, increased it when applied to individual hypercubes. We speculate that the global transform finds compromise parameters that effectively suppresses landscape-wide nonlinearity, whereas local hypercubes lack sufficient structure or signal for the same parameters to yield linearization. However, we did not probe this mechanism deeply; we note it as an observation worthy of further study.

In summary, we have developed and demonstrated a viable concept: Power Transform methods – specifically, based on Yeo-Johnson transformation – can be applied to large fitness landscapes, specifically obtained by (quasi-)random mutagenesis. The broader implications and future utility of this approach remain to be explored.

Ethical considerations

Not applicable.

Data availability

Underlying data

Figshare: https://doi.org/10.6084/m9.figshare.30921005 (Petrov, Ivankov, 2025). All scripts for generating data and pictures from the original GFP data (Sarkisyan et al., 2016) are available in the repository.

Data are available under the terms of the Creative Commons Attribution 4.0 International license (CC-BY 4.0).

Reporting guidelines

Not applicable.

References

Anderson DW, McKeown AN, Thornton JW: Intermolecular epistasis shaped the function and evolution of an ancient transcription factor and its DNA binding sites. elife. 2015 Jun 15; 4: e07864. PubMed Abstract | Publisher Full Text | Free Full Text
Box GEP, Cox DR: An Analysis of Transformations. J. R. Stat. Soc. 1964 Jul; 26(2): 211–243. Publisher Full Text
Bundy A, Wallen L: Breadth-First Search. Bundy A, Wallen L, editors. Catalogue of Artificial Intelligence Tools. Symbolic Computation. Berlin, Heidelberg: Springer; 1984. Publisher Full Text
Cheverud JM, Routman EJ: Epistasis and its contribution to genetic variance components. Genetics. 1995 Mar; 139(3): 1455–1461. PubMed Abstract | Publisher Full Text | Free Full Text
Cordell HJ: Epistasis: what it means, what it doesn’t mean, and statistical methods to detect it in humans. Hum. Mol. Genet. 2002 Oct 1; 11(20): 2463–2468. PubMed Abstract | Publisher Full Text
Esteban LA, Lonishin LR, Bobrovskiy D, et al.: HypercubeME: two hundred million combinatorially complete datasets from a single experiment. Bioinformatics. 2019 Nov 19; 36(6): 1960–1962. Epub ahead of print. PubMed Abstract | Publisher Full Text | Free Full Text
Fisher RA: XV.—The Correlation between Relatives on the Supposition of Mendelian Inheritance. Transactions of the Royal Society of Edinburgh. 1919; 52(2): 399–433. Publisher Full Text
Hall DW, Agan M, Pope SC: Fitness epistasis among 6 biosynthetic loci in the budding yeast Saccharomyces cerevisiae. J. Hered. 2010 Mar-Apr; 101 Suppl 1: S75–S84. Epub 2010 Mar 1. PubMed Abstract | Publisher Full Text
Ivankov DN, Finkelstein AV, Kondrashov FA: A structural perspective of compensatory evolution. Curr. Opin. Struct. Biol. 2014 Jun; 26(100): 104–112. Epub 2014 Jun 28. PubMed Abstract | Publisher Full Text | Free Full Text
Johnson MS, Reddy G, Desai MM: Epistasis and evolution: recent advances and an outlook for prediction. BMC Biol. 2023 May 24; 21(1): 120. PubMed Abstract | Publisher Full Text | Free Full Text
Johnston KE, Almhjell PJ, Watkins-Dulaney EJ, et al.: A combinatorially complete epistatic fitness landscape in an enzyme active site. Proc. Natl. Acad. Sci. USA. 2024 Aug 6; 121(32): e2400439121. Epub 2024 Jul 29. PubMed Abstract | Publisher Full Text | Free Full Text
Khan AI, Dinh DM, Schneider D, et al.: Negative epistasis between beneficial mutations in an evolving bacterial population. Science. 2011 Jun 3; 332(6034): 1193–1196. PubMed Abstract | Publisher Full Text
Mackay TF: Epistasis and quantitative traits: using model organisms to study gene-gene interactions. Nat. Rev. Genet. 2014 Jan; 15(1): 22–33. Epub 2013 Dec 3. PubMed Abstract | Publisher Full Text | Free Full Text
Moore JH, Williams SM: Epistasis and its implications for personal genetics. Am. J. Hum. Genet. 2009 Sep; 85(3): 309–320. PubMed Abstract | Publisher Full Text | Free Full Text
Olson CA, Wu NC, Sun R: A comprehensive biophysical description of pairwise epistasis throughout an entire protein domain. Curr. Biol. 2014 Nov 17; 24(22): 2643–2651. Epub 2014 Oct 16. PubMed Abstract | Publisher Full Text | Free Full Text
Petrov DA, Ivankov DN: Power Transform for fitness landscapes. figshare. Software. 2025. Publisher Full Text
Phillips PC: Epistasis – the essential role of gene interactions in the structure and evolution of genetic systems. Nat. Rev. Genet. 2008 Nov; 9(11): 855–867. PubMed Abstract | Publisher Full Text | Free Full Text
Poelwijk FJ, Krishna V, Ranganathan R: The Context-Dependence of Mutations: A Linkage of Formalisms. PLoS Comput. Biol. 2016 Jun 23; 12(6): e1004771. PubMed Abstract | Publisher Full Text | Free Full Text
Poelwijk FJ, Socolich M, Ranganathan R: Learning the pattern of epistasis linking genotype and phenotype in a protein. Nat. Commun. 2019 Sep 16; 10(1): 4213. PubMed Abstract | Publisher Full Text | Free Full Text
Pokusaeva VO, Usmanova DR, Putintseva EV, et al.: An experimental assay of the interactions of amino acids from orthologous sequences shaping a complex fitness landscape. PLoS Genet. 2019 Apr 10; 15(4): e1008079. PubMed Abstract | Publisher Full Text | Free Full Text
Sailer ZR, Harms MJ: Detecting High-Order Epistasis in Nonlinear Genotype-Phenotype Maps. Genetics. 2017 Mar; 205(3): 1079–1088. Epub 2017 Jan 18. PubMed Abstract | Publisher Full Text | Free Full Text
Sarkisyan KS, Bolotin DA, Meer MV, et al.: Local fitness landscape of the green fluorescent protein. Nature. 2016 May 19; 533(7603): 397–401. Epub 2016 May 11. PubMed Abstract | Publisher Full Text | Free Full Text
Tawfik DS: Messy biology and the origins of evolutionary innovations. Nat. Chem. Biol. 2010 Oct; 6(10): 692–696. PubMed Abstract | Publisher Full Text
Verhoeven KJ, Casella G, McIntyre LM: Epistasis: obstacle or advantage for mapping complex traits? PLoS One. 2010 Aug 26; 5(8): e12264. PubMed Abstract | Publisher Full Text | Free Full Text
de Visser JA , Cooper TF, Elena SF: The causes of epistasis. Proc. Biol. Sci. 2011 Dec 22; 278(1725): 3617–3624. Epub 2011 Oct 5. PubMed Abstract | Publisher Full Text | Free Full Text
de Visser JA , Park SC, Krug J: Exploring the effect of sex on empirical fitness landscapes. Am. Nat. 2009 Jul; 174 Suppl 1: S15–S30. PubMed Abstract | Publisher Full Text
Weinreich DM, Lan Y, Wylie CS, et al.: Should evolutionary geneticists worry about higher-order epistasis? Curr. Opin. Genet. Dev. 2013 Dec; 23(6): 700–707. Epub 2013 Nov 27. PubMed Abstract | Publisher Full Text | Free Full Text
Yeo IK, Johnson RA: A new family of power transformations to improve normality or symmetry. Biometrika. 2000 Dec 1; 87(4): 954–959. Publisher Full Text
Zhou J, Wong MS, Chen WC, et al.: Higher-order epistasis and phenotypic prediction. Proc. Natl. Acad. Sci. USA. 2022 Sep 27; 119(39): e2204233119. Epub 2022 Sep 21. PubMed Abstract | Publisher Full Text | Free Full Text

Comments on this article Comments (0)

Version 1

VERSION 1 PUBLISHED 31 Dec 2025

Author details Author details

¹ Center for Molecular and Cellular Biology, Skolkovo Institute of Science and Technology, Moscow, 121205, Russian Federation

Dmitry A. Petrov
Roles: Formal Analysis, Investigation, Methodology, Software, Validation, Visualization, Writing – Original Draft Preparation

Dmitry N. Ivankov
Roles: Conceptualization, Data Curation, Funding Acquisition, Project Administration, Resources, Supervision, Writing – Original Draft Preparation, Writing – Review & Editing

Competing interests

No competing interests were disclosed.

Grant information

The research was funded by the Russian Science Foundation, grant No. 25-14-00491, https://rscf.ru/project/25-14-00491/
The funders had no role in study design, data collection and analysis, decision to publish, or preparation of the manuscript.

Article Versions (1)

version 1

Published: 31 Dec 2025, 14:1478

https://doi.org/10.12688/f1000research.175373.1

Copyright

© 2025 Petrov DA and Ivankov DN. This is an open access article distributed under the terms of the Creative Commons Attribution License, which permits unrestricted use, distribution, and reproduction in any medium, provided the original work is properly cited.

Download

Export To

metrics

	Views	Downloads
F1000Research	-	-
PubMed Central Data from PMC are received and updated monthly.	-	-

Citations

0

SEE MORE DETAILS

CITE

how to cite this article

Petrov DA and Ivankov DN. Assessing nonlinearities in the GFP random mutagenesis landscape using the Power Transform [version 1; peer review: awaiting peer review]. F1000Research 2025, 14:1478 (https://doi.org/10.12688/f1000research.175373.1)

NOTE: If applicable, it is important to ensure the information in square brackets after the title is included in all citations of this article.

track

receive updates on this article

Track an article to receive email alerts on any updates to this article.

Open Peer Review

Comments on this article Comments (0)

Version 1

VERSION 1 PUBLISHED 31 Dec 2025

Open Peer Review

Reviewer Status

AWAITING PEER REVIEW

Comments on this article

All Comments(0)

Add a comment

Sign up for content alerts

Browse by related subjects

[1] Anderson DW, McKeown AN, Thornton JW: Intermolecular epistasis shaped the function and evolution of an ancient transcription factor and its DNA binding sites. elife. 2015 Jun 15; 4: e07864. PubMed Abstract | Publisher Full Text | Free Full Text

[2] Box GEP, Cox DR: An Analysis of Transformations. J. R. Stat. Soc. 1964 Jul; 26(2): 211–243. Publisher Full Text

[3] Bundy A, Wallen L: Breadth-First Search. Bundy A, Wallen L, editors. Catalogue of Artificial Intelligence Tools. Symbolic Computation. Berlin, Heidelberg: Springer; 1984. Publisher Full Text

[4] Cheverud JM, Routman EJ: Epistasis and its contribution to genetic variance components. Genetics. 1995 Mar; 139(3): 1455–1461. PubMed Abstract | Publisher Full Text | Free Full Text

[5] Cordell HJ: Epistasis: what it means, what it doesn’t mean, and statistical methods to detect it in humans. Hum. Mol. Genet. 2002 Oct 1; 11(20): 2463–2468. PubMed Abstract | Publisher Full Text

[6] Esteban LA, Lonishin LR, Bobrovskiy D, et al.: HypercubeME: two hundred million combinatorially complete datasets from a single experiment. Bioinformatics. 2019 Nov 19; 36(6): 1960–1962. Epub ahead of print. PubMed Abstract | Publisher Full Text | Free Full Text

[7] Fisher RA: XV.—The Correlation between Relatives on the Supposition of Mendelian Inheritance. Transactions of the Royal Society of Edinburgh. 1919; 52(2): 399–433. Publisher Full Text

[8] Hall DW, Agan M, Pope SC: Fitness epistasis among 6 biosynthetic loci in the budding yeast Saccharomyces cerevisiae. J. Hered. 2010 Mar-Apr; 101 Suppl 1: S75–S84. Epub 2010 Mar 1. PubMed Abstract | Publisher Full Text

[9] Ivankov DN, Finkelstein AV, Kondrashov FA: A structural perspective of compensatory evolution. Curr. Opin. Struct. Biol. 2014 Jun; 26(100): 104–112. Epub 2014 Jun 28. PubMed Abstract | Publisher Full Text | Free Full Text

[10] Johnson MS, Reddy G, Desai MM: Epistasis and evolution: recent advances and an outlook for prediction. BMC Biol. 2023 May 24; 21(1): 120. PubMed Abstract | Publisher Full Text | Free Full Text

[11] Johnston KE, Almhjell PJ, Watkins-Dulaney EJ, et al.: A combinatorially complete epistatic fitness landscape in an enzyme active site. Proc. Natl. Acad. Sci. USA. 2024 Aug 6; 121(32): e2400439121. Epub 2024 Jul 29. PubMed Abstract | Publisher Full Text | Free Full Text

[12] Khan AI, Dinh DM, Schneider D, et al.: Negative epistasis between beneficial mutations in an evolving bacterial population. Science. 2011 Jun 3; 332(6034): 1193–1196. PubMed Abstract | Publisher Full Text

[13] Mackay TF: Epistasis and quantitative traits: using model organisms to study gene-gene interactions. Nat. Rev. Genet. 2014 Jan; 15(1): 22–33. Epub 2013 Dec 3. PubMed Abstract | Publisher Full Text | Free Full Text

[14] Moore JH, Williams SM: Epistasis and its implications for personal genetics. Am. J. Hum. Genet. 2009 Sep; 85(3): 309–320. PubMed Abstract | Publisher Full Text | Free Full Text

[15] Olson CA, Wu NC, Sun R: A comprehensive biophysical description of pairwise epistasis throughout an entire protein domain. Curr. Biol. 2014 Nov 17; 24(22): 2643–2651. Epub 2014 Oct 16. PubMed Abstract | Publisher Full Text | Free Full Text

[16] Petrov DA, Ivankov DN: Power Transform for fitness landscapes. figshare. Software. 2025. Publisher Full Text

[17] Phillips PC: Epistasis – the essential role of gene interactions in the structure and evolution of genetic systems. Nat. Rev. Genet. 2008 Nov; 9(11): 855–867. PubMed Abstract | Publisher Full Text | Free Full Text

[18] Poelwijk FJ, Krishna V, Ranganathan R: The Context-Dependence of Mutations: A Linkage of Formalisms. PLoS Comput. Biol. 2016 Jun 23; 12(6): e1004771. PubMed Abstract | Publisher Full Text | Free Full Text

[19] Poelwijk FJ, Socolich M, Ranganathan R: Learning the pattern of epistasis linking genotype and phenotype in a protein. Nat. Commun. 2019 Sep 16; 10(1): 4213. PubMed Abstract | Publisher Full Text | Free Full Text

[20] Pokusaeva VO, Usmanova DR, Putintseva EV, et al.: An experimental assay of the interactions of amino acids from orthologous sequences shaping a complex fitness landscape. PLoS Genet. 2019 Apr 10; 15(4): e1008079. PubMed Abstract | Publisher Full Text | Free Full Text

[21] Sailer ZR, Harms MJ: Detecting High-Order Epistasis in Nonlinear Genotype-Phenotype Maps. Genetics. 2017 Mar; 205(3): 1079–1088. Epub 2017 Jan 18. PubMed Abstract | Publisher Full Text | Free Full Text

[22] Sarkisyan KS, Bolotin DA, Meer MV, et al.: Local fitness landscape of the green fluorescent protein. Nature. 2016 May 19; 533(7603): 397–401. Epub 2016 May 11. PubMed Abstract | Publisher Full Text | Free Full Text

[23] Tawfik DS: Messy biology and the origins of evolutionary innovations. Nat. Chem. Biol. 2010 Oct; 6(10): 692–696. PubMed Abstract | Publisher Full Text

[24] Verhoeven KJ, Casella G, McIntyre LM: Epistasis: obstacle or advantage for mapping complex traits? PLoS One. 2010 Aug 26; 5(8): e12264. PubMed Abstract | Publisher Full Text | Free Full Text

[25] de Visser JA , Cooper TF, Elena SF: The causes of epistasis. Proc. Biol. Sci. 2011 Dec 22; 278(1725): 3617–3624. Epub 2011 Oct 5. PubMed Abstract | Publisher Full Text | Free Full Text

[26] de Visser JA , Park SC, Krug J: Exploring the effect of sex on empirical fitness landscapes. Am. Nat. 2009 Jul; 174 Suppl 1: S15–S30. PubMed Abstract | Publisher Full Text

[27] Weinreich DM, Lan Y, Wylie CS, et al.: Should evolutionary geneticists worry about higher-order epistasis? Curr. Opin. Genet. Dev. 2013 Dec; 23(6): 700–707. Epub 2013 Nov 27. PubMed Abstract | Publisher Full Text | Free Full Text

[28] Yeo IK, Johnson RA: A new family of power transformations to improve normality or symmetry. Biometrika. 2000 Dec 1; 87(4): 954–959. Publisher Full Text

[29] Zhou J, Wong MS, Chen WC, et al.: Higher-order epistasis and phenotypic prediction. Proc. Natl. Acad. Sci. USA. 2022 Sep 27; 119(39): e2204233119. Epub 2022 Sep 21. PubMed Abstract | Publisher Full Text | Free Full Text

Assessing nonlinearities in the GFP random mutagenesis landscape using the Power Transform

Abstract

Abstract*

Background

Methods

Results

Conclusions

Keywords

Introduction

Methods

Identification of combinatorially complete datasets

Power transform with box-cox transformation

(1)

(2)

(3)

Power transform with Yeo-Johnson transformation

(4)

(5)

Set of combinatorially complete datasets

Identification of connected components

Calculation of epistatic coefficients

(6)

(7)

(8)

(9)

Statistical comparison of distributions

Estimating uncertainty in epistatic coefficients

(10)

Results

Dataset

Application of power transform to individual combinatorially complete datasets

Figure 1. Distribution of pairwise epistatic coefficients computed (A) before Power Transform, (B) after the Box-Cox-based Power Transform, and (C) after the Yeo-Johnson-based Power Transform.

Figure 2. Distribution of third-order epistatic coefficients computed (A) before Power Transform, (B) after the Box-Cox-based Power Transform, and (C) after the Yeo-Johnson-based Power Transform.

Changes in epistatic coefficients

Figure 3. Distribution of changes in absolute values of second-order epistatic coefficients (A) after application of the Box-Cox-based Power Transform, (B) after application of the Yeo-Johnson-based Power Transform.

Figure 4. Distribution of changes in absolute values of third-order epistatic coefficients (A) after application of the Box-Cox-based Power Transform, (B) after application of the Yeo-Johnson-based Power Transform.

Application of power transform to the whole landscape

Discussion

Ethical considerations

Data availability

Underlying data

Reporting guidelines

References

Comments on this article Comments (0)

Open Peer Review

Comments on this article Comments (0)

Open Peer Review

Reviewer Status

Comments on this article

Browse by related subjects

Competing Interests Policy

Stay Updated