Using Akaike’s information theoretic criterion in population analysis: a simulation study

Erik Olofsen; Albert Dahan

doi:10.12688/f1000research.2-71.v1

Home Browse Using Akaike’s information theoretic criterion in population analysis:...

ALL Metrics

Views

Downloads

Get PDF

Get XML

Export

▬

✚

Research Article

Using Akaike’s information theoretic criterion in population analysis: a simulation study

[version 1; peer review: 2 approved with reservations, 1 not approved]

Erik Olofsen¹, Albert Dahan¹

PUBLISHED 04 Mar 2013

Author details Author details

¹ Department of Anesthesiology, Leiden University Medical Center, PO Box 9600, 2300 RC Leiden, The Netherlands

OPEN PEER REVIEW

REVIEWER STATUS

Abstract

Akaike’s information-theoretic criterion for model discrimination (AIC) is often stated to “overfit”, i.e., it selects models with a higher dimension than the dimension of the model that generated the data. However, when no fixed-dimensional correct model exists, for example for pharmacokinetic data, AIC, or its bias-corrected version (AICc) might be the selection criterion of choice if the objective is to minimize prediction error. The present simulation study was designed to assess the behavior of AICc when applying it to the analysis of population data, for various degrees of interindividual variability. The simulation study showed that, at least in a relatively simple mixed effects modeling context, minimal mean AICc corresponded to best predictive performance even in the presence of large interindividual variability.

Keywords

population model, pharmacokinetics, Akaike, information theoretic criterion

Corresponding author: Erik Olofsen

Competing interests: No competing interests were disclosed.

Grant information: This work was funded by institutional resources.
The funders had no role in study design, data collection and analysis, decision to publish, or preparation of the manuscript.

Copyright: © 2013 Olofsen E and Dahan A. This is an open access article distributed under the terms of the Creative Commons Attribution License, which permits unrestricted use, distribution, and reproduction in any medium, provided the original work is properly cited. Data associated with the article are available under the terms of the Creative Commons Zero "No rights reserved" data waiver (CC0 1.0 Public domain dedication).

How to cite: Olofsen E and Dahan A. Using Akaike’s information theoretic criterion in population analysis: a simulation study [version 1; peer review: 2 approved with reservations, 1 not approved]. F1000Research 2013, 2:71 (https://doi.org/10.12688/f1000research.2-71.v1) First published: 04 Mar 2013, 2:71 (https://doi.org/10.12688/f1000research.2-71.v1) Latest published: 27 Jul 2015, 2:71 (https://doi.org/10.12688/f1000research.2-71.v3)

Introduction

Population data consist of one or more measurements in two or more individuals. Such data can be characterized by mixed-effects models, where the mixed effects consist of fixed and random effects. Fixed effects are, for example, the times at which the measurements are obtained, and covariates such as demographic characteristics of the individuals. When mixed-effects models are fitted to population data, the question arises how many of those effects should be incorporated in the model. This is the so-called problem of variable selection¹.

One strategy is to observe the change in goodness-of-fit by adding one more parameter and testing the significance of that change². In the maximum likelihood approach, the objective function value (OFV), being the minus two logarithm of the likelihood function, is minimized. To attain a p-value of e.g., 0.05 or less, the decrease in OFV, when adding one parameter, should be 3.84 or more².

Another strategy is to apply Akaike's information theoretic criterion (AIC), which can be written as

AIC = OFV + 2 \cdot D, (1)

where D is the number of parameters in the model^1–4. The model with the lowest value of AIC is considered the best one. In the case of just adding one parameter, the OFV needs to decrease only 2 points or more to be incorporated in the model, so the associated p-value > 0.05 seems too high to justify this strategy.

When additional model parameters are incorporated, the significance of one model parameter might change, but the interpretation of AIC does not⁴. However, when multiple significance tests are performed, the significance level of each individual test should be corrected to a lower value, so a decrease of 2 points for one parameter does again seem to be too low.

Even if the strategy of using AIC leads to optimal variable selection, the question arises if this is also the case when using mixed-effects models. In theory, the model that is best according to AIC is the one that minimizes prediction error^3,5; and this is also true for a mixed effects model when predicting data for individuals for which no data have been obtained so far⁵.

In the literature, simulation studies have assessed the performance of AIC in selecting the model with the lowest prediction error, but to our knowledge these were never done for population data. In this article, we will define a toy pharmacokinetic model and observe the performance of AIC when adding fixed effects to this model, as well as when adding interindividual variability.

Methods

A hypothetical pharmacokinetic model

Consider the following function y(t), an infinite sum of exponentials, and its relationship with a (negative) power of time⁶:

y (t) = \int_{0}^{\infty} \exp (- λ t) d λ = - \frac{1}{t} \cdot \exp (- λ t) |_{0}^{\infty} = \frac{1}{t} for t > 0 . (2)

Figure 1A shows that this function looks like a typical pharmacokinetic profile after bolus administration. This model is to be regarded as a toy model, because we do not expect it to adequately describe pharmacokinetic data, although variations of power functions of time have been shown to fit pharmacokinetic data well⁶. Here we will use the fact that if we approximate y(t) = 1/t by the following sum of M exponentials with K nonzero coefficients α and M fixed parameters λ (as chosen in the next subsections):

\hat{y} (t_{j}; α, λ) = \sum_{m = 1}^{M} α_{m} \exp (- λ_{m} t_{j}) . (3)

that with M time instants t_j, we would need no less than K = M exponentials to obtain a perfect fit. Moreover, with noisy data, it might be that for K < M an optimal fit is obtained in the sense that the associated prediction error of the model is minimal. Figure 1B shows how eleven (in this case error-free) samples from this function can be approximated by sums of exponentials.

Figure 1.

A: function y(t) = 1/t, and B: approximations obtained by fitting six and three exponentials to the depicted eleven samples. Note the log-lin and log-log scales for panels A and B, respectively. Time has arbitrary units.

Data simulation

In the following, the time instants t_j, j = 1, …, M, centered around 1, were chosen within [1/t_max,t_max] according to

t_{j} = {(\frac{j}{M + 1 - j})}^{γ}, (4)

with γ = log(t_max)/log(M); t_max was set to 100 (see the time axis of Figure 1B for an example with M = 11). Simulated data were generated via

y (t_{j}) = \frac{1}{t_{j}} \cdot (1 + ϵ_{j}), (5)

where ε_j denotes Gaussian measurement noise with variance σ². The M time constants λ were fixed according to λ_m = 1/t_m, m = 1, …, M. In this setting the model eq. (3) can be fitted to simulated data using weighted linear least squares regression, with weight factors ω(t_j) = 1/t_j (note that no precaution is needed against ε ≤ –1).

Population data simulation and modeling

Population data consisting of N individuals were simulated via

y_{i} (t_{j}) = \frac{1}{t_{j}} \cdot (\exp (η_{i}) + ϵ_{i j}) with i = 1, \dots, N, (6)

where η_i denotes interindividual variability with variance ω². The nonlinear mixed effects model for the population data was then written as:

{\hat{y}}_{i} (t_{j}; α, λ) = \sum_{m = 1}^{M} α_{m} \exp (- λ_{m} t_{j} + η_{i}) . (7)

Note that with N > 1, a perfect fit is no longer obtained with K = M, because the ε_i,j are generally different for different i (individuals).

Statistical analysis

Simulation data were generated via eq. (6), with random generators in R⁷. Model fitting was also done in R, with function "lm()" from package "stats", except for nonlinear mixed-effects model fitting for simulated data with ω² > 0, which was done in NONMEM version 7.3 (beta version a6.5)⁸. Parameters α (see eq. (7)) were not constrained to be positive, so that it was not possible for parameters to become essentially fixed to zero, reducing the dimensionality of the model. Prediction error (ν²) was calculated with

ν^{2} = \frac{1}{N \cdot M} {\sum_{i = 1}^{N} \sum_{j = 1}^{M} (\frac{z_{i} (t_{j}) - {\hat{y}}_{i} (t_{j})}{w (t_{j})})}^{2}, (8)

using predictions based on eq. (7) with the random effects η_i = 0, and validation data z_i(t_j) also generated via eq. (6), but with different realizations of ε_ij and η_i. The objective function OFV was also calculated at the estimated parameters using the validation data, denoted OFV_v, which should on average be approximately equal to Akaike's criterion (see Supplementary material). OFV_v was compared with AIC and also with Akaike's criterion with a correction for small sample sizes (AIC_c)⁴:

{AIC}_{c} = OFV + 2 \cdot D \cdot (1 + \frac{D + 1}{N \cdot M - D - 1}) (9)

The above criteria were normalized by dividing them by the number of observations, and averaged over 1000 runs (unless otherwise stated; and runs where NONMEM's minimization was not successful were excluded). For plotting purposes, 95% confidence intervals or confidence regions for means were determined using R's packages "gplots" and "car", under the assumption that averages over 1000 variables are normally distributed.

Selection of parameter values

Simulation parameters M and σ² are expected to determine the number of exponentials K; if M increases and/or σ² decreases, K will increase. Without inter-individual variance, so ω² = 0, the information in the data increases as N increases, so that K is also expected to increase. With N = 2, M = 11 and σ² = 0.5, pilot simulations indicated a K ≈ 4. When ω² > 0, the prediction error will increase, but it is less easy to predict what its effect will be on K. For ω² values of 0, 0.1, and 0.5 were selected - values that are encountered in practice. Because there is only one random effect in the mixed effects model, the relatively low number of individuals N = 5 was selected.

For a certain choice of M, there are 2^M – 1 possible combinations of λs to choose for the terms exp(–λ_mt_j) in the sum of exponentials (excluding the case of zero exponentials). Because accurate evaluation of all models at different parameter values is not feasible with respect to computer time, the set of possible combinations was reduced to one with evenly spaced λs. Table 1 gives an example for the case M = 11.

Table 1. Selecting K = 1, …, M = 11 evenly spaced rate constants from λ: 0 and 1 denote α_m to be fixed to zero, and a free parameter to be estimated, respectively (see eq. (7)).

K	m : 1	2	3	4	5	6	7	8	9	10	11
1	0	0	0	0	0	1	0	0	0	0	0
2	1	0	0	0	0	0	0	0	0	0	1
3	1	0	0	0	0	1	0	0	0	0	1
4	1	0	0	1	0	0	0	1	0	0	1
5	1	0	0	1	0	1	0	1	0	0	1
6	1	0	1	0	1	0	1	0	1	0	1
7	1	0	1	1	0	1	0	1	1	0	1
8	1	1	0	1	1	0	1	1	0	1	1
9	1	1	0	1	1	1	1	1	0	1	1
10	1	1	1	1	1	0	1	1	1	1	1
11	1	1	1	1	1	1	1	1	1	1	1

Results

Figure 2 shows the averaged prediction error versus number of exponentials for all possible choices of λ, with N = 2, M = 11, σ² = 0.5, and ω² = 0. From the figure it is clear that prediction error may indeed increase if the number of exponentials selected is too large. The bigger solid circles correspond to the models chosen in Table 1; in general the evenly spaced selection of exponents resulted in models with the smallest prediction error.

Figure 2.

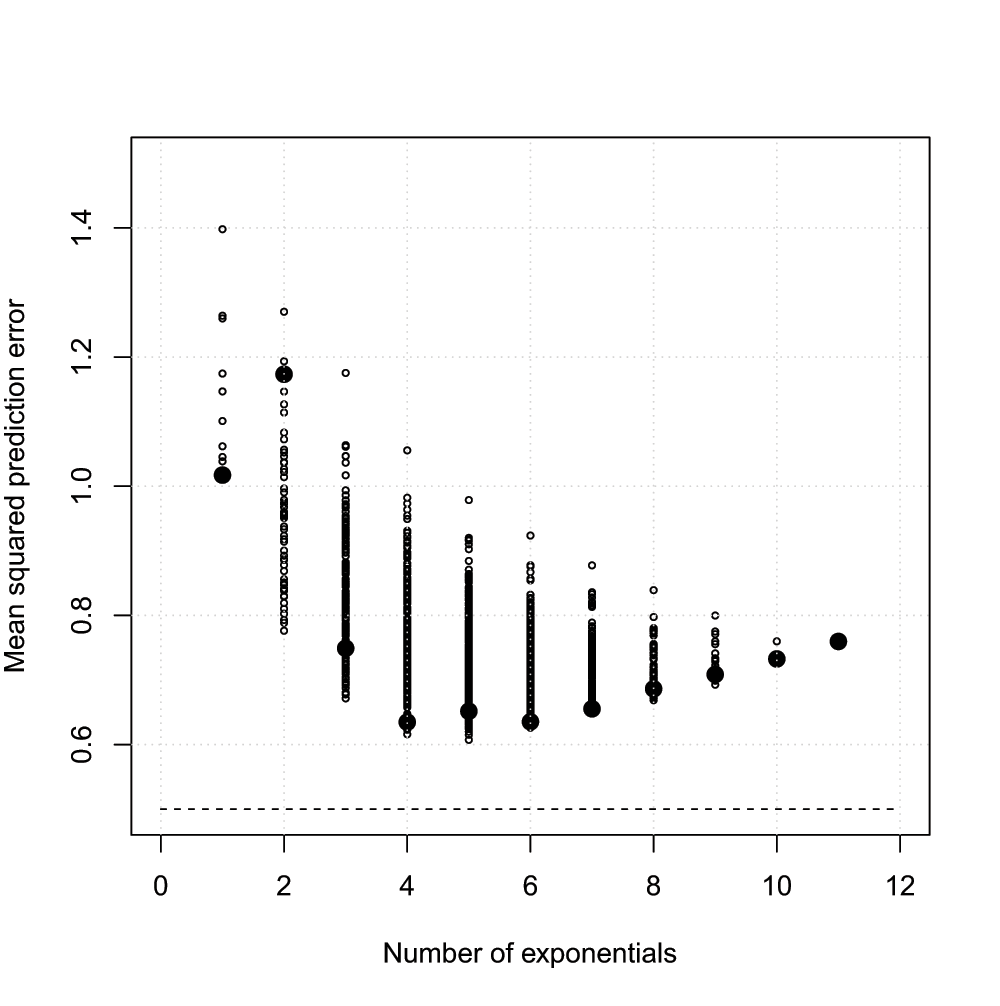
Mean squared prediction error ν² (eq. (8)) as a function of the number of exponentials, with 2047 models, averaged over 100 runs, N = 2, M = 11, σ² = 0.5, ω² = 0. The dashed line represents the prediction error from the true model, so that ν² = σ². The bigger solid circles correspond to the models chosen in Table 1.

Figure 3 shows simulation results using the model set defined in Table 1, starting from K = 4, with parameters N = 5, M = 11, σ² = 0.5, and ω² = 0. The model with K = 6 exponentials had both minimal mean OFV_v and minimal mean AIC_c (and minimal prediction error v² (not shown)). With N = 5, M = 11, there are still visible differences between AIC_c and AIC; although AIC would in this case also select the optimal model, AIC appears to favor more complex models. Note that the sizes of the confidence intervals and confidence regions can be made arbitrarily small by choosing the number of runs higher than the selected number of 1000 (at the expense of computer time).

Figure 3.

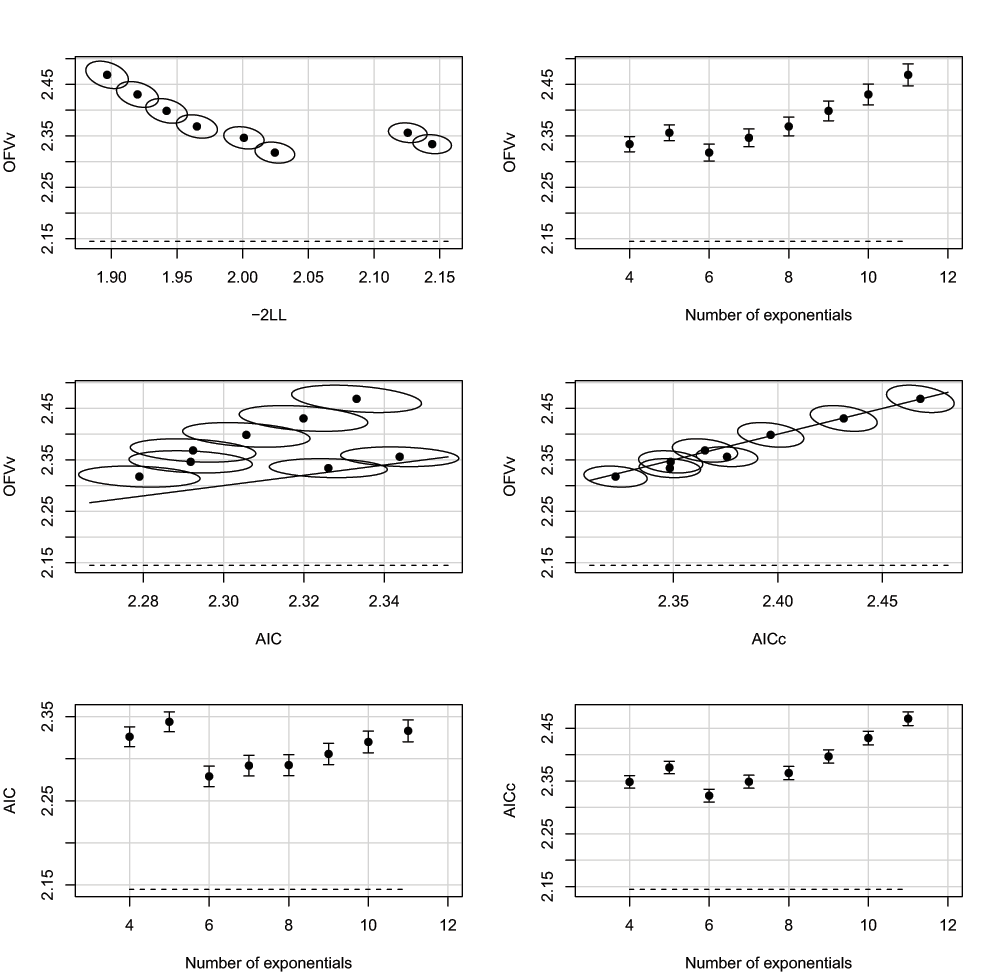
Mean OFV_v as a function minus of two log likelihood (-2LL), the number of exponentials, AIC and AIC_c (top four panels), and AIC and AIC_c as a function of the number of exponentials (lower two panels), averaged over 1000 runs, N = 5, M = 11, σ² = 0.5, ω² = 0. The dashed lines represent the theoretical values for an infinite amount of data (see Supplementary material). Error bars and ellipses denote 95% confidence intervals and confidence regions, respectively. Each solid line in the middle panels denotes the line of identity.

Figure 4 shows simulation results with ω² = 0.1; mixed-effects analysis was used to fit the population data. The main difference with the results of data with ω² = 0 is the overall increase in OFV_v and AIC_c. The optimal number of exponentials remained K = 6.

Figure 4. Mean OFV_ν, AIC_c and prediction error ν² as a function of the number of exponentials, for ω² = 0.1; parameters otherwise identical.

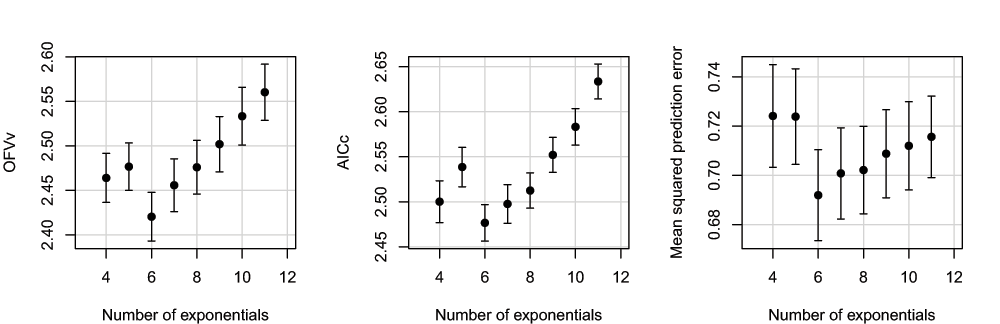
Figure 5 shows simulation results with ω² set at the higher value of 0.5. The main differences with the results of data with ω² = 0.1 are again the overall increase in OFV_v, AIC_c and prediction error, and also in the variability in the prediction error. The optimal number of exponentials remained K = 6, although AIC_c begins to favor the models with larger K (a simulation with N increased to 7, both OFV_v and AIC_c favored larger models; data not shown).

Figure 5. Mean OFV_v and AIC_c as a function of the number of exponentials, AIC and AIC_c, for ω² = 0.5; parameters otherwise identical.

Discussion

With the objective of creating a simulation context resembling pharmacokinetic analysis where concentration data are approximated by a sum of exponentials, the toy model y(t) = 1/t was chosen. In this setting, reality - the reality of the toy model - is always underfitted. When mixed effects models were fitted to simulated data, mean AIC_c was approximately equal to the validation criterion mean OFV_v, and their minima coincided. With large interindividual variability, mean expected prediction error (ν², see eq. (8), with random effects fixed to zero), was less discriminative between models, so that it became less suitable as a validation criterion.

Akaike's versus the conditional Akaike information criterion

Vaida and Blanchard proposed a conditional Akaike information criterion to be used in model selection for the "cluster focus"⁵. It is important to stress that the cluster focus as they defined is the situation where data are to be predicted of a cluster that was also used to build the predictive model. In that case, the random effects have been estimated, and then the question arises how many parameters that required. In our case, a cluster is the data from an individual; AIC was used in the situation of predicting population data consisting of individual data that were not used to build the model. This would seem to be the most common situation in clinical practice. Furthermore, AIC for the population focus is asymptotically equivalent with leave-one-individual-out cross-validation; AIC for the individual focus with leave-one-observation-out cross-validation⁹.

Akaike's versus the Bayesian information criterion

We chose to perform simulations using the model given by eq. (2) because approximating data with a sum of exponentials is daily practice in pharmacokinetic analysis where data are obtained from "infinitely complex" systems, and we cannot hope to find the "correct" model. The Bayesian information criterion (BIC) is consistent in the sense that it selects the correct model, given an infinite amount of data⁴. The reason that AIC can be used in "real-life" problems is that as the amount of data goes to infinity, the complexity, or dimension, of the model that should be applied should also go infinity¹⁰. Burnham and Anderson show that it is possible to choose the prior probability distribution for BIC in such a way that it incorporates the knowledge that more complex models should be favored if the amount of data increases, and so that the BIC "reduces" to AIC^4,10. In the situation that the correct model set belongs to the set of evaluated models, a selection criterion that both finds the correct model and minimizes prediction error would be preferable - but Yang concluded that this may not be possible¹¹.

In pharmacokinetic analysis, it may not really be appropriate to test (using a hypothesis test assuming a X² distribution for the objective function) whether an added exponential is statistically significant¹². Here the hypothesis H₀: the data originate from a K-exponential model (and H_A: the data originate from a higher dimensional model) is almost certain to be false. Furthermore, when taking a low p-value, it is also almost certain that the model selected has worse predictive properties. If a model is to be applied in clinical practice, for example for drug administration in a patient never studied before, the model should be as predictive as possible. However, it may be sensible to test whether a certain fixed effect has both a clinically and statistically significant effect, if it is costly to reach a false conclusion, for example in case of increased risks for patients, or in the field of drug development.

Model selection criterion AIC and predictive performance

Intuitively, predicting data for an individual that cannot be "individualized" seems problematic because the data are predicted using a random effect η_i set to zero, instead of the value fitting for that individual. However, AIC is related to the expected model output; and for individual data not used in building the predictive model, the expected model of output is obtained with mixed effects set to zero, although nonlinearities may bias expectation - but this is also true for nonlinear models without mixed effects.

Furthermore, it should be noted that minimizing AIC has a more general interpretation, namely optimally capturing the information contained in the data⁴. Independent or future population data z are not just predicted by ŷ; also the distributions of the expected random effects ε and η are characterized by σ̂² and ω̂². That is why OFV_v is the criterion to be used to assess the predictive performance of a model.

Regression weights as functions of the model output

The simulated data were analyzed using weighted (non)linear regression, see eq. (6), where measurement noise was weighted according to the exact function value. In practice, when the weights are unknown, a choice must be made to weight the data according to the measurements or to the model output, depending on which is likely to be the most accurate. To match the latter case, simulated data should be generated (cf. eq. (6)) via

y_{i} (t_{j}) = \frac{1}{t_{j}} \cdot \exp (η_{i}) \cdot (1 + ϵ_{i j}) . (10)

The likelihood function and AIC are both still well-defined if the model output ŷ_i(t_j) ≠ 0. Prediction errors are to be calculated with

v^{2} = \frac{1}{N \cdot M} ​ \sum_{i = 1}^{N} {\sum_{j = 1}^{M} (\frac{z_{i} (t_{j}) - {\hat{y}}_{i} (t_{j}) ​}{{\hat{y}}_{i ​} (t_{j})})}^{2}, (11)

where ŷ possibly becomes arbitrarily close to zero for less than optimal models, and v² may be based on long-tailed distributed numbers. To be able to compare prediction errors from different models, the weight factors could be chosen identical for all K to the model output of the largest model - see the Supplementary material for further analysis.

Limitations of the study

We recognize the following limitations of our study:

The model contained only one random effect, and therefore the number of random effect (co)variances was fixed to one. While the number of (co)variance parameters should be counted as ordinary parameters⁵, at least in well behaved situations¹³, we did not investigate the process of optimizing this part of a random effects model.
The nonlinearity in the mixed-effects model was simply due to a multiplicative factor exp(η) in the model output. Usually, random effects in pharmacokinetic models have more complex influence on the model output. However, the lognormal nature of exp(η) is a characteristic property of both our toy model and general pharmacokinetic models.
The characteristics of the exponentials incorporated in the regression models were evenly spaced, and the values of the rate constants λ were fixed. We expect that with more freedom in the specification of the set of models, prediction errors with overfitted models may be worse. However, the agreement between AIC_c and prediction error should persist.
We did not evaluate all possible models within their definition, but only those listed in Table 1, and it makes sense to limit the model set to avoid overfitting the data^4,11. We did not address how to optimally select the rate constants λ. Stepwise selection methods have their disadvantages¹². With stepwise forward selection, AIC_c may even perform worse than AIC¹⁴.
We did not evaluate the process of covariate selection. However, the set of exponentials may be viewed as a number of (somewhat correlated) predictors. It is therefore expected that the present findings also hold for other types of covariates.

Conclusion

In conclusion, the present simulation study demonstrated that in the presence of inter-individual variability in a relatively simple mixed effects modeling context, minimum mean AIC_c coincided with best predictive performance.

Author contributions

EO performed the numerical analyses, and EO and AD contributed to the interpretation of the results and the preparation of the manuscript; both authors have agreed to its final content.

Competing interests

No competing interests were disclosed.

Grant information

This work was funded by institutional resources.

Acknowledgments

The authors would like to thank J. de Goede for many fruitful discussions.

Supplementary material

In the following, we summarize theory on the maximum likelihood approach and AIC relevant to this paper. Suppose the model for measured data y_j, j = 1, …, M is given by (cf. eq. (5), eq. (6), and eq. (10))

y_{i} = {\hat{y}}_{j} + w_{j} . ϵ_{j}, (12)

where ŷ_j is the model output, w_j are weight factors, and ε_j are independent normally distributed with mean zero and variance σ². The likelihood function L for this data set is then given by

L (y; θ) = \prod_{j = 1}^{M} \frac{1}{w_{j} σ \sqrt{(2 π)}} ​ \exp [- \frac{1}{2} {(\frac{y_{j} - {\hat{y}}_{j}}{w_{j} σ})}^{2}], (13)

where the set of parameters θ contains σ² and those needed to calculate ŷ. The objective function value (OFV) is defined as minus two times the natural logarithm of the likelihood:

OFV = - 2 \log (L (y; θ)) = \sum_{j = 1}^{M} \log (w_{j}^{2}) + M \log (σ^{2}) + M \log (2 π) + \frac{1}{σ^{2}} ​ {\sum_{j = 1}^{M} (\frac{y_{j} - {\hat{y}}_{j}}{w_{j}})}^{2} . (14)

Note that in writing "OFV", the data and parameters it depends on have been omitted. Now maximum likelihood is obtained when OFV is minimal; constant terms such as M log(2π) may then be discarded (for example, in NONMEM's calculation of the the objective function). The minimum is attained for certain values of parameters of ŷ, and for the parameter value of σ², when the derivative of OFV with respect to that parameter is zero:

\frac{\partial OFV}{\partial σ^{2}} ​ = \frac{M}{σ^{2}} ​ - ​ \frac{1}{{(σ^{2})}^{2}} {\sum_{j = 1}^{M} (\frac{y_{j} - {\hat{y}}_{j}}{w_{j}})}^{2} = 0, (15)

so the maximum likelihood estimator of σ² is

{\hat{σ}}^{2} = \frac{1}{M} {\sum_{j = 1}^{M} (\frac{y_{j} - {\hat{y}}_{j}}{w_{j}})}^{2} . (16)

By subsituting this estimate in eq. (14), we obtain

OFV = \sum_{j = 1}^{M} \log (w_{j}^{2}) + M \log ({\hat{σ}}^{2}) + M \log (2 π) + M . (17)

By substituting this result in eq. (1), we have

AIC = \sum_{j = 1}^{M} \log (w_{j}^{2}) + M \log ({\hat{σ}}^{2}) + M \log (2 π) + M + 2 D . (18)

The term 2D arises from the fact that in minimizing the Kullback-Leibler information, i.e., a measure of the distance between reality and the best approximating model, expectations have to be taken over a data space leading to estimates of parameters θ (and hence ŷ, and possibly ω (see below)) and over a second independent data space y⁴. So AIC as defined above should on average be approximately equal the value of OFV eq. (14), with estimated values for the parameters and validation data z_j, denoted OFV_v:

{OFV}_{v} = \sum_{j = 1}^{M} \log (w_{j}^{2}) + M \log ({\hat{σ}}^{2}) + M \log (2 π) + \frac{1}{{\hat{σ}}^{2}} . {\sum_{j = 1}^{M} (\frac{z_{j} - {\hat{y}}_{j}}{w_{j}})}^{2} . (19)

So when OFV and AIC are both minimized, the latter term - the sum of squared weighted prediction errors - should also be minimal. For the plots in this paper, the measures OFV, OFV_v, AIC, and AIC_c, were normalized by dividing them by the number of data samples. With an infinite amount of data, and σ̂² = σ², the normalized criteria should attain the value of log(σ² )+log(2π)+1.

Note that if the weights w_j are taken as stated in subsection "Data simulation", the term ∑log(w_j²) vanishes (this is a just a curiosity of that choice of weights); if the w_j are taken as the measurements y_j, the expectation of this term is the same for every K (for every model considered here). However, if the weights are taken as the model output ŷ_j, the expectation of the term will not vanish for a less than perfect model, and will differ between different models. To compare their v², the weights for all models could be fixed to the model output of the best model - but since that is unknown at this point - to the output of the largest model.

For population data, the likelihood function is the product across individual marginal likelihoods where the random effects η contained in eq. (13), when ŷ is given by eq. (6), have been integrated out. Usually, these integrals need to be numerically approximated, e.g., as is done here, by NONMEM. So the context of AIC is then also the one where the ηs have been integrated out (but with the parameters at their estimated values), which is to be done when all data are acquired. So while the characteristics of the set of (validation) data are optimally captured, this context is different from the case where prediction errors are calculated with the random effects set to zero instead of being integrated out. In that case, the above AIC and OFV_v criteria do not match, as the components of the likelihood in eq. (13) are no longer independent (they can only be independent if the true values of η for the individuals are also zero). Note however, that from the higher perspective of optimally characterizing a future set of population data, this is a less important case.

Finally, it should be noted that the parameter estimates may not be consistent (i.e., do not converge to their true values when the amount of data goes to infinity if the ŷ_j do not properly account for heteroscedasticity)¹⁵. In the derivation of AIC⁴, it is only required that the likelihood function is maximized; consistency is not required.

References

1. Hastie T, Tibshirani RJ, Friedman JH: The elements of statistical learning. Data mining, inference, and prediction (2nd ed), Springer, New York (2009).
2. Bonate PL: Pharmacokinetic-pharmacodynamic modeling and simulation. (2nd ed.), Springer, New York (2011).
3. Akaike H: A new look at the statistical model identification. IEEE Trans Automat Contr. (1974); 19: 716–23.
4. Burnham KP, Anderson DR: Model selection and multimodel inference. (2nd ed.), Springer, New York (2002); 488.
5. Vaida F, Blanchard S: Conditional Akaike information for mixed-effects models. Biometrika. (2005); 92: 351–70.
6. Norwich KH: Noncompartmental models of whole-body clearance of tracers: A review. Ann Biomed Eng. (1997); 25: 421–39.
7. R Development Core Team, R: A language and environment for statistical computing. R Foundation for Statistical Computing. Vienna, Austria (2012) ISBN 3-900051-07-0.
8. Beal SL, Sheiner LB, Boeckmann AJ, et al:NONMEM User’s Guides. Icon Development Solutions, Hanover, MD, USA (1989–2012).
9. Fang Y: Asymptotic equivalence between cross-validations and Akaike information criteria in mixed-effects models. J Data Sci. (2011); 9: 15–21.
10. Burnham KP, Anderson DR: Multimodel inference: Understanding AIC and BIC in model selection. Sociol Meth Res. (2004); 33: 261–304.
11. Yang Y: Can the strengths of AIC and BIC be shared? A conflict between model identification and regression estimation. Biometrika. (2005); 92: 937–50.
12. Steyerberg EW: Clinical prediction models. A practical approach to development, validating, and updating. Springer, New York (2009); 497.
13. Greven S, Kneib T: On the behaviour of marginal and conditional AIC in linear mixed effects models. Biometrika. (2010); 97: 773–89.
14. Olofsen E: The performance of model selection criteria in the absence of a fixed-dimensional correct model.(2007); Page 16, Abstr 1198.
15. van Houwelingen JC: Use and abuse of variance models in regression. Biometrics. (1988); 44: 1073–81.

Comments on this article Comments (0)

Version 3

VERSION 3 PUBLISHED 04 Mar 2013

Author details Author details

¹ Department of Anesthesiology, Leiden University Medical Center, PO Box 9600, 2300 RC Leiden, The Netherlands

Competing interests

No competing interests were disclosed.

Grant information

This work was funded by institutional resources.
The funders had no role in study design, data collection and analysis, decision to publish, or preparation of the manuscript.

Article Versions (3)

version 3

Revised

Published: 27 Jul 2015, 2:71

https://doi.org/10.12688/f1000research.2-71.v3

version 2

Revised

Published: 28 May 2014, 2:71

https://doi.org/10.12688/f1000research.2-71.v2

version 1

Published: 04 Mar 2013, 2:71

https://doi.org/10.12688/f1000research.2-71.v1

© 2013 Olofsen E and Dahan A. This is an open access article distributed under the terms of the Creative Commons Attribution License, which permits unrestricted use, distribution, and reproduction in any medium, provided the original work is properly cited. Data associated with the article are available under the terms of the Creative Commons Zero "No rights reserved" data waiver (CC0 1.0 Public domain dedication).

Download

Export To

metrics

	Views	Downloads
F1000Research	-	-
PubMed Central Data from PMC are received and updated monthly.	-	-

Citations

SEE MORE DETAILS

CITE

how to cite this article

Olofsen E and Dahan A. Using Akaike’s information theoretic criterion in population analysis: a simulation study [version 1; peer review: 2 approved with reservations, 1 not approved]. F1000Research 2013, 2:71 (https://doi.org/10.12688/f1000research.2-71.v1)

NOTE: If applicable, it is important to ensure the information in square brackets after the title is included in all citations of this article.

track

receive updates on this article

Track an article to receive email alerts on any updates to this article.

Open Peer Review

Current Reviewer Status: ?

Key to Reviewer Statuses VIEW HIDE

ApprovedThe paper is scientifically sound in its current form and only minor, if any, improvements are suggested

Approved with reservations A number of small changes, sometimes more significant revisions are required to address specific details and improve the papers academic merit.

Not approvedFundamental flaws in the paper seriously undermine the findings and conclusions

Version 1

VERSION 1

PUBLISHED 04 Mar 2013

Views

Reviewer Report 21 Oct 2013

Julie Bertrand, UCL Genetics Institute, University College London, London, UK

Approved with Reservations

https://doi.org/10.5256/f1000research.869.r1693

The title should indeed specify that this work focuses on pharmacokinetics (PK). However I must add that the model function considered is unusual enough that it seems difficult to extend their conclusions to a real PK study analysis.

The abstract is too general and more details should be provided on the simulation study (model function, number of samples, number of subjects, number of random effects) and the results (differences between selection on OFV, AIC and AICc, impact of increasing the random effect variance).

The whole methodology is very well described. But one aspect is missing, as underlined by the other reviewer: the (very direct here) link with the best sum of exponential model and the information in the design. I was not much surprised that K=6 (or 5) exponential got the best AIC when you have 11 evenly spaced samples and the candidate models all had evenly spaced rate constants. Also, why not investigate the performance of BIC (with log(N) and log(NxM)) ?

Finally, the conclusions are balanced in the sense that the authors have rightly identified the limit of their exercise which is the generalization of their results to a real PK data analysis: only one random effect, no covariance parameters, only slope parameters, etc...

Competing Interests: No competing interests were disclosed.

I confirm that I have read this submission and believe that I have an appropriate level of expertise to confirm that it is of an acceptable scientific standard, however I have significant reservations, as outlined above.

CITE

Report a concern

Respond or Comment

Views

Reviewer Report 07 May 2013

Frank Harrell, Department of Biostatistics, Vanderbilt University School of Medicine, Nashville, TN, USA

Not Approved

https://doi.org/10.5256/f1000research.869.r928

CITE

Report a concern

Respond or Comment

Views

Reviewer Report 05 Mar 2013

Paul Eilers, Department of Biostatistics, Erasmus Medical Center, Rotterdam, The Netherlands

Approved with Reservations

https://doi.org/10.5256/f1000research.869.r809

CITE

Report a concern

Author Response 05 Mar 2013

Erik Olofsen, Department of Anesthesiology, Leiden University Medical Center, PO Box 9600, 2300 RC Leiden, The Netherlands

05 Mar 2013

Author Response

Thank you for your comments. Vaida and Blanchard (ref. 5 above) discuss two settings: model focus and cluster focus. In the former setting, the effective number of parameters equals the ... Continue reading Thank you for your comments. Vaida and Blanchard (ref. 5 above) discuss two settings: model focus and cluster focus. In the former setting, the effective number of parameters equals the number of fixed effects parameters and variance components (p.354); in the latter setting, the effective number of parameters needs to be estimated in the way you outlined. The first setting, corresponding to the situation of predicting data of "new" subjects, is the one for which the study results should be valid.
Thank you for your comments. Vaida and Blanchard (ref. 5 above) discuss two settings: model focus and cluster focus. In the former setting, the effective number of parameters equals the number of fixed effects parameters and variance components (p.354); in the latter setting, the effective number of parameters needs to be estimated in the way you outlined. The first setting, corresponding to the situation of predicting data of "new" subjects, is the one for which the study results should be valid.
Competing Interests: No competing interests were disclosed. Close
Report a concern
Respond or Comment

COMMENTS ON THIS REPORT

Author Response 05 Mar 2013

Erik Olofsen, Department of Anesthesiology, Leiden University Medical Center, PO Box 9600, 2300 RC Leiden, The Netherlands

05 Mar 2013

Author Response

Thank you for your comments. Vaida and Blanchard (ref. 5 above) discuss two settings: model focus and cluster focus. In the former setting, the effective number of parameters equals the ... Continue reading Thank you for your comments. Vaida and Blanchard (ref. 5 above) discuss two settings: model focus and cluster focus. In the former setting, the effective number of parameters equals the number of fixed effects parameters and variance components (p.354); in the latter setting, the effective number of parameters needs to be estimated in the way you outlined. The first setting, corresponding to the situation of predicting data of "new" subjects, is the one for which the study results should be valid.
Thank you for your comments. Vaida and Blanchard (ref. 5 above) discuss two settings: model focus and cluster focus. In the former setting, the effective number of parameters equals the number of fixed effects parameters and variance components (p.354); in the latter setting, the effective number of parameters needs to be estimated in the way you outlined. The first setting, corresponding to the situation of predicting data of "new" subjects, is the one for which the study results should be valid.
Competing Interests: No competing interests were disclosed. Close
Report a concern

Comments on this article Comments (0)

Version 3

VERSION 3 PUBLISHED 04 Mar 2013

Open Peer Review

Reviewer Status

Reviewer Reports

	Invited Reviewers
	1	2	3
Version 3 (revision) 27 Jul 15	read	read
Version 2 (revision) 28 May 14	read		read
Version 1 04 Mar 13	read	read	read

Paul Eilers, Erasmus Medical Center, Rotterdam, The Netherlands
Frank Harrell, Vanderbilt University School of Medicine, Nashville, TN, USA
Julie Bertrand, University College London, London, UK

Comments on this article

All Comments(0)

Add a comment

Browse by related subjects

Back to all reports

Reviewer Report

10 Views

16 Nov 2015 | for Version 3

Frank Harrell, Department of Biostatistics, Vanderbilt University School of Medicine, Nashville, TN, USA

10 Views Cite this report Responses(0)

Approved

I have read the authors revisions and am satisfied that they have answered my concerns.

Competing Interests

No competing interests were disclosed.

I confirm that I have read this submission and believe that I have an appropriate level of expertise to confirm that it is of an acceptable scientific standard.

Respond to this report

Responses (0)

Back to all reports

Reviewer Report

9 Views

06 Aug 2015 | for Version 3

Paul Eilers, Department of Biostatistics, Erasmus Medical Center, Rotterdam, The Netherlands

9 Views Cite this report Responses(0)

Approved

The revised version is fine with me.

Competing Interests

No competing interests were disclosed.

I confirm that I have read this submission and believe that I have an appropriate level of expertise to confirm that it is of an acceptable scientific standard.

Respond to this report

Responses (0)

Back to all reports

Reviewer Report

12 Views

22 Aug 2014 | for Version 2

Paul Eilers, Department of Biostatistics, Erasmus Medical Center, Rotterdam, The Netherlands

12 Views Cite this report Responses(0)

Approved

The explanation in the authors' response, about the effective degrees of freedom, clarifies the matter. That will be helpful to the readers.

I noticed a typo in the second paragraph of the Introduction, explaining the OFV. Change to "... (OFV), being minus two times the logarithm ...".

Competing Interests

No competing interests were disclosed.

I confirm that I have read this submission and believe that I have an appropriate level of expertise to confirm that it is of an acceptable scientific standard.

Respond to this report

Responses (0)

Back to all reports

Reviewer Report

29 Views

24 Jun 2014 | for Version 2

Julie Bertrand, UCL Genetics Institute, University College London, London, UK

29 Views Cite this report Responses(2)

Approved With Reservations

Abstract:

"[W]ith three degrees of inter... volume of distribution" This does not make sense, as no mention of the volume parameter is made afterward in the body of the text.

Introduction:

"Fixed effects are ... the measurements obtained", Usually the fixed effects are the population/average/mean values of the model parameters, so this sounds incorrect perhaps because it's out of context.

Methods:

The authors should be clearer about the model parameters that are estimated : K non-zero parameters α_m (?),as K doesn't even appear in equation (3)?
What are those α_m? Do they correspond to dose/volume in an IV bolus equation? Then I'm not sure one can identify M in such parameters?
"Note that with N > 1, a perfect fit is no longer obtained with K = M nonzero coefficients α, because the ϵij are generally different for different i (individuals)" The authors should add that it is the case here because in their model there is only one random effect per individual.
The constraint/absence of constraint on the α_m is not clear; those parameters were not constrained so they could be equal to zero? The authors should be more explicit.
"[U]sing predictions based on equation (7) with the random effectsηi= 0, and validation data zi(tj) also generated via equation (6), but with different realizations of ϵij and ηi" It is not clear to me how are those predictions were obtained? How are the random effect and residual errors generated (type and parameter values of the distributions)?
"The above criteria were normalized by dividing them by the number of observations, and averaged over 1000 runs" Seems incorrect or not explained enough. In mixed effect models you cannot compare two designs soley on the total number of observations. The information is not the same for n_tot=20 resulting from i) 2 subjects with 10 samples each and ii) 5 subjects with 4 samples each.
In Figure 3, the plots of OFV versus -2LL, AIC and AICc do not make sense to me as the relationship is evident from the equations, plus there is no explanation about what the separate points correspond to.

Discussion:

I am not convinced by the section on BIC as the claims are rather strong in absence of comparison on the simulations. I suggest the authors shorten it.
The first section of "Model selection criterion AIC and predictive performance" does not make sense to me, are the authors talking about AIC capability to select a model that would predict new subjects? I thought that was the criteria they actually used.
Also in "Model selection criterion AIC and predictive performance" the last section seems full of strong claims again (as for BIC) not justified through the present simulation study; I would suggest the authors remove the 1st and last sections I've mentioned.
"In practice, when the weights are unknown, a choice must be made to weight the data according to the measurements or to the model output, depending on which is likely to be the most accurate." There is literature about NOT using the measurements but the model output, that should be corrected.

Competing Interests

No competing interests were disclosed.

Respond to this report

Responses (2)

Author Response

30 Jun 2014

Erik Olofsen, Department of Anesthesiology, Leiden University Medical Center, PO Box 9600, 2300 RC Leiden, The Netherlands

We thank the reviewer for pointing out those parts of the text that are unclear. Changes to the article will be based on the following observations.

The simulated interindividual variation influences the concentration level, which is related to volume, and no other disposition characteristics - an explanation will be added to the description of the population model.
The term "fixed effect" is perhaps not well defined in the literature. In the linear fixed effects model Y = X.β, X (the design matrix) as well as β (the coefficients) are sometimes called fixed effects. In NONMEM's guide V, time - which would be part of the design matrix - is called a fixed effect. Time influences the model output in a non-random manner; how it influences the output depends on the model, and on model parameters. Therefore, a population value of a model parameter is similar to the value of a "fixed effect parameter", and then time could be called a "fixed effect factor".
The coefficients α are related to disposition characteristics and are parameters to be estimated. This was stated explicitly only in the legend of Table 1, so we agree this should be better explained. Because of the link between the considered sum of exponentials and the integral in equation (2), one would expect the α to be positive, but this constraint was not imposed. The M time constants λ are fixed and have distinct values, so that M coefficients α are identifiable. M-K coefficients were fixed to zero according to Table 1, to obtain models with K free parameters. Indeed, to obtain a perfect fit with more than one individual, M random effects are needed.
The log likelihood function with known parameter values and homoscedastic random effects is both linear in the number of observations per subject and in the number of subjects. Then the expected values of the log likelihoods for the two designs that you give are equal. The ratio of the estimated log likelihood and the total number of observations is a measure of the entropy in the data due to the random effects (the dashed lines in figure 3), with a deviation due to estimation error (possibly different for the two designs). But although this is interesting, the normalization is indeed also confusing and not essential for our study.
The plot of OFVv versus -2LL should demonstrate that a lower objective function does not imply a lower prediction error and the plots of OFVv versus AIC and AICc that it is AICc, and not AIC, which corresponds closely to prediction error. Only plots of AIC and AICc versus -2LL would be relatively trivial. We agree that the number of exponentials should be indicated next to the dots.
We expect the claims on BIC versus AIC in the literature to hold for mixed effect models, but we we agree that the range of effective sample sizes used in the present study is not sufficient to provide firm additional support.
The first section of "Model selection criterion AIC and predictive performance" is best deleted and the second section slightly rewritten. Interindividual variation in a new set of data is predicted by a distribution rather than only its mode.
To compare models with AIC in weighted regression, the weights should be the same, which is true when using the measurements, and not so when using the model output as weights, because the models are different. Therefore the model output of the best model could be used as weights. On the other hand, the output of the models should be quite similar, so that the postulated likelihood function approximately holds for the data, which might not hold as well when using the measurements as weights.

View more View less

Competing Interests

No competing interests were disclosed.

Author Response

19 Mar 2015

Erik Olofsen, Department of Anesthesiology, Leiden University Medical Center, PO Box 9600, 2300 RC Leiden, The Netherlands

The normalization of the likelihood by dividing by the total number of measurements was done to have a "target" value for the estimates indicated in the figures. When the between individuals variance is zero, the normalized value is independent of the number of measurements and individuals. When the between individuals variance is greater than zero, and the number of measurements per individual M is finite, the normalized value is larger, and in a nonlinear fashion depending on M, than this target. Therefore the two designs mentioned above are indeed different. This will be addressed in the next version.

View more View less

Competing Interests

No competing interests were disclosed.

Back to all reports

Reviewer Report

27 Views

21 Oct 2013 | for Version 1

Julie Bertrand, UCL Genetics Institute, University College London, London, UK

27 Views Cite this report Responses(0)

Approved With Reservations

Competing Interests

No competing interests were disclosed.

Respond to this report

Responses (0)

Back to all reports

Reviewer Report

54 Views

07 May 2013 | for Version 1

Frank Harrell, Department of Biostatistics, Vanderbilt University School of Medicine, Nashville, TN, USA

54 Views Cite this report Responses(0)

Not Approved

The title and abstract do not place the potentially useful study in the right context. 'Population' can have many meanings and the scope is too wide. Consider narrowing the implied scope to mixed effects PK modeling.AIC can be an excellent metric for selecting from among a very limited number of models. If used in a stepwise process it can result in all the severe problems that stepwise variable selection has. The authors need to be much more careful about multiplicity and model uncertainty. This needs to be carefully discussed, and the authors would add to the literature if they can derive the maximum number of models that can be compared with AIC before the method breaks down.

Competing Interests

No competing interests were disclosed.

I confirm that I have read this submission and believe that I have an appropriate level of expertise to state that I do not consider it to be of an acceptable scientific standard, for reasons outlined above.

Respond to this report

Responses (0)

Back to all reports

Reviewer Report

32 Views

05 Mar 2013 | for Version 1

Paul Eilers, Department of Biostatistics, Erasmus Medical Center, Rotterdam, The Netherlands

32 Views Cite this report Responses(1)

Approved With Reservations

This is an interesting and useful study, written in a relaxed style. I believe we need more studies like this, because there is a lot of folklore around AIC, mainly claiming that is generally over-fits.

I have one major objection: the effective dimension (ED) of a mixed model is less than the number of parameters (D), because shrinking takes place. The easiest way to obtain ED is to compute the trace of the “hat” matrix. In linear models this is relatively easy. In non-linear models it is harder. What one needs is (in LaTeX notation) $h_{ii} = \partial \hat y_i/ \partial y_i$. I can provide more details if needed. I don’t know if NONMEM can provide the needed quantities.

Competing Interests

No competing interests were disclosed.

Respond to this report

Responses (1)

Author Response

05 Mar 2013

Erik Olofsen, Department of Anesthesiology, Leiden University Medical Center, PO Box 9600, 2300 RC Leiden, The Netherlands

Thank you for your comments. Vaida and Blanchard (ref. 5 above) discuss two settings: model focus and cluster focus. In the former setting, the effective number of parameters equals the number of fixed effects parameters and variance components (p.354); in the latter setting, the effective number of parameters needs to be estimated in the way you outlined. The first setting, corresponding to the situation of predicting data of "new" subjects, is the one for which the study results should be valid.

View more View less

Competing Interests

No competing interests were disclosed.

Alongside their report, reviewers assign a status to the article:

Approved - the paper is scientifically sound in its current form and only minor, if any, improvements are suggested

Approved with reservations - A number of small changes, sometimes more significant revisions are required to address specific details and improve the papers academic merit.

Not approved - fundamental flaws in the paper seriously undermine the findings and conclusions

[1] 1. Hastie T, Tibshirani RJ, Friedman JH: The elements of statistical learning. Data mining, inference, and prediction (2nd ed), Springer, New York (2009).

[2] 2. Bonate PL: Pharmacokinetic-pharmacodynamic modeling and simulation. (2nd ed.), Springer, New York (2011).

[3] 3. Akaike H: A new look at the statistical model identification. IEEE Trans Automat Contr. (1974); 19: 716–23.

[4] 4. Burnham KP, Anderson DR: Model selection and multimodel inference. (2nd ed.), Springer, New York (2002); 488.

[5] 5. Vaida F, Blanchard S: Conditional Akaike information for mixed-effects models. Biometrika. (2005); 92: 351–70.

[6] 6. Norwich KH: Noncompartmental models of whole-body clearance of tracers: A review. Ann Biomed Eng. (1997); 25: 421–39.

[7] 7. R Development Core Team, R: A language and environment for statistical computing. R Foundation for Statistical Computing. Vienna, Austria (2012) ISBN 3-900051-07-0.

[8] 8. Beal SL, Sheiner LB, Boeckmann AJ, et al:NONMEM User’s Guides. Icon Development Solutions, Hanover, MD, USA (1989–2012).

[9] 9. Fang Y: Asymptotic equivalence between cross-validations and Akaike information criteria in mixed-effects models. J Data Sci. (2011); 9: 15–21.

[10] 10. Burnham KP, Anderson DR: Multimodel inference: Understanding AIC and BIC in model selection. Sociol Meth Res. (2004); 33: 261–304.

[11] 11. Yang Y: Can the strengths of AIC and BIC be shared? A conflict between model identification and regression estimation. Biometrika. (2005); 92: 937–50.

[12] 12. Steyerberg EW: Clinical prediction models. A practical approach to development, validating, and updating. Springer, New York (2009); 497.

[13] 13. Greven S, Kneib T: On the behaviour of marginal and conditional AIC in linear mixed effects models. Biometrika. (2010); 97: 773–89.

[14] 14. Olofsen E: The performance of model selection criteria in the absence of a fixed-dimensional correct model.(2007); Page 16, Abstr 1198.

[15] 15. van Houwelingen JC: Use and abuse of variance models in regression. Biometrics. (1988); 44: 1073–81.

K	m : 1	2	3	4	5	6	7	8	9	10	11
1	0	0	0	0	0	1	0	0	0	0	0
2	1	0	0	0	0	0	0	0	0	0	1
3	1	0	0	0	0	1	0	0	0	0	1
4	1	0	0	1	0	0	0	1	0	0	1
5	1	0	0	1	0	1	0	1	0	0	1
6	1	0	1	0	1	0	1	0	1	0	1
7	1	0	1	1	0	1	0	1	1	0	1
8	1	1	0	1	1	0	1	1	0	1	1
9	1	1	0	1	1	1	1	1	0	1	1
10	1	1	1	1	1	0	1	1	1	1	1
11	1	1	1	1	1	1	1	1	1	1	1

K	m : 1	2	3	4	5	6	7	8	9	10	11
1	0	0	0	0	0	1	0	0	0	0	0
2	1	0	0	0	0	0	0	0	0	0	1
3	1	0	0	0	0	1	0	0	0	0	1
4	1	0	0	1	0	0	0	1	0	0	1
5	1	0	0	1	0	1	0	1	0	0	1
6	1	0	1	0	1	0	1	0	1	0	1
7	1	0	1	1	0	1	0	1	1	0	1
8	1	1	0	1	1	0	1	1	0	1	1
9	1	1	0	1	1	1	1	1	0	1	1
10	1	1	1	1	1	0	1	1	1	1	1
11	1	1	1	1	1	1	1	1	1	1	1

Using Akaike’s information theoretic criterion in population analysis: a simulation study

Abstract

Keywords

Introduction

Methods

A hypothetical pharmacokinetic model

Figure 1.

Data simulation

Population data simulation and modeling

Statistical analysis

Selection of parameter values

Table 1. Selecting K = 1, …, M = 11 evenly spaced rate constants from λ: 0 and 1 denote αm to be fixed to zero, and a free parameter to be estimated, respectively (see eq. (7)).

Results

Figure 2.

Figure 3.

Figure 4. Mean OFVν, AICc and prediction error ν2 as a function of the number of exponentials, for ω2 = 0.1; parameters otherwise identical.

Figure 5. Mean OFVv and AICc as a function of the number of exponentials, AIC and AICc, for ω2 = 0.5; parameters otherwise identical.

Discussion

Akaike's versus the conditional Akaike information criterion

Akaike's versus the Bayesian information criterion

Model selection criterion AIC and predictive performance

Regression weights as functions of the model output

Limitations of the study

Conclusion

Author contributions

Competing interests

Grant information

Acknowledgments

Supplementary material

References

Comments on this article Comments (0)

Open Peer Review

Comments on this article Comments (0)

Open Peer Review

Reviewer Status

Reviewer Reports

Comments on this article

Browse by related subjects

Competing Interests Policy

Stay Updated

Table 1. Selecting K = 1, …, M = 11 evenly spaced rate constants from λ: 0 and 1 denote α_m to be fixed to zero, and a free parameter to be estimated, respectively (see eq. (7)).

Figure 4. Mean OFV_ν, AIC_c and prediction error ν² as a function of the number of exponentials, for ω² = 0.1; parameters otherwise identical.

Figure 5. Mean OFV_v and AIC_c as a function of the number of exponentials, AIC and AIC_c, for ω² = 0.5; parameters otherwise identical.

K	m : 1	2	3	4	5	6	7	8	9	10	11
1	0	0	0	0	0	1	0	0	0	0	0
2	1	0	0	0	0	0	0	0	0	0	1
3	1	0	0	0	0	1	0	0	0	0	1
4	1	0	0	1	0	0	0	1	0	0	1
5	1	0	0	1	0	1	0	1	0	0	1
6	1	0	1	0	1	0	1	0	1	0	1
7	1	0	1	1	0	1	0	1	1	0	1
8	1	1	0	1	1	0	1	1	0	1	1
9	1	1	0	1	1	1	1	1	0	1	1
10	1	1	1	1	1	0	1	1	1	1	1
11	1	1	1	1	1	1	1	1	1	1	1