Keywords
pyramidal cells, neuroscience, patch clamps
pyramidal cells, neuroscience, patch clamps
Our manuscript has been revised to address the various comments raised by the reviewers. Among these revisions, we note in particular: (i) a new figure showing rebound spiking as recorded in CA1 pyramidal cells in this whole hippocampus preparation, and the new data has been added, (ii) a change in the representation of the model equations (including I shift ), which does not change the model itself, (iii) 4 additional references have been included.
See the authors' detailed response to the review by Alla Borisyuk
See the authors' detailed response to the review by Farzan Nadim and Haroon Anwar
Networks of excitatory and inhibitory neurons are essential components constituting the functional structures of our brains. Dysfunction is thought to occur when inappropriate excitation-inhibition balances occur1. From a modeling perspective, these balances are determined by the choice of parameters in the equations representing neurons and networks. Mathematical models of neurons and networks are developed so that they can be used to determine the mechanisms underlying brain functions. However, it is difficult to assess whether the mechanisms determined from mathematical models actually occur biologically2,3. Furthermore, it is well known that cellular models used in building network models affect and can dictate the network output4,5. To address this recognized difficulty we are developing models that are based on well-defined experimental contexts in which both cellular and population (network) aspects can be characterized6,7. That is, we are building network models that are constrained based on experimental preparations in which intracellular and extracellular recordings (local field potentials) are simultaneously recorded, as described in other studies8,9. Using such models, we aim to determine, predict and test mechanisms underlying population network output occurring in biological systems.
Here we use a well-defined experimental context of an in vitro intact, whole hippocampus preparation in which spontaneous population theta and theta-gamma rhythms are expressed10,11. Access to many cellular details is possible in vitro, and with a physiologically relevant output of theta and theta-gamma rhythms, a reasonable and functional scenario is also present. We have previously developed models of CA1 fast-spiking inhibitory cells in the same experimental context, and used them to show that model inhibitory networks of these fast-spiking cells exhibit sharp transitions between random and coherent firings at high frequencies (>90 Hz) when connectivity constraints were imposed6. In this article, we present the result of CA1 pyramidal cell models developed in the same context of this in vitro whole hippocampus preparation. Similar to our previous cellular model developments6, the models presented here are biologically-based at the cellular level, but do not have a biophysical representation in terms of conductance-based model representations. These CA1 models use a simple two variable mathematical formulation based on Izhikevich12 and they include rebound firing and adaptation characteristics. Using these simple, yet biologically-based models, we are building and examining large network models that are aligned with the biology8,9. Subsequent analyses of these large network models could determine the mechanisms by which particular cellular characteristics critically contribute to the population activities observed in our experimental context.
Animals. Three mice (two female, post-natal day 20–29) were used. We used transgenic mice that expressed a fluorescent protein, tdTomato, under the control of the PV promoter. PV-Cre homozygote mice (strain name: B6;129P2-Pvalbtm1(cre)Arbr/J, stock number: 008069, Jackson Laboratory) were mated with a reporter line, Ai9 homozygote mice (strain name: B6;129S6-Gt(ROSA)26Sortm9(CAG-tdTomato)Hze/J, stock number: 007905, Jackson Laboratory) to generate PV-tdTomato mice. The mouse lines are on genetic backgrounds that are mixtures of C57BL/6 and a type of 129 mice; PV-Cre mice are C57BL/6;129P2 and Ai9 mice are C57BL/6;129S6. Mice were bred in-house at the Douglas animal facility and kept in standard laboratory cages with standard bedding and environmental enrichment. They were housed in a temperature-controlled room with a 12:12 hours dark/light cycle with food and water provided ad libitum. All animals were treated according to protocols and guidelines approved by McGill University and the Canadian Council of Animal Care (CCAC). Ethical approval was obtained to conduct this study (approval number: 2010-5827). The authors note that the use of scissors to decapitate mice at that age without administering anesthesia (which could have altered synaptic transmission) was approved by the CCAC.
Intact hippocampal preparation. The acute preparation containing the whole hippocampus was obtained from PV-tdTomato mice according to a previously described protocol10. Briefly, after decapitation using scissors, the brain was quickly removed from the skull and placed in ice-cold high-sucrose solution, containing (in mM) 252 sucrose, 24 NaHCO3, 10 glucose, 3 KCl, 2 MgCl2, 1.25 NaH2PO4 and 1 CaCl2 (pH 7.3, oxygenated with 95% O2-5% CO2). From a hemisected brain, the septum and hippocampus along with the interconnecting fibers were carefully and rapidly dissected out using a microspatula. The preparation was trimmed in ice-cold high-sucrose solution (same contents as the high-sucrose solution listed above) using fine scissors to remove any remaining cortical tissue and the septum. Then, the surface of the preparation was cut at a ~45° angle to expose the pyramidal layer of CA1. The cut enabled visually guided patch-clamp recordings of pyramidal cells which yielded a higher success rate for whole-cell recordings compared to the blind-patch technique used previously10. The visual approach allowed identification of CA1 pyramidal cells by their soma location, morphology and the lack of PV-tdTomato fluorescence in the soma. The hippocampal preparation was then left to equilibrate in oxygenated room-temperature high-sucrose solution for 30 min – 1 h before recording. The preparation from only one hemisphere was used for recording from each mouse, and the preparation from either the left or the right hemisphere was chosen randomly for each experiment. Three mice were used in total; we used three intact hippocampal preparations from these mice (one from each mouse) and one pyramidal cell was recorded from each preparation, except for one preparation from which two cells were recorded.
All electrophysiological recordings were performed at 30 ± 2ºC, using artificial cerebrospinal fluid (aCSF) containing (in mM) 126 NaCl, 24 NaHCO3, 10 glucose, 4.5 KCl, 2 MgSO4, 1.25 NaH2PO4, 0.4 ascorbic acid and 2 CaCl2 (pH 7.3, oxygenated with 95% O2-5% CO2). The hippocampal preparation was placed in a custom-made submerged recording chamber lined with a nylon mesh, and firmly stabilized by carefully placing several lead weights at both septal and temporal poles of the hippocampal preparation. We placed the hippocampal preparation in the recording chamber, such that the CA1 was the most superficial and accessible sub-region for visualization and whole-cell recordings. Recordings were restricted to neurons located within the middle portion of the hippocampus (intermediate between septal and temporal poles of the preparation). The preparation’s stability in the recording chamber was extremely important as aCSF was perfused at the rate of 20–25 ml/min during recordings. Since the tissue is several millimeters thick, such a fast perfusion rate is necessary to ensure sufficient oxygenation. This fast perfusion rate is also required to generate intrinsic theta oscillations from intact hippocampal preparations10. In order to achieve temperature stability, aCSF was pre-heated using an electric skillet and further regulated via an automatic temperature controller (Warner Instruments, Hamden, CT). The electrophysiology setup was equipped with an upright BX51W1 Olympus microscope, a 20× water-immersion objective, Nomarsky optics, an infrared camera (Cohu, San Diego, CA), a variable-wavelength fluorescence system (PTI, Monmouth Junction, NJ) and a monochrome digital camera for fluorescence imaging (DAGE-MTI, Michigan City, IN). Patch pipettes were pulled from borosilicate glass capillaries (2.5–4 MΩ) and filled with the intra-pipette solution containing (in mM) 144 K-gluconate, 10 HEPES, 3 MgCl2, 2 Na2ATP, 0.3 GTP, 0.2 EGTA, adjusted to pH 7.2 with KOH. The patch electrode was controlled using a motorized micromanipulator (Sutter Instruments, Novato, CA). An Axopatch-1C amplifier (Axon Instruments, Foster City, CA) and pClamp9 software (Molecular Devices, Sunnyvale, CA) were used for recording. The junction potential was estimated at -15.2 mV and was corrected for. All drugs were obtained from Sigma-Aldrich (St. Louis, MO), unless otherwise noted.
Intrinsic property characterization. Intrinsic properties were characterized in current-clamp mode following published protocols with minor modifications13. A mixture of synaptic blockers was used to inhibit synaptic activity: 5 μM 6,7-dinitroquinoxaline-2,3-dione disodium salt (DNQX), 5 μM bicuculline and 25 μM DL-2-amino-5-phosphonopentanoic acid sodium salt (DL-AP5) (Abcam, Toronto, Canada). Data analysis was done using custom Matlab software (MathWorks, Natick, MA). Once the whole-cell configuration was achieved, the cell’s resting membrane potential was noted and its spontaneous firing, if any, was recorded for 30 s. Access resistance and resting membrane potential were checked at regular intervals (every ~5 min) throughout the recording of the cell.
The frequency-current (f-I) profiles of the pyramidal cells are important to characterize, as we aim for our single cell model to respond to a variety of synaptic input strengths with frequencies similar to that observed experimentally. These f-I curves were determined by applying depolarizing current steps of 1 s duration to cells held in current clamp. Amplitudes were increased incrementally with step sizes of 25 pA for one of four cells, and 10 pA for three of four cells. The initial firing frequency was determined based on the inverse of the first inter-spike interval, and the final frequency was based on the inverse of the last inter-spike interval in the 1-second depolarizing step. For each cell, the approximate linear slope of the f-I curve above 5 Hz was determined using a least squares method. These values were chosen since above 5 Hz the slope was well-approximated by linearization. In addition, the minimum amount of current required to initiate a spike, the rheobase current (Irheo in pA), was determined. The action potential threshold was set to be the first voltage point such that the slope of the membrane potential exceeded 20 mV/ms14. The spike width was determined at the threshold value. In addition, the spike height from threshold and the minimum membrane potential reached following the spike were measured. Recordings were kept for analysis only if the neuron remained stationary; spikes overshot 0 mV (-15 mV junction potential corrected) and access resistance < 30 MΩ. While the cell was held at -52 mV in current clamp, as series of 1 s hyperpolarizing steps (25 pA increments) were used to record the post-hyperpolarization rebound spiking. For the figure showing this rebound spiking (Figure 1), the spike artifact in the current clamp input trace (shown in grey) was removed and replaced with the mean current for visualization purposes.
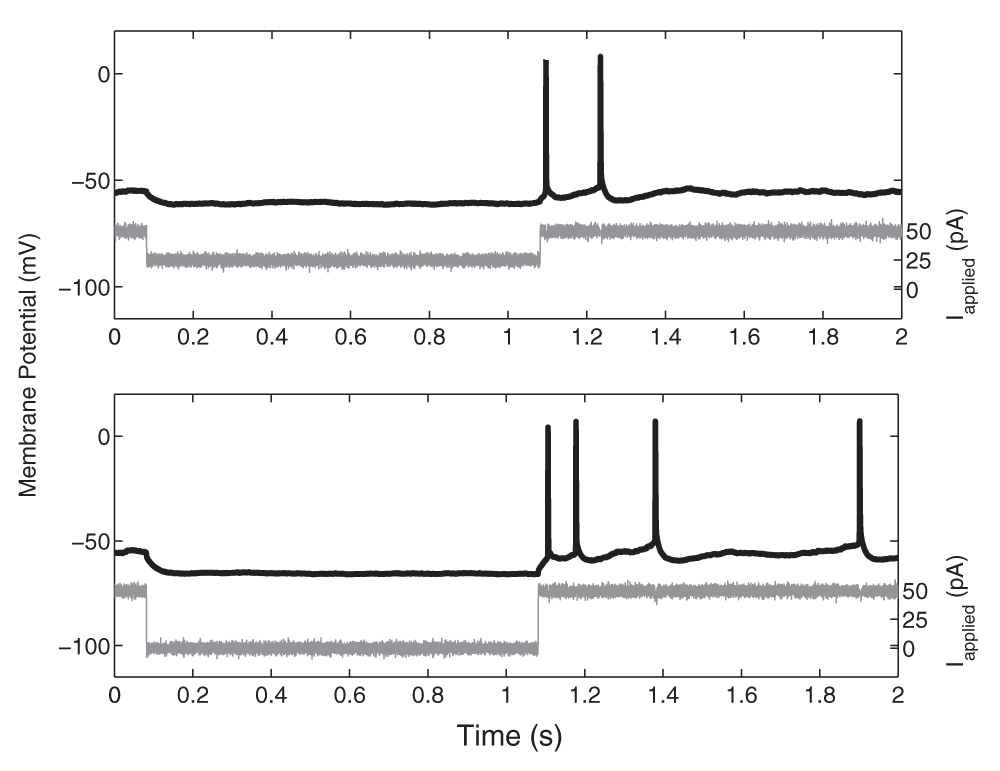
While the cell was held at -52 mV in current clamp, two 1-s hyperpolarizing steps (shown in grey; top: 25 pA, bottom: 50 pA) were used to record the post-hyperpolarization rebound spiking (voltage traces shown in black). For visualization purposes, the spike artifact in the current clamp input trace was removed and replaced with the mean current.
We built a pyramidal cell model based on Izhikevich’s12 simple spiking model structure. We chose this model as it captures the cell’s ability to produce rebound spiking, the approximate spike shape, and the frequency-current profile of the cell, including spike-adaptation. Thus, this model is relatively simple, but allows one to capture important biophysical properties of pyramidal cells.
The model has a fast variable representing the membrane potential, V (mV), and a slow “recovery” current given by the variable u (pA). In order to capture the spike width at threshold, we slightly modified the Izhikevich model by using a different “k” parameter above and below the spike threshold (khigh and klow respectively). The model is given by:
Cm = k(V–vr) (V–vt) – u + Iapplied + Ishift
= a[b(V – vr) – u] (1)
if V ≥ vpeak, then V ← c, u ← u + d
Where k = klow if V ≤ vt; k = khigh if V > vt
The parameters are as follows:
Cm (pF) is the membrane capacitance.
vr (mV) is the resting membrane potential.
vt (mV) is the instantaneous threshold potential.
vpeak (mV) is the spike cut-off value.
Iapplied (pA) is the applied current, and represents the applied input into the cell.
Ishift is a current that shifts the f-I curve laterally to allow the model to easily capture the rheobase current.
a (ms-1) is the recovery time constant of the adaptation current.
b (nS) describes the sensitivity of the adaptation current to subthreshold fluctuations. Greater values couple V and u more strongly resulting in possible subthreshold oscillations and low-threshold spiking dynamics. Further, the sign of b determines whether the effect of u is amplifying (b < 0) or resonant (b > 0).
c (mV) is the voltage reset value.
d (pA) is the total amount of outward minus inward currents activated during the spike and affecting the after-spike behaviour.
k (nS/mV) represents a scaling factor. khigh is used to adjust the spike width after the threshold.
As with the experimental frequency-current (f-I) curve frequencies, we exhibited the “initial” and “final” f-I curves for each model, where the initial curves were based on the inverse of the first inter-spike interval (ISI) due to a one second current step, and the final curves were based on the inverse of the last ISI. A linear fit based on the least squares method (on frequencies over 10 Hz) was done for each curve (using 5 Hz gave essentially the same results). We then chose parameters in which our models exhibited similar initial and final f-I curves to those of the experimental pyramidal cells. To do so, we first set the resting membrane potential at the rheobase, the spike threshold, the minimum potential reached by the spike after-hyperpolarization, the spike peak, and the spike width at threshold (providing us with values for vr, vt, c, vpeak, and khigh respectively) based on our experimentally determined values (see Results). The threshold is defined in “Intrinsic Property Characterization”. Since our pyramidal cells exhibited resonant properties, we considered b values such that b > 0. We initially held b and klow constant (at 0.2 nS and 0.05 nS/mV), and varied a between 0 and 1 with an initial step size of 0.01, and d between 0 and 20 with a step size of 1. Choosing our a and d parameters that returned the best fits to our initial and final slopes, we then varied b between 0.1 and 10, and klow between 0 and 20 (both with a step size of 0.1). Noting that we required more adaptation, we then returned to vary a between 0 and 0.1 with an initial step size of 0.0001, and d again between 0 and 20 with a step size of 1. The model was simulated using Brian software15.
Using the described whole hippocampal preparation and recordings from four CA1 pyramidal cells (from three mice), we developed our simple biologically-based cellular models. Our goal is to obtain representative CA1 pyramidal cell models that capture the essence of the experimental data in the described experimental context. By biologically-based, we mean that passive properties and spike characteristics are captured. Specifically, resting potential, spike threshold, spike width, spike peak and after-hyperpolarization potentials were incorporated into our models. In addition, the adaptation characteristics determined from the frequency-current (f-I) curves (see Methods) are captured. Rebound firing (from inhibition or hyperpolarization) has been shown in several experimental studies16,17 and is an important consideration in population theta activities. As shown in Figure 1, we could obtain rebound firing in our CA1 pyramidal cells, thus justifying their inclusion in our models.
Analysis of the experimental data yielded the following: at rheobase, the pyramidal cell membrane potential rested at -61.8 ± 2.9 mV (mean ± SEM), the spike threshold was -57.0 ± 2.2 mV, the after hyperpolarizing potential reached a minimum of -65.8 ± 3.83 mV, and the spike reached a peak at 22.6 ± 19.9 mV (n=4 cells). The spike width at threshold, was 3.6 ± 0.48 ms. Thus, we set vr = -61.8 mV, vt = -57.0 mV, c = -65.8 mV, vpeak = 22.6 mV, and khigh = 3.3 nS/mV in our models (see Methods). The remaining model parameters were chosen such that the rheobase and f-I curves of the cell model were similar to those of the cell recordings. To do so, we first considered the f-I curves of the cell recordings (Figure 2). To demonstrate the amount of adaptation that the cell exhibited, we created two f-I curves for each cell: one based on the first inter-spike interval (ISI) of the cell’s spiking during a one second current step (denoted initial curve, data points shown as asterisks in Figure 2), and one based on the last (final curve, data points shown as squares in Figure 2). If the cell only had one spike in the 1s trace, a frequency of 1 Hz was given. We note that two of our recordings (Pyramidal cell 1 and Pyramidal cell 2, shown in red and blue in Figure 2) exhibited stronger adaptation than the other two (Pyramidal cell 3 and 4, shown in green and black in Figure 2). Thus, we created pyramidal cell models based on the strongly adapting cells and the weakly adapting cells separately. While adaptation clearly exists (e.g., here 18,19), biological variability, precise protocols and contexts need to be considered. As such, we did not aim to exactly capture adaptation characteristics, but rather to capture strongly and weakly adapting cells as represented by the data here. Also, since our model has a simple, mathematical structure, it is limited in the extent of biologically-based characteristics that it can encompass.
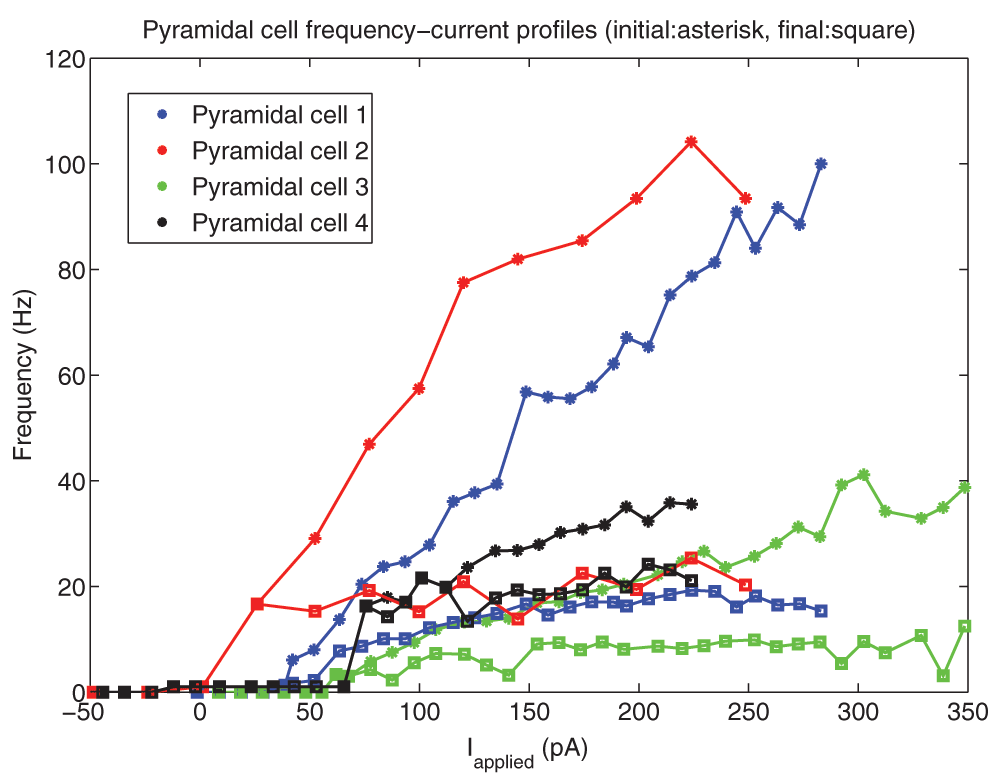
10 pA depolarizing steps were taken for all cells except Pyramidal cell 2 (25 pA steps). The initial (final) frequencies are shown by asterisks (squares), and the lines interpolate between the data points. Pyramidal cells 1 and 2 (shown in blue and red) have higher initial frequencies, and exhibit more adaptation than Pyramidal cells 3 and 4 (shown in light green and black).
It is important that our model f-I curve captures two important properties of the experimental data: the rheobase current (i.e. the minimum amount of current required to initiate a spike), and the approximate slope of the curve. If these properties are captured, then the model will spike with similar frequencies as the physiological cell given the same level of synaptic input, at least to a first approximation. We found that for the two strongly adapting pyramidal cells (1 and 2), the slope of the linear least squares approximation of the f-I curves above 5 Hz were 0.376 and 0.385 for the initial curves, and 0.030 and 0.040 for the final curves. Again, the initial frequencies are based on the inverse of the first inter-spike interval due to a one second current step, and the final frequencies are based on the last inter-spike interval. A series of depolarizing (25 and 10 pA) steps were used to determine the rheobase currents, which were 1.2 pA and 38.7 pA for the two strongly adapting cells (f-I curves, red and blue curves in Figure 2 or data in Figure 3).

The initial data points are shown as asterisks and the final points shown as squares. The initial model curve is shown as a solid line (initial slope: 0.432), and the final curve shown as a dashed line (final slope: 0.099). The model rheobase (~0 pA) and slope approximate those determined experimentally.
We kept our previously determined parameters constant (i.e. vr = -61.8 mV, vt = -57.0 mV, c = -65.8 mV, vpeak = 22.6 mV, and khigh = 3.3 nS/mV), and set our membrane capacitance to Cm = 115 pA. We then varied the parameters a, b, d, and klow to produce multiple models. We determined the rheobase current and the slope of the initial and final f-I curve over 10 Hz (using a least squares approach) for each model in order to settle upon a final model in which our initial and final f-I slopes and rheobase approximated that which we determined biologically. We determined that a = 0.0012 ms-1, b = 3 nS, klow = 0.1 nS/mV, d = 10 pA, and Ishift = 0 pA. This gave us a model f-I initial slope of 0.432, a final slope of 0.099, and a rheobase of ~0 pA (see Figure 2). As shown in Figure 4, the model shows strongly adapting firing (Figure 4A) and rebound firing when hyperpolarized (Figure 4B).
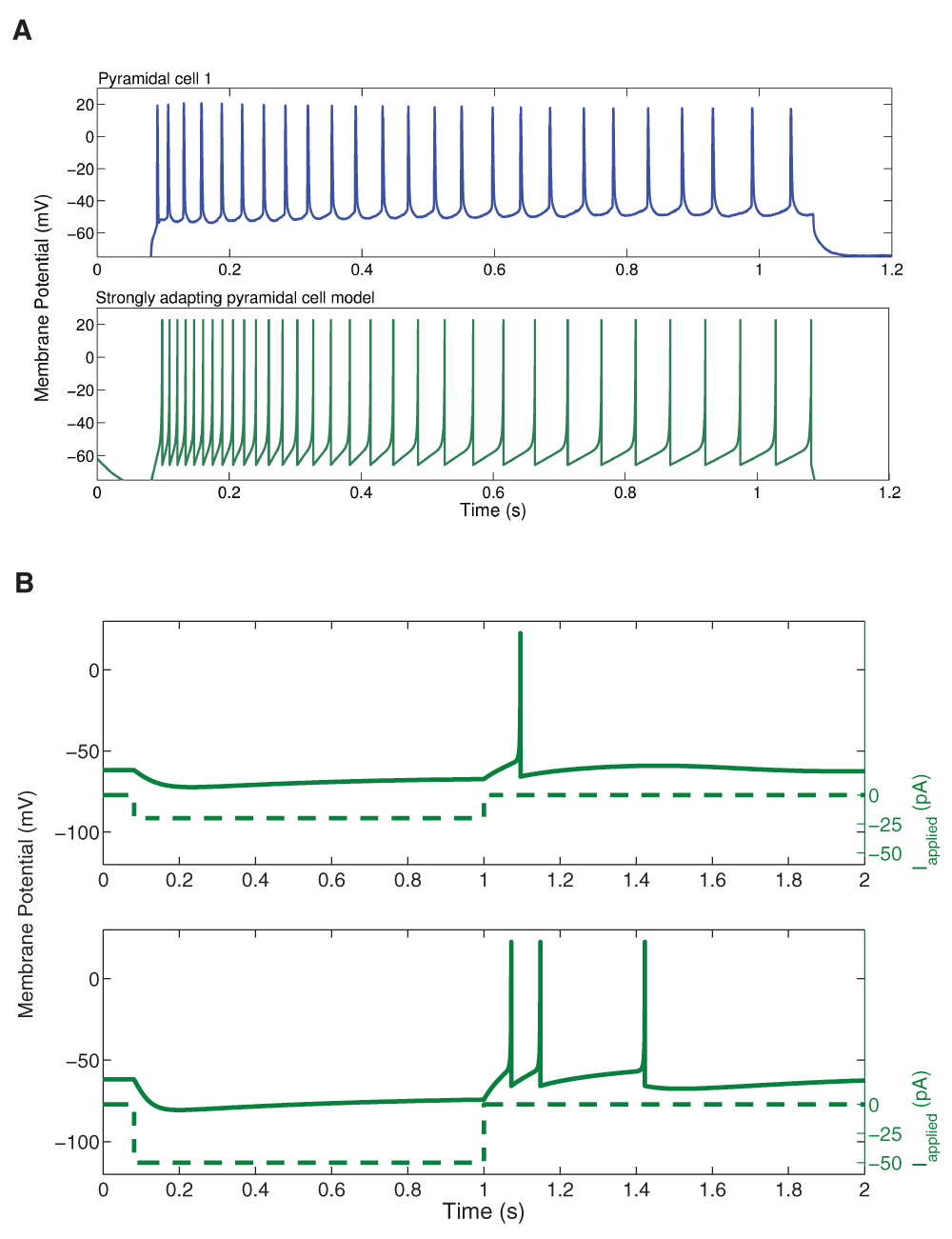
A: An example intracellular recording of Pyramidal cell 1 during current clamp with applied current of 188 pA (top, blue) is compared with the firing of our strongly adapting pyramidal cell model, also with an applied current of 188 pA (bottom, dark green). The firing rates and amount of adaptation of the model are similar to those of the experiment. B: Two examples of rebound firing in our strongly adapting model. In each case, a one-second step of hyperpolarizing input is applied (shown as dashed lines; top: 20 pA step, bottom: 50 pA step). In each case, the strongly adapting model produces rebound spiking (solid line), where more spiking occurs for larger amounts of hyperpolarizing input.
Following a similar methodology, we created two separate models for the weakly adapting pyramidal cells: the first better captures the cell’s weak adaptation, especially for larger currents, but has a steep final slope, whereas the second captures the more gradual slope of the final f-I curve, but doesn’t exhibit the cell’s weak level of adaptation.
We found that for the two weakly adapting pyramidal cells, the slope of the linear least squares approximation of the f-I curves were 0.119 and 0.138 for the initial curves, and 0.013 and 0.044 for the final curves (values relating to experimental, data green and black in Figure 2 and Figure 5). A series of depolarizing (10 pA) steps were used to precisely determine the rheobase currents, which were 62.0 pA and -12.1 pA for the two weakly adapting cells. We kept our previously determined parameters constant (i.e. vr = -61.8 mV, vt = -57.0 mV, c = -65.8 mV, vpeak = 22.6 mV, and khigh = 3.3 nS/mV), and set our membrane capacitance to Cm = 300 pA, which allowed us to obtain the gradual f-I slope. We then varied the parameters a, b, d, and klow to produce multiple models, and again determined the rheobase current and the slope of the initial and final f-I curve over 10 Hz (using a least squares approach) for each model. For our first model, we determined that a = 0.001 ms-1, b = 3 nS, klow = 0.5 nS/mV, d = 5 pA, and Ishift = –45 pA. This gave us a model f-I initial slope of 0.136, a final slope of 0.089, and a rheobase of 5 pA (see purple solid and dashed lines in Figure 5). The second weakly adapting model is identical to the first, except that we explored smaller a parameter values in order to capture the gradual slope of the final f-I curve. For this model, a = 0.00008 ms-1, which gave an initial f-I slope of 0.136, a final slope of 0.048, and a rheobase of 5 pA (see purple solid and magenta dashed lines in Figure 5). An example of the weak adaptation in this case is shown in Figure 6A, and rebound firing for model 1 is shown in Figure 6B.
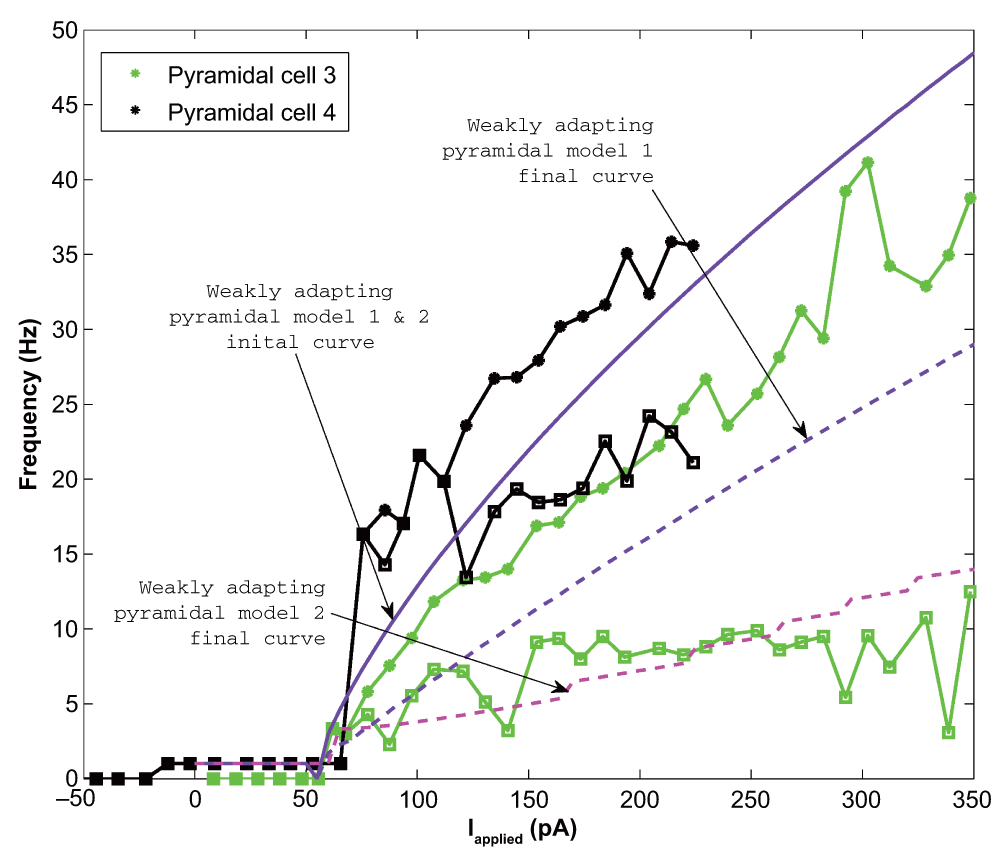
The initial data points are shown as asterisks and the final points shown as squares. The initial model curve is shown as a solid line (initial slope: 0.136), and the final curves are shown as dashed lines. Model 1 exhibits less adaptation (final slope for model 1: 0.089; final slope for model 2: 0.048), but higher final frequencies than model 2 (compare purple and magenta dashed lines). The model rheobase (5 pA) and slopes approximate those determined experimentally.

A: An example intracellular recording of Pyramidal cell 3 during current clamp with applied current of 154 pA (top, light green) is compared with the firing of our weakly adapting pyramidal cell models, also with an applied current of 154 pA (model 1: middle, purple; model 2: bottom, magenta). The firing rates and amount of adaptation of the model are similar to those of the experiment. B: An example of rebound firing in our weakly adapting model 1. A one-second step of 1000 pA hyperpolarizing input is applied (dashed line). The weakly adapting model produces rebound spiking (solid line), but requires a reasonably large amount of applied input. The weakly adapting model 2 does not produce rebound spiking following steps of hyperpolarizing input in the physiological range.
We have developed simple, biologically-based cellular models of pyramidal cells from CA1 hippocampus. These models capture the frequency-current profiles of both strongly and weakly adapting cells. Importantly, we have used pyramidal cell recordings from a well-defined experimental context as a basis for our model development. We note that even though other simple pyramidal cell models exist with a conductance-based biophysical representation20, it is challenging to have clear links with adaptation or rebound firing characteristics as exists in pyramidal cells (e.g., see 21). We note that while modifications have been done to such simple models (e.g., Stark et al.22 used the Olfusen et al. model23 which incorporated sodium currents, potassium current, voltage-dependent M currents, and a leak current, and added an h-current based on 24 to incorporate rebound capabilities), the resulting cellular model outputs constraints with respect to experimental data are unclear, and as such, we consider them not to be biologically-based per se.
Our models do not include the multiple voltage-gated channels known to be present in pyramidal cells, and are not spatially extended by being multi-compartment in nature. Multi-compartment, biophysical models of CA1 pyramidal cells exist25 as well as single-compartment biophysical models26 with various voltage-gated channels, but the goals in developing those models are different. Here, we are interested in capturing cellular characteristics in a well-defined experimental context (for subsequent large network explorations that take advantage of the experimental context), whereas these other studies have considered, for example, conductance balances to understand how they contribute to cellular output. We further note that the richness of detail in CA1 pyramidal cells is expanding (e.g., see 19 in which countermodulation by metabotropic receptors in bursting or regular spiking pyramidal cells was shown). In essence, it is always the case that the mathematical models are a limited representation of the biology.
In previous work, we used adaptation characteristics from the literature to develop simple models of CA3 pyramidal cell models, and showed that population bursting could occur in excitatory networks if the adaptation characteristics were in line with the experimental data27. In this work we had a full set of experimental recordings and so could capture appropriate cellular characteristics more directly. Although there should not be large differences in some cellular characteristics (e.g., spike widths etc.), there could be differences in characteristics such as rheobase and adaptation amounts due to varying experimental contexts (e.g., solutions, recording setup details and so on – see 16–19). Coupled with biological variability, it would be additionally challenging to be clear about model limitations in subsequent model usage. Here, with our simple mathematical model representation and knowledge of the biological variability in hand, one is easily aware of any changes in the parameters of the model that would result in large deviations from the experimental data. In doing this work, we have been clear about the rationale and manner in which the parameter choices were made. Generalization of the parameter choices are possible and could be considered, but should be done such that modeling and experimental details and contexts are not completely separated.
We note that robust fitting strategies of experimental data to simple, mathematical representations of neurons are being developed28. However, there are some differences in the modeling goals. In the paper by Hertäg et al.28, the goal was to use the developed models based on in vitro recordings to predict spiking in an in vivo context. Here, we have developed our cellular models in the experimental context for which we are building network models to help determine mechanisms occurring in the biological system8,9. One can consider using our models in other contexts, keeping in mind the limitations associated with the models as developed. In essence, when incorporating various cellular characteristics, one should express the choices, rationale and reasoning behind the model development, which naturally stem from the modeling goals.
In conclusion, with our simple, developed models as presented here, we can proceed to considering very large networks that include these models in this experimental context. Furthermore, our simple model representations will also allow us to take advantage of developed theoretical analyses29,30.
ZENODO: Data set of CA1 pyramidal cell recordings using an intact whole hippocampus preparation, including recordings of rebound firing (V2), DOI: 10.5281/zenodo.1779431
ModelDB: CA1 pyramidal neuron, available at http://senselab.med.yale.edu/ModelDB/ShowModel.cshtml?model=182515.
KAF and FKS conceived the study. CYLH, BA, SW designed the experiments. CYLH, BA carried out the experiments. KAF carried out the modeling and data analysis. FKS and KAF prepared the first draft of the manuscript. All authors were involved in the revision of the draft manuscript and have agreed to the final content.
This work has been supported by the Canadian Institutes of Health Research (CIHR Grant number MOP-102573) (SW), Natural Sciences and Engineering Research Canada (NSERC Grant Number: RGPIN-203700 (FKS), and an Ontario Graduate Scholarship (KAF).
The funders had no role in study design, data collection and analysis, decision to publish, or preparation of the manuscript.
| Views | Downloads | |
|---|---|---|
| F1000Research | - | - |
|
PubMed Central
Data from PMC are received and updated monthly.
|
- | - |
Competing Interests: No competing interests were disclosed.
Competing Interests: No competing interests were disclosed.
Alongside their report, reviewers assign a status to the article:
| Invited Reviewers | ||
|---|---|---|
| 1 | 2 | |
|
Version 2 (revision) 03 Jun 15 |
||
|
Version 1 09 May 14 |
read | read |
Provide sufficient details of any financial or non-financial competing interests to enable users to assess whether your comments might lead a reasonable person to question your impartiality. Consider the following examples, but note that this is not an exhaustive list:
Sign up for content alerts and receive a weekly or monthly email with all newly published articles
Already registered? Sign in
The email address should be the one you originally registered with F1000.
You registered with F1000 via Google, so we cannot reset your password.
To sign in, please click here.
If you still need help with your Google account password, please click here.
You registered with F1000 via Facebook, so we cannot reset your password.
To sign in, please click here.
If you still need help with your Facebook account password, please click here.
If your email address is registered with us, we will email you instructions to reset your password.
If you think you should have received this email but it has not arrived, please check your spam filters and/or contact for further assistance.
Comments on this article Comments (0)