Niche Genetic Algorithms are better than traditional Genetic Algorithms for <i>de novo</i> Protein Folding

Michael Scott Brown; Tommy Bennett; James A. Coker

doi:10.12688/f1000research.5412.1

Home Browse Niche Genetic Algorithms are better than traditional Genetic Algorithms...

ALL Metrics

Views

Downloads

Get PDF

Get XML

Export

▬

✚

Software Tool Article

Niche Genetic Algorithms are better than traditional Genetic Algorithms for de novo Protein Folding

[version 1; peer review: 2 not approved]

Michael Scott Brown¹, Tommy Bennett¹, James A. Coker ¹

PUBLISHED 07 Oct 2014

Author details Author details

¹ University of Maryland, University College, The Graduate School, Largo College park, MD 20774, USA

OPEN PEER REVIEW

REVIEWER STATUS

This article is included in the Bioinformatics gateway.

Abstract

Here we demonstrate that Niche Genetic Algorithms (NGA) are better at computing de novo protein folding than traditional Genetic Algorithms (GA). Previous research has shown that proteins can fold into their active forms in a limited number of ways; however, predicting how a set of amino acids will fold starting from the primary structure is still a mystery. GAs have a unique ability to solve these types of scientific problems because of their computational efficiency. Unfortunately, GAs are generally quite poor at solving problems with multiple optima. However, there is a special group of GAs called Niche Genetic Algorithms (NGA) that are quite good at solving problems with multiple optima. In this study, we use a specific NGA: the Dynamic-radius Species-conserving Genetic Algorithm (DSGA), and show that DSGA is very adept at predicting the folded state of proteins, and that DSGA is better than a traditional GA in deriving the correct folding pattern of a protein.

Corresponding author: James A. Coker

Competing interests: No competing interests were disclosed.

Grant information: The author(s) declared that no grants were involved in supporting this work.

Copyright: © 2014 Brown MS et al. This is an open access article distributed under the terms of the Creative Commons Attribution License, which permits unrestricted use, distribution, and reproduction in any medium, provided the original work is properly cited. Data associated with the article are available under the terms of the Creative Commons Zero "No rights reserved" data waiver (CC0 1.0 Public domain dedication).

How to cite: Brown MS, Bennett T and Coker JA. Niche Genetic Algorithms are better than traditional Genetic Algorithms for de novo Protein Folding [version 1; peer review: 2 not approved]. F1000Research 2014, 3:236 (https://doi.org/10.12688/f1000research.5412.1) First published: 07 Oct 2014, 3:236 (https://doi.org/10.12688/f1000research.5412.1) Latest published: 07 Oct 2014, 3:236 (https://doi.org/10.12688/f1000research.5412.1)

Introduction

Proteins are one of the basic building blocks of all life and we have learned much about them since they were ‘discovered’ about 200 years ago¹, including their shapes, functionality, and uses. However, there are still many basic questions such as how proteins are able to transform from a useless linear assemblage of amino acids (primary structure) into a functional three-dimensional native structure, that remain unanswered². The ability to accurately predict the functional form of a protein from its primary sequence would revolutionize many fields and has long been considered a ‘holy grail’ in Life Sciences research³.

The solution to the problem of computationally determining how proteins fold will involve multiple disciplines of science making it a very interesting topic to address. At its heart, it is a biochemical issue, rooted in both geometry and physics, which is faced by every cell on Earth. In Mathematical terms, it is an application of the ‘self-avoiding walk’ problem⁴ with some additional constraints. Since we know that there are many physical constraints on achieving a properly folded protein, it is also an NP-hard problem⁵ and therefore highly applicable to Computer Science.

Proteins are made up of a sequence of amino acids, of which there are many types but only 20 are typically used in biological proteins⁶. Each amino acid type can be placed into one of two categories: hydrophilic (P) and hydrophobic (H). While a protein’s primary sequence dictates the ordering of the amino acids, it must fold into a three-dimensional structure to be active⁷. Therefore, the goal of solving how proteins fold computationally is to determine the folding pattern of any protein starting from the primary sequence.

For the last 100 years, the two most employed methods for determining the folding pattern of a given protein are x-ray crystallography⁸ and nuclear magnetic resonance (NMR)⁹. Both can provide high resolution images of the folded-state of a protein but rely on the ability of scientists to purify the protein of interest to concentrations of 1 molar (NMR) to greater than 10 molar (x-ray crystallography), which is not an easy task. The x-ray crystallography method is further complicated by the need to determine the conditions for the growth of crystals of the protein and then waiting for those crystals to grow to a usable size and dimension¹⁰. The NMR method requires less purified protein, compared to x-ray crystallography; however, it is limited by the size of protein that can be analyzed¹⁰. Both of these more traditional methods also require a significant investment of time in order to achieve the folding pattern of a protein. Despite the significant time investment, these methods have persisted due to the fact that they are a very reliable way to determine protein structure. However, with the recent explosion of genomes being sequenced, which has resulted in the discovery of a plethora of new proteins and protein families, newer methods that will reliably determine the folding pattern of a protein in a shorter amount of time are called for¹¹. One of these methods, de novo protein folding, uses only the primary sequence of a protein and a set of computer algorithms to determine its active, folded form. This may seem overly daunting at first, since even a relatively small protein can have a nearly infinite number of possible folding patterns. However, over the past 50–60 years biochemists have determined that the way a protein folds is quite conserved in a protein family¹² and that chemical/physical forces significantly reduce the number of ways a protein can fold^13–15. These two findings are very important and have the very real implication that computers can be used to predict the active, folded forms of a protein in a very short period of time.

One method often used to computationally determine how proteins fold is a Genetic Algorithm (GA). GAs are a type of optimization algorithm that models biological selection^16,17 and are part of a family of optimizations algorithms called Heuristics¹⁸, which attempts to solve a problem by determining a solution and iteratively making the solution better. GAs have been very good at optimization of large complex domains, are a product of the field of Artificial Intelligence and can theoretically solve any problem that can be represented as the optimization of a continuous function. The theory behind GAs states that after many generations the intermediate solutions will eventually converge upon the correct answer¹⁹. Even in cases where GAs could not fully solve the problem, the answer produced was valuable, which is an aspect of GAs that makes them superior to other algorithms.

At their core, GAs model biological selection and provide multiple possible answers termed individuals, which are comprised of a string of characters. The GA begins by randomly generating a number of individuals (first generation) and then goes through multiple iterations of selection, crossover and mutation. In selection, pairs of individuals are picked for crossover. Individuals with higher fitness, as determined by a fitness function, are given an increased probability of being selected and an individual can be selected for crossover multiple times. In crossover, two individuals are picked and each is broken into two substrings at a randomly selected position that is at the same position in the string of characters for both thereby creating two new individuals. In mutation, the value of some of the characters in each individual can change based on a probability parameter. The processes described above results in a new generation of individuals and the process then repeats using the new generation (Table 1).

Table 1. GA vs. DSGA Pseudo-code.

Line	GA Pseudo-code	DSGA Pseudo-code
1	Loop until termination condition	Loop until termination condition
2	Select()	Seed Selection()
3	Crossover()	Selection()
4	Mutation()	Crossover()
5	End loop	Mutation()
6		Seed Conservation()
7		If (RLC mod Generation # = 0)
8		Put current seeds on Tabu List
9		Put any individuals with CL more identical individuals on Tabu List
10		Replace all individuals put on Tabu List with randomly generated individuals
11		Increase radius by radius delta
12		End if
13		End loop

Although GAs are good at solving the optimization of a continuous function, they have a difficult time solving multi-optima problems²⁰. When multiple optima exist a traditional GA will often locate only one optimum and there is no guarantee that it is the global optimum and not a local one. To overcome this problem, specialized GAs, called Niche Genetic Algorithms (NGA), have been developed that can locate multiple optima^20,21. There are a number of NGAs including De Jong²², Crowding Clustering Genetic Algorithm (CCGA)²³ and Species Conserving Genetic Algorithm (SCGA)²⁴. One NGA has been shown to be especially adept at solving problems with multiple optima²¹. It is called the Dynamic-radius Species-conserving Genetic Algorithm (DSGA)²⁰ and is basically a modification of the SCGA²⁴. DSGA enhances the traditional GA by the addition of seeds, a Tabu List²⁰ and the ability to change the radius. A seed is a locally strong individual based upon some radius that is identified in each iteration of the loop and conserved (i.e. propagated into the next generation by replacing a locally weak individual). A Tabu List’s function, whose name comes from the Tabu Search²⁵, is to store strong candidates for the global optima, which is determined by the Reevaluation Loop Count (RLC) and the Convergence Limit (CL).

Here we show that protein folding is a multi-optima problem and as a result NGAs are better suited for a solution. The DSGA has not previously been applied to the immense task of de novo protein folding. Therefore, as a proof of concept, we have shown two important results below: (1) the DSGA is very adept at predicting the folded state of proteins, which was shown by selecting a 20 amino acid protein and modeling the folds and all possible combinations; (2) the DSGA is better than a traditional GA and better able to derive the correct folding pattern of a protein. Below we present some preliminary testing data and have provided the source code, which is available for download at Zenodo.org (https://zenodo.org/record/11902).

Materials and methods

Seed Selection method

Each individual is evaluated from the most to the least fit. If no other seeds exist within the radius (r) of the individual then the individual is a seed. In the Seed Conservation method each seed will replace an individual in the newly created generation. If there are individuals in the next generation within r of the seed, the seed will replace the weakest of these individuals. If there are no individuals within r of the seed in the next generation, the seed will replace the globally weakest individual. But these seeds have to re-compete to be seeds in the next generation.

Generating the Tabu List

The Tabu List stores potential candidates for the global optima. As individuals are put on the Tabu List, the DSGA attempts to seek optima in other locations by using a Shared Fitness. Shared Fitness will decrease the fitness of an individual if it is too close to individuals on the Tabu List. This encourages exploration in other areas of the domain. The Shared Fitness function is defined in equation 1.

Shared Fitness (i) = (Fitness (i) / m_{i}) + 1 (1)

In equation 1, m_i is defined by equation 2 where TLj is the jth individual on the Tabu List, Length(i) is the number of characters in individual i and Distance(i, TLj) is the distance between individual i and individual TLj.

m_{i} = \sum_{j = 1}^{TabuSize} (Length (i) - (\frac{distance (i, TLj)}{Length (i) / 10})) (2)

The final term in the Shared Fitness equation is + 1. Individuals with a fitness of zero have no chance of being selected for crossover. By incrementing all Shared Fitness values by one, this gives these individuals a chance at selection and propagation into later generations.

Distance measurement

For this study, we selected chromosomal difference using Equation 3 below to calculate the distance between two individuals (i₁ and i₂).

distance (i_{1}, i_{2}) = \sum_{x = 1}^{x = length (i_{1})} if i_{1} .charAt (x) = i_{2} .charAt (x), 1 (3)

Fitness function

This function determines how fit an individual is in relation to the fold it has adopted. The value of this function is determined by calculating the Free Energy and the algorithm prioritizes individuals with a greater ability to fold spontaneously (i.e. low value for Free Energy). Here, we calculated Free Energy by summing all of the possible contacts between adjacent, but not neighboring, hydrophobic amino acids as has been done previously²⁶. The free energy between any two amino acids (i and j) can be found using the following formula:

ε_{ij} = {\begin{matrix} -1.0 & the pair of H and H residues \\ 0.0 & others \end{matrix} (4)

The free energy (E) for a protein can be found by summing the free energy between all of the amino acids as follows:

E = Σ Δr_ijε_ij

Where {Δr}_{ij} = {\begin{matrix} 1.0 & S_{i} and S_{j} are adjacent but not neighbor amino acids \\ 0.0 & others \end{matrix} (5)

Although proteins are three dimensional structures, it is common to use two dimensions. Using two dimensions reduces the search space in the domain. Issues with the algorithms can be addressed and future research can be published using three-dimensional models. This research uses a two dimensional model for protein folding.

Model for folding

In order to model protein folding, a simple method was selected where each gene of an individual has a value of zero, one, two or three. In our method, a zero, one, two or three denotes placing the next amino acid above, right, below or left the previous one, respectively. This method allows for greater simplicity and saves computing time as the number of genes needed in the individual is one less than the number of amino acids in the protein.

Keep Going

In some cases the model may produce a folding that isn’t physically possible (i.e. two amino acids occupying the same space). For example, the series of genes ‘13’ would not be physically possible as the second amino acid would be over top of the first. To handle these cases we employ a method we titled the Keep Going method. When directed to place an amino acid in a location that is already occupied, the algorithm will look for other positions to place it using a predictable pattern. If the folding sequence indicates placement of an amino acid in an occupied position, the algorithm will place it in the next available position in a clock-wise direction; however, if all positions are taken then the algorithm resolves this by setting the fitness to zero.

System requirements and input/output data

The Java-based DSGA and GA used here have been reliably run on a 1.86 GHz processor with 4 GB of memory (i.e. a standard MacBook Air). Minimal system requirements are a functional system that is able to support Java. Sample input data can be found in Supplementary File 1 but are basically an amino acid sequence with amino acids translated into hydrophilic (P) and hydrophobic (H) and the parameters for the DSGA. Sample output data are also provided (Supplementary File 2) but is basically a list of the best individuals with their corresponding calculated Free Energy value. All positive free energy values in the output should be interpreted as negative values, and vice versa. For example, a free energy value of ‘8’ for an individual in the output should be interpreted as ‘-8’. This is quite important as negative free energy values indicate spontaneous folding and positive values indicate that energy needs to be added to the system to get the protein to fold.

Results

To demonstrate that de novo protein folding is better addressed by DSGA, we have used two different methods. Two simple proteins and a method to model the protein folding were selected. All possible combinations of the folding were computed to demonstrate that there are multiple optima. Second a traditional GA was compared to DSGA to solve for a 20 amino acid protein.

Multioptimum problem

We selected a simple protein of four residues with the following sequence of hydrophilic (P) and hydrophobic (H) residues: HPHPP. The individual, which best represents how to fold the protein is 0121 (Figure 1). The first amino acid is placed in the center with the second one above (0121) the third to the right (0121), the fourth below (0121) and the last to the right (0121).

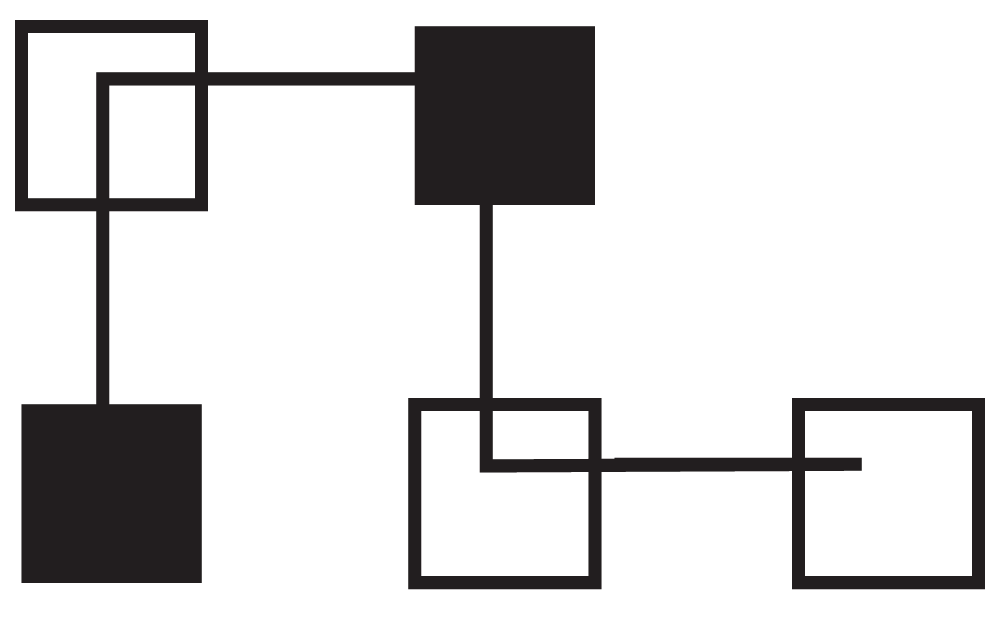
Figure 1. 0121 Folding of HPHPP.

Hydrophilic (P) residues are represented as non-shaded squares and hydrophobic (H) residues are shown as shaded squares.

Next, we moved to a more complex protein with ten amino acids, which translated into the following sequence of H and P residues: HPPHPPHPPH, and determined all the possible ways it could fold using the model described above. Since it has 10 amino acids, all the individuals generated by our DSGA will have nine genes. The values for each range from 000000000 (complete set of amino acids one above the other) to 333333333 (complete set of amino acids each one to the left of the other). Since there are four directions to place the next amino acids, there are 4⁹ or 262,144 different ways to fold the amino acids.

Figure 2 shows a graph of all of the different ways to fold HPPHPPHPPH. The X-axis contains the different ways to fold the protein. The Y-axis is the free energy for the folding method. With this folding method there are eight global optima that each have a value of four and local optima with values of three, two or one. The optimal folding is seen in Figure 3.

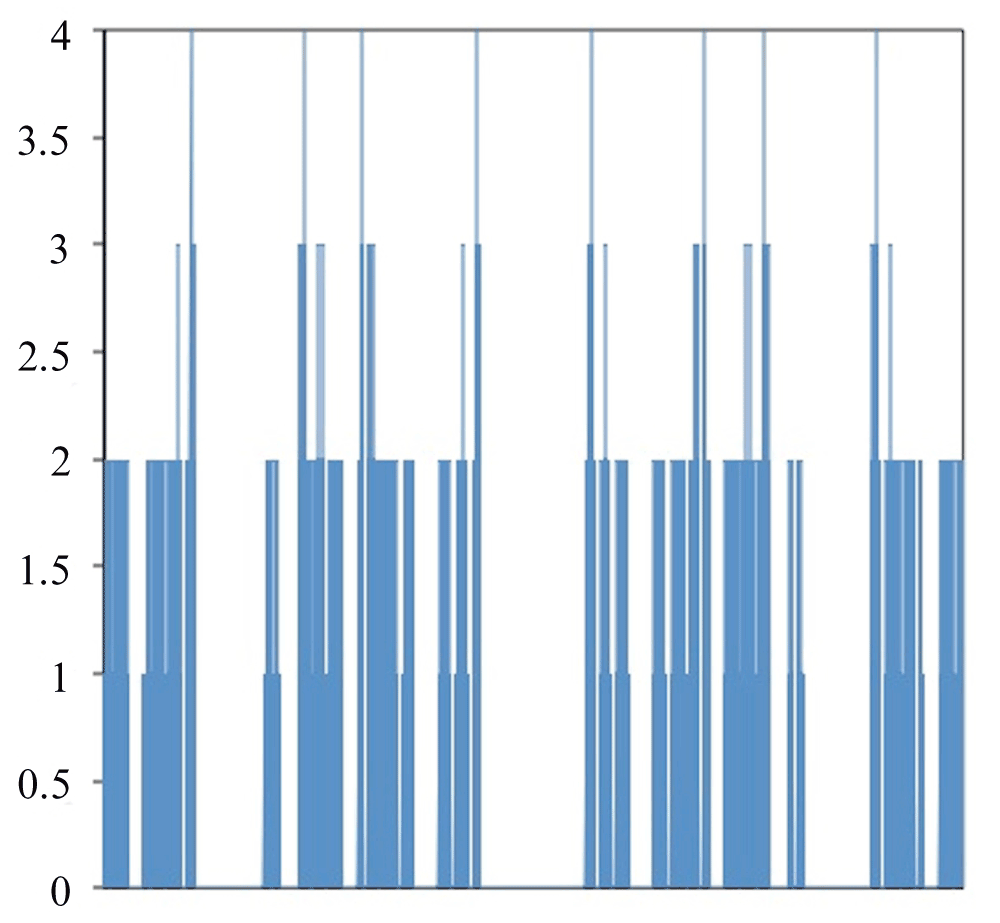
Figure 2. Free Energy for all methods to fold HPPHPPHPPH.

Left side of X-axis corresponds to 000000000 while the right side corresponds to 333333333.

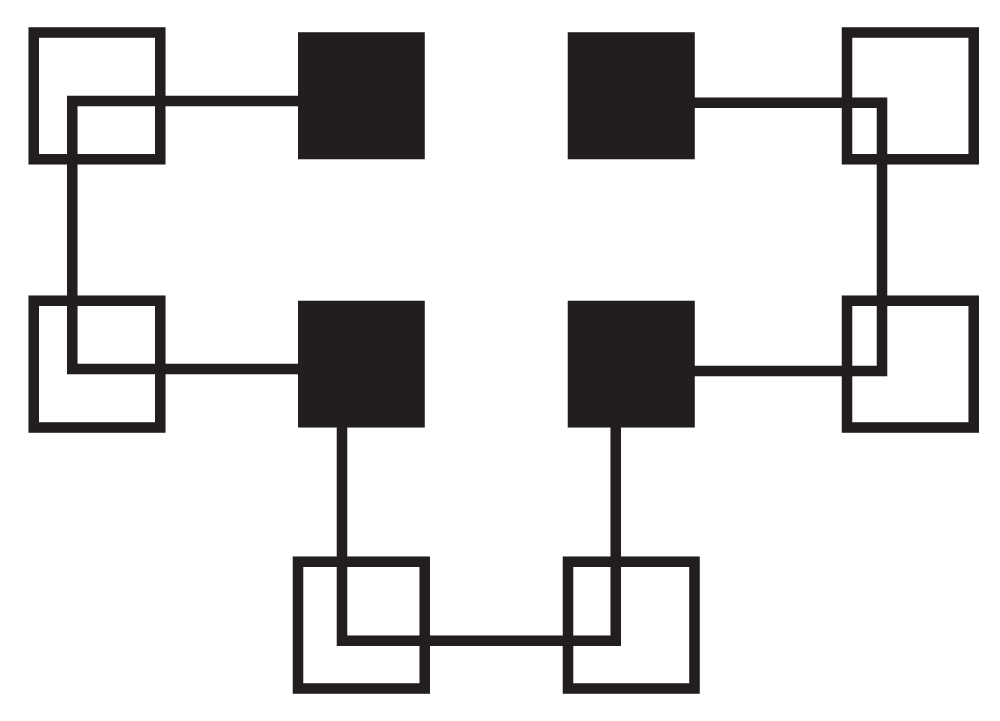
Figure 3. Correct Folding of HPPHPPHPPH.

Hydrophilic (P) residues are represented as non-shaded squares and hydrophobic (H) residues are shown as shaded squares.

Compare Traditional Genetic Algorithm to Niche Genetic Algorithm

Next, we executed our DSGA and a traditional GA²⁶ (Table 1) at solving the folding for the following: HPHPPHHPHPPHPHHPPHPH. This protein of 20 amino acids was used previously^27,28,29 and found to have an optimal folding pattern that resulted in a free energy of -9. Since DSGA usually takes longer to run than a traditional GA, two sets of results were created for the traditional GA. One contained the same number of generations as DSGA. The other had additional generations to get the total run-time the same between the two algorithms.

The parameters between DSGA and the traditional GA were kept consistent when possible; however, DSGA does have some additional parameters not used in traditional GAs (Table 2). The first set of results was from the traditional GA running the same number of generations as DSGA. The second set of results was the traditional GA running for the same amount of time as DSGA. In this example, a traditional GA running for 6,000 generations takes about the same amount of time as DSGA running for 1,000 generations. Table 3 shows the best individuals produced for each algorithm in 15 trials. In the case of DSGA the optimum is the best individual on the Tabu List. For the traditional GA the optimum is the best individual in the last generation.

Table 2. Parameter Values.

Parameter	DSGA	GA	GA Running Same Amount of Time
Population Size	200	200	200
Number of Generations	1,000	1,000	6,000
Mutation Rate (per gene)	0.03	0.03	0.03
Initial Radius	4.0	N/A	N/A
Radius Delta	1.0	N/A	N/A
Reevaluation Loop Count	250	N/A	N/A
Convergence Limit	4	N/A	N/A

Table 3. Results of DSGA and GA attempting to fold HPHPPHHPHPPHPHHPPHPH.

Trial	DSGA	GA	GA Running Same Amount of Time
1	9	4	3
2	9	4	3
3	9	4	4
4	9	4	5
5	9	2	4
6	9	3	3
7	9	3	3
8	9	3	3
9	9	3	4
10	9	4	3
11	9	3	4
12	9	3	3
13	9	3	3
14	9	3	4
15	9	2	3

Conclusion

Here we showed that even employing a simple modeling method for protein folding results in the generation of multiple local and global optima. The above also shows that using the DSGA, which is specialized for multiple optima domains, produces better results than a traditional GA. This should be instructive to researchers working on de novo techniques as many algorithms applied to protein folding are actually hybrid applications that use a GA^27–29. It is possible that previous poor results could be caused by the GA’s weakness of finding local optima. Using an NGA in these algorithms could overcome this and produce improved results.

Software availability

Archived source code as at the time of publication

Zenodo: DSGA and GA from ‘Niche Genetic Algorithms are better than traditional Genetic Algorithms for de novo Protein Folding’ doi: 10.5281/zenodo.11902³⁰

Software license

MIT License.

Author contributions

MB and JAC conceived the study and designed the experiments. MB and TB did the coding of the DSGA. MB performed the experiments. MB and JAC analyzed the data. JAC, MB, and TB wrote the paper.

Competing interests

No competing interests were disclosed.

Grant information

The author(s) declared that no grants were involved in supporting this work.

Acknowledgements

The authors would like to thank UMUC and all the members of the ITS Department for providing a positive space to perform our research.

Supplementary material

Supplementary File 1: Sample input data. This file contains a sample amino acid sequence (input data) and the meanings of each parameter that needs to be set.

Dynamic-radius Species-conserving Genetic Algorithm for de novo Protein Folding Instructions.

Dynamic-radius Species-conserving Genetic Algorithm for de novo Protein Folding is a Java application written in Java version 1.7, but it should run on other versions of Java.

There are 10 command line parameters that should be set:

# position 1 - population size

# position 2 - number of generations

# position 3 - mutation rate (decimal)

# position 4 - initial radius (decimal)

# position 5 - radius delta (decimal)

# position 6 - reevaluation loop count

# position 7 - convergence limit

# position 8 - protein

# position 9 - output file location

# position 10 - log status 0 few logs; 1 more logs; 2 most logs

An output file path must be placed in the file location for position 9.

Here is an example for running the application:

java -jar /Users/mbrown15/NetBeansProjects/DSGAProteinFolding/dist/DSGAProteinFoldingKG.jar 1000 2000 0.03 8.0 -1.0 500 4 HPPHPPHPPH //Users//mbrown15//Documents//genetic-algorithm-files// 1

This method allows multiple runs to be placed in a batch file, which can be set up as follows:

java -jar /Users/mbrown15/NetBeansProjects/DSGAProteinFolding/dist/DSGAProteinFoldingKG.jar 1000 2000 0.03 8.0 -1.0 500 4 HPPHPPHPPH //Users//mbrown15//Documents//genetic-algorithm-files// 1

1000 12000 0.03 8.0 -1.0 500 4 HPPHPPHPPH //Users//mbrown15//Documents//genetic-algorithm-files// 1

1000 20000 0.03 8.0 -1.0 500 4 HPPHPPHPPH //Users//mbrown15//Documents//genetic-algorithm-files// 1

Supplementary File 2: Sample output data. This file contains a sample of the output data.

TABU LIST

Individual 032321213 natural fittness 4.0

Individual 032320213 natural fittness 4.0

Individual 032320203 natural fittness 4.0

Individual 210012230 natural fittness 3.0

Individual 210212230 natural fittness 3.0

Individual 200212230 natural fittness 3.0

Individual 210212200 natural fittness 3.0

Individual 200212200 natural fittness 3.0

Individual 123320123 natural fittness 3.0

Individual 123310123 natural fittness 3.0

Individual 031321013 natural fittness 3.0

Individual 301133022 natural fittness 3.0

Individual 301133021 natural fittness 3.0

Best individual(s)

Individual = 032321213 4.0

Individual = 032320213 4.0

Individual = 032320203 4.0

Sample output data above are the result from the following input:

Population Size: 50

Number of generations: 5000

Mutation rate: 0.003

Initial radius: 12.0

Radius delta: -2.0

Reevaluation loop counter: 1000

Convergence limit: 3

Protein: HPPHPPHPPH

The output of the program is the full Tabu List and the best individuals for that run. The best individuals are determined by an individual’s free energy value. Free energy values are the last number in each row of the output data. So for the above sample output all three best individuals have a free energy value of -4.

NOTE: All positive free energy values in the output should be interpreted as negative values, and vice versa. For example, the above free energy value of ‘4’ for the best individuals should be interpreted as ‘-4’. This is quite important as negative free energy values indicate spontaneous folding and positive values indicate that energy needs to be added to the system to get the protein to fold.

Faculty Opinions recommended

References

1. Teich M, Needham DM: in A Documentary History of Biochemistry, 1770–1940. (Rutherford, NJ : Fairleigh Dickinson University Press). 1992. Reference Source
2. Khoury GA, Smadbeck J, Kieslich CA, et al.: Protein folding and de novo protein design for biotechnological applications. Trends Biotechnol. 2014; 32(2): 99–109. PubMed Abstract | Publisher Full Text | Free Full Text
3. Dill KA, MacCallum JL: The protein-folding problem, 50 years on. Science. 2012; 338(6110): 1042–1046. PubMed Abstract | Publisher Full Text
4. Foster DP, Pinettes C: Statistical mechanics of the two-dimensional hydrogen-bonding self-avoiding walk including solvent effects. Phys Rev E Stat Nonlin Soft Matter Phys. 2008; 77(2 Pt 1): 021115. PubMed Abstract | Publisher Full Text
5. Unger R, Moult J: Genetic algorithms for protein folding simulations. J Mol Bio. 1993; 231(1): 75–81. PubMed Abstract | Publisher Full Text
6. Alberts B, Johnson A, Lewis J, et al.: Molecular Biology of the Cell, Fifth Edition. (Garland Science). 2007. Reference Source
7. Jung J, Han KY, Koh HR, et al.: Effect of single-base mutation on activity and folding of 10–23 deoxyribozyme studied by three-color single-molecule ALEX FRET. J Phys Chem B. 2012; 116(9): 3007–12. PubMed Abstract | Publisher Full Text
8. Coontz R, Fahrekamp-Uppenbrink J, Lavine M, et al.: Going from Strength to Strength. Science. 2014; 343(6175): 1091. PubMed Abstract | Publisher Full Text
9. Marion D: An introduction to biological NMR spectroscopy. Mol Cell Proteomics. 2013; 12(11): 3006–25. PubMed Abstract | Publisher Full Text | Free Full Text
10. Henen MA, Coudevylle N, Geist L, et al.: Toward rational fragment-based lead design without 3D structures. J Med Chem. 2012; 55(17): 7909–19. PubMed Abstract | Publisher Full Text | Free Full Text
11. Pantazes RJ, Grisewood MJ, Maranas CD: Recent advances in computational protein design. Curr Opin Struct Biol. 2011; 21(4): 467–72. PubMed Abstract | Publisher Full Text
12. Durand P, Lehn P, Callebaut I, et al.: Active-site motifs of lysosomal acid hydrolases: invariant features of clan GH-A glycosyl hydrolases deduced from hydrophobic cluster analysis. Glycobiology. 1997; 7(2): 277–84. PubMed Abstract | Publisher Full Text
13. Anfinsen CB: Principles that govern the folding of protein chains. Science. 1973; 181(4096): 223–230. PubMed Abstract | Publisher Full Text
14. Martí-Renom MA, Stuart AC, Fiser A, et al.: Comparative protein structure modeling of genes and genomes. Annu Rev Biophys Biomol Struct. 2000; 29: 291–325. PubMed Abstract | Publisher Full Text
15. Kaczanowski S, Zielenkiewicz P: Why similar protein sequences encode similar three-dimensional structures? Theor Chem Acc. 2009; 125(3–6): 643–50. Publisher Full Text
16. Mitchell M: in An Introduction to Genetic Algorithms. (Cambridge, MA: MIT Press). 1996. Reference Source
17. Wang C, Lefkowitz EJ: Genomic multiple sequence alignments: refinement using a genetic algorithm. BMC Bioinformatics. 2005; 6: 200. PubMed Abstract | Publisher Full Text | Free Full Text
18. Ahn N, Park S: Finding an upper bound for the number of contacts in hydrophobic-hydrophilic protein structure prediction model. J Comput Biol. 17(4): 647–56. PubMed Abstract | Publisher Full Text
19. Holland JH: in Adaptation in Natural and Artificial Systems. (Ann Arbor, MI: University of Michigan Press). 1975. Reference Source
20. Brown MS: A Species-Conserving Genetic Algorithm for Multimodal Optimization (Doctoral dissertation). Available from Dissertations and Theses database. (UMI No. 3433233). 2010. Reference Source
21. Brown MS, Pelsoi MJ, Dirska H: Dynamic-Radius Species-Conserving Genetic Algorithm for the Financial Forecasting of Dow Jones Index Stocks. Machine Learning and Data Mining in Pattern Recognition. Ed. P. Perner (Berlin: Springer). 2013; 7988: 27–41. Publisher Full Text
22. De Jong KA: An analysis of the behavior of a class of genetic adaptive systems. (Doctoral dissertation, University of Michigan). Diss Abstr Int. 1975; 36(10): 5140B. (University Microfilms No. 76–9381). Reference Source
23. Ling Q, Wa G, Yang Z, et al.: Crowding clustering genetic algorithm for multimodal function optimization. Appl Soft Comput. 2008; 8(1): 88–95. Publisher Full Text
24. Li JP, Balazs ME, Parks GT, et al.: A species conserving genetic algorithm for multimodal function optimization. Evol Comput. 2002; 10(3): 207–234. PubMed Abstract | Publisher Full Text
25. Glover F: Tabu Search – Part I. ORSA Journal on Computing. 1989; 1(3): 190–206. Publisher Full Text
26. Bremermann HJ: The Evolution of Intelligence: The Nervous System as a Model of its Environment. (Technical Report, No.1, Contract No. 477, Issue 17). Seattle WA: Department of Mathematics, University of Washington. 1958. Reference Source
27. Huang C, Yang X, He Z: Protein folding simulations of 2D HP model by the genetic algorithm based on optimal secondary structures. Comput Biol Chem. 2010; 34(3): 137–142. PubMed Abstract | Publisher Full Text
28. Su SC, Lin CJ, Ting CK: An effective hybrid of hill climbing and genetic algorithm for 2D triangular protein structure prediction. Proteome Sci. 2011; 9(Suppl 1): S19. PubMed Abstract | Publisher Full Text | Free Full Text
29. Jiang T, Cui Q, Shi G, et al.: Protein folding simulations of the hydrophobic-hydrophilic model by combing tabu search with genetic algorithms. J Chem Phys. 2003; 119(8) 4592–4596. Publisher Full Text
30. Brown M, Bennett T, Coker JA: DSGA and GA from ‘Niche Genetic Algorithms are better than traditional Genetic Algorithms for de novo Protein Folding’ Zenodo. 2014. Data Source

Comments on this article Comments (0)

Version 1

VERSION 1 PUBLISHED 07 Oct 2014

Author details Author details

¹ University of Maryland, University College, The Graduate School, Largo College park, MD 20774, USA

Competing interests

No competing interests were disclosed.

Grant information

The author(s) declared that no grants were involved in supporting this work.

Article Versions (1)

version 1

Published: 07 Oct 2014, 3:236

https://doi.org/10.12688/f1000research.5412.1

© 2014 Brown MS et al. This is an open access article distributed under the terms of the Creative Commons Attribution License, which permits unrestricted use, distribution, and reproduction in any medium, provided the original work is properly cited. Data associated with the article are available under the terms of the Creative Commons Zero "No rights reserved" data waiver (CC0 1.0 Public domain dedication).

Download

Export To

metrics

	Views	Downloads
F1000Research	-	-
PubMed Central Data from PMC are received and updated monthly.	-	-

Citations

SEE MORE DETAILS

CITE

how to cite this article

Brown MS, Bennett T and Coker JA. Niche Genetic Algorithms are better than traditional Genetic Algorithms for de novo Protein Folding [version 1; peer review: 2 not approved]. F1000Research 2014, 3:236 (https://doi.org/10.12688/f1000research.5412.1)

NOTE: If applicable, it is important to ensure the information in square brackets after the title is included in all citations of this article.

track

receive updates on this article

Track an article to receive email alerts on any updates to this article.

Open Peer Review

Version 1

VERSION 1

PUBLISHED 07 Oct 2014

Views

Reviewer Report 03 Jun 2015

Kenneth De Jong, Department of Computer Science, George Mason University, Fairfax, VA, USA

Not Approved

https://doi.org/10.5256/f1000research.5780.r7946

My concern with this article in its current form is two-fold:

As a software tool article, the discussion seems quite dated. The field of Evolutionary Computation has moved well beyond discussions and/or demonstrations of the form XXX is better than a

My concern with this article in its current form is two-fold:

As a software tool article, the discussion seems quite dated. The field of Evolutionary Computation has moved well beyond discussions and/or demonstrations of the form XXX is better than a simple GA. In fact, almost everything is! From a software tool perspective, the key issue here is how one deals with multimodal fitness landscapes. Various forms of nicheing GAs have been developed for this purpose since the 1980s. Additionally, other approaches such as embedding internal restart mechanisms have been developed and studied. To be of interest in 2015, the authors need to compare their approach with state-of-the-art alternatives.
The particular application chosen is an important one, but the discussion also seems quite dated. The bioinformatics community has moved well beyond the simple hydrophobic-hydrophilic and on-lattice models used in this paper. To offer a credible tool to this community, one again has to do so in the context of the current state of the art. See, for example, Zhang Y (2008), or Liu J et al. (2013).

Competing Interests: No competing interests were disclosed.

I confirm that I have read this submission and believe that I have an appropriate level of expertise to state that I do not consider it to be of an acceptable scientific standard, for reasons outlined above.

CITE

Report a concern

Respond or Comment

Views

Reviewer Report 30 Apr 2015

Nathan Alexander, Department of Pharmacology, Case Western Reserve University, Cleveland, OH, USA

Not Approved

https://doi.org/10.5256/f1000research.5780.r8529

The authors attempt to demonstrate niche genetic algorithms outperform traditional GA at de novo protein folding. They select a specific NGA, termed DSGA, to compare to traditional GA. They simplify the task of de novo protein folding into a two-dimensional problem and model amino acid interactions as hydrophilic or hydrophobic. The protein energetics use a binary approximation where the “energy” of the protein is improved by 1.0 for every pair of residues that are hydrophobic and ”adjacent but not neighbor amino acids”. Amino acid placements are limited to two-dimensional grid coordinates.

The authors demonstrate that their model of protein folding can produce local optima using one ten-amino-acid sequence.

The authors next use a sequence of twenty amino acids to test whether DSGA can produce a better conformation, according to their fitness function, than a traditional GA. The authors present the results of fifteen independent optimization trajectories for DSGA, traditional GA, and traditional GA that is allowed to run for additional generations. This is important because DSGA is more computationally demanding, so there would be no advantage to DSGA over traditional GA, if GA could accomplish equivalent performance to DSGA just by running additional generations to make up for the increased computational time of DSGA. The results show that DSGA is able to find the globally optimal conformation for all fifteen optimization trials, while traditional GA and traditional GA with additional generations find the optimal conformation in none of the fifteen trials.

It is unclear until examination of Figure 1 what configurations on the grid are considered “adjacent” (i.e. are amino acids diagonally placed to one another considered adjacent?).
The authors refer to their fitness function as calculating the free energy of the protein. However, they give no data of how their fitness function quantitatively relates to free energy. Therefore, the authors must not refer to “free energy”, but should use terms such as “fitness function” or “score”. This would also remove the discrepancy that the authors refer to free energy, but large positive values resulting from their method indicate success. The authors include twice the explanation that positive values resulting from their method should be interpreted as negative values of free energy, and negative values resulting from their method should be interpreted as positive values of free energy. This explanation will be unnecessary and it will be easier for the reader to understand the results, which provides readability incentive in addition to the scientific necessity for the authors to remove the use of the term “free energy”.
As this is submitted as a Software Tool Article, in the Materials and Methods section, the authors should give explanations and any related references for what is happening in steps six through thirteen in their implementation of the DSGA pseudo-code in Table 1.
The authors should provide a reference for the basis of their traditional GA implementation.
In the Results section, the purpose of Figure 1 and the purpose of the description of the four amino acid protein are unclear. Does it demonstrate that with only four amino acids there already exist multiple optima? If so, a plot similar to Figure 2 should be shown. Is it just to give a simple demonstrative example of the model for protein folding? If so, it should not fall under the heading of “Multioptimum problem”.
The title for Figure 2 should be revised because the use of the word “methods” is ambiguous.
In the Conclusions section, the authors claim that “…DSGA, which is specialized for multiple optima domains, produces better results than a traditional GA”. This statement must be qualified to fall within the scope of their study: using their model of protein folding, DSGA “produces better results than a traditional GA” on one twenty-amino-acid sequence. The authors must specify what they mean when they say “better results”. Perhaps, they mean “configurations with higher fitness function values”. Within the constraints of their model for protein folding, the scope of the study could be broadened by testing amino acid sequences with shorter and larger length and differing hydrophobic and hydrophilic composition. This could for example demonstrate at what length is traditional GA successful and at what length does DSGA fail.

Similarly, the results and conclusions summarized in the last paragraph of the Introduction must be revised to fall within the scope of the experiments. Specifically:
1. “Here we show that protein folding is a multi-optima problem…” The authors need to change the wording to reflect the scope of their study. The authors only show that a simple model of protein folding produces a multi-optima problem. The authors could state that protein folding is a multi-optima problem and provide a reference, and then state that they show a simple model recapitulates the multi-optima nature of the problem.
2. “…and as a result NGAs are better suited for a solution.” Is this the authors’ hypothesis? The authors should clarify their hypothesis and make it clear when they are stating their hypothesis. Are the authors attempting to show NGAs are “better suited” due to the problem having multiple optima? Are they only trying to show NGAs are “better suited”? The use of the phrase “…as a result…” suggests the former. However, the experiments performed suggest the latter ‑ that the authors are hypothesizing only about the performance of DSGA versus traditional GA. The experiments and results don’t provide any evidence as to what could be the reason for the performance difference. The authors perform no experiments to test whether the improved performance is due to an ability to overcome multi-optima ‑ such as a control experiment utilizing a single-optimum problem or sequence. When clarifying their hypothesis, the authors must specify in relation to what are NGAs better than. The hypothesis should not refer to the general class of NGAs, when only a single specific type, DSGA, is tested. Further, the authors need to define how they quantitatively measure “better suited”. Lastly, the authors need to define what they mean by “solution”.
3. “(1) the DSGA is very adept at predicting the folded state of proteins, which was shown by selecting a 20 amino acid protein and modeling all the folds and all possible combinations;” The results do not provide evidence to support this conclusion. The results cannot show DSGA is “very adept” because the authors do not specify a quantitative measure by which “very adept” is defined, so there is no way to conclude this. Additionally, the ability of DSGA to successfully optimize the conformation of a single twenty amino acid sequence cannot be extrapolated to mean that DSGA can successfully optimize the conformation of amino acid sequences in general. Further, the phrase “folded state of proteins” must be qualified to fall within the scope of the study; specifically, that the folded state of a protein in the study is represented by a hydrophilic-hydrophobic model of amino acids on a two-dimensional grid coordinate system.
4. "(2) the DSGA is better than a traditional GA and better able to derive the correct folding pattern of a protein.” Similarly to the statement in the Conclusion section and above, this statement must be qualified to fall within the scope of their study. The results do not support the unqualified statement that “DSGA is better than a traditional GA”. The protein folding problem presented in the paper and used to compare DSGA to traditional GA is only a single, very specific optimization problem. This single specific optimization problem cannot be used to make the general statement that “DSGA is better than traditional GA”. It is unclear what the authors are comparing DSGA to when they state that DSGA is “…better able to derive the correct folding pattern of a protein”. Also, the authors need to specify how they measure “better” and qualify that the “folding pattern of a protein” is represented by a hydrophilic-hydrophobic model of amino acids on a two-dimensional grid coordinate system. The authors must clarify that “a protein” is a specific twenty amino acid sequence. The appropriate conclusion the results support is that, using the authors’ model of protein folding and their fitness function to score conformations, DSGA produces conformations that score better than a traditional GA on a specific amino acid sequence with length of twenty amino acids.
Similarly, the conclusions in the Abstract must be revised to fall within the scope of the experiments.
1. “DSGA is very adept at predicting the folded state of proteins”. Please see comments in 7.3. above.
2. “DSGA is better than a traditional GA in deriving the correct folding pattern of a protein”. Please see comments in 7.4. above.
Lastly, the title must be revised to clarify the scope of the study:
1. “Niche Genetic Algorithms are better than traditional Genetic Algorithms for de novo Protein Folding.” The title must indicate the extent to which de novo protein folding is simplified: using a two-dimensional grid with a hydrophobic-hydrophilic amino acid model and binary scoring scheme. The title must also indicate the comparison between niche genetic algorithms and traditional genetic algorithms was made using a single specific niche genetic algorithm. Further, the title must indicate the two algorithms were compared using a single specific twenty-amino-acid sequence.

Competing Interests: No competing interests were disclosed.

CITE

Report a concern

Author Response (F1000Research Advisory Board Member) 28 May 2015

James Coker, Johns Hopkins University, Baltimore, USA

28 May 2015

Author Response F1000Research Advisory Board Member

We thank the reviewer for his time and review of our work. Since there is currently only one review submitted (7 months after submission) we have decided to hold off ... Continue reading We thank the reviewer for his time and review of our work. Since there is currently only one review submitted (7 months after submission) we have decided to hold off on making adjustments to the manuscript until we hear back from other reviewers. That being said we have mentioned possible revisions in our responses below and will incorporate them based on the responses from other reviewers. Below we have cut and pasted the reviewer’s comments (numbered) and our responses to each.

1. It is unclear until examination of Figure 1 what configurations on the grid are considered “adjacent” (i.e. are amino acids diagonally placed to one another considered adjacent?).

The use of the term “adjacent” in HP models has been established for over 25 years. It refers to residues that are directly left, right, up, or down (not diagonal) from a particular amino acid that is not neighboring, i.e. the previous or next amino acid (n-1 or n+1). We understand that this can be confusing for a reader unfamiliar with the field. Therefore we have made a slight modification in the “Fitness Function” section, which is the first mention of adjacent amino acids. Here we mention that these terms have been defined and used previously and list two references so readers unfamiliar with the field can learn more.

2. The authors refer to their fitness function as calculating the free energy of the protein. However, they give no data of how their fitness function quantitatively relates to free energy. Therefore, the authors must not refer to “free energy”, but should use terms such as “fitness function” or “score”. This would also remove the discrepancy that the authors refer to free energy, but large positive values resulting from their method indicate success. The authors include twice the explanation that positive values resulting from their method should be interpreted as negative values of free energy, and negative values resulting from their method should be interpreted as positive values of free energy. This explanation will be unnecessary and it will be easier for the reader to understand the results, which provides readability incentive in addition to the scientific necessity for the authors to remove the use of the term “free energy”.

The use of the term ‘Free Energy’ is widely accepted in this field using the conditions we have set. See reference # 26 (Huang et al.), as well as F. Liang and W. H. Wong, J.: Chem. Phys. 2001; 115: 3374, Lau and Dill: Macromolecules. 1989: 3986-3997 (just to name a few over the past 25 years). As a result, we decided to keep the term “Free Energy” in the manuscript to be consistent with previous work.
We understand that the positive values resulting from the DSGA can be confusing as positive Free Energy values correspond with a lack of spontaneous folding, which is why, as the reviewer pointed out, we twice mention that the positive results from the DSGA should be interpreted as negative values. We do understand the reviewer’s concerns. Therefore we have removed the reference to the fact that the DSGA returns values of the opposite sign in the text of the manuscript and have kept the correctly reported values. We have moved the explanation of the negative/positive values from the DSGA to the two supplementary files. In this way the reading of the manuscript will be clear and for those that choose to use the program it will be clear how it functions and how to interpret the results.

3. As this is submitted as a Software Tool Article, in the Materials and Methods section, the authors should give explanations and any related references for what is happening in steps six through thirteen in their implementation of the DSGA pseudo-code in Table 1.

Steps six to thirteen basically show the portions of Dynamic-radius Species-conserving Genetic Algorithm that make it separate from a genetic algorithm. These steps include: the generation of seeds, a Tabu List, and manipulating the Tabu List and generating its final version. All of these are already explained in the Materials and Methods section and well cited. Therefore it seems redundant to put this information in Table 1.
As a result we have altered Table 1 to direct the reader to the relevant section of the Materials and Methods section, etc. where further explanations/references about each step can be found.

4. The authors should provide a reference for the basis of their traditional GA implementation.

We are a little uncertain as to what the reviewer is referring to here. References 16, 17, and 18 are related to Genetic Algorithms and their traditional application in sequence alignment and protein structure prediction. References 16 and 27 are in the manuscript as they are two of the most commonly sited references in relation to Genetic Algorithms.

5. In the Results section, the purpose of Figure 1 and the purpose of the description of the four amino acid protein are unclear. Does it demonstrate that with only four amino acids there already exist multiple optima? If so, a plot similar to Figure 2 should be shown. Is it just to give a simple demonstrative example of the model for protein folding? If so, it should not fall under the heading of “Multioptimum problem”.

The reason Figure 1 is present in the manuscript is to provide a clear and relatively simple example of the output of the DSGA. This figure was placed where it is to serve as an introduction and explanation to the Multioptimum problem. We do not contend or intend to suggest that every protein will have a multi-optima folding method, just the opposite. Clearly the protein in Figure 1 does not have multi-optima.

6. The title for Figure 2 should be revised because the use of the word “methods” is ambiguous.

The title of Figure 2 has been changed to ‘Free Energy for all possible folded forms of HPPHPPHPPH’.

7. In the Conclusions section, the authors claim that “…DSGA, which is specialized for multiple optima domains, produces better results than a traditional GA”. This statement must be qualified to fall within the scope of their study: using their model of protein folding, DSGA “produces better results than a traditional GA” on one twenty-amino-acid sequence. The authors must specify what they mean when they say “better results”. Perhaps, they mean “configurations with higher fitness function values”. Within the constraints of their model for protein folding, the scope of the study could be broadened by testing amino acid sequences with shorter and larger length and differing hydrophobic and hydrophilic composition. This could for example demonstrate at what length is traditional GA successful and at what length does DSGA fail.

Similarly, the results and conclusions summarized in the last paragraph of the Introduction must be revised to fall within the scope of the experiments. Specifically:
1.“Here we show that protein folding is a multi-optima problem…” The authors need to change the wording to reflect the scope of their study. The authors only show that a simple model of protein folding produces a multi-optima problem. The authors could state that protein folding is a multi-optima problem and provide a reference, and then state that they show a simple model recapitulates the multi-optima nature of the problem.
2.“…and as a result NGAs are better suited for a solution.” Is this the authors’ hypothesis? The authors should clarify their hypothesis and make it clear when they are stating their hypothesis. Are the authors attempting to show NGAs are “better suited” due to the problem having multiple optima? Are they only trying to show NGAs are “better suited”? The use of the phrase “…as a result…” suggests the former. However, the experiments performed suggest the latter ‑ that the authors are hypothesizing only about the performance of DSGA versus traditional GA. The experiments and results don’t provide any evidence as to what could be the reason for the performance difference. The authors perform no experiments to test whether the improved performance is due to an ability to overcome multi-optima ‑ such as a control experiment utilizing a single-optimum problem or sequence. When clarifying their hypothesis, the authors must specify in relation to what are NGAs better than. The hypothesis should not refer to the general class of NGAs, when only a single specific type, DSGA, is tested. Further, the authors need to define how they quantitatively measure “better suited”. Lastly, the authors need to define what they mean by “solution”.
3. “(1) the DSGA is very adept at predicting the folded state of proteins, which was shown by selecting a 20 amino acid protein and modeling all the folds and all possible combinations;” The results do not provide evidence to support this conclusion. The results cannot show DSGA is “very adept” because the authors do not specify a quantitative measure by which “very adept” is defined, so there is no way to conclude this. Additionally, the ability of DSGA to successfully optimize the conformation of a single twenty amino acid sequence cannot be extrapolated to mean that DSGA can successfully optimize the conformation of amino acid sequences in general. Further, the phrase “folded state of proteins” must be qualified to fall within the scope of the study; specifically, that the folded state of a protein in the study is represented by a hydrophilic-hydrophobic model of amino acids on a two-dimensional grid coordinate system.
4."(2) the DSGA is better than a traditional GA and better able to derive the correct folding pattern of a protein.” Similarly to the statement in the Conclusion section and above, this statement must be qualified to fall within the scope of their study. The results do not support the unqualified statement that “DSGA is better than a traditional GA”. The protein folding problem presented in the paper and used to compare DSGA to traditional GA is only a single, very specific optimization problem. This single specific optimization problem cannot be used to make the general statement that “DSGA is better than traditional GA”. It is unclear what the authors are comparing DSGA to when they state that DSGA is “…better able to derive the correct folding pattern of a protein”. Also, the authors need to specify how they measure “better” and qualify that the “folding pattern of a protein” is represented by a hydrophilic-hydrophobic model of amino acids on a two-dimensional grid coordinate system. The authors must clarify that “a protein” is a specific twenty amino acid sequence. The appropriate conclusion the results support is that, using the authors’ model of protein folding and their fitness function to score conformations, DSGA produces conformations that score better than a traditional GA on a specific amino acid sequence with length of twenty amino acids.

We understand the reviewer’s concerns here; however, the end result of the logic in these comments is that no one can ever really know if one algorithm is better than another since there will always be a condition that is left untested since it is impossible to test every protein and every condition. Here we show that some proteins create multi-optima problems (i.e. Figure 2), and we believe that the body of knowledge from Genetic Algorithms should encourage the use of Niche Genetic Algorithms. Our paper goes one step further and shows a test case in which, a NGA does a better job of solving the protein folding problem than a traditional GA.
It is well understood by the community that currently there is no algorithm that can solve the folding problem de novo for all proteins. Even the best de novo algorithms have a low overall success rate. Also 2D models are simplifications of the actual 3D models. With that being said it is common in this field of research to make statements that the review claims to be unfounded. Consider the following quotes.
Huang, C., Yang, X. & He, Z. (2010). Protein folding simulations of 2D HP model by the genetic algorithm based on optimal secondary structure, Computational Biology and Chemistry 34, pp 137-142.
“GAOSS would be an efficient tool for the protein structure predictions (PSP).”
Su, S., Lin, C. & Ting, C. (2011). An effective hybrid of hill climbing and genetic algorithm for 2D triangular protein structure prediction, Proteome Science 9(Suppl. 1).
“The simulation results show that ERS-GA and HHGA can successfully be applied to the problem of protein structure prediction. The satisfactory simulation results validate the effectiveness of the proposed algorithms”
Liang, F. and Wong, W. H. (2001). Evolutionary Monte Carlo for protein folding simulations, Journal of Chemical Physics 115(7), pp. 3374-3380.
“We showed that the evolutionary Monte Carlo algorithm can be effectively applied to simulations of protein folding on lattice models.”

That being said we also understand the spirit of the reviewer’s comments that we have analyzed a small number of protein sequences. Since we have analyzed more sequences we have now included that information as well. We have also revised the language of the conclusion section.

8.Similarly, the conclusions in the Abstract must be revised to fall within the scope of the experiments.
1.“DSGA is very adept at predicting the folded state of proteins”. Please see comments in 7.3. above.
2.“DSGA is better than a traditional GA in deriving the correct folding pattern of a protein”. Please see comments in 7.4. above.

Just as we have now modified the Conclusion section we have also modified the Abstract as well.

9.Lastly, the title must be revised to clarify the scope of the study:
1.“Niche Genetic Algorithms are better than traditional Genetic Algorithms for de novo Protein Folding.” The title must indicate the extent to which de novo protein folding is simplified: using a two-dimensional grid with a hydrophobic-hydrophilic amino acid model and binary scoring scheme. The title must also indicate the comparison between niche genetic algorithms and traditional genetic algorithms was made using a single specific niche genetic algorithm. Further, the title must indicate the two algorithms were compared using a single specific twenty-amino-acid sequence.

We are uncertain as to how all of the reviewer’s comments here can be included in a title or how it would improve the title. DSGA is a niche genetic algorithm and we have shown that it predicts the optimally folded configuration for a protein more reliably (i.e. performs better) than a traditional genetic algorithm. Since the title does not constitute an untrue statement we do not see a valid reason to change it in the reviewer’s comments. That being said we understand that the plural form of NGA might be confusing as we use one NGA in the manuscript. Therefore we have changed the title to “A Niche Genetic Algorithm is better than traditional genetic algorithms for de novo protein folding”.
We thank the reviewer for his time and review of our work. Since there is currently only one review submitted (7 months after submission) we have decided to hold off on making adjustments to the manuscript until we hear back from other reviewers. That being said we have mentioned possible revisions in our responses below and will incorporate them based on the responses from other reviewers. Below we have cut and pasted the reviewer’s comments (numbered) and our responses to each.

1. It is unclear until examination of Figure 1 what configurations on the grid are considered “adjacent” (i.e. are amino acids diagonally placed to one another considered adjacent?).

The use of the term “adjacent” in HP models has been established for over 25 years. It refers to residues that are directly left, right, up, or down (not diagonal) from a particular amino acid that is not neighboring, i.e. the previous or next amino acid (n-1 or n+1). We understand that this can be confusing for a reader unfamiliar with the field. Therefore we have made a slight modification in the “Fitness Function” section, which is the first mention of adjacent amino acids. Here we mention that these terms have been defined and used previously and list two references so readers unfamiliar with the field can learn more.

2. The authors refer to their fitness function as calculating the free energy of the protein. However, they give no data of how their fitness function quantitatively relates to free energy. Therefore, the authors must not refer to “free energy”, but should use terms such as “fitness function” or “score”. This would also remove the discrepancy that the authors refer to free energy, but large positive values resulting from their method indicate success. The authors include twice the explanation that positive values resulting from their method should be interpreted as negative values of free energy, and negative values resulting from their method should be interpreted as positive values of free energy. This explanation will be unnecessary and it will be easier for the reader to understand the results, which provides readability incentive in addition to the scientific necessity for the authors to remove the use of the term “free energy”.

The use of the term ‘Free Energy’ is widely accepted in this field using the conditions we have set. See reference # 26 (Huang et al.), as well as F. Liang and W. H. Wong, J.: Chem. Phys. 2001; 115: 3374, Lau and Dill: Macromolecules. 1989: 3986-3997 (just to name a few over the past 25 years). As a result, we decided to keep the term “Free Energy” in the manuscript to be consistent with previous work.
We understand that the positive values resulting from the DSGA can be confusing as positive Free Energy values correspond with a lack of spontaneous folding, which is why, as the reviewer pointed out, we twice mention that the positive results from the DSGA should be interpreted as negative values. We do understand the reviewer’s concerns. Therefore we have removed the reference to the fact that the DSGA returns values of the opposite sign in the text of the manuscript and have kept the correctly reported values. We have moved the explanation of the negative/positive values from the DSGA to the two supplementary files. In this way the reading of the manuscript will be clear and for those that choose to use the program it will be clear how it functions and how to interpret the results.

3. As this is submitted as a Software Tool Article, in the Materials and Methods section, the authors should give explanations and any related references for what is happening in steps six through thirteen in their implementation of the DSGA pseudo-code in Table 1.

Steps six to thirteen basically show the portions of Dynamic-radius Species-conserving Genetic Algorithm that make it separate from a genetic algorithm. These steps include: the generation of seeds, a Tabu List, and manipulating the Tabu List and generating its final version. All of these are already explained in the Materials and Methods section and well cited. Therefore it seems redundant to put this information in Table 1.
As a result we have altered Table 1 to direct the reader to the relevant section of the Materials and Methods section, etc. where further explanations/references about each step can be found.

4. The authors should provide a reference for the basis of their traditional GA implementation.

We are a little uncertain as to what the reviewer is referring to here. References 16, 17, and 18 are related to Genetic Algorithms and their traditional application in sequence alignment and protein structure prediction. References 16 and 27 are in the manuscript as they are two of the most commonly sited references in relation to Genetic Algorithms.

5. In the Results section, the purpose of Figure 1 and the purpose of the description of the four amino acid protein are unclear. Does it demonstrate that with only four amino acids there already exist multiple optima? If so, a plot similar to Figure 2 should be shown. Is it just to give a simple demonstrative example of the model for protein folding? If so, it should not fall under the heading of “Multioptimum problem”.

The reason Figure 1 is present in the manuscript is to provide a clear and relatively simple example of the output of the DSGA. This figure was placed where it is to serve as an introduction and explanation to the Multioptimum problem. We do not contend or intend to suggest that every protein will have a multi-optima folding method, just the opposite. Clearly the protein in Figure 1 does not have multi-optima.

6. The title for Figure 2 should be revised because the use of the word “methods” is ambiguous.

The title of Figure 2 has been changed to ‘Free Energy for all possible folded forms of HPPHPPHPPH’.

7. In the Conclusions section, the authors claim that “…DSGA, which is specialized for multiple optima domains, produces better results than a traditional GA”. This statement must be qualified to fall within the scope of their study: using their model of protein folding, DSGA “produces better results than a traditional GA” on one twenty-amino-acid sequence. The authors must specify what they mean when they say “better results”. Perhaps, they mean “configurations with higher fitness function values”. Within the constraints of their model for protein folding, the scope of the study could be broadened by testing amino acid sequences with shorter and larger length and differing hydrophobic and hydrophilic composition. This could for example demonstrate at what length is traditional GA successful and at what length does DSGA fail.

Similarly, the results and conclusions summarized in the last paragraph of the Introduction must be revised to fall within the scope of the experiments. Specifically:
1.“Here we show that protein folding is a multi-optima problem…” The authors need to change the wording to reflect the scope of their study. The authors only show that a simple model of protein folding produces a multi-optima problem. The authors could state that protein folding is a multi-optima problem and provide a reference, and then state that they show a simple model recapitulates the multi-optima nature of the problem.
2.“…and as a result NGAs are better suited for a solution.” Is this the authors’ hypothesis? The authors should clarify their hypothesis and make it clear when they are stating their hypothesis. Are the authors attempting to show NGAs are “better suited” due to the problem having multiple optima? Are they only trying to show NGAs are “better suited”? The use of the phrase “…as a result…” suggests the former. However, the experiments performed suggest the latter ‑ that the authors are hypothesizing only about the performance of DSGA versus traditional GA. The experiments and results don’t provide any evidence as to what could be the reason for the performance difference. The authors perform no experiments to test whether the improved performance is due to an ability to overcome multi-optima ‑ such as a control experiment utilizing a single-optimum problem or sequence. When clarifying their hypothesis, the authors must specify in relation to what are NGAs better than. The hypothesis should not refer to the general class of NGAs, when only a single specific type, DSGA, is tested. Further, the authors need to define how they quantitatively measure “better suited”. Lastly, the authors need to define what they mean by “solution”.
3. “(1) the DSGA is very adept at predicting the folded state of proteins, which was shown by selecting a 20 amino acid protein and modeling all the folds and all possible combinations;” The results do not provide evidence to support this conclusion. The results cannot show DSGA is “very adept” because the authors do not specify a quantitative measure by which “very adept” is defined, so there is no way to conclude this. Additionally, the ability of DSGA to successfully optimize the conformation of a single twenty amino acid sequence cannot be extrapolated to mean that DSGA can successfully optimize the conformation of amino acid sequences in general. Further, the phrase “folded state of proteins” must be qualified to fall within the scope of the study; specifically, that the folded state of a protein in the study is represented by a hydrophilic-hydrophobic model of amino acids on a two-dimensional grid coordinate system.
4."(2) the DSGA is better than a traditional GA and better able to derive the correct folding pattern of a protein.” Similarly to the statement in the Conclusion section and above, this statement must be qualified to fall within the scope of their study. The results do not support the unqualified statement that “DSGA is better than a traditional GA”. The protein folding problem presented in the paper and used to compare DSGA to traditional GA is only a single, very specific optimization problem. This single specific optimization problem cannot be used to make the general statement that “DSGA is better than traditional GA”. It is unclear what the authors are comparing DSGA to when they state that DSGA is “…better able to derive the correct folding pattern of a protein”. Also, the authors need to specify how they measure “better” and qualify that the “folding pattern of a protein” is represented by a hydrophilic-hydrophobic model of amino acids on a two-dimensional grid coordinate system. The authors must clarify that “a protein” is a specific twenty amino acid sequence. The appropriate conclusion the results support is that, using the authors’ model of protein folding and their fitness function to score conformations, DSGA produces conformations that score better than a traditional GA on a specific amino acid sequence with length of twenty amino acids.

We understand the reviewer’s concerns here; however, the end result of the logic in these comments is that no one can ever really know if one algorithm is better than another since there will always be a condition that is left untested since it is impossible to test every protein and every condition. Here we show that some proteins create multi-optima problems (i.e. Figure 2), and we believe that the body of knowledge from Genetic Algorithms should encourage the use of Niche Genetic Algorithms. Our paper goes one step further and shows a test case in which, a NGA does a better job of solving the protein folding problem than a traditional GA.
It is well understood by the community that currently there is no algorithm that can solve the folding problem de novo for all proteins. Even the best de novo algorithms have a low overall success rate. Also 2D models are simplifications of the actual 3D models. With that being said it is common in this field of research to make statements that the review claims to be unfounded. Consider the following quotes.
Huang, C., Yang, X. & He, Z. (2010). Protein folding simulations of 2D HP model by the genetic algorithm based on optimal secondary structure, Computational Biology and Chemistry 34, pp 137-142.
“GAOSS would be an efficient tool for the protein structure predictions (PSP).”
Su, S., Lin, C. & Ting, C. (2011). An effective hybrid of hill climbing and genetic algorithm for 2D triangular protein structure prediction, Proteome Science 9(Suppl. 1).
“The simulation results show that ERS-GA and HHGA can successfully be applied to the problem of protein structure prediction. The satisfactory simulation results validate the effectiveness of the proposed algorithms”
Liang, F. and Wong, W. H. (2001). Evolutionary Monte Carlo for protein folding simulations, Journal of Chemical Physics 115(7), pp. 3374-3380.
“We showed that the evolutionary Monte Carlo algorithm can be effectively applied to simulations of protein folding on lattice models.”

That being said we also understand the spirit of the reviewer’s comments that we have analyzed a small number of protein sequences. Since we have analyzed more sequences we have now included that information as well. We have also revised the language of the conclusion section.

8.Similarly, the conclusions in the Abstract must be revised to fall within the scope of the experiments.
1.“DSGA is very adept at predicting the folded state of proteins”. Please see comments in 7.3. above.
2.“DSGA is better than a traditional GA in deriving the correct folding pattern of a protein”. Please see comments in 7.4. above.

Just as we have now modified the Conclusion section we have also modified the Abstract as well.

9.Lastly, the title must be revised to clarify the scope of the study:
1.“Niche Genetic Algorithms are better than traditional Genetic Algorithms for de novo Protein Folding.” The title must indicate the extent to which de novo protein folding is simplified: using a two-dimensional grid with a hydrophobic-hydrophilic amino acid model and binary scoring scheme. The title must also indicate the comparison between niche genetic algorithms and traditional genetic algorithms was made using a single specific niche genetic algorithm. Further, the title must indicate the two algorithms were compared using a single specific twenty-amino-acid sequence.

We are uncertain as to how all of the reviewer’s comments here can be included in a title or how it would improve the title. DSGA is a niche genetic algorithm and we have shown that it predicts the optimally folded configuration for a protein more reliably (i.e. performs better) than a traditional genetic algorithm. Since the title does not constitute an untrue statement we do not see a valid reason to change it in the reviewer’s comments. That being said we understand that the plural form of NGA might be confusing as we use one NGA in the manuscript. Therefore we have changed the title to “A Niche Genetic Algorithm is better than traditional genetic algorithms for de novo protein folding”.
Competing Interests: No competing interests were disclosed. Close
Report a concern
Respond or Comment

COMMENTS ON THIS REPORT

Author Response (F1000Research Advisory Board Member) 28 May 2015

James Coker, Johns Hopkins University, Baltimore, USA

28 May 2015

Author Response F1000Research Advisory Board Member

We thank the reviewer for his time and review of our work. Since there is currently only one review submitted (7 months after submission) we have decided to hold off ... Continue reading We thank the reviewer for his time and review of our work. Since there is currently only one review submitted (7 months after submission) we have decided to hold off on making adjustments to the manuscript until we hear back from other reviewers. That being said we have mentioned possible revisions in our responses below and will incorporate them based on the responses from other reviewers. Below we have cut and pasted the reviewer’s comments (numbered) and our responses to each.

1. It is unclear until examination of Figure 1 what configurations on the grid are considered “adjacent” (i.e. are amino acids diagonally placed to one another considered adjacent?).

The use of the term “adjacent” in HP models has been established for over 25 years. It refers to residues that are directly left, right, up, or down (not diagonal) from a particular amino acid that is not neighboring, i.e. the previous or next amino acid (n-1 or n+1). We understand that this can be confusing for a reader unfamiliar with the field. Therefore we have made a slight modification in the “Fitness Function” section, which is the first mention of adjacent amino acids. Here we mention that these terms have been defined and used previously and list two references so readers unfamiliar with the field can learn more.

2. The authors refer to their fitness function as calculating the free energy of the protein. However, they give no data of how their fitness function quantitatively relates to free energy. Therefore, the authors must not refer to “free energy”, but should use terms such as “fitness function” or “score”. This would also remove the discrepancy that the authors refer to free energy, but large positive values resulting from their method indicate success. The authors include twice the explanation that positive values resulting from their method should be interpreted as negative values of free energy, and negative values resulting from their method should be interpreted as positive values of free energy. This explanation will be unnecessary and it will be easier for the reader to understand the results, which provides readability incentive in addition to the scientific necessity for the authors to remove the use of the term “free energy”.

The use of the term ‘Free Energy’ is widely accepted in this field using the conditions we have set. See reference # 26 (Huang et al.), as well as F. Liang and W. H. Wong, J.: Chem. Phys. 2001; 115: 3374, Lau and Dill: Macromolecules. 1989: 3986-3997 (just to name a few over the past 25 years). As a result, we decided to keep the term “Free Energy” in the manuscript to be consistent with previous work.
We understand that the positive values resulting from the DSGA can be confusing as positive Free Energy values correspond with a lack of spontaneous folding, which is why, as the reviewer pointed out, we twice mention that the positive results from the DSGA should be interpreted as negative values. We do understand the reviewer’s concerns. Therefore we have removed the reference to the fact that the DSGA returns values of the opposite sign in the text of the manuscript and have kept the correctly reported values. We have moved the explanation of the negative/positive values from the DSGA to the two supplementary files. In this way the reading of the manuscript will be clear and for those that choose to use the program it will be clear how it functions and how to interpret the results.

3. As this is submitted as a Software Tool Article, in the Materials and Methods section, the authors should give explanations and any related references for what is happening in steps six through thirteen in their implementation of the DSGA pseudo-code in Table 1.

Steps six to thirteen basically show the portions of Dynamic-radius Species-conserving Genetic Algorithm that make it separate from a genetic algorithm. These steps include: the generation of seeds, a Tabu List, and manipulating the Tabu List and generating its final version. All of these are already explained in the Materials and Methods section and well cited. Therefore it seems redundant to put this information in Table 1.
As a result we have altered Table 1 to direct the reader to the relevant section of the Materials and Methods section, etc. where further explanations/references about each step can be found.

4. The authors should provide a reference for the basis of their traditional GA implementation.

We are a little uncertain as to what the reviewer is referring to here. References 16, 17, and 18 are related to Genetic Algorithms and their traditional application in sequence alignment and protein structure prediction. References 16 and 27 are in the manuscript as they are two of the most commonly sited references in relation to Genetic Algorithms.

5. In the Results section, the purpose of Figure 1 and the purpose of the description of the four amino acid protein are unclear. Does it demonstrate that with only four amino acids there already exist multiple optima? If so, a plot similar to Figure 2 should be shown. Is it just to give a simple demonstrative example of the model for protein folding? If so, it should not fall under the heading of “Multioptimum problem”.

The reason Figure 1 is present in the manuscript is to provide a clear and relatively simple example of the output of the DSGA. This figure was placed where it is to serve as an introduction and explanation to the Multioptimum problem. We do not contend or intend to suggest that every protein will have a multi-optima folding method, just the opposite. Clearly the protein in Figure 1 does not have multi-optima.

6. The title for Figure 2 should be revised because the use of the word “methods” is ambiguous.

The title of Figure 2 has been changed to ‘Free Energy for all possible folded forms of HPPHPPHPPH’.

7. In the Conclusions section, the authors claim that “…DSGA, which is specialized for multiple optima domains, produces better results than a traditional GA”. This statement must be qualified to fall within the scope of their study: using their model of protein folding, DSGA “produces better results than a traditional GA” on one twenty-amino-acid sequence. The authors must specify what they mean when they say “better results”. Perhaps, they mean “configurations with higher fitness function values”. Within the constraints of their model for protein folding, the scope of the study could be broadened by testing amino acid sequences with shorter and larger length and differing hydrophobic and hydrophilic composition. This could for example demonstrate at what length is traditional GA successful and at what length does DSGA fail.

Similarly, the results and conclusions summarized in the last paragraph of the Introduction must be revised to fall within the scope of the experiments. Specifically:
1.“Here we show that protein folding is a multi-optima problem…” The authors need to change the wording to reflect the scope of their study. The authors only show that a simple model of protein folding produces a multi-optima problem. The authors could state that protein folding is a multi-optima problem and provide a reference, and then state that they show a simple model recapitulates the multi-optima nature of the problem.
2.“…and as a result NGAs are better suited for a solution.” Is this the authors’ hypothesis? The authors should clarify their hypothesis and make it clear when they are stating their hypothesis. Are the authors attempting to show NGAs are “better suited” due to the problem having multiple optima? Are they only trying to show NGAs are “better suited”? The use of the phrase “…as a result…” suggests the former. However, the experiments performed suggest the latter ‑ that the authors are hypothesizing only about the performance of DSGA versus traditional GA. The experiments and results don’t provide any evidence as to what could be the reason for the performance difference. The authors perform no experiments to test whether the improved performance is due to an ability to overcome multi-optima ‑ such as a control experiment utilizing a single-optimum problem or sequence. When clarifying their hypothesis, the authors must specify in relation to what are NGAs better than. The hypothesis should not refer to the general class of NGAs, when only a single specific type, DSGA, is tested. Further, the authors need to define how they quantitatively measure “better suited”. Lastly, the authors need to define what they mean by “solution”.
3. “(1) the DSGA is very adept at predicting the folded state of proteins, which was shown by selecting a 20 amino acid protein and modeling all the folds and all possible combinations;” The results do not provide evidence to support this conclusion. The results cannot show DSGA is “very adept” because the authors do not specify a quantitative measure by which “very adept” is defined, so there is no way to conclude this. Additionally, the ability of DSGA to successfully optimize the conformation of a single twenty amino acid sequence cannot be extrapolated to mean that DSGA can successfully optimize the conformation of amino acid sequences in general. Further, the phrase “folded state of proteins” must be qualified to fall within the scope of the study; specifically, that the folded state of a protein in the study is represented by a hydrophilic-hydrophobic model of amino acids on a two-dimensional grid coordinate system.
4."(2) the DSGA is better than a traditional GA and better able to derive the correct folding pattern of a protein.” Similarly to the statement in the Conclusion section and above, this statement must be qualified to fall within the scope of their study. The results do not support the unqualified statement that “DSGA is better than a traditional GA”. The protein folding problem presented in the paper and used to compare DSGA to traditional GA is only a single, very specific optimization problem. This single specific optimization problem cannot be used to make the general statement that “DSGA is better than traditional GA”. It is unclear what the authors are comparing DSGA to when they state that DSGA is “…better able to derive the correct folding pattern of a protein”. Also, the authors need to specify how they measure “better” and qualify that the “folding pattern of a protein” is represented by a hydrophilic-hydrophobic model of amino acids on a two-dimensional grid coordinate system. The authors must clarify that “a protein” is a specific twenty amino acid sequence. The appropriate conclusion the results support is that, using the authors’ model of protein folding and their fitness function to score conformations, DSGA produces conformations that score better than a traditional GA on a specific amino acid sequence with length of twenty amino acids.

We understand the reviewer’s concerns here; however, the end result of the logic in these comments is that no one can ever really know if one algorithm is better than another since there will always be a condition that is left untested since it is impossible to test every protein and every condition. Here we show that some proteins create multi-optima problems (i.e. Figure 2), and we believe that the body of knowledge from Genetic Algorithms should encourage the use of Niche Genetic Algorithms. Our paper goes one step further and shows a test case in which, a NGA does a better job of solving the protein folding problem than a traditional GA.
It is well understood by the community that currently there is no algorithm that can solve the folding problem de novo for all proteins. Even the best de novo algorithms have a low overall success rate. Also 2D models are simplifications of the actual 3D models. With that being said it is common in this field of research to make statements that the review claims to be unfounded. Consider the following quotes.
Huang, C., Yang, X. & He, Z. (2010). Protein folding simulations of 2D HP model by the genetic algorithm based on optimal secondary structure, Computational Biology and Chemistry 34, pp 137-142.
“GAOSS would be an efficient tool for the protein structure predictions (PSP).”
Su, S., Lin, C. & Ting, C. (2011). An effective hybrid of hill climbing and genetic algorithm for 2D triangular protein structure prediction, Proteome Science 9(Suppl. 1).
“The simulation results show that ERS-GA and HHGA can successfully be applied to the problem of protein structure prediction. The satisfactory simulation results validate the effectiveness of the proposed algorithms”
Liang, F. and Wong, W. H. (2001). Evolutionary Monte Carlo for protein folding simulations, Journal of Chemical Physics 115(7), pp. 3374-3380.
“We showed that the evolutionary Monte Carlo algorithm can be effectively applied to simulations of protein folding on lattice models.”

That being said we also understand the spirit of the reviewer’s comments that we have analyzed a small number of protein sequences. Since we have analyzed more sequences we have now included that information as well. We have also revised the language of the conclusion section.

8.Similarly, the conclusions in the Abstract must be revised to fall within the scope of the experiments.
1.“DSGA is very adept at predicting the folded state of proteins”. Please see comments in 7.3. above.
2.“DSGA is better than a traditional GA in deriving the correct folding pattern of a protein”. Please see comments in 7.4. above.

Just as we have now modified the Conclusion section we have also modified the Abstract as well.

9.Lastly, the title must be revised to clarify the scope of the study:
1.“Niche Genetic Algorithms are better than traditional Genetic Algorithms for de novo Protein Folding.” The title must indicate the extent to which de novo protein folding is simplified: using a two-dimensional grid with a hydrophobic-hydrophilic amino acid model and binary scoring scheme. The title must also indicate the comparison between niche genetic algorithms and traditional genetic algorithms was made using a single specific niche genetic algorithm. Further, the title must indicate the two algorithms were compared using a single specific twenty-amino-acid sequence.

We are uncertain as to how all of the reviewer’s comments here can be included in a title or how it would improve the title. DSGA is a niche genetic algorithm and we have shown that it predicts the optimally folded configuration for a protein more reliably (i.e. performs better) than a traditional genetic algorithm. Since the title does not constitute an untrue statement we do not see a valid reason to change it in the reviewer’s comments. That being said we understand that the plural form of NGA might be confusing as we use one NGA in the manuscript. Therefore we have changed the title to “A Niche Genetic Algorithm is better than traditional genetic algorithms for de novo protein folding”.
We thank the reviewer for his time and review of our work. Since there is currently only one review submitted (7 months after submission) we have decided to hold off on making adjustments to the manuscript until we hear back from other reviewers. That being said we have mentioned possible revisions in our responses below and will incorporate them based on the responses from other reviewers. Below we have cut and pasted the reviewer’s comments (numbered) and our responses to each.

1. It is unclear until examination of Figure 1 what configurations on the grid are considered “adjacent” (i.e. are amino acids diagonally placed to one another considered adjacent?).

The use of the term “adjacent” in HP models has been established for over 25 years. It refers to residues that are directly left, right, up, or down (not diagonal) from a particular amino acid that is not neighboring, i.e. the previous or next amino acid (n-1 or n+1). We understand that this can be confusing for a reader unfamiliar with the field. Therefore we have made a slight modification in the “Fitness Function” section, which is the first mention of adjacent amino acids. Here we mention that these terms have been defined and used previously and list two references so readers unfamiliar with the field can learn more.

2. The authors refer to their fitness function as calculating the free energy of the protein. However, they give no data of how their fitness function quantitatively relates to free energy. Therefore, the authors must not refer to “free energy”, but should use terms such as “fitness function” or “score”. This would also remove the discrepancy that the authors refer to free energy, but large positive values resulting from their method indicate success. The authors include twice the explanation that positive values resulting from their method should be interpreted as negative values of free energy, and negative values resulting from their method should be interpreted as positive values of free energy. This explanation will be unnecessary and it will be easier for the reader to understand the results, which provides readability incentive in addition to the scientific necessity for the authors to remove the use of the term “free energy”.

The use of the term ‘Free Energy’ is widely accepted in this field using the conditions we have set. See reference # 26 (Huang et al.), as well as F. Liang and W. H. Wong, J.: Chem. Phys. 2001; 115: 3374, Lau and Dill: Macromolecules. 1989: 3986-3997 (just to name a few over the past 25 years). As a result, we decided to keep the term “Free Energy” in the manuscript to be consistent with previous work.
We understand that the positive values resulting from the DSGA can be confusing as positive Free Energy values correspond with a lack of spontaneous folding, which is why, as the reviewer pointed out, we twice mention that the positive results from the DSGA should be interpreted as negative values. We do understand the reviewer’s concerns. Therefore we have removed the reference to the fact that the DSGA returns values of the opposite sign in the text of the manuscript and have kept the correctly reported values. We have moved the explanation of the negative/positive values from the DSGA to the two supplementary files. In this way the reading of the manuscript will be clear and for those that choose to use the program it will be clear how it functions and how to interpret the results.

3. As this is submitted as a Software Tool Article, in the Materials and Methods section, the authors should give explanations and any related references for what is happening in steps six through thirteen in their implementation of the DSGA pseudo-code in Table 1.

Steps six to thirteen basically show the portions of Dynamic-radius Species-conserving Genetic Algorithm that make it separate from a genetic algorithm. These steps include: the generation of seeds, a Tabu List, and manipulating the Tabu List and generating its final version. All of these are already explained in the Materials and Methods section and well cited. Therefore it seems redundant to put this information in Table 1.
As a result we have altered Table 1 to direct the reader to the relevant section of the Materials and Methods section, etc. where further explanations/references about each step can be found.

4. The authors should provide a reference for the basis of their traditional GA implementation.

We are a little uncertain as to what the reviewer is referring to here. References 16, 17, and 18 are related to Genetic Algorithms and their traditional application in sequence alignment and protein structure prediction. References 16 and 27 are in the manuscript as they are two of the most commonly sited references in relation to Genetic Algorithms.

5. In the Results section, the purpose of Figure 1 and the purpose of the description of the four amino acid protein are unclear. Does it demonstrate that with only four amino acids there already exist multiple optima? If so, a plot similar to Figure 2 should be shown. Is it just to give a simple demonstrative example of the model for protein folding? If so, it should not fall under the heading of “Multioptimum problem”.

The reason Figure 1 is present in the manuscript is to provide a clear and relatively simple example of the output of the DSGA. This figure was placed where it is to serve as an introduction and explanation to the Multioptimum problem. We do not contend or intend to suggest that every protein will have a multi-optima folding method, just the opposite. Clearly the protein in Figure 1 does not have multi-optima.

6. The title for Figure 2 should be revised because the use of the word “methods” is ambiguous.

The title of Figure 2 has been changed to ‘Free Energy for all possible folded forms of HPPHPPHPPH’.

7. In the Conclusions section, the authors claim that “…DSGA, which is specialized for multiple optima domains, produces better results than a traditional GA”. This statement must be qualified to fall within the scope of their study: using their model of protein folding, DSGA “produces better results than a traditional GA” on one twenty-amino-acid sequence. The authors must specify what they mean when they say “better results”. Perhaps, they mean “configurations with higher fitness function values”. Within the constraints of their model for protein folding, the scope of the study could be broadened by testing amino acid sequences with shorter and larger length and differing hydrophobic and hydrophilic composition. This could for example demonstrate at what length is traditional GA successful and at what length does DSGA fail.

Similarly, the results and conclusions summarized in the last paragraph of the Introduction must be revised to fall within the scope of the experiments. Specifically:
1.“Here we show that protein folding is a multi-optima problem…” The authors need to change the wording to reflect the scope of their study. The authors only show that a simple model of protein folding produces a multi-optima problem. The authors could state that protein folding is a multi-optima problem and provide a reference, and then state that they show a simple model recapitulates the multi-optima nature of the problem.
2.“…and as a result NGAs are better suited for a solution.” Is this the authors’ hypothesis? The authors should clarify their hypothesis and make it clear when they are stating their hypothesis. Are the authors attempting to show NGAs are “better suited” due to the problem having multiple optima? Are they only trying to show NGAs are “better suited”? The use of the phrase “…as a result…” suggests the former. However, the experiments performed suggest the latter ‑ that the authors are hypothesizing only about the performance of DSGA versus traditional GA. The experiments and results don’t provide any evidence as to what could be the reason for the performance difference. The authors perform no experiments to test whether the improved performance is due to an ability to overcome multi-optima ‑ such as a control experiment utilizing a single-optimum problem or sequence. When clarifying their hypothesis, the authors must specify in relation to what are NGAs better than. The hypothesis should not refer to the general class of NGAs, when only a single specific type, DSGA, is tested. Further, the authors need to define how they quantitatively measure “better suited”. Lastly, the authors need to define what they mean by “solution”.
3. “(1) the DSGA is very adept at predicting the folded state of proteins, which was shown by selecting a 20 amino acid protein and modeling all the folds and all possible combinations;” The results do not provide evidence to support this conclusion. The results cannot show DSGA is “very adept” because the authors do not specify a quantitative measure by which “very adept” is defined, so there is no way to conclude this. Additionally, the ability of DSGA to successfully optimize the conformation of a single twenty amino acid sequence cannot be extrapolated to mean that DSGA can successfully optimize the conformation of amino acid sequences in general. Further, the phrase “folded state of proteins” must be qualified to fall within the scope of the study; specifically, that the folded state of a protein in the study is represented by a hydrophilic-hydrophobic model of amino acids on a two-dimensional grid coordinate system.
4."(2) the DSGA is better than a traditional GA and better able to derive the correct folding pattern of a protein.” Similarly to the statement in the Conclusion section and above, this statement must be qualified to fall within the scope of their study. The results do not support the unqualified statement that “DSGA is better than a traditional GA”. The protein folding problem presented in the paper and used to compare DSGA to traditional GA is only a single, very specific optimization problem. This single specific optimization problem cannot be used to make the general statement that “DSGA is better than traditional GA”. It is unclear what the authors are comparing DSGA to when they state that DSGA is “…better able to derive the correct folding pattern of a protein”. Also, the authors need to specify how they measure “better” and qualify that the “folding pattern of a protein” is represented by a hydrophilic-hydrophobic model of amino acids on a two-dimensional grid coordinate system. The authors must clarify that “a protein” is a specific twenty amino acid sequence. The appropriate conclusion the results support is that, using the authors’ model of protein folding and their fitness function to score conformations, DSGA produces conformations that score better than a traditional GA on a specific amino acid sequence with length of twenty amino acids.

We understand the reviewer’s concerns here; however, the end result of the logic in these comments is that no one can ever really know if one algorithm is better than another since there will always be a condition that is left untested since it is impossible to test every protein and every condition. Here we show that some proteins create multi-optima problems (i.e. Figure 2), and we believe that the body of knowledge from Genetic Algorithms should encourage the use of Niche Genetic Algorithms. Our paper goes one step further and shows a test case in which, a NGA does a better job of solving the protein folding problem than a traditional GA.
It is well understood by the community that currently there is no algorithm that can solve the folding problem de novo for all proteins. Even the best de novo algorithms have a low overall success rate. Also 2D models are simplifications of the actual 3D models. With that being said it is common in this field of research to make statements that the review claims to be unfounded. Consider the following quotes.
Huang, C., Yang, X. & He, Z. (2010). Protein folding simulations of 2D HP model by the genetic algorithm based on optimal secondary structure, Computational Biology and Chemistry 34, pp 137-142.
“GAOSS would be an efficient tool for the protein structure predictions (PSP).”
Su, S., Lin, C. & Ting, C. (2011). An effective hybrid of hill climbing and genetic algorithm for 2D triangular protein structure prediction, Proteome Science 9(Suppl. 1).
“The simulation results show that ERS-GA and HHGA can successfully be applied to the problem of protein structure prediction. The satisfactory simulation results validate the effectiveness of the proposed algorithms”
Liang, F. and Wong, W. H. (2001). Evolutionary Monte Carlo for protein folding simulations, Journal of Chemical Physics 115(7), pp. 3374-3380.
“We showed that the evolutionary Monte Carlo algorithm can be effectively applied to simulations of protein folding on lattice models.”

That being said we also understand the spirit of the reviewer’s comments that we have analyzed a small number of protein sequences. Since we have analyzed more sequences we have now included that information as well. We have also revised the language of the conclusion section.

8.Similarly, the conclusions in the Abstract must be revised to fall within the scope of the experiments.
1.“DSGA is very adept at predicting the folded state of proteins”. Please see comments in 7.3. above.
2.“DSGA is better than a traditional GA in deriving the correct folding pattern of a protein”. Please see comments in 7.4. above.

Just as we have now modified the Conclusion section we have also modified the Abstract as well.

9.Lastly, the title must be revised to clarify the scope of the study:
1.“Niche Genetic Algorithms are better than traditional Genetic Algorithms for de novo Protein Folding.” The title must indicate the extent to which de novo protein folding is simplified: using a two-dimensional grid with a hydrophobic-hydrophilic amino acid model and binary scoring scheme. The title must also indicate the comparison between niche genetic algorithms and traditional genetic algorithms was made using a single specific niche genetic algorithm. Further, the title must indicate the two algorithms were compared using a single specific twenty-amino-acid sequence.

We are uncertain as to how all of the reviewer’s comments here can be included in a title or how it would improve the title. DSGA is a niche genetic algorithm and we have shown that it predicts the optimally folded configuration for a protein more reliably (i.e. performs better) than a traditional genetic algorithm. Since the title does not constitute an untrue statement we do not see a valid reason to change it in the reviewer’s comments. That being said we understand that the plural form of NGA might be confusing as we use one NGA in the manuscript. Therefore we have changed the title to “A Niche Genetic Algorithm is better than traditional genetic algorithms for de novo protein folding”.
Competing Interests: No competing interests were disclosed. Close
Report a concern

Comments on this article Comments (0)

Version 1

VERSION 1 PUBLISHED 07 Oct 2014

Open Peer Review

Reviewer Status

Reviewer Reports

	Invited Reviewers
	1	2
Version 1 07 Oct 14	read	read

Nathan Alexander, Case Western Reserve University, Cleveland, USA
Kenneth De Jong, George Mason University, Fairfax, USA

Comments on this article

All Comments(0)

Add a comment

Browse by related subjects

Back to all reports

Reviewer Report

29 Views

03 Jun 2015 | for Version 1

Kenneth De Jong, Department of Computer Science, George Mason University, Fairfax, VA, USA

29 Views Cite this report Responses(0)

Not Approved

My concern with this article in its current form is two-fold:

As a software tool article, the discussion seems quite dated. The field of Evolutionary Computation has moved well beyond discussions and/or demonstrations of the form XXX is better than a simple GA. In fact, almost everything is! From a software tool perspective, the key issue here is how one deals with multimodal fitness landscapes. Various forms of nicheing GAs have been developed for this purpose since the 1980s. Additionally, other approaches such as embedding internal restart mechanisms have been developed and studied. To be of interest in 2015, the authors need to compare their approach with state-of-the-art alternatives.
The particular application chosen is an important one, but the discussion also seems quite dated. The bioinformatics community has moved well beyond the simple hydrophobic-hydrophilic and on-lattice models used in this paper. To offer a credible tool to this community, one again has to do so in the context of the current state of the art. See, for example, Zhang Y (2008), or Liu J et al. (2013).

Competing Interests

No competing interests were disclosed.

Respond to this report

Responses (0)

Back to all reports

Reviewer Report

36 Views

30 Apr 2015 | for Version 1

Nathan Alexander, Department of Pharmacology, Case Western Reserve University, Cleveland, OH, USA

36 Views Cite this report Responses(1)

Not Approved

It is unclear until examination of Figure 1 what configurations on the grid are considered “adjacent” (i.e. are amino acids diagonally placed to one another considered adjacent?).
The authors refer to their fitness function as calculating the free energy of the protein. However, they give no data of how their fitness function quantitatively relates to free energy. Therefore, the authors must not refer to “free energy”, but should use terms such as “fitness function” or “score”. This would also remove the discrepancy that the authors refer to free energy, but large positive values resulting from their method indicate success. The authors include twice the explanation that positive values resulting from their method should be interpreted as negative values of free energy, and negative values resulting from their method should be interpreted as positive values of free energy. This explanation will be unnecessary and it will be easier for the reader to understand the results, which provides readability incentive in addition to the scientific necessity for the authors to remove the use of the term “free energy”.
As this is submitted as a Software Tool Article, in the Materials and Methods section, the authors should give explanations and any related references for what is happening in steps six through thirteen in their implementation of the DSGA pseudo-code in Table 1.
The authors should provide a reference for the basis of their traditional GA implementation.
In the Results section, the purpose of Figure 1 and the purpose of the description of the four amino acid protein are unclear. Does it demonstrate that with only four amino acids there already exist multiple optima? If so, a plot similar to Figure 2 should be shown. Is it just to give a simple demonstrative example of the model for protein folding? If so, it should not fall under the heading of “Multioptimum problem”.
The title for Figure 2 should be revised because the use of the word “methods” is ambiguous.
In the Conclusions section, the authors claim that “…DSGA, which is specialized for multiple optima domains, produces better results than a traditional GA”. This statement must be qualified to fall within the scope of their study: using their model of protein folding, DSGA “produces better results than a traditional GA” on one twenty-amino-acid sequence. The authors must specify what they mean when they say “better results”. Perhaps, they mean “configurations with higher fitness function values”. Within the constraints of their model for protein folding, the scope of the study could be broadened by testing amino acid sequences with shorter and larger length and differing hydrophobic and hydrophilic composition. This could for example demonstrate at what length is traditional GA successful and at what length does DSGA fail.

Similarly, the results and conclusions summarized in the last paragraph of the Introduction must be revised to fall within the scope of the experiments. Specifically:
1. “Here we show that protein folding is a multi-optima problem…” The authors need to change the wording to reflect the scope of their study. The authors only show that a simple model of protein folding produces a multi-optima problem. The authors could state that protein folding is a multi-optima problem and provide a reference, and then state that they show a simple model recapitulates the multi-optima nature of the problem.
2. “…and as a result NGAs are better suited for a solution.” Is this the authors’ hypothesis? The authors should clarify their hypothesis and make it clear when they are stating their hypothesis. Are the authors attempting to show NGAs are “better suited” due to the problem having multiple optima? Are they only trying to show NGAs are “better suited”? The use of the phrase “…as a result…” suggests the former. However, the experiments performed suggest the latter ‑ that the authors are hypothesizing only about the performance of DSGA versus traditional GA. The experiments and results don’t provide any evidence as to what could be the reason for the performance difference. The authors perform no experiments to test whether the improved performance is due to an ability to overcome multi-optima ‑ such as a control experiment utilizing a single-optimum problem or sequence. When clarifying their hypothesis, the authors must specify in relation to what are NGAs better than. The hypothesis should not refer to the general class of NGAs, when only a single specific type, DSGA, is tested. Further, the authors need to define how they quantitatively measure “better suited”. Lastly, the authors need to define what they mean by “solution”.
3. “(1) the DSGA is very adept at predicting the folded state of proteins, which was shown by selecting a 20 amino acid protein and modeling all the folds and all possible combinations;” The results do not provide evidence to support this conclusion. The results cannot show DSGA is “very adept” because the authors do not specify a quantitative measure by which “very adept” is defined, so there is no way to conclude this. Additionally, the ability of DSGA to successfully optimize the conformation of a single twenty amino acid sequence cannot be extrapolated to mean that DSGA can successfully optimize the conformation of amino acid sequences in general. Further, the phrase “folded state of proteins” must be qualified to fall within the scope of the study; specifically, that the folded state of a protein in the study is represented by a hydrophilic-hydrophobic model of amino acids on a two-dimensional grid coordinate system.
4. "(2) the DSGA is better than a traditional GA and better able to derive the correct folding pattern of a protein.” Similarly to the statement in the Conclusion section and above, this statement must be qualified to fall within the scope of their study. The results do not support the unqualified statement that “DSGA is better than a traditional GA”. The protein folding problem presented in the paper and used to compare DSGA to traditional GA is only a single, very specific optimization problem. This single specific optimization problem cannot be used to make the general statement that “DSGA is better than traditional GA”. It is unclear what the authors are comparing DSGA to when they state that DSGA is “…better able to derive the correct folding pattern of a protein”. Also, the authors need to specify how they measure “better” and qualify that the “folding pattern of a protein” is represented by a hydrophilic-hydrophobic model of amino acids on a two-dimensional grid coordinate system. The authors must clarify that “a protein” is a specific twenty amino acid sequence. The appropriate conclusion the results support is that, using the authors’ model of protein folding and their fitness function to score conformations, DSGA produces conformations that score better than a traditional GA on a specific amino acid sequence with length of twenty amino acids.
Similarly, the conclusions in the Abstract must be revised to fall within the scope of the experiments.
1. “DSGA is very adept at predicting the folded state of proteins”. Please see comments in 7.3. above.
2. “DSGA is better than a traditional GA in deriving the correct folding pattern of a protein”. Please see comments in 7.4. above.
Lastly, the title must be revised to clarify the scope of the study:
1. “Niche Genetic Algorithms are better than traditional Genetic Algorithms for de novo Protein Folding.” The title must indicate the extent to which de novo protein folding is simplified: using a two-dimensional grid with a hydrophobic-hydrophilic amino acid model and binary scoring scheme. The title must also indicate the comparison between niche genetic algorithms and traditional genetic algorithms was made using a single specific niche genetic algorithm. Further, the title must indicate the two algorithms were compared using a single specific twenty-amino-acid sequence.

Competing Interests

No competing interests were disclosed.

Respond to this report

Responses (1)

Author Response F1000Research Advisory Board Member

28 May 2015

James Coker, Johns Hopkins University, Baltimore, USA

We thank the reviewer for his time and review of our work. Since there is currently only one review submitted (7 months after submission) we have decided to hold off on making adjustments to the manuscript until we hear back from other reviewers. That being said we have mentioned possible revisions in our responses below and will incorporate them based on the responses from other reviewers. Below we have cut and pasted the reviewer’s comments (numbered) and our responses to each.

1. It is unclear until examination of Figure 1 what configurations on the grid are considered “adjacent” (i.e. are amino acids diagonally placed to one another considered adjacent?).

The use of the term “adjacent” in HP models has been established for over 25 years. It refers to residues that are directly left, right, up, or down (not diagonal) from a particular amino acid that is not neighboring, i.e. the previous or next amino acid (n-1 or n+1). We understand that this can be confusing for a reader unfamiliar with the field. Therefore we have made a slight modification in the “Fitness Function” section, which is the first mention of adjacent amino acids. Here we mention that these terms have been defined and used previously and list two references so readers unfamiliar with the field can learn more.

2. The authors refer to their fitness function as calculating the free energy of the protein. However, they give no data of how their fitness function quantitatively relates to free energy. Therefore, the authors must not refer to “free energy”, but should use terms such as “fitness function” or “score”. This would also remove the discrepancy that the authors refer to free energy, but large positive values resulting from their method indicate success. The authors include twice the explanation that positive values resulting from their method should be interpreted as negative values of free energy, and negative values resulting from their method should be interpreted as positive values of free energy. This explanation will be unnecessary and it will be easier for the reader to understand the results, which provides readability incentive in addition to the scientific necessity for the authors to remove the use of the term “free energy”.

The use of the term ‘Free Energy’ is widely accepted in this field using the conditions we have set. See reference # 26 (Huang et al.), as well as F. Liang and W. H. Wong, J.: Chem. Phys. 2001; 115: 3374, Lau and Dill: Macromolecules. 1989: 3986-3997 (just to name a few over the past 25 years). As a result, we decided to keep the term “Free Energy” in the manuscript to be consistent with previous work.
We understand that the positive values resulting from the DSGA can be confusing as positive Free Energy values correspond with a lack of spontaneous folding, which is why, as the reviewer pointed out, we twice mention that the positive results from the DSGA should be interpreted as negative values. We do understand the reviewer’s concerns. Therefore we have removed the reference to the fact that the DSGA returns values of the opposite sign in the text of the manuscript and have kept the correctly reported values. We have moved the explanation of the negative/positive values from the DSGA to the two supplementary files. In this way the reading of the manuscript will be clear and for those that choose to use the program it will be clear how it functions and how to interpret the results.

3. As this is submitted as a Software Tool Article, in the Materials and Methods section, the authors should give explanations and any related references for what is happening in steps six through thirteen in their implementation of the DSGA pseudo-code in Table 1.

Steps six to thirteen basically show the portions of Dynamic-radius Species-conserving Genetic Algorithm that make it separate from a genetic algorithm. These steps include: the generation of seeds, a Tabu List, and manipulating the Tabu List and generating its final version. All of these are already explained in the Materials and Methods section and well cited. Therefore it seems redundant to put this information in Table 1.
As a result we have altered Table 1 to direct the reader to the relevant section of the Materials and Methods section, etc. where further explanations/references about each step can be found.

4. The authors should provide a reference for the basis of their traditional GA implementation.

We are a little uncertain as to what the reviewer is referring to here. References 16, 17, and 18 are related to Genetic Algorithms and their traditional application in sequence alignment and protein structure prediction. References 16 and 27 are in the manuscript as they are two of the most commonly sited references in relation to Genetic Algorithms.

5. In the Results section, the purpose of Figure 1 and the purpose of the description of the four amino acid protein are unclear. Does it demonstrate that with only four amino acids there already exist multiple optima? If so, a plot similar to Figure 2 should be shown. Is it just to give a simple demonstrative example of the model for protein folding? If so, it should not fall under the heading of “Multioptimum problem”.

The reason Figure 1 is present in the manuscript is to provide a clear and relatively simple example of the output of the DSGA. This figure was placed where it is to serve as an introduction and explanation to the Multioptimum problem. We do not contend or intend to suggest that every protein will have a multi-optima folding method, just the opposite. Clearly the protein in Figure 1 does not have multi-optima.

6. The title for Figure 2 should be revised because the use of the word “methods” is ambiguous.

The title of Figure 2 has been changed to ‘Free Energy for all possible folded forms of HPPHPPHPPH’.

7. In the Conclusions section, the authors claim that “…DSGA, which is specialized for multiple optima domains, produces better results than a traditional GA”. This statement must be qualified to fall within the scope of their study: using their model of protein folding, DSGA “produces better results than a traditional GA” on one twenty-amino-acid sequence. The authors must specify what they mean when they say “better results”. Perhaps, they mean “configurations with higher fitness function values”. Within the constraints of their model for protein folding, the scope of the study could be broadened by testing amino acid sequences with shorter and larger length and differing hydrophobic and hydrophilic composition. This could for example demonstrate at what length is traditional GA successful and at what length does DSGA fail.

Similarly, the results and conclusions summarized in the last paragraph of the Introduction must be revised to fall within the scope of the experiments. Specifically:
1.“Here we show that protein folding is a multi-optima problem…” The authors need to change the wording to reflect the scope of their study. The authors only show that a simple model of protein folding produces a multi-optima problem. The authors could state that protein folding is a multi-optima problem and provide a reference, and then state that they show a simple model recapitulates the multi-optima nature of the problem.
2.“…and as a result NGAs are better suited for a solution.” Is this the authors’ hypothesis? The authors should clarify their hypothesis and make it clear when they are stating their hypothesis. Are the authors attempting to show NGAs are “better suited” due to the problem having multiple optima? Are they only trying to show NGAs are “better suited”? The use of the phrase “…as a result…” suggests the former. However, the experiments performed suggest the latter ‑ that the authors are hypothesizing only about the performance of DSGA versus traditional GA. The experiments and results don’t provide any evidence as to what could be the reason for the performance difference. The authors perform no experiments to test whether the improved performance is due to an ability to overcome multi-optima ‑ such as a control experiment utilizing a single-optimum problem or sequence. When clarifying their hypothesis, the authors must specify in relation to what are NGAs better than. The hypothesis should not refer to the general class of NGAs, when only a single specific type, DSGA, is tested. Further, the authors need to define how they quantitatively measure “better suited”. Lastly, the authors need to define what they mean by “solution”.
3. “(1) the DSGA is very adept at predicting the folded state of proteins, which was shown by selecting a 20 amino acid protein and modeling all the folds and all possible combinations;” The results do not provide evidence to support this conclusion. The results cannot show DSGA is “very adept” because the authors do not specify a quantitative measure by which “very adept” is defined, so there is no way to conclude this. Additionally, the ability of DSGA to successfully optimize the conformation of a single twenty amino acid sequence cannot be extrapolated to mean that DSGA can successfully optimize the conformation of amino acid sequences in general. Further, the phrase “folded state of proteins” must be qualified to fall within the scope of the study; specifically, that the folded state of a protein in the study is represented by a hydrophilic-hydrophobic model of amino acids on a two-dimensional grid coordinate system.
4."(2) the DSGA is better than a traditional GA and better able to derive the correct folding pattern of a protein.” Similarly to the statement in the Conclusion section and above, this statement must be qualified to fall within the scope of their study. The results do not support the unqualified statement that “DSGA is better than a traditional GA”. The protein folding problem presented in the paper and used to compare DSGA to traditional GA is only a single, very specific optimization problem. This single specific optimization problem cannot be used to make the general statement that “DSGA is better than traditional GA”. It is unclear what the authors are comparing DSGA to when they state that DSGA is “…better able to derive the correct folding pattern of a protein”. Also, the authors need to specify how they measure “better” and qualify that the “folding pattern of a protein” is represented by a hydrophilic-hydrophobic model of amino acids on a two-dimensional grid coordinate system. The authors must clarify that “a protein” is a specific twenty amino acid sequence. The appropriate conclusion the results support is that, using the authors’ model of protein folding and their fitness function to score conformations, DSGA produces conformations that score better than a traditional GA on a specific amino acid sequence with length of twenty amino acids.

We understand the reviewer’s concerns here; however, the end result of the logic in these comments is that no one can ever really know if one algorithm is better than another since there will always be a condition that is left untested since it is impossible to test every protein and every condition. Here we show that some proteins create multi-optima problems (i.e. Figure 2), and we believe that the body of knowledge from Genetic Algorithms should encourage the use of Niche Genetic Algorithms. Our paper goes one step further and shows a test case in which, a NGA does a better job of solving the protein folding problem than a traditional GA.
It is well understood by the community that currently there is no algorithm that can solve the folding problem de novo for all proteins. Even the best de novo algorithms have a low overall success rate. Also 2D models are simplifications of the actual 3D models. With that being said it is common in this field of research to make statements that the review claims to be unfounded. Consider the following quotes.
Huang, C., Yang, X. & He, Z. (2010). Protein folding simulations of 2D HP model by the genetic algorithm based on optimal secondary structure, Computational Biology and Chemistry 34, pp 137-142.
“GAOSS would be an efficient tool for the protein structure predictions (PSP).”
Su, S., Lin, C. & Ting, C. (2011). An effective hybrid of hill climbing and genetic algorithm for 2D triangular protein structure prediction, Proteome Science 9(Suppl. 1).
“The simulation results show that ERS-GA and HHGA can successfully be applied to the problem of protein structure prediction. The satisfactory simulation results validate the effectiveness of the proposed algorithms”
Liang, F. and Wong, W. H. (2001). Evolutionary Monte Carlo for protein folding simulations, Journal of Chemical Physics 115(7), pp. 3374-3380.
“We showed that the evolutionary Monte Carlo algorithm can be effectively applied to simulations of protein folding on lattice models.”

That being said we also understand the spirit of the reviewer’s comments that we have analyzed a small number of protein sequences. Since we have analyzed more sequences we have now included that information as well. We have also revised the language of the conclusion section.

8.Similarly, the conclusions in the Abstract must be revised to fall within the scope of the experiments.
1.“DSGA is very adept at predicting the folded state of proteins”. Please see comments in 7.3. above.
2.“DSGA is better than a traditional GA in deriving the correct folding pattern of a protein”. Please see comments in 7.4. above.

Just as we have now modified the Conclusion section we have also modified the Abstract as well.

9.Lastly, the title must be revised to clarify the scope of the study:
1.“Niche Genetic Algorithms are better than traditional Genetic Algorithms for de novo Protein Folding.” The title must indicate the extent to which de novo protein folding is simplified: using a two-dimensional grid with a hydrophobic-hydrophilic amino acid model and binary scoring scheme. The title must also indicate the comparison between niche genetic algorithms and traditional genetic algorithms was made using a single specific niche genetic algorithm. Further, the title must indicate the two algorithms were compared using a single specific twenty-amino-acid sequence.

We are uncertain as to how all of the reviewer’s comments here can be included in a title or how it would improve the title. DSGA is a niche genetic algorithm and we have shown that it predicts the optimally folded configuration for a protein more reliably (i.e. performs better) than a traditional genetic algorithm. Since the title does not constitute an untrue statement we do not see a valid reason to change it in the reviewer’s comments. That being said we understand that the plural form of NGA might be confusing as we use one NGA in the manuscript. Therefore we have changed the title to “A Niche Genetic Algorithm is better than traditional genetic algorithms for de novo protein folding”.

View more View less

Competing Interests

No competing interests were disclosed.

Alongside their report, reviewers assign a status to the article:

Approved - the paper is scientifically sound in its current form and only minor, if any, improvements are suggested

Approved with reservations - A number of small changes, sometimes more significant revisions are required to address specific details and improve the papers academic merit.

Not approved - fundamental flaws in the paper seriously undermine the findings and conclusions

[1] 1. Teich M, Needham DM: in A Documentary History of Biochemistry, 1770–1940. (Rutherford, NJ : Fairleigh Dickinson University Press). 1992. Reference Source

[2] 2. Khoury GA, Smadbeck J, Kieslich CA, et al.: Protein folding and de novo protein design for biotechnological applications. Trends Biotechnol. 2014; 32(2): 99–109. PubMed Abstract | Publisher Full Text | Free Full Text

[3] 3. Dill KA, MacCallum JL: The protein-folding problem, 50 years on. Science. 2012; 338(6110): 1042–1046. PubMed Abstract | Publisher Full Text

[4] 4. Foster DP, Pinettes C: Statistical mechanics of the two-dimensional hydrogen-bonding self-avoiding walk including solvent effects. Phys Rev E Stat Nonlin Soft Matter Phys. 2008; 77(2 Pt 1): 021115. PubMed Abstract | Publisher Full Text

[5] 5. Unger R, Moult J: Genetic algorithms for protein folding simulations. J Mol Bio. 1993; 231(1): 75–81. PubMed Abstract | Publisher Full Text

[6] 6. Alberts B, Johnson A, Lewis J, et al.: Molecular Biology of the Cell, Fifth Edition. (Garland Science). 2007. Reference Source

[7] 7. Jung J, Han KY, Koh HR, et al.: Effect of single-base mutation on activity and folding of 10–23 deoxyribozyme studied by three-color single-molecule ALEX FRET. J Phys Chem B. 2012; 116(9): 3007–12. PubMed Abstract | Publisher Full Text

[8] 8. Coontz R, Fahrekamp-Uppenbrink J, Lavine M, et al.: Going from Strength to Strength. Science. 2014; 343(6175): 1091. PubMed Abstract | Publisher Full Text

[9] 9. Marion D: An introduction to biological NMR spectroscopy. Mol Cell Proteomics. 2013; 12(11): 3006–25. PubMed Abstract | Publisher Full Text | Free Full Text

[10] 10. Henen MA, Coudevylle N, Geist L, et al.: Toward rational fragment-based lead design without 3D structures. J Med Chem. 2012; 55(17): 7909–19. PubMed Abstract | Publisher Full Text | Free Full Text

[11] 11. Pantazes RJ, Grisewood MJ, Maranas CD: Recent advances in computational protein design. Curr Opin Struct Biol. 2011; 21(4): 467–72. PubMed Abstract | Publisher Full Text

[12] 12. Durand P, Lehn P, Callebaut I, et al.: Active-site motifs of lysosomal acid hydrolases: invariant features of clan GH-A glycosyl hydrolases deduced from hydrophobic cluster analysis. Glycobiology. 1997; 7(2): 277–84. PubMed Abstract | Publisher Full Text

[13] 13. Anfinsen CB: Principles that govern the folding of protein chains. Science. 1973; 181(4096): 223–230. PubMed Abstract | Publisher Full Text

[14] 14. Martí-Renom MA, Stuart AC, Fiser A, et al.: Comparative protein structure modeling of genes and genomes. Annu Rev Biophys Biomol Struct. 2000; 29: 291–325. PubMed Abstract | Publisher Full Text

[15] 15. Kaczanowski S, Zielenkiewicz P: Why similar protein sequences encode similar three-dimensional structures? Theor Chem Acc. 2009; 125(3–6): 643–50. Publisher Full Text

[16] 16. Mitchell M: in An Introduction to Genetic Algorithms. (Cambridge, MA: MIT Press). 1996. Reference Source

[17] 17. Wang C, Lefkowitz EJ: Genomic multiple sequence alignments: refinement using a genetic algorithm. BMC Bioinformatics. 2005; 6: 200. PubMed Abstract | Publisher Full Text | Free Full Text

[18] 18. Ahn N, Park S: Finding an upper bound for the number of contacts in hydrophobic-hydrophilic protein structure prediction model. J Comput Biol. 17(4): 647–56. PubMed Abstract | Publisher Full Text

[19] 19. Holland JH: in Adaptation in Natural and Artificial Systems. (Ann Arbor, MI: University of Michigan Press). 1975. Reference Source

[20] 20. Brown MS: A Species-Conserving Genetic Algorithm for Multimodal Optimization (Doctoral dissertation). Available from Dissertations and Theses database. (UMI No. 3433233). 2010. Reference Source

[21] 21. Brown MS, Pelsoi MJ, Dirska H: Dynamic-Radius Species-Conserving Genetic Algorithm for the Financial Forecasting of Dow Jones Index Stocks. Machine Learning and Data Mining in Pattern Recognition. Ed. P. Perner (Berlin: Springer). 2013; 7988: 27–41. Publisher Full Text

[22] 22. De Jong KA: An analysis of the behavior of a class of genetic adaptive systems. (Doctoral dissertation, University of Michigan). Diss Abstr Int. 1975; 36(10): 5140B. (University Microfilms No. 76–9381). Reference Source

[23] 23. Ling Q, Wa G, Yang Z, et al.: Crowding clustering genetic algorithm for multimodal function optimization. Appl Soft Comput. 2008; 8(1): 88–95. Publisher Full Text

[24] 24. Li JP, Balazs ME, Parks GT, et al.: A species conserving genetic algorithm for multimodal function optimization. Evol Comput. 2002; 10(3): 207–234. PubMed Abstract | Publisher Full Text

[25] 25. Glover F: Tabu Search – Part I. ORSA Journal on Computing. 1989; 1(3): 190–206. Publisher Full Text

[26] 26. Bremermann HJ: The Evolution of Intelligence: The Nervous System as a Model of its Environment. (Technical Report, No.1, Contract No. 477, Issue 17). Seattle WA: Department of Mathematics, University of Washington. 1958. Reference Source

[27] 27. Huang C, Yang X, He Z: Protein folding simulations of 2D HP model by the genetic algorithm based on optimal secondary structures. Comput Biol Chem. 2010; 34(3): 137–142. PubMed Abstract | Publisher Full Text

[28] 28. Su SC, Lin CJ, Ting CK: An effective hybrid of hill climbing and genetic algorithm for 2D triangular protein structure prediction. Proteome Sci. 2011; 9(Suppl 1): S19. PubMed Abstract | Publisher Full Text | Free Full Text

[29] 29. Jiang T, Cui Q, Shi G, et al.: Protein folding simulations of the hydrophobic-hydrophilic model by combing tabu search with genetic algorithms. J Chem Phys. 2003; 119(8) 4592–4596. Publisher Full Text

[30] 30. Brown M, Bennett T, Coker JA: DSGA and GA from ‘Niche Genetic Algorithms are better than traditional Genetic Algorithms for de novo Protein Folding’ Zenodo. 2014. Data Source

Trial	DSGA	GA	GA Running Same Amount of Time
1	9	4	3
2	9	4	3
3	9	4	4
4	9	4	5
5	9	2	4
6	9	3	3
7	9	3	3
8	9	3	3
9	9	3	4
10	9	4	3
11	9	3	4
12	9	3	3
13	9	3	3
14	9	3	4
15	9	2	3

Trial	DSGA	GA	GA Running Same Amount of Time
1	9	4	3
2	9	4	3
3	9	4	4
4	9	4	5
5	9	2	4
6	9	3	3
7	9	3	3
8	9	3	3
9	9	3	4
10	9	4	3
11	9	3	4
12	9	3	3
13	9	3	3
14	9	3	4
15	9	2	3

Niche Genetic Algorithms are better than traditional Genetic Algorithms for de novo Protein Folding

Abstract

Introduction

Table 1. GA vs. DSGA Pseudo-code.

Materials and methods

Seed Selection method

Generating the Tabu List

Distance measurement

Fitness function

Model for folding

Keep Going

System requirements and input/output data

Results

Multioptimum problem

Figure 1. 0121 Folding of HPHPP.

Figure 2. Free Energy for all methods to fold HPPHPPHPPH.

Figure 3. Correct Folding of HPPHPPHPPH.

Compare Traditional Genetic Algorithm to Niche Genetic Algorithm

Table 2. Parameter Values.

Table 3. Results of DSGA and GA attempting to fold HPHPPHHPHPPHPHHPPHPH.

Conclusion

Software availability

Archived source code as at the time of publication

Software license

Author contributions

Competing interests

Grant information

Acknowledgements

Supplementary material

References

Comments on this article Comments (0)

Open Peer Review

Comments on this article Comments (0)

Open Peer Review

Reviewer Status

Reviewer Reports

Comments on this article

Browse by related subjects

Competing Interests Policy

Stay Updated

Trial	DSGA	GA	GA Running Same Amount of Time
1	9	4	3
2	9	4	3
3	9	4	4
4	9	4	5
5	9	2	4
6	9	3	3
7	9	3	3
8	9	3	3
9	9	3	4
10	9	4	3
11	9	3	4
12	9	3	3
13	9	3	3
14	9	3	4
15	9	2	3