Semi-automated Modular Program Constructor for physiological modeling: Building cell and organ models

Bartholomew Jardine; Gary M. Raymond; James B. Bassingthwaighte

doi:10.12688/f1000research.7476.1

Home Browse Semi-automated Modular Program Constructor for physiological modeling:...

ALL Metrics

Views

Downloads

Get PDF

Get XML

Export

▬

✚

Software Tool Article

Semi-automated Modular Program Constructor for physiological modeling: Building cell and organ models

[version 1; peer review: 1 approved with reservations]

Bartholomew Jardine¹, Gary M. Raymond¹, James B. Bassingthwaighte¹

PUBLISHED 16 Dec 2015

Author details Author details

¹ Department of Bioengineering, University of Washington, Seattle, WA, 98195, USA

OPEN PEER REVIEW

REVIEWER STATUS

Abstract

The Modular Program Constructor (MPC) is an open-source Java based utility, built upon JSim's Mathematical Modeling Language (MML) (http://www.physiome.org/jsim/) that uses directives embedded in model code to construct larger, more complicated models quickly and with less error than manually combining models. A major obstacle in writing complex programs for modeling physiological processes is the large amount of time it takes to code the myriad processes taking place simultaneously in cells, tissues, and organs. MPC replaces this task by code-generating algorithms that take the code from several different modules and produce model code for a new JSim model. This is particularly useful during multi-scale model development where many variants are to be configured and tested against data. MPC is implemented in Java and requires JSim to use its output. MPC source code and documentation are available at http://www.physiome.org/software/MPC/.

Keywords

multi-scale modeling, JSim, systems biology, physiological modeling, reproducibility, uncertainty quantification

Corresponding author: Bartholomew Jardine

Competing interests: The authors declared no competing interests.

Grant information: Research has been supported by NIH grants HL088516 (J.B. Bassingthwaighte) and HL073598 (J.B. Bassingthwaighte), BE08417 (J.B. Bassingthwaighte), the Virtual Physiological Rat program GM094503 (PI: D.A. Beard), and the Cardiac Energy Grid HL199122 (PI: J.B. Bassingthwaighte).
The funders had no role in study design, data collection and analysis, decision to publish, or preparation of the manuscript.

Copyright: © 2015 Jardine B et al. This is an open access article distributed under the terms of the Creative Commons Attribution License, which permits unrestricted use, distribution, and reproduction in any medium, provided the original work is properly cited.

How to cite: Jardine B, Raymond GM and Bassingthwaighte JB. Semi-automated Modular Program Constructor for physiological modeling: Building cell and organ models [version 1; peer review: 1 approved with reservations]. F1000Research 2015, 4:1461 (https://doi.org/10.12688/f1000research.7476.1) First published: 16 Dec 2015, 4:1461 (https://doi.org/10.12688/f1000research.7476.1) Latest published: 16 Jun 2016, 4:1461 (https://doi.org/10.12688/f1000research.7476.3)

Introduction

Many attempts have been made to provide modular programming systems for physiological applications (Erson et al., 2012; Krause et al., 2010; Mirschel et al., 2009; Smith et al., 2009). We describe our system as a semi-automated modular programming construction. It is simple and not conceptually novel, but is easy to learn and use. For developing a series of models of increasing complexity, Modular Program Constructor (MPC) can serve well as the basis of the modeling code. The perspective is to take a modular approach; this means that for multi-scale modeling one builds from simple elements initially and then uses multi-modular constructs as modules in higher level systems.

In MPC, a module can be any set of variable declarations, parameter declarations and mathematical equations that represent a process. This broad definition of a module has a broad variety of applications: from a simple first order enzyme reaction, to a complete model of coronary blood flow through heart muscle, which can then be incorporated into a yet larger systemic model.

Based on ModelBuilder, which used FORTRAN to parse code and define directives (Raymond, 2008), we designed the current version in Java and renamed it MPC. It is now refined, simplified, robust, and used to develop several new applications (Raymond et al., 2011; Raymond et al., 2012). The models include time-dependent two-dimensional models in both Cartesian and cylindrical coordinates (Raymond et al., 2011; Raymond et al., 2012), as well as whole organ models with heterogeneous flow re-implementing earlier complex whole organ models of substrate metabolism (Bassingthwaighte et al., 1989).

Methods

MPC implementation

MPC is a pre-compiler written in Java. It reads a text input file, parses the file for directives, and generates a text output file based on those directives. MPC is built upon the Mathematical Modeling Language (MML) of JSim (http://www.physiome.org/jsim/) (Butterworth et al., 2014). It has been designed to work with JSim's MML and currently requires JSim to run the model output file that MPC produces. Through JSim, the final constructed model can be exported into Systems Biology Markup Language (SBML, http://sbml.org/Main_Page), CellML (https://www.cellml.org/), and downloaded from these sources to other simulation platforms (Smith et al., 2014). MPC currently is executed as command line utility and requires the Java runtime environment (https://java.com/).

MPC has three components:

1. MML, the mathematical modeling language of JSim, is a declarative language designed for solving all the equations simultaneously; it is not procedural. MML is used for declaring parameters and variables, for defining algebraic equations, ordinary differential equations, and partial differential equations with their associated constraints, and initial and boundary conditions.
2. Modules, are sets of MML code libraries which are variable declarations, parameter declarations, or mathematical equations for a particular process, for example, flow along a capillary, diffusion within a region, a chemical reaction, transport across a membrane, or even a whole organ. These are archived, forming libraries of operational code. This allows the user to generate multi-scale models with different sub-models to use in testing a hypothesis against data, i.e. validity testing. For example, there have been a variety of models developed to describe the transmembrane sodium pump, NaKATPase which uses ATP to pump sodium out of, and potassium into, the cell. All of these models have the same essential external influences: the Na and K ion concentrations and the transmembrane electrical potential. Having a library of the MML code for the variant modules allows one to insert one's choice quickly into the template for the cell model. Changing combination(s) rapidly to match solutions with experimental results is invaluable for the early phases of developing alternative hypotheses.
3. Directives, the third component, comprises the set of instructions used by the MPC program to select processes and gather the code from existing modules, renaming parameters and variables to reflect the new purposes for which they will function, and automatically combining the mathematical structures into new structures. The directives control the identification, fetching and relabeling of variables and parameters, and the assembly and recombination of code into new equations. All MPC directives start with '//%'.

Selecting and arranging components using directives – A simple example

The MPC input file guides the construction of a model made of previously existing modules. It combines MML with “directives” embedded as comments. It uses code from other JSim model files that have been annotated so that they can be read by MPC, yet without interfering with their operability. MPC may also combine models with other models or with modules of preconstructed code from libraries. These modules are specified within a library with the START and END directive. A library with a few elementary operators from which we will build a model in out next step is illustrated below:

CodeLibrary.mod:

//------------------------- ODE DOMAINS
//%START     odeDomains     // START...END directives used to specify a module.
realDomain t s; t.min=0; t.max=16; t.delta = 0.1;
//%END     odeDomains
//------------------------- flowCalc
//%START      flowCalc
C:t = (F/V)*(Cin-C);
//%END       flowCalc
//------------------------- EXCHANGE CACULATIONS
//%START      exchangeCalc
C1:t = PS/V1*(C2-C1);    // Exchange between two compartments
C2:t = PS/V2*(C1-C2);
//%END           exchangeCalc
//------------------------- REACTION A->B
//%START     reactionCalc
real G = 5 ml/(g*min);   // Const reaction rate.
A:t = -G/V*A;
B:t = G/V*A;
//%END           reactionCalc
//------------------------- MM REACTION A->B
//%START    MMreactionCalc
real KmA =1.0 mM, VmaxA =2 umol/(g*min); // MM constant and max velocity of rxn
real G(t) ml/(g*min);    // MM reaction rate
G = (VmaxA/(KmA+A));
A:t = -G*(A)/V;
B:t =  G*(A)/V;
//%END       MmreactionCalc

In JSim's MML, the colon signifies the derivative: C:t means dC/dt. Within MPC we can write MML code directly or import code from operational JSim models that have been annotated to identify components. An example is a three species (A, B, C), two compartment model with two reactions in compartment two (Figure 1) with species concentrations described by ordinary differential equations (ODE). Species A enters, with flow F, a compartment with volume V1 and passive exchange between a second compartment with volume V2, where A reacts at rate GA2B to form B and B reacts with C at rate GB2C, a Michaelis-Menten reaction.

Figure 1. Two compartment, three species model (A, B, C) with volumes V₁, V₂, respectively.

A_in is A entering compartment 1 with flow F (No flow in for species B, C). Passive exchange between compartments for all three species and reactions only occur in compartment 2.

The MPC file defines the domain, parameters, variables, and initial conditions first. Using directives listed in ‘Example.mpc’, model code is extracted from the file ‘CodeLibrary.mod’ shown above. Values and variable names needing replacement throughout the final model are specified by the REPLACE directive along with the '%symbol%' placeholder. The use of the REPLACE, GET, COLLECT, INSERTSTART and INSERTEND directives are used in Example.mpc shown below:

Example.mpc:

//%REPLACE %CL% =("CodeLibrary.mod") // Library to get code from, replace all
                 // occurrences of %CL% with CodeLibrary.mod
//%REPLACE (%N%=(“1”,”2”), %vol%=("0.05","0.05")) // Two compartments with volumes, replace
    	      // all occurrences of %N% with 1,2 and %vol% with 0.05, 0.15
//%REPLACE (%AB%=("A","B","C") %PS3%=("6","5","4")) // 3 species, PS init values.
import nsrunit; unit conversion on; // Use SI units for this model.
math example {         // model declaration
// INDEPENDENT VARIABLES
//%GET %CL% odeDomains()   // Get odeDomains section from CodeLibrary.mod
//%INSERTSTART a2bParmsVars  // Specify params and vars section
// PARAMETERS
real Flow = 1 ml/(g*min);    // Flow rate
real PS%AB%12 = %PS3% ml/(g*min); // Conductances: PSA12,PSB12,PSC12
real V%N% = %vol% ml/g;	 // Volume of V1, V2
extern real %AB%in(t) mM; // Inflowing concentrations
// DEPENDENT VARIABLES
real %AB%%N%(t) mM;       // A1,A2,B1,B2,C1,C2
// INITIAL CONDITIONS (IC's)
when(t=t.min)  %AB%%N%=0;      // Defines IC's for the ODEs
//%INSERTEND a2bParmsVars      // End params and var sec
//%INSERTSTART a2bCalc      // Specify calc section
// ODE CALCULATIONS
//%GET %CL% reactionCalc ("A=A2","B=B2","V=V2","G=Ga2b") // A->B reaction
//%GET %CL% MMreactionCalc ("A=B2","B=C2","V=V2","G=Gb2c", // B ->C MM reaction
//% "KmA=KmB2",“VmaxA = VmaxB2", "KmA = KmB2")        // B ->C MM reaction continued
//%GET %CL% flowCalc ("Cin=%AB%in","C=%AB%1","V=V1","F=Flow","D=D%AB%1")
//%GET %CL% exchangeCalc ("C1=%AB%1","PS=PS%AB%12","C2=%AB%2")
//%COLLECT("%AB%%N%:t")     //Group all ODE calculations for a species together
//%INSERTEND a2bCalc
} // curly bracket ends model

The GET directive warrants further explanation: it identifies a code library file and module name within the library to insert into the model, and changes old names (names of parameters and variables in the module) to new model names. From the example above, //%GET %CL% reactionCalc ("A=A2","B=B2","V=V2","G=Ga2b") will get the module named 'reactionCalc' in file 'CodeLibrary.mod' and replace the variable names with the new model names ("A=A2", etc).

The MPC directives control the identification, fetching, relabeling of variables and parameters, and assembling and recombining code into new equations. The directives extract equations from files, changing the names of the module variables to application specific names and assemble the code into combined equations. The code resulting from these instructions provides a complete program (Example.mod), with no further intervention on the part of the user except to adjust parameters, solution time step length and set up graphics in JSim to display solutions, as shown in Figure 2.

Figure 2. Solution to two compartment model generated from MPC.

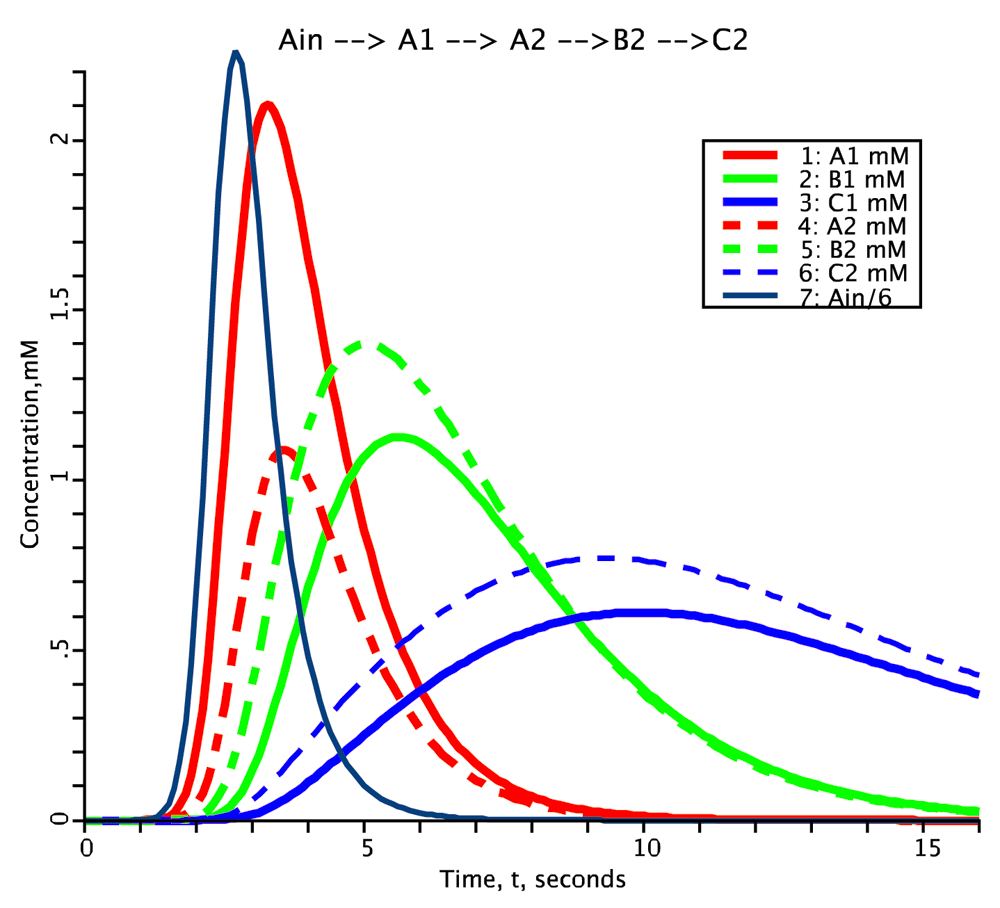
Species concentrations plotted as a function of time. Species A (red), B (green), C (blue). Compartment 1: solid line, Compartment 2: dashed line. External input for species A is A_in, the black solid line.

MPC Output - Example.mod:

import nsrunit; unit conversion on;   // Use cgs units
math example {           // model declaration
// INDEPENDENT VARIABLES
realDomain t s; t.min=0; t.max=16; t.delta = 0.1;
//%START a2bParmsVars        // Specify parameters and variables sect.
// PARAMETERS
real Flow = 1 ml/(g*min);   // Flow rate
real PSA12 = 6 ml/(g*min);  // Conductance
real PSB12 = 5 ml/(g*min);  // Conductance
real PSC12 = 4 ml/(g*min);  // Conductance
real V1 = 0.05 ml/g;        // Volume
real V2 = 0.05 ml/g;        // Volume
extern real Ain(t) mM;      // Inflowing concentration
extern real Bin(t) mM;      // Inflowing concentration, set to zero
extern real Cin(t) mM;      // Inflowing concentration, set to zero
// DEPENDENT VARIABLES
real A1(t) mM; real A2(t) mM; real B1(t) mM;
real B2(t) mM; real C1(t) mM; real C2(t) mM;
// INITIAL CONDITIONS (IC's)
when(t=t.min)  A1=0;
when(t=t.min)  A2=0;
when(t=t.min)  B1=0;
when(t=t.min)  B2=0;
when(t=t.min)  C1=0;
when(t=t.min)  C2=0;
//%END a2bParmsVars    // End parameters and variables section
//%START a2bCalc    // Specify calculations section
real Ga2b = 5 ml/(g*min);   // A ->B Const reaction rate.
real KmB2 =1.0 mM, VmaxB2 =2 umol/(g*min);// MM constant and max velocity of rxn
real Gb2c(t) ml/(g*min);      // B ->C MM reaction rate
Gb2c = (VmaxB2/(KmB2+B2));
// ODE CALCULATIONS
A2:t = -Ga2b/V2*A2 +PSA12/V2*(A1-A2);
B2:t = Ga2b/V2*A2 -Gb2c*(B2)/V2 +PSB12/V2*(B1-B2);
C2:t = Gb2c*(B2)/V2 +PSC12/V2*(C1-C2);
A1:t = (Flow/V1)*(Ain-A1) +PSA12/V1*(A2-A1);
B1:t = (Flow/V1)*(Bin-B1) +PSB12/V1*(B2-B1);
C1:t = (Flow/V1)*(Cin-C1) +PSC12/V1*(C2-C1);
//%END a2bCalc
} // curly bracket ends model

The process above is hardly worthwhile for small models but is highly efficient for larger models where flexibility in structure is desired. In the example above, converting the Ordinary Differential Equations (ODEs) to Partial Differential Equations (PDEs) requires a three line change. Addition of a new PDE e.g. for red blood cells in a capillary, takes four lines. For a five species, three region model, a three line change generates a 15 PDE model.

The small set of directives builds complex models from simple processes. MPC allows one to reliably reuse existing models in larger, multi-scale models. MPC encodes and preserves information about how a complex model is built from its modules allowing quick substitution of modules. The amount of actual code a user needs to write is reduced, especially for more complicated models. In MPC we have generated a full organ model with heterogeneity of flow, competitive transporters on the cell membranes, and reactions for multiple species (Bassingthwaighte et al., 2012) e.g. for adenosine processing in the heart. It is a 7-path, three region model that involves five species (adenosine, inosine, hypoxanthine, xanthine, and uric acid) in a sequential reaction chain. The model contains over 100 PDEs for convection, diffusion, and reactions.

Discussion

MPC and Uncertainty Quantification (UQ)

Though a MPC-generated model is checked for syntax and unit balance through JSim, verification is required: analytical solutions can be written into the code to match specific limiting cases, but otherwise one depends on testing for mass, charge, or energy balances. Validation requires testing against data, independent of the construction method. These are key steps toward reproducibility and the VVUQ process. (VVUQ = verify, validate, uncertainty quantification; the latter defining predictive accuracy.) MPC as is, depends on semantic consistency throughout the libraries and models used. Automated systems using ontologies will help craft models (Gennari et al., 2011), but the great efficiency of MPC for construction begins to show when there are many modules in series/parallel arrangements as in biochemical networks or circulatory or airway mechanical modeling. UQ includes uncertainty in inputs and parameters, readily handled by JSim's Monte Carlo analysis, and in model structure. Structural uncertainty, a major challenge, defines a major role for MPC: inserting different choices from amongst similar but differently functioning modules, into a large, multi-modular model, and solving the system many times with the variant constituents illustrating uncertainty in the projected outcomes.

Summary

A limited set of directives in MPC, our Modular Program Constructor, allows us to build complex models using small models for simple processes. MPC encodes and preserves information about how a complex model is built from its modules allowing the researcher to quickly substitute or update modules to validate a hypothesis. The amount of actual code a user needs to write is reduced, especially for more complicated models.

Future updates will improve collection and insertion of model code, better identify external module 'connections' for easier incorporation into larger models, and more intelligent reconciliation of similar code between modules. The long-term strategy is to integrate MPC within JSim allowing the user to take advantage of JSim's MML compiler and graphical user interface to quickly merge code with less user intervention.

Software availability

Software access

The Java code for MPC, the examples presented here, some more detailed examples, and instructions are available at http://www.physiome.org/software/MPC/.

Source code as at the time of publication

https://github.com/F1000Research/MPC/releases/tag/v1.0

Archived source code as at the time of publication

http://dx.doi.org/10.5281/zenodo.34208

Software license

MPC is released under a 3-clause ‘revised’ BSD license:

Developed by the National Simulation Resource

Department of Bioengineering, Box 355061

University of Washington, Seattle, WA 98195-5061.

Dr. J. B. Bassingthwaighte, Director

Redistribution and use in source and binary forms, with or without modification, are permitted provided that the following conditions are met:

* Redistributions of source code must retain the above copyright notice, this list of conditions and the following disclaimer.
* Redistributions in binary form must reproduce the above copyright notice, this list of conditions and the following disclaimer in the documentation and/or other materials provided with the distribution.
* Neither the name of the University of Washington nor the names of its contributors may be used to endorse or promote products derived from this software without specific prior written permission.

Data availability

MPC generated models for review at www.physiome.org are:

• Concentration profiles in capillary and tissue when exchange is diffusion-limited (http://www.physiome.org/jsim/models/webmodel/NSR/DiffusionLimitedProfiles/).
• ODE model of actin polymerization and depolymerization with tracking of bound nucleotide (http://www.physiome.org/jsim/models/webmodel/NSR/ActinCycle1/).
• Multiple tracer dilution estimates of D- and 2-deoxy-D-glucose uptake by the heart (http://www.physiome.org/jsim/models/webmodel/NSR/Kuikka1986BTEX30MP/).

Author contributions

Gary Raymond developed MPC. Bart Jardine currently maintains MPC source code and James Bassingthwaighte provides guidance and requirements for MPC development. All authors contributed to the design and organization of the paper and its writing and editing. All authors have seen and agreed to the final content of the manuscript.

Competing interests

The authors declared no competing interests.

Grant information

Research has been supported by NIH grants HL088516 (J.B. Bassingthwaighte) and HL073598 (J.B. Bassingthwaighte), BE08417 (J.B. Bassingthwaighte), the Virtual Physiological Rat program GM094503 (PI: D.A. Beard), and the Cardiac Energy Grid HL199122 (PI: J.B. Bassingthwaighte). Grants supported whole group.

The funders had no role in study design, data collection and analysis, decision to publish, or preparation of the manuscript.

Faculty Opinions recommended

References

Bassingthwaighte JB, Wang CY, Chan IS: Blood-tissue exchange via transport and transformation by capillary endothelial cells. Circ Res. 1989; 65(4): 997–1020. PubMed Abstract | Publisher Full Text | Free Full Text
Bassingthwaighte JB, Raymond GM, Chan JI: Tracer washout from an organ is predicted from the tracer center of mass. FASEB J. 2012; 26: 905.16. Reference Source
Butterworth E, Jardine BE, Raymond GM, et al.: JSim, an open-source modeling system for data analysis [version 3; referees: 2 approved]. F1000Res. 2014; 2: 288. PubMed Abstract | Publisher Full Text | Free Full Text
Erson EZ, Cavuşoğlu MC: Design of a framework for modeling, integration and simulation of physiological models. Comput Methods Programs Biomed. 2012; 107(3): 524–37. PubMed Abstract | Publisher Full Text
Gennari J, Neal ML, Galdzicki M, et al.: Multiple ontologies in action: Composite annotations for biosimulation models. J Biomed Informatics. 2011; 44(1): 146–154. PubMed Abstract | Publisher Full Text | Free Full Text
Krause F, Uhlendorf J, Lubitz T, et al.: Annotation and merging of SBML models with semanticSBML. Bioinformatics. 2010; 26(3): 421–422. PubMed Abstract | Publisher Full Text
Mirschel S, Steinmetz K, Rempel M, et al.: PROMOT: modular modeling for systems biology. Bioinformatics. 2009; 25(5): 687–689. PubMed Abstract | Publisher Full Text | Free Full Text
Raymond GM: Reusable modular code for multi-scale physiological systems modeling. Oral presentation 3rd MEI International symposium. 2008. Reference Source
Raymond GM, Bassingthwaighte JB: Automating modular model construction using JSim. FASEB J. 2011; 25: 863.9. Reference Source
Raymond GM, Bassingthwaighte JB: JSim models of two-dimensional concentrations in capillary-tissue systems relating center-of-mass of retained tracer to washout kinetics. FASEB J. 2012; 26: 905.17. Reference Source
Smith LP, Bergmann FT, Chandran D, et al.: Antimony: a modular model definition language. Bioinformatics. 2009; 25(18): 2452–2454. PubMed Abstract | Publisher Full Text | Free Full Text
Smith LP, Butterworth E, Bassingthwaighte JB, et al.: SBML and CellML translation in Antimony and JSim. Bioinformatics. 2014; 30(7): 903–907. PubMed Abstract | Publisher Full Text | Free Full Text

Comments on this article Comments (0)

Version 3

VERSION 3 PUBLISHED 16 Dec 2015

Author details Author details

¹ Department of Bioengineering, University of Washington, Seattle, WA, 98195, USA

Competing interests

The authors declared no competing interests.

Grant information

Article Versions (3)

version 3

Revised

Published: 16 Jun 2016, 4:1461

https://doi.org/10.12688/f1000research.7476.3

version 2

Revised

Published: 06 Apr 2016, 4:1461

https://doi.org/10.12688/f1000research.7476.2

version 1

Published: 16 Dec 2015, 4:1461

https://doi.org/10.12688/f1000research.7476.1

© 2015 Jardine B et al. This is an open access article distributed under the terms of the Creative Commons Attribution License, which permits unrestricted use, distribution, and reproduction in any medium, provided the original work is properly cited.

Download

Export To

metrics

	Views	Downloads
F1000Research	-	-
PubMed Central Data from PMC are received and updated monthly.	-	-

Citations

SEE MORE DETAILS

CITE

how to cite this article

Jardine B, Raymond GM and Bassingthwaighte JB. Semi-automated Modular Program Constructor for physiological modeling: Building cell and organ models [version 1; peer review: 1 approved with reservations]. F1000Research 2015, 4:1461 (https://doi.org/10.12688/f1000research.7476.1)

NOTE: If applicable, it is important to ensure the information in square brackets after the title is included in all citations of this article.

track

receive updates on this article

Track an article to receive email alerts on any updates to this article.

Open Peer Review

Version 1

VERSION 1

PUBLISHED 16 Dec 2015

Views

Reviewer Report 05 Jan 2016

Dagmar Waltemath, Department of Systems Biology and Bioinformatics, University of Rostock, Rostock, Germany

Approved with Reservations

https://doi.org/10.5256/f1000research.8055.r11594

The manuscript at hand describes MPC, a tool that supports modelers in constructing complex models from smaller ones. MPC also keeps information about the single modules, making their exchange and further coupling even easier.

The manuscript provides several examples (on code and abstract level) of how to use MPC, but it does not give details on how the algorithm itself works.

My suggestions for improvements are mainly on the terminology used throughout the manuscript, and on the discussion of related work.

Unifying terms: In the abstract alone you speak about programs, utilities, code; about models, processes, model code and modules. Maybe you could - not only in the abstract but throughout the manuscript - unify your wording a little bit more to make the text more comprehensive.
Related work: I missed a discussion of related systems, e.g. the model merge tool for SBML, semanticSBML, or the semantic-based system (there was a new publication just recently¹). While you mention them in the beginning of your introduction, I did not see a discussion of these systems, and how they differ from your approach. I, as a reader, would be interested to know which system is best to use when.

Furthermore, I have the following smaller comments:

Page 2, Introduction: "The models include time-dependent..." -- Here it was not clear to me what you mean by "models".
Page 2, MPC implementation: "Through JSim, the final constructed model...." -- I understand here, that you can upload your constructed models from JSim into an open model repository, and then directly download them into other simulation platforms. I am not sure that it is as easy as this, particularly for BioModels there will be a curation process in between, and there is thus no immediate reuse. The way the sentence is written now, a reader may assume that models can directly and immediately be exchanged through these resources, which is in my opinion misleading.
Page 2, MPC implementation: "These are archived, forming libraries of operational code" -- I would be interested to know how you archive the modules, where, and how/if/to what degree they are accessible/reusable?
Figure 1: I would like to suggest using an SBGN-compliant notation for the toy model.
Summary: "MPC encodes and preserves..." -- This is an important information for the users, and I would like to suggest to add this information to the abstract.

References

1. Neal ML, Carlson BE, Thompson CT, James RC, et al.: Semantics-Based Composition of Integrated Cardiomyocyte Models Motivated by Real-World Use Cases.PLoS One. 2015; 10 (12): e0145621 PubMed Abstract | Publisher Full Text

Competing Interests: No competing interests were disclosed.

I confirm that I have read this submission and believe that I have an appropriate level of expertise to confirm that it is of an acceptable scientific standard, however I have significant reservations, as outlined above.

CITE

Report a concern

Author Response 07 Apr 2016

Bartholomew Jardine, Department of Bioengineering, University of Washington, Seattle, 98195, USA

07 Apr 2016

Author Response
Our responses to Referee Dagmar Waltemath's review:
1. My suggestions for improvements are mainly on the terminology used throughout the manuscript, and on the discussion of related work. Unifying terms: In the
... Continue reading
Our responses to Referee Dagmar Waltemath's review:
My suggestions for improvements are mainly on the terminology used throughout the manuscript, and on the discussion of related work. Unifying terms: In the abstract alone you speak about programs, utilities, code; about models, processes, model code and modules. Maybe you could - not only in the abstract but throughout the manuscript - unify your wording a little bit more to make the text more comprehensive.

Author Response: Yes, we updated the abstract and paper as a whole to try to use consistent and unifying wording when discussing model code, processes, modules, etc. These changes are most notable in the abstract and introduction.

Related work: I missed a discussion of related systems, e.g. the model merge tool for SBML, semanticSBML, or the semantic-based system (there was a new publication just recently1). While you mention them in the beginning of your introduction, I did not see a discussion of these systems, and how they differ from your approach. I, as a reader, would be interested to know which system is best to use when.

Author Response: Added a paragraph in the Introduction that briefly discusses other tools in relation to MPC:

"Modular model creation and construction rely, to varying degrees, on meta-data to assist in reusing and merging previous models into a new one. Antimony (Smith 2009) is the simplest approach. It requires the user to be familiar with the model and just specify that you want to import it into the new model. It relies on the user to resolve discrepancies between models. SemanticSBML(Krause 2010), SemGen (Genari 2011, Neal 2015), and Phy-Sim (Erson 2012) make use of standard semantic and ontological descriptions of a biological model to allow large models to be broken down easily, without much user guidance, into biologically meaningful components linked to their mathematical description. Semantic and ontological metadata assists the construction of new models by providing suggested connections or relationships between models. This approach requires the user to invest time in complete annotation of models with standardized meta-data. The payoff is models that can be constructed and merged together using biological rather than mathematical terms. ProMot (Mirschel 2009) enforces an object-oriented approach to modeling (defining external interfaces for each object) and attempts to use network theory to describe biological systems through specifying elements and coupling elements (Mirschel 2009). MPC relies on the user to modularize a model using directives to specify them. MPC then requires the user to specify how the new model makes use of the modules. MPC only imposes unit balance constraints, indirectly, through the JSim MML compiler (Butterworth 2014)."
Furthermore, I have the following smaller comments:
Page 2, Introduction: "The models include time-dependent..." -- Here it was not clear to me what you mean by "models".

Author Response: Clarified sentence to make it clearer (Page 2, Introduction, 4th paragraph):

Some MPC built models include time-dependent two-dimensional spatial models in both Cartesian and cylindrical coordinates (Raymond et al., 2011; 2012), requiring PDEs, and whole organ models with heterogeneous flows, and substrate metabolism, including reconstructing Bassingthwaighte et al., 1989 blood-tissue exchange model.

Page 2, MPC implementation: "Through JSim, the final constructed model...." -- I understand here, that you can upload your constructed models from JSim into an open model repository, and then directly download them into other simulation platforms. I am not sure that it is as easy as this, particularly for BioModels there will be a curation process in between, and there is thus no immediate reuse. The way the sentence is written now, a reader may assume that models can directly and immediately be exchanged through these resources, which is in my opinion misleading.

Author Response: That sentence is confusing and not what we wanted to say. Changed to:

Through JSim, the final constructed model can be exported into Systems Biology Markup Language (SBML, http://sbml.org/Main_Page) or CellML (https://www.cellml.org/), and imported to other SBML or CellML supported simulation platforms [Smith et al., 2014].

Page 2, MPC implementation: "These are archived, forming libraries of operational code" -- I would be interested to know how you archive the modules, where, and how/if/to what degree they are accessible/reusable?

Author Response: Modules created and used by our team are currently available for download at physiome.org (http://physiome.org/software/MPC/) or search on term "mpc" (http://physiome.org/Models/modelDB/). At this time there are a very limited set of MPC modules available. Soon (May/June 2016) we will have individual MPC annotated modules accessible directly from our search page with all file dependencies listed and available for download as well as links to full JSim models that may use them. Contributions to our model repository are encouraged (Any modeling language accepted).

Sentence inserted on page 2, in MPC implementation, paragraph 2, Modules: "These are archived, forming libraries of operational module code that can be publicly distributed (some are available at http://www.physiome.org/software/MPC/)."

Figure 1: I would like to suggest using an SBGN-compliant notation for the toy model.

Author Response: Thank you for the suggestion, for this particular figure we would like to keep it as is, but since we are currently modeling cardiac metabolism at the sub-cellular level we will be adopting SBGN notation where possible. Arrowheads in figure are made smaller.

Summary: "MPC encodes and preserves..." -- This is an important information for the users, and I would like to suggest to add this information to the abstract.

Author Response: Added this sentence to the abstract.
Our responses to Referee Dagmar Waltemath's review:
My suggestions for improvements are mainly on the terminology used throughout the manuscript, and on the discussion of related work. Unifying terms: In the abstract alone you speak about programs, utilities, code; about models, processes, model code and modules. Maybe you could - not only in the abstract but throughout the manuscript - unify your wording a little bit more to make the text more comprehensive.

Author Response: Yes, we updated the abstract and paper as a whole to try to use consistent and unifying wording when discussing model code, processes, modules, etc. These changes are most notable in the abstract and introduction.

Related work: I missed a discussion of related systems, e.g. the model merge tool for SBML, semanticSBML, or the semantic-based system (there was a new publication just recently1). While you mention them in the beginning of your introduction, I did not see a discussion of these systems, and how they differ from your approach. I, as a reader, would be interested to know which system is best to use when.

Author Response: Added a paragraph in the Introduction that briefly discusses other tools in relation to MPC:

"Modular model creation and construction rely, to varying degrees, on meta-data to assist in reusing and merging previous models into a new one. Antimony (Smith 2009) is the simplest approach. It requires the user to be familiar with the model and just specify that you want to import it into the new model. It relies on the user to resolve discrepancies between models. SemanticSBML(Krause 2010), SemGen (Genari 2011, Neal 2015), and Phy-Sim (Erson 2012) make use of standard semantic and ontological descriptions of a biological model to allow large models to be broken down easily, without much user guidance, into biologically meaningful components linked to their mathematical description. Semantic and ontological metadata assists the construction of new models by providing suggested connections or relationships between models. This approach requires the user to invest time in complete annotation of models with standardized meta-data. The payoff is models that can be constructed and merged together using biological rather than mathematical terms. ProMot (Mirschel 2009) enforces an object-oriented approach to modeling (defining external interfaces for each object) and attempts to use network theory to describe biological systems through specifying elements and coupling elements (Mirschel 2009). MPC relies on the user to modularize a model using directives to specify them. MPC then requires the user to specify how the new model makes use of the modules. MPC only imposes unit balance constraints, indirectly, through the JSim MML compiler (Butterworth 2014)."
Furthermore, I have the following smaller comments:
Page 2, Introduction: "The models include time-dependent..." -- Here it was not clear to me what you mean by "models".

Author Response: Clarified sentence to make it clearer (Page 2, Introduction, 4th paragraph):

Some MPC built models include time-dependent two-dimensional spatial models in both Cartesian and cylindrical coordinates (Raymond et al., 2011; 2012), requiring PDEs, and whole organ models with heterogeneous flows, and substrate metabolism, including reconstructing Bassingthwaighte et al., 1989 blood-tissue exchange model.

Page 2, MPC implementation: "Through JSim, the final constructed model...." -- I understand here, that you can upload your constructed models from JSim into an open model repository, and then directly download them into other simulation platforms. I am not sure that it is as easy as this, particularly for BioModels there will be a curation process in between, and there is thus no immediate reuse. The way the sentence is written now, a reader may assume that models can directly and immediately be exchanged through these resources, which is in my opinion misleading.

Author Response: That sentence is confusing and not what we wanted to say. Changed to:

Through JSim, the final constructed model can be exported into Systems Biology Markup Language (SBML, http://sbml.org/Main_Page) or CellML (https://www.cellml.org/), and imported to other SBML or CellML supported simulation platforms [Smith et al., 2014].

Page 2, MPC implementation: "These are archived, forming libraries of operational code" -- I would be interested to know how you archive the modules, where, and how/if/to what degree they are accessible/reusable?

Author Response: Modules created and used by our team are currently available for download at physiome.org (http://physiome.org/software/MPC/) or search on term "mpc" (http://physiome.org/Models/modelDB/). At this time there are a very limited set of MPC modules available. Soon (May/June 2016) we will have individual MPC annotated modules accessible directly from our search page with all file dependencies listed and available for download as well as links to full JSim models that may use them. Contributions to our model repository are encouraged (Any modeling language accepted).

Sentence inserted on page 2, in MPC implementation, paragraph 2, Modules: "These are archived, forming libraries of operational module code that can be publicly distributed (some are available at http://www.physiome.org/software/MPC/)."

Figure 1: I would like to suggest using an SBGN-compliant notation for the toy model.

Author Response: Thank you for the suggestion, for this particular figure we would like to keep it as is, but since we are currently modeling cardiac metabolism at the sub-cellular level we will be adopting SBGN notation where possible. Arrowheads in figure are made smaller.

Summary: "MPC encodes and preserves..." -- This is an important information for the users, and I would like to suggest to add this information to the abstract.

Author Response: Added this sentence to the abstract.
Competing Interests: None. Close
Report a concern
Respond or Comment

COMMENTS ON THIS REPORT

Author Response 07 Apr 2016

Bartholomew Jardine, Department of Bioengineering, University of Washington, Seattle, 98195, USA

07 Apr 2016

Author Response
Our responses to Referee Dagmar Waltemath's review:
1. My suggestions for improvements are mainly on the terminology used throughout the manuscript, and on the discussion of related work. Unifying terms: In the
... Continue reading
Our responses to Referee Dagmar Waltemath's review:
My suggestions for improvements are mainly on the terminology used throughout the manuscript, and on the discussion of related work. Unifying terms: In the abstract alone you speak about programs, utilities, code; about models, processes, model code and modules. Maybe you could - not only in the abstract but throughout the manuscript - unify your wording a little bit more to make the text more comprehensive.

Author Response: Yes, we updated the abstract and paper as a whole to try to use consistent and unifying wording when discussing model code, processes, modules, etc. These changes are most notable in the abstract and introduction.

Related work: I missed a discussion of related systems, e.g. the model merge tool for SBML, semanticSBML, or the semantic-based system (there was a new publication just recently1). While you mention them in the beginning of your introduction, I did not see a discussion of these systems, and how they differ from your approach. I, as a reader, would be interested to know which system is best to use when.

Author Response: Added a paragraph in the Introduction that briefly discusses other tools in relation to MPC:

"Modular model creation and construction rely, to varying degrees, on meta-data to assist in reusing and merging previous models into a new one. Antimony (Smith 2009) is the simplest approach. It requires the user to be familiar with the model and just specify that you want to import it into the new model. It relies on the user to resolve discrepancies between models. SemanticSBML(Krause 2010), SemGen (Genari 2011, Neal 2015), and Phy-Sim (Erson 2012) make use of standard semantic and ontological descriptions of a biological model to allow large models to be broken down easily, without much user guidance, into biologically meaningful components linked to their mathematical description. Semantic and ontological metadata assists the construction of new models by providing suggested connections or relationships between models. This approach requires the user to invest time in complete annotation of models with standardized meta-data. The payoff is models that can be constructed and merged together using biological rather than mathematical terms. ProMot (Mirschel 2009) enforces an object-oriented approach to modeling (defining external interfaces for each object) and attempts to use network theory to describe biological systems through specifying elements and coupling elements (Mirschel 2009). MPC relies on the user to modularize a model using directives to specify them. MPC then requires the user to specify how the new model makes use of the modules. MPC only imposes unit balance constraints, indirectly, through the JSim MML compiler (Butterworth 2014)."
Furthermore, I have the following smaller comments:
Page 2, Introduction: "The models include time-dependent..." -- Here it was not clear to me what you mean by "models".

Author Response: Clarified sentence to make it clearer (Page 2, Introduction, 4th paragraph):

Some MPC built models include time-dependent two-dimensional spatial models in both Cartesian and cylindrical coordinates (Raymond et al., 2011; 2012), requiring PDEs, and whole organ models with heterogeneous flows, and substrate metabolism, including reconstructing Bassingthwaighte et al., 1989 blood-tissue exchange model.

Page 2, MPC implementation: "Through JSim, the final constructed model...." -- I understand here, that you can upload your constructed models from JSim into an open model repository, and then directly download them into other simulation platforms. I am not sure that it is as easy as this, particularly for BioModels there will be a curation process in between, and there is thus no immediate reuse. The way the sentence is written now, a reader may assume that models can directly and immediately be exchanged through these resources, which is in my opinion misleading.

Author Response: That sentence is confusing and not what we wanted to say. Changed to:

Through JSim, the final constructed model can be exported into Systems Biology Markup Language (SBML, http://sbml.org/Main_Page) or CellML (https://www.cellml.org/), and imported to other SBML or CellML supported simulation platforms [Smith et al., 2014].

Page 2, MPC implementation: "These are archived, forming libraries of operational code" -- I would be interested to know how you archive the modules, where, and how/if/to what degree they are accessible/reusable?

Author Response: Modules created and used by our team are currently available for download at physiome.org (http://physiome.org/software/MPC/) or search on term "mpc" (http://physiome.org/Models/modelDB/). At this time there are a very limited set of MPC modules available. Soon (May/June 2016) we will have individual MPC annotated modules accessible directly from our search page with all file dependencies listed and available for download as well as links to full JSim models that may use them. Contributions to our model repository are encouraged (Any modeling language accepted).

Sentence inserted on page 2, in MPC implementation, paragraph 2, Modules: "These are archived, forming libraries of operational module code that can be publicly distributed (some are available at http://www.physiome.org/software/MPC/)."

Figure 1: I would like to suggest using an SBGN-compliant notation for the toy model.

Author Response: Thank you for the suggestion, for this particular figure we would like to keep it as is, but since we are currently modeling cardiac metabolism at the sub-cellular level we will be adopting SBGN notation where possible. Arrowheads in figure are made smaller.

Summary: "MPC encodes and preserves..." -- This is an important information for the users, and I would like to suggest to add this information to the abstract.

Author Response: Added this sentence to the abstract.
Our responses to Referee Dagmar Waltemath's review:
My suggestions for improvements are mainly on the terminology used throughout the manuscript, and on the discussion of related work. Unifying terms: In the abstract alone you speak about programs, utilities, code; about models, processes, model code and modules. Maybe you could - not only in the abstract but throughout the manuscript - unify your wording a little bit more to make the text more comprehensive.

Author Response: Yes, we updated the abstract and paper as a whole to try to use consistent and unifying wording when discussing model code, processes, modules, etc. These changes are most notable in the abstract and introduction.

Related work: I missed a discussion of related systems, e.g. the model merge tool for SBML, semanticSBML, or the semantic-based system (there was a new publication just recently1). While you mention them in the beginning of your introduction, I did not see a discussion of these systems, and how they differ from your approach. I, as a reader, would be interested to know which system is best to use when.

Author Response: Added a paragraph in the Introduction that briefly discusses other tools in relation to MPC:

"Modular model creation and construction rely, to varying degrees, on meta-data to assist in reusing and merging previous models into a new one. Antimony (Smith 2009) is the simplest approach. It requires the user to be familiar with the model and just specify that you want to import it into the new model. It relies on the user to resolve discrepancies between models. SemanticSBML(Krause 2010), SemGen (Genari 2011, Neal 2015), and Phy-Sim (Erson 2012) make use of standard semantic and ontological descriptions of a biological model to allow large models to be broken down easily, without much user guidance, into biologically meaningful components linked to their mathematical description. Semantic and ontological metadata assists the construction of new models by providing suggested connections or relationships between models. This approach requires the user to invest time in complete annotation of models with standardized meta-data. The payoff is models that can be constructed and merged together using biological rather than mathematical terms. ProMot (Mirschel 2009) enforces an object-oriented approach to modeling (defining external interfaces for each object) and attempts to use network theory to describe biological systems through specifying elements and coupling elements (Mirschel 2009). MPC relies on the user to modularize a model using directives to specify them. MPC then requires the user to specify how the new model makes use of the modules. MPC only imposes unit balance constraints, indirectly, through the JSim MML compiler (Butterworth 2014)."
Furthermore, I have the following smaller comments:
Page 2, Introduction: "The models include time-dependent..." -- Here it was not clear to me what you mean by "models".

Author Response: Clarified sentence to make it clearer (Page 2, Introduction, 4th paragraph):

Some MPC built models include time-dependent two-dimensional spatial models in both Cartesian and cylindrical coordinates (Raymond et al., 2011; 2012), requiring PDEs, and whole organ models with heterogeneous flows, and substrate metabolism, including reconstructing Bassingthwaighte et al., 1989 blood-tissue exchange model.

Page 2, MPC implementation: "Through JSim, the final constructed model...." -- I understand here, that you can upload your constructed models from JSim into an open model repository, and then directly download them into other simulation platforms. I am not sure that it is as easy as this, particularly for BioModels there will be a curation process in between, and there is thus no immediate reuse. The way the sentence is written now, a reader may assume that models can directly and immediately be exchanged through these resources, which is in my opinion misleading.

Author Response: That sentence is confusing and not what we wanted to say. Changed to:

Through JSim, the final constructed model can be exported into Systems Biology Markup Language (SBML, http://sbml.org/Main_Page) or CellML (https://www.cellml.org/), and imported to other SBML or CellML supported simulation platforms [Smith et al., 2014].

Page 2, MPC implementation: "These are archived, forming libraries of operational code" -- I would be interested to know how you archive the modules, where, and how/if/to what degree they are accessible/reusable?

Author Response: Modules created and used by our team are currently available for download at physiome.org (http://physiome.org/software/MPC/) or search on term "mpc" (http://physiome.org/Models/modelDB/). At this time there are a very limited set of MPC modules available. Soon (May/June 2016) we will have individual MPC annotated modules accessible directly from our search page with all file dependencies listed and available for download as well as links to full JSim models that may use them. Contributions to our model repository are encouraged (Any modeling language accepted).

Sentence inserted on page 2, in MPC implementation, paragraph 2, Modules: "These are archived, forming libraries of operational module code that can be publicly distributed (some are available at http://www.physiome.org/software/MPC/)."

Figure 1: I would like to suggest using an SBGN-compliant notation for the toy model.

Author Response: Thank you for the suggestion, for this particular figure we would like to keep it as is, but since we are currently modeling cardiac metabolism at the sub-cellular level we will be adopting SBGN notation where possible. Arrowheads in figure are made smaller.

Summary: "MPC encodes and preserves..." -- This is an important information for the users, and I would like to suggest to add this information to the abstract.

Author Response: Added this sentence to the abstract.
Competing Interests: None. Close
Report a concern

Comments on this article Comments (0)

Version 3

VERSION 3 PUBLISHED 16 Dec 2015

Open Peer Review

Reviewer Status

Reviewer Reports

	Invited Reviewers
	1	2
Version 3 (revision) 16 Jun 16	read
Version 2 (revision) 06 Apr 16	read	read
Version 1 16 Dec 15	read

Dagmar Waltemath, University of Rostock, Rostock, Germany
Vanessa Díaz-Zuccarini, University College London, London, UK

Comments on this article

All Comments(0)

Add a comment

Browse by related subjects

Back to all reports

Reviewer Report

2 Views

01 Aug 2016 | for Version 3

Dagmar Waltemath, Department of Systems Biology and Bioinformatics, University of Rostock, Rostock, Germany

2 Views Cite this report Responses(0)

Approved

Thank you for the latest revision. Please consider changing the last sentence of the first paragraph in the introduction to: "and then use" --> "and then uses".

Competing Interests

No competing interests were disclosed.

I confirm that I have read this submission and believe that I have an appropriate level of expertise to confirm that it is of an acceptable scientific standard.

Respond to this report

Responses (0)

Back to all reports

Reviewer Report

5 Views

19 May 2016 | for Version 2

Vanessa Díaz-Zuccarini, UCL Mechanical Engineering , Multiscale Cardiovascular Engineering Group, University College London, London, UK

5 Views Cite this report Responses(1)

Approved

I think after the previous corrections the article is much more readable. It would be extremely helpful if the authors could update the manuscript with hyperlinks to concrete databases/examples and to provide a concrete example to illustrate their point about 'The amount of actual code a user needs to write is reduced, especially for more complicated models'.

I strongly believe one of the roadblocks to a more widespread use of markup languages and the reusability of code is the perceived challenge by modellers/users of the task(s) involved into make their models 'shareable' and 'reusable'. A contrast between 2 examples or simply a better description of the effort it would concretely entail, would make their case much clearer.

This isn't absolutely necessary for the article but since the authors are trying to make a point and for other researchers to use the tools they have developed and use for their own research, I believe this would be useful.

Competing Interests

No competing interests were disclosed.

I confirm that I have read this submission and believe that I have an appropriate level of expertise to confirm that it is of an acceptable scientific standard.

Respond to this report

Responses (1)

Author Response

17 Jun 2016

Bartholomew Jardine, Department of Bioengineering, University of Washington, Seattle, 98195, USA

I think, after the previous corrections, the article is much more readable. It would be extremely helpful if the authors could update the manuscript with hyperlinks to concrete databases/examples and to provide a concrete example to illustrate their point about 'The amount of actual code a user needs to write is reduced, especially for more complicated models'.

Author: On page 7 in final paragraph before the “Discussion” section added the following sentence, with links:

"Please see more detailed examples in the Data Availability and Software Availability sections below.”

Listed in these sections are specific examples of models available on our website (physiome.org) created using MPC.

I strongly believe one of the roadblocks to a more widespread use of markup languages and the reusability of code is the perceived challenge by modellers/users of the task(s) involved into make their models 'shareable' and 'reusable'. A contrast between 2 examples or simply a better description of the effort it would concretely entail, would make their case much clearer.

This isn't absolutely necessary for the article but since the authors are trying to make a point and for other researchers to use the tools they have developed and use for their own research, I believe this would be useful.

Author: We added this paragraph in the Data availability section (page 8) to address this important point:

“The two compartment MPC built model, demonstrated here, is available at www.physiome.org (TwoCompExampMPC, Model # 0345). As it is an ODE model it could be translated to SBML or CellML, allowing researchers whose simulation systems support one of these markup languages to run this model. However, for this presentation we have provided only the MPC annotation in order to retain its simplicity.”

View more View less

Competing Interests

None

Back to all reports

Reviewer Report

6 Views

18 Apr 2016 | for Version 2

Dagmar Waltemath, Department of Systems Biology and Bioinformatics, University of Rostock, Rostock, Germany

6 Views Cite this report Responses(1)

Approved

Thank you for revising the manuscript. It was nice reading it. I only have a few minor things to note

Last sentence of first paragraph in the introduction: I suggest to generalise the sentence and cut "for multi-scale modeling". Also, I think it should be "uses" instead of "use".
Last sentence of first paragraph in Methods: "MPC currently is executed as command line utility" - I would write "as a command line utility".
in Methods, in the listing of the three components, I suggest to remove "not procedural like Fortran or Matlab", as it is hard to follow the sentence structure and the information not essential. Also, is MML really designed to solve equations? Or rather to provide the information to solve them?
in Methods, second point in the above listing: You mention several models ("For example, there have been a variety of models...") - would it be possible to link to these specific works, e.g., using citations?
Last sentence on page 3: "A "library" with a few..." - I think it should read "in our next step" (instead of "in out next step")
End of first paragraph on page 4: "Species A enters, with flow F, a compartment... I had problems following the sentence, specifically because of "passive exchange between"... Can simplify the sentence structure or use two sentences instead?
First sentence in Discussion: Should it be "Though an MPC-generated..." (instead of "a")?
same paragraph: "These are key steps towards reproducibility and the VVUQ process." I would have found it helpful to get a reference to the VVUQ process. Can you add one?
Grant information, last sentence: Please use a capital letter to start the sentence, and add two "the" - "The grants supported the whole group."

Competing Interests

No competing interests were disclosed.

I confirm that I have read this submission and believe that I have an appropriate level of expertise to confirm that it is of an acceptable scientific standard.

Respond to this report

Responses (1)

Author Response

17 Jun 2016

Bartholomew Jardine, Department of Bioengineering, University of Washington, Seattle, 98195, USA

Responses reflected in version 3 of manuscript.

Last sentence of first paragraph in the introduction: I suggest to generalise the sentence and cut "for multi-scale modeling". Also, I think it should be "uses" instead of "use".

Author: Changed last two sentences of first paragraph (page 3) to generalize: “For developing a series of models of increasing complexity, Modular Program Constructor (MPC) can serve well as the primary basis for coding new model components and for incorporating modules of previously developed modeling code. The perspective is to take a modular approach; this means that one builds from simple modeling elements initially and then use multi-modular constructs as modules in higher level models."
Last sentence of first paragraph in Methods: "MPC currently is executed as command line utility" - I would write "as a command line utility".

Author: Made change as suggested.
in Methods, in the listing of the three components, I suggest to remove "not procedural like Fortran or Matlab", as it is hard to follow the sentence structure and the information not essential. Also, is MML really designed to solve equations? Or rather to provide the information to solve them?

Author: Updated and clarified sentence (page 3, Methods 1. MML, paragraph): “MML, the mathematical modeling language of JSim, is a declarative language specifying all the model equations, leaving the sequencing and solving of equations to the JSim compiler and simulator.”
in Methods, second point in the above listing: You mention several models ("For example, there have been a variety of models...") - would it be possible to link to these specific works, e.g., using citations?

Author: added the following references (page 3, Methods 2. Modules, paragraph):

- Chapman JB, Johnson EA, and Kootsey JM, Electrical and Biochemical Properties of an Enzyme Model of the Sodium Pump, Journal of Membrane Biology 74., 139-153, 1983
- Demir S, Clark J, Murphey C, and Giles W, A mathematical model of a rabbit sinoatrial node cell. Am. J. Physiol. Cell Physiol. 266: C832-C852, 1994
- Goldman David E. Potential, impedance, and rectification in membranes, J Gen Physiol 27: 37-60, 1943.
- Hille B. Ionic Channels of Excitable Membranes. 3rd Ed, Sunderland, MA, Sinauer, 2001.
- Hodgkin AL and Huxley AF. A quantitative description of membrane current and its application to conduction and excitation in nerve. J Physiol. 500-544, 1952d.
- Lauger P, Electrogenic Ion Pumps, 2nd Ed, Sinauer, Sunderland MA 1991
- Winslow RL, Rice J, Jafri S, Marban E, and O'Rourke B, Mechanisms of altered excitation-contraction coupling in canine tachycardia-induced heart failure, II: model studies. Circ Res. 1999 Mar 19;84(5):571-86.
Last sentence on page 3: "A "library" with a few..." - I think it should read "in our next step" (instead of "in out next step")

Author: Fixed typo (page 4, "Selecting and arranging..." paragraph): “A `library` with a few elementary operators from which we will build a model in our next step is illustrated below:”
End of first paragraph on page 4: "Species A enters, with flow F, a compartment... I had problems following the sentence, specifically because of "passive exchange between"... Can simplify the sentence structure or use two sentences instead?

Author: Made into two sentences to make more readable (page 5, first paragraph):

“Species A enters, with flow F, a compartment with volume V1 and passive exchange between a second compartment with volume V2. In the second compartment, A reacts at rate GA2B to form B and B reacts to form C at rate GB2C, a Michaelis-Menten reaction.”
First sentence in Discussion: Should it be "Though an MPC-generated..." (instead of "a")?

Author: Agree. Corrected (page 8, first paragraph); an M is an aspirate.
same paragraph: "These are key steps towards reproducibility and the VVUQ process." I would have found it helpful to get a reference to the VVUQ process. Can you add one?

Author: Rewrote the first paragraph (page 8) of the “Discussion” section and added the following reference:

- R.H. Johnstone, et al., Uncertainty and variability in models of the cardiac action potential: Can we build trustworthy models?, J Mol Cell Cardiol (2015), http://dx.doi.org/10.1016/j.yjmcc.2015.11.018

Updated paragraph:

A prerequisite to using MPC is semantic consistency throughout the libraries and modules. Automated systems using ontologies will help craft models ( Gennari et al., 2011), but the great efficiency of MPC for model construction begins to show when there are many model modules as in biochemical networks and circulatory or airway models. The VVUQ process (Johnstone et al. 2015) provides key steps toward reproducibility (VVUQ = Verification, Validation, Uncertainty Quantification, the latter defining predictive accuracy). Though an MPC-generated model is checked for syntax and unit balance through JSim, further verification is required: analytical solutions can be written into the code to match specific limiting cases, but otherwise one depends on testing for mass, charge, or energy balances. Validation requires testing against data, independent of the construction method; model solutions should not be in contradiction to the data. Quantification of the uncertainty is needed for making predictions from the model: UQ includes uncertainty in parameters, handled by JSim's Monte Carlo analysis, and in inputs/environment and model structure. Structural uncertainty, a major challenge, defines a major role for MPC: inserting different choices from amongst similar but differently functioning modules, into a large, multi-modular model, and solving the system many times with the variant constituents illustrating uncertainty in the projected outcomes.

I. Grant information, last sentence: Please use a capital letter to start the sentence, and add two "the" - "The grants supported the whole group."

Author: updated sentence as suggested.

View more View less

Competing Interests

None.

Back to all reports

Reviewer Report

11 Views

05 Jan 2016 | for Version 1

Dagmar Waltemath, Department of Systems Biology and Bioinformatics, University of Rostock, Rostock, Germany

11 Views Cite this report Responses(1)

Approved With Reservations

Unifying terms: In the abstract alone you speak about programs, utilities, code; about models, processes, model code and modules. Maybe you could - not only in the abstract but throughout the manuscript - unify your wording a little bit more to make the text more comprehensive.
Related work: I missed a discussion of related systems, e.g. the model merge tool for SBML, semanticSBML, or the semantic-based system (there was a new publication just recently¹). While you mention them in the beginning of your introduction, I did not see a discussion of these systems, and how they differ from your approach. I, as a reader, would be interested to know which system is best to use when.

Furthermore, I have the following smaller comments:

Page 2, Introduction: "The models include time-dependent..." -- Here it was not clear to me what you mean by "models".
Page 2, MPC implementation: "Through JSim, the final constructed model...." -- I understand here, that you can upload your constructed models from JSim into an open model repository, and then directly download them into other simulation platforms. I am not sure that it is as easy as this, particularly for BioModels there will be a curation process in between, and there is thus no immediate reuse. The way the sentence is written now, a reader may assume that models can directly and immediately be exchanged through these resources, which is in my opinion misleading.
Page 2, MPC implementation: "These are archived, forming libraries of operational code" -- I would be interested to know how you archive the modules, where, and how/if/to what degree they are accessible/reusable?
Figure 1: I would like to suggest using an SBGN-compliant notation for the toy model.
Summary: "MPC encodes and preserves..." -- This is an important information for the users, and I would like to suggest to add this information to the abstract.

References

Competing Interests

No competing interests were disclosed.

Respond to this report

Responses (1)

Author Response

07 Apr 2016

Bartholomew Jardine, Department of Bioengineering, University of Washington, Seattle, 98195, USA

Our responses to Referee Dagmar Waltemath's review:

My suggestions for improvements are mainly on the terminology used throughout the manuscript, and on the discussion of related work. Unifying terms: In the abstract alone you speak about programs, utilities, code; about models, processes, model code and modules. Maybe you could - not only in the abstract but throughout the manuscript - unify your wording a little bit more to make the text more comprehensive.

Author Response: Yes, we updated the abstract and paper as a whole to try to use consistent and unifying wording when discussing model code, processes, modules, etc. These changes are most notable in the abstract and introduction.
Related work: I missed a discussion of related systems, e.g. the model merge tool for SBML, semanticSBML, or the semantic-based system (there was a new publication just recently1). While you mention them in the beginning of your introduction, I did not see a discussion of these systems, and how they differ from your approach. I, as a reader, would be interested to know which system is best to use when.

Author Response: Added a paragraph in the Introduction that briefly discusses other tools in relation to MPC:

"Modular model creation and construction rely, to varying degrees, on meta-data to assist in reusing and merging previous models into a new one. Antimony (Smith 2009) is the simplest approach. It requires the user to be familiar with the model and just specify that you want to import it into the new model. It relies on the user to resolve discrepancies between models. SemanticSBML(Krause 2010), SemGen (Genari 2011, Neal 2015), and Phy-Sim (Erson 2012) make use of standard semantic and ontological descriptions of a biological model to allow large models to be broken down easily, without much user guidance, into biologically meaningful components linked to their mathematical description. Semantic and ontological metadata assists the construction of new models by providing suggested connections or relationships between models. This approach requires the user to invest time in complete annotation of models with standardized meta-data. The payoff is models that can be constructed and merged together using biological rather than mathematical terms. ProMot (Mirschel 2009) enforces an object-oriented approach to modeling (defining external interfaces for each object) and attempts to use network theory to describe biological systems through specifying elements and coupling elements (Mirschel 2009). MPC relies on the user to modularize a model using directives to specify them. MPC then requires the user to specify how the new model makes use of the modules. MPC only imposes unit balance constraints, indirectly, through the JSim MML compiler (Butterworth 2014)."

Furthermore, I have the following smaller comments:

Page 2, Introduction: "The models include time-dependent..." -- Here it was not clear to me what you mean by "models".

Author Response: Clarified sentence to make it clearer (Page 2, Introduction, 4th paragraph):

Some MPC built models include time-dependent two-dimensional spatial models in both Cartesian and cylindrical coordinates (Raymond et al., 2011; 2012), requiring PDEs, and whole organ models with heterogeneous flows, and substrate metabolism, including reconstructing Bassingthwaighte et al., 1989 blood-tissue exchange model.
Page 2, MPC implementation: "Through JSim, the final constructed model...." -- I understand here, that you can upload your constructed models from JSim into an open model repository, and then directly download them into other simulation platforms. I am not sure that it is as easy as this, particularly for BioModels there will be a curation process in between, and there is thus no immediate reuse. The way the sentence is written now, a reader may assume that models can directly and immediately be exchanged through these resources, which is in my opinion misleading.

Author Response: That sentence is confusing and not what we wanted to say. Changed to:

Through JSim, the final constructed model can be exported into Systems Biology Markup Language (SBML, http://sbml.org/Main_Page) or CellML (https://www.cellml.org/), and imported to other SBML or CellML supported simulation platforms [Smith et al., 2014].
Page 2, MPC implementation: "These are archived, forming libraries of operational code" -- I would be interested to know how you archive the modules, where, and how/if/to what degree they are accessible/reusable?

Author Response: Modules created and used by our team are currently available for download at physiome.org (http://physiome.org/software/MPC/) or search on term "mpc" (http://physiome.org/Models/modelDB/). At this time there are a very limited set of MPC modules available. Soon (May/June 2016) we will have individual MPC annotated modules accessible directly from our search page with all file dependencies listed and available for download as well as links to full JSim models that may use them. Contributions to our model repository are encouraged (Any modeling language accepted).

Sentence inserted on page 2, in MPC implementation, paragraph 2, Modules: "These are archived, forming libraries of operational module code that can be publicly distributed (some are available at http://www.physiome.org/software/MPC/)."
Figure 1: I would like to suggest using an SBGN-compliant notation for the toy model.

Author Response: Thank you for the suggestion, for this particular figure we would like to keep it as is, but since we are currently modeling cardiac metabolism at the sub-cellular level we will be adopting SBGN notation where possible. Arrowheads in figure are made smaller.
Summary: "MPC encodes and preserves..." -- This is an important information for the users, and I would like to suggest to add this information to the abstract.

Author Response: Added this sentence to the abstract.

View more View less

Competing Interests

None.

Alongside their report, reviewers assign a status to the article:

Approved - the paper is scientifically sound in its current form and only minor, if any, improvements are suggested

Approved with reservations - A number of small changes, sometimes more significant revisions are required to address specific details and improve the papers academic merit.

Not approved - fundamental flaws in the paper seriously undermine the findings and conclusions

[1] Bassingthwaighte JB, Wang CY, Chan IS: Blood-tissue exchange via transport and transformation by capillary endothelial cells. Circ Res. 1989; 65(4): 997–1020. PubMed Abstract | Publisher Full Text | Free Full Text

[2] Bassingthwaighte JB, Raymond GM, Chan JI: Tracer washout from an organ is predicted from the tracer center of mass. FASEB J. 2012; 26: 905.16. Reference Source

[3] Butterworth E, Jardine BE, Raymond GM, et al.: JSim, an open-source modeling system for data analysis [version 3; referees: 2 approved]. F1000Res. 2014; 2: 288. PubMed Abstract | Publisher Full Text | Free Full Text

[4] Erson EZ, Cavuşoğlu MC: Design of a framework for modeling, integration and simulation of physiological models. Comput Methods Programs Biomed. 2012; 107(3): 524–37. PubMed Abstract | Publisher Full Text

[5] Gennari J, Neal ML, Galdzicki M, et al.: Multiple ontologies in action: Composite annotations for biosimulation models. J Biomed Informatics. 2011; 44(1): 146–154. PubMed Abstract | Publisher Full Text | Free Full Text

[6] Krause F, Uhlendorf J, Lubitz T, et al.: Annotation and merging of SBML models with semanticSBML. Bioinformatics. 2010; 26(3): 421–422. PubMed Abstract | Publisher Full Text

[7] Mirschel S, Steinmetz K, Rempel M, et al.: PROMOT: modular modeling for systems biology. Bioinformatics. 2009; 25(5): 687–689. PubMed Abstract | Publisher Full Text | Free Full Text

[8] Raymond GM: Reusable modular code for multi-scale physiological systems modeling. Oral presentation 3rd MEI International symposium. 2008. Reference Source

[9] Raymond GM, Bassingthwaighte JB: Automating modular model construction using JSim. FASEB J. 2011; 25: 863.9. Reference Source

[10] Raymond GM, Bassingthwaighte JB: JSim models of two-dimensional concentrations in capillary-tissue systems relating center-of-mass of retained tracer to washout kinetics. FASEB J. 2012; 26: 905.17. Reference Source

[11] Smith LP, Bergmann FT, Chandran D, et al.: Antimony: a modular model definition language. Bioinformatics. 2009; 25(18): 2452–2454. PubMed Abstract | Publisher Full Text | Free Full Text

[12] Smith LP, Butterworth E, Bassingthwaighte JB, et al.: SBML and CellML translation in Antimony and JSim. Bioinformatics. 2014; 30(7): 903–907. PubMed Abstract | Publisher Full Text | Free Full Text

Semi-automated Modular Program Constructor for physiological modeling: Building cell and organ models

Abstract

Keywords

Introduction

Methods

MPC implementation

Selecting and arranging components using directives – A simple example

Figure 1. Two compartment, three species model (A, B, C) with volumes V1, V2, respectively.

Figure 2. Solution to two compartment model generated from MPC.

Discussion

MPC and Uncertainty Quantification (UQ)

Summary

Software availability

Software access

Source code as at the time of publication

Archived source code as at the time of publication

Software license

Data availability

Author contributions

Competing interests

Grant information

References

Comments on this article Comments (0)

Open Peer Review

Comments on this article Comments (0)

Open Peer Review

Reviewer Status

Reviewer Reports

Comments on this article

Browse by related subjects

Competing Interests Policy

Stay Updated

Figure 1. Two compartment, three species model (A, B, C) with volumes V₁, V₂, respectively.