Keywords
early pregnancy loss, embryo mortality, human chorionic gonadotrophin, fecundability
early pregnancy loss, embryo mortality, human chorionic gonadotrophin, fecundability
This new version includes more formal definitions of conditional probabilities that are quantified in the study. It is hoped that this will clarify the meaning of the estimates.
See the author's detailed response to the review by Alan O. Trounson
See the author's detailed response to the review by Stephen J. Senn
Estimates of natural human embryo mortality have been derived using speculative calculations1, mathematical modelling2, pregnancy surveys3, and a unique collection of surgical material4,5. Three well-designed studies (henceforth referred to as the Wilcox6, Zinaman7 and Wang8 studies) have shown that approximately two-thirds of menstrual cycles in which elevated human chorionic gonadotrophin (hCG) is detected approximately 1 week after ovulation proceed to a live birth. hCG is produced by the trophoblast cells of the embryo9 and its earliest detection indicates that implantation has commenced10–12. Hence, these studies provide no direct measure of embryo loss before implantation. The only measure of pre-implantation loss is the “scanty data of Hertig”13 which have generated estimates4,5 that are “difficult to defend with any precision”2. Estimates of embryo mortality from fertilisation onwards are therefore subject to considerable uncertainty owing to the absence of suitable data for the 5–7 day period between fertilisation and implantation.
Fecundability is the probability of reproductive success per cycle. Compared to other animals, fecundability in humans is low and has been estimated at <35%14,15. Red deer hinds, by contrast, achieve pregnancy rates of >85% per natural mating16. Clearly, as fecundability increases, the range of plausible values for embryo mortality narrows. Crude estimates of live birth fecundability can be calculated from prospective study data: 19.2% (136 births from 707 cycles6), 18.2% (79 births from 432 cycles7) and 23.9–25.9% (373 births and 31 ongoing pregnancies from 1,561 cycles8). These represent lower limits for fecundability, since optimal conditions for reproductive success were not achieved in every cycle17. However, some published estimates of embryo mortality, e.g., 76%2,18 and 78%1 can only be reconciled with these data if it is assumed that almost every non-birth cycle in these studies resulted in successful fertilisation and subsequent embryonic or fetal death, an extreme and improbable condition. Higher estimates of embryo mortality, including >85%19 and 90%20, are even less plausible. Furthermore, it is self-evident that not all observed reproductive failure is necessarily due to embryo or fetal mortality: other biological causes include mistimed coitus and failure of fertilisation despite in vivo co-localisation of ovum and sperm. Estimates of embryo mortality based on fecundability must take this into account.
The objective of this study is to obtain plausible estimates of fecundability and early human embryo mortality from available published data6–8. To do this, a simple quantitative framework is proposed to define a successful reproductive cycle. Hence, for a menstrual cycle to conclude with a live infant several distinct biological stages must be completed, each with its own probability (π) of success. These stages (and conditional probabilities) are defined as follows: (1) sexual activity within a cycle resulting in sperm-ovum-co-localisation (πSOC); (2) subsequent successful fertilisation (πFERT); (3) initiation of implantation approximately 1 week after fertilisation as indicated by increased levels of hCG (πHCG); (4) progression to a clinical pregnancy (πCLIN): the earliest typical clinical indication is an absent menstrual period approximately 14 days after fertilisation, although definitions of clinical pregnancy vary between studies; (5) survival of a clinical pregnancy to a live birth (πLB). Conditional probabilities are defined more formally as follows:
If P(A|B) is the probability of event A, conditional on event B, then:
i. πLB = P(A|B), where A is a live birth, and B is a clinical pregnancy
ii. πCLIN = P(A|B), where A is a clinical pregnancy, and B is a positive hCG test
iii. πHCG = P(A|B), where A is a positive hCG test, and B is successful fertilisation
iv. πFERT = P(A|B), where A is successful fertilisation, and B is the in vivo co-localisation of ovum and sperm
v. πSOC = P(A|B), where A is the in vivo co-localisation of ovum and sperm, and B a single menstrual cycle
It is therefore possible to calculate four different fecundabilities (broadly following Leridon21):
1. Total (All fertilisations): FECTOT = πSOC × πFERT
2. Detectable (Implantation): FECHCG = πSOC × πFERT × πHCG
3. Apparent (Clinical): FECCLIN = πSOC × πFERT × πHCG × πCLIN
4. Effective (Live Birth): FECLB = πSOC × πFERT × πHCG × πCLIN × πLB
Quantitative differences between these fecundabilities reflect intrauterine mortality at different developmental stages. Hence, the probability that a fertilised egg will perish prior to implantation is [1 − πHCG], and prior to clinical recognition is [1 – (πHCG × πCLIN)]. In theory, embryonic mortality may be estimated at all stages although in practice this depends on available data.
In 1969, Barrett & Marshall analysed the relationship between coital patterns and conception and concluded that fecundability increased with coital frequency up to 68% for daily intercourse22. Schwartz’s re-analysis of the same data revealed a similar pattern, although at higher coital frequencies estimated fecundability was lower, at 49% for daily intercourse23. These analyses indicate that failure to conceive at coital frequencies of less than once per day is, in part, due to mistimed coitus and not solely failure of fertilisation and/or embryo mortality. The difference in their estimates of fecundability arises because of key differences between the two analyses. Firstly, Schwartz analysed 2,192 cycles, 294 more than Barrett & Marshall. Secondly, the measures of conception differed: Barrett & Marshall used “absence of menstruation, after ovulation”, approximately 2 weeks after ovulation, whereas for Schwartz conception was “defined as a pregnancy lasting at least 2 months from the last menstrual period”, i.e., approximately 6 weeks from the day of ovulation. It is not surprising therefore that Schwartz values were lower since they will not have captured pregnancies that failed between 2 and 6 weeks post-fertilisation. Thirdly, and importantly, Schwartz introduced a new term, ‘cycle viability’, into the analytical model.
Schwartz modelled the probability of conceiving during a cycle (i.e., fecundability, FEC) as the product of three conditional probabilities as follows: FEC = PoPfPv. Po, Pf and Pv were the probabilities that (i) a fertilisable egg is produced (Po), (ii) it is fertilised once produced (Pf), and (iii) it survives to be detected as a conception (Pv). Pf was modelled as a function of coital frequency. Cycle viability (k) was defined as k = PoPv, and allows for the possibility that optimally-timed coitus would not result in a detected conception. It implies that there is a proportion of cycles that are infertile irrespective of coital activity. Although Schwartz did not explicitly report statistical data demonstrating that the extra parameter (k = 52%) improved the quality of the model, a comparison of the Barrett & Marshall and Schwartz models using the Wilcox study data6 provided compelling statistical evidence to this effect, and concluded that only 37% of cycles were ‘viable’24.
Since cycle viability (k) includes terms defining reproductive success both before (Po = successful ovulation) and after (Pv = embryo survival) fertilisation, it is not possible to use this term to make direct inferences about early embryo mortality. Nevertheless, Schwartz assumed that Po = 100%, thereby interpreting all cycle non-viability as a consequence of embryo loss at a rate of 48% during the first 6 weeks after fertilisation. Similar logic applied to the Wilcox study24 would conclude an equivalent estimate of 63% embryo mortality. Schwartz also concluded that Pf = 94% for daily intercourse (0.49/0.52). Hence, Schwartz attributed almost all the observed reproductive inefficiency to embryo mortality and other processes of the reproductive process were, by implication, considered to work almost perfectly. By contrast, referring to fertilisation, Hertig noted that “it seems unlikely that such a complicated process should work perfectly every time”5. It has also been correctly pointed out that preimplantation loss is statistically indistinguishable from other causes of cycle non-viability including male factors15. It seems that this interpretation of reproductive inefficiency has contributed to a widespread impression that early human embryo mortality is very high.
What are the potential explanations for cycle non-viability? Incorporation of a between-couple random effect into the modelling of these data has confirmed that cycle viability is heterogeneous between couples15. A subject-specific random effects modelling approach also resulted in a more consistent cycle by cycle estimate of cycle viability25. These analyses formally demonstrate that within the cohorts of women used in this study, there were individual differences in fecundability. Furthermore, in the Wilcox study, 14 out of 221 women were unable to conceive within 24 months6: this observation alone suggests that a proportion of the study participants were sub-fertile.
Each of the three hCG studies sought to recruit normally fertile, non-contracepting women who intended to conceive. Subjects either had “no known fertility problems”6, or were excluded if they had any “known risk factors for infertility”7 or “had tried unsuccessfully to get pregnant for ≥1 year at any time in the past”8. However, such criteria cannot guarantee complete exclusion of sub-fertile or infertile couples, and in each study pregnancy rates declined in successive cycles as the presumed proportion of sub-fertile women remaining increased. Hence, calculations based on overall aggregate data underestimate fecundability in normally fertile women. Even estimates based on first cycle data are likely to be biased since a proportion of sub-fertile of women would be in the starting cohort. The extent of the bias of such estimates will depend on factors including the heterogeneity of the population and the number of cycles studied.
Estimates for FECHCG of 30%7 and 40%8, and for FECCLIN of 30%8 and 25%6 probably underestimate the fecundability of reproductively healthy women owing to a mixed fertile/sub-fertile population in these studies. The object of the present analysis was to determine whether the published aggregate data supported this hypothesis and to estimate fecundability for any sub-cohorts identified. The modelling approach is conceptually simple; nevertheless, the results strongly indicate that the hypothesis is true and therefore provide less biased estimates of fecundability for reproductively normal women. These higher estimates of fecundability narrow the range of plausible values for embryo mortality in normal fertile women.
Data were obtained from Table 2 of Wilcox6, Table 3 and Figure 1 of Zinaman7 and Table 2 of Wang8 studies. Fourteen women who did not conceive after 24 months were included in the analysis of the Wilcox data (1 reproductive cycle per month was assumed). A subsequent publication reported an extra cycle and an extra hCG pregnancy26; however, it is not clear in which cycle this occurred, and so the original report data6 have been used. In Wilcox and Wang, for each study cycle, the number of (i) women starting each cycle, (ii) hCG pregnancies, and (iii) clinical pregnancies were recorded. The number of women who finished the study without becoming clinically pregnant and the number of women who dropped out at the end of each cycle were also reported. Women who conceived an hCG positive pregnancy but not a clinical pregnancy in a cycle continued in the study. Wilcox reported data for a maximum of nine cycles per subject and Wang for 14. The Zinaman study was similar, except that hCG data were obtained for only the first three study cycles. In the subsequent nine cycles only clinical pregnancy was recorded. Also, only the first pregnancy, whether hCG or clinical was reported.
Probabilities and percentages were estimated as logits (base 10). Standard errors are shown. Actual probabilities with 95% confidence intervals are reported in Figure 1. Two alternatively parameterised (Model 0 & Model 00) but statistically identical models were used to obtain standard errors for FECHCG and FECCLIN since FECCLIN = FECHCG × πCLIN (ELS = extended least squares; dof = degrees of freedom.)
Degrees of freedom (dof) is the difference in the number of estimated parameters between the models. χ2 is the difference in objective function values (ELS) for the two models. P values were calculated using likelihood ratio tests. The models are defined in brackets. H0 is the null hypothesis. H1 is the alternative hypothesis. NONMEM control files are named according to the study and the model, e.g., Model 0 for the Wang data is WANG0.ctl.
Estimates of hCG (FECHCG) and clinical (FECCLIN) fecundabilities and πCLIN are derived from three hCG pregnancy studies as described in the text. πLB is calculated from published values in Wilcox6, Zinaman7 and Wang8 study reports. Estimates of fertilised egg loss up to implantation, clinical recognition and birth are provided, based on three scenarios: (i) high implantation probability (πHCG = 90%); (ii) equal implantation and fertilisation probabilities (πFERT = πHCG); (iii) high fertilisation probability (πFERT = 90%). The probability of sperm-ovum-co-localisation (πSOC) was assumed to be 0.80.
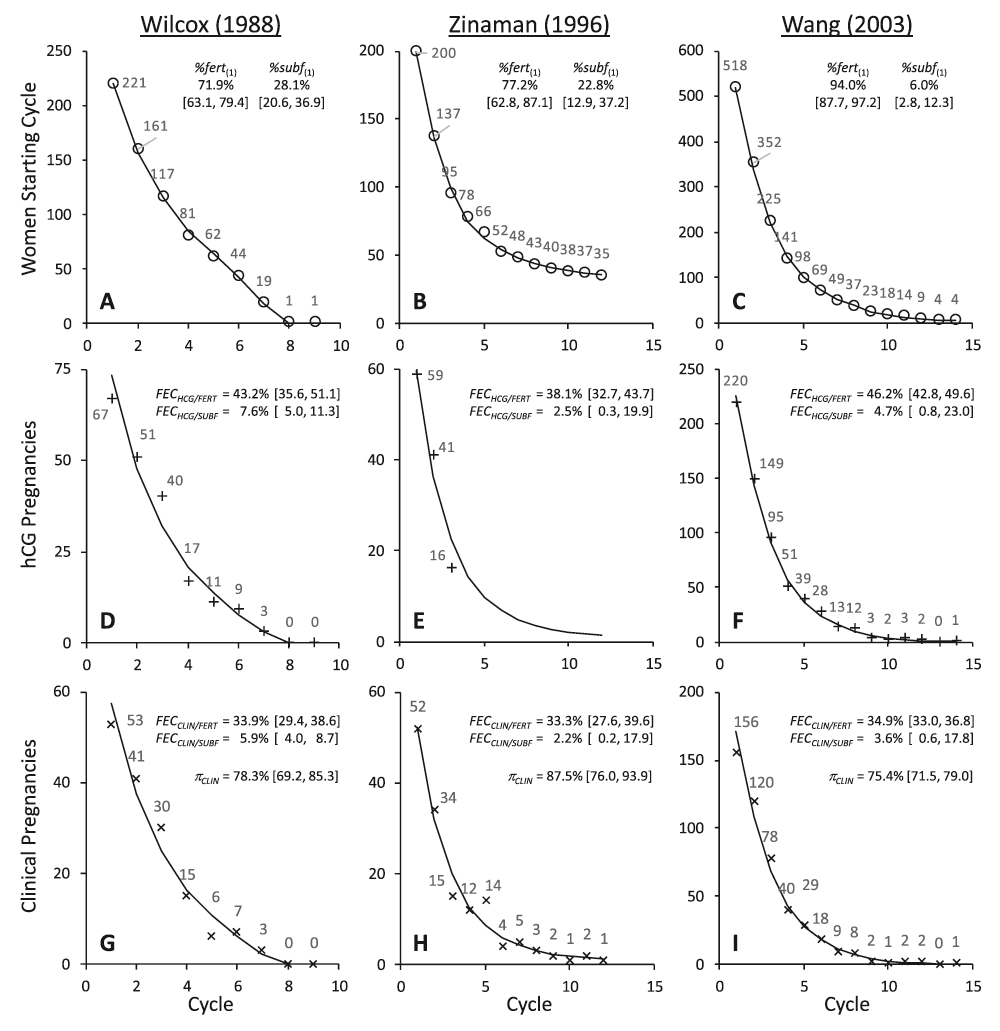
Each panel shows the data value from the study for each point (○ = women starting cycle; + = hCG pregnancies; × = clinical pregnancies). The line indicates the best fit models as defined in Table 1. Parameter estimates and [95% confidence intervals] from these models are also shown.
Observed data were modelled to estimate the following parameters: (1) %fert(1) = the percentage of fertile women in the starting cohort; (2) FECHCG = the probability of conceiving an hCG pregnancy per cycle; (3) FECCLIN the probability of becoming clinically pregnant per cycle. Alternative parameterisation allowed the probability of an hCG pregnancy progressing to a clinical pregnancy (πCLIN) to also be determined. The percentage of sub-fertile women in the starting cohort was %subf(1) = 100% – %fert(1). FECHCG, FECCLIN and πCLIN were determined for both fertile and sub-fertile sub-cohorts. The following expressions define the relationship between the parameters and the modelled estimates.
Where: N(#) is the number of women starting cycle # (for cycle 1, N(1) was fixed for each set of study data; Wilcox = 221; Zinaman = 200; Wang = 518); NFERT(#) and NSUBF(#) are the modelled number of fertile and sub-fertile women starting cycle #; PREGHCG/FERT(#) and PREGCLIN/FERT(#) are predicted numbers of hCG and clinical pregnancies in fertile women in cycle # (and analogously for sub-fertile women); FIN(#) is the number of women who finished the study without becoming clinically pregnant in cycle #; DROP(#) is the number of women who withdrew from the study at the end of cycle #; %fert(#) is the percentage of women starting cycle # who were fertile (and analogously for sub-fertile women); NONPREG(#) is the number of non-pregnant women after # cycles (equation (9) was only used to incorporate 14 non-pregnant women after 24 months into the Wilcox data model). Model expansion to allow three fertility sub-cohorts and contraction to a single fertility sub-cohort enabled hypotheses about parameters and sub-cohorts to be statistically evaluated.
All probabilities and percentages were estimated as logits (base 10). Residual unexplained variance (RUV) was modelled as a function of predicted values (PRED) as follows:
…where σ is an estimated parameter defining residual error and γ a coefficient defining the relationship between the dependent variables and PRED. When γ = 0, the residual model is homoscedastic. When γ = 2, the residual coefficient of variation is a constant.Data were analysed with NONMEM 7.3.0 (Icon PLC, Dublin, Eire) and implemented using Wings for NONMEM (http://wfn.sourceforge.net/). Parameters were estimated using a maximum likelihood algorithm (First Order Conditional Estimate with Interaction) and standard errors derived using the inverse Hessian (MATRIX = R). The objective function in NONMEM is the Extended Least Squares (ELS)27. Statistical hypotheses of nested models (Table 2) were tested using likelihood ratio tests (LRT). Control and data files are available online. Control files are named from the study and the model, e.g., WANG0.ctl is the control file for Model 0 applied to the Wang study data.
Figure 1 shows the original data values and the fitted models plotted by cycle. Parameter estimates are also shown and output from the models is given in Table 1. These models incorporate discrete fertile and sub-fertile sub-cohorts with differing FECHCG but common πCLIN values. Statistical comparison of alternative models strongly indicated that reducing the dimensionality of the model to a single FECHCG value substantially reduced its quality (Table 2, Hypothesis 1), whereas expanding the model to allow for three different FECHCG values did not improve the quality of the model (Table 2, Hypothesis 2). These statistical results indicate that the data are consistent with bi-modal study populations comprising two distinct fertility sub-cohorts. There was no statistical indication that πCLIN differed between these sub-cohorts (Table 2, Hypothesis 3). Evidence for heteroscedasticity in the residual error was strong for the Wilcox and Wang studies, and weak for the Zinaman study (Table 2, Hypothesis 4).
Figure 2 illustrates the estimated parameter values. Notwithstanding the differences between the studies, there is considerable agreement in the estimates. One noteworthy difference is in the proportion of sub-fertile women. This was low (6.0%) in the Wang study compared to the other two which were approximately 25%. Zinaman et al. commented on the high proportion of apparently infertile women in their study despite their efforts during recruitment7. The estimate of 22.8% sub-fertile women is consistent with their estimate of 18% infertility, bearing in mind that sub-fertile women may conceive, albeit with a lower probability. The Wang study was conducted in young Chinese women and had the highest FECHCG/FERT (46.2%) and lowest πCLIN (75.4%) values. This may reflect the Bayesian methodology used to detect hCG positive cycles, the identification of DDT (dichlorodiphenyltrichloroethane), present at unusually high levels in this group28, as a positive predictor of pre-clinical pregnancy loss29, or even a higher incidence of gestational tropho-blastic disease in Asian women30.
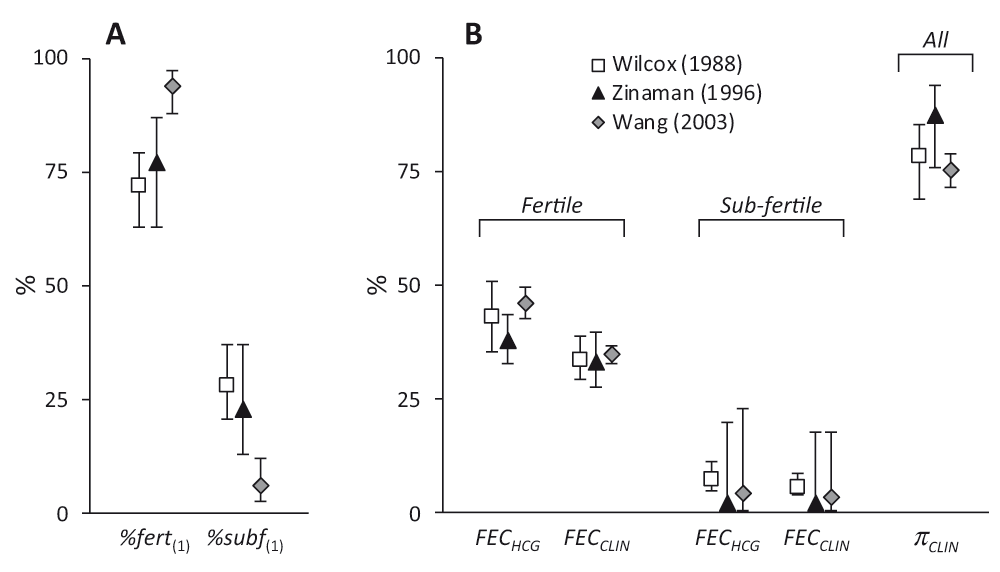
Values are shown for Wilcox (□), Zinaman (▲) and Wang ( ) studies. Panel A shows the proportions in the starting cohorts modelled as fertile or sub-fertile (%fert(1) & %subf(1)). Panel B shows the hCG (FECHCG) and clinical (FECCLIN) fecundabilities and the probability of hCG pregnancies progressing to clinical pregnancies (πCLIN). Values are derived from modelled parameter estimates (Table 1) and error bars indicate 95% confidence intervals.
) studies. Panel A shows the proportions in the starting cohorts modelled as fertile or sub-fertile (%fert(1) & %subf(1)). Panel B shows the hCG (FECHCG) and clinical (FECCLIN) fecundabilities and the probability of hCG pregnancies progressing to clinical pregnancies (πCLIN). Values are derived from modelled parameter estimates (Table 1) and error bars indicate 95% confidence intervals.
The analysis also indicates that fewer hCG pregnancies in the Zinaman study (12.5%) failed to progress to clinical recognition, compared to either the Wilcox (21.7%) or Wang (24.6%) studies. This may reflect differences in methodology for detecting hCG, the fact that they made fewer hCG measurements or differences in the definition of clinical pregnancy. Wilcox and Wang defined clinical pregnancy as those that lasted for up to 6 weeks after the last menstrual period6,8,17,26. In Zinaman, clinical pregnancy was determined following serum testing if a woman’s anticipated menses was just one day late7. Hence, the window for pre-clinical embryo loss was approximately 1–4 weeks post-fertilisation for Wilcox and Wang and 1–2 weeks for Zinaman. This different definition of clinical pregnancy would not only contribute to the higher πCLIN value from Zinaman but also the increased clinical loss of 21.0% compared to 12–13% observed by Wilcox and Wang.
Quantifying the outcome of clinical pregnancies is relatively straightforward. Excluding those lost to follow-up and induced abortions, the probability of a clinical pregnancy progressing to a live birth (πLB) was: Wilcox, 87.7% (136/155); Zinaman, 79.0% (79/100); and Wang, 87.1% (373/428). Combining these values with the modelled πCLIN provides an estimate for embryo loss from implantation to live birth of 31.3% (Wilcox), 30.9% (Zinaman) and 34.2% (Wang) (Table 3).
Estimating embryo loss prior to hCG detection is less straightforward. For sub-fertile participants, it is impossible to know why they struggled to become pregnant: there are many causes of sub-fertility31. However, for normally fertile women the modelled hCG fecundability values can be used to put limits on fertilisation (πFERT) and implantation (πHCG) conditional probabilities. As noted above, fecundability is the product of the conditional probabilities of success for each stage of the reproductive cycle. Hence for Wang:
FECHCG = πSOC × πFERT × πHCG = 0.462
Since probabilities cannot be greater than 1, the lowest possible value for πHCG must be 0.462, indicating a maximum possible loss from fertilisation up to implantation in these women of 53.8%. However, it is unlikely that all other probabilities equal 1. Sperm-ovum-co-localisation is dependent on both behavioural and biological factors. As previously noted, the analyses of Barrett & Marshall22,32 and Schwartz23 show that daily intercourse is more reproductively effective than alternate day intercourse. Hence, at coital frequencies less than once per day, πSOC must be less than 1. Specifically, a reduction of fecundability from 0.49 with daily to 0.39 for alternate day intercourse23 points towards a reduction in πSOC of approximately 20%. Volunteers in these hCG studies wished to become pregnant and were undoubtedly aware of the importance of well-timed intercourse. However, they were not required to have daily intercourse and it is likely that in some of the 3,137 cycles intercourse was not always ideally timed. Indeed, in 360/625 cycles in the Wilcox study, intercourse occurred from zero to two times during the 6 days before ovulation, and intercourse occurred on only 40% of the 6 pre-ovulatory days in 625 cycles17. It seems likely therefore that πSOC and hence fecundability were not maximised in these studies.
Furthermore, not all cycles are ovulatory. Leridon suggested that levels of anovulation lie between 5 and 15%33. Among normal healthy women, the incidence of anovulation ranged from 5.5–12.8% depending on the detection method used34. Therefore, considering behavioural and biological factors together, it seems reasonable to suppose that πSOC < 1.
It also seems unlikely that either fertilisation or implantation probabilities equal 1. Hence, Table 3 shows derived values for πFERT and πHCG assuming that πSOC = 0.80, and under conditions where: (i) πFERT = 0.90; (ii) πFERT = πHCG; and (iii) πHCG = 0.90. Based on this analysis, a plausible range for total embryo loss from fertilisation to birth is 40–60%. This is consistent with estimates from both older35 and more recent36 text books. Even with the wide range of mathematically possible outcomes, it is likely that estimates of 90%20, 83%37, 80–85%38, 78%1, 76%2 and 70%10,12 total human embryonic loss are excessive.
In 1980, Schwartz wrote that Barrett & Marshall’s estimate of fecundability of 0.68 for daily intercourse “seems to be high”. It implies an absolute maximum limit of embryo mortality of 32%. Schwartz contrasted this with Leridon’s estimate of 44% embryo loss in the first 6 weeks following fertilisation3. However, Leridon’s estimates for early intrauterine mortality are substantially dependent on data and analysis from Hertig4,5, which are themselves of questionable precision2,13,39. Widespread pessimism about human reproductive efficiency may have become a self-fulfilling prophecy in the absence of relevant good quality data.
Nevertheless, Schwartz’s analysis is a useful improvement on that of Barrett & Marshall and points clearly to the presence of infertile or non-viable cycles. The challenge arises in assigning a mechanistic cause for this “non-viability”. Previous reports draw attention to the difficulty of teasing apart distinct components, e.g., egg viability versus uterine receptivity24, or male and female factors15, and alternative modelling approaches will yield “different interpretations of the parameters related to cycle viability”15. The advantage of the present models is that the unit of analysis remains the cycle, i.e., fecundability, but the heterogeneity of the population is also acknowledged and explicitly incorporated. The model for estimating embryo loss also accommodates other plausible mechanisms for reproductive failure, rather that accrediting all unaccounted reproductive inefficiency to pre-implantation embryo mortality. Although the model does not provide a definitive answer, it does offer plausible limits within which the answer may lie.
The results of this analysis offer a statistically clear picture of bi-modal study populations comprising couples with two discrete levels of fertility. This dichotomous division of the study populations is arguably artificial: it is unlikely to capture all the quantitative subtlety that subsists in the original data. Nevertheless, expanding the model to three levels does not improve this picture and the published data do not support a model of uni-modal, albeit varied, fecundability. Put simply, there was a significant proportion of couples in these studies who were, for unknowable reasons, infertile or clearly sub-fertile. Incorporation of data derived from such couples in calculations to determine normal fecundability will therefore result in biased estimates. By analytically separating the study population into reproductively normal and sub-fertile sub-cohorts, more accurate estimates for normal reproductive function and embryo mortality have been obtained. Such estimates apply primarily to the specific study populations, which are not necessarily fully representative of a general population. The extrapolation of quantitative conclusions into other contexts and circumstances must always be done with appropriate caution.
The analysis presented here cannot be satisfactorily completed owing, in part, to a lack of data on fertilisation success rates in vivo40,41. Consequently, the range for pre-implantation loss, at approximately 10–40%, is wide, although inclusive of Hertig’s pre-implantation loss estimate of 30%4,5. Despite the imperfections and weaknesses in the available data, it is apparent that plausible values for embryo mortality are considerably less than some figures published in the scientific literature. It is concluded that a plausible range for natural human embryo mortality from fertilisation to live birth in normal healthy women is approximately 40–60%.
F1000Research: Dataset 1. Raw data Wilcox et al. study, 10.5256/f1000research.9479.d13395142
F1000Research: Dataset 2. Raw data Zinaman et al. study, 10.5256/f1000research.9479.d13395243
F1000Research: Dataset 3. Raw data Wang et al. study, 10.5256/f1000research.9479.d13395344
Thanks are due to Professor David Paton for providing helpful comments and suggestions during the writing of this paper.
| Views | Downloads | |
|---|---|---|
| F1000Research | - | - |
|
PubMed Central
Data from PMC are received and updated monthly.
|
- | - |
References
1. Macklon NS, Geraedts JP, Fauser BC: Conception to ongoing pregnancy: the 'black box' of early pregnancy loss.Hum Reprod Update. 8 (4): 333-43 PubMed AbstractCompeting Interests: No competing interests were disclosed.
References
1. Makubate B, Senn S: Planning and analysis of cross-over trials in infertility.Stat Med. 2010; 29 (30): 3203-10 PubMed Abstract | Publisher Full TextCompeting Interests: No competing interests were disclosed.
Alongside their report, reviewers assign a status to the article:
| Invited Reviewers | ||
|---|---|---|
| 1 | 2 | |
|
Version 2 (revision) 06 Dec 16 |
||
|
Version 1 26 Aug 16 |
read | read |
Click here to access the data.
Spreadsheet data files may not format correctly if your computer is using different default delimiters (symbols used to separate values into separate cells) - a spreadsheet created in one region is sometimes misinterpreted by computers in other regions. You can change the regional settings on your computer so that the spreadsheet can be interpreted correctly.
Click here to access the data.
Spreadsheet data files may not format correctly if your computer is using different default delimiters (symbols used to separate values into separate cells) - a spreadsheet created in one region is sometimes misinterpreted by computers in other regions. You can change the regional settings on your computer so that the spreadsheet can be interpreted correctly.
Click here to access the data.
Spreadsheet data files may not format correctly if your computer is using different default delimiters (symbols used to separate values into separate cells) - a spreadsheet created in one region is sometimes misinterpreted by computers in other regions. You can change the regional settings on your computer so that the spreadsheet can be interpreted correctly.
Provide sufficient details of any financial or non-financial competing interests to enable users to assess whether your comments might lead a reasonable person to question your impartiality. Consider the following examples, but note that this is not an exhaustive list:
Sign up for content alerts and receive a weekly or monthly email with all newly published articles
Already registered? Sign in
The email address should be the one you originally registered with F1000.
You registered with F1000 via Google, so we cannot reset your password.
To sign in, please click here.
If you still need help with your Google account password, please click here.
You registered with F1000 via Facebook, so we cannot reset your password.
To sign in, please click here.
If you still need help with your Facebook account password, please click here.
If your email address is registered with us, we will email you instructions to reset your password.
If you think you should have received this email but it has not arrived, please check your spam filters and/or contact for further assistance.
Comments on this article Comments (0)