A pilot study: Can heart rate variability (HRV) be determined using short-term photoplethysmograms?

Mohamed Elgendi; Ian Norton; Matt Brearley; Socrates Dokos; Derek Abbott; Dale Schuurmans

doi:10.12688/f1000research.9556.1

Home Browse A pilot study: Can heart rate variability (HRV) be determined using...

ALL Metrics

-

Views

-

Downloads

Get PDF

Get XML

Export

▬

✚

Research Article

A pilot study: Can heart rate variability (HRV) be determined using short-term photoplethysmograms?

[version 1; peer review: 2 approved with reservations]

Mohamed Elgendi^1-3, Ian Norton⁴, Matt Brearley⁴, Socrates Dokos⁵, Derek Abbott⁶, Dale Schuurmans³

Mohamed Elgendi^1-3, Ian Norton⁴, [...] Matt Brearley⁴, Socrates Dokos⁵, Derek Abbott⁶, Dale Schuurmans³

PUBLISHED 22 Sep 2016

Author details Author details

¹ Department of Obstetrics & Gynecology, University of British Columbia, Vancouver, Canada
² Department of Electrical and Computer Engineering, University of British Columbia, Vancouver, Canada
³ Department of Computing Science, University of Alberta, Edmonton, Canada
⁴ National Critical Care and Trauma Response Centre, Darwin, Australia
⁵ Graduate School of Biomedical Engineering, University of New South Wales, Sydney, Australia
⁶ School of Electrical and Electronic Engineering, University of Adelaide, Adelaide, Australia

OPEN PEER REVIEW

REVIEWER STATUS

Abstract

To date, there have been no studies that investigate the independent use of the photoplethysmogram (PPG) signal to determine heart rate variability (HRV). However, researchers have demonstrated that PPG signals offer an alternative way of measuring HRV when electrocardiogram (ECG) and PPG signals are collected simultaneously. Based on these findings, we take the use of PPGs to the next step and investigate a different approach to show the potential independent use of short 20-second PPG signals collected from healthy subjects after exercise in a hot environment to measure HRV. Our hypothesis is that if the PPG--HRV indices are negatively correlated with age, then short PPG signals are appropriate measurements for extracting HRV parameters. The PPGs of 27 healthy male volunteers at rest and after exercise were used to determine the HRV indices: standard deviation of heartbeat interval (SDNN) and the root-mean square of the difference of successive heartbeats (RMSSD). The results indicate that the use of the $aa$ interval, derived from the acceleration of PPG signals, is promising in determining the HRV statistical indices SDNN and RMSSD over 20-second PPG recordings. Moreover, the post-exercise SDNN index shows a negative correlation with age. There tends to be a decrease of the PPG--SDNN index with increasing age, whether at rest or after exercise. This new outcome validates the negative relationship between HRV in general with age, and consequently provides another evidence that short PPG signals have the potential to be used in heart rate analysis without the need to measure lengthy sequences of either ECG or PPG signals.

Keywords

Mobile health, Point-of-care device, Affordable healthcare, Moving averages

Corresponding author: Mohamed Elgendi

Competing interests: No competing interests were disclosed.

Grant information: Funding for the research project was provided by the Government of the Commonwealth of Australia.

The funders had no role in study design, data collection and analysis, decision to publish, or preparation of the manuscript.

Copyright: © 2016 Elgendi M et al. This is an open access article distributed under the terms of the Creative Commons Attribution License, which permits unrestricted use, distribution, and reproduction in any medium, provided the original work is properly cited. The author(s) is/are employees of the US Government and therefore domestic copyright protection in USA does not apply to this work. The work may be protected under the copyright laws of other jurisdictions when used in those jurisdictions.

How to cite: Elgendi M, Norton I, Brearley M et al. A pilot study: Can heart rate variability (HRV) be determined using short-term photoplethysmograms? [version 1; peer review: 2 approved with reservations]. F1000Research 2016, 5:2354 (https://doi.org/10.12688/f1000research.9556.1) First published: 22 Sep 2016, 5:2354 (https://doi.org/10.12688/f1000research.9556.1) Latest published: 22 Sep 2016, 5:2354 (https://doi.org/10.12688/f1000research.9556.1)

Introduction

The most commonly accepted heart rate variability (HRV) metric to measure both instantaneous heart rate (HR) and RR intervals is derived from electrocardiogram (ECG) signals. Metrics used to describe HRV in literature include heart period variability, cycle length variability, RR interval tachogram, and RR variability.

HRV measurement captures HR variations of the mean HR, while providing information on the stability of the sympathetic–parasympathetic autonomic system. This in turn provides information on the risk of sudden cardiac death. An example of this can be seen when continuous subjection to dry heat occurs with subjects. Dry heat exposure provokes a stress response that is designated by increased HR, which occurs due to a significant reduction in parasympathetic control of the HR, which is signified by reduced HRV¹.

The traditional method of identifying heartbeats in ECGs is by detecting R peaks. In almost every study, comparisons are made between HRV calculated from ECG signals and those calculated from photoplethysmogram (PPG) signals. In these studies, the feasibility of using PPGs as an alternative simple, inexpensive, and convenient diagnostic tool was explored in parallel with the use of ECGs. The overall results showed that PPG is potentially an ideal stand-alone alternative but it has not been explored independently, possibly explaining why there are no known investigations into the alternate use of PPG signals to measure HR and HRV.

It is noted that accurately detecting inter-beat intervals from fingertip PPG signals is challenging^2–4. Bernston et al.², noted these challenges and recommended using RR intervals from ECG signals to determine inter-beat intervals. Even with the use of a peak detection algorithm that is sophisticated, using intra-arterial pressure pulses is likely acceptable but indirect PPG signal measures need further validation. The contour of the PPG can measure HRV through the detection of the heartbeat, and thus HRV can be measured⁵.

Giardino et al.⁴ demonstrated that it is sufficient to use the distal pulse pressure, under resting conditions, to determine the heart rate as shown in Figure 1(a). The authors also recommended further investigations into the test-retest reliability evaluation for different data collection techniques.

Figure 1.

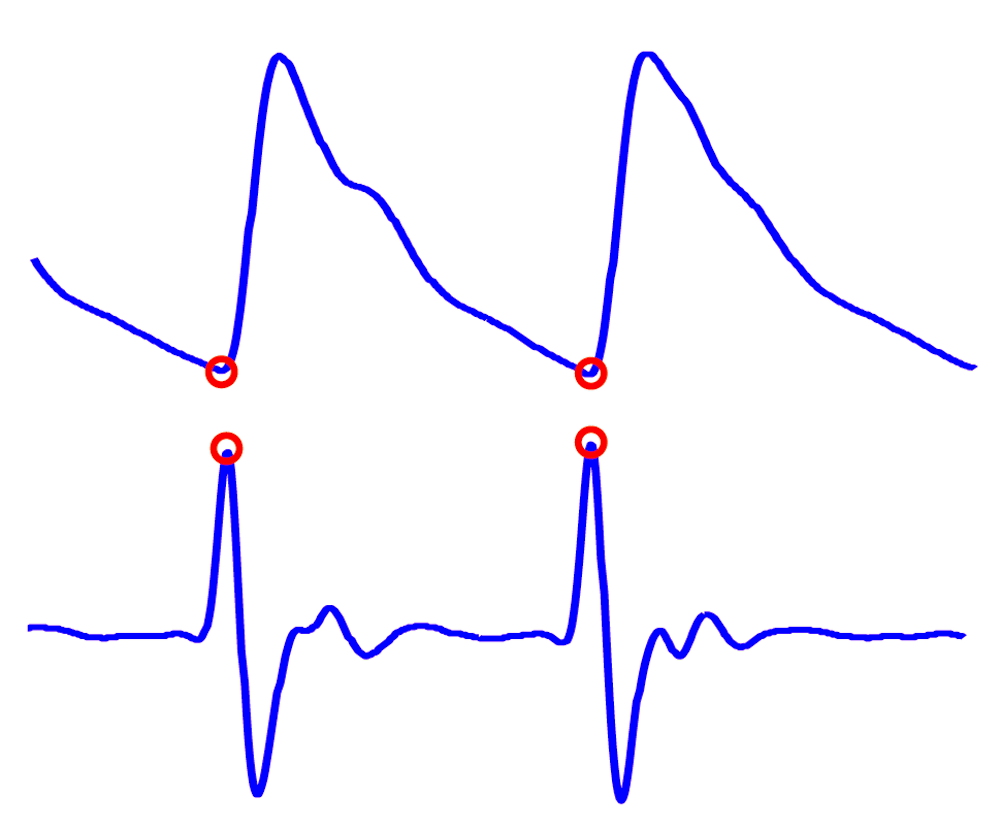
Two successive beats in (a) fingertip photoplethysmogram (PPG) signal (b) second derivative wave of photoplethysmogram (APG) signal.

These cautious evaluations may explain the reason for limited investigation into the use of PPG signals (rather than ECG) to measure HR and HRV.

The contour of the PPG can be utilized to detect the heart beat and therefore HRV can be measured from the contour⁵. In Figure 1(a) two circles, with the smallest positive PPG amplitudes, represent two consecutive heartbeats. Reliable detection of the heartbeats using the PPG contour is, however, challenging due to noise and the nature of its associated interference with hemodynamic variables⁶. These identified challenges can be addressed by using the second derivative of the photoplethysmogram waveform, also known as the acceleration plethysmogram (APG). In Figure 1(b), two circles with the largest positive amplitudes, represent two consecutive heartbeats of the APG signal. The heart rate is more accurately detected using the APG signal due to the clearly defined peaks in the APG, when compared to the peaks in the PPG contour (more specifically the a wave), as shown in Figure 2(b).

Figure 2. Fingertip photoplethysmogram signal measurement⁷.

(a) Fingertip photoplethysmogram. (b) Second derivative wave of photoplethysmogram. The photoplethysmogram waveform consists of one systolic wave and one diastolic wave, while the second derivative photoplethysmogram waveform consists of four systolic waves (a, b, c, and d waves) and one diastolic wave (e wave).

We therefore sought to validate the usefulness of PPGs using an alternative method without the collection of ECGs based on the already established negative correlation between HRV and age⁸. We hypothesized that if the PPG–HRV indices calculated from short PPG signals are negatively correlated with age then a short PPG signal is an appropriate measurement for extracting HRV parameters. In this study, only the standard deviation of the heartbeat interval (SDNN) and the root-mean square of the difference of successive heartbeats (RMSSD) indices are investigated, as they are suitable for short recordings based on the recommendation in 9. Herein we investigate if the SDNN and RMSSD calculated from short PPG signals measured before and after exercise can potentially be correlated with age.

Materials and methods

Ethics statement

Charles Darwin University (CDU) has one annotated PPG database available with data collected, in 2006. The dataset includes participant recordings during rest (before exercise) and after one hour of exercise (walking) on a treadmill in the climate control chamber at the Northern Territory Institute of Sport (Darwin, Australia). PPG data was collected on three separate occasions during each rest period as shown in Figure 3.

Figure 3. Measurement Protocol.

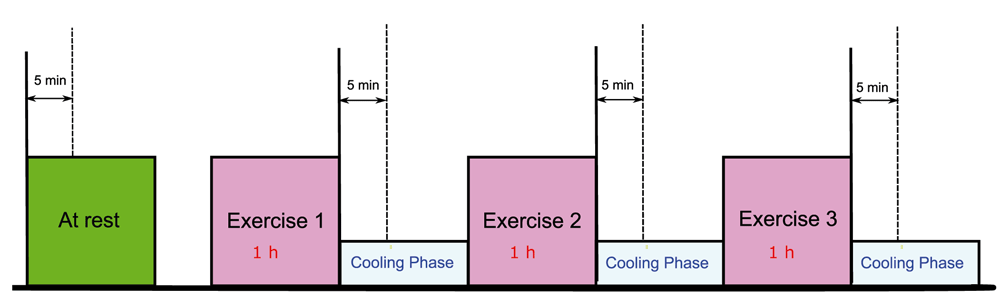
The duration of the whole experiment was approximately 4 hours, each exercise consumed approximately 1 hr while the PPG signals collected during the 5 minutes break of each exercise at a sampling rate of 200 Hz. The length of each PPG recording is 20 seconds.

Exercise was set to moderate intensity, with the treadmill speed set at 5 km/h with a 1% incline increment (which corresponds to effort required to walk on 8 kg of webbing). Details on the project are found at 10. Written consent was obtained from all subjects before participating in the Charels Darwin University Ethics Committee approved study and was conducted in accordance with applicable guidelines and regulations.

Database used

A photoplethysmography device (Salus APG, Japan) was used to measure PPG recordings from 27 healthy male volunteers (mean ± SD age of 27 ± 6.9). Sensors were placed on the second digit of the left hand on the cuticle. Measurements were recorded for each subject at rest on a chair. Data were collected at a sampling rate of 200 Hz, with recording duration of 20 seconds.

We used one PPG oximeter to collect the data from all subjects measured after each exercise. It was not plausible to collect data for a longer period of time as we needed to measure other subjects waiting in line. The longer the waiting time, the more the heat stress impact due to cooling of the body is lost. Therefore, it was convenient to collect data for a consistent recording length of 20 seconds. Preliminary feasibility was also tested with this method, since the collected of a shorter recording length is preferred in a clinical setting.

The beat annotations were performed by a cardiologist, and each beat was labeled as an a wave after processing the PPG signals with a second-order bandpass Butterworth filter from 0.5–8 Hz of the unfiltered PPG signal, based on the recommendation in 11. There were a total of 584 heartbeats founds in signals measured before exercise (during rest). A total of 885 heartbeats were founds in the PPG signals collected post one hour of exercise and also contained fast rhythm PPG signals.

Methodology

Detection of a wave. In this study, the a wave detection algorithm published in 12 will be used. Elgendi proposed an algorithm in 2013¹¹ that was used to detect systolic waves in PPG signals, QRS complexes in ECG signals¹³, and to detect c, d, and e waves in APG signals¹⁴. The algorithm is adapted for this paper and the same approach will be utilized to detect the a waves, which has four stages: bandpass filtering, squaring, generating potential blocks, and thresholding and uses five parameters F₁, F₂, MA_peak, MA_beat, and β. Each stage is explained in more detail as follows.

• Bandpass filter: A zero-phase second-order Butterworth filter, with bandpass 0.5–15 Hz, was implemented to remove frequency components that do not contribute to the a wave, such as the baseline wander and high frequencies. A filtered S[n] signal was produced by applying the output of the zero-phase Butterworth filter the PPG signal—at rest and post exercise—produced a filtered signal Therefore, F₁ = 0.5 Hz and F₂ = 15 Hz based on a brute force search that is discussed in the parameter optimization section in 12.
• Second derivative: The second derivative was used on the filtered PPG to obtain and analyze the APG signals. Non-causal filters are represented by the Equation 1 and Equation 2. Using a delay of only two samples, the three-point centre derivative was created.

S^{'} [n] = \frac{d S}{d t} |_{t = n T} = \frac{1}{2 T} (S [n + 1] - S [n - 1]), (1)

Z [n] = \frac{d S^{'}}{d t} |_{t = n T} = \frac{1}{2 T} (S^{'} [n + 1] - S^{'} [n - 1]), (2)

T is the sampling interval and equals the reciprocal of the sampling frequency and n is the number of data points.
• Cancellation of b wave: Emphasis of the APG a wave is necessary to make it distinct for detection, which can be accomplished by cutting out the negative parts of the APG signal (Z[n] = 0, if Z[n] < 0).
• Squaring: Large differences that result from a wave are emphasized by squaring. Small differences from the diastolic wave and noise are suppressed, resulting in the output.
y[n] = Z[n]², (3)
This is important for improving the accuracy in distinguishing the a wave segment in APG signals.
• Generating blocks of interest: Using two event-related moving averages, blocks of interest are created, that demarcate the a wave and heartbeat areas.
In this procedure, the first moving average (MA_peak) is used to emphasize the a wave area, and is given by

M A_{p e a k} [n] = \frac{1}{W_{1}} (y [n - (W_{1} - 1) / 2] + ... + y [n] + ... + y [n + (W_{1} - 1) / 2]), (4)

where W₁ represents the window size of the systolic-peak duration. The resulting value is rounded to the nearest odd integer. The exact value for W₁ of 175 ms is determined based on a brute force search and is further discussed in the parameter optimization section in 12.
The beat area is emphasized by the second moving average (MA_beat) that will be used as a threshold for the first moving average, and is given by

M A_{b e a t} [n] = \frac{1}{W_{2}} (y [n - (W_{2} - 1) / 2] + ... + y [n] + ... + y [n + (W_{2} - 1) / 2]), (5)

where W₂ represents a window size of approximately one beat duration and is rounded to the nearest odd integer. A brute force search is used to determine the exact value of W₂ of 1000 ms and is further in the parameter optimization section in 12.
Thresholding: Determining the offset level is done using the following equation: (α) is β z, where β = 0 based on a brute force search and is discussed further in the parameter optimization section in 12, while z is the statistical mean of the squared filtered PPG signal. The first dynamic threshold value was calculated by shifting the MA_beat signal with an offset level α, as follows:
THR₁ = MA_beat[n] + α. (6)
By comparing the MA_peak signal with THR₁ blocks of interest were generated, resulting in the generation of many blocks of interest. Some will contain the APG feature (a wave), while others will mainly contain noise. Thus, block rejection for blocks that result from noise must be carried out next and is based on the anticipated systolic-peak width. For the purpose of this paper, rejection of undesired blocks using THR₂, which is a threshold that rejects the blocks containing diastolic wave and noise. Applying the THR₂ threshold, will result in only accepting blocks that contain a waves only,
THR₂ = W₁. (7)
As previously mentioned, the threshold THR₂ corresponds to the anticipated a wave duration. Classification of an a wave takes place when a block is wider than or equal to THR₂, otherwise it will be classified as noise. The final step in this process is to identify the maximum absolute value within each block to detect the a wave. Note that not all the blocks hold potential a waves, since some blocks are created by noise and need to be eliminated. Rejection of blocks will also take place when a block is smaller than the expected width for the a wave duration and are considered as noisy blocks. Accepted blocks are considered to hold an a wave. Detected a waves are compared against the annotated a waves to determine whether they were correctly detected.

Performance of the a wave detector. We used two statistical measures to evaluate the a wave detection performance: sensitivity (SE) and positive predictivity (+P); whereas SE = TP/(TP + FN) and +P = TP/(TP + FP). TP represents the total number of true positives (a wave detected as an a wave), FN represents the total number of false negatives (a wave has not been detected), and FP represents the total number of false positives (non-a wave detected as an a wave). The percentage of true, correctly detected a waves by the algorithm is reported by SE. The +P reports the percentage of the detected a waves that were true a waves. MATLAB 2012a (The MathWorks, Inc., Natick, MA, USA) was used to implement the a wave detector.

Calculation of HRV indices. The detected a waves (heartbeats) are used to calculate the duration of each consecutive aa interval, as follows: aa[i] = A[i + 1] − A[i], where A represents the annotated a waves in each PPG signal, and aa represents the aa intervals. Note that the main interest is to analyze the aa duration rather than the amplitude, no preprocessing is needed. It is known that HRV decreases with normal based on the analysis of R peaks in ECG signals^15–17. Therefore, based on using a waves in PPG signals, if the correlation between HRV and age is decreasing, PPG signals can potentially measure HRV. The correlation between age and HRV is found by calculating and comparing two time-domain HRV parameters and are typically used with ECG signals. The first parameter, SDNN, is the SD of heartbeat duration; here, the RR interval is replaced by aa intervals. The SDNN is calculated, as follows:

S D N N = (1 / N) \sum_{i = 1}^{N} {(a a [i])}^{2} - {(1 / N) \sum_{i = 1}^{N} (a a [i])}^{2} . (8)

The second parameter is RMSSD, which is calculated as follows:

R M S S D = \sqrt{(1 / N) \sum_{i = 1}^{N} {(a a [i])}^{2}} . (9)

Analysis of trend As we have a small sample size, there is a need to examine both the correlation coefficient (r) and the slope. Note that it is common to obtain a small correlation with a small sample size, and therefore the slope can be used as an alternative to determine the relationship. Here, r is calculated as follows: $r = \frac{C o v (u, v)}{σ_{u} σ_{v}},$ where Cov(u, v) is the covariance between data u and data v, σ_u is the SD of data u and σ_v is the SD of data v. Here, u and v refer to the HRV indices.

Significance of trend. To test the significance of the slope, we performed a multilinear regression of the responses in y on the predictors in x for all lines in Figure 4 and Figure 5. The null hypothesis states that the slope is equal to zero, and the alternative hypothesis states that the slope is not equal to zero. MATLAB 2012a (The MathWorks, Inc., Natick, MA, USA) was used to calculated the significance of trend.

Results and discussion

To date, several studies have evaluated the agreement between HRV calculated from PPG and ECG signals; however, some results remain controversial^18,19. This disagreement is due to applying inappropriate methodologies or inefficient experimental settings. A recent study by Chen et al.²⁰ showed that the accuracy of HRV obtained from PPG is mostly incommensurable across 26 unhealthy subjects. However, it has been proven that the HRV calculated from PPG signal is sufficient in its accuracy for only healthy (and mostly younger) subjects at rest²¹. Therefore, in our study, fit and healthy subjects were only considered. Because of this selection, it is expected that there will be no apparent differences between subjects. Moreover, we can focus on the age impact— without any dependencies such as arrhythmia, transvenous cardiac pacing, and heart transplant—as an indirect assessment for the usefulness of HRV calculated from PPG signals.

It is worth noting that the heat stress PPG data were collected for this study as a part of the project funded by the Australian Department of Defence. As mentioned in the ’Database used’ subsection, there was no exercise test with the same subjects in a cooler (or normal) environment included in the main project protocol. Therefore, we are unable comment, compare or discuss the HRV calculation in two different conditions, hot and cool environments.

The designed exercise length for the heat stress test was four hours; however, only 16 out of 27 subjects completed the full duration. All subjects were able to complete the first 1-hr exercise, and therefore we analyzed all PPG signals collected only after 1-hr exercise.

After collecting the PPG signals, perhaps the question was how can we calculate the HRV from these PPG signals more accurately. In the literature, we found that the second derivative of the PPG signal enhances its frequencies and improves waveform characteristics especially in heat stressed PPG signals²². Moreover, we found that detection of a waves in APG signals slightly increases the accuracy of detecting heart beats compared to systolic peaks in PPG signals. For example, the overall a wave detection rate was 99.9%¹², while the overall systolic wave detection rate was 99.8%¹¹. Therefore, we applied the second derivative to the PPG signal to obtain APG signals and then applied the a wave detection algorithm described in the 'Methodology’ section.

The a wave detection algorithm was evaluated using 27 records, containing 1,540 heartbeats (584 heartbeats measured at rest and 956 heartbeats measured after 1-hr exercise), with an overall SE of 99.8%, and the overall +P of 100%. The overall accuracy was sufficient enough to calculate the HRV indices automatically.

After the automatic detection of a waves, SDNN and RMSSD indices are calculated for 27 healthy subjects using PPG recordings each of 20 seconds duration during rest and after exercise. Figure 4(a) & (b) show the relationship between age and the SDNN index at rest and after exercise, respectively. The SDNN index at rest is more negatively correlated with age (r = −0.271) and has a steeper negative slope (−0.004) than after exercise (r = −0.12 and slope = −0.001). The slope significance for SDNN before exercise was p = 0.001, and the slope significance for SDNN after exercise was p = 0.04.

Figure 4. Correlation between age and SDNN index.

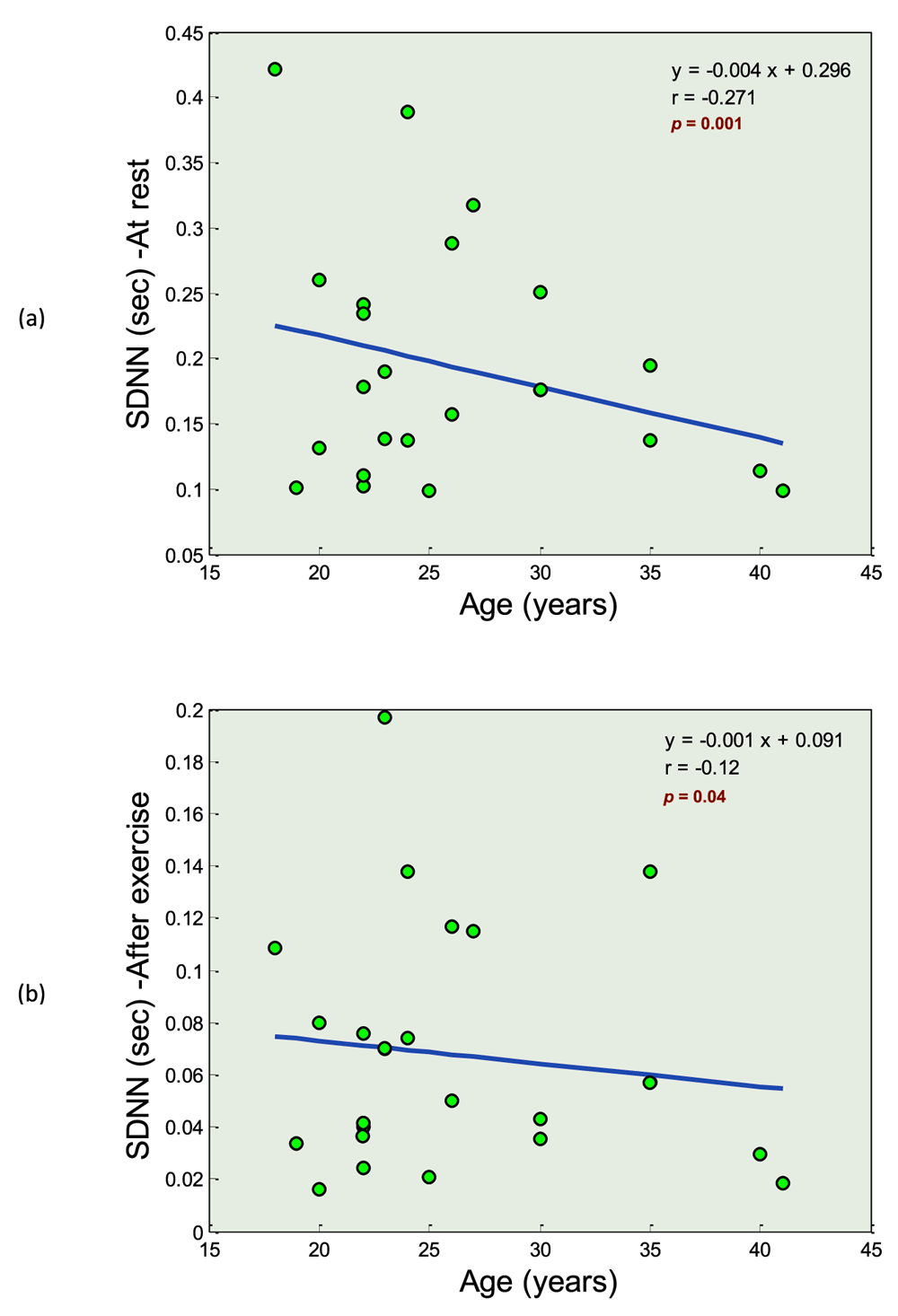
(a) Age and SDNN calculated from PPG signals for all subjects measured at rest, (b) age and SDNN calculated from PPG signals for all subjects measured after exercise. It is clear that the SDNN index is more negatively correlated with age for 20-second PPG signals measured at rest compared to after-exercise measurements. Here, the p-value shows the significance for testing the slope of the linear regression.

Figure 5(a) shows the relationship between the age and the RMSSD index at rest and Figure 5(b) shows the relationship between the age and the RMSSD index after exercise. The RMSSD index at rest is more negatively correlated with age (r = −0.217) and has a more negative slope (−0.004) than the RMSSD index after exercise (r = −0.091 and slope = −0.001). The slope significance was achieved by RMSSD before exercise with p = 0.04, while it failed for RMSSD after exercise as p = 0.18.

Figure 5. Correlation between age and RMSSD index.

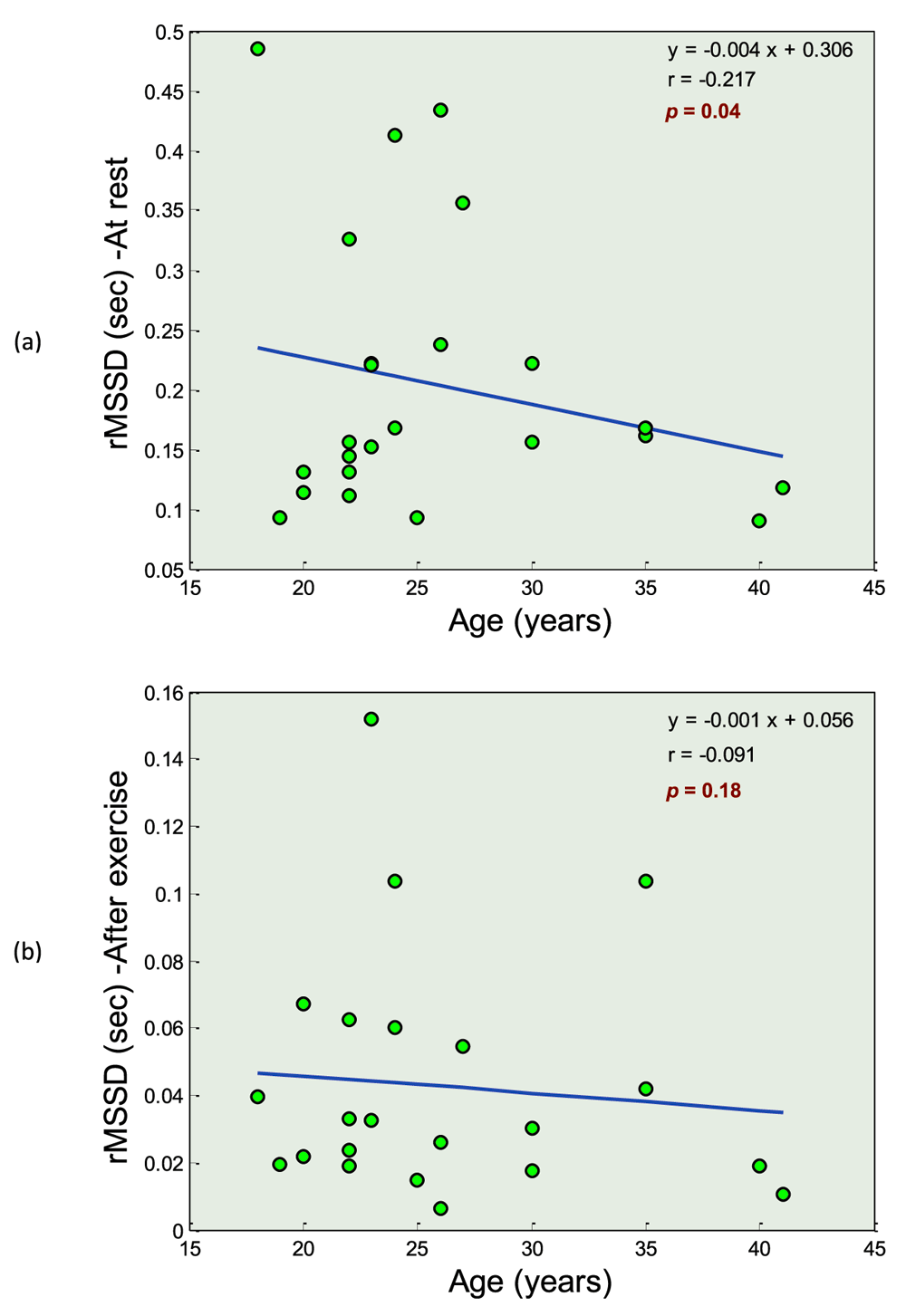
(a) Age and RMSSD calculated from PPG signals for all subjects measured at rest, (b) age and RMSSD calculated from PPG signals for all subjects measured after exercise. It is clear that the RMSSD index is more negatively correlated with age for 20-second PPG signals measured at rest compared to after-exercise measurements. Here, the p-value shows the significance for testing the slope of the linear regression.

It is worth mentioning that the remainder of the correlations are not as strong, specifically the correlation between SDNN and age and that between RMSSD and age. Nevertheless, the slope demonstrates significance between HRV indices measured at rest and after exercise. The combination of the correlation coefficient and the slope provides a more precise evaluation for the trend analysis. Note that PPGs measured at rest have a greater negative slope compared to those measured after exercise. Although it was known that long-term exercise exerts significant effects on the HRV²³, it has not been investigated over short PPG signals. This study is important because it reports the effect of exercise on HRVs calculated from short PPG signals and compared their results in subjects measured at rest and after exercise.

The results of various cross-sectional studies have shown a linear decrease in HRV during exercise with increasing age using only ECG signals^8,15,24. Interestingly, our results confirm the inverse linear relationship between HRV measures (SDNN and RMSSD) and age. Moreover, SDNN is statistically significant with age for PPG measured before and after exercise. This new outcome shows that HRV can potentially be measured using short PPG signals.

Healthy subjects were the focus of this study and the proposed method was successfully implemented only on these subjects. Subject physiology changes significantly depending on the current health status, and this was typically reflected in the PPG signal. Thus, due to these changes, the robustness of the proposed algorithm needs to be tested on and verified on recordings from unhealthy subjects. The next step, based on results from this study, is to examine the HRV indices calculated from PPG signals in the diagnosis and monitoring of abnormalities, such as arrhythmia, diabetes, hypertension, and hyperlipidemia. The HRV indices are usually calculated over a period of five minutes from the ECG signals; however, the PPG recordings in this study were very short (20 seconds). Additional studies to demonstrate the 20-second recordings are equivalent in terms of usefulness to the standard length of time (5 minutes) are needed to further validate our findings. Studies that evaluate the extracted HRV indices as a function of PPG duration are recommended. The PPG database contains signals collected from subjects of approximately the same age (about 22 years old), which creates imbalance in the age distribution. Therefore, a larger and more diverse sample size with a balanced age distribution is needed to generalize the findings of this study.

Conclusion

The findings of this preliminary study build on previous studies that discussed the potential use of only PPG to measure HRV (i.e., without collecting ECG data). Suitable indices for short duration signals include SDNN and RMSSD, which can be used with 20-second PPG recordings. A negative correlation with age at rest has been demonstrated for both indices. Interestingly, only SDNN shows significance for after exercise measurements. Since long signal measurement can be challenging due to perspiration, calculating SDNN using short PPG measurements from subjects after exercise in hot and humid weather is an appealing approach that needs to be explored on a larger scale. The overall result of this study indicates that an alternative potential modality for HRV analysis and the identification of individuals at risk, is the use of short PPG signals.

Data availability

In agreement with the Australian Department of Defence, the raw dataset could not be made available because the data could not be sufficiently anonymised to protect subject confidentiality. Upon request and review, the dataset is available at CDU (http://www.cdu.edu.au/ehse). The PPGs are human subject data and will be made available upon request from appropriate investigators after approval by Charles Darwin University Human Research Ethics Committee (http://www.cdu.edu.au/research/ori/human-ethics).

Author contributions

ME and IN designed the experiment. ME, DA, SD, and DS performed the statistical analysis. ME, IN, MB, DA, SD, and DS conceived of the study, and participated in its design and coordination and helped to draft the manuscript. All authors read and approved the final manuscript.

Competing interests

No competing interests were disclosed.

Grant information

Funding for the research project was provided by the Government of the Commonwealth of Australia.

The funders had no role in study design, data collection and analysis, decision to publish, or preparation of the manuscript.

Acknowledgments

Authors gratefully acknowledge the Northern Territory Institute of Sport (Darwin, Australia) and Charles Darwin University for initiating and sharing this line of research.

Faculty Opinions recommended

References

1. Bruce-Low SS, Cotterrell D, Jones GE: Heart rate variability during high ambient heat exposure. Aviat Space Environ Med. 2006; 77(9): 915–920. PubMed Abstract
2. Berntson GG, Bigger JT Jr, Eckberg DL, et al.: Heart rate variability: origins, methods, and interpretive caveats. Psychophysiology. 1997; 34(6): 623–648. PubMed Abstract | Publisher Full Text
3. Constant I, Laude D, Murat I, et al.: Pulse rate variability is not a surrogate for heart rate variability. Clin Sci (Lond). 1999; 97(4): 391–397. PubMed Abstract | Publisher Full Text
4. Giardino ND, Lehrer PM, Edelberg R: Comparison of finger plethysmograph to ECG in the measurement of heart rate variability. Psychophysiology. 2002; 39(2): 246–253. PubMed Abstract
5. Lu S, Zhao H, Ju K, et al.: Can photoplethysmography variability serve as an alternative approach to obtain heart rate variability information? J Clin Monit Comput. 2008; 22(1): 23–9. PubMed Abstract | Publisher Full Text
6. Weng J, Ye Z, Weng J: An Improved Pre-processing Approach for Photoplethysmographic Signal. Conf Proc IEEE Eng Med Biol Soc. 2005; 1: 41–44. PubMed Abstract | Publisher Full Text
7. Elgendi M: On the analysis of fingertip photoplethysmogram signals. Curr Cardiol Rev. 2012; 8(1): 14–25. PubMed Abstract | Publisher Full Text | Free Full Text
8. O’Brien IA, O’Hare P, Corrall RJ: Heart rate variability in healthy subjects: effect of age and the derivation of normal ranges for tests of autonomic function. Br Heart J. 1986; 55(4): 348–354. PubMed Abstract | Publisher Full Text | Free Full Text
9. Wang HM, Huang SC: SDNN/RMSSD as a surrogate for LF/HF: a revised investigation. Modelling and Simulation in Engineering. 2012; 2012: 931943. Publisher Full Text
10. Matsuyama A: ECG and APG Signal Analysis during Exercise in a Hot Environment. PhD Thesis, Charles Darwin University, Darwin, Australia, 2009. Reference Source
11. Elgendi M, Norton I, Brearley M, et al.: Systolic peak detection in acceleration photoplethysmograms measured from emergency responders in tropical conditions. PLoS One. 2013; 8(10): e76585. PubMed Abstract | Publisher Full Text | Free Full Text
12. Elgendi M, Norton I, Brearley M, et al.: Detection of a and b waves in the acceleration photoplethysmogram. Biomed Eng Online. 2014; 13(1): 139. PubMed Abstract | Publisher Full Text | Free Full Text
13. Elgendi M: Fast QRS detection with an optimized knowledge-based method: evaluation on 11 standard ECG databases. PLoS One. 2013; 8(9): e73557. PubMed Abstract | Publisher Full Text | Free Full Text
14. Elgendi M: Detection of c, d, and e waves in the acceleration photoplethysmogram. Comput Methods Programs Biomed. 2014; 117(2): 125–136. PubMed Abstract | Publisher Full Text
15. Umetani K, Singer DH, McCraty R, et al.: Twenty-four hour time domain heart rate variability and heart rate: relations to age and gender over nine decades. J Am Coll Cardiol. 1998; 31(3): 593–601. PubMed Abstract | Publisher Full Text
16. Bansal D, Khan M, Salhan AK: A review of measurement and analysis of heart rate variability. In Proc International Conference on Computer and Automation Engineering. Bangkok, Thailand, 2009; 243–246. Publisher Full Text
17. Laguna P, Caminal P, Jané R, et al.: Evaluation of HRV by PP and RR interval analysis using a new time delay estimate. In Proc IEEE Computers in Cardiology. Chicago, USA. 1990; 63–66. Publisher Full Text
18. Gil E, Orini M, Bailón R, et al.: Photoplethysmography pulse rate variability as a surrogate measurement of heart rate variability during non-stationary conditions. Physiol Meas. 2010; 31(9): 1271–1290. PubMed Abstract | Publisher Full Text
19. Wong JS, Lu WA, Wu KT, et al.: A comparative study of pulse rate variability and heart rate variability in healthy subjects. J Clin Monit Comput. 2012; 26(2): 107–114. PubMed Abstract | Publisher Full Text
20. Chen X, Huang YY, Yun F, et al.: Effect of changes in sympathovagal balance on the accuracy of heart rate variability obtained from photoplethysmography. Exp Ther Med. 2015; 10(6): 2311–2318. PubMed Abstract | Publisher Full Text | Free Full Text
21. Schäfer A, Vagedes J: How accurate is pulse rate variability as an estimate of heart rate variability? A review on studies comparing photoplethysmographic technology with an electrocardiogram. Int J Cardiol. 2013; 166(1): 15–29. PubMed Abstract | Publisher Full Text
22. Elgendi M, Fletcher RR, Norton I, et al.: Frequency analysis of photoplethysmogram and its derivatives. Comput Methods Programs Biomed. 2015; 122(3): 503–512. PubMed Abstract | Publisher Full Text
23. Zhang J: Effect of age and sex on heart rate variability in healthy subjects. J Manipulative Physiol Ther. 2007; 30(5): 374–379. PubMed Abstract | Publisher Full Text
24. Yeragani VK, Sobolewski E, Kay J, et al.: Effect of age on long-term heart rate variability. Cardiovasc Res. 1997; 35(1): 35–42. ISSN 0008-6363. PubMed Abstract | Publisher Full Text

Comments on this article Comments (0)

Version 1

VERSION 1 PUBLISHED 22 Sep 2016

Author details Author details

¹ Department of Obstetrics & Gynecology, University of British Columbia, Vancouver, Canada
² Department of Electrical and Computer Engineering, University of British Columbia, Vancouver, Canada
³ Department of Computing Science, University of Alberta, Edmonton, Canada
⁴ National Critical Care and Trauma Response Centre, Darwin, Australia
⁵ Graduate School of Biomedical Engineering, University of New South Wales, Sydney, Australia
⁶ School of Electrical and Electronic Engineering, University of Adelaide, Adelaide, Australia

Competing interests

No competing interests were disclosed.

Grant information

Funding for the research project was provided by the Government of the Commonwealth of Australia.

The funders had no role in study design, data collection and analysis, decision to publish, or preparation of the manuscript.

Article Versions (1)

version 1

Published: 22 Sep 2016, 5:2354

https://doi.org/10.12688/f1000research.9556.1

Copyright

© 2016 Elgendi M et al. This is an open access article distributed under the terms of the Creative Commons Attribution License, which permits unrestricted use, distribution, and reproduction in any medium, provided the original work is properly cited. The author(s) is/are employees of the US Government and therefore domestic copyright protection in USA does not apply to this work. The work may be protected under the copyright laws of other jurisdictions when used in those jurisdictions.

Download

Export To

metrics

	Views	Downloads
F1000Research	-	-
PubMed Central Data from PMC are received and updated monthly.	-	-

Citations

0

SEE MORE DETAILS

CITE

how to cite this article

Elgendi M, Norton I, Brearley M et al. A pilot study: Can heart rate variability (HRV) be determined using short-term photoplethysmograms? [version 1; peer review: 2 approved with reservations]. F1000Research 2016, 5:2354 (https://doi.org/10.12688/f1000research.9556.1)

NOTE: If applicable, it is important to ensure the information in square brackets after the title is included in all citations of this article.

track

receive updates on this article

Track an article to receive email alerts on any updates to this article.

Open Peer Review

Version 1

VERSION 1

PUBLISHED 22 Sep 2016

Views

13

Reviewer Report 10 Oct 2016

Albert Avolio, Department of Biomedical Sciences, Macquarie University, Sydney, NSW, Australia

Approved with Reservations

https://doi.org/10.5256/f1000research.10293.r16498

The authors propose a means of detecting heart rate variability (HRV) from the photoplethysmographic (PPG) signal. As presented, the study is only marginally informative and the following issues require consideration.

From the references cited

The authors propose a means of detecting heart rate variability (HRV) from the photoplethysmographic (PPG) signal. As presented, the study is only marginally informative and the following issues require consideration.

From the references cited in relation to the available database of PPG signals, it appears that the ECG was also recorded in the same subjects. If so, it begs the question as to why the HRV obtained from the ECG signal was not compared to the HRV obtained from the PPG signal.It is not clear why secondary associations with age needed to be invoked to provide a rather indirect justification of the fact that HRV can be obtained from the PPG signals recorded for 20 seconds.
If there were no ECG signals available, there is still a significant limitation in the study due to the very uneven distribution of age in the cohort. There are very few subjects in the age range 30-40 compared to 20-30. Given the low correlation, it is not clear if this could even be an indirect demonstration.
Abstract: correct $aa$
Page 4. Right column. 1st paragraph. Correct: “..since the collected of a shorter…”
Page 6. L column Lines 1-3. Sentence unclear.

Competing Interests: No competing interests were disclosed.

I confirm that I have read this submission and believe that I have an appropriate level of expertise to confirm that it is of an acceptable scientific standard, however I have significant reservations, as outlined above.

CITE

Report a concern

Respond or Comment

Views

19

Reviewer Report 03 Oct 2016

Mariusz Oszust, Department of Computer and Control Engineering, Rzeszów University of Technology, Rzeszów, Poland

Approved with Reservations

https://doi.org/10.5256/f1000research.10293.r16497

In the paper, heart rate variability (HRV) is determined using the photoplethysmogram (PPG) signal. The demonstrated findings are based on the calculation of the standard deviation of heartbeat interval (SDNN) and the root-mean square of the difference of successive heartbeats ... Continue reading

In the paper, heart rate variability (HRV) is determined using the photoplethysmogram (PPG) signal. The demonstrated findings are based on the calculation of the standard deviation of heartbeat interval (SDNN) and the root-mean square of the difference of successive heartbeats (RMSSD). These indices were determined using the second derivative wave of photoplethysmogram (APG) signal. The presented methodology seems valid. However, there are some issues that should be addressed.

Since authors in their previous works used 20-second PPGs for calculation of HRV indices (SDNN and RMSDD), it cannot be said that “To date, there have been no studies that investigate the independent use of the photoplethysmogram (PPG) signal to determine heart rate variability (HRV)”. Please refer e.g., to: M Elgendi, M Jonkman, F De Boer.: Applying the APG to measure Heart Rate Variability, ICCAE 2010, DOI: 10.1109/ICCAE.2010.5452042.
Authors claim that “if the PPG--HRV indices are negatively correlated with age, then short PPG signals are appropriate measurements for extracting HRV parameters”. The work “Applying the APG to measure Heart Rate Variability” (in the comment 1), as well as the paper: M Elgendi, M Jonkman, F De Boer.: Heart Rate Variability and the Acceleration Plethysmogram Signals Measured at Rest, Third International Joint Conference, BIOSTEC 2010, Valencia, Spain, January 20-23, 2010, DOI: 10.1007/978-3-642-18472-7_21, have already proven that short PPG signals are appropriate for extracting HRV parameters. In my opinion, the main novelty here is in showing the correlation of HRV indices measured before and after exercise with age, and such correlation with age should be emphasized, referring to these works, since it strengthens their findings. The title of the paper should also reflect this – the question in the title (“Can heart rate variability (HRV) be determined using short-term photoplethysmograms?”) was answered in 2010. The works above should be added to the literature. Figure 1 can be also found in these papers.
Data were collected at a sampling rate of 200 Hz, with recording duration of 20 seconds, and the duration was limited since subjects were waiting after exercise for the measurement. This suggests a need of different organisation of the data collection, in which a line of participants is not formed and does not affect the experiment. However, since “short” is a relative term, it would be desirable to assess the shortest duration that can be used for meaningful calculation of the correlation between HRV indices measured at rest and after exercise with age. Here, for example, p-value for different lengths of PPG signals can be shown (in e.g., range 5-20s). Please add to the investigation the correlation of the HRV indices with the heart rate in order to make the conclusions more general (see your works in my second comment).
The PPG database contains samples with imbalanced age distribution. This certainly influences the results and drawn conclusions on the age correlation of HRV indices, i.e., they can be wrong. Since new samples cannot be simply added to the database, the imbalanced data should be handled appropriately in order to obtain reliable results. There are many approaches to handle imbalanced datasets, e.g., undersampling (see Longadge, Rushi, and Snehalata Dongre. "Class imbalance problem in data mining review." arXiv preprint arXiv:1305.1707 (2013). http://arxiv.org/pdf/1305.1707). I strongly advise applying at least one such technique.

References

1. Elgendi M, Jonkman M, De Boer F: Applying the APG to measure heart rate variability. Computer and Automation Engineering (ICCAE). 2010; 3: 514-517 Publisher Full Text
2. Elgendi M, Jonkman M, De Boer F: Heart Rate Variability and the Acceleration Plethysmogram Signals Measured at Rest. International Joint Conference on Biomedical Engineering Systems and Technologies. 2010; 127: 266-277 Reference Source
3. Longadge R, Dongre S: Class imbalance problem in data mining review.arXiv preprint arXiv. 2013; 1305.1707. Reference Source

Competing Interests: No competing interests were disclosed.

I confirm that I have read this submission and believe that I have an appropriate level of expertise to confirm that it is of an acceptable scientific standard, however I have significant reservations, as outlined above.

CITE

Report a concern

Respond or Comment

Comments on this article Comments (0)

Version 1

VERSION 1 PUBLISHED 22 Sep 2016

Open Peer Review

Reviewer Status

Reviewer Reports

	Invited Reviewers
	1	2
Version 1 22 Sep 16	read	read

Mariusz Oszust, Rzeszów University of Technology, Rzeszów, Poland
Albert Avolio, Macquarie University, Sydney, Australia

Comments on this article

All Comments(0)

Add a comment

Sign up for content alerts

Browse by related subjects

Back to all reports

Reviewer Report

13 Views

10 Oct 2016 | for Version 1

Albert Avolio, Department of Biomedical Sciences, Macquarie University, Sydney, NSW, Australia

13 Views Cite this report Responses(0)

Approved With Reservations

The authors propose a means of detecting heart rate variability (HRV) from the photoplethysmographic (PPG) signal. As presented, the study is only marginally informative and the following issues require consideration.

From the references cited in relation to the available database of PPG signals, it appears that the ECG was also recorded in the same subjects. If so, it begs the question as to why the HRV obtained from the ECG signal was not compared to the HRV obtained from the PPG signal.It is not clear why secondary associations with age needed to be invoked to provide a rather indirect justification of the fact that HRV can be obtained from the PPG signals recorded for 20 seconds.
If there were no ECG signals available, there is still a significant limitation in the study due to the very uneven distribution of age in the cohort. There are very few subjects in the age range 30-40 compared to 20-30. Given the low correlation, it is not clear if this could even be an indirect demonstration.
Abstract: correct $aa$
Page 4. Right column. 1st paragraph. Correct: “..since the collected of a shorter…”
Page 6. L column Lines 1-3. Sentence unclear.

Competing Interests

No competing interests were disclosed.

I confirm that I have read this submission and believe that I have an appropriate level of expertise to confirm that it is of an acceptable scientific standard, however I have significant reservations, as outlined above.

Respond to this report

Responses (0)

Back to all reports

Reviewer Report

19 Views

03 Oct 2016 | for Version 1

Mariusz Oszust, Department of Computer and Control Engineering, Rzeszów University of Technology, Rzeszów, Poland

19 Views Cite this report Responses(0)

Approved With Reservations

In the paper, heart rate variability (HRV) is determined using the photoplethysmogram (PPG) signal. The demonstrated findings are based on the calculation of the standard deviation of heartbeat interval (SDNN) and the root-mean square of the difference of successive heartbeats (RMSSD). These indices were determined using the second derivative wave of photoplethysmogram (APG) signal. The presented methodology seems valid. However, there are some issues that should be addressed.

Since authors in their previous works used 20-second PPGs for calculation of HRV indices (SDNN and RMSDD), it cannot be said that “To date, there have been no studies that investigate the independent use of the photoplethysmogram (PPG) signal to determine heart rate variability (HRV)”. Please refer e.g., to: M Elgendi, M Jonkman, F De Boer.: Applying the APG to measure Heart Rate Variability, ICCAE 2010, DOI: 10.1109/ICCAE.2010.5452042.
Authors claim that “if the PPG--HRV indices are negatively correlated with age, then short PPG signals are appropriate measurements for extracting HRV parameters”. The work “Applying the APG to measure Heart Rate Variability” (in the comment 1), as well as the paper: M Elgendi, M Jonkman, F De Boer.: Heart Rate Variability and the Acceleration Plethysmogram Signals Measured at Rest, Third International Joint Conference, BIOSTEC 2010, Valencia, Spain, January 20-23, 2010, DOI: 10.1007/978-3-642-18472-7_21, have already proven that short PPG signals are appropriate for extracting HRV parameters. In my opinion, the main novelty here is in showing the correlation of HRV indices measured before and after exercise with age, and such correlation with age should be emphasized, referring to these works, since it strengthens their findings. The title of the paper should also reflect this – the question in the title (“Can heart rate variability (HRV) be determined using short-term photoplethysmograms?”) was answered in 2010. The works above should be added to the literature. Figure 1 can be also found in these papers.
Data were collected at a sampling rate of 200 Hz, with recording duration of 20 seconds, and the duration was limited since subjects were waiting after exercise for the measurement. This suggests a need of different organisation of the data collection, in which a line of participants is not formed and does not affect the experiment. However, since “short” is a relative term, it would be desirable to assess the shortest duration that can be used for meaningful calculation of the correlation between HRV indices measured at rest and after exercise with age. Here, for example, p-value for different lengths of PPG signals can be shown (in e.g., range 5-20s). Please add to the investigation the correlation of the HRV indices with the heart rate in order to make the conclusions more general (see your works in my second comment).
The PPG database contains samples with imbalanced age distribution. This certainly influences the results and drawn conclusions on the age correlation of HRV indices, i.e., they can be wrong. Since new samples cannot be simply added to the database, the imbalanced data should be handled appropriately in order to obtain reliable results. There are many approaches to handle imbalanced datasets, e.g., undersampling (see Longadge, Rushi, and Snehalata Dongre. "Class imbalance problem in data mining review." arXiv preprint arXiv:1305.1707 (2013). http://arxiv.org/pdf/1305.1707). I strongly advise applying at least one such technique.

References

1. Elgendi M, Jonkman M, De Boer F: Applying the APG to measure heart rate variability. Computer and Automation Engineering (ICCAE). 2010; 3: 514-517 Publisher Full Text
2. Elgendi M, Jonkman M, De Boer F: Heart Rate Variability and the Acceleration Plethysmogram Signals Measured at Rest. International Joint Conference on Biomedical Engineering Systems and Technologies. 2010; 127: 266-277 Reference Source
3. Longadge R, Dongre S: Class imbalance problem in data mining review.arXiv preprint arXiv. 2013; 1305.1707. Reference Source

Competing Interests

No competing interests were disclosed.

I confirm that I have read this submission and believe that I have an appropriate level of expertise to confirm that it is of an acceptable scientific standard, however I have significant reservations, as outlined above.

Respond to this report

Responses (0)

[1] 1. Bruce-Low SS, Cotterrell D, Jones GE: Heart rate variability during high ambient heat exposure. Aviat Space Environ Med. 2006; 77(9): 915–920. PubMed Abstract

[2] 2. Berntson GG, Bigger JT Jr, Eckberg DL, et al.: Heart rate variability: origins, methods, and interpretive caveats. Psychophysiology. 1997; 34(6): 623–648. PubMed Abstract | Publisher Full Text

[3] 3. Constant I, Laude D, Murat I, et al.: Pulse rate variability is not a surrogate for heart rate variability. Clin Sci (Lond). 1999; 97(4): 391–397. PubMed Abstract | Publisher Full Text

[4] 4. Giardino ND, Lehrer PM, Edelberg R: Comparison of finger plethysmograph to ECG in the measurement of heart rate variability. Psychophysiology. 2002; 39(2): 246–253. PubMed Abstract

[5] 5. Lu S, Zhao H, Ju K, et al.: Can photoplethysmography variability serve as an alternative approach to obtain heart rate variability information? J Clin Monit Comput. 2008; 22(1): 23–9. PubMed Abstract | Publisher Full Text

[6] 6. Weng J, Ye Z, Weng J: An Improved Pre-processing Approach for Photoplethysmographic Signal. Conf Proc IEEE Eng Med Biol Soc. 2005; 1: 41–44. PubMed Abstract | Publisher Full Text

[7] 7. Elgendi M: On the analysis of fingertip photoplethysmogram signals. Curr Cardiol Rev. 2012; 8(1): 14–25. PubMed Abstract | Publisher Full Text | Free Full Text

[8] 8. O’Brien IA, O’Hare P, Corrall RJ: Heart rate variability in healthy subjects: effect of age and the derivation of normal ranges for tests of autonomic function. Br Heart J. 1986; 55(4): 348–354. PubMed Abstract | Publisher Full Text | Free Full Text

[9] 9. Wang HM, Huang SC: SDNN/RMSSD as a surrogate for LF/HF: a revised investigation. Modelling and Simulation in Engineering. 2012; 2012: 931943. Publisher Full Text

[10] 10. Matsuyama A: ECG and APG Signal Analysis during Exercise in a Hot Environment. PhD Thesis, Charles Darwin University, Darwin, Australia, 2009. Reference Source

[11] 11. Elgendi M, Norton I, Brearley M, et al.: Systolic peak detection in acceleration photoplethysmograms measured from emergency responders in tropical conditions. PLoS One. 2013; 8(10): e76585. PubMed Abstract | Publisher Full Text | Free Full Text

[12] 12. Elgendi M, Norton I, Brearley M, et al.: Detection of a and b waves in the acceleration photoplethysmogram. Biomed Eng Online. 2014; 13(1): 139. PubMed Abstract | Publisher Full Text | Free Full Text

[13] 13. Elgendi M: Fast QRS detection with an optimized knowledge-based method: evaluation on 11 standard ECG databases. PLoS One. 2013; 8(9): e73557. PubMed Abstract | Publisher Full Text | Free Full Text

[14] 14. Elgendi M: Detection of c, d, and e waves in the acceleration photoplethysmogram. Comput Methods Programs Biomed. 2014; 117(2): 125–136. PubMed Abstract | Publisher Full Text

[15] 15. Umetani K, Singer DH, McCraty R, et al.: Twenty-four hour time domain heart rate variability and heart rate: relations to age and gender over nine decades. J Am Coll Cardiol. 1998; 31(3): 593–601. PubMed Abstract | Publisher Full Text

[16] 16. Bansal D, Khan M, Salhan AK: A review of measurement and analysis of heart rate variability. In Proc International Conference on Computer and Automation Engineering. Bangkok, Thailand, 2009; 243–246. Publisher Full Text

[17] 17. Laguna P, Caminal P, Jané R, et al.: Evaluation of HRV by PP and RR interval analysis using a new time delay estimate. In Proc IEEE Computers in Cardiology. Chicago, USA. 1990; 63–66. Publisher Full Text

[18] 18. Gil E, Orini M, Bailón R, et al.: Photoplethysmography pulse rate variability as a surrogate measurement of heart rate variability during non-stationary conditions. Physiol Meas. 2010; 31(9): 1271–1290. PubMed Abstract | Publisher Full Text

[19] 19. Wong JS, Lu WA, Wu KT, et al.: A comparative study of pulse rate variability and heart rate variability in healthy subjects. J Clin Monit Comput. 2012; 26(2): 107–114. PubMed Abstract | Publisher Full Text

[20] 20. Chen X, Huang YY, Yun F, et al.: Effect of changes in sympathovagal balance on the accuracy of heart rate variability obtained from photoplethysmography. Exp Ther Med. 2015; 10(6): 2311–2318. PubMed Abstract | Publisher Full Text | Free Full Text

[21] 21. Schäfer A, Vagedes J: How accurate is pulse rate variability as an estimate of heart rate variability? A review on studies comparing photoplethysmographic technology with an electrocardiogram. Int J Cardiol. 2013; 166(1): 15–29. PubMed Abstract | Publisher Full Text

[22] 22. Elgendi M, Fletcher RR, Norton I, et al.: Frequency analysis of photoplethysmogram and its derivatives. Comput Methods Programs Biomed. 2015; 122(3): 503–512. PubMed Abstract | Publisher Full Text

[23] 23. Zhang J: Effect of age and sex on heart rate variability in healthy subjects. J Manipulative Physiol Ther. 2007; 30(5): 374–379. PubMed Abstract | Publisher Full Text

[24] 24. Yeragani VK, Sobolewski E, Kay J, et al.: Effect of age on long-term heart rate variability. Cardiovasc Res. 1997; 35(1): 35–42. ISSN 0008-6363. PubMed Abstract | Publisher Full Text

A pilot study: Can heart rate variability (HRV) be determined using short-term photoplethysmograms?

Abstract

Keywords

Introduction

Figure 1.

Figure 2. Fingertip photoplethysmogram signal measurement7.

Materials and methods

Ethics statement

Figure 3. Measurement Protocol.

Database used

Methodology

Results and discussion

Figure 4. Correlation between age and SDNN index.

Figure 5. Correlation between age and RMSSD index.

Conclusion

Data availability

Author contributions

Competing interests

Grant information

Acknowledgments

References

Comments on this article Comments (0)

Open Peer Review

Comments on this article Comments (0)

Open Peer Review

Reviewer Status

Reviewer Reports

Comments on this article

Browse by related subjects

Competing Interests Policy

Stay Updated

Figure 2. Fingertip photoplethysmogram signal measurement⁷.