Keywords
mixed effect models, regression analysis, statistical models, physiological responses, functional magnetic resonance imaging
This article is included in the INCF gateway.
mixed effect models, regression analysis, statistical models, physiological responses, functional magnetic resonance imaging
We describe a procedure for analyzing fMRI time-courses across multiple subjects in pre-determined regions without an a priori pattern or timing of expected response. Functional MRI analyses usually require defining a model and identifying voxels whose time courses follow that model; other model-free event-related approaches test for responses that are coincident in time or duration. However, certain tasks elicit neural responses that vary in pattern and timing. For example, responses to physiological challenges typically occur across neural structures in a sequence rather than simultaneously, and the patterns differ according to structure1–3. While existing software like SPM does allow for model-free assessment of responses, such as identifying the hemodynamic response based on a finite impulse response function in SPM124, those approaches can be complex to implement and interpret. The present method arose out of our research group’s need to perform basic time-trend analyses of fMRI signals in specific regions.
The approach we propose is analyzing fMRI time series using repeated measures analysis of variance (RMANOVA), allowing for detection of within-group responses relative to a baseline or resting state, and of between-group differences in response. As with any analysis of variance (ANOVA), RMANOVA tests the equality of means that are assumed to be normally distributed. However, RMANOVA also accounts for the correlation between repeated measures within subjects, whereas ANOVA does not. In addition to assessment of significant reactions relative to a baseline period, or of significant group differences in response, the method allows for identifying specific time-points when these differences occur. Therefore, transient, late-developing, and complex sequences of increasing and decreasing signal changes can be distinguished with RMANOVA. The technique is suited to analysis of longer task paradigms evoking a complex pattern of responses. We present an implementation of RMANOVA in the programming language SAS (SAS Institute Inc., Cary, NC).
Functional MRI data collected in one or more groups of subjects are preprocessed, typically with slice timing and motion correction, and the images may be spatially normalized. An additional, optional step is detrending to remove global effects. In traditional cluster analyses, global effects may be accounted for within the analysis steps using, for example, SPM5. Intensity normalization using proportional scaling has been the most common approach to removing such effects, but for the example presented here, removal of global signal changes is performed on the preprocessed images prior to analysis with RMANOVA using a custom technique6.
Volumes-of-interest (VOI) are defined, usually by outlining a structure of interest on an image volume and saving that outline as a binary image, or mask. The VOI may be defined individually on a subject-by-subject basis, or globally for all subjects on a template (the latter case assumes subjects’ images are accurately spatially normalized to the template). The mask is used to extract the intensity of only those voxels within the VOI, at each time point in the fMRI series. For each time point, the average of those voxel values is recorded, resulting in a time-series corresponding to the blood oxygen level dependent (BOLD) signal time course of that VOI in the fMRI series. The procedure is repeated for all subjects, resulting in one time trend for each subject per VOI. The time trends may optionally be deconvolved with a hemodynamic response function (HRF), allowing the timing of significant responses to be inferred as neural, rather than BOLD. The resulting VOI time trends are subjected to RMANOVA.
Repeated measures ANOVA can be implemented using a mixed effect model, a generalization of the standard linear model which allows for correlation and non-constant variability within the data7. The methodology described here assumes use of the SAS function PROC MIXED, although other software packages also perform RMANOVA. However, SAS is very flexible, and includes a wide range of diagnostics tests. (See white paper “Comparing the SAS® GLM and MIXED Procedures for Repeated Measurements Analysis,” Russ Wolfinger and Ming Chang, SUGI Proceedings, 1995; available at https://support.sas.com/rnd/app/stat/papers/abstracts/mixedglm.html). The statistical procedures calculate the variance-covariance matrix based on the dependencies defined by repeated measurements within subjects, and by group classification of subjects in the case of more than one group (REPEATED and GROUP options within PROC MIXED; by convention, SAS syntax is in upper case)7.
A classification variable (t) representing baseline and time-points in the task or challenge period is created, with values of t during the baseline or reference period constant, and values increasing for each time point in the series. For example, we have collected fMRI data during physiological challenges with one minute of baseline followed by 90 sec of challenge, at a repetition time of 6 seconds (25 volumes total); thus, t is 0 for the first 10 scans, and 1 for the 11th volume, 2 for the 12th, and so on until 15 for the 25th. Note that for data collected at higher sampling rates or across longer time periods, the time-classification variable may include multiple data points, as opposed to the individual data points of the fMRI time-series; for example, we have classified instantaneous (beat-by-beat) heart rates recorded throughout a two minute period into twelve 10 sec epochs8. If more than one group of subjects is being analyzed, a second classification variable is defined at each time point with a value representing the group to which that series belongs. An example of such a format in an Excel file is shown in Appendix A; these data may be imported into SAS.
Before assessing the fMRI time-trend results of the RMANOVA analysis (see sections below for full details), certain residual and influence diagnostic tests should be performed to ensure that the model does not seriously violate underlying assumptions. A relevant subset of such tests is described in sections below. Many practical applications of RMANOVA violate the model assumptions to some degree, but the approach is considered robust to moderate departures of these assumptions. In the present application to fMRI data, a key test is to ensure that the residual distributions are not seriously skewed. We suggest the flowing checks. First determine the s residuals, which are scaled so that more than 95% should fall within the critical limits of the appropriate Student’s t distribution, which for most purposes can be assumed to be within ± 1.96 (and centered on 0). The shape of the histogram for each group of the studentized residuals should be bell-shaped. There should also be no effect of time, so each group plot of the studentized residuals by time should not show a trend. We recommend using locally-weighted-scatter-plot (lowess) curves to identify such trends. In the case where the diagnostic tests fail, there may still be some value in continuing with the model, but we suggest presenting the results of the residual diagnostics along with the findings, to allow readers to assess for themselves the validity of the model. Further options are explained in sections below, along with other possible diagnostic tests.
There are two levels of results produced by RMANOVA: the significance of the overall model at the group, time, and group-by-time levels, and the significance of between-group and within-group effects at each time point (see section below). According to the Tukey-Fisher criterion for multiple comparisons, the model is first assessed at the overall level for significance before investigating time-point specific effects; i.e., if the overall group-by-time effect is not significant, the between-group effects at each time point are not considered, regardless of their reported significance level. Similarly, if the overall time effect is not significant, then within-group effects at each time point are not considered.
Specific programming details are presented in the next sections to facilitate replication.
Data are arranged in rows per subject. Each subject is identified by a unique classification variable (SUBJECT, which may be the subject name), and similarly, the group to which that subject belongs is designated by the GROUP classification variable e.g., 1, 2, …etc.). The fMRI times series values are arranged in adjacent columns, with one column for each time point (image volume), and with the value representing the average of the voxels within the VOI at that time point for that subject (row in Figure 1). Values are in percentage change relative to a baseline period. The column headings for the time points take the format of a root (“val” in Figure 1 and the example code in next section) followed by a number indicating the sequence of values, starting at 0 (e.g., val0, val1, val2, …etc.).
The SAS code for importing these data into a library “voilib” is as follows:
LIBNAME voilib ‘[sas_library_folder]’;
PROC IMPORT OUT=voilib.data
DATAFILE = '[fn]'
DBMS=EXCEL2000 REPLACE;
RANGE = '[worksheet]'
GETNAMES=YES;
RUN;
where [sas_library_folder] is the path to where the SAS library files will be stored, [fn] is the Excel file name, and [worksheet] is the name of the worksheet within the Excel file containing the data.
SAS can also import data from a text file, which is useful for series with more that 250 time points, or for systems without Excel. The SAS help has details on importing such files.
Note that SAS code is not case dependent. In the examples presented here, capitals are used to indicate SAS commands, and bolded names within square brackets are used to indicate user-specified variables. The remaining lowercase names are variables specific to these examples.
A simple example of formatting the data is illustrated with the following SAS code, where a variable “epoch” classifies all time points as baseline epoch or epoch number corresponding to task scan number, with the assumption that one baseline period is followed by the task period:
PROC FORMAT;
VALUE ynft 1='yes' 0='no';
VALUE gft 1='[group1]' 2 = '[group2]';
RUN;
DATA voilib.formated; SET voilib.data;
ARRAY y{[num_tp]} val0 – val [num_tp-1];
DO i=1 TO [num_tp];
time=i; val=y{i};
IF 0 < time <= [bl] THEN epoch=[bl];
IF time > [bl] THEN epoch=time;
IF 0 < time <= [bl] THEN chal=’baseline’;
IF time > [bl] THEN chal=’challenge’;
OUTPUT;
END;
KEEP subject group time epoch chal;
RUN;
where [num_tp] is the number of values in the time-series and [bl] is the last baseline scan. The names for each group may be entered in place of [group1] and [group2]. The above formatting code can be modified according to the fMRI task timing. For time series with large numbers of samples, the epoch variable can be used to combine multiple values within a time period.
The RMANOVA, along with formatting and output filtering, is implemented as follows:
PROC MIXED NOITPRINT NOCLPRINT DATA=voilib.formated EMPIRICAL;
CLASS group epoch subject;
MODEL val = group epoch group*epoch / OUTP = prediction RESIDUAL;
REPEATED / TYPE=CS SUB=subject(group) group=group;
LSMEANS group*epoch / DIFF;
ODS LISTING EXCLUDE LSMEANS;
ODS OUTPUT LSMEANS= voilib.means;
ODS LISTING EXCLUDE DIFFS;
ODS OUTPUT DIFFS= voilib.differences;
ODS OUTPUT COVPARMS= voilib.covparams;
ODS OUTPUT LRT= voilib.likelihoodratiotest;
ODS OUTPUT TESTS3= voilib.type3tests;
RUN;
where the italicized statements define the model, and the remaining control the output (including residuals). Note that the RESIDUAL option, which directs studentized residuals to be calculated, is only available from SAS version 9.1. The CLASS statement determines classification variables.
The EMPIRICAL option in the proc mixed command line uses the Huber-White sandwich estimator of variance, rather than the default, as it is more conservative but considered more robust, particularly if the assumption of normality is violated (as is often the case).
The output from this step contains numerous descriptors of the model. The “Null Model Likelihood Ratio Test” gives the probability of the null model being true (column heading “Pr > ChiSq”). If the model passes the Tukey-Fisher criterion for multiple comparisons, i.e., the probability of the null model is less the 0.05, the model is investigated at the variable level using the “Type 3 Tests of Fixed Effects” output. Probabilities of the null contribution to the model by individual independent variables are presented in the “Pr > F” column for the group, epoch and group*epoch. “Group” represents a group effect, which is often not significant for fMRI data presented in percent change relative to baseline. The variable epoch represents a time effect, corresponding to within-group significant responses. The group*epoch term represents a group-by-time effect, corresponding to between-group differences across time. Again considering the Tukey-Fisher criterion, if for any of these variables the likelihood of the null model is greater than 0.05, then that variable is determined to be not significant. If less than the threshold, the model is investigated further at each time point.
Further code is needed to select the relevant output for determining the time points of within and between group significant differences. The code below is one of several possible ways to extract the relevant results.
DATA voilib.means; SET voilib.means;
RENAME estimate=adjmean;
DROP effect df tValue Probt;
RUN;
PROC SORT DATA= voilib.means; BY group epoch; RUN;
DATA voilib.differences; SET voilib.differences;
DROP effect df;
RENAME estimate=meandiff;
LABEL estimate='mean diff' _epoch='vs epoch' _group='vs group' probt='p value';
RUN;
DATA voilib.betweengroup; SET voilib.differences;
IF epoch ne _epoch THEN delete;
DROP _epoch;
RUN;
PROC SORT DATA= voilib.betweengroup; BY epoch group; RUN;
DATA voilib.withingroup; SET voilib.differences;
IF group NE _group THEN delete;
DROP _group;
IF epoch NE 28 THEN delete;
RUN;
PROC SORT DATA= voilib.withingroup; BY group _epoch; RUN;
The above code will create Withingroup and Betweengroup tables in the SAS library voilib.
If “epoch” showed a significant effect in the Type 3 tests (above), the time points where this difference appeared may be determined by examining the Withingroup table. As shown in Figure 2, each row in the table compares baseline (labeled “epoch”) vs subsequent epochs (labeled “vs epoch”), with a mean difference, standard error and P value; if the latter indicates significance (< 0.05), that time point is considered to have a significant response relative to baseline for that group.
Similarly, if “group*epoch” showed a significant effect in the Type 3 tests (above), the time-points where this difference appeared may be determined by examining the Betweengroup table. As shown in Figure 3, each row corresponds to a time point (labeled “epoch”) and compares one group vs the other, with a mean difference, standard error and P value; if the latter indicates significance (< 0.05), that time point is considered to have a significant group difference.
The RMANOVA method has a number of underlying assumptions which should be considered. The assumptions of the RMANOVA method which differ from ANOVA are that 1) the means are linear over time, 2) multivariate normality, 3) homogeneity of covariance matrices, and 4) independence. The method is reasonably robust to violations of the second and third assumptions. Violations of independence produce a non-normal distribution of the residuals, which invalidates the F-ratio. The most common violations of independence occur when either random selection or random assignment is not used or the compound symmetry covariance assumption is inappropriate. Violation of the homogeneity of covariance matrices generally results in the overall test having a higher Type I error rate than nominally set.
In the current application, a subset of key diagnostic and residual checks is suggested with the implementation of this technique.
Plots of predicted and observed data, to visually determine any major bias.
Residual checks of normality, including 95% of Studentized residuals falling within ±1.96, showing approximately normal group distributions, and scatter plots over time with lowess curves superimposed to ensure lack of group trends with time. Formal tests of normality may also be performed, although these will typically fail.
Assuming the “RESIDUAL” option in PROC MIXED has been used, which implements the studentized residuals, the following SAS code implements the tests:
PROC SORT DATA=voilib.formatted; BY group epoch; RUN;
PROC SORT DATA=voilib.means; BY group epoch; RUN;
PROC SORT DATA=voilib.prediction; BY group epoch; RUN;
DATA voilib.residuals;
MERGE voilib.formatted voilib.means voilib.prediction;
BY group epoch;
resid = val - adjmean;
LABEL resid='residual errors';
absresid = abs(resid);
RUN;
PROC UNIVARIATE NORMAL PLOT DATA=voilib.residuals;
VAR resid; BY group;
TITLE 'Residual Analysis';
RUN;
SYMBOL1 I=NONE V=STAR; * C=BLACK; *;
PROC GPLOT DATA=voilib.residuals;
PLOT resid*adjmean / VREF=0; BY group;
TITLE 'Residuals';
RUN;
DATA voilib.resid_count; SET voilib.residuals;
IF (-1.96<=resid<=1.96) THEN StudResidCount = 0;
ELSE IF (resid ne.) THEN StudResidCount = 1;
TITLE 'Residual Count (StudResidCount = 0 should be >=95%)';
RUN;
PROC FREQ; TABLE StudResidCount; RUN;
PROC LOESS DATA = voilib.residuals;
ODS OUTPUT OutputStatistics=voilib.smresid;
MODEL resid = epoch / smooth = 0.4;
BY group;
RUN;
SYMBOL1 i=none c=green v=dot;
SYMBOL 2 i=none c=red v=dot;
SYMBOL 3 i=spline c=green v=none l=2 w=5;
SYMBOL 4 i=spline c=red v=none l=2 w=5;
LEGEND1 label=('Residuals');
LEGEND2 label=('Loess Curve');
axis1 order=(-10 to 10 by 2);
PROC GPLOT data=voilib.smresid;
PLOT DepVar*epoch=group / vaxis = axis1 legend = LEGEND1;
PLOT2 Pred*epoch=group / vaxis = axis1 legend = LEGEND2;
TITLE 'Residuals by Time (should be no trend)';
RUN;
* plotting observed vs predicted *;
SYMBOL1 I=NONE C=GREEN V=TRIANGLE;
SYMBOL2 I=NONE C=RED V=HASH;
SYMBOL3 I=JOIN C=GREEN V=TRIANGLE L=2 W=4;
SYMBOL4 I=JOIN C=RED V=HASH L=2 W=4;
LEGEND1 LABEL=('Observed');
LEGEND2 LABEL=('Predicted');
PROC GPLOT DATA=voilib.residuals;
PLOT adjmean*epoch=group / LEGEND = LEGEND1; /* VAXIS = -7 to 7 ; * To set axis limits if different for each plot; */
PLOT2 pred*epoch=group / LEGEND = LEGEND2; * VAXIS = -7 to 7 ;
FORMAT adjmean 8.1;
TITLE 'Predicted vs Observed';
RUN;
The quantitative tests of normality in the proc univariate results give likelihoods of the each variable being normally distributed; for multivariable normality, all variables should be normally distributed, although this assumption is usually violated to some degree. The output of the UNIVARIATE procedure includes histograms of residuals (for assessing whether shape of distribution is approximately normal) and side-by-side box plots of residual distribution by group (Figure 3 and Figure 4).
Further possible tests include influence diagnostics, to determine whether particular subjects have undue effect on the model. If undue bias due to individual subjects is suspected, the approach we suggest is to use the influence measures to investigate whether one or more subjects are consistently and substantially discrepant from the others. In SAS these tests may be run by adding the INFLUENCE statement [e.g., after in PROC MIXED after “RESIDUAL” add “INFLUENCE (EFFECT=subject ITER=5)” and ODS SELECT INFLUENCE]; note that this requires SAS version 9.1 or greater. This test produces the restricted likelihood distance, PRESS statistic and Cook’s distance (known as Cook’s D) for each subject. If a discrepant subject is found, an attempt is made to determine whether there is some reason for this. If a reason can be found, then they might legitimately be excluded. A “sensitivity” analysis may be run (a comparison analysis including and excluding that patient) to see if there is a material difference in the conclusions or results of interest. The homogeneity of covariance matrices can also be assessed in a similar manner using the ESTIMATES option in the INFLUENCE statement. Although these influence diagnostics may be useful in some cases, they have less relevance in fMRI analyses due to the controlled nature of typical experiments and are presented here as optional.
If the residuals are non-normal but symmetrical around 0 then the model is probably robust. However, if the residuals are both non-normal and non-symmetrical (i.e., skewed) then estimate biases may appear. For a large number of patients or observations, results are typically robust to moderate amount of skew, but for smaller numbers the model is likely to be robust for no more than a small amount of skew. If the data are seriously skewed, the typical options include making transformations (log, power transformations, etc.), identifying and omitting unusual patients (see above), using another more appropriate analytical technique, introduce covariates into the model, or not analyze the data. For fMRI studies, omitting unusual patients and adding covariates are the most likely approaches. As mentioned earlier, if the findings from the model are considered of value, then we suggests researchers report them along with the diagnostics test results so that the reader can assess for themselves the validity of the results.
RMANOVA has additional limitations which may be less applicable to fMRI data, but are detailed below for completeness. The constraints of the assumptions result in weaknesses of the approach, including:
Although not usually relevant to fMRI studies, cases with missing data will be entirely deleted from the analysis, causing both conceptual and analytical difficulties. Imputation methods can be employed to circumvent this issue.
Tests of within-subjects effects assume sphericity, but this was not directly evaluated. The data can be tested for sphericity, but this evaluation is complex within the proc mixed framework, and is not addressed here. In theory, Mauchly’s test of spherericity can be used, for example, when any within-subjects factor has three or more trials. (If the within-subject factor fails to meet the assumption of sphericity, then either the multivariate approach can be used or the univariate results can be adjusted using a correction factor, e.g., the Huynh-Feldt Epsilon correction method [the Greenhouse-Geisser method has been shown to be too conservative]).
The choice of the within-subject correlation matrix form is dependent upon sphericity assumptions, and we suggest a compound symmetric matrix (“type = cs” option in proc mixed) to allow for different variance patterns across groups. If different variance patterns across time are suspected, then heterogeneous compound symmetry could be used (“type = csh” option). However, this process is extremely computationally intensive, and in tests we performed, made no notable difference to the fit of the model.
Finally, the SAS library voilib created with the above SAS code contains numerous tables of data including predicted values, observations, model fit statistics, and residuals. These tables can be examined further either within SAS or by exporting them to a graph package, such as Excel.
We used fMRI data collected from two obstructive sleep apnea and two healthy control subjects as part of a pilot project; data are available online9. The data were chosen to illustrate the RMANOVA methodology, and do not constitute a sample that is sufficient to test scientific hypotheses. The Institutional Review Board of UCLA approved this study (IRB# 10-001012), which was in compliance with the Declaration of Helsinki; participants provided informed, written consent after the nature of the procedures was explained. Following a baseline scanning period, subjects performed a series of four respiratory challenges (30 s maximal inspiratory apnea), which were expected to elicit abnormal physiological responses in the patient group, based on earlier demonstrations of impaired neural responses to physiologic challenges10–13. A standard fMRI whole-brain protocol with repetition time of 2.5 s was implemented on a 3T Siemens Trio MRI scanner, and high-resolution T1-weighted anatomical scans were also collected (voxel size = 0.9 × 0.9 × 1 mm). The fMRI data were preprocessed using SPM routines, including realignment, spatial normalization, and smoothing. Smoothed images were intensity normalized to minimize global effects. VOI derived from the “AAL” toolbox in SPM were used to extract timetrends from the processed data14, and eight were selected to illustrate a variety of patterns highlighted by the approach. For each VOI, the time-series were analyzed using RMANOVA across the groups of two subjects, with challenges combined. Accompanying SAS and Excel files for each VOI are included online with this publication (Data availability).
Preprocessing was performed using MATLAB 7 (The Mathworks, Inc., Natwick, MA, USA), SPM (http://www.fil.ion.ucl.ac.uk/spm/) and a custom detrending routine6. VOI were drawn using MRIcroN software15, and RMANOVA was implemented in SAS 9.47.
A set of results is presented in Figure 6, illustrating a variety of statistical responses for eight VOI within the same fMRI dataset. This section describes the analytic steps needed to arrive at these results.
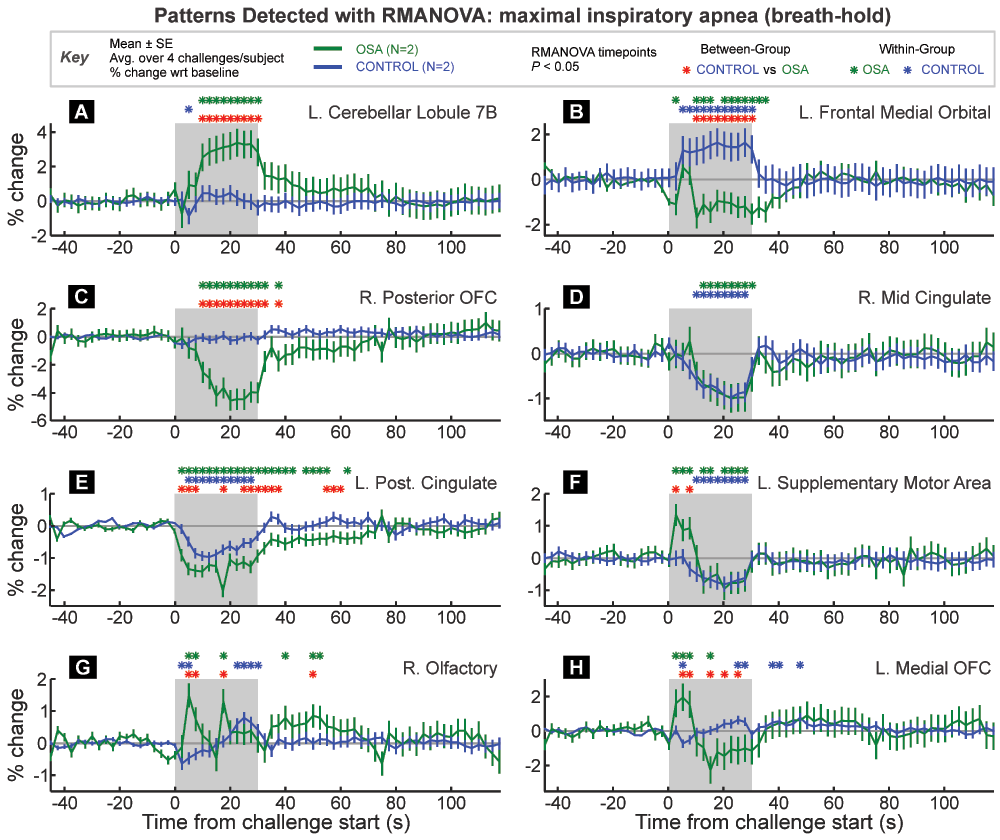
VOI are from the Automatic Anatomical Labelling toolbox extension to SPM. Time-points of between and within-group significant responses relative to baseline period are indicated by color-coded “*” symbols. The graphs are in percent signal change relative to baseline, and each trace is a group/challenge average (± between-subject SE).
Residual tests of the RMANOVA assumptions. The tests described in Appendix C were performed. The predicted responses were similar to the observed responses. Distributional tests of the Studentized residuals tests determined that the data were not precisely normally-distributed, as determined by the statistical tests with the PROC UNIVARIATE procedure. However, over 95% of the residuals were within ± 1.96, and visual inspection of the plots of residuals and predicted versus observed values showed only minor skew, and therefore the data were considered to be adequately modeled by the RMANOVA.
Patterns highlighted by RMANOVA. All significant effects were BOLD signal responses. To infer neuronal responses, these patterns should be deconvolved with an HRF; this approach was not applied here.
The Tukey-Fisher criterion for multiple comparisons was applied, and the highlighted VOI did show significant overall effects (Figure 6A–H).
The three VOI in Figure 6A–C would all be highlighted as having significant group differences in response using conventional SPM analyses. However, RMANOVA is one way to illustrate the manner in which the groups differ. Figure 6A illustrates a typical fMRI pattern of difference, with one group showing increased signal throughout the challenge, and the other group essentially no change. Figure 6B illustrates an opposite response between the groups, with on increasing and the other decreasing during the challenge period. Figure 6C shows a decrease in one group with no change in the other.
Figure 6D illustrates a simple case of a similar change in both groups; thus the within-group timepoints of difference are highlighted during the challenge period, corresponding to an equivalent decrease in OSA and control subjects. Figure 6E shows both groups changing in the same direction, but with a greater magnitude of response in the OSA group, thus leading to significant between-group differences across multiple time-points. Figure 6E also illustrates a pattern of changes that lasts over 30 seconds into the recovery period.
Transient differences are shown in Figure 6F–H. Figure 6F shows a pattern of initial increased response in the OSA group and sustained decreased response in the control group. However, unlike previous examples, the trends in the OSA group change 10–15 seconds into the challenge from an increase to a decrease below baseline. Figure 6G shows a an opposite pattern in control subjects (initial decrease, latter increase), and in OSA two large peaks are identified as differing significantly both between group and within group relative to baseline. Finally, Figure 6H shows a switch between greater OSA signal at the start of the challenge followed by a lower signal during the second half of the task period. These examples illustrate the capability of RMANOVA to detect the timing of within and between group differences in fMRI data.
The results illustrate two advantages of RMANOVA: firstly, no prior model of expected response of either signal intensity or timing is assumed, and for the type of challenge shown here, a variety of significant response patterns was detected by RMANOVA. Secondly, once a significant effect is found, RMANOVA provides an objective, statistically rigorous assessment of the time when responses or differences occurred, and the precise response pattern. A group difference highlighted by a traditional SPM analysis does not differentiate between a group increase vs. no change, a group increase vs. a decrease, no change vs. a decrease, or a larger increase vs. a smaller increase.
The procedure allows analysis of multiple subjects within multiple groups. The within-group and between-group are all performed with one analysis, allowing the contributions of subject and group factors to be accounted for in the final results.
Note that if all expected responses to the fMRI task are “on/off” or boxcar in nature, then the advantages of RMANOVA compared with cluster analysis are diminished.
Another advantage lies in processing timetrends from VOI drawn in different locations across different subjects. Spatial normalization is only accurate to within several millimeters16, and therefore small brain structures, such as those in the brainstem cannot be accurately depicted on VOI across multiple spatially normalized scans. By allowing a group analysis of timetrends from varying sites, RMANOVA can be more accurate compared with conventional fMRI analyses in depicting group responses within a particular structure. For regions such as the dorsal medulla, VOI analysis using RMANOVA is particularly helpful for determining group patterns.
Two disadvantages of RMANOVA relate to defining the VOI. The procedure requires manual definition of the VOI, perhaps for each subject, or at least for each structure of interest. A second disadvantage is that no whole-brain search is performed, and only a priori defined areas are studied. For this reason, we believe that a combination of a traditional SPM analysis with RMANOVA allows for a complete and powerful approach to analysis of fMRI data where the time-course of responses is of interest.
The approach does not consider or allow for variations in the shape of the HRF. A standard HRF may be used to deconvolve each time series, resulting in an inferred neural response time series, or a different HRF may be used for different VOI (to account for the spatial variation in HRF shape).
Temporal autocorrelation between repeated measures is not accounted for, which likely leads to some loss of power. Nevertheless, we have found the technique highlights many patterns of interest, and thus this limitation does not negate the usefulness of the technique.
Procedural disadvantages with the proposed method include the requirement for detrending images prior to analysis, the extraction of the VOI time-trends from the images, and in the example presented here, the use of SAS. The former requires computation routines which are typically not included in fMRI analysis software, and the latter requires routines for exporting the data, availability of software, and some familiarity with this software.
There are a number of assumptions underlying the RMANOVA method, which are fully described above along with their associated limitations. As with any statistical model, RMANOVA should be used with problems that match those assumptions.
Analyzing timetrends from VOI’s using RMANOVA can highlight temporal patterns of response to a challenge not readily apparent using conventional model-based approaches. Our research group has used this method extensively to assess fMRI responses to physiological challenges with complex responses over periods of tens of seconds to minutes. RMANOVA allows insight into the precise timing of changes from baseline, and response differences between groups. For complex paradigms, the technique can be a useful addition to conventional whole-brain model-based approaches.
F1000Research: Dataset 1. Processed data, as well as the SAS code for running each VOI analysis, 10.5256/f1000research.8252.d11747917
Harvard Dataverse: Macey, Paul. 2016. Pilot fMRI of breath-hold in OSA, http://dx.doi.org/10.7910/DVN/EZUMI99
PMM and RMH conceived the study; PMM and PJS designed the methodology; PMM, KEM and RMH collected the test data and performed analysis and evaluation; all authors contributed to the manuscript and have agreed to the final content.
Supported by the National Institutes of Health National Institute of Nursing Research NR 013693.
The funders had no role in study design, data collection and analysis, decision to publish, or preparation of the manuscript.
| Views | Downloads | |
|---|---|---|
| F1000Research | - | - |
|
PubMed Central
Data from PMC are received and updated monthly.
|
- | - |
Competing Interests: No competing interests were disclosed.
Competing Interests: No competing interests were disclosed.
Alongside their report, reviewers assign a status to the article:
| Invited Reviewers | ||
|---|---|---|
| 1 | 2 | |
|
Version 2 (revision) 08 Jul 16 |
read | read |
|
Version 1 05 Apr 16 |
read | read |
Click here to access the data.
Spreadsheet data files may not format correctly if your computer is using different default delimiters (symbols used to separate values into separate cells) - a spreadsheet created in one region is sometimes misinterpreted by computers in other regions. You can change the regional settings on your computer so that the spreadsheet can be interpreted correctly.
Provide sufficient details of any financial or non-financial competing interests to enable users to assess whether your comments might lead a reasonable person to question your impartiality. Consider the following examples, but note that this is not an exhaustive list:
Sign up for content alerts and receive a weekly or monthly email with all newly published articles
Already registered? Sign in
The email address should be the one you originally registered with F1000.
You registered with F1000 via Google, so we cannot reset your password.
To sign in, please click here.
If you still need help with your Google account password, please click here.
You registered with F1000 via Facebook, so we cannot reset your password.
To sign in, please click here.
If you still need help with your Facebook account password, please click here.
If your email address is registered with us, we will email you instructions to reset your password.
If you think you should have received this email but it has not arrived, please check your spam filters and/or contact for further assistance.
Comments on this article Comments (0)