Keywords
Dose-finding studies, oncology, Phase I clinical trial, individualized dose-finding, precision medicine
Dose-finding studies, oncology, Phase I clinical trial, individualized dose-finding, precision medicine
Despite advances in Bayesian adaptive designs1,2 and model-based dose-finding3, oncology dose-finding studies remain conceptually in the thrall of the maximum tolerated dose (MTD). This concept stands opposed to the long-recognized heterogeneity of cancer patients’ pharmacokinetics and pharmacodynamics (PK/PD), and to the diversity of their individual values and goals of care. Under this conceptual yoke, these dose-finding studies constitute a significant choke-point in drug development, where a severe discount may be applied to the potential value in new molecules through the hobbling of subsequent ‘efficacy’ trials by inadequate individual-level dosing4.
Strangely, Bayesian innovation in dose-finding studies has proceeded apace without issuing a meaningful challenge to the inherently frequentist conception of an MTD as determined by whole-cohort frequencies of dose-limiting toxicities (DLTs). Thus, even as Bayesianism has made progress toward the ethical imperative of efficient use of data5 in such studies, it has neglected to confront the distinct ethical dimension of individualism6. This seems a great irony, as the dynamic learning model of Bayesianism is equally suited, and indeed equally essential, to solving the latter problem.
This paper demonstrates individualized dose-finding in a simulated Phase I study of a cytotoxic chemotherapy drug for which neutropenia constitutes the critical dose-limiting toxicity. Importantly, myelosuppression is interpreted also as a monotone index of therapeutic efficacy, without a dose-response ‘plateau’7 of the type postulated for molecularly targeted agents (MTAs). This creates a problem setting where simple heuristics apply, simplifying the demonstration undertaken here. The aim of this exercise is to elaborate a concrete setting in which ‘dose-finding study’ may be seen as a misnomer. Under the view advanced here, early-phase studies of this kind should be conceived as dose titration algorithm tuning (DTAT) studies.
The idea that ‘dose finding studies’ should yield dose titration algorithms is not new. More than a quarter-century ago, Sheiner and colleagues8 advocated a learn-as-you-go concept for “dose-ranging studies”, addressing concerns about “parallel-dose designs” that are not far removed from the motivations for the present paper. As in the advocacy of Sheiner et al., parametric models play an important role in this paper, although in keeping with a spirit of pragmatism this dependence is relaxed to some extent by means of a semiparametric dynamic on-line learning heuristic.
A hypothetical cytotoxic drug is considered, modeled notionally after docetaxel, to be infused in multiple 3-week cycles. The pharmacokinetics are taken to follow a 2-compartment model with parameters as estimated for docetaxel in a recent population pharmacokinetic study9. Chemotherapy-induced neutropenia (CIN) is taken to follow a myelosuppression model due to Friberg et al.10. Together, these models form a population pharmacokinetic/pharmacodynamic (PK/PD) model within which dose titration algorithms may be simulated and tuned for optimality. For simulation purposes, and anticipating the future value of ready access to a variety of inference procedures in follow-on work, this PK/PD model is implemented in R package pomp11. R version 3.3.2 was used12.
Basic behaviors of the models are illustrated by simulation graphics generated for 25 individuals randomly generated from the population PK/PD model. Properties with specific relevance to absolute neutrophil count nadir (ANCnadir)-targeted dose titration are then investigated, with an eye to demonstrating the predictability of nadir timing. In particular, an approximate linearization of neutrophil nadir level and timing is demonstrated, achieved through suitable power-law transformation of infusion doses and logarithmic transformation of neutrophil concentration. Within this transformed parameter space, a simple recursive dose titration algorithm is defined on the basic heuristic of the Newton-Raphson method for root-finding. For simplicity, monitoring of CIN is not modeled endogenously to this algorithm, but is treated as exogenous such that nadir timing and level are known precisely. A ‘DTAT’ study is simulated and visualized for 25 patients, with the tuning parameters of the recursive titration algorithm held fixed. The visualization supports a discussion of how these parameters might be tuned over the course of a Phase I study. All simulations and figures in this paper were generated by a single R script, archived on OSF13.
We take the population pharmacokinetics of our cytotoxic drug to obey a 2-compartment model, with parameters drawn notionally from estimates published for docetaxel [9, Table 2]; see Table 1.
CL: clearance; Q: intercompartmental clearance; Vc: volume of central compartment; Vp volume of peripheral compartment; CV: coefficient of variation. (*) A CV for Vc was unavailable in 9 and has been set arbitrarily to 0.1.
| Param | Units | Mean | CV |
|---|---|---|---|
| CL | L/hour | 32.6 | 0.295 |
| Q | L/hour | 5.34 | 0.551 |
| Vc | L | 5.77 | 0.1* |
| Vp | L | 11.0 | 0.598 |
Figure 1 shows illustrative pharmacokinetic profiles for 25 randomly-generated individuals from this population, administered a 100 mg dose.
Chemotherapy-induced neutropenia is simulated using the 5-compartment model of Friberg et al. [10, Table 4], in which myelocytes (here, neutrophils) arise from progenitor cells in a proliferative compartment, mature through a series of 3 transitional states, and emerge into the systemic circulation; see Figure 2. Transit between successive compartments in this model is a Poisson process with time constant ktr, total mean transit time being therefore given by MTT = 4/ktr. See Table 2.

Prol: proliferative compartment; Transitn: maturation compartments; Circ: systemic circulation; ktr: transition rate; kprol: rate of proliferation of progenitor cells, regulated by a negative-feedback loop parametrized by γ > 0.
Circ0: baseline neutrophil concentration; MTT : mean transit time between the 5 model compartments; γ: exponent of feedback loop; EC50, Emax: parameters of a model (of the standard Emax type) governing docetaxel-induced depletion in the proliferative compartment.
| Param | Units | Mean | CV |
|---|---|---|---|
| Circ0 | cells/mm3 | 5050 | 0.42 |
| MTT | hours | 89.3 | 0.16 |
| γ | - | 0.163 | 0.039 |
| Emax | µM | 83.9 | 0.33 |
| EC50 | µM | 7.17 | 0.50 |
Figure 3 shows illustrative myelosuppression profiles for 25 randomly-generated individuals from this population, administered a 100 mg dose.

Note how a chemotherapeutic ‘shock’ to the proliferative compartment Prol propagates through the maturation compartments Tx1,2,3 and thence to the systemic circulation Circ. (ANC: absolute neutrophil count.)
When parametrized by , individuals’ trajectories in (log(ANCnadir)×timenadir)-space may be approximately linearized, as shown in Figure 4. A consequence of this rough linearity is that we may hold out some hope that a linear predictive model could be a suitable basis for an adaptive dose titration scheme.
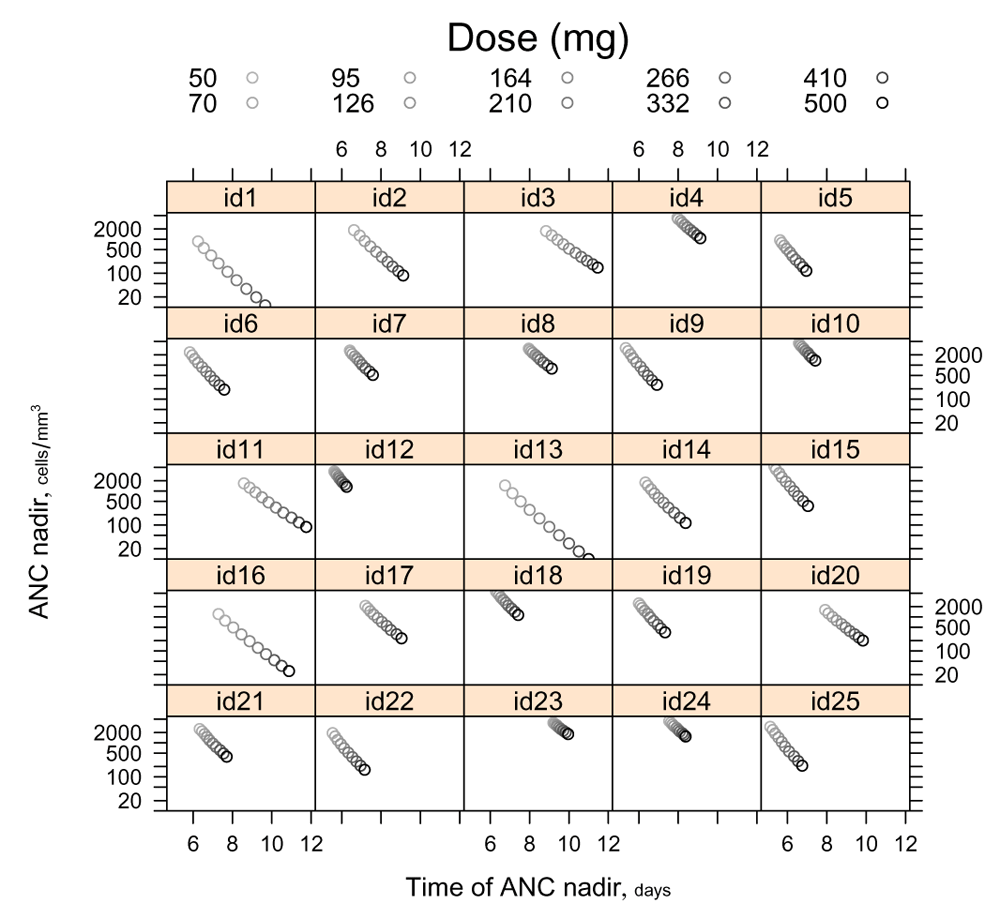
The 10 doses plotted are evenly spaced on a fourth-root scale. Not only are the trajectories themselves nearly linear in (log(ANC) × time)-space, but each one is traversed at roughly ‘constant velocity’ with respect to .
Recursive nonlinear filtering, as implemented in the extended Kalman filter (EKF) or its more modern adaptations14, constitutes a powerful conceptual framework for approaching model-based dose titration15. Under a suitable linearization of the dynamics, as for example suggested by Figure 4, even the linear Kalman filter16 might succeed admirably. The ‘tuning’ in ‘DTAT’ has itself been suggested by the practice of tuning a Kalman filter for optimal performance.
For present purposes, however, it suffices to implement a model-free recursive titration algorithm built on the Newton-Raphson method, with a numerically-estimated derivative based on most recent infusion doses and their corresponding ANC nadirs. In this algorithm, a relaxation factor ω = 0.75 is applied to any proposed dose increase, with safety in mind. Whereas the slope of log(ANCnadir) with respect to is expected to be strictly negative at steady state, hysteresis effects arising during initial steps of dose titration do sometimes yield positive numerical estimates for this slope; so the slope estimates are constrained to be ≤ 0. The infusion dose for cycle 1 is 50 mg, and the cycle-2 dose is calculated conservatively using a slope −2.0, which is larger (in absolute terms) than for any of our simulated patients except id1 and id13; see Figure 4. For reference, these starting values for the tuning parameters of the titration algorithm are collected in Table 3.
| Param | Description | Value |
|---|---|---|
| ω | Relaxation factor | 0.75 |
| slope1 | Slope for cycle-2 dosing | −2.0 |
| dose1 | Initial (cycle-1) dose | 50 mg |
With the illustrative purpose of this article again in mind, we treat neutropenia monitoring as an exogenous process yielding precise nadir timing and levels. This enables a demonstration of the main point without the encumbrance of additional modeling infrastructure peripheral to the main point.
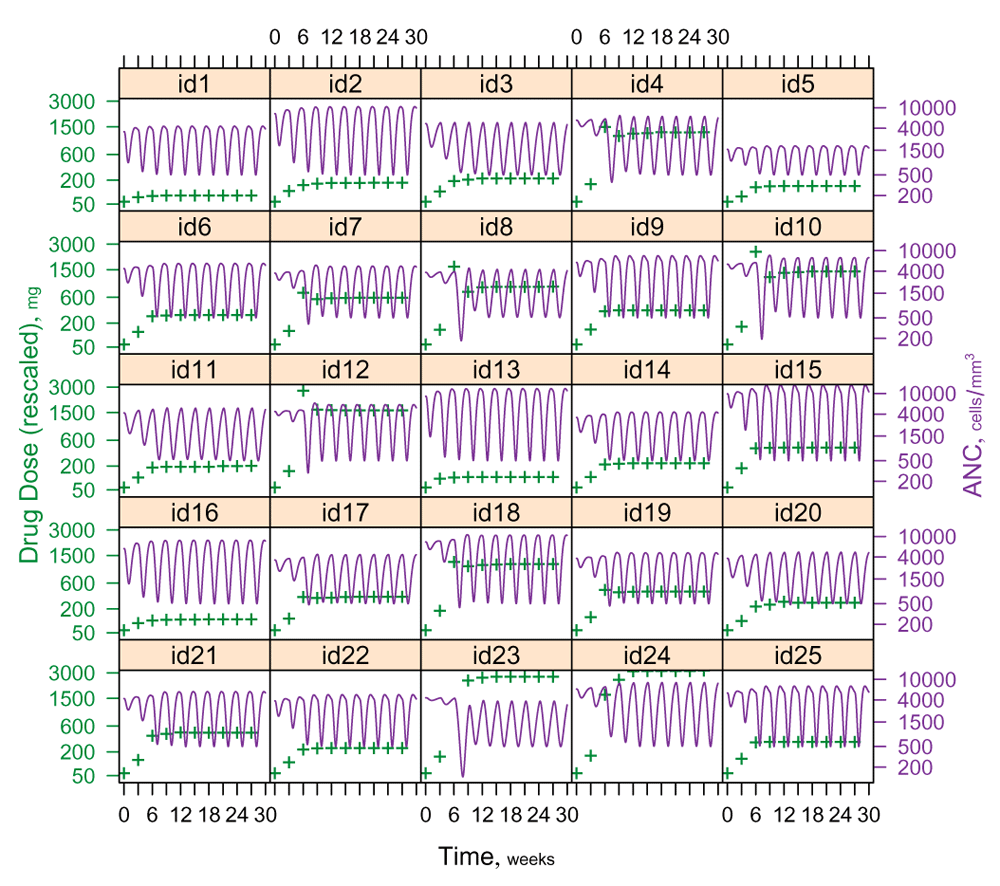
If one considers Figure 5 as a sequence of titration outcomes emerging in serially enrolled study subjects, it becomes clear that even quite early in the study it will seem desirable to ‘retune’ the titration algorithm. For example, provided that course-1 CIN monitoring is implemented with sufficient intensity to deliver advance warning of an impending severely neutropenic nadir, so that timely colony-stimulating factor may be administered prophylactically17, then upon review of the titration courses in the first 10 subjects it may well appear desirable to increase dose1 from 50mg to 100mg. Likewise, given the third-dose overshooting that occurs in 4 of the first 10 subjects, it may seem desirable to adjust the relaxation factor ω downward. Of note, at any given time any such proposed retuning may readily be subjected to a ‘dry run’ using retrospective data from all convergent titration courses theretofore collected. (Hysteresis effects would however be inaccessible to a strictly data-driven dry run absent formal modeling.) Furthermore, the ‘tuning’ idea readily generalizes to the fundamental modification or even wholesale replacement of a dose titration algorithm; the overshooting seen for subjects id10, id12 and id23, for example, inspires further thought about refining (or replacing) the admittedly very naive Newton-Raphson method employed herein.
Cc and Cp are drug concentrations in the central and peripheral compartments, respectively.
A further dimension of ‘tuning’ that must be discussed is the potential for driving the tuning parameters using statistical models built on baseline covariates. Surely, to the extent that the great heterogeneity in final dosing evident in Figure 5 could be predicted based on age, sex, weight or indeed on pharmacogenomic testing, then dose1 should be made a function of these covariates. The recalibration of such models as data accumulate from successive study subjects is very much a part of the full concept of ‘tuning’ I wish to advance.
Finally, whereas I have discussed ‘tuning’ here largely in terms of reflective, organic decision-making such as occurs in the creative refinement of algorithms or in data-driven statistical model development, I do not mean to exclude more formal approaches to algorithm tuning. A decision-theoretic framing of the tuning problem should enable formal algorithm tuning to be specified and carried out meaningfully. Such framing would also have the salutary effect of bringing into view objectively the important matter of patients’ heterogeneity with respect to values and goals of care. It seems quite likely that the balance of benefits from aggressive titration versus harms of toxicities will generally differ from one patient to another. Dose titration algorithms should most emphatically be tuned to these factors as well.
It is where pharmacometrics meets the field of optimal control that the current literature seems to make its closest point of contact with the DTAT concept I am advancing here. In optimal-control investigations of chemotherapy18–23, as in DTAT, relatively large decision spaces are explored. Indeed, the infinite-dimensional spaces of control functions posited for exploration in optimal control applications dwarf the finite-dimensional spaces of tuning parameters in DTAT as dramatically as the latter dwarf the finite sets of discrete doses trialed in now-standard Phase I studies. This intermediate ‘cardinality’ of DTAT reflects an important advantage in an era when, to almost universal chagrin, the detested 3+3 dose-finding design retains its hegemony due partly to widespread resistance to modeling24. In such an era, optimal control applications that involve detailed mathematical modeling of tumor biology and dynamics sadly seem consigned to the fringes of practice. Acceptance of such ambitious problem formulations, expressing as they do the spirit of a future age, must await deep cultural changes in the medical sciences and clinical practice.
As easy as it is, however, to disparage ‘resistance to modeling’ as some kind of antediluvian attitude, this resistance does rightfully assert the importance of unmodeled complexities that necessitate application of organic forms of clinical judgment25. It should be clear from the above discussion of ‘tuning’ that DTAT readily accommodates and veritably invites scrutiny, supervision and modification by clinical judgment. For example, if during the course of a DTAT study adverse effects other than neutropenia were to emerge as occasional dose-limiting toxicities, then the full concept of ‘tuning’ advanced above would invite dynamic, ‘learn-as-you-go’ modifications of the titration algorithm. Such modifications may begin with decreasing the relaxation factor ω, but might also involve efforts to classify and predict these new DLTs, and to incorporate such new understanding explicitly into the dose titration algorithm yielded by the study. Indeed, whatever philosophical challenge DTAT embodies is likely to take the form of requiring an intensified commitment to clinical judgment, in a learn-as-you-go world where the always-provisional nature of medical knowledge must frankly be acknowledged6,26.
I have advanced a concept of dose titration algorithm tuning (DTAT), drawing connections with recursive filtering and optimal control. I have illustrated key elements of DTAT by simulating neutrophil-nadir-targeted titration of a hypothetical cytotoxic chemotherapy drug with pharmacokinetics and myelosuppressive dynamics patterned on previously estimated population models for docetaxel. I believe DTAT presents a prima facie case for discarding the outmoded concept of ‘the’ maximum tolerated dose (MTD) of a chemotherapy drug. This argument should be of interest to a wide range of stakeholders, from cancer patients with a stake in receiving optimal individualized ‘MTDi’ dosing, to shareholders in pharmaceutical innovation with a stake in efficient dose-finding before Phase III trials.
Open Science Framework: Code and Figures for v1 of F1000Research submission: Dose Titration Algorithm Tuning (DTAT) should supersede the Maximum Tolerated Dose (MTD) concept in oncology dose-finding trials, doi 10.17605/osf.io/vwnqz13
Daniela Conrado (Associate Director, Quantitative Medicine at Critical Path Institute) confirms that the author has an appropriate level of expertise to conduct this research, and confirms that the submission is of an acceptable scientific standard. Daniela Conrado declares she has no competing interests.
The author operates a scientific and statistical consultancy focused on precision-medicine methodologies such as those advanced in this article.
Author Endorsement: Daniela Conrado (Associate Director, Quantitative Medicine at Critical Path Institute) confirms that the author has an appropriate level of expertise to conduct this research, and confirms that the submission is of an acceptable scientific standard. Daniela Conrado declares she has no competing interests.
| Views | Downloads | |
|---|---|---|
| F1000Research | - | - |
|
PubMed Central
Data from PMC are received and updated monthly.
|
- | - |
Competing Interests: No competing interests were disclosed.
Competing Interests: No competing interests were disclosed.
Alongside their report, reviewers assign a status to the article:
| Invited Reviewers | ||||
|---|---|---|---|---|
| 1 | 2 | 3 | 4 | |
|
Version 3 (update) 17 Jul 17 |
||||
|
Version 2 (revision) 30 Mar 17 |
read | read | ||
|
Version 1 07 Feb 17 |
read | read | ||
Provide sufficient details of any financial or non-financial competing interests to enable users to assess whether your comments might lead a reasonable person to question your impartiality. Consider the following examples, but note that this is not an exhaustive list:
Sign up for content alerts and receive a weekly or monthly email with all newly published articles
Already registered? Sign in
The email address should be the one you originally registered with F1000.
You registered with F1000 via Google, so we cannot reset your password.
To sign in, please click here.
If you still need help with your Google account password, please click here.
You registered with F1000 via Facebook, so we cannot reset your password.
To sign in, please click here.
If you still need help with your Facebook account password, please click here.
If your email address is registered with us, we will email you instructions to reset your password.
If you think you should have received this email but it has not arrived, please check your spam filters and/or contact for further assistance.
Comments on this article Comments (0)