Effectiveness of model-based clustering in analyzing <i>Plasmodium falciparum </i>RNA-seq time-course data

Jelili Oyelade; Itunuoluwa Isewon; Damilare Olaniyan; Solomon O Rotimi; Jumoke Soyemi

doi:10.12688/f1000research.12360.2

Home Browse Effectiveness of model-based clustering in analyzing Plasmodium falciparum...

ALL Metrics

Views

Downloads

Get PDF

Get XML

Export

▬

✚

Research Article

Revised

Effectiveness of model-based clustering in analyzing Plasmodium falciparum RNA-seq time-course data

[version 2; peer review: 1 approved, 1 approved with reservations, 1 not approved]

Jelili Oyelade ^1,2, Itunuoluwa Isewon^1,2, Damilare Olaniyan¹, Solomon O Rotimi^2,3, Jumoke Soyemi^2,4

Jelili Oyelade ^1,2, Itunuoluwa Isewon^1,2, [...] Damilare Olaniyan¹, Solomon O Rotimi^2,3, Jumoke Soyemi^2,4

PUBLISHED 25 May 2018

Author details Author details

¹ Department of Computer and Information Sciences, Covenant University, Ota, Nigeria
² Covenant University Bioinformatics Research (CUBRE), Covenant University, Ota, Nigeria
³ Department of Biological Sciences, Covenant University, Ota, Nigeria
⁴ Department of Computer Science, Federal Polytechnic, Ilaro, Nigeria

Jelili Oyelade
Roles: Conceptualization, Methodology, Project Administration, Resources, Supervision, Validation, Writing – Original Draft Preparation, Writing – Review & Editing

Itunuoluwa Isewon
Roles: Methodology, Resources, Writing – Original Draft Preparation, Writing – Review & Editing

Damilare Olaniyan
Roles: Formal Analysis, Investigation, Methodology, Software

Solomon O Rotimi
Roles: Data Curation, Investigation, Validation, Writing – Review & Editing

Jumoke Soyemi
Roles: Formal Analysis, Validation, Writing – Review & Editing

OPEN PEER REVIEW

REVIEWER STATUS

This article is included in the Pathogens gateway.

Abstract

Background: The genomics and microarray technology played tremendous roles in the amount of biologically useful information on gene expression of thousands of genes to be simultaneously observed. This required various computational methods of analyzing these amounts of data in order to discover information about gene function and regulatory mechanisms.
Methods: In this research, we investigated the usefulness of hidden markov models (HMM) as a method of clustering Plasmodium falciparum genes that show similar expression patterns. The Baum-Welch algorithm was used to train the dataset to determine the maximum likelihood estimate of the Model parameters. Cluster validation was conducted by performing a likelihood ratio test.
Results: The fitted HMM was able to identify 3 clusters from the dataset and sixteen functional enrichment in the cluster set were found. This method efficiently clustered the genes based on their expression pattern while identifying erythrocyte membrane protein 1 as a prominent and diverse protein in P. falciparum.
Conclusion: The ability of HMM to identify 3 clusters with sixteen functional enrichment from the 2000 genes makes this a useful method in functional cluster analysis for P. falciparum

Keywords

Genomics, Plasmodium falciparum, microarray, Hidden markov model, clustering, Functional Enrichment.

Corresponding author: Jelili Oyelade

Competing interests: There is no competing interests declared.

Grant information: The author(s) declared that no grants were involved in supporting this work.

Copyright: © 2018 Oyelade J et al. This is an open access article distributed under the terms of the Creative Commons Attribution License, which permits unrestricted use, distribution, and reproduction in any medium, provided the original work is properly cited. Data associated with the article are available under the terms of the Creative Commons Zero "No rights reserved" data waiver (CC0 1.0 Public domain dedication).

How to cite: Oyelade J, Isewon I, Olaniyan D et al. Effectiveness of model-based clustering in analyzing Plasmodium falciparum RNA-seq time-course data [version 2; peer review: 1 approved, 1 approved with reservations, 1 not approved]. F1000Research 2018, 6:1706 (https://doi.org/10.12688/f1000research.12360.2) First published: 19 Sep 2017, 6:1706 (https://doi.org/10.12688/f1000research.12360.1) Latest published: 25 May 2018, 6:1706 (https://doi.org/10.12688/f1000research.12360.2)

Revised Amendments from Version 1

We have responded and implemented detailed explanations of the methodology, and the Go Term enriched (p-value) has been provided. The normalized and discretized data sets used have been provided as Dataset 1.

See the authors' detailed response to the review by Ashis Das, P.A. Boopathi and Shibashish Choudhury

Introduction

Technological advancement in bioinformatics such as the high through put sequencing technology has resulted in the availability of a very large amount of informative data¹. Expressions of thousands of genes are now being measured concurrently under various experimental conditions using microarray technology. Microarray consists of many thousands of short, single stranded sequences, each immobilized as individual elements on a solid support, that are complementary to the cDNA strand representing a single gene. Gene expression measurements can be obtained for thousands of genes simultaneously using microarray technology. In a cell, genes are transcribed into mRNA molecules which in turn can be translated into proteins, and it is these proteins that perform biological functions, give cellular structure and in turn regulate gene expression².

Various researches had been carried out on the analysis and extraction of useful biological information such as detection of differential expression, clustering and predicting sample characteristics³. One of the important of gene expression data is the ability to infer biological function from genes with similar expression patterns⁴. Due to large number of genes and complexity of the data and networks, research has suggested clustering to be a very useful and appropriate technique for the analysis of gene expression data which can be used to determine gene coregulation⁵, subpopulation⁶, cellular processes, gene function⁷ and understanding disease processes⁸.

Clustering algorithms as described by 9 can either be distance based or model based. Distance-based clustering such as the k means¹⁰ does not consider dependencies between time points while the model based approach embeds time dependencies and uses statistical models to cluster data. Other approaches include Self Organizing Maps¹¹, Principal Component Analysis, hierarchical clustering⁴, graph theory approach¹², genetic algorithms and the Support Vector Machine¹³. These algorithms has been successfully applied to various time series data but still have various shortcoming such as determining the optimal number of clusters and choosing the best algorithm for clustering since most of them are based on heuristics. The algorithms are also not very effective especially when a particular gene is associated with different clusters and performs multiple functions.

This research focuses on clustering of genes with similar expression patterns using Hidden Markov Models (HMM) for time course data because they are able to model the temporal and stochastic nature of the data. A Markov process is a stochastic process such that the state at every time belongs to a finite set, the evolution occurs in a discrete time and the probability distribution of a state at a given time is explicitly dependent only on the last state and not on all the others. This refers to as first-order Markov process (Markov chain) for which the probability distribution of a state at a given time is explicitly dependent only on the previous state and not on all the others. That is, the probability of the next (“future”) state is directly dependent only on the present state and the preceding (“past”) states are irrelevant once the present state is given¹⁴. Fonzo et al.¹⁴ defined HMM as a generalization of a Markov chain in which each (“internal”) state is not directly observable (hidden) but produces (“emits”) an observable random output (“external”) state, also called “emission” state. Schliep et al.⁹ proposed a partially supervised clustering method to account for horizontal dependencies along the time axis and to cope with the missing values and noise in time course data. This approach used k means algorithm and the Baum welch algorithm for parameter estimation. Further analysis on the cluster was done with the Viterbi algorithm which gives a fine grain, homogeneous decomposition of the clusters. The partial supervised learning was done by adding labeled data to the initial collection of clusters. Ji et al.¹⁵ developed an application to cluster and mine useful biological information from gene expression data. The dataset was first normalized to a mean of zero and variance of one and then discretized into expression fluctuation symbol with each symbol representing either an increase, decrease or no change in the expression measurement. A simple HMM was constructed for these fluctuation sequences. The model was trained using the Baum-Welch EM algorithm and the probability of a sequence given a HMM was calculated using the forward-backward algorithm. Several copies of the HMM was made so that each copy represent a single cluster. These clusters were made to specialize by using a weighted Baum-Welch algorithm where the weight is proportional to the probability of the sequence given the model. The Rand Index and Figure of Merit was used to validate the optimal number of cluster results.

Geng et al.¹⁶ developed a gene function prediction tool based on HMM where they studied yeast function classes who had sufficient number of open reading frame (ORF) in Munich Information Center for Protein Sequences (MIPS). Each class was labeled as a distinct HMM. The process was performed on three stages; the discretization, training and inference stages and data used for this analysis was the yeast time series expression data. Lees et al.¹⁷ proposed another methodology to cluster gene expression data using HMM and transcription factor information to remove noise and reduce bias clustering. A single HMM was designed for the entire data set to see if it would affect clustering results. Each path in the HMM represents a cluster, transition between states in a path is set to a probability of 1 and transition between states on different path is set to a probability of 0. Genes were allocated to clusters by calculating the probability of each sequence produced by the HMM. Clusters were validated using the likelihood ratio test which computes the difference in the log-likelihood of a complex model to that of a simpler model. Zeng and Garcia-Frias¹⁸ implemented the profile HMM as a self-organizing map, this profile HMM is a special case of the left to right inhomogeneous HMM which is able to model the temporal nature of the data. This makes it very useful for real life applications. The profile HMM is trained using the Baum-Welch algorithm¹⁹ and clustering was done using the Viterbi algorithm and the algorithm was implemented on the fibroblast and the sporulation datasets. Beal et al.²⁰ implemented the Hierarchical Dirichlet Process Hidden Markov Model (HDP-HMM) for clustering gene expression data with countably infinite HMM. Gibbs sampling method was used to reduce the time complexity of the inference. The data used for the implementation was derived from Lyer et al.²¹ and Cho et al.²² which was normalized and standardized to a log ratio of 1 at time t = 1. Baum Welch algorithm was used for Estimation Maximization. In this work, we adopted the work of Lee et al.¹⁷ and applied HMM on the Plasmodium falciparum RNA-seq dataset.

Materials and methods

In this work, data was extracted and normalized to a mean of 1 and standard deviation of 0. Discretization was done on the data to improve the clustering results. The HMM forward-backward algorithm and Baum-Welch training algorithm was implemented to cluster the gene expression data. Genes were then assigned to cluster using the forward algorithm and inference was done by obtaining functionally enriched genes in the cluster set using FunRich tool. The data used was published by 23, they used the Illumina based sequencing technology to extract expressions of 5270 P. falciparum genes at seven different time points every 8hrs for 42hrs. The clustering algorithms was implemented by first randomly initializing all the HMM parameters, then, forward algorithm was implemented to calculate the forward probabilities of the observation and Baum-Welch algorithm was used for data fitting, then the likelihood of each HMM was calculated iteratively until the optimal likelihood is obtained. This process is repeated for all the different sized HMMs used.

Definitions and notation

HMMs can be viewed as probabilistic functions of a Markov chain²⁴ such that each state can produce emissions according to emission probabilities.

Definition 1. (Hidden Markov Model). Let O = (O₁,…) be a sequence over an alphabet ∈. A Hidden Markov Model λ is determined by the following parameters:

• S_i, the states i = 1, … N
• π_i, the probability of starting in state S_i,
• α_ij, the transition probability from state S_i to state S_j, and
• b_i(ω), the emission probability function of a symbol ω ∈ Σ in state S_i.

Definition 2. (Hidden Markov Cluster Problem). Given a set O = {O¹, O²,…, Oⁿ} of n sequences, not necessarily of equal length, and a fixed integer K ≪ n. Compute a partition C = (C₁, C₂,…, C_k) of O and HMMs λ₁,…, λ_k as to maximize the objective function

f (c) = \prod_{k = 1}^{k} \prod_{O_{i} ϵ C_{k}} L (O^{i} | λ_{k}) (1)

Where L(Oⁱ | λ_k) denotes the likelihood function for generating sequence Oⁱ by model λ_k:

Data preprocessing

The preprocessing was done in two stages. The first stage was the normalization and the second stage was discretization. The normalization was done with the R statistical package using the normalize library. Normalization removes static variation in the microarray experiment which affects the gene expression level. Normalization also helps in speeding up the learning phase. Missing values are also removed during normalization. The data used after normalization is given in Data Availability as normalized.xsl. Discretization was done by converting the time points to symbols depending on whether the expression value has increased, decreased or not changed, as given in Data Availability as Discretized_Data.txt. This is done by using the equation below.

S_{i} = {\begin{array}{l} 0 & i f E_{i} - E_{i + 1} < a \\ 1 & i f E_{i + 1} - E_{i} \geq a \\ 2 & i f E_{i} - E_{i + 1} \geq a \end{array} (2)

Where:

S_i = fluctuation level between time i and i + 1

E_i = expression level at time point i

L = number of time points.

a = threshold value between timepoints.

HMM for clustering gene expression data

In this work, we implemented a model-based HMM clustering algorithm where a cluster represents a path in the HMM model. Therefore, as the number of cluster increases, the number of paths through the model increases and the HMM becomes larger and larger. The number of hidden state is the number of clusters multiplied by the sequence length. Research has also shown that HMM that transverse from left to right best models time series data, therefore HMM moves from only right-to-left. The structure of the HMM is shown in Figure 1.

Figure 1. HMM design from cluster 2 to w.

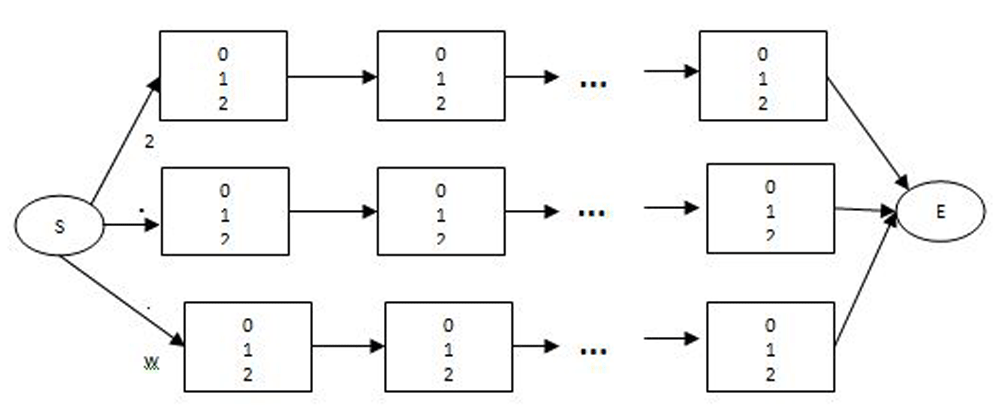
The number 0, 1, and 2 represents the emmission symbols at each state.

For an HMM to be used for real world applications, there are three basic problems of interest that needs to be solved.

1. Given an observation sequence O = {O₁ … O_n}, and a model λ = (A, B, π), how can we effectively compute the probability of observation given the model, i.e P(O/λ)
2. Given an observation sequence and a model λ, how do we choose a state sequence which best explains the observation.
3. How do we adjust the model parameter to optimize P(O/λ).

Problem 1 is the evaluation problem and solution allows us to choose the model that best matches the observation. This can be solved using the forward-backward algorithm. Problem 2 aims to discover the hidden state in the model and find correct state for each observation. It is also known as the inference problem. There is no correct solution for this problem but an optimal solution can be reached based on a stated optimality criterion. This problem can be solved using the Viterbi algorithm. The third and most difficult problem aims to adjust the model parameter to optimize the HMM and is also known as training the HMM. It is usually solved using the Baum-Welch training algorithm. In this work, we implemented the HMM clustering algorithm in C++ programming language. HMM structure for clustering was first created. A cluster is represented as a path in the HMM, for example, for x cluster the model increases proportionally with x paths through the HMM. The prior, transition and observation probability are then estimated for each cluster size by using the solution to problem 3 to optimize each model. Then, genes are assigned to each cluster by choosing the best model/cluster that fits an observation using the forward algorithm.

The left to right model has the property that, as the time increases, the state transition increases, that is, the states moves from left to right. This process is conveniently able to model data whose properties change over time.

The forward algorithm calculates the forward probabilities of a sequence of observation. This is the probability of getting a series of observation given that the HMM parameters (A, B, π) are known. This computation is usually expensive computationally. The time invariance of the probabilities can however be used to reduce the complexity of this algorithm by calculating the probabilities recursively. These probabilities are calculated by computing the partial probabilities for each state from times t = 1 to t = T. The sum of all the final probabilities for each states is the probability of observing the sequence given the HMM and this was used in this research to compute the likelihood of a sequence given the HMM. The algorithm is in 3 stages and illustrated as follows:

Initialization stage

This initializes the forward probability, which is the joint probability of starting at state and initially observing O₁.

\begin{matrix} α_{i} (1) = π b_{i} (O_{i}) & 1 \leq i \leq N \end{matrix}

Induction stage

\begin{matrix} α_{i} (t + 1) = [\sum_{i = 1}^{N} α_{i} (t) α_{ij}] b_{j} (O_{t + 1}), & 1 \leq t \leq T - 1 \end{matrix}

This is the joint probability of observation and state 3 at time t + 1 via state at time t (i.e. the joint probability of observing o at state 3 at time t+1 and form state and time t). This is performed at all states and is iterated for all times from t = 1 to T-1.

Termination stage

This computes all the forward variables, which is the P(o|M).

P (o | M) = \sum_{i = 1}^{N} α_{i} (T)

Where:

α_ij = transition from state i to j

b_i(o) = probability of emitting a symbol in a particular state

t = time

M = model

α_i = forward variable of state i

π = probability of starting at a particular state

The backward algorithm like the forward algorithm calculates backward probabilities instead. The backward probability is the probability of starting in a state at a time t and generating the rest of the observation sequence O_{t + 1},…, O_T. The backward probability can be calculated by using a variant of the forward algorithm. Therefore, instead of starting at time t = 1, the algorithm starts at time t = T and moves backwards from O_T to O_{t + 1}. In this work, the backward algorithm was used alongside the forward algorithm to re-estimate the HMM parameters. This algorithm also involves three steps and is illustrated below.

Initialization

This is the initial probability of being in a state S_i at time T and generating nothing. The value of this computation is usually 1.

\begin{matrix} β_{i} (T) = 1, & 1 \leq i \leq N \end{matrix}

Induction

This step calculates the probabilities of partial sequence observation from t+1 to end given state at time t and the model λ.

β_{i} (t) = \sum_{j = 1}^{N} α_{i j} b_{j} (O_{t + 1}) β_{t + 1} (j) t = T - 1, T - 2, \dots, 1 .

Termination

It calculates all the backward variables which is the P(O_t+1, …, O_T|Q₁ = S_i).

P (O_{t + 1}, \dots, O_{T} | Q_{1} = S_{i}) = \sum_{T}^{t = 1} β_{i} (t)

Where:

α_ij = transition from state i to j

b_j(o) = probability of emitting a symbol in a particular

β_t(j) = backward variable of state i in time t

The Baum-Welch algorithm, sometimes called the forward-backward algorithm makes use of the results derived from this algorithm to make inference. The Baum-Welch algorithm is a special form of the Expectation Maximization algorithm used for finding the maximum likelihood estimate of the parameters of the HMM. It was used in this work to train the various sized HMM parameters.

The E part of the algorithm calculates the expectation count for both the state and observation. The expectation of state count is denoted by γ_t(i). It is the probability of being in state at time t giving observation sequence and the model.

γ_{t} (i) = \frac{P (q_{t} = i | λ)}{P (o | λ)} = \frac{α_{i} (t) b_{i} (t)}{\sum_{j = 1}^{N} α_{i} (t) b_{j} (t)} (3)

The expectation of transition count is denoted by ε_ij(t). it is the probability of being in state S_i at time t and state S_j at time t + 1 given an observation sequence and the model.

ε_{i j} (t) = P (q_{t} = i, q_{t + 1} = j | o, λ) = \frac{α_{i} (t) α_{i j} b_{j} (t + 1) b_{j} (o_{t + 1})}{\sum_{i = 1}^{N} \sum_{i = 1}^{N} α_{i} (t) α_{i j} b_{j} (t + 1) b_{j} (o_{t + 1})} (4)

Based on the expectation probabilities, we can now estimate the parameters that will maximize the new model. This is the M step of the algorithm.

The new initial probability distribution can be calculated as follows.

π^{'} = γ_{i} (1) (5)

The re-estimated transition probability distribution is also calculated as follows:

{α^{'}}_{i j} = \frac{\sum_{t = 1}^{T - 1} ε_{i j} (t)}{\sum_{t = 1}^{T - 1} γ_{i} (t)} (6)

Finally, the new observation matrix is calculated using the formula below

{b^{'}}_{i j} = \frac{\sum_{t = 1}^{T - 1} γ_{i} (t) 1 (o_{t} = k)}{\sum_{t = 1}^{T - 1} γ_{i} (t)}

The pseudo code of the training algorithm is represented below:

i. Begin with some randomly initialized or preselected model, π
ii. Run O through the current model to estimate the expectations of each model parameter using the forward backward algorithm.
iii. Change the model to maximize the values of each path using the new π′, α′_ij and b′_i(t).
iv. Repeat until change in log likelihood is less than a threshold value or when the maximum number of iterations is reached.

For global optimal results, this algorithm is usually iterated depending on the size of the dataset.

Results and discussion

Likelihood estimation

After implementing the HMM algorithms, the discretized data was parsed into the program. The dataset was trained using HMMs with cluster size from cluster 2 to 10. The likelihood of each HMM was calculated using likelihood ratio test and three clusters were identified. The likelihood ratio test of the dataset from cluster 2 to 10 is shown in Table 1 below. A positive LRT show that increasing the number of parameters is still worthwhile while a negative LRT shows that increasing the parameter would not give a better model.

Table 1. Table showing LRT calculations.

The LRT becomes negative after three (3) clusters giving the optimal number as 3.

K	Log Likelihood	LR (Likelihood Ratio)	LRT(Likelihood Ratio Test)
2	-143.34
3	-102.28	41.06	7.02E+01
4	-95.62	6.66	1.42E+00
5	-89.17	6.45	1.00E+00
6	-86.89	2.28	-7.34E+00
7	-84.8	2.09	-7.72E+00
8	-8.44E+01	0.38	-1.11E+01
9	-8.27E+01	1.71	-8.48E+00
10	-8.10E+01	1.75	-8.40E+00

This test is used because the HMM are hierarchically nested and adding clusters will increase the likelihood of the data fitting the model until a certain point is reached when there is no significant change in the likelihood when parameters are added.

Likelihood Ratio Test is defined mathematically as:

LRT = LR – CR.

LT is the difference in the log likelihood of a more complex model to a simple model. The formula to calculate LR is illustrated below.

LR = 2(L_c – L_s)

where:

L_c = log likelihood of the complex model.

L_s = log likelihood of the simple model.

CH is the statistical chi square distribution with the number of extra parameter at a certain p –value.

This parameter is calculated by: L(Z–1).

where:

L = sequence length

Z = number of emission symbols

From the calculations below, the optimal number of clusters in the dataset based on the likelihood ratio test is 3. The log likelihoods of each cluster is also illustrated in Figure 2 below. It shows that the log likelihood increases with more parameters added initially but from cluster 3, there was no significant increase in log likelihood showing that the optimal number of clusters has been attained.

Figure 2. Log likelihoods for different numbers of clusters.

The log likelihood values increase with the number of clusters sizes. After 3 clusters, there is not a significant increase in the log likelihood.

Clustering results

The dataset was trained using the Baum-Welch algorithm and the probability that an observation sequence belongs to a cluster was calculated using the forward algorithm. Genes with discretized value of zeros were also removed. After the likelihood ratio test was calculated and the optimal number of clusters found, each data was then separated into clusters using the forward algorithm. The first cluster consists of 502 genes, the second cluster had 481 genes and the third cluster had 668 genes. These results are represented in the Figure 3.

Figure 3. clustering results showing all the genes in each cluster.

The x-axis shows the likelihood of each genes in each of the cluster and the y-axis shows the total number of genes in each cluster.

Functional-induced/determined clustering of plasmodium falciparum protein by the algorithm

Erythrocyte membrane protein1(pfEMP1) –Clusters 1 and 2

The clustering algorithm efficiently clustered the differentially expressed genes into 3 clusters based on their functions. It is noteworthy that the most abundant genes are the erythrocyte membrane protein 1 (PfEMP1). The proteins are grouped in cluster 1 and cluster 2. PfEMP1 is an ubiquitously expressed protein during the intraerythrocytic stage of the parasite growth that determined the pathogenicity of P. Falciparum²⁵. The virulence of P. falciparum infections is associated with the type of P. falciparum PfEMP1 expressed on the surface of infected erythrocytes to anchor these to the vascular lining. PfEMP1 represents an immunogenic and diverse group of protein family that mediate adhesion through specific binding to host receptors²⁵. The Var genes encode the PfEMP1 family, and each parasite genome contains ~60 diverse Var genes. The differential expression of the proteins in this family has been reported to determine morbidity from P. falciparum infection²⁶. Apart from clustering cell adhesion proteins into a sub-cluster, the algorithm also clustered the proteins involved in actin binding, transmembrane transportation and ATP binding. While the genes involved in ATP binding a largely conserved with their functions yet to be experimentally determined, the transport proteins are bet3 transport protein and aquaporin. Aquaporin is a membrane spanning transport proteins that is essential in the maintenance of fluid homeostasis and transport of water molecules and it has been identified as good therapeutic target²⁷. Bet3 transport protein on the other hand is involved in the transport of proteins by the fusion of endoplasmic reticulum to Golgi transport vesicles with their acceptor compartment²⁸.

The second cluster also has sub-cluster of PfEMP1 with other sub-clusters for GTP and ATP binding /ATP-dependent helicase activity as well as structural components of ribosome and ubiquitin protein ligase activity. Apart from PfEMP1, other sub-clusters are involved in protein turnover-protein synthesis and degradation²⁹. These include the RNA helicases that prepare the RNA for translation and initiate translation, the ribosomal and GTP binding proteins that are integral part of the ribosome assembly involved in translation and the ubiquitin-conjugating enzymes are carry out the ubiquitination reaction that targets a protein for degradation via the proteasome^30–32.

The genes coding for proteins involved in catabolic activities such as breakdown of proteins and hydrolysis of lipids are clustered in cluster 3. This cluster also included sub-clusters for genes involved in motor activity and DNA structural elements. The DNA structural elements include histone proteins and transcriptional initiator elements which are involved in epigenetic control of gene expression³³. The ability of P. falciparum to grow and multiply both in the warm-blooded humans and cold-blooded insects is known to be under tight epigenetic regulation and it has been suggested as a good therapeutic target²⁵.

Functional annotation

The Functional Enrichment analysis tool was used to determine functionally enriched genes in each cluster. Each cluster was loaded separately based on their unique gene identifier. Genes are matched against the UniProt background database or by using a custom database that allows users load their own predefined Gene Ontology Term (GOTerm). Statistical cut-off of enrichment analyses in FunRich software was kept as default with a p-value <0.05. We used the custom database and loaded annotations downloaded from PlasmoDB for our functional enrichment. The result of the 3 clusters is summarized in Table 2. FunRich was only able to identify 164 of the 502 genes in cluster 1. Cluster 1 has five functional annotations, 7.3% of the genes are functionally annotated with cell adhesion molecule, receptor activity, 1.2% are annotated with acting binding, 1.2% with transporter activity and 3.7% with ATP binding as shown in Figure 4. The remaining genes has no GO functions. We can deduce that since these genes are in the same cluster, they are likely to have functions as the genes with GO annotation.

Table 2. Functional annotation of each clusters.

Cluster 1 has four GO annotations, cluster 2 has five and cluster 3 has seven functional annotations.

CLUSTERS	GO-ANNOTATION	GENE ID	NUMBER OF GENES
Cluster 1	Cell adhesion molecule, receptor activity	PFD0005w PFD1015c PFE0005w PFD0635c PFD1005c PFF0845c PF07_0048 PF07_0049 PF07_0050 MAL7P1.55 MAL7P1.56 PF08_0142	12
	Acting binding	PFE0880c PFE1420w	2
	Transporter activity	PFD0895c PF08_0097	2
	ATP binding	PFB0115w PFD0365c PFD0735c PFF0390w PF07_0074 PF08_0101	6
Cluster 2	Structural constituent of the ribosome	PFB0455w PFB0830w PFB0885w PFC0200w PFC0290w PFC0295c PFC0300c PFC1020c PFD0770c PFD1055w PFE0185c PFE0300c PFE0350c PFE0845c PFE0975c PFF0700c PFF0885w PF07_0043 PF07_0079 PF07_0080 PF08_0039 PF08_0075	22
	Cell adhesion molecule receptor activity	PFA0005w PFD0020c PFD0615c PFD0625c PFD0995c PFF0010w PFF1580c MAL7P1.50 PF07_0051 PF08_0103 PF08_0107 PF08_0140	12
	ATP binding and ATP dependent in a helicase activity	PFB0860c PFD0245c PFD1060w PFE1390w PF08_0042	5
	Ubiquitin protein ligase activity	PFC0255c PFE1350c MAL8P1.23	3
	GTP binding	PFC0565w PFE1215c PFE1435c PFF0625w	4
Cluster 3	Cysteine-type peptide activity	PFB0330c PFB0335c PFB0340c PFB0345c PFB0350c PFB0360c PFD0230c	7
	Endopeptidase activity	PFA0400c PFC0745c PFE0915c PFF0420c PF07_0112 MAL8P1.14 2	6
	Hydrolase activity	PFC0065c PFE0910w PFD0185c PF07_0040	4
	ATP binding, action binding and monitor activity	PFE0175c PFF0675c	2
	DNA binding	PFD0325w PFE0305w PF07_0035	3
	Unfolded protein binding	PFF0860c PFF0865w	2
	DNA binding, protein heterodimerization activity	PFE0595w PF07_0103	2

Figure 4. Functional annotation of cluster 1.

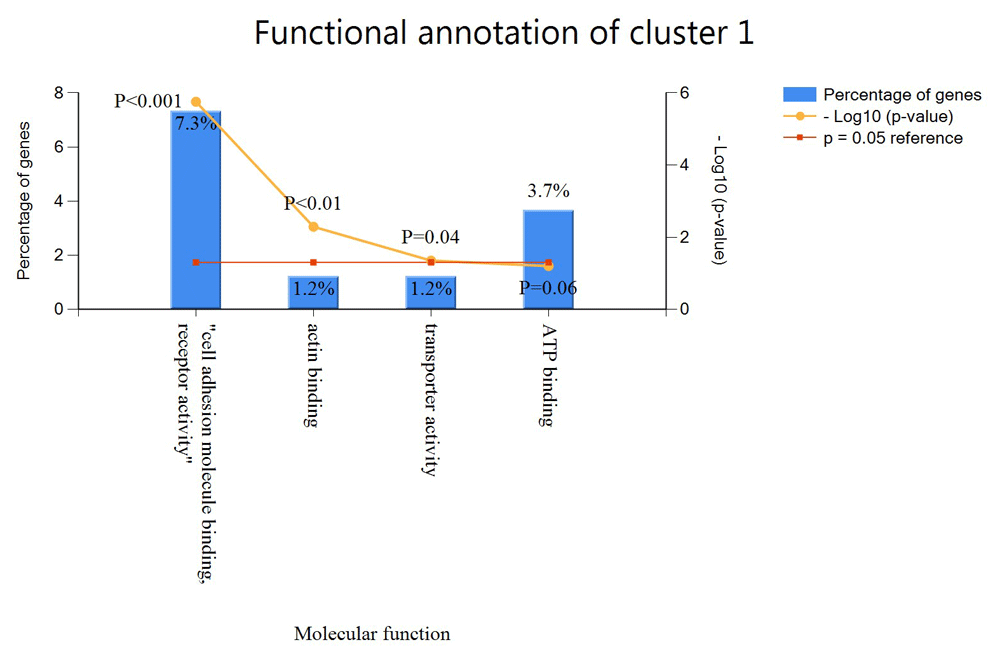
The x-axis shows the percentage genes in the cluster with specific functional annotation while the y-axis shows the function of these genes.

In cluster 2, FunRich was able to identify 308 genes. In cluster 2, 7.1% of the genes are functionally annotated with the structural constituent of the ribosome, 3.9% with cell adhesion molecule receptor activity, 1.6% with ATP binding and ATP-dependent in a helicase activity, 1.0% with ubiquitin protein ligase activity and 1.3% with GTP binding which gives a total of five functional annotations as shown in Figure 5. The rest of the genes in cluster 2 are also predicted to have similar functions as with the genes with known GO annotation.

Figure 5. Functional annotation of cluster 2.

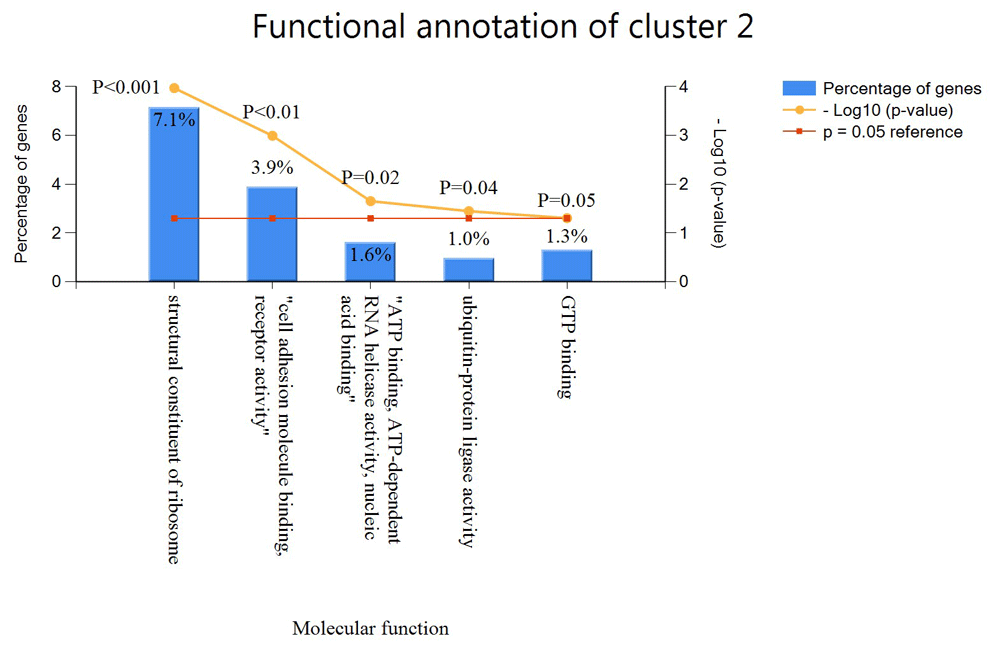
The x-axis shows the percentage genes in the cluster with specific functional annotation while the y-axis shows the function of these genes.

In cluster 3, FunRich was able to identify 249 of the 668 genes in the cluster set. This cluster has the largest GO annotation as it is enriched with seven functions. 2.8% of the genes are enriched with cysteine-type peptide activity, 2.4% with endopeptidase activity, 1.6% with hydrolase activity, 0.8% with ATP binding, action binding and monitor activity, 1.2% with DNA binding, 0.8% with unfolded protein binding and 0.8% with DNA binding, protein heterodimerization activity as shown in Figure 6. We can also deduce that in cluster 3, the genes with unknown functions are also predicted to have the same functions as with the known ones.

Figure 6. Functional annotation of cluster 3.

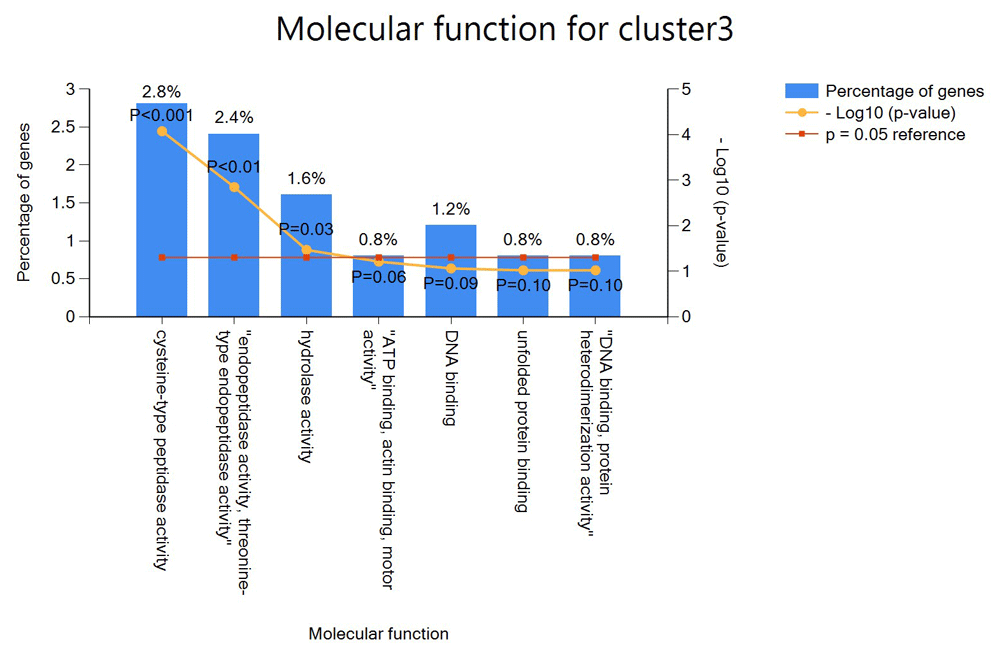
The x-axis shows the percentage genes in the cluster with specific functional annotation while the y-axis shows the function of these genes.

Dataset 1.This .zip contains the normalized (normalized.xsl) and discretized (Discretized_Data.txt) data sets used34.

Conclusion

Clustering has been found to be a very useful technique in analyzing gene expression data. It has the ability to display large datasets in a more interpretable format. Several approaches have been developed to cluster gene expression data. The HMM has a better advantage over them because of its strong mathematical background and its ability to model gene expression data successfully. The HMM algorithms were implemented to perform cluster analysis on the P. falciparum gene expression dataset. 2000 genes were used and 3 clusters were identified. Sixteen major functional enrichment were identified for the clusters.

Data availability

1. The data sets used in this study are freely available in www.ncbi.nlm.nih.gov/pubmed/20141604

Dataset 1. This .zip contains the normalized (normalized.xsl) and discretized (Discretized_Data.txt) data sets used. 10.5256/f1000research.12360.d204230

Competing interests

There is no competing interests declared.

Grant information

The author(s) declared that no grants were involved in supporting this work.

Acknowledgements

We are grateful to Covenant University for providing the platform to carrying out this research.

Faculty Opinions recommended

References

1. Huang QW, Wu LY, Qu JB, et al.: Analyzing time-course gene expression data using profile-state hidden Markov model. In: Systems Biology (ISB), IEEE International Conference. 2011; 351–355. Publisher Full Text
2. Spellman PT, Sherlock G, Zhang MQ, et al.: Comprehensive identification of cell cycle–regulated genes of the yeast Saccharomyces cerevisiae by microarray hybridization. Mol Biol Cell. 1998; 9(12): 3273–3297. PubMed Abstract | Publisher Full Text | Free Full Text
3. Slonim DK: From patterns to pathways: gene expression data analysis comes of age. Nat Genet. 2002; 32 Suppl:502–508. PubMed Abstract | Publisher Full Text
4. Eisen MB, Spellman PT, Brown PO, et al.: Cluster analysis and display of genome-wide expression patterns. Proc Natl Acad Sci U S A. 1998; 95(25): 14863–14868. PubMed Abstract | Publisher Full Text | Free Full Text
5. Segal E, Shapira M, Regev A, et al.: Module networks: identifying regulatory modules and their condition-specific regulators from gene expression data. Nat Genet. 2003; 34(2): 166–176. PubMed Abstract | Publisher Full Text
6. Howell GR, Macalinao DG, Sousa GL, et al.: Molecular clustering identifies complement and endothelin induction as early events in a mouse model of glaucoma. J Clin Invest. 2011; 121(4): 1429–44. PubMed Abstract | Publisher Full Text | Free Full Text
7. Hughes TR, Marton MJ, Jones AR, et al.: Functional discovery via a compendium of expression profiles. Cell. 2000; 102(1): 109–126. PubMed Abstract | Publisher Full Text
8. Hopcroft LE, McBride MW, Harris KJ, et al.: Predictive response-relevant clustering of expression data provides insights into disease processes. Nucleic Acids Res. 2010; 38(20): 6831–6840. PubMed Abstract | Publisher Full Text | Free Full Text
9. Schliep A, Schönhuth A, Steinhoff C: Using hidden Markov models to analyze gene expression time course data. Bioinformatics. 2003; 19 Suppl 1:i255–i263. PubMed Abstract | Publisher Full Text
10. Tavazoie S, Hughes JD, Campbell MJ, et al.: Systematic determination of genetic network architecture. Nat Genet. 1999; 22(3): 281–285. PubMed Abstract | Publisher Full Text
11. Tamayo P, Slonim D, Mesirov J, et al.: Interpreting patterns of gene expression with self-organizing maps: methods and application to hematopoietic differentiation. Proc Natl Acad Sci U S A. 1999; 96(6): 2907–2912. PubMed Abstract | Publisher Full Text | Free Full Text
12. Friedman N: Inferring cellular networks using probabilistic graphical models. Science. 2004; 303(5659): 799–805. PubMed Abstract | Publisher Full Text
13. Brown MP, Grundy WN, Lin D, et al.: Knowledge-based analysis of microarray gene expression data by using support vector machines. Proc Natl Acad Sci U S A. 2000; 97(1): 262–267. PubMed Abstract | Publisher Full Text | Free Full Text
14. De Fonzo V, Aluffi-Pentini F, Parisi V: Hidden Markov Models in Bioinformatics. Curr Bioinform. 2007; 2(1): 49–61. Publisher Full Text
15. Ji X, Li-Ling J, Sun Z: Mining gene expression data using a novel approach based on hidden Markov models. FEBS Lett. 2003; 542(1–3): 125–131. PubMed Abstract | Publisher Full Text
16. Geng H, Deng X, Ali HH: Applications of Hidden Markov Models in Microarray Gene Expression Data. Huimin Department of Computer Science, University of Nebraska at Omaha, Omaha, NE 68182 USA. Publisher Full Text
17. Lees KT: Identifying Gene Clusters and Regulatory Themes using Time Course Expression Data, Hidden Markov Models and Transcription Factor Information. Bioinformatics. 2006. Reference Source
18. Zeng Y, Garcia-Frias J: A novel HMM-based clustering algorithm for the analysis of gene expression time-course data. Comput Stat Data Anal. 2006; 50(9): 247–2494. Publisher Full Text
19. Durbin RM, Eddy SR, Krogh A, et al.: Biological Sequence Analysis: Probabilistic Models of Proteins and Nucleic Acids (1st ed.). Cambridge: Cambridge University Press, 1998. Publisher Full Text
20. Beal M, Krishnamurthy P: Gene expression time course clustering with countably infinite hidden markov model. arXiv preprint arViv: 1206.6824. Reference Source
21. Iyer VR, Eisen MB, Ross DT, et al.: The transcriptional program in the response of human fibroblasts to serum. Science. 1999; 283(5398): 83–87. PubMed Abstract | Publisher Full Text
22. Cho RJ, Campbell MJ, Winzeler EA, et al.: A genome-wide transcriptional analysis of the mitotic cell cycle. Mol Cell. 1998; 2(1): 65–73. PubMed Abstract | Publisher Full Text
23. Otto TD, Wilinski D, Assefa S, et al.: New insights into the blood-stage transcriptome of Plasmodium falciparum using RNA-Seq. Mol Microbiol. 2010; 76(1): 12–24. PubMed Abstract | Publisher Full Text | Free Full Text
24. Knab B, Schliep A, Steckemetz B, et al.: Model-Based Clustering With Hidden Markov Models and its Application to Financial Time-Series Data. Between Data Science and Applied Data Analysis. Springer. 561–569. Publisher Full Text
25. Ay F, Bunnik EM, Varoquaux N, et al.: Multiple dimensions of epigenetic gene regulation in the malaria parasite Plasmodium falciparum: gene regulation via histone modifications, nucleosome positioning and nuclear architecture in P. falciparum. Bioessays. 2015; 37(2): 182–194. PubMed Abstract | Publisher Full Text | Free Full Text
26. Besteiro S, Williams RA, Coombs GH, et al.: Protein turnover and differentiation in Leishmania. Int J Parasitol. 2007; 37(10): 1063–1075. PubMed Abstract | Publisher Full Text | Free Full Text
27. Hansen M, Beitz E, Schultz JE: An Aquaporin Gene in Plasmodium Falciparum: Molecular cloning and functional expression. Molecular Biology and Physiology of Water and Solute Transport. Springer. 2000; 389–392. Publisher Full Text
28. Jankowsky A, Guenther UP, Jankowsky E: The RNA helicase database. Nucleic Acids Res. 2011; 39(Database issue): D338–41. PubMed Abstract | Publisher Full Text | Free Full Text
29. Lavstsen T, Turner L, Saguti F, et al.: Plasmodium falciparum erythrocyte membrane protein 1 domain cassettes 8 and 13 are associated with severe malaria in children. Proc Natl Acad Sci U S A. 2012; 109(26): E1791–E1800. PubMed Abstract | Publisher Full Text | Free Full Text
30. Meena LS, Rajni: Cloning and characterization of engA, a GTP-binding protein from Mycobacterium tuberculosis H₃₇Rv. Biologicals. 2011; 39(2): 94–99. PubMed Abstract | Publisher Full Text
31. Nandi D, Tahiliani P, Kumar A, et al.: The ubiquitin-proteasome system. J Biosci. 2006; 31(1): 137–155. PubMed Abstract
32. Rossi G, Kolstad K, Stone S, et al.: BET3 encodes a novel hydrophilic protein that acts in conjunction with yeast SNAREs. Mol Biol Cell. 1995; 6(12): 1769–1780. PubMed Abstract | Publisher Full Text | Free Full Text
33. Rottmann M, Lavstsen T, Mugasa JP, et al.: Differential expression of var gene groups is associated with morbidity caused by Plasmodium falciparum infection in Tanzanian children. Infect Immun. 2006; 74(7): 3904–39. PubMed Abstract | Publisher Full Text | Free Full Text
34. Oyelade J, Isewon I, Olaniyan D, et al.: Dataset 1 in: Effectiveness of model-based clustering in analyzing Plasmodium falciparum RNA-seq time-course data. F1000Research. 2018. Data Source

Comments on this article Comments (0)

Version 2

VERSION 2 PUBLISHED 19 Sep 2017

Author details Author details

Jelili Oyelade
Roles: Conceptualization, Methodology, Project Administration, Resources, Supervision, Validation, Writing – Original Draft Preparation, Writing – Review & Editing

Itunuoluwa Isewon
Roles: Methodology, Resources, Writing – Original Draft Preparation, Writing – Review & Editing

Damilare Olaniyan
Roles: Formal Analysis, Investigation, Methodology, Software

Solomon O Rotimi
Roles: Data Curation, Investigation, Validation, Writing – Review & Editing

Jumoke Soyemi
Roles: Formal Analysis, Validation, Writing – Review & Editing

Competing interests

There is no competing interests declared.

Grant information

The author(s) declared that no grants were involved in supporting this work.

Article Versions (2)

version 2

Revised

Published: 25 May 2018, 6:1706

https://doi.org/10.12688/f1000research.12360.2

version 1

Published: 19 Sep 2017, 6:1706

https://doi.org/10.12688/f1000research.12360.1

© 2018 Oyelade J et al. This is an open access article distributed under the terms of the Creative Commons Attribution License, which permits unrestricted use, distribution, and reproduction in any medium, provided the original work is properly cited. Data associated with the article are available under the terms of the Creative Commons Zero "No rights reserved" data waiver (CC0 1.0 Public domain dedication).

Download

Export To

metrics

	Views	Downloads
F1000Research	-	-
PubMed Central Data from PMC are received and updated monthly.	-	-

Citations

SEE MORE DETAILS

CITE

how to cite this article

Oyelade J, Isewon I, Olaniyan D et al. Effectiveness of model-based clustering in analyzing Plasmodium falciparum RNA-seq time-course data [version 2; peer review: 1 approved, 1 approved with reservations, 1 not approved]. F1000Research 2018, 6:1706 (https://doi.org/10.12688/f1000research.12360.2)

NOTE: If applicable, it is important to ensure the information in square brackets after the title is included in all citations of this article.

track

receive updates on this article

Track an article to receive email alerts on any updates to this article.

Open Peer Review

Current Reviewer Status: ?

Key to Reviewer Statuses VIEW HIDE

ApprovedThe paper is scientifically sound in its current form and only minor, if any, improvements are suggested

Approved with reservations A number of small changes, sometimes more significant revisions are required to address specific details and improve the papers academic merit.

Not approvedFundamental flaws in the paper seriously undermine the findings and conclusions

Version 2

VERSION 2

PUBLISHED 25 May 2018

Revised

Views

Reviewer Report 18 Jul 2018

Thomas D Otto, University of Glasgow, Glasgow, UK

Not Approved

https://doi.org/10.5256/f1000research.16296.r34395

First, it is weird that my comments were not addressed by the authors.

Second, I don't see an improvement compared to the first version

Mixing microarray and RNA-Seq
Claiming the importance

CITE

Report a concern

Respond or Comment

Views

Reviewer Report 10 Jul 2018

Ashis Das, Molecular Parasitology and Systems Biology Lab, Department of Biological Sciences, Birla Institute of Technology and Science (BITS), Pilani, India

P.A. Boopathi, Department of Biological Sciences, Birla Institute of Technology and Science (BITS), Pilani, India

Approved with Reservations

https://doi.org/10.5256/f1000research.16296.r34396

Major

In Otto TD et.al., (2010), it was reported that 4871 transcripts were found expressed during the erythrocytic stages. However, in this study only 2000 filtered genes were considered for clustering. Why this difference between the

Major

In Otto TD et.al., (2010), it was reported that 4871 transcripts were found expressed during the erythrocytic stages. However, in this study only 2000 filtered genes were considered for clustering. Why this difference between the studies? In other words, the possible reason behind the normalization strategy adopted, which has resulted in the filtering out of so many genes. This should be discussed in results section.
Lees K et.al., (2006) suggested that this method could produce biologically meaningful information if applied to different datasets. I feel that applying this method to different P. falciparum expression datasets would further validate the present study. In the discussion part, limitations of this study should be discussed. If the comparison is not possible, please mention limitations of this approach.

Minor
The study reported here deals with RNASeq data, any mentioning about microarray technology should be removed wherever necessary. For instance, in Material and Methods under Data Preprocessing section the sentence “Normalization removes static variations in the microarray experiment”. Discuss in relation to RNASeq data.

Also in Material and Methods first discuss about the study from which RNASeq data was obtained and then discuss further steps used in the present study. Mention “Illumina based RNA sequencing technology”.

In Introduction and Abstract section there is no mentioning of RNASeq technology but microarray technology was briefly discussed. Both microarray and RNASeq technologies have been utilized in malaria research community and had helped to understand the biology of malaria parasites. Application of RNA Seq technology in P. falciparum along with results obtained should be discussed very briefly in Introduction section.

In Table 1, What about the LR and LRT values for the cluster number 2?

In Results and discussion section briefly discuss about number of genes considered initially and how many genes were filtered out in pre-processing steps. Finally come down to the number that’s been considered for clustering.

Please check the legends to the “functional enrichment of clusters” figures.

Pg10 of 19 “can deduce “should be changed to “hypothesize” pending further experimental validation.

Supplementary data
Brief explanation of supplementary data supplied should be mentioned. For instance the type of normalization applied and what does rows and columns signify. Provide the gene symbol instead only the row number.

Also in similar way explain for the discretized data. Why only 5174 rows present in this data? Provide this data with gene symbol with the time points.

Competing Interests: No competing interests were disclosed.

We confirm that we have read this submission and believe that we have an appropriate level of expertise to confirm that it is of an acceptable scientific standard, however we have significant reservations, as outlined above.

CITE

Report a concern

Respond or Comment

Version 1

VERSION 1

PUBLISHED 19 Sep 2017

Views

Reviewer Report 31 Jan 2018

Ashis Das, Molecular Parasitology and Systems Biology Lab, Department of Biological Sciences, Birla Institute of Technology and Science (BITS), Pilani, India

P.A. Boopathi, Department of Biological Sciences, Birla Institute of Technology and Science (BITS), Pilani, India

Shibashish Choudhury, Department of Biological Sciences, Birla Institute of Technology and Science (BITS), Pilani, India

Approved with Reservations

https://doi.org/10.5256/f1000research.13384.r29434

The paper discusses the application of HMM to RNA seq time course data from in-vitro P. falciparum culture to cluster the data into 3 clusters and 16 major functional enrichment was seen for these. Although there has been appreciable analysis ... Continue reading

The data pre-processing step mentioned in this article was not clear. What type of input data was used here and how the filtering was done? It was mentioned that normalize library from R package was used. Is it appropriate for normalizing RNA Seq based transcriptome studies, since it was mentioned as used for microarray studies (Is it upgraded for RNA Seq based studies?)
What is the criterion used to assign the expression of a particular gene across seven different time points? It is unclear with the brief explanation of Discretization. Is this determining the expression status of a particular gene?
Availability of data used after normalization would help in reproducibility.
Overall I suggest detailed explanation of methodology adopted and its execution with the data used. Proper discussion of the same is also necessary.
The RNA Seq based transcriptome data was generated from highly synchronous culture data. The discussion of PfEMP1 linking with the pathology is unnecessary and misleading. Especially the statement “This differential expression during infection and among patients could have accounted for its clustering into 2 different clusters by the algorithm” is not acceptable since the data is from in-vitro culture.
I recommend the use of this method to other transcriptome based studies of P.falciparum at different time points (microarray, RNASeq) to validate the results obtained in the present study. Discussion about the results obtained in this study with other transcriptome based studies is also necessary. This will reveal the robustness of the approach employed in this paper.
The criteria for GO Term enriched (p-value) should be provided in the discussion although it has been mentioned only in the Figures.
Since data was taken from different time points, the stochastic nature of the HMM process may not be appropriate to cluster gene expression data which have strong dependency.
It would be interesting to classify the var genes obtained in the different clusters. PfEMPI as encoded by the var gene family is divided into subfamilies with different functional domains. Are the different clusters showing segregation of different subfamilies? In the IDC time course experiment which was performed in-vitro based on which the RNA Seq data has been taken is there a difference in the var gene subfamily expression at different time points?
As mentioned in the materials and methods RNA seq based expression data of 5270 P.falciparum genes were considered. However in conclusion it has been mentioned that only 2000 genes were used for clustering. What is the implication of this statement?

Is the work clearly and accurately presented and does it cite the current literature?

Partly
Is the study design appropriate and is the work technically sound?

Partly
Are sufficient details of methods and analysis provided to allow replication by others?

No
If applicable, is the statistical analysis and its interpretation appropriate?

No
Are all the source data underlying the results available to ensure full reproducibility?

Partly
Are the conclusions drawn adequately supported by the results?

No

Competing Interests: No competing interests were disclosed.

Reviewer Expertise: Malaria molecular biology, transcriptomics

CITE

Report a concern

Author Response 25 May 2018

Jelili Oyelade, Department of Computer and Information Sciences, Covenant University, Ota, Nigeria

25 May 2018

Author Response

1. The data pre-processing step mentioned in this article was not clear. What type of input data was used here and how the filtering was done? It was mentioned that ... Continue reading 1. The data pre-processing step mentioned in this article was not clear. What type of input data was used here and how the filtering was done? It was mentioned that normalize library from R package was used. Is it appropriate for normalizing RNA Seq based transcriptome studies, since it was mentioned as used for microarray studies (Is it upgraded for RNA Seq based studies?)

Response
The input data was RNA-SEQ, The data was normalized to a mean of 1 and standard deviation of 0. Yes it is based on this paper. Zyprych-Walczak, J., Szabelska, A., Handschuh, L., Górczak, K., Klamecka, K., Figlerowicz, M., & Siatkowski, I. (2015). The impact of normalization methods on RNA-Seq data analysis. BioMed research international, 2015.

2. What is the criterion used to assign the expression of a particular gene across seven different time points? It is unclear with the brief explanation of Discretization. Is this determining the expression status of a particular gene?

Response
Discretization was conducted by converting the time points to symbols depending on whether the expression value has increased, decreased or not changed. This method has been used by Huimin Geng et al. (2003) and Lees et al (2007) and has been able to justify the reliability of this discretization process.

3. Availability of data used after normalization would help in reproducibility.

Response
The availability of the data used after normalization has been provided

4. Overall I suggest detailed explanation of methodology adopted and its execution with the data used. Proper discussion of the same is also necessary.

Response
The detailed explanation of the methodology has been improved and a proper discussion of the findings has been added

5. The RNA Seq based transcriptome data was generated from highly synchronous culture data. The discussion of PfEMP1 linking with the pathology is unnecessary and misleading. Especially the statement “This differential expression during infection and among patients could have accounted for its clustering into 2 different clusters by the algorithm” is not acceptable since the data is from in-vitro culture.

Response
“This differential expression during infection and among patients could have accounted for its clustering into 2 different clusters by the algorithm.” has been removed from discussion

6. I recommend the use of this method to other transcriptome based studies of P.falciparum at different time points (microarray, RNASeq) to validate the results obtained in the present study. Discussion about the results obtained in this study with other transcriptome based studies is also necessary. This will reveal the robustness of the approach employed in this paper.

Response
This is very good suggestion but, this work, is based on the work of Karen Lees , Jennifer Taylor ,Gerton Lunter , and Jotun Hein titled: “Identifying Gene Clusters and Regulatory Themes using Time Course Expression Data, Hidden Markov Models and Transcription Factor Information” which has actually proved the robustness of the approach.

7. The criteria for GO Term enriched (p-value) should be provided in the discussion although it has been mentioned only in the Figures.

Response
The GO criteria - “Statistical cut-off of enrichment analyses in FunRich software was kept as default with a p-value <0.05.” has been provided in the discussion.

8. Since data was taken from different time points, the stochastic nature of the HMM process may not be appropriate to cluster gene expression data which have strong dependency.

Response
Gene expression is a fundamentally stochastic process, with randomness in transcription and translation leading to significant cell-to-cell variations in mRNA and protein levels. Model-based clustering approaches are effective when structural properties of the data can be explicitly expressed and HMM can be used by these types of approaches to partition gene expression time-series data into clusters. The process starts with an initial collection of HMMs that encompass typical qualitative behavior and the process iteratively find cluster models such a way that the joint likely hood of the clustering is maximized. This method is also robust with respect to noisy and frequently missing data.

9. It would be interesting to classify the var genes obtained in the different clusters. PfEMPI as encoded by the var gene family is divided into subfamilies with different functional domains. Are the different clusters showing segregation of different subfamilies? In the IDC time course experiment which was perfomed in-vitro based on which the RNA Seq data has been taken, is there a difference in the var gene subfamily expression at different time points.

Response
Yes, it is possible, different clusters can also show segregation of different subfamilies and there is no difference in the var gene subfamily expression at different time points.

10. As mentioned in the materials and methods RNA seq based expression data of 5270 P.falciparum genes were considered. However in conclusion it has been mentioned that only 2000 genes were used for clustering. What is the implication of this statement?

Response
The normalization and discretization process reduced the data and we removed all missing values and noise reduce the data to about 2000 genes.

1. The data pre-processing step mentioned in this article was not clear. What type of input data was used here and how the filtering was done? It was mentioned that normalize library from R package was used. Is it appropriate for normalizing RNA Seq based transcriptome studies, since it was mentioned as used for microarray studies (Is it upgraded for RNA Seq based studies?)

Response
The input data was RNA-SEQ, The data was normalized to a mean of 1 and standard deviation of 0. Yes it is based on this paper. Zyprych-Walczak, J., Szabelska, A., Handschuh, L., Górczak, K., Klamecka, K., Figlerowicz, M., & Siatkowski, I. (2015). The impact of normalization methods on RNA-Seq data analysis. BioMed research international, 2015.

2. What is the criterion used to assign the expression of a particular gene across seven different time points? It is unclear with the brief explanation of Discretization. Is this determining the expression status of a particular gene?

Response
Discretization was conducted by converting the time points to symbols depending on whether the expression value has increased, decreased or not changed. This method has been used by Huimin Geng et al. (2003) and Lees et al (2007) and has been able to justify the reliability of this discretization process.

3. Availability of data used after normalization would help in reproducibility.

Response
The availability of the data used after normalization has been provided

4. Overall I suggest detailed explanation of methodology adopted and its execution with the data used. Proper discussion of the same is also necessary.

Response
The detailed explanation of the methodology has been improved and a proper discussion of the findings has been added

5. The RNA Seq based transcriptome data was generated from highly synchronous culture data. The discussion of PfEMP1 linking with the pathology is unnecessary and misleading. Especially the statement “This differential expression during infection and among patients could have accounted for its clustering into 2 different clusters by the algorithm” is not acceptable since the data is from in-vitro culture.

Response
“This differential expression during infection and among patients could have accounted for its clustering into 2 different clusters by the algorithm.” has been removed from discussion

6. I recommend the use of this method to other transcriptome based studies of P.falciparum at different time points (microarray, RNASeq) to validate the results obtained in the present study. Discussion about the results obtained in this study with other transcriptome based studies is also necessary. This will reveal the robustness of the approach employed in this paper.

Response
This is very good suggestion but, this work, is based on the work of Karen Lees , Jennifer Taylor ,Gerton Lunter , and Jotun Hein titled: “Identifying Gene Clusters and Regulatory Themes using Time Course Expression Data, Hidden Markov Models and Transcription Factor Information” which has actually proved the robustness of the approach.

7. The criteria for GO Term enriched (p-value) should be provided in the discussion although it has been mentioned only in the Figures.

Response
The GO criteria - “Statistical cut-off of enrichment analyses in FunRich software was kept as default with a p-value <0.05.” has been provided in the discussion.

8. Since data was taken from different time points, the stochastic nature of the HMM process may not be appropriate to cluster gene expression data which have strong dependency.

Response
Gene expression is a fundamentally stochastic process, with randomness in transcription and translation leading to significant cell-to-cell variations in mRNA and protein levels. Model-based clustering approaches are effective when structural properties of the data can be explicitly expressed and HMM can be used by these types of approaches to partition gene expression time-series data into clusters. The process starts with an initial collection of HMMs that encompass typical qualitative behavior and the process iteratively find cluster models such a way that the joint likely hood of the clustering is maximized. This method is also robust with respect to noisy and frequently missing data.

9. It would be interesting to classify the var genes obtained in the different clusters. PfEMPI as encoded by the var gene family is divided into subfamilies with different functional domains. Are the different clusters showing segregation of different subfamilies? In the IDC time course experiment which was perfomed in-vitro based on which the RNA Seq data has been taken, is there a difference in the var gene subfamily expression at different time points.

Response
Yes, it is possible, different clusters can also show segregation of different subfamilies and there is no difference in the var gene subfamily expression at different time points.

10. As mentioned in the materials and methods RNA seq based expression data of 5270 P.falciparum genes were considered. However in conclusion it has been mentioned that only 2000 genes were used for clustering. What is the implication of this statement?

Response
The normalization and discretization process reduced the data and we removed all missing values and noise reduce the data to about 2000 genes.
Competing Interests: No Competing interests Close
Report a concern
Respond or Comment

COMMENTS ON THIS REPORT

Author Response 25 May 2018

Jelili Oyelade, Department of Computer and Information Sciences, Covenant University, Ota, Nigeria

25 May 2018

Author Response

1. The data pre-processing step mentioned in this article was not clear. What type of input data was used here and how the filtering was done? It was mentioned that ... Continue reading 1. The data pre-processing step mentioned in this article was not clear. What type of input data was used here and how the filtering was done? It was mentioned that normalize library from R package was used. Is it appropriate for normalizing RNA Seq based transcriptome studies, since it was mentioned as used for microarray studies (Is it upgraded for RNA Seq based studies?)

Response
The input data was RNA-SEQ, The data was normalized to a mean of 1 and standard deviation of 0. Yes it is based on this paper. Zyprych-Walczak, J., Szabelska, A., Handschuh, L., Górczak, K., Klamecka, K., Figlerowicz, M., & Siatkowski, I. (2015). The impact of normalization methods on RNA-Seq data analysis. BioMed research international, 2015.

2. What is the criterion used to assign the expression of a particular gene across seven different time points? It is unclear with the brief explanation of Discretization. Is this determining the expression status of a particular gene?

Response
Discretization was conducted by converting the time points to symbols depending on whether the expression value has increased, decreased or not changed. This method has been used by Huimin Geng et al. (2003) and Lees et al (2007) and has been able to justify the reliability of this discretization process.

3. Availability of data used after normalization would help in reproducibility.

Response
The availability of the data used after normalization has been provided

4. Overall I suggest detailed explanation of methodology adopted and its execution with the data used. Proper discussion of the same is also necessary.

Response
The detailed explanation of the methodology has been improved and a proper discussion of the findings has been added

5. The RNA Seq based transcriptome data was generated from highly synchronous culture data. The discussion of PfEMP1 linking with the pathology is unnecessary and misleading. Especially the statement “This differential expression during infection and among patients could have accounted for its clustering into 2 different clusters by the algorithm” is not acceptable since the data is from in-vitro culture.

Response
“This differential expression during infection and among patients could have accounted for its clustering into 2 different clusters by the algorithm.” has been removed from discussion

6. I recommend the use of this method to other transcriptome based studies of P.falciparum at different time points (microarray, RNASeq) to validate the results obtained in the present study. Discussion about the results obtained in this study with other transcriptome based studies is also necessary. This will reveal the robustness of the approach employed in this paper.

Response
This is very good suggestion but, this work, is based on the work of Karen Lees , Jennifer Taylor ,Gerton Lunter , and Jotun Hein titled: “Identifying Gene Clusters and Regulatory Themes using Time Course Expression Data, Hidden Markov Models and Transcription Factor Information” which has actually proved the robustness of the approach.

7. The criteria for GO Term enriched (p-value) should be provided in the discussion although it has been mentioned only in the Figures.

Response
The GO criteria - “Statistical cut-off of enrichment analyses in FunRich software was kept as default with a p-value <0.05.” has been provided in the discussion.

8. Since data was taken from different time points, the stochastic nature of the HMM process may not be appropriate to cluster gene expression data which have strong dependency.

Response
Gene expression is a fundamentally stochastic process, with randomness in transcription and translation leading to significant cell-to-cell variations in mRNA and protein levels. Model-based clustering approaches are effective when structural properties of the data can be explicitly expressed and HMM can be used by these types of approaches to partition gene expression time-series data into clusters. The process starts with an initial collection of HMMs that encompass typical qualitative behavior and the process iteratively find cluster models such a way that the joint likely hood of the clustering is maximized. This method is also robust with respect to noisy and frequently missing data.

9. It would be interesting to classify the var genes obtained in the different clusters. PfEMPI as encoded by the var gene family is divided into subfamilies with different functional domains. Are the different clusters showing segregation of different subfamilies? In the IDC time course experiment which was perfomed in-vitro based on which the RNA Seq data has been taken, is there a difference in the var gene subfamily expression at different time points.

Response
Yes, it is possible, different clusters can also show segregation of different subfamilies and there is no difference in the var gene subfamily expression at different time points.

10. As mentioned in the materials and methods RNA seq based expression data of 5270 P.falciparum genes were considered. However in conclusion it has been mentioned that only 2000 genes were used for clustering. What is the implication of this statement?

Response
The normalization and discretization process reduced the data and we removed all missing values and noise reduce the data to about 2000 genes.

1. The data pre-processing step mentioned in this article was not clear. What type of input data was used here and how the filtering was done? It was mentioned that normalize library from R package was used. Is it appropriate for normalizing RNA Seq based transcriptome studies, since it was mentioned as used for microarray studies (Is it upgraded for RNA Seq based studies?)

Response
The input data was RNA-SEQ, The data was normalized to a mean of 1 and standard deviation of 0. Yes it is based on this paper. Zyprych-Walczak, J., Szabelska, A., Handschuh, L., Górczak, K., Klamecka, K., Figlerowicz, M., & Siatkowski, I. (2015). The impact of normalization methods on RNA-Seq data analysis. BioMed research international, 2015.

2. What is the criterion used to assign the expression of a particular gene across seven different time points? It is unclear with the brief explanation of Discretization. Is this determining the expression status of a particular gene?

Response
Discretization was conducted by converting the time points to symbols depending on whether the expression value has increased, decreased or not changed. This method has been used by Huimin Geng et al. (2003) and Lees et al (2007) and has been able to justify the reliability of this discretization process.

3. Availability of data used after normalization would help in reproducibility.

Response
The availability of the data used after normalization has been provided

4. Overall I suggest detailed explanation of methodology adopted and its execution with the data used. Proper discussion of the same is also necessary.

Response
The detailed explanation of the methodology has been improved and a proper discussion of the findings has been added

5. The RNA Seq based transcriptome data was generated from highly synchronous culture data. The discussion of PfEMP1 linking with the pathology is unnecessary and misleading. Especially the statement “This differential expression during infection and among patients could have accounted for its clustering into 2 different clusters by the algorithm” is not acceptable since the data is from in-vitro culture.

Response
“This differential expression during infection and among patients could have accounted for its clustering into 2 different clusters by the algorithm.” has been removed from discussion

6. I recommend the use of this method to other transcriptome based studies of P.falciparum at different time points (microarray, RNASeq) to validate the results obtained in the present study. Discussion about the results obtained in this study with other transcriptome based studies is also necessary. This will reveal the robustness of the approach employed in this paper.

Response
This is very good suggestion but, this work, is based on the work of Karen Lees , Jennifer Taylor ,Gerton Lunter , and Jotun Hein titled: “Identifying Gene Clusters and Regulatory Themes using Time Course Expression Data, Hidden Markov Models and Transcription Factor Information” which has actually proved the robustness of the approach.

7. The criteria for GO Term enriched (p-value) should be provided in the discussion although it has been mentioned only in the Figures.

Response
The GO criteria - “Statistical cut-off of enrichment analyses in FunRich software was kept as default with a p-value <0.05.” has been provided in the discussion.

8. Since data was taken from different time points, the stochastic nature of the HMM process may not be appropriate to cluster gene expression data which have strong dependency.

Response
Gene expression is a fundamentally stochastic process, with randomness in transcription and translation leading to significant cell-to-cell variations in mRNA and protein levels. Model-based clustering approaches are effective when structural properties of the data can be explicitly expressed and HMM can be used by these types of approaches to partition gene expression time-series data into clusters. The process starts with an initial collection of HMMs that encompass typical qualitative behavior and the process iteratively find cluster models such a way that the joint likely hood of the clustering is maximized. This method is also robust with respect to noisy and frequently missing data.

9. It would be interesting to classify the var genes obtained in the different clusters. PfEMPI as encoded by the var gene family is divided into subfamilies with different functional domains. Are the different clusters showing segregation of different subfamilies? In the IDC time course experiment which was perfomed in-vitro based on which the RNA Seq data has been taken, is there a difference in the var gene subfamily expression at different time points.

Response
Yes, it is possible, different clusters can also show segregation of different subfamilies and there is no difference in the var gene subfamily expression at different time points.

10. As mentioned in the materials and methods RNA seq based expression data of 5270 P.falciparum genes were considered. However in conclusion it has been mentioned that only 2000 genes were used for clustering. What is the implication of this statement?

Response
The normalization and discretization process reduced the data and we removed all missing values and noise reduce the data to about 2000 genes.
Competing Interests: No Competing interests Close
Report a concern

Views

Reviewer Report 20 Dec 2017

Thomas D Otto, University of Glasgow, Glasgow, UK

Not Approved

https://doi.org/10.5256/f1000research.13384.r28431

The paper describes an HMM clustering methods of a data set that I published.

I would have liked to be able to run the model. It is difficult from the definitions to understand how it runs and performs. Therefore I would suggest that the author make the source code available. I will not further comment the cluster method itself.

Assuming I would implement the method, I would not be able to replicate the analysis. The dataset has expression values from 7 time points: 0 hours - 48 hours for 5500 genes. They can be read counts or RPKM. It is not clear which input data were used and how those were then filtered ( alpha threshold in Le Roch et al.¹).

We think that at least 3300 genes are expressed, but in this analysis, just 1700 are clustered. In the blood stage of plasmodium, expressed genes follow a clear pattern, as can be seen in Bozdech et al.², and the results should be compared to this and other similar papers (at least mentioned in the introduction).

To emphasize the PfEMP1 is interesting, but those genes should not be expressed in parasites in culture(or at least their expression has no biological context), and they are expressed at around the same time.

Just as a suggestion, the paper would also more robust if other datasets would be used and the results compared: López-Barragán et al.³

Minor:

The dataset was generated from RNA-Seq data, not microarray, as mentioned in two parts of the paper.
It would be good to have the version of the GO terms. I think that those GO terms were significantly represented, what the cut-off?
40% of Plasmodium genes are of unknown function. Those won't have any GO terms. I think is wrong to deduce that they are likely to have the same function if occurring in the same cluster.

Is the work clearly and accurately presented and does it cite the current literature?

Partly
Is the study design appropriate and is the work technically sound?

No
Are sufficient details of methods and analysis provided to allow replication by others?

No
If applicable, is the statistical analysis and its interpretation appropriate?

No
Are all the source data underlying the results available to ensure full reproducibility?

Yes
Are the conclusions drawn adequately supported by the results?

No

References

1. Le Roch KG, Zhou Y, Blair PL, Grainger M, et al.: Discovery of gene function by expression profiling of the malaria parasite life cycle.Science. 2003; 301 (5639): 1503-8 PubMed Abstract | Publisher Full Text
2. Bozdech Z, Llinás M, Pulliam BL, Wong ED, et al.: The transcriptome of the intraerythrocytic developmental cycle of Plasmodium falciparum.PLoS Biol. 2003; 1 (1): E5 PubMed Abstract | Publisher Full Text
3. López-Barragán MJ, Lemieux J, Quiñones M, Williamson KC, et al.: Directional gene expression and antisense transcripts in sexual and asexual stages of Plasmodium falciparum.BMC Genomics. 2011; 12: 587 PubMed Abstract | Publisher Full Text

Competing Interests: The paper describes an HMM clustering methods of a data set that I published.

Reviewer Expertise: Bioinformatics, malaria, genomics, RNA-Seq

I confirm that I have read this submission and believe that I have an appropriate level of expertise to state that I do not consider it to be of an acceptable scientific standard, for reasons outlined above.

CITE

Report a concern

Respond or Comment

Views

Reviewer Report 01 Nov 2017

Hilary Ann Coller, Department of Molecular, Cell and Developmental Biology (MCDB), University of California, Los Angeles (UCLA), Los Angeles, CA, USA

Approved

https://doi.org/10.5256/f1000research.13384.r27477

The authors present the application of an approach to model-based clustering of RNA seq time course data to data on the life cycle of Plasmodium falciparum. The clustering was performed with an iterative training based approach based on Hidden Markov Models. An advantage of this approach is that there is objective information on the optimal number of clusters that best fit the data, which was 3 in this case. The clusters that were discovered with this method separated proteins with distinct functional roles into different clusters. For instance, genes involved in catabolic activities were clustered together in cluster 3, which also contained some structural elements. The authors use software to clearly define the extent of enrichment of different functional categories in each of the three clusters identified. The findings may prove valuable to researchers working to identify new therapeutic targets to combat P. falciparum.

Is the work clearly and accurately presented and does it cite the current literature?

Yes
Is the study design appropriate and is the work technically sound?

Yes
Are sufficient details of methods and analysis provided to allow replication by others?

Yes
If applicable, is the statistical analysis and its interpretation appropriate?

Yes
Are all the source data underlying the results available to ensure full reproducibility?

Yes
Are the conclusions drawn adequately supported by the results?

Yes

Competing Interests: No competing interests were disclosed.

I confirm that I have read this submission and believe that I have an appropriate level of expertise to confirm that it is of an acceptable scientific standard.

CITE

Report a concern

Respond or Comment

Comments on this article Comments (0)

Version 2

VERSION 2 PUBLISHED 19 Sep 2017

Open Peer Review

Reviewer Status

Reviewer Reports

	Invited Reviewers
	1	2	3
Version 2 (revision) 25 May 18		read	read
Version 1 19 Sep 17	read	read	read

Hilary Ann Coller, University of California, Los Angeles (UCLA), Los Angeles, USA
Thomas D Otto, University of Glasgow, Glasgow, UK
Ashis Das, Birla Institute of Technology and Science (BITS), Pilani, India

P.A. Boopathi, Birla Institute of Technology and Science (BITS), Pilani, India

Shibashish Choudhury, Birla Institute of Technology and Science (BITS), Pilani, India

Comments on this article

All Comments(0)

Add a comment

Browse by related subjects

Back to all reports

Reviewer Report

15 Views

18 Jul 2018 | for Version 2

Thomas D Otto, University of Glasgow, Glasgow, UK

15 Views Cite this report Responses(0)

Not Approved

First, it is weird that my comments were not addressed by the authors.

Second, I don't see an improvement compared to the first version

Mixing microarray and RNA-Seq
Claiming the importance of PfEMP1 which makes no sense in in vitro experiments, more over as generally just the exon2 have random expressions.
Not explaining why they filter 60% of the genes away, and figure 3 suggest less than 1700 genes were used.
Why not using a different dataset, as another reviewer mentioned to prove the results.

Third, the code should be made available.

Fourth, a lot of little things. The dataset was over 48h, from 0h - 48h. Genes are expressed, not proteins.

Competing Interests

I generated the used dataset (reference 23)

Reviewer Expertise

Bioinformatics, malaria, genomics, RNA-Seq

Respond to this report

Responses (0)

Back to all reports

Reviewer Report

20 Views

10 Jul 2018 | for Version 2

Ashis Das, Molecular Parasitology and Systems Biology Lab, Department of Biological Sciences, Birla Institute of Technology and Science (BITS), Pilani, India

P.A. Boopathi, Department of Biological Sciences, Birla Institute of Technology and Science (BITS), Pilani, India

20 Views Cite this report Responses(0)

Approved With Reservations

Major

In Otto TD et.al., (2010), it was reported that 4871 transcripts were found expressed during the erythrocytic stages. However, in this study only 2000 filtered genes were considered for clustering. Why this difference between the studies? In other words, the possible reason behind the normalization strategy adopted, which has resulted in the filtering out of so many genes. This should be discussed in results section.
Lees K et.al., (2006) suggested that this method could produce biologically meaningful information if applied to different datasets. I feel that applying this method to different P. falciparum expression datasets would further validate the present study. In the discussion part, limitations of this study should be discussed. If the comparison is not possible, please mention limitations of this approach.

Competing Interests

No competing interests were disclosed.

Respond to this report

Responses (0)

Back to all reports

Reviewer Report

30 Views

31 Jan 2018 | for Version 1

Ashis Das, Molecular Parasitology and Systems Biology Lab, Department of Biological Sciences, Birla Institute of Technology and Science (BITS), Pilani, India

P.A. Boopathi, Department of Biological Sciences, Birla Institute of Technology and Science (BITS), Pilani, India

Shibashish Choudhury, Department of Biological Sciences, Birla Institute of Technology and Science (BITS), Pilani, India

30 Views Cite this report Responses(1)

Approved With Reservations

The data pre-processing step mentioned in this article was not clear. What type of input data was used here and how the filtering was done? It was mentioned that normalize library from R package was used. Is it appropriate for normalizing RNA Seq based transcriptome studies, since it was mentioned as used for microarray studies (Is it upgraded for RNA Seq based studies?)
What is the criterion used to assign the expression of a particular gene across seven different time points? It is unclear with the brief explanation of Discretization. Is this determining the expression status of a particular gene?
Availability of data used after normalization would help in reproducibility.
Overall I suggest detailed explanation of methodology adopted and its execution with the data used. Proper discussion of the same is also necessary.
The RNA Seq based transcriptome data was generated from highly synchronous culture data. The discussion of PfEMP1 linking with the pathology is unnecessary and misleading. Especially the statement “This differential expression during infection and among patients could have accounted for its clustering into 2 different clusters by the algorithm” is not acceptable since the data is from in-vitro culture.
I recommend the use of this method to other transcriptome based studies of P.falciparum at different time points (microarray, RNASeq) to validate the results obtained in the present study. Discussion about the results obtained in this study with other transcriptome based studies is also necessary. This will reveal the robustness of the approach employed in this paper.
The criteria for GO Term enriched (p-value) should be provided in the discussion although it has been mentioned only in the Figures.
Since data was taken from different time points, the stochastic nature of the HMM process may not be appropriate to cluster gene expression data which have strong dependency.
It would be interesting to classify the var genes obtained in the different clusters. PfEMPI as encoded by the var gene family is divided into subfamilies with different functional domains. Are the different clusters showing segregation of different subfamilies? In the IDC time course experiment which was performed in-vitro based on which the RNA Seq data has been taken is there a difference in the var gene subfamily expression at different time points?
As mentioned in the materials and methods RNA seq based expression data of 5270 P.falciparum genes were considered. However in conclusion it has been mentioned that only 2000 genes were used for clustering. What is the implication of this statement?

Is the work clearly and accurately presented and does it cite the current literature?

Partly
Is the study design appropriate and is the work technically sound?

Partly
Are sufficient details of methods and analysis provided to allow replication by others?

No
If applicable, is the statistical analysis and its interpretation appropriate?

No
Are all the source data underlying the results available to ensure full reproducibility?

Partly
Are the conclusions drawn adequately supported by the results?

No

Competing Interests

No competing interests were disclosed.

Reviewer Expertise

Malaria molecular biology, transcriptomics

Respond to this report

Responses (1)

Author Response

25 May 2018

Jelili Oyelade, Department of Computer and Information Sciences, Covenant University, Ota, Nigeria

1. The data pre-processing step mentioned in this article was not clear. What type of input data was used here and how the filtering was done? It was mentioned that normalize library from R package was used. Is it appropriate for normalizing RNA Seq based transcriptome studies, since it was mentioned as used for microarray studies (Is it upgraded for RNA Seq based studies?)

Response
The input data was RNA-SEQ, The data was normalized to a mean of 1 and standard deviation of 0. Yes it is based on this paper. Zyprych-Walczak, J., Szabelska, A., Handschuh, L., Górczak, K., Klamecka, K., Figlerowicz, M., & Siatkowski, I. (2015). The impact of normalization methods on RNA-Seq data analysis. BioMed research international, 2015.

2. What is the criterion used to assign the expression of a particular gene across seven different time points? It is unclear with the brief explanation of Discretization. Is this determining the expression status of a particular gene?

Response
Discretization was conducted by converting the time points to symbols depending on whether the expression value has increased, decreased or not changed. This method has been used by Huimin Geng et al. (2003) and Lees et al (2007) and has been able to justify the reliability of this discretization process.

3. Availability of data used after normalization would help in reproducibility.

Response
The availability of the data used after normalization has been provided

4. Overall I suggest detailed explanation of methodology adopted and its execution with the data used. Proper discussion of the same is also necessary.

Response
The detailed explanation of the methodology has been improved and a proper discussion of the findings has been added

5. The RNA Seq based transcriptome data was generated from highly synchronous culture data. The discussion of PfEMP1 linking with the pathology is unnecessary and misleading. Especially the statement “This differential expression during infection and among patients could have accounted for its clustering into 2 different clusters by the algorithm” is not acceptable since the data is from in-vitro culture.

Response
“This differential expression during infection and among patients could have accounted for its clustering into 2 different clusters by the algorithm.” has been removed from discussion

6. I recommend the use of this method to other transcriptome based studies of P.falciparum at different time points (microarray, RNASeq) to validate the results obtained in the present study. Discussion about the results obtained in this study with other transcriptome based studies is also necessary. This will reveal the robustness of the approach employed in this paper.

Response
This is very good suggestion but, this work, is based on the work of Karen Lees , Jennifer Taylor ,Gerton Lunter , and Jotun Hein titled: “Identifying Gene Clusters and Regulatory Themes using Time Course Expression Data, Hidden Markov Models and Transcription Factor Information” which has actually proved the robustness of the approach.

7. The criteria for GO Term enriched (p-value) should be provided in the discussion although it has been mentioned only in the Figures.

Response
The GO criteria - “Statistical cut-off of enrichment analyses in FunRich software was kept as default with a p-value <0.05.” has been provided in the discussion.

8. Since data was taken from different time points, the stochastic nature of the HMM process may not be appropriate to cluster gene expression data which have strong dependency.

Response
Gene expression is a fundamentally stochastic process, with randomness in transcription and translation leading to significant cell-to-cell variations in mRNA and protein levels. Model-based clustering approaches are effective when structural properties of the data can be explicitly expressed and HMM can be used by these types of approaches to partition gene expression time-series data into clusters. The process starts with an initial collection of HMMs that encompass typical qualitative behavior and the process iteratively find cluster models such a way that the joint likely hood of the clustering is maximized. This method is also robust with respect to noisy and frequently missing data.

9. It would be interesting to classify the var genes obtained in the different clusters. PfEMPI as encoded by the var gene family is divided into subfamilies with different functional domains. Are the different clusters showing segregation of different subfamilies? In the IDC time course experiment which was perfomed in-vitro based on which the RNA Seq data has been taken, is there a difference in the var gene subfamily expression at different time points.

Response
Yes, it is possible, different clusters can also show segregation of different subfamilies and there is no difference in the var gene subfamily expression at different time points.

10. As mentioned in the materials and methods RNA seq based expression data of 5270 P.falciparum genes were considered. However in conclusion it has been mentioned that only 2000 genes were used for clustering. What is the implication of this statement?

Response
The normalization and discretization process reduced the data and we removed all missing values and noise reduce the data to about 2000 genes.

View more View less

Competing Interests

No Competing interests

Back to all reports

Reviewer Report

27 Views

20 Dec 2017 | for Version 1

Thomas D Otto, University of Glasgow, Glasgow, UK

27 Views Cite this report Responses(0)

Not Approved

The dataset was generated from RNA-Seq data, not microarray, as mentioned in two parts of the paper.
It would be good to have the version of the GO terms. I think that those GO terms were significantly represented, what the cut-off?
40% of Plasmodium genes are of unknown function. Those won't have any GO terms. I think is wrong to deduce that they are likely to have the same function if occurring in the same cluster.

Is the work clearly and accurately presented and does it cite the current literature?

Partly
Is the study design appropriate and is the work technically sound?

No
Are sufficient details of methods and analysis provided to allow replication by others?

No
If applicable, is the statistical analysis and its interpretation appropriate?

No
Are all the source data underlying the results available to ensure full reproducibility?

Yes
Are the conclusions drawn adequately supported by the results?

No

References

Competing Interests

The paper describes an HMM clustering methods of a data set that I published.

Reviewer Expertise

Bioinformatics, malaria, genomics, RNA-Seq

Respond to this report

Responses (0)

Back to all reports

Reviewer Report

20 Views

01 Nov 2017 | for Version 1

Hilary Ann Coller, Department of Molecular, Cell and Developmental Biology (MCDB), University of California, Los Angeles (UCLA), Los Angeles, CA, USA

20 Views Cite this report Responses(0)

Approved

Is the work clearly and accurately presented and does it cite the current literature?

Yes
Is the study design appropriate and is the work technically sound?

Yes
Are sufficient details of methods and analysis provided to allow replication by others?

Yes
If applicable, is the statistical analysis and its interpretation appropriate?

Yes
Are all the source data underlying the results available to ensure full reproducibility?

Yes
Are the conclusions drawn adequately supported by the results?

Yes

Competing Interests

No competing interests were disclosed.

I confirm that I have read this submission and believe that I have an appropriate level of expertise to confirm that it is of an acceptable scientific standard.

Respond to this report

Responses (0)

Alongside their report, reviewers assign a status to the article:

Approved - the paper is scientifically sound in its current form and only minor, if any, improvements are suggested

Approved with reservations - A number of small changes, sometimes more significant revisions are required to address specific details and improve the papers academic merit.

Not approved - fundamental flaws in the paper seriously undermine the findings and conclusions

Click here to access the data.

Downloaded data do not display as expected? Download the data

[1] 1. Huang QW, Wu LY, Qu JB, et al.: Analyzing time-course gene expression data using profile-state hidden Markov model. In: Systems Biology (ISB), IEEE International Conference. 2011; 351–355. Publisher Full Text

[2] 2. Spellman PT, Sherlock G, Zhang MQ, et al.: Comprehensive identification of cell cycle–regulated genes of the yeast Saccharomyces cerevisiae by microarray hybridization. Mol Biol Cell. 1998; 9(12): 3273–3297. PubMed Abstract | Publisher Full Text | Free Full Text

[3] 3. Slonim DK: From patterns to pathways: gene expression data analysis comes of age. Nat Genet. 2002; 32 Suppl:502–508. PubMed Abstract | Publisher Full Text

[4] 4. Eisen MB, Spellman PT, Brown PO, et al.: Cluster analysis and display of genome-wide expression patterns. Proc Natl Acad Sci U S A. 1998; 95(25): 14863–14868. PubMed Abstract | Publisher Full Text | Free Full Text

[5] 5. Segal E, Shapira M, Regev A, et al.: Module networks: identifying regulatory modules and their condition-specific regulators from gene expression data. Nat Genet. 2003; 34(2): 166–176. PubMed Abstract | Publisher Full Text

[6] 6. Howell GR, Macalinao DG, Sousa GL, et al.: Molecular clustering identifies complement and endothelin induction as early events in a mouse model of glaucoma. J Clin Invest. 2011; 121(4): 1429–44. PubMed Abstract | Publisher Full Text | Free Full Text

[7] 7. Hughes TR, Marton MJ, Jones AR, et al.: Functional discovery via a compendium of expression profiles. Cell. 2000; 102(1): 109–126. PubMed Abstract | Publisher Full Text

[8] 8. Hopcroft LE, McBride MW, Harris KJ, et al.: Predictive response-relevant clustering of expression data provides insights into disease processes. Nucleic Acids Res. 2010; 38(20): 6831–6840. PubMed Abstract | Publisher Full Text | Free Full Text

[9] 9. Schliep A, Schönhuth A, Steinhoff C: Using hidden Markov models to analyze gene expression time course data. Bioinformatics. 2003; 19 Suppl 1:i255–i263. PubMed Abstract | Publisher Full Text

[10] 10. Tavazoie S, Hughes JD, Campbell MJ, et al.: Systematic determination of genetic network architecture. Nat Genet. 1999; 22(3): 281–285. PubMed Abstract | Publisher Full Text

[11] 11. Tamayo P, Slonim D, Mesirov J, et al.: Interpreting patterns of gene expression with self-organizing maps: methods and application to hematopoietic differentiation. Proc Natl Acad Sci U S A. 1999; 96(6): 2907–2912. PubMed Abstract | Publisher Full Text | Free Full Text

[12] 12. Friedman N: Inferring cellular networks using probabilistic graphical models. Science. 2004; 303(5659): 799–805. PubMed Abstract | Publisher Full Text

[13] 13. Brown MP, Grundy WN, Lin D, et al.: Knowledge-based analysis of microarray gene expression data by using support vector machines. Proc Natl Acad Sci U S A. 2000; 97(1): 262–267. PubMed Abstract | Publisher Full Text | Free Full Text

[14] 14. De Fonzo V, Aluffi-Pentini F, Parisi V: Hidden Markov Models in Bioinformatics. Curr Bioinform. 2007; 2(1): 49–61. Publisher Full Text

[15] 15. Ji X, Li-Ling J, Sun Z: Mining gene expression data using a novel approach based on hidden Markov models. FEBS Lett. 2003; 542(1–3): 125–131. PubMed Abstract | Publisher Full Text

[16] 16. Geng H, Deng X, Ali HH: Applications of Hidden Markov Models in Microarray Gene Expression Data. Huimin Department of Computer Science, University of Nebraska at Omaha, Omaha, NE 68182 USA. Publisher Full Text

[17] 17. Lees KT: Identifying Gene Clusters and Regulatory Themes using Time Course Expression Data, Hidden Markov Models and Transcription Factor Information. Bioinformatics. 2006. Reference Source

[18] 18. Zeng Y, Garcia-Frias J: A novel HMM-based clustering algorithm for the analysis of gene expression time-course data. Comput Stat Data Anal. 2006; 50(9): 247–2494. Publisher Full Text

[19] 19. Durbin RM, Eddy SR, Krogh A, et al.: Biological Sequence Analysis: Probabilistic Models of Proteins and Nucleic Acids (1st ed.). Cambridge: Cambridge University Press, 1998. Publisher Full Text

[20] 20. Beal M, Krishnamurthy P: Gene expression time course clustering with countably infinite hidden markov model. arXiv preprint arViv: 1206.6824. Reference Source

[21] 21. Iyer VR, Eisen MB, Ross DT, et al.: The transcriptional program in the response of human fibroblasts to serum. Science. 1999; 283(5398): 83–87. PubMed Abstract | Publisher Full Text

[22] 22. Cho RJ, Campbell MJ, Winzeler EA, et al.: A genome-wide transcriptional analysis of the mitotic cell cycle. Mol Cell. 1998; 2(1): 65–73. PubMed Abstract | Publisher Full Text

[23] 23. Otto TD, Wilinski D, Assefa S, et al.: New insights into the blood-stage transcriptome of Plasmodium falciparum using RNA-Seq. Mol Microbiol. 2010; 76(1): 12–24. PubMed Abstract | Publisher Full Text | Free Full Text

[24] 24. Knab B, Schliep A, Steckemetz B, et al.: Model-Based Clustering With Hidden Markov Models and its Application to Financial Time-Series Data. Between Data Science and Applied Data Analysis. Springer. 561–569. Publisher Full Text

[25] 25. Ay F, Bunnik EM, Varoquaux N, et al.: Multiple dimensions of epigenetic gene regulation in the malaria parasite Plasmodium falciparum: gene regulation via histone modifications, nucleosome positioning and nuclear architecture in P. falciparum. Bioessays. 2015; 37(2): 182–194. PubMed Abstract | Publisher Full Text | Free Full Text

[26] 26. Besteiro S, Williams RA, Coombs GH, et al.: Protein turnover and differentiation in Leishmania. Int J Parasitol. 2007; 37(10): 1063–1075. PubMed Abstract | Publisher Full Text | Free Full Text

[27] 27. Hansen M, Beitz E, Schultz JE: An Aquaporin Gene in Plasmodium Falciparum: Molecular cloning and functional expression. Molecular Biology and Physiology of Water and Solute Transport. Springer. 2000; 389–392. Publisher Full Text

[28] 28. Jankowsky A, Guenther UP, Jankowsky E: The RNA helicase database. Nucleic Acids Res. 2011; 39(Database issue): D338–41. PubMed Abstract | Publisher Full Text | Free Full Text

[29] 29. Lavstsen T, Turner L, Saguti F, et al.: Plasmodium falciparum erythrocyte membrane protein 1 domain cassettes 8 and 13 are associated with severe malaria in children. Proc Natl Acad Sci U S A. 2012; 109(26): E1791–E1800. PubMed Abstract | Publisher Full Text | Free Full Text

[30] 30. Meena LS, Rajni: Cloning and characterization of engA, a GTP-binding protein from Mycobacterium tuberculosis H₃₇Rv. Biologicals. 2011; 39(2): 94–99. PubMed Abstract | Publisher Full Text

[31] 31. Nandi D, Tahiliani P, Kumar A, et al.: The ubiquitin-proteasome system. J Biosci. 2006; 31(1): 137–155. PubMed Abstract

[32] 32. Rossi G, Kolstad K, Stone S, et al.: BET3 encodes a novel hydrophilic protein that acts in conjunction with yeast SNAREs. Mol Biol Cell. 1995; 6(12): 1769–1780. PubMed Abstract | Publisher Full Text | Free Full Text

[33] 33. Rottmann M, Lavstsen T, Mugasa JP, et al.: Differential expression of var gene groups is associated with morbidity caused by Plasmodium falciparum infection in Tanzanian children. Infect Immun. 2006; 74(7): 3904–39. PubMed Abstract | Publisher Full Text | Free Full Text

[34] 34. Oyelade J, Isewon I, Olaniyan D, et al.: Dataset 1 in: Effectiveness of model-based clustering in analyzing Plasmodium falciparum RNA-seq time-course data. F1000Research. 2018. Data Source

Effectiveness of model-based clustering in analyzing Plasmodium falciparum RNA-seq time-course data

Abstract

Keywords

Revised Amendments from Version 1

Introduction

Materials and methods

Definitions and notation

Data preprocessing

HMM for clustering gene expression data

Figure 1. HMM design from cluster 2 to w.

Results and discussion

Likelihood estimation

Table 1. Table showing LRT calculations.

Figure 2. Log likelihoods for different numbers of clusters.

Clustering results

Figure 3. clustering results showing all the genes in each cluster.

Functional-induced/determined clustering of plasmodium falciparum protein by the algorithm

Functional annotation

Table 2. Functional annotation of each clusters.

Figure 4. Functional annotation of cluster 1.

Figure 5. Functional annotation of cluster 2.

Figure 6. Functional annotation of cluster 3.

Conclusion

Data availability

Competing interests

Grant information

Acknowledgements

References

Comments on this article Comments (0)

Open Peer Review

Comments on this article Comments (0)

Open Peer Review

Reviewer Status

Reviewer Reports

Comments on this article

Browse by related subjects

The problem

How to fix it

Competing Interests Policy

Stay Updated