Keywords
graph mining, protein-protein interaction, pseudo-absence, semi-supervised learning, support vector machine
This article is included in the Bioconductor gateway.
This article is included in the RPackage gateway.
This article is included in the Machine learning: life sciences collection.
This article is included in the Interactive Figures collection.
graph mining, protein-protein interaction, pseudo-absence, semi-supervised learning, support vector machine
The functions of many proteins remain unknown. This is a big challenge in functional genomics. As proteins that consist of the same protein complex are often involved in the same cellular process, the pattern of protein-protein interactions (PPIs) can give information regarding protein function. Thus PPI databases can be useful to predict protein function, complementing conventional approaches based on protein sequence analyses.
Many databases store information on protein-protein interactions as well as protein complexes. For example, the Biological General Repository for Interaction Datasets (BioGRID) includes over 500,000 manually annotated interactions1. The STRING database aims to provide a critical assessment and integration of protein-protein interactions, including direct (physical) as well as indirect (functional) associations. The basic interaction unit in STRING is the functional association, i.e. a specific and productive functional relationship between two proteins2.
Once the PPI has been obtained experimentally, there are numerous methods to analyze the network. A neighbor counting method for protein function prediction was developed3,4. The theory of Markov random fields was used to infer functions using protein-protein interaction data and the functional annotations of its interaction protein partners5. There are many algorithms that try to integrate multiple sources of data to infer functions6–8. We propose a method that can infer the putative functions of proteins by solving classification problems and thus identifying closely connected proteins known to be involved in a certain process.
We use the kernel method for the graph as a similarity measure between proteins, instead of using the first or second level neighbors, and thus our proposed method provides scores or distances derived from a graph kernel. The main advantage of the proposed method is that the neighbors of a set of proteins can be ranked in terms of scores. Generally, we need two or more classes for classification problem. Although we only know the target, we want to apply semi-supervised learning techniques to the PPI through this package. Thus, the main idea of this method is how to find another class so that two classes can be used for classification problem. Eventually, we can classify proteins to identify such closely related proteins by using this package. Finally, functional enrichment analyses such as ORA and GSEA are incorporated to predict the protein function from the closely related proteins.
The support vector machine (SVM) is one of most widely used methods for classification9. Suppose we have a dataset in the real space and that each point in our dataset has a corresponding class label. A SVM is involved in a convex optimization problem to separate data points in the dataset according to their class, by maximizing distance between class and minimizing a penalty for misclassification for each class, at the same time. Unfortunately, the graph data is not in the real space. Cover’s theorem10 provides the useful idea behind a nonlinear SVM, which is to find an optimal separating hyperplane in high-dimensional feature space mapped by using a suitable kernel function, just as we did for the linear SVM in original space.
Graph (network) data is ubiquitous and graph mining tries to extract novel and insightful information from data. Graph kernels are defined in the form of kernel matrices, based on the normalized Laplacian matrix for a graph. The best-known kernel in a graph is the diffusion kernel11. The motivation is that it is often easier to describe the local neighborhood than to describe the structure of the whole space12. Another method is called a regularized Laplacian matrix13 and is widely used in areas such as spectral graph theory, where properties of graphs are studied in terms of their eigenvalues and vectors of adjacency matrices14. Broadly speaking, kernels can be thought of as functions that produce similarity matrices15. In the package, we choose only the regularized Laplacian matrix as a graph kernel for the PPI.
In many biological problems, datasets are often compounded by imbalanced class distribution, known as the imbalanced data problem, in which the size of one class is significantly larger than that of the other class. Many classification algorithms such as a SVM are sensitive to data with an imbalanced class problem, leading to a suboptimal classification. It is desirable to compensate the imbalance effect in model training for more accurate classification. A possible solution to this problem is to use the one-class SVM (OCSVM) by learning from the target class only16. In one-class classification, it is assumed that only information of one of the classes, the target class, is available, and no information is available from the other class, known as the background. The OCSVM can be solely applied because we have only one class, the target. However, it is known that one-class classifiers seldom outperform two-class classifiers when the data from two class are available17.
The strategy of this package is to make use of the OCSVM and classical SVM, sequentially. First, we apply the OCSVM by training a one-class classifier using the data from the known class only. Let n be the number of proteins in the target class. This model is used to identify distantly related proteins among remaining N – n proteins in the background. Indeed, we do not know whether or not each of proteins in the background interacts with the proteins of the target. Thus, it does not always imply that proteins in the background do not interact with the target. In fact, their associations with the target are not observed to date yet. Proteins with zero similarity with the target class are extracted. Then they are potentially defined as the other class by pseudo-absence selection methods18 from spatial statistics. The target class can be seen as real presence data. The main idea of the proposed method is to adopt the pseudo-absence class. For the data to be balanced, assume that two classes contain the same number of proteins. Next, by the classical SVM, these two classes are used to identify closely related proteins whose scores ranging from -1 to 1 are close to 1 among remaining N – 2n proteins. Semi-supervised learning can be applied to make use of large unlabeled data and small labeled data. Some of these methods directly try to label the unlabeled data. Eventually, those found by this procedure can be functionally linked to the target proteins. This is usually based on the assumption that unannotated proteins have similar functions as their interacting proteins.
We need a list of proteins and the kernel matrix to infer functionally related proteins. With the STRING database for mouse, it is supposed that the target is the set of proteins in the Ras signaling pathway from the KEGG pathway (http://www.genome.jp/kegg-bin/show_pathway?mmu04014).
library(PPInfer)
# download the kernel matrix from http://ge-lab.org/dm/K10090.rds
K.10090 <- readRDS("K10090.rds")# remove prefix
rownames(K.10090) <- sub(".*\\.", "", rownames(K.10090))# load target
library(limma)
kegg.mmu <- getGeneKEGGLinks(species.KEGG = "mmu")
index <- which(kegg.mmu[,2] == "path:mmu04014")
path.04014 <- kegg.mmu[index,1]# infer functionally related proteins
path.04014.infer <- ppi.infer.mouse(path.04014, K.10090, input = "entrezgene",
output = "entrezgene", nrow(K.10090))
genes <- path.04014.infer$top# load gene sets for gene ontology
library(org.Mm.eg.db)
library(GO.db)
xx <- sapply(as.list(org.Mm.egGO2EG), unique)# ORA with top 100 proteins
resORA <- ORA(xx, genes[1:100])
ORAsummary <- na.omit(data.frame(resORA, AnnotationDbi::select(GO.db,
rownames(resORA), "TERM")))
head(ORAsummary)
p <- ORA.dotplot(ORAsummary, category = "TERM", count = "Count", size = "Size",
pvalue = "pvalue", sort = "pvalue", p.adjust.methods = "fdr", numChar = 60,
top = 50) + scale_colour_gradient(low = "red", high = "yellow")# interactive figure
library(plotly)
config(ggplotly(p), showLink = TRUE)# GSEA
index <- !is.na(path.04014.infer$score)
genes <- path.04014.infer$top[index]
scores <- path.04014.infer$score[index]
scaled.scores <- as.numeric(scale(scores))
names(scaled.scores) <- genes
set.seed(1)
resGSEA <- fgsea(xx, scaled.scores, nperm = 1000)
GSEAsummary <- na.omit(data.frame(resGSEA, AnnotationDbi::select(GO.db,
resGSEA$pathway, "TERM")))
head(GSEAsummary)
p <- GSEA.barplot(GSEAsummary, category = "TERM", score = "NES", pvalue = "padj",
top = 50, sort = "NES", decreasing = TRUE, numChar = 50) +
scale_fill_continuous(low = "red", high = "blue")# interactive figure
p <- ggplotly(p + guides(fill = FALSE))
config(p, showLink = TRUE)The tyrosine kinase receptor binds to a ligand in the extracellular space. Then its cytoplasmic domain undergoes conformational change that forms dimerization, resulting in transphophotyrosine. The SH2 domain recognizes this phosphotyrosine. The Grb2 adaptor protein containing SH2 binds these receptors and recruits Sos, which is the Ras-GEF inducing Ras, to release its GDP and bind a GTP instead. The Ras protein is activated by this guanine nucleotide exchange factor. GTP-activated Ras can activate PI3K. Once PIP3 is formed by PI3K, an Akt/PKB kinase can become tethered via its PH domain. Once activated, Akt/PKB proceeds to phosphorylate a series of protein substrates, leading to aiding survival by reducing the possibility of apoptotic suicide program. For this reason, several GO terms about the RTK and PI3K pathways are shown in Figure 1. We can find cell migration due to the integrin and FAK. MAP kinase activity, which is a downstream of Ras signaling and causes cell proliferation, is statistically significant.
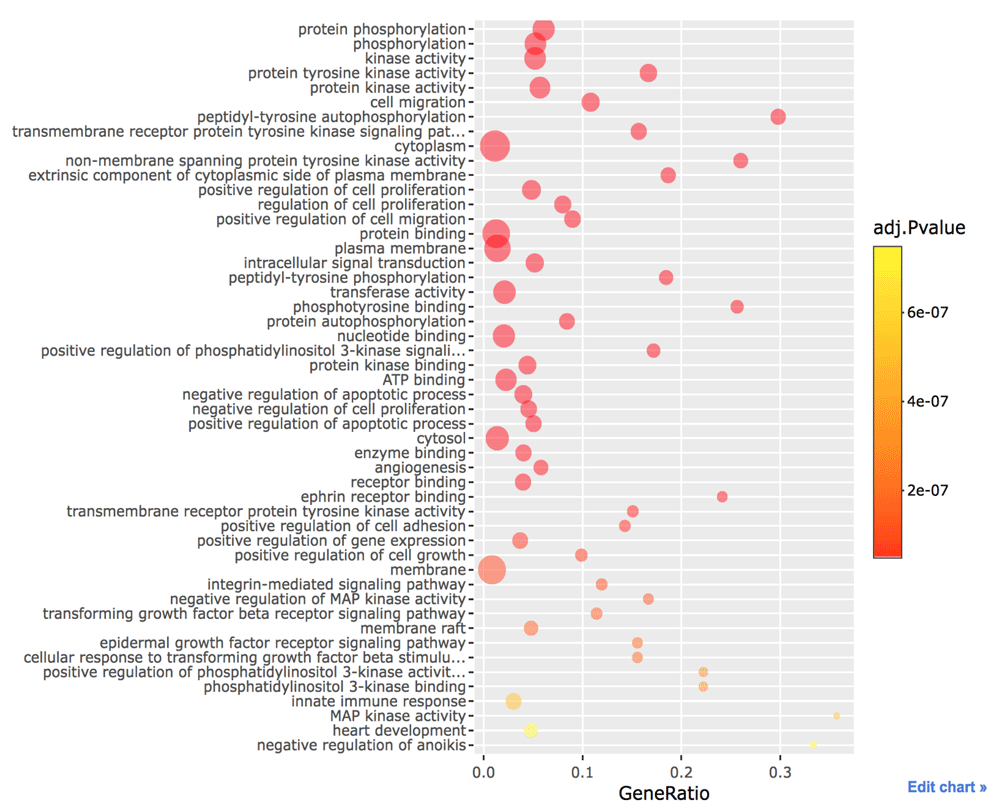
This figure was generated with Plotly (https://plot.ly/).
In the GSEA, the gene list is sorted by the standardized score showing how much they are functionally close to the target. Genes with higher scores are functionally more related to the target. The positive values of the enrichment score indicate enrichment at the top of the ranked gene list. Proteins that are closely related to the target are enriched in categories with high enrichment scores. In other words, these proteins are depleted in categories with low enrichment scores. We can see the RTK, MAPK and Wnt signaling pathways in Figure 2. One possible reason is that Akt can activate β-catenin both indirectly and indirectly.
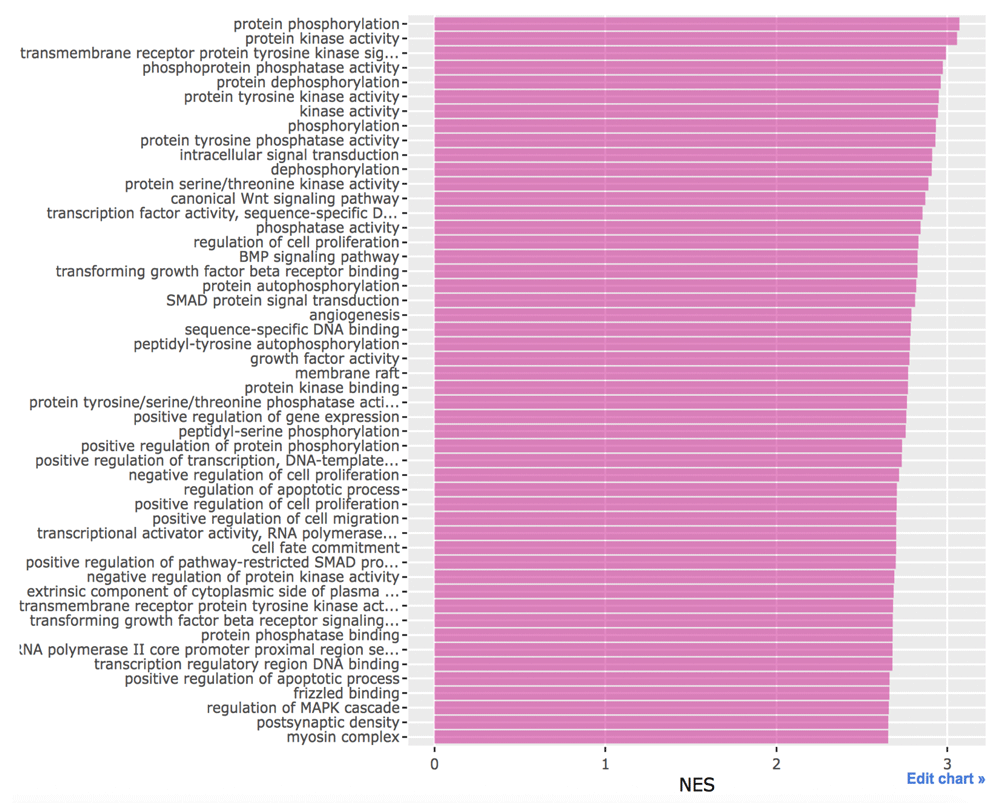
This figure was generated with Plotly (https://plot.ly/).
# gene sets for GO and KEGG pathway
GO.TERM <- AnnotationDbi::select(GO.db, names(xx), "TERM")[,2]
names(xx) <- GO.TERM
library(KEGG.db)
pathway.id <- unique(kegg.mmu[,2])
yy <- list()
for(i in 1:length(pathway.id))
{
index <- which(kegg.mmu[,2] == pathway.id[i])
yy[[i]] <- kegg.mmu[index,1]
}
library(Category)
names(yy) <- getPathNames(sub("[[:alpha:]]+....", "", pathway.id))
yy[which(names(yy) == "NA")] <- NULL# remove duplicate categories
yy[intersect(names(xx), names(yy))] <- NULL# GSEA
set.seed(1)
GSEAsummary <- fgsea(c(xx, yy), scaled.scores, nperm = 1000)
index <- which(GSEAsummary[,1] == names(yy[1]))
groups <- 0
groups[1:(index-1)] <- "GO"
groups[index:nrow(GSEAsummary)] <- "KEGG"
index <- match(data.frame(GSEAsummary[,1])[,1], names(c(xx, yy)))# network visualization
g <- enrich.net(GSEAsummary, c(xx, yy)[index], node.id = "pathway", numChar = 60,
pvalue = "pval", edge.cutoff = 0.2, pvalue.cutoff = 0.05, degree.cutoff = 1,
n = 200, group = groups, vertex.label.cex = 0.6, vertex.label.color = "black")# interactive figure
vs <- V(g)
es <- as.data.frame(get.edgelist(g))
Nv <- length(vs)
Ne <- length(es[1]$V1)# create nodes
L <- layout.kamada.kawai(g)
Xn <- L[,1]
Yn <- L[,2]
group <- ifelse(V(g)$shape == "circle", "GO", "KEGG")
network <- plot_ly(x = ~Xn, y = ~Yn, type = "scatter", mode = "markers",
marker = list(color = V(g)$color, size = V(g)$size*2,
symbol= ~V(g)$shape, line = list(color = "gray", width = 2)),
hoverinfo = "text", text = ~paste("</br>", group, "</br>", names(vs))) %>%
add_annotations( x = ~Xn, y = ~Yn, text = names(vs), showarrow = FALSE,
font = list(color = "gray", size = 10))# create edges
edge_shapes <- list()
for(i in 1:Ne)
{
v0 <- es[i,]$V1
v1 <- es[i,]$V2
index0 <- match(v0, names(V(g)))
index1 <- match(v1, names(V(g)))
edge_shape <- list(type = "line", line = list(color = "#030303",
width = E(g)$width[i]), x0 = Xn[index0], y0 = Yn[index0],
x1 = Xn[index1], y1 = Yn[index1])
edge_shapes[[i]] <- edge_shape
}# create network
axis <- list(title = "", showgrid = FALSE, showticklabels = FALSE, zeroline = FALSE)
h <- layout(network, title = "Enrichment Network", shapes = edge_shapes,
xaxis = axis, yaxis = axis)
config(h, showLink = TRUE)In Figure 3, the network visualization of the functional enrichment analysis is displayed. Nodes indicate GO terms and KEGG pathways. The connection between two nodes depends on the proportion of overlapping genes of corresponding two categories19. The size of nodes is proportional to the number of genes in their categories. The more significant categories are, the less transparent their nodes are. This network may be useful to see the overview of the functional enrichment.
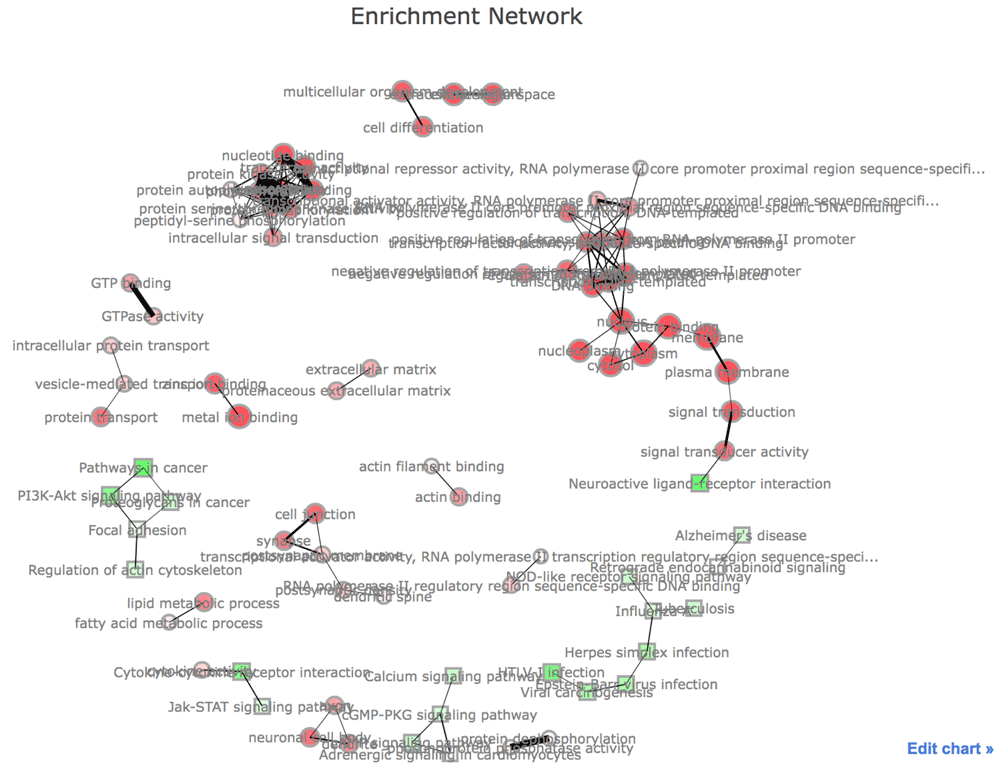
This figure was generated with Plotly (https://plot.ly/).
The proposed method is highly dependent on protein interaction networks. There are many prominent databases that include extensive information on protein interactions, and interactions are also reported in thousands of literature references. Therefore, the choice of data can be critical. Another issue is a technical problem. The one-class support vector machine can be sensitive to the choice of kernels and parameters. However, there is potential in inferring putative functions of proteins from PPIs, complementing conventional methods based on protein sequence analyses.
The PPInfer package is available at: http://bioconductor.org/packages/PPInfer/
Source code is available at: https://github.com/Bioconductor-mirror/PPInfer
Archived source code as at the time of publication: https://doi.org/doi:10.5281/zenodo.103512820
License: Artistic-2.0
This material is based upon work supported by the National Science Foundation/EPSCoR Grant Number IIA-1355423 and by the State of South Dakota.
The funders had no role in study design, data collection and analysis, decision to publish, or preparation of the manuscript.
| Views | Downloads | |
|---|---|---|
| F1000Research | - | - |
|
PubMed Central
Data from PMC are received and updated monthly.
|
- | - |
Is the rationale for developing the new software tool clearly explained?
Partly
Is the description of the software tool technically sound?
Yes
Are sufficient details of the code, methods and analysis (if applicable) provided to allow replication of the software development and its use by others?
No
Is sufficient information provided to allow interpretation of the expected output datasets and any results generated using the tool?
No
Are the conclusions about the tool and its performance adequately supported by the findings presented in the article?
No
Competing Interests: No competing interests were disclosed.
Alongside their report, reviewers assign a status to the article:
| Invited Reviewers | ||
|---|---|---|
| 1 | 2 | |
|
Version 3 (revision) 12 Mar 18 |
read | |
|
Version 2 (revision) 08 Dec 17 |
read | read |
|
Version 1 07 Nov 17 |
read | |
Provide sufficient details of any financial or non-financial competing interests to enable users to assess whether your comments might lead a reasonable person to question your impartiality. Consider the following examples, but note that this is not an exhaustive list:
Sign up for content alerts and receive a weekly or monthly email with all newly published articles
Already registered? Sign in
The email address should be the one you originally registered with F1000.
You registered with F1000 via Google, so we cannot reset your password.
To sign in, please click here.
If you still need help with your Google account password, please click here.
You registered with F1000 via Facebook, so we cannot reset your password.
To sign in, please click here.
If you still need help with your Facebook account password, please click here.
If your email address is registered with us, we will email you instructions to reset your password.
If you think you should have received this email but it has not arrived, please check your spam filters and/or contact for further assistance.
Comments on this article Comments (0)