Analyzing DECREASE trials to estimate evidence of data manipulation

Chris H.J. Hartgerink; E.M. Kemper; Markus W. Hollmann; Gerben ter Riet

doi:10.12688/f1000research.12584.1

Home Browse Analyzing DECREASE trials to estimate evidence of data manipulation

ALL Metrics

-

Views

-

Downloads

Get PDF

Get XML

Export

▬

✚

Research Article

Analyzing DECREASE trials to estimate evidence of data manipulation

[version 1; peer review: 1 approved, 1 approved with reservations]

Chris H.J. Hartgerink¹, E.M. Kemper², Markus W. Hollmann³, Gerben ter Riet⁴

PUBLISHED 13 Nov 2017

Author details Author details

¹ Department of Methods and Statistics, Tilburg University, Tillburg, 5037AB, The Netherlands
² Department of Pharmacy, Amsterdam Medisch Centrum (AMC), Amsterdam, 1105AZ, The Netherlands
³ Department of General Practice/Family Medicine, Amsterdam Medisch Centrum (AMC), Amsterdam, 1105AZ, The Netherlands
⁴ Department of Anesthesiology, Amsterdam Medisch Centrum (AMC), Amsterdam, 1105AZ, The Netherlands

Chris H.J. Hartgerink
Roles: Conceptualization, Data Curation, Formal Analysis, Investigation, Methodology, Project Administration, Resources, Software, Visualization, Writing – Original Draft Preparation, Writing – Review & Editing

E.M. Kemper
Roles: Conceptualization, Writing – Original Draft Preparation, Writing – Review & Editing

Markus W. Hollmann
Roles: Writing – Review & Editing

Gerben ter Riet
Roles: Conceptualization, Writing – Original Draft Preparation, Writing – Review & Editing

OPEN PEER REVIEW

REVIEWER STATUS

This article is included in the Interactive Figures collection.

Abstract

Background: The effect of beta-blockers on perioperative mortality in non-cardiac surgery has been controversial due to concerns regarding the scientific integrity of the DECREASE-I and DECREASE-IV trials. Previous meta-analyses indicated beta-blockade might increase mortality after removing the DECREASE trials from the evidence base.
Methods: In this report, we statistically investigate the DECREASE trials and model their veracity (i.e., the probability that these effects or more extreme occurred naturally) and estimate how many data points might have been manipulated in the DECREASE trials using the inversion method.
Results: Our research indicates that the DECREASE trials are nearly impossible if we assume they investigate the same effect as the non-DECREASE trials and under that assumption. Our results also provide evidence that at least some data points were manipulated.
Conclusions: The DECREASE trials are likely to be manipulated under the assumption that they investigate the same effect as the non-DECREASE trials on beta-blockade. However, these differences might also be due to different conceptual approaches as to how beta-blockade might prevent mortality in non-cardiac surgery. Considering this, we recommend new and more extensively controlled, confirmatory trials to determine whether there is any use in administering beta-blockers in order to decrease perioperative mortality.

Keywords

beta-blocker, DECREASE, data manipulation, inversion method, misconduct

Corresponding author: Chris H.J. Hartgerink

Competing interests: No competing interests were disclosed.

Grant information: CHJH was funded by the Office of Research Integrity during part of this project (HHS-ORI; ORIIR160019).
The funders had no role in study design, data collection and analysis, decision to publish, or preparation of the manuscript.

This is an open access article, made available under the Creative Commons Public Domain Dedication. This work may be copied, modified, distributed and performed, even for commercial purposes, all without asking permission. How to cite: Hartgerink CHJ, Kemper EM, Hollmann MW and ter Riet G. Analyzing DECREASE trials to estimate evidence of data manipulation [version 1; peer review: 1 approved, 1 approved with reservations]. F1000Research 2017, 6:1995 (https://doi.org/10.12688/f1000research.12584.1) First published: 13 Nov 2017, 6:1995 (https://doi.org/10.12688/f1000research.12584.1) Latest published: 13 Nov 2017, 6:1995 (https://doi.org/10.12688/f1000research.12584.1)

Introduction

The effect of beta-blockers on perioperative mortality in non-cardiac surgery has been controversial¹ due to concerns regarding the scientific integrity in two related clinical trials^2–6. Three meta-analyses that included the trials subject to concerns concluded that beta-blockers decrease perioperative mortality^7–9, whereas a meta-analysis that excluded the suspect trials concluded that beta-blockers increase perioperative mortality⁹. In these studies, perioperative mortality was defined as the death rate of patients in the perioperative setting, including the period of admission, anaesthesia with surgery, and postoperative recovery.

The trials subject to concerns regarding scientific integrity were the Dutch DECREASE-I and DECREASE-IV trials^4–6. The committees that investigated the integrity of the DECREASE trials reported that data manipulation was likely, but that the extent of the data manipulation remained unclear^4–6. Moreover, the latest guidelines still recommend the usage of beta-blockers in the perioperative period in certain cases^10,11, where some of these guidelines are based on other work by the PI of the DECREASE trials. Considering the potential harmful consequences of guidelines based on work by someone who has been repeatedly investigated for breaching scientific integrity, we aim to estimate the extent of data manipulation in the DECREASE studies^2–6 to further stimulate the debate on using beta-blockers in the perioperative period for patients undergoing non-cardiac surgery.

The reports on the integrity of the DECREASE trials primarily focused on the provenance of the raw data but did not investigate the extent to which the DECREASE trials deviated from comparable trials. Provenance is primarily concerned with the origins of the data, verifying things such as (but not limited to) the informed consent and whether data correspond to patient files. However, the committee reports did not neglect statistical evaluation; according to the report a statistical expert assessed the applicability of forensic statistical methods⁶ to evaluate results of trials separately (i.e., DECREASE-I, DECREASE-IV), although the report lacks details as to how this evaluation took place. The expert concluded that the methods previously applied by him were not applicable for use in this case. Nonetheless, in the present study we compare across trials, which is a method that has previously been used to monitor trial data quality or to test for potential data anomalies^12,13. Moreover, comparing across trials instead of evaluating them separately has previously proven to be effective in detecting data manipulation¹⁴. Comparing the DECREASE trials to other published trials studying the effectiveness of beta-blockers with respect to perioperative mortality could prove informative of the potential extent of the manipulation in the DECREASE trials.

The effectiveness of perioperative beta-blockade is obfuscated by the afflicted DECREASE trials, potentially interacting with the type of beta-blocker and the way that beta-blockers were administered (i.e., dose and duration of treatment). In the randomized trials on beta-blockers, patients were administered various types of beta-blockers (e.g., metroprolol, bisoprolol, atenolol) and in various ways (e.g., intravenously, orally; half an hour before surgery or multiple days before surgery; with or without titration based on heart rate). Factors such as dosage and duration can have an effect on the pharmacological effectiveness with respect to perioperative mortality. Moreover, the highly discrepant results from the DECREASE trials⁹ might partly be caused by such differences¹⁵ and not purely due to data manipulation (given that not all data points can be considered manipulated at this point).

To statistically investigate the evidence for data manipulation in the DECREASE studies^2,3, we took three steps. First, we reproduced the findings from the 2014 meta-analysis by Bouri et al.⁹, which contained sufficient information to estimate the deviation of the DECREASE trials from other published trials on beta-blockers. We also included type of beta-blocker to inspect whether this is predictive of the effect of beta-blockers on perioperative mortality. Second, we evaluated the probability that the DECREASE trials (or more extreme effects) arose from the same effect distribution as the non-DECREASE trials, which are assumed to be the true effect of beta-blockers on perioperative mortality in patients undergoing non-cardiac surgery. Third, we estimated how many data points would have to be manipulated in order to reproduce the results of the DECREASE trials if the initial, non-manipulated results arose from the effect estimates as obtained from the non-DECREASE trials. Considering the committees investigating the scientific integrity of the DECREASE trials were unable to assess this, we consider it worthwhile to investigate this further.

Step 1: Reproducing meta-analysis of Bouri et al. (2014)

Methods

To ensure that we used similar analysis procedures as in the 2014 meta-analysis⁹, we initially reproduced Bouri et al.'s estimates. This ensured that (1) their results are reproducible and (2) we are using the correct estimates in subsequent steps of our analyses. Using Figure 2 and Figure 3 from the original paper⁹, we extracted the raw event data for the 2 (control vs experimental) by 2 (event vs no event) design, which we used to recompute the natural logarithm of the risk ratio and its standard error. The extracted event data is available at osf.io/aykeh and our analysis plan was preregistered at osf.io/vnmzc.

We computed the log risk ratio (i.e., log RR) for each study and pooled these using v2.0.0 of the R package metafor¹⁶. We estimated a weighted random-effects model using the restricted maximum-likelihood estimator (i.e., REML)¹⁷ to estimate the variance of effects. We used the default weighting procedure in the metafor package. We added 0.5 to each cell count, as is common in meta-analyses on risk- and odds ratios in order to prevent computational artefacts¹⁸. The 2014 meta-analysis⁹ did not specify the variance estimate used; hence, (minor) discrepancies between our estimates and the original estimates could be due to differences in the estimation procedure.

Results

We were able to closely reproduce the estimates for the different sets of studies (Figure 2 of the 2014 meta-analysis⁹). Bouri et al. differentiated between the estimates from the non-DECREASE trials (k = 9) and the DECREASE trials (k = 2). We confirmed the effect size estimates and the variance estimates for both the non-DECREASE and the DECREASE trials, except for some discrepancies at the second decimal level for the estimated effect sizes and a somewhat larger difference between the variance estimates of the DECREASE studies. Table 1 depicts the original and reproduced values for both sets of studies.

Table 1. The original- and reproduced meta-analytic results based on the data provided in the 2014 meta-analysis by Bouri et al.⁹.

		Risk ratio	RR Confidence interval	τ²
Non-DECREASE (k=9)	Original	1.27	[1.01; 1.60]	0
	Reproduced	1.27	[1.01; 1.61]	0
DECREASE (k=2)	Original	0.42	[0.15; 1.23]	0.29
	Reproduced	0.47	[0.19; 1.15]	0.14

Second, we meta-analyzed all studies combined, including a dummy predictor for the DECREASE and non-DECREASE studies to reproduce results presented in Figure 4 of the 2014 meta-analysis⁹. Our results showed a bit more evidence against equal subgroups than the original meta-analysis⁹ (original: χ²(1) = 3.91, p = .05; reproduced: χ²(1) = 6.12, p = 0.013). Additionally, the original analyses showed substantial residual heterogeneity (I² = 74.4%), whereas we found no residual heterogeneity (I² = 0%). Different variance estimates (e.g., DerSimonian-Laird instead of REML) did not resolve this difference. We tried to clarify these discrepancies by e-mailing the original authors (including a reminder after several weeks), but did not receive a response. Nonetheless, the broad strokes of the meta-regression confirmed that the DECREASE trials were the determining predictor for the effectiveness of beta-blockers (including DECREASE: RR = 0.509; excluding DECREASE: RR = 1.275).

Additionally, and exploratively, we evaluated the predictive effect of the type of beta-blocker used in the trials. Descriptively, the DECREASE trials remained predictive of decreased mortality (RR = 0.509), whereas the non-DECREASE trials provide tentative evidence that atenolol results in lower mortality (RR = 0.777). Nonetheless, for other beta-blockers in the non-DECREASE trials, there is descriptive evidence that beta-blockers could increase mortality (bisoprolol: RR = 2.973; metoprolol: RR = 1.303; propranolol: RR = 1.7). Table 2 shows the meta-regression results in full. We do note that the DECREASE studies only use bisoprolol and any estimates for other beta-blockers are extrapolations.

Table 2. Meta-regression results (k=11) for log(RR), including dummy predictors for DECREASE trials (reference: non-DECREASE trials) and type of beta-blockers used in the trial (reference: atenolol).

	Estimate	95% CI
Intercept	-0.252	-1.228; 0.724
Non-DECREASE	-	-
DECREASE	-1.765	-5.05; 1.519
Atenolol	-	-
Bisoprolol	1.342	-2.015; 4.698
Metoprolol	0.517	-0.49; 1.523
Propranolol	0.783	-1.5; 3.065

Step 2: Evaluating the veracity of DECREASE studies

Based on the effect estimates for the non-DECREASE trials from Step 1, we estimated the probability that the observed effects from the DECREASE studies (or more extreme) occurred naturally. We assumed that the non-DECREASE studies estimated the true effect distribution of perioperative beta-blockade on mortality, not perturbed by publication bias due to statistical (non)significance. Publication bias was assumed to not be a problem because a substantial number of nonsignificant effects are included in the dataset (9 of 11 results are nonsignificant). Based on this effect distribution, we estimated the veracity of the DECREASE trials separately, which is the estimated probability of the observed data (or more extreme) under a given true effect¹⁹.

Method

Based on the estimated effect distribution from the non-DECREASE trials, we calculated the probability of each DECREASE trial result, or a more extreme result. In other words, we computed the two-tailed p-value for the null hypothesis that the DECREASE trials arose from the same effect distribution as the non-DECREASE trials (H₀: $μ_{{\bar{x}}_{1} - {\bar{x}}_{2}}$ = 0). To this end, we applied a Welch t-test²⁰. As means, we used the observed log RR for the DECREASE trials (i.e., DECREASE-I: -1.44; DECREASE-IV: -0.452) and the meta-analyzed log RR for the non-DECREASE trials (i.e., 0.243). As standard deviations, we used the standard error for the DECREASE trials (i.e., DECREASE-I: 0.061; DECREASE-IV: 0.018) and the standard error of the estimated log RR for the non-DECREASE trials (i.e., 0.002). We initially preregistered that the DECREASE trials would be regarded as fixed in the computation of the veracity, which was erroneous because these also have their own standard error; hence, we applied the Welch test to take into account the uncertainty in the estimates of both the DECREASE and non-DECREASE trials.

Results

Results indicate that the DECREASE trials are highly unlikely under the estimated effect distribution from the non-DECREASE trials. More specifically, the results from DECREASE-I (or more extreme) have a probability of approximately 1 in 10 000 (t(8) = –6.75, p = 0.000145) and the results from DECREASE-IV (or more extreme) have a probability of approximately 1 in 1000 (t(8) = –4.996, p = 0.0010587). This indicates that the DECREASE trial results are unlikely to have come from the same population effect distribution as the non-DECREASE trials. Moreover, observing two of such extremely unlikely results jointly, as in the DECREASE trials, would occur in only 2 out of 10 million sets of two trials (i.e., 0.0000002) according to this model. Hence, this result indicates that the DECREASE trials are severely different from the non-DECREASE trials.

Results from Step 1 indicated that no between-trial variance (i.e., homogeneity; τ² = 0) of the effects was observed; given the small number of trials included (i.e., 9), however, this estimate is highly uncertain. The total N across the non-DECREASE trials was 10529. We conducted sensitivity analyses to see how dependent results are on the heterogeneity estimate (not preregistered; osf.io/vnmzc). Fixing the variance estimate τ² to .5, indicates that the probability of observing the DECREASE trials jointly is approximately 1.2 out of 100 000 (see Figure 1). To put these numbers into context, a variance of 0.25 would suggest that results of perioperative beta-blockade vary substantially due to contextual circumstances of the study, even if perioperative beta-blockade has no effect whatsoever (RRs between 0.779 and 1.284 in ~64% of the cases).

Figure 1. Sensitivity analyses for the p-value that indicates the probability of observing the results from the DECREASE studies, or more extreme results, based on the estimated true effect (non-DECREASE trials) and the accompanying variance estimate.

Step 3: Estimating the amount of manipulated data

We estimated the number of data points that would need to be manipulated to arrive at the estimates from the DECREASE trials, given that the non-DECREASE trials represent the true effect of perioperative beta-blockade. In contrast to Step 2, which assumes no data manipulation occurred and that the DECREASE trials occurred naturally from the same effect distribution as the non-DECREASE trials, Step 3 assumes that the DECREASE trials might in fact contain manipulated data. The estimates from Step 3 provide an indication of the extent of potential data manipulation in the DECREASE studies^4–6,9.

Method

In order to estimate the number of manipulated data points, we first estimated the probability of perioperative mortality (in log odds) in each trial arm for each trail stratum. As such, we estimate mortality odds four times: once per condition (beta-blocker or control) per trial stratum (DECREASE- and non-DECREASE trials). For all four combinations of condition and trial type, we ran a meta-analysis applying similar methods used in Step 1, resulting in four meta-analytic absolute mortality estimates with corresponding effect variances. Throughout the simulations, we used the point estimates (i.e., fixed effect) to simulate genuine and manipulated data, but supplemented this by using distribution estimates (i.e., random effects) as sensitivity analyses.

We applied the inversion method to estimate the number of manipulated data points in the DECREASE trials²¹. We assumed that if data are manipulated, each data point is manipulated in the same way and to the same extent. The inversion method iteratively hypothesizes that X out of N data points were manipulated (i.e., X = 0,1,..., N), assuming they were manipulated in the same way. For each combination of X and trial, we simulated 10000 datasets. Each simulated dataset contained X manipulated data points and N-X genuine data points. For each simulated dataset (exact simulation procedure in the next paragraph), we determined the likelihood of the results with

L = π_{E}^{n_{11}} {(1 - π_{E})}^{n_{12}} \times π_{C}^{n_{21}} {(1 - π_{C})}^{n_{22}}

where π_{_E} indicates the mortality rate in the beta-blocker condition as drawn from the meta-analytic effect distribution (π_{_C} indicates the mortality rate in the control condition). We estimated those parameters using the meta-analytic procedure described in the previous paragraph, resulting in the estimates depicted in Table 3. The likelihood was computed under both the manipulated effect estimates (i.e., L_{_manipulated}) and the genuine data (i.e., L_{_genuine}). Table 4 indicates which cell sizes the various n_XX refer to within the (simulated) data. After computing the likelihoods, we compared them to determine whether the simulated data were more likely to arise from the genuine trials (L_{_genuine} > L_{_manipulated}) or from the manipulated trials (L_{_manipulated} > L_{_genuine}). Note that comparing the likelihoods is a minor deviation from the preregistration, where we initially planned on using p-value comparisons (osf.io/vnmzc).

Table 3. Mortality estimates per condition, per trial stratum.

We used these parameters to estimate the number of manipulated data points with the inversion method.

		log(odds)	τ
DECREASE (k=2)	Beta-blocker	-3.629	0.588
	Control	-2.498	1.644
Non-DECREASE (k=9)	Beta-blocker	-3.034	0.712
	Control	-3.208	1.001

Table 4. Outcome possibilities within a simulated 2 (beta-blocker v control) by 2 (dead v alive) clinical trial.

	Dead	Alive
Beta-blockers	n₁₁	n₁₂
Control	n₂₁	n₂₂

For each hypothesis of X out of N manipulated data points, we computed the probability that the manipulated data are more likely than the genuine data (p_{_M} = P(L_{_manipulated} > L_{_genuine})). Based on p_{_M}, we computed the confidence interval for the estimated X manipulated data points (i.e., X_LB; X_UB). For a 95% confidence interval, the lower bound is equal to the p_{_M} closest to .025, whereas the upperbound is equal to the p_{_M} closest to .975.

We computed p_{_M} for all X out of N manipulated data points in 10000 randomly generated datasets, which were generated in three steps. For each dataset we:

1. Sampled (across conditions, without replacement) X fictitious participants that would be the result of data manipulation.

2. Determined the population mortality rate for each condition (i.e., for each cell based on the estimates from Table 3). The meta-analytic point estimate was used or a population effect was randomly drawn from the meta-analytic effect distribution.

3. Simulated the number of deaths for the different conditions using a binomial distribution based on the mortality rate as determined in 2, resulting in the cell counts as in Table 4.

Based on the meta-analytic effect from 2 and the cell sizes from 3, we computed the likelihoods L_{_manipulated} and L_{_genuine} using Equation 1. As mentioned before, we computed p_{_M}, which indicates the probability that the data are more likely under the estimates resulting from the (allegedly) manipulated data (i.e., the DECREASE trials) than under the estimates resulting from the genuine data (i.e., the non-DECREASE trials; p_{_M} = P(L_{_manipulated} > L_{_genuine})).

Results

For DECREASE-I (N = 112), the 95% confidence interval for the estimated number of manipulated data points is [0 – 112] or [0 – 112] when based on a point estimate or a more uncertain distribution estimate, respectively. The left column of Figure 2 depicts the p_{_M} per X manipulated data points (top panel) and the bounds of the confidence interval when the degree of confidence is altered (lower panel). Staying clearly between the dotted lines in the top panel, depicting the 95% CI (top: .975; bottom: .025), it becomes apparent that the degree of uncertainty is too high to make any reasonable estimates about the number of manipulated data points with sufficient confidence. This is partly due to the small sample size of the DECREASE-I trial (i.e., N = 112) and the availability of just the summary results. Only when the degree of confidence is lowered to around 75% does the interval not span the entire sample size. As such, based on the summary results, little can be said about the extent of the data manipulation that occurred in the DECREASE-I trial, affirming the conclusions of the original committee report⁶.

Figure 2. Inversion method results used to estimate the number of data points manipulated in the DECREASE-I and DECREASE-IV trials.

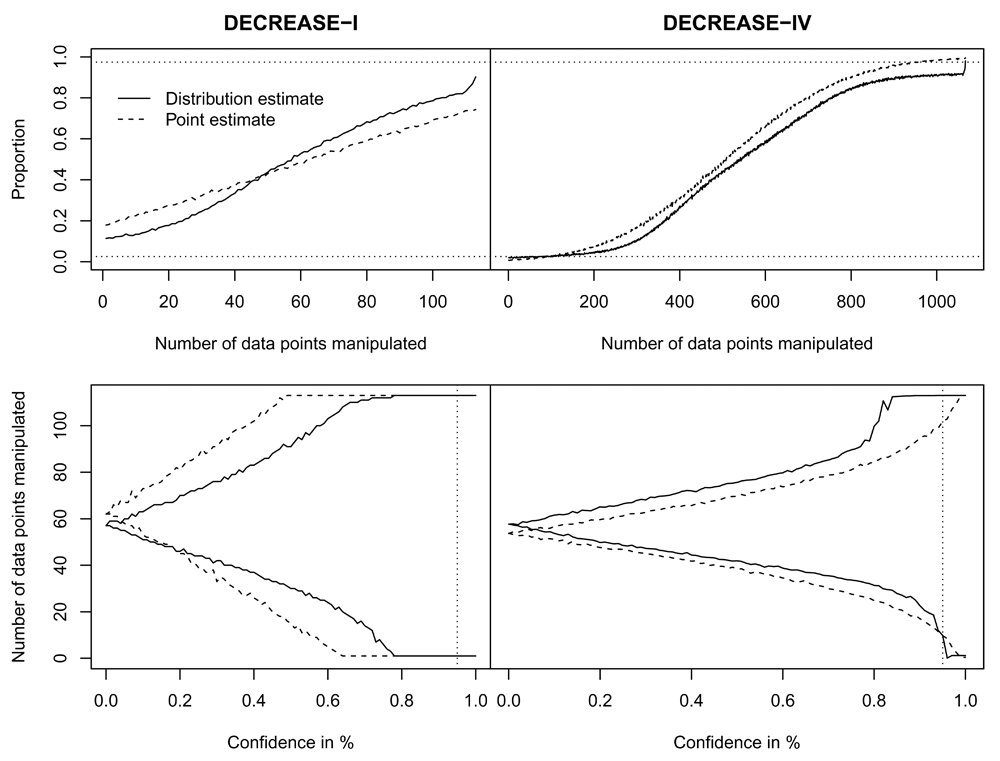
The top row panels indicate p_{_M} (y-axis) for all X out of N manipulated data points (x-axis). The bottom row indicates the estimated interval of manipulated data points (y-axis) when varying the degree of confidence (x-axis). Dotted lines indicate the bounds for a 95 percent CI. The online version of this figure is interactive.

For DECREASE-IV (N = 1066), the 95% confidence interval for the estimated number of manipulated data points is [3 – 1066] or [10 – 1066] when based on a point estimate or a more uncertain distribution estimate, respectively. The relatively minor difference between the estimates indicates that there is a high degree of confidence that data manipulation did occur based on the difference of the trial results alone. Nonetheless, the range of potentially manipulated data points is still estimated at approximately 1000; this indicates that the summary results are insufficient to provide more than an estimated lower bound. This indicates that it is possible not all data were manipulated (i.e., N = 1066), but at least some were, increasing the importance of well-documented data provenance to discern between genuine and falsified data.

Discussion

The effect of beta-blockade on perioperative mortality was already unclear based on the investigations regarding scientific integrity; our results strongly affirm that the empirical evidence from the DECREASE trials is highly discrepant from other trials supposedly studying the same effect (i.e., the effectiveness of beta-blockers in decreasing perioperative mortality). Our results indicate that the results from the DECREASE trials are nearly impossible to have arisen from the same effect inspected by the non-DECREASE trials, except when we assume at least some of the data were manipulated. As such, the scientific validity of the DECREASE-I and DECREASE-IV trials should be regarded as highly problematic and untrustworthy when assessing the effectiveness of beta-blockade on perioperative mortality if they truly investigate the same effects as the non-DECREASE trials, as is often assumed⁹. Nonetheless, the original papers that presented these trial results are not yet retracted^2,3, despite the integrity reports^4–6.

Our approach to estimating the number of manipulated data points has one major limitation that we would like to highlight: multiplicity. For each estimated proportion of manipulated data points, there is another smaller (or larger) proportion with more (or less) extremely manipulated data points. This problem is similar to how various samples can give rise to the same mean, but contain vastly different individual scores within them (e.g., -2.5 and +2.5 versus -100 and +100; both give the mean zero). Nonetheless, this limitation does still allow us to estimate whether any data manipulation occurred because there is no multiplicity in not manipulating data.

The ESC/ESA and ACC/AHA guidelines^11,22 on perioperative beta-blockade already excluded the DECREASE trials in their assessment, but also explicitly state that other trials by Poldermans are excluded. However, upon close inspection of the reference lists, the ACC/AHA guidelines still cites four trials including Poldermans as author as evidence for the guidelines^2,23–25, of which two were already inspected by the scientific integrity committees of Erasmus MC^2,23. In the ACC/AHA guidelines, the following is said about studies conducted by Poldermans:

"If nonretracted DECREASE publications and/or other derivative studies by Poldermans are relevant to the topic, they can only be cited in the text with a comment about the finding compared with the current recommendation but should not form the basis of that recommendation or be used as a reference for the recommendation."¹¹

Nonetheless, references are made without clear comments. Given the confirmation of problems in the DECREASE-I and DECREASE-IV trials in our results, it stresses that there is reason to distrust trials by Poldermans. For the integrity of the guidelines and the safety of the patients, we pose that investigations should be initiated into works where Poldermans was involved and which were not cleared by the scientific committees of Erasmus MC in their misconduct investigations. In particular those papers cited as evidence in the ACC/AHA guidelines should be investigated, considering that they affect patients and their treatment directly.

Previously, further investigation of trials by Poldermans was deemed unfeasible due to the lack of raw data; here we indicate methods that do make it feasible. Based on just event-count data and trials that supposedly investigate the same effect, we were able to estimate whether part of the data were in fact manipulated and whether the results were within reason of trials investigating the same effect. The results clearly indicated they were not within such reason.

The results of our analyses also highlight that, despite the lack of raw data availability, summary results from larger samples allow for more precise estimates of the number of manipulated data points when similar trials are available. Moreover, larger trials result in relatively more certainty (e.g., DECREASE-IV) about the estimated number of manipulated data points, when using the inversion method, compared to smaller trials (e.g., DECREASE-I). This increased certainty is due to decreased standard errors of the estimated effects, resulting in higher sensitivity to data anomalies. Nonetheless, much residual uncertainty remains and simply less information is available in summary results when compared to raw data. As such, raw data availability would improve the options open to detect potential anomalies (note: raw data are available for DECREASE VI, but upon a freedom of information request by the first author, Erasmus MC refused to share these data; see osf.io/zv953/ for original Dutch correspondence). The results also highlight that in order to prevent detection, it would be in the manipulator's interest to fabricate small and imprecise studies (assuming the manipulator wants to remain undetected), which ultimately detracts from the scientific value of such a study and hence the individual reward for manipulation through reduced impact (hopefully).

With respect to clinical practice, the results provide some tentative evidence that type of beta-blockade can severely influence perioperative mortality. Our reanalysis of the Bouri et al.⁹ data indicates that type of beta-blockade can reverse the effect on perioperative mortality, even after taking into account whether a study belongs to the DECREASE family. As such, atenolol seems to tentatively decrease perioperative mortality, whereas the others (metoprolol, propranolol, bisoprolol) increase perioperative mortality. However, there seems to be covariation with respect to treatment administration, duration, and dose, which further confounds whether the treatment effect is due to type of beta-blocker or due to one of these other parameters. There are too few studies (k = 11) to properly discern the various treatments from each other, requiring a new randomized trial with high statistical power to determine moderating factors (if any). This affirms the statement from the ESC/ESA guidelines that "high priority needs to be given to new randomized clinical trials to better identify which patients derive benefit from beta-blocker therapy in the perioperative setting, and to determine the optimal method of beta-blockade"²².

Moreover, the DECREASE and non-DECREASE trials seem to apply beta-blockade from different conceptual viewpoints that could confound the effectiveness of beta-blockade. The non-DECREASE trials seem to focus purely on the application of beta-blockers in itself, whereas the DECREASE trials use beta-blockade as a proxy to decrease resting heart rate^2,3. As such, the DECREASE studies applied beta-blockade at least a week in advance, specifically in order to lower patient's resting heart rate to <70BPM and potentially habituate the patient to the effects of the beta-blockade. Other studies apply the beta-blockade just prior to the surgery (maximum: one day prior), and therefore seem to regard the treatment specifically and not the proxy of lowered BPM. As such, the differences between the DECREASE and non-DECREASE trials might also in part be a consequence of the different approaches in the various trials. Whether these differences matter in treatment decisions is worthy of further research in a clinical trial with high statistical power to find such differences.

In summary, our research indicates that the DECREASE trials are nearly impossible if we assume they investigate exactly the same effect as the non-DECREASE trials and, under that assumption, our results provide some evidence that at least some data points were manipulated. However, these differences might also be due to different conceptual approaches as to how beta-blockade might prevent mortality in non-cardiac surgery. We recommend renewed investigations into Poldermans’ work given these findings — especially those works still referenced by guidelines on the use of beta-blockers without proper notice. Moreover, it remains unclear whether beta-blockers might be effective in preventing mortality rates in non-cardiac surgery patients. Considering this, we recommend new and more extensively controlled, confirmatory trials to determine whether there is any use in administering beta-blockers in order to decrease perioperative mortality — at the moment there is insufficient evidence to determine any positive effect of beta-blockers on mortality rates.

Data availability

All manuscript materials are available at https://github.com/chartgerink/2015poldermans and are preserved at Zenodo (doi.org/10.5281/zenodo.845354²⁶).

Competing interests

The authors declare no competing interests.

Grant information

CHJH was funded by the Office of Research Integrity during part of this project (HHS-ORI; ORIIR160019).

The funders had no role in study design, data collection and analysis, decision to publish, or preparation of the manuscript.

Supplementary material

Supplementary File 1: Session info.

Click here to access the data.

Faculty Opinions recommended

References

1. Cole GD, Francis DP: Perioperative β blockade: guidelines do not reflect the problems with the evidence from the DECREASE trials. BMJ. 2014; 349: g5210. PubMed Abstract | Publisher Full Text
2. Poldermans D, Boersma E, Bax JJ, et al.: The effect of bisoprolol on perioperative mortality and myocardial infarction in high-risk patients undergoing vascular surgery. Dutch Echocardiographic Cardiac Risk Evaluation Applying Stress Echocardiography Study Group. N Engl J Med. 1999; 341(24): 1789–1794. PubMed Abstract | Publisher Full Text
3. Dunkelgrun M, Boersma E, Schouten O, et al.: Bisoprolol and fluvastatin for the reduction of perioperative cardiac mortality and myocardial infarction in intermediate-risk patients undergoing noncardiovascular surgery: A randomized controlled trial (DECREASE-IV). Ann Surg. 2009; 249(6): 921–926. PubMed Abstract | Publisher Full Text
4. Onderzoekscommissie Wetenschappelijke Integriteit: Onderzoek Naar Mogelijke Schending van de Wetenschappelijke Integriteit: Beknopte Versie. Erasmus MC; 2011. Reference Source
5. Commissie Vervolgonderzoek 2012: Rapport Vervolgonderzoek Naar Mogelijke Schending van de Wetenschappelijke Integriteit. Erasmus MC; 2012. Reference Source
6. Commissie Vervolgonderzoek Wetenschappelijke Integriteit 2013: Rapport. Erasmus MC; 2014. Reference Source
7. Devereaux PJ, Beattie WS, Choi PT, et al.: How strong is the evidence for the use of perioperative beta blockers in non-cardiac surgery? Systematic review and meta-analysis of randomised controlled trials. BMJ. 2005; 331(7512): 313–321. PubMed Abstract | Publisher Full Text | Free Full Text
8. Angeli F, Verdecchia P, Karthikeyan G, et al.: ß-Blockers reduce mortality in patients undergoing high-risk non-cardiac surgery. Am J Cardiovasc Drugs. 2010; 10(4): 247–259. PubMed Abstract | Publisher Full Text
9. Bouri S, Shun-Shin MJ, Cole GD, et al.: Meta-analysis of secure randomised controlled trials of β-blockade to prevent perioperative death in non-cardiac surgery. Heart. 2014; 100(6): 456–464. PubMed Abstract | Publisher Full Text | Free Full Text
10. ESC/ESA: Guidelines on non-cardiac surgery: Cardiovascular assessment and management. Eur Heart J. 2014; 35: 2383–2243. Reference Source
11. Fleisher LA, Fleischmann KE, Auerbach AD, et al.: 2014 ACC/AHA guideline on perioperative cardiovascular evaluation and management of patients undergoing noncardiac surgery: executive summary: a report of the American College of Cardiology/American Heart Association Task Force on Practice Guidelines. Circulation. 2014; 130(24): 2215–2245. PubMed Abstract | Publisher Full Text
12. Buyse M, George SL, Evans S, et al.: The role of biostatistics in the prevention, detection and treatment of fraud in clinical trials. Stat Med. 1999; 18(24): 3435–3451. PubMed Abstract | Publisher Full Text
13. Carlisle JB: Data fabrication and other reasons for non-random sampling in 5087 randomised, controlled trials in anaesthetic and general medical journals. Anaesthesia. 2017; 72(8): 944–952. PubMed Abstract | Publisher Full Text
14. Knepper D, Lindblad AS, Sharma G, et al.: Statistical monitoring in clinical trials: Best practices for detecting data anomalies suggestive of fabrication or misconduct. Ther Innov Regul Sci. 2016; 50(2): 144–154. Publisher Full Text
15. van Klei WA: [Which is the preferred perioperative beta-blocker?]. Ned Tijdschr Geneeskd. 2015; 159: A9798. PubMed Abstract
16. Viechtbauer W: Conducting meta-analyses in R with the metafor package. J Stat Softw. 2010; 36(3): 1–48. Publisher Full Text
17. Viechtbauer W: Bias and efficiency of meta-analytic variance estimators in the Random-Effects model. J Educ Behav Stat. 2005; 30(3): 261–293. Publisher Full Text
18. Agresti A: Categorical Data Analysis. Hoboken NJ: John Wiley & Sons Inc.; 2002. Reference Source
19. Peters CFW, Klaassen CAJ, van de Wiel MA: Evaluating the Scientific Veracity of Publications by Dr. Jens Forster. University of Amsterdam; 2015. Reference Source
20. Welch BL: The generalisation of student’s problems when several different population variances are involved. Biometrika. 1947; 34(1–2): 28–35. PubMed Abstract | Publisher Full Text
21. Casella G, Berger RL: Statistical Interference. Pacific Grove, CA:Duxbury; 2002. Reference Source
22. Kristensen SD, Knuuti J, Saraste A, et al.: 2014 ESC/ESA Guidelines on non-cardiac surgery: cardiovascular assessment and management: The Joint Task Force on non-cardiac surgery: cardiovascular assessment and management of the European Society of Cardiology (ESC) and the European Society of Anaesthesiology (ESA). Eur J Anaesthesiol. 2014; 31(10): 517–573. PubMed Abstract | Publisher Full Text
23. Boersma E, Poldermans D, Bax JJ, et al.: Predictors of cardiac events after major vascular surgery: Role of clinical characteristics, dobutamine echocardiography, and beta-blocker therapy. JAMA. 2001; 285(14): 1865–73. PubMed Abstract | Publisher Full Text
24. van Kuijk JP, Flu WJ, Schouten O, et al.: Timing of noncardiac surgery after coronary artery stenting with bare metal or drug-eluting stents. Am J Cardiol. 2009; 104(9): 1229–1234. PubMed Abstract | Publisher Full Text
25. Flu WJ, van Kuijk JP, Chonchol M, et al.: Timing of pre-operative Beta-blocker treatment in vascular surgery patients: influence on post-operative outcome. J Am Coll Cardiol. 2010; 56(23): 1922–1929. PubMed Abstract | Publisher Full Text
26. Hartgerink C: chartgerink/2015poldermans: Zenodo DOI creation. Zenodo. 2017. Data Source

Comments on this article Comments (0)

Version 1

VERSION 1 PUBLISHED 13 Nov 2017

Author details Author details

¹ Department of Methods and Statistics, Tilburg University, Tillburg, 5037AB, The Netherlands
² Department of Pharmacy, Amsterdam Medisch Centrum (AMC), Amsterdam, 1105AZ, The Netherlands
³ Department of General Practice/Family Medicine, Amsterdam Medisch Centrum (AMC), Amsterdam, 1105AZ, The Netherlands
⁴ Department of Anesthesiology, Amsterdam Medisch Centrum (AMC), Amsterdam, 1105AZ, The Netherlands

Chris H.J. Hartgerink
Roles: Conceptualization, Data Curation, Formal Analysis, Investigation, Methodology, Project Administration, Resources, Software, Visualization, Writing – Original Draft Preparation, Writing – Review & Editing

E.M. Kemper
Roles: Conceptualization, Writing – Original Draft Preparation, Writing – Review & Editing

Markus W. Hollmann
Roles: Writing – Review & Editing

Gerben ter Riet
Roles: Conceptualization, Writing – Original Draft Preparation, Writing – Review & Editing

Competing interests

No competing interests were disclosed.

Grant information

CHJH was funded by the Office of Research Integrity during part of this project (HHS-ORI; ORIIR160019).
The funders had no role in study design, data collection and analysis, decision to publish, or preparation of the manuscript.

Article Versions (1)

version 1

Published: 13 Nov 2017, 6:1995

https://doi.org/10.12688/f1000research.12584.1

Copyright

This is an open access article, made available under the Creative Commons Public Domain Dedication. This work may be copied, modified, distributed and performed, even for commercial purposes, all without asking permission.

Download

Export To

metrics

	Views	Downloads
F1000Research	-	-
PubMed Central Data from PMC are received and updated monthly.	-	-

Citations

0

SEE MORE DETAILS

CITE

how to cite this article

Hartgerink CHJ, Kemper EM, Hollmann MW and ter Riet G. Analyzing DECREASE trials to estimate evidence of data manipulation [version 1; peer review: 1 approved, 1 approved with reservations]. F1000Research 2017, 6:1995 (https://doi.org/10.12688/f1000research.12584.1)

NOTE: If applicable, it is important to ensure the information in square brackets after the title is included in all citations of this article.

track

receive updates on this article

Track an article to receive email alerts on any updates to this article.

Open Peer Review

Version 1

VERSION 1

PUBLISHED 13 Nov 2017

Views

22

Reviewer Report 14 Jun 2018

Stephen Senn, Statistical Consultant, Edinburgh, UK

Approved

https://doi.org/10.5256/f1000research.13628.r34206

An initial observation as regards my review is that I am unfamiliar with the background to this story and I have reviewed this paper only. The authors make a number of claims regarding facts that could probably be checked by ... Continue reading

An initial observation as regards my review is that I am unfamiliar with the background to this story and I have reviewed this paper only. The authors make a number of claims regarding facts that could probably be checked by reading some of the references. I have not done this. My comments are limited to the internal logic of the paper only.

Whether or not one agrees with the conclusions, this is an interesting investigation. I have some reservations as regards emphasis in the conclusions, which I shall explain in due course, but first I shall explain why statisticians with my background may have a slightly different point of view to the authors.

Since the time in which I worked in the pharmaceutical industry (1987-1995), I have been interested in drug regulatory science. An attitude that (rightly or wrongly) is accepted as being the norm in both sides of the regularity divide is that evidence of efficacy for one drug in a class cannot (usually) be used as evidence of efficacy of another. In fact, so strong is this point of view that when it is sought to use the proof of efficacy of one formulation for another, proof of equivalence is required. Thus, not only is it the case that different molecules cannot be regarded as having the same efficacy, this carries over to doses and formulations. Some, no doubt, will see this as a conspiracy to inhibit generic competition. However, during my own time in drug development I twice worked on alternative formulations (that is to say developed by the innovator company) that had to be abandoned. In one case a clinical trial of the new formulation revealed it had one quarter the potency of the existing formulation¹.

This ‘no pooling of products’ attitude also holds for ‘proving’ safety. For different formulation ‘proof’ of equivalence would be required and for different molecules usually a whole new programme. (Biosimilars might be a controversial exception.) However, regulators do generally consider that observed safety problems in one molecule in a class create a potential concern. The FDA’s attitude as regards development of treatments in diabetes, partly as a response to Nissen and Wolski’s meta-analysis of rosiglitazone, is a case in point².

Thus, there is a general aversion in drug-development and regulation, not necessarily shared by the evidence-based medicine movement, to pooling different molecules in a meta-analysis. Nevertheless, I consider that such pooling is legitimate for one purpose, namely that of testing the hypothesis that no drug in among those pooled has the effect being studied. If this is adopted as a null hypothesis and a fixed effect analysis suggests the null hypothesis should be rejected, then the hypothesis to assert becomes the hypothesis that at least one drug in the class has an effect. (See my paper on overstating evidence³ p3. ) Further investigations are then necessary to determine what the practical implications of this are, but asserting the alternative hypothesis that all drugs have an effect is clearly not warranted.

In fact, I can put it cynically like this. We seem to live in an era in which everyone believes in personalised medicine (thus in patient by treatment interaction) but we are unconcerned about the differences between the main effects of treatment.

However, a further consequence of my time in the pharmaceutical industry, is that I share a general mistrust of investigator led-trials (with some notable exceptions). The fact that previously, raw data from pharmaceutical trials were not shared with the wider public, has been the subject of much criticism. Nevertheless, such trials were examined by the regulator and this, in my opinion, has done much to improve the quality of pharmaceutical industry trials. Without such external scrutiny the danger is that independent trials may suffer in quality.

I now come to my specific comments.

It is clear from the authors’ paper that in the meta-analysis different drugs are pooled. This implies that one explanation that should not be dismissed on the basis of the statistical analysis alone, is that the effects vary from treatment to treatment in the class. To be fair to the authors, they do discuss this in more than one place but I feel that they do not appreciate fully the reservations that apply generally to pooling drugs. Again, to be fair, they do provide the extremely helpful table 2, which provides an analysis by table. It would be nice to see, just to complete the picture, if there is a connected network, what a network meta-analysis would show. (If there is not a connected network then this must be that the problem with the different experimental treatments also applies to the controls.) For example, this would permit formal comparison of different drugs. Again, it should be noted that the authors do include what might be regarded as a sort of network analysis, however, all other treatments are lumped together and this suffers from a problem discussed in point 4 below. I am not suggesting that the authors need to do this analysis (it could a be task for future work), I am just suggesting that the fact that this has not been done is a limitation that needs to be reflected in the discussion.
By the same token, this means that it would be highly debatable anyway, irrespective of any particular doubts about the reliability of the DECREASE I & IV trials, to use these as proof of efficacy of beta-blockade generally. Again, to be fair to the authors, they do suggest that more trials are needed.
However, if the data from the DECREASE I & IV trials have not been audited, then in my opinion nobody is obliged to accept the results anyway. Checkability is the standard by which claims should be judged.
I have some reservations regarding the use of the one degree of freedom chi-square tests in step 1. It should be appreciated that the analysis is one that is strictly speaking only valid if pre-specified without any access to results. It is not an analysis that is valid when comparing observed extreme results with others⁴.
I did not understand the argument in the last paragraph of Step 3. This is probably just due to my being obtuse. The robustness of the results and the implication of the results, if true, seemed to me to get mixed up.

However, these comments do not alter my opinion that this is an interesting paper.

Is the work clearly and accurately presented and does it cite the current literature?

Yes
Is the study design appropriate and is the work technically sound?

Yes
Are sufficient details of methods and analysis provided to allow replication by others?

Yes
If applicable, is the statistical analysis and its interpretation appropriate?

Partly
Are all the source data underlying the results available to ensure full reproducibility?

Yes
Are the conclusions drawn adequately supported by the results?

Partly

References

1. Senn S, Lillienthal J, Patalano F, Till D: An incomplete blocks cross-over in asthma: a case study in collaboration, Cross-over Clinical Trials. Fischer: Stuttgart. 1997. 3-26
2. Nissen SE, Wolski K: Effect of rosiglitazone on the risk of myocardial infarction and death from cardiovascular causes.N Engl J Med. 2007; 356 (24): 2457-71 PubMed Abstract | Publisher Full Text
3. Senn SJ: Overstating the evidence: double counting in meta-analysis and related problems.BMC Med Res Methodol. 2009; 9: 10 PubMed Abstract | Publisher Full Text
4. Senn S, Harrell F: On Wisdom after the Event. J Clin Epidemiol. 1997; 50 (7): 749-751

Competing Interests: I have no competing interests that I am aware of. However, I maintain a full declaration here: http://www.senns.demon.co.uk/Declaration_Interest.htm

Reviewer Expertise: Statistical methods in drug development

I confirm that I have read this submission and believe that I have an appropriate level of expertise to confirm that it is of an acceptable scientific standard.

CITE

Report a concern

Respond or Comment

Views

35

Reviewer Report 20 Feb 2018

Bob Siegerink, Center for Stroke Research Berlin (CSB), Charité Universitätsmedizin Berlin, Berlin, Germany

Sean Kelley, Center for Stroke Research Berlin (CSB), Charité Universitätsmedizin Berlin, Berlin, Germany

Approved with Reservations

https://doi.org/10.5256/f1000research.13628.r30658

The paper by Hartgerink et al. sought to determine whether or not there is evidence for data manipulation in the DECREASE-I and Decrease-IV trials. First, the authors reproduced the results of a previous meta-analysis from Bouri et al., using raw ... Continue reading

The paper by Hartgerink et al. sought to determine whether or not there is evidence for data manipulation in the DECREASE-I and Decrease-IV trials. First, the authors reproduced the results of a previous meta-analysis from Bouri et al., using raw event data to calculate the ln(relative risk) and its standard error. Next, they modeled the probability that the results from the DECREASE trials could have occurred from the effect distribution of the non-DECREASE trials. Finally, by creating simulated datasets that were subsequently manipulated they determined the probability that the likelihood of the manipulated data (DECREASE meta-analytic effect distribution) is larger than the likelihood of the genuine data (non-DECREASE meta-analytic effect distribution).

Even though the motivating case for the paper is the questioned reliability of the data within the DECREASE trials that tries to answer a very concrete clinical question (should we use perioperatively use beta blockers to reduce mortality?), the paper ultimately tries to answer a question that is much broader: can we use forensics statistics even when individual data records are not available. In our opinion, the authors succeeded in part to answer that underlying question.

General Comments:

Some circular reasoning in step 2, In step 2 the authors provide clear evidence that the results of the DECREASE trials are quite unlikely, however, they employ some circular reasoning in their argumentation. Because we know the DECREASE values are extreme, when a p-value is calculated for the DECREASE effect is calculated based off of the non-DECREASE effect distribution it will of course be very small. The results of this approach are methodically sound but suffer from circular reasoning and do not seem to add much to the goal of determining whether data manipulation occurred. Although this step might be useful to help ease the reader into the following steps, the limited added value of these analyses should be recognized.
Robustness of approach In Step 3, the combination of adding simulated datasets with a likelihood calculation is an interesting approach to try to determine data manipulation when only summary statistics are available. In the second paragraph of the methods, when describing the inversion method, the authors say “We assumed that if data are manipulated, each data point is manipulated in the same way and to the same extent.” We have a feeling that this is a very strong assumption that is likely not to hold true and might drive the results. An exploration of the robustness, in text or analyses, could help strengthen the argument for the approach the authors apply. Additionally, since the DECREASE-IV trials have approximately 10x the sample size as DECREASE-I we expected a reduction in the confidence interval, yet the confidence interval still spans almost the entire range. Further deliberations on this phenomenon would help the reader understand the robustness of the applied technique.
Interpretation of results. In general, the results show that the data simulation does not give a lot of precision when it comes to pinpointing the number of manipulated datapoints. In some sense, and as also described by the authors, this is also not needed as the lower boundary of the confidence interval of manipulated datapoints should always include 0. In fact, the authors claim that “there is a high degree of confidence that data manipulation did occur based on the difference of the trial results alone”. We do follow that reasoning, but do not fully understand why the authors adhere so much to the difference between the results of the two trials. There does not seem to be a material difference in the 95% confidence intervals between DECREASE-I and DECREASE-IV since in both cases the confidence interval spans essentially the entire range of possible outcomes. Nonetheless, the authors seem to put a lot more emphasis on the analyses of DECREASE IV with its higher sample size, in part because the results show that the lower boundary of the confidence interval does not span the 0 but ranges from 3-1066 or 10-1066, depending on the method used. Given the unknown robustness of this approach, we wonder whether the implied relevance of the small difference between the results of the DECREASE I and DECREASE IV is justified.
Conclusion. In the discussion section, we take issue with the sentence beginning “Our results indicate that the results from the DECREASE trials ... at least some of the data were manipulated”. The word manipulated implies an intention to manipulate data, yet there are numerous ways for data to become incorrectly classified without overt and intended manipulation. Although the authors show it is likely that something altered the data, we believe that strong claims about the provenance of that change based on the analyses provided in this paper should be avoided. However, we agree with the authors that DECREASE I and DECREASE IV should be regarded as "highly problematic and untrustworthy when assessing the effect of beta blockade in perioperative mortality", but that is only when we place the results from this paper in the context of the reports on scientific integrity of the DECREASE trials.

Next to these general comments, we also have some specific suggestions or questions, mainly to help increase the readability in a potential second version of the manuscript :

It would be helpful to have a forest plot of Table 1, to better visualize the results and compare DECREASE vs. non-DECREASE. In Table 2, the authors could report the relative risk (RR) instead of the log(RR) to improve the table’s readability and help the reader understand the magnitude of the different effects depicted. We would also be interested whether some more general information on this topic, especially regarding the non-DECREASE trials to put the DECREASE trials and their data into perspective. (e.g. how many non decrease trials were registered but not published; or whether there is any other evidence or suggestion for non-publication of relevant data that could alter some of the conclusions in this paper.)
A minor point, re-label the subscripts of the Likelihood function as DECREASE and non-DECREASE to avoid the loaded terminology of manipulated and genuine which seem to presuppose the conclusion.
We suggest rewording the second paragraph under the results section, and specifically address the sentence that begins “The relatively minor difference…”. This sentence first references “estimates”, but it is unclear what these estimates are referring to.
In Figure 2 please address why, in the bottom lower panel, the confidence interval for the point estimate is larger than the distribution estimate. Because the distribution estimate has more error in it, we were expecting that the confidence interval of the distribution estimate would be larger than that of the point estimate.

This peer review report was made in collaboration with Sean Walter Kelley, as part of his training.

Is the work clearly and accurately presented and does it cite the current literature?

Yes
Is the study design appropriate and is the work technically sound?

Yes
Are sufficient details of methods and analysis provided to allow replication by others?

Yes
If applicable, is the statistical analysis and its interpretation appropriate?

Partly
Are all the source data underlying the results available to ensure full reproducibility?

Yes
Are the conclusions drawn adequately supported by the results?

Partly

Competing Interests: No competing interests were disclosed.

Reviewer Expertise: Methodology, epidemiology

We confirm that we have read this submission and believe that we have an appropriate level of expertise to confirm that it is of an acceptable scientific standard, however we have significant reservations, as outlined above.

CITE

Report a concern

Respond or Comment

Comments on this article Comments (0)

Version 1

VERSION 1 PUBLISHED 13 Nov 2017

Open Peer Review

Reviewer Status

Reviewer Reports

	Invited Reviewers
	1	2
Version 1 13 Nov 17	read	read

Bob Siegerink, Charité Universitätsmedizin Berlin, Berlin, Germany

Sean Kelley, Charité Universitätsmedizin Berlin, Berlin, Germany
Stephen Senn, Statistical Consultant, Edinburgh, UK

Comments on this article

All Comments(0)

Add a comment

Sign up for content alerts

Browse by related subjects

Back to all reports

Reviewer Report

22 Views

14 Jun 2018 | for Version 1

Stephen Senn, Statistical Consultant, Edinburgh, UK

22 Views Cite this report Responses(0)

Approved

An initial observation as regards my review is that I am unfamiliar with the background to this story and I have reviewed this paper only. The authors make a number of claims regarding facts that could probably be checked by reading some of the references. I have not done this. My comments are limited to the internal logic of the paper only.

Whether or not one agrees with the conclusions, this is an interesting investigation. I have some reservations as regards emphasis in the conclusions, which I shall explain in due course, but first I shall explain why statisticians with my background may have a slightly different point of view to the authors.

Since the time in which I worked in the pharmaceutical industry (1987-1995), I have been interested in drug regulatory science. An attitude that (rightly or wrongly) is accepted as being the norm in both sides of the regularity divide is that evidence of efficacy for one drug in a class cannot (usually) be used as evidence of efficacy of another. In fact, so strong is this point of view that when it is sought to use the proof of efficacy of one formulation for another, proof of equivalence is required. Thus, not only is it the case that different molecules cannot be regarded as having the same efficacy, this carries over to doses and formulations. Some, no doubt, will see this as a conspiracy to inhibit generic competition. However, during my own time in drug development I twice worked on alternative formulations (that is to say developed by the innovator company) that had to be abandoned. In one case a clinical trial of the new formulation revealed it had one quarter the potency of the existing formulation¹.

This ‘no pooling of products’ attitude also holds for ‘proving’ safety. For different formulation ‘proof’ of equivalence would be required and for different molecules usually a whole new programme. (Biosimilars might be a controversial exception.) However, regulators do generally consider that observed safety problems in one molecule in a class create a potential concern. The FDA’s attitude as regards development of treatments in diabetes, partly as a response to Nissen and Wolski’s meta-analysis of rosiglitazone, is a case in point².

Thus, there is a general aversion in drug-development and regulation, not necessarily shared by the evidence-based medicine movement, to pooling different molecules in a meta-analysis. Nevertheless, I consider that such pooling is legitimate for one purpose, namely that of testing the hypothesis that no drug in among those pooled has the effect being studied. If this is adopted as a null hypothesis and a fixed effect analysis suggests the null hypothesis should be rejected, then the hypothesis to assert becomes the hypothesis that at least one drug in the class has an effect. (See my paper on overstating evidence³ p3. ) Further investigations are then necessary to determine what the practical implications of this are, but asserting the alternative hypothesis that all drugs have an effect is clearly not warranted.

In fact, I can put it cynically like this. We seem to live in an era in which everyone believes in personalised medicine (thus in patient by treatment interaction) but we are unconcerned about the differences between the main effects of treatment.

However, a further consequence of my time in the pharmaceutical industry, is that I share a general mistrust of investigator led-trials (with some notable exceptions). The fact that previously, raw data from pharmaceutical trials were not shared with the wider public, has been the subject of much criticism. Nevertheless, such trials were examined by the regulator and this, in my opinion, has done much to improve the quality of pharmaceutical industry trials. Without such external scrutiny the danger is that independent trials may suffer in quality.

I now come to my specific comments.

It is clear from the authors’ paper that in the meta-analysis different drugs are pooled. This implies that one explanation that should not be dismissed on the basis of the statistical analysis alone, is that the effects vary from treatment to treatment in the class. To be fair to the authors, they do discuss this in more than one place but I feel that they do not appreciate fully the reservations that apply generally to pooling drugs. Again, to be fair, they do provide the extremely helpful table 2, which provides an analysis by table. It would be nice to see, just to complete the picture, if there is a connected network, what a network meta-analysis would show. (If there is not a connected network then this must be that the problem with the different experimental treatments also applies to the controls.) For example, this would permit formal comparison of different drugs. Again, it should be noted that the authors do include what might be regarded as a sort of network analysis, however, all other treatments are lumped together and this suffers from a problem discussed in point 4 below. I am not suggesting that the authors need to do this analysis (it could a be task for future work), I am just suggesting that the fact that this has not been done is a limitation that needs to be reflected in the discussion.
By the same token, this means that it would be highly debatable anyway, irrespective of any particular doubts about the reliability of the DECREASE I & IV trials, to use these as proof of efficacy of beta-blockade generally. Again, to be fair to the authors, they do suggest that more trials are needed.
However, if the data from the DECREASE I & IV trials have not been audited, then in my opinion nobody is obliged to accept the results anyway. Checkability is the standard by which claims should be judged.
I have some reservations regarding the use of the one degree of freedom chi-square tests in step 1. It should be appreciated that the analysis is one that is strictly speaking only valid if pre-specified without any access to results. It is not an analysis that is valid when comparing observed extreme results with others⁴.
I did not understand the argument in the last paragraph of Step 3. This is probably just due to my being obtuse. The robustness of the results and the implication of the results, if true, seemed to me to get mixed up.

However, these comments do not alter my opinion that this is an interesting paper.

Is the work clearly and accurately presented and does it cite the current literature?

Yes
Is the study design appropriate and is the work technically sound?

Yes
Are sufficient details of methods and analysis provided to allow replication by others?

Yes
If applicable, is the statistical analysis and its interpretation appropriate?

Partly
Are all the source data underlying the results available to ensure full reproducibility?

Yes
Are the conclusions drawn adequately supported by the results?

Partly

References

1. Senn S, Lillienthal J, Patalano F, Till D: An incomplete blocks cross-over in asthma: a case study in collaboration, Cross-over Clinical Trials. Fischer: Stuttgart. 1997. 3-26
2. Nissen SE, Wolski K: Effect of rosiglitazone on the risk of myocardial infarction and death from cardiovascular causes.N Engl J Med. 2007; 356 (24): 2457-71 PubMed Abstract | Publisher Full Text
3. Senn SJ: Overstating the evidence: double counting in meta-analysis and related problems.BMC Med Res Methodol. 2009; 9: 10 PubMed Abstract | Publisher Full Text
4. Senn S, Harrell F: On Wisdom after the Event. J Clin Epidemiol. 1997; 50 (7): 749-751

Competing Interests

I have no competing interests that I am aware of. However, I maintain a full declaration here: http://www.senns.demon.co.uk/Declaration_Interest.htm

Reviewer Expertise

Statistical methods in drug development

I confirm that I have read this submission and believe that I have an appropriate level of expertise to confirm that it is of an acceptable scientific standard.

Respond to this report

Responses (0)

Back to all reports

Reviewer Report

35 Views

20 Feb 2018 | for Version 1

Bob Siegerink, Center for Stroke Research Berlin (CSB), Charité Universitätsmedizin Berlin, Berlin, Germany

Sean Kelley, Center for Stroke Research Berlin (CSB), Charité Universitätsmedizin Berlin, Berlin, Germany

35 Views Cite this report Responses(0)

Approved With Reservations

The paper by Hartgerink et al. sought to determine whether or not there is evidence for data manipulation in the DECREASE-I and Decrease-IV trials. First, the authors reproduced the results of a previous meta-analysis from Bouri et al., using raw event data to calculate the ln(relative risk) and its standard error. Next, they modeled the probability that the results from the DECREASE trials could have occurred from the effect distribution of the non-DECREASE trials. Finally, by creating simulated datasets that were subsequently manipulated they determined the probability that the likelihood of the manipulated data (DECREASE meta-analytic effect distribution) is larger than the likelihood of the genuine data (non-DECREASE meta-analytic effect distribution).

Even though the motivating case for the paper is the questioned reliability of the data within the DECREASE trials that tries to answer a very concrete clinical question (should we use perioperatively use beta blockers to reduce mortality?), the paper ultimately tries to answer a question that is much broader: can we use forensics statistics even when individual data records are not available. In our opinion, the authors succeeded in part to answer that underlying question.

General Comments:

Some circular reasoning in step 2, In step 2 the authors provide clear evidence that the results of the DECREASE trials are quite unlikely, however, they employ some circular reasoning in their argumentation. Because we know the DECREASE values are extreme, when a p-value is calculated for the DECREASE effect is calculated based off of the non-DECREASE effect distribution it will of course be very small. The results of this approach are methodically sound but suffer from circular reasoning and do not seem to add much to the goal of determining whether data manipulation occurred. Although this step might be useful to help ease the reader into the following steps, the limited added value of these analyses should be recognized.
Robustness of approach In Step 3, the combination of adding simulated datasets with a likelihood calculation is an interesting approach to try to determine data manipulation when only summary statistics are available. In the second paragraph of the methods, when describing the inversion method, the authors say “We assumed that if data are manipulated, each data point is manipulated in the same way and to the same extent.” We have a feeling that this is a very strong assumption that is likely not to hold true and might drive the results. An exploration of the robustness, in text or analyses, could help strengthen the argument for the approach the authors apply. Additionally, since the DECREASE-IV trials have approximately 10x the sample size as DECREASE-I we expected a reduction in the confidence interval, yet the confidence interval still spans almost the entire range. Further deliberations on this phenomenon would help the reader understand the robustness of the applied technique.
Interpretation of results. In general, the results show that the data simulation does not give a lot of precision when it comes to pinpointing the number of manipulated datapoints. In some sense, and as also described by the authors, this is also not needed as the lower boundary of the confidence interval of manipulated datapoints should always include 0. In fact, the authors claim that “there is a high degree of confidence that data manipulation did occur based on the difference of the trial results alone”. We do follow that reasoning, but do not fully understand why the authors adhere so much to the difference between the results of the two trials. There does not seem to be a material difference in the 95% confidence intervals between DECREASE-I and DECREASE-IV since in both cases the confidence interval spans essentially the entire range of possible outcomes. Nonetheless, the authors seem to put a lot more emphasis on the analyses of DECREASE IV with its higher sample size, in part because the results show that the lower boundary of the confidence interval does not span the 0 but ranges from 3-1066 or 10-1066, depending on the method used. Given the unknown robustness of this approach, we wonder whether the implied relevance of the small difference between the results of the DECREASE I and DECREASE IV is justified.
Conclusion. In the discussion section, we take issue with the sentence beginning “Our results indicate that the results from the DECREASE trials ... at least some of the data were manipulated”. The word manipulated implies an intention to manipulate data, yet there are numerous ways for data to become incorrectly classified without overt and intended manipulation. Although the authors show it is likely that something altered the data, we believe that strong claims about the provenance of that change based on the analyses provided in this paper should be avoided. However, we agree with the authors that DECREASE I and DECREASE IV should be regarded as "highly problematic and untrustworthy when assessing the effect of beta blockade in perioperative mortality", but that is only when we place the results from this paper in the context of the reports on scientific integrity of the DECREASE trials.

Next to these general comments, we also have some specific suggestions or questions, mainly to help increase the readability in a potential second version of the manuscript :

It would be helpful to have a forest plot of Table 1, to better visualize the results and compare DECREASE vs. non-DECREASE. In Table 2, the authors could report the relative risk (RR) instead of the log(RR) to improve the table’s readability and help the reader understand the magnitude of the different effects depicted. We would also be interested whether some more general information on this topic, especially regarding the non-DECREASE trials to put the DECREASE trials and their data into perspective. (e.g. how many non decrease trials were registered but not published; or whether there is any other evidence or suggestion for non-publication of relevant data that could alter some of the conclusions in this paper.)
A minor point, re-label the subscripts of the Likelihood function as DECREASE and non-DECREASE to avoid the loaded terminology of manipulated and genuine which seem to presuppose the conclusion.
We suggest rewording the second paragraph under the results section, and specifically address the sentence that begins “The relatively minor difference…”. This sentence first references “estimates”, but it is unclear what these estimates are referring to.
In Figure 2 please address why, in the bottom lower panel, the confidence interval for the point estimate is larger than the distribution estimate. Because the distribution estimate has more error in it, we were expecting that the confidence interval of the distribution estimate would be larger than that of the point estimate.

This peer review report was made in collaboration with Sean Walter Kelley, as part of his training.

Is the work clearly and accurately presented and does it cite the current literature?

Yes
Is the study design appropriate and is the work technically sound?

Yes
Are sufficient details of methods and analysis provided to allow replication by others?

Yes
If applicable, is the statistical analysis and its interpretation appropriate?

Partly
Are all the source data underlying the results available to ensure full reproducibility?

Yes
Are the conclusions drawn adequately supported by the results?

Partly

Competing Interests

No competing interests were disclosed.

Reviewer Expertise

Methodology, epidemiology

We confirm that we have read this submission and believe that we have an appropriate level of expertise to confirm that it is of an acceptable scientific standard, however we have significant reservations, as outlined above.

Respond to this report

Responses (0)

[1] 1. Cole GD, Francis DP: Perioperative β blockade: guidelines do not reflect the problems with the evidence from the DECREASE trials. BMJ. 2014; 349: g5210. PubMed Abstract | Publisher Full Text

[2] 2. Poldermans D, Boersma E, Bax JJ, et al.: The effect of bisoprolol on perioperative mortality and myocardial infarction in high-risk patients undergoing vascular surgery. Dutch Echocardiographic Cardiac Risk Evaluation Applying Stress Echocardiography Study Group. N Engl J Med. 1999; 341(24): 1789–1794. PubMed Abstract | Publisher Full Text

[3] 3. Dunkelgrun M, Boersma E, Schouten O, et al.: Bisoprolol and fluvastatin for the reduction of perioperative cardiac mortality and myocardial infarction in intermediate-risk patients undergoing noncardiovascular surgery: A randomized controlled trial (DECREASE-IV). Ann Surg. 2009; 249(6): 921–926. PubMed Abstract | Publisher Full Text

[4] 4. Onderzoekscommissie Wetenschappelijke Integriteit: Onderzoek Naar Mogelijke Schending van de Wetenschappelijke Integriteit: Beknopte Versie. Erasmus MC; 2011. Reference Source

[5] 5. Commissie Vervolgonderzoek 2012: Rapport Vervolgonderzoek Naar Mogelijke Schending van de Wetenschappelijke Integriteit. Erasmus MC; 2012. Reference Source

[6] 6. Commissie Vervolgonderzoek Wetenschappelijke Integriteit 2013: Rapport. Erasmus MC; 2014. Reference Source

[7] 7. Devereaux PJ, Beattie WS, Choi PT, et al.: How strong is the evidence for the use of perioperative beta blockers in non-cardiac surgery? Systematic review and meta-analysis of randomised controlled trials. BMJ. 2005; 331(7512): 313–321. PubMed Abstract | Publisher Full Text | Free Full Text

[8] 8. Angeli F, Verdecchia P, Karthikeyan G, et al.: ß-Blockers reduce mortality in patients undergoing high-risk non-cardiac surgery. Am J Cardiovasc Drugs. 2010; 10(4): 247–259. PubMed Abstract | Publisher Full Text

[9] 9. Bouri S, Shun-Shin MJ, Cole GD, et al.: Meta-analysis of secure randomised controlled trials of β-blockade to prevent perioperative death in non-cardiac surgery. Heart. 2014; 100(6): 456–464. PubMed Abstract | Publisher Full Text | Free Full Text

[10] 10. ESC/ESA: Guidelines on non-cardiac surgery: Cardiovascular assessment and management. Eur Heart J. 2014; 35: 2383–2243. Reference Source

[11] 11. Fleisher LA, Fleischmann KE, Auerbach AD, et al.: 2014 ACC/AHA guideline on perioperative cardiovascular evaluation and management of patients undergoing noncardiac surgery: executive summary: a report of the American College of Cardiology/American Heart Association Task Force on Practice Guidelines. Circulation. 2014; 130(24): 2215–2245. PubMed Abstract | Publisher Full Text

[12] 12. Buyse M, George SL, Evans S, et al.: The role of biostatistics in the prevention, detection and treatment of fraud in clinical trials. Stat Med. 1999; 18(24): 3435–3451. PubMed Abstract | Publisher Full Text

[13] 13. Carlisle JB: Data fabrication and other reasons for non-random sampling in 5087 randomised, controlled trials in anaesthetic and general medical journals. Anaesthesia. 2017; 72(8): 944–952. PubMed Abstract | Publisher Full Text

[14] 14. Knepper D, Lindblad AS, Sharma G, et al.: Statistical monitoring in clinical trials: Best practices for detecting data anomalies suggestive of fabrication or misconduct. Ther Innov Regul Sci. 2016; 50(2): 144–154. Publisher Full Text

[15] 15. van Klei WA: [Which is the preferred perioperative beta-blocker?]. Ned Tijdschr Geneeskd. 2015; 159: A9798. PubMed Abstract

[16] 16. Viechtbauer W: Conducting meta-analyses in R with the metafor package. J Stat Softw. 2010; 36(3): 1–48. Publisher Full Text

[17] 17. Viechtbauer W: Bias and efficiency of meta-analytic variance estimators in the Random-Effects model. J Educ Behav Stat. 2005; 30(3): 261–293. Publisher Full Text

[18] 18. Agresti A: Categorical Data Analysis. Hoboken NJ: John Wiley & Sons Inc.; 2002. Reference Source

[19] 19. Peters CFW, Klaassen CAJ, van de Wiel MA: Evaluating the Scientific Veracity of Publications by Dr. Jens Forster. University of Amsterdam; 2015. Reference Source

[20] 20. Welch BL: The generalisation of student’s problems when several different population variances are involved. Biometrika. 1947; 34(1–2): 28–35. PubMed Abstract | Publisher Full Text

[21] 21. Casella G, Berger RL: Statistical Interference. Pacific Grove, CA:Duxbury; 2002. Reference Source

[22] 22. Kristensen SD, Knuuti J, Saraste A, et al.: 2014 ESC/ESA Guidelines on non-cardiac surgery: cardiovascular assessment and management: The Joint Task Force on non-cardiac surgery: cardiovascular assessment and management of the European Society of Cardiology (ESC) and the European Society of Anaesthesiology (ESA). Eur J Anaesthesiol. 2014; 31(10): 517–573. PubMed Abstract | Publisher Full Text

[23] 23. Boersma E, Poldermans D, Bax JJ, et al.: Predictors of cardiac events after major vascular surgery: Role of clinical characteristics, dobutamine echocardiography, and beta-blocker therapy. JAMA. 2001; 285(14): 1865–73. PubMed Abstract | Publisher Full Text

[24] 24. van Kuijk JP, Flu WJ, Schouten O, et al.: Timing of noncardiac surgery after coronary artery stenting with bare metal or drug-eluting stents. Am J Cardiol. 2009; 104(9): 1229–1234. PubMed Abstract | Publisher Full Text

[25] 25. Flu WJ, van Kuijk JP, Chonchol M, et al.: Timing of pre-operative Beta-blocker treatment in vascular surgery patients: influence on post-operative outcome. J Am Coll Cardiol. 2010; 56(23): 1922–1929. PubMed Abstract | Publisher Full Text

[26] 26. Hartgerink C: chartgerink/2015poldermans: Zenodo DOI creation. Zenodo. 2017. Data Source

Analyzing DECREASE trials to estimate evidence of data manipulation

Abstract

Keywords

Introduction

Step 1: Reproducing meta-analysis of Bouri et al. (2014)

Methods

Results

Table 1. The original- and reproduced meta-analytic results based on the data provided in the 2014 meta-analysis by Bouri et al.9.

Table 2. Meta-regression results (k=11) for log(RR), including dummy predictors for DECREASE trials (reference: non-DECREASE trials) and type of beta-blockers used in the trial (reference: atenolol).

Step 2: Evaluating the veracity of DECREASE studies

Method

Results

Figure 1. Sensitivity analyses for the p-value that indicates the probability of observing the results from the DECREASE studies, or more extreme results, based on the estimated true effect (non-DECREASE trials) and the accompanying variance estimate.

Step 3: Estimating the amount of manipulated data

Method

Table 3. Mortality estimates per condition, per trial stratum.

Table 4. Outcome possibilities within a simulated 2 (beta-blocker v control) by 2 (dead v alive) clinical trial.

Results

Figure 2. Inversion method results used to estimate the number of data points manipulated in the DECREASE-I and DECREASE-IV trials.

Discussion

Data availability

Competing interests

Grant information

Supplementary material

References

Comments on this article Comments (0)

Open Peer Review

Comments on this article Comments (0)

Open Peer Review

Reviewer Status

Reviewer Reports

Comments on this article

Browse by related subjects

Competing Interests Policy

Stay Updated

Table 1. The original- and reproduced meta-analytic results based on the data provided in the 2014 meta-analysis by Bouri et al.⁹.