Keywords
practical significance, statistical significance, research evidence, p-values, Bayes factors, reproducibility, replicability
practical significance, statistical significance, research evidence, p-values, Bayes factors, reproducibility, replicability
Minor changes incorporating reviewers’ recommendations:
See the authors' detailed response to the review by Stephen Senn
See the authors' detailed response to the review by Patrizio Tressoldi
See the authors' detailed response to the review by Juan Carro Ramos
Seeking to address the lack of research reproducibility due to the high rate of false positives in the literature, Benjamin et al. (2017a); Benjamin et al. (2017b) propose a pragmatic solution which “aligns with the training undertaken by many researchers, and might quickly achieve broad acceptance” (also Savehn, 2017): to use a stricter p < 0.005 standard for statistical significance when claiming evidence of new discoveries.
The proposal is subject to several constrains in its application: (1) to claims of discovery of new effects (thus, not necessarily to replication studies); (2) when using null hypothesis significance testing (arguably Fisher’s approach, perhaps even Neyman-Pearson’s, but excluding other p-value-generating approaches such as resampling); (3) in fields with too flexible standards (namely 5% or above); (4) when the prior odds of alternative-to-null hypothesis is in the range 1-to-5, to 1-to-40 (stricter standards are required with lower odds); (5) for researcher’s consumption (thus, not a standard for journal rejection, although “journals can help transition to the new statistical significance threshold”; also, “journals editors and funding institutions could easily enforce the proposal”, Wagenmakers, 2017; and “its implementation only requires journal editors to agree on the new threshold”, Machery, 2017); (6) while still keeping findings with probability up to 5% as suggestive (and meriting publication if so “properly labelled”); (7) despite many of the proponents believing that the proposal is nonsense, anyway (that is, it is a quick fix, not a credible one; also Ioannidis in Easwaran, 2017; Resnick, 2017; Wagenmakers, 2017; Wagenmakers & Gronau, 2017).
The main analyses supporting the proposal were the following: (a) a calibration of p-values to Bayes factors under certain plausible alternatives (their Figure 1, Benjamin et al., 2017b, p. 2); (b) an estimated false positive rate under certain plausible prior odds of alternative-to-null hypotheses as a function of power (their Figure 2, Benjamin et al., 2017b, p. 3); and (c) a “critical mass of researchers now endors[ing] this change” (a.k.a., the 72 co-authors). Meanwhile, the proposal downplays the costs due to increasing sample size in order to ensure enough research power, the potential increase in false negatives and misconduct, and the existence of alternative solutions well known by, at least, some of the authors (despite Machery’s, 2017, claim to the contrary).
Notwithstanding its potential impact, Benjamin et al.’s (2017a); Benjamin et al.’s (2017b) proposal is not recognizant of the entire engine of science (Figure 1), which has motivated an even larger mass of authors to offer their counter-arguments.
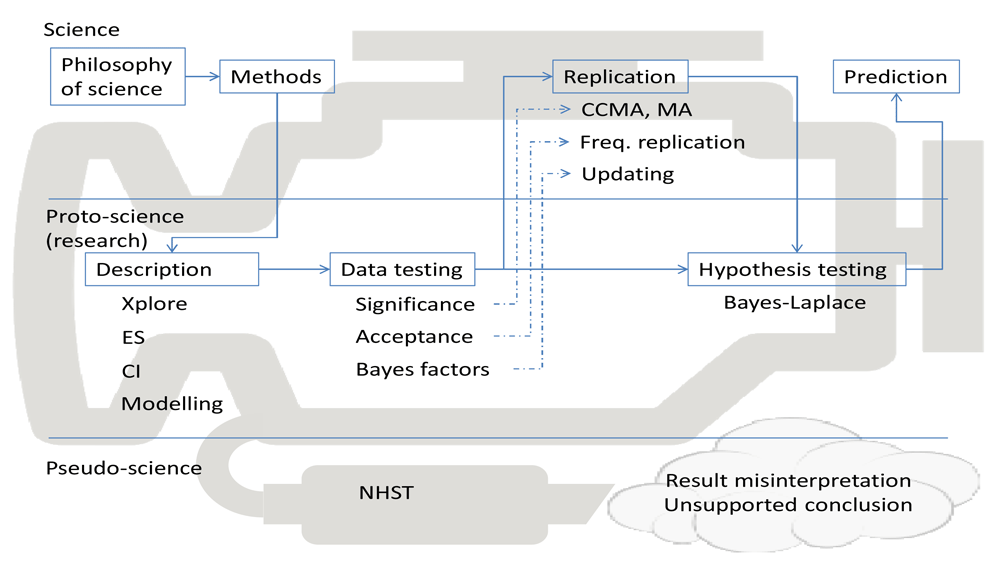
Xplore = exploratory data analysis; ES = effect size; CI = confidence interval, credible interval; CCMA = continuous cumulating meta-analysis; MA = meta-analysis; Freq. replication = frequentist replication; NHST = null hypothesis significance testing (as in Perezgonzalez, 2015).
From Philosophy of science, Mayo (2017a), in particular, provides important counter-arguments against the philosophical standing of Benjamin et al.’s proposal. Quoting Greenland et al. (2016), Mayo asserts that whether p-values exaggerate the evidence against the null hypothesis depends on the philosophical background within which such claim is made: It may seem so from a Bayesian perspective, but both from a frequentist and an error statistics perspective, it is the Bayes factor which exaggerates the evidence (also 2017e). “I find it especially troubling”—she continues—“to spoze an error statistician…ought to use a Bayes Factor as the future gold standard for measuring his error statistical tool…even though Bayes Factors don’t control or measure error probabilities” (2017b). Furthermore, Mayo pinpoints the (old) fallacy of transposing the conditional, whereby the (error) probability of a test is confused with the (posterior) probability of a belief (also Trafimow et al., 2017). And despite “60 years (sic) old…demonstrations [showing] that with reasonable tests and reasonable prior probabilities, the disparity vanishes…they still mean different things” (2017c). In particular, “in an adequate account [of severity testing], the improbability of a claim must be distinguished from its having been poorly tested. (You need to be able to say things like, ‘it’s plausible, but that’s a lousy test of it.’)” (2017d). And “the method for such checking is significance tests!” (2017b).
From Methodology, a large number of critics have faulted Benjamin et al.’s disregard of what is really affecting replication in order to focus on a relatively minor issue. Mayo, for example, lists biasing selection effects, cherry-picking, multiple testing, hunting for significance, optional stopping, violated statistical assumptions, missing or irrelevant statistical-substantive links, and questionable measurements as the main culprits in flawed findings and lack of reproducibility (2017a–e; also Gelman & McShane, 2017; Gelman, 2017b). Lakens et al. (2017) add lack of experimental redundancy, logical traps, research opacity, and poor accounting of sources of error, as well as the risks of reduced generalisability and research breadth were Benjamin et al.’s proposal to succeed. Methodological concerns were also raised by Amrhein & Greenland (2017); Black (2017); Byrd (2017); Chapman (2017); Crane (2017); Ferreira & Henderson (2017); Greenland (2017); Hamlin (2017); Kong (2017); Lew (2017); Llewelyn (2017); Martin (2017); McShane et al. (2017); Passin (2017); Steltenpohl (2017); Trafimow et al. (2017); Young (2017); Zollman (2017); and Morey (2017). Some researchers even propose the use of preregistration as a way of minimizing above problems (Hamlin, 2017; Llewelyn, 2017; van der Zee, 2017)
The pseudoscientific NHST element (as conceptualized in Perezgonzalez, 2015) is the cornerstone of Benjamin et al.’s proposal, as it mixes Fisher’s tests of significance with Neyman-Pearson’s alternative hypotheses, Type II errors and power estimation, and with Bayesian prior probabilities, in order to argue about the false positive rate as the culprit for the lack of replicability. Indeed, the false positive rate argument has been heavily criticized by several authors: Mayo (2017b; also Byrd, 2017) chiefly derides as questionable the prior probabilities given to the hypotheses; Colquhoun (2017) denounces the credibility of Benjamin et al.’s false positive rate calculation for some of the prior probabilities used, which he sees as a rather liberal rate; Chapman (2017; also Byrd, 2017) claims that the prior probability ratios for the hypotheses are not realistic; Llewelyn (2017) raises an argument on prior probabilities and their combination with accumulated evidence in order to estimate the probability of future replication, not finding a more restrictive level of significance an adequate antecedent for increasing such probability; Krueger (2017) adds that, under the new proposal, the proportion of false negatives rises faster than the speed at which false positives drops, leading Phaf (2017) to wonder whether, because of it, “it makes more sense to increase, rather than reduce, the significance level for novel findings”; Kong (2017) states that the false positive rate formula is misleading and finds the expected false positive rate when testing the conventional 5% threshold.
Furthermore, Perezgonzalez (2017) argued that the misinterpretation of p-values as evidence in favour or against a hypothesis has more to do with the pseudoscientific use of NHST than with frequentist testing proper (also Amrhein & Greenland, 2017; Mayo, 2017b; McShane et al., 2017). As Benjamin et al.’s proposal is made within the pseudo-philosophical argument of NHST (e.g., confusing statistical and substantive significance; Mayo, 2017c), a lower threshold of significance does not improve such ‘magical thinking’ (also Argamon, 2017; Diebold, 2017; Greenland, 2017; Krueger, 2017; Phaf, 2017). Lakens et al. (2017; also Morey, 2017; O’Rourke, 2017) equally warn that the proposal exaggerates the focus on single p-values in scientific practice, education, decision making and publication.
Unsupported conclusions are another consequence of pseudoscientific thinking, and McShane et al. (2017) and Amrhein & Greenland (2017) highlight the risks of studies published under the new banner exaggerating effect sizes and overconfidence in significant results while discounting non-significant findings. De Brigard (2017) argues, instead, for the need to be humbler and not generalize to populations, irrespective of statistical significance, effects that may only be present in the sample.
The descriptive data analysis element was briefly touched upon by Mayo (2017a)—who recommends abandoning significance testing in favour of inferring the magnitudes that are well (or poorly) indicated by the data (a.k.a., CIs)—and Lew (2017), Phaf (2017), and McShane et al. (2017)—whom argue for the need to interpret evidence in the context of other findings and theoretical models in lieu of NHST.
Regarding data testing, Mayo (2017a); Mayo (2017b) and Perezgonzalez (2017) have no particular problem with a lower level of significance although both reckon Benjamin et al.’s proposal does not address anything in particular with frequentist testing proper. Mayo equally sees such lowering unnecessary as “you might not want to be too demanding before claiming evidence of a [null] model violation” (2017b), while the “lack of replication is effectively uncovered thanks to statistical significance tests” (2017e). Young (2017) reminds us of the appropriate use of significance tests in experimental contexts. McShane et al. (2017) also argues the credibility of uniformly most powerful priors and tests and the loss of its connection to Bayesianism as for justifying Benjamin et al.’s proposal (but see Wagenmakers & Gronau’s counter-argument, 2017).
Other authors recommend continuing using p-values either as part of frequentist tests proper (Bates, 2017) or without significance testing, the latter including Colquhoun (2017), Mayo (2017b; who also proposes estimating false positive rates), Greenland (2017, who proposes transforming them to bits of information against the null hypothesis), Diebold (2017); Funder (2017); Lakens et al. (2017, who recommend justifying whatever thresholds may be used at the design stage), McShane et al. (2017, who recommend using them as descriptives among other neglected factors—but see Wagenmakers & Gronau’s, 2017, counter-argument, and Gelman’s, 2017a, counter-counter-argument), and Amrhein & Greenland (2017). Argamon (2017) suggests substituting Bayesian statistics, instead.
Addressing replication directly, Chapman (2017) and Trafimow et al. (2017) point out that the problem with replication is not too many false positives but insufficient power. Krueger (2017; also McShane et al., 2017, Trafimow et al., 2017) chides Benjamin et al. for the incoherence of considering replication as order-dependent and inverting the exploratory-confirmatory nature of replication by proposing to make the former more difficult to achieve and the latter more liberal. He further chides them on whether they would disallow their own past findings at the 5% threshold. Lakens et al. (2017; also Crane, 2017) found biases in the analyses done by Benjamin et al., and conclude that there is no [Bayesian] evidence that a lower level of significance improves replicability. They also warn of the risks of fewer availability of replication studies were the proposal to succeed (also Greenland, 2017). Gelman (2017b); Hamlin (2017); Ickes (2017); Kong (2017); Roberts (2017), and Trafimow et al. (2017) propose to stop the proverbial beating around the bushes and perform direct replications as a straightforward measure of replicability.
The hypothesis testing element (namely full Bayesian hypothesis testing) has been seldom touched upon but briefly by Llewelyn (2017), who extended the need for prior probabilities and even more accumulated evidence as pre-requisite for estimating the probability of hypotheses being ‘true’.
In conclusion, despite Benjamin et al.’s best intentions, their proposal only reinforces the NHST pseudoscientific approach with a stricter bright-line threshold for claiming evidence it cannot possibly claim—irrespective of how well it calibrates with Bayes factors under certain conditions—while dismissing potential consequences such as the stifling of research and its publication, an increase in false negatives, an increase in misbehaviour, and a continuation of pseudoscientific practices. Furthermore, theirs is a frequentist solution many of their Bayesian proponents do not even believe in, born out of a false belief of lacking equally simple but better-suited alternatives (Machery, 2017).
In reality, an equally simple and better suited alternative exists, perhaps the only one the authors could be entitled to make from their Jeffresian perspective, hence our own recommendation: Use JASP, the stand-alone, free-to-download, R-based statistical software with user-friendly interface, developed by Wagenmakers’ team (https://jasp-stats.org1). JASP allows for analysing the same dataset using frequentist (Fisher’s tests of significance) and Bayesian tools (Jeffreys’s Bayes factors2) without necessarily forcing a mishmash of philosophies of science (e.g., see Supplementary File 1). JASP allows for the Popperian (also Meehl’s, Mayo’s) approach to severely testing a null hypothesis but also to ascertain the credibility of tests based on the observed data. JASP allows researchers to qualitatively calibrate their significance tests to Bayes factors but also the possibility of calibrating Bayes factors to frequentist tests so as to ascertain their error probabilities. JASP is an existing simple and easy application that shows two interpretations of the same data, which aligns well with the training undertaken by frequentist and Jeffreysian researchers alike while allowing them the opportunity to learn the alternative philosophy—irrespective of which they will choose for publication—and may as well help diminish the misinterpretation of results and the reaching of unsupported conclusions. In so doing, it may even help improve replicability.
1Worthy alternatives are Morey’s R package for Bayes factors (http://bayesfactorpcl.r-forge.r-project.org), Morey’s Bayes factor calculator (http://pcl.missouri.edu/bayesfactor), and Dienes’s Bayes factor calculator (http://www.lifesci.sussex.ac.uk/home/Zoltan_Dienes/inference/Bayes.htm). Even better would be to skip comparing models altogether and go for full Bayesian hypothesis testing (e.g., Kruschke, 2011). Yet none of those alternatives surpass, at present, JASP’s interface and its flexibility for parallel analysis.
2The latest versions of JASP (e.g. 0.8.4.0; 0.8.5.1) also allows for choosing informed priors based on Cauchy, Normal, and t-distributions.
This publication was financially supported by Massey University Research Fund (MURF) Mini Grant 2017 for Open Access publication, Massey University, New Zealand.
The funders had no role in study design, data collection and analysis, decision to publish, or preparation of the manuscript.
We wish to thank the reviewers, P. Tressoldi, J. C. Ramos, and S. Senn for their reviews and suggestions for improvement.
Supplementary file 1: Parallel statistical analysis via JASP. Example of data analysis using both frequentist (Fisher) and Bayesian (Jeffreys) approaches.
| Views | Downloads | |
|---|---|---|
| F1000Research | - | - |
|
PubMed Central
Data from PMC are received and updated monthly.
|
- | - |
Is the topic of the opinion article discussed accurately in the context of the current literature?
Partly
Are all factual statements correct and adequately supported by citations?
Partly
Are arguments sufficiently supported by evidence from the published literature?
Partly
Are the conclusions drawn balanced and justified on the basis of the presented arguments?
Partly
References
1. Senn S: Two cheers for P-values?. J Epidemiol Biostat. 2001; 6 (2): 193-204; discussion 205 PubMed AbstractCompeting Interests: No competing interests were disclosed.
Reviewer Expertise: Biostatistics, Drug Development, Statistical Inference
Is the topic of the opinion article discussed accurately in the context of the current literature?
Yes
Are all factual statements correct and adequately supported by citations?
Yes
Are arguments sufficiently supported by evidence from the published literature?
Yes
Are the conclusions drawn balanced and justified on the basis of the presented arguments?
Yes
Competing Interests: No competing interests were disclosed.
Is the topic of the opinion article discussed accurately in the context of the current literature?
Yes
Are all factual statements correct and adequately supported by citations?
Yes
Are arguments sufficiently supported by evidence from the published literature?
Yes
Are the conclusions drawn balanced and justified on the basis of the presented arguments?
Yes
Competing Interests: No competing interests were disclosed.
Alongside their report, reviewers assign a status to the article:
| Invited Reviewers | |||
|---|---|---|---|
| 1 | 2 | 3 | |
|
Version 2 (revision) 16 Feb 18 |
|||
|
Version 1 12 Dec 17 |
read | read | read |
Provide sufficient details of any financial or non-financial competing interests to enable users to assess whether your comments might lead a reasonable person to question your impartiality. Consider the following examples, but note that this is not an exhaustive list:
Sign up for content alerts and receive a weekly or monthly email with all newly published articles
Already registered? Sign in
The email address should be the one you originally registered with F1000.
You registered with F1000 via Google, so we cannot reset your password.
To sign in, please click here.
If you still need help with your Google account password, please click here.
You registered with F1000 via Facebook, so we cannot reset your password.
To sign in, please click here.
If you still need help with your Facebook account password, please click here.
If your email address is registered with us, we will email you instructions to reset your password.
If you think you should have received this email but it has not arrived, please check your spam filters and/or contact for further assistance.
I believe Benjamin et al. would have made more sense proposing a double analysis frequentist/Jeffresian (it prompts you to know what's the knowledge each approach warrants) than proposing a reduction of significance just because it calibrates with Bayes Factors under certain conditions (which suggests p-values and BF are different tools measuring the same thing, like the Celsius and Fahrenheit temperature scales).
Of course, this doesn't mean that the double analysis is the quick fix-all solution, though. I think Gelman (or is it Senn?) has also been wondering why BF when we could go for a full Bayesian analysis instead. I also understand Mayo's point focused on error statistics. Yet all those perspective are focusing on the problem from different points-of-views, and such points-of-view need to be understood in order to make sense of each claim.
In a nutshell, next time I go to the doctor for a test, I want that test to be pretty good at reducing false positives (Fisher). I also want it to be pretty good at reducing false negatives (Neyman-Pearson; BF). And not only that, I want such test validated under the frequentist approach. And yet, I don't want my diagnosis been determined by the test. Indeed, I want my doctor to make the diagnosis (Bayes). Hopefully, she will recommend further tests or follow ups (some form of frequentist replication, or Bayesian updating). I need (and want) all those approaches!
I believe Benjamin et al. would have made more sense proposing a double analysis frequentist/Jeffresian (it prompts you to know what's the knowledge each approach warrants) than proposing a reduction of significance just because it calibrates with Bayes Factors under certain conditions (which suggests p-values and BF are different tools measuring the same thing, like the Celsius and Fahrenheit temperature scales).
Of course, this doesn't mean that the double analysis is the quick fix-all solution, though. I think Gelman (or is it Senn?) has also been wondering why BF when we could go for a full Bayesian analysis instead. I also understand Mayo's point focused on error statistics. Yet all those perspective are focusing on the problem from different points-of-views, and such points-of-view need to be understood in order to make sense of each claim.
In a nutshell, next time I go to the doctor for a test, I want that test to be pretty good at reducing false positives (Fisher). I also want it to be pretty good at reducing false negatives (Neyman-Pearson; BF). And not only that, I want such test validated under the frequentist approach. And yet, I don't want my diagnosis been determined by the test. Indeed, I want my doctor to make the diagnosis (Bayes). Hopefully, she will recommend further tests or follow ups (some form of frequentist replication, or Bayesian updating). I need (and want) all those approaches!