Keywords
lifespan, human lifespan, contradictory findings, ageing, life history, refutation
This article is included in the Preclinical Reproducibility and Robustness gateway.
lifespan, human lifespan, contradictory findings, ageing, life history, refutation
Recent findings by Dong et al.1 suggested fixed upper limits to the human life span. Using the same data, we replicated their analysis to obtain an entirely different result: the upper limit of human life is rapidly increasing.
Dong et al. conclude that the maximum reported age at death (MRAD) is limited to 125 years in humans1 and that lifespan increases above age 110 are highly unlikely, due to the reduced rate of increase in life expectancy at advanced ages.
We repeated Dong et al.’s1 analysis using identical data (SI). Replicating these findings requires the inclusion of rounding errors, treating zero-rounded values as log(1) and the incorrect pooling of populations.
The Human Mortality Database (HMD) data provide both the age-specific probability of survival (qx) and the survival rates of a hypothetical cohort of 100,000 individuals (lx). However, lx survival rates are rounded off to the nearest integer value.
The magnitude and frequency of lx rounding errors increases as the probability of survival approaches 1 in 100,000. These rounding errors mask variation in survival rates at advanced ages: over half of lx survival data are rounded to zero above age 90 (Figure 1b).

(a) Figure modified after Dong et al. Figure 1b, showing rounded survival data (red points), rounded survival data with log(0)=log(1) (black points), the resulting linear regression in Dong et al. (solid red line) and observed survival data (pink points). (b) Rounding errors in survival data (box-whisker plots; 95% CI) and the proportion of survival data rounded to zero in males (blue line) and females (red line). (c) Survival data from (a) with rounding errors removed, showing variation outside the 1900-1990 period (vertical dotted lines). (d) The rate of change in late-life mortality since 1900 with (dotted lines) and without (solid lines) rounding errors (after Dong et al. Figure 1c).
Dong et al. appear to have used these rounded-off survival data in their models1 and incorrectly treated log(0) values as log(1) in log-linear regressions (Figure 1a–d; SI).
These errors have considerable impact. Re-calculating cohort survival from raw data or excluding zero-rounded figures eliminates the proposed decline in old-age survival gains (Figure 1d; SI).
Likewise, recalculating these data removed their proposed limits to the age of greatest survival gain (SI), which in 15% of cases were the result of the artificial 110-year age limit placed on HMD data2.
We also found that variation in the probability of death was masked by date censoring1. Major non-linear shifts in old-age survival occur outside the 1900-1990 period used by Dong et al. (Figure 1c). Why these data were excluded from this regression, but included elsewhere, is unclear.
Evidence based on observed survival above age 110 appears to support a late-life deceleration in survival gains1. For the period 1960–2005 Dong et al. present data1 from 4 of the 15 countries in the International Database on Longevity3 (IDL). In their pooled sample of these countries, there is a non-significant (p=0.3) reduction in MRAD between 1995 and 2006 (Figure 2a).
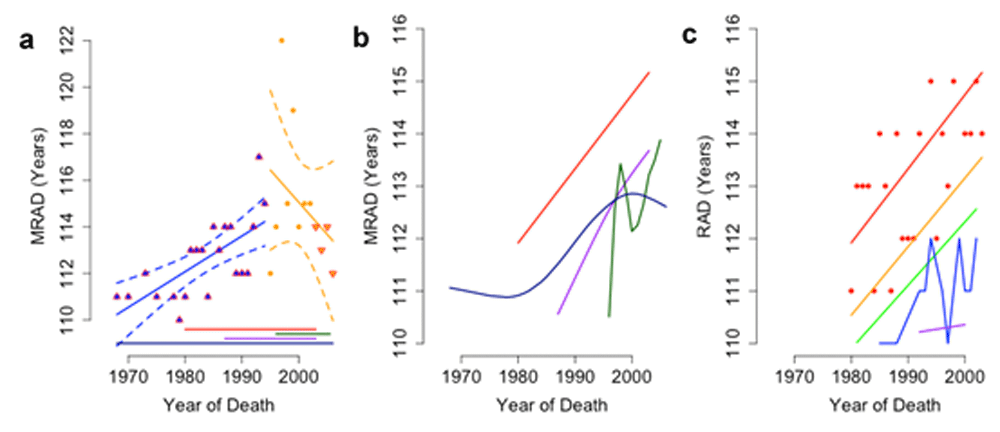
(a) Reproduction of Dong et al. Figure 2a, including 95% CI for increasing (p<0.0001) and falling (p=0.3) maximum recorded age at death (MRAD), showing data biased by the addition and removal (up and down arrows) of populations. (b) Locally weighted smoothed splines of MRAD in Japan (green), the USA (red), the UK (dark blue) and France (purple). (c) Locally weighted trends of MRAD in the USA across the oldest 5 reported ages at death (red, orange, green, blue and purple lines show rank 1–5 respectively).
The declining MRAD reported by Dong et al.1 arises from the use of falling sample sizes. According to the Gerontology Research Group (GRG), 62% of validated supercentenarians alive in 2007 resided in France and the USA. However, these countries are not surveyed3 by the IDL after 2003 (Figure 2a). The proposed post-1995 decline in MRAD results from this dramatic fall in sample size.
Viewed individually, all four countries have an upward trend in the mean reported age at death (RAD; Figure 2b) of supercentenarians (SI) and the top 5 ranked RADs (Figure 2c). All four countries achieved record lifespans since 1995, as did 80% of the countries in the IDL. Without the pooling of IDL data used by Dong et al. there is no evidence for a plateau in late-life survival gains.
We attempted to reproduce Dong et al.’s supporting analysis of GRG records. The text and Extended Data Figure 6 of Dong et al. do not match annual MRAD records from 1972 as stated1. However, they do match deaths of the world’s oldest person titleholders from 1955 (GRG Table C, Revision 9) with all deaths in May and June removed (SI).
Actual MRAD data from the GRG support a significant decline in the top-ranked age at death since 1995 (r = -0.47; p = 0.03, MSE = 3.2). However, this trend is not significant if only Jeanne Clament is removed (p = 0.9). Linear models fit to lower-ranked RADs have an order of magnitude better fit, and all indicate an increase in maximum lifespan since 1995 (N= 64; SI).
Collectively, these data indicate an ongoing rebound of upper lifespan limits since 1950, with a progressive increase in observed upper limit of human life. To estimate theoretical limits, we developed a simple approximation of the upper limit of human life.
Mortality rates double with age in human populations (Figure 3a and b). Log-linear models fit to this rate-increase closely approximate the observed age-specific probability of death4. These models also provide a simple method of predicting upper limits to human life span that is independent of population size.

(a) In humans, the probability of death q at age x (qx; red line) increases at an approximately log-linear rate with age (black lines; 95% CI), shown here for the birth cohort of Jeanne Clament (d.122.5 years; circle). Projection of this log-linear increase to log(q) = 0 provides the MSA, the upper limit of human survival, shown here for (b) observed and projected global populations5 and (c) 40 historic HMD populations 1751–2014.
We fit log-linear models to age-specific mortality rates from the HMD data used by Dong et al.1, and used these models to predict the age at which the probability of death intercepts one. This maximum survivable age (MSA) provides a simple, conservative estimate of the upper limit of human life (Figure 3c).
Log-linear models closely approximate the observed probability of death in HMD populations for both period and cohort life tables (median R2 = 0.99; 4501 population-years). These models predict an MSA exceeding 125 years within observed historic periods (Figure 3b and c; SI).
Furthermore, period data indicate that MSA is steadily increasing from a historic low c.1956 (Figure 3b and c) and that the MRAD is expected to rise over the next century. This result is supported by trends in global mortality data from the United Nations5, sampled across 194 nations (Figure 3b).
This analysis provides an estimate of human lifespan limits that is conservatively low. Log-linear mortality models assume no late-life deceleration in mortality rates6, which, if present, would increase the upper limits of human lifespan7. In addition, these models are fit to population rates and cannot provide an estimate of individual variation in the rate of mortality acceleration.
Given historical flexibility in lifespan limits and the possibility of late-life mortality deceleration in humans8, these models should, however, be treated with caution.
A claim might be made for a general, higher 130-year bound to the human lifespan. However, an even higher limit is possible and should not be ruled out simply because it exceeds observed historical limits.
Life table data were downloaded from the United Nations5 (UN) and the Human Mortality Database (HMD) and lifespan records from the International Database on Longevity (IDL) and the Gerontology Research Group (GRG).
Least squared linear models were fit to life table data on the log-transformed age-specific probability of death (qx), and projected to qx=1 to predict the maximum survivable age in each population (Figure 1b and c; SI). Maximum lifespan within GRG and IDL data was annually aggregated and fit by locally weighted smoothed splines9 (Figure 3b and c).
We reproduced the analysis of Dong et al. in R version10 3.2.1 (SI), using the code in Supplementary File 1.
An earlier version of this article can be found on bioRxiv (doi: 10.1101/124800).
The authors declare that all data are available within the paper and its supplementary material.
S.J.N. wrote the analysis and code, and reproduced Dong et al.’s analysis. S.J.N. and S.E. developed the analysis, methods and statistical design, and co-wrote the manuscript.
Supplementary File 1: Supplementary information guide. The supplementary information supplied here constitutes two sections of integrated code in the R statistical language:
1. R code required to calculate the maximum survivable age or MSA from both public data and the human mortality data used by Dong et al., and required to reproduce our findings in full.
2. R code required to reproduce Dong et al.1 with original errors, often including several error-corrected or partially corrected versions.
Both sections are wrapped in the same script, and require several package dependencies and datasets outlined in the annotated code.
| Views | Downloads | |
|---|---|---|
| F1000Research | - | - |
|
PubMed Central
Data from PMC are received and updated monthly.
|
- | - |
Is the work clearly and accurately presented and does it cite the current literature?
Yes
Is the study design appropriate and is the work technically sound?
Yes
Are sufficient details of methods and analysis provided to allow replication by others?
Yes
If applicable, is the statistical analysis and its interpretation appropriate?
Yes
Are all the source data underlying the results available to ensure full reproducibility?
Yes
Are the conclusions drawn adequately supported by the results?
Yes
References
1. Dong X, Milholland B, Vijg J: Evidence for a limit to human lifespan.Nature. 2016; 538 (7624): 257-259 PubMed Abstract | Publisher Full TextCompeting Interests: No competing interests were disclosed.
Reviewer Expertise: Aging; Evolution of demography
Is the work clearly and accurately presented and does it cite the current literature?
Yes
Is the study design appropriate and is the work technically sound?
Partly
Are sufficient details of methods and analysis provided to allow replication by others?
Yes
If applicable, is the statistical analysis and its interpretation appropriate?
Partly
Are all the source data underlying the results available to ensure full reproducibility?
Yes
Are the conclusions drawn adequately supported by the results?
Partly
Competing Interests: No competing interests were disclosed.
Reviewer Expertise: Biodemography
Alongside their report, reviewers assign a status to the article:
| Invited Reviewers | |||
|---|---|---|---|
| 1 | 2 | 3 | |
|
Version 2 (revision) 09 Jun 17 |
read | ||
|
Version 1 26 Apr 17 |
read | read | |
Provide sufficient details of any financial or non-financial competing interests to enable users to assess whether your comments might lead a reasonable person to question your impartiality. Consider the following examples, but note that this is not an exhaustive list:
Sign up for content alerts and receive a weekly or monthly email with all newly published articles
Already registered? Sign in
The email address should be the one you originally registered with F1000.
You registered with F1000 via Google, so we cannot reset your password.
To sign in, please click here.
If you still need help with your Google account password, please click here.
You registered with F1000 via Facebook, so we cannot reset your password.
To sign in, please click here.
If you still need help with your Facebook account password, please click here.
If your email address is registered with us, we will email you instructions to reset your password.
If you think you should have received this email but it has not arrived, please check your spam filters and/or contact for further assistance.
Comments on this article Comments (0)