Keywords
diabetes, carbohydrate metabolism, clinical trials, nonlinear models, multivariate analysis
This article is included in the RPackage gateway.
diabetes, carbohydrate metabolism, clinical trials, nonlinear models, multivariate analysis
Disorders of carbohydrate metabolism contribute substantially to overall disease burden throughout the world. According to the International Diabetes Foundation (International Diabetes Federation: IDF Diabetes Atlas, 2015), over 400 million individuals are diabetic, and numbers afflicted continue to rise.
Various tests are used to diagnose diabetes or assess risk of diabetes. In the oral glucose tolerance test (OGTT), a specified quantity of glucose is ingested orally. Plasma concentrations of glucose and insulin are measured at specific times after ingestion. Panels (a) and (b) of Figure 1 illustrate trajectories of glucose and insulin concentrations in a single patient performing the 120 minute protocol.
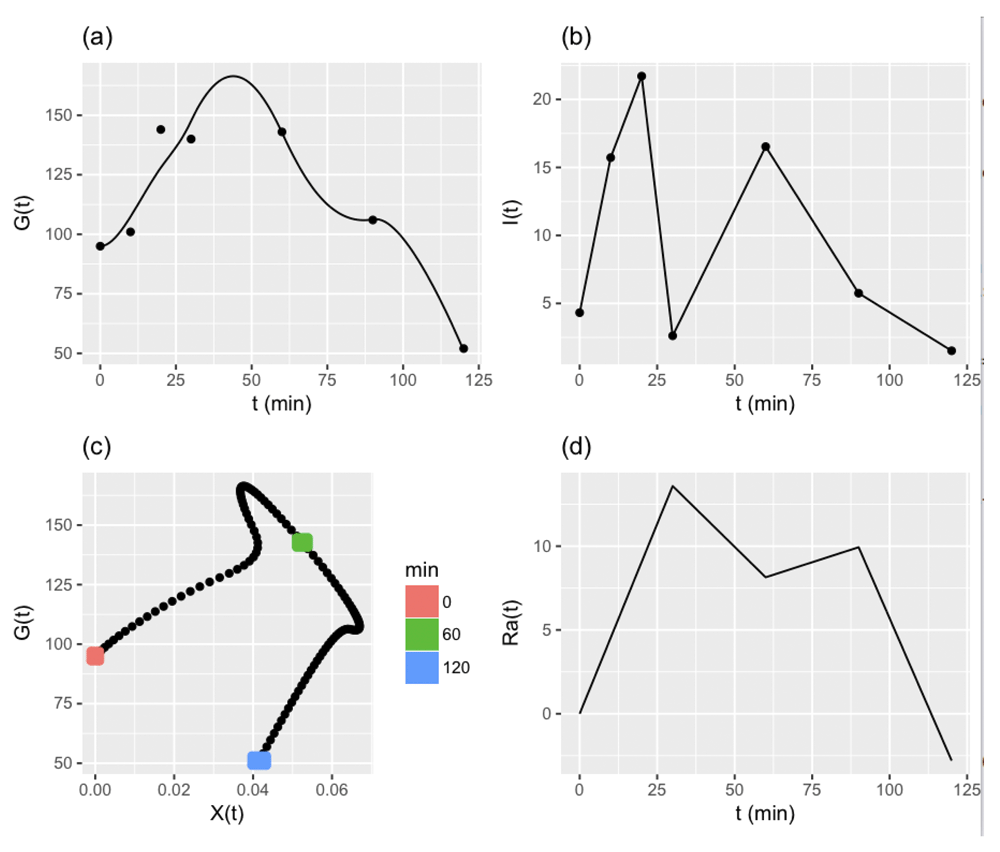
(a) The observed glucose concentrations (dots) and predictions (line). (b) Insulin concentrations (dots) and linear interpolation. (c) Predicted glucose vs. insulin action X(t). (d) Rate of appearance of glucose, Ra(t).
Methods for administering, analyzing, and clinically interpreting OGTT results are subjects of active research. Concerns with the use of individualized compartmental models for OGTT analysis are discussed in the work of Theodorakis et al. (2017). These authors propose population level nonlinear modeling for estimation of insulin sensitivity, and demonstrate that empirical Bayes procedures have desirable properties for computation and interpretation.
In this report, we describe an open-source software, ogttMetrics, for the management and analysis of OGTT series collected in large cohorts, and illustrate the application of models and metrics to a cross-over clinical trial (Sacks et al. (2014)) of effects of varying glycemic index and carbohydrate content of controlled diets. A widely cited proprietary software tool for fitting compartmental models to OGTT data is SAAM-II (Barrett et al. (1998)). We developed ogttMetrics to allow open investigation into properties of OGTT series, for which the SAAM-II models yield untenable estimates or do not converge. In addition, we saw an opportunity to develop a formal structure for collections of large numbers of OGTT series. We adopted the Bioconductor MultiAssayExperiment structure for this purpose, and introduced methods for interactive visualization and quality assessment of OGTT series, exploiting structures and functions of this package to simplify the coding.
Following Bergman et al. (1979), let G(t) and I(t) denote time-dependent plasma concentrations of glucose and insulin respectively. Various time-dependent factors affect the trajectories of these concentration functions, and we will assume that derivatives of these function with respect to time, and partial derivatives of these functions with respect to relevant time-dependent variables, can be defined. Let Ġ denote the rate of change of glucose concentration in plasma over time. Glucose effectiveness is defined as E = –∂Ġ/∂G. This is described as “the quantitative enhancement of glucose disappearance due to an increase in the plasma glucose concentration” (Bergman et al., 1979, p. E673). At steady state, insulin sensitivity is SI = ∂E/∂I. A four compartment model (model VI of Bergman et al. (1979)) leads to differential equations
G′(t) = (p1 – X(t))G(t) + B0
and
X′(t) = p2X(t) + p3I(t)
where X(t) is an abstract time-dependent function representing insulin action, G(t) is the time-dependent function representing glucose concentration, I(t) represents time-dependent insulin concentration, and B0 represents “glucose balance” (difference between rates of hepatic release to circulation and uptake in peripheral tissue) extrapolated to zero glucose concentration. By the definition of glucose effectiveness, the first differential equation implies E(t) = X(t) – p1, and, at steady state, XSS = –ISSp3/p2. This final expression is substituted into the expression for E just obtained, and after formal partial differentiation by I, we obtain SI = –p3/p2.
In the following,
G(t) is the plasma glucose concentration (mg/dl),
I(t) is the plasma insulin concentration (μU/ml),
Gb and Ib are the baseline values of glucose and insulin,
X(t) represents insulin action on glucose production and disposal (min–1),
SI is insulin sensitivity (min–1/μU · ml–1),
p2 is a rate constant for dynamics of insulin action (min–1),
Ra(α, t) denotes a time-dependent function representing appearance of glucose in plasma, with parameters α (mg · min–1/kg),
V is volume of distribution (dl/kg), and
SG is glucose effectiveness per unit volume (min-1).
We consider the specific formalism for the dalla Man et al. minimal model given by Burattini et al. (2006):
with initial conditions G(0) = Gb and X(0) = 0.
The procedure of Dalla Man et al. (2002) involves two phases. In the first phase, the system of ordinary differential equations (ODE) above is solved on the basis of provisional settings of unknown parameters. The solution yields pointwise predictions of glucose concentrations Ĝt with t ranging over the sampling time course of the OGTT. In the second phase, parameters of the ODE system are updated using non-linear least squares. The phases are iterated until the sum of squared discrepancies ∑t(Gt – Ĝt)2 converges to a minimum. Inputs to the algorithm are measured time series of glucose and insulin concentrations, and individual body weight; other quantities, such as glucose effectiveness (SG) fraction of ingested dose absorbed (FA), and volume of distribution (V) are taken as fixed constants, with values derived from results of other experiments.
The kernel of fitOneMinMod in the ogttMetrics package is
model <- function(t, Y, parameters) {
with(as.list(parameters), {
dy1 = -(Sg + Y[2]) * Y[1] + Sg * Gb + (ra(a1, a2,
a3, t, BW, D, FA, DC)/V)
dy2 = -p2 * Y[2] + p2 * SI * (Insulin(t) - Ib)
list(c(dy1, dy2))
})
}
Here the interface to lsoda in the deSolve package is employed (Hindmarsh, 1983; Petzold, 1983). The formal variables Y[1] and Y[2] represent G(t) and X(t) respectively; ra() and Insulin() are specially defined functions that return, for any given time in the course of the OGTT, the rate of glucose appearance, and insulin concentration, respectively. The lsoda solver is invoked in the function mmsolfn, whose inputs a1, a2, a3 are free parameters of a piecewise linear model for Ra(t), the rate of appearance of glucose; input SI is the target quantity of interest, the measure of insulin sensitivity. The values of free parameters are obtained by minimizing the sum of squared differences between observed glucose g and values predicted by the ODE system for current values of the unknown parameters:
mmsolfn = function(a1, a2, a3, SI) lsoda(c(Gb, 0), t, model,
c(a1 = a1, a2 = a2, a3 = a3, SI = SI))
fit = nls(g ~ mmsolfn(a1, a2, a3, SI)[, 2], start = nlsinit,
trace = nlstrace, control = fullNLScontrol)Additional quantities BW, D, FA, DC are used to implement the constraint of Dalla Man et al. (2002)
in which BW is participant body weight, D is the dose of glucose ingested, and FA is the fraction of ingested glucose that is actually absorbed; DC is constant that determines the rate of exponential decay of glucose concentration in plasma past minute 120.
For concreteness, Figure 1 displays all components of a minimal model fitted to a single 120 minute OGTT.
In practice, OGTT series can be collected according to different protocols and may include additional biomarkers such as c-peptide concentrations. For flexible data management and analysis, we adopted the data structure of the MultiAssayExperiment package of Bioconductor. We extended this structure in a class called ogttCohort, which includes metadata about timing of concentration measures. Each biomarker series for each individual is stored as a column of an R matrix, with rows and columns coordinated across assays. Arbitrary additional sample-level information can be linked to assay data. High level functions getMinmodSIs and addMatsuda120 fit the minimal model or compute the Matsuda index for each series, and append results to the data container. Because the minimal model may be time-consuming to fit, support is provided for parallel computation of multiple models. Use of a compact formal representation of all the OGTT data collected on a cohort simplifies creation of generic reports and visualizations. Figure 2 is based on the QCplots function, that can be applied to any ogttCohort instance. The top two panels display aspects of marginal (time-specific) distributions using boxplots. The bottom two panels are views of joint distributions of features and samples using the biplot methodology of Gabriel (1971). Calibrated outlier detection, proceeding under the assumption that the OGTT series are multivariate normal with a common mean vector and unspecified covariance matrix, can be conducted for glucose and insulin series separately, using mvOutliers. The procedure of Caroni & Prescott (1992) is used.

Top two panels are time-specific boxplots, bottom two are biplots based on principal components analysis of the 50x2 7-dimensional vectors of glucose and insulin concentrations in the dataset.
Theodorakis et al. (2017) mentions that the standard (proprietary, closed source) software tool SAAM-II (Barrett et al. (1998)) failed to produce accceptable estimates of insulin sensitivity in over one-third of 106 samples. Similar difficulties were encountered in the OMNICarb study. These challenges motivated us to create an open source solution that would foster investigation of aspects of glucose and insulin series for which the minimal model fails to converge, and allow comparison of alternative metrics of carbohydrate metabolism on large datasets. Figure 3 displays the SIexplorer interactive interface. Given a collection of OGTT results in an ogttCohort structure, the SI vs Matsuda panel shows the association between estimated SI, Matsuda’s index, and convergence status of the Burattini et al. formulation of the minimal model. The display is made with transformed axes (log10 for SI, square root for Matsuda’s index). Negative estimates of SI are Winsorized to the smallest positive estimate observed in the data. Positive correlation between the indices is apparent, and the general trend appears to be obeyed for the majority of estimates of SI for which the dalla Man et al., algorithm does not converge.
We created the ogttMetrics package to analyze data from the OMNICarb study (Sacks et al. (2014)). This study involved over 150 overweight individuals (BMI > 25kg=m2) whose systolic blood pressure was in the interval 120–159 mmHg, or diastolic blood pressure in the interval 70–90 mmHg. Individuals with diagnoses of diabetes, cardiovascular disease, or chronic kidney disease were excluded. Four experimental diets were designed to provide contrasting values of overall carbohydrate content and glycemic index of foods consumed. Carbohydrate and glycemic index each had two levels denoted C and c (G and g) respectively, leading to the set (CG, Cg, cG, cg) of experimental diets. Each patient received a randomly ordered sequence of diets from this set, consuming each assigned diet for five weeks, with a pause of two weeks between diets. At the end of each feeding period a 120-minute OGTT protocol was administered. As noted previously, attempts to fit the Bergman minimal model with SAAM-II frequently failed to produce acceptable values, and so the study report of effects on insulin sensitivity used Matsuda’s index. We have used the ogttMetrics package to structure the data and compute both Matsuda’s index and the minimal model SI. Figure 4 shows how the diet effects are estimated using these two indices. Confidence intervals are presented for five different contrasts. The left panel of Figure 4 is identical in content to the Insulin sensitivity panel of Figure 3 of Sacks et al. (2014). The right panel shows results based on SI that are qualitatively similar to those found with Matsuda’s index, with the exception of the estimated effect of lowering glycemic index in the context of high overall carbohydrate content. With Matsuda’s index, the 95% confidence interval excludes zero, but this is not observed when SI is used. Further work on optimizing estimation of insulin sensitivity from the 120 minute OGTT protocol is warranted; the empirical Bayes approach of Theodorakis et al. (2017) is of particular interest as individual-level estimation in that procedure borrows strength from information assembled for the cohort as a whole.
Installation of ogttMetrics can be accomplished using R 3.4 via devtools::install_github("vjcitn/ogttMetrics", dependencies=c("Depends", "Imports", “Suggests")). The key infrastructure components required for ogttMetrics are CRAN package deSolve for minimal model estimation, and Bioconductor package MultiAssayExperiment for data management. The SIexplorer utility employs the shiny package. These key components have extensive dependencies among other CRAN packages, but these dependencies are automatically resolved by the install_github() command given above. All example data analyzed or visualized in this paper are accessible using the data() function. For example, to reproduce Figure 1, use the commands library(ogttMetrics); data(obaSamp); m1 = minmodByID(obaSamp, "1"); plot_OGTT_fit(m1). For Figure 2, in the same session, use QCplots(obasamp).
Users may import data managed in spreadsheets (CSV format) for use with this software. An executable example is available with example(csvImport).
The reference assay for glucose metabolism is the hyperinsulinemic-euglycemic clamp (Soonthornpun et al. (2003)). Because it is less expensive and much less invasive, the OGTT is an attractive assay for assessing insulin sensitivity, particularly in large studies. We have presented, and made freely available (at http://github.com/vjcitn/ogttMetrics), a collection of data structures and functions in the R programming language that help manage and interpret OGTT series collected in cohort studies and clinical trials.
We and others have found that the minimal model frequently fails to generate reasonable values for SI in OGTT series encountered in practice. In part this is manifested in non-convergence of the basic nonlinear model for the glucose trajectory. However, we have not observed a striking disparity between rankings of participants using the estimate of SI based on an unsatisfactory minimal model fit, and rankings obtained when the closed form Matsuda index is computed on the same OGTT data (Figure 3, Spearman correlation between Matsuda and estimated SI = 0.5782, p < .0001). The estimated SI may be good enough for practical use, but further investigation of features of OGTT data associated with non-convergence of the minimal model, and biologically motivated elaborations of the model that yield successful fits more generally, should be undertaken.
The tools for multivariate analysis and interactive model visualization in the SIexplorer component of ogttMetrics will be useful for gaining additional insight into subtyping of patients according to features of glucose and insulin trajectories.
Software and all data analyzed in this paper are available from: http://github.com/vjcitn/ogttMetrics
Archived source code as at time of publication: DOI, 10.5281/zenodo.570174 (Carey, 2017)
License: GPL-3
Benjamin Stubbs and Keith Frankston developed software and visualizations, analyzed the data, and participated in manuscript development. Marcel Ramos developed the MultiAssayExperiment package of Bioconductor. Frank M. Sacks and Nancy Laranjo conceived and executed the OMNICarb study created the database from which ogttMetrics data are derived, and participated in manuscript development. Vincent Carey acquired funding for software development, developed software and visualizations, and wrote the manuscript.
This work was supported by US National Institutes of Health, National Institute of Diabetes and Digestive and Kidney Diseases (5R21DK098720-02; V. Carey, PI), and National Cancer Institute (5U24 CA180996-04; M. Morgan, PI.)
The funders had no role in study design, data collection and analysis, decision to publish, or preparation of the manuscript.
| Views | Downloads | |
|---|---|---|
| F1000Research | - | - |
|
PubMed Central
Data from PMC are received and updated monthly.
|
- | - |
Is the rationale for developing the new software tool clearly explained?
Yes
Is the description of the software tool technically sound?
Partly
Are sufficient details of the code, methods and analysis (if applicable) provided to allow replication of the software development and its use by others?
Partly
Is sufficient information provided to allow interpretation of the expected output datasets and any results generated using the tool?
Yes
Are the conclusions about the tool and its performance adequately supported by the findings presented in the article?
Yes
Competing Interests: No competing interests were disclosed.
Alongside their report, reviewers assign a status to the article:
| Invited Reviewers | |
|---|---|
| 1 | |
|
Version 1 16 May 17 |
read |
Provide sufficient details of any financial or non-financial competing interests to enable users to assess whether your comments might lead a reasonable person to question your impartiality. Consider the following examples, but note that this is not an exhaustive list:
Sign up for content alerts and receive a weekly or monthly email with all newly published articles
Already registered? Sign in
The email address should be the one you originally registered with F1000.
You registered with F1000 via Google, so we cannot reset your password.
To sign in, please click here.
If you still need help with your Google account password, please click here.
You registered with F1000 via Facebook, so we cannot reset your password.
To sign in, please click here.
If you still need help with your Facebook account password, please click here.
If your email address is registered with us, we will email you instructions to reset your password.
If you think you should have received this email but it has not arrived, please check your spam filters and/or contact for further assistance.
Comments on this article Comments (0)