Do funding applications where peer reviewers disagree have higher citations? A cross-sectional study

Adrian G Barnett; Scott R. Glisson; Stephen Gallo

doi:10.12688/f1000research.15479.1

Home Browse Do funding applications where peer reviewers disagree have higher...

ALL Metrics

Views

Downloads

Get PDF

Get XML

Export

▬

✚

Research Article

Negative/null result

Do funding applications where peer reviewers disagree have higher citations? A cross-sectional study

[version 1; peer review: 2 approved]

Adrian G Barnett ¹, Scott R. Glisson², Stephen Gallo²

PUBLISHED 09 Jul 2018

Author details Author details

¹ Institute of Health and Biomedical Innovation & School of Public Health and Social Work, Queensland University of Technology, Brisbane, QLD, 4059, Australia
² American Institute of Biological Sciences, Reston, Virginia, VA 20191, USA

Adrian G Barnett
Roles: Conceptualization, Formal Analysis, Methodology, Software, Visualization, Writing – Original Draft Preparation

Scott R. Glisson
Roles: Data Curation, Project Administration, Writing – Review & Editing

Stephen Gallo
Roles: Conceptualization, Data Curation, Investigation, Methodology, Writing – Review & Editing

OPEN PEER REVIEW

REVIEWER STATUS

This article is included in the Research on Research, Policy & Culture gateway.

Abstract

Background: Decisions about which applications to fund are generally based on the mean scores of a panel of peer reviewers. As well as the mean, a large disagreement between peer reviewers may also be worth considering, as it may indicate a high-risk application with a high return.
Methods: We examined the peer reviewers' scores for 227 funded applications submitted to the American Institute of Biological Sciences between 1999 and 2006. We examined the mean score and two measures of reviewer disagreement: the standard deviation and range. The outcome variable was the relative citation ratio, which is the number of citations from all publications associated with the application, standardised by field and publication year.
Results: There was a clear increase in relative citations for applications with a higher mean. There was no association between relative citations and either of the two measures of disagreement.
Conclusions: We found no evidence that reviewer disagreement was able to identify applications with a higher than average return. However, this is the first study to empirically examine this association, and it would be useful to examine whether reviewer disagreement is associated with research impact in other funding schemes and in larger sample sizes.

Keywords

meta-research, research funding, peer review, citations, research impact

Corresponding author: Adrian G Barnett

Competing interests: No competing interests were disclosed.

Grant information: AB receives funding from the Australian National Health and Medical Research Council (APP1117784).
The funders had no role in study design, data collection and analysis, decision to publish, or preparation of the manuscript.

Copyright: © 2018 Barnett AG et al. This is an open access article distributed under the terms of the Creative Commons Attribution License, which permits unrestricted use, distribution, and reproduction in any medium, provided the original work is properly cited.

How to cite: Barnett AG, Glisson SR and Gallo S. Do funding applications where peer reviewers disagree have higher citations? A cross-sectional study [version 1; peer review: 2 approved]. F1000Research 2018, 7:1030 (https://doi.org/10.12688/f1000research.15479.1) First published: 09 Jul 2018, 7:1030 (https://doi.org/10.12688/f1000research.15479.1) Latest published: 15 Oct 2018, 7:1030 (https://doi.org/10.12688/f1000research.15479.2)

Introduction

Winning funding is an important stage of the research process and researchers spend large amounts of their time preparing applications¹. Applications are typically assessed using relatively small panels of 3 to 12 peer reviewers, sometimes including external reviewers with additional expertise, which is similar to the journal process of editors and reviewers. Given the importance of funding processes to researchers’ careers and the progress of science, there is surprisingly little research on whether funding systems reliably identify the best research. A recent systematic review found there are many unanswered questions in funding peer review, and concluded, “there is a need for open, transparent experimentation and evaluation of different ways to fund research”². A prior systematic review similarly concluded that studies to examine the accuracy and soundness of funding peer review are “urgently needed”³. Whilst a systematic review of innovations for effectiveness and efficiency in peer review funding found only eight studies and called for more studies⁴.

The majority of funding systems rank applications using the mean score from the review panel, and award funding from the highest to the lowest ranked applications, stopping when the budget is exhausted (exceptions are sometimes made for applications below the funding line because of national research priorities). An interesting recent idea is that an application’s mean score may not be the only statistic worth considering, and that the standard deviation in peer reviewers’ scores may also be a useful statistic for ranking applications⁵. A zero standard deviation means all panel members gave the same score. Larger standard deviations indicate more disagreement between panel members, and this disagreement may be useful for identifying high-risk research that may also have a higher return.

Using the mean score for ranking may allow panel members to “sink” an application by awarding a low score that pulls the mean below the funding line. Including a measure of reviewer disagreement in funding could ameliorate such “sinking” and allow applications that have strong support from a few reviewers to be supported. This may also increase the diversity in what kinds of applications are funded. Some peer review systems already recognise this issue by giving each panel member a wildcard which allows them to “float” an application above the funding line regardless of other panel members’ scores. At least one funding scheme also includes patient and stakeholder reviewers to increase the diversity of viewpoints⁶.

A recent systematic review found “suggestive” evidence that funding peer review can have an anti-innovation bias² and that innovation and risk may not often be sufficiently addressed in review feedback⁷. There is evidence that riskier cross-disciplinary research has lower success rates⁸. Some researchers feel they need to write conservative applications that please all members of the panel to achieve a good average score⁹. However, supporting risky research can have huge benefits for society when it pays off¹⁰. In a survey of Australian researchers, 90% agreed with the statement: “I think the NHMRC [the main Australian funding body for health and medical research] should fund risky research that might fail but, if successful, would change the scientific field”¹¹.

Previous studies have investigated the association between an application’s mean score (or ranking based on the mean) and subsequent citations, where citations are used as a measure of success. Many studies using large sample sizes found either no association or only a weak association between the mean score and the citations of subsequent publications^12–16. Other studies have shown a positive association between higher mean peer review scores and increased citations^17,18, including a study that used the same data analyzed here¹⁹. To our knowledge, no previous study has empirically estimated how the disagreement in peer reviewers’ scores may also predict citations.

Methods

Application data

We examined 227 successful grant applications submitted to the American Institute of Biological Sciences between the years 1999 to 2006. These successful applications came from 2,063 total applications (overall 11% success rate). The applications covered a wide range of biomedical research areas, including vision, drug abuse, nutrition, blood-related cancer, kidney disease, autoimmune diseases, malaria, tuberculosis, osteoporosis, arthritis and autism. Applications were assessed by between 2 and 18 peer reviewers, with a median of 10 reviewers. Panels evaluated an average of 25 applications over two days. Ninety percent of applications were reviewed by on-site panels with an average size of 10 reviewers, and 10% of applications were reviewed via teleconferences of 3 reviewers. Further details on the funding process is available in a previous study of how the applications’ mean scores predicted citations¹⁹.

Our key predictor is the peer reviewers’ scores. Individual peer reviewers, who were not conflicted, scored applications between 1.0 (best) to 5.0 (worst) in 0.1 increments. To determine funding, the score was averaged across all reviewers. In this study we also consider statistics that measure within-panel disagreement, which are the standard deviation and the range (largest minus smallest score).

Citation counts

The primary outcome is the citation counts from publications associated with the successful application. The publication data for the funded applications were taken from the mandatory final reports submitted by the applicants. On average, these reports were submitted 5 years after the application’s peer review. Publications were produced from 1 to 8 (average 4.3) years after the review date. Only peer-reviewed publications were counted, confirmed through PubMed and Web of Knowledge searches. Publications listed in the final report as “submitted” or “in preparation”, were included if they could be found as peer-reviewed published papers. Citations were counted in 2014 using Web of Knowledge.

This analysis used 20,313 citations from 805 peer reviewed publications. The total citation level per funded application was the cumulative citations of all publications. As citations are time-dependent they were standardized using the average citation level of all publications by scientific field and year, using data from a published calculation using the Thomson Reuters Essential Science Indicators database²⁰. These published average rates were determined for 2000–2010 by scientific field, assessed in 2011 and displayed a linear relationship with time (e.g., R² = 0.99 for the field of molecular biology). We chose molecular biology because it was the highest cited field and in general was the field most applicable to the funded applications.

Because the Reuters curve was assessed in 2011, we extended the curve for 2014, back calculating using a linear fit which had a very high R² of 0.99. In this way, we could most accurately standardize the data for the relationship between publication date and citation level and could calculate the Total Relative Citation per application. A total relative citation of 1 meant the application achieved the average number of citations, whereas values above 1 meant a higher than average number of citations.

We note that a recent study that used both unadjusted citation counts and relative citations, found the two measures gave similar results when used as the key outcome variable²¹.

Statistical analyses

The total relative citations were modelled using a multiple regression model. We ran two models with the three application variables:

1. Review year, mean score, score standard deviation
2. Review year, mean score, score range

Our aim was to examine two measures of panel disagreement: the standard deviation and range. We included mean score because it has already been shown to be an important predictor for these data¹⁹ and we were interested in the additional value of a measure of disagreement. We adjusted for review year (1999 to 2006) because there was a difference in the application score statistics over time, and because year was associated with citation numbers, hence it was a potential confounder.

The citations were first base e log-transformed because of their positive skew. We added a small positive constant of 0.1 before using the log-transform because some citations were zero. The estimates were back-transformed and plotted to show the results on the original relative citations scale. Using equations the multiple regression model was:

\begin{array}{l} \log_{e} (Y_{i} + 0.1) \sim N (μ_{i}, σ^{2}), i = 1, \dots, N, \\ μ_{i} = β_{0} + \sum_{j = 1}^{3} β_{j} f (X_{i, j}) + γ_{p (i)}, \\ γ_{k} \sim N (0, σ_{γ}^{2}), k = 1, \dots, M, \end{array}

where Y are the citations and γ are random intercepts to adjust for the potential within-panel correlation in citations (where p(i) is the panel number for application i and M is the total number of panels). The mean (µ) had a constant (β₀) and the three application predictors (X) which were first transformed using a fractional polynomial function.

Associations between the score statistics and citation outcomes could be non-linear, for example a larger difference in citations for a change in mean score from 1.0 to 1.1 compared with a change from 2.0 to 2.1. To model this potential non-linearity we used fractional polynomials to examine a range of non-linear associations between the scores and citations²². The fractional polynomial function is:

f (X_{i}) = {\begin{array}{l} \begin{array}{l} X_{i}^{P}, P \neq 0, \\ \log_{e} (X_{i}), P = 0. \end{array} \end{array}

We examined the eight transformations of: P = {−2, −1, −0.5, 0, 0.5, 1, 2, 3} and chose the optimal P using the deviance. The optimal P was chosen for each of the three predictors, meaning we examined 8³ = 512 models in total. We only present results for the best model with the smallest deviance. We checked the distribution of the model residuals for multi-modality and outliers, and used Cook’s distance to find influential observations.

Missing data

Sixteen (7%) observations were missing the score standard deviation and 32 (14%) observations were missing the score range because the individual peer reviewer scores were no longer available for some applications at the time of this retrospective analysis. These missing observations were imputed using linear regression with the application variables: review year, mean score, score standard deviation, minimum score, maximum score and range. We used five multiple imputations.

All analyses were made using R version 3.4.4²³ with the imputations using the “MICE” package²⁴. The code and anonymized data are available here: http://doi.org/10.5281/zenodo.1299384²⁵.

We report our results using the STROBE guidelines for observational research²⁶.

Results

The histograms in Figure 1 show the distributions of total relative citations and the application score statistics: mean, standard deviation, minimum, maximum and range (maximum minus minimum). There was a strong positive skew in citations with one outlying relative citation of 104; the next largest citation was 34. To counter this positive skew we used a base e log transform in later analyses. There was also a positive skew in the score standard deviation and range, and we also log-transform these predictors.

Figure 1. Histograms of total relative citations (green) and application score statistics (blue).

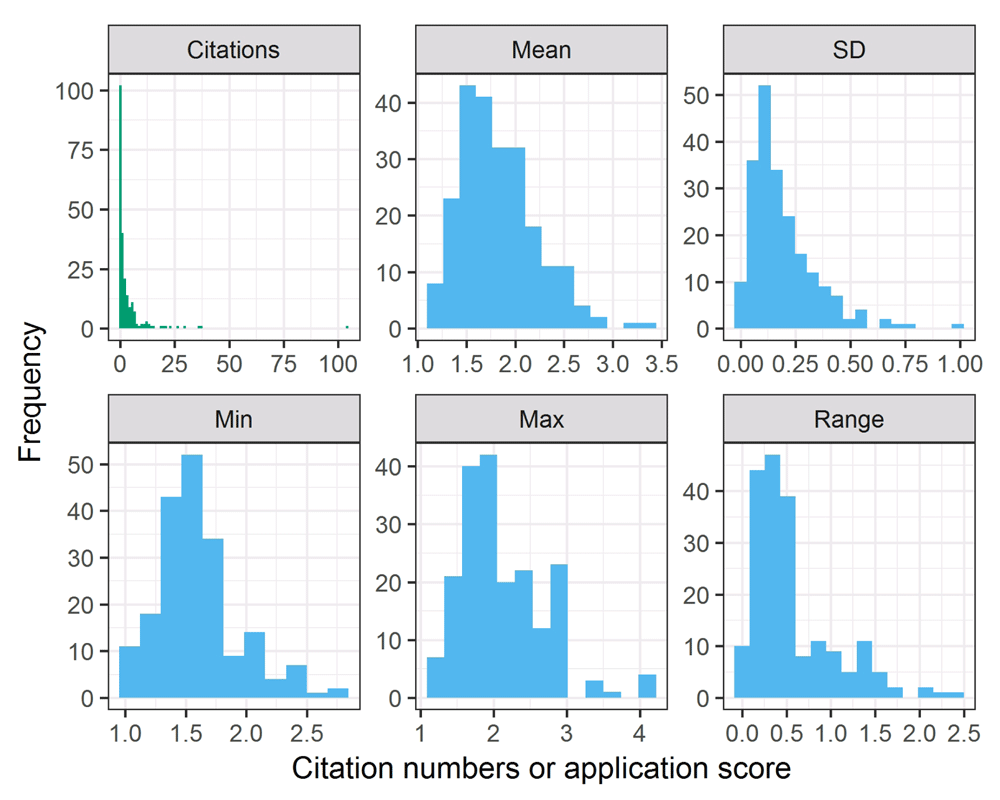
The lower the mean score, the better the application did in peer review.

The scatter-plots in Figure 2 show the associations between the application score statistics. There was a strong correlation between the standard deviation and maximum (0.80), but not between the standard deviation and minimum (0.05). This indicates the largest disagreement is where at least one panel member has given a poor score (remembering lower scores are better). Applications where there was one dissenting panel member with a good score were unlikely to be funded as their mean score would not be competitive, and hence are not in this sample. There was a strong positive correlation between the two measures of panel disagreement, the standard deviation and range (0.93).

Figure 2. Scatter-plots and Pearson correlations of application score statistics.

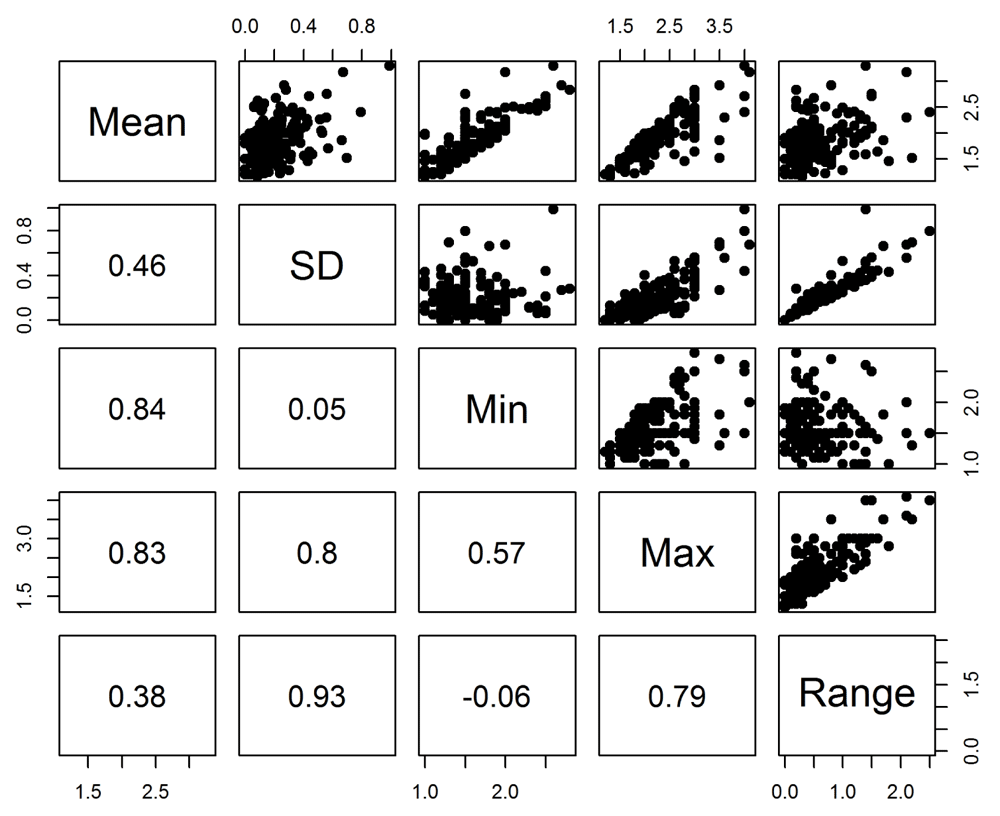
The numbers in the bottom-left diagonal of the plot matrix are the Pearson correlations.

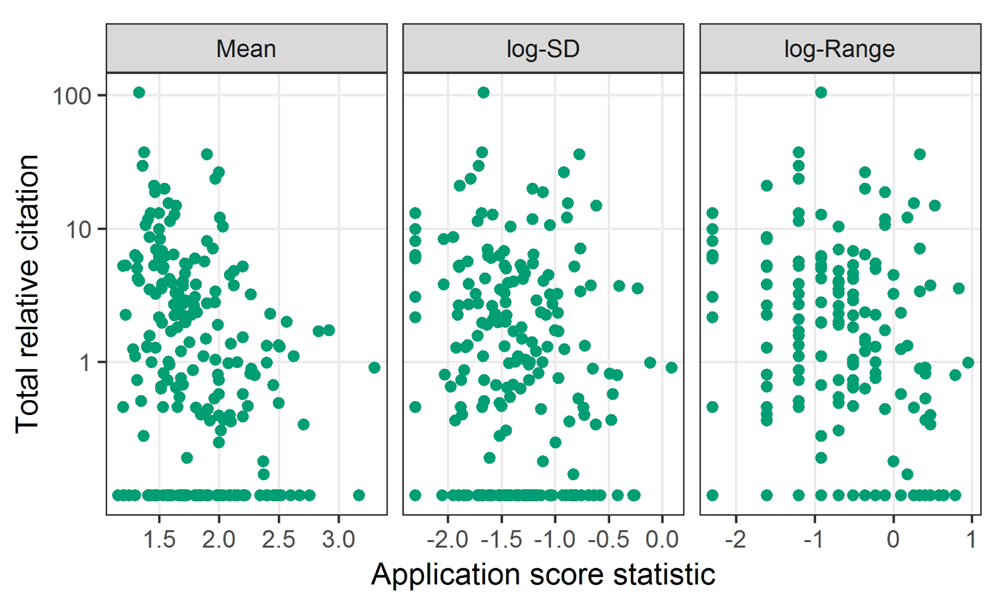
The scatter-plots in Figure 3 show the association between total relative citations and the score statistics. We used the log-transformed citations and the standard deviation and range to remove the skew and so show a clearer association. The variance in log-citations appears relatively stable over the score statistics, somewhat confirming the validity of log-transforming the citations²⁷. The points along the bottom of the y-axis are the 74 applications (33%) with no citations. Some association between mean score and citations is visible, with a generally downward pattern in citations for increasing score. There is no clear association between citations and either the standard deviation or range.

Figure 3. Scatter-plots of log-transformed total relative citations against application score statistics.

The results from the multiple linear regression models are in Table 1. Only the application’s mean score had a statistically significant association with citation numbers.

Table 1. Parameter estimates for the multiple regression models predicting citation numbers.

FP = fractional polynomial.

Model 1	FP	Mean (95% CI)
Mean score	–0.5	5.9 (2.6 to 9.1)
Standard deviation	3	0.7 (–1.3 to 2.7)
Review year	–0.5	–1.2 (–3.0 to 0.6)
Model 2	FP	Mean (95% CI)
Mean score	–0.5	5.4 (2.2 to 8.7)
Range	–0.5	–0.1 (–1.0 to 0.8)
Review year	–0.5	–1.2 (–3.0 to 0.6)

The predictions from the multiple linear regression models are in Figure 4. There was a reduction in citations for applications with a higher (worse) mean score. The mean lines are flat for both the standard deviation and range, indicating no association between these score statistics and citation numbers. The 95% confidence intervals for the standard deviation are very wide for large standard deviations. The application with the largest standard deviation was influential according to Cook’s statistic, and removing this application had little impact on the mean line but did reduce these wide intervals (see additional results at https://github.com/agbarnett/funding.disagree). The model residuals had an approximately symmetric and unimodal distribution with no outliers.

Figure 4. Predicted relative citations using the best fractional polynomial for the application score statistics.

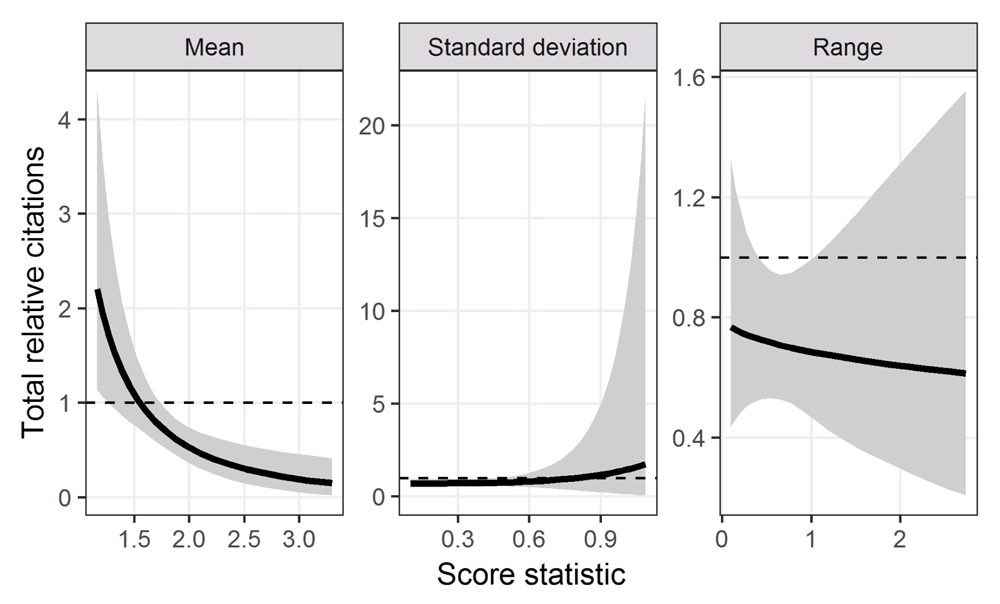
The solid lines are the means and the grey areas are 95% confidence intervals. The dotted horizontal line at 1 represents the average citations, so values above this are better than average.

Discussion

We found a statistically significant association between an application’s mean score and subsequent citation counts, with the result in the expected direction because applications with better scores had more citations (on average). The largest size of the increase is also practically significant as the highest scores have a mean of 2 (Figure 4), meaning double the average citations.

We found no association between the two measures of reviewer disagreement and citations counts. It appears that any disagreement between peer reviewers did not indicate an application with a potentially high return.

Disagreements between reviewers about an application can stem from different sources. Disagreements about the proposed methods may mean the study is not viable and would struggle to produce valid results and/or publish papers. Disagreements about the application’s goals may reflect a difference of opinion about the potential impact, and it is these disagreements that are likely more subjective and hence where a higher return is possible if one reviewer is right. Disagreements between reviewers can also occur for more trivial reasons such as the dynamics of the panel and personal disagreements²⁸. A more sophisticated measure of panel disagreement to those used here may be more predictive of the benefits of the research, but such measures would need to be well-defined and prospectively recorded at the panel meeting. Some reviews already breakdown scores into separate areas, such as track record and innovation, and reviewer disagreement could be examined using these separate scores. Each reviewer brings their own experience and biases to the funding process and such intellectual differences influence application scores^29,30. Indeed, some recent research has recently indicated that there is more variability in score across reviewers than across proposals³¹ and previous results indicate inter-rater reliability as very low³². An application’s average score is somewhat due to the “luck of the draw” of what reviewers were selected³³. Variations can also occur because of the way the application is summarised at the panel meeting^28,34. If a larger disagreement leads to high-risk returns then we might expect an increase in the variance in citations for larger score standard deviations and ranges. This is because there might be more “failures” with zero citations, but also more big returns. Our multiple regression models only examined a change in mean citations and a different statistical model would be needed to examine a change in variance. However, the scatter-plots in Figure 3 show no sign of an increasing variance in citations for higher standard deviations or ranges.

Limitations

Some have argued that studies like ours are invalid because: 1) they only consider funded applications and do not include unfunded studies, 2) an application’s score is not the only criteria used to award funding (e.g., applications with low scores awarded funding because of national priorities), and 3) because budgets are frequently cut, meaning the actual research may differ from the application³⁵. Studies that follow funded and unfunded fellowship applicants are possible, e.g., 36, but this is very difficult when examining projects that need specific funding³⁷. We believe, despite the limitations of bibliometric measures, it is reasonable to expect a dose-response association between scores and citations within funded applications. Samples that include applications that were funded for reasons other than their mean score, such as national priorities, increase the variance in the key predictors of application scores statistics and hence increase statistical power. Cuts to the budget are important and can hinder the planned research. However, assuming the reviewers believed the study was still viable with the reduced budget, such studies still test the ability of a panel to predict what research will have the greatest return.

Citations are an imperfect measure of the impact of research because many citations have little worth and scientists often report that their most highly cited work is not their best³⁸. Studies that examine more detailed outcomes such as translation into practice or cost-benefits would be incredibly useful, however these studies would themselves require funding as it would involve further data collection, analyses and interviews of the applicants. Our results may not be generalisable to other funding schemes, especially as there are large differences between fields in their perceptions of what makes a good application²⁸. It would be useful to examine whether reviewer disagreement is associated with research impact in other funding schemes and in larger sample sizes.

Conclusions

We found no association between two measures of reviewer disagreement when assessing an application and the subsequent research impact of that application as measured by citation counts.

Data availability

The code and anonymized data are available here: http://doi.org/10.5281/zenodo.1299384²⁵.

Competing interests

No competing interests were disclosed.

Grant information

AB receives funding from the Australian National Health and Medical Research Council (APP1117784).

The funders had no role in study design, data collection and analysis, decision to publish, or preparation of the manuscript.

Acknowledgements

We thank the AIBS SPARS staff for their work in implementing these reviews for nearly a decade.

Faculty Opinions recommended

References

1. Herbert DL, Barnett AG, Clarke P, et al.: On the time spent preparing grant proposals: an observational study of Australian researchers. BMJ Open. 2013; 3(5): pii: e002800. PubMed Abstract | Publisher Full Text | Free Full Text
2. Guthrie S, Ghiga I, Wooding S: What do we know about grant peer review in the health sciences? [version 2; referees: 2 approved]. F1000Res. 2018; 6: 1335. PubMed Abstract | Publisher Full Text | Free Full Text
3. Demicheli V, Di Pietrantonj C: Peer review for improving the quality of grant applications. Cochrane Database Syst Rev. 2007; (2): MR000003. PubMed Abstract | Publisher Full Text
4. Shepherd J, Frampton GK, Pickett K, et al.: Peer review of health research funding proposals: A systematic map and systematic review of innovations for effectiveness and efficiency. PLoS One. 2018; 13(5): e0196914. PubMed Abstract | Publisher Full Text | Free Full Text
5. Linton JD: Improving the peer review process: Capturing more information and enabling high-risk/high-return research. Research Policy. 2016; 45(9): 1936–1938. Publisher Full Text
6. Fleurence RL, Forsythe LP, Lauer M, et al.: Engaging patients and stakeholders in research proposal review: the patient-centered outcomes research institute. Ann Intern Med. 2014; 161(2): 122–130. PubMed Abstract | Publisher Full Text
7. Gallo S, Thompson L, Schmaling K, et al.: Risk evaluation in peer review of grant applications. Environment Systems and Decisions. 2018; 38(2): 216–229. Publisher Full Text
8. Bromham L, Dinnage R, Hua X: Interdisciplinary research has consistently lower funding success. Nature. 2016; 534(7609): 684–687. PubMed Abstract | Publisher Full Text
9. Fang FC, Casadevall A: NIH peer review reform--change we need, or lipstick on a pig? Infect Immun. 2009; 77(3): 929–932. PubMed Abstract | Publisher Full Text | Free Full Text
10. Braben DW: Promoting the Planck Club: How Defiant Youth, Irreverent Researchers and Liberated Universities Can Foster Prosperity Indefinitely. Wiley, 2014; ISBN 9781118546383. Reference Source
11. Barnett AG: Ask the researcher: The experience of applying for health and medical research funding in Australia Survey results. 2017. Reference Source
12. Scheiner SM, Bouchie LM: The predictive power of NSF reviewers and panels. Frontiers in Ecology and the Environment. 2013; 11(8): 406–407. Publisher Full Text
13. Kaltman JR, Evans FJ, Danthi NS, et al.: Prior publication productivity, grant percentile ranking, and topic-normalized citation impact of NHLBI cardiovascular R01 grants. Cir Res. 2014; 115(7): 617–624. PubMed Abstract | Publisher Full Text | Free Full Text
14. Lauer MS, Danthi NS, Kaltman J, et al.: Predicting productivity returns on investment: Thirty years of peer review, grant funding, and publication of highly cited papers at the National Heart, Lung, and Blood Institute. Circ Res. 2015; 117(3): 239–243. PubMed Abstract | Publisher Full Text | Free Full Text
15. Doyle JM, Quinn K, Bodenstein YA, et al.: Association of percentile ranking with citation impact and productivity in a large cohort of de novo NIMH-funded R01 grants. Mol Psychiatry. 2015; 20(9): 1030–1036. PubMed Abstract | Publisher Full Text | Free Full Text
16. Fang FC, Bowen A, Casadevall A: NIH peer review percentile scores are poorly predictive of grant productivity. eLife. 2016; 5. pii: e13323. PubMed Abstract | Publisher Full Text | Free Full Text
17. Danthi N, Wu CO, Shi P, et al.: Percentile ranking and citation impact of a large cohort of National Heart, Lung, and Blood Institute-funded cardiovascular R01 grants. Circ Res. 2014; 114(4): 600–606. PubMed Abstract | Publisher Full Text | Free Full Text
18. Li D, Agha L: Research funding. Big names or big ideas: do peer-review panels select the best science proposals? Science. 2015; 348(6233): 434–8. PubMed Abstract | Publisher Full Text
19. Gallo SA, Carpenter AS, Irwin D, et al.: The validation of peer review through research impact measures and the implications for funding strategies. PLoS One. 2014; 9(9): e106474. PubMed Abstract | Publisher Full Text | Free Full Text
20. Times Higher Education: Citation averages, 2000-2010, by fields and years. 2011. Reference Source
21. Lindner MD, Torralba KD, Khan NA: Scientific productivity: An exploratory study of metrics and incentives. PLoS One. 2018; 13(4): e0195321. PubMed Abstract | Publisher Full Text | Free Full Text
22. Royston P, Ambler G, Sauerbrei W: The use of fractional polynomials to model continuous risk variables in epidemiology. Int J Epidemiol. 1999; 28(5): 964–974. PubMed Abstract | Publisher Full Text
23. R Core Team: A Language and Environment for Statistical Computing. R Foundation for Statistical Computing, Vienna, Austria, 2018. Reference Source
24. van Buuren S, Groothuis-Oudshoorn K: mice: Multivariate imputation by chained equations in R. J Stat Softw. 2011; 45(3): 1–67. Publisher Full Text
25. Barnett AG: agbarnett/funding.disagree: First release of funding disagreement code and data (version v1.0). 2018. Publisher Full Text
26. von Elm E, Altman DG, Egger M, et al.: The Strengthening the Reporting of Observational Studies in Epidemiology (STROBE) statement: guidelines for reporting observational studies. PLoS Med. 2007; 4(10): e296. PubMed Abstract | Publisher Full Text | Free Full Text
27. Manning WG: The logged dependent variable, heteroscedasticity, and the retransformation problem. J Health Econ. 1998; 17(3): 283–95. PubMed Abstract | Publisher Full Text
28. Coveney J, Herbert DL, Hill K, et al.: ‘Are you siding with a personality or the grant proposal?’: observations on how peer review panels function. Res Integr Peer Rev. 2017; 2(1): 19. PubMed Abstract | Publisher Full Text | Free Full Text
29. Boudreau KJ, Guinan EC, Lakhani KR, et al.: Looking Across and Looking Beyond the Knowledge Frontier: Intellectual Distance, Novelty, and Resource Allocation in Science. Manage Sci. 2016; 62(10): 2765–2783. PubMed Abstract | Publisher Full Text | Free Full Text
30. Gallo SA, Sullivan JH, Glisson SR: The Influence of Peer Reviewer Expertise on the Evaluation of Research Funding Applications. PLoS One. 2016; 11(10): e0165147. PubMed Abstract | Publisher Full Text | Free Full Text
31. Pier EL, Brauer M, Filut A, et al.: Low agreement among reviewers evaluating the same NIH grant applications. Proc Natl Acad Sci U S A. 2018; 115(12): 2952–2957. PubMed Abstract | Publisher Full Text | Free Full Text
32. Cicchetti DV: The reliability of peer review for manuscript and grant submissions: A cross-disciplinary investigation. Behavioral and Brain Sciences. 1991; 14(1): 119–135. Publisher Full Text
33. Graves N, Barnett AG, Clarke P: Funding grant proposals for scientific research: retrospective analysis of scores by members of grant review panel. BMJ. 2011; 343: d4797. PubMed Abstract | Publisher Full Text | Free Full Text
34. Gregorius S, Dean L, Cole DC, et al.: The peer review process for awarding funds to international science research consortia: a qualitative developmental evaluation [version 3; referees: 2 approved]. F1000Res. 2018; 6: 1808. PubMed Abstract | Publisher Full Text | Free Full Text
35. Lindner MD, Nakamura RK: Examining the Predictive Validity of NIH Peer Review Scores. PLoS One. 2015; 10(6): e0126938. PubMed Abstract | Publisher Full Text | Free Full Text
36. Bornmann L, Wallon G, Ledin A: Does the committee peer review select the best applicants for funding? An investigation of the selection process for two European molecular biology organization programmes. PLoS One. 2008; 3(10): e3480. PubMed Abstract | Publisher Full Text | Free Full Text
37. Decullier E, Huot L, Chapuis FR: Fate of protocols submitted to a French national funding scheme: A cohort study. PLoS One. 2014; 9(6): e99561. PubMed Abstract | Publisher Full Text | Free Full Text
38. Ioannidis JP, Boyack KW, Small H, et al.: Bibliometrics: Is your most cited work your best? Nature. 2014; 514(7524): 561–562. PubMed Abstract | Publisher Full Text

Comments on this article Comments (0)

Version 2

VERSION 2 PUBLISHED 09 Jul 2018

Author details Author details

Adrian G Barnett
Roles: Conceptualization, Formal Analysis, Methodology, Software, Visualization, Writing – Original Draft Preparation

Scott R. Glisson
Roles: Data Curation, Project Administration, Writing – Review & Editing

Stephen Gallo
Roles: Conceptualization, Data Curation, Investigation, Methodology, Writing – Review & Editing

Competing interests

No competing interests were disclosed.

Grant information

AB receives funding from the Australian National Health and Medical Research Council (APP1117784).
The funders had no role in study design, data collection and analysis, decision to publish, or preparation of the manuscript.

Article Versions (2)

version 2

Revised

Published: 15 Oct 2018, 7:1030

https://doi.org/10.12688/f1000research.15479.2

version 1

Published: 09 Jul 2018, 7:1030

https://doi.org/10.12688/f1000research.15479.1

© 2018 Barnett AG et al. This is an open access article distributed under the terms of the Creative Commons Attribution License, which permits unrestricted use, distribution, and reproduction in any medium, provided the original work is properly cited.

Download

Export To

metrics

	Views	Downloads
F1000Research	-	-
PubMed Central Data from PMC are received and updated monthly.	-	-

Citations

SEE MORE DETAILS

CITE

how to cite this article

Barnett AG, Glisson SR and Gallo S. Do funding applications where peer reviewers disagree have higher citations? A cross-sectional study [version 1; peer review: 2 approved]. F1000Research 2018, 7:1030 (https://doi.org/10.12688/f1000research.15479.1)

NOTE: If applicable, it is important to ensure the information in square brackets after the title is included in all citations of this article.

track

receive updates on this article

Track an article to receive email alerts on any updates to this article.

Open Peer Review

Version 1

VERSION 1

PUBLISHED 09 Jul 2018

Views

Reviewer Report 24 Sep 2018

Shahar Avin, Centre for the Study of Existential Risk, University of Cambridge, Cambridge, UK

Steven Wooding, Centre for Science and Policy, University of Cambridge, Cambridge, UK

Approved

https://doi.org/10.5256/f1000research.16873.r37261

Rank proposals based on their mean scores until funding runs out.
Pool proposals based on their mean score into buckets, rounding to the nearest integer. Fund all proposals with a mean of 1 (1.0-1.49, n=45), then from the bucket with a mean of 2 (1.5-2.49, n=114) rank proposals based on their standard deviation and fund until funding runs out.

Under both methods, all proposals with a mean of 1 are funded, for a total TRC of 319.9. When we look at the proposals in the second bucket, when funding according to method 1, the total TRC for this bucket is 224.2, whereas for method 2 it is 195.5. However, the highest citation-receiving proposal in the second bucket under method 1 has a TRC of 19.9, whereas the highest citation-receiving proposal from the second bucket under method 2 has a TRC of 35.9 (the third highest TRC in the entire sample). This fits with Gillies' description of peer-review as going for less risky proposals, but at the cost of throwing out the occasional exceptional proposal. This is also born out by the distribution of TRCs, with the standard deviation of TRCs for the second bucket under method 1 being 4.2, and under method 2 being 6.2.

Thirdly, it would be valuable to understand what sorts of disagreement exist in the scoring of all the applications (both successful and unsuccessful). It could be argued that the type of disagreement likely to indicate high risk/high return proposals would be bi-modal – some good reviews maybe with scores of 1-1.5, some very poor reviews maybe with scores of 3-4. Given the small fraction of applications funded, very few applications of this nature would be funded (due to the understandable aggregation in the shared data we could not examine the exact number, but fewer than 10 applications have a score lower than 3). Do such applications with such bi-modal review scores exist? Or is the level of disagreement seen in the successful applications similar to that of the unsuccessful applications?

The above questions only suggest that there is further complexity here that needs to be explored, with more complex, higher power studies. We thank the authors for paving the path for such studies, and for making their underlying data and analysis available in a form that is easy to explore.

Two small notes:

It might be easier to read the paper if scores were consistently referred to as best/worst and better/worse – using ‘higher' is confusing when better scores are lower.
It would be more elegant to give 'e.g., Bornmann et al, 2008' rather than 'e.g., 36'.

Is the work clearly and accurately presented and does it cite the current literature?

Yes
Is the study design appropriate and is the work technically sound?

Yes
Are sufficient details of methods and analysis provided to allow replication by others?

Yes
If applicable, is the statistical analysis and its interpretation appropriate?

Yes
Are all the source data underlying the results available to ensure full reproducibility?

Yes
Are the conclusions drawn adequately supported by the results?

Yes

References

1. Linton J: Improving the Peer review process: Capturing more information and enabling high-risk/high-return research. Research Policy. 2016; 45 (9): 1936-1938 Publisher Full Text
2. Greenberg D: Chance and grants. The Lancet. 1998; 351 (9103). Publisher Full Text
3. Gillies D: How should research be organised?. College Publications. 2008.

Competing Interests: No competing interests were disclosed.

We confirm that we have read this submission and believe that we have an appropriate level of expertise to confirm that it is of an acceptable scientific standard.

CITE

Report a concern

Author Response 15 Oct 2018

Adrian Barnett, Institute of Health and Biomedical Innovation & School of Public Health and Social Work, Queensland University of Technology, Brisbane, 4059, Australia

15 Oct 2018

Author Response
The notion that disagreements amongst reviewers might indicate a promising high-risk/high-reward project certainly has currency amongst those who consider how the system might be improved. In addition to the framework ... Continue reading
The notion that disagreements amongst reviewers might indicate a promising high-risk/high-reward project certainly has currency amongst those who consider how the system might be improved. In addition to the framework of Linton (2016)1, the idea is also present in the model of Brezis (2007) and is implied by several works on the anti-innovation bias of grant peer review (e.g. Greenberg, 1998 2; Gillies, 2008 3). However, this intuitive notion has yet to be put to the test, until the current study, which is a welcome contribution.
Thanks for the interesting references, we have now mentioned Brezis in our Introduction.
The experimental design and statistical analysis are compelling for an initial study, though as the authors note further complications could be addressed in later work.
Given the prevailing policy and academic discussions the negative result is surprising and it rules out some suggested approaches to reform of the grant allocation system; however, the dataset limits the generality of the conclusions that can be drawn (through no fault of the authors) – the key limitation being that only 11% of applications can be analysed (the funded ones), a set that is heavily skewed towards the top scoring applications.
We agree this is a key limitation, and it would be useful to repeat the study in a more generous scheme, where a greater proportion of applications were funded.
For example, as shown in Figure 4 there is plenty of potential for SD to be associated with increased citation, but not enough data to tell. The authors note that the application with the largest SD drove this large uncertainty – it could be that this application is an outlier, or it could be that it is typical of applications with large SDs but there are very few of them in the dataset because they tended to fall below the funding line.
This is entirely possible, and if there are a small number of extremely high pay-off projects then we would need a much larger sample to robustly test if there is a consistent pattern of more high pay-off projects associated with greater disagreement. We have now mentioned this in the limitations.
Through its analysis, the study forces a refinement of the question of what sorts of disagreements (in extent and driven by what underlying logics) should be considered useful indicators. We suggest the study raises the following THREE questions for future work:
Firstly it would be valuable to understand the reasons and logics behind the disagreements that arise between reviewers, from the fact that "disagreements between reviewers about an application can stem from different sources". While the authors suggest addressing this with further information about scores, we can also ask if different score means might indicate different "regimes" for disagreement, e.g. disagreement along the lines of "not sure this will work" or "this goes against received wisdom" at relatively high score means, and disagreements along the lines of "not sure what this is about" or "hasn't this been tried before?" at lower score means. Qualitative research asking reviewers about their scoring behaviour could help understand the reasoning that goes with different scoring.
This is a good point. “Disagreement” is likely to be too general a word, and future studies could look in far more detail at the types of disagreement. We have previously used a qualitative researcher as an observer of funding panel dynamics, and we have now added this potential approach to our discussion.
Secondly, we could reframe the question to address the lack of information on unfunded applications by asking how can funding best be allocated if the amount of funding available is cut by 50%.
To test this, we reanalysed the data provided by the authors with the following question: assuming only half the funding was available, which of the following selection methods would perform better?
Rank proposals based on their mean scores until funding runs out.
Pool proposals based on their mean score into buckets, rounding to the nearest integer. Fund all proposals with a mean of 1 (1.0-1.49, n=45), then from the bucket with a mean of 2 (1.5-2.49, n=114) rank proposals based on their standard deviation and fund until funding runs out.
Under both methods, all proposals with a mean of 1 are funded, for a total TRC of 319.9. When we look at the proposals in the second bucket, when funding according to method 1, the total TRC for this bucket is 224.2, whereas for method 2 it is 195.5. However, the highest citation-receiving proposal in the second bucket under method 1 has a TRC of 19.9, whereas the highest citation-receiving proposal from the second bucket under method 2 has a TRC of 35.9 (the third highest TRC in the entire sample). This fits with Gillies' description of peer-review as going for less risky proposals, but at the cost of throwing out the occasional exceptional proposal. This is also born out by the distribution of TRCs, with the standard deviation of TRCs for the second bucket under method 1 being 4.2, and under method 2 being 6.2.
This is an interesting comment and thanks for the new analysis. As an aside, we note that only by sharing our data can we have such an in-depth discussion with our reviewers. We have added R code to run these suggested analyses to our results on github (https://github.com/agbarnett/funding.disagree).
It is an interesting approach to use the mean for the “top” tier of applications and the standard deviation for the second tier. This may appeal to funders and panel members, because we believe there will always be a desire to fund those applications with the best mean. This two-tier approach may also be easier to explain than the Black–Scholes approach suggested by Linton, which combines the mean and variance in scores using an equation.
We are wary of using the standard deviation in the total relative citations because of the strong positive skew in its distribution, and the inter-quartile range in citations is actually larger for the approach using the mean at 4.3, compared with 2.9 when using the standard deviation.
Thirdly, it would be valuable to understand what sorts of disagreement exist in the scoring of all the applications (both successful and unsuccessful). It could be argued that the type of disagreement likely to indicate high risk/high return proposals would be bi-modal – some good reviews maybe with scores of 1-1.5, some very poor reviews maybe with scores of 3-4. Given the small fraction of applications funded, very few applications of this nature would be funded (due to the understandable aggregation in the shared data we could not examine the exact number, but fewer than 10 applications have a score lower than 3). Do such applications with such bi-modal review scores exist? Or is the level of disagreement seen in the successful applications similar to that of the unsuccessful applications?
Unfortunately our data only contains the summary statistics on the applications’ scores and so we can’t examine these distributions. We have added this as a limitation.
The above questions only suggest that there is further complexity here that needs to be explored, with more complex, higher power studies. We thank the authors for paving the path for such studies, and for making their underlying data and analysis available in a form that is easy to explore.
Thanks, we agree that larger studies are needed.
Two small notes:

It might be easier to read the paper if scores were consistently referred to as best/worst and better/worse – using ‘higher' is confusing when better scores are lower.

Agreed and changed. We’ve also added text labels to Figure 5 and the new Figure 4.

It would be more elegant to give 'e.g., Bornmann et al, 2008' rather than 'e.g., 36'.

Changed as suggested.
The notion that disagreements amongst reviewers might indicate a promising high-risk/high-reward project certainly has currency amongst those who consider how the system might be improved. In addition to the framework of Linton (2016)1, the idea is also present in the model of Brezis (2007) and is implied by several works on the anti-innovation bias of grant peer review (e.g. Greenberg, 1998 2; Gillies, 2008 3). However, this intuitive notion has yet to be put to the test, until the current study, which is a welcome contribution.
Thanks for the interesting references, we have now mentioned Brezis in our Introduction.
The experimental design and statistical analysis are compelling for an initial study, though as the authors note further complications could be addressed in later work.
Given the prevailing policy and academic discussions the negative result is surprising and it rules out some suggested approaches to reform of the grant allocation system; however, the dataset limits the generality of the conclusions that can be drawn (through no fault of the authors) – the key limitation being that only 11% of applications can be analysed (the funded ones), a set that is heavily skewed towards the top scoring applications.
We agree this is a key limitation, and it would be useful to repeat the study in a more generous scheme, where a greater proportion of applications were funded.
For example, as shown in Figure 4 there is plenty of potential for SD to be associated with increased citation, but not enough data to tell. The authors note that the application with the largest SD drove this large uncertainty – it could be that this application is an outlier, or it could be that it is typical of applications with large SDs but there are very few of them in the dataset because they tended to fall below the funding line.
This is entirely possible, and if there are a small number of extremely high pay-off projects then we would need a much larger sample to robustly test if there is a consistent pattern of more high pay-off projects associated with greater disagreement. We have now mentioned this in the limitations.
Through its analysis, the study forces a refinement of the question of what sorts of disagreements (in extent and driven by what underlying logics) should be considered useful indicators. We suggest the study raises the following THREE questions for future work:
Firstly it would be valuable to understand the reasons and logics behind the disagreements that arise between reviewers, from the fact that "disagreements between reviewers about an application can stem from different sources". While the authors suggest addressing this with further information about scores, we can also ask if different score means might indicate different "regimes" for disagreement, e.g. disagreement along the lines of "not sure this will work" or "this goes against received wisdom" at relatively high score means, and disagreements along the lines of "not sure what this is about" or "hasn't this been tried before?" at lower score means. Qualitative research asking reviewers about their scoring behaviour could help understand the reasoning that goes with different scoring.
This is a good point. “Disagreement” is likely to be too general a word, and future studies could look in far more detail at the types of disagreement. We have previously used a qualitative researcher as an observer of funding panel dynamics, and we have now added this potential approach to our discussion.
Secondly, we could reframe the question to address the lack of information on unfunded applications by asking how can funding best be allocated if the amount of funding available is cut by 50%.
To test this, we reanalysed the data provided by the authors with the following question: assuming only half the funding was available, which of the following selection methods would perform better?
Rank proposals based on their mean scores until funding runs out.
Pool proposals based on their mean score into buckets, rounding to the nearest integer. Fund all proposals with a mean of 1 (1.0-1.49, n=45), then from the bucket with a mean of 2 (1.5-2.49, n=114) rank proposals based on their standard deviation and fund until funding runs out.
Under both methods, all proposals with a mean of 1 are funded, for a total TRC of 319.9. When we look at the proposals in the second bucket, when funding according to method 1, the total TRC for this bucket is 224.2, whereas for method 2 it is 195.5. However, the highest citation-receiving proposal in the second bucket under method 1 has a TRC of 19.9, whereas the highest citation-receiving proposal from the second bucket under method 2 has a TRC of 35.9 (the third highest TRC in the entire sample). This fits with Gillies' description of peer-review as going for less risky proposals, but at the cost of throwing out the occasional exceptional proposal. This is also born out by the distribution of TRCs, with the standard deviation of TRCs for the second bucket under method 1 being 4.2, and under method 2 being 6.2.
This is an interesting comment and thanks for the new analysis. As an aside, we note that only by sharing our data can we have such an in-depth discussion with our reviewers. We have added R code to run these suggested analyses to our results on github (https://github.com/agbarnett/funding.disagree).
It is an interesting approach to use the mean for the “top” tier of applications and the standard deviation for the second tier. This may appeal to funders and panel members, because we believe there will always be a desire to fund those applications with the best mean. This two-tier approach may also be easier to explain than the Black–Scholes approach suggested by Linton, which combines the mean and variance in scores using an equation.
We are wary of using the standard deviation in the total relative citations because of the strong positive skew in its distribution, and the inter-quartile range in citations is actually larger for the approach using the mean at 4.3, compared with 2.9 when using the standard deviation.
Thirdly, it would be valuable to understand what sorts of disagreement exist in the scoring of all the applications (both successful and unsuccessful). It could be argued that the type of disagreement likely to indicate high risk/high return proposals would be bi-modal – some good reviews maybe with scores of 1-1.5, some very poor reviews maybe with scores of 3-4. Given the small fraction of applications funded, very few applications of this nature would be funded (due to the understandable aggregation in the shared data we could not examine the exact number, but fewer than 10 applications have a score lower than 3). Do such applications with such bi-modal review scores exist? Or is the level of disagreement seen in the successful applications similar to that of the unsuccessful applications?
Unfortunately our data only contains the summary statistics on the applications’ scores and so we can’t examine these distributions. We have added this as a limitation.
The above questions only suggest that there is further complexity here that needs to be explored, with more complex, higher power studies. We thank the authors for paving the path for such studies, and for making their underlying data and analysis available in a form that is easy to explore.
Thanks, we agree that larger studies are needed.
Two small notes:

It might be easier to read the paper if scores were consistently referred to as best/worst and better/worse – using ‘higher' is confusing when better scores are lower.

Agreed and changed. We’ve also added text labels to Figure 5 and the new Figure 4.

It would be more elegant to give 'e.g., Bornmann et al, 2008' rather than 'e.g., 36'.

Changed as suggested.
Competing Interests: No competing interests were disclosed. Close
Report a concern
Respond or Comment

COMMENTS ON THIS REPORT

Author Response 15 Oct 2018

Adrian Barnett, Institute of Health and Biomedical Innovation & School of Public Health and Social Work, Queensland University of Technology, Brisbane, 4059, Australia

15 Oct 2018

Author Response
The notion that disagreements amongst reviewers might indicate a promising high-risk/high-reward project certainly has currency amongst those who consider how the system might be improved. In addition to the framework ... Continue reading
The notion that disagreements amongst reviewers might indicate a promising high-risk/high-reward project certainly has currency amongst those who consider how the system might be improved. In addition to the framework of Linton (2016)1, the idea is also present in the model of Brezis (2007) and is implied by several works on the anti-innovation bias of grant peer review (e.g. Greenberg, 1998 2; Gillies, 2008 3). However, this intuitive notion has yet to be put to the test, until the current study, which is a welcome contribution.
Thanks for the interesting references, we have now mentioned Brezis in our Introduction.
The experimental design and statistical analysis are compelling for an initial study, though as the authors note further complications could be addressed in later work.
Given the prevailing policy and academic discussions the negative result is surprising and it rules out some suggested approaches to reform of the grant allocation system; however, the dataset limits the generality of the conclusions that can be drawn (through no fault of the authors) – the key limitation being that only 11% of applications can be analysed (the funded ones), a set that is heavily skewed towards the top scoring applications.
We agree this is a key limitation, and it would be useful to repeat the study in a more generous scheme, where a greater proportion of applications were funded.
For example, as shown in Figure 4 there is plenty of potential for SD to be associated with increased citation, but not enough data to tell. The authors note that the application with the largest SD drove this large uncertainty – it could be that this application is an outlier, or it could be that it is typical of applications with large SDs but there are very few of them in the dataset because they tended to fall below the funding line.
This is entirely possible, and if there are a small number of extremely high pay-off projects then we would need a much larger sample to robustly test if there is a consistent pattern of more high pay-off projects associated with greater disagreement. We have now mentioned this in the limitations.
Through its analysis, the study forces a refinement of the question of what sorts of disagreements (in extent and driven by what underlying logics) should be considered useful indicators. We suggest the study raises the following THREE questions for future work:
Firstly it would be valuable to understand the reasons and logics behind the disagreements that arise between reviewers, from the fact that "disagreements between reviewers about an application can stem from different sources". While the authors suggest addressing this with further information about scores, we can also ask if different score means might indicate different "regimes" for disagreement, e.g. disagreement along the lines of "not sure this will work" or "this goes against received wisdom" at relatively high score means, and disagreements along the lines of "not sure what this is about" or "hasn't this been tried before?" at lower score means. Qualitative research asking reviewers about their scoring behaviour could help understand the reasoning that goes with different scoring.
This is a good point. “Disagreement” is likely to be too general a word, and future studies could look in far more detail at the types of disagreement. We have previously used a qualitative researcher as an observer of funding panel dynamics, and we have now added this potential approach to our discussion.
Secondly, we could reframe the question to address the lack of information on unfunded applications by asking how can funding best be allocated if the amount of funding available is cut by 50%.
To test this, we reanalysed the data provided by the authors with the following question: assuming only half the funding was available, which of the following selection methods would perform better?
Rank proposals based on their mean scores until funding runs out.
Pool proposals based on their mean score into buckets, rounding to the nearest integer. Fund all proposals with a mean of 1 (1.0-1.49, n=45), then from the bucket with a mean of 2 (1.5-2.49, n=114) rank proposals based on their standard deviation and fund until funding runs out.
Under both methods, all proposals with a mean of 1 are funded, for a total TRC of 319.9. When we look at the proposals in the second bucket, when funding according to method 1, the total TRC for this bucket is 224.2, whereas for method 2 it is 195.5. However, the highest citation-receiving proposal in the second bucket under method 1 has a TRC of 19.9, whereas the highest citation-receiving proposal from the second bucket under method 2 has a TRC of 35.9 (the third highest TRC in the entire sample). This fits with Gillies' description of peer-review as going for less risky proposals, but at the cost of throwing out the occasional exceptional proposal. This is also born out by the distribution of TRCs, with the standard deviation of TRCs for the second bucket under method 1 being 4.2, and under method 2 being 6.2.
This is an interesting comment and thanks for the new analysis. As an aside, we note that only by sharing our data can we have such an in-depth discussion with our reviewers. We have added R code to run these suggested analyses to our results on github (https://github.com/agbarnett/funding.disagree).
It is an interesting approach to use the mean for the “top” tier of applications and the standard deviation for the second tier. This may appeal to funders and panel members, because we believe there will always be a desire to fund those applications with the best mean. This two-tier approach may also be easier to explain than the Black–Scholes approach suggested by Linton, which combines the mean and variance in scores using an equation.
We are wary of using the standard deviation in the total relative citations because of the strong positive skew in its distribution, and the inter-quartile range in citations is actually larger for the approach using the mean at 4.3, compared with 2.9 when using the standard deviation.
Thirdly, it would be valuable to understand what sorts of disagreement exist in the scoring of all the applications (both successful and unsuccessful). It could be argued that the type of disagreement likely to indicate high risk/high return proposals would be bi-modal – some good reviews maybe with scores of 1-1.5, some very poor reviews maybe with scores of 3-4. Given the small fraction of applications funded, very few applications of this nature would be funded (due to the understandable aggregation in the shared data we could not examine the exact number, but fewer than 10 applications have a score lower than 3). Do such applications with such bi-modal review scores exist? Or is the level of disagreement seen in the successful applications similar to that of the unsuccessful applications?
Unfortunately our data only contains the summary statistics on the applications’ scores and so we can’t examine these distributions. We have added this as a limitation.
The above questions only suggest that there is further complexity here that needs to be explored, with more complex, higher power studies. We thank the authors for paving the path for such studies, and for making their underlying data and analysis available in a form that is easy to explore.
Thanks, we agree that larger studies are needed.
Two small notes:

It might be easier to read the paper if scores were consistently referred to as best/worst and better/worse – using ‘higher' is confusing when better scores are lower.

Agreed and changed. We’ve also added text labels to Figure 5 and the new Figure 4.

It would be more elegant to give 'e.g., Bornmann et al, 2008' rather than 'e.g., 36'.

Changed as suggested.
The notion that disagreements amongst reviewers might indicate a promising high-risk/high-reward project certainly has currency amongst those who consider how the system might be improved. In addition to the framework of Linton (2016)1, the idea is also present in the model of Brezis (2007) and is implied by several works on the anti-innovation bias of grant peer review (e.g. Greenberg, 1998 2; Gillies, 2008 3). However, this intuitive notion has yet to be put to the test, until the current study, which is a welcome contribution.
Thanks for the interesting references, we have now mentioned Brezis in our Introduction.
The experimental design and statistical analysis are compelling for an initial study, though as the authors note further complications could be addressed in later work.
Given the prevailing policy and academic discussions the negative result is surprising and it rules out some suggested approaches to reform of the grant allocation system; however, the dataset limits the generality of the conclusions that can be drawn (through no fault of the authors) – the key limitation being that only 11% of applications can be analysed (the funded ones), a set that is heavily skewed towards the top scoring applications.
We agree this is a key limitation, and it would be useful to repeat the study in a more generous scheme, where a greater proportion of applications were funded.
For example, as shown in Figure 4 there is plenty of potential for SD to be associated with increased citation, but not enough data to tell. The authors note that the application with the largest SD drove this large uncertainty – it could be that this application is an outlier, or it could be that it is typical of applications with large SDs but there are very few of them in the dataset because they tended to fall below the funding line.
This is entirely possible, and if there are a small number of extremely high pay-off projects then we would need a much larger sample to robustly test if there is a consistent pattern of more high pay-off projects associated with greater disagreement. We have now mentioned this in the limitations.
Through its analysis, the study forces a refinement of the question of what sorts of disagreements (in extent and driven by what underlying logics) should be considered useful indicators. We suggest the study raises the following THREE questions for future work:
Firstly it would be valuable to understand the reasons and logics behind the disagreements that arise between reviewers, from the fact that "disagreements between reviewers about an application can stem from different sources". While the authors suggest addressing this with further information about scores, we can also ask if different score means might indicate different "regimes" for disagreement, e.g. disagreement along the lines of "not sure this will work" or "this goes against received wisdom" at relatively high score means, and disagreements along the lines of "not sure what this is about" or "hasn't this been tried before?" at lower score means. Qualitative research asking reviewers about their scoring behaviour could help understand the reasoning that goes with different scoring.
This is a good point. “Disagreement” is likely to be too general a word, and future studies could look in far more detail at the types of disagreement. We have previously used a qualitative researcher as an observer of funding panel dynamics, and we have now added this potential approach to our discussion.
Secondly, we could reframe the question to address the lack of information on unfunded applications by asking how can funding best be allocated if the amount of funding available is cut by 50%.
To test this, we reanalysed the data provided by the authors with the following question: assuming only half the funding was available, which of the following selection methods would perform better?
Rank proposals based on their mean scores until funding runs out.
Pool proposals based on their mean score into buckets, rounding to the nearest integer. Fund all proposals with a mean of 1 (1.0-1.49, n=45), then from the bucket with a mean of 2 (1.5-2.49, n=114) rank proposals based on their standard deviation and fund until funding runs out.
Under both methods, all proposals with a mean of 1 are funded, for a total TRC of 319.9. When we look at the proposals in the second bucket, when funding according to method 1, the total TRC for this bucket is 224.2, whereas for method 2 it is 195.5. However, the highest citation-receiving proposal in the second bucket under method 1 has a TRC of 19.9, whereas the highest citation-receiving proposal from the second bucket under method 2 has a TRC of 35.9 (the third highest TRC in the entire sample). This fits with Gillies' description of peer-review as going for less risky proposals, but at the cost of throwing out the occasional exceptional proposal. This is also born out by the distribution of TRCs, with the standard deviation of TRCs for the second bucket under method 1 being 4.2, and under method 2 being 6.2.
This is an interesting comment and thanks for the new analysis. As an aside, we note that only by sharing our data can we have such an in-depth discussion with our reviewers. We have added R code to run these suggested analyses to our results on github (https://github.com/agbarnett/funding.disagree).
It is an interesting approach to use the mean for the “top” tier of applications and the standard deviation for the second tier. This may appeal to funders and panel members, because we believe there will always be a desire to fund those applications with the best mean. This two-tier approach may also be easier to explain than the Black–Scholes approach suggested by Linton, which combines the mean and variance in scores using an equation.
We are wary of using the standard deviation in the total relative citations because of the strong positive skew in its distribution, and the inter-quartile range in citations is actually larger for the approach using the mean at 4.3, compared with 2.9 when using the standard deviation.
Thirdly, it would be valuable to understand what sorts of disagreement exist in the scoring of all the applications (both successful and unsuccessful). It could be argued that the type of disagreement likely to indicate high risk/high return proposals would be bi-modal – some good reviews maybe with scores of 1-1.5, some very poor reviews maybe with scores of 3-4. Given the small fraction of applications funded, very few applications of this nature would be funded (due to the understandable aggregation in the shared data we could not examine the exact number, but fewer than 10 applications have a score lower than 3). Do such applications with such bi-modal review scores exist? Or is the level of disagreement seen in the successful applications similar to that of the unsuccessful applications?
Unfortunately our data only contains the summary statistics on the applications’ scores and so we can’t examine these distributions. We have added this as a limitation.
The above questions only suggest that there is further complexity here that needs to be explored, with more complex, higher power studies. We thank the authors for paving the path for such studies, and for making their underlying data and analysis available in a form that is easy to explore.
Thanks, we agree that larger studies are needed.
Two small notes:

It might be easier to read the paper if scores were consistently referred to as best/worst and better/worse – using ‘higher' is confusing when better scores are lower.

Agreed and changed. We’ve also added text labels to Figure 5 and the new Figure 4.

It would be more elegant to give 'e.g., Bornmann et al, 2008' rather than 'e.g., 36'.

Changed as suggested.
Competing Interests: No competing interests were disclosed. Close
Report a concern

Views

Reviewer Report 20 Sep 2018

Jonathan Shepherd, Southampton Health Technology Assessments Centre, University of Southampton, Southampton, UK

Jeremy C. Wyatt, Wessex Institute, University of Southampton, Southampton, SO40 7AA, UK

Approved

https://doi.org/10.5256/f1000research.16873.r36742

We thank the authors for this very interesting study. We have some comments and suggestions which we think will enhance the manuscript.

1. The primary outcome measure is the citation counts from publications associated with the successful application. Publications were produced from 1 to 8 years after the peer review date (average 4.3 years). This does not appear to take account of varying time since the projects were funded (i.e. 7 year gap between projects that were funded from 1999 to 2006). Thus, older studies would have had more time for publications to be produced and cited. We therefore suggest a more meaningful outcome measure would be either the number of citations per year per study, or the total number of citations in, say, the 5 years following the final project report, or some other standardised project milestone. Adding the review year to the model does not seem to adequately control for this factor (though qualified statistical advice is needed to clarify this). We think this is the issue that likely affects the interpretation of the results the most in our critique.

2. The number of citations was standardised by academic field – i.e. molecular biology. Was there any variation in study designs within this field that might also change the expected number of citations (e.g. systematic reviews may attract more citations than primary experimental studies in some fields)? It would be useful for context if there could be a table with some basic aggregate details of the funded studies, such as types of study design, molecular biological application, study sample characteristics, duration of study etc. This would help to put the results into context.

3. The impact of a piece of research on which referees could not agree might be either lower or higher than those on which they could. So, it would be useful to plot the standard deviation of the citations against the standard deviation of the peer review score.

4. As well as using multiple imputation to correct for missing data, a sensitivity analysis in which cases with missing data are omitted would be useful.

5. Some measure of the model fit would be useful, eg. adjusted R squared

6. There was a wide variation in the number of reviewers per article from 2 to 18. Was this due to differences in the kind of research, amount of funding requested or some other perceived risk on behalf of the funder? Could this artificially influence the standard deviation of the score, confounding any association with citations?

7. Fractional polynomial model results are only presented for the best fitting model with the smallest deviance. This is acceptable in principle, but it would be useful for the authors to comment on whether there was any variation in the results according to the other fractional polynomial transformations (if available). This will provide confidence in the robustness of the findings.

8. Reference is made in the first paragraph to a “recent systematic review” by Guthrie et al (2018¹) (and also in the third paragraph). We note that this publication doesn’t refer to itself as being a systematic review, and indeed, it is an update of a 2009 review which describes itself as a non-systematic review. We would suggest using the tern “non-systematic review”, or just “literature review”.

9. Thank you for citing our own recent systematic review on peer review of grants in health. You mention that the review included eight studies and called for further research in this area, which is correct. However, the review focused specifically on studies aiming to improve the effectiveness and efficiency of peer review. These were drawn from a wider set of 83 studies on peer review which we systematically mapped. In the map there were some studies which focused on assessing the impact of funded research, eg. In terms of bibliometrics. Thus, there is a body of evidence on this topic, though we didn't systematically review it in detail. We are happy to provide you with a list of these studies.

10. The sentence on page 3 beginning “A recent systematic review found “suggestive” evidence that funding peer review can have an anti-innovation bias² and that innovation and risk may not often be sufficiently addressed in review feedback⁷” needs re-wording as not only is the Guthrie et al paper a non-systematic review, but the second reference cited in that sentence by Gallo et al is a survey (i.e. not a review at all). The way the sentence is phrased implies that it is a systematic review.

11. Suggest amending the sentence on page 3 “Many studies using large sample sizes found either no association or only a weak association between the mean score and the VOLUME of citations of subsequent publications”

Is the work clearly and accurately presented and does it cite the current literature?

Yes
Is the study design appropriate and is the work technically sound?

Partly
Are sufficient details of methods and analysis provided to allow replication by others?

Yes
If applicable, is the statistical analysis and its interpretation appropriate?

Partly
Are all the source data underlying the results available to ensure full reproducibility?

Yes
Are the conclusions drawn adequately supported by the results?

Yes

References

1. Guthrie S, Ghiga I, Wooding S: What do we know about grant peer review in the health sciences?. F1000Res. 2017; 6: 1335 PubMed Abstract | Publisher Full Text

Competing Interests: No competing interests were disclosed.

We confirm that we have read this submission and believe that we have an appropriate level of expertise to confirm that it is of an acceptable scientific standard.

CITE

Report a concern

Author Response 15 Oct 2018

Adrian Barnett, Institute of Health and Biomedical Innovation & School of Public Health and Social Work, Queensland University of Technology, Brisbane, 4059, Australia

15 Oct 2018

Author Response

1. The primary outcome measure is the citation counts from publications associated with the successful application. Publications were produced from 1 to 8 years after the peer review date (average ... Continue reading 1. The primary outcome measure is the citation counts from publications associated with the successful application. Publications were produced from 1 to 8 years after the peer review date (average 4.3 years). This does not appear to take account of varying time since the projects were funded (i.e. 7 year gap between projects that were funded from 1999 to 2006). Thus, older studies would have had more time for publications to be produced and cited. We therefore suggest a more meaningful outcome measure would be either the number of citations per year per study, or the total number of citations in, say, the 5 years following the final project report, or some other standardized project milestone. Adding the review year to the model does not seem to adequately control for this factor (though qualified statistical advice is needed to clarify this). We think this is the issue that likely affects the interpretation of the results the most in our critique.
Thanks for the comment. Actually, the citation values are normalized per publication year, thus older studies would not have an advantage as the resultant citations from publications are normalized by year. It is true that more time post peer review date would allow more publications, but all of these products were derived from the final reports, which were submitted on average five years after peer review. Thus, whatever is reported by the principal investigator in their final report is what was measured, which is what is presented by funding agencies as the output of the grant.

2. The number of citations was standardised by academic field – i.e. molecular biology. Was there any variation in study designs within this field that might also change the expected number of citations (e.g. systematic reviews may attract more citations than primary experimental studies in some fields)? It would be useful for context if there could be a table with some basic aggregate details of the funded studies, such as types of study design, molecular biological application, study sample characteristics, duration of study etc. This would help to put the results into context.
This is interesting, but would likely need to be a much larger, separate study to go back into each application and characterize the study design, sample characteristics, etc., and is out of the current scope. That said, the applications included in this analysis were submitted to a 4-year, R01-style support mechanism. In every program year there was a significant proportion of both applied and basic research applications, with many applications encompassing varying degrees of both basic and applied research in their aims. There was a wide variety of research topic areas, including vision, drug abuse, nutrition, blood-related cancer, kidney disease, autoimmune diseases, malaria, tuberculosis, osteoporosis, arthritis, and autism research, among others. This is described in more detail in our original publication: https://journals.plos.org/plosone/article?id=10.1371/journal.pone.0106474.

3. The impact of a piece of research on which referees could not agree might be either lower or higher than those on which they could. So, it would be useful to plot the standard deviation of the citations against the standard deviation of the peer review score.
We have now plotted the inter-quartile range in citations against the application score mean and standard deviation. We used the inter-quartile range instead of the standard deviation because of the strong skew in citations, and the standard deviation was strongly influenced by the application with the highest citations.
The new results show moderate support for a greater return for applications with a higher agreement between peer reviewers. See new Figure 4, with new explanatory paragraph in the “Statistical Methods” section, and an updated discussion.

4. As well as using multiple imputation to correct for missing data, a sensitivity analysis in which cases with missing data are omitted would be useful.
We have added a complete case analysis to the more detailed results available on github (https://github.com/agbarnett/funding.disagree). All the results were very similar to the imputed data.

5. Some measure of the model fit would be useful, eg. adjusted R squared
We are not certain that the R-squared statistic would be useful here. The adjusted R-squared can be useful for comparing between alternative models, or where the goal is accurate prediction. Here we were just looking for any signal between application scores and citations, assuming that the detection of any signal could lead to improvements in the design of funding systems. We have investigated the residuals to look for poor model fit.

6. There was a wide variation in the number of reviewers per article from 2 to 18. Was this due to differences in the kind of research, amount of funding requested or some other perceived risk on behalf of the funder? Could this artificially influence the standard deviation of the score, confounding any association with citations?
The majority (90%) of applications were reviewed in panels (roughly 10 to 15 reviewers). Some were reviewed via a mail review mechanism (2 to 3 reviewers). The determination of review mechanism largely depended on the topic area. We don’t believe this should be a large confounder of the results.
We have now included a sensitivity analysis using just the larger panels and excluding the mail review panels. The results were similar to the analysis using all panels. These new results are available on github (https://github.com/agbarnett/funding.disagree).

7. Fractional polynomial model results are only presented for the best fitting model with the smallest deviance. This is acceptable in principle, but it would be useful for the authors to comment on whether there was any variation in the results according to the other fractional polynomial transformations (if available). This will provide confidence in the robustness of the findings.
We have examined the predictions for the best five models and the average results were similar in terms of the mean. However, the confidence intervals for the second best model had a much narrow confidence interval for citation predictions using the application score standard deviation. In hindsight we prefer this model, as it has only a slightly poorer deviance, but a much more believable confidence interval. It would have been better to have a multi-criteria decision for the “best” model, that used both the deviance and average confidence interval width. This has been a useful lesson for future studies, but we continue to present the model with the wider CI in the main results because we feel we should stick to our original protocol.
These new results are available on github (https://github.com/agbarnett/funding.disagree).

8. Reference is made in the first paragraph to a “recent systematic review” by Guthrie et al (2018 1) (and also in the third paragraph). We note that this publication doesn’t refer to itself as being a systematic review, and indeed, it is an update of a 2009 review which describes itself as a non-systematic review. We would suggest using the term “non-systematic review”, or just “literature review”.
Thank you for flagging this. We have now used “literature review”.

9. Thank you for citing our own recent systematic review on peer review of grants in health. You mention that the review included eight studies and called for further research in this area, which is correct. However, the review focused specifically on studies aiming to improve the effectiveness and efficiency of peer review. These were drawn from a wider set of 83 studies on peer review which we systematically mapped. In the map there were some studies which focused on assessing the impact of funded research, eg. In terms of bibliometrics. Thus, there is a body of evidence on this topic, though we didn't systematically review it in detail. We are happy to provide you with a list of these studies.
We have changed our language to make the goal of your review clearer. We would gladly see the study list. Perhaps this is best uploaded to our github page for this project (if it can be made public): https://github.com/agbarnett/funding.disagree then click “upload file”, you will need a github account (free) and request write access to our project.

10. The sentence on page 3 beginning “A recent systematic review found “suggestive” evidence that funding peer review can have an anti-innovation bias2 and that innovation and risk may not often be sufficiently addressed in review feedback7” needs re-wording as not only is the Guthrie et al paper a non-systematic review, but the second reference cited in that sentence by Gallo et al is a survey (i.e. not a review at all). The way the sentence is phrased implies that it is a systematic review.
Thank you for flagging this. We have now used “literature review” and added the fact that the second study is a survey.

11. Suggest amending the sentence on page 3 “Many studies using large sample sizes found either no association or only a weak association between the mean score and the VOLUME of citations of subsequent publications”
We have changed the text to read “number of citations”.
1. The primary outcome measure is the citation counts from publications associated with the successful application. Publications were produced from 1 to 8 years after the peer review date (average 4.3 years). This does not appear to take account of varying time since the projects were funded (i.e. 7 year gap between projects that were funded from 1999 to 2006). Thus, older studies would have had more time for publications to be produced and cited. We therefore suggest a more meaningful outcome measure would be either the number of citations per year per study, or the total number of citations in, say, the 5 years following the final project report, or some other standardized project milestone. Adding the review year to the model does not seem to adequately control for this factor (though qualified statistical advice is needed to clarify this). We think this is the issue that likely affects the interpretation of the results the most in our critique.
Thanks for the comment. Actually, the citation values are normalized per publication year, thus older studies would not have an advantage as the resultant citations from publications are normalized by year. It is true that more time post peer review date would allow more publications, but all of these products were derived from the final reports, which were submitted on average five years after peer review. Thus, whatever is reported by the principal investigator in their final report is what was measured, which is what is presented by funding agencies as the output of the grant.

2. The number of citations was standardised by academic field – i.e. molecular biology. Was there any variation in study designs within this field that might also change the expected number of citations (e.g. systematic reviews may attract more citations than primary experimental studies in some fields)? It would be useful for context if there could be a table with some basic aggregate details of the funded studies, such as types of study design, molecular biological application, study sample characteristics, duration of study etc. This would help to put the results into context.
This is interesting, but would likely need to be a much larger, separate study to go back into each application and characterize the study design, sample characteristics, etc., and is out of the current scope. That said, the applications included in this analysis were submitted to a 4-year, R01-style support mechanism. In every program year there was a significant proportion of both applied and basic research applications, with many applications encompassing varying degrees of both basic and applied research in their aims. There was a wide variety of research topic areas, including vision, drug abuse, nutrition, blood-related cancer, kidney disease, autoimmune diseases, malaria, tuberculosis, osteoporosis, arthritis, and autism research, among others. This is described in more detail in our original publication: https://journals.plos.org/plosone/article?id=10.1371/journal.pone.0106474.

3. The impact of a piece of research on which referees could not agree might be either lower or higher than those on which they could. So, it would be useful to plot the standard deviation of the citations against the standard deviation of the peer review score.
We have now plotted the inter-quartile range in citations against the application score mean and standard deviation. We used the inter-quartile range instead of the standard deviation because of the strong skew in citations, and the standard deviation was strongly influenced by the application with the highest citations.
The new results show moderate support for a greater return for applications with a higher agreement between peer reviewers. See new Figure 4, with new explanatory paragraph in the “Statistical Methods” section, and an updated discussion.

4. As well as using multiple imputation to correct for missing data, a sensitivity analysis in which cases with missing data are omitted would be useful.
We have added a complete case analysis to the more detailed results available on github (https://github.com/agbarnett/funding.disagree). All the results were very similar to the imputed data.

5. Some measure of the model fit would be useful, eg. adjusted R squared
We are not certain that the R-squared statistic would be useful here. The adjusted R-squared can be useful for comparing between alternative models, or where the goal is accurate prediction. Here we were just looking for any signal between application scores and citations, assuming that the detection of any signal could lead to improvements in the design of funding systems. We have investigated the residuals to look for poor model fit.

6. There was a wide variation in the number of reviewers per article from 2 to 18. Was this due to differences in the kind of research, amount of funding requested or some other perceived risk on behalf of the funder? Could this artificially influence the standard deviation of the score, confounding any association with citations?
The majority (90%) of applications were reviewed in panels (roughly 10 to 15 reviewers). Some were reviewed via a mail review mechanism (2 to 3 reviewers). The determination of review mechanism largely depended on the topic area. We don’t believe this should be a large confounder of the results.
We have now included a sensitivity analysis using just the larger panels and excluding the mail review panels. The results were similar to the analysis using all panels. These new results are available on github (https://github.com/agbarnett/funding.disagree).

7. Fractional polynomial model results are only presented for the best fitting model with the smallest deviance. This is acceptable in principle, but it would be useful for the authors to comment on whether there was any variation in the results according to the other fractional polynomial transformations (if available). This will provide confidence in the robustness of the findings.
We have examined the predictions for the best five models and the average results were similar in terms of the mean. However, the confidence intervals for the second best model had a much narrow confidence interval for citation predictions using the application score standard deviation. In hindsight we prefer this model, as it has only a slightly poorer deviance, but a much more believable confidence interval. It would have been better to have a multi-criteria decision for the “best” model, that used both the deviance and average confidence interval width. This has been a useful lesson for future studies, but we continue to present the model with the wider CI in the main results because we feel we should stick to our original protocol.
These new results are available on github (https://github.com/agbarnett/funding.disagree).

8. Reference is made in the first paragraph to a “recent systematic review” by Guthrie et al (2018 1) (and also in the third paragraph). We note that this publication doesn’t refer to itself as being a systematic review, and indeed, it is an update of a 2009 review which describes itself as a non-systematic review. We would suggest using the term “non-systematic review”, or just “literature review”.
Thank you for flagging this. We have now used “literature review”.

9. Thank you for citing our own recent systematic review on peer review of grants in health. You mention that the review included eight studies and called for further research in this area, which is correct. However, the review focused specifically on studies aiming to improve the effectiveness and efficiency of peer review. These were drawn from a wider set of 83 studies on peer review which we systematically mapped. In the map there were some studies which focused on assessing the impact of funded research, eg. In terms of bibliometrics. Thus, there is a body of evidence on this topic, though we didn't systematically review it in detail. We are happy to provide you with a list of these studies.
We have changed our language to make the goal of your review clearer. We would gladly see the study list. Perhaps this is best uploaded to our github page for this project (if it can be made public): https://github.com/agbarnett/funding.disagree then click “upload file”, you will need a github account (free) and request write access to our project.

10. The sentence on page 3 beginning “A recent systematic review found “suggestive” evidence that funding peer review can have an anti-innovation bias2 and that innovation and risk may not often be sufficiently addressed in review feedback7” needs re-wording as not only is the Guthrie et al paper a non-systematic review, but the second reference cited in that sentence by Gallo et al is a survey (i.e. not a review at all). The way the sentence is phrased implies that it is a systematic review.
Thank you for flagging this. We have now used “literature review” and added the fact that the second study is a survey.

11. Suggest amending the sentence on page 3 “Many studies using large sample sizes found either no association or only a weak association between the mean score and the VOLUME of citations of subsequent publications”
We have changed the text to read “number of citations”.
Competing Interests: No competing interests were disclosed. Close
Report a concern
Respond or Comment

COMMENTS ON THIS REPORT

Author Response 15 Oct 2018

Adrian Barnett, Institute of Health and Biomedical Innovation & School of Public Health and Social Work, Queensland University of Technology, Brisbane, 4059, Australia

15 Oct 2018

Author Response

1. The primary outcome measure is the citation counts from publications associated with the successful application. Publications were produced from 1 to 8 years after the peer review date (average ... Continue reading 1. The primary outcome measure is the citation counts from publications associated with the successful application. Publications were produced from 1 to 8 years after the peer review date (average 4.3 years). This does not appear to take account of varying time since the projects were funded (i.e. 7 year gap between projects that were funded from 1999 to 2006). Thus, older studies would have had more time for publications to be produced and cited. We therefore suggest a more meaningful outcome measure would be either the number of citations per year per study, or the total number of citations in, say, the 5 years following the final project report, or some other standardized project milestone. Adding the review year to the model does not seem to adequately control for this factor (though qualified statistical advice is needed to clarify this). We think this is the issue that likely affects the interpretation of the results the most in our critique.
Thanks for the comment. Actually, the citation values are normalized per publication year, thus older studies would not have an advantage as the resultant citations from publications are normalized by year. It is true that more time post peer review date would allow more publications, but all of these products were derived from the final reports, which were submitted on average five years after peer review. Thus, whatever is reported by the principal investigator in their final report is what was measured, which is what is presented by funding agencies as the output of the grant.

2. The number of citations was standardised by academic field – i.e. molecular biology. Was there any variation in study designs within this field that might also change the expected number of citations (e.g. systematic reviews may attract more citations than primary experimental studies in some fields)? It would be useful for context if there could be a table with some basic aggregate details of the funded studies, such as types of study design, molecular biological application, study sample characteristics, duration of study etc. This would help to put the results into context.
This is interesting, but would likely need to be a much larger, separate study to go back into each application and characterize the study design, sample characteristics, etc., and is out of the current scope. That said, the applications included in this analysis were submitted to a 4-year, R01-style support mechanism. In every program year there was a significant proportion of both applied and basic research applications, with many applications encompassing varying degrees of both basic and applied research in their aims. There was a wide variety of research topic areas, including vision, drug abuse, nutrition, blood-related cancer, kidney disease, autoimmune diseases, malaria, tuberculosis, osteoporosis, arthritis, and autism research, among others. This is described in more detail in our original publication: https://journals.plos.org/plosone/article?id=10.1371/journal.pone.0106474.

3. The impact of a piece of research on which referees could not agree might be either lower or higher than those on which they could. So, it would be useful to plot the standard deviation of the citations against the standard deviation of the peer review score.
We have now plotted the inter-quartile range in citations against the application score mean and standard deviation. We used the inter-quartile range instead of the standard deviation because of the strong skew in citations, and the standard deviation was strongly influenced by the application with the highest citations.
The new results show moderate support for a greater return for applications with a higher agreement between peer reviewers. See new Figure 4, with new explanatory paragraph in the “Statistical Methods” section, and an updated discussion.

4. As well as using multiple imputation to correct for missing data, a sensitivity analysis in which cases with missing data are omitted would be useful.
We have added a complete case analysis to the more detailed results available on github (https://github.com/agbarnett/funding.disagree). All the results were very similar to the imputed data.

5. Some measure of the model fit would be useful, eg. adjusted R squared
We are not certain that the R-squared statistic would be useful here. The adjusted R-squared can be useful for comparing between alternative models, or where the goal is accurate prediction. Here we were just looking for any signal between application scores and citations, assuming that the detection of any signal could lead to improvements in the design of funding systems. We have investigated the residuals to look for poor model fit.

6. There was a wide variation in the number of reviewers per article from 2 to 18. Was this due to differences in the kind of research, amount of funding requested or some other perceived risk on behalf of the funder? Could this artificially influence the standard deviation of the score, confounding any association with citations?
The majority (90%) of applications were reviewed in panels (roughly 10 to 15 reviewers). Some were reviewed via a mail review mechanism (2 to 3 reviewers). The determination of review mechanism largely depended on the topic area. We don’t believe this should be a large confounder of the results.
We have now included a sensitivity analysis using just the larger panels and excluding the mail review panels. The results were similar to the analysis using all panels. These new results are available on github (https://github.com/agbarnett/funding.disagree).

7. Fractional polynomial model results are only presented for the best fitting model with the smallest deviance. This is acceptable in principle, but it would be useful for the authors to comment on whether there was any variation in the results according to the other fractional polynomial transformations (if available). This will provide confidence in the robustness of the findings.
We have examined the predictions for the best five models and the average results were similar in terms of the mean. However, the confidence intervals for the second best model had a much narrow confidence interval for citation predictions using the application score standard deviation. In hindsight we prefer this model, as it has only a slightly poorer deviance, but a much more believable confidence interval. It would have been better to have a multi-criteria decision for the “best” model, that used both the deviance and average confidence interval width. This has been a useful lesson for future studies, but we continue to present the model with the wider CI in the main results because we feel we should stick to our original protocol.
These new results are available on github (https://github.com/agbarnett/funding.disagree).

8. Reference is made in the first paragraph to a “recent systematic review” by Guthrie et al (2018 1) (and also in the third paragraph). We note that this publication doesn’t refer to itself as being a systematic review, and indeed, it is an update of a 2009 review which describes itself as a non-systematic review. We would suggest using the term “non-systematic review”, or just “literature review”.
Thank you for flagging this. We have now used “literature review”.

9. Thank you for citing our own recent systematic review on peer review of grants in health. You mention that the review included eight studies and called for further research in this area, which is correct. However, the review focused specifically on studies aiming to improve the effectiveness and efficiency of peer review. These were drawn from a wider set of 83 studies on peer review which we systematically mapped. In the map there were some studies which focused on assessing the impact of funded research, eg. In terms of bibliometrics. Thus, there is a body of evidence on this topic, though we didn't systematically review it in detail. We are happy to provide you with a list of these studies.
We have changed our language to make the goal of your review clearer. We would gladly see the study list. Perhaps this is best uploaded to our github page for this project (if it can be made public): https://github.com/agbarnett/funding.disagree then click “upload file”, you will need a github account (free) and request write access to our project.

10. The sentence on page 3 beginning “A recent systematic review found “suggestive” evidence that funding peer review can have an anti-innovation bias2 and that innovation and risk may not often be sufficiently addressed in review feedback7” needs re-wording as not only is the Guthrie et al paper a non-systematic review, but the second reference cited in that sentence by Gallo et al is a survey (i.e. not a review at all). The way the sentence is phrased implies that it is a systematic review.
Thank you for flagging this. We have now used “literature review” and added the fact that the second study is a survey.

11. Suggest amending the sentence on page 3 “Many studies using large sample sizes found either no association or only a weak association between the mean score and the VOLUME of citations of subsequent publications”
We have changed the text to read “number of citations”.
1. The primary outcome measure is the citation counts from publications associated with the successful application. Publications were produced from 1 to 8 years after the peer review date (average 4.3 years). This does not appear to take account of varying time since the projects were funded (i.e. 7 year gap between projects that were funded from 1999 to 2006). Thus, older studies would have had more time for publications to be produced and cited. We therefore suggest a more meaningful outcome measure would be either the number of citations per year per study, or the total number of citations in, say, the 5 years following the final project report, or some other standardized project milestone. Adding the review year to the model does not seem to adequately control for this factor (though qualified statistical advice is needed to clarify this). We think this is the issue that likely affects the interpretation of the results the most in our critique.
Thanks for the comment. Actually, the citation values are normalized per publication year, thus older studies would not have an advantage as the resultant citations from publications are normalized by year. It is true that more time post peer review date would allow more publications, but all of these products were derived from the final reports, which were submitted on average five years after peer review. Thus, whatever is reported by the principal investigator in their final report is what was measured, which is what is presented by funding agencies as the output of the grant.

2. The number of citations was standardised by academic field – i.e. molecular biology. Was there any variation in study designs within this field that might also change the expected number of citations (e.g. systematic reviews may attract more citations than primary experimental studies in some fields)? It would be useful for context if there could be a table with some basic aggregate details of the funded studies, such as types of study design, molecular biological application, study sample characteristics, duration of study etc. This would help to put the results into context.
This is interesting, but would likely need to be a much larger, separate study to go back into each application and characterize the study design, sample characteristics, etc., and is out of the current scope. That said, the applications included in this analysis were submitted to a 4-year, R01-style support mechanism. In every program year there was a significant proportion of both applied and basic research applications, with many applications encompassing varying degrees of both basic and applied research in their aims. There was a wide variety of research topic areas, including vision, drug abuse, nutrition, blood-related cancer, kidney disease, autoimmune diseases, malaria, tuberculosis, osteoporosis, arthritis, and autism research, among others. This is described in more detail in our original publication: https://journals.plos.org/plosone/article?id=10.1371/journal.pone.0106474.

3. The impact of a piece of research on which referees could not agree might be either lower or higher than those on which they could. So, it would be useful to plot the standard deviation of the citations against the standard deviation of the peer review score.
We have now plotted the inter-quartile range in citations against the application score mean and standard deviation. We used the inter-quartile range instead of the standard deviation because of the strong skew in citations, and the standard deviation was strongly influenced by the application with the highest citations.
The new results show moderate support for a greater return for applications with a higher agreement between peer reviewers. See new Figure 4, with new explanatory paragraph in the “Statistical Methods” section, and an updated discussion.

4. As well as using multiple imputation to correct for missing data, a sensitivity analysis in which cases with missing data are omitted would be useful.
We have added a complete case analysis to the more detailed results available on github (https://github.com/agbarnett/funding.disagree). All the results were very similar to the imputed data.

5. Some measure of the model fit would be useful, eg. adjusted R squared
We are not certain that the R-squared statistic would be useful here. The adjusted R-squared can be useful for comparing between alternative models, or where the goal is accurate prediction. Here we were just looking for any signal between application scores and citations, assuming that the detection of any signal could lead to improvements in the design of funding systems. We have investigated the residuals to look for poor model fit.

6. There was a wide variation in the number of reviewers per article from 2 to 18. Was this due to differences in the kind of research, amount of funding requested or some other perceived risk on behalf of the funder? Could this artificially influence the standard deviation of the score, confounding any association with citations?
The majority (90%) of applications were reviewed in panels (roughly 10 to 15 reviewers). Some were reviewed via a mail review mechanism (2 to 3 reviewers). The determination of review mechanism largely depended on the topic area. We don’t believe this should be a large confounder of the results.
We have now included a sensitivity analysis using just the larger panels and excluding the mail review panels. The results were similar to the analysis using all panels. These new results are available on github (https://github.com/agbarnett/funding.disagree).

7. Fractional polynomial model results are only presented for the best fitting model with the smallest deviance. This is acceptable in principle, but it would be useful for the authors to comment on whether there was any variation in the results according to the other fractional polynomial transformations (if available). This will provide confidence in the robustness of the findings.
We have examined the predictions for the best five models and the average results were similar in terms of the mean. However, the confidence intervals for the second best model had a much narrow confidence interval for citation predictions using the application score standard deviation. In hindsight we prefer this model, as it has only a slightly poorer deviance, but a much more believable confidence interval. It would have been better to have a multi-criteria decision for the “best” model, that used both the deviance and average confidence interval width. This has been a useful lesson for future studies, but we continue to present the model with the wider CI in the main results because we feel we should stick to our original protocol.
These new results are available on github (https://github.com/agbarnett/funding.disagree).

8. Reference is made in the first paragraph to a “recent systematic review” by Guthrie et al (2018 1) (and also in the third paragraph). We note that this publication doesn’t refer to itself as being a systematic review, and indeed, it is an update of a 2009 review which describes itself as a non-systematic review. We would suggest using the term “non-systematic review”, or just “literature review”.
Thank you for flagging this. We have now used “literature review”.

9. Thank you for citing our own recent systematic review on peer review of grants in health. You mention that the review included eight studies and called for further research in this area, which is correct. However, the review focused specifically on studies aiming to improve the effectiveness and efficiency of peer review. These were drawn from a wider set of 83 studies on peer review which we systematically mapped. In the map there were some studies which focused on assessing the impact of funded research, eg. In terms of bibliometrics. Thus, there is a body of evidence on this topic, though we didn't systematically review it in detail. We are happy to provide you with a list of these studies.
We have changed our language to make the goal of your review clearer. We would gladly see the study list. Perhaps this is best uploaded to our github page for this project (if it can be made public): https://github.com/agbarnett/funding.disagree then click “upload file”, you will need a github account (free) and request write access to our project.

10. The sentence on page 3 beginning “A recent systematic review found “suggestive” evidence that funding peer review can have an anti-innovation bias2 and that innovation and risk may not often be sufficiently addressed in review feedback7” needs re-wording as not only is the Guthrie et al paper a non-systematic review, but the second reference cited in that sentence by Gallo et al is a survey (i.e. not a review at all). The way the sentence is phrased implies that it is a systematic review.
Thank you for flagging this. We have now used “literature review” and added the fact that the second study is a survey.

11. Suggest amending the sentence on page 3 “Many studies using large sample sizes found either no association or only a weak association between the mean score and the VOLUME of citations of subsequent publications”
We have changed the text to read “number of citations”.
Competing Interests: No competing interests were disclosed. Close
Report a concern

Comments on this article Comments (0)

Version 2

VERSION 2 PUBLISHED 09 Jul 2018

Open Peer Review

Reviewer Status

Reviewer Reports

	Invited Reviewers
	1	2
Version 2 (revision) 15 Oct 18
Version 1 09 Jul 18	read	read

Jonathan Shepherd, University of Southampton, Southampton, UK

Jeremy C. Wyatt, University of Southampton, Southampton, UK
Shahar Avin, University of Cambridge, Cambridge, UK

Steven Wooding, University of Cambridge, Cambridge, UK

Comments on this article

All Comments(0)

Add a comment

Browse by related subjects

Back to all reports

Reviewer Report

25 Views

24 Sep 2018 | for Version 1

Shahar Avin, Centre for the Study of Existential Risk, University of Cambridge, Cambridge, UK

Steven Wooding, Centre for Science and Policy, University of Cambridge, Cambridge, UK

25 Views Cite this report Responses(1)

Approved

Rank proposals based on their mean scores until funding runs out.
Pool proposals based on their mean score into buckets, rounding to the nearest integer. Fund all proposals with a mean of 1 (1.0-1.49, n=45), then from the bucket with a mean of 2 (1.5-2.49, n=114) rank proposals based on their standard deviation and fund until funding runs out.

It might be easier to read the paper if scores were consistently referred to as best/worst and better/worse – using ‘higher' is confusing when better scores are lower.
It would be more elegant to give 'e.g., Bornmann et al, 2008' rather than 'e.g., 36'.

Is the work clearly and accurately presented and does it cite the current literature?

Yes
Is the study design appropriate and is the work technically sound?

Yes
Are sufficient details of methods and analysis provided to allow replication by others?

Yes
If applicable, is the statistical analysis and its interpretation appropriate?

Yes
Are all the source data underlying the results available to ensure full reproducibility?

Yes
Are the conclusions drawn adequately supported by the results?

Yes

References

Competing Interests

No competing interests were disclosed.

We confirm that we have read this submission and believe that we have an appropriate level of expertise to confirm that it is of an acceptable scientific standard.

Respond to this report

Responses (1)

Author Response

15 Oct 2018

Adrian Barnett, Institute of Health and Biomedical Innovation & School of Public Health and Social Work, Queensland University of Technology, Brisbane, 4059, Australia

The notion that disagreements amongst reviewers might indicate a promising high-risk/high-reward project certainly has currency amongst those who consider how the system might be improved. In addition to the framework of Linton (2016)1, the idea is also present in the model of Brezis (2007) and is implied by several works on the anti-innovation bias of grant peer review (e.g. Greenberg, 1998 2; Gillies, 2008 3). However, this intuitive notion has yet to be put to the test, until the current study, which is a welcome contribution.
Thanks for the interesting references, we have now mentioned Brezis in our Introduction.
The experimental design and statistical analysis are compelling for an initial study, though as the authors note further complications could be addressed in later work.
Given the prevailing policy and academic discussions the negative result is surprising and it rules out some suggested approaches to reform of the grant allocation system; however, the dataset limits the generality of the conclusions that can be drawn (through no fault of the authors) – the key limitation being that only 11% of applications can be analysed (the funded ones), a set that is heavily skewed towards the top scoring applications.
We agree this is a key limitation, and it would be useful to repeat the study in a more generous scheme, where a greater proportion of applications were funded.
For example, as shown in Figure 4 there is plenty of potential for SD to be associated with increased citation, but not enough data to tell. The authors note that the application with the largest SD drove this large uncertainty – it could be that this application is an outlier, or it could be that it is typical of applications with large SDs but there are very few of them in the dataset because they tended to fall below the funding line.
This is entirely possible, and if there are a small number of extremely high pay-off projects then we would need a much larger sample to robustly test if there is a consistent pattern of more high pay-off projects associated with greater disagreement. We have now mentioned this in the limitations.
Through its analysis, the study forces a refinement of the question of what sorts of disagreements (in extent and driven by what underlying logics) should be considered useful indicators. We suggest the study raises the following THREE questions for future work:
Firstly it would be valuable to understand the reasons and logics behind the disagreements that arise between reviewers, from the fact that "disagreements between reviewers about an application can stem from different sources". While the authors suggest addressing this with further information about scores, we can also ask if different score means might indicate different "regimes" for disagreement, e.g. disagreement along the lines of "not sure this will work" or "this goes against received wisdom" at relatively high score means, and disagreements along the lines of "not sure what this is about" or "hasn't this been tried before?" at lower score means. Qualitative research asking reviewers about their scoring behaviour could help understand the reasoning that goes with different scoring.
This is a good point. “Disagreement” is likely to be too general a word, and future studies could look in far more detail at the types of disagreement. We have previously used a qualitative researcher as an observer of funding panel dynamics, and we have now added this potential approach to our discussion.
Secondly, we could reframe the question to address the lack of information on unfunded applications by asking how can funding best be allocated if the amount of funding available is cut by 50%.
To test this, we reanalysed the data provided by the authors with the following question: assuming only half the funding was available, which of the following selection methods would perform better?
Rank proposals based on their mean scores until funding runs out.
Pool proposals based on their mean score into buckets, rounding to the nearest integer. Fund all proposals with a mean of 1 (1.0-1.49, n=45), then from the bucket with a mean of 2 (1.5-2.49, n=114) rank proposals based on their standard deviation and fund until funding runs out.
Under both methods, all proposals with a mean of 1 are funded, for a total TRC of 319.9. When we look at the proposals in the second bucket, when funding according to method 1, the total TRC for this bucket is 224.2, whereas for method 2 it is 195.5. However, the highest citation-receiving proposal in the second bucket under method 1 has a TRC of 19.9, whereas the highest citation-receiving proposal from the second bucket under method 2 has a TRC of 35.9 (the third highest TRC in the entire sample). This fits with Gillies' description of peer-review as going for less risky proposals, but at the cost of throwing out the occasional exceptional proposal. This is also born out by the distribution of TRCs, with the standard deviation of TRCs for the second bucket under method 1 being 4.2, and under method 2 being 6.2.
This is an interesting comment and thanks for the new analysis. As an aside, we note that only by sharing our data can we have such an in-depth discussion with our reviewers. We have added R code to run these suggested analyses to our results on github (https://github.com/agbarnett/funding.disagree).
It is an interesting approach to use the mean for the “top” tier of applications and the standard deviation for the second tier. This may appeal to funders and panel members, because we believe there will always be a desire to fund those applications with the best mean. This two-tier approach may also be easier to explain than the Black–Scholes approach suggested by Linton, which combines the mean and variance in scores using an equation.
We are wary of using the standard deviation in the total relative citations because of the strong positive skew in its distribution, and the inter-quartile range in citations is actually larger for the approach using the mean at 4.3, compared with 2.9 when using the standard deviation.
Thirdly, it would be valuable to understand what sorts of disagreement exist in the scoring of all the applications (both successful and unsuccessful). It could be argued that the type of disagreement likely to indicate high risk/high return proposals would be bi-modal – some good reviews maybe with scores of 1-1.5, some very poor reviews maybe with scores of 3-4. Given the small fraction of applications funded, very few applications of this nature would be funded (due to the understandable aggregation in the shared data we could not examine the exact number, but fewer than 10 applications have a score lower than 3). Do such applications with such bi-modal review scores exist? Or is the level of disagreement seen in the successful applications similar to that of the unsuccessful applications?
Unfortunately our data only contains the summary statistics on the applications’ scores and so we can’t examine these distributions. We have added this as a limitation.
The above questions only suggest that there is further complexity here that needs to be explored, with more complex, higher power studies. We thank the authors for paving the path for such studies, and for making their underlying data and analysis available in a form that is easy to explore.
Thanks, we agree that larger studies are needed.
Two small notes:

It might be easier to read the paper if scores were consistently referred to as best/worst and better/worse – using ‘higher' is confusing when better scores are lower.

Agreed and changed. We’ve also added text labels to Figure 5 and the new Figure 4.

It would be more elegant to give 'e.g., Bornmann et al, 2008' rather than 'e.g., 36'.

Changed as suggested.

View more View less

Competing Interests

No competing interests were disclosed.

Back to all reports

Reviewer Report

25 Views

20 Sep 2018 | for Version 1

Jonathan Shepherd, Southampton Health Technology Assessments Centre, University of Southampton, Southampton, UK

Jeremy C. Wyatt, Wessex Institute, University of Southampton, Southampton, SO40 7AA, UK

25 Views Cite this report Responses(1)

Approved

Is the work clearly and accurately presented and does it cite the current literature?

Yes
Is the study design appropriate and is the work technically sound?

Partly
Are sufficient details of methods and analysis provided to allow replication by others?

Yes
If applicable, is the statistical analysis and its interpretation appropriate?

Partly
Are all the source data underlying the results available to ensure full reproducibility?

Yes
Are the conclusions drawn adequately supported by the results?

Yes

References

1. Guthrie S, Ghiga I, Wooding S: What do we know about grant peer review in the health sciences?. F1000Res. 2017; 6: 1335 PubMed Abstract | Publisher Full Text

Competing Interests

No competing interests were disclosed.

We confirm that we have read this submission and believe that we have an appropriate level of expertise to confirm that it is of an acceptable scientific standard.

Respond to this report

Responses (1)

Author Response

15 Oct 2018

Adrian Barnett, Institute of Health and Biomedical Innovation & School of Public Health and Social Work, Queensland University of Technology, Brisbane, 4059, Australia

1. The primary outcome measure is the citation counts from publications associated with the successful application. Publications were produced from 1 to 8 years after the peer review date (average 4.3 years). This does not appear to take account of varying time since the projects were funded (i.e. 7 year gap between projects that were funded from 1999 to 2006). Thus, older studies would have had more time for publications to be produced and cited. We therefore suggest a more meaningful outcome measure would be either the number of citations per year per study, or the total number of citations in, say, the 5 years following the final project report, or some other standardized project milestone. Adding the review year to the model does not seem to adequately control for this factor (though qualified statistical advice is needed to clarify this). We think this is the issue that likely affects the interpretation of the results the most in our critique.
Thanks for the comment. Actually, the citation values are normalized per publication year, thus older studies would not have an advantage as the resultant citations from publications are normalized by year. It is true that more time post peer review date would allow more publications, but all of these products were derived from the final reports, which were submitted on average five years after peer review. Thus, whatever is reported by the principal investigator in their final report is what was measured, which is what is presented by funding agencies as the output of the grant.

2. The number of citations was standardised by academic field – i.e. molecular biology. Was there any variation in study designs within this field that might also change the expected number of citations (e.g. systematic reviews may attract more citations than primary experimental studies in some fields)? It would be useful for context if there could be a table with some basic aggregate details of the funded studies, such as types of study design, molecular biological application, study sample characteristics, duration of study etc. This would help to put the results into context.
This is interesting, but would likely need to be a much larger, separate study to go back into each application and characterize the study design, sample characteristics, etc., and is out of the current scope. That said, the applications included in this analysis were submitted to a 4-year, R01-style support mechanism. In every program year there was a significant proportion of both applied and basic research applications, with many applications encompassing varying degrees of both basic and applied research in their aims. There was a wide variety of research topic areas, including vision, drug abuse, nutrition, blood-related cancer, kidney disease, autoimmune diseases, malaria, tuberculosis, osteoporosis, arthritis, and autism research, among others. This is described in more detail in our original publication: https://journals.plos.org/plosone/article?id=10.1371/journal.pone.0106474.

3. The impact of a piece of research on which referees could not agree might be either lower or higher than those on which they could. So, it would be useful to plot the standard deviation of the citations against the standard deviation of the peer review score.
We have now plotted the inter-quartile range in citations against the application score mean and standard deviation. We used the inter-quartile range instead of the standard deviation because of the strong skew in citations, and the standard deviation was strongly influenced by the application with the highest citations.
The new results show moderate support for a greater return for applications with a higher agreement between peer reviewers. See new Figure 4, with new explanatory paragraph in the “Statistical Methods” section, and an updated discussion.

4. As well as using multiple imputation to correct for missing data, a sensitivity analysis in which cases with missing data are omitted would be useful.
We have added a complete case analysis to the more detailed results available on github (https://github.com/agbarnett/funding.disagree). All the results were very similar to the imputed data.

5. Some measure of the model fit would be useful, eg. adjusted R squared
We are not certain that the R-squared statistic would be useful here. The adjusted R-squared can be useful for comparing between alternative models, or where the goal is accurate prediction. Here we were just looking for any signal between application scores and citations, assuming that the detection of any signal could lead to improvements in the design of funding systems. We have investigated the residuals to look for poor model fit.

6. There was a wide variation in the number of reviewers per article from 2 to 18. Was this due to differences in the kind of research, amount of funding requested or some other perceived risk on behalf of the funder? Could this artificially influence the standard deviation of the score, confounding any association with citations?
The majority (90%) of applications were reviewed in panels (roughly 10 to 15 reviewers). Some were reviewed via a mail review mechanism (2 to 3 reviewers). The determination of review mechanism largely depended on the topic area. We don’t believe this should be a large confounder of the results.
We have now included a sensitivity analysis using just the larger panels and excluding the mail review panels. The results were similar to the analysis using all panels. These new results are available on github (https://github.com/agbarnett/funding.disagree).

7. Fractional polynomial model results are only presented for the best fitting model with the smallest deviance. This is acceptable in principle, but it would be useful for the authors to comment on whether there was any variation in the results according to the other fractional polynomial transformations (if available). This will provide confidence in the robustness of the findings.
We have examined the predictions for the best five models and the average results were similar in terms of the mean. However, the confidence intervals for the second best model had a much narrow confidence interval for citation predictions using the application score standard deviation. In hindsight we prefer this model, as it has only a slightly poorer deviance, but a much more believable confidence interval. It would have been better to have a multi-criteria decision for the “best” model, that used both the deviance and average confidence interval width. This has been a useful lesson for future studies, but we continue to present the model with the wider CI in the main results because we feel we should stick to our original protocol.
These new results are available on github (https://github.com/agbarnett/funding.disagree).

8. Reference is made in the first paragraph to a “recent systematic review” by Guthrie et al (2018 1) (and also in the third paragraph). We note that this publication doesn’t refer to itself as being a systematic review, and indeed, it is an update of a 2009 review which describes itself as a non-systematic review. We would suggest using the term “non-systematic review”, or just “literature review”.
Thank you for flagging this. We have now used “literature review”.

9. Thank you for citing our own recent systematic review on peer review of grants in health. You mention that the review included eight studies and called for further research in this area, which is correct. However, the review focused specifically on studies aiming to improve the effectiveness and efficiency of peer review. These were drawn from a wider set of 83 studies on peer review which we systematically mapped. In the map there were some studies which focused on assessing the impact of funded research, eg. In terms of bibliometrics. Thus, there is a body of evidence on this topic, though we didn't systematically review it in detail. We are happy to provide you with a list of these studies.
We have changed our language to make the goal of your review clearer. We would gladly see the study list. Perhaps this is best uploaded to our github page for this project (if it can be made public): https://github.com/agbarnett/funding.disagree then click “upload file”, you will need a github account (free) and request write access to our project.

10. The sentence on page 3 beginning “A recent systematic review found “suggestive” evidence that funding peer review can have an anti-innovation bias2 and that innovation and risk may not often be sufficiently addressed in review feedback7” needs re-wording as not only is the Guthrie et al paper a non-systematic review, but the second reference cited in that sentence by Gallo et al is a survey (i.e. not a review at all). The way the sentence is phrased implies that it is a systematic review.
Thank you for flagging this. We have now used “literature review” and added the fact that the second study is a survey.

11. Suggest amending the sentence on page 3 “Many studies using large sample sizes found either no association or only a weak association between the mean score and the VOLUME of citations of subsequent publications”
We have changed the text to read “number of citations”.

View more View less

Competing Interests

No competing interests were disclosed.

Alongside their report, reviewers assign a status to the article:

Approved - the paper is scientifically sound in its current form and only minor, if any, improvements are suggested

Approved with reservations - A number of small changes, sometimes more significant revisions are required to address specific details and improve the papers academic merit.

Not approved - fundamental flaws in the paper seriously undermine the findings and conclusions

[1] 1. Herbert DL, Barnett AG, Clarke P, et al.: On the time spent preparing grant proposals: an observational study of Australian researchers. BMJ Open. 2013; 3(5): pii: e002800. PubMed Abstract | Publisher Full Text | Free Full Text

[2] 2. Guthrie S, Ghiga I, Wooding S: What do we know about grant peer review in the health sciences? [version 2; referees: 2 approved]. F1000Res. 2018; 6: 1335. PubMed Abstract | Publisher Full Text | Free Full Text

[3] 3. Demicheli V, Di Pietrantonj C: Peer review for improving the quality of grant applications. Cochrane Database Syst Rev. 2007; (2): MR000003. PubMed Abstract | Publisher Full Text

[4] 4. Shepherd J, Frampton GK, Pickett K, et al.: Peer review of health research funding proposals: A systematic map and systematic review of innovations for effectiveness and efficiency. PLoS One. 2018; 13(5): e0196914. PubMed Abstract | Publisher Full Text | Free Full Text

[5] 5. Linton JD: Improving the peer review process: Capturing more information and enabling high-risk/high-return research. Research Policy. 2016; 45(9): 1936–1938. Publisher Full Text

[6] 6. Fleurence RL, Forsythe LP, Lauer M, et al.: Engaging patients and stakeholders in research proposal review: the patient-centered outcomes research institute. Ann Intern Med. 2014; 161(2): 122–130. PubMed Abstract | Publisher Full Text

[7] 7. Gallo S, Thompson L, Schmaling K, et al.: Risk evaluation in peer review of grant applications. Environment Systems and Decisions. 2018; 38(2): 216–229. Publisher Full Text

[8] 8. Bromham L, Dinnage R, Hua X: Interdisciplinary research has consistently lower funding success. Nature. 2016; 534(7609): 684–687. PubMed Abstract | Publisher Full Text

[9] 9. Fang FC, Casadevall A: NIH peer review reform--change we need, or lipstick on a pig? Infect Immun. 2009; 77(3): 929–932. PubMed Abstract | Publisher Full Text | Free Full Text

[10] 10. Braben DW: Promoting the Planck Club: How Defiant Youth, Irreverent Researchers and Liberated Universities Can Foster Prosperity Indefinitely. Wiley, 2014; ISBN 9781118546383. Reference Source

[11] 11. Barnett AG: Ask the researcher: The experience of applying for health and medical research funding in Australia Survey results. 2017. Reference Source

[12] 12. Scheiner SM, Bouchie LM: The predictive power of NSF reviewers and panels. Frontiers in Ecology and the Environment. 2013; 11(8): 406–407. Publisher Full Text

[13] 13. Kaltman JR, Evans FJ, Danthi NS, et al.: Prior publication productivity, grant percentile ranking, and topic-normalized citation impact of NHLBI cardiovascular R01 grants. Cir Res. 2014; 115(7): 617–624. PubMed Abstract | Publisher Full Text | Free Full Text

[14] 14. Lauer MS, Danthi NS, Kaltman J, et al.: Predicting productivity returns on investment: Thirty years of peer review, grant funding, and publication of highly cited papers at the National Heart, Lung, and Blood Institute. Circ Res. 2015; 117(3): 239–243. PubMed Abstract | Publisher Full Text | Free Full Text

[15] 15. Doyle JM, Quinn K, Bodenstein YA, et al.: Association of percentile ranking with citation impact and productivity in a large cohort of de novo NIMH-funded R01 grants. Mol Psychiatry. 2015; 20(9): 1030–1036. PubMed Abstract | Publisher Full Text | Free Full Text

[16] 16. Fang FC, Bowen A, Casadevall A: NIH peer review percentile scores are poorly predictive of grant productivity. eLife. 2016; 5. pii: e13323. PubMed Abstract | Publisher Full Text | Free Full Text

[17] 17. Danthi N, Wu CO, Shi P, et al.: Percentile ranking and citation impact of a large cohort of National Heart, Lung, and Blood Institute-funded cardiovascular R01 grants. Circ Res. 2014; 114(4): 600–606. PubMed Abstract | Publisher Full Text | Free Full Text

[18] 18. Li D, Agha L: Research funding. Big names or big ideas: do peer-review panels select the best science proposals? Science. 2015; 348(6233): 434–8. PubMed Abstract | Publisher Full Text

[19] 19. Gallo SA, Carpenter AS, Irwin D, et al.: The validation of peer review through research impact measures and the implications for funding strategies. PLoS One. 2014; 9(9): e106474. PubMed Abstract | Publisher Full Text | Free Full Text

[20] 20. Times Higher Education: Citation averages, 2000-2010, by fields and years. 2011. Reference Source

[21] 21. Lindner MD, Torralba KD, Khan NA: Scientific productivity: An exploratory study of metrics and incentives. PLoS One. 2018; 13(4): e0195321. PubMed Abstract | Publisher Full Text | Free Full Text

[22] 22. Royston P, Ambler G, Sauerbrei W: The use of fractional polynomials to model continuous risk variables in epidemiology. Int J Epidemiol. 1999; 28(5): 964–974. PubMed Abstract | Publisher Full Text

[23] 23. R Core Team: A Language and Environment for Statistical Computing. R Foundation for Statistical Computing, Vienna, Austria, 2018. Reference Source

[24] 24. van Buuren S, Groothuis-Oudshoorn K: mice: Multivariate imputation by chained equations in R. J Stat Softw. 2011; 45(3): 1–67. Publisher Full Text

[25] 25. Barnett AG: agbarnett/funding.disagree: First release of funding disagreement code and data (version v1.0). 2018. Publisher Full Text

[26] 26. von Elm E, Altman DG, Egger M, et al.: The Strengthening the Reporting of Observational Studies in Epidemiology (STROBE) statement: guidelines for reporting observational studies. PLoS Med. 2007; 4(10): e296. PubMed Abstract | Publisher Full Text | Free Full Text

[27] 27. Manning WG: The logged dependent variable, heteroscedasticity, and the retransformation problem. J Health Econ. 1998; 17(3): 283–95. PubMed Abstract | Publisher Full Text

[28] 28. Coveney J, Herbert DL, Hill K, et al.: ‘Are you siding with a personality or the grant proposal?’: observations on how peer review panels function. Res Integr Peer Rev. 2017; 2(1): 19. PubMed Abstract | Publisher Full Text | Free Full Text

[29] 29. Boudreau KJ, Guinan EC, Lakhani KR, et al.: Looking Across and Looking Beyond the Knowledge Frontier: Intellectual Distance, Novelty, and Resource Allocation in Science. Manage Sci. 2016; 62(10): 2765–2783. PubMed Abstract | Publisher Full Text | Free Full Text

[30] 30. Gallo SA, Sullivan JH, Glisson SR: The Influence of Peer Reviewer Expertise on the Evaluation of Research Funding Applications. PLoS One. 2016; 11(10): e0165147. PubMed Abstract | Publisher Full Text | Free Full Text

[31] 31. Pier EL, Brauer M, Filut A, et al.: Low agreement among reviewers evaluating the same NIH grant applications. Proc Natl Acad Sci U S A. 2018; 115(12): 2952–2957. PubMed Abstract | Publisher Full Text | Free Full Text

[32] 32. Cicchetti DV: The reliability of peer review for manuscript and grant submissions: A cross-disciplinary investigation. Behavioral and Brain Sciences. 1991; 14(1): 119–135. Publisher Full Text

[33] 33. Graves N, Barnett AG, Clarke P: Funding grant proposals for scientific research: retrospective analysis of scores by members of grant review panel. BMJ. 2011; 343: d4797. PubMed Abstract | Publisher Full Text | Free Full Text

[34] 34. Gregorius S, Dean L, Cole DC, et al.: The peer review process for awarding funds to international science research consortia: a qualitative developmental evaluation [version 3; referees: 2 approved]. F1000Res. 2018; 6: 1808. PubMed Abstract | Publisher Full Text | Free Full Text

[35] 35. Lindner MD, Nakamura RK: Examining the Predictive Validity of NIH Peer Review Scores. PLoS One. 2015; 10(6): e0126938. PubMed Abstract | Publisher Full Text | Free Full Text

[36] 36. Bornmann L, Wallon G, Ledin A: Does the committee peer review select the best applicants for funding? An investigation of the selection process for two European molecular biology organization programmes. PLoS One. 2008; 3(10): e3480. PubMed Abstract | Publisher Full Text | Free Full Text

[37] 37. Decullier E, Huot L, Chapuis FR: Fate of protocols submitted to a French national funding scheme: A cohort study. PLoS One. 2014; 9(6): e99561. PubMed Abstract | Publisher Full Text | Free Full Text

[38] 38. Ioannidis JP, Boyack KW, Small H, et al.: Bibliometrics: Is your most cited work your best? Nature. 2014; 514(7524): 561–562. PubMed Abstract | Publisher Full Text

Do funding applications where peer reviewers disagree have higher citations? A cross-sectional study

Abstract

Keywords

Introduction

Methods

Application data

Citation counts

Statistical analyses

Missing data

Results

Figure 1. Histograms of total relative citations (green) and application score statistics (blue).

Figure 2. Scatter-plots and Pearson correlations of application score statistics.

Figure 3. Scatter-plots of log-transformed total relative citations against application score statistics.

Table 1. Parameter estimates for the multiple regression models predicting citation numbers.

Figure 4. Predicted relative citations using the best fractional polynomial for the application score statistics.

Discussion

Limitations

Conclusions

Data availability

Competing interests

Grant information

Acknowledgements

References

Comments on this article Comments (0)

Open Peer Review

Comments on this article Comments (0)

Open Peer Review

Reviewer Status

Reviewer Reports

Comments on this article

Browse by related subjects

Competing Interests Policy

Stay Updated