Keywords
decision making, RCT, sample size, waste in research
-
Views
-
Downloads
How to cite this article
Graves N, Barnett AG, Burn E and Cook D. Smaller clinical trials for decision making; a case study to show p-values are costly [version 2; peer review: 1 approved, 2 approved with reservations]. F1000Research 2018, 7:1176 (https://doi.org/10.12688/f1000research.15522.2)
NOTE: If applicable, it is important to ensure the information in square brackets after the title is included in all citations of this article.
Export Citation
Sciwheel
EndNote
Ref. Manager
Bibtex
ProCite
Sente
▬
✚
Research Article
Revised
Smaller clinical trials for decision making; a case study to show p-values are costly
[version 2; peer review: 1 approved, 2 approved with reservations]
Previously titled: Smaller clinical trials for decision making; using p-values could be costly
PUBLISHED 27 Sep 2018
OPEN PEER REVIEW
REVIEWER STATUS
Abstract
Corresponding author:
Nicholas Graves
Competing interests:
No competing interests were disclosed.
Grant information:
The author(s) declared that no grants were involved in supporting this work.
Copyright:
© 2018 Graves N et al.
This is an open access article distributed under the terms of the Creative Commons Attribution License, which permits unrestricted use, distribution, and reproduction in any medium, provided the original work is properly cited.
Data associated with the article are available under the terms of the Creative Commons Zero "No rights reserved" data waiver (CC0 1.0 Public domain dedication).
How to cite: Graves N, Barnett AG, Burn E and Cook D. Smaller clinical trials for decision making; a case study to show p-values are costly [version 2; peer review: 1 approved, 2 approved with reservations]. F1000Research 2018, 7:1176 (https://doi.org/10.12688/f1000research.15522.2)
First published: 02 Aug 2018, 7:1176 (https://doi.org/10.12688/f1000research.15522.1)
Latest published: 27 Sep 2018, 7:1176 (https://doi.org/10.12688/f1000research.15522.2)
Revised Amendments from Version 1
This is an update in response to the review from Stephen Senn. The title has been changed, there is a new Figure 3, we have added a new "Counter-exmple of no treatment" sub-heading in the Methods section, and have expanded the Discussions section.
See the authors' detailed response to the review by Stephen Senn
Introduction
Informed patients, thoughtful clinicians and rational health planners make decisions about the services and treatments provided using the best information available, and all decisions are made under conditions of uncertainty1,2. We examine a situation where sufficient evidence arises from a clinical trial to inform a decision about changing services before the conventional statistical stopping point for a clinical trial is reached. This paper is about the tension between the ‘precision’ and the ‘impact’ of a scientific measurement3 and how that tension might dictate the sample size of a clinical trial.
Imagine a new treatment is compared against the best contemporary alternative in a well conducted randomised controlled trial (RCT). The design requires 800 participants in total based on a standard sample size calculation of 5% type 1 error and 80% power. The new treatment is more efficacious, prolongs life of high quality and saves more money than it costs to implement. The evidence to support these conclusions can be seen in the data after only 200 trial participants have been recruited, but primary outcomes are not yet statistically significant. Clinical equipoise, the cornerstone of ethical treatment allocation is lost, yet the conventions of hypothesis testing and arbitrary power calculation demand a further 600 participants are recruited. The information arising from the additional 600 participants is unlikely to change the actions of a rational decision maker who wishes to adopt the new treatment. Yet scarce research funds are used up meaning opportunities to fund other research are lost, and some patients have been consented and allocated to a treatment that we could not recommend, nor would we chose for ourselves or our families.
The utility of clinical trials for those managing health services and making clinical decisions is under debate and traditional paradigms are being challenged4. The chief claim of this paper is that an RCT designed to test a hypothesis using traditional rules of inference might have more participants than required, if the goal is to make a good decision. Waste in research arises from routine use of arbitrary levels of statistical confidence5 and because the trial data are considered in isolation6. The marginal value of the information acquired for the purpose of making a good decision is not made explicit. Important information for the purpose of decision making often lies outside the clinical trial process. The plausibility of our claim is demonstrated by re-analysing a recent RCT7.
Choosing a sample size for hypothesis testing
For the design of superiority trial, the aim is to have a high likelihood of sufficient evidence to confidently reject a null hypothesis that two treatments are equivalent when treatments differ by a specified difference. This difference is usually based on either clinical importance or a best guess of the true treatment effect. Inference based on this approach has two types of potential errors. A false-positive or type I error of rejecting the null hypothesis when there is no difference, with probability α. A false negative or type II error of not rejecting the null hypothesis when there is an effect, with probability β. The sample size of the trial is calculated to give an acceptable type I error rate and power (1–β), typically 0.05 for α and 0.8 to 0.9 for the power. The final analysis summarises the incompatibility between the data and the null hypothesis8. If the p-value is below the standard 5% limit the null hypothesis of no effect is rejected. A ‘statistically significant’ result is then celebrated and typically used to support a decision to make a change to health services.
Choosing a sample size for decision making
We assume the objective of decision-makers who manages health services is to improve outcomes for the populations they serve. Because this challenge will be addressed with finite resources not every service or new technology can be made available for a population. Decision-makers therefore require knowledge of the health foregone from not funding services displaced by the services that are funded9. The services that are provided should generate more health benefits per dollar of cost when compared to those that are not. With this criterion satisfied the opportunity cost from the services not provided is minimised. A rational decision maker will logically follow these rules: do not adopt programmes that worsen health outcomes and increase cost; adopt programmes that improve health outcomes and decrease costs; and, when they face a situation of increased cost for increased health outcomes they prioritise programmes that provide additional health benefits for the lowest extra cost10. They will continue choosing cost-effective services until available health budgets are exhausted. An appropriate and generic measure of health benefit is the quality adjusted life year (QALY)11. While this approach does not consider how health benefits are distributed among the population there is a framework for including health inequalities in the economic assessment of health care programmes12.
In choosing a sample size for a clinical trial to evaluate a new service or technology a decision-maker will consider the uncertainty in the conclusion about how costs and health benefits change by adoption. The aim is to reduce the likelihood of making the wrong decision. They will make rational and good decisions, and they will manage uncertainty rather than demand an arbitrarily high probability of rejecting a null hypothesis. Methods are available to estimate the expected value of information and so the optimal sample size for a trial is dependent on the context specific costs and benefits of acquiring extra information13. Each decision is context dependent and the ‘one size fits all’ approach to sample size calculation is arbitrary and potentially wasteful. This holistic approach should be a priority for designing, monitoring and analysing clinical trials.
Methods
The TEXT ME RCT: A case study
A case study to illustrate the differing evidential requirements of the ‘hypothesis-testing’ and ‘decision-making’ approaches is provided by the RCT of the Tobacco, Exercise and Diet Messages (TEXT ME) intervention14. This health services program targeted multiple influential risk factors in patients with coronary heart disease, with SMS text messages. Advice and motivation was provided to improve health behaviours and it was supplementary to usual care. The hypothesis was that the intervention would lower plasma low-density lipoprotein cholesterol by 4.5 mg/dL at 6 months for participants compared with those receiving usual care15. The required sample size was 704 participants for 90% power15 and the trial recruited and randomised 710 participants7. The mean difference between the intervention and control group was –5 mg/dL, (95% CI –9 to 0 mg/dL). With a p-value of 0.04, the null hypothesis was rejected. Evidence for health effects were also sought on other biomedical and behavioural risk factors, quality of life, primary care use and re-hospitalisations. Clinically and statistically significant effects were also found for systolic blood pressure (mean difference –8 mmHg, p<0.001), body mass index (–1.3 kg/m2, p<0.001) and current smoking (relative risk of 0.61, p<0.001).
The TEXT ME trial data were used to inform an economic evaluation of the potential change to costs and health benefits measured in quality adjusted life years to the community from a decision to adopt the programme16. The observed differences in low-density lipoprotein cholesterol, systolic blood pressure and smoking were combined with reliable external epidemiological evidence to estimate the reduction in acute coronary events, myocardial infarction and stroke and were extrapolated over the patients expected remaining life times. The costs of providing the intervention, the projected costs of the treatment of acute events and general primary care use and expected mortality were all informed by data sources external to the primary trial16. The findings revealed that TEXT ME was certainly going to lead to better health outcomes and cost savings. The conclusion was that a rational decision-maker should fund and implement the TEXT ME program. Once available an informed clinician would then recommend TEXT ME to coronary patients, and enough patients would sign up to create benefits for individuals and the health system. Using the TEXT ME study, we consider whether the same decision could have been made at an earlier stage with fewer participants enrolled in the primary trial.
Data analysis
We examine the effect of a reduced sample size on the results of both the hypothesis-testing analysis for differences in low-density lipoprotein cholesterol, and the economic evaluation of the intervention. From the original 710 participants, smaller samples between 100 and 700 patients in increments of 100 were considered with the resampling done with replacement. The ‘p-value’ and ‘economic’ analyses were re-run using the data provided by the randomly selected patients and this process was repeated 500 times for each sample size. The simulations and figures were created using R (version 3.1.0). The code is available on GitHub https://github.com/agbarnett/smaller.trials but we are unable to share the primary data from the TEXT ME RCT.
Counter-example of no treatment effect
To illustrate this approach with treatments that are equally effective, we used the same methods as above, but created data using the TEXT ME trial where the two groups had equivalent outcomes. We did this by randomly allocating patients to the TEXT ME intervention or usual care, and then resampling with replacement to create a new version of the study sample. We assumed there was no risk reduction for the TEXT ME group, and used the same uncertainty in risk reduction as per the previous model.
Results
The effect of reducing the sample size for hypothesis-testing objectives was to simulate studies that traditional hypothesis testing approaches would deem underpowered, see Figure 1.
Figure 1. P-values increase as sample sizes decrease for the observed differences in low-density lipoprotein cholesterol (based on 500 simulations per sample size).
The dotted horizontal line is the standard 5% threshold. The boxes are the 25th and 75th percentiles with the median as the central line. The upper whisker extends from the third quartile to the largest value no further than 1.5 * IQR from the quartile (where IQR is the inter-quartile range). The lower whisker extends from the 1st quartile to the smallest value at most 1.5 * IQR of the quartile. Data beyond the end of the whiskers are called ‘outlying’ points and are plotted individually.
Only for a sample size of 500 participants or more would the majority of trials find a statistically significant difference in average low-density lipoprotein cholesterol between groups (Figure 1). Even at a sample size of 700 around 30% of trials would be expected to make the ‘wrong’ inference of not rejecting the null hypothesis. This is consistent with a priori analytic estimates of sample size to address the hypothesis.
To inform decision making using cost-effectiveness as the criterion, reducing the sample size has little effect on the conclusion of whether to fund, recommend and participate in TEXT ME, see Figure 2. For every simulation for each sample size the decision to adopt TEXT ME led to cost savings shown on the y-axis and gains to health, measured by QALYs shown on the x-axis.
Figure 2. The conclusion for decision-making becomes more uncertain but does not change with decreasing sample size.
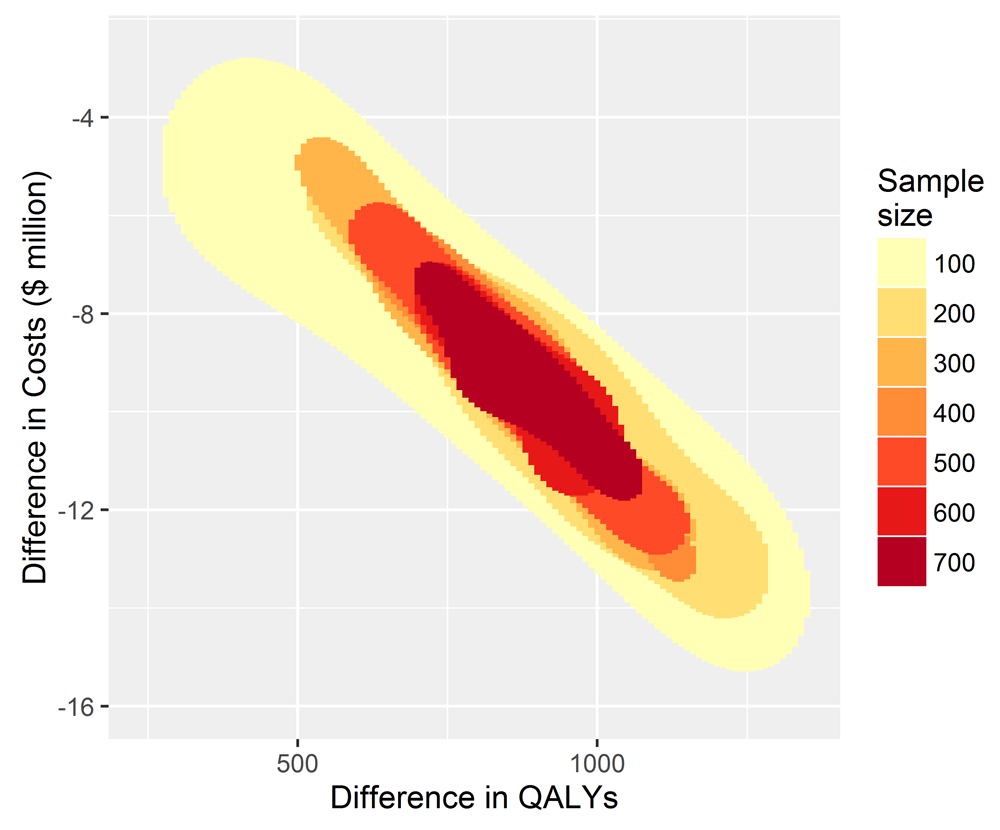
The x-axis shows the QALY gains for TEXT ME over usual care, and the y-axis shows the cost savings.
A sample size of 100 or more in the primary trial would convince a risk neutral and rational decision maker that TEXT ME is both cost-saving and health improving, and so should be adopted. The imprecision surrounding this inference increases as the sample size reduces, but the decision-making inference does not change. If the goal is to make a good decision about whether TEXT ME should be adopted widely, then that could have been achieved with a much smaller trial, one that enrolled as few as 100 patients. This would have been a cheaper and quicker research project releasing scarce research dollars for other important projects.
When we simulated studies where there was no treatment effect, all the costs of implementing the TEXT ME program of around 1.5 million dollars for the cohort of 50,000 patients were incurred, but none of the health benefits and associated cost savings were realised. The estimates of change to health benefits straddled the zero line with a spread covering a relatively small change in QALYs of around 20 lost to 12 gained. The inference for decision makers is clear at any sample size that adoption would be a poor decision (Figure 3).
Figure 3. The conclusion for decision-making is clear when there is no treatment effect, costs are increased for no change to health benefits for all sample sizes.
Dataset 1.Data used for a simulation of Figure 2.
Discussion
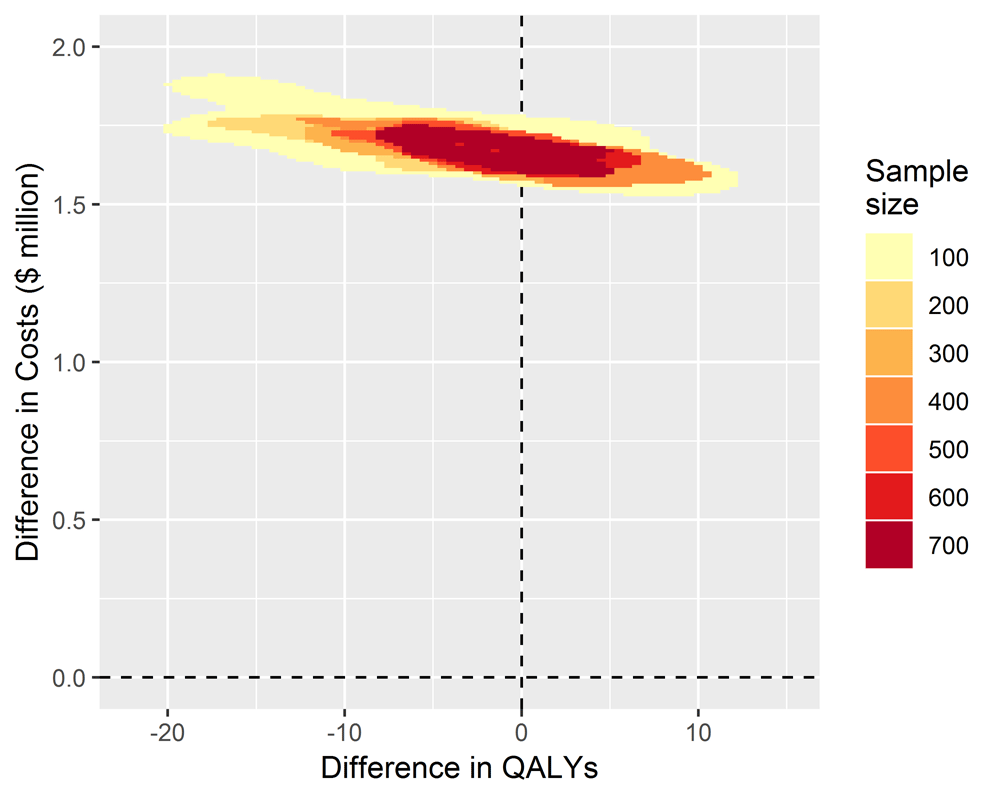
RCTs have become “massive bureaucratic and corporate enterprises, demanding costly infrastructure for research design, patient care, record keeping, ethical review, and statistical analysis”17. A single phase 3 RCT could today cost $30 million or more18 and take several years from inception to finalisation. These trials are powered for arbitrary rules of statistical significance. Critics of this approach3 argue “that some of the sciences have made a mistake, by basing decisions on statistical significance” and that “in daily use it produces unchecked a loss of jobs, justice, profit, and even life”. The mistake made by the so called ‘sizeless scientist’ is to favour ‘Precision’ over ‘Oomph’. A ‘sizeless scientist’ is more interested in how precisely an outcome is estimated and less interested in the size of the implications for society or health services of any observed change in the outcome. They do not appear interested in the facts that “significant does not mean important and insignificant does not mean unimportant”. Even experts in statistics have been shown to interpret evidence poorly, based on whether the p-value crosses the threshold of 5% for statistical significance19.
Researchers today are calling for a shift towards research designed for decision making20. Yet this is not new, in 1967 Schwartz & Lellouch21 made a distinction between ‘explanatory’ and ‘pragmatic’ approaches. The former seeks ‘proof’ of the efficacy of a new treatment and the latter is about ‘choosing’ the best from two treatments. Patients, clinicians and payers of health care are interested in whether some novel treatment or health programme should be adopted over the alternatives.
There are many choices to be evaluated and many useful clinical trials to be undertaken, yet research budgets to support these are insufficient22. Funding a larger number of smaller trials to enable correct decisions about how to organise health services more frequently is a sensible goal. A hypothesis-testing approach maintains that a uniform level of certainty around these decisions is desirable, and needed by all stakeholders: managers, clinicians and patients. Yet the costs and benefits of every decision made are context-specific. Striving to eliminate uncertainty is likely to be inefficient use of research funding, where the benefit of achieving a given level of certainty is low or the prescribed precision unnecessary. We are not the only group that are advocating for this approach, and others have used cost-effectiveness as a criteria for dynamically deciding the necessary size of an ongoing trial23. There is a wider literature on decision making including economic data. Decision-making should address the costs and benefits throughout the life cycle of an intervention24, with consideration of whether decisions could be made based on current evidence and whether additional research needs to be undertaken25. Other considerations for decision making under conditions of uncertainty have been established and reviewed in detail26.
Our observations contradict advice by Nagendran et al.27 who suggest researchers aim to “conduct studies that are larger and properly powered to detect modest effects”. This approach promotes using p-values for decision making without a more encompassing evaluation of all outcomes that are relevant for decision-making.
We suggest the decision making approach to sample size calculation would often lead to smaller trials, but not always. If rare adverse events had a substantial impact on cost and health outcomes the trial may be larger than a hypothesis testing trial powered for a single outcome, which was not the adverse event. This may especially be the case for trials of new drugs. There are some good arguments against smaller trials. A large trial with lots of data might help future proof an adoption decision. If costs, frequencies of adverse events or baseline risks change over time then a large trial might render sufficient information to defend the adoption decision in the future as compared to a small trial. There might also not be another opportunity to run an RCT, for ethical or funding reasons, and so gathering a lot of data when the chance arises could be wise. Smaller trials, despite being well designed, might find a positive result that overestimates the real effect28. This may have happened with our example of TEXT ME and a more conservative estimate of the intervention effect would likely come from a meta-analysis or repeated trial. Indeed Prasad et al.29 found from 2,044 articles published over 10 years in a leading medical journal, 1,344 were about a medical practice, 363 of them tested an established medical practice and for 146 (40%) the finding was that practice was no better or worse than the comparator implying a reversal of practice. Those who deliver health services are unlikely to be rational and risk neutral. There is often scepticism and inertia when a change to practice is suggested and some clinicians will only change when evidence is overwhelming. Lau et al.30 did a cumulative meta-analysis of intravenous streptokinase for acute myocardial infarction with mortality as the primary outcome. They showed the probability the treatment reduced mortality was greater than 97.5% by 1973 after 2,432 patients had been enrolled in eight trials. By 1977, after 4,084 patients had been enrolled in thirteen trials the probability the treatment was effective was more than 99.5%. By 1988, 36 trials had been completed with 36,974 patients included confirming the previous conclusion.
Our case study demonstrates - for a single carefully conducted trial - that more information might have been collected than was necessary for a good decision to be made about a decision to adopt the intervention. We did not cherry pick this trial, but selected it because it was a recent economic analysis and had broad implications for health. The differences in necessary sample sizes and evidence will depend on context and design of trials. It might often be that smaller and so faster and cheaper trials are sufficient for good decision-making. This would release scarce research dollars that funding bodies could use for other valuable projects. Our approach is part of the drive toward increasing the value of health and medical research, which currently has a poor return with an estimated 85% of investment wasted31. Further, as adaptive trials gain traction, decision based designs provide flexibility, facilitating faster evolution of implementable findings.
Data availability
The datasets used and/or analysed for the TEXT ME trial are not publicly available due to data sharing not being approved by the local ethics committee. To access the data, the corresponding author of the primary trial should be contacted (cchow@georgeinstitute.org.au).
A random sample of the TEXT ME clinical trial data that has similar features to the TEXT ME data is provided in the code used to create the simulations and figures, which is available on GitHub: https://github.com/agbarnett/trials.smaller
Archived code as at time of publication: http://doi.org/10.5281/zenodo.132245932
Dataset 1: Data used for a simulation of Figure 2. DOI, 10.5256/f1000research.15522.d21237733
Download
Export To
metrics
| Views | Downloads | |
|---|---|---|
| F1000Research | - | - |
|
PubMed Central
Data from PMC are received and updated monthly.
|
- | - |
Citations
CITE
how to cite this article
Graves N, Barnett AG, Burn E and Cook D. Smaller clinical trials for decision making; a case study to show p-values are costly [version 2; peer review: 1 approved, 2 approved with reservations]. F1000Research 2018, 7:1176 (https://doi.org/10.12688/f1000research.15522.2)
NOTE: If applicable, it is important to ensure the information in square brackets after the title is included in all citations of this article.
track
receive updates on this article
Track an article to receive email alerts on any updates to this article.
Open Peer Review
Current Reviewer Status:
Key to Reviewer Statuses
VIEW
HIDE
ApprovedThe paper is scientifically sound in its current form and only minor, if any, improvements are suggested
Approved with reservations
A number of small changes, sometimes more significant revisions are required to address specific details and improve the papers academic merit.
Not approvedFundamental flaws in the paper seriously undermine the findings and conclusions
Version 2
VERSION 2
PUBLISHED 27 Sep 2018
Revised
Views
24
How to cite this report:
Mark DB. Reviewer Report For: Smaller clinical trials for decision making; a case study to show p-values are costly [version 2; peer review: 1 approved, 2 approved with reservations]. F1000Research 2018, 7:1176 (https://doi.org/10.5256/f1000research.17883.r151315)
The direct URL for this report is:
https://f1000research.com/articles/7-1176/v2#referee-response-151315
https://f1000research.com/articles/7-1176/v2#referee-response-151315
NOTE: it is important to ensure the information in square brackets after the title is included in this citation.
Reviewer Report 11 Oct 2022
Daniel Benjamin Mark,
Division of Cardiology, Department of Medicine, Duke University Medical Center, Durham, NC, USA
Approved with Reservations
VIEWS 24
This article addresses an important and provocative idea, namely that we are making our clinical trials larger and more expensive than is necessary for rational decision making. I suspect the authors are correct but would offer several general reasons why
... Continue reading
CITE
HOW TO CITE THIS REPORT
Mark DB. Reviewer Report For: Smaller clinical trials for decision making; a case study to show p-values are costly [version 2; peer review: 1 approved, 2 approved with reservations]. F1000Research 2018, 7:1176 (https://doi.org/10.5256/f1000research.17883.r151315)
The direct URL for this report is:
https://f1000research.com/articles/7-1176/v2#referee-response-151315
https://f1000research.com/articles/7-1176/v2#referee-response-151315
NOTE: it is important to ensure the information in square brackets after the title is included in all citations of this article.
Views
10
How to cite this report:
Julious S. Reviewer Report For: Smaller clinical trials for decision making; a case study to show p-values are costly [version 2; peer review: 1 approved, 2 approved with reservations]. F1000Research 2018, 7:1176 (https://doi.org/10.5256/f1000research.17883.r46419)
The direct URL for this report is:
https://f1000research.com/articles/7-1176/v2#referee-response-46419
https://f1000research.com/articles/7-1176/v2#referee-response-46419
NOTE: it is important to ensure the information in square brackets after the title is included in this citation.
Reviewer Report 09 Sep 2019
Steven Julious,
Medical Statistics Group, University of Sheffield, Sheffield, UK
Approved
VIEWS 10
While I agree with the sentiments of the authors that there can be instances where a conventional sample size calculation may not be appropriate. I do have an issue with the generalisations they are making from a single trial to
... Continue reading
CITE
HOW TO CITE THIS REPORT
Julious S. Reviewer Report For: Smaller clinical trials for decision making; a case study to show p-values are costly [version 2; peer review: 1 approved, 2 approved with reservations]. F1000Research 2018, 7:1176 (https://doi.org/10.5256/f1000research.17883.r46419)
The direct URL for this report is:
https://f1000research.com/articles/7-1176/v2#referee-response-46419
https://f1000research.com/articles/7-1176/v2#referee-response-46419
NOTE: it is important to ensure the information in square brackets after the title is included in all citations of this article.
Views
35
How to cite this report:
Senn S. Reviewer Report For: Smaller clinical trials for decision making; a case study to show p-values are costly [version 2; peer review: 1 approved, 2 approved with reservations]. F1000Research 2018, 7:1176 (https://doi.org/10.5256/f1000research.17883.r38819)
The direct URL for this report is:
https://f1000research.com/articles/7-1176/v2#referee-response-38819
https://f1000research.com/articles/7-1176/v2#referee-response-38819
NOTE: it is important to ensure the information in square brackets after the title is included in this citation.
Reviewer Report 09 Oct 2018
Approved with Reservations
VIEWS 35
First let me apologise for a stupid slip in my first review. I referred to sampling without replacement and the authors quite rightly corrected me and pointed out that they sampled with replacement. That is, in fact, what I meant
... Continue reading
CITE
HOW TO CITE THIS REPORT
Senn S. Reviewer Report For: Smaller clinical trials for decision making; a case study to show p-values are costly [version 2; peer review: 1 approved, 2 approved with reservations]. F1000Research 2018, 7:1176 (https://doi.org/10.5256/f1000research.17883.r38819)
The direct URL for this report is:
https://f1000research.com/articles/7-1176/v2#referee-response-38819
https://f1000research.com/articles/7-1176/v2#referee-response-38819
NOTE: it is important to ensure the information in square brackets after the title is included in all citations of this article.
-
Author Response 31 Oct 2019Nicholas Graves, Institute of Health and Biomedical Innovation, Queensland University of Technology, Brisbane, 4059, Australia31 Oct 2019Author ResponseWe thank the reviewer for the additional comments and try to respond to the key issue that arose in the first review.
The reviewer says “simulating only from the case where ... Continue reading
COMMENTS ON THIS REPORT
-
Author Response 31 Oct 2019Nicholas Graves, Institute of Health and Biomedical Innovation, Queensland University of Technology, Brisbane, 4059, Australia31 Oct 2019Author ResponseWe thank the reviewer for the additional comments and try to respond to the key issue that arose in the first review.
The reviewer says “simulating only from the case where ... Continue reading
Version 1
VERSION 1
PUBLISHED 02 Aug 2018
Views
26
How to cite this report:
Senn S. Reviewer Report For: Smaller clinical trials for decision making; a case study to show p-values are costly [version 2; peer review: 1 approved, 2 approved with reservations]. F1000Research 2018, 7:1176 (https://doi.org/10.5256/f1000research.16927.r37678)
The direct URL for this report is:
https://f1000research.com/articles/7-1176/v1#referee-response-37678
https://f1000research.com/articles/7-1176/v1#referee-response-37678
NOTE: it is important to ensure the information in square brackets after the title is included in this citation.
Reviewer Report 07 Sep 2018
Approved with Reservations
VIEWS 26
The authors propose that when a clinical trial is sought to inform practical decision-making, conventional standards of 'proof' may be too stringent and in consequence resources may be wasted. They illustrate this by simulating from a particular clinical trial, the
... Continue reading
CITE
HOW TO CITE THIS REPORT
Senn S. Reviewer Report For: Smaller clinical trials for decision making; a case study to show p-values are costly [version 2; peer review: 1 approved, 2 approved with reservations]. F1000Research 2018, 7:1176 (https://doi.org/10.5256/f1000research.16927.r37678)
The direct URL for this report is:
https://f1000research.com/articles/7-1176/v1#referee-response-37678
https://f1000research.com/articles/7-1176/v1#referee-response-37678
NOTE: it is important to ensure the information in square brackets after the title is included in all citations of this article.
-
Author Response 27 Sep 2018Nicholas Graves, Duke NUS Graduate Medical School, Singapore27 Sep 2018Author ResponseThe authors propose that when a clinical trial is sought to inform practical decision-making, conventional standards of 'proof' may be too stringent and in consequence resources may be wasted. They ... Continue reading
COMMENTS ON THIS REPORT
-
Author Response 27 Sep 2018Nicholas Graves, Duke NUS Graduate Medical School, Singapore27 Sep 2018Author ResponseThe authors propose that when a clinical trial is sought to inform practical decision-making, conventional standards of 'proof' may be too stringent and in consequence resources may be wasted. They ... Continue reading
Comments on this article Comments (0)