Keywords
heart rate variability, time, frequency, non-linear, entropy, horses, equine
heart rate variability, time, frequency, non-linear, entropy, horses, equine
Beat-to-beat alterations in heart rate, termed heart rate variability (HRV), is an intrinsic property that may be affected by distinct physiological states, such as exercise. Exercise-related sudden cardiac arrest remains a significant problem, affecting young athletes who are otherwise healthy with structurally normal hearts. Previously, our group has employed mouse models for studying cardiac electrophysiological properties1. However, these bear the disadvantages of having important differences compared to humans, such as a ten-fold higher heart rates and the lack of a plateau phase during repolarization.
Therefore, the use of alternative animal models offers an important and complementary approach. For example, horses show similar heart rate patterns compared to humans, with capacity of increasing from 40 bpm to 200 bpm during exercise. This suggests that horses could be useful for exploring the consequences of exercise-induced electrophysiological changes2. However, few studies in the literature have quantified HRV in horses. We quantified beat-to-beat variability in heart rate by applying time-domain, frequency-domain and non-linear techniques for the first time to electrocardiograms obtained from horses at rest and during exercise.
Heart rate data of horses were obtained from a publicly available dataset published online with the study protocol previously described3. Briefly, healthy Thoroughbred horses in race training presented for workups at an equine hospital were screened. This yielded a total of seven horses with electrocardiographic recordings for 10 to 18 minutes. HRV analysis was performed using Kubios HRV Standard software (Version 3.0.2). The following time-domain measures were obtained: 1) mean RR interval; 2) standard deviation (SD) of RR intervals; 3) coefficient of variation (CoV) for RR intervals, 4) root mean square (RMSSD) of successive differences of RR intervals; 5) NN50, number of successive RR interval pairs that differ more than 50 ms; 6) pNN50, relative number of successive RR interval pairs that differ more than 50 ms; 7) HRV triangular index, the integral of the RR interval histogram divided by the height of the histogram; 8) Triangular interpolation of normal-to-normal intervals (TINN). 9) mean HR; 10) SD of HR; 11) CoV for HR; 12) minimum HR; 13) maximum HR.
Frequency-domain analysis was performed using the Fast Fourier Transform method4 with sampling frequency set at 8 Hz. The power in the repolarization spectrum between 0.04 and 0.4 Hz was defined as total power (TP). The power in the heart rate spectrum was divided into three different frequency bands: very low frequency power (VLF, 0 to 0.04 Hz), low frequency power (LF, 0.04 to 0.15 Hz) and high frequency power (HF, 0.15 to 0.4 Hz).
Non-linear properties of HRV were studied as follow. Poincaré plots are graphical representations of the correlation between successive RR intervals, in which RRn+1 is plotted against RRn. From this plot, the SD of the points perpendicular to the line-of-identity (SD1) describing short-term variability, and the SD of the points along the line-of-identity (SD2) describing the long-term variability, can be determined. The SD2/SD1 ratio is a measure of long-term variability relative to the short-term variability. The approximate entropy provides a measure of the irregularity of the signal. It is computed as follows:
Firstly, a set of length m vectors uj is formed:
uj = (RRj ; RRj+1,…, RRj+m-1); j = 1; 2; …N – m + 1
where m is the embedding dimension and N is the number of measured RR intervals. The distance between these vectors is defined as the maximum absolute difference between the corresponding elements:
d(uj, uk) = max {|RRj+n – RRk+n| | n=0, …, m-1}
for each uj the relative number of vectors uk for which d(uj, uk) ≤ r is calculated. This index is denoted with Cmj (r) and can be written in the form
Taking the natural logarithms gives:
The approximate entropy is then defined as:
Lower approximate entropy values reflect a more regular signal, whereas higher values reflect a more irregular signal.
The sample entropy also provides a measure of signal irregularity but is less susceptible to bias compared to approximate entropy. This is given by:
Averaging then yields:
The sample entropy is then given by:
Finally, detrended fluctuation analysis (DFA) was performed to determine long-range correlations in non-stationary physiological time series5, yielding both short-term fluctuation (α1) and long-term fluctuation (α2) slopes. The point at which the slopes α1 and α2 is the crossover point.
Statistical analyses were conducted using Origin Pro 2017. All values were expressed as mean ± standard deviation (SD). Numerical data were compared by one-way analysis of variance (ANOVA). P<0.05 was considered statistically significant and was denoted by * in the figures.
Representative time series data for RR intervals at rest and during exercise from a single horse are shown in Figure 1A and Figure 1B, respectively, with their frequency distributions shown in Figure 1C and Figure 1D. Their corresponding heart rate time series are shown in Figure 2A and Figure 2B, and frequency distributions in Figure 2C and Figure 2D. Under resting conditions, the mean RR interval was 1392±224 ms, decreasing to 541±84 with exercise (n=7 horses) (Figure 3A). The mean standard deviation (SD) was 65±43 ms (Figure 3B) and coefficient of variation (CoV) was 5±2% (Figure 3C), which decreased to 8±4 ms and 1±1%, respectively, after exercise (ANOVA, P<0.05). Similarly, the root mean square of successive RR interval differences (RMSSD) decreased from 89±92 to 6±4 ms (Figure 3D). The number of interval differences of successive NN intervals greater than 50 ms (NN50) and the proportion derived by dividing NN50 by the total number of NN intervals (pNN50) were decreased from 85±55 to 0±1 ms and from 21±12 to 0±1%, respectively (ANOVA, P<0.05). The HRV triangular index, which is integral of the RR interval histogram divided by the height of the histogram, also decreased from 8.37±2.87 to 2.03±0.45 (ANOVA, P<0.05), as was the triangular interpolation of normal-to-normal intervals (TINN), the baseline width of the RR interval histogram (445± 240 to 40±26 ms; ANOVA, P<0.05). These corresponded to a mean heart rate of 44±8 bpm (Figure 4A), SD was 7±2 bpm (Figure 4B) and CoV (Figure 4C) of 16±4%. With exercise, HR increased to 113±17 bpm, whereas SD, CoV and RMSSD decreased to 4±2 bpm, 3±2% and 6±4 ms, respectively. Finally, the minimum and maximum heart rates (Figure 4D and 4E) at rest were 34±5 and 79±16 bpm, respectively, increasing to 101±16 and 129±15 bpm.
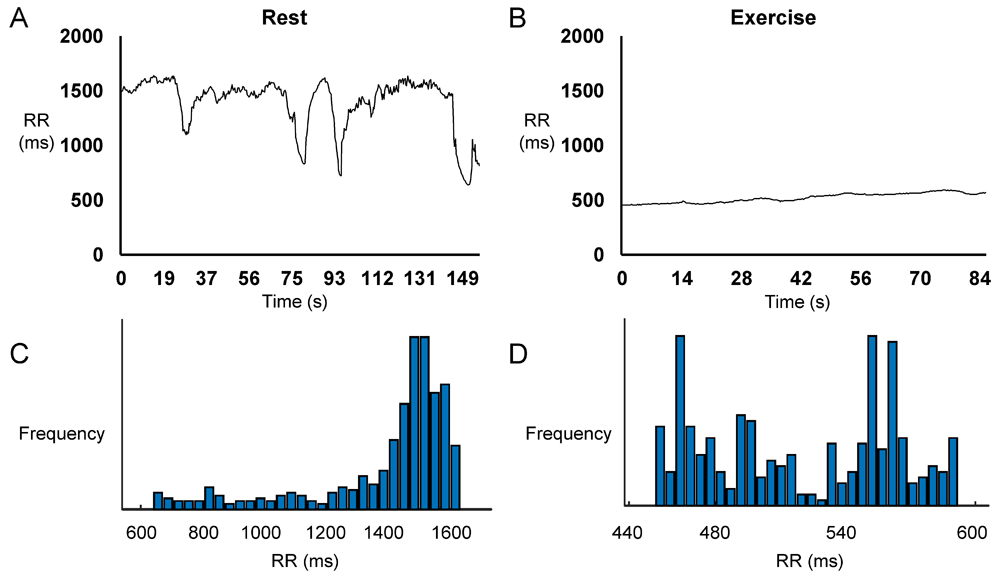
Representative time series data for RR intervals at rest (A) and during exercise (B) and the corresponding histograms (C and D) from a single horse.
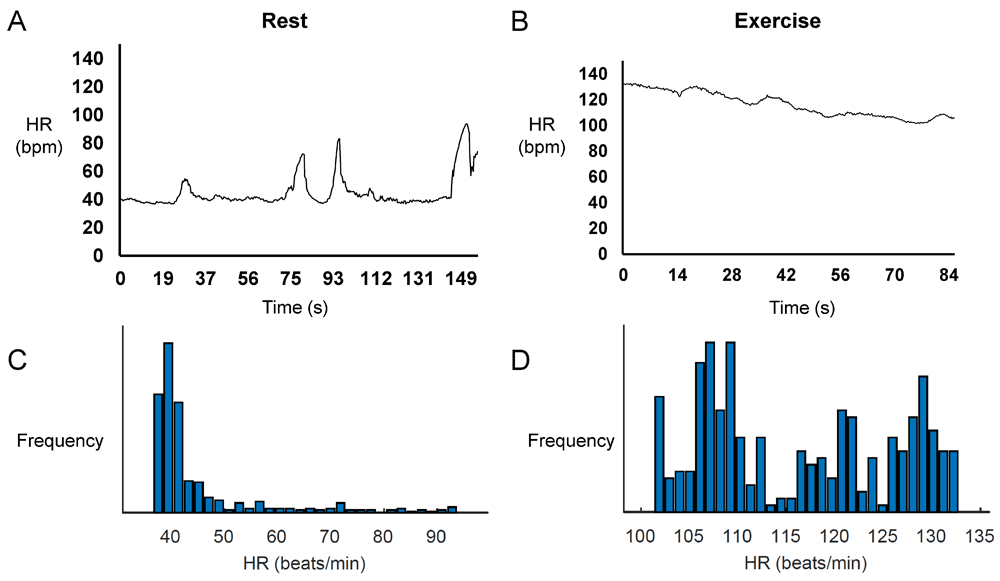
Representative time series data for heart rates at rest (A) and during exercise (B) and the corresponding histograms (C and D) from a single horse.
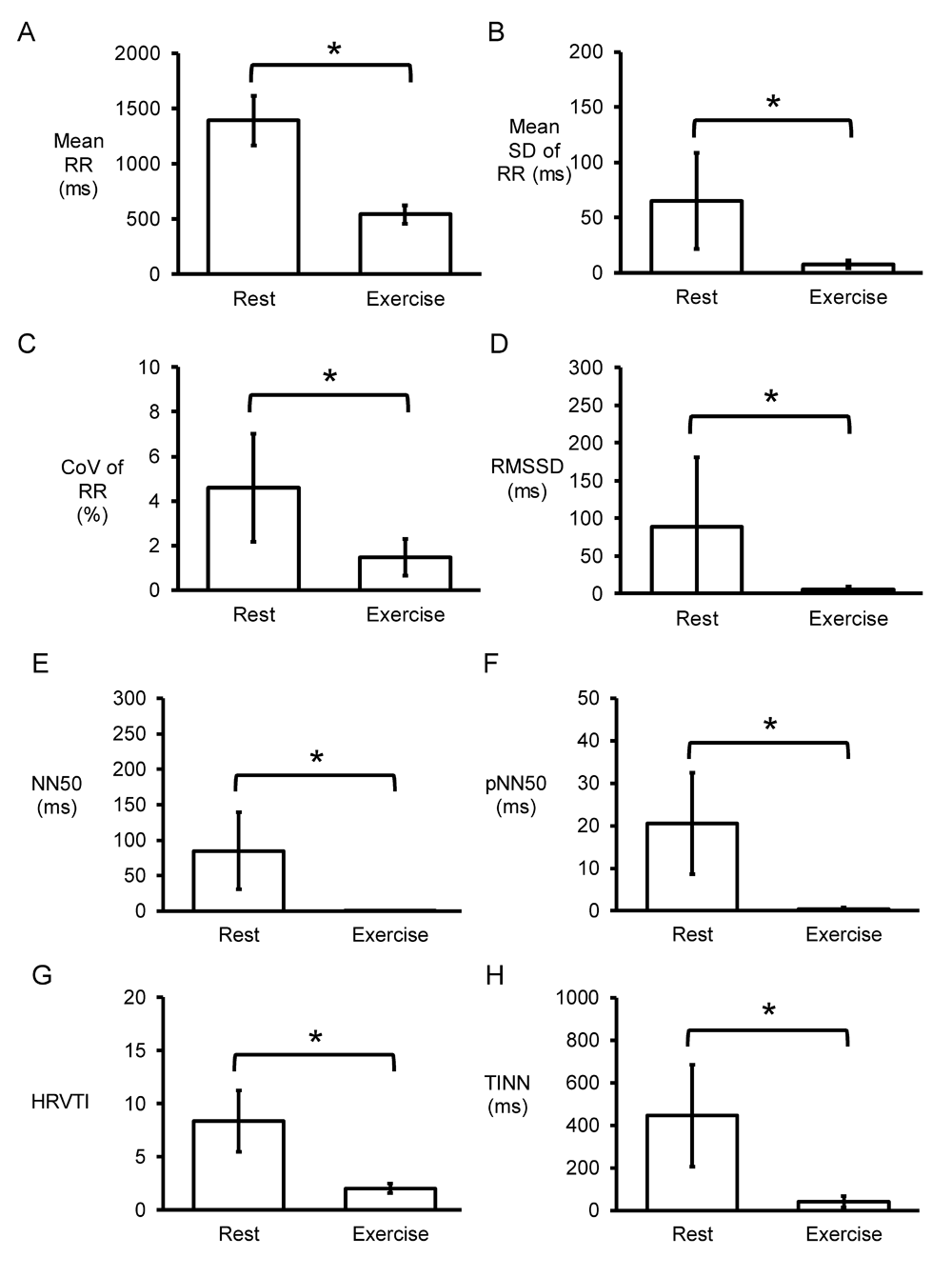
Time-domain analysis (n=7 horses) yielding mean RR intervals (A), standard deviation (SD) of RR intervals (B), coefficient of variation (CoV) given by SD/mean x 100% (C), root mean square of successive RR interval differences (RMSSD) (D), number of interval differences of successive NN intervals greater than 50 ms (NN50) (E), proportion derived by dividing NN50 by the total number of NN intervals (pNN50) (F), heart rate variability triangular index (HRVTI), the integral of the RR interval histogram divided by the height of the histogram (G) and triangular interpolation of normal-to-normal intervals (TINN), the baseline width of the RR interval histogram (H).
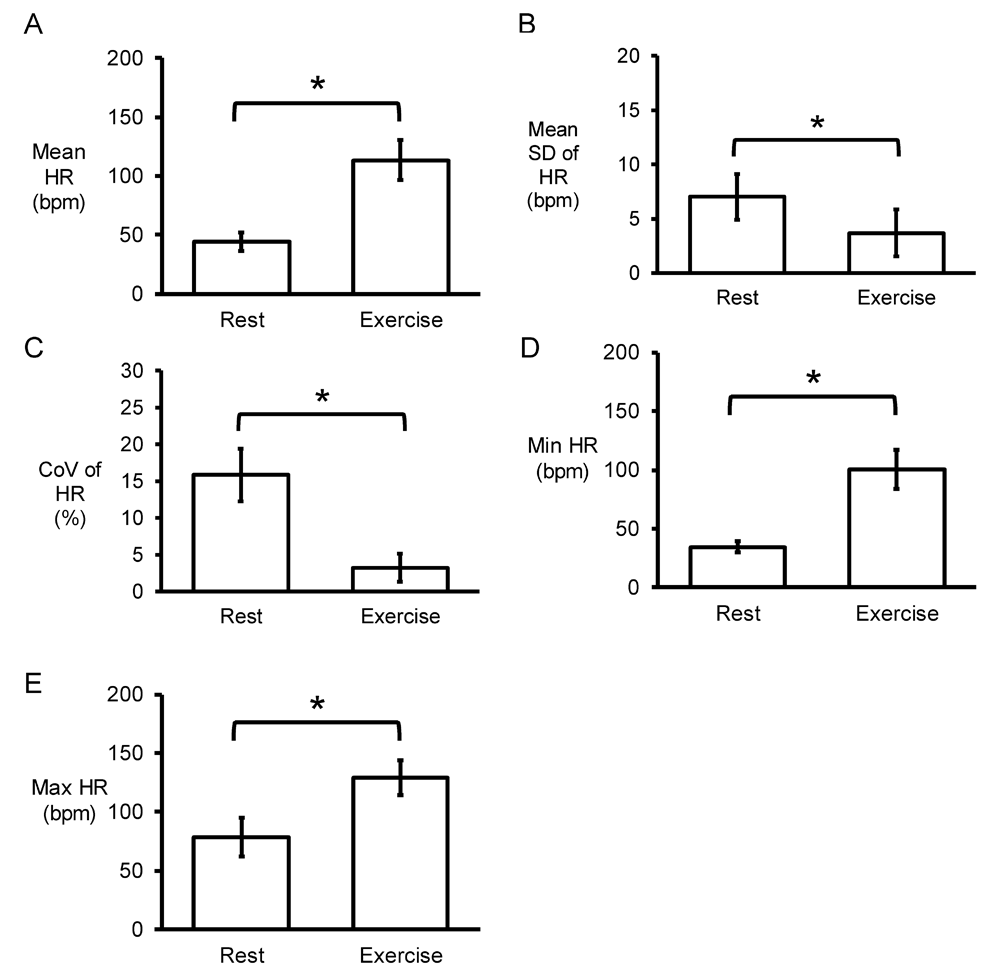
Time-domain analysis yielding mean heart rate (HR) (A), standard deviation (SD) of HR (B), coefficient of variation (CoV) given by standard deviation (SD)/mean x 100% (C), minimum HR (D) and maximum HR (E).
Next, the Fast Fourier Transform method was used for frequency-domain analyses. An example of the power spectrum plot against frequency before and after exercise is shown in Figure 5A and 5B, respectively. Strikingly, the peaks for very low-, low- and high-frequency were not altered by exercise (0.04 ± 0.00 vs. 0.04 ± 0.00 Hz; 0.10 ± 0.03 vs. 0.09±0.03 Hz; 0.19 ± 0.03 vs. 0.18±0.03 Hz, respectively) (Figures 5C to E). Similarly, their percentage powers remained unchanged (2±1 vs. 4±5%; 59±9 vs. 64±20%; 39±10 vs. 32±19%, respectively, P>0.05) (Figures 5F to 5H). By contrast, very low-frequency, low-frequency, and high-frequency powers were significantly reduced from 29±17 to 2±5 ms2, 1138±372 to 22±22 ms2 and 860±564 to 9±6 ms2, respectively (P<0.05) (Figures 6A to 6C), as was the total power (in logarithms) from 7.52±0.52 to 3.25±0.73 (P<0.05) (Figures 6D).
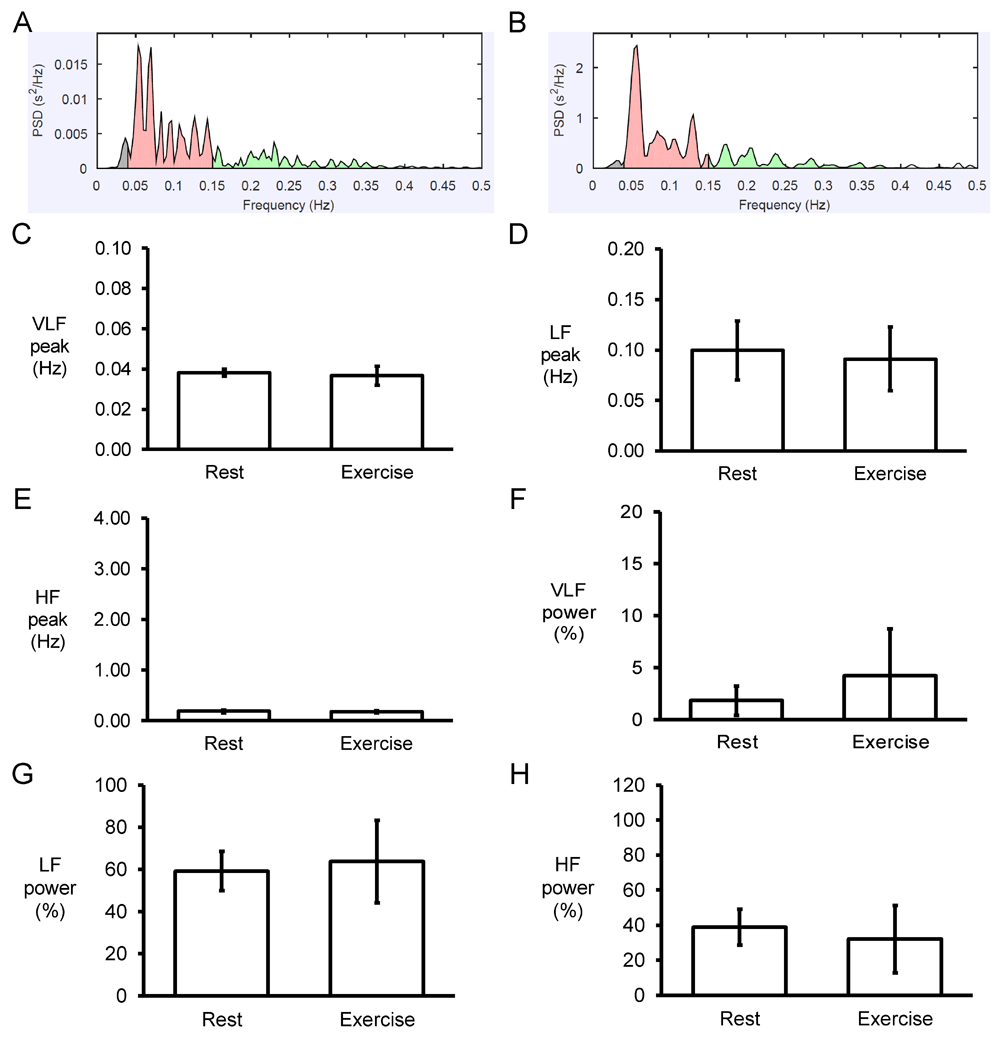
Examples of frequency spectra using the Fast Fourier Transform method for RR time series obtained before (A) and after (B) exercise. Peaks for very low-frequency (VLF) (C), low-frequency (LF) (D) and high-frequency (HF) (E) and their percentage powers (F to H).
Poincaré plots expressing RRn+1 as a function of RRn were constructed, with typical examples from a single horse before and after exercise shown in Figure 7A and 7B. In all of the hearts studied, circular shapes of the data points were observed. The SD perpendicular to the line-of-identity (SD1) and SD along the line-of-identity (SD2) are shown in Figure 7C and 7D, respectively. The mean SD1 and SD2 were 63±65 and 62±17, respectively, corresponding to a SD2/SD1 ratio of 1.33±0.45 (Figure 7E). After exercise, SD1 and SD2 decreased significantly to 5±3 and 9±5, respectively, which corresponded to increased SD2/SD1 ratio to 2.19±0.72 (P<0.05). Moreover, approximate and sample entropy took values of 0.97±0.23 (Figure 7F) and 1.14±0.43 (Figure 7G), respectively. These values were not altered after exercise (0.82±0.22 and 1.37±0.49, respectively; P>0.05). Detrended fluctuation analysis plotting the detrended fluctuations F(n) as a function of n in a log-log scale was performed for the RR intervals (Figure 8A and 8B). This revealed short- (α1) and long-term (α2) fluctuation slopes of 0.76±0.27 (Figure 8C) and 0.16±0.11 (Figure 8D) before exercise. After exercise, α1 was not significantly different (1.18±0.55; P>0.05) but α2 was significantly increased to 0.50±0.16 (P<0.05).
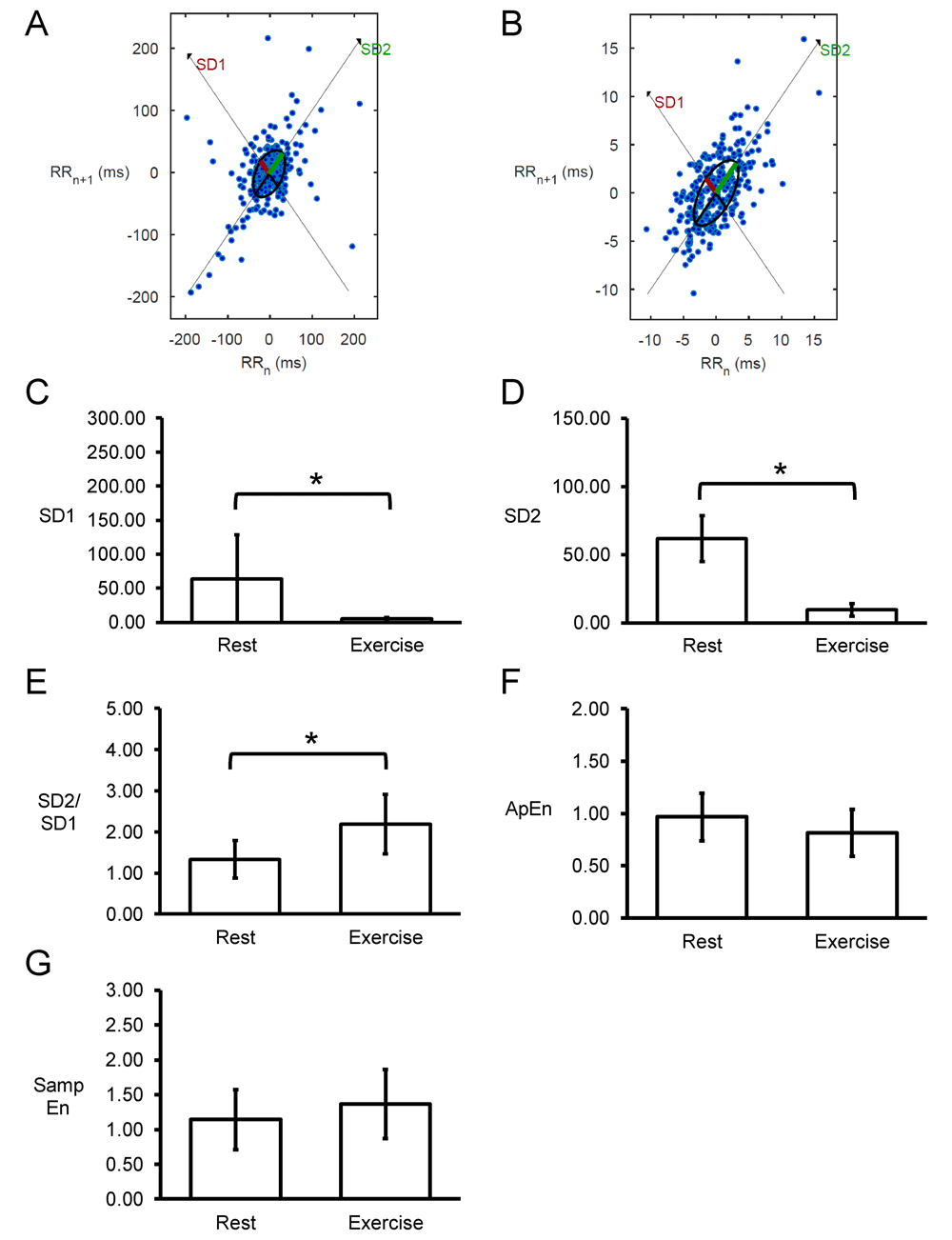
Representative Poincaré plots of RRn+1 against RRn before (A) or after exercise (B) from a single horse. Summary data (n=7) for standard deviation (SD) along the line-of-identity (SD1) (C) and SD perpendicular to the line-of-identity (SD2) (D), and the SD2/SD1 ratio (E), approximate entropy (ApEn) (F) and sample entropy (Samp En) (G).
In this study, we investigated HRV of equine athletes before and after exercise. The main findings are that 1) variability in heart rate can be detected using time-domain, frequency-domain and non-linear methods; 2) exercise led to reduced HRV as revealed using time-domain, frequency-domain and linear methods, 3) no change in signal entropy was observed after exercise.
The heart shows variability in their electrical signals both spatially and temporally6–8, and this signal variability can be detected at different levels of complexity, from whole organs down to single ion channels9–11. A certain degree of HRV is present in normal, healthy individuals12–16. However, it can become altered in pathological states and in turn associated with atrial fibrillation, ventricular arrhythmias and sudden cardiac arrest14. HRV has been investigated in the context of aging17, massage18 and pregnancy19. To date, there have only been a handful of studies that have evaluated HRV from equine athletes in the context of exercise20–34. Consistent with previous findings22,29,30, we found that exercise decreased HRV as determined by time-domain methods. Thus, SD of RR intervals, CoV, RMSSD, NN50, pNN50, HRV triangular index, and TINN were all significantly reduced.
From frequency-domain analysis, we did not detect significant changes in the low- and high-frequency peaks, or their percentage powers after exercise. These findings are in contrast to some of the previously reported findings. Thus, an increase in high-frequency peak29, higher low-frequency and lower high-frequency components30, and increased high-frequency to low-frequency ratios during gallop31 were observed. By contrast, we observed significantly reductions in the absolute values for very low frequency power, lower frequency power and high frequency power and total power but no change in low frequency/high frequency power ratio after exercise. These findings are consistent with previous demonstrations that power in all bands was reduced by exercise31.
Significantly, non-linear analyses of RR intervals yielded further insights. Thus, Poincaré plots showed ellipsoid shapes in all of the horses studied at rest with SD2/SD1 ratio close to 1, suggesting similar short-term and long-term variability. By contrast, exercise led to significant decreases in both SD1 and SD2, but an increase in SD2/SD1 ratio, indicated greater long-term variability under these stressed conditions. These findings are consistent with a recent report showing significant reductions in both SD1 and SD222. Furthermore, the present findings also quantified approximate and sample entropy for the first time in equine athletes, demonstrating a degree of entropy present. Entropy is the amount of disorder in a given system and reflects the signal regularity or complexity35,36. However, this was not altered by exercise.
Finally, detrended fluctuation analysis (DFA) was applied, to the best of our knowledge, for the first time in equine athletes. Previosu studies have used this method for investigating long-range correlations in non-stationary physiological time series5. In DFA, the mean fluctuation is plotted against the number of beats on a double logarithmic scale. This would then yield the scaling exponents, α1 and α2, respectively. For uncorrelated data, α takes a value of 0.5. By contrast, the presence of correlation will be reflected by α taking values below or above 0.5. In our study, α1 was 0.76±0.27 and α2 was 0.16±0.11 before exercise. With exercise α2 was increased to 0.50±0.16, suggesting that the long-term correlation was lost. Previous studies have applied DFA to HRV in other species. For example, in rabbits with hypertrophic cardiomyopathy, greater values of the scaling exponent were observed compared to those with the disease37. Moreover, in humans, a reduction in α1 was found during sympathetic activation, indicating a breakdown of the short-term fractal organization of heart rate38. Normal α1 and decreased α2 were observed in patients with atrial fibrillation (AF) compared to those without AF39. Our findings suggest that exercise does indeed alter scaling exponents for long-term correlations, which may be important in diseased states related to sudden cardiac arrest.
Compared to rodent hearts with a significantly higher resting heart rate, equine hearts serve as more representative model system for electrophysiological studies. However, it is known that horses frequently show spontaneous AF due to their high vagal tone and enlarged atria. This needs to be evaluated in future studies, as detailed in other studies40–43. Nevertheless, equine athletes undergo a similar sequence to humans from an athletic life course perspective, through from training to peak performance and retirement from competitive activity. This allows for more insightful investigation into electrophysiological changes in competitive human athletes but not in the general human population, where standard-breed equine models will be more appropriate. Further studies should be conducted on larger equine sample sizes against human counterparts at different life course intervals namely training, peak performance and retirement to better match the electrophysiological changes between the two cardiac models.
The present findings report that exercise leads to a decrease in HRV but did not affect signal entropy in horses. Time-domain, frequency-domain and non-linear analyses all provided unique insights into signal variability, regularity and complexity.
The dataset used in this analysis is available as part of Li et al. (2018)3
PLoS One: S1 Dataset. Excel file of dataset of electrocardiographic intervals in all horses.
https://doi.org/10.1371/journal.pone.0194008.s0013
License: CC BY 4.0 Attribution
GT is currently supported by a Clinical Assistant Professorship from the Croucher Foundation of Hong Kong.
The funders had no role in study design, data collection and analysis, decision to publish, or preparation of the manuscript.
| Views | Downloads | |
|---|---|---|
| F1000Research | - | - |
|
PubMed Central
Data from PMC are received and updated monthly.
|
- | - |
Is the work clearly and accurately presented and does it cite the current literature?
Yes
Is the study design appropriate and is the work technically sound?
Yes
Are sufficient details of methods and analysis provided to allow replication by others?
Partly
If applicable, is the statistical analysis and its interpretation appropriate?
Partly
Are all the source data underlying the results available to ensure full reproducibility?
Yes
Are the conclusions drawn adequately supported by the results?
Yes
Competing Interests: No competing interests were disclosed.
Reviewer Expertise: Computational Cardiology
Is the work clearly and accurately presented and does it cite the current literature?
Yes
Is the study design appropriate and is the work technically sound?
Partly
Are sufficient details of methods and analysis provided to allow replication by others?
Partly
If applicable, is the statistical analysis and its interpretation appropriate?
Partly
Are all the source data underlying the results available to ensure full reproducibility?
Yes
Are the conclusions drawn adequately supported by the results?
Yes
References
1. French AS, Holden AV: Alias-free sampling of neuronal spike trains.Kybernetik. 1971; 8 (5): 165-71 PubMed AbstractCompeting Interests: No competing interests were disclosed.
Reviewer Expertise: Computational biology, time series analysis, nonlinear dynamics
Alongside their report, reviewers assign a status to the article:
| Invited Reviewers | ||
|---|---|---|
| 1 | 2 | |
|
Version 1 04 Feb 19 |
read | read |
Provide sufficient details of any financial or non-financial competing interests to enable users to assess whether your comments might lead a reasonable person to question your impartiality. Consider the following examples, but note that this is not an exhaustive list:
Sign up for content alerts and receive a weekly or monthly email with all newly published articles
Already registered? Sign in
The email address should be the one you originally registered with F1000.
You registered with F1000 via Google, so we cannot reset your password.
To sign in, please click here.
If you still need help with your Google account password, please click here.
You registered with F1000 via Facebook, so we cannot reset your password.
To sign in, please click here.
If you still need help with your Facebook account password, please click here.
If your email address is registered with us, we will email you instructions to reset your password.
If you think you should have received this email but it has not arrived, please check your spam filters and/or contact for further assistance.
Comments on this article Comments (0)