Projection layers improve deep learning models of regulatory DNA function

Alex Hawkins-Hooker; Henry Kenlay; John E. Reid

doi:10.12688/f1000research.17125.1

Home Browse Projection layers improve deep learning models of regulatory DNA function

ALL Metrics

-

Views

-

Downloads

Get PDF

Get XML

Export

▬

✚

Method Article

Projection layers improve deep learning models of regulatory DNA function

[version 1; peer review: 1 approved, 1 approved with reservations]

Alex Hawkins-Hooker¹, Henry Kenlay¹, John E. Reid^1,2

PUBLISHED 05 Feb 2019

Author details Author details

¹ MRC Biostatistics Unit, University of Cambridge, Cambridge, CB2 0SR, UK
² Alan Turing Institute, London, NW1 2DB, UK

Alex Hawkins-Hooker
Roles: Conceptualization, Methodology, Project Administration, Software, Supervision, Validation, Visualization, Writing – Review & Editing

Henry Kenlay
Roles: Data Curation, Formal Analysis, Investigation, Methodology, Software, Writing – Review & Editing

John E. Reid
Roles: Conceptualization, Data Curation, Formal Analysis, Investigation, Methodology, Software, Validation, Visualization, Writing – Original Draft Preparation, Writing – Review & Editing

OPEN PEER REVIEW

REVIEWER STATUS

This article is included in the Artificial Intelligence and Machine Learning gateway.

Abstract

With the increasing application of deep learning methods to the modelling of regulatory DNA sequences has come an interest in exploring what types of architecture are best suited to the domain. Networks designed to predict many functional characteristics of noncoding DNA in a multitask framework have to recognise a large number of motifs and as a result benefit from large numbers of convolutional filters in the first layer. The use of large first layers in turn motivates an exploration of strategies for addressing the sparsity of output and possibility for overfitting that result. To this end we propose the use of a dimensionality-reducing linear projection layer after the initial motif-recognising convolutions. In experiments with a reduced version of the DeepSEA dataset we find that inserting this layer in combination with dropout into convolutional and convolutional-recurrent architectures can improve predictive performance across a range of first layer sizes. We further validate our approach by incorporating the projection layer into a new convolutional-recurrent architecture which achieves state of the art performance on the full DeepSEA dataset. Analysis of the learned projection weights shows that the inclusion of this layer simplifies the network’s internal representation of the occurrence of motifs, notably by projecting features representing forward and reverse-complement motifs to similar positions in the lower dimensional feature space output by the layer.

Keywords

sequence analysis, deep learning, gene regulation

Corresponding authors: Alex Hawkins-Hooker, John E. Reid

Competing interests: No competing interests were disclosed.

Grant information: This work was funded by the UK Medical Research Council (Grant Ref MC_U105260799).
The funders had no role in study design, data collection and analysis, decision to publish, or preparation of the manuscript.

Copyright: © 2019 Hawkins-Hooker A et al. This is an open access article distributed under the terms of the Creative Commons Attribution License, which permits unrestricted use, distribution, and reproduction in any medium, provided the original work is properly cited.

How to cite: Hawkins-Hooker A, Kenlay H and Reid JE. Projection layers improve deep learning models of regulatory DNA function [version 1; peer review: 1 approved, 1 approved with reservations]. F1000Research 2019, 8:151 (https://doi.org/10.12688/f1000research.17125.1) First published: 05 Feb 2019, 8:151 (https://doi.org/10.12688/f1000research.17125.1) Latest published: 05 Feb 2019, 8:151 (https://doi.org/10.12688/f1000research.17125.1)

Introduction

The abundance of data characterising the function of noncoding DNA at high resolution facilitates the use of complex data-driven methods to learn the sequence features known as ‘motifs’ that encode this function¹. A number of works have used neural networks to model human regulatory DNA, taking as input fixed-length regions of DNA sequence and predicting properties such as transcription factor binding, chromatin accessibility and histone marks using data collected by ENCODE and other consortia^2–7. Several of these networks are intended to simultaneously model a wide variety of the functional characteristics of the input region, by predicting hundreds or even thousands of such measurements across multiple cell types in a multi-task learning framework. With hundreds of known regulatory motifs recorded in databases such as JASPAR⁸, machine learning models capable of fully characterising a significant variety of the measurable functional properties of human noncoding DNA must be able to recognise a large number of distinct patterns in the input sequence. Indeed while existing approaches have varied in the details of their neural network architectures, they have tended to share the use of relatively large numbers of convolutions as motif scanners in the first layer, and differed mainly in the subsequent layers where standard convolutions, dilated convolutions and recurrent layers have all been used to model interactions between features^2–6. The best reported performance on the DeepSEA benchmark was achieved by a network having 1024 convolutional kernels in its first layer⁴; indeed even when experimenting with single-output networks designed to predict binding for a single transcription factor⁹, observed that the performance of convolutional networks continued increasing with the number of filters in the first layer up to over 100 filters¹.

The use of a sufficient number of first layer filters to capture the variety of motifs relevant to the task at hand thus appears to be an important consideration in the design of neural networks for processing noncoding DNA sequences. At the same time, it raises questions. For one thing, the use of a large number of parameters in the first layer raises the possibility of overfitting. Moreover, first layers designed to recognise large numbers of specific motifs are bound to produce outputs which are relatively sparse and high-dimensional, which may hamper learning in subsequent layers¹⁰. Finally, these layers are computationally expensive, particularly when applied to long sequences, both due to the cost of computing the activations by convolving the input at each point in the sequence, and the cost in the next layer of processing sequences of high-dimensional activation vectors.

Standard regularisation techniques such as dropout¹¹ may be expected to help alleviate the problem of overfitting, and have been applied to the first convolutional layer in previous works. But there is room for further work both in terms of characterising the extent of the problem and investigating alternative solutions. Projection layers, which can be used to reduce the dimensionality of a representation without reducing its resolution, are a popular component of deep networks in computer vision where they are often referred to as 1 × 1 convolutions^12,14,15. Reducing the dimensionality of a layer’s activations reduces the number of parameters required in the subsequent layer, as well as the cost of computing that layer’s activations. At the same time, depending on the nature of the features learned in the first layer, the denser representation resulting from the projection may well preserve much of the information contained therein. Even random projections are well known to preserve distances in dense representations^16,17.

The common practice of including amongst the training inputs both forward and reverse-complement versions of each target sequence in particular motivates the exploration of a more compressed representation. Models are forced by this form of data augmentation to recognise distinct instances (forward and reverse-complement) of functionally equivalent motifs. Methods capable of identifying these two instantiations therefore offer the same capacity at potentially lower representational cost. Recognition of this issue has motivated the development of layers specially adapted to ensure the identity of forward and reverse-complementary sequences¹⁸. The use of projections offers an alternative approach to this problem. Here we focus on the design choices related to the capacity of multi-task networks to recognise a sufficient variety of motifs in input sequences, by jointly exploring both the effect of the number of first layer filters and the use of projection and dropout as approaches designed to mitigate the disadvantages of a large first layer. We choose to address these questions using the DeepSEA dataset², since this has previously been used to benchmark different network architectures^4,6. Initially using a reduced version of the dataset with shortened input regions, we vary the number of first layer filters for standard convolutional and convolutional-recurrent architectures with and without a projection layer and dropout, with our results indicating the importance of regularisation and the performance benefits of projection. We incorporate the projection layer into a convolutional recurrent neural network architecture with a number of modifications from the DanQ architecture proposed by 4. This new architecture achieves state of the art performance on the full DeepSEA dataset.

Methods

Baseline architectures

We experiment with modifications to two classes of architecture which have been successfully applied for multitask prediction in regulatory genomics. Details of the hyperparameters we used when training versions of these models are provided in the sections describing the relevant experiments.

1. Convolutional neural network (CNN): Both DeepSEA² and Basset³ use 3 layer CNNs, consisting of a stack of 3 convolution and max-pooling operations followed by one or more fully connected layers. DeepSEA’s convolutional layers are regularized using dropout and a global L2 penalty, whereas Basset applies batch normalization after each convolutional layer.
2. DanQ: The DanQ convolutional-recurrent architecture consists of a single convolutional layer followed by a pooling layer and a bidirectional long short-term memory (LSTM)¹⁹. The full sequence of LSTM outputs are passed through two fully connected layers in order to generate predictions⁴. reported results for two versions of this architecture, DanQ and DanQ-JASPAR, differing in the sizes of the layers and in the initialization used for the first layer, with half of the better-performing DanQ-JASPAR’s 1024 first-layer filters being initialized using known motifs from the JASPAR database. Like DeepSEA, both DanQ architectures use dropout after their single convolutional layer.

Linear projection layer

We investigate the use of a linear projection applied to the pooled activations of the first layer of architectures of both types. In detail, suppose that the first layer has m 1D convolutional filters and that after pooling the length of the sequence representation is l. Then the pooled activations form a sequence (a₁, a₂ … a_l) of m-dimensional vectors. The output of the projection layer is a sequence (v₁, v₂ … v_l ) of k-dimensional vectors (k < m):

v_{i} = P a_{i} (1)

where P is a weight matrix of size k × m. The projection layer’s output is a sequence of the same length as the sequence of the first layer’s pooled filter activations, but whose members are vectors of a lower dimension, with the same projection matrix P being used to reduce the dimension at each point in the sequence. All the results reported below were obtained using a value of k = 64, which seemed to represent a good trade-off between dimensionality reduction and preservation of information.

Improved convolutional-recurrent architecture

The best previously reported performance on the DeepSEA dataset was achieved by the DanQ-JASPAR architecture which uses a single large convolutional layer followed by a max-pooling layer with stride and pool size of 15. This layer summarises the presence of the motifs identified by the convolutional layer across relatively large 15bp stretches of input. Pooling so aggressively has the advantage of controlling the length of sequence to be fed into the LSTM, preventing computation in the recurrent layer from becoming prohibitively time consuming.

We hypothesise that this pooling involves throwing out useful positional information, which could be better preserved by splitting the downsampling across two sets of convolution and pooling layers rather than a single one. Therefore we propose an alternative convolutional recurrent (CRNN) architecture, which adds a projection layer, a second convolutional layer and a second pooling operation between the pooled outputs of the first convolutional layer and the bidirectional LSTM. To ensure fair comparison, the overall level of downsampling in the convolution and pooling layers is the same as in the DanQ-JASPAR networks, such that the length of the sequence of inputs to the bidirectional LSTM is the same (64) in both cases. In common with the DanQ networks we use a single fully-connected hidden layer before the output layer, but in order to control overfitting we use as input to this layer not the full sequence of LSTM outputs but their global mean. The proposed network, full details of which are given below, has far fewer parameters than DanQ-JASPAR and trains faster.

Experiments

The DeepSEA dataset. The DeepSEA dataset consists of sequences of 1000 bp from the human noncoding genome, labelled for the presence of a peak in the central 200 bp in the signal for each of 919 chromatin features taken from ENCODE and Roadmap^20,21. These features represent a range of transcription factor binding, chromatin accessibility and histone modification measurements across a variety of cell types. Both forward and reverse-complement versions of the sequence corresponding to each set of targets are included in the dataset, meaning that models must be capable of learning both forward and reverse-complement motifs. We use the original training, validation and test splits and follow⁴ in using as our primary evaluation metric test set area under the precision recall curve (AUPRC), which is calculated after averaging predictions across forward and reverse complement versions of each sequence.

Design choices related to first layer on reduced DeepSEA dataset. In our first set of experiments we seek to rigorously explore the optimal configuration of the early layers of instantiations of both CNN and DanQ network designs. We vary the number of first layer filters, the use of dropout immediately after the first pooling layer, and the use of a projection layer (we fix the output dimension of this layer at each point in the sequence to 64) while keeping other hyperparameters fixed for a version of each class of architecture. When dropout and projection are used together, the dropout is applied after the projection layer. A dropout rate of 0.2 is used in all cases, which is the same as that applied to the activations of the first convolutional layer in both the DeepSEA and DanQ architectures. Other modifications to the original architectures were made in the interests of retaining comparable performance while reducing computational cost and are described below.

The CNN model that we choose to explore here takes from Basset the use of 3 convolutional layers, with kernel sizes of 19, 11 and 7 respectively, but varying in several other details. We use max pooling operations of sizes 6, 2, and 2 after the convolutional layers. The number of filters in the second and third convolutional layers is held fixed at 128 and 256 respectively. The outputs of the final pooling operation are fed into a single hidden layer of 2048 neurons to which dropout with dropout factor of 0.5 is applied. Leaky ReLUs²² are used for all activations. Our DanQ architectures follow the original in most details other than those under investigation, except for the use of Leaky ReLU rather than ReLU activations, and the use of a reduced number of LSTM cells (100) in each direction. To mitigate the cost of these experiments, we run them on a reduced version of the DeepSEA dataset, using only the central 500 bp of each 1000 bp sequence. For all networks we use the Adam optimizer²³ with an initial learning rate of 3 × 10⁻⁴ to minimize the multitask binary cross entropy loss via mini-batch gradient descent with a batch size of 256. The learning rate was reduced by a factor of 5 if the validation loss did not decrease for two epochs. Training was terminated if the validation loss did not improve for five epochs. All models were implemented in Keras²⁴ using the Theano backend²⁵.

Evaluation of CRNN architecture on full DeepSEA dataset. For the second set of experiments we use the full 1000 bp for each sequence and seek to compare the performance of our improved CRNN architecture to that of DeepSEA and the two DanQ architectures. For comparison with the two variants of DanQ, DanQ and DanQ-JASPAR, which have, respectively, 320 and 1024 filters in the first layer, we explore two variants of our CRNN architecture with 320 and 700 filters of length 30 in the first layer. To evaluate the contribution of the projection layer, for each CRNN variant we train one network with projection after the first pooling operation, and one network without projection but otherwise identical to the first. All networks use a second convolutional layer with 128 filters of length 11 whose activations are pooled and fed into a bidirectional LSTM with 300 units in each direction. Max-pooling with stride and pool size of 7 after the first convolutional layer and 2 after the second convolutional layer together with unpadded convolutions ensure that the sequence of inputs to the LSTM is of the same length as in the DanQ-JASPAR model. Dropout with a rate of 0.15 is applied to the projected first layer activations if projection is used, and to the pooled first layer activations if not. Recurrent dropout²⁶ with a rate of 0.2 is applied to the LSTM. Leaky ReLUs are used for all layer activations. Networks are trained using the same learning rate schedules as in the previous set of experiments. We compare the average test set AUPRCs of our models with those of the publicly available trained DeepSEA and DanQ networks.

The source code for all models and experiments is available on GitHub and Zenodo²⁷.

Results

Effects of first layer design choices on reduced-size dataset

In both fully convolutional and convolutional-recurrent architectures consistent benefits were achieved by increasing the number of first layer filters, with gradual saturation of performance (as measured by test set AUPRC averaged across the tasks) at around 1000 filters in both cases (Figure 1). In the fully convolutional networks the benefit of the projection layer was very clear, with all networks which used projection outperforming those that didn’t, often by considerable margins. A combination of dropout and projection achieved the best performance in every case. There is less evidence of benefit in the case of the networks using DanQ-style architectures, with networks with regularisation sometimes outperforming those without, but a lack of a clear pattern in the results, at least under the test set AUPRC metric. This is despite models incorporating dropout and the projection layer consistently achieving lower cross-entropy loss on the validation set. One factor in the difference between the two types of architectures is the degree of overfitting that the standard, unregularised architecture suffers. We observed that fully convolutional architectures showed a much greater tendency to overfit than convolutional-recurrent architectures (Figure 2). We note that unlike a convolutional layer, an LSTM already learns its own projection in the form of the weight matrix which transforms the inputs into the internal state space within the input and forget gates. These internal projections may help reduce both the tendency to overfit and the potential performance improvement associated with incorporating an additional projection layer. In contrast, inserting a projection layer into a CNN architecture substantially reduces the degree of overfitting (Figure 2), which allows CNN networks including projection layers continue to benefit from adding additional filters in the first layer, whereas without projection, CNN performance hardly improves beyond 500 first layer filters, as the benefit of extra feature detectors is offset by the increased likelihood of overfitting.

Figure 1. Test set AUPRC as function of first layer size for CNNs (left) and DanQ networks (right) with and without projection layer (projecting down to 64 dimensions) and dropout (dropout rate of 0.2).

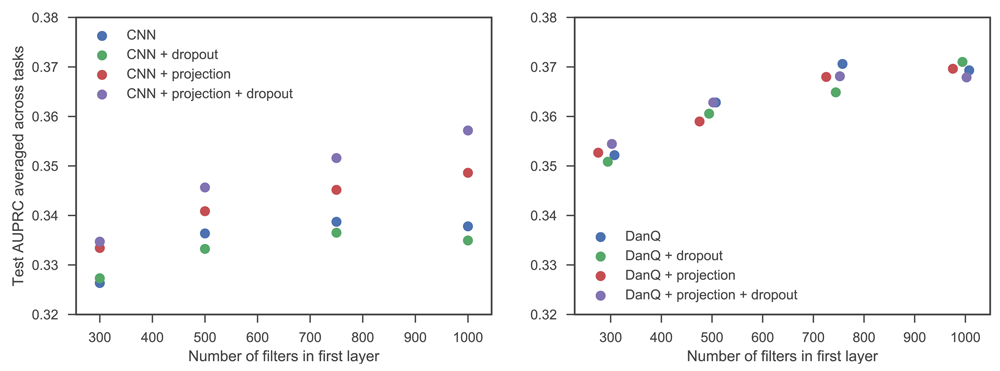
Jitter was added to the number of first layer filters for DanQ architectures to enable the points to be distinguished.

Figure 2. Validation set loss curves for CNN (left) and DanQ (right) models with 500 first layer filters, either with or without the two regularisation strategies.

The CNN network shows much more evidence of overfitting.

Projection layer helps improved CRNN architecture outperform other models on full DeepSEA data

Table 1 shows the cross entropy losses on the validation and test sets for our best-performing convolutional recurrent (CRNN) models as well as published baselines. CRNN-700 achieves the best average test set AUPRC of the compared models while being significantly less costly to train than DanQ-JASPAR, and without requiring the use of any known motifs to initialize first layer filters, as DanQ-JASPAR does. For both CRNN models we also compare the performance of models with and without the projection layer. In both cases, the projection layer leads to a clear increase in performance and a reduction in the cost per epoch of training the network.

Table 1. Performance of CRNN models with and without projection layer compared to DeepSEA and DanQ networks.

CRNN-n is a model with 2 convolutional layers with n and 128 filters respectively, with kernel sizes of 30 and 11, followed by a bidirectional LSTM with 300 units in each direction, whose outputs are averaged and fed through a hidden layer with 919 units which in turn feeds into the output layer. CRNN-n-projection is identical to CRNN-n except for the inclusion of a projection layer between the first and second convolution layers, which effectively reduces the dimension of the first layer’s activations from n to 64. Losses and AUPRCs for DanQ and DeepSEA networks are calculated using the publicly available model weights files. AUPRCs for all models are calculated after averaging predictions for forward and reverse complement versions of each test sequence, whereas forward and reverse complement versions of each sequence contribute independently to the reported losses.

Model	Parameters	Valid Loss	Test Loss	Test AUPRC
DeepSEA	155,159,839	0.0509	0.0554	0.343
DanQ	46,926,479	0.0491	0.0538	0.371
DanQ-JASPAR	67,892,175	0.0482	0.0533	0.379
CRNN-320-projection	2,477,479	0.0485	0.0532	0.383
CRNN-320	2,727,335	0.0489	0.0540	0.375
CRNN-700-projection	2,547,779	0.0475	0.0526	0.391
CRNN-700	3,174,595	0.0484	0.0533	0.385

Projection layer simplifies learning by unifying representations for forward and reverse-complement motifs

To understand the nature of the performance benefits brought by the use of the projection layer, we can investigate the relationship between the projection weights learned and the motifs learned by the first convolutional layer. To associate a motif with each filter in the first layer we follow a procedure similar to that introduced by 1: several thousand sequences from the training set are passed through the trained model, and for each first layer convolutional filter we record the identities of the nucleotides at each position in the maximally-activating stretch of input in each sequence in which that filter is activated. From this we construct a PFM which can be converted into a motif representing the typical input pattern recognised by the filter. Using TOMTOM²⁸ to search the JASPAR 2018 database⁸ we find that 257 of the 700 learned motifs of the best-performing CRNN-700-projection model have at least one significant match (q < 0.01). Each learned motif is also associated with one of the columns in the 64 × 700 weight matrix of the projection layer. Suppose for example that at a certain point in an input sequence, the motif recognised by the i^th convolutional filter occurs. Assuming none of the other filters are activated by this motif or its neighbouring region, the network’s representation of this region of the input will then just be the vector obtained by multiplying each weight in the i^th column of the projection matrix by the filter’s activation. Thus the i^th column of the projection matrix can be interpreted as representing an embedding of the motif learned by the i^th convolutional filter. To visualise these embeddings, we choose to focus on a subset of the learned motifs which have the best matches to known motifs, selecting only the 44 learned motifs with q-values less than 10⁻⁸. The result of performing a PCA on the 44 columns of the projection weight matrix associated with these motifs is shown in Figure 3. Most strikingly, different versions of the same motif tend to cluster together, with the embeddings for filters which learn to recognise the forward version of a particular motif very often close to those for filters which recognise the reverse complement of the same motif. This suggests that the projection layer allows for a more efficient internal representation of motifs, recognising that forward and reverse complement patterns are functionally equivalent although completely different and therefore requiring different feature extractors at the sequence level. This representation of functional equivalence allows networks with a projection layer to harness the benefits of reverse-complement data augmentation without paying a price in terms of representational complexity.

Figure 3. PCA of projection weights corresponding to learned motifs with best matches to known motifs in JASPAR database.

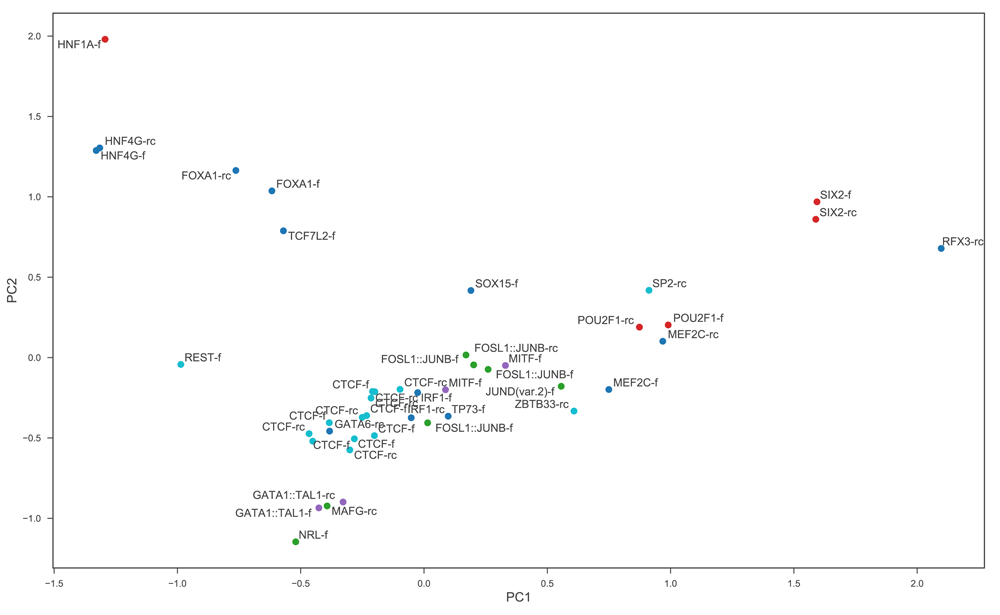
Each point represents one of the 64 dimensional column vectors of the projection weight matrix. Only columns corresponding to learned motifs with a match with q -value less than 10⁻⁸ are included in the PCA to aid visualisation. Points are labelled by name of matched motif and whether it is the forward (f) or the reverse complement (rc) version of the known motif that is matched. Points are coloured by transcription factor family (cyan: C2H2 zinc finger, green: basic leucine zipper, red: homeodomain, purple: basic helix-loop-helix, blue: all other).

Discussion

Despite the recent progress in the application of deep learning methods to model genomic data there remains work to be done in understanding the types of architecture and design choices best suited to the domain. We provide further evidence here that the performance of networks whose goal is to predict hundreds of functional properties from the DNA sequence is strongly dependent on the number of convolutional filters in the first layer. In networks where the subsequent layer is also convolutional, performance can be further improved by inserting a dimensionality-reducing projection layer between the two sets of convolutions. A similar use of projection layers in networks designed to predict enhancers was independently proposed by²⁹ while we were finalising this manuscript. Their network takes as input both DNA sequences and chromatin accessibility information, and intersperses projections and convolutions on each of the two data modalities. While their work shows that projections can be used in highly performing architectures for regulatory genomics problems, they did not explore the role of projections in achieving this performance. Here our aim is to draw particular attention to the performance benefits and mode of functioning of a single projection layer, inserted directly after a first DNA motif-recognising convolutional layer, since we believe these point to its potential utility beyond any single application. In particular, we show that the projection layer is capable of learning the identity between forward and reverse-complement versions of functionally equivalent motifs and thereby simplifying the representation of the functional content of the sequence. It also reduces the number of parameters required in the subsequent layer, leading to less overfitting (particularly in combination with dropout) and reducing the computational cost. Incorporating the projection layer into a convolutional-recurrent network architecture similar to the DanQ architecture leads to improved performance on the DeepSEA dataset with fewer parameters and shorter per-epoch training times. Although we have only tested the use of the projection layer on the DeepSEA dataset, we believe that its use could be of important benefit in other situations in which accurate prediction of the targets requires recognition of a large variety of motifs in the input sequence.

Data availability

DeepSEA dataset: the full dataset, including train, test and validations splits, may be downloaded from http://deepsea.princeton.edu/help/.

Software availability

Source code for models and experiments available at: https://github.com/alex-hh/motif_projection.

Archived source code at time of publication: https://doi.org/10.5281/zenodo.2543796²⁹.

License: MIT license.

Author contributions

AHH proposed the use of the projection layer, implemented and trained the models, ran the evaluations and wrote the paper. HK prototyped, implemented and trained early versions of the models and designed the evaluations. JR initiated the project, helped with the interpretation of the results and helped write the paper.

Grant information

This work was funded by the UK Medical Research Council (Grant Ref MC_U105260799).

The funders had no role in study design, data collection and analysis, decision to publish, or preparation of the manuscript.

Footnotes

1 For comparison, top performing networks on ImageNet^12,13 make do with only 64 filters in the first layer despite the output dimension being comparable to that of DeepSEA. This discrepancy may perhaps be explained by the fact that while the features learned by the first layers of image processing networks are small, generic and only gradually composed into more specific features by subsequent layers, the features learned by the first layers of networks in regulatory genomics are by design highly specific motifs, typically 10–20bp in length.

Faculty Opinions recommended

References

1. Alipanahi B, Delong A, Weirauch MT, et al.: Predicting the sequence specificities of DNA- and RNA-binding proteins by deep learning. Nat Biotechnol. 2015; 33(8): 831–8. PubMed Abstract | Publisher Full Text
2. Zhou J, Troyanskaya OG: Predicting effects of noncoding variants with deep learning-based sequence model. Nat Methods. 2015; 12(10): 931–4. PubMed Abstract | Publisher Full Text | Free Full Text
3. Kelley DR, Snoek J, Rinn JL: Basset: Learning the regulatory code of the accessible genome with deep convolutional neural networks. Genome Res. 2016; 26(7): 990–9. PubMed Abstract | Publisher Full Text | Free Full Text
4. Quang D, Xie X: DanQ: a hybrid convolutional and recurrent deep neural network for quantifying the function of DNA sequences. Nucleic Acids Res. 2016; 44(11): e107. PubMed Abstract | Publisher Full Text | Free Full Text
5. Kelley DR, Reshef YA: Sequential regulatory activity prediction across chromosomes with convolutional neural networks. Genome Res. 2018; 28(5): 739–750. PubMed Abstract | Publisher Full Text | Free Full Text
6. Gupta A, Rush AM: Dilated convolutions for modeling long-distance genomic dependencies. ArXiv e-prints. 2017. Reference Source
7. Zhou J, Theesfeld CL, Yao K, et al.: Deep learning sequence-based ab initio prediction of variant effects on expression and disease risk. Nat Genet. 2018; 50(8): 1171–1179. PubMed Abstract | Publisher Full Text | Free Full Text
8. Khan A, Fornes O, Stigliani A, et al.: JASPAR 2018: update of the open-access database of transcription factor binding profiles and its web framework. Nucleic Acids Res. 2018; 46(D1): D1284. PubMed Abstract | Publisher Full Text | Free Full Text
9. Zeng H, Edwards MD, Liu G, et al.: Convolutional neural network architectures for predicting DNA-protein binding. Bioinformatics. 2016; 32(12): i121–i127. PubMed Abstract | Publisher Full Text | Free Full Text
10. Bengio Y, Ducharme R, Vincent P, et al.: A neural probabilistic language model. J Mach Learn Res. 2003; 3: 1137–1155. Reference Source
11. Srivastava N, Hinton G, Krizhevsky A, et al.: Dropout: A simple way to prevent neural networks from overfitting. J Mach Learn Res. 2014; 15(1): 1929–1958. Reference Source
12. He K, Zhang X, Ren S, et al.: Deep residual learning for image recognition. In 2016 IEEE Conference on Computer Vision and Pattern Recognition, CVPR 2016, Las Vegas, NV USA, June 27-30, 2016. 2016; 770–778. Publisher Full Text
13. Simonyan K, Zisserman A: Very deep convolutional networks for large-scale image recognition. CoRR. 2014. Reference Source
14. Szegedy C, Liu W, Jia Y, et al.: Going deeper with convolutions. CoRR. abs/1409.4842, 2014. Reference Source
15. Lin M, Chen Q, Yan S: Network in network. CoRR. 2013. Reference Source
16. Johnson W, Lindenstrauss J: Extensions of Lipschitz mappings into a Hilbert space. In Conference in modern analysis and probability (New Haven, Conn., 1982), volume 26 of Contemporary Mathematics. American Mathematical Society, 1984; 189–206. Publisher Full Text
17. Bingham E, Mannila H: Random projection in dimensionality reduction: Applications to image and text data. In Proceedings of the Seventh ACM SIGKDD International Conference on Knowledge Discovery and Data Mining, KDD ’01, New York, NY, USA, 2001; 245–250. Publisher Full Text
18. Shrikumar A, Greenside P, Kundaje A: Reverse-complement parameter sharing improves deep learning models for genomics. bioRxiv. 2017. Reference Source
19. Graves A, Schmidhuber J: Framewise phoneme classification with bidirectional LSTM and other neural network architectures. Neural Netw. 2005; 18(5–6): 602–610. Publisher Full Text
20. The ENCODE Project Consortium: An integrated encyclopedia of DNA elements in the human genome.Nature. 2012; 489(7414): 57–74. PubMed Abstract | Publisher Full Text | Free Full Text
21. Roadmap Epigenomics Consortium, Kundaje A, Meuleman W, et al.: Integrative analysis of 111 reference human epigenomes. Nature. 2015; 518(7539): 317–330. PubMed Abstract | Publisher Full Text | Free Full Text
22. Maas AL, Hannun AY, Ng AY: Rectifier nonlinearities improve neural network acoustic models. In: in ICML Workshop on Deep Learning for Audio, Speech and Language Processing. 2013. Reference Source
23. Kingma DP, Ba J: Adam: A method for stochastic optimization. CoRR. 2014; abs/1412.6980. Reference Source
24. Chollet F, et al.: Keras. 2015. Reference Source
25. Theano Development Team: Theano: A Python framework for fast computation of mathematical expressions. arXiv e-prints. 2016; abs/1605.02688. Reference Source
26. Gal Y, Ghahramani Z: A theoretically grounded application of dropout in recurrent neural networks. In: Lee DD, Sugiyama M, Luxburg UV, et al. editors, Advances in Neural Information Processing Systems 29. Curran Associates, Inc., 2016; 1019–1027. Reference Source
27. Alex: alex-hh/motif projection preprint. (Versionpreprint). Zenodo. 2019. http://www.doi.org/10.5281/zenodo.2543797
28. Gupta S, Stamatoyannopoulos JA, Bailey TL, et al.: Quantifying similarity between motifs. Genome Biol. 2006; 8(2): R24. PubMed Abstract | Publisher Full Text | Free Full Text
29. Chen S, Gan M, Lv H, et al.: DeepCAPE: a deep convolutional neural network for the accurate prediction of enhancers. bioRxiv. 2018. Publisher Full Text

Comments on this article Comments (0)

Version 1

VERSION 1 PUBLISHED 05 Feb 2019

Author details Author details

¹ MRC Biostatistics Unit, University of Cambridge, Cambridge, CB2 0SR, UK
² Alan Turing Institute, London, NW1 2DB, UK

Alex Hawkins-Hooker
Roles: Conceptualization, Methodology, Project Administration, Software, Supervision, Validation, Visualization, Writing – Review & Editing

Henry Kenlay
Roles: Data Curation, Formal Analysis, Investigation, Methodology, Software, Writing – Review & Editing

John E. Reid
Roles: Conceptualization, Data Curation, Formal Analysis, Investigation, Methodology, Software, Validation, Visualization, Writing – Original Draft Preparation, Writing – Review & Editing

Competing interests

No competing interests were disclosed.

Grant information

This work was funded by the UK Medical Research Council (Grant Ref MC_U105260799).
The funders had no role in study design, data collection and analysis, decision to publish, or preparation of the manuscript.

Article Versions (1)

version 1

Published: 05 Feb 2019, 8:151

https://doi.org/10.12688/f1000research.17125.1

Copyright

© 2019 Hawkins-Hooker A et al. This is an open access article distributed under the terms of the Creative Commons Attribution License, which permits unrestricted use, distribution, and reproduction in any medium, provided the original work is properly cited.

Download

Export To

metrics

	Views	Downloads
F1000Research	-	-
PubMed Central Data from PMC are received and updated monthly.	-	-

Citations

0

SEE MORE DETAILS

CITE

how to cite this article

Hawkins-Hooker A, Kenlay H and Reid JE. Projection layers improve deep learning models of regulatory DNA function [version 1; peer review: 1 approved, 1 approved with reservations]. F1000Research 2019, 8:151 (https://doi.org/10.12688/f1000research.17125.1)

NOTE: If applicable, it is important to ensure the information in square brackets after the title is included in all citations of this article.

track

receive updates on this article

Track an article to receive email alerts on any updates to this article.

Open Peer Review

Version 1

VERSION 1

PUBLISHED 05 Feb 2019

Views

16

Reviewer Report 21 Oct 2019

Qin Ma, Department of Biomedical Informatics, College of Medicine, Ohio State University, Columbus, OH, USA

Approved with Reservations

https://doi.org/10.5256/f1000research.18723.r55081

The authors proposed a novel approach to model the regulatory activity of DNA sequences and, by incorporating the projection layer into a new convolutional-recurrent architecture. The proposed method obtains state-of-the-art performance on the full DeepSEA dataset. In the experiment process, ... Continue reading

The authors proposed a novel approach to model the regulatory activity of DNA sequences and, by incorporating the projection layer into a new convolutional-recurrent architecture. The proposed method obtains state-of-the-art performance on the full DeepSEA dataset. In the experiment process, the authors explore what effect the projection layer and dropout rate have on DanQ, CNN and CRNN models, and explore the role of projections in achieving this performance. Meanwhile, applying the global average pool to reduce the number of parameters, which is a method to save training time and memory. The key contribution of this article is that the projection layer and dropout rate are utilized to model regulatory DNA, which provides us a new idea about how to mitigate the disadvantage s of a large first layer. The paper is well-organized and provides new insight into modeling the regulatory activity of DNA sequences, however, there are still some improvements needed.

Major comment 1: It is not clear to me how many times the models in Table 1 are tested. Meanwhile, regarding the results shown as figure 1 and figure 2, we usually test more times and give the boxplot of the results, to avoid the randomness.
Major comment 2: The authors should descript how to optimize their model, in detail.
Major comment 3: It is awesome that the 257 of the 700 learned motifs are obtained by the CRNN-700-projection model. If some of the learned motifs are shown in the main text, this article will be more attracting. Meanwhile, the DanQ model can also be used to extract motifs, this model should be compared to the CRNN-700-projection model.
Minor comment 1: Please, ensure what the ‘4’ means, in the penult line of the Introduction.
Minor comment 2: Please, provide the expansion of PAC and PFM.
Minor comment 3: The flowchart can clarify the authors’ method, why not consider adding the flowchart of your approach.

Is the rationale for developing the new method (or application) clearly explained?

Yes
Is the description of the method technically sound?

Partly
Are sufficient details provided to allow replication of the method development and its use by others?

Partly
If any results are presented, are all the source data underlying the results available to ensure full reproducibility?

Yes
Are the conclusions about the method and its performance adequately supported by the findings presented in the article?

Yes

Competing Interests: No competing interests were disclosed.

Reviewer Expertise: Bioinformatics, Computational Systems Biology

I confirm that I have read this submission and believe that I have an appropriate level of expertise to confirm that it is of an acceptable scientific standard, however I have significant reservations, as outlined above.

CITE

Report a concern

Respond or Comment

Views

28

Reviewer Report 18 Feb 2019

David R. Kelley, Calico Life Sciences LLC, South San Francisco, CA, USA

Approved

https://doi.org/10.5256/f1000research.18723.r44128

Summary
The authors suggest the use of “projection” layers for modeling the regulatory activity of DNA sequences. “Projection” layers perform a linear transformation from a large representation size to a smaller one, by applying a width one convolution. They ... Continue reading

Summary
The authors suggest the use of “projection” layers for modeling the regulatory activity of DNA sequences. “Projection” layers perform a linear transformation from a large representation size to a smaller one, by applying a width one convolution. They present experiments with two previously studied architectures in which the addition of these layers improves performance. They suggest that inserting this layer after the initial convolution layer, which most closely resembles position weight matrices, enables the model to more easily capture the similarity of forward and reverse complement motifs for some tasks.

This technique has been studied in the larger neural network literature, often by the name of bottleneck layers. The authors should consider citing Lin et al. Network in network (https://arxiv.org/abs/1312.4400) for readers who would like to learn more about the technique.

The experiments appear solid and align with my own experiences using similar layers. One difference with my previous experiments is that I've always applied a nonlinearity after the "projection", effectively making it a more standard neural network layer. The authors might consider benchmarking this version.

In addition to the projection layers, the authors observation that the final prediction layers for these tasks can use drastically fewer parameters by applying a global average pool is insightful.

Overall, I expect this report will be useful to future practitioners of neural networks for DNA sequence analysis.

Is the rationale for developing the new method (or application) clearly explained?

Yes
Is the description of the method technically sound?

Yes
Are sufficient details provided to allow replication of the method development and its use by others?

Yes
If any results are presented, are all the source data underlying the results available to ensure full reproducibility?

Yes
Are the conclusions about the method and its performance adequately supported by the findings presented in the article?

Yes

Competing Interests: No competing interests were disclosed.

Reviewer Expertise: Regulatory sequence machine learning

I confirm that I have read this submission and believe that I have an appropriate level of expertise to confirm that it is of an acceptable scientific standard.

CITE

Report a concern

Respond or Comment

Comments on this article Comments (0)

Version 1

VERSION 1 PUBLISHED 05 Feb 2019

Open Peer Review

Reviewer Status

Reviewer Reports

	Invited Reviewers
	1	2
Version 1 05 Feb 19	read	read

David R. Kelley, Calico Life Sciences LLC, South San Francisco, USA
Qin Ma, Ohio State University, Columbus, USA

Comments on this article

All Comments(0)

Add a comment

Sign up for content alerts

Browse by related subjects

Back to all reports

Reviewer Report

16 Views

21 Oct 2019 | for Version 1

Qin Ma, Department of Biomedical Informatics, College of Medicine, Ohio State University, Columbus, OH, USA

16 Views Cite this report Responses(0)

Approved With Reservations

The authors proposed a novel approach to model the regulatory activity of DNA sequences and, by incorporating the projection layer into a new convolutional-recurrent architecture. The proposed method obtains state-of-the-art performance on the full DeepSEA dataset. In the experiment process, the authors explore what effect the projection layer and dropout rate have on DanQ, CNN and CRNN models, and explore the role of projections in achieving this performance. Meanwhile, applying the global average pool to reduce the number of parameters, which is a method to save training time and memory. The key contribution of this article is that the projection layer and dropout rate are utilized to model regulatory DNA, which provides us a new idea about how to mitigate the disadvantage s of a large first layer. The paper is well-organized and provides new insight into modeling the regulatory activity of DNA sequences, however, there are still some improvements needed.

Major comment 1: It is not clear to me how many times the models in Table 1 are tested. Meanwhile, regarding the results shown as figure 1 and figure 2, we usually test more times and give the boxplot of the results, to avoid the randomness.
Major comment 2: The authors should descript how to optimize their model, in detail.
Major comment 3: It is awesome that the 257 of the 700 learned motifs are obtained by the CRNN-700-projection model. If some of the learned motifs are shown in the main text, this article will be more attracting. Meanwhile, the DanQ model can also be used to extract motifs, this model should be compared to the CRNN-700-projection model.
Minor comment 1: Please, ensure what the ‘4’ means, in the penult line of the Introduction.
Minor comment 2: Please, provide the expansion of PAC and PFM.
Minor comment 3: The flowchart can clarify the authors’ method, why not consider adding the flowchart of your approach.

Is the rationale for developing the new method (or application) clearly explained?

Yes
Is the description of the method technically sound?

Partly
Are sufficient details provided to allow replication of the method development and its use by others?

Partly
If any results are presented, are all the source data underlying the results available to ensure full reproducibility?

Yes
Are the conclusions about the method and its performance adequately supported by the findings presented in the article?

Yes

Competing Interests

No competing interests were disclosed.

Reviewer Expertise

Bioinformatics, Computational Systems Biology

I confirm that I have read this submission and believe that I have an appropriate level of expertise to confirm that it is of an acceptable scientific standard, however I have significant reservations, as outlined above.

Respond to this report

Responses (0)

Back to all reports

Reviewer Report

28 Views

18 Feb 2019 | for Version 1

David R. Kelley, Calico Life Sciences LLC, South San Francisco, CA, USA

28 Views Cite this report Responses(0)

Approved

Summary
The authors suggest the use of “projection” layers for modeling the regulatory activity of DNA sequences. “Projection” layers perform a linear transformation from a large representation size to a smaller one, by applying a width one convolution. They present experiments with two previously studied architectures in which the addition of these layers improves performance. They suggest that inserting this layer after the initial convolution layer, which most closely resembles position weight matrices, enables the model to more easily capture the similarity of forward and reverse complement motifs for some tasks.

This technique has been studied in the larger neural network literature, often by the name of bottleneck layers. The authors should consider citing Lin et al. Network in network (https://arxiv.org/abs/1312.4400) for readers who would like to learn more about the technique.

The experiments appear solid and align with my own experiences using similar layers. One difference with my previous experiments is that I've always applied a nonlinearity after the "projection", effectively making it a more standard neural network layer. The authors might consider benchmarking this version.

In addition to the projection layers, the authors observation that the final prediction layers for these tasks can use drastically fewer parameters by applying a global average pool is insightful.

Overall, I expect this report will be useful to future practitioners of neural networks for DNA sequence analysis.

Is the rationale for developing the new method (or application) clearly explained?

Yes
Is the description of the method technically sound?

Yes
Are sufficient details provided to allow replication of the method development and its use by others?

Yes
If any results are presented, are all the source data underlying the results available to ensure full reproducibility?

Yes
Are the conclusions about the method and its performance adequately supported by the findings presented in the article?

Yes

Competing Interests

No competing interests were disclosed.

Reviewer Expertise

Regulatory sequence machine learning

I confirm that I have read this submission and believe that I have an appropriate level of expertise to confirm that it is of an acceptable scientific standard.

Respond to this report

Responses (0)

[1] 1. Alipanahi B, Delong A, Weirauch MT, et al.: Predicting the sequence specificities of DNA- and RNA-binding proteins by deep learning. Nat Biotechnol. 2015; 33(8): 831–8. PubMed Abstract | Publisher Full Text

[2] 2. Zhou J, Troyanskaya OG: Predicting effects of noncoding variants with deep learning-based sequence model. Nat Methods. 2015; 12(10): 931–4. PubMed Abstract | Publisher Full Text | Free Full Text

[3] 3. Kelley DR, Snoek J, Rinn JL: Basset: Learning the regulatory code of the accessible genome with deep convolutional neural networks. Genome Res. 2016; 26(7): 990–9. PubMed Abstract | Publisher Full Text | Free Full Text

[4] 4. Quang D, Xie X: DanQ: a hybrid convolutional and recurrent deep neural network for quantifying the function of DNA sequences. Nucleic Acids Res. 2016; 44(11): e107. PubMed Abstract | Publisher Full Text | Free Full Text

[5] 5. Kelley DR, Reshef YA: Sequential regulatory activity prediction across chromosomes with convolutional neural networks. Genome Res. 2018; 28(5): 739–750. PubMed Abstract | Publisher Full Text | Free Full Text

[6] 6. Gupta A, Rush AM: Dilated convolutions for modeling long-distance genomic dependencies. ArXiv e-prints. 2017. Reference Source

[7] 7. Zhou J, Theesfeld CL, Yao K, et al.: Deep learning sequence-based ab initio prediction of variant effects on expression and disease risk. Nat Genet. 2018; 50(8): 1171–1179. PubMed Abstract | Publisher Full Text | Free Full Text

[8] 8. Khan A, Fornes O, Stigliani A, et al.: JASPAR 2018: update of the open-access database of transcription factor binding profiles and its web framework. Nucleic Acids Res. 2018; 46(D1): D1284. PubMed Abstract | Publisher Full Text | Free Full Text

[9] 9. Zeng H, Edwards MD, Liu G, et al.: Convolutional neural network architectures for predicting DNA-protein binding. Bioinformatics. 2016; 32(12): i121–i127. PubMed Abstract | Publisher Full Text | Free Full Text

[10] 10. Bengio Y, Ducharme R, Vincent P, et al.: A neural probabilistic language model. J Mach Learn Res. 2003; 3: 1137–1155. Reference Source

[11] 11. Srivastava N, Hinton G, Krizhevsky A, et al.: Dropout: A simple way to prevent neural networks from overfitting. J Mach Learn Res. 2014; 15(1): 1929–1958. Reference Source

[12] 12. He K, Zhang X, Ren S, et al.: Deep residual learning for image recognition. In 2016 IEEE Conference on Computer Vision and Pattern Recognition, CVPR 2016, Las Vegas, NV USA, June 27-30, 2016. 2016; 770–778. Publisher Full Text

[13] 13. Simonyan K, Zisserman A: Very deep convolutional networks for large-scale image recognition. CoRR. 2014. Reference Source

[14] 14. Szegedy C, Liu W, Jia Y, et al.: Going deeper with convolutions. CoRR. abs/1409.4842, 2014. Reference Source

[15] 15. Lin M, Chen Q, Yan S: Network in network. CoRR. 2013. Reference Source

[16] 16. Johnson W, Lindenstrauss J: Extensions of Lipschitz mappings into a Hilbert space. In Conference in modern analysis and probability (New Haven, Conn., 1982), volume 26 of Contemporary Mathematics. American Mathematical Society, 1984; 189–206. Publisher Full Text

[17] 17. Bingham E, Mannila H: Random projection in dimensionality reduction: Applications to image and text data. In Proceedings of the Seventh ACM SIGKDD International Conference on Knowledge Discovery and Data Mining, KDD ’01, New York, NY, USA, 2001; 245–250. Publisher Full Text

[18] 18. Shrikumar A, Greenside P, Kundaje A: Reverse-complement parameter sharing improves deep learning models for genomics. bioRxiv. 2017. Reference Source

[19] 19. Graves A, Schmidhuber J: Framewise phoneme classification with bidirectional LSTM and other neural network architectures. Neural Netw. 2005; 18(5–6): 602–610. Publisher Full Text

[20] 20. The ENCODE Project Consortium: An integrated encyclopedia of DNA elements in the human genome.Nature. 2012; 489(7414): 57–74. PubMed Abstract | Publisher Full Text | Free Full Text

[21] 21. Roadmap Epigenomics Consortium, Kundaje A, Meuleman W, et al.: Integrative analysis of 111 reference human epigenomes. Nature. 2015; 518(7539): 317–330. PubMed Abstract | Publisher Full Text | Free Full Text

[22] 22. Maas AL, Hannun AY, Ng AY: Rectifier nonlinearities improve neural network acoustic models. In: in ICML Workshop on Deep Learning for Audio, Speech and Language Processing. 2013. Reference Source

[23] 23. Kingma DP, Ba J: Adam: A method for stochastic optimization. CoRR. 2014; abs/1412.6980. Reference Source

[24] 24. Chollet F, et al.: Keras. 2015. Reference Source

[25] 25. Theano Development Team: Theano: A Python framework for fast computation of mathematical expressions. arXiv e-prints. 2016; abs/1605.02688. Reference Source

[26] 26. Gal Y, Ghahramani Z: A theoretically grounded application of dropout in recurrent neural networks. In: Lee DD, Sugiyama M, Luxburg UV, et al. editors, Advances in Neural Information Processing Systems 29. Curran Associates, Inc., 2016; 1019–1027. Reference Source

[27] 27. Alex: alex-hh/motif projection preprint. (Versionpreprint). Zenodo. 2019. http://www.doi.org/10.5281/zenodo.2543797

[28] 28. Gupta S, Stamatoyannopoulos JA, Bailey TL, et al.: Quantifying similarity between motifs. Genome Biol. 2006; 8(2): R24. PubMed Abstract | Publisher Full Text | Free Full Text

[29] 29. Chen S, Gan M, Lv H, et al.: DeepCAPE: a deep convolutional neural network for the accurate prediction of enhancers. bioRxiv. 2018. Publisher Full Text

Projection layers improve deep learning models of regulatory DNA function

Abstract

Keywords

Introduction

Methods

Baseline architectures

Linear projection layer

Improved convolutional-recurrent architecture

Experiments

Results

Effects of first layer design choices on reduced-size dataset

Figure 1. Test set AUPRC as function of first layer size for CNNs (left) and DanQ networks (right) with and without projection layer (projecting down to 64 dimensions) and dropout (dropout rate of 0.2).

Figure 2. Validation set loss curves for CNN (left) and DanQ (right) models with 500 first layer filters, either with or without the two regularisation strategies.

Projection layer helps improved CRNN architecture outperform other models on full DeepSEA data

Table 1. Performance of CRNN models with and without projection layer compared to DeepSEA and DanQ networks.

Projection layer simplifies learning by unifying representations for forward and reverse-complement motifs

Figure 3. PCA of projection weights corresponding to learned motifs with best matches to known motifs in JASPAR database.

Discussion

Data availability

Software availability

Author contributions

Grant information

Footnotes

References

Comments on this article Comments (0)

Open Peer Review

Comments on this article Comments (0)

Open Peer Review

Reviewer Status

Reviewer Reports

Comments on this article

Browse by related subjects

Competing Interests Policy

Stay Updated