Keywords
evolution, gene networks, fitness landscape learning
evolution, gene networks, fitness landscape learning
To respond to the reviewers' comments, in this revision, we extended the discussion. For the key point that the network modifies the thresholds by a simply feedback mechanism we point to regulation via enhancers.
In order to explain in more detail the regulation we added a new section
2.5 on "Gene regulation networks". Two new figures (Figure 1 and Figure
2) show results of numerical simulations based on the ``strong selection weak mutation'' (SSWM) algorithm.
In the discussion of Theorem 3.2 we added a paragraph on rare mutants and giving some intuitions towards the proof of Theorem 3.2 as it is based on estimates of the accuracy of the Nagylaki equations. For the main Lemma 4.5 for the proof of Theorem 3.2. we add a transparent interpretation.
Additional references pointed out by the reviewers are incorporated into version 2 of the paper.
To read any peer review reports and author responses for this article, follow the "read" links in the Open Peer Review table.
A central idea of modern biology is that evolution proceeds by mutation and selection. This process may be represented as a walk in a fitness landscape leading to fitness increase and slow adaptation1. According to classical ideas this walk can be considered a sequence of small random steps with small phenotypic effects. Nevertheless, there is a limited amount of experimental support for this idea2 and some experimental evidence that evolution can involve genetic changes of a relatively large effect and that the total number of changes are surprisingly small3. Another intriguing fact is that organisms are capable of making adaptive predictions of environmental changes4.
To explain those facts new evolutionary concepts have been suggested (see the review by 5 and references therein). The main idea is that a population can “learn” (recognize) fitness landscapes5–7. The approach developed in these works is a generalization of ideas from machine learning in which learning (regression to data) is viewed as selection and generalization (interpolation or extrapolation) is viewed as adaptation.
A mathematical basis for investigation of evolution learning problems has been developed by 8. However, this work uses a simplified model, where organisms are represented as Boolean circuits seeking an “ideal answer” to environmental challenges. These circuits involve Ng Boolean variables that can be interpreted as genes, and the ideal circuit answer maximizes the fitness. A similar model was studied numerically by 7 to confirm the theory of “facilitated variation” explaining the appearance of genetic variations which can lead to large phenotypic ones. In the work by 9 a theory of the evolution of these Boolean circuits was advanced. It was shown that, under some conditions—weak selection, see 10—a polynomially large population over polynomially many generations (polynomial in Ng) will end up almost surely consisting exclusively of assignments, which satisfy all constraints. This theorem can shed light on the problem of the evolution of complex adaptations since that satisfiability problem can be considered as a rough mathematical model of adaptation to many constraints.
In 6 it is shown that, in the regime of weak selection, population evolution can be described by the multiplicative weight update algorithm (MWUA), which is a powerful tool, well known in theoretical computer science and a generalization of such famous algorithms as Adaboost and others11. Note that in 6 infinitely large populations are investigated whereas the results of 9 hold only for finite populations and take into account genetic drift.
Evolution Computation(EC) problems are considered recently by many papers12–16 mainly for artificial test fitness functions like OneMax or LeadingOnes (for an overwiew of EC problems, see 17).
In this paper, we investigate adaptation and the fitness landscape learning problem for more realistic fitness function This fitness can model adaptation for insects and connected with a fundamental hard combinatorial problem: K-SAT.
The main results can be outlined as follows. We show that, in a fixed environment, genes can serve as learners in the machine learning sense. Indeed, if an organism has survived for a long period, this fact alone constitutes important information, which can be used. The biological interpretation of this fact is simple: if a population is large enough and mutations are sufficiently rare, deleterious mutations are eliminated by purifying selection. Hence, those non-neutral mutant alleles which have become fixed in natural populations will, with probability close to 1, be adaptive and cause a positive increment of fitness (see Theorem 3.1 and Theorem 3.2 in Subsection 3.1 and Subsection 3.2). We obtain mathematical results, which allows us to estimate the reduction of mutation number due to that learning landscape procedure. Learning can sharply reduce the number of mutations needed to form a phenotypic trait useful for adaptation that is consistent with experimental data mentioned above (see 3).
Another important result is as follows. We estimate the accuracy of fundamental Nagylaki equations6,10 for a realistic population model, where the population size is bounded and a non-zero mutation rate is taken into account (in the case of asexual reproduction). Those accuracy estimates are fulfilled for all possible values of mutation rates and population sizes.
In this section, we describe our model and mathematical approach.
We assume that the genotype can be described by Boolean strings of length Ng, where Ng is the number of genes. Then
where si = 1 means that gene i is activated (switched on) and si = 0 means that it is repressed (switched off). Correspondence between Boolean hypercube and genotypes is considered for example in 12.
Although phenotype is controlled by genes, it is also influenced by environmental conditions and various epigenetic processes. In this paper, we suppose that phenotypic traits are controlled by genotype only. We consider levels fj of expressions of those traits as real variables in the interval (0, 1). Then the vector f = (f1, . . . , fNb) can be considered to represent the organismal phenotype. We suppose that
where fj ∈ (0, 1) is a real valued function of the Boolean string s, the genotype.
Only a part of si is involved in fj. Namely, for each j we have a set of indices Kj = {i1, i2, . . ., inj} such that fj depends on si with i ∈ Kj, so that
where il ∈ Kj and nj is the number of genes involved in the control of the trait expression.
The representation of phenotype by the quantities fj is suggestive of quantitative traits because the fj are real valued. The limiting values of 0 or 1 suggest another interpretation, however, in terms of cell type. Multicellular organisms consist of cells of different types. One can suppose that the organismal phenotype is defined completely by the corresponding cell pattern. The cell type j is determined by morphogenes, which can be identified as gene products or signaling molecules that can change cell type (or genes that code for signaling molecules that can determine cell types or cell-cell interactions and then finally the cell pattern). The morphogene activity is defined by (2.2).
We further suppose:
Assumption M. Assume activities fj have the following properties.
The sets Kj are independent uniformly random subsets of Sg = {1, . . . Ng}
We denote the total number of genes involved in regulation of all fj by Nr, where
Assumption M implies that the genetic control of the phenotype is organized, in a sense, randomly, and that only a portion of the full set of genes controls phenotypic traits. That modularity of gene control is well known from experimental data (see 18, 19) and for evolution computation problems it was studied, for example, in 16.
Consider an example, where the assumption M holds, where we have a saturated expression, inspired by earlier work20,21. Let
where j = 1, . . . , Nb. Here σ(z) is a sigmoidal function of real z such that
and wij, hj are some coefficients (their meaning will be explained below). As an example, we can take σ(S) = (1 + exp(−bS))−1, where b > 0 is a sharpness parameter. Note that for large b this sigmoidal function tends to the step function and for b = +∞ our model becomes a Boolean one. The parameters hj defines thresholds for trait expression20. The relation (2.4) can be interpreted as a simple mathematical model for quantitative trait locus (QTL) action.
To understand the role of hj consider a trait fj and suppose that for a well adapted organism fj ≈ 1. Let, for simplicity, wij take the values 1, 0, or −1. Then the parameter hj defines how many genes involved in the control of the fj expression should be activators and how many should be repressors. Let the numbers of activator and repressor genes be , respectively.
Then fj ≈ 1 if
One can suppose that hj describes a direct influence of environment on phenotype, such as stress, that can exert epigenetic effects. In Section 2.6 using data from 22 we will show that the model defined by (2.4) are capable to describe main topological characteristics of really observed fitness functions in the case of mimicry, camouflage and thermoregulation for insects.
Let us introduce the matrix W of size Nb × Ng with the entries wij. The coefficients wji determine the effects of terminal differentiation genes (see 23), and hence encodes the genotype-phenotype map. We assume that the coefficients wji are random, with the probability that wji > 0 or that wji < 0 is β/2N, where β > 0 is a parameter. This quantity β << N defines a genetic redundancy, i.e., averaged numbers of genes that control a trait. Note that then large β ≫ 1 one has nj < 4β with the probability Prβ, which is exponentially close to 1: Prβ > 1 – exp(−0.1β), thus, the number nj are bounded.
We know little about the details of how fitness relates to the phenotype of multicellular organisms, and for that reason classic neo-Darwinian theory takes fitness to be a function of genotype. Some models which take account of epistasis have been proposed24. The random field models assign fitness values to genotypes independently from a fixed probability distribution. They are close to mutation selection models introduced by 25, and can be named House of Cards (HoC) model. The best known model of this kind is the NK model introduced by Kauffman and Weinberger26, where each locus interacts with K other loci. Rough Mount Fuji (RMF) models are obtained by combining a random HoC landscape with an additive landscape models27. In evolution computations (EC) some artificial fitness models were used, for example OneMax and Leading Ones to test evolution algorithms, see for example15.
In this work, we use the classical approach of R. Fisher by introducing an explicit representation of phenotype, f, and allow it to determine fitness through interaction with an environment b. That is, we assume that the phenotype is completely determined by the phenotype trait expression, and thus the fitness depends on the genotype s via fj.
We express the relative fitness F and its dependence on environment b via an auxiliary function W via the relation
where KF is a positive constant and b = (b1,..., bNb) is a vector consisting of coefficients bj, respectively. Below we refer to W as a fitness potential, and we assume that
Sometimes, if the parameter b is fixed, we shall omit the corresponding argument in notation for W and F.
We consider fitness as a numerical measure of interactions between the phenotype and an environment. For a fixed environment, this idea gives us the fitness of classical population genetics. A part of the fitness, however, depends on the organism developing properly and for now we represent it as independent of the environment, although we are aware that this is not always the case. Note that some coefficients bj may be negative and others may be positive, and that the model (2.7) can describe gene epistatic effects via dependence of fj on s if fj are nonlinear in s.
The expression (2.7) can serve as a rough approximation of the fitness function in the case of insects such as grasshoppers or fruit flies. In fact, important factors, which determine insect survival, are thermoregulation, mimicry and camouflage levels18,22,28. All those factors depend on colour pigmentation pattern. Blackwhite pigmentation patterns can be roughly described by vectors f = (f1, f2,..., fNb), where fj ≈ 1 and fj ≈ 0 mean that the cell j is black, or white, respectively, Then thermoregulation depends on The mimicry level can be approximately defined by expression , where f* is a target pattern corresponding to an insect to mimic. Colour patterns can be also described by classical RGB formalism.
The representation of the fitness as a sum of terms (2.7) is of course a rough approximation; however if assumption M holds that representation is consistent with important observed facts. First, mutations have been identified that alter one part of the pigment pattern without affecting any other. This independence of different pattern parts can be explained by the modular organization of the genetic regulation that controls pigmentation. In the course of evolution, different aspects of the pigment pattern have clearly evolved independently of each other18. Second, the topology of the fitness landscapes was studied in 22 by field experiments in the case of insect mimicry. Main conclusions are as follows. A number of studies of fitness landscapes in natural populations have demonstrated low fitness of intermediate phenotypes, i.e., existence of valley in the fitness landscape. It is found22 that natural selection promotes genetic architecture preventing the expression of intermediate phenotypes. Close fitness peaks are separated by ridges, favouring colour pattern switches and allowing drift from local peaks.
In Section 2.6 we will show that the fitness model defined by (2.4) and (2.7) have those topological properties.
For simplicity, we consider populations with asexual reproduction. (Although a part of the results remain valid for sexual reproduction, as we discuss at the end of this subsection). We choose initial genotypes randomly from a gene pool and assign them to organisms. This choice is invariant with respect to the population member, i.e,. the probability to assign a given genotype s to a member of the population does not depend on that member.
In each generation, there are Npop(t) individuals, the genome of each of which is denoted by s(t), where t = 0, 1, 2,... stands for the evolution step number). Following the classical Wright-Fisher ideas, we suppose that generations do not overlap. In each generation (i.e., for each t), the following three steps are performed:
1. Each individual s at each evolution step can mutate with probability pmut per gene;
2. At evolution step t each individual with a genotype s produces k progeny, where k is a random non-negative integer, distributed according to the Poisson law
where q = F(s) is the fitness of that individual;
3. To take into account ecological restrictions on the population size, we introduce the maximal population size Npopmax. If (t) > Npopmax, where (t) is the number of progeny produced by the population at step t, we kill randomly selected individuals in a population-dependent manner. The probability of the death of an individual is given by pkill() = 1 − (Npopmax/(t)). If (t) ≤ Npopmax, we do nothing. We refer to this as the “massacre procedure.”
Conditions 1 and 2 imply that mutations in the genotypes create a new genetic pool and then a new round of selection starts. Condition 3 expresses the fundamental ecological limitation that all environments can only support populations of a limited size. If Npopmax ≫ 1 then by (2.8) and the Central Limit Theorem one can show, under some additional conditions, (see Section 4) that fluctuations of the population size are small, and thus the population is ecologically stable and Npop(t) ≈ Npopmax.
In the limit case of infinitely large populations we will write the discrete dynamical equation for the time evolution of the frequency X(s, t) of the genotype s in the population as
where (t) is the average fitness of the population at the moment t defined by
where S(t) is the set of genotypes existing in the population at time t (the genetic pool) and X(s, t) = N(s, t)/Npop(t) is the frequency of the genotype s. Here N(s, t) denotes the number of the population members with the genotype s at the step t.
The equations (2.9) do not take mutations into account. They only describe changes in the genotype frequencies because of selection at the t-th time step. The same equations govern evolution in the case of sexual reproduction in the limit of weak selection6,10. Note that for an evolution defined by (2.9), the average fitness (t) defined by (2.10) satisfies Fisher’s theorem, so that this function increases at each time step t: (t + 1) ≥ (t).
In this section, we follow ideas of the classic paper29: the model should include a regulatory network, which evolves itself.
Regulatory genes as well as environmental factors, such as temperature, can influence the trait expression. This effect can be realized via thresholds hj (we shall describe it below), or via a regulation of coefficients wij (see 30). In fact, these approaches are similar for sharp sigmoidal functions σ that are close to step functions, as can be shown by ideas from 31. Consider the expression
involved in relation (2.4). Suppose following 31 that wij take the values γ, 0 or −γ, where γ is a parameter, which can be regulated. Let hj ≪ γ be fixed.
Assume that at an evolution step we have Si > dS, where dS > 0 is a parameter, which is more than γ. According to our Theorems this fact indicates, that for a well adapted organism the trait fj(s) ≈ 1 and the corresponding coefficient bj = 1. On the contrary, if Si < −dS, then one can expect that bj = −1 and fj(s) must be 0.
In the both cases, we can regulate the trait expression by a feedback so that whenever Si attains a critical level, i.e., a trait is well expressed, then γ should be increased. In our numerical simulations we use an alternative model, where we change hj. The alternative model, which is used in our numerical simulations, can be described as follows. We suppose that depending on activity of some regulatory genes or proteins (such as Hsp90), the threshold value can take three values , and such that
where Dh > 1 is a large parameter that defines the number of genes involved in trait specification (see Subsection 2.2). Thus, hj can take large negative or positive values, and also a neutral value close to 0. The feedback can be described as follows: if Si > 0 is large enough and hi is small, then hi = −Dh; if Si < 0 and is large enough and hi is small, then hi = Dh; otherwise, we do not change hi.
In our simulations, each ΔT evolution steps we modify hi from 0 to −Dh or Dh for the trait with the maximal value .
Such a regulation produces a good adaptation even when the number of genes is essentially less than the number of the traits. The plot in Figure 3 shows a difference between an evolution without any regulation and with the regulation by (2.12) described above.
However, the evolution of gene regulation via hi has an advantage: it makes phenotype more robust. In fact, the traits with large are non-sensitive with respect to mutations. The effect produced by this robustness is shown on Figure 1.
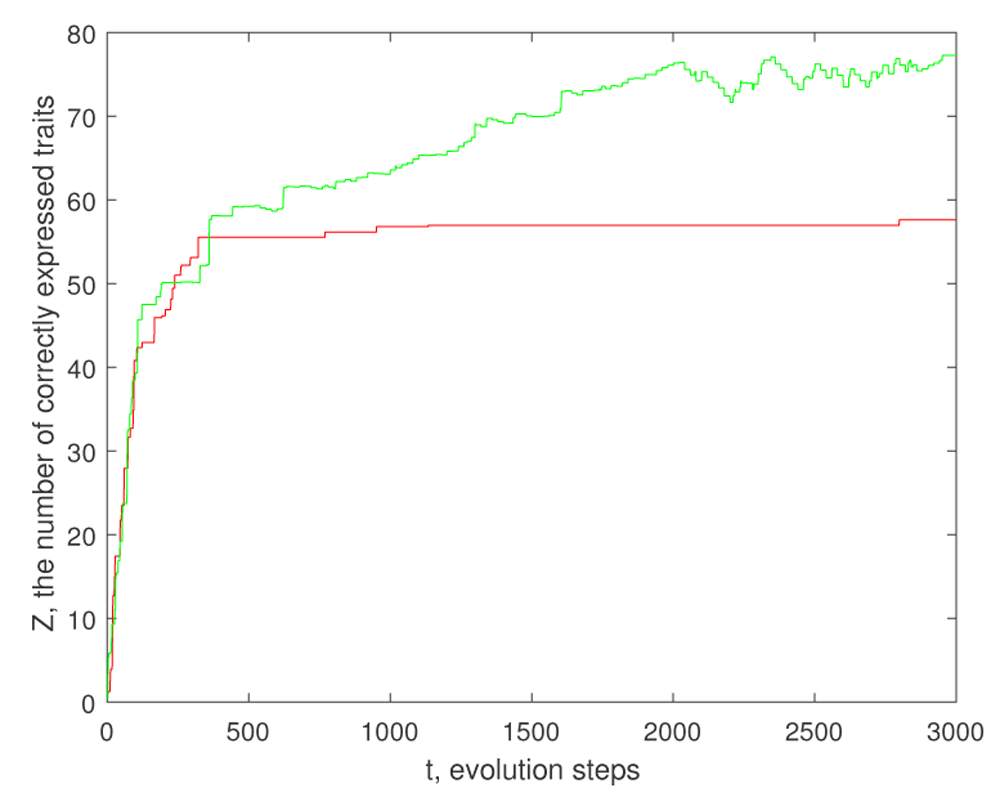
The parameters are Ng = 50, M = 300, the mutation rate pmut = 0.01, γ = 1 and K = 4. Non-zero coefficients wij are random numbers distributed according to the standard normal law. The initial genome is a random binary string, where each value is 0 or 1 with probability 1/2. The coefficients bi are either 1 or −1, where the probability of 1 is pb = 0.8.
This regulation is even more effective, if we consider the modular evolution, following the recent paper32. Indeed, biological systems are characterized by a high degree of modularity. This modularity allows biological systems to vary only in a small subset of traits at each evolution round. Figure 2 shows an effect of this modularity. We consider a toy example, where a system with only 10 genes should be adapted to 200 constraints. Without regulation, we have no chances to make an adaptation (only about 10 traits are correctly adapted, see the green curve). It is a consequence of a formidable pleiotropy (20 traits on 1 gene). However, if at each evolution stage an organism should be adapted to 4 traits whereas the remaining ones are made robust by high , then already 66 traits are correctly expressed after 20000 evolution steps. Note that the learning plays a key role in the regulation. In fact, the sign of the regulation threshold hi depends on the sign of the corresponding coefficient bi, and the knowledge of that sign gives us important information on the fitness landscape.
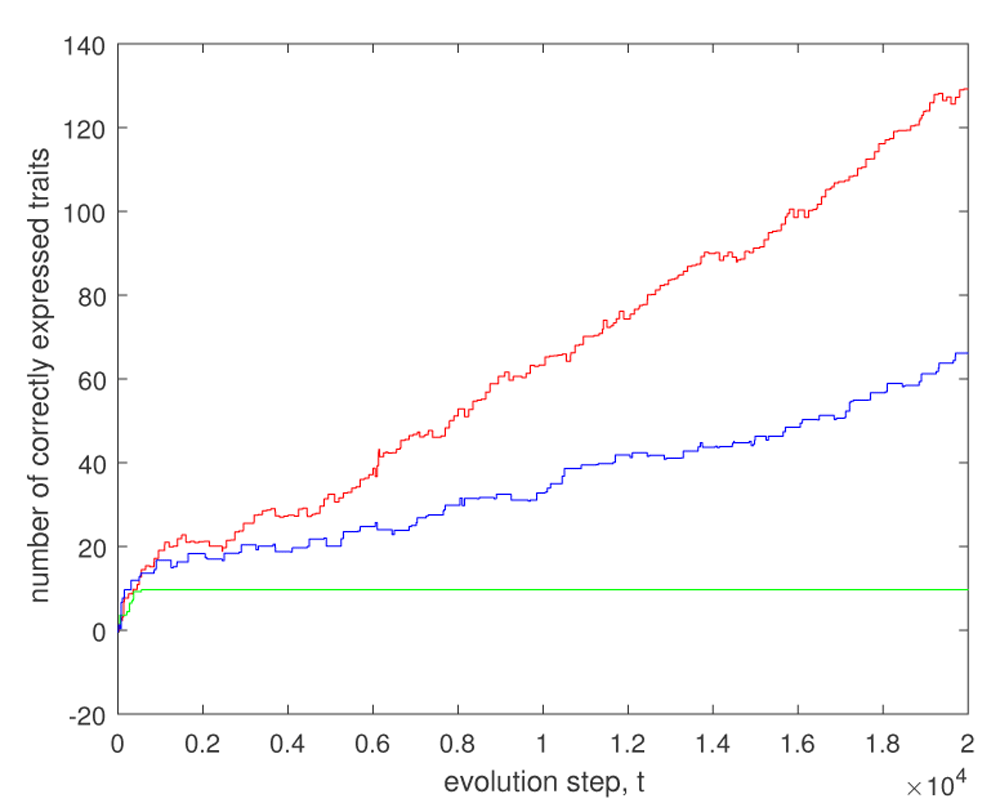
This means that we have a very big pleiotropy. Evolution proceeds in 20000 steps. The green curve corresponds to random walk with fixed small h without any evolution of gene regulation. We observe that with 10 genes 9 traits are correctly expressed. If evolution goes into 50 rounds then 66 traits are correctly adapted, and if evolution goes in 190 rounds then 129 traits are correctly adapted (the red curve). In that last case, at each step we make adaptation to at most one trait. Parameters are as follows. The mutation rate pmut = 0.01 and K = 5. Nonzero coefficients wij are random numbers distributed according to the standard normal law. The initial genome is a random binary string, where each value is 0 or 1 with probability 1/2. The coefficients bi are either 1 or –1, where the probability of 1 is pb = 0.8.
Adaptation (i.e., maximization of fitness in a changing environment) is a very hard problem since over evolutionary history we observe the coevolution of many traits accompanied by changes in many genes. In its general context, this is a problem in the theory of macroevolution, which in general requires the integration of population genetics and developmental biology for its full understanding. There are two key components of this problem. First, development is itself a dynamical process operating over time. Second, there is a combinatorial component of development wherein different combinations of gene must be expressed in different cell types. This combinatorial aspect of the problem means that straightforward theoretical methods of considering the relationship between gene expression and a changing environment that have been very successful in single celled organisms33 cannot be applied to metazoa. In this work, for the sake of tractability, we focus on the combinatorial aspect of the problem and neglect developmental dynamics. Even at the highly simplified level of our model, adaptation is a hard computational problem, as we now demonstrate.
Consider the case, where fj are defined by relations (2.4) and assume that
As a consequence of the second assumption, F attains its maximum for f1 = 1, f2 = 1,..., fNb = 1. Let us show that, even in this particular case, the problem of the fitness maximization with respect to s is very complex. In fact, for a choice of hj it reduces to the famous NP-complete problem, so-called K-SAT, which has received a great deal of attention in the last few decades (see 34–39). The K-SAT can be formulated as follows.
K-SAT problem. Let us consider the set Vn = {s1,..., sn} of Boolean variables si ∈ {0, 1} and a set 𝒞m of m clauses. The clauses Cj are disjunctions (logical ORs) involving K literals zi1, zi2,..., zik, where each zi is either si or the negation i of si. The problem is to test whether one can satisfy all of the clauses by an assignment of Boolean variables.
Cook and Levin34,35 have shown that the K-SAT problem is NP-complete and therefore in general it is not feasible in a reasonable running time. In subsequent studies—for instance, by 36 —it was shown that K-SAT of a random structure is feasible under the condition that Nb < αc(K)Ng, where αc(K) ≈ 2K log 2 for large K.
The set 𝒞K of solutions of random K-SAT has a nontrivial structure depending on parameter α = Nb/Ng37,39. For sufficiently small α < αg(K), where αg(K) ≈ 2K log(K)/K is some critical parameter, the set 𝒞K forms a giant cluster, where nearest solutions are connected by a single flip and one can go from a solution to another by a sequence of single flips (pointed mutations)39. For α ∈ (αg, αd), where αd(k) < αc is another critical value, solutions form a set of disconnected clusters. The local search algorithms do not work in the domain α > αg.
Probably, for evolution context K-SAT was applied first in 40, where it was used for an investigation of speciation problem.
To see the connection of our model with K-SAT, consider equation (2.4) supposing that wij ∈ {1, 0, −1} and hj = −Cj + 0.5, where Cj is the number of negative wji in the sum We set m = Nb and n = Ng. Under this choice of hj, the terms σ(Sj) can be represented as disjunctions of literals zj. Each literal zj equals either sj or j, where j denotes negation of sj. To maximize the fitness, we must assign sj such that all disjunctions will be satisfied. If we fix the number nj of the literals participating in each disjunction (clause) and set nj = K, this assignment problem is precisely the K-SAT problem formulated above.
Reduction to the K-SAT problem is a transparent way of representing the idea that multiple constraints need to be satisfied. The number K defines the gene redundancy and the probability of gene pleiotropy. Remind that pleiotropy occurs when one gene influences two or more seemingly unrelated phenotypic traits. The threshold hj and K define the number of genes which need be flipped in order to attain a high expression of the trait fj. Note that gene pleiotropy is a fundamental characteristics41, which is studied for real organisms only recently (see 19). We can compare experimental observations and consequence of model (2.4), which is a generalisation of K-SAT (compare plot Figure 3 and plots on Figure 1 in 19). So, we can fit our model parameters using real data. Moreover, we can check validity of our model by the following arguments.
We note that, in the case of giant cluster formation, the topological properties of the solution set 𝒞K, mentioned above, outline the properties of really observed fitness landscapes22: existence of many peaks, valleys and ridges connecting peaks. Namely, existence of many solutions of K-SAT, when a giant cluster exists, means that the landscape has a number of peaks separated by valleys. On the other hand, connectance of solutions within the giant cluster can be interpreted that there exist ridges that connect peaks.
Note that there are important differences between K-SAT in Theoretical Computer Science and fitness maximization problems. First, the signs of bj are unknown for real biological situations since the fitness landscape is unknown. Second, our adaptation problem involves the threshold parameters hj (see (2.4)). In contrast to K-SAT, in our case the Boolean circuit is plastic, because the hj are not fixed.
If the bj are unknown, the adaptation (fitness maximization) problem becomes even harder because we do not know the function to optimize. Therefore, many algorithms for K-SAT are useless for biological adaptation problems. Below we will nonetheless obtain some analytical results based on the assumption that bj are random.
The subsequent material is organized as follows. First we formulate a result on regulation mechanism power. Furthermore, we prove two fitness landscape learning theorems.
For simplicity, we consider asexual reproduction. To obtain similar results for sexual reproduction, one can consider a weak selection regime and use the results of 10, where eq. (2.9) are derived.
Let us introduce two sets of indices I+ and I−, such that I+ ∪ I− = {1,..., Nb}. We refer to these sets in the sequel as positive and negative sets, respectively. We have
The biological interpretation of that definition is transparent: the expression of the traits fj with j ∊ I+ increases the fitness and for j ∊ I– expression of the trait decreases the fitness.
Let s and be two genotypes. Then we denote by Diff(s, ) the set of positions i such that si ≠ i:
The set Diff(s, ) indicates which genes in s should be flipped in order to obtain .
We formulate two theorems on fitness landscape learning. First we consider the case of infinitely large populations.
Theorem 3.1. Suppose that the evolution of the genotype frequencies X(s, t) is determined by equations (2.9) and (2.10). Moreover, assume that
I for all t ∊ [T1, T1 + Tc], where T1, Tc > 0 are integers, the population contains two genotypes s and such that the frequencies X(s, t) and X(, t) satisfy
II we have
for some j. In other words, the genes si such that si ≠ i are involved in a single regulation set Kj; and finally,
III Let
and
Then, if
we have j ∊ I+. If fj(s) > fj(), then j ∊ I–.
Before proving this, let us make some comments. The biological meaning of the theorem is simple: for simple fitness models, where unknown parameters bj are involved in a linear way, in the limit of infinitely large populations fitness landscape learning is possible.
Moreover, note that we do not make any specific assumptions about the nature of mutation, but only that all genetic variation between s and are contained in a single regulatory set Kj.
The assertion of Theorem 3.1 is not valid if the set Diff(s, ) belongs to a union of different regulation sets Kj , j = j1, . . . , jp with p > 1. This effect of belonging to different sets Kj is pleiotropy in gene regulation. Note that if Nb ≪ Ng then the pleiotropy probability is small for large genome lengths Ng. On the contrary, if Nb ≫ Ng then assumption II is invalid.
Assumption II looks natural if when we deal with point mutations. In fact, if is obtained from s by a single point mutation then condition (3.4) always holds for some j. For small mutation rates the probability of two point mutations is essentially below than the probability of a single mutation.
To conclude let us note that Theorem gives a rough estimate for the learning time Tc:
Proof. The main idea is simple. Negative mutations lead to elimination of mutant genotypes from the population, and the corresponding frequencies become, for large times, exponentially small.
Assume that (3.7) holds. Let j ∊ I−, and thus bj < 0. Consider the quantity
According to assumption II
Assumption III entails that
Relations (2.6) and (3.10) imply
By (2.9) and the last inequality we find that for T > T1
Consider inequality (3.11) for T = T1 + Tc. Let us note that in the relation Q(T1) = X(s, T1)/X(, T1) the numerator is p0 whereas the denominator ≤ 1. Thus, Q(T1) ≥ p0. The same arguments show that Q(T1 + Tc ) ≤ 1/p1. Therefore, by (3.11) one obtains that
This inequality leads to a contradiction for Tc satisfying (3.6), thus completing the proof.
Theorem 3.1 can be extended to the case of finite populations and non-zero mutation rates. is small. To formulate this generalization, we need an additional assumption about the fitness function. Suppose that
where cF, CF > 0 are constants independent of t. For example, if
then cF = KF exp(–γ) and CF = KF exp(γ) and (3.13) holds if KF > exp(γ).
Condition (3.13) means that each individual gives birth to at least cF and at most CF descendants, where those bounds do not depend on the population size and evolution step.
Let
Note that for simplicity in the next Theorem 3.2 we consider point mutations (bit flipping) only. The model used here cannot represent mutations of arbitrarily small effect, but it can include insertions or deletions. In contrast to Theorem 3.2, Theorem 3.1 is valid for all kinds of mutations.
Then we have
Theorem 3.2. Consider the population dynamics defined by model 1-3 in Subsection 2.4. Assume conditions (3.14) and M hold, and assumptions (3.3), (3.4), (3.5), (3.7) of Theorem 3.1 are satisfied. Suppose
Then if j ∊ I– the inequality
is fulfilled with the probability Prv such that
where for large Npopmax and pmut → 0
Interpretation of Theorem 3.2
It is interesting to compare Theorem 3.1 and Theorem 3.2. The previous one asserts that for infinite populations the probability of the event j ∊ I− is zero whereas the second one claims that this probability becomes exponentially small as the population size increases.
This theorem also shows that evolution can make a statistical test checking the hypothesis H– that j ∊ I– against the hypothesis H+ that j ∊ I+. Suppose that H– is true. Let V be the event that the frequency X(, t) of the genotype in the population is larger than p1 within a sufficiently large time Tc. According to estimate (3.18), the probability of the event V is so small that it is almost unbelievable. Therefore, the hypothesis H– should be rejected. We will refer Tc as the checking time.
Rare mutants. In this Theorem we assume that the frequencies p0 and p1 of genotypes (wild and mutant) are fixed and our estimate is valid as pmut → 0. I.e., we do not consider mutants with a very small frequencies (fractions). Of course, a large population always contains a small number of such mutants. In numerical simulations we assume that evolution is successful and population is perfectly adapted, if, say, 95 or 99 percents of population members have the maximal fitness.
Ideas for the proof. The main idea is the same as that for the previous theorem: we compare the frequencies of the organisms with the genotype and the organisms with the genotype s. However, the proof includes a number of technical details connected with estimates of mutation effects and fluctuations. The formal proof can be found in Section 4. It is based on estimates of the accuracy of the Nagylaki equations (2.9). The main Lemma 4.5 for the proof of Theorem 3.2. admits a transparent interpretation. We show that fraction X(s, t) of genotype s evolves in time in such a way that the estimates.
are satisfied, where F(s) is a fitness of genotype s, is average population fitness, and r(pmut, Npop)) are small corrections, which converge to zero uniformly in s as the mutation rate pmut → 0 and the population size Npopmax → ∞. This means that in the limit pmut → 0, Npopmax → ∞ we have equation (2.9). The main problem with the application of Theorem 3.2 is how it allows to perform fitness landscape learning. It can be done by a regulation, as is detailed in the following section.
Let us prove Theorem 3.2.
Let us introduce notation and make some preliminary remarks. Remind that we denote by N(s, t) the number of the population members with the genotype s at the moment t. Let X(t) be the set of all population members at the moment t. For each x ∊ X(t) let us denote by (x, t) the number of progeny born by the individual x at the moment t before the massacre (see point 3 of model from Subsection 2.4). Let sg (x) be the genotype of x. Then, according to (2.8), the mean of (x, t) is
where EX denotes the expected value of X. By (s, t) we denote the number of all progeny born by individuals with the genotype s at the moment t before the massacre. Since all progeny are produced independently and randomly, the previous relation gives
Our main analytical tools are the Chernoff bounds and the Hoeffding inequalities. We also use the Markov inequality: for a positive random quantity X and a > 0 one has
Moreover, we use two elementary estimates. Let 𝒜 be an event in stochastic population dynamics. We denote by Not𝒜 the negation (complement) of 𝒜 and by Pr(𝒜|ℬ) the conditional probability of 𝒜 under the condition ℬ. For events 𝒜 , ℬ1, . . . , ℬn we have
For two events 𝒜, ℬ one has
Lemma 4.1. Let Xi be independent random quantities, where i = 1, . . . , n. Let each Xi be distributed according to the Poisson law with the average EXi = μi. Let us denote
Then for all δ > 0
where
Similarly,
Proof. Note that for any λ > 0
Since Xj are independent quantities, we have
The straight forward computation shows that
Therefore, due to the Markov inequality (4.3) and estimate (4.8) one has
where
We minimize f with respect to λ and obtain (4.6). To derive (4.7), we use
and repeat the same arguments. The Lemma is proved.
Lemma 4.2. Let Xi be independent random quantities, where i = 1, . . . , n such that Xi ∊ {0, 1} and EXi = p. Then
where
Proof. Note that for any λ > 0
Since Xj are independent quantities, we have
Note that E exp(−λXj) = p exp(−λ) + 1 − p. Let
We take λ = ln 2 and find that G(ln 2, p) = −g(p). Now by using the Markov inequality (4.3) and estimate (4.12) one obtains (4.10). The Lemma is proved.
We also use the following Chernoff-Hoeffding theorem. Let Xi be i.i.d. quantities such that Xi ∊ {0, 1} and EXi = p, where i = 1, . . . , n. Then for one has
where D(x||y) is the Kullback-Leibler divergence
Moreover, we will use the Hoeffding Theorem: if i.i.d. quantities Xi ∊ [0, 1] with the probability 1 then
First we estimate the population size fluctuations.
Lemma 4.3. Let (t) be the number of all progeny, born in the population at the moment t before the massacre, and ε1 > 0 be a small number. Then
with probability
where
Proof. Let (x, t) denote the number of progeny produced by the individual x before the massacre at the t-th evolution step. The number (t) is the sum
of the mutually independent random quantities. According to (4.2), the average E (x, t) is F(sg (x)). Therefore,
We set
and use the Lemma 4.1 that gives us (4.17).
Lemma 4.4. Let ε2 ∊ (0, 1) be fixed and condition (3.13) be fulfilled. Assume, moreover, that
where
and cF > 1 is defined by (3.13). Let us define the event 𝒟ε2 (t) by
Then one has
where
and
Proof. Let ξ(x) be random quantities defined as follows: ξ(x) = 1 if the individual x is survived as a result of massacre (see point 3 of our model from Subsection 2.4), and ξ(x) = 0 otherwise. Let (t) be the set of progeny produced by all individuals from the population. Then the number Nsur(t) = Npop(t + 1) of finally survived progeny can be computed as follows:
Note that |(t)| = (t). Moreover, Eξ(x ) = Npopmax/(t) for (t) ≥ Npopmax. Therefore, if (t) ≥ Npopmax then
Let us define the event
where the interval Jε(t) is defined by (4.16) and is defined by (4.27). By (4.4) we have
Now we apply the Hoeffding inequality (4.15). For each ε2 > 0 we obtain
If ℬ (t) takes place, then (t) ≥ Npopmax and consequently
Therefore,
Moreover, by Lemma 4.3
Inequalities (4.30), (4.32) and (4.33) prove (4.25).
The following lemma, in particular, allows us to obtain equations (2.9) and (2.10) in the limit of infinite populations and for small mutation probabilities.
Recall that denotes the number of non-mutated progeny generated by the individuals with the genotype s before the massacre. Let Nsur(s, t) be the number of those progeny that survived after that massacre.
Lemma 4.5. Let ε0 be a positive number satisfying (4.75) and
Then one has
with the probability Prs,t,+ such that
where
Similarly,
with the probability Prs,t,− such that
Proof. Step 1, estimates of fluctuations. First let us estimate the fluctuations of the number . For each ε2 > 0 let us define the event
By Lemma 4.1 one has
Note that
As a result, by (4.46) we obtain
Step 2. Here we estimate the number of progeny that survived as a result of the massacre procedure (point 3 of the population dynamics model, see subsection 2.9). Let X' (s, t) be the set of progeny produced by individuals with the genotype s. Then the number Nsur(s, t) of survived progeny x for individuals x belonging to the set Z' (s, t) is
where ξ(x) are defined in the proof of the previous Lemma. For ε3 > 0 we consider the event
Let us estimate the probability Pr(𝒜sur,s(t)). According to the Hoeffding Theorem (4.15)
Note that ξ(x) and ξ(y) are independent quantities for different x and y, thus under the condition > Npopmax
therefore,
Let us define the events ℬs(t) and ℬ(t) by
Then using (4.4) one has
We observe that under conditions ℬs(t) and ℬ(t)
In that estimate let us set ε2 = 0.5 and ε1 = 1. Taking into account that E = Npop(t) < 2CFNpopmax, we have that
where
Moreover, according to (4.47)
and due to (4.17)
where R1,R2 are defined by (4.37) and (4.38). Finally,
Step 3, estimate of the number of mutants.
Let us estimate how many individuals with genotypes s can mutate. The probability of mutation is pmut. Let Nmut(s, t) be the number of such mutants. Let us define the event 𝒜mut,s(t) by
Since the random quantity Nmut(s, t) is subject to the Bernoulli law, we can apply the Chernoff-Hoeffding inequality (4.13). Then we obtain that
where, according to definition (4.14) of D(x||y), one has
and g is defined by (4.11).
Using (4.4) one has
As a result, by Lemma 4.3 one finds
where R4,R5 are defined by (4.40) and (4.41).
To prove (4.35), we set ε3 = ε0/2. Taking into account condition (4.75) for ε0 we see that if the both events Not 𝒜mut,s(t) and Not 𝒜sur,s,ε0/2(t) take place, then inequality (4.35) is fulfilled. Thus
where Ri are defined by (4.37)–(4.41).
Finally, taking into account the results of steps 1, 2 and 3 we see that estimate (4.35) holds with the probability Prt,+. It completes the proof of (4.35). The second inequality (4.42) can be obtained in the same way.
We use the same idea that in the proof of Theorem 3.1 but first we establish uniform bounds for the population size and other quantities involved in the proof.
Step 1 Here we estimate the population size. Let us set
in Lemma 4.4. Let us consider the events 𝒟ε2(t) defined by (4.24) in Lemma 4.4. If the events 𝒟ε2(t) take place for all t ∈ [T1, T1 + Tc] and Npop(0) = Npopmax, we have that
Then conditions (3.15), (3.16) of Theorem 3.2 imply
Those inequalities imply the following estimates for the quantities Ri defined by (4.37)–(4.41):
where qi are defined by
where
and
where = 1 – (κcF)–1, and
For each p ∈ (0, 1) let us define an auxiliary function
where qi, are defined by relations (4.68)–(4.72). We can find asymptotics of ρ under natural assumptions that pmut → 0 and Npopmax → ∞ while all the rest parameters are fixed. Then the leading term in the right hand side of (4.36) is q4 and As a result, we have
Step 2. Let Q(t) is defined by (3.8) and, moreover, let j ∈ I−. We use Lemma 4.5 inductively for genotypes s and . Let us set
where ε is defined by (4.75). We remark that the inequality
holds with a probability PrQ,t > 0. Let us obtain a uniform estimate of that probability. Let ℰ(t) be the event that (4.78) holds at the step t. Using (4.4) we have
where, according to Lemma 4.4, the probability of the event Not 𝒟ε2(t) is less than η, where η is defined by (4.25), and
We conclude by (4.5) that
where is defined by (4.74). This estimate is uniform in t ∈ [1, . . . , Tc]. By (4.80) we obtain then that the inequality
is satisfied with the probability Prv such that
For ε0 defined by (4.75). one has
Now repeating the same arguments that in the end of the proof of Theorem 3.1, and taking into account asymptotics (4.77), we obtain the conclusion of Theorem 3.2.
In this paper, we proposed a model for fitness landscape learning, which extends earlier work by 7–9 in two ways. First, we use hybrid circuits involving two kinds of variables. The first class of variables are real valued in the interval (0, 1) and can be interpreted as relative levels of phenotypic traits, other variables are Boolean and can be interpreted as genes. Second, we use a threshold scheme of regulation, which is inspired by ideas of the paper by 20. All variables are involved in gene regulation via thresholds.
The work presented here is a major extension of a long term effort to explicitly model the effects of phenotypic buffering in evolution by considering a class of Boolean and mixed Boolean-continuous models in which the phenotype is represented explicitly and the degree of phenotypic buffering can be controlled in various ways. For example, we have demonstrated that the idea of an “evolutionary capacitor”42,43 can be implemented by explicit control of phenotypic buffering in a hub-and-spokes architecture23 and that in a more general class of genetic architecture numerical simulations show that an intermediate level of buffering is optimal for evolution in a changing environment31.
The results reported here are very promising, since they are consistent with the results of recent experiments by 44 and 45 on heat shock stress. The essential mechanism is that the exploration of the fitness landscape by the genetic network in such a way that future mutations are more likely to be adaptive. We have shown that, at least for some fitness landscapes, rapid evolutionary changes—perhaps instances of the “hopeful monsters” of Goldschmidt46—can be created by a combination of random small mutations and epigenetic effects. The main idea is that small mutations pave the way for large epigenetic or genetic changes. The hypothetical mechanism, which we propose, can be outlined as follows (see Figure 4, Figure 5).
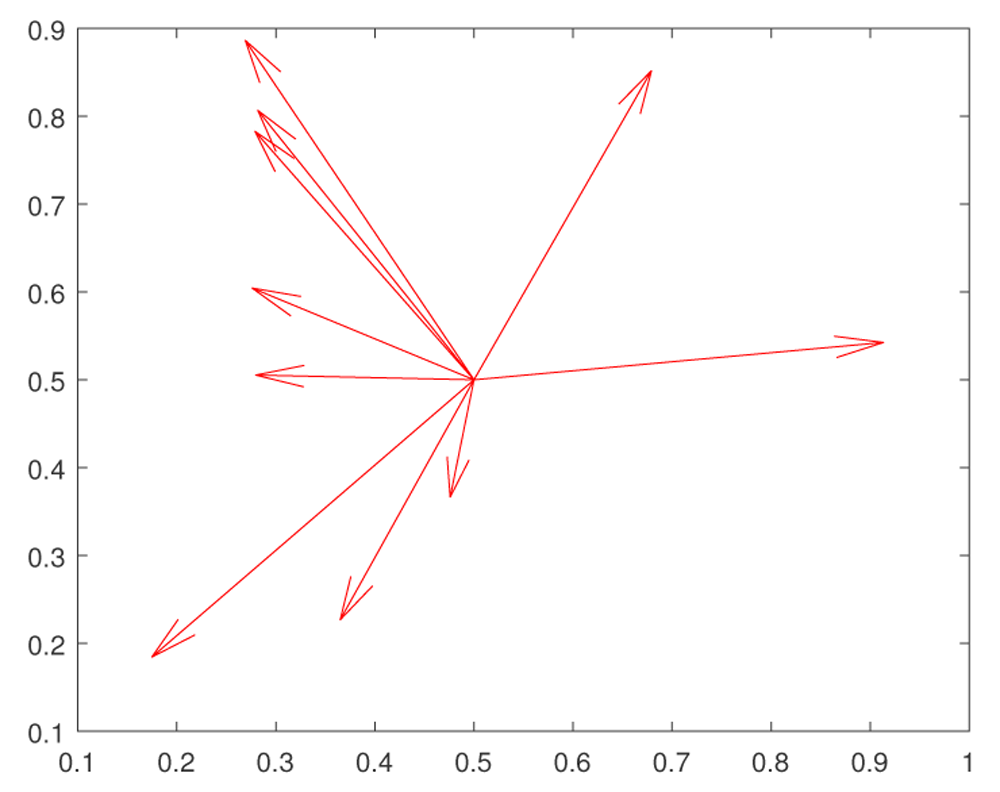
At the initial moment the trait expressions take the values x = 0.5, y = 0.5. According to Fisher’s ideas, random large mutations decrease the fitness F = KF exp(W). (Changes of x = F1, y = f2, which are induced by mutations, are shown by red vectors.) Thus such mutations produce non-viable organisms.

At the initial time the trait expressions take the values x = 0.5, y = 0.5. Evolutionary changes go in two stages. First we make small random mutations (shown by red vectors), which explore the fitness landscape. If such a mutation is not eliminated from the population, this means that a correct evolution direction is found, and gene regulation system makes a big leap (shown by the green vector) in the direction of that small mutation. Such a two step model can be called clever Goldshmidt leaps. Note that evolution is gradual, and the existence of clusters of almost identical genes involved in the same QTL increases the chances to create a clever Goldschmidt hopeful monster.
This network modifies the thresholds by a simple feedback mechanism. Although we are not aware of clear experimental evidence for the existence of such a mechanism, we nevertheless think that such a mechanism can be connected with regulations via enhancers47,48, where enhancer action is described by deep network models based on thermodynamics, and chemical kinetics, and those models contain threshold parameters. Alternative variants involve modifications of weights. To some extent, both mechanisms are mathematically equivalent. However, the regulation via thresholds has an important advantage: it makes phenotypes robust with respect to mutations. In this second version of the paper we included a subsection about regulation and two pictures, which show results of numerical simulations based on the “strong selection weak mutation” (SSWM) algorithm. As is the case for threshold signs, they of course should have different signs. The key question is how an individual obtains information about the fitness landscape. In our model that information is the sign of bj. If the bj is positive the corresponding threshold must be negative, otherwise, it should be negative. Actually, we think that the gene of individuals have that information! According to the main theorems proved in this paper, the fact that a mutated individual survives for a sufficient long period of time gives us that information. The very fact of the existence of the individual carries the most important information. Look at the mutations of its genotype and you will know where evolution should go!
As is described in Subsection 2.5, we assume that expression of genes involved in the expression of phenotypic traits depends on threshold parameters hj, which take three values: a large negative one, a neutral value close to zero and a large positive one. First the threshold parameter hj is small and thus the phenotypic trait is sensitive with respect to even small mutations. Those mutations play a fundamental role working as scouts exploring environments (see Figure 4). If a mutation occurred and the corresponding mutant has survived within Tc ≫ 1 generations then according to Theorem 3.1 and Theorem 3.2 these events mean that that mutation increases the fitness that allows the network to estimate the correct direction of evolution. Then gene regulation detects that increase to change the threshold according to simple rules. Namely, if the trait is less expressed in that mutant with respect to wild type parent, the gene regulation system decreases the threshold up to the large negative value. On the contrary, if the trait is strongly expressed in the mutant, the gene regulation system increases the threshold up to the large positive value. This simple regulation control not only sharply reduces the number of mutations needed for adaptation, but also canalizes the phenotype since for large thresholds the trait expression level becomes insensitive with respect to mutations. We suppose that these threshold modifications can be inherited.
So, we propose the mechanism: small mutations serve as scouts finding the way for large epigenetic or genetic changes, which can be performed by gene regulatory system.
The mechanism may also explain the results of 4 on prediction of environmental changes. In fact, let us suppose that environment varies in time. The first, perhaps relatively small, variations can trigger the threshold mechanism described above. As a result, the population will be adapted to the subsequent changes in advance.
Our results show that evolution can proceed rapidly because it reduces the number of mutations required for adaptive change.
The primary limitation of our results is that the representation of the evolving genetic network is limited to the network of gene controlling phenotype, represented here by the Boolean strings s. Other model variables represent the coarse-grained activities of genes. One class is the terminal differentiation genes represented by wij, and another are the genes or epigenetic factors controlling the thresholds h and their associated learning rules. A more careful consideration of the relationship of these moieties to observable molecular entities is an important objective of future work. At the mathematical level, the key analytical results were obtained in a simplified context that falls short of a realistic level of pleiotropy and thus of the level of NP-hard complexity exhibited by fully pleotropic forms of our model. We believe that our analytical results can be generalized, which we plan to address in future work.
All data underlying the results are available as part of the article and no additional source data are required.
| Views | Downloads | |
|---|---|---|
| F1000Research | - | - |
|
PubMed Central
Data from PMC are received and updated monthly.
|
- | - |
Competing Interests: No competing interests were disclosed.
Reviewer Expertise: Theoretical evolutionary biology
Competing Interests: No competing interests were disclosed.
Is the work clearly and accurately presented and does it cite the current literature?
Partly
Is the study design appropriate and is the work technically sound?
Yes
Are sufficient details of methods and analysis provided to allow replication by others?
Yes
If applicable, is the statistical analysis and its interpretation appropriate?
Not applicable
Are all the source data underlying the results available to ensure full reproducibility?
No source data required
Are the conclusions drawn adequately supported by the results?
Partly
References
1. Hinton GE, Nowlan SJ: How Learning Can Guide Evolution. Complex Systems. 1987; 1.Competing Interests: No competing interests were disclosed.
Reviewer Expertise: Theoretical/Mathematical Systems and Evolutionary Biology.
Is the work clearly and accurately presented and does it cite the current literature?
Yes
Is the study design appropriate and is the work technically sound?
Partly
Are sufficient details of methods and analysis provided to allow replication by others?
Partly
If applicable, is the statistical analysis and its interpretation appropriate?
Not applicable
Are all the source data underlying the results available to ensure full reproducibility?
No source data required
Are the conclusions drawn adequately supported by the results?
Partly
References
1. Jiang P, Kreitman M, Reinitz J: The relationship between robustness and evolution. bioRxiv. 2018. Publisher Full TextCompeting Interests: No competing interests were disclosed.
Reviewer Expertise: Theoretical evolutionary biology
Alongside their report, reviewers assign a status to the article:
| Invited Reviewers | ||
|---|---|---|
| 1 | 2 | |
|
Version 2 (revision) 13 Sep 19 |
read | read |
|
Version 1 01 Apr 19 |
read | read |
Provide sufficient details of any financial or non-financial competing interests to enable users to assess whether your comments might lead a reasonable person to question your impartiality. Consider the following examples, but note that this is not an exhaustive list:
Sign up for content alerts and receive a weekly or monthly email with all newly published articles
Already registered? Sign in
The email address should be the one you originally registered with F1000.
You registered with F1000 via Google, so we cannot reset your password.
To sign in, please click here.
If you still need help with your Google account password, please click here.
You registered with F1000 via Facebook, so we cannot reset your password.
To sign in, please click here.
If you still need help with your Facebook account password, please click here.
If your email address is registered with us, we will email you instructions to reset your password.
If you think you should have received this email but it has not arrived, please check your spam filters and/or contact for further assistance.
Comments on this article Comments (0)