Keywords
machine learning, unsupervised machine learning, supervised machine learning, clustering, clinical informatics, mixed data, mixed-type data, clinical data
This article is included in the RPackage gateway.
This article is included in the Artificial Intelligence and Machine Learning gateway.
machine learning, unsupervised machine learning, supervised machine learning, clustering, clinical informatics, mixed data, mixed-type data, clinical data
In response to the comments from Reviewer 1, we:
1. Added a sentence to the abstract to clarify the meaning of "mixed type data".
2. Expanded the captions on Figures 2, 3, and 4 in order to make them easier to understand.
3. Added several paragraphs to the "Implementation" section to highlight the use of S4 classes in our R package.
See the authors' detailed response to the review by Julia Wrobel
As large clinical databases expand and data mining of the electronic medical record (EMR) improves, the scale and potential of data available for clinical knowledge discovery is increasing dramatically. Expanding size and complexity of data demands new analytics approaches and paves the way for applications of machine learning (ML) in novel clinical contexts1,2. However, clinical data are characterized by heterogeneity, including measurement and data collection noise, individual biological variation, variable data set size, and mixed data types, which raises new challenges for ML analyses1. Clinical data sets vary widely in scale, from early-stage clinical trials with fewer than 100 patients to prospective cohorts following 10,000 patients to large-scale mining of electronic health records. They consist of data collected in the clinical setting, including demographic information, laboratory values, results of physical exams, disease and symptom histories, dates of visits or hospital length-of-stay, pharmacologic medications and dosing, and procedures performed, possibly with associated ICD-9 or -10 codes. The most salient, identifying feature of clinical data is that it is of mixed-type, containing continuous, categorical, and binary data. The result of this heterogeneity is an ML milieu characterized by methodological experimentation, without consensus best methods to apply to challenging clinical data3.
Developing and evaluating best practice methodologies for ML on clinical data demands a known validation standard for comparison. Previously, we described an approach using “biological validation”: testing an ML methodology in a disease with well-understood relationships between patient features and outcomes. Thus, we allow known biological truths uncovered (or absent) in a solution to validate a method3. However, biological validation fails to capture interaction effects or allow the validation of emergent discoveries. By far, a superior solution would be to validate novel methods on data with known “ground truth.” Artificial clinical data, simulated with known assignments, can serve to rigorously test and validate ML algorithms.
Simulating realistic clinical data poses challenges. The wide range in feature spaces and sample sizes demands simulation solutions that vary by orders of magnitude. Rather than simulating data of a single type, simulated clinical data must be of mixed-type and must reflect the variable mixtures of types found in clinical scenarios, where one type may predominate over others4–6. In addition, in order to conclusively test algorithms for use in clinical contexts, simulations of clinical data must replicate the noisiness of these data that results from variation of human and technological features in measurement and the biological variation between individuals.
A real need exists for noisy, realistic, clinically meaningful simulated data to advance ML in clinical contexts. The user finds few tools currently available, and those pose problematic restrictions. For example, the KAMILA (k-means for mixed large data) R package can be used to generate complex mixed-type clusters with a high degree of user specificity, but can only be used to generate two clusters7. Because many important problems face the analyst beyond distinguishing two groups in data, the need presents itself in the literature for more comprehensive, mixed-type simulation tools.
Here, we present Umpire 2.0, a tool that facilitates generation of complex, noisy, simulated clinical and mixed-type data sets. Umpire 2.0 provides broad functionality across sample sizes, feature spaces, and data types to allow the user to simulate correlated, heterogeneous binary, continuous, categorical, or mixed type data from the scale of a small clinical trial to data on thousands of patients drawn from the EMR. These realistic clinical simulations are vital for testing and developing superior ML techniques for new clinical data challenges.
The original Umpire R package (1.0) could be used to simulate complex, correlated, continuous gene expression data with known subgroup identities and both dichotomous and survival outcomes, as previously described8. Two core ideas underlie Umpire. First, biological data are correlated in blocks of variable size, simulating the functioning of genes, tissues, or symptoms in biological networks and pathways. Second, motivated by the multi-hit theory of cancer, subgroups (or clusters) of patients are defined by a number of informative, latent variables called “hits”. Each patient receives a combination of multiple “hits,” simulating population heterogeneity. These latent hits are used to link simulated alterations in patient data to outcome data in the form of dichotomous outcomes and time-to-event data.
Umpire 2.0 expands the Umpire simulation engine for clinical and mixed-type data through a flexible pipeline. Users can vary the characteristics and the number of subgroups, features, hits, and correlated blocks. Using Umpire, they can control the level of patient-to-patient heterogeneity in various configurations of mixed-type data. Users can also generate multiple data sets (for example, training and test) of unlimited sizes from the same underlying distributional models.
Umpire 2.0 enables users to incorporate individual and population heterogeneity in multiple ways. First, as above, latent hits are used to simulate features in correlated blocks, using multivariate normal distributions, with variation between individual members of a subgroup. Second, users can simulate clusters of equal or unequal size. Third, users can apply additive noise modeling measurement error and individual biological variation to simulations.
Because we know that clusters of equal size are unrealistic (outside of pre-defined case-control studies), we enable users to simulate clusters of equal or unequal sizes. In the equal case, we set the population proportions equal and sample data using a multinomial distribution. In the unequal case, we first sample a vector, r ∼ Dirichlet(α1, . . . , αk), setting the expected proportions of k clusters from the Dirichlet distribution. For small numbers of clusters (k ≤ 8), we set all α = 10. For more clusters (k > 8), we set one quarter each of the α parameters to 1, 2, 4, and 8, respectively, accepting only a vector of cluster sizes r in which every cluster contains at least 1% of patients.
The initial data simulated by Umpire represents the true, unadulterated biological signal. To these data, Umpire can add noise, mimicking biological variation and experimental random error. Marlin and colleagues9 argue that all clinical data “must be treated as fundamentally uncertain” due to human error in measurement and manual recording, variability in sampling frequencies, and variation within automatic monitoring equipment. Clinical experience teaches us that variability in clinical data arises from many sources, including human error, measurement error, and individual biological variation. However, because clinical measurements are integral to the provision of patient care, demanding high accuracy and reliability, we also assume that many clinical variables have low measurement error, such as tightly calibrated laboratory tests. For a given feature f measured on patient i, we model the clinically observed value Y from additive measurement noise E applied to the true biological signal S as
We model the additive noise following the normal distribution E ∼ N(0, τ) with mean 0 and standard deviation τ, where τ follows the gamma distribution τ ∼ Γ (c, b) such that bc = 0.05. Thus, we create a distribution in which most features have very low noise while some are subject to very high noisiness.
Umpire 2.0 generates binary and categorical data by discretizing raw, continuous features along meaningful cutoffs. To convert a continuous feature into a binary vector, we select a cutoff and assign values on one side of this demarcation to “zero” and the others to “one.” We begin by calculating a “bimodality index” (BI) for the continuous vector10. To compute the bimodality index, we model the data as a mixture of two normal distributions, and take:
Here π is the fraction of members in one population and δ = (µ1 − µ2)/σ is the standardized distance between the two means. The recommended cutoff of 1.1 to define bimodality was determined by simulation10. If the continuous data are bimodal, we split them midway between the means. For continuous features without a bimodal distribution, we partition them to binary features by randomly selecting an arbitrary cutoff between 5% to 35%. Although arbitrariness feels uncomfortable in an informatics sphere, we believe that this approach reflects a fundamental arbitrariness in many clinical definitions. For example, an adult female with a hemoglobin of 12.0 is said to be anemic, even though the clinical presentation and symptoms of a woman with a hemoglobin of 11.9 probably do not differ from those of a woman with a hemoglobin of 12.1. The choice of an arbitrary cutoff reflects these clinical decision-making processes: along a spectrum of phenotype, a value is chosen based on experience to define the edge of the syndrome. By choosing an arbitrary cutoff, we replicate this process. To reduce bias that could result if all low values were assigned “0” and all larger values were assigned “1,” we randomly choose whether values above or below the cutoff are assigned 0. We mark binary features in which 10% or fewer values fall into one category as asymmetric and mark the remainder as symmetric binary features.
To simulate a categorical feature, we rank a continuous feature from low to high and bin its components into categories, which we label numerically (i.e., 1, 2, 3, 4, 5). Distributing an equal number of observations into each bin does not reflect the realities we see in clinical data, and dividing a continuous feature by values (e.g., dividing a feature of 500 observations between 1 and 100 into units of 1–10, 11–20, etc.) could lead to overly disparate distributions of observations into categories, especially at the tails. Here, for c categories, we model a vector of R sizes along the Dirichlet distribution,
such that we create categories of unequal membership without overly sparse tails. To generate an ordinal categorical feature, we bin a continuous feature and number its bins sequentially by value of observations (e.g., 1, 2, 3, 4, 5). To generate a nominal categorical feature, we number these bins in random order (e.g., 4, 2, 5, 1, 3).
The user may choose to simulate continuous, binary, nominal, or ordinal data, or any mixture thereof.
Umpire 2.0 has been implemented as a package for R 3.6.3 and R 4.0. It is freely available on RForge and CRAN. Any system (Linux, Windows, MacOS) capable of running R 3.6.3 or R 4.0 is sufficient for implementing Umpire.
Umpire 2.0 provides a 4-part workflow to generate simulations and save parameters for downstream reuse (Figure 1). The original Umpire 1.0 functionality and the Umpire 2.0 extension are arranged as a series of interchangeable modules (e.g., Engines, NoiseModels) within a parallel workflow. For a more thorough, guided introduction to the Umpire functions, please see the package vignettes. For clinical simulations, the user begins by generating a ClinicalEngine, consisting of a correlated block structure to generate population heterogeneity, a model of subgroup membership, and a survival model, which is used to generate a raw (continuous, not-noisy) data set. Next, clinically representative noise is applied. The user discretizes these data to mixed-type. Finally, Engine parameters, the ClinicalNoiseModel, and mixed data definitions are stored in a MixedTypeEngine to easily generate downstream simulations from the same parameter set.
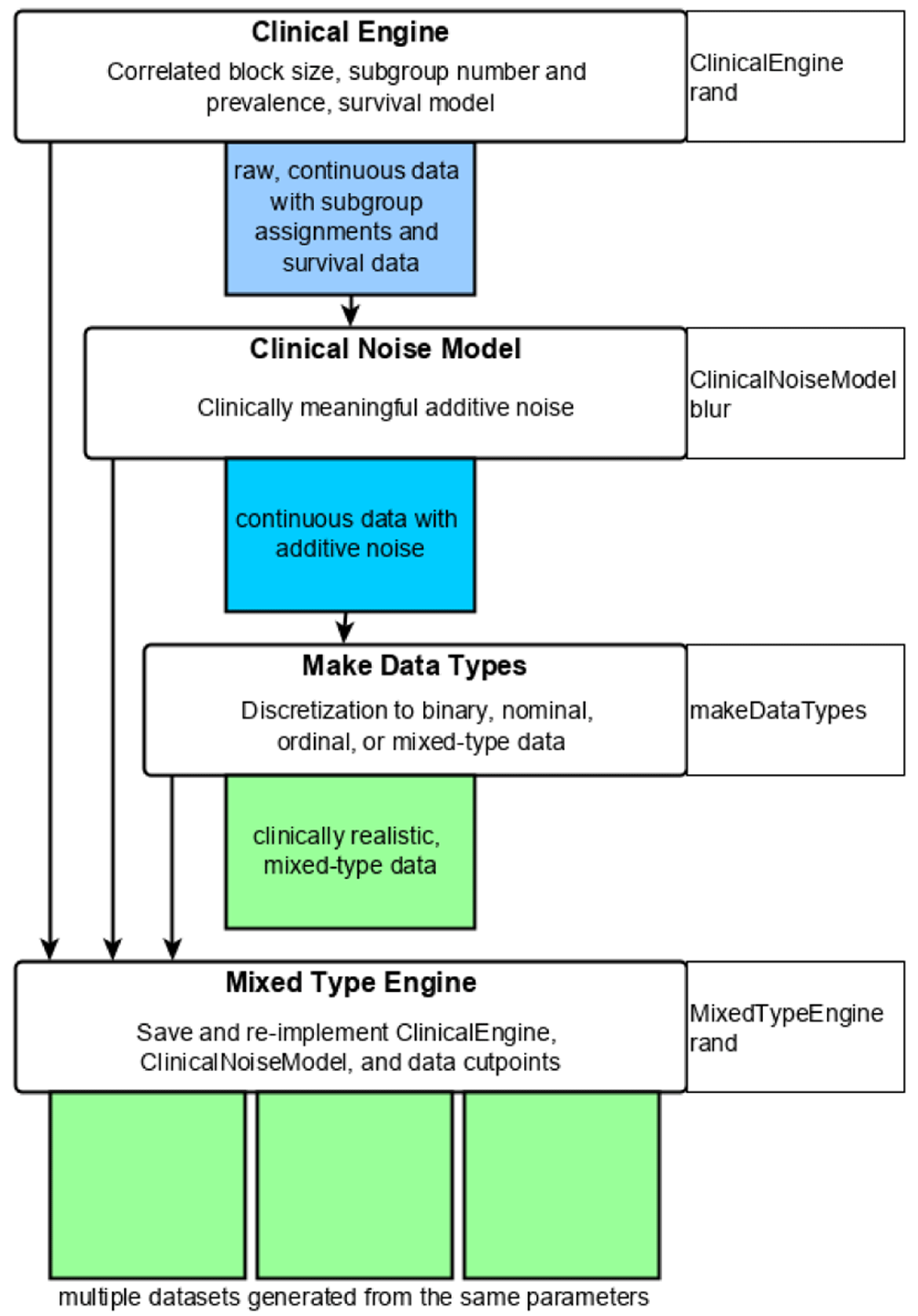
The user begins by generating a ClinicalEngine to define correlated block structure, latent hits, subgroup prevalences, and a survival model. This is used to generate a raw, continuous data set. The user generates a clinically meaningful ClinicalNoiseModel, and applies it to the raw data. Next, the data are discretized to mixed type. Finally, the parameters of the ClinicalEngine, the ClinicalNoiseModel, and the discretized cutpoints are stored in a MixedTypeEngine to generate future simulations with the same parameters.
The Umpire package makes extensive use of the S4 object-oriented capabilities in R. The core class is an “Engine”. In statistical terms, an Engine is an abstract representation of a random vector generator, implemented as a list of “components”. The package includes three classes that can be used as components: “IndependentNormal”, “IndependentLogNormal”, and “MVN” (for multivariate normal distributions). Both the Engine and each of its components must support three newly defined methods. First, the “rand” method generates a random vector. Next, the “alterMean” and “alterSD” methods must change the corresponding statistical properties in order to represent systematic differences, for example, between different subtypes of samples. Users can extend the capabilities of the Umpire package by designing their own classes that can respond to these three methods.
At a higher level, the “CancerEngine” contains two engines, one representing expression in normal samples, and the other in cancer samples. It unites these engines with a nested pair of classes. First, the “SurvivalModel” implements an underlying exponential distribution for survival curves. Second, the “CancerModel” combines the SurvivalModel with a vector of parameters that represent latent factors modifying the hazard ratio. It also includes a vector describing how the same factors will modify a binary outcome through a logistic model. In version 1.0 of Umpire, the data simulated by a CancerModel represented “perfect” data, with variability attributable solely to biological differences between samples. An additional class, the “NoiseModel” was used to represent additional sources of variation arising from measurement errors.
Version 2.0 of Umpire extended these S4 classes in two ways. First, we added a “ClinicalEngine” function. Note that there is no corresponding class with this name. The new function actually creates a “CancerEngine”, with a new set of default parameters selected to provide a better representation of clinical data instead of gene expression data. The main goal here was ease-of-use for people who wanted to produce useful simulations without diving as deeply into the underlying structure. The second extension did involve the creation of a new class, the “MixedTypeEngine”. The MixedTypeEngine is derived from a CancerEngine using the core objectoriented principle of inheritance. It has all the properties and behaviors of a CancerEngine. but adds additional features. Specifically, it includes its own NoiseModel, with parameters chosen from a Gamma distribution to represent the more highly variable noise structures one would expect in clinical data. The MixedTypeEngine also includes a set of “cut points” used to convert continuous data into categorical or dichotomous data types. So, unlike the CancerModel that can only generate “raw” continuous data, the MixedType Engine can also generate “noisy” continuous data along with data that has been “binned” after discretization of some components. These new features are illustrated in the use cases below.
In this section, we present several examples explaining how Umpire can be used to simulate data relevant to important clinical questions.
Unsupervised machine learning algorithms, designed to discover the subtypes inherent in a given data set, form one of the major branches in the field. In the clinical literature, these algorithms are being applied to data with variable feature sizes, including some studies with fewer than 10 features4,11. The number of subtypes (or clusters) identified in the literature also spans a fairly wide range4,5,12,13. At present, however, there is no consensus on which unsupervised ML algorithms are most effective, nor is it clear if different algorithms work better for different numbers of patients, clusters, features, or mixtures of data types.
Since one idea at the core of Umpire is that cohorts of patients tend to be heterogeneous, it is perfectly positioned to perform simulations to evaluate unsupervised ML algorithms in the clinical context. As an illustration, we start by construcing a ClinicalEngine with four subtypes of patients.
> library(Umpire) > set.seed(36475) > numFeat <- 100 > ce0 <- ClinicalEngine(nFeatures = numFeat, # clinical variables. + nClusters = 4, # subtypes, + isWeighted = FALSE) # about the same size.
Internally, the ClinicalEngine simulates latent variables that affect both the expression of the clinical covariates and the outcomes in each of the four patient clusters. You can visualize which latent variables affect which clusters by extracting the “hit pattern” nested inside the ClinicalEngine (Figure 2).
> library(Polychrome) > dk <- alphabet.colors(26)[c("red", "navy", "forest", "amethyst", + "turquoise", "sea", "wine")]
> res <- 300 > png(filename = "heatpattern.png", width=6*res, height= 6*res, res=res, + bg="white") > heatmap(ce0@cm@hitPattern, scale="none", ColSideColors = dk[1:4], + col = c("gray", "black")) > dev.off()

Black pixels mark the presence of latent variables, or hits, within a cluster. The top dendrogram shows the true relationships between clusters, which are driven by the presence of shared latent variables. The left dendrogram shows the relationships between hits, which are based on their co-occurrence within clusters.
Note that this heatmap shows the true underlying structure relating the clusters to the latent variables, and not any simulated data sets. By design, however, the ClinicalEngine can only simulate “perfect” continuous data reflecting the true signal. In order to simulate realistic mixed-type data, we must first add noise to these data, and then discretize some of the features to create binary or nominal features.
Data collected in the clinic includes many different kinds of values. Demographic values include a small number of nominal demographic values (e.g., ethnicity, marital status) with four to five categories. Physical exam values include binary indicators (such as presence or absence of enlarged liver). Most of the values assessed on patients are continuous, such as heart rate, blood pressure, and laboratory values. We assume that most of these values have low error. For example, clinical laboratory values are tightly calibrated. However, some measurements, such as physical exam values, were assessed by chart review from the medical record. Others, such as blood pressure, were measured by hand and typed into the record at the time of the visit. Thus, a few values may be very prone to measurement and human error. Here we apply a ClinicalNoiseModel to our features that reflects our beliefs about the noisiness of our data, with the standard deviation following a gamma distribution defined by shape and scale parameters. Then, we construct a MixedTypeEngine.
> cnm <- ClinicalNoiseModel(numFeat, shape = 1.02, scale = 0.05) > mte <- MixedTypeEngine(ce0, # a clinical engine + cnm, # a noise model + cutpoints = list(N = 200, + pCont = 0.6, + pBin = 0.2, + pCat = 0.2, + pNominal = 1, + range = c(4,5))) > rm(cnm) > summary(mte)
A ’MixedTypeEngine’ (MTE) based on:
A ’CancerEngine’ using the cancer model:
--------------
Clinical Simulation Model (Raw), a CancerModel object constructed via:
CancerModel(name = "Clinical Simulation Model (Raw)", nPossible = NP,
nPattern = nClusters, HIT = hitfn, SURV = SURV, OUT = OUT,
survivalModel = survivalModel, prevalence = Prevalence(isWeighted,
nClusters))
Pattern prevalences:
[1] 0.2206505 0.2998339 0.2343084 0.2452072
Survival effects:
Min. 1st Qu. Median Mean 3rd Qu. Max.
-0.43931 -0.12208 0.08784 0.08932 0.32549 0.51441
Outcome effects:
Min. 1st Qu. Median Mean 3rd Qu. Max.
-0.46565 -0.16604 -0.03749 -0.03927 0.13257 0.40766
--------------
Base expression given by:
An Engine with 33 components.
Altered expression given by:
An Engine with 33 components.
---------------
The MTE uses the following noise model:
A ’NoiseModel’ with:
additive offset = 0
additive scale distributed as:
Min. 1st Qu. Median Mean 3rd Qu. Max.
0.001204 0.015000 0.041432 0.051332 0.069693 0.249882
multiplicative scale = 0
---------------
The MTE simulates clinical data of these types:
asymmetric binary continuous nominal symmetric binary
1 60 23 15Note that the cm slot of the clinical engine is retained as a slot in the mixed-type engine, so the heatmap shown above can be recreated with the command
> # Not run > heatmap(mte@cm@hitPattern, scale="none", ColSideColors = dk[1:4], + col = c("gray", "black"))
At this point, we still haven’t simulated any actual data. For that purpose, we use the rand method.
> mtData <- rand(mte, 500, keepall = TRUE)
We now take a look inside the simulated data
> names(mtData)
[1] "raw" "clinical" "noisy" "binned"> sapply(mtData, dim) raw clinical noisy binned [1,] 99 500 99 500 [2,] 500 4 500 99
> summary(mtData$clinical) CancerSubType Outcome LFU Event Min. :1.00 Bad :234 Min. : 0.00 Mode :logical 1st Qu.:2.00 Good:266 1st Qu.: 7.00 FALSE:136 Median :3.00 Median :16.00 TRUE :364 Mean :2.56 Mean :19.79 3rd Qu.:4.00 3rd Qu.:29.00 Max. :4.00 Max. :71.00
There are four components:
1. “clinical” contains the subtype, a binary outcome, and a time-to-event outcome represented by the last follow up time (LFU) and a logical indicator of whether the event occurred.
2. “raw” contains the continuous data simulated by the clinical engine.
3. “noisy” contains the same data, with noise added.
4. “binned” contains the mixed type data, after discretization of some features.
Note that using keepall = FALSE will not preserve the raw or noisy components. Also, the raw and noisy components are arranged in the “omics” style, where rows are features and columns are patients. By contrast, the binned component is transposed into the usual clinical style, where rows are patients and columns are features.
As an illustration, we visualize clusters for the noisy, continuous data compared to the discretized, mixed-type data. We use the daisy function from the cluster R package to compute distances between mixed-type data, and we use the Rtsne package for visualization (Figure 3).
> myClustColor <- dk[mtData$clinical$CancerSubType] > library(cluster) > dtypes <- getDaisyTypes(mte) > dai <- daisy(mtData$binned, type = dtypes) > dai <- as.dist(dai) > library(Rtsne) > tsN <- Rtsne(t(mtData$noisy)) # transpose from omics-style to clinical-style > tsM <- Rtsne(dai, is_distance=TRUE)
> png(filename = "daisy.png", width=10*res, height=5*res, res=res, bg="white") > opar <- par(mfrow=c(1,2)) > plot(tsN$Y, pch=19, col = myClustColor, main="Noisy, Continuous Data") > plot(tsM$Y, pch=19, col = myClustColor, main="Mixed-Type Data") > par(opar) > dev.off()
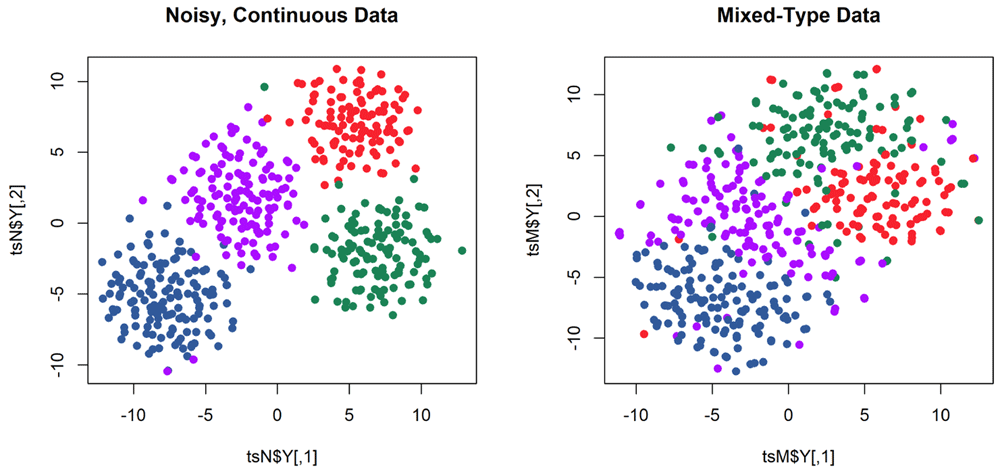
Colors are the same as in Figure 2, and indicate the true cluster membership created by the simulation.
Based on the literature results referenced above, we constructed simulation parameters to represent common problems in clinical data (Table 1). These included a range of feature sizes (9–243), patient sizes (200– 3200), and number of clusters (2–16). In essence, this simulation was equivalent to evaluating a set of nested for-loops:
> # Not Run > for (F in featureSize) { + cnm <- ClinicalNoiseModel(F, shape = 1.02, scale = 0.05) + for (K in clusterSize) { + for (P in patientSize) { + mte <- MixedTypeEngine(list(nFeatures = F, # num features + nClusters = K, # num clusters + isWeighted = TRUE), + cnm, + cutpoints = list(N = 200, + pCont = 0.6, + pBin = 0.2, + pCat = 0.2, + pNominal = 0.5)) + simdata <- rand(mte, P, keepall = TRUE) # num patients + save(simdata, file = SOMEFILENAME) # for evaluation later + } + } + }
Parameters were chosen to reflect data set sizes from a Phase II clinical trial to a large EHR data set or cohort.
| Patients | 200, 800, 3200 |
|---|---|
| Features | 9, 27, 81, 243 |
| Clusters | 2, 6, 16 |
| Data types and mixtures | Single data type: continuous, binary, nominal, ordinal, mixed categorical1 Mixtures: balanced, continuous unbalanced, binary unbalanced, categorical unbalanced |
One could also vary other parameters, with the most likely candidates being the “cutpoints” parameters that control the fraction of continuous, binary, or categorical features in the data.
The primary benefit of these simulations for assessing clustering algorithms is that Umpire generates data with known, gold-standard cluster assignments. Using simulation parameters in Table 2, we examined hierarchical clustering (HC) with Euclidean distance, a method commonly found in the literature5,14–16, We compared HC to partitioning around medoids (PAM) and self-organizing maps (SOM)17,18. We also compared Euclidean distance to the mixed-type distance measure, DAISY. We were able to assess accuracy and quality of each clustering solution against a known ground truth using the Adjusted Rand Index (ARI)19. Summarized results are shown in Figure 4.
Three algorithms (hierarchical clustering with Ward’s criterion, Partitioning Around Medoids, and Self-Organizing Maps) were implemented with a single-distance metric (Euclidean distance) and a mixed-type metric and tested on single- and mixedtype simulations generated with Umpire.
| Algorithm | Single-Distance Metric | Mixed-Type Metric |
|---|---|---|
| Hierarchical clustering | Euclidean | DAISY |
| Partitioning Around Medoids (PAM) | Euclidean | DAISY |
| Self-organizing maps (SOM) | Euclidean | Supersom |
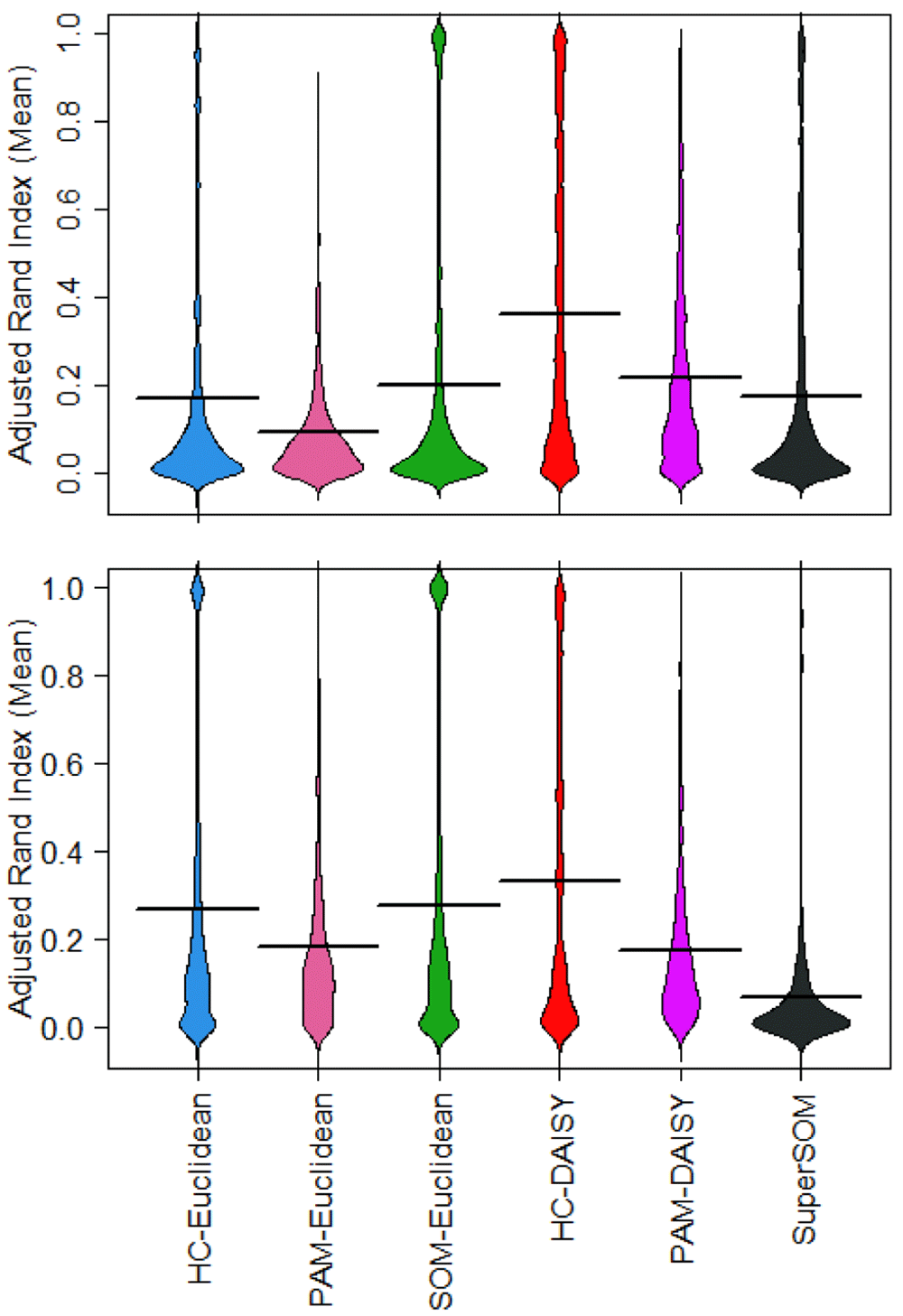
DAISY outperformed all other methods on both balanced (top) and unbalanced continuous (bottom) data mixtures. Algorithm performance varied between data mixtures, with improved performance of hierarchical clustering (HC) and self-organizing maps (SOM) with Euclidean distance on unbalanced continuous data.
Time to response or adverse event is a core clinical question in clinical trials of pharmaceutical and device interventions. Here, we use Umpire to simulate time-to-event data for clinical trials to inform study design or methods development.
We begin by customizing a SurvivalModel, which in this case will simulate a trial with 5 years of patient accrual and 1 year of follow up. The user may customize length and units of follow up, as well as the base hazard rate. (Internally, Umpire uses this hazard rate in an exponential survival function.)
> library(Umpire) > set.seed(83552) # for reproducibility > sm <- SurvivalModel(baseHazard = 1/5, + accrual = 5, + followUp = 1, + units = 12, + unitName = "months")
Here, we illustrate the impact of altering the base hazard on the simulated mortality rate. We simulate three different survival models, using the default values for accrual and follow up (Figure 5).
> library(survival) > set.seed(12345) > sm3 <- SurvivalModel(baseHazard = 1/3) > dat3 <- rand(sm3, 200) > sm5 <- SurvivalModel(baseHazard = 1/5) > dat5 <- rand(sm5, 200) > sm8 <- SurvivalModel(baseHazard = 1/5) > dat8 <- rand(sm8, 200)
> png(filename = "hazards.png", width=10*res, height=4*res, res= res, bg="white") > opar <- par(pty="s", mfrow=c(1,3)) > plot(survfit(Surv(LFU, Event) ~ 1, data=dat8), + main="Base Hazard = 1/8") > plot(survfit(Surv(LFU, Event) ~ 1, data=dat5), + main="Base Hazard = 1/5") > plot(survfit(Surv(LFU, Event) ~ 1, data=dat3), + main="Base Hazard = 1/3") > par(opar) > dev.off()
The survival model is an argument to the constructor for a ClinicalEngine; if omitted, a default survival model is used. Here we explicitly use our survival model to construct a clinical engine with four balanced subtypes.
> set.seed(64321) > ce <- ClinicalEngine(nFeatures = 40, # clinical variables. + nClusters = 4, # subtypes, + isWeighted = FALSE, # designed to be the same size. + survivalModel = sm) # outcomes.
Because the latent variables affect the survival outcomes (by changing the hazard ratio) in the four patient clusters, you can generate different clinical engines from the same underlying parameters and obtain cohorts with different survival patterns (Figure 6). Note that we create different clinical engines to select different latent variables and create different populations. Using the rand function multiple times with the same engine would generate different samples from the same population, which would be useful for creating separate training and test data sets.
> set.seed(11111) > ce1 <- ClinicalEngine(nFeatures = 40, nClusters = 4, isWeighted = FALSE, + survivalModel = sm) > cdat1 <- rand(ce1, 100) > > ce2 <- ClinicalEngine(nFeatures = 40, nClusters = 4, isWeighted = FALSE, + survivalModel = sm) > cdat2 <- rand(ce2, 100) > > ce3 <- ClinicalEngine(nFeatures = 40, nClusters = 4, isWeighted = FALSE, + survivalModel = sm) > cdat3 <- rand(ce3, 100)
> png(filename = "varce.png", height=4*res, width=10*res, res=res, bg="white") > opar <- par(pty="s", mfrow=c(1,3)) > plot(survfit(Surv(LFU, Event) ~ CancerSubType, data=cdat1$clinical), + main="Simulation 1", col = dk, lwd = 2) > plot(survfit(Surv(LFU, Event) ~ CancerSubType, data=cdat2$clinical), + main="Simulation 2", col = dk, lwd=2) > plot(survfit(Surv(LFU, Event) ~ CancerSubType, data=cdat3$clinical), + main="Simulation 3", col = dk, lwd = 2) > par(opar) > dev.off()
It is important to realize that the subtypes generated as part of a clinical engine or a mixed-type engine are unlikely to represent the arms of an actual clinical trial. They are, after all, based on patterns of latent variables that, by definition, would be unobserved by the team running the clinical trial. One might want to view the simulations as a single-arm trial, where different unknown subgroups of patients respond to the therapy differently, and the goal is to use the covariate to identify a subset of patients who respond. In that case, the ability of Umpire to generate another data set from the same mixed-type engine could be used to provide independent validation of the method.
A sensible approach might be to simulate a two-arm clinical trial where one arm receives a placebo (or the current standard-of-care), while the second arm receives a new (or additional) therapy. Again, one possible goal is to identify the subset of patients in the experimental arm with better response. We can achieve this in Umpire by adding a control group.
> cec <- addControl(ce) > summary(cec)
A ’CancerEngine’ using the cancer model:
--------------
Clinical Simulation Model (Raw) plus control, a CancerModel object constructed via:
CancerModel(name = "Clinical Simulation Model (Raw)", nPossible = NP,
nPattern = nClusters, HIT = hitfn, SURV = SURV, OUT = OUT,
survivalModel = survivalModel, prevalence = Prevalence(isWeighted,
nClusters))
Pattern prevalences:
[1] 0.5000000 0.1197993 0.1096268 0.1340680 0.1365059
Survival effects:
Min. 1st Qu. Median Mean 3rd Qu. Max.
-0.13793 -0.03038 0.03760 0.07660 0.18176 0.50587
Outcome effects:
Min. 1st Qu. Median Mean 3rd Qu. Max.
-0.284222 -0.228845 -0.040243 0.001858 0.129494 0.616201
--------------
Base expression given by:
An Engine with 40 components.
Altered expression given by:
An Engine with 40 components.The control arm is now subtype 1, and the experimental arm is given by the collection of all other (heterogeneous) subtypes.
We note here that one of the default parameters to the CancerModel constructor that is used inside a clinical engine defines the distribution of the beta-parameters in a Cox proportional hazards model. By default, these are chosen from a normal distribution with mean 0 and standard deviation 0.3. As a consequence, each latent variable is just as likely to make the hazard ratio worse rather than better. For purposes of illustration, we are going to cheat and adjust the beta parameters to bias them toward an improved outcome in the experimental group:
> beta <- cec@cm@survivalBeta > if (sum(beta) > 0) cec@cm@survivalBeta <- -beta
Of course, the better way to accomplish this goal would have been to set that parameter when we constructed the ClinicalEngine orginally, to something like SURV = function(n) rnorm(n, 0.2, 0.3).
Here is an example of a simulated trial.
> cnm <- ClinicalNoiseModel(40, shape = 1.02, scale = 0.05) > mte <- MixedTypeEngine(cec, + cnm, + cutpoints = list(N = 200, + pCont = 0.6, + pBin = 0.2, + pCat = 0.2, + pNominal = 1, + range = c(4,5))) > trialData <- rand(mte, 200) > # make a factor for trial arm > isExp <- 1 + 1*(trialData$clinical$CancerSubType > 1) > trialData$clinical$Arm <- factor(c("Control", "Experimental")[isExp]) > summary(trialData$clinical)
CancerSubType Outcome LFU Event Arm
Min. :1.00 Bad :101 Min. : 0.00 Mode :logical Control :104
1st Qu.:1.00 Good: 99 1st Qu.:14.00 FALSE:101 Experimental: 96
Median :1.00 Median :23.00 TRUE :99
Mean :2.25 Mean :27.53
3rd Qu.:4.00 3rd Qu.:40.25
Max. :5.00 Max. :70.00Now we compute the Cox proportional hazards model that we would see from the two-arm trial.
> fit <- coxph(Surv(LFU, Event) ~ Arm, data = trialData$clinical) > summary(fit)
Call:
coxph(formula = Surv(LFU, Event) ~ Arm, data = trialData$clinical)
n= 200, number of events= 99
coef exp(coef) se(coef) z Pr(>|z|)
ArmExperimental -0.5974 0.5502 0.2075 -2.879 0.00399 **
---
Signif. codes: 0 ’***’ 0.001 ’**’ 0.01 ’*’ 0.05 ’.’ 0.1 ’ ’ 1
exp(coef) exp(-coef) lower .95 upper .95
ArmExperimental 0.5502 1.817 0.3664 0.8264
Concordance= 0.57 (se = 0.027 )
Likelihood ratio test= 8.56 on 1 df, p=0.003
Wald test = 8.29 on 1 df, p=0.004
Score (logrank) test = 8.53 on 1 df, p=0.003Thanks in part to the bias we built into the simulation, the experimental group does significantly better than the control group. We can also fit the model that would be obtained if the trial designers were omniscient and could see the subtypes defined by the latent variables.
> latentfit <- coxph(Surv(LFU, Event) ~ factor(CancerSubType), + data = trialData$clinical) > latentfit
Call:
coxph(formula = Surv(LFU, Event) ~ factor(CancerSubType), data = trialData$clinical)
coef exp(coef) se(coef) z p
factor(CancerSubType)2 0.08847 1.09250 0.30651 0.289 0.7729
factor(CancerSubType)3 -0.62841 0.53344 0.37710 -1.666 0.0956
factor(CancerSubType)4 -0.91522 0.40043 0.35797 -2.557 0.0106
factor(CancerSubType)5 -0.90929 0.40281 0.37737 -2.410 0.0160
Likelihood ratio test=15.31 on 4 df, p=0.004102
n= 200, number of events= 99
Here we see that one of the four subtypes is equivalent to the control group, while all three other subtypes appear to do better. Finally, we plot the resulting Kaplan-Meirer curves for both models (Figure 7).
> png(filename = "fitplots.png", width=10*res, height=5*res, res=res,bg="white") > opar <- par(mfrow =c(1,2)) > plot(survfit(Surv(LFU, Event) ~ Arm, data = trialData$clinical), + col=dk[c(1, 6)], lwd=2) > legend("bottomleft", levels(trialData$clinical$Arm), lwd=2, col = dk[c(1, 6)]) > > plot(survfit(Surv(LFU, Event) ~ factor(CancerSubType), data = trialData$clinical), + col =dk, lwd=2) > legend("bottomleft", legend = 1:5, lwd=2, col = dk) > par(opar) > dev.off()

As in the first use case, you can run a set of nested loops to vary the parameters of interest. As noted previously, one possible application would be to test algorithms for finding clinical variables that define patient subgroups with better (or worse) responses than the control group.
Large epidemiological cohorts are a foundational data type in public health research. Here, we simulate an extensive patient cohort and assess for a binary outcome.
Epidemiological cohorts may aggregate data from multiple data collection instruments, possibly including chart review, laboratory data, and survey. Here, we generate mixed type data consisting of continuous laboratory data gathered at time of study entry and an extensive survey, which contains both nominal and ordinal (Likert scale) categorical responses. We simulate a ClinicalEngine with a large feature space and 6 latent clusters of unequal size, taking the default noise and survival models. We generate data for 4,000 patients.
> set.seed(1000) > ce <- ClinicalEngine(nFeatures = 300, + nClusters = 6, + isWeighted = TRUE, + OUT = function(n) rnorm(n, -0.1, 0.3)) # bias favorable > cnm <- ClinicalNoiseModel(300) > mixed <- MixedTypeEngine(ce, cnm, + list(N=200, pCont = .3, pCat = .7, pBin=0, + pNominal = .5, range = c(3,7))) > table(getDataTypes(mixed))
continuous nominal ordinal 77 97 123 > simdata <- rand(mixed, 4000) > sapply(simdata, dim) binned clinical [1,] 4000 4000 [2,] 297 4 > summary(simdata$clinical) CancerSubType Outcome LFU Event Min. :1.000 Bad :1233 Min. : 0.00 Mode :logical 1st Qu.:2.000 Good:2767 1st Qu.:14.00 FALSE:2095 Median :4.000 Median :25.00 TRUE :1905 Mean :3.762 Mean :28.31 3rd Qu.:5.000 3rd Qu.:42.00 Max. :6.000 Max. :71.00
Now we are going to fit univariate models to determine which features are associated with the binary outcome. For continuous variables, we perform a t-test comparing the values in the two outcome groups. For discrete variables (binary or categorical), we perform a chi-squared test.
> DT <- getDataTypes(mixed) > results <- data.frame(Test=NA, Statistic = NA, PValue = NA)[-1,] > for (J in 1:ncol(simdata$binned)) { + if (DT[J] == "continuous") { + test <- t.test(simdata$binned[simdata$clinical$Outcome == "Bad", J], + simdata$binned[simdata$clinical$Outcome == "Good", J]) + results <- rbind(results, + data.frame(Test = "T", + Statistic = test$statistic, + PValue = test$p.value)) + } else { # discrete = binary or categorical + tab <- table(feature = simdata$binned[, J], + outcome = simdata$clinical$Outcome) + test <- chisq.test(tab) + results <- rbind(results, + data.frame(Test = "ChiSq", + Statistic = test$statistic, + PValue = test$p.value)) + } + } > summary(results)
Test Statistic PValue
Length:297 Min. :-9.300 Min. :0.00000
Class :character 1st Qu.: 1.266 1st Qu.:0.00371
Mode :character Median : 4.960 Median :0.23660
Mean : 9.104 Mean :0.32206
3rd Qu.: 9.924 3rd Qu.:0.58628
Max. :87.610 Max. :0.99882To account for multiple testing, we fit a beta-uniform-mixture (BUM) model to estimate the false discovery rate (FDR)20. We show the results by overlaying the fitted model on a histogram of p-values (Figure 8).
> suppressMessages( library(ClassComparison) ) > bum <- Bum(results$PValue) > png(filename = "fig8-bum.png", width=5*res, height=4*res, res=res, bg="white") > hist(bum) > dev.off()
There is clear evidence of an enrichment of small p-values indicating features that are associated with the clinical outcome in univariate models. We can determine the number of significant features and the nominal p-value cutoff associated with any given FDR.
> countSignificant(bum, alpha = 0.01, by = "FDR") [1] 76 > cutoff <- cutoffSignificant(bum, alpha = 0.01, by = "FDR") > cutoff [1] 0.004186874
We can also count the number of significant “discoveries” associated with each block of correlated genes, but this requires some spelunking into the depths of the mixed-type engine.
> A <- get("altered", mixed@localenv) > N <- nComponents(A) > am <- sapply(A@components, function(x) length(x@mu)) > block <- rep(1:N, times = am) > table(results$PValue < cutoff, block)
block
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24
FALSE 10 11 10 11 8 6 6 6 3 8 11 7 4 9 11 6 2 0 8 7 11 11 11 11
TRUE 1 0 1 0 3 5 5 5 8 3 0 4 7 2 0 5 9 11 3 4 0 0 0 0
block
25 26 27
FALSE 11 11 11
TRUE 0 0 0We can compare this table with a heatmap of the hit pattern (Figure 9). Only 20 of the 27 blocks were included as possible hits, and blocks 2, 4, 11, and 15 were unused. The table shows that none of the identified features were included in any of those blocks, suggesting that we made no false discoveries.
> png(filename = "heatpattern2.png", width=6*res, height=6*res, res=res, bg="white") > heatmap(mixed@cm@hitPattern, scale="none", ColSideColors = dk[1:6], + col = c("gray", "black")) > dev.off()
The Umpire R-package provides a series of tools to simulate complex, correlated, heterogenous data for methods development and testing for omics and clinical data. The Umpire 2.0 package version described here provides an easy, user-friendly pipeline to generate clinically realistic, mixed-type data to interrogate analytic problems in clinical data. Alongside data sets with meaningful noise and complex feature interrelationships, Umpire simulates subgroup or cluster identities with known ground truth and single- and multi-group dichotomous and survival outcomes. Thus, Umpire facilitates the creation of simulations to explore a variety of methodological problems.
Umpire offers the user a streamlined workflow with ample opportunities for fine-tuning and flexibility. Although this paper describes applications for clinical data, we have previously described Umpire’s tools for simulating omics data8. Furthermore, the modules of the package (e.g., Engines, NoiseModels, and make-DataTypes) may be used interchangeably. Thus, the user may choose to generate omics-scale data of noncontinuous type. The user may generate elaborate simulations by varying and increasing parameters (including, but not limited to, subgroup size or number, feature space, sample size, noise, survival model) to target an inquiry.
In our use cases, we demonstrated the flexibility of Umpire for generating simulations to help evaluate a variety of applications of machine learning to clinical data. These include applications of unsupervised ML to discover subtypes (in Use case 1) and applications of supervised machine learning to find predictive or prognostic factors (in Use cases 2 and 3). The ability of Umpire to evaluate analysis methods is not confined to these use cases. Our use cases illustrating supervised ML did not exploit the fact that, using the parameters saved in a mixed-type engine, Umpire can simulate multiple data sets from the same underlying population, thus providing unlimited test and validation sets. In addition to testing algorithms head-to-head, Umpire can also be used to generate complex simulations to interrogate the “operating characteristics” of an algorithm. For instance, one of the still-unsolved problems in clustering is determining the true number of clusters. A researcher who has developed a new method that claims to solve this problem could simulate mixed-type data with a variety of different cluster numbers, prevalences, feature numbers, and patient sizes to determine which factors influence the accuracy of the method.
We expect Umpire to have wide applicability as a tool for comparing and understanding the behavior of any ML method that has the potential to be applied to clinical data.
All data underlying the results are available as part of the article and no additional source data are required.
Umpire is freely available at the Comprehensive R Archive Network: https://cran.r-project.org/ web/packages/Umpire/index.html.
Source code is available from R-Forge: https://r-forge.r-project.org/R/?group_id=1831.
Archived source code at time of publication: https://cran.r-project.org/web/packages/Umpire/index.html and https://doi.org/10.5281/zenodo.402310621.
License: Apache License, version 2.0.
CEC contributed in conceptualization, formal analysis, methodology, software, validation, visualization, and writing (both original draft preparation and review & editing). ZBA contributed in methodology, software, and writing – reviewing & editing. GB contributed in supervision and writing – reviewing & editing. KRC contributed in conceptualization, formal analysis, methodology, software, supervision, validation, and writing – reviewing and editing. All authors have approved the final version of the manuscript and agree to be accountable for all aspects of the work.
| Views | Downloads | |
|---|---|---|
| F1000Research | - | - |
|
PubMed Central
Data from PMC are received and updated monthly.
|
- | - |
Is the rationale for developing the new software tool clearly explained?
Partly
Is the description of the software tool technically sound?
Yes
Are sufficient details of the code, methods and analysis (if applicable) provided to allow replication of the software development and its use by others?
Partly
Is sufficient information provided to allow interpretation of the expected output datasets and any results generated using the tool?
Yes
Are the conclusions about the tool and its performance adequately supported by the findings presented in the article?
Yes
Competing Interests: No competing interests were disclosed.
Reviewer Expertise: Clinical research informatics, secondary use of electronic health data, electronic phenotyping, machine learning, internal medicine.
Competing Interests: No competing interests were disclosed.
Reviewer Expertise: Biomedical imaging, statistical software development, wearable technology.
Is the rationale for developing the new software tool clearly explained?
Yes
Is the description of the software tool technically sound?
Yes
Are sufficient details of the code, methods and analysis (if applicable) provided to allow replication of the software development and its use by others?
Partly
Is sufficient information provided to allow interpretation of the expected output datasets and any results generated using the tool?
No
Are the conclusions about the tool and its performance adequately supported by the findings presented in the article?
Yes
Competing Interests: No competing interests were disclosed.
Reviewer Expertise: Biomedical imaging, statistical software development, wearable technology.
Alongside their report, reviewers assign a status to the article:
| Invited Reviewers | ||
|---|---|---|
| 1 | 2 | |
|
Version 2 (revision) 05 Mar 21 |
read | read |
|
Version 1 01 Oct 20 |
read | |
Provide sufficient details of any financial or non-financial competing interests to enable users to assess whether your comments might lead a reasonable person to question your impartiality. Consider the following examples, but note that this is not an exhaustive list:
Sign up for content alerts and receive a weekly or monthly email with all newly published articles
Already registered? Sign in
The email address should be the one you originally registered with F1000.
You registered with F1000 via Google, so we cannot reset your password.
To sign in, please click here.
If you still need help with your Google account password, please click here.
You registered with F1000 via Facebook, so we cannot reset your password.
To sign in, please click here.
If you still need help with your Facebook account password, please click here.
If your email address is registered with us, we will email you instructions to reset your password.
If you think you should have received this email but it has not arrived, please check your spam filters and/or contact for further assistance.
Comments on this article Comments (0)