VTES: a stochastic Python-based tool to simulate viral transmission

Introduction

As of the start of this year (2020) a novel coronavirus originating out of Wuhan-China (which became known as severe acute respiratory syndrome coronavirus 2, or SARS-CoV-2), rapidly spread worldwide and became a global pandemic, the magnitude of which had not been seen since the Spanish influenza pandemic a century ago. At the time of writing (09/2020), SARS-CoV-2 has resulted in >27 million cases and >900,000 deaths in 188 countries worldwide¹, with a case-fatality rate of >15% in some areas^1,2.

One key factor of the disease’s devastating impact is how rapidly and pervasively it spreads throughout a population. The factors that influence the spread of infectious diseases are enormously complex, involving numerous variables, which are often initially unknown to researchers. Such variables include the rate of transmission, population density, and the disease mortality rate in a population. Therefore, it is unsurprising that dubious science and confounding arguments has resulted in mixed messages and false claims being made on how to limit the spread of this viral disease³. Misinterpreted science and these misleading reports have generally resulted in mass confusion, and in some cases, resistance to many crucial disease control techniques, such as mask wearing, social distancing, and self-isolation. This has predictably lead to a substantial rise in SARS-CoV-2 cases and deaths⁴.

Though the complexities of a pandemic are difficult to account for, simulations and models offer us a chance to both explore the mechanisms underpinning a pandemic and potential solutions to mitigate its threat. Another benefit of simulations is that, by reducing the complexity of disease spread, they can be useful educational tools for clearly demonstrating how recommendations from medical professionals will affect the course of a epidemic. Along those lines, medically-based simulations are increasingly being developed to teach and demonstrate the effects of differing courses of actions on an outcome, and the rise in SARS-Cov-2 has provided more use for these models than ever before. One example is the Washington Post’s “Coronavirus Simulator”⁵. The article utilizes several simulations and infographics to effectively demonstrate how quickly an unmitigated virus will spread within a population, and explains the basis behind different containment methods used to prevent a widespread infection. Inspired by this approach, we coded a Viral Transmission Education Simulator (VTES) - a reduced representation simulation that replicates the effects of different variables on viral transmission in a population.

VTES was designed to be modular, simple, and clear, to encourage users to interact with the script that creates the simulations. By interacting with VTES, and enabling visualization of the results, we aim to help individuals understand key variables that influence the course of the spread of the disease, including population density, population mobility, interventions that reduce transmission, and a disease’s mortality rate. In this article, we show the impact of decreasing transmission chance (achieved through actions such as social distancing, masking and self-quarantining), the process of becoming “immune” to SARS-CoV-2, and how to calculate R0. We hope VTES will help foster a deeper understanding of the parameters underpinning the spread of a virus such as SARS-CoV-2 and will be used to clearly educate those unfamiliar with such parameters, as well as in exploring how small changes to variables that influence virus spread can have large impacts on the course of a pandemic.

Methods

Implementation

The disease spread simulation script was written in Python 3 using standard libraries. The code was written in a way so that it is straightforward for programming novices to change the values for variables that influence the disease spread, and was written in a modular fashion with sections, each headed by a title and description in comments. Below we provide an explanation and describe each section of the code.

The script first introduces a function to createperson. This defines a dictionary of attributes for a “person”, or dot, and how they move around in the simulated environment. They begin as alive, uninfected, and not immune (i.e. susceptible to infection).

The next section introduces variables that influence an outbreak. These lines are what we suggest modifying to explore the effects of different variables on viral transmission in the simulated population. For example, by changing transmission_chance = 0.90 to transmission_chance = 0.70, the simulation will decrease the probability the disease is transmitted from person to person. This will result in an decreased number of “infected people” overall.

The next section creates a window, forms an environment for the simulation, generates a population, and begins the simulation by changing one “dot’s” status to person [‘infected’]= True. The code begins a loop to move dots around according to their velocity, and bouncing off encountered walls or other dots. The parameter velocity determines how quickly the dots move. Users may change the velocity to simulate how measures like social distancing impact viral transmission.

Within the loop, the section headed make a person better over infection duration determines whether or not a person recovers over the duration of infection (thus becoming non-susceptible), and if so, reassigns their status accordingly.

The next section check the interactions of all the dots at every step in the simulation. This is where transmission is determined; as dots collide, their probability of becoming infected is determined by transmission_chance. Deceased and immune (recovered/non-susceptible) dots are ignored by infectious dots, and the window is then updated.

The final section calculates statistics and plots the figures (see example in Figure 1). Statistics include the total number of cases, people infected, the total number of deceased, and the length of the pandemic in days.

Figure 1.

Plots outlining the epidemiological statistics output at the end of (A) Simulation 1, (B) Simulation 2, and (C) Simulation 3.

Use Case 1: observing the effects of modulating VTES’s parameters

We now introduce an example of how to interact with the simulation’s code, and detail the resultant effects it has on the simulation of viral transmission. We will modulate the transmission_chance from transmission_chance = 0.90 to transmission_chance = 0.70 and transmission_chance = 0.60, reducing the probability of transmission by 20% and 30%, respectively. On average, decreasing the chance of transmission will reduce the total number of both people infected and fatalities resulting from infection, as well as flatten the curve.

Results

We have provided a video of Simulation 1 (Extended data¹³) to provide an example of what the simulation looks like.

In Simulation 1, where transmission_chance = 0.90, the pandemic lasted a total of 167 days, infecting 87.73% of the 375 simulated “people”, leaving 5.07% deceased Figure 2(A). In Simulation 2, where transmission_chance = 0.70 Figure 2(B), the pandemic lasted 282 days, and resulted in a lower total number of people infected (73.87%) or deceased (3.73% of the simulated population). Simulation 3, where transmission_chance = 0.60, the pandemic lasted 128 days and displayed the lowest total number of people infected (25.87% ) and deceased (1.87%) Figure 2(C).

Figure 2.

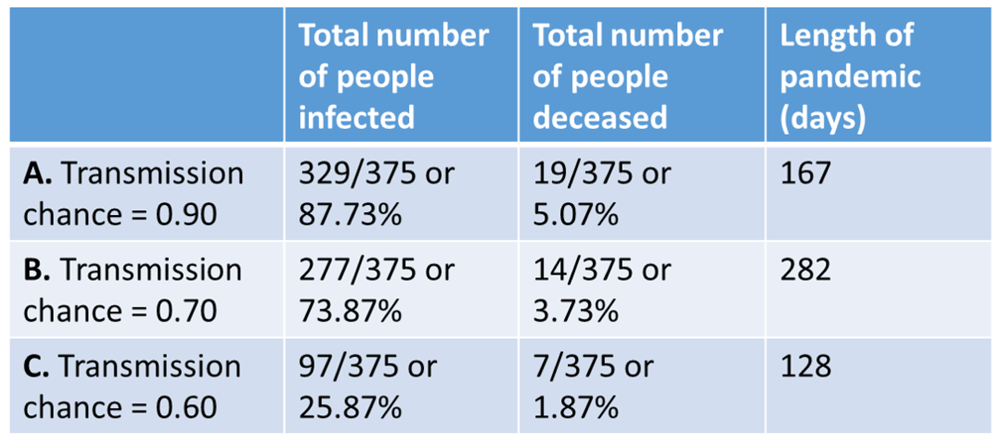
Statistics generated through running (A) Simulation 1, (B) Simulation 2, and (C) Simulation 3.

Decreasing the chance of transmission had an inverse relationship between outbreak severity and the size of the curve. The higher the chance of transmission, the more people became infected, resulting in a curve that extended beyond the hospital capacity. As transmission chance lowered, so did the number of people infected or killed by the virus, resulting in a flattened curve Figure 1.

The difference in the progression of the virus may be seen through snapshots of the Simulation 1 and Simulation 2’s progression. At first, both Simulation 1 and 2 started with one person infected Figure 3(A). However, 25 seconds into the pandemics, we can see Simulation 1 has more “people” who can continue spreading the virus, whereas Simulation 2 has fewer actively infectious “people” and more recovered\immune people Figure 3(B).

Figure 3.

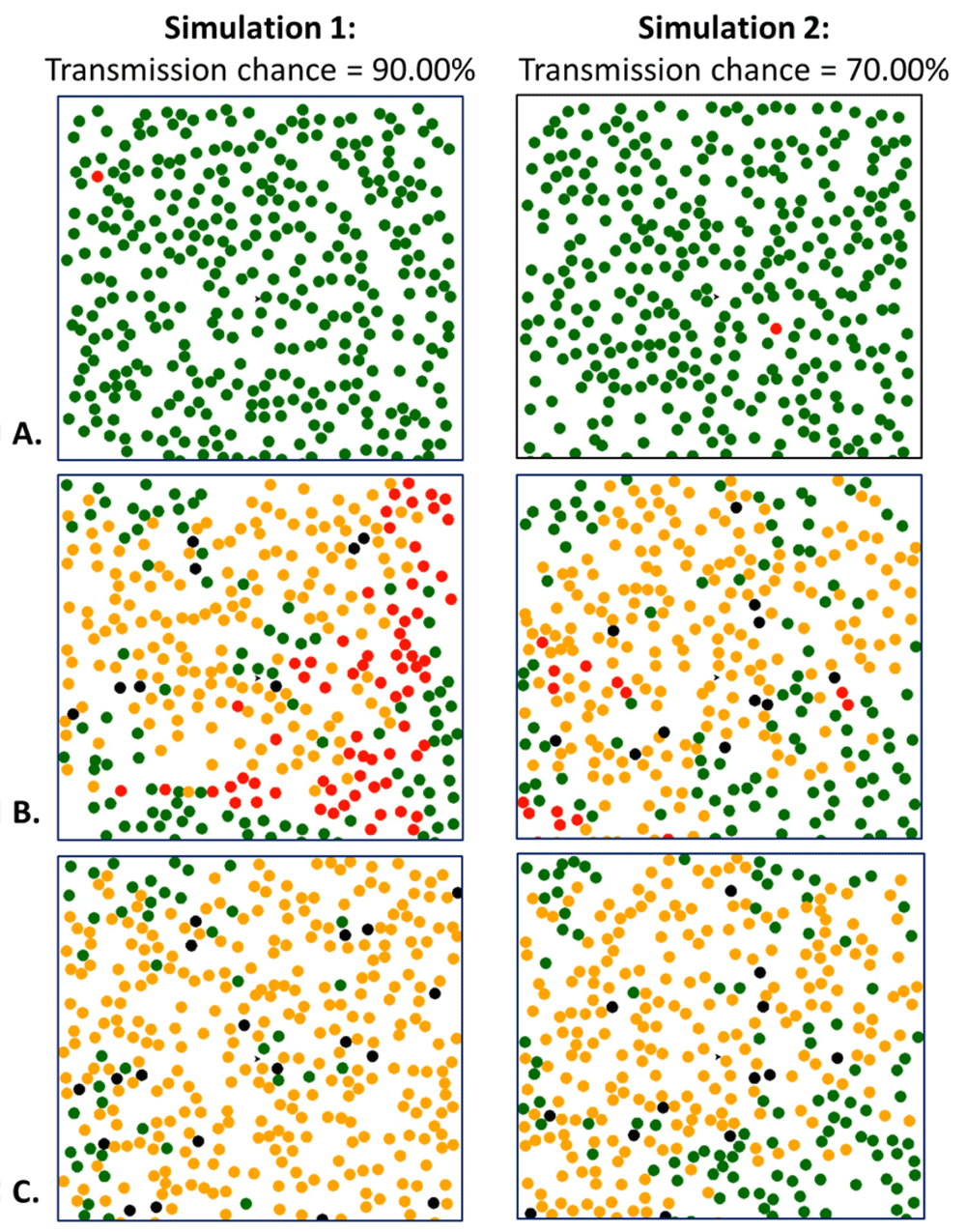
Snapshots of Simulation 1 and Simulation 2 at the start of the simulation (A), 25 seconds in to the simulation (B), and at the end of the simulations (C). Total run time was 42 seconds for Simulation 1 and 35 seconds for Simulation 2. Green dots represent those who have not been infected yet (susceptible individuals), red dots indicate infected "people", yellow dots indicate the number of recovered or immune "people" (non-susceptible individuals), and the black dots represent those deceased individuals.

We can see examples of herd immunity in both Simulation 1 and Simulation 2 Figure 4. Herd immunity occurs when a large enough proportion of the population has acquired individual immunity to the virus¹⁴. Since a virus cannot propagate through a non-susceptible population (in the case of SARS-CoV-2), herd immunity creates a buffer for those who are not yet immune, essentially protecting them from infection¹⁴. This can be seen in Figure 4, where individuals susceptible to the virus do not come into contact with infected peoples capable of transmitting the disease, thanks to the buffer created by non-susceptible others.

Figure 4. Example of susceptible individuals protected by those individuals that have ’recovered’, thereby illustrating the process of herd immunity in the simulation (in blue border).

Use Case 2: calculating R0

In order to calculate R0, we set record_contacts = True. We then ran the simulation 15 times, recording each output, the Contact_rate_for_uninfected_individuals_with_patient_zero and averaging them to produce $\overline{c}$. This resulted in $\overline{c}$ = 0.1808. With transmission_chance = 0.9 and the infection_duration = 14, we show

This is slightly lower R0 for SARS-Cov-2 as calculated in a review by Liu et al, who reported a mean R0 of 3.28 and a median of 2.79¹⁵.

Discussion

In Use Case 1, we show that lowering the transmission_chance results in fewer numbers of infected and deceased individuals in a population experiencing a viral outbreak. By modelling a reduction in transmission chance, we can draw parallels to real-world efforts to reduce the chance of transmission, such as social distancing or wearing masks. A recent meta-analysis by Chu et al (2020), aimed at investigating the optimal distance for limiting person-to-person transmission and the impact of wearing a mask on preventing transmission of CoV-1, CoV-2 and Middle East Respiratory Syndrome (MERS-CoV), found that wearing a mask may lower the chance of viral transmission and infection by 14.3% and that the risk of being infected (i.e. chance of transmission) is only 3% when 2 individuals are over 1 metre apart¹⁶. These real-world studies suggest statistics that can be used to alter the parameters of the simulation, where users can observe the effects of these alterations, and more importantly, the behaviours or processes that underpin them.

In Use Case 2, we calculated R0 and found it to be reasonably close to the established R0 for SARS-Cov-2, especially considering we did not intentionally nor precisely modify the parameters to reflect SARS-Cov-2. We note there are numerous means of calculating R0 at various time-points throughout the progression of a viral outbreak, with each equation building on the complexity of the last. Our definition was drawn from Jones¹¹. Furthermore, calculating R0 in the real world via contact tracing may not always reflect the precise infectivity of a virus¹². However, we have the luxury of running the simulation multiple times in order to obtain an average $\overline{c}$, providing a more robust R0 calculation. The strength of VTES is that it simplifies messy, complex, real-world variability. Our reduced representation can help users gain a deeper understanding of R0 - a popular, though not well understood, metric used to highlight the severity of the current SARS-Cov-2 pandemic, as well as other communicable diseases.

VTES clearly demonstrates the link between transmission control measures (e.g. wearing a mask) and it’s effects on slowing viral spread and reducing the number of infected individuals Figure 2. By modifying one of the simulations parameters, we can compare the behaviour of VTES’s simulations to current literature on SARS-CoV-2. This reduces the complexity of the real world, where dozens of factors influence the outcomes of viral transmission, to just a few key factors. Manipulating these factors allows users to draw insights into the mechanisms underpinning disease transmission. The dynamic nature of these simulations may therefore carry greater educational impact than impersonal and poorly described statistics. The simulations generated by VTES serve as tools that can help educate, train, and inform individuals on how a disease can propagate through a population.

While VTES models the parameters that underpin the dynamics of a pandemic at a high level, they do not capture many of the variables that influence disease spread in real populations. For instance, while the bouncing circles resemble the interaction between individuals, they do not fully, nor accurately, represent the way in which humans move about in a population. The software for VTES was created as a simple, modular tool that models the dynamics of viral transmission within a population, and encourages modification by users. The lessons learned from the simulations may be scaled up and are applicable to a larger population, and we hope future users who interact with the code add their own improvements. This may generate new and exciting insights that our simple, baseline simulation may not provide.

Many other features could be added by the adventurous programmer. For instance, one aspect of disease control that we currently do not account for is testing and quarantining. It would be straightforward to simulate the process of quarantining by adding to the code such that after a certain number of days of infection an infected individual would stop moving, and would thus have fewer collisions, and therefore chances to spread the disease.

Conclusions

In summary, we have used the programming language Python to build a stochastic, epidemic simulator that has dual roles as a tool for modeling the impact of different factors on the spread of disease and as an educational tool. By providing Use Cases where the transmission_chance parameter was modified and R0 was calculated, we provided examples of the sort of exploratory use we encourage from future users, and how this tool can be used for educational purposes. We hope VTES will be amended and improved per the needs of each user, and that the simulations it generates provide visual explanations for the efficacy of, and rationale behind, varying methods of slowing viral spread.

Software availability

Source code available from: https://github.com/sstagg/disease-transmission

Archived source code as at time of publication: http://doi.org/10.5281/zenodo.4041821¹⁷

License: CC-BY 4.0

Data availability