Keywords
Mathematical model, Moko, Banana, Ralstonia solanacearum, Logistic growth
This article is included in the Agriculture, Food and Nutrition gateway.
Mathematical model, Moko, Banana, Ralstonia solanacearum, Logistic growth
In this version we include the evaluators' suggestions; The explanation of the mathematical model that was not clear was included, the sensitivity and stability analysis was organized into independent items and the optimal control problem was included with the new graphs complementing the results. This improved version is longer but more complete.
To read any peer review reports and author responses for this article, follow the "read" links in the Open Peer Review table.
The banana is a fruit of great economic importance and food sovereignty, because it is found in the shopping basket of people across different social strata and because of its nutritional content. However, its production is threatened by re-emerging diseases such as Moko, caused by the bacterium Ralstonia solanacearum race 2 philotype II (Fegan & Prior, 2006), which causes wilting and deterioration of the plant. Symptoms are usually visible when there is a great spread of bacteria and adjacent plants may have already been infected (Viljoen et al., 2016). Moko is a peculiar manifestation of bacterial wilt; it is a quarantine pest that, once inside the host, moves through the vascular bundles. Being a vascular disease, this bacterium not only affects the vegetative part but also the daughter hill, promoting the spread of the disease, which is accelerated by the high optimal minimum, optimal and maximum temperatures of 10°C, 35°C and 41°C, respectively, infecting triploid plantains, heliconia (Heliconia spp.) and other ornamental Musacea plants (Jiang et al., 2017).
The development of mathematical models has contributed through the use of a wide range of techniques to the study of epidemics and diseases, helping to answer biological questions and raising new questions related to the epidemiology and ecology of pathogens and the diseases they cause; in most cases, mathematical models lead directly to applications in the control of the disease (Jeger et al., 2018). In plants, some prediction models have evaluated the control of some diseases in plantain and bananas, such as banana wilt by Xanthomonas (BXW) using mathematical models, describing a deterministic SI-type epidemic model for control of BXW focusing on the integrated management of the disease through cultural control as in Nannyonga et al. (2015), who considered the optimal control strategies associated with the prevention of transmission by the use of contaminated tools. The researchers assumed a model with three modes of transmission: vertical (from the mother plant to its child), horizontal (indirect) from the vector to plant, and through contaminated agricultural tools (Nannyonga et al., 2015).
Likewise, Nakakawa et al. (2016) presented a mathematical model for BXW propagated by an insect vector. The mathematical model they formulated takes into account inflorescence infection and vertical transmission from the mother corm to the daughter hills, but not tool-based transmission by humans (Nakakawa et al., 2016). In this context, a dynamic system is formulated based on ordinary two-dimensional differential equations that interprets the dynamics of incidence of banana Moko disease, including prevention and treatment.
In the research carried out by (Bautista-Montealegre et al., 2016), the state of the disease in 2016 is shown, these authors to contribute to the management of banana Moko disease in the department of Quindío-Colombia, evaluated the relationship between the incidence of the disease and variables related to physical and chemical properties of the soil, as well as the use of the soil and the altitudinal location in 269 farms analyzing soils and foliar tissues, as well as the symptoms of the disease to establish the effect of the variables on the probability of occurrence of the disease, finding a positive and significant correlation between the incidence of the disease, the hydraulic conductivity and the saturation of potassium in the soil; and negative and significant with the altitude, foliar copper concentration and presence of associated crops; Likewise, they argue that 10 of the 12 municipalities in the department have a high percentage of the disease, demonstrating the inadequate phytosanitary management that is still being carried out (Bautista-Montealegre et al., 2016).
Mathematical models are a tool of a growing scientific branch and of a notorious and marked interdisciplinary nature, linking mainly biologists and mathematicians, but also researchers from other areas with the challenge of applying mathematical techniques to the study of biological processes (García-Macías & Ubertini, 2019). Previously, they were used mainly in epidemiology in SI, SIS, SIR, SIRS epidemic models among others; at present, mathematical models are, therefore, a useful tool in biology, agronomy, phytopathology, chemistry, environment and among many other areas, since they allow to make a representation of a biological system, the behavior of a certain disease etc., and with them facilitate the understanding of its dynamics in order to make predictions for future decisions on actions that facilitate control (Jeger et al., 2018).
The model presents the following assumptions:
In the plantation the total plant population is assumed to be positive.
It is considered a plantation with a maximum capacity of banana plants k
It is considered that the disease of the banana Moko, follows a model Epidemic type SI (Susceptible-Infectious).
Banana plants in asymptomatic state are not considered.
Removal of infected plants is considered.
A population model with nonlinear ordinary differential equations is presented, which interprets the dynamics of the banana Moko, including a constant rate of disease prevention in the population of susceptible plants over time. A variable population of plants and a logistic growth of replanting are assumed, taking into account the maximum capacity of plants in the study region. The variables and parameters of the model are: x(t), the average number of susceptible banana plants; y(t), the average number of diseased banana plants; and P(t) = x(t) + y(t), total number of banana plants at one time t, shown in Figure 1.
The model parameters are: γ, constant overseeding rate; k, load capacity (maximum capacity) of banana plants in the study region; and β, probability of transmission of infection. Preventive controls are: g, fraction of infected banana plants removed; and f, fraction of susceptible banana plants that receive prevention of contagion of the bacteria. The dynamic system that interprets the infectious process including prevention and elimination, is formed by the following two nonlinear differential equations:
With initial conditions x(0) = x0, y(0) = y0, P(0) = x(0) + y(0), γ, k > 0, 0 < f, g, β < 1, P ≤ k, x(t) ≡ x, and y(t) ≡ y.
The region of eco-epidemiological sense is defined where the trajectories of the plant infection dynamics make sense,
In the first equation, the derivative indicates the variation of the susceptible banana plant population with respect to time in weeks t, which is given by the inflow, the growth of susceptible banana plants by replanting γx regulated by the factor minus the outflow, the incidence of banana plants λ(y)(1 – f)x, where is the infection force of banana Moko and (1 – f) is the fraction of population of susceptible banana plants on which no preventive measures were taken.
Similarly, in the second equation the derivative represents the variation of the population of infected plants with respect to time in weeks t, given by the inflow the incidence of banana plants minus the outflow the population of plants infected deleted gy.
We start by finding the equilibrium populations, the constant solutions of the system, where the population variation of susceptible plants and variation of infected plants become zero, that is,
We solve this non-linear algebraic system for x and y, determining the equilibrium point according to agricultural conditions.
From Equation (4) y = 0 o
Substituting y = 0 in Equation (3), we obtain
Of which x = 0 or x = k. Therefore, we have the point E0 = (0,0), which does not make agricultural sense, since P > 0 and the equilibrium point E1 = (k,0), disease free and in which the susceptible population equals the capacity maximum.
Solving for y from Equation (5), we obtain
Substituting Equation (6) in Equation (3), we obtain the components of equilibrium point with disease, E3 =
Considering,
We write x and y like this
In coexistence of populations and , which is true when ξ0 > 1 and ρ < 1.
Since P = x + y, the total plant population in equilibrium is, That is,
Therefore,
ξ0, indicates the average number of infected plants that an infected plant produces during the infectious period (before being killed) in the population of susceptible plants and is considered the threshold of infected plants. We can consider this threshold as a function that depends on f and g,
To determine the stability of each equilibrium point (E), we apply the Hartman-Grobman theorem (Perko, 2008), linearizing the system of non-linear Equation (1) – Equation (2), obtaining the linearization matrix (Jacobian matrix) of the form:
With the following partial derivative elements,
These elements of the matrix J (E) are the coefficients of the linear system
Where, U = (u, v)t (transposed vector).
We analyze the equilibrium points with an agricultural sense E1 = (k, 0) y E3 = For E1, we obtain the Jacobian matrix,
Because it is a triangular matrix, the eigenvalues (λi, i = 1,2)
where λ2 < 0 since the threshold ξ0 < 1.
We conclude that the free equilibrium point of Moko disease is locally and asymptomatically stable.
For case in matrix (7) we obtain the trace and the determinant of J(E3), respectively,
We conclude that the equilibrium point with susceptible plants and infected plants is locally and asymptomatically stable if the threshold inequalities (ξ0 > 1 and ρ < 1) and the inequalities are met,
These analytical results are shown in the phase planes of Figure 2, made with Maple 18 software (free trial available; SageMath is an openly available alternative), for different scenarios varying initial conditions.
The local sensitivity analysis was performed that is a measure of the relative change in a variable when its parameters change (Chitnis et al., 2008; Hamby, 1994; Rodrigues et al., 2013). That is,
Where,
y p: β, g, f, are previously defined parameters.
The indices of local sensitivity of the threshold were calculated with respect to each parameter:
With respect to the values of the threshold indices of the disease and the Figure 3., the following observations are made:
For f = 0.5 it is true that =
When the percentage of plants receiving prevention increases, the disease threshold decreases, that is, they are inversely proportional. This behavior is good in managing the disease.
For values of f,g < 0.5, the disease threshold index is lower for the elimination of infected plants (g) and in the case that f,g > 0.5, the disease threshold index is lower in the case of prevention of susceptible plants.
The disease threshold increases proportionally with respect to the transmission probability.
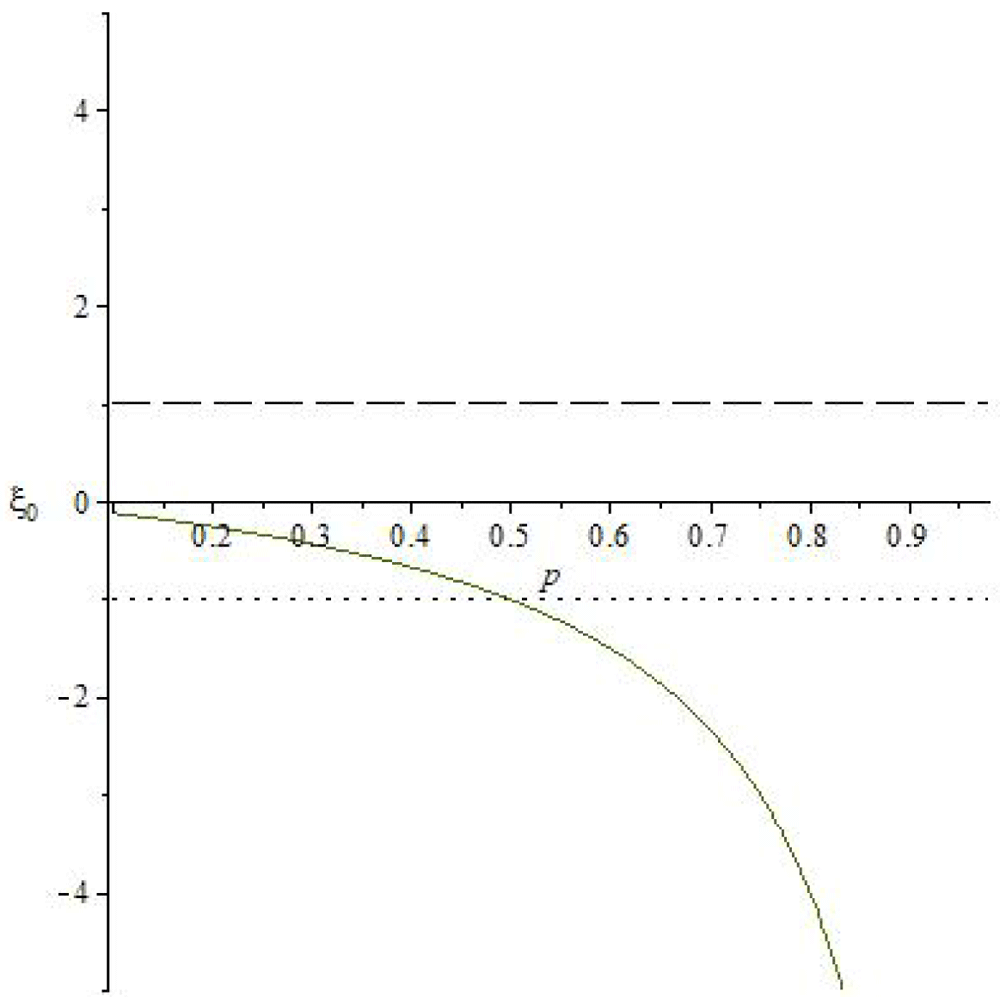
It is concluded that mathematical simulation models are a useful tool for research in banana Moko disease. With them it was determined that the elimination of banana plants infected with the disease plays an essential role in the good agronomic management of the crop.
An objective, quadratic and cost functional linked to a system is presented of nonlinear ordinary differential equations, which interprets the dynamics of banana Moko (Figure 4), including a constant rate of disease prevention in the population of susceptible plants over time. It assumes a variable population of plants and a logistic growth of replanting having taken into account the maximum capacity of plants in the study region (Cherruault & Gallego, 1985; Louadj et al., 2018). The variables and parameters of the optimal control problem are described in Table 1.
The functional objective of direct and indirect costs is proposed:
Linked to the system of differential equations:
With initial conditions x(0) = x0, y(0) = y0, P(0) = x(0) + y(0), γ, k > 0, 0 ≤ u1, u2, β ≤ 1 and P ≤ k.
It is about finding optimal control such that:
Where,
is the space of admissible controls and L2 is the space of integrable functions, and T is the control terminal time.
The Hamiltonian function or (Pontryagin function) is of the form:
where x = (x, y) is the vector of state variables, u = (u1; u2) the vector of controls, λ = (λ1, λ2) the vector of attached or conjugate variables and L is the Lagrangian. That is to say,
Applying the first order condition , the optimal control is obtained:
The conjugate system (or adjoint system) has the form:
that is to say,
Where,
with transversality conditions λi(T) = 0, i = 1,2.
The contour problem is formed by the system of state variables of the dynamics of the Moko with their respective initial conditions, the conjugated system and the terminal conditions and the optimal controls:
Numerical analysis of the contour problem: with this analysis we can observe the decrease of the infected plants varying different conditions of the controls u1 and u2, showing that when u1 and u2 are not implemented as shown in the figure at week 120, the population of infected plants tends to increase (Figure 5), and that the implementation of control u1 in approximately 45% (Figure 6) and the implementation of control u2 in approximately 60% (Figure 7), produces a complete decrease in infected plants at week 23.
With this we can determine that if both controls are implemented in 40% and 60% respectively, the banana Moko disease in a crop with good agronomic management tends to disappear, likewise it contributes to reducing the production costs associated with the loss of plants due to infection and the costs of implementing prevention strategies by 51.13% weekly, which is equivalent to 60,756 Colombian pesos.
We conclude that in order to reduce production costs and maintain the disease in a controlled state, the recommended prevention strategies should be implemented, and with greater relevance the detection and rapid elimination of infected plants.
All data underlying the results are available as part of the article and no additional source data are required.
The authors thank the Vicerrectoría de investigaciones of the University of Quindío, the Mathematical Modeling Group in Epidemiology GMME for supporting us in this study and Oscar Andrés Manrique Arias M.Sc., for their support in the numerical solution of the contour problem.
| Views | Downloads | |
|---|---|---|
| F1000Research | - | - |
|
PubMed Central
Data from PMC are received and updated monthly.
|
- | - |
Competing Interests: No competing interests were disclosed.
Reviewer Expertise: Public health, environment, sustainability, environmental management, econometrics
Competing Interests: No competing interests were disclosed.
Reviewer Expertise: Mathematical biology, applied Mathematics
Is the work clearly and accurately presented and does it cite the current literature?
Partly
Is the study design appropriate and is the work technically sound?
Yes
Are sufficient details of methods and analysis provided to allow replication by others?
Partly
If applicable, is the statistical analysis and its interpretation appropriate?
Not applicable
Are all the source data underlying the results available to ensure full reproducibility?
Yes
Are the conclusions drawn adequately supported by the results?
Partly
Competing Interests: No competing interests were disclosed.
Reviewer Expertise: Mathematical biology, applied Mathematics
Is the work clearly and accurately presented and does it cite the current literature?
Partly
Is the study design appropriate and is the work technically sound?
Yes
Are sufficient details of methods and analysis provided to allow replication by others?
Yes
If applicable, is the statistical analysis and its interpretation appropriate?
Not applicable
Are all the source data underlying the results available to ensure full reproducibility?
Yes
Are the conclusions drawn adequately supported by the results?
Partly
Competing Interests: No competing interests were disclosed.
Reviewer Expertise: Public health, environment, sustainability, environmental management, econometrics
Alongside their report, reviewers assign a status to the article:
| Invited Reviewers | ||
|---|---|---|
| 1 | 2 | |
|
Version 2 (revision) 19 Feb 21 |
read | read |
|
Version 1 10 Dec 20 |
read | read |
Provide sufficient details of any financial or non-financial competing interests to enable users to assess whether your comments might lead a reasonable person to question your impartiality. Consider the following examples, but note that this is not an exhaustive list:
Sign up for content alerts and receive a weekly or monthly email with all newly published articles
Already registered? Sign in
The email address should be the one you originally registered with F1000.
You registered with F1000 via Google, so we cannot reset your password.
To sign in, please click here.
If you still need help with your Google account password, please click here.
You registered with F1000 via Facebook, so we cannot reset your password.
To sign in, please click here.
If you still need help with your Facebook account password, please click here.
If your email address is registered with us, we will email you instructions to reset your password.
If you think you should have received this email but it has not arrived, please check your spam filters and/or contact for further assistance.
Comments on this article Comments (0)