Qualitative analysis of HIV and AIDS disease transmission: impact of awareness, testing and effective follow up

Oluwakemi E. Abiodun; Olukayode Adebimpe; James Ndako; Olajumoke Oludoun; Benedicta Aladeitan; Michael Adeniyi

doi:10.12688/f1000research.123693.1

Home Browse Qualitative analysis of HIV and AIDS disease transmission: impact...

ALL Metrics

-

Views

-

Downloads

Get PDF

Get XML

Export

▬

✚

Research Article

Qualitative analysis of HIV and AIDS disease transmission: impact of awareness, testing and effective follow up

[version 1; peer review: 1 approved, 1 approved with reservations, 1 not approved]

Oluwakemi E. Abiodun ¹, Olukayode Adebimpe², James Ndako¹, Olajumoke Oludoun¹, Benedicta Aladeitan¹, Michael Adeniyi³

Oluwakemi E. Abiodun ¹, Olukayode Adebimpe², [...] James Ndako¹, Olajumoke Oludoun¹, Benedicta Aladeitan¹, Michael Adeniyi³

PUBLISHED 07 Oct 2022

Author details Author details

¹ Physical Sciences, Landmark University, Omu Aran, Kwara, 251101, Nigeria
² Mathematics and Statistic, First Technical University, Ibadan, Nigeria, 200103, Nigeria
³ Mathematics and Statistic, Lagos State Polytechnic, Lagos, Lagos, Nigeria

Oluwakemi E. Abiodun
Roles: Formal Analysis, Investigation, Methodology, Writing – Original Draft Preparation

Olukayode Adebimpe
Roles: Supervision, Writing – Review & Editing

James Ndako
Roles: Supervision, Writing – Review & Editing

Olajumoke Oludoun
Roles: Conceptualization, Validation

Benedicta Aladeitan
Roles: Investigation, Resources

Michael Adeniyi
Roles: Methodology, Software, Writing – Review & Editing

OPEN PEER REVIEW

REVIEWER STATUS

This article is included in the Emerging Diseases and Outbreaks gateway.

This article is included in the Sociology of Health gateway.

This article is included in the Global Public Health gateway.

Abstract

Background: Since the early 1980s, human immunodeficiency virus (HIV) and its accompanying acquired immunodeficiency syndrome (AIDS) have spread worldwide, becoming one of the world's major global health issues. From the beginning of the epidemic until 2020, about 79.3 million people became infected, with 36.3 million deaths due to AIDS illnesses. This huge figure is a result of those unaware of their status due to stigmatization and invariably spreading the virus unknowingly.
Methods: Qualitative analysis through a mathematical model that will address HIV unaware individuals and the effect of an increasing defaulter on the dynamics of HIV/AIDS was investigated. The impact of treatment and the effect of inefficient follow-up on the transmission of HIV/AIDS were examined. The threshold for the effective reduction of the unaware status of HIV through testing, in response to awareness, and the significance of effective non-defaulting in treatment commonly called defaulters loss to follow-up as these individuals contribute immensely to the spread of the virus due to their increase in CD4+ count was determined in this study. Stability analysis of equilibrium points is performed using the basic reproduction number $R_0$, an epidemiological threshold that determines disease eradication or persistence in viral populations. We tested the most sensitive parameters in the basic reproduction numbers. The model of consideration in this study is based on the assumption that information (awareness) and non-stigmatization can stimulate change in the behaviours of infected individuals, and can lead to an increase in testing and adherence to treatment. This will in turn reduce the basic reproduction number, and consequently, the spread of the virus.
Results: The results portray that the early identification and treatment are inadequate for the illness to be eradicated.
Conclusions: Other control techniques, such as treatment adherence and effective condom usage, should be investigated in order to lessen the disease's burden.

Keywords

HIV/AIDS, infection-free equilibrium, defaulter lost to follow-up, endemic equilibrium, next generation matrix, basic reproduction number, stability.

Corresponding author: Oluwakemi E. Abiodun

Competing interests: No competing interests were disclosed.

Grant information: The author(s) declared that no grants were involved in supporting this work.

Copyright: © 2022 Abiodun OE et al. This is an open access article distributed under the terms of the Creative Commons Attribution License, which permits unrestricted use, distribution, and reproduction in any medium, provided the original work is properly cited.

How to cite: Abiodun OE, Adebimpe O, Ndako J et al. Qualitative analysis of HIV and AIDS disease transmission: impact of awareness, testing and effective follow up [version 1; peer review: 1 approved, 1 approved with reservations, 1 not approved]. F1000Research 2022, 11:1145 (https://doi.org/10.12688/f1000research.123693.1) First published: 07 Oct 2022, 11:1145 (https://doi.org/10.12688/f1000research.123693.1) Latest published: 28 Feb 2023, 11:1145 (https://doi.org/10.12688/f1000research.123693.2)

1. Introduction

Human immunodeficiency virus (HIV) is a sexually transmitted infection (STI) and a blood-borne illness in humans with a wide range of clinical manifestations.¹^,² HIV and its accompanying acquired immune deficiency syndrome (AIDS) have spread rapidly around the world since its discovery in the early 1980s, and it remains the world’s most serious global health and development challenge. There is, however, a global devotion to avoiding new infections and making sure that all patients diagnosed have access to treatment. In addition, 79.3 million individuals have been infected with HIV since the pandemic began, with 36.3 million people dying due to AIDS diseases. About five million individuals contracted HIV for the first time in 2003, the largest number in any one year since the pandemic began.³ Globally, the figure of persons living with HIV/AIDS has risen from 35 million in 2001 to 37.7 million in 2020, with around 3 million people dying from the illness in that year.⁴^,⁵ Around 84 percent [68 − 98 percent] of HIV-positive persons in the globe know their status in 2020, the remaining 16 percent (about 6 million people) [4.8 million-7.1 million] need to be tested for HIV. HIV testing is an important initial step in HIV prevention, treatment, care, and support.⁶^,⁷ Under Sustainable Development Goal 3, the international community pledged to work to end the AIDS pandemic by 2030. While progress has been made, it has been inconsistent, and the intermediate targets of “90-90-90” have been missed.⁷^,⁸ New diseases continue to wreak havoc on communities and undermine vital socioeconomic infrastructure all across the planet. According to the United Nations Joint Program on HIV and AIDS, the number of HIV-positive people in 2021 was 37.6 million, up from 33.2 million in 2010.⁹ 1.5 million [1.1 million-2.1 million] people contracted HIV for the first time in 2020, 690,000 [480,000-1 million] people died of AIDS-related illnesses, and antiretroviral medication was available to 27.4 million [26.5 million-27.7 million] patients in December 2020, up from 7.8 million [6.9 million-7.9 million] in 2010.⁹^–¹¹ HIV can be spread horizontally or vertically from one infected individual to another. Horizontal HIV transmission occurs when an individual comes into direct contact with an HIV-positive person, including sexual contact, or when they use a needle and syringe that has recently been utilized by a HIV-positive individual. Contrastingly, vertical transmission occurs when the virus is passed directly from an infected mother to her pregnant or newborn child.¹² HIV/AIDS transmission dynamics has piqued the interest of applied mathematicians, epidemiologists¹³^–¹⁶ and biologists¹⁷^–²² due to the disease’s worldwide menace. Various improvements have been made to May and Anderson’s early models,²³^–²⁵ and particular issues have been discussed by researchers.¹²^,²⁶^–⁴⁸ In Lu et al. 2020²⁷ fostered a compartmental model for the yearly revealed HIV/AIDS MSM in the Zhejiang Region of China between 2007 to 2019 and anticipated that 90 percent of people tested for HIV/AIDS will have received treatment by 2020, while the screened extent will remain as low as 40 percent, and that antiretroviral treatment (ART) can actually control the transmission of HIV, even within the sight of medication opposition. In Rana and Sharma, 2020³⁰ presented a simple Likely to be exposed-Infected (i.e.SI) form of HIV/AIDS mathematical model, in view of the supposition that changing from an AIDS-infected to an HIV-infected individual is conceivable, in order to understand disease dynamics and develop strategies to reduce or control disease transmission among individual. Mushanyu³² built a mathematical model for HIV acquisition using nonlinear ordinary differential equations to analyse the influence of delayed HIV diagnosis on the transmission of HIV in the year 2020. To prevent HIV from spreading further, the researchers advocated for early HIV treatment and the expansion of HIV self-testing initiatives, which would allow more people who have not been tested for HIV to learn their status. Teng¹² proposed and investigated a time-delay compartmental framework for HIV transmission in a sexually active cohort with press coverage, a disease that can result to a developed phase of infection known as acquired immunodeficiency syndrome (AIDS), as well as vertical transmission in the enrollment of people infected in 2019.³³ Saad et al. (2019) developed and considered an HIV⁺ mathematical model with the next generation matrix, the infection-free and endemic equilibrium points were identified, and the basic reproduction ratio R₀ was determined. The Lyapunov function was utilized to analyze the equilibria’s global stability, and it was observed that the equilibria’s stability is reliant on the magnitude of the fundamental reproduction ratio.³⁷ developed an HIV/AIDS epidemic model with a generic nonlinear rate of occurrence and therapy, was able to obtain the basic reproductive number R₀ using the next generating matrix technique.

Researchers have employed numerous tools to manage and eradicate HIV/AIDS diseases.³^,¹¹^,¹² These studies revealed that awareness creation/information can help to control the disease burden but cannot eliminate the disease. Furthermore, there are other techniques and tools available that can be applied to study the dynamics of disease transmission and to provide suitable control interventions. The use of mathematical modeling is foremost among these techniques.¹⁶^–¹⁹ Although many articles²⁰ have studied the impact of different controls; however, none of them have incorporated human behavior in response to information. Hence, this study identifies the threshold for effective reduction of HIV/AIDS, as a result of HIV unaware individuals and consequent effective follow up in the use treatment.

The following is the structure of the paper: Section 2 describes the model, while Section 3 examines the model’s basic features, the basic reproduction number, and equilibrium points. Section 4 employs parameter sensitivity index on the reproduction number to conduct a stability study of the equilibria (local and global), and the findings are generated from numerical simulations of data from previously published studies in Section 5. Finally, the research is examined and completed in Section 6.

2. Model formulation and description

A mathematical model on the mechanisms of horizontal and vertical transmission of HIV/AIDS was developed, by incorporating the effect of testing, defaulter lost to follow-up on treatment, and effective use of condom on the existing model. The model is available from GitHub and is archived with Zenodo.⁶⁶ The model is depicted schematically in Figure 1. The model contains six (6) state variables, namely: Susceptible, (S), representing people who are likely to become infected with HIV; Unaware HIV infectives, (H_U), Aware HIV infectives (H_A), Treated HIV infectives, (H_T); AIDS individuals (A_A) and AIDS on treatment individuals (A_T). The rate of effective contact with HIV-positive people either by immigration or emigration is given by Λ. A percentage of newborns get infected with HIV during birth at a rate of (1 − ζ) and are therefore directly enrolled into the unaware infected population H_U, at a rate ζΛ, with 0 ≤ ζ ≤ 1. $λ_{H} = c (1 - ψξ) \frac{β_{1} H_{U} + β_{2} H_{A} + β_{3} A_{A}}{N}$ is the HIV transmission contact rate. Parameter c represents the average number of sexual partners acquired by people who is vulnerable to HIV annually. In order to simulate the influence of condom usage as a significant preventive intervention, the amount of condom protection (usage and effectiveness) is given as ψξ[0, 1] based on assumption. If ξ = 0, condom use provides no protection, but ξ = 1 denotes complete protection, where ψ is the condom use. The parameters β₁, β₂ and β₃ account for the HIV transfer rates between persons at risk and (HIV unaware, HIV aware and full blown AIDS) infectives individuals, respectively. Both the HIV-infected and the AIDS-infected groups are thought to be active in the spread of HIV/AIDS amongst susceptible. Because infected patients with AIDS symptoms have a greater viral load than HIV positive people (pre-AIDS) in the H_U and H_A classes, and because viral load and infectiousness have a positive connection, we must have β₁ < β₂ < β₃. There is an evidence to suggest that individuals who know their HIV status H_A change their sexual behavior (i.e. adopt safer-sex practices), resulting in reduced transmission.²⁵ Most HIV pandemic models disregard the role of AIDS patients in HIV transmission by applying simplistic assumptions such as AIDS death being immediate or AIDS patients being incapable of mingling and gaining new sex partners. However, epidemiological data shows that AIDS patients participate in hazardous sexual activities, such as seldom wearing condoms or having several sex partners.⁶¹ As shown in the findings of²¹ a research of HIV-1-infected transfusion men and their women sex partners, severe AIDS patients are more likely to infect their partners than non-advanced immuno-compromised receivers.⁶² also reported similar findings. HIV-positive individuals with and without AIDS signs are likely to have access to antiretroviral therapy (ART). Unaware HIV-infected persons, H_U, progress to the category of aware HIV infection H_A, after testing at a rate of α, while unaware infected individual who did not go for testing progress to stage IV of AIDS, A_A; at a rate of ρ. HIV-infected aware people with no symptoms of AIDS; H_A, proceed to the group of HIV infection under ART therapy, H_T, whereas HIV-infected people with AIDS symptoms, A_A, are treated for AIDS at a rate of θ₂ on reaching the class of A_T. We presume that HIV-infected people on treatment do not spread the virus.⁴⁹^,⁵⁰ HIV-infected people who are receiving therapy but do not have AIDS symptoms, H_T, who default during treatment and become resistant to drug, will return to the HIV-infected aware individuals, H_A, and that HIV-infected persons with AIDS symptoms, A_A, who default during treatment in class A_T, become re-infected with HIV with symptoms of AIDS individuals, A_A, at a rate υ₁ and υ₂ respectively.⁵¹ It is assumed that only HIV-infected people with AIDS symptoms, A_A and A_T, die of AIDS-related causes at a rate of d_a. The following mathematical model is based on these assumptions and that the system has a natural death in each class at a rate μ.

Figure 1. HIV/AIDS compartmental flow diagram.

In order to contribute to the arduous aim of ending it by 2030 there is need to foresee the epidemic’s behaviour. One of the most significant tools we’ll utilize to attain our aim is mathematical modeling of HIV infection. Based on,⁵² the following model was developed by the inclusion of AIDS on treatment compartment (by considering treatment of both individual not showing and showing symptoms of AIDS), individual who fall-out of treatment, considering AIDS individual are able to transmit infection, condom use to control transmission rate and average number of sexual partners acquired on force of infection. A system of ordinary differential equations (ODEs) can be used to express the mathematical equations that correspond to the schematic diagram:

(1)

\begin{array}{l} \frac{dS}{dt} = Λ (1 - ζ H_{U}) - (λ_{H} + μ) S (a) \\ \frac{{dH}_{U}}{dt} = Λ ζ H_{U} + λ_{H} S - (α + ρ + μ) H_{U} (b) \\ \frac{{dH}_{A}}{dt} = α H_{U} + v_{1} H_{T} - (θ_{1} + μ) H_{A} (c) \\ \frac{{dH}_{T}}{dt} = θ_{1} H_{A} - (v_{1} + μ) H_{T} (d) \\ \frac{{dA}_{A}}{dt} = ρ H_{U} + v_{2} A_{T} - (θ_{2} + d_{a} + μ) A_{A} (e) \\ \frac{{dA}_{T}}{dt} = θ_{2} A_{A} - (v_{2} + d_{a} + μ) A_{T} (f) \end{array}

with the positive initial conditions given as:

(2)

S (0) = S_{0}, H_{U} (0) = H_{U 0}, H_{A} (0) = H_{A 0}, H_{T} (0) = H_{T 0}, A_{A} (0) = A_{A 0}, A_{T} (0) = A_{T 0}

3. Model investigation

3.1 Region of invariant

All of the parameters in the model are considered to be non-negative. System (1), on the other hand, keeps track of the human populace, hence, the state variables are always positive for all time t ≥ 0. Thus, the total human populace is given as

(3)

N (t) = S (t) + H_{U} (t) + H_{A} (t) + H_{T} (t) + A_{A} (t) + A_{T} (t)

Here equation (1) is changing at a rate

(4)

\frac{dN}{dt} = \frac{dS}{dt} + \frac{{dH}_{U}}{dt} + \frac{{dH}_{A}}{dt} + \frac{{dH}_{T}}{dt} + \frac{{dA}_{A}}{dt} + \frac{{dA}_{T}}{dt} = Λ - μN - d_{a} A_{A} - d_{a} A_{T} + φ H_{U}

In the non-existence of infection i.e for H_U = H_A = H_T = A_A = A_T = 0 we have,

(5)

\frac{dN}{dt} \leq Λ - μ

We must have (6) by separating the variables of differential inequality.

(6)

\frac{dN}{Λ - μN} \leq dt

Integrating the above equation we have

Λ - μN \geq {Ce}^{- μt}

where C is a constant to which to be determined. Let at t = 0, N = N₀. So we have,

(7)

C = Λ - μ N_{0}

From (7) we have

\begin{array}{l} Λ - μN \geq (Λ - μ N_{0}) e^{- μt} \\ \Rightarrow N (t) \leq \frac{Λ}{μ} - [\frac{Λ - μ N_{0}}{μ}] e^{- μt} \end{array}

As $t \to \infty, 0 \leq N (t) \leq \frac{Λ}{μ}$

As a result, the system (1) feasible solutions set enters the region.

Ω = \{(S, H_{U}, H_{A}, H_{T}, A_{A}, A_{T}) \in {ℛ e}_{+}^{6} : 0 \leq N \leq \frac{Λ}{μ}\}

when

N \leq \frac{Λ}{μ}

every solution with an initial condition in

{ℛ e}_{+}^{6}

stays in that region for t > 0. As a result, the model is well posed and epidemiologically relevant in the domain Ω.

3.2 Non-negativity of solutions

This section discusses the positivity of the solutions, which describes the system’s non-negativity of solutions (1).

Lemma 1: S(t) ≥ 0, H_U(t) ≥ 0, H_A(t) ≥ 0, H_T(t) ≥ 0, A_A(t) ≥ 0, A_T(t) ≥ 0 and N(t) ≥ 0 satisfied by the solutions of system (1) with initial conditions (2) for all t ≥ 0. The region $Ω \subset ℛ ⌉_{+ 0}^{6}$ is positively invariant and attracts in terms of system (1).

Proof: Take a look at the first equation in (1)

\frac{dS}{dt} = Λ (1 - ζ H_{U}) - (λ_{H} + μ) S

we have;

\frac{dS}{dt} \geq - (Λ ζ H_{U} + λ_{H} + μ) S \int \frac{1}{S} dS \int - (Λ ζ H_{U} + λ_{H} + μ) dt

S \geq S_{0} e^{- (Λ ζ H_{U} + λ_{H} + μ)} \geq 0

provided $(Λ ζ H_{U} + λ_{H} + μ) < \infty$

As a result, S ≥ 0

Likewise, for system (1)’s second equation, we have

\frac{{dH}_{U}}{dt} = Λ ζ H_{U} + λ_{H} S - (α + ρ + μ) H_{U}

\frac{{dH}_{U}}{dt} \geq - (α + ρ + μ) H_{U} \int \frac{1}{H_{U}} {dH}_{U} \int - (α + ρ + μ) dt

H_{U} \geq H_{U 0} e^{- (α + ρ + μ)} \geq 0

provided $(α + ρ + μ) < \infty$

Hence, H_U ≥ 0

similarly it can be shown that H_A ≥ 0, H_T ≥ 0, A_A ≥ 0, A_T ≥ 0 for all t > 0

Thus the solutions S, H_U, H_A, H_T, A_A, A_T remain positive forever.

3.3 Equilibrium point and basic reproduction number; R₀

The model (1) has exactly one disease-free equilibrium (DFE) point and the equilibrium point E₀ is given by $(S_{0}, H_{U 0}, H_{A 0}, H_{T 0}, A_{A 0}, A_{T 0}) = (\frac{Λ}{μ}, 0, 0, 0, 0, 0) .$ In the absence of infection, the total population changes in proportion to the ratio of recruitment rate to the death rate.

The total population dynamics can be altered when an individual with an HIV/AIDS is introduced into a population. For the endemic equilibrium, there is an existence of infection hence H_U≠H_A≠H_T≠A_A≠A_T≠0. It is denoted by E_*. Setting equation (1a-1f) equal to zero which exist when R₀ > 1 we have

(8)

S_{*} = \frac{(M_{1} - ζ Λ) (M_{4} M_{5} - υ_{2} θ_{2})}{λρ M_{5}} {A_{A}}^{*}

(9)

H_{U *} = \frac{(M_{4} M_{5} - υ_{2} θ_{2})}{ρ M_{5}} {A_{A}}^{*}

(10)

H_{A *} = \frac{α M_{3} (- υ_{2} θ_{2} + M_{4} M_{5})}{(M_{2} M_{3} - υ_{1} θ_{1})} {A_{A}}^{*}

(11)

H_{T *} = \frac{θ_{1} α M_{3} (υ_{2} θ_{2} - M_{4} M_{5})}{M_{3} (M_{2} M_{3} - υ_{1} θ_{1})} {A_{A}}^{*}

(12)

A_{A *} = \frac{Λ ρ M_{5} λ}{M_{1} (M_{4} M_{5} - υ_{2} θ_{2}) λ + μ (M_{1} - ζ Λ) (M_{4} M_{5} - υ_{4} θ_{2})}

(13)

A_{T *} = \frac{θ_{2}}{M_{5}} A_{A *}

M₁ = α + ρ + μ, M₂ = θ₁ + μ, M₃ = υ₁ + μ, M₄ = θ₂ + d_a + μ, M₅ = υ₂ + d_a + μ.

Theorem 1: There exists a positive endemic equilibrium if R₀ > 1

Reference 53 presented a better method for determining R₀ which was an improved technique of solving the reproduction number firstly developed by Ref. 54 that is widely accepted because it represents the biological meaning of R₀. By considering only the infective classes, we were able to obtain the system’s (1) basic reproduction number, R0, which is the spectral radius (ρ) of the next generation matrix, NGM, i.e. $R_{0} = ρ ({FV}^{- 1})$ . The rate of emergence of new infections in compartments i, while V denotes the rate of transfer of individual into and out of the compartment i by all other means. Where F and V are the m × m matrices defined as:

$F = \frac{\partial F_{i (xo)}}{\partial_{xj}} and V = \frac{\partial V_{i (xo)}}{\partial_{xj}} with i \leq i, j \leq m$

F is non-negative and V is non-singular matrix.

Then,

(14)

F = (\begin{array}{c} c (1 - ψξ) β_{1} & c (1 - ψξ) β_{2} & 0 & c (1 - ψξ) β_{3} & 0 \\ 0 & 0 & 0 & 0 & 0 \\ 0 & 0 & 0 & 0 & 0 \\ 0 & 0 & 0 & 0 & 0 \\ 0 & 0 & 0 & 0 & 0 \end{array}) and V = (\begin{array}{c} M_{1} - Λ ζ & 0 & 0 & 0 & 0 \\ - α & M_{2} & - υ_{1} & 0 & 0 \\ 0 & - θ_{1} & M_{3} & 0 & 0 \\ - ρ & 0 & 0 & M_{4} & - υ_{2} \\ 0 & 0 & 0 & - θ_{2} & M_{5} \end{array}) F V^{- 1} = [\begin{array}{c} \frac{c (1 - ψξ) β_{1}}{Λ ζ - M_{1}} + \frac{c (1 - ψξ) β_{2} α M_{3}}{Λ ζ M_{2} M_{3} - Λ {ζθ}_{1} υ_{1} - M_{1} M_{2} M_{3} + M_{1} θ_{1} υ_{1}} + \frac{c (1 - ψξ) β_{3} ρ M_{4}}{Λ ζ M_{4}^{2} - Λ {ζθ}_{2} υ_{2} - M_{1} k_{4}^{2} + M_{1} θ_{2} υ_{2}} & \frac{c (1 - ψξ) β_{2} M_{3}}{M_{2} M_{3} - θ_{1} υ_{1}} & \frac{c (1 - ψξ) β_{2} υ_{1}}{M_{2} M_{3} - θ_{1} υ_{1}} & \frac{c (1 - ψξ) β_{3} M_{4}}{M_{4}^{2} - θ_{2} υ_{2}} & \frac{c (1 - ψξ) β_{3} υ_{2}}{M_{4}^{2} - θ_{2} υ_{2}} \\ 0 & 0 & 0 & 0 & 0 \\ 0 & 0 & 0 & 0 & 0 \\ 0 & 0 & 0 & 0 & 0 \\ 0 & 0 & 0 & 0 & 0 \end{array}]

where M₁ = α + μ + ρ, M₂ = θ₁ + μ, M₃ = v₁ + μ, M₄ = θ₂ + d_a + μ, M₅ = v₂ + d_a + μ

The model reproduction number, denoted by R₀ is thus given by $R_{0} = ρ ({FV}^{- 1}) = R = R_{1} + R_{2} + R_{3}$ , the spectral radius of the NGM FV⁻¹.

Here,

\begin{array}{l} R_{1} = \frac{c (1 - ψξ) β_{1}}{ζ Λ - M_{1}} \\ R_{2} = \frac{c (1 - ψξ) β_{2} α M_{3}}{(M_{2} M_{3} - θ_{1} υ_{1}) (ζ Λ - M_{1})} \\ R_{3} = \frac{c (1 - ψξ) β_{3} ρ M_{4}}{(M_{4}^{2} - θ_{2} υ_{2}) (ζ Λ - M_{1})} \end{array}

4. Equilibria stability analysis

4.1 Disease-free equilibrium stability on a local and global scale, E₀

Theorem 2: For all R₀, the disease-free equilibrium E₀ exists, and it is locally asymptotically stable for R₀ < 1 and unstable otherwise.

Proof: The resulting matrix from linearized model $\frac{dx}{dt} = AX,$ where $X = {(x_{1}, x_{2}, x_{3}, x_{4}, x_{5}, x_{6})}^{T}, (x_{1}, x_{2}, x_{3}, x_{4}, x_{5}, x_{6}) \in R_{+}^{6}$ , and

(15)

A = (\begin{array}{c} g 1 - μ & g 2 - Λ ζ & g 5 & \frac{c (1 - ψξ) (β_{2} H_{A} + β_{3} A_{A} + H_{U} β_{1}) S}{{(S + H_{U} + H_{A} + H_{T} + A_{A} + A_{T})}^{2}} & g 7 & \frac{c (1 - ψξ) (β_{2} H_{A} + β_{3} A_{A} + H_{U} β_{1}) S}{{(S + H_{U} + H_{A} + H_{T} + A_{A} + A_{T})}^{2}} \\ g 3 & ζ Λ - α + g 4 - μ - ρ & g 6 & - \frac{c (1 - ψξ) (β_{2} H_{A} + β_{3} A_{A} + H_{U} β_{1}) S}{{(S + H_{U} + H_{A} + H_{T} + A_{A} + A_{T})}^{2}} & g 8 & - \frac{c (1 - ψξ) (β_{2} H_{A} + β_{3} A_{A} + H_{U} β_{1}) S}{{(S + H_{U} + H_{A} + H_{T} + A_{A} + A_{T})}^{2}} \\ 0 & α & - θ_{1} - μ & υ_{1} & 0 & 0 \\ 0 & 0 & θ_{1} & - υ_{1} - μ & 0 & 0 \\ 0 & ρ & 0 & 0 & - θ_{2} - d_{a} - μ & υ_{2} \\ 0 & 0 & 0 & 0 & θ_{2} & - υ_{2} - d_{a} - μ \end{array})

g_{1} = \frac{c (1 - ψξ) (β_{2} H_{A} + β_{3} A_{A} + H_{U} β_{1}) S}{{(S + H_{U} + H_{A} + H_{T} + A_{A} + A_{T})}^{2}} - \frac{c (1 - ψξ) (β_{2} H_{A} + β_{3} A_{A} + H_{U} β_{1})}{S + H_{U} + H_{A} + H_{T} + A_{A} + A_{T}},

g_{2} = \frac{c (1 - ψξ) (β_{2} H_{A} + β_{3} A_{A} + H_{U} β_{1}) S}{{(S + H_{U} + H_{A} + H_{T} + A_{A} + A_{T})}^{2}} - \frac{c (1 - ψξ) β_{1} S}{S + H_{U} + H_{A} + H_{T} + A_{A} + A_{T}},

g_{3} = \frac{c (1 - ψξ) (β_{2} H_{A} + β_{3} A_{A} + H_{U} β_{1})}{S + H_{U} + H_{A} + H_{T} + A_{A} + A_{T}} - \frac{c (1 - ψξ) (β_{2} H_{A} + β_{3} A_{A} + H_{U} β_{1}) S}{{(S + H_{U} + H_{A} + H_{T} + A_{A} + A_{T})}^{2}},

g_{4} = \frac{c (1 - ψξ) β_{1} S}{S + H_{U} + H_{A} + H_{T} + A_{A} + A_{T}} - \frac{c (1 - ψξ) (β_{2} H_{A} + β_{3} A_{A} + H_{U} β_{1}) S}{{(S + H_{U} + H_{A} + H_{T} + A_{A} + A_{T})}^{2}},

g_{5} = \frac{c (1 - ψξ) (β_{2} H_{A} + β_{3} A_{A} + H_{U} β_{1}) S}{{(S + H_{U} + H_{A} + H_{T} + A_{A} + A_{T})}^{2}} - \frac{c (1 - ψξ) β_{2} S}{S + H_{U} + H_{A} + H_{T} + A_{A} + A_{T}},

g_{6} = \frac{c (1 - ψξ) β_{2} S}{S + H_{U} + H_{A} + H_{T} + A_{A} + A_{T}} - \frac{c (1 - ψξ) (β_{2} H_{A} + β_{3} A_{A} + H_{U} β_{1}) S}{{(S + H_{U} + H_{A} + H_{T} + A_{A} + A_{T})}^{2}}

g_{7} = \frac{c (1 - ψξ) (β_{2} H_{A} + β_{3} A_{A} + H_{U} β_{1}) S}{{(S + H_{U} + H_{A} + H_{T} + A_{A} + A_{T})}^{2}} - \frac{c (1 - ψξ) β_{3} S}{S + H_{U} + H_{A} + H_{T} + A_{A} + A_{T}},

g_{8} = \frac{c (1 - ψξ) β_{3} S}{S + H_{U} + H_{A} + H_{T} + A_{A} + A_{T}} - \frac{c (1 - ψξ) (β_{2} H_{A} + β_{3} A_{A} + H_{U} β_{1}) S}{{(S + H_{U} + H_{A} + H_{T} + A_{A} + A_{T})}^{2}}

The resulting Jacobian matrix of (14) at E₀ is

(16)

| A - λI | = |\begin{array}{c} - μ - λ & - Λ ζ - c (1 - ψξ) β_{1} & - c (1 - ψξ) β_{2} & 0 & - c (1 - ψξ) β_{3} & 0 \\ 0 & Λ ζ + c (1 - ψξ) β_{1} - α - ρ - μ - λ & c (1 - ψξ) β_{2} & 0 & c (1 - ψξ) β_{3} & 0 \\ 0 & α & - θ_{1} - μ - λ & υ_{1} & 0 & 0 \\ 0 & 0 & θ_{1} & - υ_{1} - μ - λ & 0 & 0 \\ 0 & ρ & 0 & 0 & - θ_{2} - d_{a} - μ - λ & υ_{2} \\ 0 & 0 & 0 & 0 & θ_{2} & - υ_{2} - d_{a} - μ - λ \end{array}|

from (15) the first three eigenvalues are given as $λ_{1} = - μ, λ_{2} = - (v_{1} + μ), λ_{3} = - (θ_{1} + μ)$ and the roots of the resulting quadratic equation is obtained as:

(17)

\begin{array}{l} f (λ) = λ^{3} + (c {ψξβ}_{1} - ζ Λ - c β_{1} + M_{1} + M_{2} + M_{3}) λ^{2} + (β_{3} cψρξ + cψξ M_{2} β_{1} + cψξ M_{3} β_{1} - Λ ζ M_{2} - Λ ζ M_{3} - β_{3} cρ \\ - {cM}_{2} β_{1} - {cM}_{3} β_{1} + M_{1} M_{2} + M_{1} M_{3} + M_{2} M_{3} - θ_{2} υ_{2}) λ + β_{3} cψρξ M_{3} + cψξ M_{2} M_{3} β_{1} - c {ψξβ}_{1} θ_{2} υ_{2} \\ - Λ ζ M_{2} M_{3} + Λ {ζθ}_{2} υ_{2} - β_{3} cρ M_{3} - {cM}_{2} M_{3} β_{1} + c β_{1} θ_{2} υ_{2} + M_{1} M_{2} M_{3} - M_{1} θ_{2} υ_{2} \end{array}

Because all parameters of the model are assumed to be positive, λ₄ < 0, λ₅ < 0, λ₆ < 0. Evidently, if R₀ < 1, the roots of f(λ) have negative real parts, implying that E₀ is locally asymptotically stable (LAS) when R₀ < 1; if R₀ > 1, the roots of f(λ) are real and some are positive, implying that E₀ is unstable.

Theorem 3: If R₀ < 1, the disease free equilibrium is asymptotically stable globally for system (1).

Proof: The comparison theorem, as demonstrated by Ref. 55 proves the global stability of the disease-free equilibrium. We rename the infected class: $\frac{dx}{dt} = (F - V) X - JX, X = (H_{U}, H_{A}, H_{T}, A_{A}, A_{T})$ where,

(18)

F = (\begin{array}{c} c (1 - ψξ) β_{1} & c (1 - ψξ) β_{2} & 0 & c (1 - ψξ) β_{3} & 0 \\ 0 & 0 & 0 & 0 & 0 \\ 0 & 0 & 0 & 0 & 0 \\ 0 & 0 & 0 & 0 & 0 \\ 0 & 0 & 0 & 0 & 0 \end{array}), V = (\begin{array}{c} M_{1} - Λ ζ & 0 & 0 & 0 & 0 \\ - α & M_{2} & - υ_{1} & 0 & 0 \\ 0 & - θ_{1} & M_{3} & 0 & 0 \\ - ρ & 0 & 0 & M_{4} & - υ_{2} \\ 0 & 0 & 0 & - θ_{2} & M_{5} \end{array})

Then all of the matrix F − V eigenvalues have negative real parts, i.e So that

(19)

J = (1 - \frac{S}{N}) |\begin{array}{c} c (1 - ψξ) β_{1} + Λ ζ - M_{1} - λ & c (1 - ψξ) β_{2} & 0 & c (1 - ψξ) β_{3} & 0 \\ α & - M_{2} - λ & υ_{1} & 0 & 0 \\ 0 & θ_{1} & - M_{3} - λ & 0 & 0 \\ ρ & 0 & 0 & - M_{4} - λ & υ_{2} \\ 0 & 0 & 0 & θ_{2} & - M_{5} - λ \end{array}| = 0

(20)

\begin{array}{l} λ^{5} - (c β_{1} - c {ψξβ}_{1} + Λ ζ - M_{1} - M_{2} - M_{3} - M_{4} - M_{5}) λ^{4} - (Λ ζ M_{2} + Λ ζ M_{3} + Λ ζ M_{4} + Λ ζ M_{5} - ξc {ψβ}_{2} α - c {ψρξβ}_{3} \\ - cψξ M_{2} β_{1} - cψξ M_{3} β_{1} - cψξ M_{4} β_{1} - cψξ M_{5} β_{1} + c β_{2} α + ρc β_{3} + {cM}_{2} β_{1} + {cM}_{3} β_{1} + {cM}_{4} β_{1} + {cM}_{5} β_{1} - M_{2} M_{1} - M_{3} M_{1} \\ - M_{4} M_{1} - M_{1} M_{5} - M_{3} M_{2} - M_{2} M_{4} - M_{2} M_{5} - M_{3} M_{4} - M_{3} M_{5} - M_{4} M_{5} + υ_{1} θ_{1} + θ_{2} υ_{2}) λ^{3} - (Λ ζ M_{2} M_{3} + Λ ζ M_{2} M_{4} \\ + Λ ζ M_{2} M_{5} + Λ ζ M_{3} M_{4} + Λ ζ M_{3} M_{5} + Λ ζ M_{4} M_{5} - αcψξ M_{3} β_{2} - αcψξ M_{4} β_{2} - αcψξ M_{5} β_{2} - cψρξ M_{2} β_{3} - cψρξ M_{3} β_{3} \\ - cψρξ M_{5} β_{3} - cψξ M_{2} M_{3} β_{1} - cψξ M_{2} M_{4} β_{1} - cψξ M_{2} M_{5} β_{1} - cψξ M_{3} M_{4} β_{1} - cψξ M_{3} M_{5} β_{1} - cψξ M_{4} M_{5} β_{1} + c {ψξβ}_{1} θ_{1} υ_{1} \\ + c {ψξβ}_{1} θ_{2} υ_{2} - Λ {ζθ}_{1} υ_{1} - Λ {ζθ}_{2} υ_{2} + α {cM}_{3} β_{2} + α {cM}_{4} β_{2} + α {cM}_{5} β_{2} + cρ M_{2} β_{3} + cρ M_{3} β_{3} + cρ M_{5} β_{3} + {cM}_{2} M_{3} β_{1} \\ + {cM}_{2} M_{4} β_{1} + {cM}_{2} M_{5} β_{1} + {cM}_{3} M_{4} β_{1} + {cM}_{3} M_{5} β_{1} + {cM}_{4} M_{5} β_{1} - c β_{1} θ_{1} υ_{1} - c β_{1} θ_{2} υ_{2} - M_{1} M_{2} M_{3} - M_{1} M_{2} M_{4} - M_{1} M_{2} M_{5} \\ - M_{1} M_{3} M_{4} - M_{1} M_{3} M_{5} - M_{1} M_{4} M_{5} + M_{1} θ_{1} υ_{1} + M_{1} θ_{2} υ_{2} - M_{2} M_{3} M_{4} - M_{2} M_{3} M_{5} - M_{2} M_{4} M_{5} + M_{2} θ_{2} υ_{2} - M_{3} M_{4} M_{5} \\ + M_{3} θ_{2} υ_{2} + M_{4} θ_{1} υ_{1} + M_{5} θ_{1} υ_{1}) λ^{2} - (αc {ψξβ}_{2} θ_{2} υ_{2} - αcψξ M_{3} M_{4} β_{2} - αcψξ M_{3} M_{5} β_{2} - αcψξ M_{4} M_{5} β_{2} - cψρξ M_{2} M_{3} β_{3} \\ - cψρξ M_{2} M_{5} β_{3} - cψρξ M_{3} M_{5} β_{3} + c {ψρξβ}_{3} θ_{1} υ_{1} - cψξ M_{2} M_{3} M_{4} β_{1} - cψξ M_{2} M_{3} M_{5} β_{1} - cψξ M_{2} M_{4} M_{5} β_{1} + cψξ M_{2} β_{1} θ_{2} υ_{2} \\ - cψξ M_{3} M_{4} M_{5} β_{1} + cψξ M_{3} β_{1} θ_{2} υ_{2} + cψξ M_{4} β_{1} θ_{1} υ_{1} + cψξ M_{5} β_{1} θ_{1} υ_{1} + Λ ζ M_{2} M_{3} M_{4} + Λ ζ M_{2} M_{3} M_{5} + Λ ζ M_{2} M_{4} M_{5} \\ - Λ ζ M_{2} θ_{2} υ_{2} + Λ ζ M_{3} M_{4} M_{5} - Λ ζ M_{3} θ_{2} υ_{2} - Λ ζ M_{4} θ_{1} υ_{1} - Λ ζ M_{5} θ_{1} υ_{1} + α {cM}_{3} M_{4} β_{2} + α {cM}_{3} M_{5} β_{2} + α {cM}_{4} M_{5} β_{2} \\ - αc β_{2} θ_{2} υ_{2} + cρ M_{2} M_{3} β_{3} + cρ M_{2} M_{5} β_{3} + cρ M_{3} M_{5} β_{3} - c {ρβ}_{3} θ_{1} υ_{1} + {cM}_{2} M_{3} M_{4} β_{1} + {cM}_{2} M_{3} M_{5} β_{1} + {cM}_{2} M_{4} M_{5} β_{1} \\ - {cM}_{2} β_{1} θ_{2} υ_{2} + {cM}_{3} M_{4} M_{5} β_{1} - {cM}_{3} β_{1} θ_{2} υ_{2} - {cM}_{4} β_{1} θ_{1} υ_{1} - {cM}_{5} β_{1} θ_{1} υ_{1} - M_{1} M_{2} M_{3} M_{4} - M_{1} M_{2} M_{3} M_{5} - M_{1} M_{2} M_{4} M_{5} \\ + M_{1} M_{2} θ_{2} υ_{2} - M_{1} M_{3} M_{4} M_{5} + M_{1} M_{3} θ_{2} υ_{2} + M_{1} M_{4} θ_{1} υ_{1} + M_{1} M_{5} θ_{1} υ_{1} - M_{2} M_{3} M_{4} M_{5} + M_{2} M_{3} θ_{2} υ_{2} + M_{4} M_{5} θ_{1} υ_{1} \\ - θ_{1} θ_{2} υ_{1} υ_{2}) λ + αcψξ M_{3} M_{4} M_{5} β_{2} - αcψξ M_{3} β_{2} θ_{2} υ_{2} + cψρξ M_{2} M_{3} M_{5} β_{3} - cψρξ M_{5} β_{3} θ_{1} υ_{1} + cψξ M_{2} M_{3} M_{4} M_{5} β_{1} \\ - cψξ M_{2} M_{3} β_{1} θ_{2} υ_{2} - cψξ M_{4} M_{5} β_{1} θ_{1} υ_{1} + c {ψξβ}_{1} θ_{1} θ_{2} υ_{1} υ_{2} - Λ ζ M_{2} M_{3} M_{4} M_{5} + Λ ζ M_{2} M_{3} θ_{2} υ_{2} + Λ ζ M_{4} M_{5} θ_{1} υ_{1} \\ - Λ {ζθ}_{1} θ_{2} υ_{1} υ_{2} - α {cM}_{3} M_{4} M_{5} β_{2} + α {cM}_{3} β_{2} θ_{2} υ_{2} - cρ M_{2} M_{3} M_{5} β_{3} + cρ M_{5} β_{3} θ_{1} υ_{1} - {cM}_{2} M_{3} M_{4} M_{5} β_{1} \\ + {cM}_{2} M_{3} β_{1} θ_{2} υ_{2} + {cM}_{4} M_{5} β_{1} θ_{1} υ_{1} - c β_{1} θ_{1} θ_{2} υ_{1} υ_{2} + M_{1} M_{2} M_{3} M_{4} M_{5} - M_{1} M_{2} M_{3} θ_{2} υ_{2} - M_{1} M_{4} M_{5} θ_{1} υ_{1} + M_{1} θ_{1} θ_{2} υ_{1} υ_{2} \end{array}

Equation (20) has four (4) negative roots by Descartes rule of signs if

\begin{array}{l} ({αcψξM}_{3} M_{4} M_{5} β_{2} - {αcψξM}_{3} β_{2} θ_{2} υ_{2} + {cψρξM}_{2} M_{3} M_{5} β_{3} - {cψρξM}_{5} β_{3} θ_{1} υ_{1} + {cψξM}_{2} M_{3} M_{4} M_{5} β_{1} - {cψξM}_{2} M_{3} β_{1} θ_{2} υ_{2} \\ - {cψξM}_{4} M_{5} β_{1} θ_{1} υ_{1} + {cψξβ}_{1} θ_{1} θ_{2} υ_{1} υ_{2} - Λ {ζM}_{2} M_{3} M_{4} M_{5} + Λ {ζM}_{2} M_{3} θ_{2} υ_{2} + Λ {ζM}_{4} M_{5} θ_{1} υ_{1} - Λ {ζθ}_{1} θ_{2} υ_{1} υ_{2} - {αcM}_{3} M_{4} M_{5} β_{2} \\ + {αcM}_{3} β_{2} θ_{2} υ_{2} - {cρM}_{2} M_{3} M_{5} β_{3} + {cρM}_{5} β_{3} θ_{1} υ_{1} - {cM}_{2} M_{3} M_{4} M_{5} β_{1} + {cM}_{2} M_{3} β_{1} θ_{2} υ_{2} + {cM}_{4} M_{5} β_{1} θ_{1} υ_{1} - {cβ}_{1} θ_{1} θ_{2} υ_{1} υ_{2} \\ + M_{1} M_{2} M_{3} M_{4} M_{5} - M_{1} M_{2} M_{3} θ_{2} υ_{2} - M_{1} M_{4} M_{5} θ_{1} υ_{1} + M_{1} θ_{1} θ_{2} υ_{1} υ_{2}) < [({cβ}_{1} - {cψξβ}_{1} + Λ ζ - M_{1} - M_{2} - M_{3} - M_{4} - M_{5}) \\ \times (Λ {ζM}_{2} + Λ {ζM}_{3} + Λ {ζM}_{4} + Λ {ζM}_{5} - {ξcψβ}_{2} α - {cψρξβ}_{3} - {cψξM}_{2} β_{1} - {cψξM}_{3} β_{1} - {cψξM}_{4} β_{1} - {cψξM}_{5} β_{1} + {cβ}_{2} α + {ρcβ}_{3} \\ + {cM}_{2} β_{1} + {cM}_{3} β_{1} + {cM}_{4} β_{1} + {cM}_{5} β_{1} - M_{2} M_{1} - M_{3} M_{1} - M_{4} M_{1} - M_{1} M_{5} - M_{3} M_{2} - M_{2} M_{4} - M_{2} M_{5} - M_{3} M_{4} - M_{3} M_{5} - M_{4} M_{5} \\ + υ_{1} θ_{1} + θ_{2} υ_{2}) (Λ {ζM}_{2} M_{3} + Λ {ζM}_{2} M_{4} + Λ {ζM}_{2} M_{5} + Λ {ζM}_{3} M_{4} + Λ {ζM}_{3} M_{5} + Λ {ζM}_{4} M_{5} - {αcψξM}_{3} β_{2} - {αcψξM}_{4} β_{2} \\ - {αcψξM}_{5} β_{2} - {cψρξM}_{2} β_{3} - {cψρξM}_{3} β_{3} - {cψρξM}_{5} β_{3} - {cψξM}_{2} M_{3} β_{1} - {cψξM}_{2} M_{4} β_{1} - {cψξM}_{2} M_{5} β_{1} - {cψξM}_{3} M_{4} β_{1} - {cψξM}_{3} M_{5} β_{1} \\ - {cψξM}_{4} M_{5} β_{1} + {cψξβ}_{1} θ_{1} υ_{1} + {cψξβ}_{1} θ_{2} υ_{2} - Λ {ζθ}_{1} υ_{1} - Λ {ζθ}_{2} υ_{2} + {αcM}_{3} β_{2} + {αcM}_{4} β_{2} + {αcM}_{5} β_{2} + {cρM}_{2} β_{3} + {cρM}_{3} β_{3} \\ + {cρM}_{5} β_{3} + {cM}_{2} M_{3} β_{1} + {cM}_{2} M_{4} β_{1} + {cM}_{2} M_{5} β_{1} + {cM}_{3} M_{4} β_{1} + {cM}_{3} M_{5} β_{1} + {cM}_{4} M_{5} β_{1} - {cβ}_{1} θ_{1} υ_{1} - {cβ}_{1} θ_{2} υ_{2} - M_{1} M_{2} M_{3} \\ - M_{1} M_{2} M_{4} - M_{1} M_{2} M_{5} - M_{1} M_{3} M_{4} - M_{1} M_{3} M_{5} - M_{1} M_{4} M_{5} + M_{1} θ_{1} υ_{1} + M_{1} θ_{2} υ_{2} - M_{2} M_{3} M_{4} - M_{2} M_{3} M_{5} - M_{2} M_{4} M_{5} \\ + M_{2} θ_{2} υ_{2} - M_{3} M_{4} M_{5} + M_{3} θ_{2} υ_{2} + M_{4} θ_{1} υ_{1} + M_{5} θ_{1} υ_{1}) ({αcψξβ}_{2} θ_{2} υ_{2} - {αcψξM}_{3} M_{4} β_{2} - {αcψξM}_{3} M_{5} β_{2} - {αcψξM}_{4} M_{5} β_{2} \\ - {cψρξM}_{2} M_{3} β_{3} - {cψρξM}_{2} M_{5} β_{3} - {cψρξM}_{3} M_{5} β_{3} + {cψρξβ}_{3} θ_{1} υ_{1} - {cψξM}_{2} M_{3} M_{4} β_{1} - {cψξM}_{2} M_{3} M_{5} β_{1} - {cψξM}_{2} M_{4} M_{5} β_{1} \\ + {cψξM}_{2} β_{1} θ_{2} υ_{2} - {cψξM}_{3} M_{4} M_{5} β_{1} + {cψξM}_{3} β_{1} θ_{2} υ_{2} + {cψξM}_{4} β_{1} θ_{1} υ_{1} + {cψξM}_{5} β_{1} θ_{1} υ_{1} + Λ {ζM}_{2} M_{3} M_{4} + Λ {ζM}_{2} M_{3} M_{5} \\ + Λ {ζM}_{2} M_{4} M_{5} - Λ {ζM}_{2} θ_{2} υ_{2} + Λ {ζM}_{3} M_{4} M_{5} - Λ {ζM}_{3} θ_{2} υ_{2} - Λ {ζM}_{4} θ_{1} υ_{1} - Λ {ζM}_{5} θ_{1} υ_{1} + {αcM}_{3} M_{4} β_{2} + {αcM}_{3} M_{5} β_{2} + {αcM}_{4} M_{5} β_{2} \\ - {αcβ}_{2} θ_{2} υ_{2} + {cρM}_{2} M_{3} β_{3} + {cρM}_{2} M_{5} β_{3} + {cρM}_{3} M_{5} β_{3} - {cρβ}_{3} θ_{1} υ_{1} + {cM}_{2} M_{3} M_{4} β_{1} + {cM}_{2} M_{3} M_{5} β_{1} + {cM}_{2} M_{4} M_{5} β_{1} \\ - {cM}_{2} β_{1} θ_{2} υ_{2} + {cM}_{3} M_{4} M_{5} β_{1} - {cM}_{3} β_{1} θ_{2} υ_{2} - {cM}_{4} β_{1} θ_{1} υ_{1} - {cM}_{5} β_{1} θ_{1} υ_{1} - M_{1} M_{2} M_{3} M_{4} - M_{1} M_{2} M_{3} M_{5} - M_{1} M_{2} M_{4} M_{5} \\ + M_{1} M_{2} θ_{2} υ_{2} - M_{1} M_{3} M_{4} M_{5} + M_{1} M_{3} θ_{2} υ_{2} + M_{1} M_{4} θ_{1} υ_{1} + M_{1} M_{5} θ_{1} υ_{1} - M_{2} M_{3} M_{4} M_{5} + M_{2} M_{3} θ_{2} υ_{2} + M_{4} M_{5} θ_{1} υ_{1} - θ_{1} θ_{2} υ_{1} υ_{2})] \end{array}

Since $S (t) \leq \frac{Λ}{μ}$ in the invariant set, J is a non-negative matrix. Hence, it follows that

\frac{dx}{dt} \leq (F - V) X

When R₀ < 1, the eigenvalues of the matrix F − V are negative. As a result, the linearized differential equation is stable whenever R₀ < 1 is positive. Since $(H_{U}, H_{A}, H_{T}, A_{A}, A_{T}) \to (0, 0, 0, 0, 0)$ as $t \to \infty$ . According to the comparison theorem, $(H_{U}, H_{A}, H_{T}, A_{A}, A_{T}) \to (0, 0, 0, 0, 0)$ as $t \to \infty$ . Substituting H_U = H_A = H_T = A_A = A_T = 0 in (1) gives $S (t) \to S_{0}$ as $t \to \infty$ . Thus, $(S, H_{U}, H_{A}, H_{T}, A_{A}, A_{T}) \to (S_{0}, 0, 0, 0, 0, 0)$ as $t \to \infty$ for R₀ < 1. Thus, E₀ is globally asymptotically stable if R₀ < 1.

4.2 The endemic equilibrium’s local and global stability; E^*

Theorem 4: The endemic steady state $E^{*} (S^{*}, {H_{u}}^{*}, H_{A}^{*}, H_{T}^{*}, A_{A}^{*}, A_{T}^{*})$ of the model is locally asymptotically stable (LAS) If R₀ > 1.

Proof: We must now demonstrate the local stability of the endemic steady state. Assume R0 > 1.

The Jacobian matrix for the variables of system (1) is computed in the proof of Theorem 2 as in (14).

Hence, for the endemic equilibrium $(S^{*}, H_{U}^{*}, H_{A}^{*}, H_{T}^{*}, A_{A}^{*}, A_{T}^{*})$ , the Jacobian matrix and the determinantal equation at the endemic equilibrium is given as matrix in (15)

Clearly, the equation reduces to:

(21)

(- θ_{1} - μ - λ) (- v_{1} - μ - λ) (- v_{2} - d_{a} - μ - λ) (- θ_{2} - d_{a} - μ - λ) |\begin{array}{l} g_{1} - μ - λ & - Λ ζ + g_{2} \\ g_{3} & Λ ζ - α + g_{4} - μ - ρ - λ \end{array}| = 0

The first four eigenvalues of (21) are given as:

λ_{1} = - (θ_{1} + μ), λ_{2} = - (v_{1} + μ), λ_{3} = - (v_{2} + d_{a} + μ), λ_{4} = - (θ_{2} + d_{a} + μ)

The eigenvalue of the remaining 2 × 2 is obtained from the characteristics equation below:

(22)

λ^{2} + (+ α - Λ ζ - g_{1} - g 4 + 2 μ + ρ) λ + Λ ζ g_{1} + Λ ζ g_{3} - Λ ζμ - α g_{1} + αμ + g_{1} g_{4} - g_{1} μ - g_{1} ρ - g_{2} g_{3} - g_{4} μ + μ^{2} + μρ

The determinants of the characteristic polynomial from (22) yield the following result:

f (λ) = λ_{2} + a_{1} λ + a_{0} .

Polynomials of order 2 satisfy the Routh-Hurwitz criterion, We know that f(λ) = 0 using Routh-Hurwitz criterion polynomials of order 2 is stable if and only if both coefficients in (22) satisfy the following conditions: a_i > 0 From Eq. (22) the condition is satisfied. Therefore, EE is locally asymptotically stable.

Theorem 5: when R₀<1, the equations of the model have a positive distinct endemic equilibrium, which is said to be globally asymptotically stable.

Proof: Considering the Lyapunov function, which is defined as

L (S^{*}, H_{U}^{*}, {H_{A}}^{*}, H_{T}^{*}, A_{A}^{*}, A_{T}^{*}) = (S - S^{*} ln (\frac{S}{S^{*}})) + (H_{U} - H_{U}^{*} ln (\frac{H_{U}}{H_{U}^{*}})) + (H_{A} - H_{A}^{*} ln (\frac{H_{A}}{H_{A}^{*}})) + (H_{T} - H_{T}^{*} ln (\frac{H_{T}}{H_{T}^{*}})) + (A_{A} - A_{A}^{*} ln (\frac{A_{A}}{A_{A}^{*}})) + (A_{T} - A_{T}^{*} ln (\frac{A_{T}}{A_{T}^{*}}))

where L directly takes its derivative along the system as:

\frac{dL}{dt} = (1 - \frac{S^{*}}{S}) \frac{dS}{dt} + (1 - \frac{H_{U}^{*}}{H_{U}}) \frac{{dH}_{U}}{dt} + (1 - \frac{H_{A}^{*}}{H_{A}}) \frac{{dH}_{A}}{dt} + (1 - \frac{H_{T}^{*}}{H_{T}}) \frac{{dH}_{T}}{dt} + (1 - \frac{A_{A}^{*}}{A_{A}}) \frac{{dA}_{A}}{dt} + (1 - \frac{A_{T}^{*}}{A_{T}}) \frac{{dA}_{T}}{dt}

\begin{array}{l} \frac{dL}{dt} = (1 - \frac{S^{*}}{S}) 〈 Λ (1 - ζ H_{U}) - ((\frac{{cb}_{h} (1 - ψξ) β_{1} H_{U} + β_{2} H_{A} + β_{3} A_{A}}{N}) + μ) S 〉 \\ + (1 - \frac{H_{U}^{*}}{H_{U}}) 〈 (\frac{{cb}_{h} (1 - ψξ) β_{1} H_{U} + β_{2} H_{A} + β_{3} A_{A}}{N}) S - (α + ρ + μ) H_{U} + Λ ζ H_{U} 〉 \\ + (1 - \frac{H_{A}^{*}}{H_{A}}) 〈 α H_{U} + υ_{1} H_{T} - (θ_{1} + μ) H_{A} 〉 + (1 - \frac{H_{T}^{*}}{H_{T}}) 〈 θ_{1} H_{A} - (υ + μ) H_{T} 〉 \\ + (1 - \frac{A_{A}^{*}}{A_{A}}) 〈 ρ H_{U} + υ_{2} A_{T} - (θ_{2} + d_{a} + μ) A_{A} 〉 + (1 - \frac{A_{T}^{*}}{A_{T}}) 〈 θ_{2} A_{A} - (υ_{2} + d_{a} + μ) A_{T} 〉 \end{array}

At equilibrium

Λ (1 - ζ H_{U}) = {cb}_{h} (1 - ψξ) (\frac{β_{1} H_{U}^{*} + β_{2} H_{A}^{*} + β_{3} A_{A}^{*}}{N^{*}}) S^{*} + μ S^{*}

(α + ρ + μ + Λ ζ) = {cb}_{h} (1 - ψξ) (\frac{β_{1} H_{U}^{*} + β_{2} H_{A}^{*} + β_{3} A_{A}^{*}}{{H_{U}}^{*} N^{*}}) S^{*}

(θ_{1} + μ) = \frac{α H_{U}^{*} + υ_{1} H_{T}^{*}}{H_{A}^{*}}

(υ_{1} + μ) = \frac{θ_{1} H_{A}^{*}}{H_{T}^{*}}

(θ_{2} + d_{a} + μ) = \frac{ρ H_{U}^{*}}{A_{A}^{*}} + \frac{υ_{2} A_{T}^{*}}{A_{A}^{*}}

(υ_{2} + d_{a} + μ) = \frac{θ_{2} A_{A}^{*}}{A_{T}^{*}}

\begin{array}{l} \frac{dL}{dt} = (1 - \frac{S^{*}}{S}) 〈 (\frac{{cb}_{h} (1 - ψξ) β_{1} H_{U}^{*} + β_{2} H_{A}^{*} + β_{3} A_{A}^{*}}{N^{*}}) S^{*} + μ S^{*} - 〈 (\frac{{cb}_{h} (1 - ψξ) β_{1} H_{U} + β_{2} H_{A} + β_{3} A_{A}}{N}) + μ 〉 S 〉 \\ + (1 - \frac{H_{U}^{*}}{H_{U}}) 〈 (\frac{{cb}_{h} (1 - ψξ) β_{1} H_{U} + β_{2} H_{A} + β_{3} A_{A}}{N}) S - (\frac{{cb}_{h} (1 - ψξ) (β_{1} H_{U}^{*} + β_{2} H_{A}^{*} + β_{3} A_{A}^{*})}{H_{U}^{*} N^{*}}) S^{*} H_{U} \\ + (1 - \frac{H_{A}^{*}}{H_{A}}) 〈 α H_{U} + υ_{1} H_{T} - (\frac{α H_{U}^{*}}{H_{A}^{*}} + \frac{υ_{1} H_{T}^{*}}{H_{A}^{*}}) H_{A} 〉 + (1 - \frac{H_{T}^{*}}{H_{T}}) 〈 θ_{1} H_{A} - (\frac{θ_{1} H_{A}^{*}}{H_{T}}) H_{T} 〉 \\ + (1 - \frac{A_{A}^{*}}{A_{A}}) 〈 ρ H_{U} + υ_{2} A_{T} - (\frac{ρ H_{U}^{*}}{A_{A}^{*}} + \frac{υ_{2} A_{T}^{*}}{A_{A}^{*}}) A_{A} 〉 + (1 - \frac{A_{T}^{*}}{A_{T}}) 〈 θ_{2} A_{A} - \frac{θ_{2} A_{A}^{*}}{A_{T}^{*}} A_{T} 〉 \end{array}

\begin{array}{l} = (1 - \frac{S^{*}}{S}) 〈 \frac{{cb}_{h} (1 - ψξ) β_{1} H_{U}^{*}}{N^{*}} S^{*} + \frac{{cb}_{h} (1 - ψξ) β_{2} H_{A}^{*}}{N^{*}} S^{*} + \frac{{cb}_{H} (1 - ψξ) β_{3} A_{A}^{*}}{N^{*}} S^{*} + μ S^{*} - \frac{{cb}_{h} (1 - ψξ) β_{1} H_{U}}{N} S \\ - \frac{{cb}_{h} (1 - ψξ) β_{2} H_{A}}{N} S - \frac{{cb}_{h} (1 - ψξ) β_{3} A_{A}}{N} S - μS 〉 + (1 - \frac{H_{U}^{*}}{H_{U}}) 〈 \frac{{cb}_{h} (1 - ψξ) β_{1} H_{U}}{N} S + \frac{{cb}_{h} (1 - ψξ) β_{2} H_{A}}{N} S \\ + \frac{{cb}_{h} (1 - ψξ) β_{3} A_{A}}{N} S - \frac{{cb}_{h} (1 - ψξ) β_{1} H_{U}^{*} S^{*} H_{U}}{H_{U}^{*} N^{*}} - \frac{{cb}_{h} (1 - ψξ) β_{2} H_{A}^{*} S^{*} H_{U}}{H_{U}^{*} N^{*}} - \frac{{cb}_{h} (1 - ψξ) β_{3} A_{A}^{*} S^{*} H_{U}}{H_{U}^{*} N^{*}} S 〉 \\ + (1 - \frac{H_{A}^{*}}{H_{A}}) 〈 α H_{U} + υ_{1} H_{T} - \frac{α H_{U}^{*} H_{A}}{H_{A}^{*}} - \frac{υ_{1} H_{T}^{*} H_{A}}{H_{A}^{*}} 〉 + (1 - \frac{H_{T}^{*}}{H_{T}}) (θ_{1} H_{A} - \frac{θ_{1} H_{A}^{*} H_{T}}{H_{T}}) \\ + (1 - \frac{A_{A}^{*}}{A_{A}}) 〈 ρ H_{U} + υ_{2} A_{T} - \frac{ρ H_{U}^{*} A_{A}}{A_{A}^{*}} - \frac{υ_{2} A_{T}^{*} A_{A}}{A_{A}^{*}} 〉 + (1 - \frac{A_{T}^{*}}{A_{T}}) (θ_{2} A_{A} - \frac{θ_{2} A_{A} A_{T}}{A_{T}^{*}}) \end{array}

\begin{array}{l} = (1 - \frac{S^{*}}{S}) 〈 \frac{{cb}_{h} (1 - ψξ) β_{1} H_{U}^{*} S}{N} (1 - \frac{H_{U}^{*} S^{*} N}{H_{U} {SN}^{*}}) - {cb}_{h} (1 - ψξ) β_{2} H_{A} S (1 - \frac{H_{A}^{*} S^{*} N}{H_{A} {SN}^{*}}) \\ - {cb}_{h} (1 - ψξ) β_{3} A_{A} S (1 - \frac{H_{A}^{*} S^{*} N}{A_{A} {SN}^{*}}) - μS (1 - \frac{S^{*}}{S}) + (1 - \frac{H_{U}^{*}}{H_{U}}) \\ 〈 \frac{{cb}_{h} (1 - ψξ) β_{1} H_{U} S}{N} (1 - \frac{H_{U}^{*} S^{*} N}{H_{U}^{*} {SN}^{*}}) + \frac{{cb}_{h} (1 - ψξ) β_{2} H_{A} S}{N} (1 - \frac{H_{A}^{*} S^{*} H_{U}}{H_{A} {SH}_{U}^{*} N^{*}}) + \frac{{cb}_{h} (1 - ψξ) β_{3} A_{A} S}{N} (1 - \frac{A_{A}^{*} S^{*} H_{U}}{A_{A} {SH}_{U}^{*} N^{*}}) 〉 \\ + (1 - \frac{H_{A}^{*}}{H_{A}}) 〈 α H_{U} (1 - \frac{H_{U}^{*}}{H_{U}}) (1 - \frac{H_{A}^{*}}{H_{A}}) + υ H_{T} (1 - \frac{H_{T}^{*}}{H_{T}}) (1 - \frac{H_{A}^{*}}{H_{A}}) 〉 \\ + (1 - \frac{H_{T}^{*}}{H_{T}}) 〈 (θ_{1} H_{A} (1 - \frac{H_{A}^{*}}{H_{A}}) (1 - \frac{H_{T}^{*}}{H_{T}}) 〉 + (1 - \frac{A_{A}^{*}}{A_{A}}) 〈 ρ H_{U} (1 - \frac{H_{U}^{*}}{H_{U}}) (1 - \frac{A_{A}^{*}}{A_{A}}) + υ_{2} A_{T} (1 - \frac{A_{T}^{*}}{A_{T}} (1 - \frac{A_{A}^{*}}{A_{A}}) 〉 \\ + (1 - \frac{A_{T}^{*}}{A_{T}}) ⟨ θ_{2} A_{A} (1 - \frac{A_{A}^{*}}{A_{A}}) (1 - \frac{A_{T}^{*} A_{T}}{A_{T}}) = - μS {(1 - \frac{S^{*}}{S})}^{2} + P_{1} (S, H_{U}, H_{A}, H_{T}, A_{A}, A_{T}) + P_{2} (S, H_{U}, H_{A}, H_{T}, A_{A}, A_{T}) \end{array}

where

P_{1} (S, H_{U}, H_{A}, H_{T}, A_{A}, A_{T}) = - \frac{{cb}_{h} (1 - ψξ) β_{1} H_{U} S}{N} (1 - \frac{S^{*}}{S}) (1 - \frac{H_{U}^{*} S^{*} N}{H_{U} {SN}^{*}}) - \frac{{cb}_{h} (1 - ψξ) β_{2} H_{A}^{*} S^{*} N}{H_{A} {SN}^{*}} (1 - \frac{S^{*}}{S}) (1 - \frac{H_{A}^{*} S^{*} N}{H_{A} {SN}^{*}}) - \frac{{cb}_{h} (1 - ψξ) β_{3} A_{A} S}{N} (1 - \frac{S^{*}}{S}) (1 - \frac{A_{A}^{*} S^{*} N}{A_{A} {SN}^{*}})

P_{2} (S, H_{U}, H_{A}, H_{T}, A_{A}, A_{T}) = All others

(23)

P_{1} \leq 0 whenever H_{U} {SN}^{*} \geq H_{U}^{*} S^{*} N, H_{A} {SN}^{*} \geq H_{A}^{*} S^{*} N, A_{A} {SN}^{*} \geq A_{A}^{*} S^{*} N

(24)

\begin{array}{l} P_{2} \leq 0 whenever {H_{U}}^{*} {SN}^{*} \geq H_{U}^{*} S^{*} N, H_{A} {SH}_{U}^{*} N^{*} \geq H_{A}^{*} S^{*} H_{U}, A_{A} {SH}_{U}^{*} N^{*} \geq A_{A}^{*} S^{*} H_{U}, H_{U} H_{A}^{*} \geq H_{U}^{*} H_{A}, H_{T}^{*} H_{A}, \\ H_{U} A_{A}^{*} \geq H_{U}^{*} A_{A}, A_{A} A_{T} \geq A_{A}^{*} A_{T} \end{array}

Thus

\frac{dL}{dt} \leq 0

if (23) and (24) holds.

Hence, by Lasalle theorem, the equilibrium is globally asymptotically stable in the feasible region $R_{+}^{6}$ .

4.3 Sensitivity indices

Knowing the relative relevance of the different factors involved in HIV transmission and prevalence is vital for deciding how effectively to minimize human morbidity and mortality rate due to HIV infections. Sensitivity analysis is performed in this sub-section to assess the resilience of factors that have a strong impact on the basic reproduction number, R₀, so that suitable intervention strategies may be implemented.

The effect of HIV testing and treatment on HIV/AIDS dynamics was studied using the elasticity of ReH with respect to α and θ. Using the method described in⁵⁷^,⁶⁴^,⁶⁵ to compute the elasticity⁵⁸ of R_eH with respect to α and θ as shown in Equation (25)

(25)

\frac{αθ}{R_{eH}} \frac{\partial R_{eH}}{\partial αθ} = \frac{c (1 - ψξ)}{ζ Λ - M_{1}} + \frac{c (1 - ψξ) α M_{3}}{(M_{2} M_{3} - θ_{1} υ_{1}) (ζ Λ - M_{1})} + \frac{c (1 - ψξ) ρ M_{4}}{(M_{4}^{2} - θ_{2} υ_{2}) (ζ Λ - M_{1})}

Interpretation of the sensitivity indices

Table 1’s sensitivity indices are read as follows: Positive indices indicate that the corresponding basic reproduction number increases (decreases) as those parameters increase (decrease). Negative indices, on the other hand, indicate that increasing (decreasing) those parameters reduces the associated basic reproduction number (increases).

Table 1. Sensitivity indices of R_0.

Parameter	Sensitivity index	Parameter	Sensitivity index
Λ	+	α	-
ζ	+	μ	-
β₁	+	ρ	-
β₂	+	d_a	-
β₃	+	θ₁	-
c	+	θ₂	-
υ₁	+
υ₂	+

The endemicity of HIV infection increases when the values of β_i, i = 1, 2, 3, υ, and c are increased; when the values of alpha and mu are decreased, the endemicity of HIV infection decreases.

As a result, interventions should aim to reduce the annual average number of sexual partners acquired, c, the number of defaulters lost to follow-up, υ, and the likelihood of HIV transmission per sexual contact, β_i, i = 1, 2, 3, because the rate of progression from HIV to AIDS is increasing, ρ, indicates rapid progression to AIDS. In addition, effective condom use should be mandated as a precautionary measure to reduce the rate of HIV/AIDS transmission.

5. Numerical simulation

To affirm the model’s theoretical prognosis, simulation studies of the system (1) are run with the estimated parameter values listed below:

Simulation 1. Take into account the parametric data in Table 2 c = 3, ψ = 0, ξ = 0, β₁ = 0.050, β₂ = 0.055, β₃ = 0.060, μ = 0.2, Λ = 29, α = 0.7, ρ = 0.322, ζ = 0.02, υ₁ = 0.0169, υ₂ = 0.0169, θ₁ = 1.6949, θ₂ = 1.6949, d_a = 0.0333: Hence, R₀ = 0.698 and the infection-free equilibrium is (145.000;0;0;0;0;0): We can see in Figure 2 that by changing the initial values, the solution trajectories intersect to (145.00;0;0;0;0;0): This confirms the fact that if R₀ < 1, the virus-free equilibrium is globally asymptotically stable:

Table 2. Definition of Parameters values for the HIV model.

Parameters	Description	Parameters value	Source
Λ	Recruitment rate	29 yr⁻1	³
ζ	Rate of newborns infected with HIV	0.02	[Assumed]
c	Contact rate	3 patners/yr	³
β_i, i = 1, 2, 3	Transmission rate for the infective HIV and AIDS	[0.050, 0.055, 0.060]	Assumed
μ	Natural mortality	0.2	[Assumed]
α	Testing rate	0.7	[Assumed]
ρ	Progression rate from Unaware HIV to AIDS	0.322	[Assumed]
υ_i, i = 1, 2	HIV and AIDS defaulters from treatment	0.0169	⁵¹
θ₁, i = 1, 2	HIV and AIDS treatment rate	1.6949	²⁷
d_a	Mortality due to AIDS	0.0333	[Assumed]
ψ	condom effectiveness	[0,1]	[Assumed]
ξ	condom usage	[0,1]	[Assumed]

Figure 2. (Simulation 1) if R₀ < 1, the infection-free equilibrium is asymptotically stable.

Simulation 2. Let c = 6, ψ = 0, ξ = 0, β₁ = 0.080, β₂ = 0.085, β₃ = 0.090, μ = 0.2, Λ = 29, α = 0.7, ρ = 0.322, ζ = 0.02, υ₁ = 0.0169, υ₂ = 0.0169, θ₁ = 1.6949, θ₂ = 1.6949, d_a = 0.0333: Hence, R₀ = 2.197. Moreover, the endemic equilibrium is (64.197;13.225;5.251;41.035;2.348;15.905): We can see in Figure 3 that by changing the initial conditions, the solution trajectories intersect to (64.197;13.225;5.251;41.035; 2.348;15.905): This proves Theorem 5: if R₀ > 1, the endemic stability is globally stable.

Figure 3. (Simulation 2) If R₀ > 1, the endemic stability is asymptotically stable.

Figure 4. (Simulation 3) Take ψ = 1 and ξ = 1,to check the impact of condom use and effectiveness on the population when there’s no contact.

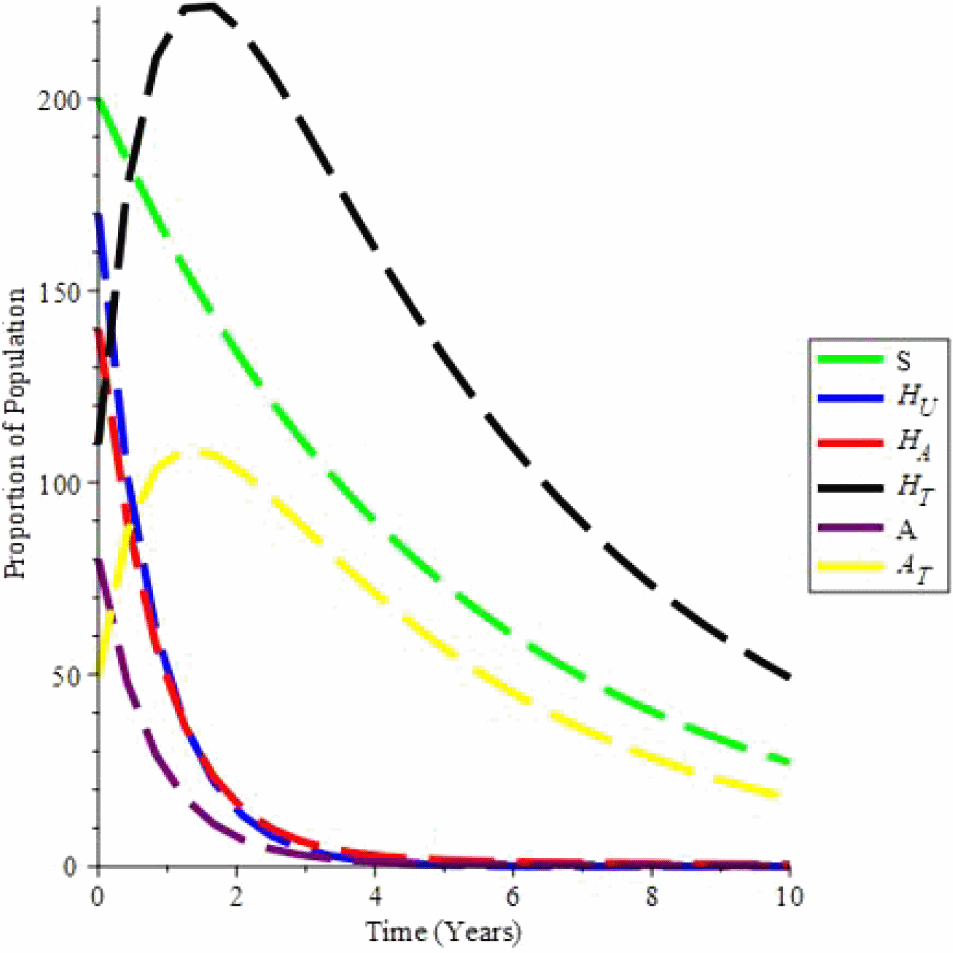
Simulation 3 depicts the distribution of individual proportions over time in various classes where there are no new infected children ζ or recruitment Λ, and contact c i.e. taking c = 0, ζ = 0, Λ = 0 when ψ = 1 and ξ = 1, (condom usage and effectiveness)i.e when there is full protection keeping every other values at endemic equilibrum constant, the value of R₀ = 0.

The impact of perinatal transmission in the system, i.e. the incidence of new recruits of infected children directly into the infective group, is pointedly demonstrated in simulation 4.

Figure 5(a) shows that as the proportion of infected newborns (ζ) rises, so does the proportion of the general population who is unaware. Figure 5(b) shows that increasing the value of (ζ) causes the proportion of the AIDS population to decrease over time, then raise until it reaches its stable state. As a result, if newborns infected with the virus are treated, the total infective group will be better controlled, minimizing the AIDS individuals. Figure 5(c) shows that as the number of infected children born rises, so does the treated populace.

Figure 5. (Simulation 4) Variation in the infected individual for different ζ values.

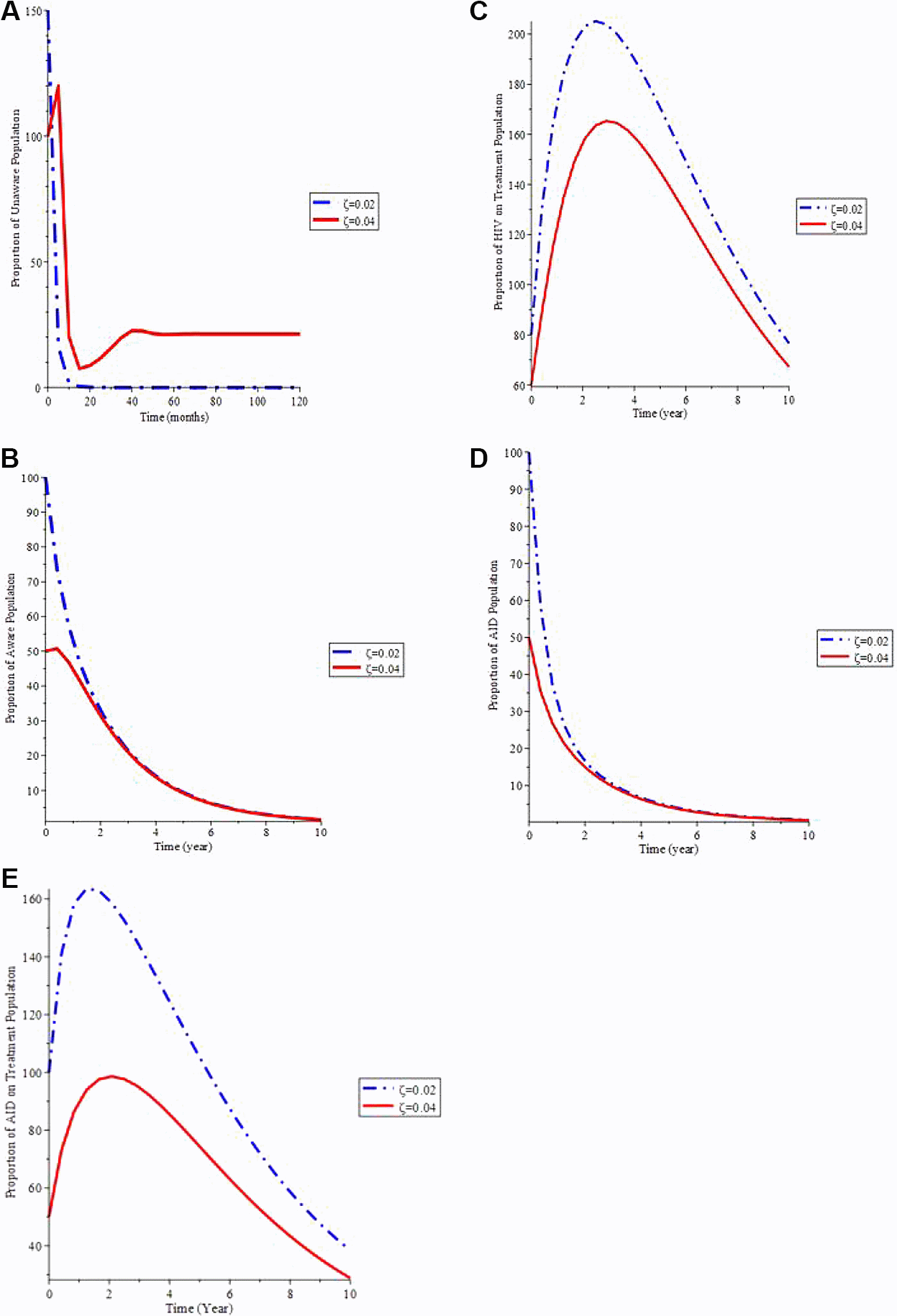
A. Variation of Unaware HIV population for different values of ζ. B. Variation of Aware HIV population for different values of ζ. C. Variation of HIV on Treatment population for different values of ζ. D. Variation of AIDS population for different values of ζ. E. Variation of AIDS on Treatment population for differnet values of ζ.

The effect of defaulters on treatment lost to follow-up in the model is examined in simulation 5.

Figure 6(a) shows that as the rate of defaulters (υ) increases, so does the proportion of the population that is aware, whereas the proportion of HIV patients on treatment decreases (b). Figure 6(c) shows how increasing upsilon causes the proportion of the AIDS population to increase over time while decreasing the proportion of the AIDS population on treatment until equilibrium is reached. As a result, if the HIV-aware infected population follows adheres therapy, the infectious individual as a whole would then remain under control, lowering the HIV-aware and AIDS number of individuals.

Figure 6. (Simulation 5) Variation of the infected individual for different fallout, υ values.

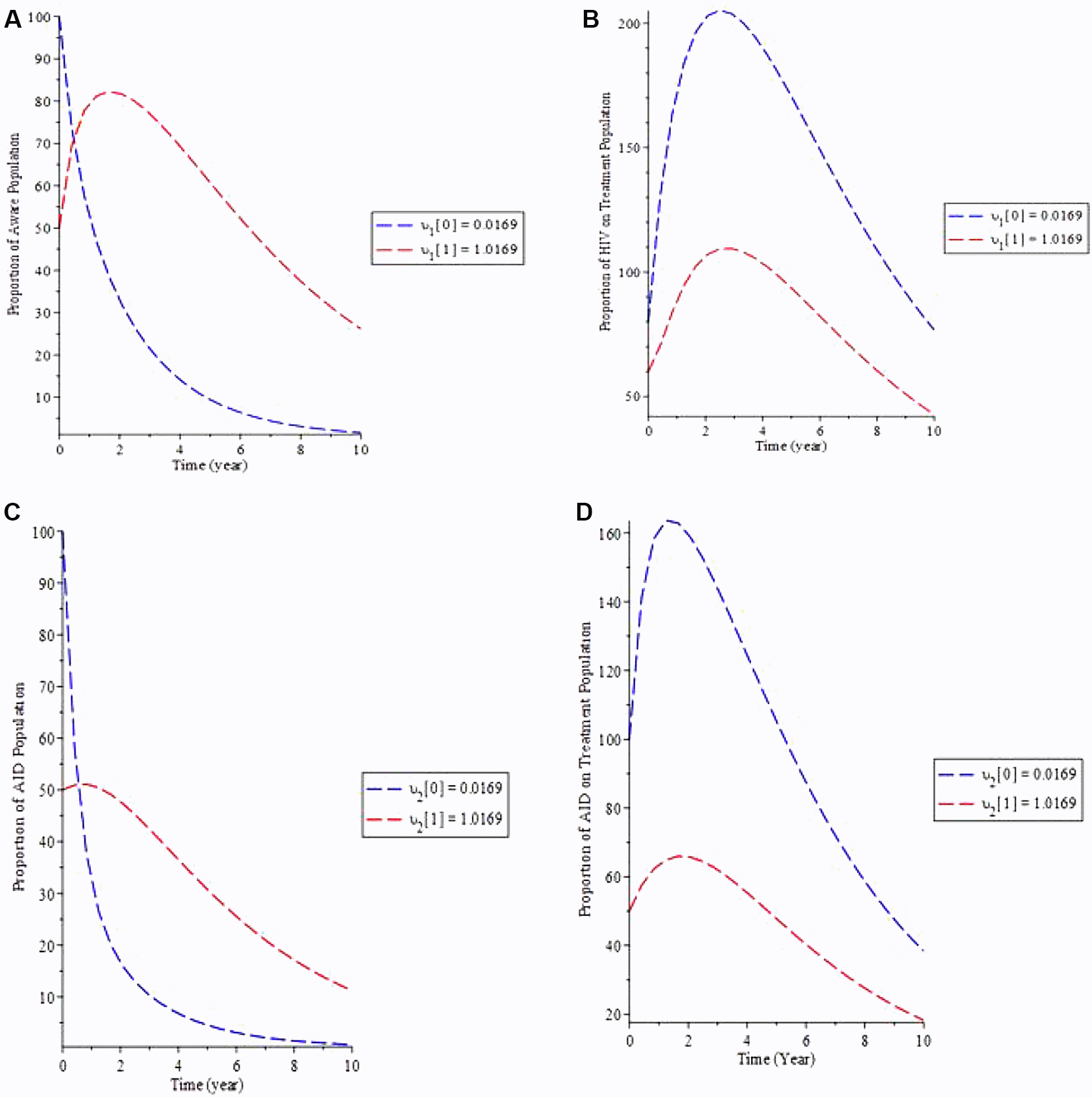
A. Variation of HIV Aware population for different values of υ. B. Variation of HIV on Treatment population for different values of υ. C. Variation of AIDS population for different values of υ. D. Variation of AIDS on Treatment population for different values of υ.

The increasing effect of testing and treatment on the model is examined in simulation 6.

From Figure 7(a-d), it is observed that if testing rate and treatment rate is increase,the unaware HIV decrease,while aware HIV and AIDS individual decrease with time due to treatment. Furthermore, the susceptible individual increases, and as treatment increases, so does the population of HIV and AIDS patients on treatment. As a result, increasing HIV screening and treatment is the first procedure to UNAIDS’ 90-90-90 aspirations.

Figure 7. (Simulation 6) Proportion of different Population at the increased values of α and θ.

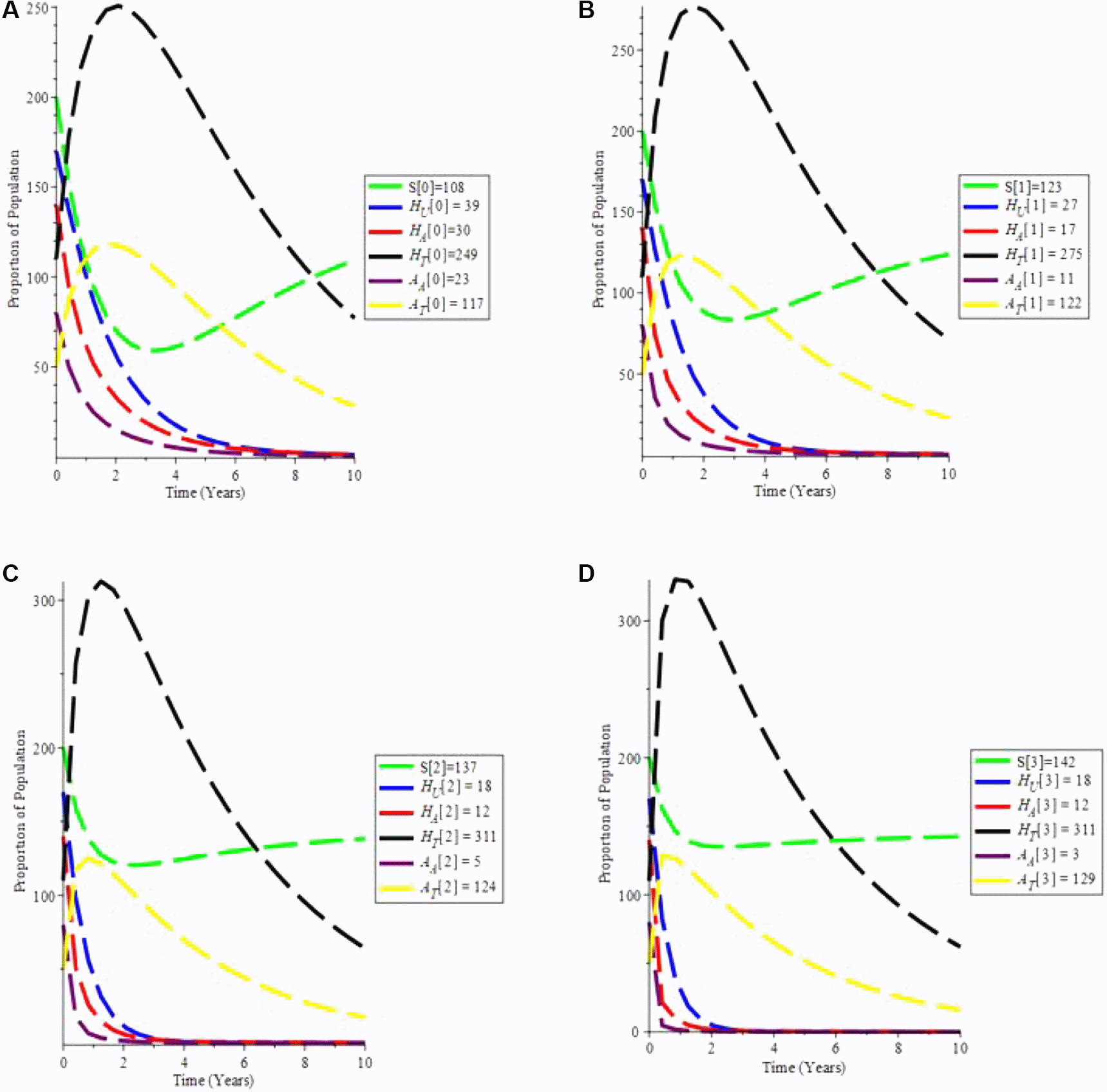
A. Proporation of Population when α = 0.7 and θ = 1.6949. B. Proporation of Population when α = 0.9 and θ = 2.6949. C. Proporation of Population when α = 1.5 and θ = 4.6949. D. Proporation of Population when α = 1.9 and θ = 9.6949.

Figure 8 shows the effect of treatment fall out on the reproduction number. When the number of infected individual on treatment that fallout is 19.8 percent then R₀ = 0.041. The linear graphical representation also revealed that if 40.1 percent of the population drops out of treatment, the reproduction number rises to 0.043. This simply means that, as defaulters lost to follow-up increase, the reproduction number also increases. Hence, reducing high-risk habits, mainly through education, is the most effective way to reduce the overall number of HIV/AIDS patients.

Figure 8. Impact of treatment fall out on HIV reproduction number.

6. Conclusions and recommendations

This study investigated the effect of testing and ART on the vertical and horizontal transmission dynamics of HIV/AIDS infection using an improved compartmental model and the dynamics theory of SI infectious diseases.

Reducing high-risk behaviours, primarily through education on the importance of HIV/AIDS status awareness and treatment adherence, is the best option for reducing the total number of HIV/AIDS patients.

Increased HIV testing is the first step toward UNAIDS’s 90-90-90 objectives, although many countries still face significant obstacles in attaining this goal. Early detection allows for prompt antiretroviral therapy, which lowers HIV viral load and hence slows the transmission of the virus. We believe that increasing HIV/AIDS diagnosis rates will increase the number of HIV/AIDS patients treated in the short term but decrease the number in the long term. WHO advises HIV self-testing as a complementary strategy,⁵⁹ which can improve the efficiency of HIV testing.⁶⁰

The current research showed that these intervention strategies are effective in combating the HIV/AIDS epidemic. This also emphasizes the need of behavioral and biologic therapies in preventing HIV transmission among pregnant women. This study has flaws, as well. First, statistics on drug resistance may be skewed because not all treated patients are tested early on, and secondly, homosexual transmission was not included in the model. Finally, certain characteristics were chosen on the basis of assumptions and may not really reflect reality.

In conclusion, the model implies that, in addition to HIV testing, behavioural and biologic strategies, effective condom use, and stringent adherence to ART are required for HIV prevention among individuals and pregnant women. Even in the face of medication resistance, ART and effective condom use can successfully limit the transmission of HIV. The 90-90-90 strategy may not be sufficient on its own to end the global HIV/AIDS outbreak.

Data availability

The data in this article come from Mukandivire et al., 2010, Zu et al., 2016, Lu et al., 2020, and other assumed/estimated data.

Software availability

Source code available from: https://github.com/OE-Abiodun/release/tag/v3.1.2

Archived source code at time of publication: https://doi.org/10.5281/zenodo.6894864.⁶⁶

License: GNU General Public License v3.0

References

1. Mayo Clinic:2020. - Hepatitis C - Symptoms and causes. [Accessed December 15, 2020].Reference Source
2. Public Health Agency of Canada: HIV transmission risk: A summary of the evidence2012. [Accessed December 15, 2020].
3. Mukandavire Z, Das P, Chiyaka C, et al.: Global analysis of an HIV/AIDS epidemic model. World J. Model. Simul. 2010; 6(3): 231–240.
4. UNAIDS:2019.Reference Source
5. UNAIDS: Global HIV and AIDS statistics – 2020 fact sheet.2020. [Accessed February 2021]Reference Source
6. HIV.ORG: The Global HIV/AIDS Epidemic statistics-2020.2020.Reference Source
7. UNAIDS: Start Free Stay Free AIDS Free - 2020 report.07 July 2020.Reference Source
8. global-statistics:2017. [Accessed June 2021].
9. UNAIDS: Global HIV and AIDS statistics – 2021 Fact sheet, Preliminary UNAIDS 2021 epidemiological estimates.2021. [Accessed June 2021].Reference Source
10. UNAIDS: Data Book [pdf]2018.
11. Kaiser Family Foundation (KFF): The Global HIV/AIDS Epidemic, Global Health Policy.2021. [Accessed June 2021].Reference Source
12. Teng TRY, De Lara-Tuprio EP, Macalalag JMR: An HIV/AIDS epidemic model with media coverage, vertical transmission and time delays. AIP Conference Proceedings 2192, 060021 2019. Published Online: 19 December 2019. Publisher Full Text
13. Oluwakemi A, Mohammed I, Olukayode A, et al.:Dynamical Analysis of Salmonella Epidemic Model with Saturated Incidence Rate.Yang XS, Sherratt S, Dey N, et al., editors. Proceedings of Sixth International Congress on Information and Communication Technology. Lecture Notes in Networks and Systems. Singapore:Springer;2022; (217. ). Publisher Full Text
14. Olajumoke O, Olukayode A, James N, et al.:Global Stability Analysis of HBV Epidemics with Vital Dynamics.Yang XS, Sherratt S, Dey N, et al., editors. Proceedings of Sixth International Congress on Information and Communication Technology. Lecture Notes in Networks and Systems. Singapore:Springer;2022; (217. ). Publisher Full Text
15. Adebimpe O, et al.:Dynamical Modeling of Measles with Different Saturated Incidence Rate.Yang XS, Sherratt S, Dey N, et al., editors. Proceedings of Sixth International Congress on Information and Communication Technology. Lecture Notes in Networks and Systems. Singapore:Springer;2022; (217. ). Publisher Full Text
16. Oludoun O, Adebimpe O, Ndako J, et al.: The impact of testing and treatment on the dynamics of Hepatitis B virus. F1000Res. 2021; 10: 936. PubMed Abstract | Publisher Full Text
17. Hajhamed M, Hajhamed M: ATI Treatment for HIV.2021; 3(1): 2021.
18. Saxena SK, Khurana SMP: NanoBioMedicine. NanoBioMedicine. 2020. Publisher Full Text
19. Sagar M: HIV-1 transmission biology: selection and characteristics of infecting viruses. J. Infect. Dis. 2010; 202 Suppl 2(Suppl 2): S289–S296. PubMed Abstract | Publisher Full Text
20. Pinto CMA, Carvalho A: Effects of treatment, awareness and condom use in a coinfection model for HIV and HCV in MSM. J. Biol. Syst. 2015; 23(2): 165–193. Publisher Full Text
21. Hamouda O: Epidemiology of HIV and AIDS. MMW-Fortschritte Der Medizin 2010; 152(17): 27–30. PubMed Abstract | Publisher Full Text
22. Oguntibeju OO, van den Heeve WMJ, Van Schalkwyk FE: A Review of the Epidemiology, Biology and Pathogenesis of HIV. J. Biol. Sci. 2007; 7: 1296–1304. Publisher Full Text
23. Anderson RM: The role of mathematical models in the study of HIV transmission and the epidemiology of AIDS. J. AIDS. 1988; 1: 241–256.
24. Anderson RM, Medly GF, May RM, et al.: A preliminary study of the transmission dynamics of the Human Immunodeficiency Virus (HIV), the causative agent of AIDS. IMA J. Math. Appl. Med. Biol. 1986; 3: 229–263. PubMed Abstract | Publisher Full Text
25. May RM, Anderson RM: Transmission dynamics of HIV infection. Nature 1987; 326: 137–142. Publisher Full Text
26. Attaullah, Sohaib M: Mathematical modeling and numerical simulation of HIV infection model. Results Appl. Math. 2020; 7: 100118. Publisher Full Text
27. Lu Z, Wang L, Wang LP, et al.: A mathematical model for HIV prevention and control among men who have sex with men in China. Epidemiol. Infect. 2020; 148: e224. PubMed Abstract | Publisher Full Text
28. Iqbal Z, Ahmed N, Baleanu D, et al.: Positivity and boundedness preserving numerical algorithm for the solution of fractional nonlinear epidemic model of HIV/AIDS transmission. Chaos, Solitons Fractals. 2020; 134: 109706. Publisher Full Text
29. Jawaz M, Ahmed N, Baleanu D, et al.: Positivity Preserving Technique for the Solution of HIV/AIDS Reaction Diffusion Model With Time Delay. Front. Phys. 2020; 7(January): 1–10. 10.3389/.
30. Rana PS, Sharma N: Mathematical modeling and stability analysis of a SI type model for HIV/AIDS. J. Interdiscip. Math. 2020; 23(1): 257–273. Publisher Full Text
31. Munawwaroh DA, Sutimin H, Heri R, et al.: Analysis stability of HIV/AIDS epidemic model of different infection stage in closed community. J. Phys. Conf. Ser. 2020; 1524(1): 012130. Publisher Full Text
32. Mushanyu J: A note on the impact of late diagnosis on HIV/AIDS dynamics: a mathematical modelling approach. BMC. Res. Notes 2020; 13(1): 340–348. PubMed Abstract | Publisher Full Text
33. Saad FT, Sanlidag T, Hincal E, et al.:Global stability analysis of HIV+ model. Advances in Intelligent Systems and Computing. Springer International Publishing;2019; (Vol. 896). Publisher Full Text
34. Theses E, Ngina PM, Citation R: Mathematical modelling of In-vivo HIV optimal therapy and management Mathematical Modelling of In-vivo HIV Optimal Therapy and Management.2018.
35. Li Z, Teng Z, Miao H: Modeling and Control for HIV/AIDS Transmission in China Based on Data from 2004 to 2016. Comput. Math. Methods Med. 2017; 2017: 1–13. PubMed Abstract | Publisher Full Text
36. Senthilkumaran M, Narmatha K: Mathematical Analysis of an HIV/AIDS Epidemic Model with delay 1 Introduction. 2(January), 63–762017. Publisher Full Text
37. Jia J, Qin G: Stability analysis of HIV/AIDS epidemic model with nonlinear incidence and treatment. Adv. Differ. Equ. 2017; 2017(1). Publisher Full Text
38. Rani P, Jain D, Saxena VP: Stability analysis of HIV/AIDS transmission with treatment and role of female sex workers. Int. J. Nonlinear Sci. Numer. Simul. 2017; 18(6): 457–467. Publisher Full Text
39. Ogunlaran OM, Oukouomi Noutchie SC: Mathematical model for an effective management of HIV infection. Biomed. Res. Int. 2016; 2016: 1–6. PubMed Abstract | Publisher Full Text
40. Zu G, Mo I, Danbaba A, et al.: Mathematical Modelling for Screening and Migration in Horizontal and Vertical Transmission of HIV/AIDS.2016; 5(1): 4–10.
41. Bozkurt F, Peker F: Mathematical modelling of HIV epidemic and stability analysis. Adv. Differ. Equ. 2014; 2014(1): 1–17. Publisher Full Text
42. Li Q, Cao S, Chen X, et al.: Stability analysis of an HIV/AIDS dynamics model with drug resistance. Discret. Dyn. Nat. Soc. 2012; 2012: 1–13. Publisher Full Text
43. Daabo MI, Seidu B: Modelling the Effect of Irresponsible Infective Immigrants on the Transmission Dynamics of HIV/AIDS.2012; 3(1): 31–40.
44. Al-sheikh S: Stability Analysis of an HIV/AIDS Epidemic Model with Screening.2011; 6(66): 3251–3273.
45. Nyabadza F, Mukandavire Z, Hove-Musekwa SD: Modelling the HIV/AIDS epidemic trends in South Africa: Insights from a simple mathematical model. Nonlinear Anal. Real World Appl. 2011; 12(4): 2091–2104. Publisher Full Text
46. Akpa OM, Oyejola BA: Modeling the transmission dynamics of HIV/AIDS epidemics: An introduction and a review. J. Infect. Dev. Ctries. 2010; 4(10): 597–608. PubMed Abstract | Publisher Full Text
47. Cai L, Li X, Ghosh M, et al.: Stability analysis of an HIV/AIDS epidemic model with treatment. J. Comput. Appl. Math. 2009; 229(1): 313–323. Publisher Full Text
48. Marks G, Crepaz N, Senterfitt JW, et al.: Meta-analysis of high-risk sexual behavior in persons aware and unaware they are infected with hiv in the united states: implications for hiv prevention programs. J. Acquir. Immune Defic. Syndr. 2005; 39: 446–453. PubMed Abstract | Publisher Full Text
49. Eshleman SH: HHS Public Access. Physiol. Behav. 2019; 176(3): 139–148. PubMed Abstract | Publisher Full Text
50. Ping L-H, Jabara CB, Rodrigo AG, et al.: HIV-1 Transmission during Early Antiretroviral Therapy: Evaluation of Two HIV-1 Transmission Events in the HPTN 052 Prevention Study. PLoS One. 2013; 8(9): e71557. PubMed Abstract | Publisher Full Text
51. Zhimin S, Dong C, Li P, et al.: A mathematical modeling study of the HIV epidemics at two rural townships in the Liangshan Prefecture of the Sichuan Province of China. J. Infect. Dis. Model. 2016; 1: 3–10.
52. Zu G, Mo I, Danbaba A, et al.: Mathematical Modelling for Screening and Migration in Horizontal and Vertical Transmission of HIV/AIDS.2016; 5(1): 4–10.
53. van den Driessche P , Watmough J: Reproduction numbers and subthreshold endemic equilibria for compartmental models of disease transmission. Math. Biosci. 2002; 180: 29–48. PubMed Abstract | Publisher Full Text
54. Diekmann O, Hesterbeek JAP, Metz JAJ: On the definition and the computation of the basic reproduction ratio R ₀ in models for infectious diseases in heterogeneous populations. J. Math. Biol. 1990; 28: 365–382. PubMed Abstract
55. Okuonghae 2016.
56. Brauer F, Castillo-Chaavez C: Mathematical models for communicable diseases, volume 84. SIAM.2012.
57. Chitnis N, Hyman JM, Cushing JM: Determining important parameters in the spread of malaria through the sensitivity analysis of a mathematical model. Bull. Math. Biol. 2008; 70(5): 1272–1296. PubMed Abstract | Publisher Full Text
58. Caswell H: Construction, analysis, and interpretation. Sunderland:Sinauer;2001.
59. WHO Guidelines on HIV Self-Testing and Partner Notification: Supplement to Consolidated Guidelines on HIV Testing Services. Geneva:World Health Organization;2016.
60. Tang W, et al.: What happens after HIV self-testing? Results from a longitudinal cohort of Chinese men who have sex with men. BMC Infect. Dis. 2019; 19: 807. PubMed Abstract | Publisher Full Text
61. Lansky A, Nakashima A, Jones J: Risk behaviors related to heterosexual transmission from HIV2 38 infected persons. Sex. Transm. Dis. 2000; 27: 483–489. PubMed Abstract | Publisher Full Text
62. Nicolosi A, Musicco M, et al.: Risk factors for woman-to-man sexual transmission 255 of the human immunodeficiency virus. J. Acquir. Immune Defic. Syndr. 1994; 7: 296–300. PubMed Abstract
63. OBrien T, Busch M, et al.: Heterosexual transmission of human 257 immunodeficiency virus type 1 from transfusion recipients to their sex partners. J. Acquir. Immune Defic. Syndr. 1994; 7: 705–710.
64. Brauer F, Castillo-Chaavez C: Mathematical models for communicable diseases. SIAM;2012; vol. 84.
65. Brauer F, Castillo-Chavez C: Mathematical models in population biology and epidemiology. Springer;2001; vol. 40.
66. Abiodun OE: OE-Abiodun/OE-Abiodun: F1000: HIV ONLY MODEL (v3.1.2). [Software] Zenodo.2022. Publisher Full Text

Comments on this article Comments (0)

Version 2

VERSION 2 PUBLISHED 07 Oct 2022

Author details Author details

¹ Physical Sciences, Landmark University, Omu Aran, Kwara, 251101, Nigeria
² Mathematics and Statistic, First Technical University, Ibadan, Nigeria, 200103, Nigeria
³ Mathematics and Statistic, Lagos State Polytechnic, Lagos, Lagos, Nigeria

Oluwakemi E. Abiodun
Roles: Formal Analysis, Investigation, Methodology, Writing – Original Draft Preparation

Olukayode Adebimpe
Roles: Supervision, Writing – Review & Editing

James Ndako
Roles: Supervision, Writing – Review & Editing

Olajumoke Oludoun
Roles: Conceptualization, Validation

Benedicta Aladeitan
Roles: Investigation, Resources

Michael Adeniyi
Roles: Methodology, Software, Writing – Review & Editing

Competing interests

No competing interests were disclosed.

Grant information

The author(s) declared that no grants were involved in supporting this work.

Article Versions (2)

version 2

Revised

Published: 28 Feb 2023, 11:1145

https://doi.org/10.12688/f1000research.123693.2

version 1

Published: 07 Oct 2022, 11:1145

https://doi.org/10.12688/f1000research.123693.1

Copyright

© 2022 Abiodun OE et al. This is an open access article distributed under the terms of the Creative Commons Attribution License, which permits unrestricted use, distribution, and reproduction in any medium, provided the original work is properly cited.

Download

Export To

metrics

	Views	Downloads
F1000Research	-	-
PubMed Central Data from PMC are received and updated monthly.	-	-

Citations

0

SEE MORE DETAILS

CITE

how to cite this article

Abiodun OE, Adebimpe O, Ndako J et al. Qualitative analysis of HIV and AIDS disease transmission: impact of awareness, testing and effective follow up [version 1; peer review: 1 approved, 1 approved with reservations, 1 not approved]. F1000Research 2022, 11:1145 (https://doi.org/10.12688/f1000research.123693.1)

NOTE: If applicable, it is important to ensure the information in square brackets after the title is included in all citations of this article.

track

receive updates on this article

Track an article to receive email alerts on any updates to this article.

Open Peer Review

Current Reviewer Status: ?

Key to Reviewer Statuses VIEW HIDE

ApprovedThe paper is scientifically sound in its current form and only minor, if any, improvements are suggested

Approved with reservations A number of small changes, sometimes more significant revisions are required to address specific details and improve the papers academic merit.

Not approvedFundamental flaws in the paper seriously undermine the findings and conclusions

Version 1

VERSION 1

PUBLISHED 07 Oct 2022

Views

12

Reviewer Report 25 Jan 2023

Ropo Ebenzer Ogunsakin, Discipline of Public Health Medicine, School of Nursing & Public Health, College of Health Sciences, University of KwaZulu-Natal, Durban, South Africa

Approved

https://doi.org/10.5256/f1000research.135825.r159237

In this paper, the authors developed a new mathematical model for the transmission dynamics of HIV and AIDS and the model was rigorously analysed. The authors considered the impact of three major strategies (impact of awareness, testing and follow up) ... Continue reading

In this paper, the authors developed a new mathematical model for the transmission dynamics of HIV and AIDS and the model was rigorously analysed. The authors considered the impact of three major strategies (impact of awareness, testing and follow up) which are important in controlling the transmission dynamics of HIV/AIDS. The six- compartmental model of HIV/AID presented are: Susceptible, (S), representing people who prone to be infected with HIV in engage in risk habits/factors, those who are unaware of their HIV status (HU), those who become aware after testing (HA), those who are placed on treatment after becoming aware (HT); the AIDS individuals (AA) due to non-adherence to treatment and the AIDS on treatment population (AT). The author showed that the model is positive through a given region in their analyses and the reproduction number of the model was correctly worked out. The effects of the strategies were graphically represented in the numerical simulations. The title is peaks a volume to the context of the article.

The work is well organized and approved for indexing. I have the following observation/comment on the paper:

The overall command of English looks good, however there are some grammatical errors in the paper. Also the authors should check for incomplete sentences in the paper.
Some representation can be made to reduce the size of the matrices as they are big or boxes should be adjusted.
It is necessary that the biological meaning of R0 be properly stated.
In the sensitivity section, the authors can as well placed the real values of the indices.
The conclusion looks good, the novelty of the work is discussed.

Is the work clearly and accurately presented and does it cite the current literature?

Yes
Is the study design appropriate and is the work technically sound?

Yes
Are sufficient details of methods and analysis provided to allow replication by others?

Yes
If applicable, is the statistical analysis and its interpretation appropriate?

Partly
Are all the source data underlying the results available to ensure full reproducibility?

Yes
Are the conclusions drawn adequately supported by the results?

Yes

Competing Interests: No competing interests were disclosed.

Reviewer Expertise: Statistician, Biological and Computational Mathematics

I confirm that I have read this submission and believe that I have an appropriate level of expertise to confirm that it is of an acceptable scientific standard.

CITE

Report a concern

Respond or Comment

Views

17

Reviewer Report 05 Jan 2023

Fatmawati Fatmawati, Department of Mathematics, Faculty of Science and Technology, Universitas Airlangga, Surabaya, Indonesia

Not Approved

https://doi.org/10.5256/f1000research.135825.r158041

I have read this article. Some of my critical comments include:

Please explore the novelty of this article. What is the difference between this article and previous research that already exists.

I have read this article. Some of my critical comments include:

Please explore the novelty of this article. What is the difference between this article and previous research that already exists.
I don't see the connection between the existence of the endemic equilibrium point and basic reproduction number (R0). Likewise to prove the stability of the disease-free equilibrium. The authors only mention that if R0 < 1 then the disease-free equilibrium is LAS, while depending on R0 cannot be proven exactly
Please also check for proof of global stability of the disease-free equilibrium.
The authors must proofread very carefully the language of the manuscript.
Carefully check in whole manuscript, dot, and comma after each equation.
Then numerical results need to be discussed in more details.
The conclusion sections should highlight the main findings of this study.
References should be up to date and must follow the style correctly.

Is the work clearly and accurately presented and does it cite the current literature?

Partly
Is the study design appropriate and is the work technically sound?

Partly
Are sufficient details of methods and analysis provided to allow replication by others?

Partly
If applicable, is the statistical analysis and its interpretation appropriate?

Partly
Are all the source data underlying the results available to ensure full reproducibility?

No
Are the conclusions drawn adequately supported by the results?

Partly

Competing Interests: No competing interests were disclosed.

Reviewer Expertise: Mathematical modeling in life science, optimal control, fractional modelling.

I confirm that I have read this submission and believe that I have an appropriate level of expertise to state that I do not consider it to be of an acceptable scientific standard, for reasons outlined above.

CITE

Report a concern

Respond or Comment

Views

22

Reviewer Report 18 Nov 2022

Adedapo Loyinmi, Department of Mathematics, Tai Solarin University of Education, Ijebu ode, Nigeria

Approved with Reservations

https://doi.org/10.5256/f1000research.135825.r152688

The article proposed a mathematical model for the transmission dynamics of HIV and AIDS considering three control/preventive strategies: the impact of awareness, testing and follow up. The work presented a six- compartmental model of HIV/AID which are Susceptible, (S), representing ... Continue reading

The article proposed a mathematical model for the transmission dynamics of HIV and AIDS considering three control/preventive strategies: the impact of awareness, testing and follow up. The work presented a six- compartmental model of HIV/AID which are Susceptible, (S), representing people who are likely to become infected with HIV; Unaware HIV infective, (HU), Aware HIV infective (HA), Treated HIV infective, (HT); AIDS individuals (AA) and AIDS on treatment individuals (AT). Analysis of the model showed that the model is positively invariant. Also, the reproduction number of the model was accurately worked out. The stability of the model showed that the disease free and endemic equilibrium is stable if necessary conditions are satisfied. The numerical simulations graphically showed the effect of the control strategies. The work is well organized and suitable for indexing.

However, a few issues should be addressed:

The manuscript needs to be properly arranged as some of the matrices are too big. The boxes should be adjusted.
Under stability analysis of the DFE, the R0 is not clearly shown. Since conclusion depends on the value of R0, it is necessary that R0 is properly substituted in the equation.
In the sensitivity section, the sensitivity value need to be presented in order to know how sensitive each parameters are. The + and - signs are not enough
Graphs are not bold enough.
Revisit the conclusion under stability of DFE to drive home your findings
In figure 5, I suggest that more than two values of ζ be used.
In the conclusion, the novelty of the work is not elaborately discussed. Please rewrite this part to show what the contribution to knowledge is.
There should be a paragraph discussing earlier work on diseases such as Ebola, covid-19 and the likes threatening global health. Such articles like, but not limited to 'qualitative analysis and dynamical behaviour of a Lassa haemorrhagic fever model with exposed rodents and saturated incidence rate' would help.

Is the work clearly and accurately presented and does it cite the current literature?

Yes
Is the study design appropriate and is the work technically sound?

Yes
Are sufficient details of methods and analysis provided to allow replication by others?

Yes
If applicable, is the statistical analysis and its interpretation appropriate?

Yes
Are all the source data underlying the results available to ensure full reproducibility?

Yes
Are the conclusions drawn adequately supported by the results?

Yes

Competing Interests: No competing interests were disclosed.

Reviewer Expertise: Biological and computational Mathematics

I confirm that I have read this submission and believe that I have an appropriate level of expertise to confirm that it is of an acceptable scientific standard, however I have significant reservations, as outlined above.

CITE

Report a concern

Respond or Comment

Comments on this article Comments (0)

Version 2

VERSION 2 PUBLISHED 07 Oct 2022

Open Peer Review

Reviewer Status

Reviewer Reports

	Invited Reviewers
	1	2	3
Version 2 (revision) 28 Feb 23	read	read
Version 1 07 Oct 22	read	read	read

Adedapo Loyinmi, Tai Solarin University of Education, Ijebu ode, Nigeria
Fatmawati Fatmawati, Universitas Airlangga, Surabaya, Indonesia
Ropo Ebenzer Ogunsakin, University of KwaZulu-Natal, Durban, South Africa

Comments on this article

All Comments(0)

Add a comment

Sign up for content alerts

Browse by related subjects

Back to all reports

Reviewer Report

8 Views

13 Mar 2023 | for Version 2

Fatmawati Fatmawati, Department of Mathematics, Faculty of Science and Technology, Universitas Airlangga, Surabaya, Indonesia

8 Views Cite this report Responses(0)

Approved

The authors have addressed most of the issues raised in my report, and improved the paper accordingly.

Competing Interests

No competing interests were disclosed.

Reviewer Expertise

Mathematical modeling in life science, optimal control, fractional modelling.

I confirm that I have read this submission and believe that I have an appropriate level of expertise to confirm that it is of an acceptable scientific standard.

Respond to this report

Responses (0)

Back to all reports

Reviewer Report

5 Views

08 Mar 2023 | for Version 2

Adedapo Loyinmi, Department of Mathematics, Tai Solarin University of Education, Ijebu ode, Nigeria

5 Views Cite this report Responses(0)

Approved

All observed lapses are corrected. The article is now fit for indexing.

Competing Interests

No competing interests were disclosed.

Reviewer Expertise

Biological and computational Mathematics

I confirm that I have read this submission and believe that I have an appropriate level of expertise to confirm that it is of an acceptable scientific standard.

Respond to this report

Responses (0)

Back to all reports

Reviewer Report

12 Views

25 Jan 2023 | for Version 1

Ropo Ebenzer Ogunsakin, Discipline of Public Health Medicine, School of Nursing & Public Health, College of Health Sciences, University of KwaZulu-Natal, Durban, South Africa

12 Views Cite this report Responses(0)

Approved

In this paper, the authors developed a new mathematical model for the transmission dynamics of HIV and AIDS and the model was rigorously analysed. The authors considered the impact of three major strategies (impact of awareness, testing and follow up) which are important in controlling the transmission dynamics of HIV/AIDS. The six- compartmental model of HIV/AID presented are: Susceptible, (S), representing people who prone to be infected with HIV in engage in risk habits/factors, those who are unaware of their HIV status (HU), those who become aware after testing (HA), those who are placed on treatment after becoming aware (HT); the AIDS individuals (AA) due to non-adherence to treatment and the AIDS on treatment population (AT). The author showed that the model is positive through a given region in their analyses and the reproduction number of the model was correctly worked out. The effects of the strategies were graphically represented in the numerical simulations. The title is peaks a volume to the context of the article.

The work is well organized and approved for indexing. I have the following observation/comment on the paper:

The overall command of English looks good, however there are some grammatical errors in the paper. Also the authors should check for incomplete sentences in the paper.
Some representation can be made to reduce the size of the matrices as they are big or boxes should be adjusted.
It is necessary that the biological meaning of R0 be properly stated.
In the sensitivity section, the authors can as well placed the real values of the indices.
The conclusion looks good, the novelty of the work is discussed.

Is the work clearly and accurately presented and does it cite the current literature?

Yes
Is the study design appropriate and is the work technically sound?

Yes
Are sufficient details of methods and analysis provided to allow replication by others?

Yes
If applicable, is the statistical analysis and its interpretation appropriate?

Partly
Are all the source data underlying the results available to ensure full reproducibility?

Yes
Are the conclusions drawn adequately supported by the results?

Yes

Competing Interests

No competing interests were disclosed.

Reviewer Expertise

Statistician, Biological and Computational Mathematics

I confirm that I have read this submission and believe that I have an appropriate level of expertise to confirm that it is of an acceptable scientific standard.

Respond to this report

Responses (0)

Back to all reports

Reviewer Report

17 Views

05 Jan 2023 | for Version 1

Fatmawati Fatmawati, Department of Mathematics, Faculty of Science and Technology, Universitas Airlangga, Surabaya, Indonesia

17 Views Cite this report Responses(0)

Not Approved

I have read this article. Some of my critical comments include:

Please explore the novelty of this article. What is the difference between this article and previous research that already exists.
I don't see the connection between the existence of the endemic equilibrium point and basic reproduction number (R0). Likewise to prove the stability of the disease-free equilibrium. The authors only mention that if R0 < 1 then the disease-free equilibrium is LAS, while depending on R0 cannot be proven exactly
Please also check for proof of global stability of the disease-free equilibrium.
The authors must proofread very carefully the language of the manuscript.
Carefully check in whole manuscript, dot, and comma after each equation.
Then numerical results need to be discussed in more details.
The conclusion sections should highlight the main findings of this study.
References should be up to date and must follow the style correctly.

Is the work clearly and accurately presented and does it cite the current literature?

Partly
Is the study design appropriate and is the work technically sound?

Partly
Are sufficient details of methods and analysis provided to allow replication by others?

Partly
If applicable, is the statistical analysis and its interpretation appropriate?

Partly
Are all the source data underlying the results available to ensure full reproducibility?

No
Are the conclusions drawn adequately supported by the results?

Partly

Competing Interests

No competing interests were disclosed.

Reviewer Expertise

Mathematical modeling in life science, optimal control, fractional modelling.

I confirm that I have read this submission and believe that I have an appropriate level of expertise to state that I do not consider it to be of an acceptable scientific standard, for reasons outlined above.

Respond to this report

Responses (0)

Back to all reports

Reviewer Report

22 Views

18 Nov 2022 | for Version 1

Adedapo Loyinmi, Department of Mathematics, Tai Solarin University of Education, Ijebu ode, Nigeria

22 Views Cite this report Responses(0)

Approved With Reservations

The article proposed a mathematical model for the transmission dynamics of HIV and AIDS considering three control/preventive strategies: the impact of awareness, testing and follow up. The work presented a six- compartmental model of HIV/AID which are Susceptible, (S), representing people who are likely to become infected with HIV; Unaware HIV infective, (HU), Aware HIV infective (HA), Treated HIV infective, (HT); AIDS individuals (AA) and AIDS on treatment individuals (AT). Analysis of the model showed that the model is positively invariant. Also, the reproduction number of the model was accurately worked out. The stability of the model showed that the disease free and endemic equilibrium is stable if necessary conditions are satisfied. The numerical simulations graphically showed the effect of the control strategies. The work is well organized and suitable for indexing.

However, a few issues should be addressed:

The manuscript needs to be properly arranged as some of the matrices are too big. The boxes should be adjusted.
Under stability analysis of the DFE, the R0 is not clearly shown. Since conclusion depends on the value of R0, it is necessary that R0 is properly substituted in the equation.
In the sensitivity section, the sensitivity value need to be presented in order to know how sensitive each parameters are. The + and - signs are not enough
Graphs are not bold enough.
Revisit the conclusion under stability of DFE to drive home your findings
In figure 5, I suggest that more than two values of ζ be used.
In the conclusion, the novelty of the work is not elaborately discussed. Please rewrite this part to show what the contribution to knowledge is.
There should be a paragraph discussing earlier work on diseases such as Ebola, covid-19 and the likes threatening global health. Such articles like, but not limited to 'qualitative analysis and dynamical behaviour of a Lassa haemorrhagic fever model with exposed rodents and saturated incidence rate' would help.

Is the work clearly and accurately presented and does it cite the current literature?

Yes
Is the study design appropriate and is the work technically sound?

Yes
Are sufficient details of methods and analysis provided to allow replication by others?

Yes
If applicable, is the statistical analysis and its interpretation appropriate?

Yes
Are all the source data underlying the results available to ensure full reproducibility?

Yes
Are the conclusions drawn adequately supported by the results?

Yes

Competing Interests

No competing interests were disclosed.

Reviewer Expertise

Biological and computational Mathematics

I confirm that I have read this submission and believe that I have an appropriate level of expertise to confirm that it is of an acceptable scientific standard, however I have significant reservations, as outlined above.

Respond to this report

Responses (0)

[1] 1. Mayo Clinic:2020. - Hepatitis C - Symptoms and causes. [Accessed December 15, 2020].Reference Source

[2] 2. Public Health Agency of Canada: HIV transmission risk: A summary of the evidence2012. [Accessed December 15, 2020].

[3] 3. Mukandavire Z, Das P, Chiyaka C, et al.: Global analysis of an HIV/AIDS epidemic model. World J. Model. Simul. 2010; 6(3): 231–240.

[4] 4. UNAIDS:2019.Reference Source

[5] 5. UNAIDS: Global HIV and AIDS statistics – 2020 fact sheet.2020. [Accessed February 2021]Reference Source

[6] 6. HIV.ORG: The Global HIV/AIDS Epidemic statistics-2020.2020.Reference Source

[7] 7. UNAIDS: Start Free Stay Free AIDS Free - 2020 report.07 July 2020.Reference Source

[8] 8. global-statistics:2017. [Accessed June 2021].

[9] 9. UNAIDS: Global HIV and AIDS statistics – 2021 Fact sheet, Preliminary UNAIDS 2021 epidemiological estimates.2021. [Accessed June 2021].Reference Source

[10] 10. UNAIDS: Data Book [pdf]2018.

[11] 11. Kaiser Family Foundation (KFF): The Global HIV/AIDS Epidemic, Global Health Policy.2021. [Accessed June 2021].Reference Source

[12] 12. Teng TRY, De Lara-Tuprio EP, Macalalag JMR: An HIV/AIDS epidemic model with media coverage, vertical transmission and time delays. AIP Conference Proceedings 2192, 060021 2019. Published Online: 19 December 2019. Publisher Full Text

[13] 13. Oluwakemi A, Mohammed I, Olukayode A, et al.:Dynamical Analysis of Salmonella Epidemic Model with Saturated Incidence Rate.Yang XS, Sherratt S, Dey N, et al., editors. Proceedings of Sixth International Congress on Information and Communication Technology. Lecture Notes in Networks and Systems. Singapore:Springer;2022; (217. ). Publisher Full Text

[14] 14. Olajumoke O, Olukayode A, James N, et al.:Global Stability Analysis of HBV Epidemics with Vital Dynamics.Yang XS, Sherratt S, Dey N, et al., editors. Proceedings of Sixth International Congress on Information and Communication Technology. Lecture Notes in Networks and Systems. Singapore:Springer;2022; (217. ). Publisher Full Text

[15] 15. Adebimpe O, et al.:Dynamical Modeling of Measles with Different Saturated Incidence Rate.Yang XS, Sherratt S, Dey N, et al., editors. Proceedings of Sixth International Congress on Information and Communication Technology. Lecture Notes in Networks and Systems. Singapore:Springer;2022; (217. ). Publisher Full Text

[16] 16. Oludoun O, Adebimpe O, Ndako J, et al.: The impact of testing and treatment on the dynamics of Hepatitis B virus. F1000Res. 2021; 10: 936. PubMed Abstract | Publisher Full Text

[17] 17. Hajhamed M, Hajhamed M: ATI Treatment for HIV.2021; 3(1): 2021.

[18] 18. Saxena SK, Khurana SMP: NanoBioMedicine. NanoBioMedicine. 2020. Publisher Full Text

[19] 19. Sagar M: HIV-1 transmission biology: selection and characteristics of infecting viruses. J. Infect. Dis. 2010; 202 Suppl 2(Suppl 2): S289–S296. PubMed Abstract | Publisher Full Text

[20] 20. Pinto CMA, Carvalho A: Effects of treatment, awareness and condom use in a coinfection model for HIV and HCV in MSM. J. Biol. Syst. 2015; 23(2): 165–193. Publisher Full Text

[21] 21. Hamouda O: Epidemiology of HIV and AIDS. MMW-Fortschritte Der Medizin 2010; 152(17): 27–30. PubMed Abstract | Publisher Full Text

[22] 22. Oguntibeju OO, van den Heeve WMJ, Van Schalkwyk FE: A Review of the Epidemiology, Biology and Pathogenesis of HIV. J. Biol. Sci. 2007; 7: 1296–1304. Publisher Full Text

[23] 23. Anderson RM: The role of mathematical models in the study of HIV transmission and the epidemiology of AIDS. J. AIDS. 1988; 1: 241–256.

[24] 24. Anderson RM, Medly GF, May RM, et al.: A preliminary study of the transmission dynamics of the Human Immunodeficiency Virus (HIV), the causative agent of AIDS. IMA J. Math. Appl. Med. Biol. 1986; 3: 229–263. PubMed Abstract | Publisher Full Text

[25] 25. May RM, Anderson RM: Transmission dynamics of HIV infection. Nature 1987; 326: 137–142. Publisher Full Text

[26] 26. Attaullah, Sohaib M: Mathematical modeling and numerical simulation of HIV infection model. Results Appl. Math. 2020; 7: 100118. Publisher Full Text

[27] 27. Lu Z, Wang L, Wang LP, et al.: A mathematical model for HIV prevention and control among men who have sex with men in China. Epidemiol. Infect. 2020; 148: e224. PubMed Abstract | Publisher Full Text

[28] 28. Iqbal Z, Ahmed N, Baleanu D, et al.: Positivity and boundedness preserving numerical algorithm for the solution of fractional nonlinear epidemic model of HIV/AIDS transmission. Chaos, Solitons Fractals. 2020; 134: 109706. Publisher Full Text

[29] 29. Jawaz M, Ahmed N, Baleanu D, et al.: Positivity Preserving Technique for the Solution of HIV/AIDS Reaction Diffusion Model With Time Delay. Front. Phys. 2020; 7(January): 1–10. 10.3389/.

[30] 30. Rana PS, Sharma N: Mathematical modeling and stability analysis of a SI type model for HIV/AIDS. J. Interdiscip. Math. 2020; 23(1): 257–273. Publisher Full Text

[31] 31. Munawwaroh DA, Sutimin H, Heri R, et al.: Analysis stability of HIV/AIDS epidemic model of different infection stage in closed community. J. Phys. Conf. Ser. 2020; 1524(1): 012130. Publisher Full Text

[32] 32. Mushanyu J: A note on the impact of late diagnosis on HIV/AIDS dynamics: a mathematical modelling approach. BMC. Res. Notes 2020; 13(1): 340–348. PubMed Abstract | Publisher Full Text

[33] 33. Saad FT, Sanlidag T, Hincal E, et al.:Global stability analysis of HIV+ model. Advances in Intelligent Systems and Computing. Springer International Publishing;2019; (Vol. 896). Publisher Full Text

[34] 34. Theses E, Ngina PM, Citation R: Mathematical modelling of In-vivo HIV optimal therapy and management Mathematical Modelling of In-vivo HIV Optimal Therapy and Management.2018.

[35] 35. Li Z, Teng Z, Miao H: Modeling and Control for HIV/AIDS Transmission in China Based on Data from 2004 to 2016. Comput. Math. Methods Med. 2017; 2017: 1–13. PubMed Abstract | Publisher Full Text

[36] 36. Senthilkumaran M, Narmatha K: Mathematical Analysis of an HIV/AIDS Epidemic Model with delay 1 Introduction. 2(January), 63–762017. Publisher Full Text

[37] 37. Jia J, Qin G: Stability analysis of HIV/AIDS epidemic model with nonlinear incidence and treatment. Adv. Differ. Equ. 2017; 2017(1). Publisher Full Text

[38] 38. Rani P, Jain D, Saxena VP: Stability analysis of HIV/AIDS transmission with treatment and role of female sex workers. Int. J. Nonlinear Sci. Numer. Simul. 2017; 18(6): 457–467. Publisher Full Text

[39] 39. Ogunlaran OM, Oukouomi Noutchie SC: Mathematical model for an effective management of HIV infection. Biomed. Res. Int. 2016; 2016: 1–6. PubMed Abstract | Publisher Full Text

[40] 40. Zu G, Mo I, Danbaba A, et al.: Mathematical Modelling for Screening and Migration in Horizontal and Vertical Transmission of HIV/AIDS.2016; 5(1): 4–10.

[41] 41. Bozkurt F, Peker F: Mathematical modelling of HIV epidemic and stability analysis. Adv. Differ. Equ. 2014; 2014(1): 1–17. Publisher Full Text

[42] 42. Li Q, Cao S, Chen X, et al.: Stability analysis of an HIV/AIDS dynamics model with drug resistance. Discret. Dyn. Nat. Soc. 2012; 2012: 1–13. Publisher Full Text

[43] 43. Daabo MI, Seidu B: Modelling the Effect of Irresponsible Infective Immigrants on the Transmission Dynamics of HIV/AIDS.2012; 3(1): 31–40.

[44] 44. Al-sheikh S: Stability Analysis of an HIV/AIDS Epidemic Model with Screening.2011; 6(66): 3251–3273.

[45] 45. Nyabadza F, Mukandavire Z, Hove-Musekwa SD: Modelling the HIV/AIDS epidemic trends in South Africa: Insights from a simple mathematical model. Nonlinear Anal. Real World Appl. 2011; 12(4): 2091–2104. Publisher Full Text

[46] 46. Akpa OM, Oyejola BA: Modeling the transmission dynamics of HIV/AIDS epidemics: An introduction and a review. J. Infect. Dev. Ctries. 2010; 4(10): 597–608. PubMed Abstract | Publisher Full Text

[47] 47. Cai L, Li X, Ghosh M, et al.: Stability analysis of an HIV/AIDS epidemic model with treatment. J. Comput. Appl. Math. 2009; 229(1): 313–323. Publisher Full Text

[48] 48. Marks G, Crepaz N, Senterfitt JW, et al.: Meta-analysis of high-risk sexual behavior in persons aware and unaware they are infected with hiv in the united states: implications for hiv prevention programs. J. Acquir. Immune Defic. Syndr. 2005; 39: 446–453. PubMed Abstract | Publisher Full Text

[49] 49. Eshleman SH: HHS Public Access. Physiol. Behav. 2019; 176(3): 139–148. PubMed Abstract | Publisher Full Text

[50] 50. Ping L-H, Jabara CB, Rodrigo AG, et al.: HIV-1 Transmission during Early Antiretroviral Therapy: Evaluation of Two HIV-1 Transmission Events in the HPTN 052 Prevention Study. PLoS One. 2013; 8(9): e71557. PubMed Abstract | Publisher Full Text

[51] 51. Zhimin S, Dong C, Li P, et al.: A mathematical modeling study of the HIV epidemics at two rural townships in the Liangshan Prefecture of the Sichuan Province of China. J. Infect. Dis. Model. 2016; 1: 3–10.

[52] 52. Zu G, Mo I, Danbaba A, et al.: Mathematical Modelling for Screening and Migration in Horizontal and Vertical Transmission of HIV/AIDS.2016; 5(1): 4–10.

[53] 53. van den Driessche P , Watmough J: Reproduction numbers and subthreshold endemic equilibria for compartmental models of disease transmission. Math. Biosci. 2002; 180: 29–48. PubMed Abstract | Publisher Full Text

[54] 54. Diekmann O, Hesterbeek JAP, Metz JAJ: On the definition and the computation of the basic reproduction ratio R ₀ in models for infectious diseases in heterogeneous populations. J. Math. Biol. 1990; 28: 365–382. PubMed Abstract

[55] 55. Okuonghae 2016.

[56] 56. Brauer F, Castillo-Chaavez C: Mathematical models for communicable diseases, volume 84. SIAM.2012.

[57] 57. Chitnis N, Hyman JM, Cushing JM: Determining important parameters in the spread of malaria through the sensitivity analysis of a mathematical model. Bull. Math. Biol. 2008; 70(5): 1272–1296. PubMed Abstract | Publisher Full Text

[58] 58. Caswell H: Construction, analysis, and interpretation. Sunderland:Sinauer;2001.

[59] 59. WHO Guidelines on HIV Self-Testing and Partner Notification: Supplement to Consolidated Guidelines on HIV Testing Services. Geneva:World Health Organization;2016.

[60] 60. Tang W, et al.: What happens after HIV self-testing? Results from a longitudinal cohort of Chinese men who have sex with men. BMC Infect. Dis. 2019; 19: 807. PubMed Abstract | Publisher Full Text

[61] 61. Lansky A, Nakashima A, Jones J: Risk behaviors related to heterosexual transmission from HIV2 38 infected persons. Sex. Transm. Dis. 2000; 27: 483–489. PubMed Abstract | Publisher Full Text

[62] 62. Nicolosi A, Musicco M, et al.: Risk factors for woman-to-man sexual transmission 255 of the human immunodeficiency virus. J. Acquir. Immune Defic. Syndr. 1994; 7: 296–300. PubMed Abstract

[63] 63. OBrien T, Busch M, et al.: Heterosexual transmission of human 257 immunodeficiency virus type 1 from transfusion recipients to their sex partners. J. Acquir. Immune Defic. Syndr. 1994; 7: 705–710.

[64] 64. Brauer F, Castillo-Chaavez C: Mathematical models for communicable diseases. SIAM;2012; vol. 84.

[65] 65. Brauer F, Castillo-Chavez C: Mathematical models in population biology and epidemiology. Springer;2001; vol. 40.

[66] 66. Abiodun OE: OE-Abiodun/OE-Abiodun: F1000: HIV ONLY MODEL (v3.1.2). [Software] Zenodo.2022. Publisher Full Text

Qualitative analysis of HIV and AIDS disease transmission: impact of awareness, testing and effective follow up

Abstract

Keywords

1. Introduction

2. Model formulation and description

Figure 1. HIV/AIDS compartmental flow diagram.

(1)

(2)

3. Model investigation

3.1 Region of invariant

(3)

(4)

(5)

(6)

(7)

3.2 Non-negativity of solutions

3.3 Equilibrium point and basic reproduction number; R0

(8)

(9)

(10)

(11)

(12)

(13)

(14)

4. Equilibria stability analysis

4.1 Disease-free equilibrium stability on a local and global scale, E0

(15)

(16)

(17)

(18)

(19)

(20)

4.2 The endemic equilibrium’s local and global stability; E*

(21)

(22)

(23)

(24)

4.3 Sensitivity indices

(25)

Table 1. Sensitivity indices of R0.

5. Numerical simulation

Table 2. Definition of Parameters values for the HIV model.

Figure 2. (Simulation 1) if R0 < 1, the infection-free equilibrium is asymptotically stable.

Figure 3. (Simulation 2) If R0 > 1, the endemic stability is asymptotically stable.

Figure 4. (Simulation 3) Take ψ = 1 and ξ = 1,to check the impact of condom use and effectiveness on the population when there’s no contact.

Figure 5. (Simulation 4) Variation in the infected individual for different ζ values.

Figure 6. (Simulation 5) Variation of the infected individual for different fallout, υ values.

Figure 7. (Simulation 6) Proportion of different Population at the increased values of α and θ.

Figure 8. Impact of treatment fall out on HIV reproduction number.

6. Conclusions and recommendations

Data availability

Software availability

References

Comments on this article Comments (0)

Open Peer Review

Comments on this article Comments (0)

Open Peer Review

Reviewer Status

Reviewer Reports

Comments on this article

Browse by related subjects

Competing Interests Policy

Stay Updated

3.3 Equilibrium point and basic reproduction number; R₀

4.1 Disease-free equilibrium stability on a local and global scale, E₀

4.2 The endemic equilibrium’s local and global stability; E^*

Table 1. Sensitivity indices of R_0.

Figure 2. (Simulation 1) if R₀ < 1, the infection-free equilibrium is asymptotically stable.

Figure 3. (Simulation 2) If R₀ > 1, the endemic stability is asymptotically stable.