Keywords
Movement ecology, agent-based, individual-based, simulation, behavioural states, spatial ecology
This article is included in the Bioinformatics gateway.
This article is included in the RPackage gateway.
Movement ecology, agent-based, individual-based, simulation, behavioural states, spatial ecology
As the biodiversity crisis deepens, we are in constant need of new refined methods of mitigating human impacts on animals. Developing mitigation strategies is aided by a strong understanding of animals lives and needs. How animals move offers a window into their decisions making process,1,2 as well as how they prioritise resources,3–5 avoid threats,6 and react to anthropogenic modification of the environment.7–9 Examinations of animal movement are frequently integrated into conservation plans10 because of the insights they provide on habitat and space requirements, but also because they offer avenues to explore fundamental questions about ecology. For example, space use has been tied directly to body size connected via the energy requirements for animals,11 and movement has provided incredible insights into behaviour.12
The information gathered from animal movement studies is only as robust as the methods and analysis applied. In the past decade, the volume of animal data has exploded,13,14 and the infrastructure for collating these data has improved drastically.15 There are stand out examples of novel methods,16 and exceptionally detailed insights into animal behaviour using new bio-logging technology (e.g., Ref. 12). However, on the whole, analysis approaches to maximise the information extracted have arguably lagged behind the technological and data improvements.13 The bodily cost of attaching bio-telemetry devices (with examples from reptiles17; mammals18; and birds19), as well as the possible conservation sensitivity of study animals, means researchers have an ethical duty to maximise the value/impact of the data collected.
Maximising the value of data should include ensuring that results gained are robust and replicable. Meta-analyses have revealed that several textbook examples in ecology are not as universally replicable as once thought.20–23 Whereas lab studies can more feasibly be repeated (although such replications are far from cheap), movement studies conducted on free-ranging wild animals are difficult to repeat while satisfactorily meeting the conditions of the true replication.24 It is hard to justify placing bio-telemetry devices on more animals to repeat a study, especially when they are of conservation concern. Studies tend to focus on larger, less vulnerable species,25,26 but as the benefits of detailed movement data grow, we can expect greater demand for tracking species of conservation concern.10 With the limited scope for repeating wild movement studies, and the desire to maximise study-to-benefit ratio for sensitive species, it is imperative that we maximise the quality of the initial studies.
Expanding pre-study planning and developing better approaches to guide study design may provide a partial solution.27 Study scenarios where researchers have control over the environment, randomisation, and controls can satisfy the assumptions of many statistical approaches.28 Movement studies conducted in the wild are fraught with uncontrollable confounding variables and often further restricted by sample sizes limited by ethics, capture rates, and cost of bio-telemetry equipment. As the complexity of the research environment increases, so must the analytical approach to account for the uncontrollable –but potentially extraneous to the question– variables. Testing these analysis approaches, and their limitations therefore becomes more difficult to asses a priori.
A potential solution is virtual ecology: where synthetic data are simulated to cover a range of possible scenarios allowing researchers to explore different study approaches/designs with the aim of identifying the best for a given question.29 Exploration of analysis methods using simulations can yield useful insights even for broadly understood techniques (e.g., Generalised linear mixed model30). Such an approach has the potential to adequately recreate the complex emergent properties that could hamper analyses.30 The suite of tools for simulating aspects of ecological systems (e.g., landscapes,31 genetics,32 conservation choices,29 ecological community comparisons,33 resource selection34) is growing, and some are explicitly focusing on aiding study design. There are also examples of simulation approaches being directly tied to applied issues like human-wildlife conflict (e.g., snakes,35 tigers36).
Population monitoring studies offer a great example of a mature relationship between simulated data, study design, and applied research, implemented in a complex study environment.37 There are examples of simulated datasets being used to validate field protocols (e.g., camera trap effort 38,39) and analyses (e.g., accounting for species interactions,40 or difficult to account for variation in populations41). More recently, explicitly simulating animal movement processes rather than the population distribution has helped validate spatially-explicit capture recapture methods (SECR), while also prompting deeper questions concerning the findings generalisably to drastically different movement processes.37 Once validated with real-world data, simulated explorations of study design presents opportunities to understand the trade-offs between effort and precision.39 But similarly, disagreements on the implementation of surveying methods have led to further explorations of how we conceptualise and simulate animal processes.42
As illustrated by the SECR example, different simulation approaches and different analyses accounting for different additional complexities offer different suggestions on the optimal study design. There are a number of approaches for simulating animal movement including (but not limited to):
1. continuous movement processes, best exemplified by the R package ctmm43 and worked examples such as Ref. 44 and Ref. 37. These methods rely on a mathematically defined movement process (such as Ornstein–Uhlenbeck foraging process 45). A key aspect of animal movement they simulate is correlated speeds and central tendency (i.e., home range).
2. hidden markov models, exemplified by the simData function from the R package moveHMM.46 Their biggest contribution to simulating animal movement is the inclusion of state switching (i.e., different behaviours). They are best used in conjunction with existing movement data for parametric bootstrapping to explore estimator uncertainty.46
3. agent-based approach, is a bottom-up approach where simulations of an agent (e.g., an animal) are based upon a number of rules,47 and through repeatedly following those rules a complex output emerges. In the model we present here, this output represents the movement pathways in a landscape. Previous examples of agent-based movement models have targeted specific key components of animal movements such as movement heavily constrained by landscape features,48 simulating memory/home range,49 or migratory behaviour.50
Here we present an agent-based approach to supplement those existing simulations, which provides a unique combination of features. The agent-based approach is suited to explore a combination of the complexities of animal movement, and the emergent properties. Our model does not require fitting to prior movement data, allows for multiple predefined points of attraction/avoidance, multiple-levels of activity cycling, three behavioural states, and multiple spatial environmental covariates. A new independently developed approach to simulating animal movement will provide a additional routes to test the robustness of movement analyses.
The abmAnimalMovement package provides the functionality to simulate animal movements via an agent-based model. We wrote the model using C++ via the Rcpp v.1.0.8.3 package51–53 to ensure it runs efficiently while allowing for easier manipulation of model inputs and outputs via R (R is the most used analysis tool in movement ecology with numerous supporting packages13,54).
The model simulates animal locations over a given period of time at discrete time steps. At each time step, the agent (i.e., simulated animal) is presented with a range of movement options in the form of new locations [Figure 2], and will choose from amongst these (i.e., sum-based model as opposed to facing a series of sequential binary decisions, see Ref. 2 for an example of the latter). The possible movement options, and how the new location is selected, are influenced by several factors: behavioural state of the animal, environmental quality, and proximity to points of attraction/avoidance. By simulating these drivers of animal movement, we hope to capture aspects of the internal state (i.e., motivation to move via behaviour); motion capacity (i.e., the individual’s varying ability to move); navigation capacity (i.e., ability to plan ahead beyond the immediate movement distance); and external factors (i.e., the landscape that steers and limits movement), all of which are defined as key components of animal movement.47,55
The animal has three behavioural states, broadly defined here as state 0 - sheltering (or resting), state 1 - exploring, and state 2 - foraging. Each behavioural state modifies the movement characteristics of the animal; for example, exploring comprises of more random movements with longer distances between subsequent chosen locations, whereas resting behaviour is largely defined by stationary or very low discrete movements after returning to a shelter site. The movement characteristics are defined by two distributions: a Gamma distribution that step lengths are drawn from, and a Von-Mises that turn angles are drawn from. The resulting step length, combined with a turn angle describes the change in animal location between each time step (as selected from a given number of options). We will largely define these based on the movement capacity of the animal over a minute.
As the simulation will be running with three behavioural states, we need to define how likely an animal is to switch between the behaviours. We achieved this by creating a transition matrix that describes the probability at each time step of the animal changing to another behaviour [Figure 1], where each value describes the probability of the animal transitioning from the current behaviour (row: b0, b1, b2), to the behaviour for the next time step (columns: b0, b1, b2). The diagonal describes the probability of the animal remaining in the same behavioural state. These probabilities can be kept very high to introduce autocorrelation in the behavioural state; a high autocorrelation is required if we are modelling time steps as one minute.
## b0 b1 b2 ## b0 0.9700 0.01000 0.0010 ## b1 0.0002 0.95000 0.0008 ## b2 0.0010 0.00001 0.9900

Remain values indicate the probabilities of the animal remaining in the same behavioural state. Values correspond directly to those in the transition matrix used as a simulation input.
Animals behaviour is frequently expressed via cycles, such as day/night or diel cycles56; therefore, we want the transition matrix to vary over time. We describe a number of cycles (or waves) that can be applied to the core transition matrix impacting the probability of entering resting behaviour. For example, a diel cycle can be expressed via a Sine wave with a frequency of 12 hours and an amplitude of 0.1. At each time step we draw a value from the wave, and by added that weighting (from -0.05 to 0.05) to the transition probability of entering resting state (row 1, column 1 of the matrix); therefore, the probability of resting will increase and decrease following the Sine wave approximately a 12 hour activity pattern. We can define as many cycles as needed, and they impact the resting probability additively.
When entering the resting state the animal will seek out a shelter site. In the abmAnimalMovement package, we can supply a number of shelter sites to simulate this need and create site fidelity. As these shelter sites act as points of attraction for the animal for each rest, the animal occupies a consistent area, or something approximating a home range. Home ranges are meant to represent areas in which the animal can source all resources required for a given life stage.44 The predefined and steady state of these shelter sites provides the stability we look for in a home range, as well as a means of predefining a level of site fidelity. As the abmAnimalMovement model can have multiple attraction (rest) sites supplied, we can simulate home ranges with unequal and behaviourally influenced space use.
In addition to the predefined attraction to shelter sites, the abmAnimalMovement package allows for a more dynamic attraction to areas of high resource quality. Movements cannot be directly translated to animal preference; for example, habitat preference may miss key movement corridors57; or the habitat decisions may occur at scales different to observed movement.1 Therefore, the simulation required a mechanism that somewhat detaches the preference/choice for observed movements. When entering foraging mode, the animal randomly selects foraging destinations as a point of attraction (but weighted towards areas of higher quality) [Figure 2]. This attraction impacts the movement choices made at each time step, with the animal more likely to choose (and therefore move to) options closer to the foraging destination. Therefore, foraging destination choice operates on a different time frame to the movement and allows movements through low-quality foraging areas. This presents a critical benefit of the simulation approach, as we define the internal state decision making process of the animal. The two time frames also allow exploration of assumptions connecting observed movement choices to choices grounded in resource use, and whether downstream analyses can accurately recover a hidden decision making process.

A - the time frame of the destination choice, B - the time frame of movements at each time step.
At all times, the subsequent locations of the animal are impacted by a movement resistance matrix. Differing values represent different environmental conditions that could change how easily/likely an animal is to use that area to move towards a destination. For example, rivers or hard barriers within a landscape could present very high movement resistance and an animal would aim to avoid traversing them. Alternatively areas of lower movement resistance could aid movement, and potentially form movement corridors. The movement matrix has values that describe the weighting of movement probability (lower values indicating a lower probability of entering a cell). Whereas the resource environmental layer and shelter locations interact with destination/goal decisions, the movement resistance affects the step-by-step movement decisions.
The interplay between shelter sites, foraging quality, and movement resistance simulates the site fidelity required for home ranges, while allowing the environment to help shape the size and diffusion of that home range. Simulating a more dynamic and messy array of movements can help test how far assumptions of uniform circular animal movement are practical.
To demonstrate the variation that movement ecology methods needs to wrangle, as well as the scope of movements the agent-based model can recreate, we provide three example species. The examples cover a range of movement capacities, site fidelity, and resting/sheltering patterns. Unlike alternative methods that are built to fit and simulate movements from existing data, our examples are loosely based on summary statistics from previous published results (cited below in each example species’ section). The choice of using species specific examples is intended to provide some biological context while demonstrating a range of simulation parametrisations. Therefore, we are only interested in whether the simulated data returns the intended traits we are attempting to simulate for each example species (e.g., avoidance, site fidelity, expected step lengths). We show one example via a more detailed walk-through (badger), and the other example parametrisations are included as uses cases at the end of the manuscript (vulture, king cobra).
2.3.1 Ecology and objectives - badger
Our primary example is based on a badger. Badgers occupy setts, in our example a two home/shelter sites, to where they routinely return.58,59 When not at the sett, the badger forages, and the foraging distances are impacted by resource position and movement capacity of the badger (i.e., how far can a badger feasibly travel for food from the sett). The badger therefore expresses very high site fidelity, a range dictated by the spatial positioning of resources, and is subject to the movement resistance of the terrestrial environment.
We can draw on studies such as Refs. 58 and 60 to roughly gauge the speed of badgers (i.e., step length per minute). How this speed differs between behaviours is more difficult to estimate from existing literature, but we can use Ref. 58 reported maximum speed to guide more direct movements (e.g., state 0 - sheltering and state 1 - exploring). In particular Ref. 58 mentioned the heightened speeds moving from and to the setts. We also want to allow the exploratory (state 1) movements to be great enough to occasionally exceed the normal home range or territory.61 We can draw on statements regarding maximum distance travelled in a night from papers such as, Refs. 58, 60 and 62 to approximate how distance foraging locations could be from a sett, While also confirming the nocturnal activity cycle for the badger. For the example, we will consider badgers as fully nocturnal, and with active periods lasting for around 8 hours each night.60,63 The 8 hour active periods are not consistent throughout the year. Badger occupying temperate areas are impacted by seasonal shifts that modify daylight hours and available resources.60,63 Badger movements are also impacted by their territoriality, avoiding areas occupied by other badger groups, but also displaying occasional extra-territorial movements.59,61 This suggests a general, but not complete avoidance of areas occupied by other badger groups.
We can broadly summarise the badger ecology we want to parametrise as follows:
The abmAnimalMovement package requires links to the Rcpp (>= 1.0.8.3)51–53 and BH (>= 1.78.0.0) packages,64 and therefore requires a version of R >=3.5.065 (available from www.r-project.org). Currently the abmAnimalMovement package can be installed from Github using install_github provided by the devtools package.66
A submission to the Comprehensive R Archive Network (CRAN) is under way, which will streamline installation and ensure compatibly with a wide range of platforms.
While only the abmAnimalMovement package is required for running core simulations (abm_simulate function), to generate, organise, and review the inputs and outputs of simulations, we make use of a number of R packages. An alternative simpler implementation with no dependencies is provided as a package vignette.
# core package library(abmAnimalMovement) # data manipulation library(dplyr) library(reshape2) # visualisation library(ggplot2) library(ggforce) library(ggtext) library(ggridges) library(patchwork) # environmental matrix generation library(raster) library(NLMR)
We used R v.4.2.165 via RStudio v.2022.2.2.485,67 and used rmarkdown v.2.14,68–70 bookdown v.0.26,71,72 tinytex v.0.39,73,74 and knitr v.1.3975–77 packages to generate type-set outputs. We used the here v.1.0.1 package78 to help with relative file path definition. We used the dplyr v.1.0.9 and reshape2 v.1.4.4 packages for data manipulation.79,80 We used ggplot2 v.3.3.6 for creating figures,81,82 with the expansions: ggridges v.0.5.3,83 ggtext v.0.1.1,84 ggforce v.0.3.3,85 and patchwork v.1.1.1.86 We used the raster v.3.5.21,87 sp v.1.4.7,88–90 and NLMR v.1.191,92 for generating environmental matrices.
2.5.1 Generating environmental matrices
To ensure that the simulation completed during this example is repeatable, we set a seed. For the sake of simplicity, the year the examples was written (2022) is used.
seed ˂- 2022 set.seed(seed)
Before starting to simulate animal movement, we need to generate a landscape. The landscapes in this case will take the form of matrices, where each cell is describing the quality of foraging, shelter, and movement ease. The highest quality locations/cells are coded as 1, with quality decreasing as the values range down to 0. The 1 to 0 quality values in each cell are later used to help the animal to choose how and where it moves throughout the landscape. Depending on the behavioural state, the weighing of which matrix/layer used will change (e.g., when in a resting behavioural state the shelter site quality layer is used).
For most applications, a landscape would be known a priori, but for this demonstration and testing of methods we will use a selection of random generated landscape matrices [Figure 3], using the NLMR package (neutral landscape models).
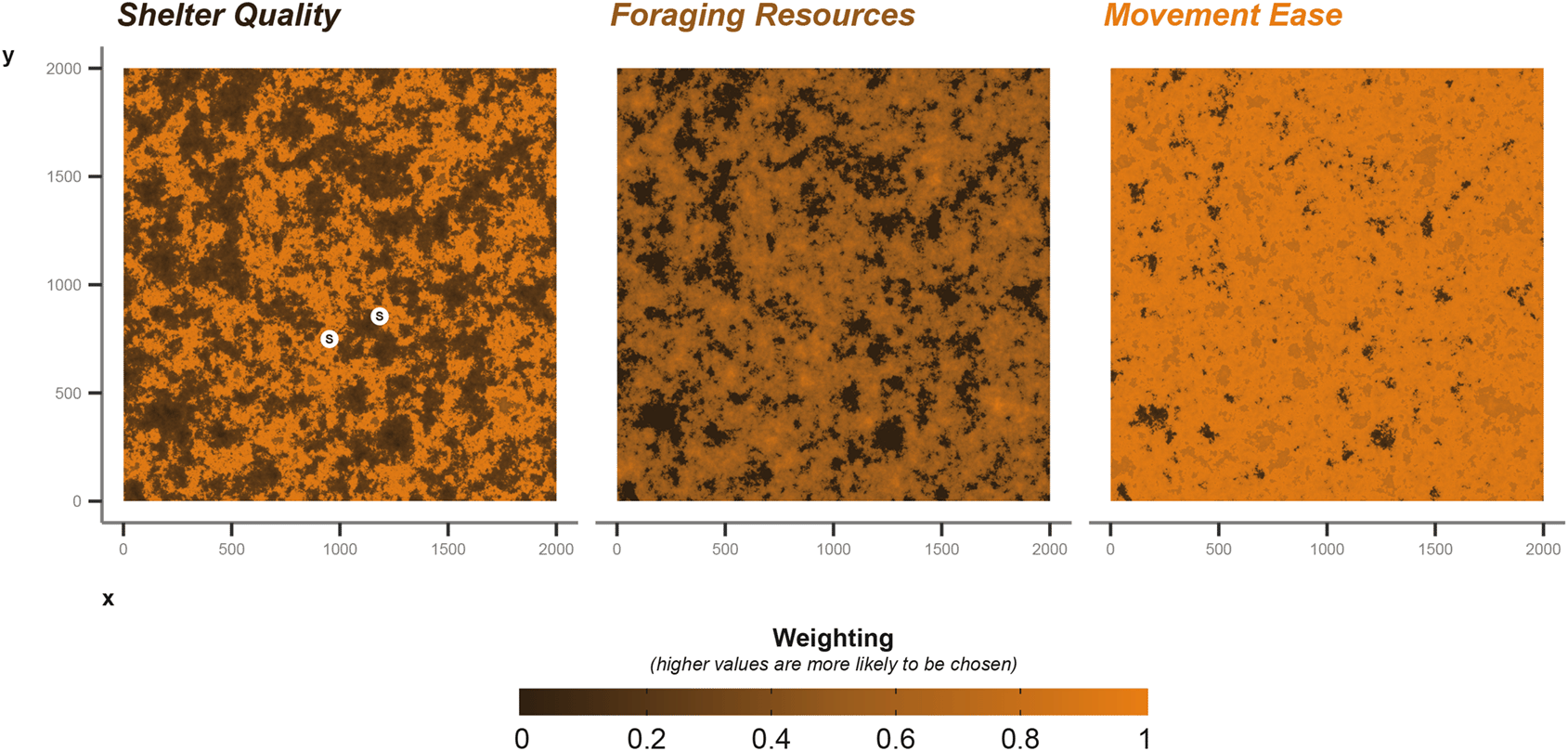
We used a Gaussian field with an autocorrelation range of 40, a magnitude of variation across the landscape of 5, a magnitude of variation in the scale of autocorrelation range of 0.2, and a mean of 0.5. For foraging, we build on the Gaussian field already produced, allocating all values lower than 0.4 as 0 (i.e., no value for foraging), then normalising the remaining values between 0 and 1.
For a baseline movement resistance layer, we take the original Gaussian field and increase areas greater than 0.6 by 0.5 to allow areas of high resource quality to be easily accessible. We also greatly increase the movement ease in “edge” habitat (+1), where values fall between 0.6 and 0.3. Again we normalise between 0 and 1, where 1 are areas easily traversed. The resulting environment is one with easily traversable edge areas, surrounding better quality foraging locations than can be moved into easily.
Shelter quality is intermediate; we increased weighting by +1 in areas where cell values were greater than 0.5 and lower than 0.7. Thereby shelter sites are more likely to occur in the areas of higher foraging quality, but not in the core (i.e., >0.7), nor in the edge areas (<0.5). This provides some balance between accessibility and proximity to resources. The three matrices described provide a baseline for our examples, but can easily be modified for different scenarios [Figure 3]. To aid balancing, we keep values between 0 and 1; any numeric value can be used, but the simulation will interpret the values as relative weights when the animal is making decisions (Note: The current implementation of cpp_get_values that extracts values from the matrices during the simulation returns -99.9 weighting when presented with NA values; therefore, -99.9 serves as a lower limit to the matrix weighting values).
Once generated will supply the core simulation function (abm_simulate) with each of these layers via the shelteringMatrix, foragingMatrix, and movementMatrix arguments.
2.5.2 Animal parameters
We predefine a suite of parameters describing the movement and behaviour characteristics of the animal (e.g., badger) loosely based on summary statistics and general statements from previous research (e.g., Refs. 58–63). We store the parameters as objects we can later input into the abm_simulate function. We complete this process for three species; the badger values are displayed below, whereas the values for vulture and king cobra examples are provided at the end of the manuscript.
We parametrise shelter information in the following ways. For the sett, we draw a two sets of coordinates from the shelter quality layer. During the simulation the badger will randomly select a sett to return to each time it enters the resting behavioural state. The choice of which sett to return to is weighted by the values supplied via the shelter quality environmental layer [Figure 3]. The coordinate data frame is provided to the core simulation function’s shelterLocations argument.
The shelterSize argument describes the radius around the shelter locations within which the animal exhibits near stationary behaviour. We specify the shelter size to be 8 m, meaning that when within 8 m of the selected shelter site the animal’s possible step lengths are decreased 100-fold. The shelter site size of 8 m allows for small movements near/within the sett during resting behaviour.
sampledShelters ˂- sampleRandom(raster(landscapeLayersList$shelter), 2, ext = extent(0.45, 0.65, 0.45, 0.65), rowcol = TRUE) BADGER_shelterLocs ˂- data.frame( "x" = sampledShelters[,2], "y" = sampledShelters[,1]) BADGER_shelterSize ˂- 8
Badger movement is set via the definition of three pairs of Gamma and Von Misses distributions. Each behavioural state is provided with a Gamma distribution to describe the step lengths between locations, and a Von Mises to describe the turn angles. When combined these two distributions provide the animal with a number of locations to choose from at each time step [Figure 2]. As we have three behavioural states, each movement parameter takes the form of a vector of length three. The step lengths require predefined shape (k) and scale (θ) parameters to describe the Gamma distributions, and we provide these to the simulate function via the k_step and s_step arguments. For the turn angles we require the mean (μ) and concentration (κ) to defined the Von Mises distributions, and provide these via the mu_angle and k_angle arguments.
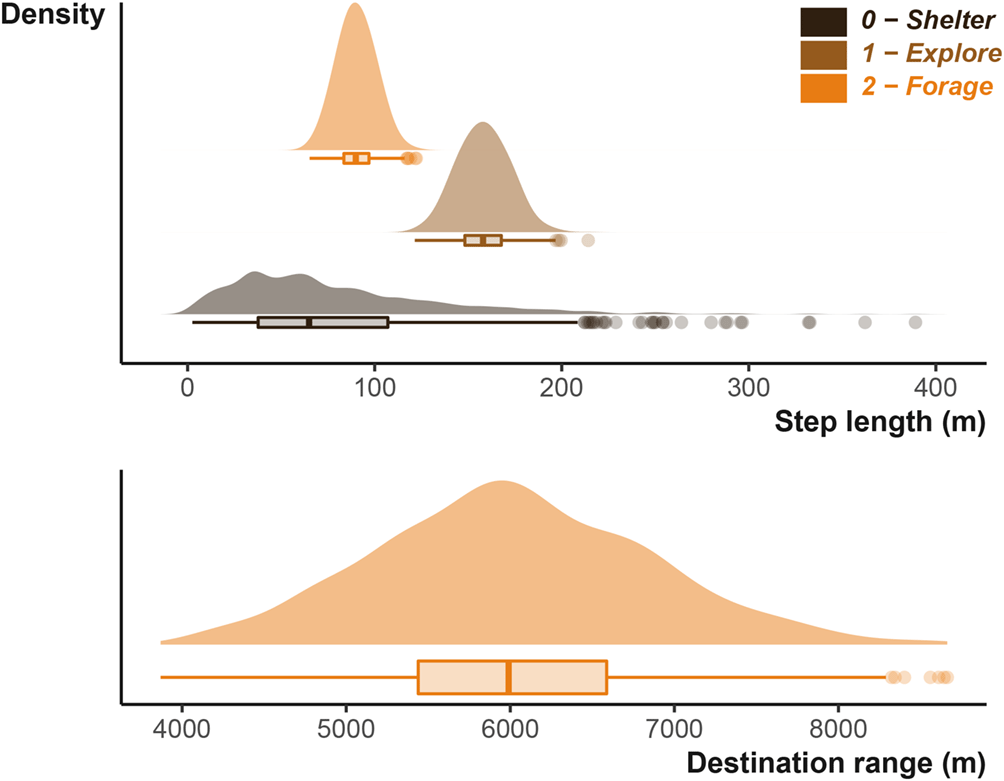
The perceptual range, in other words, where the badger decides to forage is set in a similar fashion. Where destinationRange provides the shape (k) and scale (θ) for the Gamma distribution describing distance of possible foraging locations, and destinationDirection provides the mean (μ) and concentration (κ) the Von Mises distribution describing the angle which those locations can fall [Figure 4].

The distribution displayed is generated from the same shape and scale parameters that will be input into the simulation function for the badger simulation. The lower plot shows the distribution used to generate potential foraging desintations.
We can also alter the strength of attraction to the foraging destinations. At each time step, the animal is offered a number of location options to move to next time step. The simulation calculates the distance between all options and the destination (i.e., a foraging location or shelter site), then normalises the distances between 0 and 1. The normalises values serve as weighting to increase the chances the animal will move towards its destination. We modify the weighting with the destinationTransformation and destinationModifier arguments. The destinationTransformation allows for weightings to be transformed (where 0 = no transformation, 1 = weights are square-rooted, 2 = weights are squared). Values supplied destinationModifier applies a linear multiplicative effect to all the weightings. When these weightings increase in value the animal will exhibit a stronger attraction and choose more direct movements to its current destination.
We also store a value ready for the rescale_step2cell argument. The rescale value is a simple means of adjusting the environment layers to fit with the scale/unit in which the step lengths are provided. In this case, we treat each cell as 5m by 5m, thereby ensuring that our 2000x2000 matrix is sufficient for the badger to traverse without leaving. The rescale value therefore allows high resolution movements on lower resolution environments, offering a crucial memory saving optimisation.
BADGER_k_step ˂- c(0.3*60, 1.25*60, 0.25*60) BADGER_s\_step ˂- c(0.8, 0.25, 0.5) BADGER_mu_angle ˂- c(0, 0, 0) BADGER_k_angle ˂- c(0.6, 0.99, 0.6) BADGER_destinationRange ˂- c(3, 120) BADGER_destinationDirection ˂- c(0, 0.01) BADGER_destinationTransformation ˂- 2 BADGER_destinationModifier ˂- 2 BADGER_rescale ˂- 5
The territoriality is not simulated directly via other individuals, instead we approximate it by supplying a number of point locations the badger will avoid. An alternative way of simulating this behaviour would be to create areas of high movement resistance to prevent the badger from entering. We provide a set of x, y coordinates of locations to be avoided. Alongside the locations, we need to define how strongly the badger will avoid them using avoidTransformation (distance to point is weighting squared) and avoidModifier (distance to point is weighting multiplied by 4). Both avoidTransformation and avoidModifier operate in the same way as the destination attraction arguments, but inverted; therefore, the avoidance behaviour will directly counteract the attraction to destination behaviour.
BADGER_avoidLocs ˂- data.frame( "x" = c(1205, 1500, 1165), "y" = c(980, 1090, 1250)) BADGER_avoidTransformation ˂- 2 BADGER_avoidModifier ˂- 4
We implement two cycles to capture the daily and seasonal cycles the badger experiences. Both cycles are created by describing a Sine wave defined by its amplitude, midline, offset (ϕ) and frequency (τ; via the cycle_draw function). The abm_simulate function has two arguments for wave parameters: rest_Cycle is a mandatory input to describe diel activity cycling, and additional_Cycles to define any number of additive additional cycles. For rest_Cycle we will store a vector of length 4, with values defining the amplitude, midline, offset, and frequency in that order (Frequency is supplied in hours, i.e., 60 times the time step). We set the amplitude to 0.12 and midline as 0, meaning the probability of resting will be modified by values ranging from -0.06 to 0.06 depending on the location in the wave. Our badger example requires a 24 hour cycle where the probability of resting will peak and nadir, hence offset and frequency are set to 24 hours. When combined with the base transition probability to rest, the above parametrisation creates a scenario of approximately 8 hour periods of activity every 24 hours.
To add a seasonal cycle we will use additional_Cycles. We predefine a data frame where each row contains four elements describing the amplitude, midline, offset, and frequency. Whereas our diel activity is defined by a 24 hour cycle, a seasonal cycle is 365 days and we shift the peak half a year (offset = 365/2). The seasonal wave will increase the probability of resting behaviour during a portion of the year, while not also overwhelming a relatively stable diel cycle (i.e., badger will sleep longer during one part of the year) as we have set a lower amplitude for the seasonal cycle (0.075). A more extreme implementation of the second cycle could introduce hibernation behaviour.
We also pull forward the behaviour transition matrix we showed during the overview, and rename it so all simulation input objects have the BADGER_ prefix.
BADGER_rest_Cycle ˂- c(0.12, 0, 24, 24) # additional cycle c0 ˂- c(0.075, 0, 24* (365/2), 24* 365) # seasonal BADGER_additional_Cycles ˂- rbind(c0) BADGER_additional_Cycles ## [,1] [,2] [,3] [,4] ## c0 0.075 0 4380 8760 BADGER_behaveMatrix ˂- Default_behaveMatrix BADGER_behaveMatrix ## b0 b1 b2 ## b0 0.9700 0.01000 0.0010 ## b1 0.0002 0.95000 0.0008 ## b2 0.0010 0.00001 0.9900
2.5.3 Running the simulation
We need to initially define a start location for our animal. To introduce some more individual variation, we can randomly vary this starting location, but we will restrict the start locations to be proximal to the centre of the environment. For the simulation, we need a vector of length 2, where the first value is the x location, the second is y.
startLocation ˂- sample(900:1100, 2, replace = TRUE)
We finally have some parameters that describe the scope and intensity of the simulation. The length of the simulation is provided via the timesteps argument; in our examples we are operating under the assumption that one time step is equal to one minute. Equally timesteps can be thought as the number of movement choices simulated. We also need to specify how many options will be drawn and considered by the animal at each time step. The options argument is where this is input. Similarly des_options is where we specify the number of dynamically selected foraging attraction/destinations to choose from when it enters the foraging behaviour mode (state 1).
We can then call all our settings describing badger behaviour and movement settings we stored as objects previously, and run the simulation using abm_simulate.
simSteps ˂- 24*60 *365 simRes ˂- abm_simulate( # a data frame with x and y coordinates start = startLocation, # an integer describing the length of the simulation timesteps = simSteps, # an integer describing the number of foraging destination options an animal # is offered des_options = 10, # an integer describing the number of movement options an animal is offered options = 12, # a data frame providing x and y coordinates of the shelter locations shelterLocations = BADGER_shelterLocs, # a value describing the radius around shelter sites that movement step # lengths are reduced shelterSize = BADGER_shelterSize, # a data frame providing x and y coordinates of the avoidance locations avoidPoints = BADGER_avoidLocs, # a numeric vector of length two that contains the shape and scale values # that describe the Gamma distribution for potential foraging destinations destinationRange = BADGER_destinationRange, # a numeric vector of length two that contains the mean and concentration values # that describe the Von Mises distribution for potential foraging destinations destinationDirection = BADGER_destinationDirection, # a value to chose the type of transformation applied to the animal’s # attraction to a chosen destination destinationTransformation = BADGER_destinationTransformation, # a value modifying the animal’s attraction to a chosen destination destinationModifier = BADGER_destinationModifier, # a value to chose the type of transformation applied to the animal’s # avoidance to a avoidance locations avoidTransformation = BADGER_avoidTransformation, # a value modifying the animal’s avoidance of avoidance locations avoidModifier = BADGER_avoidModifier, # a vector of three numbers describing the three behavioural state’s Gamma # distributions’ shape parameter for step lengths k_step = BADGER_k_step, # a vector of three numbers describing the three behavioural state’s Gamma # distributions’ scale parameter for step lengths s_step = BADGER_s_step, # a vector of three numbers describing the three behavioural state’s Von Mises # distributions’ mean parameter for turn angles mu_angle = BADGER_mu_angle, # a vector of three numbers describing the three behavioural state’s Von Mises # distributions’ concentration parameter for turn angles k_angle = BADGER_k_angle, # a numeric value to specify the size of the environmental matrices cells rescale_step2cell = BADGER_rescale, # a 3x3 numeric matrix describing the transition probabilities between the # three behavioural states behave_Tmat = BADGER_behaveMatrix, # A vector length 4 for amplitude, midline, offset and frequency to define the # resting/active cycle rest_Cycle = BADGER_rest_Cycle, # A data.frame 4 columns wide for amplitude, midline, offset and frequency to # define any additional activity cycles, where each row is another cycle additional_Cycles = BADGER_additional_Cycles, # Three arguments for the three matrices describing the landscape the # simulated animal occupies shelteringMatrix = BADGER_shelter, foragingMatrix = BADGER_forage, movementMatrix = BADGER_move)
The simulation function (abm_simulate) outputs a list containing: (1) a dataframe of realised movements, (2) a dataframe of options the animal had available, and (3) a list of the inputs used to simulate the movement. The realised movement dataframe (locations) describes all realised locations the animal occupied, step length information, behavioural state, and current point of attraction, where each row is equal to a time step. Note the simulation is scale agnostic, so each row can represent a different time step to the example. Other than the lack of timestamps and location error, the format largely mirrors a typical movement dataset. Our example is minute by minute; changing the time step would require a reparametrisation of step length and behavioural transition probabilities. The options dataframe describes all the options available to the animal over the entire simulation duration, where each row is equal to an option repeated for each time step.
Once simulated, we can review the movement characteristics of the three species. The simplest to examine is the movement speeds or step lengths. During the simulation parametrisation we provided rescale values for the size of the cells describing environmental information (see rescale_step2cell argument). The simulated movement will return the scaled values, so to plot something comparable to the input values, we must rescale the simulated step lengths.
We can compare the simulation’s inputs displayed in Figure 4 to the simulated/observed outputs displayed in Figure 5 and see that they largely agree as expected. The turn angles are more variable, as the destination decisions and attraction to locations heavily influence the distribution overriding the initial parametrisation of the Von Mises distribution. Figure 10 and Figure 12 in the uses cases section show the outputs for vulture and king cobra simulations.
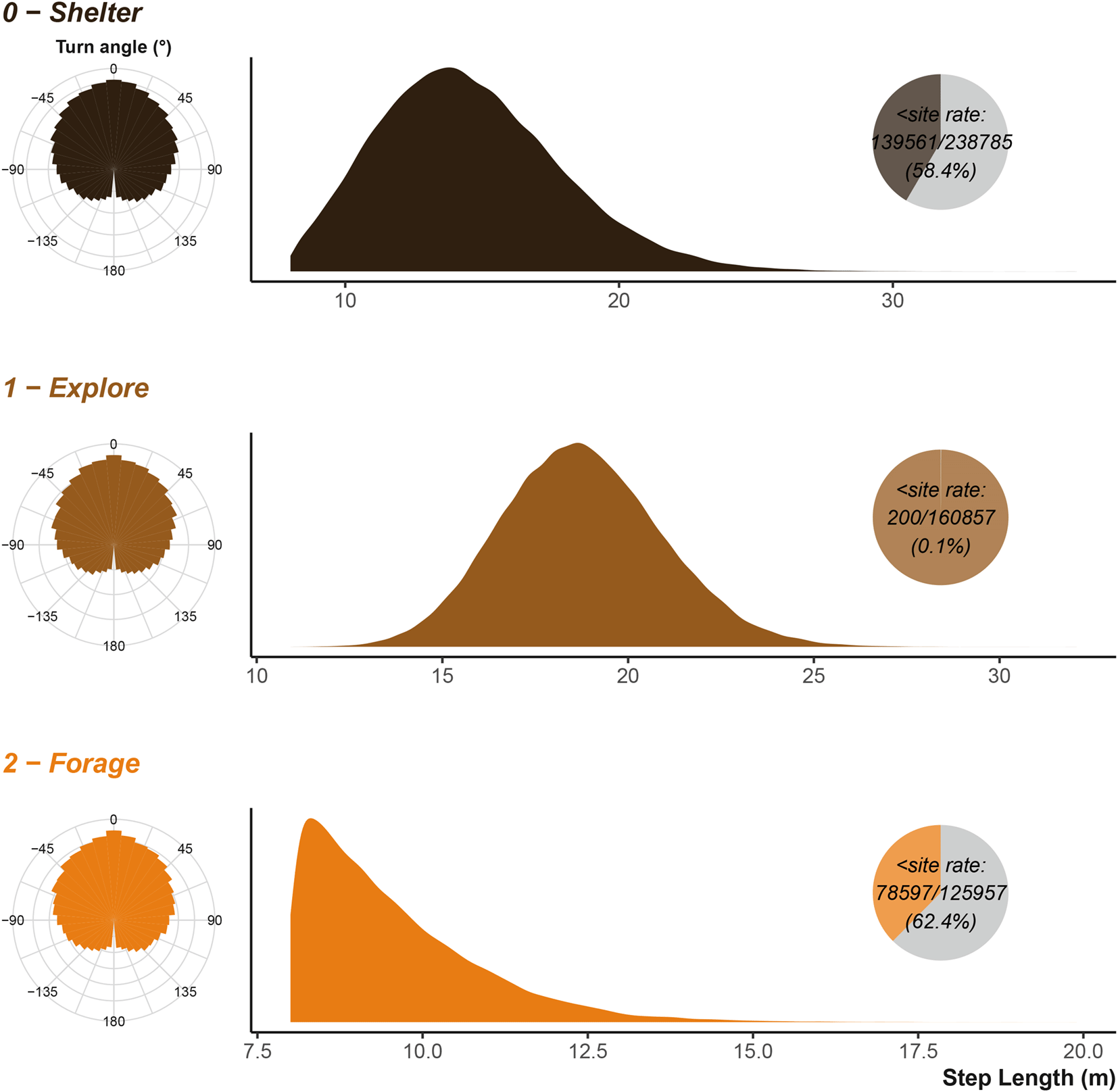
Step lengths are scaled to the input units. Inset pie chart show the number of step lengths that were below the shelter site size; the sub-shelter site step lengths are excluded from the density plot. Note that x axis is not consistent between the three plots.
We can review how the movements appear in space. With the badger example, the impact of the avoidance points is clearly visible [Figure 6A, Figure 7A], whereas the lack of or weaker avoidance in vulture [Figure 6B] and king cobra [Figure 6C] makes the avoidance less influential. The vulture’s movements and chosen foraging locations are largely to the east [Figure 7B], demonstrating the impact of the underlying foraging quality environmental layer. The king cobra plot shows the impact of a near impermeable barrier truncating the southward movements [Figure 7C].

Black points show the observed location at each time step. The orange squares show the dynamically selected foraging destinations. Circles with an interior S show the shelter site locations, and cricles with an interior A show the avoidance points. Note that the size represented by each unit on the x and y axis differs depending on the species.

Grey path shows the overall movement during that month, overlaid points indicate where the animal was in a given behavioural mode. Circles with an interior S show the shelter site locations, and cricles with an interior A show the avoidance points, black squares show the dynamically selected foraging destinations. Note that the size represented by each unit on the x and y axis differs depending on the species.
The activity cycles and the timing of behavioural shifts is a key component in the simulations. We can examine that the predefined cycles result in expected patterns. A year of data makes observing all but the broadest cycles difficult, so in Figure 8 we can look at several months of data as well as the daily cycle. Badger and vulture daily cycles are largely the same [Figure 8A & B], with a consistent daily activity cycle differing only slightly in the time spent active and balance between shifts from sheltering to foraging and exploring. Some of the differences are a result of the different behavioural transition matrix provided to simulated the two species, where both had different baseline probabilities of shifting between behavioural states. By contrast, the king cobra example demonstrates the interaction between the daily and weekly cycles [Figure 8]. We can see intermittently extended sheltering periods, punctuated by short exploratory or foraging bouts.
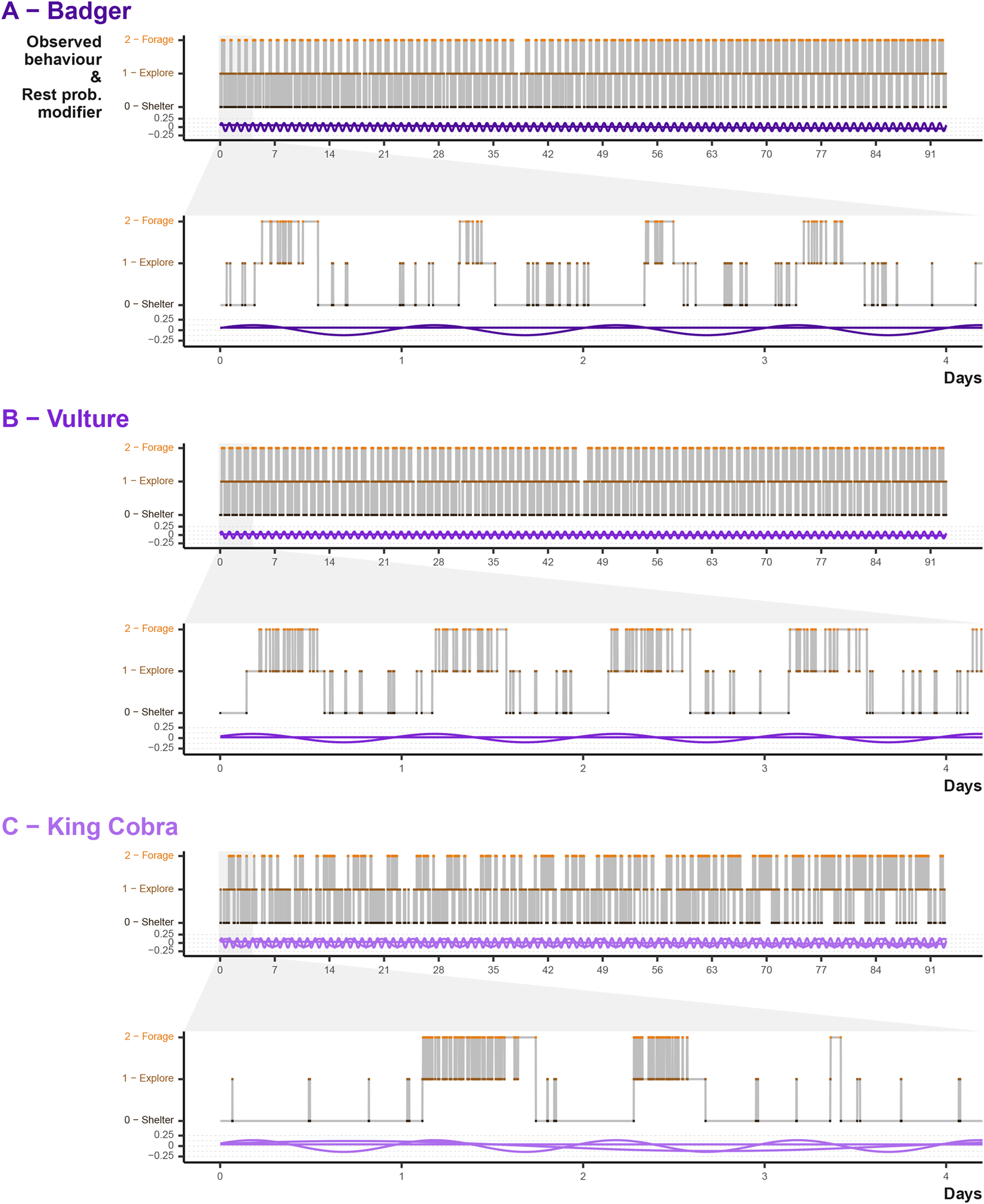
Point colour and position describe the behavioural state at each simulated time step, whereas the purple waves indicated the input values. Note that the input waves acting on the simulated animal in conjunction with the beahvioural transition matrix.
At the daily and monthly scale, we cannot see the impact of the broad scale seasonal cycles. Instead we can look at the percentage of time steps per day the animal was in sheltering behaviour [Figure 9]. Again the Badger and Vulture sheltering rates are similar, differing in intensity, but with both demonstrating a seasonal decrease in the middle of the simulation. The king cobra cycles reveal decrease in the number of days spent entirely sheltering and an overall impression that the seasonal cycle is less influential (as it is only one of three activity cycles).
Animal movement datasets are complex and require a suite of analytical approaches to tackle satisfactorily. Efforts to develop new, and test existing, analyses would be aided by access to a range of diverse datasets. While ideal simulations often accompany new analysis methods and provide superb validation for the method in question, reaffirming the method’s robustness and pushing them to new limits with a messier, more stochastic, simulation approach could greatly strengthen our confidence in results. The abmAnimalMovement package provides an independent route to test new methods that covers a range of interacting movement features, not necessarily directly tied to a single analytical method.
By including a range of features linked to movement and behaviour, the abmAnimalMovement package can be implemented to investigate a suite of questions commonly asked of movement data –from habitat selection, to behaviour detection (for examples of common themes see Ref. 13). While some of the features can appear simplistic, there remains ample flexibility to simulate a wide range of useful scenarios. For example, we conceptualise the three movement states as sheltering, exploring, and foraging. However, only several aspects are immutable: one state exhibits site fidelity (state 0), one state is free from all attraction (state 1), and one state is driven by an underlying environmental layer (state 2).
The abmAnimalMovement package has an advantage over data-driven simulation methods in scenarios where data are scarce, as much of the animal world is untracked.13,25 For the untracked animals, we may be limited to basic information of speed, activity, and resources, or such information may even need to be inferred from ecologically similar species. In such data starved situations, the abmAnimalMovement package’s low computational cost and minimal data requirements allows for a large number of alternative parametrisations to be explored. Via the explorations of different parametrisations researchers can help build a picture of the study and analysis methods best suited for their questions, with the opportunity to test those analyses on synthetic simulated data.
In cases where data cannot be shared (e.g. due to concerns over species sensitivity), using a synthetic dataset could allow researchers to provide peer reviewers a dataset to test and error-check analysis code.93 Providing data is a key component to ensuring computational reproducibility,94 and synthetic datasets provide an avenue to limit the reproducibility loss from data sharing restrictions. Additionally, such synthetic datasets could be integrated into preregistration as a means of demonstrating the validity of an analysis plan prior to undertaking a study.
Producing a range of simulated datasets that cover alternate scenarios may present researchers opportunities to test real data against a null model. For example, researchers looking to investigate whether an animal was avoiding a certain landscape feature could calibrate a number of simulations covering a range of differing avoidance strengths. The simulated results could then be compared to the real data to gauge how different the real data was from simulations exhibiting zero avoidance (i.e., a null model scenario). This approach could complement current analysis methods, akin to sensitivity analysis.
The abmAnimalMovement package provides adequate functionality to simulate a range of scenarios and movements. However, there are several aspects that will bear updating in future versions.
1. Dynamic state 0. While state 0 and the steady state of the attraction locations is key to simulating range stability (i.e., home range), there maybe scenarios where this stability is not desired. For example, simulating dispersal behaviour of juvenile or sub-adult animals there may be a desire to have shelter site dynamically chosen for a time. Currently such behaviour could be simulated, but it would require the dispersal to occur immediately, and the dispersal destination to be predefined (i.e., the sites for state 0 attraction). Therefore, in the current state the package may be limited in its ability to help predict possible dispersal destination, but potentially capable of informing dispersal routes.
2. Autocorrelated speed. We may need to improve the autocorrelation of the animal’s speed. Currently the speeds are non-independent based on the behavioural mode of the animal. The need to implement a more aggressive movement momentum/autocorrelative structure may be felt more acutely at different time frames, and for animals with a great variation in step lengths (i.e., a larger θ for the Gamma distribution). Explorations of simulated data using methods that measure autocorrelation in animal speed will reveal how much of a priority this should be.
3. Dynamic environment. All the environmental matrices are static; currently there is no system to update values during the simulation. This prevents shifts in the landscape such as seasonal variation in resources, or the development of trails. Currently, the closest solution is to run multiple simulations where the end location of simulation1 is the start location for simulation2, where simulation2 is provided with a new season-appropriate resource layer. This solution would be inadequate for trail development, as trail development would require a system within the simulation to update previously used cells for the animal at each time step.
This section provides alternative parametrisations for the secondary examples to better demonstrate the range of movement types and scenarios the abmAnimalMovement package can replicate. We provide example implementations of vulture and king cobra-like movement.
Unlike badgers and other terrestrially moving animals, vultures can move great distances with minimal obstruction [Figure 11]. Vultures can also move greater distances more rapidly,95 resulting in a more variable and distribution of step lengths96–98 [Figure 10].
The distribution displayed is generated from the same shape and scale parameters that will be input into the simulation function for the vulture simulation. The lower plot shows the distribution used to generate potential foraging desintations.
Similar to badgers vultures exhibit significant site fidelity, re-using roosting and nesting sites.99 Such shelter sites could be predefined; for example, if shelter sites were known a priori discovered via the capture and tagging of animals, which in the case of birds is more likely.
Vultures also offer an opportunity to demonstrate how the underlying resource availability impact the movements of animals. In the case of vultures, their moments have been seen to follow carcass, creating starkly contrasting areas where vultures will and will not travel9 [Figure 11].

Vultures have a very similar cycle pattern to the badgers (just inverted), one defined by a standard 12 hours of activity during the day, and 12 hours of increased resting behaviour during the night. The importance of simulating such cycles is made clear by vultures studies demonstrating that day-night cycles can impact rates of location collection.100 How the the animals’ activity cycle and the probability of collected data interact could be key consideration for some research questions. Again similar to badgers we would expect seasonal shifts in the form of an increase and decrease in activity depending on the time of year.95–97,101
We can broadly summarise the vulture ecology we want to parametrise as follows:
4.2.2 Ecology and objectives - king cobra
Whereas the previous two species have a very limited or single shelter sites, king cobras make use of a wider range of shelter sites distributed more widely over their home ranges.102,103 These sites can also be larger, comprising burrow systems or rock complexes.
What more dramatically sets king cobras, and other snakes, apart is a vastly differing rest-forage cycle. While snakes still exhibit a diel cycle, the intermittent depredation of large prey items and the time required sheltering to digest large meals results in a second broader activity cycle operating over a more widely observed diel cycle.103–106 We can conceptualise this pattern as two additive cycles, one that will describe the daily activity cycle, and a second that describes the foraging and digestion cycle. Seasonality also impacts king cobra activity. As king cobras occupy tropical regions, the seasonality they experience is not as pronounced as the badger or vulture examples. Overall king cobras have three activity cycles acting on three different scales.
In this example we can also demonstrate the movement resistance dramatically impacting movement possibilities. King cobra movement can be limited by roads,107,108 where unless provided with crossing structures king cobras are vulnerable to vehicle hits [Figure 13]. In addition to roads presenting linear barriers across the landscape, king cobras face persecution when near or in human settlements.108,109 Despite the risks, avoidance of such areas appears weak.
Finally, king cobra movement characteristics will be dramatically reduced compared to the vulture’s, but with similar shape to the badger with greater variability [Figure 12] as king cobras are known to range over large areas.102,103,110

The distribution displayed is generated from the same shape and scale parameters that will be input into the simulation function for the king cobra simulation. The lower plot shows the distribution used to generate potential foraging desintations.
We can broadly summarise the king cobra ecology we want to parametrise as follows:
1. Lower site fidelity via the use of many shelter sites102,103
2. Movement speed approximated by summary statistics from previous studies,102,103,110 with examples of very high landscape derived resistance107,108
3. A 8-12 hour activity cycle, with a approximately weekly forage-digest cycle, and weak seasonality103–106
4.2.3 Simulation inputs
Vulture Inputs Largely the vulture parametrisation matches the badger. We specified a number of predefined resting/shelter sites, assuming that bird bio-tagging is more likely to occur at known site (i.e., nests or roosts). The shelter site size is smaller than the badger sett, so is only 5 m. Step length parameters are all larger and more variable, along with destination ranges [Figure 10]. We set a larger rescale value also to ensure the vulture has a larger landscape to operate across. The rest cycle is broadly similar, with a 12 hour diel cycle and gentle seasonality. We make two small modifications to the transition matrix allows for more frequent switches between foraging and exploring. We also alter two of the environmental matrices. We maximise movement ease across the entire landscape, while also lowering the foraging quality for an area to the West reflecting lower resources in that area [Figure 11]. Finally, we specify that the vulture will not be avoiding any locations; we still require inputs for the simulation, but we can provide zeroes to negate the effect.
# predefined shelter sites
VULTURE_shelterLocs ˂- data.frame(
"x" = c(1024}, 1005, 1115),
"y" = c(1193, 1070, 882))
# shelter site radius to reduce movements
VULTURE_shelterSize ˂- 5
# parameters defining Gamma (step length) and Von Mises (turn angle) for each
# behaviour state
# Gamma shape
VULTURE_k_step ˂- c(2, 2.2*60, 1.5*60)
# Gamma scale
VULTURE_s_step ˂- c(40, 1.2, 1)
# Von Mises mean
VULTURE_mu_angle ˂- c(0, 0, 0)
# Von Mises concentration
VULTURE_k_angle ˂- c(0.6, 0.99, 0.6)
# parameters defining Gamma (shape and scale) and Von Mises (mean and
# concentration) for foraging destination options
VULTURE_destinationRange ˂- c(50, 120)
VULTURE_destinationDirection ˂- c(0, 0.01)
# the transformation (2 = squared) and strength of attraction to destinations
VULTURE_destinationTransformation ˂- 2
VULTURE_destinationModifier ˂- 2
# each cell of the environmental matrix is 20x20
VULTURE_rescale ˂- 20
# the diel resting/active cycle: amplitude, midline, offset, frequency
VULTURE_rest_Cycle ˂- c(0.1, 0, 24, 24)
# additional cycles as a dataframe: amplitude, midline, offset, frequency
c0 ˂- c(0.025, 0, 24* (365/2), 24* 365) # seasonal
VULTURE_additional_Cycles ˂- rbind(c0)
# select modifications to the default behavioural transition matrix
VULTURE_behaveMatrix ˂- Default_behaveMatrix
VULTURE_behaveMatrix[2,3] ˂- 0.0002
VULTURE_behaveMatrix[3,2] ˂- 0.000015
# maximising movement ease by changing the default movement matrix
VULTURE_movementMatrix ˂- landscapeLayersList$movement
VULTURE_movementMatrix[] ˂- 1
# reducing foraging quality in the West of the landscape
VULTURE_forageMatrix ˂- landscapeLayersList$forage
VULTURE_forageMatrix[1:950,1:2000] ˂- VULTURE_forageMatrix[1:950,1:2000] - 0.6
VULTURE_forageMatrix[VULTURE_forageMatrix[˂ 0] ˂- 0
# place holder avoidance location
VULTURE_avoidLocs ˂- data.frame(
"x" = c({1000),
"y" = c(1000))
# vulture has zero avoidance of the place holder point
VULTURE_avoidTransformation ˂- 0
VULTURE_avoidModifier ˂- 0King Cobra Inputs Compared to the vulture, the king cobra movements are smaller, but king cobras can still occupy large areas [Figure 12]. We provide a rescale value of 10 m to provide a large enough landscape to capture a potentially large range. The activity cycle provides an opportunity to demonstrate three additive cycles. The diel cycle is largely similar to the other examples, but we also define an approximately weekly cycle to cover the forage-digestion cycle as well as weak seasonal cycle. Combined the three cycles create an activity pattern quite different from either the badger or vulture. To balance the three cycles and their influence on the behaviour transitions, we make some minor adjustments to the underlying behavioural transition matrix. As mentioned in the ecology and justifications, we want to simulate a barrier limiting movement. We construct this by altering the values in the environmental matrices, minimising the weighting in cells following two perpendicular lines [Figure 13]. We also provide a set of avoidance locations and a relatively weak avoidance weighting coefficient. Finally, we can set the shelter sites. We draw 12 sites randomly based on shelter site quality, and limit the area that they can be draw from to ensure they are not on the far side of the barrier. We use a larger shelter site size, as king cobras are known to occupy large rock complexes at times.
# parameters defining Gamma (step length) and Von Mises (turn angle) for each
# behaviour state
# Gamma shape
KINGCOBRA_k_step ˂- c(30, 40, 20)
# Gamma scale
KINGCOBRA_s_step ˂- c(0.75, 1.2, 1.75)
# Von Mises mean
KINGCOBRA_mu_angle ˂- c(0, 0, 0)
# Von Mises concentration
KINGCOBRA_k_angle ˂- c(0.6, 0.99, 0.6)
# parameters defining Gamma (shape and scale) and Von Mises (mean and
# concentration) for foraging destination options
KINGCOBRA_destinationRange ˂- c(50, 10)
KINGCOBRA_destinationDirection ˂- c(0, 0.01)
# the transformation (2 = squared) and strength of attraction to destinations
KINGCOBRA_destinationTransformation ˂- 2
KINGCOBRA_destinationModifier ˂- 1.5
# each cell of the environmental matrix is 10x10
KINGCOBRA_rescale ˂- 10
# the diel resting/active cycle: amplitude, midline, offset, frequency
KINGCOBRA_rest_Cycle ˂- c(0.14, 0, 24, 24)
# additional cycles as a dataframe: amplitude, midline, offset, frequency
c0 ˂- c(0.12, 0, 24, 24*4) # digestion
c1 ˂- c(0.05, 0, 24 * (365/2), 24* 365) # seasonal
KINGCOBRA_additional_Cycles ˂- rbind(c0, c1)
# select modifications to the default behavioural transition matrix
KINGCOBRA_behaveMatrix ˂- Default_behaveMatrix
KINGCOBRA_behaveMatrix[1,1] ˂- 0.95
KINGCOBRA_behaveMatrix[1,2] ˂- 0.005
KINGCOBRA_behaveMatrix[3,1] ˂- 0.00025
KINGCOBRA_behaveMatrix[3,2] ˂- 0.000001
KINGCOBRA_behaveMatrix[3,3] ˂- 0.999
# extracting the default matrices ready for changes
KINGCOBRA_shelteringMatrix ˂- landscapeLayersList$shelter
KINGCOBRA_forageMatrix ˂- landscapeLayersList$forage
KINGCOBRA_movementMatrix ˂- landscapeLayersList$movement
# defining the start and end of strong intersections hampering movement
roadMin_x ˂- 1360
roadMax_x ˂- roadMin_x + 40
roadMin_y ˂- 660
roadMax_y ˂- roadMin_y + 40
# applying the change, dramatically reducing the weighting for all matrices
KINGCOBRA_shelteringMatrix[roadMin_x:roadMax_x,1:2000] ˂-
KINGCOBRA_shelteringMatrix[roadMin_x:roadMax_x,1:2000] - 90
KINGCOBRA_shelteringMatrix[1:2000,roadMin_y:roadMax_y] ˂-
KINGCOBRA_shelteringMatrix[1:2000,roadMin_y:roadMax_y] - 90
KINGCOBRA_shelteringMatrix[!{KINGCOBRA_shelteringMatrix >= -99.9] ˂- -99
KINGCOBRA_forageMatrix[roadMin_x:roadMax_x,1:2000] ˂-
KINGCOBRA_forageMatrix[roadMin_x:roadMax_x,1:2000] - 90
KINGCOBRA_forageMatrix[1:2000,roadMin_y:roadMax_y] <-
KINGCOBRA_forageMatrix[1:2000,roadMin_y:roadMax_y] - 90
KINGCOBRA_forageMatrix[!KINGCOBRA_forageMatrix >= -99.9] <- -99
KINGCOBRA_movementMatrix[roadMin_x:roadMax_x,1:2000] <-
KINGCOBRA_movementMatrix[roadMin_x:roadMax_x,1:2000] - 90
KINGCOBRA_movementMatrix[1:2000,roadMin_y:roadMax_y] <-
KINGCOBRA_movementMatrix[1:2000,roadMin_y:{roadMax_y] - 90
KINGCOBRA_movementMatrix[!KINGCOBRA_movementMatrix >= -99.9] <- -99
# defining a number of avoidance points
KINGCOBRA_avoidLocs <- data.frame(
"x" = c(552, 1232, 1587),
"y" = c(789, 975, 1356))
# and specifying a weak avoidance of the points
KINGCOBRA_avoidTransformation <- 2
KINGCOBRA_avoidModifier <- 1
# after the matrices have been altered, drawing 12 shelter sites based on shelter quality
sampledShelters <- sampleRandom (raster (KINGCOBRA_shelteringMatrix), 12,
ext = extent(0.35, 0.65, 0.42, 0.65),
rowcol = TRUE)
# and storing those shelter sites as a dataframe ready for the simulation function
KINGCOBRA_shelterLocs <- data.frame(
"x" = sampledShelters[,2],
"y" = sampledShelters[,1])
# specifying a larger shelter site radius
KINGCOBRA_shelterSize <- 10
Movement ease is blocked by bars of -99 weighting.
4.2.4 Simulation outputs
Figures 10 and 12 describe the inputs for the vulture and king cobra example respectively, and can be compared to Figures 14 and 15 that display the realised movements. Figures 14, and 15 also provide information on the rates of stationary behaviour, defined in the plot as step lengths less than the shelter site size. The king cobra example in particular highlights the prolonged near weekly resting periods.

Step lengths are scaled back to the input units. Inset pie chart show the number of step lengths that were below the shelter site size; the sub-shelter site step lengths are excluded from the density plot. Note that x axis is not consistent between the three plots.
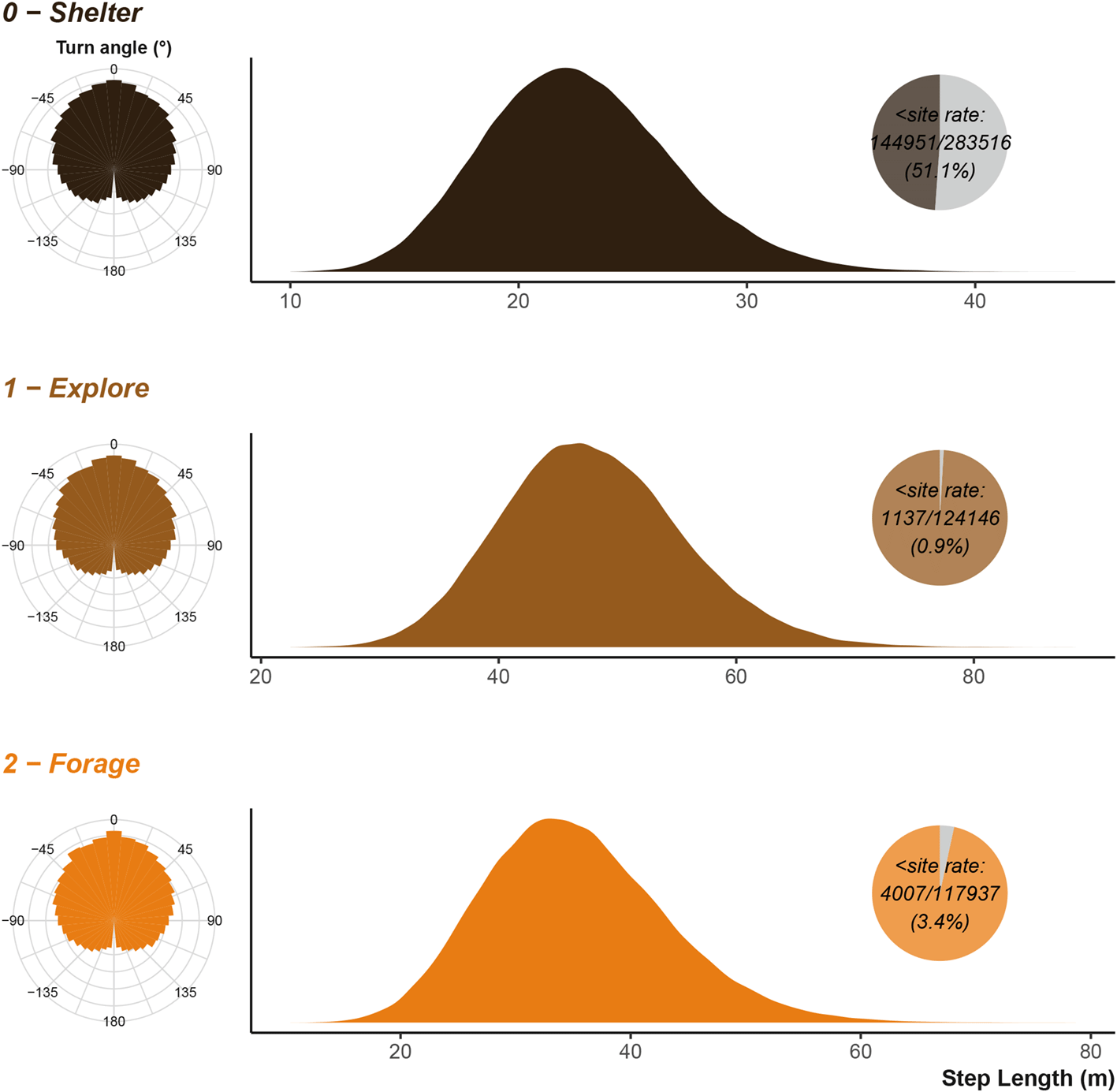
Step lengths are scaled back to the input units. Inset pie chart show the number of step lengths that were below the shelter site size; the sub-shelter site step lengths are excluded from the density plot. Note that x axis is not consistent between the three plots.
The parameters used to generate the examples (based on Refs. 58–63 for the badger example; Refs. 95–101 for the vulture example; and Refs. 102–110 for the king cobra example) presented in this study are included in the GitHub and Zenodo repositories in the file ‘notebook/manuscript/Agent-based_model_walkthrough.Rmd’.
Zenodo: Simulated data from abmAnimalMovement: An R package for simulating animal movement using an agent-based model, https://doi.org/10.5281/zenodo.6992495.111
This project contains the following underlying data:
• eg_simdata_BADGER_locations.csv (A csv file that contains the realised locations of the example badger simulation, where each row is equal to a timestep. Columns include: timestep, the timestep as a integer; x, the x coordinate of the animal; y, the y coordinate of the animal; sl, the step length between locations used during the simulation; sl_rescale the rescale factor required to return step lengths back to the input scale; ta, turning angle between locations in degrees; behave, the behavioural mode the animal was in at a given timestep; chosen, the location chosen out of the number of options available; destination_x and destination_y the point the animal was attracted to at that time (note exploratory behaviour is not subject attraction)).
• eg_simdata_BADGER_options.csv (A csv file that contains the options available to the example badger simulation over the entire simulation duration, where each row is equal to an option repeated for each timestep. Columns include: timestep, the timestep as an integer; oall_x, and oall_y show the x and y coordinates of all the options available to an animal at a timestep; oall_steplengths are the step lengths from the current location compared to all the options).
• eg_simdata_completelist.RDS (This RDS file contains a list object of length three, where the full simulation outputs from each three example is stored. Each species slot contains the “locations” dataframe (see description of locations.csv), the “options” dataframe (see description of options.csv), and a nested list containing all the “inputs” used to generate the simulated results (split into subsections: inputs_basic that contains inputs linked to simulation duration and intensity, inputs_destination that contains inputs linked to destination and attraction aspects, inputs_movement that contains inputs linked to movement capacity and behavioural switching, inputs_cycle that contains inputs linked to activity cycling, inputs_layerSeed that contains the environmental matrices and seed). A fourth object is return called “others” that captures all other outputs, mainly used internally for debugging and checking).
• eg_simdata_KINGCOBRA_locations.csv (A csv file that contains the realised locations of the example king cobra simulation, where each row is equal to a timestep. The file structure follows the same as the BADGER_options.csv file).
• eg_simdata_KINGCOBRA_options.csv (A csv file that contains the options available to the example king cobra simulation over the entire simulation duration, where each row is equal to an option repeated for each timestep. The file structure follows the same as the BADGER_options.csv file).
• eg_simdata_VULTURE_locations.csv (A csv file that contains the realised locations of the example vulture simulation, where each row is equal to a timestep. The file structure follows the same as the BADGER_locations.csv file).
• eg_simdata_VULTURE_options.csv (A csv file that contains the options available to the example vulture simulation over the entire simulation duration, where each row is equal to an option repeated for each timestep. The file structure follows the same as the BADGER_locations.csv file).
Data are available under the terms of the Creative Commons Attribution 4.0 International license (CC-BY 4.0).
Source code available from: https://github.com/BenMMarshall/abmAnimalMovement/tree/v.0.1.3.0000
Archived source code at time of publication: https://doi.org/10.5281/zenodo.6951938112
License: GPL-3.0-only
| Views | Downloads | |
|---|---|---|
| F1000Research | - | - |
|
PubMed Central
Data from PMC are received and updated monthly.
|
- | - |
Is the rationale for developing the new software tool clearly explained?
Yes
Is the description of the software tool technically sound?
Yes
Are sufficient details of the code, methods and analysis (if applicable) provided to allow replication of the software development and its use by others?
Partly
Is sufficient information provided to allow interpretation of the expected output datasets and any results generated using the tool?
No
Are the conclusions about the tool and its performance adequately supported by the findings presented in the article?
Partly
References
1. Gochanour B, Fernández‐López J, Contina A: abmR : An R package for agent‐based model analysis of large‐scale movements across taxa. Methods in Ecology and Evolution. 2023; 14 (1): 218-230 Publisher Full TextCompeting Interests: No competing interests were disclosed.
Reviewer Expertise: Movement Ecology.
Is the rationale for developing the new software tool clearly explained?
Yes
Is the description of the software tool technically sound?
Yes
Are sufficient details of the code, methods and analysis (if applicable) provided to allow replication of the software development and its use by others?
No
Is sufficient information provided to allow interpretation of the expected output datasets and any results generated using the tool?
Partly
Are the conclusions about the tool and its performance adequately supported by the findings presented in the article?
Partly
Competing Interests: No competing interests were disclosed.
Reviewer Expertise: Statistical ecology; movement ecology
Alongside their report, reviewers assign a status to the article:
| Invited Reviewers | |||
|---|---|---|---|
| 1 | 2 | 3 | |
|
Version 2 (revision) 17 Dec 25 |
read | ||
|
Version 1 17 Oct 22 |
read | read | |
Provide sufficient details of any financial or non-financial competing interests to enable users to assess whether your comments might lead a reasonable person to question your impartiality. Consider the following examples, but note that this is not an exhaustive list:
Sign up for content alerts and receive a weekly or monthly email with all newly published articles
Already registered? Sign in
The email address should be the one you originally registered with F1000.
You registered with F1000 via Google, so we cannot reset your password.
To sign in, please click here.
If you still need help with your Google account password, please click here.
You registered with F1000 via Facebook, so we cannot reset your password.
To sign in, please click here.
If you still need help with your Facebook account password, please click here.
If your email address is registered with us, we will email you instructions to reset your password.
If you think you should have received this email but it has not arrived, please check your spam filters and/or contact for further assistance.
VULTURE_behaveMatrix <- Default_behaveMatrix
Error: object 'Default_behaveMatrix' not found
VULTURE_behaveMatrix <- Default_behaveMatrix
Error: object 'Default_behaveMatrix' not found
VULTURE_behaveMatrix <- Default_behaveMatrix
Error: object 'Default_behaveMatrix' not found