Accounting for the expansion of the universe using an energy/momentum model to construct the space-time metric

Hugh James

doi:10.12688/f1000research.108648.5

Home Browse Accounting for the expansion of the universe using an energy/momentum...

ALL Metrics

Views

Downloads

Get PDF

Get XML

Export

▬

✚

Research Article

Revised

Accounting for the expansion of the universe using an energy/momentum model to construct the space-time metric

[version 5; peer review: 2 not approved]

Hugh James

PUBLISHED 18 Dec 2025

Author details Author details

Retired, AWE, Aldermaston, Reading, Berkshire, RG7 4PR, UK

Hugh James
Roles: Conceptualization, Writing – Original Draft Preparation, Writing – Review & Editing

OPEN PEER REVIEW

REVIEWER STATUS

Abstract

Background

The success of the theories of special and general relativity in describing localised phenomena, such as objects undergoing high speed motion or located in gravitational fields, needs no further elaboration. However, when applied to the evolution of the universe several problems arise which can require an additional model, e.g., inflation during the early expansion, and adjustments to parameters to account for phenomena such as the late-time acceleration of the universe.

Methods

Focusing on the difference between the ways in which space and time are measured, this paper shows that there are two paths which allow the equations of special relativity to be produced from the same basic postulates.

Results

Both the standard theory and the energy/momentum, or dynamic model, utilise the Minkowski metric, but with different coordinate systems. The dynamic model transforms Cartesian coordinates into an Euclidean form by multiplying the coordinates by functions of γ (= (1– ν ²/c ²)^-1/2). When utilising these coordinates, the relativistic equations are unchanged for local phenomena such as the Lorentz coordinate transformation and the energy/momentum equation for high-velocity objects.

Conclusions

However, the derived coordinates alter the perceived overall structure of the universe in a manner that, for the simplest model under this system, allows the reproduction of observed cosmological features, such as the intrinsic flatness of the universe and the apparent late-time acceleration of its expansion, without the need of additional models or changes in parameter values.

Keywords

Cosmology, large-scale structure of universe, relativistic processes.

Corresponding author: Hugh James

Competing interests: No competing interests were disclosed.

Grant information: The author(s) declared that no grants were involved in supporting this work.

Copyright: © 2025 James H. This is an open access article distributed under the terms of the Creative Commons Attribution License, which permits unrestricted use, distribution, and reproduction in any medium, provided the original work is properly cited.

How to cite: James H. Accounting for the expansion of the universe using an energy/momentum model to construct the space-time metric [version 5; peer review: 2 not approved]. F1000Research 2025, 11:344 (https://doi.org/10.12688/f1000research.108648.5) First published: 21 Mar 2022, 11:344 (https://doi.org/10.12688/f1000research.108648.1) Latest published: 18 Dec 2025, 11:344 (https://doi.org/10.12688/f1000research.108648.5)

Revised Amendments from Version 4

There are three main changes in this version. The pruning of a lot of repetitious text coupled with some attempted further clarification of the philosophy and mathematics behind the theory. A major change is the correction of the time v. radius relationship of the universe's expansion (Equation 30, Fig.7). Previous versions followed an incorrect path in going from the Hubble equation to its required integral. Finally the symbol for the universe's scale factor has been changed from "s" to "a" to bring it more into line with common usage.

See the author's detailed response to the review by Boudewijn F. Roukema
See the author's detailed response to the review by Jackson Levi Said

Introduction

The success of the current theories of special (SR) and general relativity (GR) in describing localised phenomena, such as objects undergoing high speed motion, located in local gravitational fields or generating gravitational waves, needs no further elaboration. However, when applied to the evolution of the universe several problems arise which require either an additional model, e.g., inflation to account for the flatness or the horizon problems, or adjustments to coefficients and/or parameters to account for phenomena such as the universe’s late-time acceleration and the lack of observable mass to match the universe’s expansion¹.

This paper is not intended as a detailed review of current cosmology and the reader is assumed conversant with the problems mentioned above, hence only the outlines of such problems will be discussed. The paper is intended as a test-of-concept investigation into whether the approach developed therein might be more fruitful in tackling some of these problems than that utilised by the Standard Cosmology Model (SCM). The ability to do so is assessed as being able to dispense with some or all of the theoretical additions needed by SCM while still providing the same standard of fit that SCM achieves to the observed expansion of the universe.

In exploring an approach which attempts to answer at least some of these cosmological problems, while still satisfying the basic postulates of relativity, it will be shown that it is possible to utilise the same Minkowski space-time metric when constructing a set of coordinates that produce an alternative overall structure of the universe. This set of coordinates is based on leaving aside any philosophical questions about what space and time “really” are and just concentrating on the phenomena that humans consider as providing realistic analogues of such phenomena, i.e., as discussed in the following section, changes in energy are considered to be analogues of changes in time (clocks) while a spatial dimensions can be considered as corresponding to a distribution in mass (rulers). It is these analogues that are used to provide quantifiable tests of relativistic theories and so are of prime importance in describing the universe. However, as also explored below, they also illustrate the problems of mixing time and space to provide the coordinate systems used to form the space-time of standard, or indeed any, theory of relativity.

When discussing coordinate systems, it will be argued that care must be taken over the definitions of what is directly observable and what can only be inferred. Changes in coordinates that occur in the observer’s present can be defined as direct observations. When transforming these changes into a dimension, we can define the resulting coordinates as being directly observed if they can be revisited and are able to have different actions carried out at their location. Inferred coordinates are those that are based on a location which can only be visited once. The former can be associated with spatial dimensions while the latter is associated with time. Any temporal dimension must be constructed from indirect observations such as the reliance on memory or artificial aids such as film. Current theories rely on such a construction to complete a four-dimensional space-time, which has been very successful but has some problems on a universal scale such as those outlined above. The alternative approach is discussed which assumes, for reasons explained below, that it is the energy and momentum of objects that are fundamental to their behaviour, and from which the time element of a four-dimensional space-time coordinate system can be inferred, rather than starting from a four-dimensional coordinate system against which the energy and momentum of objects can be measured. Such an approach using the Minkowski metric allows Cartesian coordinates to be transformed into an Euclidean form (see Equation (7)–Equation (11) below). The changes between coordinate systems will be discussed, and the consequences of such changes are explored.

Any modification of the current theory must still conform to both the observation that the speed of light (c) is a constant in all inertial frames, and to the principle that the laws of nature are the same in all inertial frames. It also must conform to the principle of consistency, i.e., any new theory has to account for the successful predictions of the Newtonian and relativistic theories that it attempts to modify.

When carrying out such modifications the alternate set of coordinates will be labelled as “Dynamic” to distinguish them from the Standard set of coordinates which are currently used. The transformation between the two sets of coordinates within a single frame of reference will be derived in the following sections.

Under the “Cosmology” section it will be shown that the simplest model of the universe that can be constructed using dynamic coordinates will create a surface of three spatial dimensions whose evolution is based entirely on SR. In this model gravitational effects are assumed to exist along this surface and are orthogonal to its expansion in the fourth dimension.

Since the resulting model of the universe does not account for gravity, it is not related to the Friedmann-Lemaître-Robertson-Walker (FLRW) models. However, its results can be compared to those from the FLRW Standard Cosmology Model (Figure 5–Figure 6) and the combined Friedmann equations (Figure 7), which are assumed by this paper to currently give the best fits to astronomical observations. Consequently, it will be argued that the fact that the dynamic theory gives a good fit to such models implies it also gives a good fit to the corresponding astronomical data without the paper being sidetracked into extensive explanations and attributions of this data. It should also be emphasised that the goodness of fit shown in the above figures is achieved without any recourse to either GR or the additional models and coefficients that make up the SCM.

To summarise, the paper is in two main parts, with both parts concentrating on using SR as the basis. The first part discusses a possible alternative way of expressing SR and how coordinates in space-time arising from this can be transformed into “Standard” coordinates (Equation 7–Equation 10a) within a given inertial frame. It also shows agreement between the two theories in the non-cosmological (or local) area which is required for the new (“Dynamic”) theory to have any validity, e.g. the Minkowski space-time is still retained (although mapped differently), while both the Lorentz transformation between inertial frames and the 4-momentum relationship are unchanged. The consequences of this approach are discussed and in the second main part (labelled “Cosmology”) are applied to give a simple model of the universe’s expansion (Equation 24, Equation 26 & Equation 30) in order to test this concept.

The basis of the dynamic theory in Special Relativity (SR)

Possible grounds for pursuing alternative coordinate systems

A possible area that could lead to more than one approach to producing an SR coordinate system arises with the need to include time as the equivalent of a spatial dimension in either of the theories (standard or dynamic) discussed in this paper. As stated in the Introduction, for the dynamic theory this paper leaves aside any philosophical questions about what space and time “really” are and just concentrates on the phenomena that humans consider as providing realistic analogues of such phenomena, i.e., as discussed below, changes in energy are considered to be analogues of changes in time (clocks) while a spatial dimension can be considered as corresponding to a distribution in mass (rulers). It is these analogues that are used to provide quantifiable tests of relativistic theories. They also illustrate the problems of mixing time and space to form the space-time of standard, or indeed any, theory of relativity.

Basically, relativistic effects are measured with a clock and a ruler. To state the obvious a ruler is composed of a distribution of matter which is taken to define a spatial dimension. For the purposes of relativistic measurements, the ruler is unchanging for an observer in the same inertial frame, i.e. the coordinates it provides along a spatial dimension are static within an inertial frame and any position on this ruler can be revisited at will (albeit at different times). In contrast a clock gives a continuous (and regular) conversion of potential into kinetic energy, which is able to do work on its surroundings, e.g. the release in energy from a clock spring to continuously move the clock’s hands, or the decay of radioactive material to activate a counter. This is intended to correspond to what an observer experiences as time, i.e. he is always trapped in the current moment in the sense that he can only influence or be influenced by events which happen in his present (memories of past events may be said to influence him, but can only do so in his present), but this moment is always changing*. Since the observer is always in his present, past events can only be accessed by memory or aids such as film. This access is of a different order to the interactions granted to events in the present. An observer can physically visit a spatial location many times and interact with what is happening at that location. The ability to physically interact with an event in time is restricted by the fact that a temporal location can only be physically visited once. Since the observer only exists in his changing present, temporal coordinates can only be inferred by integrating experiences of the changing present using memories or other recording devices. The ever-changing present has no real coordinate that can be directly observed in the sense of spatial coordinates, there are only directly observed changes in time - see definitions of observable and inferred events given in the Introduction... Hence from within an inertial frame no dimension can be directly observed in what can be assumed as the time direction. It can only be inferred.

Consequently, there are two routes that can be taken when attempting to mix space and time. The coordinate route of the standard theory keeps the spatial dimension unchanged while integrating the changing temporal view to give an inferred fourth dimension which is analogous to space. The dynamic view keeps time as an ever-changing entity but requires this to be linked to objects (including other observers) which have an ever-changing spatial position. Hence the dynamic view is based on energy and momentum while the coordinate view is based on dimensions.

Since the integral of the dynamic view will also give space-time coordinates (albeit artificially constructed), and since it has already been stated that, at least locally, the standard and dynamic theories must match for the dynamic view to have any validity, the next two sections show where the coordinates generated by the two theories coincide; where they diverge; the derivation of the dynamic metric, and the transformation between dynamic and standard coordinates within a single inertial frame.

The intersection of the standard and dynamic theories

To clarify which theory is being referred to in the following, the derivatives in the standard theory result from infinitesimal changes in intervals which are used to obtain the dimensional coordinates and can be used to construct trajectories. In this paper such changes are denoted by d(). In the dynamic theory D() are infinitesimal changes in coordinates which are derived from the magnitude of the change in energy experienced in the present (located in what can be constructed as the time direction - i.e., orthogonal to the spatial directions), and the momentum of objects in the spatial dimensions. These are changes along trajectories. Subscripts N and M denote any inertial frame, in contrast to A and B which usually have specified conditions such as which frame contains the observer and which the observed.

In the standard theory a single subscript is used to denote the frame in which the coordinates are located, e.g. dt_A, dx_B, see Equation (1) below. In the dynamic theory more than one subscript is used to describe the direct observation within a single frame (A in what follows) of how other frames appear relative to A’s measuring apparatus, e.g. two subscripts are used for time, Dt_AB, where the first subscript is the frame containing the observer and the second the frame in which the object being observed is located. For space there are three subscripts, e.g. Dt_ACB where the first and third subscripts are as in the description for time, while the middle subscript is the frame in which the ruler is located against which the spatial motion is measured. In this example A is the observer, B is the object being observed relative to A’s space and C is the frame containing the ruler against which A measures B’s motion and again is relative to A’s space. Coordinates are transformed between dynamic and standard descriptions within a given frame by Equation (7), while both dynamic and standard coordinates are transformed between different frames by Lorentz transforms. The dynamic transform is given in Table 1 and the standard in Table 2 in the sections below.

Table 1. Dynamic Lorentz transforms from the viewpoints of A and B.

Column 1	Column 2
Dx_BBG = γ(Dx_AAG – vDt_AA):	Dx_AAG = γ(Dx_BBG + vDt_BB)
Dt_BB = γ(Dt_AA – v Dx_AAG/c²):	Dt_AA = γ(Dt_BB + v Dx_BBG/c²).

Table 2. Standard Lorentz transforms derived from Equation (7) and Table 1.

Column 1	Column 2
dx_B = γ(dx_A – vdt_A):	dx_A = γ(dx_B – vdt_B)
dt_B = γ(dt_A – v dx_A/c²):	dt_A = γ(dt_B – v dx_B/c²).

Both theories must satisfy the condition that the speed of light is the same in all inertial frames.

For the standard dimensional coordinate theory, this leads to the Minkowski metric which provides the following Cartesian relationship between space and time

c^{2} d τ^{2} = c^{2} d t_{A}^{2} - d x_{A}^{2} - d y_{A}^{2} - d z_{A}^{2} = c^{2} d t_{B}^{2} - d x_{B}^{2} - d y_{B}^{2} - d z_{B}^{2} (1) .

where A and B are inertial frames of reference, and d_τ is defined as the proper time interval, i.e. it is time recorded by a clock which moves with the object of interest and is an invariant quantity. In this paper, for brevity - but without any loss of generality – the total component of spatial motion is usually assumed to be lying along the x axis. For photons d_τ = 0.

In the dynamic theory several points must be considered.

The view of all inertial frames is always done from the present of an observer, and since both theories agree that there is no such thing as a universal present, the continuous changes are seen from a single viewpoint.
The dynamic theory deals with energy and momentum, i.e. the constant change in time (where coordinates must be inferred) and space (real coordinates). For brevity, these phenomena will sometimes be referred to as “motion”. As already outlined, this motion will be denoted by Dt_NM for time – where M is the frame in which the clock resides, and N is the frame containing the observer – while Dx_NNM refers to spatial motion where M is the frame in motion relative to both a ruler (middle subscript) and observer (first subscript) located in N.

The key point in dynamic SR is that the theory assumes that the fundamental parameters are the energy/momentum (motions) of objects (which includes observers) which are used to construct a 4-vector coordinate system, and not a 4-vector coordinate system that the motion is measured against. Consequently, for the dynamic theory, when the spatial component of motion lies entirely along the x axis, the above equation has to be written as

c^{2} D t_{A B}^{2} = c^{2} D t_{A A}^{2} - D x_{A A B}^{2} and c^{2} D t_{B A}^{2} = c^{2} D t_{B B}^{2} - D x_{B B A}^{2} (2)

to preserve both the existence and equivalence of two unique viewpoints - A sees B as B sees A - as well as the constant value of the speed of light from both viewpoints, i.e. if B is a photon then Dt_AB = 0. However, as will now be shown, the grouping of the parameters and the general invariance of the time term will be different.

Concentrating on A as the observer with the single viewpoint, then in an inertial frame the only motion that he can directly experience is that of his clock (Dt_AA). He does not experience any spatial motion (Dx_AAA = 0), and any such motion that could be inferred from movement of objects outside the frame can, from A’s view, be added to the spatial motion of B. This motion A sees as being relative to A’s own ruler (Dx_AAB). However, A is able to see (for this illustration and accounting for relativistic Doppler effects) B’s clock (Dt_AB). Consequently, grouping the motion that A can see of himself, and the motion that A sees of B on separate sides of the above equation gives the infinitesimal changes in dynamic coordinates (which should be compared to the changes in standard coordinates in Equation (1)) as

c^{2} D t_{A A}^{2} = c^{2} D t_{A B}^{2} + D x_{A A B}^{2} (3) .

The same view can be seen from B with the appropriate change in subscripts, i.e.

c^{2} D t_{B B}^{2} = c^{2} D t_{B A}^{2} - D x_{B B A}^{2} (4) .

The first thing to note is that the invariant is now Dt_NN as this is the only changing parameter that N can experience of itself, and one of the main principles of SR is that nature’s laws must be the same when seen from inside an inertial frame. Since a lot of these laws are time-dependent, then if Dt_AA ≠ Dt_BB there should be an effect seen from outside the frame which cannot be ascribed to either relative velocity or gravity. No such effect has ever been reliably reported so it is a safe postulate that Dt_AA ≡ Dt_BB

The second thing is that the only coordinates that A can directly observe are spatial. Hence the three subscripts for Dx – where the middle one relates to a ruler - compared to the two subscripts for Dt. However, as already mentioned, a time coordinate can be inferred by simply integrating Dt between two recorded events. If there is to be any overlap between the dynamic and coordinate theories, we need to find the relationship between the inferred and standard coordinates and, consequently, the relationship between their differentials.

In the standard coordinate theory, it is dτ that is the invariant between inertial frames, i.e. when we look for where the two coordinate systems overlap, we are looking for specific conditions where dτ = Dt_NN. This will be shown to be along the time-like hyperbolas in Figure 1a where dτ is an invariant for all possible inertial frames that have their origin at O, i.e. frames containing OA, OB and OG all have the same value of cdτ for any given hyperbola.

Since the dynamic theory has an ever-changing present, this is equivalent in Cartesian coordinates to mapping out time-like trajectories such as OB in Figure 1a.

Figure 1a. A’s view of a quadrant of the Minkowski space-time.

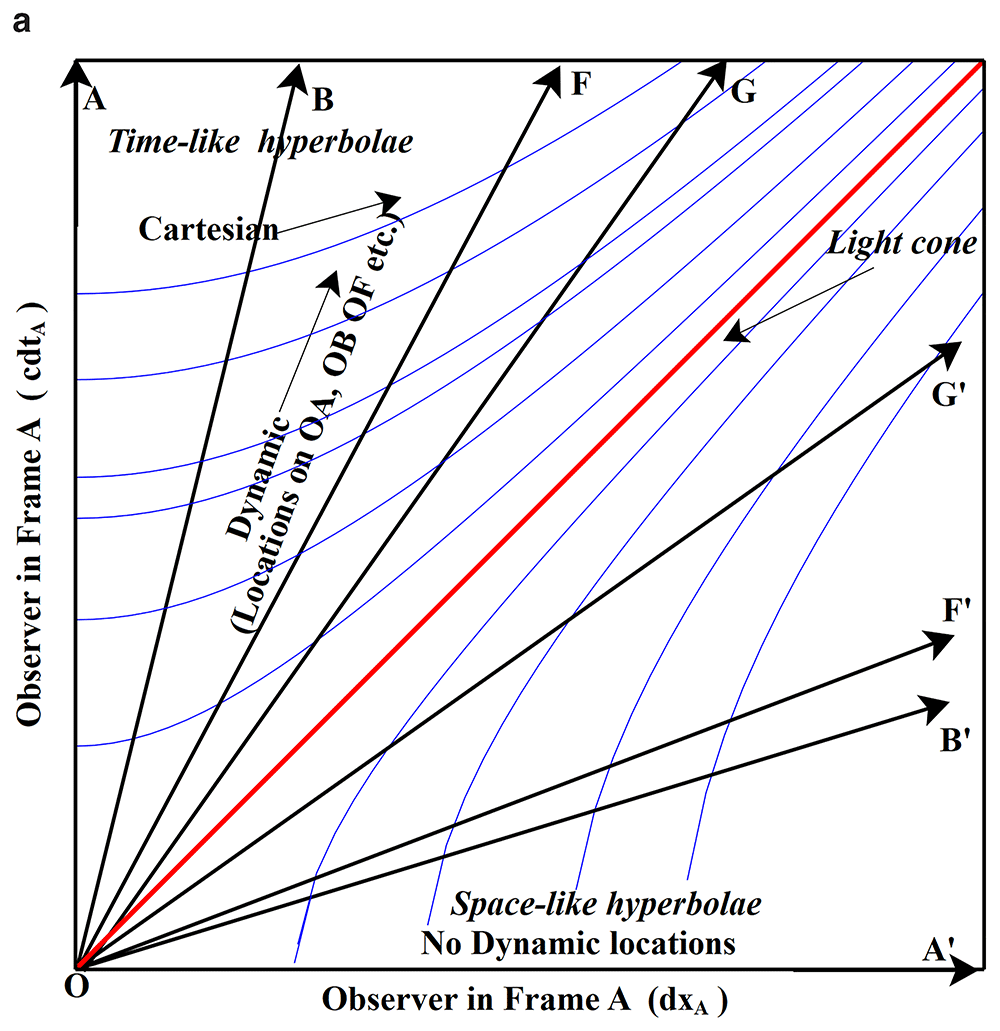
Standard coordinates follow the blue lines (hyperbolae) while dynamic coordinates follow the time-like axes OA, OB, OF etc. Note the time-like hyperbolae are also the locus of all time axes for inertial frames with an origin at O. As shown in Figure 1b, there are no dynamic locations on the space-like hyperbolae because in Equation (3), Equation (4), DX_NNN = 0, while only DX_NNM ≠ 0. (See text for nomenclature.).

In Figure 1a, A is the observer, and the condition dτ = Dt_NN can only occur where the observer and the event or object being observed lie entirely on their respective time axes, e.g. along OA, OB, OF and OG in Figure 1a. This condition corresponds to dx_N = 0 in Equation (1), and Dx_NNM = Dx_NNN = 0 in Equation (3) and Equation (4). The four sets of inertial axes (A, B, F and G) in this figure are shown from A’s viewpoint. All frames have a common initial location at O. These positions are consistent with the dynamic hypothesis that from within any inertial frame, the only features of the frame that changes are those entirely connected with changes in time (i.e. Dt_NN).

In Figure 1b it can be seen that all inertial time axes with a common origin (O) must intersect the hyperbolas defining different values of cdτ, and so these hyperbolas can be considered as the loci of intersections of all the time axes of objects undergoing different inertial spatial motions as seen from A.

Figure 1b. Comparison of the Dynamic and Standard coordinates in complete Minkowski space-time.

Consequently, for these conditions to be met, the dynamic equivalence of the Cartesian coordinate viewpoint requires that every object (and hence every observer) must be located on its own time axis, even though such an axis can only be inferred by such an observer. This corresponds to the initial definitions that were given about the dynamic condition. Every point on a given hyperbola coincides with a time axis of an object which has a given relative velocity to A, and whose velocity is different to every other point on the curve. The location of an object on its own time axis means that Dt_AA = Dt_NN. However, since this occurs at every point along this curve, in general terms, Dt_NN and dτ are both invariant along this hyperbola.

Hence, from the above along the time-like hyperbolas

D t_{N N} = d τ a t D x_{N N N} = 0 (5) .

And since

c^{2} D t_{N N}^{2} = c^{2} d τ^{2} then c^{2} D t_{N M}^{2} + D x_{N N M}^{2} + D y_{N N M}^{2} + D z_{N N M}^{2} = c^{2} d t_{N}^{2} - d x_{N}^{2} - d y_{N}^{2} - d z_{N}^{2} (6) .

Let

\begin{array}{l} D X_{N}^{2} = D x_{N N M}^{2} + D y_{N N M}^{2} + D Z_{N N M}^{2} and d X_{N}^{2} = d x_{N}^{2} + d y_{N}^{2} + d z_{N}^{2}, so \\ d X_{N} / c d t_{N} = D X_{N N M} / c D t_{N N} = υ_{N} / c, \end{array}

From this and Equation (6) we can, after some manipulation, derive the following relationships

\begin{array}{l} D t_{N N} = d τ \\ γ_{N} D t_{N N} = d t_{N} \\ γ_{N} D X_{N N M} = d X_{N} \\ γ_{N}^{2} D t_{N M} = γ_{N} d τ = d t_{N} . \end{array} (7) .

Where $γ_{N} = {(1 - υ_{N}^{2} / c^{2})}^{- 1 / 2} .$

Hence γ_{N}^{- 1} (d X_{N}, d t_{N}) = (D X_{N N M}, D t_{N N}) . (8) .

Consequently, we can rewrite the dynamic portion of Equation (6) in terms of standard coordinates to give

c^{2} d τ^{2} = γ_{N}^{- 4} c^{2} d t_{N}^{2} + γ_{N}^{- 2} d X_{N}^{2} = c^{2} d t_{N}^{2} - d X_{N}^{2} (9) .

To express the standard and dynamic coordinates in more familiar nomenclature, let

μ, v = 0 t o 3. Then c d t_{N} = d x^{0}; d x_{N} = d x^{1}; d y_{N} = d x^{2}; d z_{N} = d x^{3} .

The Minkowski metric is

{(c d τ)}^{2} = η_{μ v} d x^{μ} d x^{v} (10) .

Where in standard coordinates

η_{μ v} = \begin{array}{c} 1 & 0 & 0 & 0 \\ 0 & - 1 & 0 & 0 \\ 0 & 0 & - 1 & 0 \\ 0 & 0 & 0 & - 1 \end{array}

While the dynamic coordinates transformed into standard coordinates are

η_{μ v} = \begin{array}{l} γ_{N}^{- 4} & 0 & 0 & 0 \\ 0 & γ_{N}^{- 2} & 0 & 0 \\ 0 & 0 & γ_{N}^{- 2} & 0 \\ 0 & 0 & 0 & γ_{N}^{- 2} \end{array}

From the above it is straightforward to show the dynamic theory gives the same 4-momentum vector as the standard theory, i.e. let

U^{0} = d x^{0} / d τ = γ_{N} c D t_{N N} / d τ = c γ_{N}; and U^{1} = d x^{1} / d τ = γ_{N} D x_{N N M} / D t_{N N} = v_{1} γ_{N} e t c .

Then U^μ = γ_N(c, V) where V is the complete spatial vector, and by multiplying by the mass (m) of the object under investigation in frame M, we get

P^{μ} = m γ_{N} (c, V) (11)

which is the 4-momentum of the standard theory. The main difference between the theories is that one corresponds to an Eulerian form while the other does not. This gives rise to the following relationship between spatial motion and a changing present.

The equivalent dynamic diagram to Figure 1a is, from A’s viewpoint, given in Figure 2. However, from this Figure when B moves relative to A in the dynamic theory, it appears to A that B’s time is partly at a reduced time rate and partly as a motion against A’s spatial dimensions. In the limit a photon would appear to A as only having a spatial motion and with no time element present. Although to an imaginary observer within the photon’s frame of reference, according to the requirement of nature’s laws having to be constant, the photon’s time would appear to proceed at Dt_NN while A would only have a motion along the photon’s spatial dimension during which A’s clock would appear frozen. Hence in this limit of possible frame rotations, what appears to be time from within the frame is seen from the outside as a motion through space against the background of the outside observer’s spatial dimensions. To an observer within a frame there is no observation (as distinct from inference) of any dimension of any sort - temporal or spatial - in the time direction and so it appears that the space against which this motion takes place does not exist, i.e. it has collapsed to a point on the time axis where it corresponds to the ever-changing, dimensionless present. However, the summation of all the views from every possible frame indicates the overall framework within which any individual observation is made is of four orthogonal spatial dimensions. It is just that the individual observer can only see three of them plus a changing present (see Cosmology Section).

Figure 2. The dynamic view of inertial frames.

Similarities and differences between the theories

Time dilation. It is straightforward to show that Equation (3) can be manipulated to give to give a dynamic time dilation that is the same as for the standard theory. Indeed we note that from the transform in Equation 7 we can immediately write

d t_{A} / d τ = γ_{A} D t_{A A} / γ_{A} D t_{A B} = γ_{A} . (11) .

Length contraction. The key element when dealing with spatial dimensions in the dynamic theory is that no spatial dimension can be seen to exist by an observer in his own time direction. However, there will be items that have unchanging spatial coordinates within an inertial frame, and which can also be seen outside of that frame. Take frames A and B as being stationary relative to each other at some point in time. Both are equipped with rods of equal length along the x axis. The frames are then given a relative velocity of v, and A then compares B’s rod with his own. The dynamic equations given above can be represented by a simple axis rotation equal to ζ = sin ^–1(v/ c), and by the acknowledgement that the spatial x coordinates lie in the same direction as Dx.

For the dynamic theory let any coordinate terms be represented (e.g. the rod length) by δx, δy etc. Being a coordinate within an inertial frame, this is unchanging in time, in contrast to Dx which we have defined as constantly changing to match the ever-changing present. The subscript convention is the same as for Dx, e.g. δx_ABC where A is the observer, B the frame containing the ruler and C is the frame containing an object that A wishes to measure, and which lies in A’s x direction. For a complete four-dimensional Euclidean-type coordinate transform, A would see δx_BBB as having a component δx_BBB cos ζ in A’s spatial direction and δx_BBB sin ζ along A’s time axis. However, since there is no spatial dimension that can be observed by A along his own time axis, the length of B’s rod which is present in A’s inertial frame is seen by A to only be

δ x_{A B B} = δ x_{B B B} c o s ζ = γ_{A}^{- 1} δ x_{B B B} (12) .

This is the same length contraction result as for the standard theory, and this length contraction is independent of time since we are using δx.

Both the time and space effects in special relativity are apparent effects. The word "apparent" is used as the changes in the parameters are brought about by changes in perspective rather than any fundamental change of the value of the parameter, e.g. in the length contraction discussed above, the same contraction is seen by B in A’s rod. Fundamental changes may be assumed to only occur once gravitation (or acceleration according to Einstein’s equivalence principle) is considered, but this is beyond the scope of the present paper.

It should also be noted that in the dynamic theory while Dx_NNN and Dx_NMM are always zero (the frame cannot move relative to its own ruler), δx_NNN and δx_NMM can have non-zero values.

Lorentz transformation. This is the transformation of coordinate systems (standard and dynamic) between different frames, in contrast to Equation (7) where the transformation is between coordinate systems in the same frame.

An additional spatial motion must be used by the dynamic theory to obtain the Lorentz transformation, as Dx_NNN is zero. For all spatial motions taking place along A’s x direction, the transformation can be derived as follows.

Take frame G moving relative to both A and B, where the spatial motion of G relative to the ruler in B is observed by B to be Dx_BBG, and the spatial motion relative to a ruler in A (observed by A) is Dx_AAG. The velocity of B (observed by A) is given by v = Dx_AAB/Dt_AA; the velocity of G relative to B (observed by B) is w = Dx_BBG/Dt_BB and the velocity of G relative to A (observed by A) is u = Dx_AAG/Dt_AA.

Let

γ_{1} = {(1 - v^{2} / c^{2})}^{- 1 / 2}; γ_{2} = {(1 - u^{2} / c^{2})}^{- 1 / 2} and γ_{3} = {(1 - w^{2} / c^{2})}^{- 1 / 2}

Where in Table 1, γ = (γ₁γ₂)/γ₃ for Column 1, and γ = (γ₁γ₃)/γ₂ for Column 2.

Dividing the top row by the bottom in Column 1 gives

w = (u - v) / (1 - v u / c^{2}) (13)

while dividing the top row by the bottom in Column 2 gives

u = (w + u) / (1 + v w / c^{2}) (14) .

When comparing these equations with the standard coordinate version of the Lorentz transformation, they give both the same velocity-addition relationships and, as will be shown, the same coordinate transforms.

In Table 1 multiply both sides of each equation by γ and substituting the appropriate d() term from Equation (7). This gives substitute Table 2 in standard Cartesian coordinates which corresponds to the standard transformation.

The 4-vector, energy and momentum. As already shown the dynamic theory gives the same 4-momentum relationship as the coordinate theory, but this results in a change of interpretation of the role of rest mass energy (E₀). This result can be obtained geometrically for the dynamic theory by taking the top right-hand quadrant of Figure 2, but omitting the G axis. In the following, the terms OA, OB, OE and EB are those used in Figure 2.

Note that γ = γ₁ in the rest of the text,

Let each of the sides of the triangle OBE in this figure be divided by cDt_AB and denote them by a dashed superscript, which then gives OB′ = OB/cDt_AB; OE′ = OE/CDt_AB. Hence triangles OBE and OB′E′ are similar which gives

OB′ = OA′ = cDt_BB/cDt_AB = cDt_AA/cDt_AB = γ;

E′ B′ = Dx_AAB/cDt_AB = γv/c;

OE′ = 1.

The energy/momentum vectors can then be obtained by multiplying each of the sides by B’s rest mass energy (E₀ = mc²) where m is B’s mass. In turn this gives

OE′ = E₀.

OB′ = γE₀ = E.

E′ B′ = γmvc²/c = pc,

where p is momentum, i.e. p = γmv.

From Figure 2, OB² = OE² + EB². Hence (OB′)² = (OB′)² + (E′B′)², and so

E^{2} = E_{0}^{2} + p^{2} c^{2} (15) .

as in the standard theory.

It should be noted that the rest mass energy lies in A’s time direction and so appears to be linked to the continually changing time, which is seen from other frames of reference as having components of both spatial velocity and time. As discussed above, these components have a vector addition which always adds up to the velocity of light and so within a frame, which cannot observe any spatial motion of itself, this velocity is entirely expressed as a changing time i.e. E₀ is a kinetic rather than a static phenomenon.

In the next section it will be hypothesised that the time directions of all frames of reference lie in the local directions of the radial expansion of the dynamic model of a 4D universe. In this simple model this is the only motion that is allowed. The 3D space is everywhere orthogonal to this direction and, as discussed below, an observer can only see other frames moving in his space due to the curvature of the universe in this model and the radial expansion of this surface (see Figure 3). Consequently, despite having a total motion equivalent to the velocity of light, this is only seen from within a frame as temporal changes and is driven entirely by the expansion of the 3D surface of this universe along a radial direction in the fourth dimension. There are no objects moving along the 3D surface independently of this expansion, i.e. as previously discussed, all objects are time-like and none are space-like.

Figure 3. Simple dynamic model of the current state of the universe.

Cosmology

The standard model and its problems

In describing the universe, the standard theory has evidence of an expanding space-time which started from a singularity and was impelled outwards by the Big Bang some 13.8 billion years ago. In the simplest model the mass of the universe is assumed to be uniformly distributed and the expanding 4D space-time is taken as analogous to the surface of an expanding balloon in which all views and expansions are along the surface. Nothing is assumed to exist outside of this surface so what can be taken in an ordinary balloon as an expansion which is normal to its surface, is only seen in the standard model as a stretching surface. There are a number of problems with this model¹ which can be summarised as

The need for an inflation model. This postulates that at very early times the universe underwent a very rapid expansion which was abruptly switched on and then off and has never been seen since. There currently appears no solid physical explanation for this model^1,3 and the reason for adopting it is that it provides an explanation of some of the following observational conundrums.
The flatness problem. From observation the universe is very close to its critical mass density which means the curvature of space-time is near zero⁴. Since the universe is thought to start from a point, the inflation model is needed to suddenly expand to a surface whose curvature is locally insignificant.
The isotropic or horizon problem. The microwave background radiation is very uniform in all directions. Either we are somehow at a unique place in the cosmos, or all parts of the universe were in contact at the earliest times after the Big Bang. However, the areas that needed to be in contact exist along a line of sight that precludes even the speed of light to be fast enough to provide a connection. Again, the inflation theory can be used to provide an initial expansion that was far faster than the speed of light and so allowed such connections to exist at early times.
The existence of quantum fluctuations needed to provide the seeds of the current galaxies. The origin of such fluctuations requires the formation of virtual particles that are separated by space-time expanding too fast for them to recombine. An inflation-type model is needed for this expansion.

And some items which may not be explained by inflation.

Dark matter. There is a lack of observable mass in the universe needed to account for its expansion using the standard general relativity theory. There also appears to be too little mass to account for the rotation of galaxies. The shortfall is sometimes postulated as being due to a so-far unobserved particle and is often referred to as dark mass. To account for the dynamics of the universe’s expansion using the standard theory, this dark mass would have to consist of about 25% of the matter in the universe.
Dark energy. It has recently been found^5,6 that the expansion of the universe appears to be accelerating, rather than decaying as would be expected if the expansion were only controlled by gravitational effects (or at least, effects due to the standard theory of gravitation**). This energy would be equivalent to about 70% of the matter needed to model the universe using the standard theory.
The “Hubble tension” where the current Hubble parameter which is obtained from the cosmic wave background (i.e. the early stages of the universe’s expansion) is some 10% lower than that found from recent cosmological features (e.g. 10).

The dynamic theory will attempt to answer all of the above points based on the different structure of the universe generated by the differences between standard and dynamic relativistic models. In the dynamic theory no further models, such as inflation, will be needed. The next segment will construct the simplest model of the universe that is consistent with the dynamic theory. The last segment will compare quantitative predictions from this theory with FLRW fits to observations. The reasons and basis for this approach have been outlined at the start of this paper.

The simple dynamic model

In the simplest model the dynamic theory assumes the universe started from a singularity embedded in four spatial (not space-time) dimensions at, what we consider, the time of the Big Bang. This provides a uniform radial expansion in the four dimensions if we assume that mass is uniformly distributed throughout the history of the expansion. This is assumed to be analogous to the expanding shell of a 3D sphere, where the mass can be taken as lying at the centre of the sphere, despite all the material being located in the shell, and there is no gravitational potential along the shell normal to the radial expansion vector.

Time comes into being as soon as the expansion starts. This is the radial expansion vector and in effect the model is the opposite of the standard theory. There nothing exists apart from a 4D surface undergoing expansion, while gravitation, spatial motion etc. takes place along this surface. In the dynamic theory, assuming uniform mass, the expansion only occurs radially into a 4D space. For the model discussed in more detail below, our 3D space exists as a surface which is orthogonal to the radial expansion. This radial expansion is experienced as time from within an observer’s reference frame, but with all other frames seen as having their spatial components of motion (and gravitational effects) along this 3D surface in the same fashion as already discussed in the previous sections on SR (see Figure 3). The observer has no observation of a fourth spatial dimension; it can only be inferred from clocks as previously discussed.

Quite when this expansion transforms to a Minkowski space-time is not clear other than it is assumed by the dynamic theory to occur soon after the Big Bang. Also, like the standard theory, quantum effects should be important in these very early stages but are not considered in this paper. Equally speculation on what exists in the space outside the expanding surface is again outside the scope of the current paper.

Because this is a radial expansion and the 3D spatial surface is analogous to a sphere, an observer (A) sees a non-local galaxy (such as B) as having a spatial motion away from him as the radial expansion occurs at increasing angles to A’s time direction. This 3D spatial surface is assumed to be flat, i.e., there is zero intrinsic curvature along this surface while the curvature exists in the fourth dimension, seen locally as time, and non-locally as providing an increasing velocity of the 3D surface in relation to A, so providing a stretching surface (see Figure 3).

The trajectories of all objects are assumed in this simple model to be constant and are seen from outside their frames of reference (and inferred) to obey R = cT, R being the dynamic spatial coordinate of the surface at time cT, and T is the dynamic time coordinate relative to the Big Bang, i.e. $c T = c \int_{0}^{T} D t_{N N}$ which is the integral of Dt_NN along N’s trajectory as inferred by an observer located within N’s frame of reference. $R = \int_{0}^{R} D r_{N N P}$ and is the position of a photon in frame P, emitted at the Big Bang, in N’s spatial axes while $D r_{N N P}^{2} = D x_{N N P}^{2} + D y_{N N P}^{2} + D z_{N N P}^{2}$ All inferred surfaces are coloured blue (see Figure 4) and are the loci of all such trajectories originating from the Big Bang.

Figure 4. Simple dynamic model of the evolution of the universe.

It is worth re-emphasising that the above trajectories relate to the expansion of these surfaces and not to what we would consider to be velocities along the three spatial dimensions of the surface. The surface of the universe can be postulated as everywhere (in the dynamic non-gravitational simple model) expanding radially at the speed of light. But this is in the fourth dimension which can only be inferred in terms of trajectory and observed as changes in time. No particle with a rest mass could move along the surface with this velocity. As explained in the SR section, this leads to all particles having a time-like trajectory, and this is the only trajectory linked to the radial expansion of the universe that can be inferred from within a reference frame that also contains the observer (see Figure 3 and Figure 4).

There are some points which have to be attached to the simple 4D picture of the dynamic universe (see also Figure 3):-

There is no motion along the surface normal to the radial expansion otherwise matter will tend to clump, and the uniform mass model will be invalid. Obviously clumping does happen to an extent in the real universe due to gravitational effects along the 3D surface as galaxies etc. exist. But in this model we are taking the simplest possible mass distribution where in spatial terms it is assumed that most of the universe can be treated as having a uniformly smooth matter distribution.
Consequently, from the previous assumption, there can be no overall gravitational potential along the 3D surface as it is assumed analogous to a uniform shell of material which forms the surface of a 3D sphere in Newtonian space, where the potential gradient lies along the radius but is zero along the surface normal to this radius. Locally the same comment about non-uniformity applies as in the previous bullet.
As a consequence of the previous points General Relativistic effects can, to a first approximation, be ignored when considering the observed overall motion of this surface, in contrast to the standard theory where they dominate due to all forces having to lie along a 4D surface***.
In the standard theory the redshift in B, as seen by A, could be generated by either a receding velocity or a gravitational redshift (or a combination of both). From the previous bullets, in the dynamic theory it is assumed that to fit the simple theory the redshift is entirely provided by a receding velocity, which in turn results from the angle the radial velocity at any location makes with an observer. Hence, to reiterate previous bullets, it is assumed that there is little matter (compared to the mass of the universe) that is trapped in intense local gravitational fields (in a black hole or around stars) or moving at high speeds along the 3D surface.
The expansion velocity of the universe would be inferred to be constant (and equal to the velocity of light) once the perspective effects due to curvature have been subtracted, despite the overall expansion probably decreasing. This apparently contradictory situation results from there being no direct way for 3D observers to measure changes in the actual 4D radial expansion rate from within the universe. Any real change in radial motion will be equally seen in both the passage of time and the expansion of space (see Figure 3), so that a phenomenon such as velocity remains unchanged.

Although the time dimension does not exist when observed from within a given reference frame, the remaining analysis requires the construction of an inferred “time dimension” in order to situate the relative position of bodies and events, e.g. such as where and when A locates galaxy B, or where events are located relative to the Big Bang. It is constructed by integrating the radial motion to provide a dimension in which events lie relative to A.

There are two types of surface shown in the following diagram (Figure 4). Solid blue lines are inferred surfaces which consist of the locus of 4D trajectories from the Big Bang to the present. Each trajectory is locally constructed, e.g. OA and OB in the Figure. The present is the surface constructed from the termination of these trajectories such as at A and B. This surface is where the 4D sphere lies but is not observable other than locally since information about B can only arrive at A in B’s past.

The second type (solid red line) is the directly observed surface. Observer A sees time dilation effects in B because of the galaxy’s recessional velocity, and these, plus the time delay for photons from B to reach A (vertical lines such as CF in the figure), only allows A to see B in B’s past. This is the only directly observable surface due to observations of the Doppler effect, and as such its position is linked to the change in scale factor with time (see below for a more detailed analysis of the scale factors relating to the universe). Such observations always occur in A’s continually changing present (which is equivalent in Cartesian terms of laying down a time-like trajectory) since this is the only location at which A can interact with events or phenomena such as photons. However, that the observation is of B’s past allows A to construct B as a point on A’s own time axis, e.g. OF in Figure 4.

It should be re-emphasised that from A’s viewpoint his time axis is an inferred construct where the observable surface (solid red line) is seen in A’s present and consists of a single view of all other trajectories where the time dilated surface (solid red line), the object’s trajectory (e.g. OB) and the photon trajectory (e.g. CF) intersect. From the photon trajectory A calculates B as apparently appearing at a location OF in time relative to the Big Bang. Although the result of every intersection is seen at A, he has (in the current theory) artificially spread out these locations along an inferred dimension (OA). The method by which the events are calculated is discussed below.

Also note that temporal simultaneity occurs along the inferred surfaces such as ABL and ECK, and not along the vertical lines which connect different times such as OF and OC between the observed surface and the observer.

The quantitative dynamic model

A’s construction of the surfaces required by the simple model

Let us assume that A and B had clocks travelling with them that were set to zero at the Big Bang and have been accumulating time ever since. Because of the fourth-dimension curvature, A sees B moving at velocity v/c along A’s spatial axis. Because B has a straight radial trajectory, this velocity has not changed over time.
We are only dealing with special relativity so that A’s observation of B is from point C where OC/OB = OE/OA = (1 − v²/c²)^1/2, i.e. to A the galaxy at B has not travelled as far along OB as it should due to the time dilation factor of the apparent velocity.

The geometric construction of the surfaces can be obtained by remembering we are only dealing with concentric circles and straight lines, and by letting cT₀ = OB; cT_G = OG; cT_F = OF; cT_E = OE; X_R = CF and X₀ = BE in Figure 4. Then
The inferred present surface ABL is given by
$X_{0} / R_{0} = {[1 - {(T_{E} / T_{0})}^{2}]}^{1 / 2} (16) .$
The time-dilated observed surface (solid red line) relative to A is
$X_{0} / R_{0} = {[T_{F} / T_{0} - {(T_{F} / T_{0})}^{2}]}^{1 / 2} (17) .$

The links between these construction surfaces and the dynamic theory are explored below.

Comparison of the predictions of the dynamic and coordinate theories

The evolution of the universe is calculated in terms of the scale factor a of the universe at time T after the Big Bang, which can be expressed in Figure 4 as

a = c T_{F} / c T_{0} = R_{J} / R_{0} (18) .

Since a dynamic coordinate is being used (e.g. T or R) it should be emphasized that this is along a given trajectory (e.g. OA or OB), but inferred surfaces (e.g. FDJ in Figure 4) link constant values of a. This parameter can measure the amount of stretch in the surface between then (T) and now (T₀), and is often used when comparing experiment and theory The connection between the observed and inferred surfaces, and the scale factor is given by the location where three phenomena, discussed below, meet (C) in the example shown in Figure 4 :-

The relativistic Doppler redshift.
The only scale factor that can be directly seen by A is the value of a given by the Doppler redshift (z), and corresponds to the frequency of light emitted at any point along the trajectory OB (f_e) since B’s velocity along this trajectory is, from A’s viewpoint, a constant due to the assumption of a straight trajectory. The frequency observed at A by at locations such as F and G is f₀, where z = f_e/f₀ – 1) and a is assumed as equal to 1/(1 + z).
The Doppler redshift is then related to the recessional velocity of the object (or galaxy) by the standard relativistic relationship
$1 / a = 1 + z = {[(1 + υ / c) / (1 + υ / c)]}^{1 / 2} or on rearranging$
$υ / c = (1 - a^{2}) / (1 + a^{2}) (19) .$
In dynamic coordinates in Figure 4, sinζ = v/c, and so cosζ = (1 – v²/c²)^1/2. From this and Equation (19) we then have
$cos ζ = 2 a / (1 + a^{2}) (20) .$
This is the key equation which provides the link between construction geometry and observation, and which is further explored below. Note that Equation 20 only applies to A’s observation of scale factors resulting from B’s trajectory as cosζ is completely dependant on the Doppler velocity.
The trajectory reduction.

As already mentioned, A will see B’s trajectory foreshortened due to the space-time dilation effects of B’s relative velocity. B will have only apparently travelled to OC rather than OB.

The photon travel.
Photons travel vertically in dynamic coordinates and so while time dilation places B at OC on B’s trajectory, B appears at OF on A’s trajectory from A’s perspective. Hence from A’s viewpoint a = OF/OA and it should be noted that since simultaneity occurs along inferred surfaces, a will be constant along arc FDJ, and consequently it can be inferred that a is also equal to OD/OB.

A’s observations of B are that, because v/c is constant along OB (according to A), a location on OB is related to a location on OA by OA = OB cosζ, e.g.

cos ζ = O G / O D = O F / O C = O E / O B, (21),

where in Figure 4, OD; OC and OB are located on trajectory OB. Equally OG; OF and OE are located on OA.

However, the inferred geometric relationships in Figure 4 obtained from the concentric surfaces can be summarised as

OA = OB; OC = OE; OD = OF and by substituting such values into Equation (21), we can write

OF/OE = OE/OA which lie entirely on the OA trajectory.

Multiplying through by OE/OA gives OF/OA = (OE/OA)²

and since a = OF/OA, then OE/OA = a^1/2. These values of a also apply to a = OD/OB and a^1/2 = OC/OB.

Hence A’s view of location OC, where the Doppler effect, time dilation surface and photon trajectory intersect, can be obtained from (Equation 21) as

OF/OC.(OC/OB) = OE/OB.(OC/OB) or

O F / O B = a^{1 / 2} cos ζ (22) .

Consequently from (Equation 20 and Equation 22) the key equation for the dynamic theory can now be expressed as

T_{F} / T_{0} = 2 a^{3 / 2} / (1 + a^{2}) (23) .

Let H(T) be the Hubble parameter at time T after the Big Bang and H₀ is the present value of the parameter. Then H₀ = 1/T₀ and along a trajectory that is frozen at R₀, T₀ ≡ R_L, T_A, we have H(T) = a^–1 da/dT.

From A’s viewpoint H(T) varies along the time axis (OA) and at a point along this axis, e.g. DR_J/DT_F = dR_J/dT_F = R_J/T_F = c, (c being the velocity of light).

The observed surface on which A sees B is at R_J = cT_F. Since a = R_J/R₀ then $d a / d T = R_{0}^{- 1} d R_{J} / d T,$ and so

$H (T_{F}) = a^{- 1} d a / d T_{F} = R_{J}^{- 1} d R_{J} / d T_{F} = c / R_{J} = 1 / T_{F} .$ Hence H(T_F) = 1/T_F. So

H_{0} / H (T_{F}) = 2 a^{3 / 2} / (1 + a^{2}) (24) .

Let H(T) be designated as H. In the standard (GR-based) coordinate theory for a flat universe, we have the first Friedmann equation which is

{[\frac{1}{R} \frac{d R}{d T}]}^{2} = \frac{8 π G}{3} [Ω_{M} a^{- 3} + Ω_{R} a^{- 4} + Ω_{Λ}] - \frac{k c^{2}}{R^{2}}

where G is the universal gravitational constant and k is the curvature parameter which is zero for a flat universe.

$H_{0} = {(8 π G ρ_{0} / 3)}^{1 / 2}$ where ρ₀ is the current average universal density. So for the standard theory

H_{0} / H = {(Ω_{M} a^{- 3} + Ω_{R} a^{- 4} + Ω_{Λ})}^{- 1 / 2} (25),

where Ω_M is the current normalised density of matter. The Standard Cosmology Model (SCM) value quoted in 9 is 0.32 for this parameter; Ω_R is the normalised density of radiation equal to 5×10^–5; and the SCM value for Ω_Λ (the normalised dark energy coefficient) is 0.68.

Figure 5 shows a comparison of the two theories (Equation (24) and Equation (25)).

Figure 5. The comparison of the standard and dynamic models of the universe’s evolution.

Considering the simplicity of the model used in the dynamic theory (red line), it is remarkably close overall to the SCM coordinate theory’s values for the coefficients (black line, in the Figure) considering SCM is based on GR for a flat universe and incorporating the lambda coefficient while the dynamic theory is based on SR and the simplest assumptions about the universe’s geometry.

Figure 6. The Hubble “tension”.

The comparison of the standard and dynamic scale velocity models showing the universe’s initial deceleration and late-time acceleration (26 and 27). Note how the two SCM curves can be fitted to different regions of a single dynamic curve.

At the early time low expansion of the universe (low a or high z), a good fit is obtained to the dynamic theory by the SCM’s coefficients when this curve is reduced by 10%. This is shown in Figure 6 (blue dotted curve). Consequently, to fit to the dynamic curve over the complete range of a two SCM curves are needed, the low a (high z) curve needing a value of H₀ which is 10% lower than its value obtained from nearby (high a) cosmological data. This might allow the dynamic theory to explain the current “tension” between values of H₀ obtained from the cosmic microwave background (high z) and from more recent (low z) cosmological feature (e.g. 10).

Figure 6a. The Hubble “tension” plotted in terms of redshift (z).

Equations (26 & 27) with a = (1 + z)^–1.

It should be noted from Figure 6 that when the dynamic curve is divided by T₀ - the current age of the universe for an observer - the shape of the curve (i.e. the late time acceleration) is independent of the epoch in which the observation is made.

The differential da/dT of A’s observation of B in both the standard and dynamic theories is given by H(T) = a^–1 da/dT. Hence for the dynamic theory, substituting this into Equation (24) gives

T_{0} d a / d T = 0.5 (a^{- 1 / 2} + a^{3 / 2}) (26) .

In the standard theory a similar substitution in Equation (25) gives the SCM scale velocity as

T_{0} d a / d T = {(Ω_{M} a^{- 1} + Ω_{R} a^{- 2} + Ω_{Λ} a^{2})}^{1 / 2} (27) .

These equations are shown in terms of the scale factor (a) in Figure 6 and z_a, the redshift at the start of the recent universe’s acceleration, in Table 3 below.

Table 3. Values of z_a from both theories and observations.

z_a	Comments	Reference
0.732	Shape independent of T₀.	Dynamic Theory
0.619	Value at current epoch.	SCM⁹
0.752 +/-0.041	Astronomical data	4
0.72 +/-0.05 to 0.84 +/-0.03	5 models plus 38 measurements of H(z)	11

The match between the theories means that it is possible that dark energy (the accelerating universe represented by Ω_Λ) could be just a feature of perspective. This follows from the scale velocity (da/dT) of the observable surface that shows the universe slowing down at large redshifts - as would be expected in the standard theory from the effects of gravity - and then in the relatively recent past beginning to accelerate. In the dynamic theory this is due to the model’s geometry which is independent of gravity (see previous discussion) and yet which still provides a good fit to the trend of the SCM, as shown above in Figure 5 & Figure 6). Also the position, in terms of redshift, where the dynamic theory predicts the acceleration to start to accelerate (z_a) agrees well with results from various models based on both the standard theory and observational astronomy, and are given in Table 3.

The position versus time of the universe’s radius is given by the integral of Equation 26 for the dynamic theory, and the integral of the combination of Friedmann’s first equation (above) with his acceleration equation

\frac{1}{R} \frac{d^{2} R}{d T^{2}} = - \frac{4 π G}{3} (ρ + \frac{3 p}{c^{2}})

where ρ and p are the density and pressure in the universe at time T. Assuming pressure- free matter, negligible radiation density and spatial flatness gives an integral for the standard theory of

a = A^{1 / 3} {s i n h}^{2 / 3} (T / T_{Λ}) (28)

where $A = Ω_{M} / Ω_{Λ} a n d T_{Λ} = {(4 / [3 Λ c^{2}])}^{1 / 2} a n d Λ \approx 10^{- 35} s^{- 2} .$ To convert T_Λ to units of time it has to be multiplied by c.

Then T/cT_Λ = T/T₀.(T₀/cT_Λ) = KT/T₀. Here K is a dimensionless constant equal to 13.8Gyr divided by (4/3Λ)^1/2. Using cT_Λ ≈ 3.72x10¹⁷ s allows Equation 28 to have a scale factor of unity at T = T₀ in Figure 7. Hence Equation 28 can be rewritten as

T / T_{0} = 0.855 s i n h^{- 1} (1.4577 a^{3 / 2}) (29) .

Figure 7. Comparison of standard theory (Equation 29) with the dynamic curve (Equation 30).

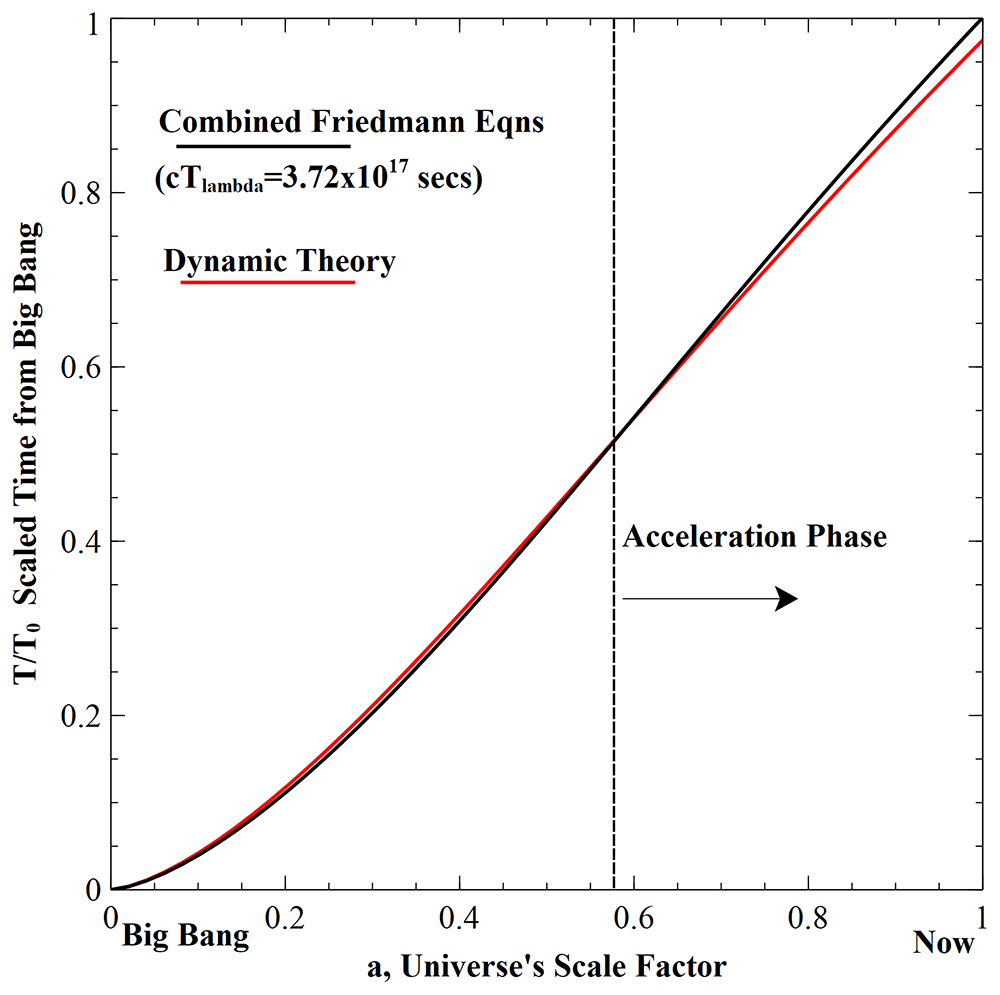
The equivalent curve from the dynamic theory is obtained by the rearrangement and integral of Equation 26, i.e.,

2 \int_{0}^{a} a^{1 / 2} d a / (1 + a^{2}) = \int_{0}^{T} d T / T_{0} .

This gives

\frac{T}{T_{0}} = \frac{1}{\sqrt{2}} l n [\frac{a + 1 - \sqrt{2 a}}{a + 1 + \sqrt{2 a}}] + \sqrt{2} [t a n^{- 1} (\frac{a - 1}{\sqrt{2 a}}) + \frac{π}{2}] (30) .

The key elements in the dynamic theory are: -

Very much like in special relativity A’s view of B is due to perspective rather than any real relationship. B’s view of A will be identical.
The match between the dynamic and coordinate theories in describing the universe’s evolution means that if there is any merit in the dynamic solution, there is no need to consider that the overwhelming proportion of dark mass (represented by Ω_M in the coordinate theory) exists. However, some must be present (or some currently unknown physical phenomenon must apply) as the rotation of galaxies requires more mass than is observable.
The match can also mean that dark energy (the accelerating universe represented by Ω_Λ) is also just a feature of perspective. This follows from the differential of the observable surface that shows the universe slowing down at large redshifts - as would be expected in the coordinate theory from the effects of gravity - and then in the relatively recent past beginning to accelerate. This is shown in Figure 6 & Figure 6a, along with the position, in terms of redshift, where the dynamic theory predicts the acceleration to start. Comparisons of this acceleration start in terms of redshift (z_a ) with results from various models based on both the coordinate theory and observational astronomy are given in Table 3

Discussion and conclusions

The basis of this paper results from a paradox. The way we measure space and time show that they are two very different entities. And yet it has also been shown beyond doubt that they need to be fused into space-time to accurately describe our universe. One may argue that “real” space and time are far removed from the way we define them, and this could well be the case. However, at its most basic construction these two entities have been defined by the ruler and the clock, and on this has been erected one of the most successful theories in science. However, it is a theory which on a cosmic scale has produced conundrums. It has been argued in this paper that such conundrums have arisen because there is more than one way that this fusion of space and time can be achieved.

The use of a dynamic theory to create such a fusion utilises the Minkowski metric, but where the standard Cartesian coordinates have been transformed into an Eulerian configuration (the dynamic coordinates) by multiplying them by a function of γ (see Equation 7–Equation 10) within a given inertial frame. The resulting two sets of coordinates (standard Cartesian and dynamic) give the same local descriptions of motion for special relativity (SR) but has these motions occurring against the background of a different universal structure.

From this paper the difference in the universe’s structure have led the following current cosmological problems to have possible dynamic solutions

The flatness problem. In the dynamic theory the curvature is always caused by the radial velocity. In turn this is always in the time direction for human observers - a direction in which locally they cannot see any sort of dimension. This is illustrated in qualitative terms by Figure 3 in which it is assumed that A can see the current (according to both A’s and B’s clocks) position of B with no account taken of time dilations or delays. See previous Sections for a more quantitatively precise description of A’s view of B in the dynamic theory. In Figure 3, A is again the main observer and B a distant galaxy. The real (i.e., total) motion of B lies along B’s time axis, which is orthogonal to the 4D surface. A directly sees only the spatial component of B’s real motion as a velocity lying parallel to A’s spatial dimension, and hence, from A’s viewpoint, projected onto it. In the Figure, a photon would have its time direction aligned with A’s spatial axis and its space direction along A’s time axis.

The dynamic universe has an extrinsic curvature, the curvature being confined to the fourth dimension. However, to any observer on this 4D surface one of these dimensions is missing (it is in the time direction) and the three remaining spatial dimensions having no intrinsic curvature appear flat.

Consequently, it is possible for this 3D space to appear flat from the viewpoint of any observer located on the 4D surface (B and A can be interchanged in terms of what each sees of the other). The only view an observer such as A has of this curvature is the projection of the radial velocity onto his 3D space by distant objects.

The horizon problem. This is simply solved in the dynamic theory because all elements of the universe are in contact in the 4D space at the location of the Big Bang. While the coordinate theory must deal with connections between various parts of the universe within an expanding surface when trying to explain the isotropic nature of the microwave radiation, the dynamic theory postulates that all parts were initially in contact and expanded radially outwards.

Dark mass and dark energy. The dark energy needed to explain the late-time acceleration of the universe in the coordinate theory, appears in the dynamic theory to be due to the perspective created by the presence of a directly observed surface (see above), i.e. in the dynamic theory there is no requirement for it to exist.

A lot of the dark mass also appears to be due to problems with the perspective and can be explained away as not required in the dynamic theory. However, this may not be true for all of it as there remains some unanswered questions about the rotation of galaxies for instance.

Inflation-type behaviour. The redshift formulation of Equation (26) tends to infinity for values of R close to zero at T = 0. Hence the inflation-type behaviour is implicit in the model without resorting to a separate phenomenon.

The “Hubble tension”. The dynamic scale velocity of the universe fits two SCM curves in different regions of the universe’s expansion (Figure 6 & Figure 6a). The SCM curves have values of H₀ that differ by 10%. This may be an interesting indicator that the dynamic model provides a better (or at least simpler) approach to solving this problem.

In Figure 5–Figure 7, considering the simplicity of the model used in the dynamic theory, it is remarkably close overall to the SCM theory considering SCM is based on GR (albeit for a flat universe in the comparisons shown) and incorporating the lambda coefficient. This is while the dynamic theory is based on SR and the simplest assumptions about the universe’s geometry.

The dynamic theory is far from the complete answer to every conundrum, but it is hoped that it may provide some alternative pathways to explore in the future.

Data

No data are associated with this article.

Author endorsement

Professor John Curtis confirms that the author has an appropriate level of expertise to conduct this research, and confirms that the submission is of an acceptable scientific standard. Professor John Curtis declares they have no competing interests. Affiliation: Atomic Weapons Establishment; Visiting Professor UCL Mathematics Department.

Acknowledgements

The author wished to thank those who initiated invaluable discussions and gave advice during the early stages of the production of this paper.

Footnotes

^*This view has a long history, e.g. Heraclitus of Ephesus (c.535-c.475BC) has an ever-present change being a fundamental essence of the universe²

^**There are theories which postulate non-standard gravitational behaviours and a large number of alternative theories exist to explain the apparent effect of dark energy. See a summary and references in 7

^***See, however⁸, for example where an eleven dimensional space is discussed.

Faculty Opinions recommended

References

1. Peebles PJE, Ratra B: The cosmological constant and dark energy. Rev Mod Phys. 2003; 75: 559–606. Publisher Full Text
2. Beris AN, Giacomin AJ: Everything flows. Appl Rheol. 2014; 24(5): 1–13. Publisher Full Text
3. Earman J, Mosterin J: A critical look at inflationary cosmology. Philos Sci. 1999; 66(1): 1–49. Publisher Full Text
4. Suzuki N, Rubin D, Lidman C, et al.: The Hubble space telescope cluster supernova survey. V. Improving the dark energy constraints above z > 1 and building an early-type-hosted supernova sample. Astron J. 2012; 746(1): 85. Publisher Full Text
5. Perlmutter S, Aldering G, Goldhaber G, et al.: Measurements of Ω and Λ from 42 high-redshift supernovae. Astron J. 1999; 517(2): 565–586. Publisher Full Text
6. Riess AG, Filippenko AV, Challis P, et al.: Observational evidence from supernovae for an accelerating universe and a cosmological constant. Astron J. 1998; 116(3): 1009–1038. Publisher Full Text
7. Rashki M, Fathi M, Mostaghel B, et al.: Interacting dark side of universe through generalized uncertainty principle. arXiv: 1901.05766v2, 2019. Publisher Full Text
8. Rostami T, Jalalzadeh S: Why the measured cosmological constant is small. arXiv: 1510.02068v1, 2015. Publisher Full Text
9. Planck Collaboration, Ade PAR, Aghanim N, et al.: Planck 2013 results. I. Overview of products and scientific results. Astron Astrophys. 2014; 571: 48. Publisher Full Text
10. Di Valentino E, Mena O, Pan S, et al.: In the realm of the Hubble tension—a review of solutions. Class Quantum Grav. 2021; 38(15): 153001. Publisher Full Text
11. Farooq O, Madiyar FR, Crandall S, et al.: Hubble parameter measurement constraints on the redshift of the deceleration-acceleration transition, dynamical dark energy, and space curvature. arXiv: 1607.03537v2give, 2016. Publisher Full Text

Comments on this article Comments (0)

Version 5

VERSION 5 PUBLISHED 21 Mar 2022

Author details Author details

Retired, AWE, Aldermaston, Reading, Berkshire, RG7 4PR, UK

Hugh James
Roles: Conceptualization, Writing – Original Draft Preparation, Writing – Review & Editing

Competing interests

No competing interests were disclosed.

Grant information

The author(s) declared that no grants were involved in supporting this work.

Article Versions (5)

version 5

Revised

Published: 18 Dec 2025, 11:344

https://doi.org/10.12688/f1000research.108648.5

version 4

Revised

Published: 27 Jan 2025, 11:344

https://doi.org/10.12688/f1000research.108648.4

version 3

Revised

Published: 30 Sep 2024, 11:344

https://doi.org/10.12688/f1000research.108648.3

version 2

Revised

Published: 30 Jan 2023, 11:344

https://doi.org/10.12688/f1000research.108648.2

version 1

Published: 21 Mar 2022, 11:344

https://doi.org/10.12688/f1000research.108648.1

© 2025 James H. This is an open access article distributed under the terms of the Creative Commons Attribution License, which permits unrestricted use, distribution, and reproduction in any medium, provided the original work is properly cited.

Download

Export To

metrics

	Views	Downloads
F1000Research	-	-
PubMed Central Data from PMC are received and updated monthly.	-	-

Citations

SEE MORE DETAILS

CITE

how to cite this article

James H. Accounting for the expansion of the universe using an energy/momentum model to construct the space-time metric [version 5; peer review: 2 not approved]. F1000Research 2025, 11:344 (https://doi.org/10.12688/f1000research.108648.5)

NOTE: If applicable, it is important to ensure the information in square brackets after the title is included in all citations of this article.

track

receive updates on this article

Track an article to receive email alerts on any updates to this article.

Open Peer Review

Version 4

VERSION 4

PUBLISHED 27 Jan 2025

Revised

Views

Reviewer Report 19 Aug 2025

Jackson Levi Said, University of Malta, Msida, Malta

Not Approved

https://doi.org/10.5256/f1000research.176897.r397419

The manuscript claims to resolve some open problems in relativity theory. Overall, the work is not robustly formulated and contains informal language throughout. A more formal analysis should involve more explicit model suggestions and some rudimentary form of data analysis since the principal issues identified are observational in nature. The confused language is unclear throughout. However, any conflict within special relativity should be explicitly shown as should any proposal beyond this theoretical framework. The author should revisit the foundations of their proposal in more detail, and formulate a better defined research hypothesis and proposal.

For these reasons, I do not recommend this manuscript for indexing in its present form. Below, I detail the precise issue to be reconsidered by the authors.

Section 1 - Introduction
The opening assumes special and general relativity as foundational building blocks, as they should be. However, the introduction then goes into the need to resolve some problematic features of special relativity. These are not explained explicitly, nor are they well defined in terms of observables associated with observers in this framework. This leaves the motivation for the work ambiguous while the research hypothesis is vague in nature. The author should describe in more detail what supposed problem appears in not giving a “good fit to the corresponding astronomical data” means and at what statistical level this appears at. In its present form, these statements are very vague and not well referenced.

Section 2 - The basis of the dynamic theory in Special Relativity (SR)
In this section, the supposed problematic features of SR are described. The first subsection qualitatively explains the potential problem in coordinate systems as related to the temporal dimension. The description is inexact in nature and lacks robustness. The author should consider putting in a more robust general analysis of the technical problem in observables, otherwise this remains a qualitative supposition. The second subsection mostly includes entry-level definitions of the Minkowski metric in textbooks and the line element. This background is not needed since it is well known. Similarly, length contraction and time dilation as well as the other properties in the final subsection are well known in the literature. Indeed, these are not so much related to cosmology except in a foundational sense.

Section 3 - Cosmology
This section contains more literature review and some original results. This opens with a discussion of the known problems in standard cosmology. These are only partially reviewed and in no great depth. The author may want to consider more recent observed issues with the theory including cosmic tensions. The next subsection describes the so-called model being proposed in this work. This is very qualitative and not exactly in nature. A more formal attempt is provided in the third subsection, but this is similarly informal and very circumstantial. Any model beyond special or general relativity should conform to the robust mathematical rigor or either framework. Section four goes back to Lorentz transformations while the fifth section covers other special relativistic effects. These do not go beyond special relativity in any meaningful way. The section closes with a minor discussion of some of the open challenges to standard cosmology. However, these are not tackled in any serious way. The author should consider a numerical analysis involving observational data.

Section 3 - Discussion and conclusions
The work closes with a short summary of the main results and a long list of observations both in SR an general relativity using these suggestions made earlier in the work.

Is the work clearly and accurately presented and does it cite the current literature?

No
Is the study design appropriate and is the work technically sound?

No
Are sufficient details of methods and analysis provided to allow replication by others?

No
If applicable, is the statistical analysis and its interpretation appropriate?

No
Are all the source data underlying the results available to ensure full reproducibility?

Partly
Are the conclusions drawn adequately supported by the results?

No

Competing Interests: No competing interests were disclosed.

Reviewer Expertise: I am a cosmologist working on the theoretical development of models to resolve open issues in observational cosmology.

I confirm that I have read this submission and believe that I have an appropriate level of expertise to state that I do not consider it to be of an acceptable scientific standard, for reasons outlined above.

CITE

Report a concern

Author Response 18 Dec 2025

Hugh James, Retired, AWE, Aldermaston, Reading, RG7 4PR, UK

18 Dec 2025

Author Response

R=Reviewer comment, A=Author response.

R.
The manuscript claims to resolve some open problems in relativity theory. Overall, the work is not robustly formulated and contains informal language throughout. A ... Continue reading R=Reviewer comment, A=Author response.

R.
The manuscript claims to resolve some open problems in relativity theory. Overall, the work is not robustly formulated and contains informal language throughout. A more formal analysis should involve more explicit model suggestions and some rudimentary form of data analysis since the principal issues identified are observational in nature. The confused language is unclear throughout. However, any conflict within special relativity should be explicitly shown as should any proposal beyond this theoretical framework. The author should revisit the foundations of their proposal in more detail, and formulate a better defined research hypothesis and proposal.

For these reasons, I do not recommend this manuscript for indexing in its present form. Below, I detail the precise issue to be reconsidered by the authors.

Section 1 - Introduction
The opening assumes special and general relativity as foundational building blocks, as they should be. However, the introduction then goes into the need to resolve some problematic features of special relativity. These are not explained explicitly, nor are they well defined in terms of observables associated with observers in this framework. This leaves the motivation for the work ambiguous while the research hypothesis is vague in nature. The author should describe in more detail what supposed problem appears in not giving a “good fit to the corresponding astronomical data” means and at what statistical level this appears at. In its present form, these statements are very vague and not well referenced.

A.
My Introduction should have been clearer and more succinct.

The paper is not intended as a review of current cosmology and the reader is assumed conversant with problems in the “Standard” approach, hence only the outlines of such problems are given in Sections 1 and 3.

This paper is intended as a test-of-concept investigation into whether an approach developed therein might be more fruitful in tackling some of these problems than the approach utilised by the Standard Cosmology Model (SCM).

In brief, with the SCM there are problems using general relativity (GR) when GR is applied to cosmology. To account for the observed flatness or horizon phenomena, an additional model (inflation) must be invoked. Equally the universe’s late-time acceleration requires Einstein’s lambda function to be included in the GR description. Neither of these “fixes” currently appear to have a solid physical justification other than to fit the theory to observation.

In the limit, where there is no gravitational field or acceleration of a given observer, GR must revert to special relativity (SR). Consequently, in this paper it is proposed that if there is an alternative way of expressing SR, this might in turn lead to solutions of some of the above problems by using it as a first approximation for the basis of modelling cosmology without the need for requiring additional phenomena such as inflation or lambda.

The paper has no problems with SR as such. However, it suggests that a different way of formulating it (see below) might be a way to obtain a more fruitful approach to modelling cosmology.

It is agreed that the Standard non-cosmological applications of SR and GR are well established. Consequently, the paper is in two main parts, with both parts concentrating on using SR as the basis. The first part (Section 2) shows the alternative way of expressing SR and how coordinates in space-time arising from this can be transformed into “Standard” coordinates (Eq.7-10a). It also shows agreement between the two theories in the non-cosmological (or local) area which is required for the new (“Dynamic”) theory to have any validity (hence the provision of this background), e.g. the Minkowski space-time is still retained (although mapped differently), while the Lorentz transformation between inertial frames and the 4-momentum relationship are unchanged.

The consequences of this approach are discussed and in the second main part (Section 3) are applied to give a simple model of the universe’s expansion (Eqns 26 & 30) in order to test this concept.

Since SCM is tuned to observational data, and it is generally accepted that its current empirical coefficients allow a good fit, it is the intention of the paper to show that just from the basis of the Dynamic SR, and some simple assumptions (Section 3), that the Dynamic theory in turn follows the trends demonstrated by the SCM (Fig 5 & 6), e.g. it shows the late-time acceleration without the need for additional models or coefficients. In following these trends, it also does so without the need of inflation to account for the flatness and horizon problems. Consequently, it is argued that the paper has gone some way to showing the Dynamic SR concept may have some validity although further work is needed (e.g. attempting to establish the possibilities of a GR theory based on this approach, and how this could be applied to cosmology).

The term “good fit…” should have been better expressed as the Dynamic theory gives a good fit to the trends shown by SCM, which in turn is tuned to give a good fit to cosmological data.

R.
Section 2 - The basis of the dynamic theory in Special Relativity (SR)
In this section, the supposed problematic features of SR are described. The first subsection qualitatively explains the potential problem in coordinate systems as related to the temporal dimension. The description is inexact in nature and lacks robustness. The author should consider putting in a more robust general analysis of the technical problem in observables, otherwise this remains a qualitative supposition. The second subsection mostly includes entry-level definitions of the Minkowski metric in textbooks and the line element. This background is not needed since it is well known. Similarly, length contraction and time dilation as well as the other properties in the final subsection are well known in the literature. Indeed, these are not so much related to cosmology except in a foundational sense.

A.
There are no problems with Standard SR, just a different way in expressing it. The paper is built entirely around SR and hence always uses inertial frames of reference.

We do not know what time and space really are. We model them in the way that we perceive them to be, i.e. using rulers and clocks. It is important to note that it is only by using these perceived models that we quantify the predictions of SR and GR. These perceptions are described in some detail in this section, leading to the observation that while space and time appear to be different phenomena, there is solid, non-cosmological evidence that they must be combined into “space-time” coordinates to provide a viable description of such behaviour as high velocity interactions or the acceleration of falling objects.

The paper argues there are two ways of providing this combination. The Standard way which keeps space as a coordinate and transforms changes in time into a “temporal dimension” using the speed of light. The Dynamic way keeps the changes in time and links them to changes in space. The first constructs space and time coordinates linked to a given inertial frame and against which the changes in coordinate positions of objects in this and other frames can be measured, although the paper emphasises the temporal coordinate always has to be inferred rather than directly observed (definitions of these terms are given in the paper). The second can only experience a change in time within an inertial frame (linked to energy changes) but not the spatial motion of the frame itself. The only changes in space coordinates are given by movements of other frames relative to an apparently fixed ruler within the observer’s frame (i.e. their observed momentums). Hence objects and observers within a given frame will only follow an (inferred) path in the temporal dimension but are fixed within their spatial dimensions. (To change their spatial position within a frame requires a non-inertial action, i.e. an acceleration followed by a deceleration to move an object to a different fixed spatial position within the original inertial frame).The consequences of the inertial behaviour are described in the paper in terms of how the Dynamic changes in time and space are combined to give a constant speed of light (Eqns 3 & 4) and which parameter has now become an invariant in the Dynamic formulation. Also, how the resulting changes in Dynamic coordinates can be transformed into changes in position given by Standard coordinates (Eqs7-10) by assuming the invariants of both theories can be equated, i.e. Eqn 8 shows the resulting transform needed between Standard changes in coordinates () and Dynamic changes within the same inertial frame that contains the observer. See paper for nomenclature and note that is always zero. Note also this transform is different to the Lorentz transform which applies to both Dynamic and Standard coordinates between frames.

The differences in how the two theories map the same Minkowski space-time are shown in Figs 1a & 1b.

R.
Section 3 - Cosmology
This section contains more literature review and some original results. This opens with a discussion of the known problems in standard cosmology. These are only partially reviewed and in no great depth. The author may want to consider more recent observed issues with the theory including cosmic tensions. The next subsection describes the so-called model being proposed in this work. This is very qualitative and not exactly in nature. A more formal attempt is provided in the third subsection, but this is similarly informal and very circumstantial. Any model beyond special or general relativity should conform to the robust mathematical rigor or either framework. Section four goes back to Lorentz transformations while the fifth section covers other special relativistic effects. These do not go beyond special relativity in any meaningful way. The section closes with a minor discussion of some of the open challenges to standard cosmology. However, these are not tackled in any serious way. The author should consider a numerical analysis involving observational data.

A.
The reason for the partial review is covered under the Introduction.

It would have been better to include the “Hubble Tension” under the list of the Standard theory’s possible shortcomings rather than trying to introduce it halfway through the section.

The last part of this review Section above, “Section four goes back to Lorentz transformations…consider a numerical analysis involving observational data.” seems to have slipped down from review Section 2. That “These do not go beyond [Standard] special relativity in any meaningful way.” Is the point as in this regime the Dynamic must agree with the Standard theory for it to have any validity (see above under Introduction). Where it does go beyond Standard SR is shown in Fig.2 and discussed in the paragraph before the sub-heading “Similarities and differences between the theories” and should have been included in that section of the paper.

“Any model…should conform to the robust mathematical rigor or [of?] either framework.” I am not sure where the additional rigor comes in. I have shown that Dynamic and Standard SR give the same results in non-cosmological regimes (GR is not considered in this paper) and where Dynamic can be extended to beyond Standard SR in the implications arising from Fig.2 and supporting paragraph. This lays the foundations of the proposed cosmology discussed in sections “The simple dynamic model” and “The quantitative dynamic model”. In turn these compare the Dynamic Hubble expansion (Eqn.26) with the SCM (Eqn.27) in Fig.6. Further discussions on where the two theories give an exact match and where (and possibly why) they run parallel are discussed in Fig.7 and supporting text.

R.
Section 3 - Discussion and conclusions
The work closes with a short summary of the main results and a long list of observations both in SR an general relativity using these suggestions made earlier in the work.

A.
The SCM relies on GR plus empirical models and coefficients briefly outlined in the paper, while the Dynamic cosmology only relies on Dynamic SR plus simple geometry. This goes some way to satisfying the aim of the paper which was to see if the Dynamic approach provides a possibly more fruitful path in describing cosmology in a way that does not require additional models or coefficients which have an unclear physical basis.
R=Reviewer comment, A=Author response.

R.
The manuscript claims to resolve some open problems in relativity theory. Overall, the work is not robustly formulated and contains informal language throughout. A more formal analysis should involve more explicit model suggestions and some rudimentary form of data analysis since the principal issues identified are observational in nature. The confused language is unclear throughout. However, any conflict within special relativity should be explicitly shown as should any proposal beyond this theoretical framework. The author should revisit the foundations of their proposal in more detail, and formulate a better defined research hypothesis and proposal.

For these reasons, I do not recommend this manuscript for indexing in its present form. Below, I detail the precise issue to be reconsidered by the authors.

Section 1 - Introduction
The opening assumes special and general relativity as foundational building blocks, as they should be. However, the introduction then goes into the need to resolve some problematic features of special relativity. These are not explained explicitly, nor are they well defined in terms of observables associated with observers in this framework. This leaves the motivation for the work ambiguous while the research hypothesis is vague in nature. The author should describe in more detail what supposed problem appears in not giving a “good fit to the corresponding astronomical data” means and at what statistical level this appears at. In its present form, these statements are very vague and not well referenced.

A.
My Introduction should have been clearer and more succinct.

The paper is not intended as a review of current cosmology and the reader is assumed conversant with problems in the “Standard” approach, hence only the outlines of such problems are given in Sections 1 and 3.

This paper is intended as a test-of-concept investigation into whether an approach developed therein might be more fruitful in tackling some of these problems than the approach utilised by the Standard Cosmology Model (SCM).

In brief, with the SCM there are problems using general relativity (GR) when GR is applied to cosmology. To account for the observed flatness or horizon phenomena, an additional model (inflation) must be invoked. Equally the universe’s late-time acceleration requires Einstein’s lambda function to be included in the GR description. Neither of these “fixes” currently appear to have a solid physical justification other than to fit the theory to observation.

In the limit, where there is no gravitational field or acceleration of a given observer, GR must revert to special relativity (SR). Consequently, in this paper it is proposed that if there is an alternative way of expressing SR, this might in turn lead to solutions of some of the above problems by using it as a first approximation for the basis of modelling cosmology without the need for requiring additional phenomena such as inflation or lambda.

The paper has no problems with SR as such. However, it suggests that a different way of formulating it (see below) might be a way to obtain a more fruitful approach to modelling cosmology.

It is agreed that the Standard non-cosmological applications of SR and GR are well established. Consequently, the paper is in two main parts, with both parts concentrating on using SR as the basis. The first part (Section 2) shows the alternative way of expressing SR and how coordinates in space-time arising from this can be transformed into “Standard” coordinates (Eq.7-10a). It also shows agreement between the two theories in the non-cosmological (or local) area which is required for the new (“Dynamic”) theory to have any validity (hence the provision of this background), e.g. the Minkowski space-time is still retained (although mapped differently), while the Lorentz transformation between inertial frames and the 4-momentum relationship are unchanged.

The consequences of this approach are discussed and in the second main part (Section 3) are applied to give a simple model of the universe’s expansion (Eqns 26 & 30) in order to test this concept.

Since SCM is tuned to observational data, and it is generally accepted that its current empirical coefficients allow a good fit, it is the intention of the paper to show that just from the basis of the Dynamic SR, and some simple assumptions (Section 3), that the Dynamic theory in turn follows the trends demonstrated by the SCM (Fig 5 & 6), e.g. it shows the late-time acceleration without the need for additional models or coefficients. In following these trends, it also does so without the need of inflation to account for the flatness and horizon problems. Consequently, it is argued that the paper has gone some way to showing the Dynamic SR concept may have some validity although further work is needed (e.g. attempting to establish the possibilities of a GR theory based on this approach, and how this could be applied to cosmology).

The term “good fit…” should have been better expressed as the Dynamic theory gives a good fit to the trends shown by SCM, which in turn is tuned to give a good fit to cosmological data.

R.
Section 2 - The basis of the dynamic theory in Special Relativity (SR)
In this section, the supposed problematic features of SR are described. The first subsection qualitatively explains the potential problem in coordinate systems as related to the temporal dimension. The description is inexact in nature and lacks robustness. The author should consider putting in a more robust general analysis of the technical problem in observables, otherwise this remains a qualitative supposition. The second subsection mostly includes entry-level definitions of the Minkowski metric in textbooks and the line element. This background is not needed since it is well known. Similarly, length contraction and time dilation as well as the other properties in the final subsection are well known in the literature. Indeed, these are not so much related to cosmology except in a foundational sense.

A.
There are no problems with Standard SR, just a different way in expressing it. The paper is built entirely around SR and hence always uses inertial frames of reference.

We do not know what time and space really are. We model them in the way that we perceive them to be, i.e. using rulers and clocks. It is important to note that it is only by using these perceived models that we quantify the predictions of SR and GR. These perceptions are described in some detail in this section, leading to the observation that while space and time appear to be different phenomena, there is solid, non-cosmological evidence that they must be combined into “space-time” coordinates to provide a viable description of such behaviour as high velocity interactions or the acceleration of falling objects.

The paper argues there are two ways of providing this combination. The Standard way which keeps space as a coordinate and transforms changes in time into a “temporal dimension” using the speed of light. The Dynamic way keeps the changes in time and links them to changes in space. The first constructs space and time coordinates linked to a given inertial frame and against which the changes in coordinate positions of objects in this and other frames can be measured, although the paper emphasises the temporal coordinate always has to be inferred rather than directly observed (definitions of these terms are given in the paper). The second can only experience a change in time within an inertial frame (linked to energy changes) but not the spatial motion of the frame itself. The only changes in space coordinates are given by movements of other frames relative to an apparently fixed ruler within the observer’s frame (i.e. their observed momentums). Hence objects and observers within a given frame will only follow an (inferred) path in the temporal dimension but are fixed within their spatial dimensions. (To change their spatial position within a frame requires a non-inertial action, i.e. an acceleration followed by a deceleration to move an object to a different fixed spatial position within the original inertial frame).The consequences of the inertial behaviour are described in the paper in terms of how the Dynamic changes in time and space are combined to give a constant speed of light (Eqns 3 & 4) and which parameter has now become an invariant in the Dynamic formulation. Also, how the resulting changes in Dynamic coordinates can be transformed into changes in position given by Standard coordinates (Eqs7-10) by assuming the invariants of both theories can be equated, i.e. Eqn 8 shows the resulting transform needed between Standard changes in coordinates () and Dynamic changes within the same inertial frame that contains the observer. See paper for nomenclature and note that is always zero. Note also this transform is different to the Lorentz transform which applies to both Dynamic and Standard coordinates between frames.

The differences in how the two theories map the same Minkowski space-time are shown in Figs 1a & 1b.

R.
Section 3 - Cosmology
This section contains more literature review and some original results. This opens with a discussion of the known problems in standard cosmology. These are only partially reviewed and in no great depth. The author may want to consider more recent observed issues with the theory including cosmic tensions. The next subsection describes the so-called model being proposed in this work. This is very qualitative and not exactly in nature. A more formal attempt is provided in the third subsection, but this is similarly informal and very circumstantial. Any model beyond special or general relativity should conform to the robust mathematical rigor or either framework. Section four goes back to Lorentz transformations while the fifth section covers other special relativistic effects. These do not go beyond special relativity in any meaningful way. The section closes with a minor discussion of some of the open challenges to standard cosmology. However, these are not tackled in any serious way. The author should consider a numerical analysis involving observational data.

A.
The reason for the partial review is covered under the Introduction.

It would have been better to include the “Hubble Tension” under the list of the Standard theory’s possible shortcomings rather than trying to introduce it halfway through the section.

The last part of this review Section above, “Section four goes back to Lorentz transformations…consider a numerical analysis involving observational data.” seems to have slipped down from review Section 2. That “These do not go beyond [Standard] special relativity in any meaningful way.” Is the point as in this regime the Dynamic must agree with the Standard theory for it to have any validity (see above under Introduction). Where it does go beyond Standard SR is shown in Fig.2 and discussed in the paragraph before the sub-heading “Similarities and differences between the theories” and should have been included in that section of the paper.

“Any model…should conform to the robust mathematical rigor or [of?] either framework.” I am not sure where the additional rigor comes in. I have shown that Dynamic and Standard SR give the same results in non-cosmological regimes (GR is not considered in this paper) and where Dynamic can be extended to beyond Standard SR in the implications arising from Fig.2 and supporting paragraph. This lays the foundations of the proposed cosmology discussed in sections “The simple dynamic model” and “The quantitative dynamic model”. In turn these compare the Dynamic Hubble expansion (Eqn.26) with the SCM (Eqn.27) in Fig.6. Further discussions on where the two theories give an exact match and where (and possibly why) they run parallel are discussed in Fig.7 and supporting text.

R.
Section 3 - Discussion and conclusions
The work closes with a short summary of the main results and a long list of observations both in SR an general relativity using these suggestions made earlier in the work.

A.
The SCM relies on GR plus empirical models and coefficients briefly outlined in the paper, while the Dynamic cosmology only relies on Dynamic SR plus simple geometry. This goes some way to satisfying the aim of the paper which was to see if the Dynamic approach provides a possibly more fruitful path in describing cosmology in a way that does not require additional models or coefficients which have an unclear physical basis.
Competing Interests: No competing interests Close
Report a concern
Respond or Comment

COMMENTS ON THIS REPORT

Author Response 18 Dec 2025

Hugh James, Retired, AWE, Aldermaston, Reading, RG7 4PR, UK

18 Dec 2025

Author Response

R=Reviewer comment, A=Author response.

R.
The manuscript claims to resolve some open problems in relativity theory. Overall, the work is not robustly formulated and contains informal language throughout. A ... Continue reading R=Reviewer comment, A=Author response.

R.
The manuscript claims to resolve some open problems in relativity theory. Overall, the work is not robustly formulated and contains informal language throughout. A more formal analysis should involve more explicit model suggestions and some rudimentary form of data analysis since the principal issues identified are observational in nature. The confused language is unclear throughout. However, any conflict within special relativity should be explicitly shown as should any proposal beyond this theoretical framework. The author should revisit the foundations of their proposal in more detail, and formulate a better defined research hypothesis and proposal.

For these reasons, I do not recommend this manuscript for indexing in its present form. Below, I detail the precise issue to be reconsidered by the authors.

Section 1 - Introduction
The opening assumes special and general relativity as foundational building blocks, as they should be. However, the introduction then goes into the need to resolve some problematic features of special relativity. These are not explained explicitly, nor are they well defined in terms of observables associated with observers in this framework. This leaves the motivation for the work ambiguous while the research hypothesis is vague in nature. The author should describe in more detail what supposed problem appears in not giving a “good fit to the corresponding astronomical data” means and at what statistical level this appears at. In its present form, these statements are very vague and not well referenced.

A.
My Introduction should have been clearer and more succinct.

The paper is not intended as a review of current cosmology and the reader is assumed conversant with problems in the “Standard” approach, hence only the outlines of such problems are given in Sections 1 and 3.

This paper is intended as a test-of-concept investigation into whether an approach developed therein might be more fruitful in tackling some of these problems than the approach utilised by the Standard Cosmology Model (SCM).

In brief, with the SCM there are problems using general relativity (GR) when GR is applied to cosmology. To account for the observed flatness or horizon phenomena, an additional model (inflation) must be invoked. Equally the universe’s late-time acceleration requires Einstein’s lambda function to be included in the GR description. Neither of these “fixes” currently appear to have a solid physical justification other than to fit the theory to observation.

In the limit, where there is no gravitational field or acceleration of a given observer, GR must revert to special relativity (SR). Consequently, in this paper it is proposed that if there is an alternative way of expressing SR, this might in turn lead to solutions of some of the above problems by using it as a first approximation for the basis of modelling cosmology without the need for requiring additional phenomena such as inflation or lambda.

The paper has no problems with SR as such. However, it suggests that a different way of formulating it (see below) might be a way to obtain a more fruitful approach to modelling cosmology.

It is agreed that the Standard non-cosmological applications of SR and GR are well established. Consequently, the paper is in two main parts, with both parts concentrating on using SR as the basis. The first part (Section 2) shows the alternative way of expressing SR and how coordinates in space-time arising from this can be transformed into “Standard” coordinates (Eq.7-10a). It also shows agreement between the two theories in the non-cosmological (or local) area which is required for the new (“Dynamic”) theory to have any validity (hence the provision of this background), e.g. the Minkowski space-time is still retained (although mapped differently), while the Lorentz transformation between inertial frames and the 4-momentum relationship are unchanged.

The consequences of this approach are discussed and in the second main part (Section 3) are applied to give a simple model of the universe’s expansion (Eqns 26 & 30) in order to test this concept.

Since SCM is tuned to observational data, and it is generally accepted that its current empirical coefficients allow a good fit, it is the intention of the paper to show that just from the basis of the Dynamic SR, and some simple assumptions (Section 3), that the Dynamic theory in turn follows the trends demonstrated by the SCM (Fig 5 & 6), e.g. it shows the late-time acceleration without the need for additional models or coefficients. In following these trends, it also does so without the need of inflation to account for the flatness and horizon problems. Consequently, it is argued that the paper has gone some way to showing the Dynamic SR concept may have some validity although further work is needed (e.g. attempting to establish the possibilities of a GR theory based on this approach, and how this could be applied to cosmology).

The term “good fit…” should have been better expressed as the Dynamic theory gives a good fit to the trends shown by SCM, which in turn is tuned to give a good fit to cosmological data.

R.
Section 2 - The basis of the dynamic theory in Special Relativity (SR)
In this section, the supposed problematic features of SR are described. The first subsection qualitatively explains the potential problem in coordinate systems as related to the temporal dimension. The description is inexact in nature and lacks robustness. The author should consider putting in a more robust general analysis of the technical problem in observables, otherwise this remains a qualitative supposition. The second subsection mostly includes entry-level definitions of the Minkowski metric in textbooks and the line element. This background is not needed since it is well known. Similarly, length contraction and time dilation as well as the other properties in the final subsection are well known in the literature. Indeed, these are not so much related to cosmology except in a foundational sense.

A.
There are no problems with Standard SR, just a different way in expressing it. The paper is built entirely around SR and hence always uses inertial frames of reference.

We do not know what time and space really are. We model them in the way that we perceive them to be, i.e. using rulers and clocks. It is important to note that it is only by using these perceived models that we quantify the predictions of SR and GR. These perceptions are described in some detail in this section, leading to the observation that while space and time appear to be different phenomena, there is solid, non-cosmological evidence that they must be combined into “space-time” coordinates to provide a viable description of such behaviour as high velocity interactions or the acceleration of falling objects.

The paper argues there are two ways of providing this combination. The Standard way which keeps space as a coordinate and transforms changes in time into a “temporal dimension” using the speed of light. The Dynamic way keeps the changes in time and links them to changes in space. The first constructs space and time coordinates linked to a given inertial frame and against which the changes in coordinate positions of objects in this and other frames can be measured, although the paper emphasises the temporal coordinate always has to be inferred rather than directly observed (definitions of these terms are given in the paper). The second can only experience a change in time within an inertial frame (linked to energy changes) but not the spatial motion of the frame itself. The only changes in space coordinates are given by movements of other frames relative to an apparently fixed ruler within the observer’s frame (i.e. their observed momentums). Hence objects and observers within a given frame will only follow an (inferred) path in the temporal dimension but are fixed within their spatial dimensions. (To change their spatial position within a frame requires a non-inertial action, i.e. an acceleration followed by a deceleration to move an object to a different fixed spatial position within the original inertial frame).The consequences of the inertial behaviour are described in the paper in terms of how the Dynamic changes in time and space are combined to give a constant speed of light (Eqns 3 & 4) and which parameter has now become an invariant in the Dynamic formulation. Also, how the resulting changes in Dynamic coordinates can be transformed into changes in position given by Standard coordinates (Eqs7-10) by assuming the invariants of both theories can be equated, i.e. Eqn 8 shows the resulting transform needed between Standard changes in coordinates () and Dynamic changes within the same inertial frame that contains the observer. See paper for nomenclature and note that is always zero. Note also this transform is different to the Lorentz transform which applies to both Dynamic and Standard coordinates between frames.

The differences in how the two theories map the same Minkowski space-time are shown in Figs 1a & 1b.

R.
Section 3 - Cosmology
This section contains more literature review and some original results. This opens with a discussion of the known problems in standard cosmology. These are only partially reviewed and in no great depth. The author may want to consider more recent observed issues with the theory including cosmic tensions. The next subsection describes the so-called model being proposed in this work. This is very qualitative and not exactly in nature. A more formal attempt is provided in the third subsection, but this is similarly informal and very circumstantial. Any model beyond special or general relativity should conform to the robust mathematical rigor or either framework. Section four goes back to Lorentz transformations while the fifth section covers other special relativistic effects. These do not go beyond special relativity in any meaningful way. The section closes with a minor discussion of some of the open challenges to standard cosmology. However, these are not tackled in any serious way. The author should consider a numerical analysis involving observational data.

A.
The reason for the partial review is covered under the Introduction.

It would have been better to include the “Hubble Tension” under the list of the Standard theory’s possible shortcomings rather than trying to introduce it halfway through the section.

The last part of this review Section above, “Section four goes back to Lorentz transformations…consider a numerical analysis involving observational data.” seems to have slipped down from review Section 2. That “These do not go beyond [Standard] special relativity in any meaningful way.” Is the point as in this regime the Dynamic must agree with the Standard theory for it to have any validity (see above under Introduction). Where it does go beyond Standard SR is shown in Fig.2 and discussed in the paragraph before the sub-heading “Similarities and differences between the theories” and should have been included in that section of the paper.

“Any model…should conform to the robust mathematical rigor or [of?] either framework.” I am not sure where the additional rigor comes in. I have shown that Dynamic and Standard SR give the same results in non-cosmological regimes (GR is not considered in this paper) and where Dynamic can be extended to beyond Standard SR in the implications arising from Fig.2 and supporting paragraph. This lays the foundations of the proposed cosmology discussed in sections “The simple dynamic model” and “The quantitative dynamic model”. In turn these compare the Dynamic Hubble expansion (Eqn.26) with the SCM (Eqn.27) in Fig.6. Further discussions on where the two theories give an exact match and where (and possibly why) they run parallel are discussed in Fig.7 and supporting text.

R.
Section 3 - Discussion and conclusions
The work closes with a short summary of the main results and a long list of observations both in SR an general relativity using these suggestions made earlier in the work.

A.
The SCM relies on GR plus empirical models and coefficients briefly outlined in the paper, while the Dynamic cosmology only relies on Dynamic SR plus simple geometry. This goes some way to satisfying the aim of the paper which was to see if the Dynamic approach provides a possibly more fruitful path in describing cosmology in a way that does not require additional models or coefficients which have an unclear physical basis.
R=Reviewer comment, A=Author response.

R.
The manuscript claims to resolve some open problems in relativity theory. Overall, the work is not robustly formulated and contains informal language throughout. A more formal analysis should involve more explicit model suggestions and some rudimentary form of data analysis since the principal issues identified are observational in nature. The confused language is unclear throughout. However, any conflict within special relativity should be explicitly shown as should any proposal beyond this theoretical framework. The author should revisit the foundations of their proposal in more detail, and formulate a better defined research hypothesis and proposal.

For these reasons, I do not recommend this manuscript for indexing in its present form. Below, I detail the precise issue to be reconsidered by the authors.

Section 1 - Introduction
The opening assumes special and general relativity as foundational building blocks, as they should be. However, the introduction then goes into the need to resolve some problematic features of special relativity. These are not explained explicitly, nor are they well defined in terms of observables associated with observers in this framework. This leaves the motivation for the work ambiguous while the research hypothesis is vague in nature. The author should describe in more detail what supposed problem appears in not giving a “good fit to the corresponding astronomical data” means and at what statistical level this appears at. In its present form, these statements are very vague and not well referenced.

A.
My Introduction should have been clearer and more succinct.

The paper is not intended as a review of current cosmology and the reader is assumed conversant with problems in the “Standard” approach, hence only the outlines of such problems are given in Sections 1 and 3.

This paper is intended as a test-of-concept investigation into whether an approach developed therein might be more fruitful in tackling some of these problems than the approach utilised by the Standard Cosmology Model (SCM).

In brief, with the SCM there are problems using general relativity (GR) when GR is applied to cosmology. To account for the observed flatness or horizon phenomena, an additional model (inflation) must be invoked. Equally the universe’s late-time acceleration requires Einstein’s lambda function to be included in the GR description. Neither of these “fixes” currently appear to have a solid physical justification other than to fit the theory to observation.

In the limit, where there is no gravitational field or acceleration of a given observer, GR must revert to special relativity (SR). Consequently, in this paper it is proposed that if there is an alternative way of expressing SR, this might in turn lead to solutions of some of the above problems by using it as a first approximation for the basis of modelling cosmology without the need for requiring additional phenomena such as inflation or lambda.

The paper has no problems with SR as such. However, it suggests that a different way of formulating it (see below) might be a way to obtain a more fruitful approach to modelling cosmology.

It is agreed that the Standard non-cosmological applications of SR and GR are well established. Consequently, the paper is in two main parts, with both parts concentrating on using SR as the basis. The first part (Section 2) shows the alternative way of expressing SR and how coordinates in space-time arising from this can be transformed into “Standard” coordinates (Eq.7-10a). It also shows agreement between the two theories in the non-cosmological (or local) area which is required for the new (“Dynamic”) theory to have any validity (hence the provision of this background), e.g. the Minkowski space-time is still retained (although mapped differently), while the Lorentz transformation between inertial frames and the 4-momentum relationship are unchanged.

The consequences of this approach are discussed and in the second main part (Section 3) are applied to give a simple model of the universe’s expansion (Eqns 26 & 30) in order to test this concept.

Since SCM is tuned to observational data, and it is generally accepted that its current empirical coefficients allow a good fit, it is the intention of the paper to show that just from the basis of the Dynamic SR, and some simple assumptions (Section 3), that the Dynamic theory in turn follows the trends demonstrated by the SCM (Fig 5 & 6), e.g. it shows the late-time acceleration without the need for additional models or coefficients. In following these trends, it also does so without the need of inflation to account for the flatness and horizon problems. Consequently, it is argued that the paper has gone some way to showing the Dynamic SR concept may have some validity although further work is needed (e.g. attempting to establish the possibilities of a GR theory based on this approach, and how this could be applied to cosmology).

The term “good fit…” should have been better expressed as the Dynamic theory gives a good fit to the trends shown by SCM, which in turn is tuned to give a good fit to cosmological data.

R.
Section 2 - The basis of the dynamic theory in Special Relativity (SR)
In this section, the supposed problematic features of SR are described. The first subsection qualitatively explains the potential problem in coordinate systems as related to the temporal dimension. The description is inexact in nature and lacks robustness. The author should consider putting in a more robust general analysis of the technical problem in observables, otherwise this remains a qualitative supposition. The second subsection mostly includes entry-level definitions of the Minkowski metric in textbooks and the line element. This background is not needed since it is well known. Similarly, length contraction and time dilation as well as the other properties in the final subsection are well known in the literature. Indeed, these are not so much related to cosmology except in a foundational sense.

A.
There are no problems with Standard SR, just a different way in expressing it. The paper is built entirely around SR and hence always uses inertial frames of reference.

We do not know what time and space really are. We model them in the way that we perceive them to be, i.e. using rulers and clocks. It is important to note that it is only by using these perceived models that we quantify the predictions of SR and GR. These perceptions are described in some detail in this section, leading to the observation that while space and time appear to be different phenomena, there is solid, non-cosmological evidence that they must be combined into “space-time” coordinates to provide a viable description of such behaviour as high velocity interactions or the acceleration of falling objects.

The paper argues there are two ways of providing this combination. The Standard way which keeps space as a coordinate and transforms changes in time into a “temporal dimension” using the speed of light. The Dynamic way keeps the changes in time and links them to changes in space. The first constructs space and time coordinates linked to a given inertial frame and against which the changes in coordinate positions of objects in this and other frames can be measured, although the paper emphasises the temporal coordinate always has to be inferred rather than directly observed (definitions of these terms are given in the paper). The second can only experience a change in time within an inertial frame (linked to energy changes) but not the spatial motion of the frame itself. The only changes in space coordinates are given by movements of other frames relative to an apparently fixed ruler within the observer’s frame (i.e. their observed momentums). Hence objects and observers within a given frame will only follow an (inferred) path in the temporal dimension but are fixed within their spatial dimensions. (To change their spatial position within a frame requires a non-inertial action, i.e. an acceleration followed by a deceleration to move an object to a different fixed spatial position within the original inertial frame).The consequences of the inertial behaviour are described in the paper in terms of how the Dynamic changes in time and space are combined to give a constant speed of light (Eqns 3 & 4) and which parameter has now become an invariant in the Dynamic formulation. Also, how the resulting changes in Dynamic coordinates can be transformed into changes in position given by Standard coordinates (Eqs7-10) by assuming the invariants of both theories can be equated, i.e. Eqn 8 shows the resulting transform needed between Standard changes in coordinates () and Dynamic changes within the same inertial frame that contains the observer. See paper for nomenclature and note that is always zero. Note also this transform is different to the Lorentz transform which applies to both Dynamic and Standard coordinates between frames.

The differences in how the two theories map the same Minkowski space-time are shown in Figs 1a & 1b.

R.
Section 3 - Cosmology
This section contains more literature review and some original results. This opens with a discussion of the known problems in standard cosmology. These are only partially reviewed and in no great depth. The author may want to consider more recent observed issues with the theory including cosmic tensions. The next subsection describes the so-called model being proposed in this work. This is very qualitative and not exactly in nature. A more formal attempt is provided in the third subsection, but this is similarly informal and very circumstantial. Any model beyond special or general relativity should conform to the robust mathematical rigor or either framework. Section four goes back to Lorentz transformations while the fifth section covers other special relativistic effects. These do not go beyond special relativity in any meaningful way. The section closes with a minor discussion of some of the open challenges to standard cosmology. However, these are not tackled in any serious way. The author should consider a numerical analysis involving observational data.

A.
The reason for the partial review is covered under the Introduction.

It would have been better to include the “Hubble Tension” under the list of the Standard theory’s possible shortcomings rather than trying to introduce it halfway through the section.

The last part of this review Section above, “Section four goes back to Lorentz transformations…consider a numerical analysis involving observational data.” seems to have slipped down from review Section 2. That “These do not go beyond [Standard] special relativity in any meaningful way.” Is the point as in this regime the Dynamic must agree with the Standard theory for it to have any validity (see above under Introduction). Where it does go beyond Standard SR is shown in Fig.2 and discussed in the paragraph before the sub-heading “Similarities and differences between the theories” and should have been included in that section of the paper.

“Any model…should conform to the robust mathematical rigor or [of?] either framework.” I am not sure where the additional rigor comes in. I have shown that Dynamic and Standard SR give the same results in non-cosmological regimes (GR is not considered in this paper) and where Dynamic can be extended to beyond Standard SR in the implications arising from Fig.2 and supporting paragraph. This lays the foundations of the proposed cosmology discussed in sections “The simple dynamic model” and “The quantitative dynamic model”. In turn these compare the Dynamic Hubble expansion (Eqn.26) with the SCM (Eqn.27) in Fig.6. Further discussions on where the two theories give an exact match and where (and possibly why) they run parallel are discussed in Fig.7 and supporting text.

R.
Section 3 - Discussion and conclusions
The work closes with a short summary of the main results and a long list of observations both in SR an general relativity using these suggestions made earlier in the work.

A.
The SCM relies on GR plus empirical models and coefficients briefly outlined in the paper, while the Dynamic cosmology only relies on Dynamic SR plus simple geometry. This goes some way to satisfying the aim of the paper which was to see if the Dynamic approach provides a possibly more fruitful path in describing cosmology in a way that does not require additional models or coefficients which have an unclear physical basis.
Competing Interests: No competing interests Close
Report a concern

Version 3

VERSION 3

PUBLISHED 30 Sep 2024

Revised

Views

Reviewer Report 18 Oct 2024

Boudewijn F. Roukema, Institute of Astronomy, Faculty of Physics, Astronomy and Informatics, Nicolaus Copernicus University of Torun, Torun, Poland

Not Approved

https://doi.org/10.5256/f1000research.172462.r328151

Version 3 of the submitted paper clarifies one issue: the author's intention is that his model is for a Minkowski metric. Thus, his intended model is a different spacetime to most of the FLRW (Friedmann-Lemaitre-Robertson-Walker) cosmological spacetimes (apart from at least one special case). It appears from the Version 3 abstract that the intention is to re-interpret a Minkowski spacetime and relate it to astronomical observations that have been used over the past century to constrain the FLRW models. However, despite the author excluding most of the FLRW models, later in the text he states that his re-interpretation of Minkowski spacetime includes a singularity. This is a mathematical contradiction. Moroever, he interprets astronomical observations within the context of the FLRW models that he has excluded.

The text has ambiguities throughout. It does not present a well-defined line of reasoning. Most of my specific concerns have not been dealt with by text corrections by the author (even the assertion that tachyons exist remains in Version 3 of the text). The revisions to this submitted paper show no sign of converging. This paper is not a research paper in physics/astronomy/cosmology.

Competing Interests: No competing interests were disclosed.

Reviewer Expertise: Observational cosmology; galaxy formation; large-scale structure; cosmic topology; inhomogeneous cosmology

CITE

Report a concern

Author Response 25 Oct 2024

Hugh James, Retired, AWE, Aldermaston, Reading, RG7 4PR, UK

25 Oct 2024

Author Response
R= reviewer's comment; A= author's response

R: However, despite the author excluding most of the FLRW models, later in the text he states that his re-interpretation of Minkowski spacetime ... Continue reading
R= reviewer's comment; A= author's response

R: However, despite the author excluding most of the FLRW models, later in the text he states that his re-interpretation of Minkowski spacetime includes a singularity. This is a mathematical contradiction.
A: The first sentence under the "Cosmology" heading is badly phrased. It should have read "In describing the universe, the standard theory has evidence of an expanding space-time which started from a singularity". The theory does not assume the Minkowski spacetime includes a singularity. Elsewhere it's stated this spacetime occurs after the singularity begins to expand, as explained in the text “In the simplest model the dynamic theory assumes the universe started as a singularity embedded in four spatial (not space-time) dimensions at, what we consider, the time of the Big Bang. This provides a uniform radial expansion in the four dimensions if we assume that..." (My italics). You can argue about the physics at this point (i.e. when can the singularity be considered as an expanding shell of radiation and start obeying Minkowski), much as the standard theory also has problems in this area since Quantum Mechanics must play an important role here.

R: Moreover, he interprets astronomical observations within the context of the FLRW models that he has excluded.
A: The FLRW Standard Cosmology Model (Fig.5) and the combined Friedmann equations (Fig.8) are assumed to currently give the best fits to the astronomical observations. Consequently, the fact that the dynamic theory gives a good fit to such models implies it also gives a good fit to the corresponding astronomical data without the paper being sidetracked into extensive explanations and attributions of this data.

R: The text has ambiguities throughout.
A: Difficult to respond to without specific instances being listed. If these are the same ambiguities raised for Version 2, I did respond at some length. The major error in that version, as the reviewer pointed out, was my assumption that I was dealing with different metrics rather than different coordinate systems. As stated above this has been clarified. One major unresolved issue is the reviewer’s insistence that I am dealing with tachyons, which is discussed below.

R: It does not present a well-defined line of reasoning.
A: I have probably included too much description and elements that more properly belong in sidebars. To try to precis the reasoning: -

Minkowski spacetime can be described by two different sets of coordinates, Cartesian (standard) and dynamic (current paper). The translation between the coordinate systems is given by Eq.7 (see * below).

The reasoning behind the dynamic coordinates leads to a different cosmological spacetime compared to FLRW models, where in the simplest case a 4D universe can be constructed using Special Relativity (SR) and without recourse to General Relativity (GR).

Even the simple model using the dynamic theory provides a good fit to the FLRW models based on GR (see above) but without needing some of the additional models (e.g. inflation) or difficulties (e.g. late time acceleration) that the standard theory has.

The dynamic theory simply points out some of the difficulties of using what are basically clocks and rulers to provide quantifiable tests of a selection of cosmological observations, using theories which have GR as a basis, and suggests a possible alternate view.

Obviously gravity must play an important part in most of cosmology, but an SR-based theory provides a surprisingly good fit to a number of scenarios where GR-based theories face problems.

* There is a typo in the last term of the last line of this equation. The term should have dt_N divided by gamma, not multiplied by it.

R: Most of my specific concerns have not been dealt with by text corrections by the author (even the assertion that tachyons exist remains in Version 3 of the text).
A: The reviewer’s idea that I am dealing with tachyons appears to arise from two points he makes in his Version 2 review. In my Version 2 reply these come under points I have labelled 2 and 5, and I will attempt to further clarify these (for the record I believe there is no solid evidence tachyons exist).
Point 2. He quotes my text “an observer…can only influence or be influenced by events which happen in the present.” Which he then interprets as my belief that tachyons exist. This is probably due to the clumsy way I originally phrased this. In the standard theory this would mean a single unchanging time coordinate which would have to be connected to the rest of the universe by spacelike worldlines, i.e. tachyons. However, what I should have made clear is this is the dynamic theory where the observer is in an everchanging present, which when translated into standard coordinates (Eq.7) gives timelike worldlines as illustrated in Fig.1b. The observer moves along these worldlines in standard coordinates, but to the observer in the dynamic theory he sees only the changing present. Eq.7 & Fig 1b show how the different ways of describing the observer can be equated and transformations between the two obtained - but only for timelike worldlines.
Point 5. Similarly he takes my meaning as the only worldlines considered are along the x axis, i.e. time coordinates are constant and again this would imply spacelike worldlines. This misunderstood my formulation of Eq.1 (which is the Minkowski standard equation) where what I was trying to say was the spatial content of this equation assumed all spatial coordinate changes (i.e. velocity vectors) in this paper could be reduced to lying in the x dimension, rather than having to write out the root of x² + y² + z² each time I wanted to use it.
R= reviewer's comment; A= author's response

R: However, despite the author excluding most of the FLRW models, later in the text he states that his re-interpretation of Minkowski spacetime includes a singularity. This is a mathematical contradiction.
A: The first sentence under the "Cosmology" heading is badly phrased. It should have read "In describing the universe, the standard theory has evidence of an expanding space-time which started from a singularity". The theory does not assume the Minkowski spacetime includes a singularity. Elsewhere it's stated this spacetime occurs after the singularity begins to expand, as explained in the text “In the simplest model the dynamic theory assumes the universe started as a singularity embedded in four spatial (not space-time) dimensions at, what we consider, the time of the Big Bang. This provides a uniform radial expansion in the four dimensions if we assume that..." (My italics). You can argue about the physics at this point (i.e. when can the singularity be considered as an expanding shell of radiation and start obeying Minkowski), much as the standard theory also has problems in this area since Quantum Mechanics must play an important role here.

R: Moreover, he interprets astronomical observations within the context of the FLRW models that he has excluded.
A: The FLRW Standard Cosmology Model (Fig.5) and the combined Friedmann equations (Fig.8) are assumed to currently give the best fits to the astronomical observations. Consequently, the fact that the dynamic theory gives a good fit to such models implies it also gives a good fit to the corresponding astronomical data without the paper being sidetracked into extensive explanations and attributions of this data.

R: The text has ambiguities throughout.
A: Difficult to respond to without specific instances being listed. If these are the same ambiguities raised for Version 2, I did respond at some length. The major error in that version, as the reviewer pointed out, was my assumption that I was dealing with different metrics rather than different coordinate systems. As stated above this has been clarified. One major unresolved issue is the reviewer’s insistence that I am dealing with tachyons, which is discussed below.

R: It does not present a well-defined line of reasoning.
A: I have probably included too much description and elements that more properly belong in sidebars. To try to precis the reasoning: -

Minkowski spacetime can be described by two different sets of coordinates, Cartesian (standard) and dynamic (current paper). The translation between the coordinate systems is given by Eq.7 (see * below).

The reasoning behind the dynamic coordinates leads to a different cosmological spacetime compared to FLRW models, where in the simplest case a 4D universe can be constructed using Special Relativity (SR) and without recourse to General Relativity (GR).

Even the simple model using the dynamic theory provides a good fit to the FLRW models based on GR (see above) but without needing some of the additional models (e.g. inflation) or difficulties (e.g. late time acceleration) that the standard theory has.

The dynamic theory simply points out some of the difficulties of using what are basically clocks and rulers to provide quantifiable tests of a selection of cosmological observations, using theories which have GR as a basis, and suggests a possible alternate view.

Obviously gravity must play an important part in most of cosmology, but an SR-based theory provides a surprisingly good fit to a number of scenarios where GR-based theories face problems.

* There is a typo in the last term of the last line of this equation. The term should have dt_N divided by gamma, not multiplied by it.

R: Most of my specific concerns have not been dealt with by text corrections by the author (even the assertion that tachyons exist remains in Version 3 of the text).
A: The reviewer’s idea that I am dealing with tachyons appears to arise from two points he makes in his Version 2 review. In my Version 2 reply these come under points I have labelled 2 and 5, and I will attempt to further clarify these (for the record I believe there is no solid evidence tachyons exist).
Point 2. He quotes my text “an observer…can only influence or be influenced by events which happen in the present.” Which he then interprets as my belief that tachyons exist. This is probably due to the clumsy way I originally phrased this. In the standard theory this would mean a single unchanging time coordinate which would have to be connected to the rest of the universe by spacelike worldlines, i.e. tachyons. However, what I should have made clear is this is the dynamic theory where the observer is in an everchanging present, which when translated into standard coordinates (Eq.7) gives timelike worldlines as illustrated in Fig.1b. The observer moves along these worldlines in standard coordinates, but to the observer in the dynamic theory he sees only the changing present. Eq.7 & Fig 1b show how the different ways of describing the observer can be equated and transformations between the two obtained - but only for timelike worldlines.
Point 5. Similarly he takes my meaning as the only worldlines considered are along the x axis, i.e. time coordinates are constant and again this would imply spacelike worldlines. This misunderstood my formulation of Eq.1 (which is the Minkowski standard equation) where what I was trying to say was the spatial content of this equation assumed all spatial coordinate changes (i.e. velocity vectors) in this paper could be reduced to lying in the x dimension, rather than having to write out the root of x² + y² + z² each time I wanted to use it.
Competing Interests: No competing interests. Close
Report a concern
Respond or Comment

COMMENTS ON THIS REPORT

Author Response 25 Oct 2024

Hugh James, Retired, AWE, Aldermaston, Reading, RG7 4PR, UK

25 Oct 2024

Author Response
R= reviewer's comment; A= author's response

R: However, despite the author excluding most of the FLRW models, later in the text he states that his re-interpretation of Minkowski spacetime ... Continue reading
R= reviewer's comment; A= author's response

R: However, despite the author excluding most of the FLRW models, later in the text he states that his re-interpretation of Minkowski spacetime includes a singularity. This is a mathematical contradiction.
A: The first sentence under the "Cosmology" heading is badly phrased. It should have read "In describing the universe, the standard theory has evidence of an expanding space-time which started from a singularity". The theory does not assume the Minkowski spacetime includes a singularity. Elsewhere it's stated this spacetime occurs after the singularity begins to expand, as explained in the text “In the simplest model the dynamic theory assumes the universe started as a singularity embedded in four spatial (not space-time) dimensions at, what we consider, the time of the Big Bang. This provides a uniform radial expansion in the four dimensions if we assume that..." (My italics). You can argue about the physics at this point (i.e. when can the singularity be considered as an expanding shell of radiation and start obeying Minkowski), much as the standard theory also has problems in this area since Quantum Mechanics must play an important role here.

R: Moreover, he interprets astronomical observations within the context of the FLRW models that he has excluded.
A: The FLRW Standard Cosmology Model (Fig.5) and the combined Friedmann equations (Fig.8) are assumed to currently give the best fits to the astronomical observations. Consequently, the fact that the dynamic theory gives a good fit to such models implies it also gives a good fit to the corresponding astronomical data without the paper being sidetracked into extensive explanations and attributions of this data.

R: The text has ambiguities throughout.
A: Difficult to respond to without specific instances being listed. If these are the same ambiguities raised for Version 2, I did respond at some length. The major error in that version, as the reviewer pointed out, was my assumption that I was dealing with different metrics rather than different coordinate systems. As stated above this has been clarified. One major unresolved issue is the reviewer’s insistence that I am dealing with tachyons, which is discussed below.

R: It does not present a well-defined line of reasoning.
A: I have probably included too much description and elements that more properly belong in sidebars. To try to precis the reasoning: -

Minkowski spacetime can be described by two different sets of coordinates, Cartesian (standard) and dynamic (current paper). The translation between the coordinate systems is given by Eq.7 (see * below).

The reasoning behind the dynamic coordinates leads to a different cosmological spacetime compared to FLRW models, where in the simplest case a 4D universe can be constructed using Special Relativity (SR) and without recourse to General Relativity (GR).

Even the simple model using the dynamic theory provides a good fit to the FLRW models based on GR (see above) but without needing some of the additional models (e.g. inflation) or difficulties (e.g. late time acceleration) that the standard theory has.

The dynamic theory simply points out some of the difficulties of using what are basically clocks and rulers to provide quantifiable tests of a selection of cosmological observations, using theories which have GR as a basis, and suggests a possible alternate view.

Obviously gravity must play an important part in most of cosmology, but an SR-based theory provides a surprisingly good fit to a number of scenarios where GR-based theories face problems.

* There is a typo in the last term of the last line of this equation. The term should have dt_N divided by gamma, not multiplied by it.

R: Most of my specific concerns have not been dealt with by text corrections by the author (even the assertion that tachyons exist remains in Version 3 of the text).
A: The reviewer’s idea that I am dealing with tachyons appears to arise from two points he makes in his Version 2 review. In my Version 2 reply these come under points I have labelled 2 and 5, and I will attempt to further clarify these (for the record I believe there is no solid evidence tachyons exist).
Point 2. He quotes my text “an observer…can only influence or be influenced by events which happen in the present.” Which he then interprets as my belief that tachyons exist. This is probably due to the clumsy way I originally phrased this. In the standard theory this would mean a single unchanging time coordinate which would have to be connected to the rest of the universe by spacelike worldlines, i.e. tachyons. However, what I should have made clear is this is the dynamic theory where the observer is in an everchanging present, which when translated into standard coordinates (Eq.7) gives timelike worldlines as illustrated in Fig.1b. The observer moves along these worldlines in standard coordinates, but to the observer in the dynamic theory he sees only the changing present. Eq.7 & Fig 1b show how the different ways of describing the observer can be equated and transformations between the two obtained - but only for timelike worldlines.
Point 5. Similarly he takes my meaning as the only worldlines considered are along the x axis, i.e. time coordinates are constant and again this would imply spacelike worldlines. This misunderstood my formulation of Eq.1 (which is the Minkowski standard equation) where what I was trying to say was the spatial content of this equation assumed all spatial coordinate changes (i.e. velocity vectors) in this paper could be reduced to lying in the x dimension, rather than having to write out the root of x² + y² + z² each time I wanted to use it.
R= reviewer's comment; A= author's response

R: However, despite the author excluding most of the FLRW models, later in the text he states that his re-interpretation of Minkowski spacetime includes a singularity. This is a mathematical contradiction.
A: The first sentence under the "Cosmology" heading is badly phrased. It should have read "In describing the universe, the standard theory has evidence of an expanding space-time which started from a singularity". The theory does not assume the Minkowski spacetime includes a singularity. Elsewhere it's stated this spacetime occurs after the singularity begins to expand, as explained in the text “In the simplest model the dynamic theory assumes the universe started as a singularity embedded in four spatial (not space-time) dimensions at, what we consider, the time of the Big Bang. This provides a uniform radial expansion in the four dimensions if we assume that..." (My italics). You can argue about the physics at this point (i.e. when can the singularity be considered as an expanding shell of radiation and start obeying Minkowski), much as the standard theory also has problems in this area since Quantum Mechanics must play an important role here.

R: Moreover, he interprets astronomical observations within the context of the FLRW models that he has excluded.
A: The FLRW Standard Cosmology Model (Fig.5) and the combined Friedmann equations (Fig.8) are assumed to currently give the best fits to the astronomical observations. Consequently, the fact that the dynamic theory gives a good fit to such models implies it also gives a good fit to the corresponding astronomical data without the paper being sidetracked into extensive explanations and attributions of this data.

R: The text has ambiguities throughout.
A: Difficult to respond to without specific instances being listed. If these are the same ambiguities raised for Version 2, I did respond at some length. The major error in that version, as the reviewer pointed out, was my assumption that I was dealing with different metrics rather than different coordinate systems. As stated above this has been clarified. One major unresolved issue is the reviewer’s insistence that I am dealing with tachyons, which is discussed below.

R: It does not present a well-defined line of reasoning.
A: I have probably included too much description and elements that more properly belong in sidebars. To try to precis the reasoning: -

Minkowski spacetime can be described by two different sets of coordinates, Cartesian (standard) and dynamic (current paper). The translation between the coordinate systems is given by Eq.7 (see * below).

The reasoning behind the dynamic coordinates leads to a different cosmological spacetime compared to FLRW models, where in the simplest case a 4D universe can be constructed using Special Relativity (SR) and without recourse to General Relativity (GR).

Even the simple model using the dynamic theory provides a good fit to the FLRW models based on GR (see above) but without needing some of the additional models (e.g. inflation) or difficulties (e.g. late time acceleration) that the standard theory has.

The dynamic theory simply points out some of the difficulties of using what are basically clocks and rulers to provide quantifiable tests of a selection of cosmological observations, using theories which have GR as a basis, and suggests a possible alternate view.

Obviously gravity must play an important part in most of cosmology, but an SR-based theory provides a surprisingly good fit to a number of scenarios where GR-based theories face problems.

* There is a typo in the last term of the last line of this equation. The term should have dt_N divided by gamma, not multiplied by it.

R: Most of my specific concerns have not been dealt with by text corrections by the author (even the assertion that tachyons exist remains in Version 3 of the text).
A: The reviewer’s idea that I am dealing with tachyons appears to arise from two points he makes in his Version 2 review. In my Version 2 reply these come under points I have labelled 2 and 5, and I will attempt to further clarify these (for the record I believe there is no solid evidence tachyons exist).
Point 2. He quotes my text “an observer…can only influence or be influenced by events which happen in the present.” Which he then interprets as my belief that tachyons exist. This is probably due to the clumsy way I originally phrased this. In the standard theory this would mean a single unchanging time coordinate which would have to be connected to the rest of the universe by spacelike worldlines, i.e. tachyons. However, what I should have made clear is this is the dynamic theory where the observer is in an everchanging present, which when translated into standard coordinates (Eq.7) gives timelike worldlines as illustrated in Fig.1b. The observer moves along these worldlines in standard coordinates, but to the observer in the dynamic theory he sees only the changing present. Eq.7 & Fig 1b show how the different ways of describing the observer can be equated and transformations between the two obtained - but only for timelike worldlines.
Point 5. Similarly he takes my meaning as the only worldlines considered are along the x axis, i.e. time coordinates are constant and again this would imply spacelike worldlines. This misunderstood my formulation of Eq.1 (which is the Minkowski standard equation) where what I was trying to say was the spatial content of this equation assumed all spatial coordinate changes (i.e. velocity vectors) in this paper could be reduced to lying in the x dimension, rather than having to write out the root of x² + y² + z² each time I wanted to use it.
Competing Interests: No competing interests. Close
Report a concern

Version 2

VERSION 2

PUBLISHED 30 Jan 2023

Revised

Views

Reviewer Report 01 Nov 2023

Boudewijn F. Roukema, Institute of Astronomy, Faculty of Physics, Astronomy and Informatics, Nicolaus Copernicus University of Torun, Torun, Poland

Not Approved

https://doi.org/10.5256/f1000research.142944.r161776

Revision 2 of this paper has not addressed the main concerns of lack of clarity (properly quantified and defined assumptions, method, results). It remains extremely difficult to try to guess what the author is proposing, and there are too many errors and verbose expressions without definitions to make it possible to guess the author's intended line of argument. There is no proper mathematical definition of the proposed model, and no separation between the model and its interpretations. The changes add material, but do not make it possible for the reader to work through the basic assumptions and method of the paper prior to trying to understand the new material.

As an example of a specific wrong physical claim that remains uncorrected, the sentence "The basis..." in paragraph 2 of the Introduction still contains an assertion that tachyons exist: "an observer ... can only influence or be influenced by events which happen in the present".

Some specific examples of problems in version 2 follow. Their correction would be necessary, but *not* sufficient, for the paper to constitute a research paper in this field.

The Introduction points the reader to Eqs (7)-(11); this requires the reader to first work through the equations starting with (1). The interpretation of (1) differs from standard SR, since the author says that d\tau is necessarily a proper time interval, contradicts himself by saying that it can be zero, and then neglects the case where (d\tau)^2 is negative, in which case d\tau is not a proper time interval.

Even more confusing in this same paragraph is that the author states that "only spatial motions along the x axis are considered". In the context of (1), which is the only equation or convention introduced by this point of the text, the lack of a definition of "spatial motion" forces the reader to speculate what this might mean. The apparently intended meaning is that the only worldlines that are considered are those "along the x axis", i.e. with constant t_A and t_B values, i.e. tachyons. On the contrary, if the author's intended meaning is that he wishes to present a pseudo-Riemannian manifold, and projections within that manifold, then that has to be presented and defined unambiguously.

The definition of Dt_{AB} prior to (1) remains obscure: there is no indication here of how a coordinate in two frames (A, B) relates to choices of coordinate systems A and B. The subscript C for the frame of a ruler "against which spatial motion is measured" leaves Dx_{ACB} undefined.

Trying to interpret the text after (4), we find that "the only coordinates that A can directly observe are spatial." This contradicts Eq (1), which has a time coordinate t_A, and also implies that clocks don't exist in the proposed model.

At three places in and around Fig. 1, a spacelike hyperbola is incorrectly described as timelike. This is wrong: a spacelike hyperbola is spacelike; it is not timelike.

Trying to continue through to (7)-(11), there is no clear way for the reader to guess the definition of the manifold being proposed.

Returning to the introduction:

Paragraph 4 of the introduction describes what appears to be the global model with the phrase "a non-local view in which this surface is expanding along four spatial dimensions"; but "is expanding" implies the existence of a fifth dimension that is timelike (let us call it x^5). The following sentence implies that one of the four spatial dimensions is to be reinterpreted as time (let us call it x^4), in which case the model must be five-dimensional with two time dimensions: x^4 and x^5.

The sentence in this paragraph "Consequently when this model ... " defines a gravitational potential which is apparently a vector field, since it refers to the potential being "normal to ...", but lacks a definition of the way in which a vector potential might be used to model gravity. The (undefined) vector potential is apparently directed in the \tau direction ("normal to its expansion").

Paragraph 5: "a vector equal to the universal expansion, shown as equivalent to the speed of light." Expansion in FLRW models is modelled as a scalar function of a time parameter; it is not a vector. The speed of light is not a vector either. Equating any of these three things ((i) a vector; (ii) universal expansion; (iii) the speed of light) to one of the other is mathematically wrong in the standard model, and this paper does not make it clear how any of these three things can be equated.

Competing Interests: No competing interests were disclosed.

Reviewer Expertise: Observational cosmology; galaxy formation; large-scale structure; cosmic topology; inhomogeneous cosmology.

CITE

Report a concern

Author Response 09 Nov 2023

Hugh James, Retired, AWE, Aldermaston, Reading, RG7 4PR, UK

09 Nov 2023

Author Response

The paragraph numbering corresponds to the Reviewer's paragraphs.

1. The verbosity was intended to provid sufficient context for the differences between the standard theory and that put forward in this ... Continue reading The paragraph numbering corresponds to the Reviewer's paragraphs.

1. The verbosity was intended to provid sufficient context for the differences between the standard theory and that put forward in this paper. The standard theory deals with coordinates and their derivatives while the dynamic theory in the paper deals with momentum (space) and energy (time) from which coordinate derivatives can be obtained. The derivatives can be linked to each other (eqs.7-11) and the reasons for differences are discussed primarily in the paragraph before Eqs. 3 & 4.

2. The paragraph referred to is simply trying to make the point that the way humans obtain a quantified measure of space and time (by rulers and clocks) has fundamental differences between these measures despite needing to amalgamate them to obtain space-time. The comment about the observer always being in his present simply reflects the human experience of time. A spatial coordinate can be visited many times, a temporal coordinate only once.
At no point do I assert tachyons exist. In the model (see under "Cosmology") the universe consists of a surface made up of the locus of all inertial frames moving outwards from a central point at what can be constued as the speed of light. This is the motion of the universe's surface, not motion along that surface which is what tachyons would require.

4. Eq.1 is the standard SR which for brevity assumes the spatial motion is along x, which saves writing
-dx²-dy²-dz² each time. According to Foster & Nightingale ("A short course in general relativity", p165, Longman, 1979) "the path through spacetime...is called its world line..and the proper time interval d\tau between points...relative to some frame K..is defined by.." and then follows my Eq.1, or in its complete form my Eq.10. The italics are their own. Further "..the proper time tau is the time recorded by a clock which moves along with the particle" Again their italics. And again on the same page "..for a particle at rest in K [or in my case A] the proper time tau is..the coordinate time t ...measured by stationary clocks in [A]." Substitute ds² for d\tau² in my Eq.1. It can then be positive, negative or zero. I have chosen the positive one as it joins up time-like intervals (Fig.1, OA, OB, OG). I have concentrated on this as A is the observer's frame in which d\tau=dt.

5. Better in the paper would be "only changes in spatial coordinates along.." and refers to the brevity discussed in 4. At that point I had not started discussing the dynamic theory.

6. Since the paper deals mainly with special relativity (SR), A, B and C are seperate inertial frames with different relative velocities and their own spatial coordinate frames and clocks. Assuming time on clocks in each frame can be seen from any other frame, then Dt_AB has A as the observer looking at the clock in frame B and comparing it to their own clock. Consequently Dt_AB (the observed clock) = Dt_AA (the observer's clock) multiplied by gamma^-1 (see text). Equally it is assumed the observer can see other frames moving relative to a ruler. Hence Dx_AAB has A observing B's change in spatial position relative to a ruler in A's frame. Dx_ACB is A observing B's space changes against a ruler in C's space. The links between observers are still given by the Lorentz transforms (Table 1 & Eqs. 14-18. Note the typo in Eq.18, the right side should be (w+v)/(1+vw/c²)).

7. This was meant to emphasise the differences between models. The standard model (Eq.1) assumes both spatial and temporal coordinates are present (dtA, dxA) while the dynamic model (Eq.4) says the only coordinates that can be directly observed are spatial, e.g. divisions on a ruler. Time coordinates have to be constructed since clocks only give changes in time, and other methods are needed to give (Dt_AA, Dx_AAB) but NOT Dx_AAA - see text.

8. See comments under 4.

9. Eq.11 defines the dynamic metric while Eq.9 defines the line element. Both are expressed in terms of standard coordinates. Fig.1 shows the Minkowski hyperbola from standard SR but constructed as the locus of the time axes of inertial frames with increasing velocities relative to a given observer (A). Eq.9 shows such a construction can also be expressed in an Euclidean form where lines of increasing velocity intersect the hyperbola.

10. The model only has 4 spatial dimensions, each frame having 3 of space and one which takes on the aspects of time. Within a frame, however, the time dimension is only inferred from memory and aids such as film. As far as direct observations and interactions with your surroundings go, the temporal dimension appears rolled up into a point which we call the present. From outside the frame (i.e. from a frame with a relative velocity to the first) this time appears as motion along a spatial set of coordinates (see paragraph after Eq.11). The observer sees a velocity but the observed sees dimensionless changing time. Consequently a "non-local" view has a universe with a surface described in 2, and under "Cosmology" in the paper.

11. The model is based on SR since any gravitational effect normal to the universe's expansion would equally affect the apparent motions of an observer in both space and time, leading to a constant expansion velocity (see Fig.3).

12. In the paper it should have been the velocity of light since it has a definite direction.
The paragraph numbering corresponds to the Reviewer's paragraphs.

1. The verbosity was intended to provid sufficient context for the differences between the standard theory and that put forward in this paper. The standard theory deals with coordinates and their derivatives while the dynamic theory in the paper deals with momentum (space) and energy (time) from which coordinate derivatives can be obtained. The derivatives can be linked to each other (eqs.7-11) and the reasons for differences are discussed primarily in the paragraph before Eqs. 3 & 4.

2. The paragraph referred to is simply trying to make the point that the way humans obtain a quantified measure of space and time (by rulers and clocks) has fundamental differences between these measures despite needing to amalgamate them to obtain space-time. The comment about the observer always being in his present simply reflects the human experience of time. A spatial coordinate can be visited many times, a temporal coordinate only once.
At no point do I assert tachyons exist. In the model (see under "Cosmology") the universe consists of a surface made up of the locus of all inertial frames moving outwards from a central point at what can be constued as the speed of light. This is the motion of the universe's surface, not motion along that surface which is what tachyons would require.

4. Eq.1 is the standard SR which for brevity assumes the spatial motion is along x, which saves writing
-dx²-dy²-dz² each time. According to Foster & Nightingale ("A short course in general relativity", p165, Longman, 1979) "the path through spacetime...is called its world line..and the proper time interval d\tau between points...relative to some frame K..is defined by.." and then follows my Eq.1, or in its complete form my Eq.10. The italics are their own. Further "..the proper time tau is the time recorded by a clock which moves along with the particle" Again their italics. And again on the same page "..for a particle at rest in K [or in my case A] the proper time tau is..the coordinate time t ...measured by stationary clocks in [A]." Substitute ds² for d\tau² in my Eq.1. It can then be positive, negative or zero. I have chosen the positive one as it joins up time-like intervals (Fig.1, OA, OB, OG). I have concentrated on this as A is the observer's frame in which d\tau=dt.

5. Better in the paper would be "only changes in spatial coordinates along.." and refers to the brevity discussed in 4. At that point I had not started discussing the dynamic theory.

6. Since the paper deals mainly with special relativity (SR), A, B and C are seperate inertial frames with different relative velocities and their own spatial coordinate frames and clocks. Assuming time on clocks in each frame can be seen from any other frame, then Dt_AB has A as the observer looking at the clock in frame B and comparing it to their own clock. Consequently Dt_AB (the observed clock) = Dt_AA (the observer's clock) multiplied by gamma^-1 (see text). Equally it is assumed the observer can see other frames moving relative to a ruler. Hence Dx_AAB has A observing B's change in spatial position relative to a ruler in A's frame. Dx_ACB is A observing B's space changes against a ruler in C's space. The links between observers are still given by the Lorentz transforms (Table 1 & Eqs. 14-18. Note the typo in Eq.18, the right side should be (w+v)/(1+vw/c²)).

7. This was meant to emphasise the differences between models. The standard model (Eq.1) assumes both spatial and temporal coordinates are present (dtA, dxA) while the dynamic model (Eq.4) says the only coordinates that can be directly observed are spatial, e.g. divisions on a ruler. Time coordinates have to be constructed since clocks only give changes in time, and other methods are needed to give (Dt_AA, Dx_AAB) but NOT Dx_AAA - see text.

8. See comments under 4.

9. Eq.11 defines the dynamic metric while Eq.9 defines the line element. Both are expressed in terms of standard coordinates. Fig.1 shows the Minkowski hyperbola from standard SR but constructed as the locus of the time axes of inertial frames with increasing velocities relative to a given observer (A). Eq.9 shows such a construction can also be expressed in an Euclidean form where lines of increasing velocity intersect the hyperbola.

10. The model only has 4 spatial dimensions, each frame having 3 of space and one which takes on the aspects of time. Within a frame, however, the time dimension is only inferred from memory and aids such as film. As far as direct observations and interactions with your surroundings go, the temporal dimension appears rolled up into a point which we call the present. From outside the frame (i.e. from a frame with a relative velocity to the first) this time appears as motion along a spatial set of coordinates (see paragraph after Eq.11). The observer sees a velocity but the observed sees dimensionless changing time. Consequently a "non-local" view has a universe with a surface described in 2, and under "Cosmology" in the paper.

11. The model is based on SR since any gravitational effect normal to the universe's expansion would equally affect the apparent motions of an observer in both space and time, leading to a constant expansion velocity (see Fig.3).

12. In the paper it should have been the velocity of light since it has a definite direction.
Competing Interests: No competing interests Close
Report a concern
Respond or Comment

COMMENTS ON THIS REPORT

Author Response 09 Nov 2023

Hugh James, Retired, AWE, Aldermaston, Reading, RG7 4PR, UK

09 Nov 2023

Author Response

The paragraph numbering corresponds to the Reviewer's paragraphs.

1. The verbosity was intended to provid sufficient context for the differences between the standard theory and that put forward in this ... Continue reading The paragraph numbering corresponds to the Reviewer's paragraphs.

1. The verbosity was intended to provid sufficient context for the differences between the standard theory and that put forward in this paper. The standard theory deals with coordinates and their derivatives while the dynamic theory in the paper deals with momentum (space) and energy (time) from which coordinate derivatives can be obtained. The derivatives can be linked to each other (eqs.7-11) and the reasons for differences are discussed primarily in the paragraph before Eqs. 3 & 4.

2. The paragraph referred to is simply trying to make the point that the way humans obtain a quantified measure of space and time (by rulers and clocks) has fundamental differences between these measures despite needing to amalgamate them to obtain space-time. The comment about the observer always being in his present simply reflects the human experience of time. A spatial coordinate can be visited many times, a temporal coordinate only once.
At no point do I assert tachyons exist. In the model (see under "Cosmology") the universe consists of a surface made up of the locus of all inertial frames moving outwards from a central point at what can be constued as the speed of light. This is the motion of the universe's surface, not motion along that surface which is what tachyons would require.

4. Eq.1 is the standard SR which for brevity assumes the spatial motion is along x, which saves writing
-dx²-dy²-dz² each time. According to Foster & Nightingale ("A short course in general relativity", p165, Longman, 1979) "the path through spacetime...is called its world line..and the proper time interval d\tau between points...relative to some frame K..is defined by.." and then follows my Eq.1, or in its complete form my Eq.10. The italics are their own. Further "..the proper time tau is the time recorded by a clock which moves along with the particle" Again their italics. And again on the same page "..for a particle at rest in K [or in my case A] the proper time tau is..the coordinate time t ...measured by stationary clocks in [A]." Substitute ds² for d\tau² in my Eq.1. It can then be positive, negative or zero. I have chosen the positive one as it joins up time-like intervals (Fig.1, OA, OB, OG). I have concentrated on this as A is the observer's frame in which d\tau=dt.

5. Better in the paper would be "only changes in spatial coordinates along.." and refers to the brevity discussed in 4. At that point I had not started discussing the dynamic theory.

6. Since the paper deals mainly with special relativity (SR), A, B and C are seperate inertial frames with different relative velocities and their own spatial coordinate frames and clocks. Assuming time on clocks in each frame can be seen from any other frame, then Dt_AB has A as the observer looking at the clock in frame B and comparing it to their own clock. Consequently Dt_AB (the observed clock) = Dt_AA (the observer's clock) multiplied by gamma^-1 (see text). Equally it is assumed the observer can see other frames moving relative to a ruler. Hence Dx_AAB has A observing B's change in spatial position relative to a ruler in A's frame. Dx_ACB is A observing B's space changes against a ruler in C's space. The links between observers are still given by the Lorentz transforms (Table 1 & Eqs. 14-18. Note the typo in Eq.18, the right side should be (w+v)/(1+vw/c²)).

7. This was meant to emphasise the differences between models. The standard model (Eq.1) assumes both spatial and temporal coordinates are present (dtA, dxA) while the dynamic model (Eq.4) says the only coordinates that can be directly observed are spatial, e.g. divisions on a ruler. Time coordinates have to be constructed since clocks only give changes in time, and other methods are needed to give (Dt_AA, Dx_AAB) but NOT Dx_AAA - see text.

8. See comments under 4.

9. Eq.11 defines the dynamic metric while Eq.9 defines the line element. Both are expressed in terms of standard coordinates. Fig.1 shows the Minkowski hyperbola from standard SR but constructed as the locus of the time axes of inertial frames with increasing velocities relative to a given observer (A). Eq.9 shows such a construction can also be expressed in an Euclidean form where lines of increasing velocity intersect the hyperbola.

10. The model only has 4 spatial dimensions, each frame having 3 of space and one which takes on the aspects of time. Within a frame, however, the time dimension is only inferred from memory and aids such as film. As far as direct observations and interactions with your surroundings go, the temporal dimension appears rolled up into a point which we call the present. From outside the frame (i.e. from a frame with a relative velocity to the first) this time appears as motion along a spatial set of coordinates (see paragraph after Eq.11). The observer sees a velocity but the observed sees dimensionless changing time. Consequently a "non-local" view has a universe with a surface described in 2, and under "Cosmology" in the paper.

11. The model is based on SR since any gravitational effect normal to the universe's expansion would equally affect the apparent motions of an observer in both space and time, leading to a constant expansion velocity (see Fig.3).

12. In the paper it should have been the velocity of light since it has a definite direction.
The paragraph numbering corresponds to the Reviewer's paragraphs.

1. The verbosity was intended to provid sufficient context for the differences between the standard theory and that put forward in this paper. The standard theory deals with coordinates and their derivatives while the dynamic theory in the paper deals with momentum (space) and energy (time) from which coordinate derivatives can be obtained. The derivatives can be linked to each other (eqs.7-11) and the reasons for differences are discussed primarily in the paragraph before Eqs. 3 & 4.

2. The paragraph referred to is simply trying to make the point that the way humans obtain a quantified measure of space and time (by rulers and clocks) has fundamental differences between these measures despite needing to amalgamate them to obtain space-time. The comment about the observer always being in his present simply reflects the human experience of time. A spatial coordinate can be visited many times, a temporal coordinate only once.
At no point do I assert tachyons exist. In the model (see under "Cosmology") the universe consists of a surface made up of the locus of all inertial frames moving outwards from a central point at what can be constued as the speed of light. This is the motion of the universe's surface, not motion along that surface which is what tachyons would require.

4. Eq.1 is the standard SR which for brevity assumes the spatial motion is along x, which saves writing
-dx²-dy²-dz² each time. According to Foster & Nightingale ("A short course in general relativity", p165, Longman, 1979) "the path through spacetime...is called its world line..and the proper time interval d\tau between points...relative to some frame K..is defined by.." and then follows my Eq.1, or in its complete form my Eq.10. The italics are their own. Further "..the proper time tau is the time recorded by a clock which moves along with the particle" Again their italics. And again on the same page "..for a particle at rest in K [or in my case A] the proper time tau is..the coordinate time t ...measured by stationary clocks in [A]." Substitute ds² for d\tau² in my Eq.1. It can then be positive, negative or zero. I have chosen the positive one as it joins up time-like intervals (Fig.1, OA, OB, OG). I have concentrated on this as A is the observer's frame in which d\tau=dt.

5. Better in the paper would be "only changes in spatial coordinates along.." and refers to the brevity discussed in 4. At that point I had not started discussing the dynamic theory.

6. Since the paper deals mainly with special relativity (SR), A, B and C are seperate inertial frames with different relative velocities and their own spatial coordinate frames and clocks. Assuming time on clocks in each frame can be seen from any other frame, then Dt_AB has A as the observer looking at the clock in frame B and comparing it to their own clock. Consequently Dt_AB (the observed clock) = Dt_AA (the observer's clock) multiplied by gamma^-1 (see text). Equally it is assumed the observer can see other frames moving relative to a ruler. Hence Dx_AAB has A observing B's change in spatial position relative to a ruler in A's frame. Dx_ACB is A observing B's space changes against a ruler in C's space. The links between observers are still given by the Lorentz transforms (Table 1 & Eqs. 14-18. Note the typo in Eq.18, the right side should be (w+v)/(1+vw/c²)).

7. This was meant to emphasise the differences between models. The standard model (Eq.1) assumes both spatial and temporal coordinates are present (dtA, dxA) while the dynamic model (Eq.4) says the only coordinates that can be directly observed are spatial, e.g. divisions on a ruler. Time coordinates have to be constructed since clocks only give changes in time, and other methods are needed to give (Dt_AA, Dx_AAB) but NOT Dx_AAA - see text.

8. See comments under 4.

9. Eq.11 defines the dynamic metric while Eq.9 defines the line element. Both are expressed in terms of standard coordinates. Fig.1 shows the Minkowski hyperbola from standard SR but constructed as the locus of the time axes of inertial frames with increasing velocities relative to a given observer (A). Eq.9 shows such a construction can also be expressed in an Euclidean form where lines of increasing velocity intersect the hyperbola.

10. The model only has 4 spatial dimensions, each frame having 3 of space and one which takes on the aspects of time. Within a frame, however, the time dimension is only inferred from memory and aids such as film. As far as direct observations and interactions with your surroundings go, the temporal dimension appears rolled up into a point which we call the present. From outside the frame (i.e. from a frame with a relative velocity to the first) this time appears as motion along a spatial set of coordinates (see paragraph after Eq.11). The observer sees a velocity but the observed sees dimensionless changing time. Consequently a "non-local" view has a universe with a surface described in 2, and under "Cosmology" in the paper.

11. The model is based on SR since any gravitational effect normal to the universe's expansion would equally affect the apparent motions of an observer in both space and time, leading to a constant expansion velocity (see Fig.3).

12. In the paper it should have been the velocity of light since it has a definite direction.
Competing Interests: No competing interests Close
Report a concern

Version 1

VERSION 1

PUBLISHED 21 Mar 2022

Views

111

Reviewer Report 18 Jul 2022

Boudewijn F. Roukema, Institute of Astronomy, Faculty of Physics, Astronomy and Informatics, Nicolaus Copernicus University of Torun, Torun, Poland

Not Approved

https://doi.org/10.5256/f1000research.120051.r139580

The aim of this paper is, apparently, to propose a differential pseudo-Riemannian manifold (a topological manifold M' endowed with a pseudo-Riemannian metric g', i.e. (M', g') that is an alternative to Minkowski spacetime (M, g) as a model for special relativity. However, the language and equations make it very difficult to guess what (M', g') is being proposed. It is unclear if the author is trying to express the relation between different coordinate systems for a single spacetime, or describe a relation between two or three spacetimes. Physically, the introductory section includes the experimentally absurd assertion that bradyons do not exist; and the so-far experimentally unestablished claim that tachyons exist ("... an observer...can only influence or be influenced by events which happen in the present").

The lack of a clear proposal for the paper's main aim - an alternative to Minkowski spacetime - makes it impossible to judge the proposal's implications for cosmological spacetimes. The author also appears to suggest that the proposed spacetime is identical to Minkowski spacetime (abstract: "the relativistic equations are unchanged for local phenomena such as the Lorentz coordinate transformation and the energy/momentum equation for high-velocity objects"), in which case there is no new proposal.

I would suggest that the author first work through Taylor & Wheeler's "Spacetime physics"¹ - a geometrical approach to special relativity, as opposed to the historical approach, before attempting to propose an alternative to Minkowski spacetime. The alternative model should be clearly defined using standard mathematical terminology of differential geometry, or of another field of mathematics if the model is not differentiable pseudo-Riemannian 4-manifold.

Some specific examples of problems follow:

The abstract states that the "equations" of special relativity following from (M', g') are identical to those for (M, g). It incorrectly states that a coordinate framework is a fundamental requirement of the theory. Special relativity assumes that bradyonic particles exist as timelike world lines in (M, g) independent of any coordinate system.

The paragraph "Basically, relativistic effects..." is an extremely confusing way of presenting the worldline of an observer in Minkowski spacetime. It asserts the existence of tachyons and rejects the existence of bradyons: "...what an observer experiences as time, i.e. he is always trapped in the current moment in the sense that he can only influence or be influenced by events which happen in the present." Influencing or being influenced by events at a constant time in a chosen reference frame (x, t) requires the use of tachyons, where these tachyons have world lines that exist along a constant t and cover an interval in x from the observer to the event being influenced or that influences the observer.

The paragraph "Time in this view appears..." fails to explain what (M', g') is being proposed. The sentence "The dynamic view keeps time as an ever-changing entity..." fails to say what time changes with respect to. If the change is with respect to time, then the simplest interpretation is that time t changes with respect to time t, yielding dt/dt = 1. This gives no difference from Minkowski spacetime, and would imply that the phrase "time... as an ever-changing entity" is an obfuscatory way of saying in words that dt/dt = 1.

The section "The intersection of the coordinate and dynamic theories" appears intended to present (M', g'), but fails to define energy and momentum. In Minkowski spacetime, these are defined in terms of the 4-momentum, and for a bradyon as the mass times the 4-velocity. We cannot know what the author's definition is prior to the definition of the spacetime itself.

More fundamentally, while the line element of metric can be expressed in terms of small changes in the values of coordinates, the author's proposal appears to combine two coordinate systems for time, and three coordinate systems for space. This leaves the reader with no help in understanding what (M', g') is being proposed. If three different metric spaces are being proposed using three different line elements written with a single coordinate system, then that should be done. The relation between the three metrics would also have to be defined.

The uses of the verbs "see" and "exist" in the text are generally confusing for the presentation of an alternative spacetime geometry to Minkowski spacetime.

One example of confusing phrases in the section "The simple dynamical model" is "This provides a uniform radial expansion in the four dimensions..." There is *no* radial expansion in any standard (Friedmann-Lemaitre-Robertson-Walker, FLRW) model, since an FLRW universe has no centre. In some cases, the embedding of the spatial section of an FLRW universe in a higher dimensional space X is useful for intuition and for calculations, but this does not imply any physical significance for the space X. The author's apparent inclusion of a "fourth dimension", which appears to be either spacelike or timelike at different points in the text, with an unclear relation to (M', g'), does not help to clarify what "radial expansion" might be intended to mean. (The observer's past time cone is radial by construction, with the observer at the centre, but constructing a spacetime by starting with the observer still requires unambiguously defining the general characteristics of the class of spacetimes that are under consideration).

Is the work clearly and accurately presented and does it cite the current literature?

Partly
Is the study design appropriate and is the work technically sound?

No
Are sufficient details of methods and analysis provided to allow replication by others?

No
If applicable, is the statistical analysis and its interpretation appropriate?

Not applicable
Are all the source data underlying the results available to ensure full reproducibility?

No source data required
Are the conclusions drawn adequately supported by the results?

No

References

1. Taylor E, Wheeler J, Bowen J: Spacetime Physics: Introduction to Special Relativity, 2nd ed.American Journal of Physics. 1993; 61 (3). Publisher Full Text

Competing Interests: No competing interests were disclosed.

Reviewer Expertise: Observational cosmology; galaxy formation; large-scale structure; cosmic topology; inhomogeneous cosmology.

CITE

Report a concern

Author Response 04 Aug 2022

Hugh James, Retired, AWE, Aldermaston, Reading, RG7 4PR, UK

04 Aug 2022

Author Response
- The paper defines a possible alternative space time (Dynamic space time, or DS) to that of Minkowski.
- It does not assert the non- existence of bradyons and
... Continue reading
The paper defines a possible alternative space time (Dynamic space time, or DS) to that of Minkowski.

It does not assert the non- existence of bradyons and the existence of tachyons, this is based on a misconception of how DS is constructed (see below).

A Cartesian coordinate system is used throughout, and only inertial frames (IFs) are considered.

The alternative spacetime is based on the differences of how space and time are measured, and leaves aside any consideration of what they might “really” be.

Space coordinates are based on a ruler - a distribution of mass to which coordinates can be assigned. A clock output is an energy release which can be equated to a continuously changing time, and from which temporal coordinates can be constructed.

Minkowski converts clock outputs to temporal coordinates to obtain a non-Euclidean spacetime (Eqn.1).

DS partners momentum to the clock energy release. An observer in an IF (e.g. labelled A) can only see a clock changing and not the IFs momentum. He also cannot see a dimension in what can be hypothesised as the time direction (orthogonal to his x,y,z space). He exists in an ever-changing present - not at a constant time (and hence nothing to do with tachyons). From this changing present can be constructed an imaginary time dimension by using memories or recording devices. A temporal coordinate in this dimension can only be physically visited once, unlike the physically real spatial coordinates which can be visited many times.

As A cannot use his own momentum, he uses his observations of a different IF (B). The combination of A’s time and A’s observation of B’s energy and momentum gives A’s Euclidean DS spacetime (Eqn.3).

The observation of these phenomena indicates that both (energy release and momentum) are relative, i.e. A’s clock is relative to (A’s observations of B’s) clock and spatial motion, which means that for a single observer dt is not just a change in time.

The verbs “see” and “exist” refer to physically-based phenomena such as spatial coordinates or a changing time, and not to an imaginary time dimension.

The derivation of A’s spacetime leads to the hypothesis that in DS it is the clock co-located with the observer that provides the invariant, in contrast to Minkowski where it is the moving clock that is invariant.

DS confines any bradyon to its own time direction (OA, OB, OG in Fig.1) and actually located at A, B, G in that Figure, which is on the time-like hyperbola provided by Minkowski. Hence only along this hyperbola can the two spacetimes (Euclidean and non-Euclidean) intersect to agree on Lorentz transformations, the 4-momentum etc. Away from this they are different and Fig.2 shows how each IF is seen from within as 3 spatial dimensions and a changing time in which any dimension has rolled up to a point. From outside this IF the changing time is seen as a motion along a spatial dimension.

This leads to the hypothesis that the universe consists of 4 spatial dimensions which, in the simplest case, has bradyons travel radially outwards from a common centre. These bradyons form a surface which is orthogonal to the radial motion, and although this radial motion is at the speed of light, this is the rate of expansion of the universe. The observed bradyon motion is the component of this expansion along the surface when seen from a different IF (Figs 3 & 4), and so does not contravene the requirement that bradyons should travel slower than the speed of light. From within the IF this radial motion is experienced as the changing time.

This is not an FLRW model, but results from an FLRW model can be compared to those from DS (Figs 5 & 6, Table 1).

The use of only IFs and not general relativity in constructing this model is discussed in the Conclusions and Discussion of the paper.
The paper defines a possible alternative space time (Dynamic space time, or DS) to that of Minkowski.

It does not assert the non- existence of bradyons and the existence of tachyons, this is based on a misconception of how DS is constructed (see below).

A Cartesian coordinate system is used throughout, and only inertial frames (IFs) are considered.

The alternative spacetime is based on the differences of how space and time are measured, and leaves aside any consideration of what they might “really” be.

Space coordinates are based on a ruler - a distribution of mass to which coordinates can be assigned. A clock output is an energy release which can be equated to a continuously changing time, and from which temporal coordinates can be constructed.

Minkowski converts clock outputs to temporal coordinates to obtain a non-Euclidean spacetime (Eqn.1).

DS partners momentum to the clock energy release. An observer in an IF (e.g. labelled A) can only see a clock changing and not the IFs momentum. He also cannot see a dimension in what can be hypothesised as the time direction (orthogonal to his x,y,z space). He exists in an ever-changing present - not at a constant time (and hence nothing to do with tachyons). From this changing present can be constructed an imaginary time dimension by using memories or recording devices. A temporal coordinate in this dimension can only be physically visited once, unlike the physically real spatial coordinates which can be visited many times.

As A cannot use his own momentum, he uses his observations of a different IF (B). The combination of A’s time and A’s observation of B’s energy and momentum gives A’s Euclidean DS spacetime (Eqn.3).

The observation of these phenomena indicates that both (energy release and momentum) are relative, i.e. A’s clock is relative to (A’s observations of B’s) clock and spatial motion, which means that for a single observer dt is not just a change in time.

The verbs “see” and “exist” refer to physically-based phenomena such as spatial coordinates or a changing time, and not to an imaginary time dimension.

The derivation of A’s spacetime leads to the hypothesis that in DS it is the clock co-located with the observer that provides the invariant, in contrast to Minkowski where it is the moving clock that is invariant.

DS confines any bradyon to its own time direction (OA, OB, OG in Fig.1) and actually located at A, B, G in that Figure, which is on the time-like hyperbola provided by Minkowski. Hence only along this hyperbola can the two spacetimes (Euclidean and non-Euclidean) intersect to agree on Lorentz transformations, the 4-momentum etc. Away from this they are different and Fig.2 shows how each IF is seen from within as 3 spatial dimensions and a changing time in which any dimension has rolled up to a point. From outside this IF the changing time is seen as a motion along a spatial dimension.

This leads to the hypothesis that the universe consists of 4 spatial dimensions which, in the simplest case, has bradyons travel radially outwards from a common centre. These bradyons form a surface which is orthogonal to the radial motion, and although this radial motion is at the speed of light, this is the rate of expansion of the universe. The observed bradyon motion is the component of this expansion along the surface when seen from a different IF (Figs 3 & 4), and so does not contravene the requirement that bradyons should travel slower than the speed of light. From within the IF this radial motion is experienced as the changing time.

This is not an FLRW model, but results from an FLRW model can be compared to those from DS (Figs 5 & 6, Table 1).

The use of only IFs and not general relativity in constructing this model is discussed in the Conclusions and Discussion of the paper.
Competing Interests: There are no competing interests Close
Report a concern
Respond or Comment

COMMENTS ON THIS REPORT

Author Response 04 Aug 2022

Hugh James, Retired, AWE, Aldermaston, Reading, RG7 4PR, UK

04 Aug 2022

Author Response
- The paper defines a possible alternative space time (Dynamic space time, or DS) to that of Minkowski.
- It does not assert the non- existence of bradyons and
... Continue reading
The paper defines a possible alternative space time (Dynamic space time, or DS) to that of Minkowski.

It does not assert the non- existence of bradyons and the existence of tachyons, this is based on a misconception of how DS is constructed (see below).

A Cartesian coordinate system is used throughout, and only inertial frames (IFs) are considered.

The alternative spacetime is based on the differences of how space and time are measured, and leaves aside any consideration of what they might “really” be.

Space coordinates are based on a ruler - a distribution of mass to which coordinates can be assigned. A clock output is an energy release which can be equated to a continuously changing time, and from which temporal coordinates can be constructed.

Minkowski converts clock outputs to temporal coordinates to obtain a non-Euclidean spacetime (Eqn.1).

DS partners momentum to the clock energy release. An observer in an IF (e.g. labelled A) can only see a clock changing and not the IFs momentum. He also cannot see a dimension in what can be hypothesised as the time direction (orthogonal to his x,y,z space). He exists in an ever-changing present - not at a constant time (and hence nothing to do with tachyons). From this changing present can be constructed an imaginary time dimension by using memories or recording devices. A temporal coordinate in this dimension can only be physically visited once, unlike the physically real spatial coordinates which can be visited many times.

As A cannot use his own momentum, he uses his observations of a different IF (B). The combination of A’s time and A’s observation of B’s energy and momentum gives A’s Euclidean DS spacetime (Eqn.3).

The observation of these phenomena indicates that both (energy release and momentum) are relative, i.e. A’s clock is relative to (A’s observations of B’s) clock and spatial motion, which means that for a single observer dt is not just a change in time.

The verbs “see” and “exist” refer to physically-based phenomena such as spatial coordinates or a changing time, and not to an imaginary time dimension.

The derivation of A’s spacetime leads to the hypothesis that in DS it is the clock co-located with the observer that provides the invariant, in contrast to Minkowski where it is the moving clock that is invariant.

DS confines any bradyon to its own time direction (OA, OB, OG in Fig.1) and actually located at A, B, G in that Figure, which is on the time-like hyperbola provided by Minkowski. Hence only along this hyperbola can the two spacetimes (Euclidean and non-Euclidean) intersect to agree on Lorentz transformations, the 4-momentum etc. Away from this they are different and Fig.2 shows how each IF is seen from within as 3 spatial dimensions and a changing time in which any dimension has rolled up to a point. From outside this IF the changing time is seen as a motion along a spatial dimension.

This leads to the hypothesis that the universe consists of 4 spatial dimensions which, in the simplest case, has bradyons travel radially outwards from a common centre. These bradyons form a surface which is orthogonal to the radial motion, and although this radial motion is at the speed of light, this is the rate of expansion of the universe. The observed bradyon motion is the component of this expansion along the surface when seen from a different IF (Figs 3 & 4), and so does not contravene the requirement that bradyons should travel slower than the speed of light. From within the IF this radial motion is experienced as the changing time.

This is not an FLRW model, but results from an FLRW model can be compared to those from DS (Figs 5 & 6, Table 1).

The use of only IFs and not general relativity in constructing this model is discussed in the Conclusions and Discussion of the paper.
The paper defines a possible alternative space time (Dynamic space time, or DS) to that of Minkowski.

It does not assert the non- existence of bradyons and the existence of tachyons, this is based on a misconception of how DS is constructed (see below).

A Cartesian coordinate system is used throughout, and only inertial frames (IFs) are considered.

The alternative spacetime is based on the differences of how space and time are measured, and leaves aside any consideration of what they might “really” be.

Space coordinates are based on a ruler - a distribution of mass to which coordinates can be assigned. A clock output is an energy release which can be equated to a continuously changing time, and from which temporal coordinates can be constructed.

Minkowski converts clock outputs to temporal coordinates to obtain a non-Euclidean spacetime (Eqn.1).

DS partners momentum to the clock energy release. An observer in an IF (e.g. labelled A) can only see a clock changing and not the IFs momentum. He also cannot see a dimension in what can be hypothesised as the time direction (orthogonal to his x,y,z space). He exists in an ever-changing present - not at a constant time (and hence nothing to do with tachyons). From this changing present can be constructed an imaginary time dimension by using memories or recording devices. A temporal coordinate in this dimension can only be physically visited once, unlike the physically real spatial coordinates which can be visited many times.

As A cannot use his own momentum, he uses his observations of a different IF (B). The combination of A’s time and A’s observation of B’s energy and momentum gives A’s Euclidean DS spacetime (Eqn.3).

The observation of these phenomena indicates that both (energy release and momentum) are relative, i.e. A’s clock is relative to (A’s observations of B’s) clock and spatial motion, which means that for a single observer dt is not just a change in time.

The verbs “see” and “exist” refer to physically-based phenomena such as spatial coordinates or a changing time, and not to an imaginary time dimension.

The derivation of A’s spacetime leads to the hypothesis that in DS it is the clock co-located with the observer that provides the invariant, in contrast to Minkowski where it is the moving clock that is invariant.

DS confines any bradyon to its own time direction (OA, OB, OG in Fig.1) and actually located at A, B, G in that Figure, which is on the time-like hyperbola provided by Minkowski. Hence only along this hyperbola can the two spacetimes (Euclidean and non-Euclidean) intersect to agree on Lorentz transformations, the 4-momentum etc. Away from this they are different and Fig.2 shows how each IF is seen from within as 3 spatial dimensions and a changing time in which any dimension has rolled up to a point. From outside this IF the changing time is seen as a motion along a spatial dimension.

This leads to the hypothesis that the universe consists of 4 spatial dimensions which, in the simplest case, has bradyons travel radially outwards from a common centre. These bradyons form a surface which is orthogonal to the radial motion, and although this radial motion is at the speed of light, this is the rate of expansion of the universe. The observed bradyon motion is the component of this expansion along the surface when seen from a different IF (Figs 3 & 4), and so does not contravene the requirement that bradyons should travel slower than the speed of light. From within the IF this radial motion is experienced as the changing time.

This is not an FLRW model, but results from an FLRW model can be compared to those from DS (Figs 5 & 6, Table 1).

The use of only IFs and not general relativity in constructing this model is discussed in the Conclusions and Discussion of the paper.
Competing Interests: There are no competing interests Close
Report a concern

Comments on this article Comments (0)

Version 5

VERSION 5 PUBLISHED 21 Mar 2022

Open Peer Review

Reviewer Status

Reviewer Reports

	Invited Reviewers
	1	2
Version 5 (revision) 18 Dec 25
Version 4 (revision) 27 Jan 25		read
Version 3 (revision) 30 Sep 24	read
Version 2 (revision) 30 Jan 23	read
Version 1 21 Mar 22	read

Boudewijn F. Roukema, Nicolaus Copernicus University of Torun, Torun, Poland
Jackson Levi Said, University of Malta, Msida, Malta

Comments on this article

All Comments(0)

Add a comment

Browse by related subjects

Back to all reports

Reviewer Report

31 Views

19 Aug 2025 | for Version 4

Jackson Levi Said, University of Malta, Msida, Malta

31 Views Cite this report Responses(1)

Not Approved

Is the work clearly and accurately presented and does it cite the current literature?

No
Is the study design appropriate and is the work technically sound?

No
Are sufficient details of methods and analysis provided to allow replication by others?

No
If applicable, is the statistical analysis and its interpretation appropriate?

No
Are all the source data underlying the results available to ensure full reproducibility?

Partly
Are the conclusions drawn adequately supported by the results?

No

Competing Interests

No competing interests were disclosed.

Reviewer Expertise

I am a cosmologist working on the theoretical development of models to resolve open issues in observational cosmology.

Respond to this report

Responses (1)

Author Response

18 Dec 2025

Hugh James, Retired, AWE, Aldermaston, Reading, RG7 4PR, UK

R=Reviewer comment, A=Author response.

R.
The manuscript claims to resolve some open problems in relativity theory. Overall, the work is not robustly formulated and contains informal language throughout. A more formal analysis should involve more explicit model suggestions and some rudimentary form of data analysis since the principal issues identified are observational in nature. The confused language is unclear throughout. However, any conflict within special relativity should be explicitly shown as should any proposal beyond this theoretical framework. The author should revisit the foundations of their proposal in more detail, and formulate a better defined research hypothesis and proposal.

For these reasons, I do not recommend this manuscript for indexing in its present form. Below, I detail the precise issue to be reconsidered by the authors.

Section 1 - Introduction
The opening assumes special and general relativity as foundational building blocks, as they should be. However, the introduction then goes into the need to resolve some problematic features of special relativity. These are not explained explicitly, nor are they well defined in terms of observables associated with observers in this framework. This leaves the motivation for the work ambiguous while the research hypothesis is vague in nature. The author should describe in more detail what supposed problem appears in not giving a “good fit to the corresponding astronomical data” means and at what statistical level this appears at. In its present form, these statements are very vague and not well referenced.

A.
My Introduction should have been clearer and more succinct.

The paper is not intended as a review of current cosmology and the reader is assumed conversant with problems in the “Standard” approach, hence only the outlines of such problems are given in Sections 1 and 3.

This paper is intended as a test-of-concept investigation into whether an approach developed therein might be more fruitful in tackling some of these problems than the approach utilised by the Standard Cosmology Model (SCM).

In brief, with the SCM there are problems using general relativity (GR) when GR is applied to cosmology. To account for the observed flatness or horizon phenomena, an additional model (inflation) must be invoked. Equally the universe’s late-time acceleration requires Einstein’s lambda function to be included in the GR description. Neither of these “fixes” currently appear to have a solid physical justification other than to fit the theory to observation.

In the limit, where there is no gravitational field or acceleration of a given observer, GR must revert to special relativity (SR). Consequently, in this paper it is proposed that if there is an alternative way of expressing SR, this might in turn lead to solutions of some of the above problems by using it as a first approximation for the basis of modelling cosmology without the need for requiring additional phenomena such as inflation or lambda.

The paper has no problems with SR as such. However, it suggests that a different way of formulating it (see below) might be a way to obtain a more fruitful approach to modelling cosmology.

It is agreed that the Standard non-cosmological applications of SR and GR are well established. Consequently, the paper is in two main parts, with both parts concentrating on using SR as the basis. The first part (Section 2) shows the alternative way of expressing SR and how coordinates in space-time arising from this can be transformed into “Standard” coordinates (Eq.7-10a). It also shows agreement between the two theories in the non-cosmological (or local) area which is required for the new (“Dynamic”) theory to have any validity (hence the provision of this background), e.g. the Minkowski space-time is still retained (although mapped differently), while the Lorentz transformation between inertial frames and the 4-momentum relationship are unchanged.

The consequences of this approach are discussed and in the second main part (Section 3) are applied to give a simple model of the universe’s expansion (Eqns 26 & 30) in order to test this concept.

Since SCM is tuned to observational data, and it is generally accepted that its current empirical coefficients allow a good fit, it is the intention of the paper to show that just from the basis of the Dynamic SR, and some simple assumptions (Section 3), that the Dynamic theory in turn follows the trends demonstrated by the SCM (Fig 5 & 6), e.g. it shows the late-time acceleration without the need for additional models or coefficients. In following these trends, it also does so without the need of inflation to account for the flatness and horizon problems. Consequently, it is argued that the paper has gone some way to showing the Dynamic SR concept may have some validity although further work is needed (e.g. attempting to establish the possibilities of a GR theory based on this approach, and how this could be applied to cosmology).

The term “good fit…” should have been better expressed as the Dynamic theory gives a good fit to the trends shown by SCM, which in turn is tuned to give a good fit to cosmological data.

R.
Section 2 - The basis of the dynamic theory in Special Relativity (SR)
In this section, the supposed problematic features of SR are described. The first subsection qualitatively explains the potential problem in coordinate systems as related to the temporal dimension. The description is inexact in nature and lacks robustness. The author should consider putting in a more robust general analysis of the technical problem in observables, otherwise this remains a qualitative supposition. The second subsection mostly includes entry-level definitions of the Minkowski metric in textbooks and the line element. This background is not needed since it is well known. Similarly, length contraction and time dilation as well as the other properties in the final subsection are well known in the literature. Indeed, these are not so much related to cosmology except in a foundational sense.

A.
There are no problems with Standard SR, just a different way in expressing it. The paper is built entirely around SR and hence always uses inertial frames of reference.

We do not know what time and space really are. We model them in the way that we perceive them to be, i.e. using rulers and clocks. It is important to note that it is only by using these perceived models that we quantify the predictions of SR and GR. These perceptions are described in some detail in this section, leading to the observation that while space and time appear to be different phenomena, there is solid, non-cosmological evidence that they must be combined into “space-time” coordinates to provide a viable description of such behaviour as high velocity interactions or the acceleration of falling objects.

The paper argues there are two ways of providing this combination. The Standard way which keeps space as a coordinate and transforms changes in time into a “temporal dimension” using the speed of light. The Dynamic way keeps the changes in time and links them to changes in space. The first constructs space and time coordinates linked to a given inertial frame and against which the changes in coordinate positions of objects in this and other frames can be measured, although the paper emphasises the temporal coordinate always has to be inferred rather than directly observed (definitions of these terms are given in the paper). The second can only experience a change in time within an inertial frame (linked to energy changes) but not the spatial motion of the frame itself. The only changes in space coordinates are given by movements of other frames relative to an apparently fixed ruler within the observer’s frame (i.e. their observed momentums). Hence objects and observers within a given frame will only follow an (inferred) path in the temporal dimension but are fixed within their spatial dimensions. (To change their spatial position within a frame requires a non-inertial action, i.e. an acceleration followed by a deceleration to move an object to a different fixed spatial position within the original inertial frame).The consequences of the inertial behaviour are described in the paper in terms of how the Dynamic changes in time and space are combined to give a constant speed of light (Eqns 3 & 4) and which parameter has now become an invariant in the Dynamic formulation. Also, how the resulting changes in Dynamic coordinates can be transformed into changes in position given by Standard coordinates (Eqs7-10) by assuming the invariants of both theories can be equated, i.e. Eqn 8 shows the resulting transform needed between Standard changes in coordinates (

) and Dynamic changes

within the same inertial frame that contains the observer. See paper for nomenclature and note that

is always zero. Note also this transform is different to the Lorentz transform which applies to both Dynamic and Standard coordinates between frames.

The differences in how the two theories map the same Minkowski space-time are shown in Figs 1a & 1b.

R.
Section 3 - Cosmology
This section contains more literature review and some original results. This opens with a discussion of the known problems in standard cosmology. These are only partially reviewed and in no great depth. The author may want to consider more recent observed issues with the theory including cosmic tensions. The next subsection describes the so-called model being proposed in this work. This is very qualitative and not exactly in nature. A more formal attempt is provided in the third subsection, but this is similarly informal and very circumstantial. Any model beyond special or general relativity should conform to the robust mathematical rigor or either framework. Section four goes back to Lorentz transformations while the fifth section covers other special relativistic effects. These do not go beyond special relativity in any meaningful way. The section closes with a minor discussion of some of the open challenges to standard cosmology. However, these are not tackled in any serious way. The author should consider a numerical analysis involving observational data.

A.
The reason for the partial review is covered under the Introduction.

It would have been better to include the “Hubble Tension” under the list of the Standard theory’s possible shortcomings rather than trying to introduce it halfway through the section.

The last part of this review Section above, “Section four goes back to Lorentz transformations…consider a numerical analysis involving observational data.” seems to have slipped down from review Section 2. That “These do not go beyond [Standard] special relativity in any meaningful way.” Is the point as in this regime the Dynamic must agree with the Standard theory for it to have any validity (see above under Introduction). Where it does go beyond Standard SR is shown in Fig.2 and discussed in the paragraph before the sub-heading “Similarities and differences between the theories” and should have been included in that section of the paper.

“Any model…should conform to the robust mathematical rigor or [of?] either framework.” I am not sure where the additional rigor comes in. I have shown that Dynamic and Standard SR give the same results in non-cosmological regimes (GR is not considered in this paper) and where Dynamic can be extended to beyond Standard SR in the implications arising from Fig.2 and supporting paragraph. This lays the foundations of the proposed cosmology discussed in sections “The simple dynamic model” and “The quantitative dynamic model”. In turn these compare the Dynamic Hubble expansion (Eqn.26) with the SCM (Eqn.27) in Fig.6. Further discussions on where the two theories give an exact match and where (and possibly why) they run parallel are discussed in Fig.7 and supporting text.

R.
Section 3 - Discussion and conclusions
The work closes with a short summary of the main results and a long list of observations both in SR an general relativity using these suggestions made earlier in the work.

A.
The SCM relies on GR plus empirical models and coefficients briefly outlined in the paper, while the Dynamic cosmology only relies on Dynamic SR plus simple geometry. This goes some way to satisfying the aim of the paper which was to see if the Dynamic approach provides a possibly more fruitful path in describing cosmology in a way that does not require additional models or coefficients which have an unclear physical basis.

View more View less

Competing Interests

No competing interests

Back to all reports

Reviewer Report

38 Views

18 Oct 2024 | for Version 3

Boudewijn F. Roukema, Institute of Astronomy, Faculty of Physics, Astronomy and Informatics, Nicolaus Copernicus University of Torun, Torun, Poland

38 Views Cite this report Responses(1)

Not Approved

Competing Interests

No competing interests were disclosed.

Reviewer Expertise

Observational cosmology; galaxy formation; large-scale structure; cosmic topology; inhomogeneous cosmology

Respond to this report

Responses (1)

Author Response

25 Oct 2024

Hugh James, Retired, AWE, Aldermaston, Reading, RG7 4PR, UK

R= reviewer's comment; A= author's response

R: However, despite the author excluding most of the FLRW models, later in the text he states that his re-interpretation of Minkowski spacetime includes a singularity. This is a mathematical contradiction.
A: The first sentence under the "Cosmology" heading is badly phrased. It should have read "In describing the universe, the standard theory has evidence of an expanding space-time which started from a singularity". The theory does not assume the Minkowski spacetime includes a singularity. Elsewhere it's stated this spacetime occurs after the singularity begins to expand, as explained in the text “In the simplest model the dynamic theory assumes the universe started as a singularity embedded in four spatial (not space-time) dimensions at, what we consider, the time of the Big Bang. This provides a uniform radial expansion in the four dimensions if we assume that..." (My italics). You can argue about the physics at this point (i.e. when can the singularity be considered as an expanding shell of radiation and start obeying Minkowski), much as the standard theory also has problems in this area since Quantum Mechanics must play an important role here.

R: Moreover, he interprets astronomical observations within the context of the FLRW models that he has excluded.
A: The FLRW Standard Cosmology Model (Fig.5) and the combined Friedmann equations (Fig.8) are assumed to currently give the best fits to the astronomical observations. Consequently, the fact that the dynamic theory gives a good fit to such models implies it also gives a good fit to the corresponding astronomical data without the paper being sidetracked into extensive explanations and attributions of this data.

R: The text has ambiguities throughout.
A: Difficult to respond to without specific instances being listed. If these are the same ambiguities raised for Version 2, I did respond at some length. The major error in that version, as the reviewer pointed out, was my assumption that I was dealing with different metrics rather than different coordinate systems. As stated above this has been clarified. One major unresolved issue is the reviewer’s insistence that I am dealing with tachyons, which is discussed below.

R: It does not present a well-defined line of reasoning.
A: I have probably included too much description and elements that more properly belong in sidebars. To try to precis the reasoning: -

Minkowski spacetime can be described by two different sets of coordinates, Cartesian (standard) and dynamic (current paper). The translation between the coordinate systems is given by Eq.7 (see * below).
The reasoning behind the dynamic coordinates leads to a different cosmological spacetime compared to FLRW models, where in the simplest case a 4D universe can be constructed using Special Relativity (SR) and without recourse to General Relativity (GR).
Even the simple model using the dynamic theory provides a good fit to the FLRW models based on GR (see above) but without needing some of the additional models (e.g. inflation) or difficulties (e.g. late time acceleration) that the standard theory has.
The dynamic theory simply points out some of the difficulties of using what are basically clocks and rulers to provide quantifiable tests of a selection of cosmological observations, using theories which have GR as a basis, and suggests a possible alternate view.
Obviously gravity must play an important part in most of cosmology, but an SR-based theory provides a surprisingly good fit to a number of scenarios where GR-based theories face problems.

* There is a typo in the last term of the last line of this equation. The term should have dt_N divided by gamma, not multiplied by it.

R: Most of my specific concerns have not been dealt with by text corrections by the author (even the assertion that tachyons exist remains in Version 3 of the text).
A: The reviewer’s idea that I am dealing with tachyons appears to arise from two points he makes in his Version 2 review. In my Version 2 reply these come under points I have labelled 2 and 5, and I will attempt to further clarify these (for the record I believe there is no solid evidence tachyons exist).
Point 2. He quotes my text “an observer…can only influence or be influenced by events which happen in the present.” Which he then interprets as my belief that tachyons exist. This is probably due to the clumsy way I originally phrased this. In the standard theory this would mean a single unchanging time coordinate which would have to be connected to the rest of the universe by spacelike worldlines, i.e. tachyons. However, what I should have made clear is this is the dynamic theory where the observer is in an everchanging present, which when translated into standard coordinates (Eq.7) gives timelike worldlines as illustrated in Fig.1b. The observer moves along these worldlines in standard coordinates, but to the observer in the dynamic theory he sees only the changing present. Eq.7 & Fig 1b show how the different ways of describing the observer can be equated and transformations between the two obtained - but only for timelike worldlines.
Point 5. Similarly he takes my meaning as the only worldlines considered are along the x axis, i.e. time coordinates are constant and again this would imply spacelike worldlines. This misunderstood my formulation of Eq.1 (which is the Minkowski standard equation) where what I was trying to say was the spatial content of this equation assumed all spatial coordinate changes (i.e. velocity vectors) in this paper could be reduced to lying in the x dimension, rather than having to write out the root of x² + y² + z² each time I wanted to use it.

View more View less

Competing Interests

No competing interests.

Back to all reports

Reviewer Report

63 Views

01 Nov 2023 | for Version 2

Boudewijn F. Roukema, Institute of Astronomy, Faculty of Physics, Astronomy and Informatics, Nicolaus Copernicus University of Torun, Torun, Poland

63 Views Cite this report Responses(1)

Not Approved

Competing Interests

No competing interests were disclosed.

Reviewer Expertise

Observational cosmology; galaxy formation; large-scale structure; cosmic topology; inhomogeneous cosmology.

Respond to this report

Responses (1)

Author Response

09 Nov 2023

Hugh James, Retired, AWE, Aldermaston, Reading, RG7 4PR, UK

The paragraph numbering corresponds to the Reviewer's paragraphs.

1. The verbosity was intended to provid sufficient context for the differences between the standard theory and that put forward in this paper. The standard theory deals with coordinates and their derivatives while the dynamic theory in the paper deals with momentum (space) and energy (time) from which coordinate derivatives can be obtained. The derivatives can be linked to each other (eqs.7-11) and the reasons for differences are discussed primarily in the paragraph before Eqs. 3 & 4.

2. The paragraph referred to is simply trying to make the point that the way humans obtain a quantified measure of space and time (by rulers and clocks) has fundamental differences between these measures despite needing to amalgamate them to obtain space-time. The comment about the observer always being in his present simply reflects the human experience of time. A spatial coordinate can be visited many times, a temporal coordinate only once.
At no point do I assert tachyons exist. In the model (see under "Cosmology") the universe consists of a surface made up of the locus of all inertial frames moving outwards from a central point at what can be constued as the speed of light. This is the motion of the universe's surface, not motion along that surface which is what tachyons would require.

4. Eq.1 is the standard SR which for brevity assumes the spatial motion is along x, which saves writing
-dx²-dy²-dz² each time. According to Foster & Nightingale ("A short course in general relativity", p165, Longman, 1979) "the path through spacetime...is called its world line..and the proper time interval d\tau between points...relative to some frame K..is defined by.." and then follows my Eq.1, or in its complete form my Eq.10. The italics are their own. Further "..the proper time tau is the time recorded by a clock which moves along with the particle" Again their italics. And again on the same page "..for a particle at rest in K [or in my case A] the proper time tau is..the coordinate time t ...measured by stationary clocks in [A]." Substitute ds² for d\tau² in my Eq.1. It can then be positive, negative or zero. I have chosen the positive one as it joins up time-like intervals (Fig.1, OA, OB, OG). I have concentrated on this as A is the observer's frame in which d\tau=dt.

5. Better in the paper would be "only changes in spatial coordinates along.." and refers to the brevity discussed in 4. At that point I had not started discussing the dynamic theory.

6. Since the paper deals mainly with special relativity (SR), A, B and C are seperate inertial frames with different relative velocities and their own spatial coordinate frames and clocks. Assuming time on clocks in each frame can be seen from any other frame, then Dt_AB has A as the observer looking at the clock in frame B and comparing it to their own clock. Consequently Dt_AB (the observed clock) = Dt_AA (the observer's clock) multiplied by gamma^-1 (see text). Equally it is assumed the observer can see other frames moving relative to a ruler. Hence Dx_AAB has A observing B's change in spatial position relative to a ruler in A's frame. Dx_ACB is A observing B's space changes against a ruler in C's space. The links between observers are still given by the Lorentz transforms (Table 1 & Eqs. 14-18. Note the typo in Eq.18, the right side should be (w+v)/(1+vw/c²)).

7. This was meant to emphasise the differences between models. The standard model (Eq.1) assumes both spatial and temporal coordinates are present (dtA, dxA) while the dynamic model (Eq.4) says the only coordinates that can be directly observed are spatial, e.g. divisions on a ruler. Time coordinates have to be constructed since clocks only give changes in time, and other methods are needed to give (Dt_AA, Dx_AAB) but NOT Dx_AAA - see text.

8. See comments under 4.

9. Eq.11 defines the dynamic metric while Eq.9 defines the line element. Both are expressed in terms of standard coordinates. Fig.1 shows the Minkowski hyperbola from standard SR but constructed as the locus of the time axes of inertial frames with increasing velocities relative to a given observer (A). Eq.9 shows such a construction can also be expressed in an Euclidean form where lines of increasing velocity intersect the hyperbola.

10. The model only has 4 spatial dimensions, each frame having 3 of space and one which takes on the aspects of time. Within a frame, however, the time dimension is only inferred from memory and aids such as film. As far as direct observations and interactions with your surroundings go, the temporal dimension appears rolled up into a point which we call the present. From outside the frame (i.e. from a frame with a relative velocity to the first) this time appears as motion along a spatial set of coordinates (see paragraph after Eq.11). The observer sees a velocity but the observed sees dimensionless changing time. Consequently a "non-local" view has a universe with a surface described in 2, and under "Cosmology" in the paper.

11. The model is based on SR since any gravitational effect normal to the universe's expansion would equally affect the apparent motions of an observer in both space and time, leading to a constant expansion velocity (see Fig.3).

12. In the paper it should have been the velocity of light since it has a definite direction.

View more View less

Competing Interests

No competing interests

Back to all reports

Reviewer Report

111 Views

18 Jul 2022 | for Version 1

Boudewijn F. Roukema, Institute of Astronomy, Faculty of Physics, Astronomy and Informatics, Nicolaus Copernicus University of Torun, Torun, Poland

111 Views Cite this report Responses(1)

Not Approved

Is the work clearly and accurately presented and does it cite the current literature?

Partly
Is the study design appropriate and is the work technically sound?

No
Are sufficient details of methods and analysis provided to allow replication by others?

No
If applicable, is the statistical analysis and its interpretation appropriate?

Not applicable
Are all the source data underlying the results available to ensure full reproducibility?

No source data required
Are the conclusions drawn adequately supported by the results?

No

References

1. Taylor E, Wheeler J, Bowen J: Spacetime Physics: Introduction to Special Relativity, 2nd ed.American Journal of Physics. 1993; 61 (3). Publisher Full Text

Competing Interests

No competing interests were disclosed.

Reviewer Expertise

Observational cosmology; galaxy formation; large-scale structure; cosmic topology; inhomogeneous cosmology.

Respond to this report

Responses (1)

Author Response

04 Aug 2022

Hugh James, Retired, AWE, Aldermaston, Reading, RG7 4PR, UK

The paper defines a possible alternative space time (Dynamic space time, or DS) to that of Minkowski.
It does not assert the non- existence of bradyons and the existence of tachyons, this is based on a misconception of how DS is constructed (see below).
A Cartesian coordinate system is used throughout, and only inertial frames (IFs) are considered.
The alternative spacetime is based on the differences of how space and time are measured, and leaves aside any consideration of what they might “really” be.
Space coordinates are based on a ruler - a distribution of mass to which coordinates can be assigned. A clock output is an energy release which can be equated to a continuously changing time, and from which temporal coordinates can be constructed.
Minkowski converts clock outputs to temporal coordinates to obtain a non-Euclidean spacetime (Eqn.1).
DS partners momentum to the clock energy release. An observer in an IF (e.g. labelled A) can only see a clock changing and not the IFs momentum. He also cannot see a dimension in what can be hypothesised as the time direction (orthogonal to his x,y,z space). He exists in an ever-changing present - not at a constant time (and hence nothing to do with tachyons). From this changing present can be constructed an imaginary time dimension by using memories or recording devices. A temporal coordinate in this dimension can only be physically visited once, unlike the physically real spatial coordinates which can be visited many times.
As A cannot use his own momentum, he uses his observations of a different IF (B). The combination of A’s time and A’s observation of B’s energy and momentum gives A’s Euclidean DS spacetime (Eqn.3).
The observation of these phenomena indicates that both (energy release and momentum) are relative, i.e. A’s clock is relative to (A’s observations of B’s) clock and spatial motion, which means that for a single observer dt is not just a change in time.
The verbs “see” and “exist” refer to physically-based phenomena such as spatial coordinates or a changing time, and not to an imaginary time dimension.
The derivation of A’s spacetime leads to the hypothesis that in DS it is the clock co-located with the observer that provides the invariant, in contrast to Minkowski where it is the moving clock that is invariant.
DS confines any bradyon to its own time direction (OA, OB, OG in Fig.1) and actually located at A, B, G in that Figure, which is on the time-like hyperbola provided by Minkowski. Hence only along this hyperbola can the two spacetimes (Euclidean and non-Euclidean) intersect to agree on Lorentz transformations, the 4-momentum etc. Away from this they are different and Fig.2 shows how each IF is seen from within as 3 spatial dimensions and a changing time in which any dimension has rolled up to a point. From outside this IF the changing time is seen as a motion along a spatial dimension.
This leads to the hypothesis that the universe consists of 4 spatial dimensions which, in the simplest case, has bradyons travel radially outwards from a common centre. These bradyons form a surface which is orthogonal to the radial motion, and although this radial motion is at the speed of light, this is the rate of expansion of the universe. The observed bradyon motion is the component of this expansion along the surface when seen from a different IF (Figs 3 & 4), and so does not contravene the requirement that bradyons should travel slower than the speed of light. From within the IF this radial motion is experienced as the changing time.
This is not an FLRW model, but results from an FLRW model can be compared to those from DS (Figs 5 & 6, Table 1).
The use of only IFs and not general relativity in constructing this model is discussed in the Conclusions and Discussion of the paper.

View more View less

Competing Interests

There are no competing interests

Alongside their report, reviewers assign a status to the article:

Approved - the paper is scientifically sound in its current form and only minor, if any, improvements are suggested

Approved with reservations - A number of small changes, sometimes more significant revisions are required to address specific details and improve the papers academic merit.

Not approved - fundamental flaws in the paper seriously undermine the findings and conclusions

[1] 1. Peebles PJE, Ratra B: The cosmological constant and dark energy. Rev Mod Phys. 2003; 75: 559–606. Publisher Full Text

[2] 2. Beris AN, Giacomin AJ: Everything flows. Appl Rheol. 2014; 24(5): 1–13. Publisher Full Text

[3] 3. Earman J, Mosterin J: A critical look at inflationary cosmology. Philos Sci. 1999; 66(1): 1–49. Publisher Full Text

[4] 4. Suzuki N, Rubin D, Lidman C, et al.: The Hubble space telescope cluster supernova survey. V. Improving the dark energy constraints above z > 1 and building an early-type-hosted supernova sample. Astron J. 2012; 746(1): 85. Publisher Full Text

[5] 5. Perlmutter S, Aldering G, Goldhaber G, et al.: Measurements of Ω and Λ from 42 high-redshift supernovae. Astron J. 1999; 517(2): 565–586. Publisher Full Text

[6] 6. Riess AG, Filippenko AV, Challis P, et al.: Observational evidence from supernovae for an accelerating universe and a cosmological constant. Astron J. 1998; 116(3): 1009–1038. Publisher Full Text

[7] 7. Rashki M, Fathi M, Mostaghel B, et al.: Interacting dark side of universe through generalized uncertainty principle. arXiv: 1901.05766v2, 2019. Publisher Full Text

[8] 8. Rostami T, Jalalzadeh S: Why the measured cosmological constant is small. arXiv: 1510.02068v1, 2015. Publisher Full Text

[9] 9. Planck Collaboration, Ade PAR, Aghanim N, et al.: Planck 2013 results. I. Overview of products and scientific results. Astron Astrophys. 2014; 571: 48. Publisher Full Text

[10] 10. Di Valentino E, Mena O, Pan S, et al.: In the realm of the Hubble tension—a review of solutions. Class Quantum Grav. 2021; 38(15): 153001. Publisher Full Text

[11] 11. Farooq O, Madiyar FR, Crandall S, et al.: Hubble parameter measurement constraints on the redshift of the deceleration-acceleration transition, dynamical dark energy, and space curvature. arXiv: 1607.03537v2give, 2016. Publisher Full Text

Accounting for the expansion of the universe using an energy/momentum model to construct the space-time metric

Abstract

Background

Methods

Results

Conclusions

Keywords

Revised Amendments from Version 4

Introduction

The basis of the dynamic theory in Special Relativity (SR)

Possible grounds for pursuing alternative coordinate systems

The intersection of the standard and dynamic theories

Table 1. Dynamic Lorentz transforms from the viewpoints of A and B.

Table 2. Standard Lorentz transforms derived from Equation (7) and Table 1.

Figure 1a. A’s view of a quadrant of the Minkowski space-time.

Figure 1b. Comparison of the Dynamic and Standard coordinates in complete Minkowski space-time.

Figure 2. The dynamic view of inertial frames.

Similarities and differences between the theories

Figure 3. Simple dynamic model of the current state of the universe.

Cosmology

The standard model and its problems

The simple dynamic model

Figure 4. Simple dynamic model of the evolution of the universe.

The quantitative dynamic model

Comparison of the predictions of the dynamic and coordinate theories

Figure 5. The comparison of the standard and dynamic models of the universe’s evolution.

Figure 6. The Hubble “tension”.

Figure 6a. The Hubble “tension” plotted in terms of redshift (z).

Table 3. Values of za from both theories and observations.

Figure 7. Comparison of standard theory (Equation 29) with the dynamic curve (Equation 30).

Discussion and conclusions

Data

Author endorsement

Acknowledgements

Footnotes

References

Comments on this article Comments (0)

Open Peer Review

Comments on this article Comments (0)

Open Peer Review

Reviewer Status

Reviewer Reports

Comments on this article

Browse by related subjects

Competing Interests Policy

Stay Updated

Table 3. Values of z_a from both theories and observations.