Computational Study Protocol: Leveraging Synthetic Data to Validate a Benchmark Study for Differential Abundance Tests for 16S Microbiome Sequencing Data

Background and rationale {6a}

Differential abundance (DA) analysis of metagenomic microbiome data has emerged as a pivotal tool in understanding the complex dynamics of microbial communities across various environments and host organisms.^3–5 Microbiome studies are crucial for identifying specific microorganisms that differ significantly in abundance between different conditions, such as health and disease states, different environmental conditions, or before and after a treatment. The insights we gain from analyzing the differential abundance of microorganisms are critical to understanding the role that microbial communities play in environmental adaptations, disease development and health of the host.⁶ Refining statistical methods for the identification of changes in microbial abundance is essential for understanding how these communities influence disease progression and other interactions with the host, which then enables new strategies for therapeutic interventions and diagnostic analyses.⁷

The statistical interpretation of microbiome data is notably challenged by its inherent sparsity and compositional nature. Sparsity refers to the disproportionate proportion of zeros in metagenomic sequencing data and requires tailored statistical methods,^8,9 e.g. to account for so-called structural zeros that originate from technical limitations rather than from real absence.¹⁰ Additionally, due to the compositional aspect of microbiome data regulation of highly abundant microbes can lead to biased quantification of low-abundant organisms.¹¹ Such bias might be erroneously interpreted as apparent regulation that is mainly due to the compositional character of the data. Such characteristics of microbiome data have a notable impact on the performance of common statistical approaches for DA analysis, delimits their applicability for microbiome data and poses challenges about the optimal selection of DA tests.

A number of benchmark studies have been conducted to evaluate the performance of DA tests in the analysis of microbiome data.^12–15 However, the results show a very heterogeneous picture and clear guidelines or rules for the appropriate selection of DA tests have yet to be established. In order to assess and contextualize the findings of those studies, additional benchmarking efforts using a rigorous methodology,^16,17 as well as further experimental and synthetic benchmark data sets are essential.

Synthetic data is frequently utilized to evaluate the performance of computational methods because for such simulated data the ‘correct’ or ‘true’ answer is known and can be used to assess whether a specific method can recover this known truth.¹⁶ Moreover, characteristics of the data can be changed to explore the relationship between data characteristics such as effect size, variability or sample size and the performance of the considered methods. Several simulation tools have been introduced for generating synthetic microbiome data.^18–23 They cover a broad range of functionality. For example, MB-GAN²² leverages generative adversarial networks to capture complex patterns and interactions present in the data, while metaSPARSim,¹⁸ sparseDOSSA2¹⁹ or nuMetaSim²⁴ employ different statistical models to generate microbiome data. Introducing a new simulation tool typically involves demonstrating its capacity to replicate key data characteristics. Nonetheless, an ongoing question persists regarding the feasibility of validating findings derived from experimental data when synthetic data, generated to embody the characteristics of the experimental data, is used in its place.

Here we refer to the recent high-impact benchmark study of Nearing et al.¹ in which the performance of a comprehensive set of 14 DA tests applied to 38 experimental 16S microbiome data sets was compared. This 16S microbiome sequencing data is used to study communities in various environments, here from human gut, soil, wastewater, freshwater, plastisphere, marine and built environments. The data sets are presented in a two group design for which DA tools are applied to identify variations in species abundances between the groups.

In this validation study we replicate the primary analysis conducted in the reference study by substituting the actual datasets with corresponding synthetic counterparts. The objective is to explore the validity of the main findings from the reference benchmark study when the analysis workflow is repeated with an independent implementation and with synthetic data, generated to recapitulate the characteristics of the original real data.

Objectives {7}

Aim 1: Synthetic data, simulated based on an experimental template, overall reflect main data characteristics.

Aim 2: Study results from Nearing et al. can be validated using synthetic data, simulated based on corresponding experimental data.

Trial design {8}

Aim 1: Exploratory comparative study

Aim 2: Confirmatory benchmark study

Summary Table

Study population/participants

In the context of our benchmark study, the study population is given by the experimental data sets from the reference study.¹

Study setting {9}

Where possible, the study is conducted analogously to the benchmark study conducted by Nearing et al.,¹ e.g. the same data and primary outcomes will be used.

All data sets as provided by Nearing et al.¹ will be included in the study. We employ two published simulation tools, metaSPARSim¹⁸ and sparseDOSSA2,¹⁹ which have been developed for simulating microbial abundance profiles as they are generated by 16s sequencing.

We also apply the same DA tests as in¹ and implementation in the R statistical programming language. In order to provide the most valuable results for the bioinformatics community, the latest versions of these implementations will be used.

Eligibility criteria {10}

Inclusion criteria

We will include the same experimental data sets and DA tests as in Ref. 1.

Exclusion criteria

There are no exclusion criteria for the data sets.

Who will take informed consent? {26a}

n/a: Data is publicly available, there is no need to obtain consent.

Additional consent provisions for collection and use of participant data and biological specimens {26b}

n/a: Data is publicly available, there is no need to obtain consent.

Explanation for the choice of comparators {6b}

For aim 1, the comparator are 43 data characteristics calculated from the 38 experimental data sets. These characteristics are chosen such that they provide a comprehensive description of count matrices and enabling unbiased comparison between experimental and synthetic data sets. They cover for example information about the sparsity in a data set, mean-variance trends of features (taxa), or effect sizes between groups of samples. Tables 4 and 5 provide a detailed summary of all data characteristic and how they are calculated.

For aim 2, 14 differential abundance (DA) tests are applied to the experimental data (ALDEx2, ANCOM-II, corncob, DESeq2, edgeR, LEfSe, limma voom (TMM), limma voom (TMMwsp), MaAsLin2, MaSsLin2 (rare), metagenomeSeq, t-test (rare), Wilcoxon test (CLR), Wilcoxon test (rare)), i.e. the outcomes (number of significant features) calculated from the experimental data sets will serve as comparator. As in Ref. 1, we analyzed unfiltered data as well as data filtered with respect to features with a sufficient number of non-zero counts.

Intervention description {11a}

The intervention consists of using synthetic data instead of experimental data.

For each of the 38 experimental data sets, synthetic data will be simulated. For the simulation two simulation tools (metaSPARSim¹⁸ and sparseDOSSA2¹⁹) will be used. Simulation parameters are calibrated using the experimental data, such that the simulated data reflect the experimental data template. Both simulation approaches offer such a calibration functionality. Multiple (N=10) data realizations will be generated for each experimental data template to assess the impact of different realizations of simulation noise and to test for significant differences between interventions and the comparator.

For aim 1, the data characteristics will be computed for each of the synthetic and experimental data sets. For aim 2, 14 DA tests will be applied to the synthetic data generated in aim1.

Criteria for discontinuing or modifying allocated interventions {11b}

For assessing the similarity of the synthetic data templates, we apply equivalence tests based on two one-sided t-tests as implemented in the TOSTER R-package with a 5% significance level. We use the SD of the respective values from all experimental data templates as lower and upper margins. Figure 1 illustrates the equivalence testing procedure for the proportion of zeros in the whole data set as an exemplary data characteristic. For equivalence testing, the combined null hypothesis that the tested values are below the lower margin or above the upper margin has to be rejected to conclude equivalence. This only occurs when the average data characteristic of synthetic data is inside both margins and not too close to those two bounds, i.e. the whole 95% CI interval of the estimated mean has to be between both margins.

Figure 1. Illustration of assessing similarity based on an equivalence test.

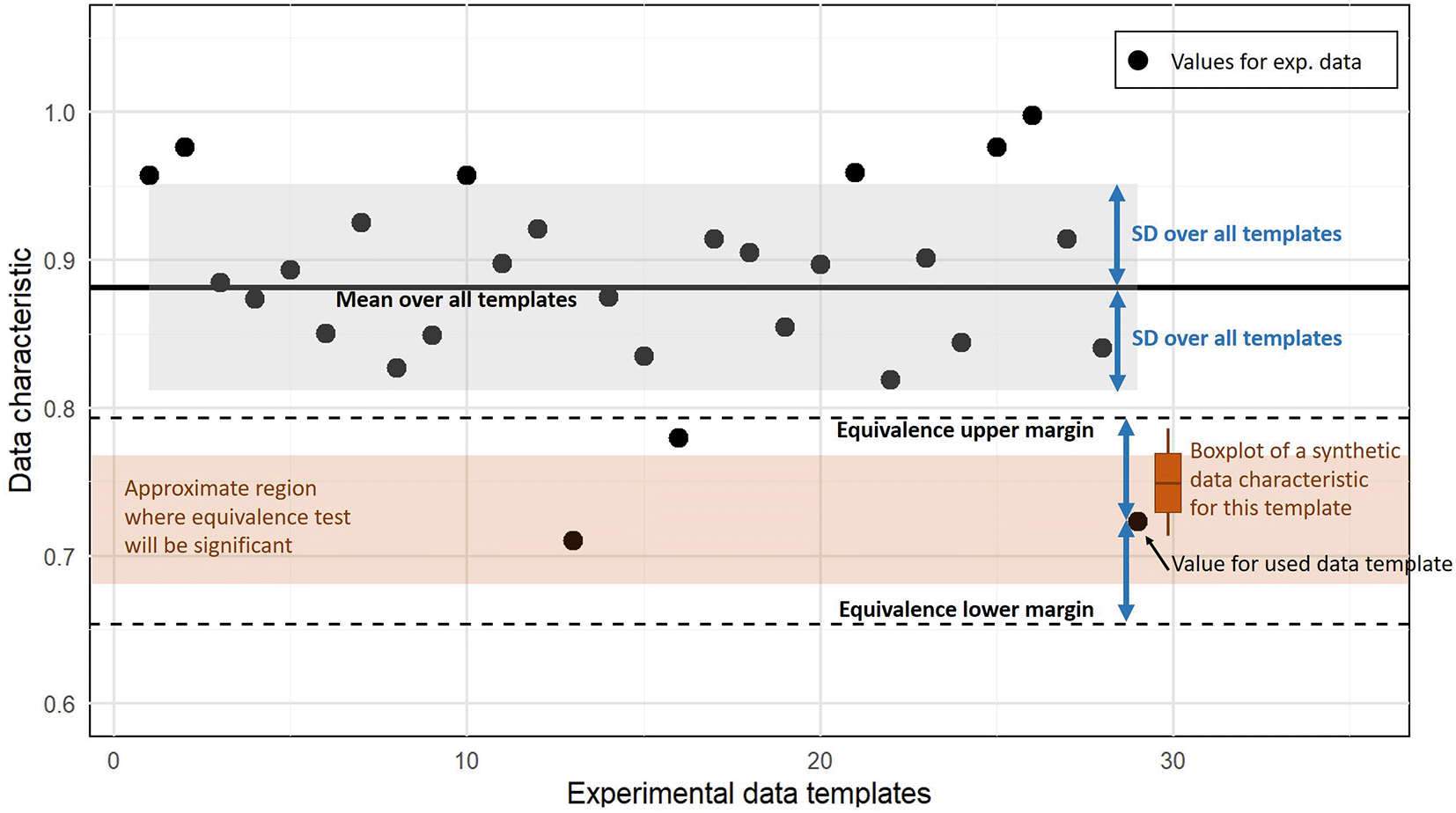
The black dots indicate a data characteristic computed for experimental data sets (here the proportion of zeros). Equivalence tests requires an interval that is considered as equivalent given by lower and upper margin bounds (dashed lines). We use the SD over all values from experimental templates to define these margins. The values computed from the synthetic data for a template are considered as equivalent if values below the lower margin and above the upper margin can be rejected according to the prespecified significance level. Depending on the variation of the characteristic for the synthetic data (here indicated by the boxplot), the average characteristic has to be inside a region (brown region) that is smaller than the interval between both margins.

Modification by adjusting the proportions of zeros and effect sizes

If equivalence tests fail, i.e. the synthetic data turns out to be partly unrealistic, we try to reduce the number of failed tests by adjusting two important characteristics, the proportion of zeros in the synthetic data sets, and the effect size, i.e., magnitude of differences between the two groups of samples.

Modifying the proportion of zeros will be performed by the following procedure for all synthetic data sets:

Since we calibrate the simulation tools for both groups separately, all simulation parameters controlling the count distribution will be different in both groups. Therefore, we anticipate that the differences between both groups might be overestimated. We therefore try to make the simulation more realistic by modifying the effect size by the following procedure for all synthetic data sets:

In addition to both individual modifications, we also apply both modification. For the following analyses, we then use the synthetic data where most data characteristics are equivalent.

Exclusion criteria

In our study, we use experimental data as templates for generating synthetic data which are then analyzed by DA methods. At both levels, generation of synthetic data and applying DA methods, we define exclusion or modification criteria in order to handle exceeding runtimes, computation errors, and unrealistic data simulation. Figure 2 shows an overview about these exclusion and modification steps.

Figure 2. Overview about the analysis workflow and the exclusion/modification strategy.

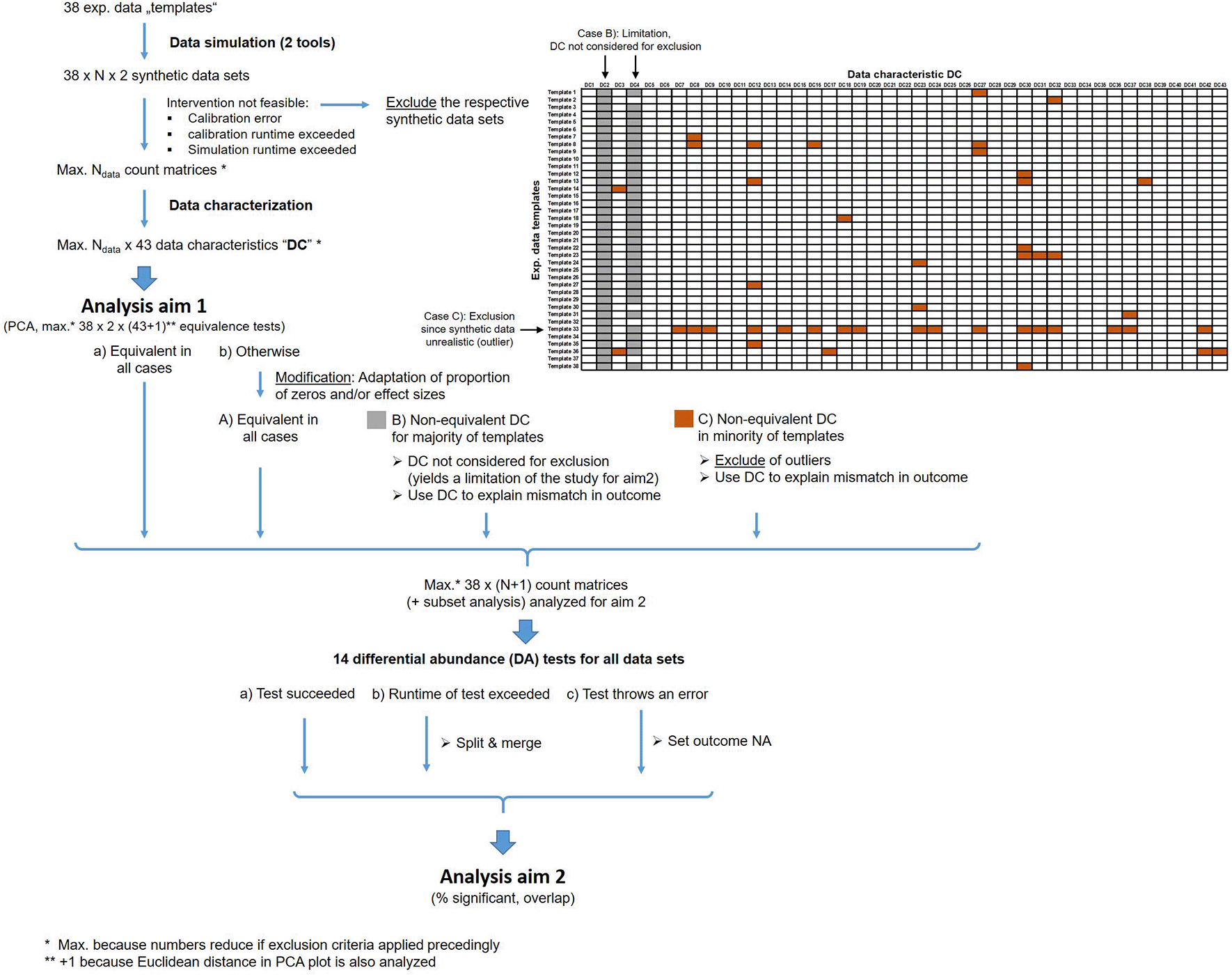
These criteria are applied to handle runtime issues, computation errors and unrealistic synthetic data.

Exclusion of simulation for a specific data template based on simulation performance

A simulation tool will be excluded for a specific data template, if calibration of the simulation parameters is not feasible. We define feasibility by the following criteria:

All computations in this study will be performed on a Linux Debian x86_64 compute server with 64 AMD EPYC 7452 32-Core Processor CPUs. Although, we will run parts of the analyses in parallel mode, the specified computation times refer to runtimes on a single core.

Exclusion of simulations for a specific data template based on deviating data properties

For aim 2, we exclude synthetic data sets that are not similar enough to the experimental data sets used as templates. The goal of the following exclusion criterion is to exclude synthetic data sets that are overall strongly dissimilar from the experimental data template, without being too stringent since the simulation tools cannot perfectly resemble all data characteristics and therefore a slight or medium amount of dissimilarity has to be accepted. In general, dissimilarities are exploited to study the impact of those characteristics by investigating the association of such deviations with dissimilarity in outcomes. For assessing similarity, the data characteristics described before and specified in detail in Table 5 are used.

We expect that a few data characteristics are very sensitive in discriminating experimental and synthetic data. To prevent loss of too many data sets, such characteristics (highlighted in gray in Figure 2) are only considered for the investigation of association between mismatch in outcome and mismatch in data characteristics but not for exclusion.

Unrealistic synthetic data will be excluded for the primary analyses of the study using the remaining data characteristics. We define the exclusion criteria due to dissimilarity from its template by one of the following criteria:

For evaluating the sensitivity with respect to exclusion, we perform an additional, secondary analysis on all synthetic data sets, regardless of similarity to the templates.

Modification of differential abundance (DA) tests

Inflated runtime

Data sets with a large number of features could lead to inflating runtimes for some statistical tests. If the runtime threshold for an individual test is exceeded for a specific data set, we split the data set, apply the test again on the subsets and afterwards merge the results. This split and merge procedure is repeated until the test runtime is below the threshold.

Here, we define the runtime threshold to be max. 1 hour per test. Then, in a worst case scenario, the 14 tests for the 10+1 data sets for each of the 38 template (5832 combinations) would need 244 days on a single core. Since we can conduct the tests on up to 64 cores, such a worst case scenario would still be manageable.

Test failure

If a DA test throws an error we omit the number of significant features and the overlap of significant features and report them as NA (not available) as it would occur in practice.

Strategies to improve adherence to interventions {11c}

n/a

Relevant concomitant care permitted or prohibited during the trial {11d}

n/a

Provisions for post-trial care {30}

n/a

Participant timeline {13}

n/a

Sample size {14}

The used 38 experimental data sets and DA tests are defined by the reference study that is being validated. In our study, we can therefore only choose the number of synthetic data sets per data template reasonably. Since there is no pilot study for the outcomes obtained from synthetic data that can be used for sample size calculations, and because a large number of outcomes are considered, the number of simulated data sets for one template was chosen to be a) feasible in terms of run time and b) should be large enough to enable valid conclusions. Based on both aspects, we decided to simulate N=10 synthetic data sets for each experimental data template, i.e., 380 synthetic data sets for each simulation tool.

For the one-sample equivalence tests with significance level 5% conducted for aim 1, N=10 synthetic data sets have a power of 89,75% to reject both the null hypothesis that the data characteristic is below -1SD and above +1SD and thereby favor the alternative hypothesis that the characteristic is equivalent to the reference value computed for the experimental data template. For this computation, we presumed that the expected mean (i.e. the bias of a characteristic in simulated data) is 0.5 SD, the standard deviation within synthetic data is 0.5 SD. Here, all specifications were made in units SD that refers to the standard deviation over all exp. templates. Assuming a smaller bias or a smaller variability for the synthetic data increases the expected power. These calculation has been conducted with Nquery version 8.7.2.0, equivalence test for one mean (MOE4-1).

For the proportions P of fulfilled hypothesis that were estimated for addressing most hypotheses in aim 2, 95% Clopper-Pearson confidence intervals (R-package DescTools) are calculated. As an example, n=380 independent samples leads to P = 0.026, 95%-CI = [0.013, 0.047] if for 10 out of 380 synthetic data sets the tested hypothesis is violated. This sample size is available for 20/27 hypotheses. However, it should be noted that such sample size considerations are limited by the fact that the data characteristics and results for synthetic data sets from a template are likely to be similar to each other and it is therefore not permissible to consider all samples as independent.

Recruitment {15}

n/a

Assignment of interventions: allocation

Sequence generation {16a}

The intervention and the comparator can be evaluated for all data sets and the order of the computations has no impact. Therefore, random allocation and sequence generation is not required.

Concealment mechanism {16b}

n/a

Implementation {16c}

n/a

Assignment of interventions: Blinding

Who will be blinded {17a}

No blinding procedure will be applied because we see no risk of bias by a non-blinded calculation of data characteristics and statistical tests.

Procedure for unblinding if needed {17b}

n/a: No blinding performed.

Plans for assessment and collection of outcomes {18a}

The analyses will be conducted by two experienced Statisticians/Bioinformaticians (E.K., C.K.) both with > 5yrs experience with differential abundance analyses. All statistical tests will adhere to the methodology outlined by Nearing et al.¹ To do so we chose the same configurations of the statistical methods as implemented in the code from Nearing et al.¹ for running the statistical tests, provided on Github (https://github.com/nearinj/Comparison_of_DA_microbiome_methods). This strategy ensures comparability between the outcomes of the reference study and our validation study.

Plans to promote participant retention and complete follow-up {18b}

n/a

Data management {19}

The 38 experimental data sets were downloaded from https://figshare.com/articles/dataset/16S_rRNA_Microbiome_Datasets/14531724 on February 9, 2024. There, Nearing et al.¹ made the data sets from their study available, therefore we incorporate the exact same data sets. We keep a local copy of this data in our Fredato research data management system https://nxc-fredato.imbi.uni-freiburg.de until 31.12.2030 and make it available if the original data is not available in the current version any more and if this does not violate legal, data protection, or copyright regulations. Generated data, analysis scripts, results and supplemental information to this study will also be stored in the Fredato research data management. In case of unexpected technical limitations, we will make data, analysis scripts and supplemental information available via https://figshare.com.

Confidentiality {27}

n/a: The experimental data is publicly available. The data generated in this project is not subject to data protection regulations.

Plans for collection, laboratory evaluation and storage of biological specimens for genetic or molecular analysis in this trial/future use {33}

n/a

Data monitoring committee {21a}

n/a: The data has already been collected and is publicly available.

Statistical methods for primary and secondary outcomes {20a}

Aim 1: For each data set (experimental and synthetic) a set of 43 data characteristics is calculated. All data characteristics are defined as a single number. These calculations are described in more detail in Table 5. As N=10 simulation realizations are generated, there will be 10 values for each data characteristic per experimental data template. For the primary outcome a PCA plot based on the scaled data characteristics is generated. Moreover, equivalence tests are applied to all 43 data characteristics as well as to the Euclidean distance in the two principal component coordinates as describe above (section “Interventions”). Based on these equivalence tests, we test a single hypothesis (equivalence of synthetic and experimental data) which is fulfilled in strict terms only when all equivalence tests are significant. We therefore do not have to control the probability of a single false positive test (i.e. the so-called family-wise error rate). Therefore, multiple testing aspects do not apply these tests.

Aim 2: All DA methods will be applied to experimental and synthetic data adhering to the methodology in Nearing et al.¹ as described in the methods section of the paper. Significant features will be identified using a 0.05 threshold for the multiple testing adjusted p-values (Benjamini-Hochberg).

For the primary outcome, it is determined how many tests jointly identify features to be significant for each data set. After visualization, the 13 hypotheses extracted from¹ will be investigated using the statistical analyses summarized in Box 1. Estimates of the target values and the respective 95% confidence intervals are used to validate the hypotheses because these values are easier to interpret than p-values and because the significance of the p-values is strongly determined by the number of cases.

For the secondary outcome, the number and proportion of significant features is extracted for each data set and test individually. After visualization, the 14 hypotheses extracted from¹ will be investigated using the statistical analyses summarized in Box 2.

Confidence intervals for the estimated proportions of cases where the hypothesis is fulfilled will be calculated as exact intervals, i.e. using Clopper-Pearson intervals (R-package DescTools). If the analyzed cases are statistically dependent, we compute hierarchical bootstrap confidence intervals by first drawing with replacement templates, and then synthetic data sets within each template.

These analyses are conducted for unfiltered data and for filtered data. As in,¹ filtered means that features found in fewer than 10% of samples are removed. Moreover, to analyze the sensitivity of our outcomes with respect to our exclusion criteria, filtered and unfiltered data are also analyzed without applying criteria that exclude non-realistic simulations.

In case we find different results for the simulated data for some hypotheses, we will analyze the association of the mismatch in the outcome with the mismatch of data characteristics to identify data characteristics that could be responsible for the disagreement. To ensure independence of the scales, we will perform these analyses after rank transformations. We will use univariate analyses (i.e. Spearman correlation) as well as a forward selection with a 5% cut-off criterion for p-values.

Interim analyses {21b}

n/a: There will be no interim analyses in this study.

Methods for additional analyses (e.g. subgroup analyses) {20b}

n/a: In this study there will be no subgroup analyses.

Methods in analysis to handle protocol non-adherence and any statistical methods to handle missing data {20c}

n/a: In this study there is no missing data.

Plans to give access to the full protocol, participant level-data and statistical code {31c}

Generated data, analysis scripts and supplemental information to this study will also be stored in the Fredato research data management. In case of unexpected technical limitations, we will make data, analysis scripts and supplemental information available via https://figshare.com.

Composition of the coordinating centre and trial steering committee {5d}

n/a

Composition of the data monitoring committee, its role and reporting structure {21a}

n/a

Adverse event reporting and harms {22}

n/a

Ancillary and post-trial care {30}

n/a

Frequency and plans for auditing trial conduct {23}

n/a

Plans for communicating important protocol amendments to relevant parties (e.g. trial participants, ethical committees) {25}

n/a