Aerodynamic Performance Enhancement of Crm Nacelle Under Transonic Flow: A Comprehensive Cfd-based Optimization Approach

J K Ajay Kumar; Sudheendra Prabhu K; A S Veerendra; Sudhir Shastry Y B; Srinivas G

doi:10.12688/f1000research.170106.1

Home Browse Aerodynamic Performance Enhancement of Crm Nacelle Under Transonic...

ALL Metrics

-

Views

Get PDF

Get XML

Export

▬

✚

Research Article

Aerodynamic Performance Enhancement of Crm Nacelle Under Transonic Flow: A Comprehensive Cfd-based Optimization Approach

[version 1; peer review: awaiting peer review]

J K Ajay Kumar¹, Sudheendra Prabhu K², A S Veerendra³, Sudhir Shastry Y B⁴, Srinivas G ⁵

J K Ajay Kumar¹, Sudheendra Prabhu K², [...] A S Veerendra³, Sudhir Shastry Y B⁴, Srinivas G ⁵

PUBLISHED 10 Nov 2025

Author details Author details

¹ Department of Aeronautical & Automobile Engineering, Manipal Academy of Higher Education, Manipal, Karnataka, 576104, India
² Department of Aeronautical & Automobile Engineering, Manipal Academy of Higher Education, Manipal, Karnataka, 576104, India
³ Department of Electrical & Electronics Engineering, Manipal Academy of Higher Education, Manipal, Karnataka, 576104, India
⁴ Department of Aerospace Engineering, Jain University Faculty of Engineering & Technology, Bengaluru, Karnataka, 560069, India
⁵ Department of Aeronautical & Automobile Engineering, Manipal Academy of Higher Education, Manipal, Karnataka, 576104, India

J K Ajay Kumar
Roles: Conceptualization, Data Curation

Sudheendra Prabhu K
Roles: Formal Analysis, Investigation

A S Veerendra
Roles: Methodology

Sudhir Shastry Y B
Roles: Resources, Software

Srinivas G
Roles: Supervision, Writing – Review & Editing

OPEN PEER REVIEW

REVIEWER STATUS AWAITING PEER REVIEW

This article is included in the Manipal Academy of Higher Education gateway.

Abstract

Background

The CRM nacelle is a benchmark model for both CFD validation and shock dominated flow interaction analysis in propulsion airframe configurations. However, accurate prediction of drag and lift remains challenging due to complex flow interaction near the nacelle surface.

Methods

This research investigates the aerodynamic performance of a CRM nacelle using the ANSYS 2023 Fluent tool with different numerical techniques like the grid independence test, different turbulence models, and different Mach number variations.

Results

At Mach 0.85, the nacelle with a fan and a 1.64 million grid size produced a C_d of 0.00245 with a 1.24% error. Similarly, out of six different models, the K-epsilon model produced the least validation error of 1.24%. Mach number variation from 0.8 to 1.3 Mach number shown a maximum C_d at 0.95 Mach followed by a decrement at 1.2 Mach. In the aerodynamic optimization, a core cone was added to the nacelle and further simulated at 0.82 Mach. Spalart-Allmara model with a 2.55 million grid size produced a C_l value of 0.01098 with an 8.54% validation error. The cone angles were varied from 15.7° by ±0.5° steps.

Conclusions

The optimized nacelle at a 13.7°cone angle showed an improved C_l of 0.011035 compared to the baseline model. The novelty of this research lies in testing the CRM nacelle under transonic flow conditions from 0.8 to 1.3 Mach and optimizing the nacelle aerodynamic performance using different numerical techniques. This research paper further helps the researchers in nacelle aerodynamics by optimizing the nacelle geometry for aerodynamic lift enhancement.

Keywords

Aerodynamics, CFD, Nacelle, CRM, Optimization

Corresponding author: Srinivas G

Competing interests: No competing interests were disclosed.

Grant information: The author(s) declared that no grants were involved in supporting this work.

Copyright: © 2025 Kumar JKA et al. This is an open access article distributed under the terms of the Creative Commons Attribution License, which permits unrestricted use, distribution, and reproduction in any medium, provided the original work is properly cited.

How to cite: Kumar JKA, K SP, Veerendra AS et al. Aerodynamic Performance Enhancement of Crm Nacelle Under Transonic Flow: A Comprehensive Cfd-based Optimization Approach [version 1; peer review: awaiting peer review]. F1000Research 2025, 14:1236 (https://doi.org/10.12688/f1000research.170106.1) First published: 10 Nov 2025, 14:1236 (https://doi.org/10.12688/f1000research.170106.1) Latest published: 10 Nov 2025, 14:1236 (https://doi.org/10.12688/f1000research.170106.1)

1. Introduction

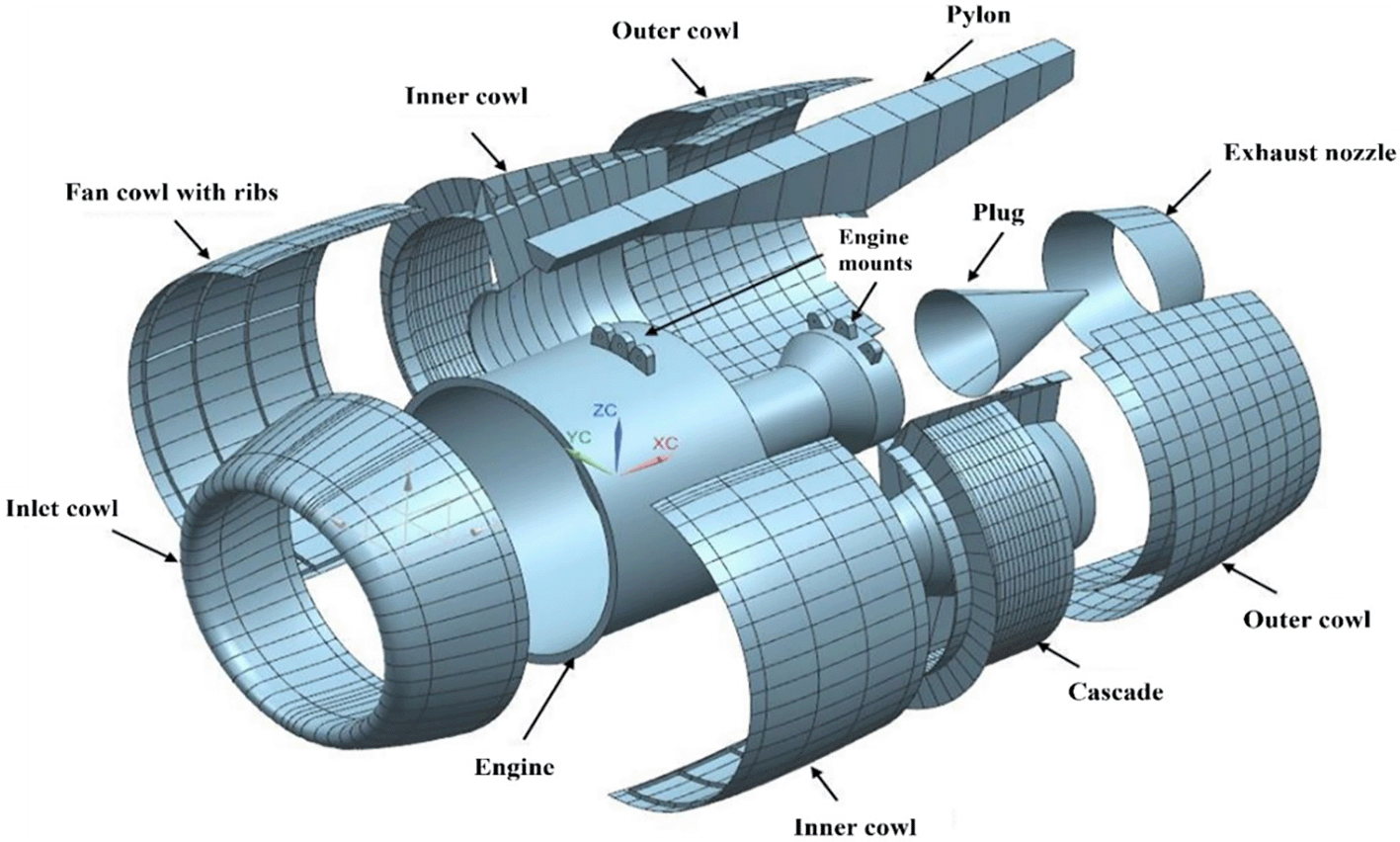
The aircraft nacelle is an integral component that houses the propulsion system and contributes significantly to the aerodynamic efficiency.¹ It includes essential subcomponents such as an inlet fan, core cowl, and exhaust duct.² The main parts of an aircraft nacelle are shown in Figure 1. The aircraft engine components manage airflow and minimize drag across various flight regimes.² Nacelle optimization³ using CFD and turbulence models helps to improve aircraft performance under transonic conditions.² Modern nacelles are integrated with acoustic liners to meet noise regulations.⁴ The nacelle shape and its mounting position concerning the aircraft wing significantly affect the engine-airframe integrations.⁵ As engine technologies evolve, nacelle design remains a key focus for aircraft performance and efficiency.

Figure 1. Main parts of an aircraft nacelle.²

Recent advancements in the aerodynamic design of the CRM nacelle have primarily focused on reducing the drag and enhancing the lift. The nacelle drag can be reduced by adopting Chinese geometries,⁶ compact nacelle configurations,^7,8 and pylon-nacelle integration.⁹ Experimental and numerical studies have demonstrated that optimized nacelle shaping can mitigate adverse vortex integrations at high angles of attack. Implementing advanced turbulence models⁹ has further improved the predictive accuracy of flow behaviour, enabling more efficient aerodynamic configurations for modern high-lift aircraft. Enhanced aerodynamic performance can be achieved by utilizing a high bypass ration nacelle and noise reduction can be achieved by using a short nacelle. Enhanced aerodynamic performance can be achieved by utilizing a high bypass ratio nacelle¹⁰ and noise reduction can be achieved by using a short nacelle.¹¹

The present research focuses on the transonic flow analysis of the CRM nacelle using the ANSYS Fluent tool. Initially, the nacelle with a fan and without a core-cone assembly was analysed and validated using various numerical techniques, including grid tests, different turbulence models, and Mach number variation from 0.8 to 1.3. Additionally, an optimized configuration was developed by assembling a core-cone structure at the fan exit of the CRM nacelle. This optimized nacelle was then analysed using various numerical techniques at 0.82 Mach. The subsequent sections present the detailed optimization procedure and the corresponding nacelle analysis results.

2. Literature review

This section explores experimental, numerical, and theoretical studies related to aircraft nacelles under various flight conditions. Additionally, this section also focuses on understanding flow behaviour, aerodynamic effects, and design strategies for better nacelle performance.

2.1 Experimental research studies on aircraft engine nacelle

Researchers performing the wind tunnel experimental studies of wing nacelle for the configurations show the importance of wind tunnel testing. Experimental wind tunnel testing is crucial in the comprehension of intricate aerodynamic processes, particularly in high and UHBR engines. Important conclusions are shock-induced separation and buffet on the lower surface of the wing caused by nacelle mounting,¹² with buffet peaks at a Strouhal number of approximately 0.4. Thrust reduction by spinning fan blades demonstrated a small decrease in landing distances,¹³ and chine design with Kriging models enhanced lift performance.¹⁴ Special wind tunnel rigs imaged windmilling phenomena and boundary layer separation via schlieren and infrared imaging.¹⁵ Utilizing imaging techniques in the experiments indicated drag savings ranging from 5 to 19% through optimized lip shapes and blowing ratios.¹⁶ Surface treatments such as superhydrophobic films minimized water retention but ice accretion was still geometry dependent.¹⁷ Engine power settings had a direct impact on lift and pressure distribution at low speeds,¹⁸ and CFD verification campaigns substantiated primary flow phenomena in HWB configurations.¹⁹ Dynamics of separation and wake influences were examined under crosswinds and windmilling conditions using clean and vaned nacelle models,^20,21 while PIV measurements recorded detailed chine-induced vortices.^22,23 Research on aircraft engine bypass geometry^24,25 and separation hysteresis²⁶ further highlighted the vulnerability of nacelle performance to design and flow conditions.

2.2 Numerical research studies on aircraft engine nacelle

Numerical studies on wing nacelle aerodynamics have fast progressed due to the use of CFD, optimization algorithms, and machine learning tools. The typical workflow starts with generating geometry, creating meshes, and performing RANS-based CFD simulations to gather flow-field data. This data is processed and used to train DNNs, which provide faster and accurate predictions of aerodynamic performance. The new approach cuts CPU time by a hefty margin.²⁷ Designers still prefer sleek, compact nacelles and typically rely on CST for quick curves. Fang et al.²⁸ showed that a RANS-CFD-based loop delivers drag and Mach estimates within a few counts. A crosswind-aware intake, run with fan-intake coupling and surrogate-based optimization, slashed DC60 distortion by 29%. That gain beat rivals that tackled only the intake.²⁹ Tests on ultra-high bypass nacelles proved mounting position matters, with peak net thrust near x/c = -0.1.³⁰ A multi-objective sweep of scarfed and drooped designs, fed by Kriging and an evolutionary routine, balanced drag, noise, and weight.³¹ Finally, NLF holding roughly 30% chordwise laminarity trimmed overall drag by 13.3%.³² Inverse pressure gradient designs allowed for shock-free, stable flow even under off-design conditions.³³ Meanwhile, ASBRO strategies improved robustness and cut computational costs by nearly 60%.³⁴ Additional studies investigated icing effects using 3D simulation methods,³⁵ the aeroelastic response of powered engine mounts³⁶ and reducing aerodynamic interference through NURBS-based free-form deformation combined with PSO.³⁷ Body-force models provided useful tools for predicting inlet distortion without needing detailed fan geometry.³⁸ Ground vortex dynamics under crosswinds were experimentally mapped in four unsteady phases, revealing their significant effect on inlet flow.³⁹ Finally, high-incidence lip separation, which is a major source of distortion, was accurately modeled using ANSYS CFX.⁴⁰ Powered intakes were shown to reduce flow distortion, improving stability and performance.⁴¹

2.3 Theoretical research studies on aircraft engine nacelle

Fine-tuning wing-nacelle setups in the transonic zone calls for a careful trade-off among gains, run time, and design handle-ability. To speedup things, newer studies mix quick-look surrogates, machine-learning tricks, and flexible shape templates. Researchers^42,43 show solid results using feed-forward nets to forecast drag and flow, cutting CPU time by almost 75% while keeping errors near 2.8% and hitting 98% on class tasks. Research⁴³ pairs that with a CNN and Sobel edge map to sharpen shock-wave spotting. Research⁴⁴ leans on a GAN loop and beats the old toolbox, turning out cleaner pressure fields and sleeker nacelle outlines. Research⁴⁵ merge CST batched with a genetic code and Kriging to tune non-axisymmetric bodies inside RANS. Meanwhile, studies like^46,47 run Gaussian Processes on a joint Pareto map, trading lift, drag, and noise via scarf angle, and trim the variable list upfront. NSGA-II optimization in⁴⁸ and advanced response surfaces in⁴⁹ enhance convergence and precision for gradient-sensitive objectives. ANN-based surrogate models in⁵⁰ and multi-fidelity ANN/Euler-RANS frameworks in⁵¹ achieve up to 92% computational saving while resolving intricate flow features. Off-design robustness including windmilling is explored in⁵² with regression/classification models. Optimization of the combustion chamber in⁵³ employs a POD-Hierarchical-Kriging approach with RMS errors less than 0.2% and good Pareto trade-offs. Parametric geometry tools in⁵⁴ illustrate CST's value for quick production of feasible nacelle designs. POD-based 3D inlet optimization under high-angle conditions in⁵⁵ captures realistic constraints. Finally,⁵⁶ combines Euler/Navier–Stokes solvers with inverse design techniques to reduce installation effects for complicated aircraft configurations.

2.4 Summary of the literature review

Experimental studies highlight the value of wind tunnel testing to understand complex phenomena like shock-induced separation, buffet, and windmilling. Techniques such as schlieren imaging, infrared thermography, and PIV showed chine vortices, boundary layer behaviour, and drag patterns. Optimized nacelle lips and active blowing achieved drag reductions of up to 19%.¹⁶ Engine power settings and surface treatments influenced lift and icing behaviour. Studies on crosswind and bypass flow noted how sensitive nacelle design is to mounting and flow conditions. Numerical research has advanced with RANS-based CFD and data-driven models. Machine learning, deep neural networks, and surrogate-based optimization greatly reduced computation time while maintaining precise aerodynamic predictions. Parametric sweeps looked at intake distortion, mounting effects, and laminar-flow designs, with some setups achieving over 13.3% drag reduction.³² Shape optimization with tools like CST, NURBS deformation, and inverse design further improved performance across drag, noise, and weight trade-offs. Ground vortex and icing simulations made intake behaviour under tough conditions more realistic. A theoretical approach combined AI-driven models with flexible geometry control for quick and solid optimization. Neural networks, GANs, and Gaussian processes predicted complex flow features with little error and computational effort. Multi-objective optimization frameworks using genetic algorithms and Kriging supported balanced trade-offs. Multi-fidelity approaches brought together CFD and surrogate models for efficient exploration of the design space.

2.5 Quantitative analysis

Table 1 presents a qualitative analysis of data from experimental, numerical, and theoretical studies focusing on nacelle aerodynamics under various flow conditions. Key model configurations, flow parameters, and control factors are listed to support aerodynamic evaluation of the aircraft nacelle. The experimental quantitative analysis explores aerodynamic behaviour using physical testing of nacelles, hybrid wings, and airfoil models, focusing on parameters like Reynolds number, Mach number, and AoA. The numerical quantitative analysis highlights CFD simulations with models such as DLR, RAE2822, and NACA airfoils incorporating advanced turbulence modeling and surrogate optimization to evaluate aerodynamic performance. The theoretical literature focus is on analysing different parameters and predicting outcomes using simpler models, Kriging surfaces, and Pareto optimization, which provide important information about how airflow behaves in perfect conditions.

Table 1. Quantitative analysis.

Experimental qualitative analysis
SL.No	Author’s Name	Model Type	Re	Mach No	Miscellaneous
¹²	Spinner Sebastian et al.	XRF1	6.6 × 10⁶	0.84	α = −4
¹³	Loginov et al.	TJTE nacelle	7.25 × 10⁵
¹⁴	Masahiro et al.	Kriging surro-gate			C_Lmax = 3.02
¹⁵	Kshitij Sabnis et al.		1.2 × 10⁶	0.65	hb/Δy = 0.159, 0.194 & 0.227
¹⁶	Lee Chern Khai et al.		3.5 × 10⁵		P = 60 Pa
¹⁷	Filomena Piscitelli et al.	M28 PZL			Ra = 1.6 μm ± 0.3
¹⁸	Silva et al.		3.05 × 10⁵		MFR = 0.75
¹⁹	Michael J et al.	Boeing 0009GM HWB
²⁰	Kshitij Sabnis et al.			1.2
²¹	Luca Boscagli et al.		1.25 × 10⁵	0.65	Mise, pre−sw ≈ 1.6
²²	Mehti Koklu et al.	CRM-HL			α = 19
²³	Hiroyuki Kato et al.	JAXA LWT1	2.2 × 10⁶	0.84
²⁴	Yong Han Yeong et al.	NASA F-15
²⁵	Ruben Hortensius et al.
²⁶	C. A. Hall et al.		2 × 10⁷	0.5
Numerical qualitative analysis
SL.No	Author’s Name	Model Type	Re	Mach No	MFCR	Miscellaneous
²⁷	GuochengTao et al.	RAE2822		0.85	0.7
²⁸	Matthew Robinson et al.			0.85	0.7	L_nac/D_fan = 0.6
²⁹	Xiaobin Yang et al.	DC60
³⁰	Andrea Magrini et al.			0.85		C_l = 0.50
³¹	Fernando Tejero et al.			0.785
³²	Chongyang YAN et al.	DLR	1.0 × 10⁶	0.85		C_m = 0.70
³³	Heng ZHANG et al.	NACA0036	3.5 × 10⁷	0.85
³⁴	Yuan YAO et al.	NLF nacelle
³⁵	Qian Yang et al.	NACA 0012
³⁶	Vladyslav Rozov et al.			0.85		C_l = 0.5
³⁷	Li Jing et al.	DLR-F6	3.0 × 10⁶	0.75		C_l = 0.50
³⁸	Yinbo Mao et al.
³⁹	Jingjing Chen et al.	DLR-F6				h/D_h = 0.25
⁴⁰	Stefan Kennedy et al.	CF-34-3A
⁴¹	M. Carnevale et al.			0.25		Δα 5
Theoretical qualitative analysis
SL.No	Author’s Name	Model Type	Re	Mach No	MFCR	Miscellaneous
⁴²	Fernando Tejero et al.			0.78		C_l = 0.82
⁴³	Sanjeeth Sureshbabu et al.		5 × 10⁵	0.85	0.7	MSE = 0.0027
⁴⁴	Cong Wangm et al.		1.0 × 10⁶	0.80
⁴⁵	Xiaoming Fang et al.		5 × 10⁵	0.80	0.7500	C_d = 0.003414
⁴⁶	Wenbin Song et al.
⁴⁷	Fernado et al.			0.80		L/D = 34.5
⁴⁸	Matthew Robinson et al.	DTLZ2		0.95	0.7	BPR = 14.3
⁴⁹	Alexander Heidebrecht et al.			0.8.	0.75
⁴⁵	Xiaoming Fang et al.		5 × 10⁵	0.80	0.75
⁵⁰	F. Tejero et al.			0.84	0.70	C_l = 0.82
⁵²	Avery Swarthout et al.			0.85	0.7
⁵¹	Francisco et al.		11.7 × 10⁶	0.84
⁵³	Shuhong Tong et al.
⁵⁴	Robert Christie et al.		40 × 10⁶	0.85
⁵⁵	Shuyue Wang et al.
⁵⁶	Roland Wilhelm et al.	DLR TAU	3 × 10⁶	0.75		α = 0.50

2.6 Research gaps

After completing the systematic literature review of experimental, numerical, and theoretical research studies, it is observed that aerodynamic flow parameters need to be improved using different numerical techniques. Transonic flow typically ranges between Mach 0.8 and 1.3, but recent studies have only focused on the Mach number up to 0.85. Currently, no much literature explores flow parameters at Mach 1.3 for transport aircraft nacelle, and there are very few experimental studies involving transport aircraft nacelle with this Mach range. A limited research has been identified at transonic flow regime especially from Mach 0.8 to 1.3. The numerical studies on transport aircraft nacelle usually includes one or two turbulence models and address one or two aerodynamic parameters such as pressure, temperature, density, Mach distribution, velocity distribution, or turbulence. Therefore, this research includes the study of flow characteristics of a 3D nacelle using various numerical techniques, including different turbulence models, boundary condition variations, grid independence tests, etc. In this research the cone-core assembly was added to the nacelle and aerodynamic analysis is performed by varying the cone-core angle.

2.7 Research objectives

The objectives of the research are:

• To analyse the aerodynamic flow characteristics of a CRM nacelle and validate the results with available findings.
• To investigate the aerodynamic performance of a CRM under transonic flow conditions from 0.8 to 1.3 Mach numbers.
• To perform aerodynamic optimization of a CRM wing to enhance lift and evaluate the optimized nacelle at 0.82 Mach number.

3. Methodology

The research starts with an experimental, numerical, and theoretical literature review. The literature review was summarized, and the research gap was identified. The methodology includes modeling of the CRM nacelle, meshing, and flow analysis. Five different grid sizes were tested, and six different turbulence models were analysed. The baseline nacelle model was only with fans, and no core was added. While comparing with the reference data,⁵⁷ the K-omega model produced the least error. For the same K-omega model, the Mach number was varied from 0.8 to 1.3. In the nacelle optimization, the nacelle core was assembled, meshed, and validated with the reference data.⁵⁸ For the best grid size, six different turbulence models were tested, and the Spalart-Allmaras model produced the least error. The cone angle was varied to enhance the lift, and optimized simulation was performed at 0.82 Mach. The methodology flow chart of the Nacelle CFD analysis can be seen from Figure 2.

Figure 2. Research methodology flowchart.

3.1 Baseline analysis

3.1.1 Nacelle baseline modeling

For the CFD analysis, the nacelle model was taken from the NASA 6^th drag prediction workshop.⁵⁹ The nacelle model was converted from a sheet body into a solid body using the ANSYS 2023 R2 Spaceclaim tool. The continuity and integrity of the model were cross-checked to prevent issues during the CFD analysis.

The major parts of the nacelle are shown in Figure 3 and the geometry specifications of the nacelle is shown in Table 2. The total length of the nacelle is 6 m, the inlet diameter of the nacelle is 3.2 m, and the exhaust diameter of the nacelle is found to be 2.7 m. Additionally, a cylindrical far field was created, and the dimensions of both the nacelle and far fields are shown in Figure 2 and Figure 4. The detailed engine specifications⁶⁰ of the CRM nacelle are shown in the Table 2.

Figure 3. CRM nacelle dimensions.

Table 2. Geometry specifications and reference quantities of the nacelle.

CRM nacelle reference quantities⁶⁰
Altitude	35,000 ft
MFCR	0.75
F_N	55,700 N
Fan nozzle pressure ratio (FNPR)	2.7
Fan pressure ratio (FPR)	1.67
Overall pressure ratio	50
Engine pitch angle	1.75^°
CRM nacelle geometry specification
Area	383.86 m²
Inlet diameter	3.2 m
Exit diameter	2.7 m
Nacelle length	6 m
Pitch angle	1.75 degree

Figure 4. Cylindrical farfield dimensions.

3.1.2 Nacelle and farfield meshing

After creating a nacelle model, the nacelle and farfield model were imported to create mesh. The ANSYS meshing module was used to mesh the model. Before meshing, an additional body of influence was created, as shown in Figure 5, which acts like a refined far field. A general unstructured tetrahedral mesh was chosen with a higher y⁺ value, and a 15-boundary layer was created around the nacelle surface. The global mesh size was fixed to 15m with high smoothness and a 1.2 growth rate. Th pre-inflation algorithm and a 5^° curvature angle resulted in a minimum orthogonal quality of 0.1 and a maximum skewness of 0.9. The mesh size for the nacelle cowl and fan faces was generated using uniform face sizing of 0.1m, while the nacelle lip region was refined with face sizing ranging from 0.045m to 0.085m. The mesh over a nacelle and farfield surfaces can be seen from the Figure 5 and the detailed mesh settings of CRM nacelle are given in the Table 3.

Figure 5. Mesh representation of wing model along with farfield and inflation layer.

Table 3. Detailed mesh settings for aerodynamic analysis of the nacelle.

Geometry	Selection type	Mesh details
Domain	Body	15 m
Nacelle cowl and fan faces	Face Sizing	0.1 m
Nacelle lip region	Face Sizing	0.045 m to 0.085 m
Wing edges	Edge Sizing	300 number of divisions
Wing Surface	First Layer Thickness	0.001 m
	Number of Layers	15
	Growth Rate	1.2

A cylindrical farfield allows a linear transition of mesh elements from coarse at the boundary to finer near the wing surface. It reduces the distortion and ensures symmetry, which helps in handling the boundary conditions. Additionally, a dome-shaped far field improves the convergence and accuracy of the CFD analysis.

3.1.3 Numerical modeling

The Fluent software solves the following Navier-Stokes equations, composed of continuity equation and momentum equations as given below (1) – (5).⁶¹

(1)

Continuity equation : \frac{∂u}{∂x} + \frac{∂v}{∂y} + \frac{∂w}{∂z} = 0

(2)

X - Momentum equation : ρ \frac{Du}{Dt} = - \frac{∂p}{\partial x} + μ (\frac{\partial^{2} u}{\partial x^{2}} + \frac{\partial^{2} u}{\partial y^{2}} + \frac{\partial^{2} u}{\partial z^{2}}) + ρ . f_{x}

(3)

Y - Momentum equation : ρ \frac{Dv}{Dt} = - \frac{∂p}{\partial y} + μ (\frac{\partial^{2} v}{\partial x^{2}} + \frac{\partial^{2} v}{\partial y^{2}} + \frac{\partial^{2} v}{\partial z^{2}}) + ρ . f_{y}

(4)

Z - Momentum equation : ρ \frac{Dw}{Dt} = - \frac{∂p}{\partial z} + μ (\frac{\partial^{2} w}{\partial x^{2}} + \frac{\partial^{2} w}{\partial y^{2}} + \frac{\partial^{2} w}{\partial z^{2}}) + ρ . f_{z}

(5)

Reynolds equation : R_{e} = \frac{ρ . v . L}{μ}

The Reynolds number is a unitless parameter that determines the nature of fluid motion, indicating whether the fluid exhibits laminar or turbulent behaviour. Equation (5) gives the expression for the Reynolds number, where ρ denotes fluid density (kg/m³), V is velocity (m/s), and μ refers to the dynamic viscosity of the fluid (kg/ms).

3.1.4 Boundary conditions for the wing analysis

The CFD setup has a cylindrical farfield with pressure-far-field boundary conditions, a symmetry plane, and a no-slip wall on the aircraft surface. Figure 6 and Table 4 the represents detailed boundary conditions are used in the aerodynamic analysis of the nacelle. Before establishing the boundary conditions, the International Standard Atmosphere (ISA) table⁶² was used to determine the following important atmospheric parameters, such as temperature (218.81 K), density (0.3796 kg/m³), and pressure (23842 Pa) of air at 35,000 ft altitude.⁵⁷

Figure 6. Boundary conditions for the nacelle aerodynamic analysis.

Table 4. Boundary conditions used in the nacelle aerodynamic analysis.

Reference boundary conditions⁵⁷			Baseline boundary conditions
Type	Named selection	Values	Type	Named selection	Values
Pressure-Farfield	Farfield	23842 Pa with 218.81 K	Pressure-Farfield	Farfield	23842 Pa with 218.81 K
Wall	Nacelle	No slip with 218.81 K	Wall	Nacelle	No slip with 218.81 K
Pressure-Inlet	Fan inlet	14396.238 Pa with 250 K	Pressure-Inlet	Fan inlet	14396.238 Pa with 250 K
Pressure-Inlet	Fan inlet	14396.238 Pa with 250 K	Pressure-Outlet	Engine exit	0 Pa with 218.81 K

The total pressure for the analysis was calculated by using the Equation 6.⁶³ Similarly, the total temperature at the inlet of the engine was calculated using the Equation 7.⁶³ By solving both Equation 1 and Equation 2, total pressure and temperature of 38238 Pa and 250K are obtained.

(6)

P_{\infty} = p_{\infty} {(1 + \frac{γ - 1}{2} M^{2})}^{\frac{γ - 1}{γ}}

(7)

T_{\infty} = t_{\infty} (1 + \frac{γ - 1}{2} M^{2})

Where P_∞ is the total pressure in P_a, p_∞ is the static pressure in P_a, M is the Mach number, γ is the specific heat ratio, T_∞ is the total temperature in K, and t_∞ is the static temperature in K. In the boundary condition, the gauge pressure is applied at the fan inlet; to calculate the gauge pressure, Equation 8⁵⁷ is used. By solving the corresponding equation, a gauge pressure of 14396.238 Pa is obtained.

(8)

P_{gauge} = (PR \times P_{\infty}) - p_{\infty}

Where P_gauge is the gauge pressure at the inlet and PR is the blowing pressure ratio.

Additionally, the SST k-epsilon model accurately captures the boundary layer effects and shock separations in transonic flows. The material property for the air was selected as the ideal gas with Sutherland viscosity, allowing the solver to accurately calculate the density of the air based on pressure and temperature input.

The nacelle surface area was taken from the reference paper,⁵⁷ and the chord length of the wing was taken as the reference length. The report definition was defined to calculate C_d at the wing surface. In this analysis, implicit method with AUSM flux type scheme was utilized. Additionally, Second-order equation blending was selected using transonic solution steering, and the “Least square based cell” scheme was used to calculate all gradients. The solution convergence was monitored until the solution reached the convergence threshold of 10⁻⁶ (i.e. 0.000001). Hybrid initialization was used in the analysis because it combines all the initialization techniques to provide accurate and effective starting point for the simulation. Since the analysis is focused on transonic flow over a wing, it is essential to opt for hybrid initialization to achieve faster convergence and improved solution quality. After initialization, the solution was iterated for 1000 iterations and due to good mesh quality, the solution converged within 350 iterations. The convergence graph of the nacelle can be seen from Figure 7.

Figure 7. Convergence graph of the nacelle analysis.

4. Results and discussions

4.1 Grid independency test

The results shown in the Figure 8 and Table 5 represent the grid independency test of a CRM nacelle at 0.85 Mach, 0^° AoA, and an altitude of 35,000 ft. From the table, the highest C_d observed is 0.00256 at 1.47 million cells with an error of 5.78%. The lowest C_d value is 0.00245, consistently observed at 1.64 million cells onwards with a reduced error of 1.24%. In the graph, the C_d shows a sharp drop as the cell count increases from 1.4 to 1.64 million; thereafter, the C_d stabilizes. The highlighted point at 1.64 million cells indicates the selected grid size for further simulation.

Figure 8. Wing grid independency plot.

Table 5. Error evaluation and grid independency test results of the nacelle aerodynamic analysis.

Number of elements (millions)	Drag coefficient. C_d	Reference⁵⁷ Drag coefficient (C_dref) for halved nacelle	Reference⁵⁷ Drag coefficient (C_dref) for full nacelle	Error (%)
1.47	0.00256	0.00121	0.00242	5.78%
1.54	0.00249	0.00121	0.00242	2.89%
1.64	0.00245	0.00121	0.00242	1.24%
1.76	0.00245	0.00121	0.00242	1.24%
1.96	0.00245	0.00121	0.00242	1.24%

The CRM nacelle underwent a grid independency test with five different mesh sizes shown in the Figure 9. From a grid size of 1.64 million elements, a constant C_d of 0.00245 was observed. At 0.85 Mach and 0^° AoA, a high pressure of 38030.69 Pa appeared near the nacelle lip region. Intermediate pressure between 12039.975 Pa and 26891.816 Pa is observed over the nacelle cowl surface. The low pressure ranging from 894.189 Pa to 8335.731 Pa is observed at the nacelle exit where the velocity is maximum. The above contour results validate accurate prediction under the grid-independency test. The continuous pressure contours on the nacelle surfaces confirms that a 1.64 million mesh size is good enough to capture the key aerodynamic parameters.

Figure 9. Grid independency test pressure contours.

4.2 CRM nacelle pressure contour comparison

The above Figure 10 represents the pressure contours of the halved nacelle. A maximum pressure of 14500 Pa is observed at the inlet fan face. The peak pressure is uniformly distributed over the fan surface, but at the inlet fan edges, an intermediate pressure is observed.

Figure 10. Pressure contour comparison of the CRM nacelle with comparison graph.

The above Figure 10 highlights pressure contours over the baseline nacelle surfaces. From the figure, a maximum pressure of 41417.2 Pa is observed at the nacelle lip and inlet fan surfaces. The peak pressure is much higher compared to the reference article because, in the baseline analysis, the full engine is used. Similarly, an intermediate pressure of 20920.07 Pa to 32632.719 Pa is observed on the cowl surface. Additionally, at the fan face the pressure ranges from 8327.015 Pa to 15752.936 Pa, and it is closer to the.⁵⁷ Additionally, variation in the pressure values of baseline and reference model can be observed from the graph.

4.3 Different turbulence model

Six different turbulence models were evaluated for a CRM nacelle at 0.85 Mach using a fixed grid size of 1.64 million cells. The table and graph highlight the C_d values for six different turbulence models. The highest C_d was 0.00245 using the K-epsilon standard model with a validation error of 1.24%. The lowest C_d was 0.00231 from the Reynolds stress model, but this model has the highest error of 4.54%. The graph clearly shows minimal grid count variation while C_d varies among turbulence models. Figure 11 and Table 6 show that the K-epsilon model has the lowest validation error of 1.24%, and this model was selected for further analysis of the CRM nacelle.

Figure 11. Number of cells vs C_d at six different turbulence models.

Table 6. C_d value for different turbulence models.

Turbulence models	Drag coefficient (C_d)	Number of elements (millions)	Error (%)
K-epsilon standard model	0.00245	1.64	1.24%
K-omega SST model	0.00235	1.64	2.89%
Spalart-Allmara vorticity-based model	0.00232	1.64	4.13%
Transition SST model	0.00238	1.64	1.65%
Transition K-Kl model	0.00239	1.64	1.24%
Reynolds stress model	0.00231	1.64	4.54%

Six different turbulence models were tested using 1.64 million mesh elements, and the k-epsilon model showed the lowest validation error of 1.24%. Compared to other turbulence models, the k-epsilon model provided more accurate results due to its robustness in predicting fully developed turbulent flows and its ability to handle high Reynolds number boundary layers in the nacelle. From the pressure contour shown in Figure 12, a high pressure of 38030.69 Pa is noticed at the nacelle lip region. Intermediate pressure between 12039.975 Pa and 26891.816 Pa appeared on the nacelle cowl surface. A low-pressure zone ranging from 894.189 Pa to 8335.731 Pa is observed near the rear exit portion, indicating flow expansion and pressure drop.

Figure 12. Pressure contours for the CRM wing using different turbulence models.

4.4 Varying Mach numbers

Figure 13 and Table 7 shows how the C_d varies with the different Mach numbers for a CRM nacelle simulated on a mesh with 1.64 million cells. The Mach number varies from 0.8 up to 1.3 under the transonic regime. The C_d is very low at subsonic speeds, starting at about 0.00165 at 0.8 Mach. As the Mach number increases towards transonic speed, the cd rises sharply, reaching a peak at 0.95 Mach and slightly dropping at 1 Mach. As the Mach number increases from 1.05 to 1.3, the C_d gradually decreases from 0.0127 to 0.0113. This trend reflects typical drag behaviour near the critical Mach number, where the drag rises sharply due to shock formation and then decreases slightly as the flow becomes fully supersonic.

Figure 13. C_d value vs different Mach numbers.

Table 7. C_d value for different Mach number.

Different Mach numbers
Number of elements (millions)	Mach number (M)	Drag coefficient (C_d)
1.64	0.8	0.001648669
1.64	0.85	0.002448422
1.64	0.9	0.007277025
1.64	0.95	0.014037617
1.64	1	0.013154485
1.64	1.05	0.012689028
1.64	1.1	0.012478685
1.64	1.15	0.012407278
1.64	1.2	0.012552771
1.64	1.25	0.011241958
1.64	1.3	0.011340093

The contour plot Figure 14 represent the complete flow analysis of the CRM nacelle at 0.8 Mach. In the velocity streamline the flow separation is observed at the nacelle lip, where the velocity reaches 375.969 m/s. The maximum velocity of 563.954 m/s appears at the nacelle exit region. An intermediate velocity between 56.395 m/s and 112.791 m/s is observed over the nacelle cowl surface. Additionally, air velocity between 250.646 m/s and 375.969 m/s is observed over the nacelle cowl. From pressure contours, the maximum pressure of 36148.5 Pa occurs at the nacelle lip due to stagnation. Intermediate pressures of 15013.665 Pa to 25581.08 Pa are seen over the cowl surface. On the diffuser, the pressure ranges from 7968.72 Pa to 11491.192 Pa. In density contours, the maximum value of 0.525 kg/m³ appears at the nacelle lip, while intermediate densities from 0.274 kg/m³ to 0.424 kg/m³ are observed over the cowl surface. Temperature contours show a high temperature of 230.705K uniformly distributed along the nacelle cowl and lip region, while the fan face experiences the intermediate temperature of 199.159K. Kinetic energy contours reveal low values between 0 and 1431.48 m²/s² covering the entire nacelle rare.

Figure 14. Flow contours at 0.8 Mach.

The flow contours shown in Figure 15 illustrate the complete CRM nacelle aerodynamic behaviour at 0.85 Mach. In the velocity streamline contour, a flow separation is observed at the nacelle lip region at 379.589 m/s stagnation velocity. The maximum velocity of 569.383 m/s occurs at the nacelle exit. Intermediate velocities ranging from 189.794 m/s to 379.589 m/s are distributed along the nacelle cowl surface, and the intermediate velocity is experienced at the fan face. The pressure contour shows a peak value of 38030.699 Pa at the nacelle lip caused by stagnation. Over the cowl surface, an intermediate pressure ranges between 15752.936 Pa and 26891.816 Pa. The diffuser experiences a pressure ranging between 8327.015 Pa and 15752.936 Pa. In density contours, the highest density of 0.545 kg/m³ is observed at the lip region, whereas intermediate densities range between 0.231 kg/m³ and 0.388 kg/m³ across the cowl surface. The temperature contour shows a high uniform temperature of 234K throughout the lip and cowl regions. The fan face experiences temperatures between 169.691K and 201.846 K. Additionally; the kinetic energy contours reveal low energy levels between 0 m²/s² and 1545.535 m²/s² across all the nacelle faces.

Figure 15. Flow contours at 0.85 Mach.

Figure 16 shows the flow contours of the CRM nacelle analysis at 0.9 Mach. Velocity streamlines indicate flow separation near the nacelle lip region, with local velocity reaching 382.18 m/s. The highest velocity is observed at the nacelle exit with a value of 573.27 m/s. An intermediate velocity between 254.787 m/s and 445.877 m/s is observed over the nacelle cowl surface, and the same velocity is also observed at the fan faces. The pressure contour shows a high pressure of 40106.301 Pa at the nacelle lip region caused by the stagnation effect. The intermediate pressure between 20532.842 Pa and 32276.918 Pa is observed on the cowl surface. The diffuser face has moderate pressure between 8788.765 Pa and 16618.148 Pa. In the density contour, a maximum density of 0.567 kg/m³ is observed at the nacelle lip, while the cowl surface shows a density range between 0.186 kg/m³ and 0.404 kg/m³. The temperature contour shows a uniform high-temperature value of 221.332K over the lip and cowl surfaces. The fan face experiences a temperature range from 172.456K to 221.332K. The kinetic energy values remain low across the nacelle region, ranging from 0.001 m²/s² to 1520 m²/s².

Figure 16. Flow contours at 0.9 Mach.

Figure 17 shows all the flow contours of the nacelle analysis at 0.95 Mach. From the velocity streamlines, flow separation is observed near the nacelle lip region with a velocity reaching 386.511 m/s. The maximum velocity at the nacelle exit is 579.767 m/s. Over the cowl surface, an intermediate velocity between 257.674 m/s and 450.93 m/s is observed. The same intermediate velocity is observed at the fan faces. From the pressure contours, a maximum pressure of 42383.199 Pa is observed at the nacelle lip region. Over the cowl surface, intermediate pressure ranges between 21635.088 Pa and 29934.332 Pa. On the diffuser surface, the pressure value further reduces between 13335.841 Pa and 21635.088 Pa. The density contour shows a maximum density of 0.592 kg/m³ near the nacelle lip region, while moderate density between 0.251 kg/m³ and 0.421 kg/m² is observed over the cowl surface. The temperature distribution is almost uniform with a value of 207.925K across the fan face, nacelle lip, and cowl regions. The kinetic energy contour indicates lower values ranging between 0.001 m²/s² and 1939.731 m²/s² across the nacelle faces.

Figure 17. Flow contours at 0.95 Mach.

Figure 18 presents the flow contours of the CRM nacelle at 1 Mach. Velocity streamlines indicate flow separation near the nacelle lip region, where the flow velocity reaches 406.556 m/s. The maximum velocity of 609.834 m/s is observed at the nacelle exit. Intermediate velocity ranging from 271.037 m/s to 406.556 m/s is observed over the cowl surface, and the same velocity is observed at the fan face. The pressure contours show a maximum pressure of 44881.102 Pa at the nacelle lip region caused by the flow stagnation. Intermediate pressure values ranging between 18213.582 Pa and 31547.344 Pa occur over the cowl surface. The diffuser faces experience a pressure between 9324 Pa and 18213.582 Pa. In the density contour, the highest density of 0.618 kg/m³ is observed at the nacelle lip region. An intermediate density value from 0.254 kg/m³ to 0.436 kg/m³ is observed on the lip and cowl surface. The temperature contour shows a uniform high temperature of 225.253K across both the cowl and lips regions. At the fan face, the temperature ranges between 225.253K and 243.733K. The kinetic energy contour reveals that nacelle faces experience a low kinetic energy between 0 m²/s² and 2492.131 m²/s².

Figure 18. Flow contours at 1 Mach.

Figure 19 displays all the flow contours of the CRM nacelle analysis at 1.05 Mach. From the velocity streamline, flow separation is observed near the nacelle lip region with a velocity reaching 412.398 m/s. A maximum velocity of 618.597 m/s is observed at the nacelle exit regions. Over the cowl surface, intermediate velocities between 247.439 m/s and 433.018 m/s are observed. The fan face of the nacelle experiences a moderate flow velocity of 247.439 m/s. The pressure contour shows a maximum value of 47615.801 Pa at the nacelle lip due to stagnation. Pressure on the cowl moderately ranges between 19268.906 Pa and 33442.352 Pa, while the diffuser face experiences a pressure between 14544.423 Pa and 19268.906 Pa. Density contour shows a maximum density value of 0.646 kg/m³ at the nacelle lip. Similarly, an intermediate density between 0.264 kg/m² and 0.455 kg/m³ is observed at the cowl and fan faces of the nacelle. Temperature contour shows a high temperature of 209.505 uniformly distributed over the nacelle cowl and lip areas. The fan faces record a temperature between 209.505K and 247.626K. Additionally, Kinetic energy values range from 0.001 m²/s² to 2507.291 m²/s² across all nacelle faces.

Figure 19. Flow contours at 1.05 Mach.

Figure 20 show all flow contours of the CRM nacelle at 1.1 Mach. Flow separation is visible near the nacelle lip, where velocity reaches 418.022 m/s. The highest velocity occurs at the nacelle exit, with a value of 627.033 m/s. Over the cowl surface, intermediate velocity ranges from 348.352 m/s to 487.692 m/s, and a moderate velocity of 250.813 m/s is observed at the fan face. From the pressure contour, a peak pressure of 50540.302 Pa is recorded at the nacelle lip due to stagnation. Intermediate pressures are distributed over the nacelle cowl surface, ranging from 20420.861 Pa to 35480.73 Pa. The diffuser faces experience a pressure between 10380.949 Pa and 15400.905 Pa. Density contours show a maximum density of 0.675 kg/m³ at the nacelle lip, and an intermediate density ranging from 0.275 kg/m³ to 0.475 kg/m³ is observed over the cowl surface. Temperature contours indicate a nearly uniform high temperature of 271.378K across the nacelle cowl and lip region. At the fan face the temperature varies between 232.154K and 271.378K. The kinetic energy remains low over nacelle faces with values ranging from 0 m²/s² to 2579.031 m²/s².

Figure 20. Flow contours at 1.1 Mach.

The Figure 21 provides flow contours of the CRM nacelle at 1.15 Mach. From the velocity streamline it is observed that flow separation appears near the nacelle lip at 381.929 m/s. At the exit, velocity reaches a maximum value of 636.548 m/s, while the cowl region and fan face show moderate velocities ranging from 190.964 m/s to 445.584 m/s. Maximum pressure of 53719.699 Pa is observed at the nacelle lip due to the stagnation effect. Intermediate pressure on the cowl ranges from 21673.746 Pa to 37696.723 Pa. The diffuser pressure lies between 10991.761 Pa and 21673.746 Pa. The lip region shows a maximum density of 0.706 kg/m³.

Figure 21. Flow contours at 1.15 Mach.

The cowl surface and fan faces have moderate density values ranging from 0.287kg/m³ to 0.497kg/m³. Temperature reaches 215.544K and it is distributed uniformly throughout the cowl surface. At the fan face, the temperature ranges from 215.544K to 276.291K. Additionally, the kinetic energy is low across all surfaces, ranging up to 2686.041 m²/s².

Figure 22 presents a detailed flow field analysis of the CRM nacelle operating at 1.2 Mach. From the velocity streamline contour, a flow separation is observed near the nacelle lip where the velocity reaches 429.099 m/s. The peak velocity of 643.649 m/s is observed at the nacelle exit region. Intermediate flow over the nacelle cowl surface ranges between 286.066 m/s and 500.616 m/s, whereas the fan face experiences a velocity between 193.095 m/s and 321.824 m/s. Pressure contour reveals a stagnation pressure of 57075 Pa at the nacelle due to incoming flow deceleration. Across the cowl surface, pressure values fall between 22999.947 Pa and 40037.473 Pa. Similarly, over the diffuser section, pressure reduces between 11641.597 Pa and 22999.947 Pa. Density contour shows a maximum density of 0.739 kg/m³ at the nacelle lip region. Intermediate densities across the cowl surface range between 0.373 kg/m³ and 0.519 kg/m³. The temperature distribution is nearly uniform, showing a value of 219.072K across the nacelle lip and cowl surface. At the fan face, the temperature varies between 239.854K and 281.419K. The turbulent kinetic energy distribution remains low over the nacelle faces with a low value between 0 to 2798.591 m²/s².

Figure 22. Flow contours at 1.2 Mach.

Figure 23 shows all the flow contours of the CRM nacelle at 1.25 Mach. Velocity streamlines indicate flow separation near the nacelle lip region, with stagnation velocity reaching 433.983 m/s. A maximum velocity of 650.974 m/s is observed at the nacelle exit. Over the nacelle surface, the intermediate velocity ranges from 361.652 m/s to 506.313 m/s. Moderate pressure between 195.292 m/s and 260.39 m/s is observed at the nacelle fan face. From the pressure contour, a maximum pressure of 60669.801 Pa is observed at the nacelle lip due to stagnation. An intermediate pressure between 30465.691 Pa and 42547.336 Pa is observed over the cowl surface. Similarly, the fan face and diffuser section experience a moderate pressure between 18384.047 Pa and 36506.512 Pa. The density contour shows a maximum density of 0.772 kg/m³ at the nacelle lip region. The cowl region shows a density between 0.389 kg/m³ and 0.466 kg/m³. The temperature contour indicates a nearly uniform temperature of 224.026K across the nacelle cowl and lip surface. The fan face experiences temperatures ranging from 224.026K to 289.008K. The turbulence kinetic energy remains low across all nacelle regions with values between 0 m²/s² and 2781.231 m²/s².

Figure 23. Flow contours at 1.25 Mach.

Figure 24 displays all the flow contours of the CRM nacelle analysis at 1.3 Mach. From the velocity streamline, flow separation is observed near the nacelle lip region with a velocity reaching 439.241 m/s. A maximum velocity of 658.862 m/s is observed at the nacelle exit regions. Over the cowl surface, intermediate velocities between 292.828 m/s and 512.448 m/s are observed. The fan face of the nacelle experiences a moderate flow velocity of 2263.545 m/s. From the pressure contour, a peak pressure of 64450.398 Pa is recorded at the nacelle lip due to stagnation. Intermediate pressures are distributed over the nacelle cowl surface, ranging from 32344.08 Pa to 45186.605 Pa.

Figure 24. Flow contours at 1.3 Mach.

The diffuser faces experience a pressure between 19501.553 Pa and 45186.605 Pa. In the density contour, a maximum density of 0.807 kg/m³ is observed at the nacelle lip, while the cowl surface shows a density range between 0.0246 kg/m³ and 0.0567 kg/m³. The temperature contour shows a high uniform temperature of 229.786K throughout the lip and cowl regions. The fan face experiences temperatures between 229.786K and 274.503K. Additionally, the kinetic energy contours reveal low energy levels between 0 m²/s² and 3029.031 m²/s² across all the nacelle faces.

4.5 CRM nacelle design optimization

4.5.1 Nacelle cone core modeling

The nacelle core assembly, which encloses and safeguards the jet engine, plays a critical role in enhancing aerodynamic efficiency, minimizing noise emissions, and facilitating maintenance accessibility. The nacelle core assembly also integrates thrust reversers to improve braking and flight safety.

During nacelle optimization, a core cone was assembled in accordance with a reference design,⁵⁸ and the baseline angle of the core cone was found to be 15.7^°. To investigate the transonic aerodynamics of the nacelle, the core-cone angle was uniformly increased from 15.7^° to 16.7^° in 0.5^° step increments and decreased down to 13.7^° in 0.5^° step decrements. The optimized nacelle was tested at 0.82 Mach to understand the nacelle's aerodynamic performance and efficiency. The cone angle variation and 3D model of the cone assembled nacelle are shown in Figure 25.

Figure 25. CRM nacelle aerodynamic design optimization.

4.5.2 Optimized nacelle grid indecency test

Figure 26 and Table 8 represent the grid independency test results of the optimized CRM nacelle model under specific flow conditions, where the AoA is 8^°, the altitude is 35000ft, and the Mach number is 0.82. The gauge pressure and total temperature are calculated using the isentropic relations corresponding to 0.82 Mach by ensuring realistic flight boundary conditions. Among the tested mesh sizes ranging from 2.3 to 2.9 million elements, the highest C_l error was 8.87%, observed at 2.3 million cells. Meanwhile, the lowest error recorded was 8.42%, consistently found at 2.55, 2.7, and 2.9 million cells. This confirms that beyond 2.55 million cells, further refinement yields negligible improvement in accuracy; therefore, this mesh size was selected for further analysis.

Figure 26. C_l vs number of cells in millions.

Table 8. Nacelle optimization grid independency test results.

Number of elements (millions)	C_l	Reference C_lref⁵⁸	Error (%)
2.3	0.010935637	0.012	8.87%
2.46	0.010974622	0.012	8.54%
2.55	0.010988883	0.012	8.42%
2.7	0.010988883	0.012	8.42%
2.9	0.010988883	0.012	8.42%

4.5.3 Different turbulence models for the optimized nacelle

The Table 9 and Figure 27 represent the performance of six different turbulence models tested at 0.82 Mach on the optimized CRM nacelle model. All simulations used a constant mesh size of 2.55 million elements, allowing a fair comparison of each turbulence model's C_l prediction and corresponding error percentage. Among the tested models, the Reynolds stress model produced the highest 0.01342 C_l value with a 13.81% error. The Spalart-Allmaras model predicted a C_l of 0.01099, yielding the lowest error of 8.42%, indicating superior agreement with the reference value. The K-epsilon and K-omega models showed moderate errors of 9.5% and 10.02%, respectively. Transition-based models, including SST and K-Kl, displayed higher deviation, with errors above 10%. Upon validation, the Spalart-Allmaras model produced a C_l value closer to the reference data and showed the least validation error of 8.42%; therefore, this turbulence model was selected for further nacelle core optimization.

Table 9. C_l at different turbulence models.

Turbulence model	C_l	Number of elements (millions)	Error (%)
K-epsilon standard model	0.010858404	2.55	9.50%
K-omega SST model	0.010797221	2.55	10.02%
Spalart-Allmara vorticity-based model	0.010988883	2.55	8.42%
Transition SST model	0.010779794	2.55	10.16%
Transition K-Kl model	0.010351854	2.55	13.73%
Reynolds stress model	0.013424512	2.55	13.81%

Figure 27. Number of cells vs C_l at six different turbulence models.

4.5.4 Optimized nacelle results and discussions

Figure 28 and corresponding Table 10 represent the results of aerodynamics optimization for nacelle core assembly at the transonic speed of 0.82 Mach. The cone angle was varied from 13.7^° to 16.7^°at a fixed mesh size of 2.55 million elements. The C_l corresponding to each cone angle was determined using CFD simulations with the Spalart-Amara turbulence model.

Figure 28. C_l vs different cone angles.

Table 10. C_l with respect to different cone angles.

Number of elements (millions)	Nacelle core angle variation in degree	C_l	Mach number (M)
2.55	16.7	0.010941599	0.82
2.55	16.2	0.010960267	0.82
2.55	15.7 (Base)	0.010988883	0.82
2.55	15.2	0.010957501	0.82
2.55	14.7	0.010977722	0.82
2.55	14.2	0.01098843	0.82
2.55	13.7	0.011035105	0.82

The highest C_l value of 0.011035 was achieved at 1.37^°, indicating an optimal cone geometry for lift enhancement. At the 15.7^° baseline angle, the C_l was 0.01098, which was lower than the optimal case, indicating suboptimal efficiency. As the cone angle increased beyond 15.7^°, the C_l progressively decreased and reached a minimum C_l value of 0.01094 at 16.7^°. The results clearly demonstrate that a reduction in cone angle below the baseline enhanced the aerodynamic performance.

Figure 29 represents all flow contours of the optimized CRM nacelle at 0.82 Mach. From the velocity streamlines, flow separation is observed near the nacelle lip region with a local velocity of 270.716 m/s. Over the cowl surface, air velocities were distributed in the range of 270.716 m/s to 406.075 m/s, and a similar velocity is observed at the fan faces. A maximum velocity of 609.112 m/s is noted at the nacelle exit.

Figure 29. Flow contours at 13.7° cone angle.

From the pressure contour it is observed that due to the stagnation effect, a maximum pressure of 36857.5 Pa is observed at the nacelle lip. An intermediate pressure between 20570.785 and 28714.143 Pa is observed over the cowl surface. At the diffuser region, the pressure values were found in the range of 8355.746 Pa to 20570.785 Pa. The density contour shows a maximum value of 0.536 kg/m³ near the nacelle lip. Over the cowl surface, density ranges from 0.24 kg/m³ to 0.358 kg/m³.

At the diffuser and fan face areas, the density values are between 0.181 kg/m³ and 0.24 kg/m³. A nearly uniform temperature of 206.688K is observed over the cowl and lip surfaces. Temperature between 144.509K and 206.688K is observed at the fan face and diffuser surface. Similarly, the kinetic energy values range from 0 m²/s² to 8482.033 m²/s² over the entire nacelle surface.

In Figure 30, the optimized nacelle is compared with the baseline nacelle. The velocity streamlines of the CRM nacelle at a 15.7° base cone angle and a 13.7° optimized cone angle show a clear aerodynamic difference due to shape refinement. In the baseline case, flow separation occurs near the lip region with a velocity of 271.89 m/s. Similarly, at the nacelle exit, the streamline reaches a maximum value of 611.571 m/s. The internal flow fields show intermediate velocities between 203.857 m/s and 407.714 m/s, indicating non-uniform fan face inflow. From the streamline contour, it is observed that the optimized nacelle produces more attached streamlines compared to the baseline. The maximum velocity of the optimized is 609.114 m/s, which is slightly less compared to the baseline. Similarly, the intermediate velocity of the optimized nacelle ranges between 237.657 m/s and 406.971 m/s; this results in smoother and reduced flow distortion. The optimized CRM nacelle resulted in better pressure recovery, reduced drag, improved lift, and stable inflow conditions.

Figure 30. Comparison of the optimized nacelle with baseline.

5. Combined results and discussions of baseline and optimized nacelle

The aerodynamic evaluation of the CRM nacelle integrated with a fan was conducted using different numerical methods, including a five-grid independency test, six different turbulence models, and Mach number variations. At 0.85 Mach, the grid with 1.64 million elements and the standard K-epsilon model produced a C_d value of 0.00245, corresponding to a validation error of 1.24%. Subsequent simulations with Mach numbers ranging from 0.8 to 1.3 revealed that the C_d values varied from 0.001348 to 0.001134. Beyond 0.95 Mach, a noticeable decline in the C_d was observed, with the C_d dropping from 0.014037 and reaching 0.01134 at 1.3 Mach. In this case nacelle with fan assembly was considered and the overall results of the CRM nacelle can be seen from the Figure 31.

Figure 31. Overall C_d values vs different numerical techniques.

The aerodynamic optimization of the nacelle was carried out by integrating a core with the existing nacelle geometry, followed by a detailed numerical study. Figure 32 represents overall results of the core assembled CRM nacelle. The methodology incorporated grid indecency tests, turbulence model evaluation, and a systematic variation of the core-cone angle. At 0.82 Mach, a mesh size of 2.55 million elements and the Spalart-Allmara model produced a C_l value of 0.01098 with a validation error of 8.24%. The core angle varied from the baseline of 15.7^° up to 16.7^° and reduced to 13.7^° with a uniform 0.5^° step variation. Among the six tested core angles, the 13.7 configuration demonstrated a better aerodynamic performance with a C_l value of 0.11035, surpassing the baseline design.

Figure 32. Overall C_l values vs different numerical techniques.

6. Conclusions and future scope

In this research article, a comprehensive numerical investigation was conducted to minimize the drag and enhance the overall lift of a CRM nacelle. At 0.85 Mach, the baseline nacelle model with a fan was evaluated using five different grid sizes. The mesh with 1.64 million elements provided the most consistent result with a C_d of 0.00245 and a validation error of 1.24% compared to reference data. Out of six turbulence models tested, the K-epsilon model produced the same error of 1.24% and was selected for further analysis. To investigate the transonic effect on the CRM nacelle, the Mach number was varied from 0.8 to 1.3 with a 0.05 step increment. At 0.95 Mach, the highest C_d of 0.014037 was observed. As the Mach number increased to 1.2, the C_d dropped to 0.012552. However, at 1.3 Mach, the C_d slightly increased to 0.01134. This is due to compressibility or shock effects in the transonic regime.

In the nacelle optimization study, the CRM nacelle was modified by adding the core-cone shape and retested at 0.82 Mach. A new grid with 2.55 million elements produced a C_l of 0.01098 with a validation error of 8.54%. Similarly, the optimized nacelle was tested using six different turbulence models, and the Spalart-Allmaras model produced the most accurate result. Subsequently, the cone angle was varied in both increasing and decreasing directions. Subsequently, the cone angle was varied from the base angle of 15.7^°. Two forward iterations up to 16.7^° and three reverse iterations down to 13.7^° with 0.5^°step variation were tested. Compared to baseline model, the optimized nacelle with 13.7^° cone angle produced a better C_l of 0.011035105.

In conclusion, this research helps to understand the transonic flow characteristics of a CRM nacelle. Nacelle core angle optimization significantly enhances the lift under varying Mach numbers. The iterative variation of the cone angle provides a clear aerodynamic improvement and offers valuable insights into efficient nacelle design strategies. Future studies focus on unsteady transonic effects using time-resolved URANS or LES simulations and PIMPLE algorithms.⁶⁴ Further exploration of cone angle optimization using machine learning-based design methods may enhance aerodynamic efficiency. Investigating off-design conditions and nacelle airframe integration can provide deeper insights into real-time flight performance.

Ethics and consent

Ethics and consent were not required.

Data availability statement

All data underlying the results presented in this article are available under a CC-BY license. The datasets and materials supporting the findings of this study, including CFD simulation outputs, mesh files, and the values used to generate all figures and tables, are freely available at https://doi.org/10.5281/zenodo.17372018.

Data are available under the terms of the Creative Commons Zero "No rights reserved" data waiver (CC0 1.0 Public domain dedication).⁶⁵

References

1. Faust GK, Mungur P: Nacelle Design, NASA Langley Research Center, Research in Natural Laminar Flow and Laminar-Flow Control, Part 3.Dec. 1, 1987.
2. Geron M, Kirkland F, Fox R, et al.: Parametric nacelle modelling to support structural design for engine integration.2023. Reference Source
3. Sadrehaghighi I: Aircraft Nacelle Design & Optimization CFD Open Series.2023. Publisher Full Text
4. Raghunathan S, et al.: Symbols Key aerodynamic technologies for aircraft engine nacelles.2006.
5. Xin Z, et al.: Nacelle-airframe integration design method for blended-wing-body transport with podded engines. Chin. J. Aeronaut. Aug. 2019; 32(8): 1860–1868. Publisher Full Text
6. Koklu M, et al.: Investigation of the Nacelle/Pylon Vortex System on the High-Lift Common Research Model. AIAA J. Sep. 2021; 59(9): 3748–3763. Publisher Full Text
7. Swarthout A, et al.: Aerodynamics of a Compact Nacelle at Take-Off Conditions. AIAA Aviation and Aeronautics Forum and Exposition, AIAA AVIATION Forum 2023. American Institute of Aeronautics and Astronautics Inc, AIAA; 2023. Publisher Full Text
8. Sánchez-Moreno F, MacManus D, Tejero F, et al.: Installed nacelle aerodynamics at cruise and windmilling conditions. Aircr. Eng. Aerosp. Technol. 2024; 96(6): 757–768. Publisher Full Text
9. Zhang S, Li H, Zhang Y: Aerodynamic Prediction of a CRM High-lift Configuration using a modified three equation turbulence model.
10. Ziogas O, Antoniou S, Panagiotou P, et al.: Assessing Nacelle Drag Increment: Implications of New Engine Technologies on Aircraft Performance EASN 2024. Basel Switzerland: MDPI; Mar. 2025; p. 49. Publisher Full Text
11. Tejero F, Robinson M, MacManus DG, et al.: Multi-objective optimisation of short nacelles for high bypass ratio engines. Aerosp. Sci. Technol. Aug. 2019; 91: 410–421. Publisher Full Text
12. Sebastian S, Ralf R: Experimental assessment of wing lower surface buffet effects induced by the installation of a UHBR nacelle. CEAS Aeronaut. J. Jan. 2024; 15(1): 49–59. Publisher Full Text
13. Loginov V, Ukrainets Y, Kravchenko I, et al.: Experimental research into aerodynamic characteristics of a nacelle with the enabled system of engine thrust neutralization. Eastern-European Journal of Enterprise Technologies. 2018; 6(8–96): 65–73. Publisher Full Text
14. Kanazaki M, Yokokawa Y, Murayama M, et al.: Nacelle Chine Installation Based on Wind-Tunnel Test Using Efficient Global Optimization.
15. Sabnis K, et al.: A Wind Tunnel Rig to Study the External Fan Cowl Separation Experienced by Compact Nacelles in Windmilling Scenarios.
16. Khai LC, Ismail MA, Azam Q, et al.: Experimental study on aerodynamic performance of nacelle lip-skin bias flow. J. Mech. Sci. Technol. Apr. 2020; 34(4): 1613–1621. Publisher Full Text
17. Piscitelli F, Palazzo S, De Nicola F: Icing Wind Tunnel Test Campaign on a Nacelle Lip-Skin to Assess the Effect of a Superhydrophobic Coating on Ice Accretion. Applied Sciences (Switzerland). Apr. 2023; 13(8). Publisher Full Text
18. Silva VT, Lundbladh A, Xisto C, et al.: Powered Low-Speed Experimental Aerodynamic Investigation of an Over-Wing-Mounted Nacelle Configuration. J. Aircr. Mar. 2024; 61(2): 415–424. Publisher Full Text
19. Schuh MJ, Garcia JA, Carter MB, et al.: NASA Environmentally Responsible Aviation Hybrid Wing Body Flow-Through Nacelle Wind Tunnel CFD.
20. Sabnis K, Babinsky H, Boscagli L, et al.: Experimental Investigation of External Fan Cowl Separation for Compact Nacelles in Windmilling Scenarios. AIAA Aviation and Aeronautics Forum and Exposition, AIAA AVIATION Forum 2023. American Institute of Aeronautics and Astronautics Inc, AIAA; 2023. Publisher Full Text
21. Boscagli L, Macmanus D, Tejero F, et al.: Characteristics of shock-induced boundary layer separation on nacelles under windmilling diversion conditions.2023.
22. Kato H, Watanabe S, Murayama M, et al.: PIV Investigation of Nacelle Chine Effects on High-Lift System Performance.2008.
23. Koklu M, et al.: AIAA Associate Fellow ‡ Research Scientist, Flow Physics and Control Branch. AIAA Associate Fellow;
24. Yeong YH, Chiles IM, Bragg MB, et al.: Wind Tunnel Testing of a Nacelle Bypass Concept for a Quiet Supersonic Aircraft.
25. Hortensius R, Elliott GS, Bragg MB: An Experimental Investigation of the Flow Through the Aft Portion of a High-Flow Nacelle Bypass Concept.2012.
26. Hall CA, Hynes TP: Measurements of intake separation hysteresis in a model fan and nacelle rig. J. Propuls. Power. 2006; 22(4): 872–879. Publisher Full Text
27. Tao G, Liu Y, Cui J: Flow field prediction and optimization of non-axisymmetric aero-engine nacelles based on deep learning. Aerosp. Sci. Technol. Apr. 2025; 159: 109990. Publisher Full Text
28. Robinson M, MacManus DG, Christie R, et al.: Nacelle design for ultra-high bypass ratio engines with CFD based optimisation. Aerosp. Sci. Technol. Jun. 2021; 113: 106191. Publisher Full Text
29. Yang X, Cao C, Wang C, et al.: Surrogate-based optimization of nacelle intake with fan-intake interaction: Mitigating flow separation under crosswind. Aerosp. Sci. Technol. Nov. 2023; 142: 108641. Publisher Full Text
30. Magrini A, Buosi D, Benini E: Analysis of installation aerodynamics and comparison of optimised configuration of an ultra-high bypass ratio turbofan nacelle. Aerosp. Sci. Technol. Sep. 2022; 128: 107756. Publisher Full Text
31. Tejero F, Christie R, MacManus D, et al.: Non-axisymmetric aero-engine nacelle design by surrogate-based methods. Aerosp. Sci. Technol. Oct. 2021; 117: 106890. Publisher Full Text
32. Yan C, Zhang Y, Zhang M: Numerical optimization of transonic natural laminar flow nacelles. Chin. J. Aeronaut. Jun. 2023; 36(6): 35–51. Publisher Full Text
33. Zhang H, Li J, Yang Z: Double-decoupled inverse design of natural laminar flow nacelle under transonic conditions. Chin. J. Aeronaut. Jun. 2023; 36(6): 1–18. Publisher Full Text
34. Yao Y, Ma D, Yang M, et al.: Adaptive-surrogate-based robust optimization of transonic natural laminar flow nacelle. Chin. J. Aeronaut. Oct. 2021; 34(10): 36–52. Publisher Full Text
35. Yang Q, Guo X, Dong W, et al.: Ice accretion and aerodynamic effects on a turbofan engine nacelle under takeoff conditions. Aerosp. Sci. Technol. Jul. 2022; 126: 107571. Publisher Full Text
36. Rozov V, Stuhlpfarrer M, Osma MF, et al.: Engine Modeling for Small-Disturbance-CFD Related to Aircraft Flutter Investigations. J Fluids Struct. Jul. 2020; 96: 103045. Publisher Full Text
37. Li J, Gao Z, Huang J, et al.: Aerodynamic design optimization of nacelle/pylon position on an aircraft. Chin. J. Aeronaut. Aug. 2013; 26(4): 850–857. Publisher Full Text
38. Mao Y, Dang TQ: A three-dimensional body-force model for nacelle-fan systems under inlet distortions. Aerosp. Sci. Technol. Nov. 2020; 106: 106085. Publisher Full Text
39. Chen J, Wu Y, Hua O, et al.: Research on the ground vortex and inlet flow field under the ground crosswind condition. Aerosp. Sci. Technol. Aug. 2021; 115: 106772. Publisher Full Text
40. Kennedy S, Robinson T, Spence S, et al.: Computational investigation of inlet distortion at high angles of attack. J. Aircr. 2014; 51(2): 361–376. Publisher Full Text
41. Carnevale M, Wang F, Green JS, et al.: Lip stall suppression in powered intakes. J. Propuls. Power. 2016; 32(1): 161–170. Publisher Full Text
42. Tejero F, MacManus DG, Sanchez-Moreno F, et al.: Neural network-based multi-point, multi-objective optimisation for transonic applications. Aerosp. Sci. Technol. May 2023; 136: 108208. Publisher Full Text
43. Sureshbabu S, Tejero F, Macmanus D, et al.: Deep-Learning Methods for Non-Linear Transonic Flow-Field Prediction. AIAA Aviation and Aeronautics Forum and Exposition, AIAA AVIATION Forum 2023. American Institute of Aeronautics and Astronautics Inc, AIAA; 2023. Publisher Full Text
44. Wang C, et al.: Framework of nacelle inverse design method based on improved generative adversarial networks. Aerosp. Sci. Technol. Feb. 2022; 121: 107365. Publisher Full Text
45. Fang X, Zhang Y, Chen H: Transonic nacelle aerodynamic optimization based on hybrid genetic algorithm 17th AIAA/ISSMO Multidisciplinary Analysis and Optimization Conference. American Institute of Aeronautics and Astronautics Inc, AIAA; 2016. Publisher Full Text
46. Song W, Keane AJ: Surrogate-based aerodynamic shape optimization of a civil aircraft engine nacelle. AIAA J. Oct. 2007; 45(10): 2565–2574. Publisher Full Text
47. Tejero F, MacManus DG, Sheaf C: Surrogate-based aerodynamic optimisation of compact nacelle aero-engines. Aerosp. Sci. Technol. Oct. 2019; 93: 105207. Publisher Full Text
48. Robinson M, MacManus DG, Heidebrecht A, et al.: An optimization method for nacelle design. AIAA SciTech Forum - 55th AIAA Aerospace Sciences Meeting. American Institute of Aeronautics and Astronautics Inc.; 2017. Publisher Full Text
49. Heidebrecht A, MacManus DG: Surrogate model of complex non-linear data for preliminary nacelle design. Aerosp. Sci. Technol. Jan. 2019; 84: 399–411. Publisher Full Text
50. Tejero F, Macmanus D, Heidebrecht A, et al.: Artificial neural network for preliminary design and optimisation of civil aero-engine nacelles. Aeronaut. J. 2024; 128: 2261–2280. Publisher Full Text
51. Sánchez-Moreno F, Macmanus DG, Tejero F, et al.: Nacelle optimisation through multi-fidelity neural networks.
52. Swarthout A, Macmanus D, Tejero F, et al.: A Comparative Assessment of Multi-Objective Optimisation Methodologies for Aero Engine Nacelles.
53. Tong S, et al.: Optimization of aero-engine combustion chambers with the assistance of Hierarchical-Kriging surrogate model based on POD downscaling method. Adv. Aerodyn. Dec. 2023; 5(1). Publisher Full Text
54. Christie R, Heidebrecht A, MacManus D: An automated approach to nacelle parameterization using intuitive class shape transformation curves. J. Eng. Gas Turbines Power. 2017; 139(6): 062601-1–062601-9. Publisher Full Text
55. Wang S, Cao C, Wang C, et al.: A nacelle inlet design approach with more three-dimensional geometric consideration. Aerosp. Sci. Technol. May 2021; 112: 106624. Publisher Full Text
56. Wilhelm R: An inverse design method for engine nacelles and wings. Aerosp. Sci. Technol. 2005; 9(1): 19–29. Publisher Full Text
57. Nambiar VR, Pachidis V: Nacelle intake flow separation reduction at cruise condition using active flow control. Propulsion and Power Research. Sep. 2022; 11(3): 337–352. Publisher Full Text
58. Stankowski TP, Macmanus DG, Robinson M, et al.: Aerodynamic effects of propulsion integration for high bypass ratio engines. J. Aircr. 2017; 54(6): 2270–2284. Publisher Full Text
59. Vassberg JC, Dehaan MA, Rivers SM, et al.: Development of a Common Research Model for Applied CFD Validation Studies.
60. Otter JJ, Stańkowski T, Robinson M, et al.: Installation aerodynamics of civil aero-engine exhaust systems. Aerosp. Sci. Technol. Jun. 2019; 89: 345–355. Publisher Full Text
61. Datta B, Goel V, Garg S, et al.: Study of Various Passive Drag Reduction Techniques on External Vehicle Aerodynamics Performance: CFD Based Approach. International Research Journal of Engineering and Technology. 2008; 1851. Reference Source
62. Young T: Performance of the Jet Transport Airplane: Analysis Methods, Flight Operations, and Regulations.2017. Publisher Full Text
63. Kumar M, Fernando DX, Kumar RM: Design and Optimization of De Lavel Nozzle to Prevent Shock Induced Flow Separation.2013. Reference Source
64. Karthik A, Srinivas G, Naik N: Implementation of higher-order PIMPLE algorithm for time marching analysis of transonic wing compressibility effects with high Mach pre-conditioning. Eng. Sci. May 2022; 20. Publisher Full Text
65. Ajay Kumar JK, Sudheendra Prabhu K, Veerendra AS, et al.: AERODYNAMIC PERFORMANCE ENHANCEMENT OF CRM NACELLE UNDER TRANSONIC FLOW: A COMPREHENSIVE CFD-BASED OPTIMIZATION APPROACH. Zenodo. 2025. Publisher Full Text

Comments on this article Comments (0)

Version 1

VERSION 1 PUBLISHED 10 Nov 2025

Author details Author details

¹ Department of Aeronautical & Automobile Engineering, Manipal Academy of Higher Education, Manipal, Karnataka, 576104, India
² Department of Aeronautical & Automobile Engineering, Manipal Academy of Higher Education, Manipal, Karnataka, 576104, India
³ Department of Electrical & Electronics Engineering, Manipal Academy of Higher Education, Manipal, Karnataka, 576104, India
⁴ Department of Aerospace Engineering, Jain University Faculty of Engineering & Technology, Bengaluru, Karnataka, 560069, India
⁵ Department of Aeronautical & Automobile Engineering, Manipal Academy of Higher Education, Manipal, Karnataka, 576104, India

J K Ajay Kumar
Roles: Conceptualization, Data Curation

Sudheendra Prabhu K
Roles: Formal Analysis, Investigation

A S Veerendra
Roles: Methodology

Sudhir Shastry Y B
Roles: Resources, Software

Srinivas G
Roles: Supervision, Writing – Review & Editing

Competing interests

No competing interests were disclosed.

Grant information

The author(s) declared that no grants were involved in supporting this work.

Article Versions (1)

version 1

Published: 10 Nov 2025, 14:1236

https://doi.org/10.12688/f1000research.170106.1

Copyright

© 2025 Kumar JKA et al. This is an open access article distributed under the terms of the Creative Commons Attribution License, which permits unrestricted use, distribution, and reproduction in any medium, provided the original work is properly cited.

Download

Export To

metrics

	Views	Downloads
F1000Research	-	-
PubMed Central Data from PMC are received and updated monthly.	-	-

Citations

0

SEE MORE DETAILS

CITE

how to cite this article

Kumar JKA, K SP, Veerendra AS et al. Aerodynamic Performance Enhancement of Crm Nacelle Under Transonic Flow: A Comprehensive Cfd-based Optimization Approach [version 1; peer review: awaiting peer review]. F1000Research 2025, 14:1236 (https://doi.org/10.12688/f1000research.170106.1)

NOTE: If applicable, it is important to ensure the information in square brackets after the title is included in all citations of this article.

track

receive updates on this article

Track an article to receive email alerts on any updates to this article.

Open Peer Review

Comments on this article Comments (0)

Version 1

VERSION 1 PUBLISHED 10 Nov 2025

Open Peer Review

Reviewer Status

AWAITING PEER REVIEW

Comments on this article

All Comments(0)

Add a comment

Sign up for content alerts

Browse by related subjects

[1] 1. Faust GK, Mungur P: Nacelle Design, NASA Langley Research Center, Research in Natural Laminar Flow and Laminar-Flow Control, Part 3.Dec. 1, 1987.

[2] 2. Geron M, Kirkland F, Fox R, et al.: Parametric nacelle modelling to support structural design for engine integration.2023. Reference Source

[3] 3. Sadrehaghighi I: Aircraft Nacelle Design & Optimization CFD Open Series.2023. Publisher Full Text

[4] 4. Raghunathan S, et al.: Symbols Key aerodynamic technologies for aircraft engine nacelles.2006.

[5] 5. Xin Z, et al.: Nacelle-airframe integration design method for blended-wing-body transport with podded engines. Chin. J. Aeronaut. Aug. 2019; 32(8): 1860–1868. Publisher Full Text

[6] 6. Koklu M, et al.: Investigation of the Nacelle/Pylon Vortex System on the High-Lift Common Research Model. AIAA J. Sep. 2021; 59(9): 3748–3763. Publisher Full Text

[7] 7. Swarthout A, et al.: Aerodynamics of a Compact Nacelle at Take-Off Conditions. AIAA Aviation and Aeronautics Forum and Exposition, AIAA AVIATION Forum 2023. American Institute of Aeronautics and Astronautics Inc, AIAA; 2023. Publisher Full Text

[8] 8. Sánchez-Moreno F, MacManus D, Tejero F, et al.: Installed nacelle aerodynamics at cruise and windmilling conditions. Aircr. Eng. Aerosp. Technol. 2024; 96(6): 757–768. Publisher Full Text

[9] 9. Zhang S, Li H, Zhang Y: Aerodynamic Prediction of a CRM High-lift Configuration using a modified three equation turbulence model.

[10] 10. Ziogas O, Antoniou S, Panagiotou P, et al.: Assessing Nacelle Drag Increment: Implications of New Engine Technologies on Aircraft Performance EASN 2024. Basel Switzerland: MDPI; Mar. 2025; p. 49. Publisher Full Text

[11] 11. Tejero F, Robinson M, MacManus DG, et al.: Multi-objective optimisation of short nacelles for high bypass ratio engines. Aerosp. Sci. Technol. Aug. 2019; 91: 410–421. Publisher Full Text

[12] 12. Sebastian S, Ralf R: Experimental assessment of wing lower surface buffet effects induced by the installation of a UHBR nacelle. CEAS Aeronaut. J. Jan. 2024; 15(1): 49–59. Publisher Full Text

[13] 13. Loginov V, Ukrainets Y, Kravchenko I, et al.: Experimental research into aerodynamic characteristics of a nacelle with the enabled system of engine thrust neutralization. Eastern-European Journal of Enterprise Technologies. 2018; 6(8–96): 65–73. Publisher Full Text

[14] 14. Kanazaki M, Yokokawa Y, Murayama M, et al.: Nacelle Chine Installation Based on Wind-Tunnel Test Using Efficient Global Optimization.

[15] 15. Sabnis K, et al.: A Wind Tunnel Rig to Study the External Fan Cowl Separation Experienced by Compact Nacelles in Windmilling Scenarios.

[16] 16. Khai LC, Ismail MA, Azam Q, et al.: Experimental study on aerodynamic performance of nacelle lip-skin bias flow. J. Mech. Sci. Technol. Apr. 2020; 34(4): 1613–1621. Publisher Full Text

[17] 17. Piscitelli F, Palazzo S, De Nicola F: Icing Wind Tunnel Test Campaign on a Nacelle Lip-Skin to Assess the Effect of a Superhydrophobic Coating on Ice Accretion. Applied Sciences (Switzerland). Apr. 2023; 13(8). Publisher Full Text

[18] 18. Silva VT, Lundbladh A, Xisto C, et al.: Powered Low-Speed Experimental Aerodynamic Investigation of an Over-Wing-Mounted Nacelle Configuration. J. Aircr. Mar. 2024; 61(2): 415–424. Publisher Full Text

[19] 19. Schuh MJ, Garcia JA, Carter MB, et al.: NASA Environmentally Responsible Aviation Hybrid Wing Body Flow-Through Nacelle Wind Tunnel CFD.

[20] 20. Sabnis K, Babinsky H, Boscagli L, et al.: Experimental Investigation of External Fan Cowl Separation for Compact Nacelles in Windmilling Scenarios. AIAA Aviation and Aeronautics Forum and Exposition, AIAA AVIATION Forum 2023. American Institute of Aeronautics and Astronautics Inc, AIAA; 2023. Publisher Full Text

[21] 21. Boscagli L, Macmanus D, Tejero F, et al.: Characteristics of shock-induced boundary layer separation on nacelles under windmilling diversion conditions.2023.

[22] 22. Kato H, Watanabe S, Murayama M, et al.: PIV Investigation of Nacelle Chine Effects on High-Lift System Performance.2008.

[23] 23. Koklu M, et al.: AIAA Associate Fellow ‡ Research Scientist, Flow Physics and Control Branch. AIAA Associate Fellow;

[24] 24. Yeong YH, Chiles IM, Bragg MB, et al.: Wind Tunnel Testing of a Nacelle Bypass Concept for a Quiet Supersonic Aircraft.

[25] 25. Hortensius R, Elliott GS, Bragg MB: An Experimental Investigation of the Flow Through the Aft Portion of a High-Flow Nacelle Bypass Concept.2012.

[26] 26. Hall CA, Hynes TP: Measurements of intake separation hysteresis in a model fan and nacelle rig. J. Propuls. Power. 2006; 22(4): 872–879. Publisher Full Text

[27] 27. Tao G, Liu Y, Cui J: Flow field prediction and optimization of non-axisymmetric aero-engine nacelles based on deep learning. Aerosp. Sci. Technol. Apr. 2025; 159: 109990. Publisher Full Text

[28] 28. Robinson M, MacManus DG, Christie R, et al.: Nacelle design for ultra-high bypass ratio engines with CFD based optimisation. Aerosp. Sci. Technol. Jun. 2021; 113: 106191. Publisher Full Text

[29] 29. Yang X, Cao C, Wang C, et al.: Surrogate-based optimization of nacelle intake with fan-intake interaction: Mitigating flow separation under crosswind. Aerosp. Sci. Technol. Nov. 2023; 142: 108641. Publisher Full Text

[30] 30. Magrini A, Buosi D, Benini E: Analysis of installation aerodynamics and comparison of optimised configuration of an ultra-high bypass ratio turbofan nacelle. Aerosp. Sci. Technol. Sep. 2022; 128: 107756. Publisher Full Text

[31] 31. Tejero F, Christie R, MacManus D, et al.: Non-axisymmetric aero-engine nacelle design by surrogate-based methods. Aerosp. Sci. Technol. Oct. 2021; 117: 106890. Publisher Full Text

[32] 32. Yan C, Zhang Y, Zhang M: Numerical optimization of transonic natural laminar flow nacelles. Chin. J. Aeronaut. Jun. 2023; 36(6): 35–51. Publisher Full Text

[33] 33. Zhang H, Li J, Yang Z: Double-decoupled inverse design of natural laminar flow nacelle under transonic conditions. Chin. J. Aeronaut. Jun. 2023; 36(6): 1–18. Publisher Full Text

[34] 34. Yao Y, Ma D, Yang M, et al.: Adaptive-surrogate-based robust optimization of transonic natural laminar flow nacelle. Chin. J. Aeronaut. Oct. 2021; 34(10): 36–52. Publisher Full Text

[35] 35. Yang Q, Guo X, Dong W, et al.: Ice accretion and aerodynamic effects on a turbofan engine nacelle under takeoff conditions. Aerosp. Sci. Technol. Jul. 2022; 126: 107571. Publisher Full Text

[36] 36. Rozov V, Stuhlpfarrer M, Osma MF, et al.: Engine Modeling for Small-Disturbance-CFD Related to Aircraft Flutter Investigations. J Fluids Struct. Jul. 2020; 96: 103045. Publisher Full Text

[37] 37. Li J, Gao Z, Huang J, et al.: Aerodynamic design optimization of nacelle/pylon position on an aircraft. Chin. J. Aeronaut. Aug. 2013; 26(4): 850–857. Publisher Full Text

[38] 38. Mao Y, Dang TQ: A three-dimensional body-force model for nacelle-fan systems under inlet distortions. Aerosp. Sci. Technol. Nov. 2020; 106: 106085. Publisher Full Text

[39] 39. Chen J, Wu Y, Hua O, et al.: Research on the ground vortex and inlet flow field under the ground crosswind condition. Aerosp. Sci. Technol. Aug. 2021; 115: 106772. Publisher Full Text

[40] 40. Kennedy S, Robinson T, Spence S, et al.: Computational investigation of inlet distortion at high angles of attack. J. Aircr. 2014; 51(2): 361–376. Publisher Full Text

[41] 41. Carnevale M, Wang F, Green JS, et al.: Lip stall suppression in powered intakes. J. Propuls. Power. 2016; 32(1): 161–170. Publisher Full Text

[42] 42. Tejero F, MacManus DG, Sanchez-Moreno F, et al.: Neural network-based multi-point, multi-objective optimisation for transonic applications. Aerosp. Sci. Technol. May 2023; 136: 108208. Publisher Full Text

[43] 43. Sureshbabu S, Tejero F, Macmanus D, et al.: Deep-Learning Methods for Non-Linear Transonic Flow-Field Prediction. AIAA Aviation and Aeronautics Forum and Exposition, AIAA AVIATION Forum 2023. American Institute of Aeronautics and Astronautics Inc, AIAA; 2023. Publisher Full Text

[44] 44. Wang C, et al.: Framework of nacelle inverse design method based on improved generative adversarial networks. Aerosp. Sci. Technol. Feb. 2022; 121: 107365. Publisher Full Text

[45] 45. Fang X, Zhang Y, Chen H: Transonic nacelle aerodynamic optimization based on hybrid genetic algorithm 17th AIAA/ISSMO Multidisciplinary Analysis and Optimization Conference. American Institute of Aeronautics and Astronautics Inc, AIAA; 2016. Publisher Full Text

[46] 46. Song W, Keane AJ: Surrogate-based aerodynamic shape optimization of a civil aircraft engine nacelle. AIAA J. Oct. 2007; 45(10): 2565–2574. Publisher Full Text

[47] 47. Tejero F, MacManus DG, Sheaf C: Surrogate-based aerodynamic optimisation of compact nacelle aero-engines. Aerosp. Sci. Technol. Oct. 2019; 93: 105207. Publisher Full Text

[48] 48. Robinson M, MacManus DG, Heidebrecht A, et al.: An optimization method for nacelle design. AIAA SciTech Forum - 55th AIAA Aerospace Sciences Meeting. American Institute of Aeronautics and Astronautics Inc.; 2017. Publisher Full Text

[49] 49. Heidebrecht A, MacManus DG: Surrogate model of complex non-linear data for preliminary nacelle design. Aerosp. Sci. Technol. Jan. 2019; 84: 399–411. Publisher Full Text

[50] 50. Tejero F, Macmanus D, Heidebrecht A, et al.: Artificial neural network for preliminary design and optimisation of civil aero-engine nacelles. Aeronaut. J. 2024; 128: 2261–2280. Publisher Full Text

[51] 51. Sánchez-Moreno F, Macmanus DG, Tejero F, et al.: Nacelle optimisation through multi-fidelity neural networks.

[52] 52. Swarthout A, Macmanus D, Tejero F, et al.: A Comparative Assessment of Multi-Objective Optimisation Methodologies for Aero Engine Nacelles.

[53] 53. Tong S, et al.: Optimization of aero-engine combustion chambers with the assistance of Hierarchical-Kriging surrogate model based on POD downscaling method. Adv. Aerodyn. Dec. 2023; 5(1). Publisher Full Text

[54] 54. Christie R, Heidebrecht A, MacManus D: An automated approach to nacelle parameterization using intuitive class shape transformation curves. J. Eng. Gas Turbines Power. 2017; 139(6): 062601-1–062601-9. Publisher Full Text

[55] 55. Wang S, Cao C, Wang C, et al.: A nacelle inlet design approach with more three-dimensional geometric consideration. Aerosp. Sci. Technol. May 2021; 112: 106624. Publisher Full Text

[56] 56. Wilhelm R: An inverse design method for engine nacelles and wings. Aerosp. Sci. Technol. 2005; 9(1): 19–29. Publisher Full Text

[57] 57. Nambiar VR, Pachidis V: Nacelle intake flow separation reduction at cruise condition using active flow control. Propulsion and Power Research. Sep. 2022; 11(3): 337–352. Publisher Full Text

[58] 58. Stankowski TP, Macmanus DG, Robinson M, et al.: Aerodynamic effects of propulsion integration for high bypass ratio engines. J. Aircr. 2017; 54(6): 2270–2284. Publisher Full Text

[59] 59. Vassberg JC, Dehaan MA, Rivers SM, et al.: Development of a Common Research Model for Applied CFD Validation Studies.

[60] 60. Otter JJ, Stańkowski T, Robinson M, et al.: Installation aerodynamics of civil aero-engine exhaust systems. Aerosp. Sci. Technol. Jun. 2019; 89: 345–355. Publisher Full Text

[61] 61. Datta B, Goel V, Garg S, et al.: Study of Various Passive Drag Reduction Techniques on External Vehicle Aerodynamics Performance: CFD Based Approach. International Research Journal of Engineering and Technology. 2008; 1851. Reference Source

[62] 62. Young T: Performance of the Jet Transport Airplane: Analysis Methods, Flight Operations, and Regulations.2017. Publisher Full Text

[63] 63. Kumar M, Fernando DX, Kumar RM: Design and Optimization of De Lavel Nozzle to Prevent Shock Induced Flow Separation.2013. Reference Source

[64] 64. Karthik A, Srinivas G, Naik N: Implementation of higher-order PIMPLE algorithm for time marching analysis of transonic wing compressibility effects with high Mach pre-conditioning. Eng. Sci. May 2022; 20. Publisher Full Text

[65] 65. Ajay Kumar JK, Sudheendra Prabhu K, Veerendra AS, et al.: AERODYNAMIC PERFORMANCE ENHANCEMENT OF CRM NACELLE UNDER TRANSONIC FLOW: A COMPREHENSIVE CFD-BASED OPTIMIZATION APPROACH. Zenodo. 2025. Publisher Full Text

Aerodynamic Performance Enhancement of Crm Nacelle Under Transonic Flow: A Comprehensive Cfd-based Optimization Approach

Abstract

Background

Methods

Results

Conclusions

Keywords

1. Introduction

Figure 1. Main parts of an aircraft nacelle.2

2. Literature review

2.1 Experimental research studies on aircraft engine nacelle

2.2 Numerical research studies on aircraft engine nacelle

2.3 Theoretical research studies on aircraft engine nacelle

2.4 Summary of the literature review

2.5 Quantitative analysis

Table 1. Quantitative analysis.

2.6 Research gaps

2.7 Research objectives

3. Methodology

Figure 2. Research methodology flowchart.

3.1 Baseline analysis

Figure 3. CRM nacelle dimensions.

Table 2. Geometry specifications and reference quantities of the nacelle.

Figure 4. Cylindrical farfield dimensions.

Figure 5. Mesh representation of wing model along with farfield and inflation layer.

Table 3. Detailed mesh settings for aerodynamic analysis of the nacelle.

(1)

(2)

(3)

(4)

(5)

Figure 6. Boundary conditions for the nacelle aerodynamic analysis.

Table 4. Boundary conditions used in the nacelle aerodynamic analysis.

(6)

(7)

(8)

Figure 7. Convergence graph of the nacelle analysis.

4. Results and discussions

4.1 Grid independency test

Figure 8. Wing grid independency plot.

Table 5. Error evaluation and grid independency test results of the nacelle aerodynamic analysis.

Figure 9. Grid independency test pressure contours.

4.2 CRM nacelle pressure contour comparison

Figure 10. Pressure contour comparison of the CRM nacelle with comparison graph.

4.3 Different turbulence model

Figure 11. Number of cells vs Cd at six different turbulence models.

Table 6. Cd value for different turbulence models.

Figure 12. Pressure contours for the CRM wing using different turbulence models.

4.4 Varying Mach numbers

Figure 13. Cd value vs different Mach numbers.

Table 7. Cd value for different Mach number.

Figure 14. Flow contours at 0.8 Mach.

Figure 15. Flow contours at 0.85 Mach.

Figure 16. Flow contours at 0.9 Mach.

Figure 17. Flow contours at 0.95 Mach.

Figure 18. Flow contours at 1 Mach.

Figure 19. Flow contours at 1.05 Mach.

Figure 20. Flow contours at 1.1 Mach.

Figure 21. Flow contours at 1.15 Mach.

Figure 22. Flow contours at 1.2 Mach.

Figure 23. Flow contours at 1.25 Mach.

Figure 24. Flow contours at 1.3 Mach.

4.5 CRM nacelle design optimization

Figure 25. CRM nacelle aerodynamic design optimization.

Figure 26. Cl vs number of cells in millions.

Table 8. Nacelle optimization grid independency test results.

Table 9. Cl at different turbulence models.

Figure 27. Number of cells vs Cl at six different turbulence models.

Figure 28. Cl vs different cone angles.

Table 10. Cl with respect to different cone angles.

Figure 29. Flow contours at 13.7° cone angle.

Figure 30. Comparison of the optimized nacelle with baseline.

5. Combined results and discussions of baseline and optimized nacelle

Figure 31. Overall Cd values vs different numerical techniques.

Figure 32. Overall Cl values vs different numerical techniques.

6. Conclusions and future scope

Ethics and consent

Data availability statement

References

Comments on this article Comments (0)

Figure 1. Main parts of an aircraft nacelle.²

Figure 11. Number of cells vs C_d at six different turbulence models.

Table 6. C_d value for different turbulence models.

Figure 13. C_d value vs different Mach numbers.

Table 7. C_d value for different Mach number.

Figure 26. C_l vs number of cells in millions.

Table 9. C_l at different turbulence models.

Figure 27. Number of cells vs C_l at six different turbulence models.

Figure 28. C_l vs different cone angles.

Table 10. C_l with respect to different cone angles.

Figure 31. Overall C_d values vs different numerical techniques.

Figure 32. Overall C_l values vs different numerical techniques.