Inferring and simulating a gene regulatory network for the sympathoadrenal differentiation from single-cell transcriptomics in human.

Data preparation

The raw data is available at GEO GSE14782.

The processed adrenal.human.seurat.scrublet.rds dataset used in this study can be found at http://pklab.med.harvard.edu/artem/adrenal/data/Seurat/.

This represents single-cell transcriptomic analysis using 10x chromium on isolated individual cells from dissected adrenal glands with surrounding tissue from human embryos at 6, 8, 9, 11, 12, and 14. The initial matrix displays the expression of 25787 genes across 72571 cells. Only cells harboring a cell doublet probability (Scrublet score) <0.2 were kept.

The cell types were annotated by the authors based upon gene expression pattern.

To elucidate the sympathoadrenal cell fate transitions in humans at a higher resolution, we focused on the 3,901 cells of SCP, chromaffin, and sympathetic fates, omitting annotated cell cycle genes. As advocated by the authors, we removed a small potentially contaminating population of cells expressing the STAR gene. This resulted in a final matrix displaying the expression level of 20807 genes in 3759 cells at six developmental time points. We verified that the UMAP generated from this dataset was in perfect agreement with Figure 2a in the original paper (see Figure 1a). UMAP was computed using the Uwot package.²² All the UMAPs were embedded within the experimental UMAP using a combination of the ret_model and umap_transform functions of the uwot package.

Figure 1. UMAP representation of the dataset.

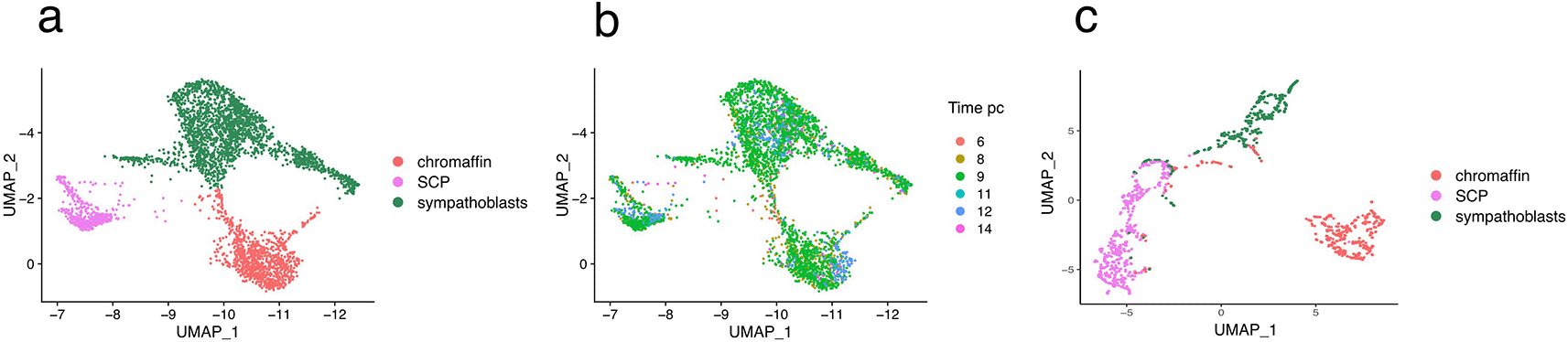
a and b: the initial 3759 cells x 20807 genes matrix. c: the final 1800 cell x 97 genes dataset after time sampling (see Figure 2). In a and c cells are color-coded according to their cell fate. In b, cells are color-coded according to their sampling time.

Stemness score

The stemness score was computed per cell as signature_SCP/signature_SCP + signature_sympatoblast + signature_chromaffin, by summing up the gene expression level for the following signature genes:

GRN inference and representation

First, we cloned the original CARDAMOM git repository at https://github.com/ogandril/cardamom. All computations were performed at the IN2P3 computing center (https://cc.in2p3.fr). The scripts used for launching CARDAMOM on a distant server are available at https://github.com/ogandril/Launching_Cardamom. All interaction values were scaled by a factor of 10 and thresholded at a value of four to maintain only the most relevant interactions.

The resulting inter.csv interaction matrix was opened with R²³ and plotted using the qgraph package.²⁴ A list of transcription factors was obtained from https://github.com/saezlab/CollecTRI.²⁵ Violin plots were drawn using the ggbeeswarm package.

GRN simulation

The simulation was performed using the CARDAMOM build-in version of HARISSA, a software for performing GRN simulations based on an underlying stochastic dynamical model driven by the transcriptional bursting phenomenon.²⁶

The dynamics of each gene is given by the following ordinary differential equations:

E_i can randomly switch from 0 to 1 (activation) with a protein-dependent rate k_on,i (P) and from 1 to 0 (inactivation) with a constant rate k_off,i.

We define the protein-dependent rate function k_on,i as in Ref. 26.

Because we simulated a mechanistic model, one needs to provide HARISSA with half-lives for both mRNAs (d _0,i) and proteins (d _1,i). Experimentally determined values for mRNAs and proteins were extracted from²⁷ and,²⁸ respectively. Genes that were not found in these datasets were attributed to the mean value of experimentally determined half-lives. Degradation rates were obtained using the following formula: degradation rate = ln(2)/half-life. The half-lives of proteins were limited by a parameter called the cell cycle, which was set to 20h.

Color code for a rapid estimation of the fit quality was as follows: given all Kantorovich distances for all genes at all times, we considered that 40 % of the values should be considered as correct (after a careful examination of the marginals) and therefore colored in green. The remaining 60% was split into two, the first half colored in orange, and the last half colored red.

Dynamical GRN representation

In CARDAMOM,we compute at each time point t_i with i ≥ 1 the value of each interaction, using

So we do obtain at each time t_i a variation in the network

T being the latest time point available.

The dynamical interactions ${\mathrm{\Theta }}_{\mathrm{i}}^{\mathrm{k},\mathrm{l}}$ can therefore be defined as:

1 being the indicator function.

Organizing the cells

Our first task was to organize the cells according to their differentiation status, as our GRN inference is anchored in the time-dependent evolution of the differentiation process. Cells were collected from human embryos at 6, 8, 9, 11, 12, and 14 weeks post-conception. First, we assessed whether this cell collection time could be a relevant framework for generating time-reconstructed data. As shown in Figure 1b, this was not the case, since all cell types were present at all collection times. This is in line with the fact that in the human adrenal gland, the transition from Schwann cell precursor (SCP) to sympathoadrenal states persists for several weeks,¹⁰ which leads to the expectation that cells at all stages of differentiation should be present at all collection times.

Therefore, we were faced with a different situation from the one we used to benchmark CARDAMOM, where the cell sampling time was in accordance with the actual process time.¹⁸

Consequently, we organized the cells according to their stemness scores ( Figure 2a).

Figure 2. Cell ordering by their stemness score.

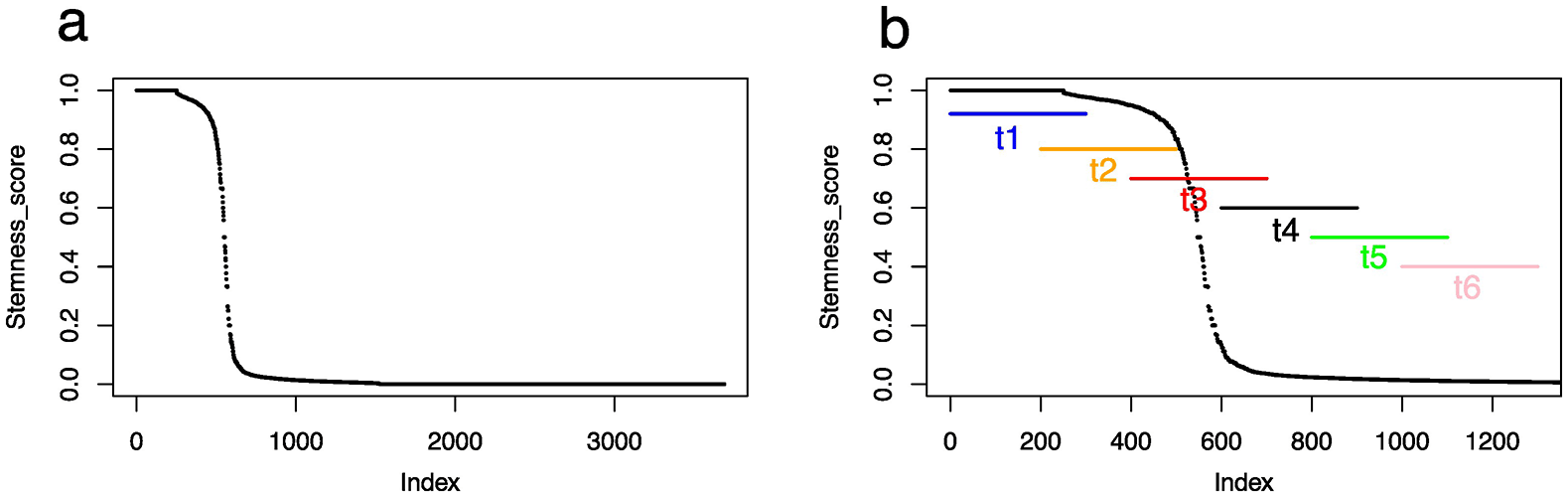
a: all cells are displayed. b: Focus on the first 1300 cells, where the “process time” are indicated. The process time is defined along six time point with sliding windows of 300 cells overlapping by 100 cells.

For this, we assumed a differentiation sequence starting with the SCP, giving rise to chromaffin cells and sympathoblasts through a bifurcation. Such a scheme is in line with the conclusions of the original paper from which we obtained dataset¹⁰ and is shared by most^6,12,13,29 but not all^4,30 authors working on sympathoadrenal differentiation in humans. This led to the definition of the stemness score (see Materials and Methods) as the ratio of SCP-signature gene expression, evolving from 1 (only the SCP signature genes are expressed) to zero (none of the SCP signature genes are expressed). This allowed us to define the “process time” ( Figure 2b) using an overlapping sliding window of 300 cells. This was defined only on the first 1300 cells since the stemness score was almost down to zero at the end of that sequence, and because we wanted to capture in detail the abrupt decrease in the stemness score. The use of an overlapping window is justified by the fact that differentiation should be considered a discontinuous nonlinear process (see e.g., Ref. 31), and therefore should allow cells to go back and forth in the gene expression space. This resulted in a 20807 genes x 1800 cells matrix.

Gene selection

We then explored the most relevant gene set to be used for the GRN inference. Because our inference and simulation scheme CARDAMOM is fundamentally rooted in exploiting the power of distributions,^18,32 we first computed a Kantorovitch distance³³ for all genes for all delta-times. Similarly, since most delta-entropic genes were shown to represent the most relevant genes for the differentiation process,³⁴ we also computed delta-entropy for all genes for all delta-times.

The combination of these two lists ( Figure 3) provided us with a list of 97 genes ( Table 1) that were used for inferring the GRN.

Figure 3. Gene selection procedure.

We first computed a Kantorovitch distance for all genes between 2 consecutive time points. We then took the union of the 133 genes harboring the largest distance for each delta-time, which left us with a list of 200 genes (some genes might be among the most distant between two or more time points), labelled MaxKD. Very similarly, we computed an entropy value for all genes between 2 consecutive time points. We then took the union of the 50 genes harboring the largest entropy for each delta-time, which left us with a list of 376 genes labelled MostDE. The union of those two lists gave us a list of 97 genes ( Table 1) that were used for inferring the GRN.

This left us with a matrix displaying the expression levels of 97 genes in 1800 cells distributed over six time points. We verified that the information contained within this matrix was sufficient to correctly capture the differentiation process of interest, as assessed by UMAP representation ( Figure 1c). It is important to note that these genes were chosen purely based on their expression patterns, irrespective of their putative biological functions (see Discussion).

GRN inference and analysis

We then applied the CARDAMOM algorithm to infer the GRN structure ( Figure 4a), resulting in a relatively densely connected network.

Figure 4. Representation of the inferred GRN structure.

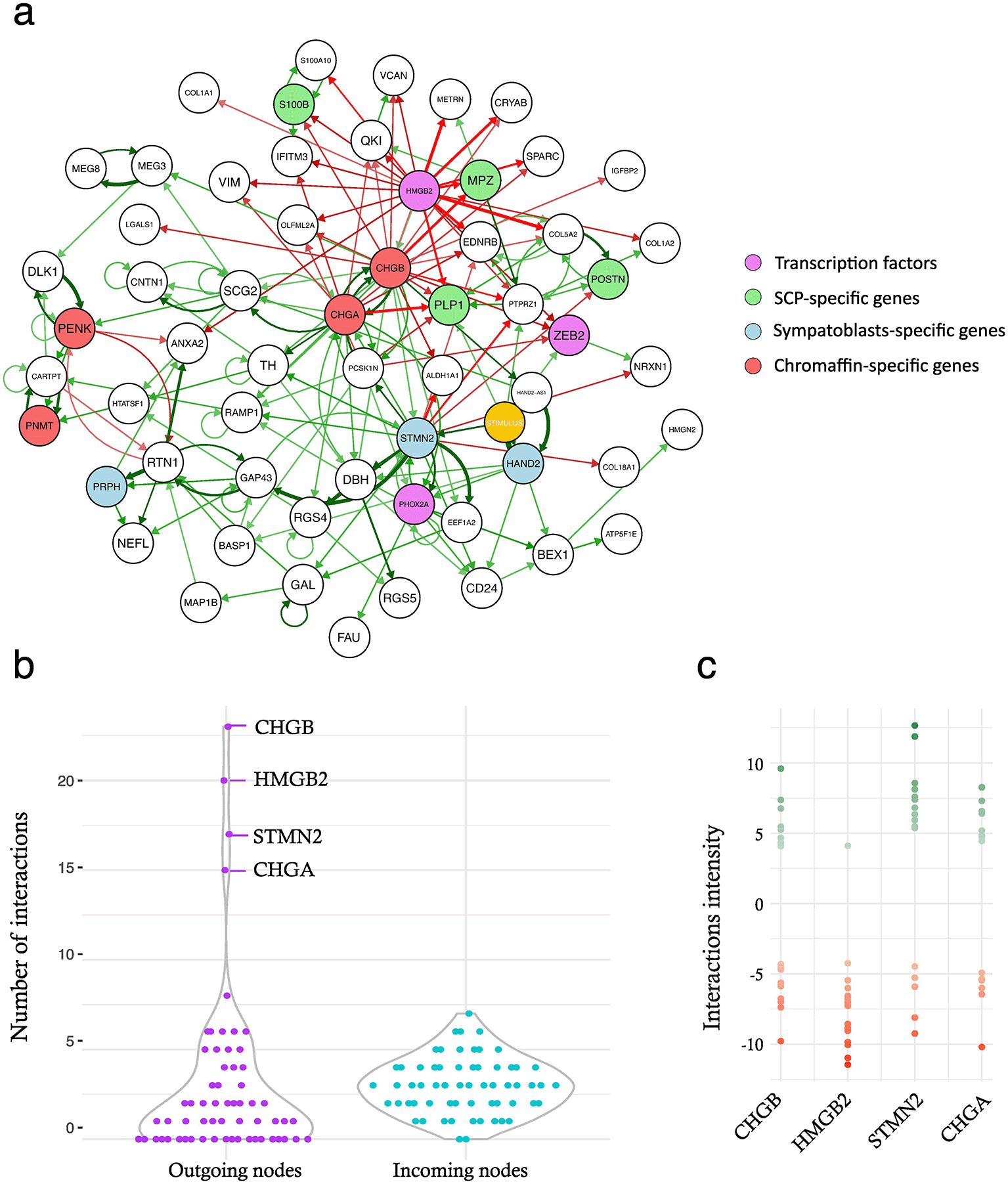
a: the full inferred GRN. Activations are displayed in green, inhibitions are displayed in red. The strength of the interaction is reflected by the arrow thickness. On the right is shown the color-code that has been applied to the GRN nodes. The stimulus is highlighted in yellow. b: violin plot representing the number of outgoing or incoming interactions per gene. c: the actual values of the outgoing interactions are shown for the four genes with the highest number of interactions.

First, we explored the network connectivity. We observed a striking difference between the distribution of the numbers of outgoing and incoming nodes ( Figure 4b). The incoming nodes were distributed according to a normal (i.e., Gaussian) distribution centered around a mean of three, whereas the outgoing nodes displayed a very heavy long tail toward higher values, as well as a large number of null values (i.e., leaves, that is, genes only receiving and not sending any signals within the GRN). The long tail was mostly due to 4 genes (CHGA, CHGB, STMN2, and HMGB2). The intensity of all outgoing interactions for these four genes is shown in Figure 4c. HMGB2 displayed a specific pattern with quasi-exclusively inhibitory interactions, whereas the other three genes displayed a relatively similar number of positive and negative interactions. It should be noted that all but HMGB2 are part of the defining gene signatures (see Materials and Methods).

One key feature of our inference process is the possibility of decomposing the overall GRN into dynamical subparts, where each edge appears at the time point transition for which it was detected with the strongest intensity by the inference algorithm ( Figure 5;¹⁸ see Materials and Methods for a formal definition).

Figure 5. Representation of the time-dependent evolution of the inferred GRN structure.

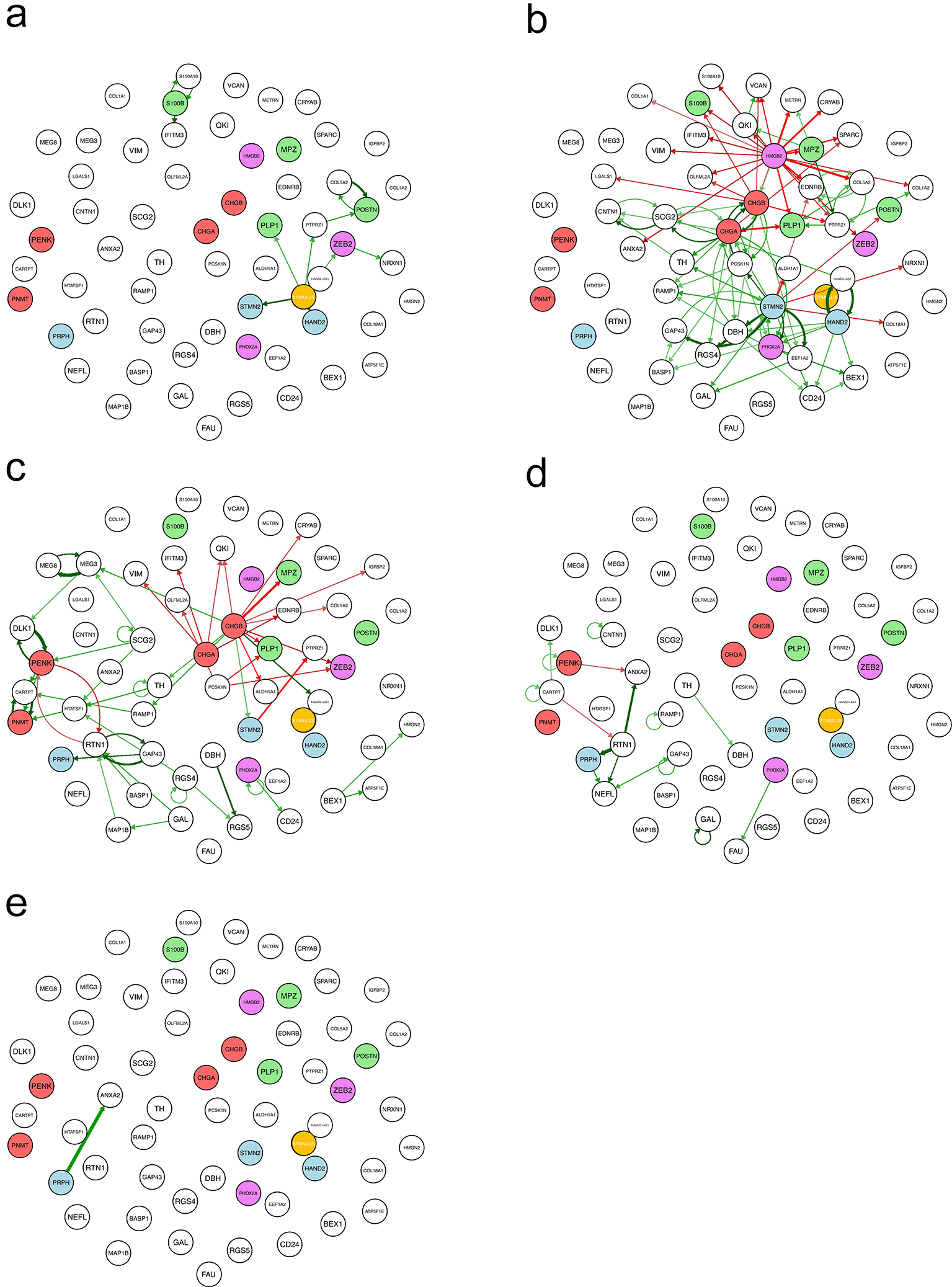
a: t1 → t2; b: t2 → t3; c: t3 → t4; d: t4 → t5; e: t5 → t6. For the time definition, see Figure 2. For the color-code applied to the GRN nodes, see Figure 4a. For the definition of the dynamical interactions displayed, see Material and methods.

The dynamics start with a small number of genes being turned on by the stimulus ( Figure 5a). In our previous studies, the stimulus was explicitly identified as an exogenous medium change/addition.^18,35 Here, it should be understood as a complex influence exerted by the cell environment, whether hormonal or through cell-cell interactions, which induces SCP cell differentiation. It is needed to “set the GRN in motion” and push the cells out of their quasi-steady state.

There was a much larger number of interactions important for the next time point ( Figure 5b), including a very large set of genes being repressed by HMGB2. All known SCP-specific genes were repressed at that point, which was expected. A CHGA-CHGB self-reinforcing loop activates genes from the chromaffin lineage, while a few sympathoblast-specific genes (STMN2, HAND2) are activated.

At the next time point, an RTN1-PENK toggle switch was apparently supported by positive loops on both sides ( Figure 5c). We can see a lot of genes being repressed by CHGA and CHGB genes. This includes the repression of MPZ-and PLP1 SCP-specific genes by CGHB, a chromaffin-specific gene.

The two latest time points showed a very small number of interactions ( Figure 5d and 5e).

It is clear that the two time points where there is a large number of interactions correspond to the times at which one observes a steep variation in the stemness score ( Figure 2). Altogether, this time decomposition offers a clear illustration of a signal propagating through the GRN in the form of waves of gene activation and repression.³⁵

Finally, we extracted from the full GRN a subset of the genes connected by specific dynamical motifs, that is, either cross-positive self-reinforcing loops or mutually repressive toggle switches ( Figure 6). Among these, only one direct toggle switch can be observed, the one linking PENK to RTN1 genes. All other motifs were positive. One can see a group of genes (COL5A2, PTPRZ1, EDRNB, POSTN), including one SCP-specific gene (POSTN) which reinforce together and are repressed concomitantly by chromaffin specific genes (CHGA and CHGB) and a sympathoblast-specific gene (STMN2).

Figure 6. Representation of a subset of the GRN showing genes involved in specific dynamical motifs.

GRN simulation

One of the main advantages of our approach is that it produces executable GRN models,³⁶ the time-dependent evolution of which can be simulated, and the resulting simulated dataset can be compared with the experimentally observed dataset.

There are many ways in which the results of a simulation can be assessed. Using a UMAP representation allows for quick evaluation of the quality of the fit. This was first used to calibrate the process times t1–t5 in real time ( Figure 7).

Figure 7. Adjusting the process time to real time values.

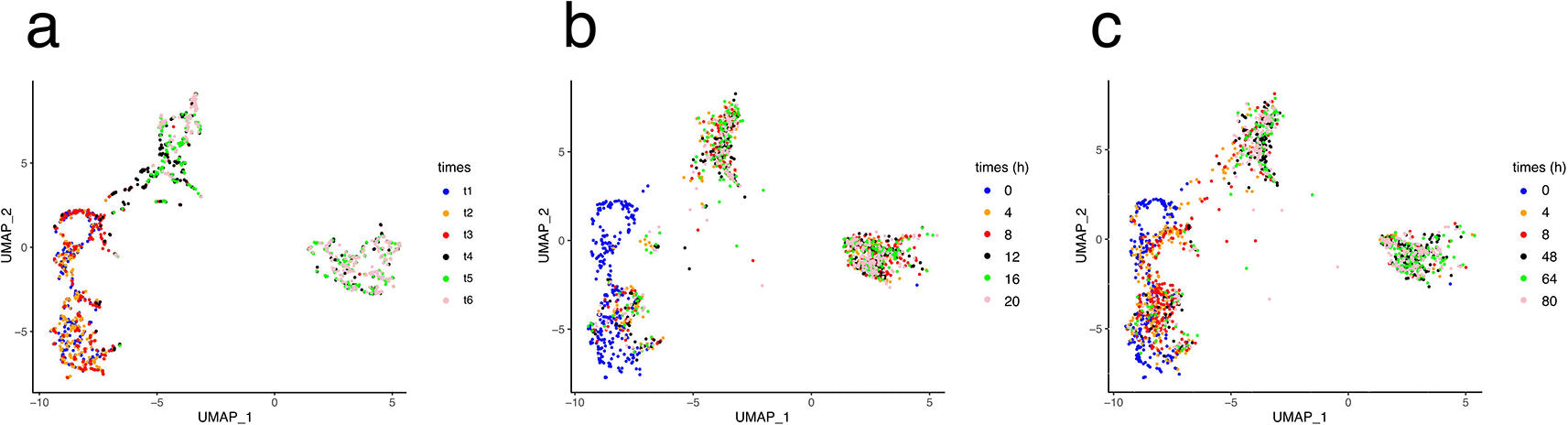
In a, the UMAP is computed on the experimental dataset and color coded according to the process times (see Figure 2). b and c: the UMAP is computed on the simulated dataset and color coded according to the model time, in hours.

We first tested an evenly spaced time frame, where each time point was set 4 h apart ( Figure 7b). All the cells were instantly projected from their t1 position to the final position of the process. Therefore, we attempted different adjustments and obtained the best visual fit using a time sequence extending up to 80 h ( Figure 7c), which was used for further simulations.

We then assessed the extent to which the simulation captured the time-dependent evolution of a few genes whose expression was characteristic of the three cell types we were trying to reproduce ( Figure 8).

Figure 8. UMAP representation of the dataset used for GRN inference (a-f ) and of the dataset obtained through GRN simulation (g-m).

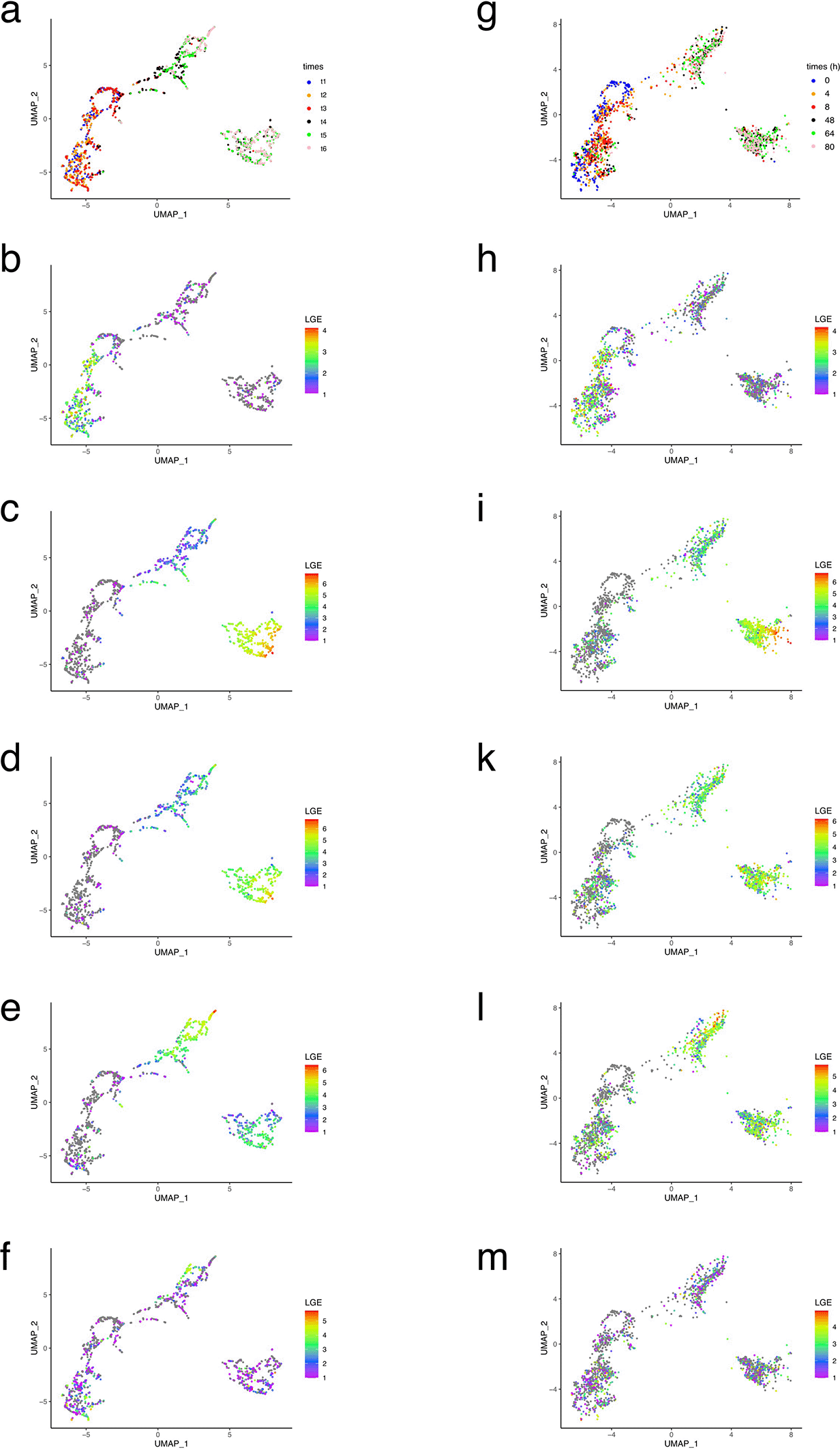
The cells are colored coded according to: (i) time (a and g); (ii) ZEB2 expression level (b and h); (iii) CHGA expression level (c and i); (iv): CHGB expression level (d and k); (v): STMN2 expression level (e and l) and (vi): HMGB2 expression level (f and m). All gene expression are log-transformed (LGE= ln(x+1)).

Overall, the gene expression pattern, when observed through its UMAP projection, was quite well reproduced by our GRN simulation. Most notably, chromaffin/sympathoblast bifurcation was quite well captured by our model.

Another way to assess the quality of the fit is to investigate the distance between the distribution of gene expression values of the experimentally observed mRNA distribution and the simulated distribution. As shown in Figure 9, there was a close proximity between the two distributions, as assessed by a low Kantorovich distance for the four genes displayed. Altogether, although some refinement could be performed (see discussion), we considered the fit quality of the experimental dataset to be quite satisfactory.

Figure 9. Fit quality for each gene at each time point as assessed by the Kantorovich distance (Kanto.dist) between the experimentally observed mRNA distribution and the simulated distribution.

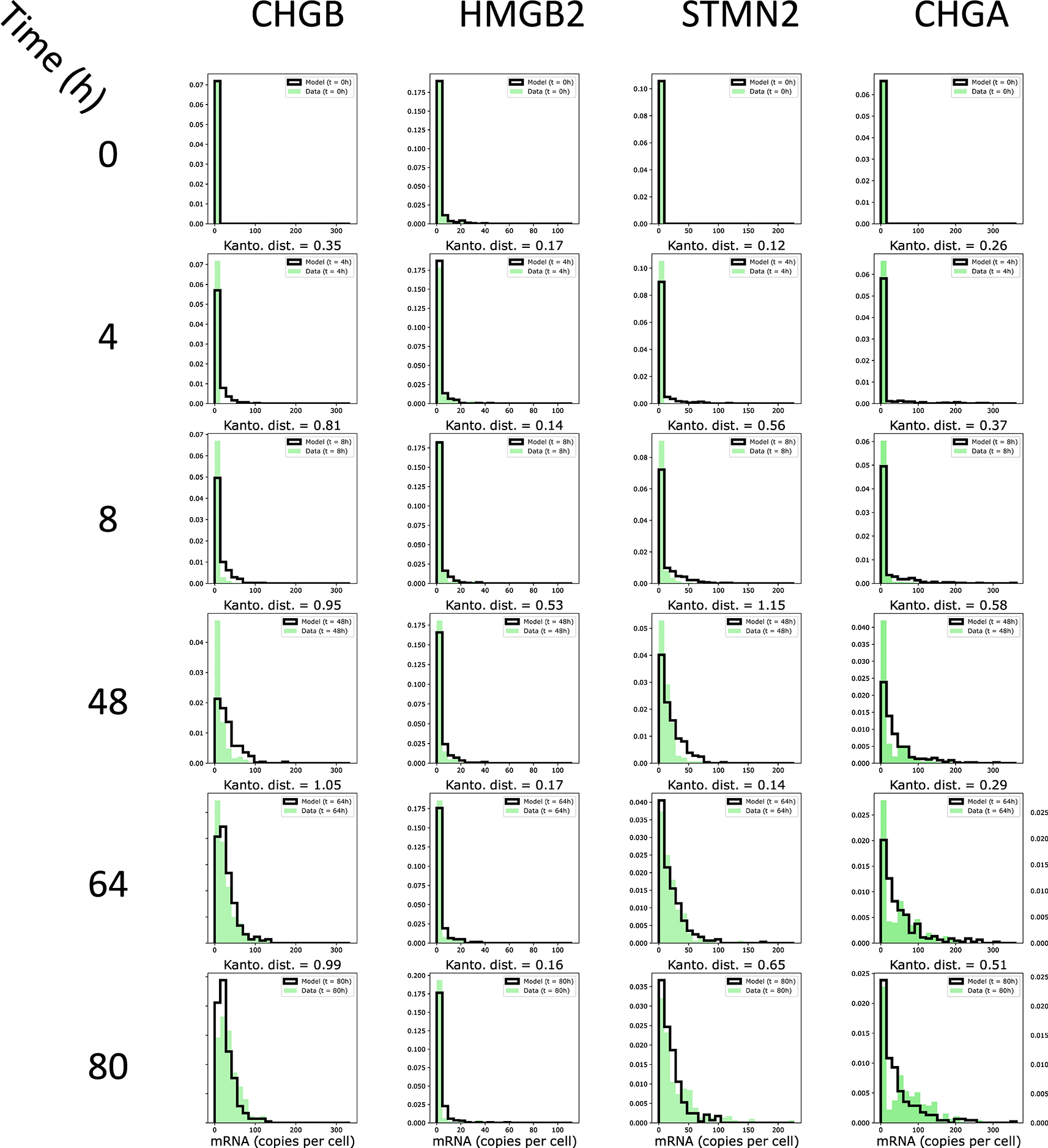
The marginals computed by the model are shown by bold-delimited bars, the experimenatlly-observed margnials are shown as plain bars in green.

We finally analyzed the run-to-run variability of the model, given the intrinsically stochastic behavior of our gene expression model (see “GRN simulation” upper). We therefore performed 10 runs of the GRN without specifying the seed, and analyzed the result by taking advantage of the clear separation of the three cell types in the 2D UMAP space ( Figure 1c). This allowed us to count the number of cells belonging to each cell type following the simulation ( Figure 10). We observed a very reproducible behavior of our model with only marginal differences between the number of cells for each cell type between different simulations.

Figure 10. The UMAP space was divided in three regions, representing SCP, sympathoblasts and chromaffin cells (see Figure 1c).

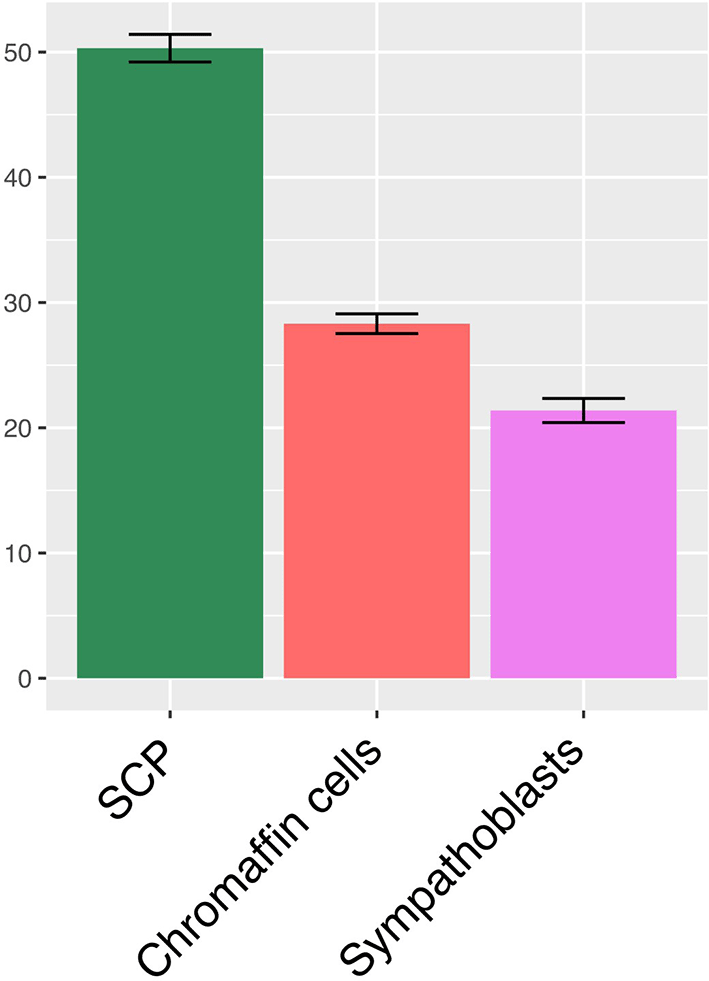
Shown the mean +/- SD of the percent of cells belonging to each cell category, as assessed by their 2D UMAP position, in 10 independent runs of the model.