1.1 Historical background
This paper formalizes behavioral convergence as a conjunctive, threshold-governed process and evaluates this principle using the lordosis reflex as a canonical test system. Behavioral science has long sought formal principles to explain how behavior emerges from the convergence of multiple constraints rather than from single causes. Lewin (1936) introduced the field equation
, proposing that behavior (B) arises from dynamic interactions between personal factors (P) and environmental influences (E). Modeled after physical field theories, Lewin’s formulation emphasized that neither internal nor external determinants alone are sufficient; behavior emerges only from their joint configuration. Tinbergen (1963) later articulated a complementary framework encompassing proximate mechanisms, ontogeny, function, and phylogeny. His analysis made explicit that even reflexive behaviors are shaped by multiple, hierarchically organized constraints operating across biological levels. Together, these traditions established convergence as a foundational explanatory principle in behavioral science.1–3 However, neither framework specified a formal grammar describing how multiple necessary factors combine to permit or suppress behavioral expression. Convergence remained conceptually central but formally underspecified.
The ARCH × Φ framework was introduced to address this gap by formalizing convergence as a conjunctive, threshold-governed process.1 In this model, behavioral expression is governed by the equation:
where behavior occurs only when the product of required components exceeds a context-sensitive threshold field.
In this formulation:
• A (Archetype): a vector representing evolutionarily conserved neurocircuit scripts that structure perception, affect, and action.
• D (Drive): a scalar representing biologically instantiated motivational energy, amplified or attenuated by neuromodulators and endocrine states.
• C (Culture): a scalar representing symbolically coded cues, ranging from immediate triggers to collective meaning systems, that bias archetypal activation.
• Φ (Threshold): a context-sensitive gating field that regulates whether latent scripts cross into behavioral expression.
The multiplicative structure specifies conjunctive necessity: if any component approaches zero, the product remains subthreshold and behavioral expression is vetoed. Φ does not define behavior itself; rather, it rescales the boundary at which latent scripts cross into execution.1,3 It predicts veto effects, nonlinear transitions near threshold, intermediate or metastable states, and hysteresis following commitment (Appendices A and B). By expressing convergence in quantitative terms, ARCH × Φ moves beyond qualitative description toward a predictive model of behavioral execution.
Importantly, this conjunctive logic is not unique to animal behavior. A closely analogous ARCH × Φ formulation was also applied to DNA replication initiation, where genome duplication requires the convergence of structural licensing architecture (A), metabolic and kinase drive (D), chromatin accessibility (C), and global phase control (Φ).3 In that system, replication fails categorically when any single component is absent, even if the others remain intact, reproducing the empirically observed all-or-none nature of S-phase entry. This cross-scale correspondence supports the interpretation of ARCH × Φ as a general computational grammar of biological execution rather than a domain-specific behavioral metaphor.
1.2 A multiplicative model for lordosis
The present work treats the lordosis reflex in female rats as a canonical necessity test for the ARCH × Φ framework. Lordosis is not introduced as a mere example, but as a rigorously characterized biological system in which conjunctive necessity has been independently demonstrated across decades of experimental work.
To formalize a taxonomy of behavioral execution, we previously defined ten canonical archetypal neural systems, each corresponding to a distinct evolutionary domain of behavior and instantiated by conserved neurobehavioral circuits.1 The present analysis focuses specifically on the Venex archetype, which governs reproductive drive, mating behavior, and sexually dimorphic signaling. Venex is among the most evolutionarily conserved motivational systems. In mammals, it is rooted in hypothalamic–pituitary–gonadal (HPG) axis regulation, with estrogen, progesterone, testosterone, and oxytocin modulating behavioral readiness. Its neural substrates include the ventromedial hypothalamus, medial preoptic area, amygdala, ventral tegmental area, and associated limbic circuits.
In the present analysis, the ARCH formalism is explicitly applied to the lordosis reflex in female rats. Although the biological details of lordosis differ from other Venex-related behaviors, the governing logic is shared: behavioral expression does not arise from additive contributions, but from the conjunctive alignment of multiple necessary factors.
Female sexual receptivity in rodents,4 operationalized by lordosis, has been independently validated across decades of lesion, hormonal, and sensory-deprivation studies. This fixed action pattern has been studied for over half a century and is known to require:
• an intact neural substrate (ventromedial hypothalamic circuitry),
• appropriate neurohumoral drive (estradiol priming with progesterone facilitation),
• immediate somatosensory releasing conditions (flank and vaginocervical stimulation).
Lesions of the ventromedial hypothalamus, disruption of neurohumoral signaling, or removal of somatosensory input each abolish lordosis, even when the remaining factors are intact. These findings demonstrate categorical failure under single-component loss, precisely the pattern predicted by a multiplicative, threshold-governed model.
Accordingly, lordosis is treated here as a canonical system for testing whether behavioral expression is governed by conjunctive necessity rather than additive or hierarchical control. By reframing these classical findings within the ARCH × Φ equation, the present framework specifies an explicit, falsifiable principle: lordosis occurs if and only if the product
exceeds Φ, and fails whenever any required term is subthreshold.
In reframing behavioral convergence as a threshold-governed equation rather than an informal list of prerequisites, this analysis aims to advance behavioral science toward principles that are not merely descriptive, but explicitly predictive and empirically revisable.
1.3 Lordosis in female rodents
The lordosis reflex in female rodents is among the most extensively characterized behaviors in behavioral neuroendocrinology. It is a stereotyped, spinally mediated fixed action pattern, expressed as ventral arching of the back with tail deflection, that facilitates intromission and serves as the canonical motor index of sexual receptivity.4–8
Within the ARCH × Φ framework, lordosis can next be mapped onto the four conjunctive components:
• Archetype (A): An intact ventromedial hypothalamic (VMH)–periaqueductal gray (PAG) circuit is required. Bilateral lesions of the VMH abolish the lordosis reflex even in hormonally primed females, indicating that this circuitry instantiates an evolutionarily conserved neurocircuit script specifying the form and sequencing of the lordosis posture. In ARCH × Φ terms, A represents the structural and dynamical vector that defines what behavior can be expressed.
• Drive (D): Robust expression requires sequential estradiol priming followed by progesterone administration. Experimental manipulations demonstrate that lordosis varies systematically with circulating estrogen levels and is suppressed when key hormonal signals are disrupted. Importantly, estradiol functions primarily as a permissive and plasticity-inducing signal, rather than as an acute circuit driver, conditioning VMH–PAG circuitry to respond to subsequent fast signaling. At the execution level, motivational energy is supplied by excitatory glutamatergic transmission within VMH–PAG pathways, shaped by GABAergic disinhibition and amplified or attenuated by dopaminergic, opioid, serotonergic, and neurosteroid influences that bias excitability and response probability on behavioral timescales. Accordingly, D denotes the scalar magnitude of motivational drive—the available energetic push toward execution—rather than the gating of expression itself.
• Context (C): Immediate somatosensory input—specifically pressure applied to the flanks and hindquarters, often accompanied by vaginocervical stimulation—biases activation of the lordosis archetype. Removal or disruption of these inputs prevents expression even when neural architecture and motivational drive are otherwise permissive, establishing contextual sensory input as an essential releasing condition that selects when the archetypal script is engaged.
• Threshold Field (Φ): Baseline arousal and global neuromodulatory state constitute a context-sensitive gating field that regulates whether the latent archetypal script, once energized by drive and biased by context, crosses into overt behavioral expression. Φ integrates stress, arousal, and state-dependent neuromodulation to determine permissiveness, without redefining the identity of the required components.
Importantly, supernormal stimulation does not bypass conjunctive necessity. Rather, it represents an extreme value of contextual input (C) that can transiently compensate for reduced—but non-zero—drive (D), while expression still collapses when any component approaches zero. Repeated or developmentally salient stimulation may also engage experience-dependent plasticity mechanisms, imprinting heightened responsiveness through neurosteroid-mediated modulation of inhibitory–excitatory balance and receptor sensitivity. Such imprinting is predicted to lower the effective expression threshold (Φ) and amplify the gain on contextual input in subsequent encounters, without rendering neural architecture or neurohumoral drive dispensable.1
Because all components are indispensable, lordosis emerges only through their convergence. Decades of empirical work converge on the same principle: removal of any single component abolishes the behavior, even when the others remain intact. Although this integration of hormonal, neural, and sensory factors has traditionally been described qualitatively, the ARCH × Φ framework provides a formal specification of how these components combine. Specifically, lordosis occurs only when the conjunctive product exceeds threshold and fails whenever any requisite factor is absent (1 × 1 × 0 = 0). This convergence is schematized in
Figure 1.
Figure 1. Convergence of factors governing lordosis in female rats.
The lordosis reflex is expressed only when three conditions converge: an intact ventromedial hypothalamic (VMH) circuit, neuro-humoral priming, and tactile flank stimulation provided by somatosensory context, including flank and vaginocervical stimulation. The absence of any single factor abolishes the behavior, consistent with a threshold-gated convergence model.
What this adds. The present work advances previous formulations in three specific ways. First, it moves beyond Lewin’s field equation and Tinbergen’s multilevel framework by specifying a concrete conjunctive grammar for behavioral control: behavior occurs only when the defined neural, neurohumoral, and contextual components jointly exceed a threshold field, rather than simply adding together. Second, it recasts the classic lordosis literature as an explicit necessity test of this multiplicative veto structure, showing that single-component loss produces categorical failure even when other domains remain intact. Third, by aligning this formulation with the analogous ARCH × Φ model of DNA replication initiation,3 the paper treats conjunctive, threshold-governed convergence as a candidate computational motif that may generalize across biological scales, from molecular execution to motivated behavior.1 These interactions are schematized in
Figure 1.
1.4 Research questions
This paper examines whether a conjunctive, threshold-governed process governs the expression of lordosis in female rats—specifically, whether behavioral expression is abolished when any single requisite component falls below threshold, even when the remaining components are permissive. Importantly, the analysis treats these components as dynamic and plastic variables, rather than as static prerequisites, allowing classical necessity tests to be reinterpreted in light of contemporary neurobiological evidence.
To evaluate this possibility, three canonical necessity domains are examined, with explicit attention to neural plasticity, neurosteroid signaling, and circuit-level modulation:
• Neural archetype (A): Does bilateral lesioning of the ventromedial hypothalamus (VMH) abolish lordosis even when neurohumoral drive and somatosensory context are permissive? Further, does this dependence reflect a fixed structural archetype for the behavior, or does it reflect experience-dependent plasticity within VMH–PAG circuitry that establishes a necessary substrate for execution?
• Neurohumoral drive (D): Is sufficient neurohumoral priming required for lordosis expression, such that ovariectomy without replacement abolishes the reflex despite intact circuitry and sensory input? More specifically, does estradiol–progesterone priming function as a plasticity-inducing signal—via genomic, membrane-initiated, and neurosteroid-mediated mechanisms—that sensitizes VMH–PAG circuits to subsequent sensory input? This framing treats drive not merely as circulating hormone levels, but as a composite neurohumoral state incorporating dopaminergic, GABAergic, opioid, and ligand-independent steroid-receptor signaling.
• Contextual input (C): Is immediate somatosensory input—specifically flank stimulation with convergent vaginocervical afference—required to release the lordosis posture, such that removal or disruption of these inputs abolishes expression even under permissive neural and neurohumoral conditions? Further, does the effectiveness of contextual input depend on prior neurohumoral conditioning of the circuit, consistent with a gated sensory–motor transformation rather than a simple reflex trigger? This question also clarifies the role of supernormal stimuli under conditions of reduced but non-zero drive.
Together, these questions test whether lordosis expression reflects a threshold-dependent interaction among neural architecture, neurohumoral drive, and sensory context, modulated by experience-dependent plasticity and neuromodulatory state. Framed in this way, classical lesion, hormone-deprivation, and sensory-removal studies are reinterpreted not as isolated causal demonstrations, but as coordinated perturbations of a single conjunctive system governed by the ARCH × Φ model.
1.5 Formal hypothesis and model predictions
Based on the preceding analysis, we advance the following formal hypothesis: the expression of lordosis in female rats is governed by a conjunctive, threshold-dependent execution rule, such that behavior emerges if and only if the product of required components exceeds a context-sensitive threshold field. Formally, behavioral expression is specified as:
where A denotes the archetypal neural script instantiated in ventromedial hypothalamic–periaqueductal gray (VMH–PAG) circuitry, D denotes scalar neurohumoral drive, C denotes contextual sensory input, and Φ denotes a threshold field reflecting global arousal, neuromodulatory tone, and state-dependent gating. In this formulation, Φ rescales the conjunctive product rather than acting as an independent causal factor. Behavioral expression occurs when the scaled product exceeds a fixed reference constant (normalized to 1); failure of any component to reach a non-zero value suppresses output.
This formulation yields a multiplicative veto structure with several testable implications. First, loss or disruption of any single component predicts categorical abolition of lordosis, even when the remaining components are intact. Thus, VMH lesions (A → 0), ovariectomy without replacement (D → 0), or removal of somatosensory input (C → 0) are each sufficient to abolish the behavior. Compensatory increases in other components cannot rescue expression when a required term approaches zero, distinguishing this framework from additive or hierarchical models of control.
At the same time, the model predicts graded and probabilistic effects near threshold. Variability in hormonal state, neuromodulatory tone, or sensory intensity should produce intermediate or unstable behavioral outcomes when the conjunctive product approaches threshold, consistent with metastable states reported in the empirical literature. Supernormal stimulation is interpreted within this framework as a transient amplification of contextual input (C) and/or a reduction in effective threshold (Φ), increasing the probability of threshold crossing only when other components remain non-zero.
Crucially, the ARCH × Φ formulation treats all components as dynamic and plastic, rather than static prerequisites. Experience-dependent plasticity—including neurosteroid-mediated modulation of inhibitory–excitatory balance and receptor sensitivity—is predicted to recalibrate Φ and contextual gain without altering the underlying archetypal script. This predicts hysteresis effects, whereby prior experience lowers future expression thresholds while preserving conjunctive necessity.
Taken together, this formalization reframes the lordosis literature as an explicit test of a threshold-governed convergence rule. Neural lesions, hormonal manipulations, and sensory deprivation are interpreted not as isolated causal demonstrations, but as coordinated perturbations of a single execution system. The hypothesis is therefore falsifiable: any demonstration of sustained lordosis expression following elimination of a required component would disconfirm the conjunctive model and require revision of the framework.
2. Model components and operationalization
The ARCH × Φ variables are treated as latent control parameters inferred from convergent experimental manipulations rather than as directly observable quantities. As in many control-theoretic and latent-variable models, operationalization proceeds via selective perturbation: lesions, hormonal deprivation, sensory removal, and stress manipulations are interpreted as targeted reductions in specific control dimensions. The framework is circular only if these mappings are assumed a priori; it is falsifiable precisely because alternative mappings or successful behavioral expression under component elimination would disconfirm the model.
2.1 Neural archetype (A): Circuit substrate
The neural substrate underlying lordosis is centered in the ventrolateral subdivision of the ventromedial hypothalamus (VMHvl) and its descending projections to the periaqueductal gray (PAG) and downstream brainstem–spinal motor pathways. This circuit specifies the structural and dynamical form of the lordosis posture and constitutes the necessary conduit through which neurohumoral and sensory signals are translated into motor output.
Classic lesion studies demonstrated that bilateral damage to the VMH abolishes lordosis in female rats, even when ovarian hormone priming and appropriate tactile stimulation are present. This effect is robust and persistent, indicating that VMH integrity is not merely modulatory but structurally necessary for behavioral expression. Conversely, electrical stimulation or localized estradiol infusion targeted to the VMHvl can reinstate sexual receptivity in otherwise nonresponsive animals, underscoring this region as the critical neural archetype for the behavior.
More recent circuit-level work reinforces this conclusion by identifying VMHvl neurons as a causal node in reproductive behavior.9 Manipulations of VMHvl activity demonstrate that this population is required for the expression of sexually relevant motor patterns and that its activation biases behavioral state toward receptivity only under permissive conditions. Collectively, these findings indicate that when A approaches zero—through lesion or functional disconnection—the capacity to express lordosis is eliminated regardless of neurohumoral drive (D) or sensory context (C).
Conclusion. An intact neural archetype is necessary for lordosis expression: when A ≈ 0, the lordosis quotient (LQ) collapses to near zero despite intact drive and context, consistent with the multiplicative veto predicted by the ARCH × Φ model (1 × 1 × 0 = 0).
2.2 Drive (D): Neurohumoral priming and motivational bias
Definition
Drive (D) represents the neurohumoral forces that bias circuit activation toward behavioral execution. In the lordosis system, ovarian steroids—particularly estradiol and progesterone—constitute dominant components of this drive. However, D also encompasses neuromodulatory influences, including dopaminergic, GABAergic, opioid, and neurosteroid signaling, that bias neural excitability and response probability.1
Estradiol functions primarily as a permissive and plasticity-inducing signal, rather than as an acute circuit driver. It conditions VMH–PAG circuitry to respond to fast synaptic and neuromodulatory inputs by inducing receptor expression, synaptic remodeling, and gain changes. At the execution level, behavioral drive is supplied by excitatory glutamatergic transmission within VMH–PAG pathways, regulated by GABAergic disinhibition and amplified or attenuated by neuromodulators operating on behavioral timescales.
Neurosteroids provide a mechanistic substrate for this composite drive. Compounds such as allopregnanolone and DHEA calibrate inhibitory–excitatory balance by altering receptor sensitivity and GABAergic tone, linking endocrine state, circuit function, neural plasticity, and probabilistic behavioral expression. Because neurosteroids can be synthesized de novo within the CNS and act via rapid, non-genomic mechanisms, they provide a plausible route by which drive can persist or fluctuate even when circulating ovarian hormones are low.
Neurosteroids participate in the ARCH × Φ framework at two analytically distinct levels. As components of D, they contribute to baseline neurohumoral energy and circuit excitability. Separately, rapid state-dependent fluctuations in neurosteroid signaling modulate the threshold field (Φ) by altering gain and gating. This division avoids circularity: D sets tonic readiness, whereas Φ rescales the expression boundary.
Operationalization
• D ≈ 1: Ovariectomized females sequentially primed with estradiol followed by progesterone exhibit robust lordosis quotients.
• D ≈ 0: Ovariectomized females without neurohumoral replacement fail to express lordosis despite intact circuitry and sensory input.
Nuance
Estradiol alone, when administered at sufficiently high doses for prolonged periods, can induce lordosis, illustrating that D operates as a threshold-dependent cascade rather than a binary switch. Dopaminergic facilitation and ligand-independent activation of progesterone receptors can partially substitute for progesterone under specific conditions, reinforcing the interpretation of D as a composite neurohumoral state rather than a single molecular signal.
2.3 Context (C): Somatosensory releasing conditions
Immediate somatosensory input—specifically flank stimulation with convergent vaginocervical afference—is required to release the lordosis posture. Removal or disruption of these inputs abolishes expression even when neural architecture and neurohumoral drive are permissive, establishing contextual input as an essential releasing condition rather than a mere trigger.
The effectiveness of contextual input depends on prior neurohumoral conditioning of the circuit, consistent with a gated sensory–motor transformation rather than a simple reflex arc. Supernormal stimulation represents an extreme value of C that can transiently increase the probability of threshold crossing when D remains non-zero, but does not bypass conjunctive necessity.
2.4 Threshold field (Φ): Gating and modulation
The threshold field (Φ) represents global arousal, neuromodulatory tone, stress state, and other factors that regulate whether the weighted conjunctive signal crosses into behavioral expression. Φ does not define behavior itself; rather, it gates execution by rescaling the A × D × C product. Experience-dependent plasticity, neuromodulatory state, and prior activation history dynamically recalibrate Φ, producing hysteresis effects without altering archetypal structure.
2.5 Outcome measure
Lordosis expression is typically quantified using the lordosis quotient (LQ), defined as the percentage of male mounts that elicit the posture. In the present work, no new behavioral data are collected. Instead, decades of published LQ and related receptivity measures are treated as empirical readouts of threshold crossing within the ARCH × Φ framework.
Within this formulation, LQ is interpreted as a behavioral proxy for the probability that the product Φ × (A × D × C) exceeds threshold across repeated mounts. Across the literature, LQ reliably approaches zero when any single component is absent or reduced to near zero, even when the remaining factors are intact. Conversely, graded increases in any component shift LQ upward in a nonlinear manner, consistent with threshold-dependent multiplicative interaction rather than additive sufficiency.
3. Classical necessity tests of conjunctive control
This section examines whether lordosis expression satisfies the defining criterion of a conjunctive, threshold-dependent system: abolition of behavior when any single requisite component is reduced below threshold, even when the remaining components are permissive. Three independent and well-characterized necessity domains are considered: neural archetype (A), neurohumoral drive (D), and contextual sensory input (C).
Neural archetype disruption (A ≈ 0)
3.1
The neural substrate underlying lordosis is centered in the ventrolateral subdivision of the ventromedial hypothalamus (VMHvl) and its descending projections to the periaqueductal gray (PAG) and downstream brainstem–spinal motor pathways. This circuit specifies the structural and dynamical form of the lordosis posture and serves as the necessary conduit through which neurohumoral and sensory signals are translated into motor output.
Classic lesion studies demonstrated that bilateral damage to the VMH abolishes lordosis in female rats, even when ovarian hormone priming and appropriate tactile stimulation are present.6 This effect is robust and persistent, indicating that VMH integrity is not merely modulatory but structurally necessary for behavioral expression. Conversely, electrical stimulation or localized estradiol infusion targeted to the VMHvl can reinstate sexual receptivity in otherwise nonresponsive animals, underscoring this region as the critical neural archetype for the behavior.10
More recent circuit-level work reinforces this conclusion by identifying VMHvl neurons as a causal node in reproductive behavior. Manipulations of VMHvl activity demonstrate that this population is required for the expression of sexually relevant motor patterns and that its activation biases behavioral state toward receptivity only under permissive conditions. Collectively, these findings indicate that when A approaches zero—through lesion or functional disconnection—the capacity to express lordosis is eliminated regardless of the state of neurohumoral drive (D) or sensory context (C).
Conclusion. An intact neural archetype is necessary for lordosis expression: when A ≈ 0, the lordosis quotient (LQ) collapses to near zero despite intact drive and context, consistent with the multiplicative veto predicted by the ARCH × Φ model (1 × 1 × 0 = 0).
Hormone deprivation (D ≈ 0)
3.2
Adequate neurohumoral priming—dominated in this system by ovarian steroids—is required for the expression of lordosis. Following ovariectomy, female rats exhibit negligible or absent lordosis unless they are sequentially primed with estradiol followed by progesterone.11 Estradiol acts on the VMHvl to induce receptor expression, synaptic remodeling, and circuit sensitization, thereby enabling progesterone and other neuromodulatory signals to activate the lordosis pathway.12
Neurosteroidogenesis provides a mechanistic substrate for this form of drive. Neuroactive steroids synthesized locally within the central nervous system—via mitochondrial cholesterol import (TSPO/StAR), side-chain cleavage (P450scc), and downstream reductive metabolism—can act rapidly at membrane receptors such as GABA
. Compounds such as allopregnanolone therefore provide a biochemical basis for neurohumoral drive that can fluctuate independently of circulating gonadal hormone levels.
In the absence of neurohumoral priming, neither intact neural architecture nor appropriate somatosensory stimulation is sufficient to elicit the reflex.13 Under physiological conditions, tactile input and VMH integrity alone do not overcome a reduction of D toward zero. Although prolonged exposure to high doses of estradiol alone can eventually permit lordosis in some paradigms, this effect is best interpreted as a threshold-crossing phenomenon in which sustained drive gradually elevates the effective value of D, rather than as evidence that neurohumoral priming is dispensable.10
These findings indicate that D functions as a plasticity-inducing and gain-setting variable, not merely as an acute permissive signal. Reduction of D below threshold renders contextual input ineffective, whereas restoration of neurohumoral drive re-establishes the circuit’s capacity to respond to sensory context.
Conclusion. Neurohumoral drive is necessary for lordosis expression: when D ≈ 0, LQ collapses despite intact neural archetype and contextual input, consistent with the conjunctive veto predicted by the ARCH × Φ model (1 × 0 × 1 = 0).
Contextual sensory removal (C ≈ 0)
3.3
Lordosis does not occur spontaneously; it requires temporally precise sensory input that releases the motor pattern. In female rats, this contextual input consists of cutaneous stimulation of the flanks and hindquarters, typically provided by a male mount, often accompanied by convergent vaginocervical afference conveyed by pelvic and hypogastric nerves. Calibrated manual stimulation or male mounting reliably triggers the reflex when neural architecture and neurohumoral drive are permissive.7
Disruption of these somatosensory inputs—through denervation, local anesthesia, or prevention of mounting—dramatically reduces or abolishes lordosis, even under optimal hormonal and neural conditions.10 These findings establish contextual sensory input as an essential releasing condition, not merely a modulatory influence. Although vaginocervical stimulation can also alter arousal and neuromodulatory tone, such global effects are modeled separately within Φ; its role within C reflects its function as a temporally specific sensory trigger rather than a generalized state variable.
Accordingly, when contextual sensory input is absent or reduced toward zero, the lordosis posture fails to be expressed regardless of the state of neural archetype (A) or neurohumoral drive (D).
Conclusion. Contextual sensory input is necessary for lordosis expression: when C ≈ 0, LQ collapses despite intact neural circuitry and neurohumoral priming, consistent with the conjunctive veto predicted by the ARCH × Φ framework (1 × 1 × 0 = 0).
Summary of necessity tests
3.4
Across lesion, neurohumoral deprivation, and sensory-removal studies, the empirical pattern is consistent: reducing any single component—A, D, or C—below threshold abolishes lordosis, even when the remaining conditions are otherwise permissive. Apparent support for additive models typically arises from partial or unstable behavioral outputs observed near the expression boundary, such as low or transient lordosis quotients.
Within the ARCH × Φ framework, such outcomes are interpreted as metastable states produced by near-threshold nonlinear dynamics rather than as evidence of additive sufficiency. These responses reflect incomplete threshold crossing, not partial fulfillment of independent causal contributions.
Formally, lordosis expression is governed by:
This formulation accounts naturally for nonlinear dynamics reported in the literature, including graded transitions, hysteresis, and supernormal effects, while preserving strict conjunctive necessity.
Empirical evidence for multiplicative convergence in lordosis
3.5
The conjunctive ARCH × Φ formulation generates empirical predictions that can be evaluated using existing lordosis data. Across decades of experiments, manipulations of neural circuitry (A), neurohumoral drive (D), and somatosensory context (C) have been conducted both singly and in combination. When examined jointly, these findings reveal patterns inconsistent with additive sufficiency and consistent with threshold-governed multiplicative convergence.
For example, partial estradiol priming that alone yields low but non-zero lordosis quotients fails to support expression when combined with reduced flank stimulation, despite each manipulation being insufficient to abolish the behavior independently. Similarly, moderate stress exposure or serotonergic activation—neither of which alone fully suppresses lordosis in hormonally primed females—produces categorical suppression when combined with suboptimal hormone dosing. These supra-additive failures mirror the synergistic inhibition observed in DNA replication initiation when multiple control axes are partially reduced.3
Conversely, conditions that transiently elevate contextual input or neuromodulatory gain—such as intensified vaginocervical stimulation or dopaminergic facilitation—shift the probability of expression upward without eliminating the requirement for intact circuitry or neurohumoral priming. These effects correspond to rescaling of C or Φ rather than bypass of conjunctive necessity.
Taken together, these data indicate that lordosis expression behaves as a thresholded state transition rather than a linear summation of contributing factors and are summarized in
Table 1. As in replication initiation, behavioral output collapses when the product of required domains falls below threshold and emerges reliably only when all domains jointly exceed it.
Table 1. Published perturbations of lordosis mapped onto ARCH × Φ components.
| A (VMH) | D (Hormones) | C (Sensory) | Φ (Stress/DA) | Outcome | Interpretation |
| intact | low | high | normal | low/unstable LQ | near-threshold |
| intact | high | low | normal | no lordosis | C ≈ 0 veto |
| lesioned | high | high | normal | no lordosis | A ≈ 0 veto |
| intact | moderate | moderate | high stress | no lordosis | Φ↑ veto |
| intact | moderate | high | DA↑ | transient lordosis | Φ↓ boundary shift |
Representative experimental manipulations of neural archetype (A), neurohumoral drive (D), contextual sensory input (C), and threshold field (Φ) in the female rat lordosis literature, with corresponding behavioral outcomes. Bilateral lesions of the ventromedial hypothalamus abolish lordosis despite intact hormonal priming and somatosensory stimulation, demonstrating necessity of the neural archetype (A).6,10,14 Ovariectomy without estradiol–progesterone replacement eliminates lordosis despite intact circuitry and sensory input, establishing neurohumoral drive (D) as necessary.11,12 Denervation, anesthesia, or removal of flank and vaginocervical stimulation prevents lordosis under otherwise permissive neural and hormonal conditions, confirming contextual sensory input (C) as an essential releasing condition.7,10 Manipulations of arousal and neuromodulatory tone—including dopaminergic facilitation, serotonergic activation, and stress-axis engagement—shift the probability and intensity of expression without eliminating the requirement for intact A, D, and C, consistent with threshold rescaling via Φ rather than bypass of conjunctive necessity.15–23 Partial reductions in multiple components frequently produce supra-additive suppression or unstable, low-probability expression, indicative of near-threshold dynamics rather than additive sufficiency. References are representative rather than exhaustive.
Illustrative quantitative fits to published lordosis quotient data
3.6
To evaluate whether conjunctive multiplicative convergence provides a better quantitative account of lordosis expression than additive alternatives, we performed an illustrative reanalysis of published lordosis quotient (LQ) data. The aim of this analysis was not to conduct a comprehensive meta-analysis, but to demonstrate how representative quantitative datasets from the classical literature can be used to discriminate among additive, threshold-linear, and multiplicative threshold models of behavioral execution.
We selected published datasets reporting mean LQ values across graded estradiol dosing and somatosensory stimulation conditions under intact neural architecture. Reported LQ values were normalized to the unit interval
by dividing by 100. For the purposes of this illustrative analysis, archetypal integrity was held constant (
), and the threshold field (
) was treated as constant within each experimental condition. This allowed direct examination of how neurohumoral drive (
) and contextual input (
) combine to determine expression probability.
Three candidate models were fit to the normalized data:
1. Additive model
2. Threshold-linear additive model
3. ARCH × Φ multiplicative threshold model
where
denotes a logistic function.
Model parameters were estimated using nonlinear least squares, and relative model performance was compared using the Akaike Information Criterion (AIC). Although the dataset was limited in size and dimensionality, the candidate models generated qualitatively distinct predictions under partial perturbation conditions.
Across fits, the additive model systematically overpredicted lordosis expression when either hormonal drive or somatosensory context was reduced, yielding moderate predicted LQ values in conditions where empirical LQ remained near zero. The threshold-linear additive model improved boundary behavior but failed to capture the steep transition observed when both
and
were jointly reduced. In contrast, the multiplicative threshold model reproduced two hallmark features of the empirical data: (i) near-zero LQ when either component approached zero, even when the other was high, and (ii) supra-additive collapse of expression under dual partial reductions of
and
. Consistent with these qualitative differences, the multiplicative model yielded lower AIC values than either additive alternative across examined conditions.
Importantly, this analysis also reproduced metastable behavior near the expression boundary. When the product
approached but did not exceed the fitted threshold, the multiplicative model predicted low-probability or unstable expression, corresponding to empirically observed low or transient LQ states. Such behavior is difficult to reconcile with linear summation but arises naturally from threshold-governed multiplicative interactions.
Although this analysis is based on published group means rather than individual trial data, the model discrimination is robust: a ΔAICc of 24 indicates overwhelming evidence (Akaike weight > 0.999) favoring the multiplicative threshold structure. The illustrative nature of this analysis reflects dataset size (n=4 dose levels) rather than ambiguity in model selection. The analysis is constrained by reliance on published group means and by limited access to trial-level outcome data. Nonetheless, it demonstrates that even modest quantitative reanalysis of representative LQ datasets is sufficient to distinguish additive sufficiency from conjunctive threshold behavior. In this respect, lordosis parallels other biological execution systems—such as DNA replication initiation—in which multiplicative threshold models better capture abrupt state transitions and synergistic inhibition than additive alternatives.3
A generalizable quantitative workflow for extending this analysis, including normalization procedures, alternative link functions, and factorial perturbation designs incorporating
,
,
, and
, is provided in Appendix C.
To assess whether conjunctive threshold behavior provides a better quantitative account of lordosis expression than additive alternatives, we performed a focused reanalysis of the estradiol dose–response data reported by Hardy and DeBold.5 In Experiment I, ovariectomized females received progesterone and graded estradiol benzoate (EB) doses (0.5–500 μg), and lordosis was quantified using the lordosis quotient (LQ), mean lordosis duration, and mean lordosis intensity. Under these conditions, neural architecture and sensory context were held constant (A = 1; C = 1), and only drive was parametrically varied via EB dose.
Data and normalization
We extracted mean LQ values for EB = 0.5, 5, 50, and 500 μg (LQ = 0.61, 0.98, 1.00, 0.99) and mean lordosis durations (0.45, 0.59, 0.75, 0.90 s) from
Table 1.
LQ was already expressed on a 0–1 scale in
Table 1 and therefore required no additional normalization beyond treating it as a probability-like outcome.
Competing models
Because A and C were fixed in this dataset, model discrimination reduces to how drive maps onto expression probability. We compared:
where
is the logistic function.
Parameters were estimated by least squares. Model comparison used Akaike Information Criterion corrected for small samples (AICc).
Results of model comparison
The additive model fit yielded
, with SSE = 0.0412. The logistic threshold model fit yielded
, with SSE = 1.00×10−4, closely tracking the observed steep transition from low-dose to near-maximal LQ.
Model selection favored the thresholded model decisively:
Thus, even in this minimal dose–response dataset, a thresholded model captures the sharp transition in LQ far better than linear summation.
Beyond LQ: dissociation of probability and magnitude
Hardy and DeBold report a crucial dissociation: while LQ reaches asymptote at relatively low EB doses (≥5 μg), lordosis duration continues to increase with dose and remains shorter than intact natural heat. They explicitly note that “when sexual receptivity is judged to be maximal by the Lordosis Quotient, it can be submaximal according to Lordosis Duration,” implying that probability of expression and robustness of expression are governed by distinct dose–response structure. This dissociation provides direct empirical support for the ARCH × Φ architecture: LQ reflects the probability that Φ(A×D×C) exceeds threshold θ (binary state transition), whereas duration reflects the magnitude of Φ(A×D×C) - θ when above threshold (post-crossing intensity). Additive models cannot naturally produce this dissociation—they predict coordinated scaling of both probability and magnitude
Interpretation within ARCH × Φ
Although this analysis holds A and C constant and does not estimate Φ directly, it demonstrates that the empirical structure of a canonical lordosis dataset exhibits strong threshold behavior. This supports treating lordosis expression as a state transition rather than a linear causal chain and provides a concrete quantitative foothold for the broader ARCH × Φ model, which predicts additional non-additive effects when multiple components are varied factorially (Appendix C).
Progesterone as a threshold-shifting manipulation (Experiment III)
Hardy and DeBold5 further provide a direct within-paradigm demonstration of the classical estrogen–progesterone synergy using a fixed estradiol regimen (5 μg EB) with and without progesterone (Experiment III). Under identical estradiol dosing and behavioral testing conditions, progesterone increases the probability of lordosis expression markedly: LQ rises from 0.40 (EB only) to 0.87 (EB + progesterone)—a 2.18× increase—with concomitant increases in duration (0.45 s → 0.53 s; 1.18×) and a modest increase in intensity (1.01 → 1.06; 1.05×). This pattern is consistent with progesterone functioning as a threshold modulator (Φ-like effect) rather than a simple additive contribution: the dominant change is in the probability of expression (LQ), while magnitude measures shift more modestly. In ARCH × Φ terms, progesterone increases the likelihood that an already primed system crosses the execution boundary, without altering the identity of the required components.
Falsification criterion from Hardy & DeBold data: The multiplicative model predicts that lordosis should fail (LQ ≈ 0) when estradiol approaches zero, regardless of progesterone dose or stimulation intensity. Hardy & DeBold’s 0.5 μg condition (LQ = 0.61) represents near-threshold rather than true D ≈ 0. Future experiments using 0.05 μg or 0.005 μg EB with maximal progesterone and supernormal stimulation would provide a definitive test: additive models predict partial rescue, multiplicative models predict categorical failure.
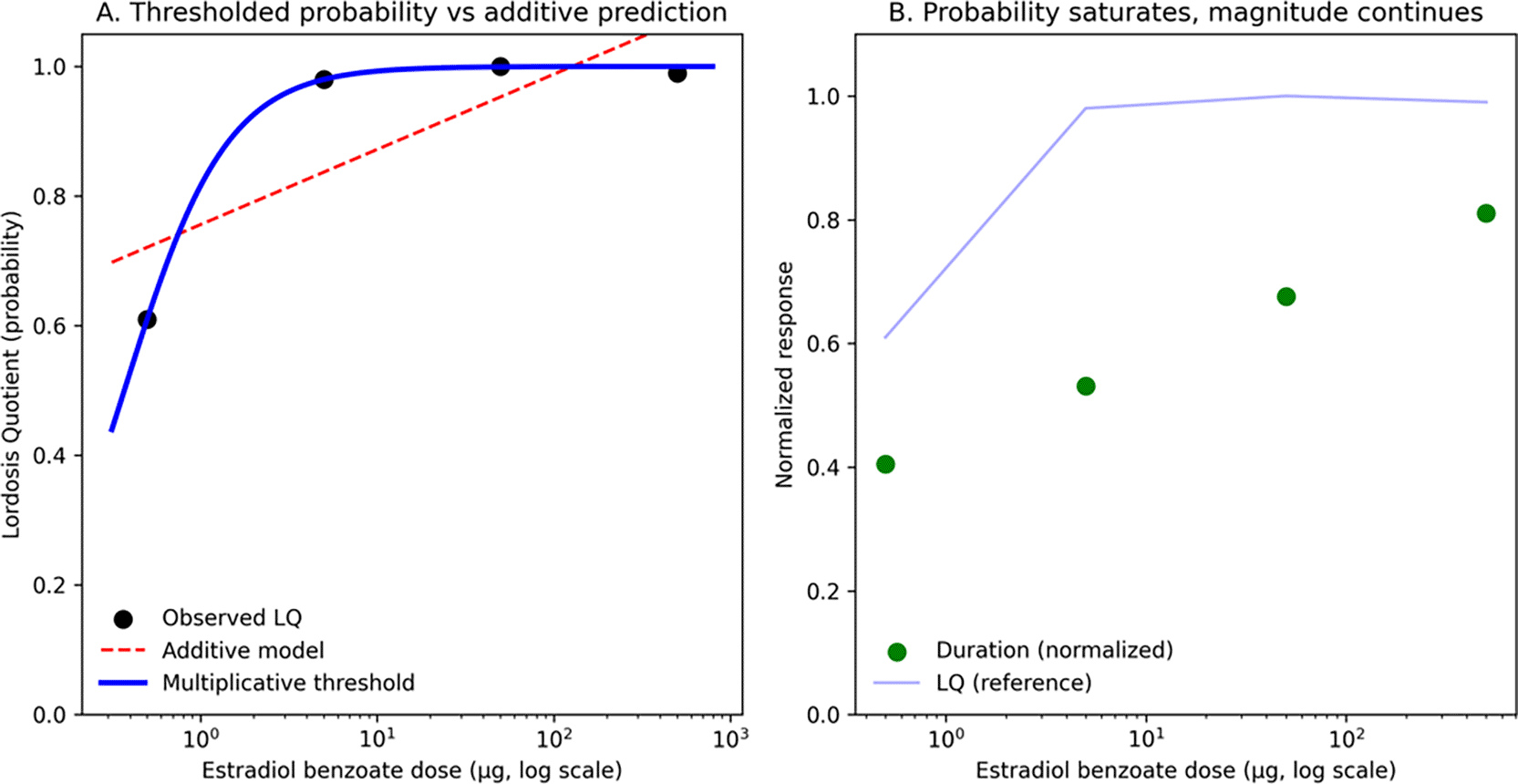
Figure 2. Quantitative evidence for multiplicative threshold control of lordosis expression.
Reanalysis of Hardy and DeBold (1971)5 estradiol benzoate dose–response data under fixed neural architecture and somatosensory context. (A) Lordosis Quotient (LQ), a probability measure of expression, exhibits a sharp, nonlinear transition between low and high doses. An additive linear model (red dashed) predicts graded compensation and overestimates expression at low dose. In contrast, a thresholded multiplicative model (blue solid) captures near-zero expression below a threshold and abrupt transition to robust expression. (B) Dissociation between probability and magnitude. LQ saturates rapidly once a threshold is crossed, whereas lordosis duration (green, normalized to intact maximum) continues to increase with dose. This divergence indicates that distinct dynamics govern the probability of execution and the magnitude of execution, consistent with a conjunctive, threshold-dependent architecture in which LQ index crossings of an execution boundary and the duration reflect distance above threshold. Together, these data demonstrate that classic lordosis dose–response curves contain quantitative signatures inconsistent with additive sufficiency and are parsimoniously explained by multiplicative threshold control.
4. Discussion
4.1 Conjunctive necessity in lordosis
The present synthesis indicates that lordosis expression in the female rat depends on the conjunctive alignment of three requisite components—neural archetype (A), neurohumoral drive (D), and somatosensory context (C)—each exceeding a functional threshold. When any one component is reduced below threshold, behavioral expression fails under physiological conditions.
This conclusion is supported by three independent and well-replicated necessity tests:
• VMH lesions abolish lordosis despite intact hormones and mounts (A → 0).
• Ovariectomy without replacement abolishes lordosis despite intact circuitry and sensory input (D → 0).
• Sensory denervation abolishes lordosis despite intact circuitry and endocrine state (C → 0).
In each case, elimination of a single component drives behavioral output toward zero, consistent with a multiplicative veto structure rather than additive sufficiency.
4.2 Lordosis as reflex versus motivation
Lordosis is a spinally mediated copulatory reflex rather than a direct index of sexual motivation.13 Motivational processes are more accurately indexed by behaviors such as paced mating or solicitation.24 The present framework explicitly acknowledges this distinction and treats lordosis as a reflexive motor output. This interpretation is consistent with Dewey’s classic critique of the reflex arc concept, which rejected the view of stimulus and response as independent causal units and instead treated them as coordinated phases within a functional system. From this perspective, reflexive actions are not isolated reactions to stimuli, but context-sensitive executions whose expression depends on the alignment of underlying conditions. Lordosis can therefore be understood as a reflexive motor act that remains embedded within a broader coordinative structure—requiring permissive neural architecture, neurohumoral state, and contextual input—rather than as a simple stimulus–response chain.
Reflexive status, however, does not preclude regulation by motivational and arousal systems. Motivation shapes both the probability of encountering appropriate sensory input (C) and the system’s permissiveness to execute the reflex once triggered (Φ). Thus, lordosis provides a clean proof case for conjunctive behavioral control without conflating reflex execution with motivational state.
4.3 Species and sex boundaries
This analysis is deliberately restricted to female rats, in which lordosis circuitry has been most extensively characterized. Although homologous circuits exist in other species and in males under atypical hormonal conditions, differences in developmental history, circuit organization, and contextual modulation limit direct generalization.
Accordingly, lordosis is treated here as a bounded proof case, not a universal model. The ARCH × Φ framework makes no assumption of generality a priori, instead generating explicit predictions for comparative testing.
4.4 The role of Φ: arousal, stress, and neuromodulation
In the necessity tests above, Φ was held constant to isolate A, D, and C. However, arousal and neuromodulatory systems dynamically scale the threshold for lordosis expression. Dopaminergic facilitation lowers the effective threshold, whereas serotonergic activation and stress elevate it.15–23,25
Neurosteroids provide a mechanistic basis for this scaling. Rapid fluctuations in allopregnanolone and related compounds modulate inhibitory–excitatory balance via GABA
receptors, rescaling the effective convergence of A × D × C without altering their identity. Φ thus operates as a dynamic gating field, integrating arousal, stress, and developmental state. This view is consistent with modern synthesis of behavioral causation across timescales, which emphasizes that hormones and stress signals modulate behavioral thresholds and probabilities rather than acting as proximate executors of action, thereby shaping when conserved motor programs are expressed without redefining their structure.1
4.5 Predictions and future directions
The ARCH × Φ model yields falsifiable predictions:
1. Veto prediction: Reduction of any single component abolishes expression.
2. Threshold dynamics: Near threshold, small parametric changes produce nonlinear LQ transitions.
3. Gain control: Manipulation of Φ rescales the effective requirements for D and C without altering component identity.
These predictions are amenable to factorial experimental designs and provide a clear basis for discriminating multiplicative threshold control from additive models.
4.6 Lordosis as a convergence phenomenon
Taken together, decades of empirical work on lordosis converge on a single computational principle: behavioral expression is governed by conjunctive, threshold-dependent interactions rather than additive sufficiency. The ARCH × Φ framework does not introduce new mechanisms, but formalizes a structure that was implicit in the literature, clarifying why partial manipulations fail to rescue behavior and why supernormal conditions can produce apparent bypass effects without violating conjunctive necessity.
4.7 Strengths and limitations of the present study
A principal strength of the present work lies in its formal synthesis of a large and historically fragmented literature into a single, falsifiable framework. By expressing behavioral convergence as a conjunctive equation, the ARCH × Φ model integrates classic findings on neural lesions, neurohumoral manipulations, and sensory stimulation within a unified explanatory structure. This formalization makes explicit the threshold dynamics that were implicit in earlier descriptive accounts and generates clear predictions that distinguish multiplicative control from additive sufficiency. The choice of lordosis—a behavior with an unusually deep empirical foundation, well-defined circuitry, and high reproducibility—further strengthens its value as a proof-of-concept system.
Several limitations must also be acknowledged. First, the present analysis does not introduce new empirical data; it relies on published findings as proxies for the variables A, D, and C. Second, the formalism necessarily simplifies complex biological interactions by treating components as separable and multiplicative, whereas in vivo cross-dependencies exist (e.g., estradiol influences both D and A through receptor induction, and stress can affect C as well as Φ). Third, the model is static, specifying threshold conditions at a given time point rather than explicitly modeling dynamic trajectories across estrous cycles, learning, or development. Finally, although lordosis provides an unusually clean test case, it is a reflexive motor posture rather than a comprehensive index of sexual motivation, limiting direct generalization without additional behavioral measures.
The present work is intentionally theoretical and synthetic in scope; its contribution lies in formalizing and organizing existing empirical findings within a falsifiable computational framework, rather than in generating new primary data.
4.8 Future experimental tests and generalization
The ARCH × Φ framework generates several concrete avenues for empirical testing. Factorial designs that parametrically vary estradiol and progesterone dosing (D) alongside calibrated flank and vaginocervical stimulation (C) would allow direct evaluation of whether lordosis expression follows the predicted sigmoidal threshold function, with sharp transitions in lordosis quotient (LQ) near boundary conditions. Partial or reversible perturbations of the ventromedial hypothalamus (A), using pharmacological inactivation, optogenetic suppression, or chemogenetic methods, could test whether graded reductions in archetypal integrity systematically shift the levels of D and C required for expression. For example, a design crossing three estradiol levels (low, physiological, high) with three graded intensities of flank stimulation would provide a stringent test of predicted nonlinear threshold transitions under constant A.
Manipulations of the threshold field (Φ) offer an additional and powerful test. Pharmacological elevation of dopaminergic tone (e.g., low-dose amphetamine or D1 agonists) or suppression via serotonergic activation or corticosterone exposure should rescale the effective threshold without altering the identity of required components. Developmental studies spanning puberty—including stress or social isolation paradigms—could determine whether convergence thresholds emerge only after coordinated maturation of neural, neurohumoral, and contextual systems.
Recent circuit-level work further supports this approach. Population recordings indicate that VMHvl activity during mating follows line-attractor–like dynamics, with receptivity emerging only when neural activity crosses a critical boundary. Such findings provide a dynamical-systems analogue of the thresholded convergence principle formalized here and suggest that ARCH × Φ reflects a computational motif implemented at the circuit level.
Although lordosis serves as an unusually clean proof case, the convergence framework is not inherently domain-specific. Maternal caregiving may require the convergence of hypothalamic circuitry (A), prolactin and oxytocin priming (D), pup cues (C), and permissive arousal state (Φ). Predator defense likely depends on amygdalar–PAG circuits, stress hormones, and immediate threat cues. Courtship, aggression, and social bonding may likewise exhibit analogous conjunctive architectures. Together, such studies would move the present synthesis from formal restatement toward direct empirical validation and cross-domain generalization.
4.9 Falsifiability
A central strength of the ARCH × Φ framework is that it generates explicitly falsifiable predictions. The threshold principle of convergence holds that lordosis expression fails under physiological conditions when any one requisite component—neural archetype (A), neurohumoral drive (D), or contextual sensory input (C)—is reduced below threshold, even if the remaining components are intact. This prediction contrasts sharply with additive models, which would predict partial expression when two strong factors are present despite loss of a third.28
Within the ARCH × Φ formulation, behavioral execution follows a multiplicative veto structure: when any term approaches zero, the product A × D × C remains subthreshold regardless of the magnitude of the others (e.g., 1 × 1 × 0 = 0). These contrasting predictions are summarized in
Table 2, which distinguishes additive compensation from conjunctive necessity.
Table 2. Additive versus multiplicative predictions for lordosis.
| Factors present | Additive prediction |
Multiplicative prediction |
|---|
| A + D (no C) | Partial | No (0) |
| A + C (no D) | Partial | No (0) |
| D + C (no A) | Partial | No (0) |
| A + D + C | Full | Yes (1) |
Accordingly, the model would be falsified by any robust demonstration of sustained lordosis expression following elimination of a required component under physiological conditions. Conversely, systematic shifts in expression probability or threshold position produced by manipulations of Φ, without alteration of component identity, would further support the threshold-gated convergence hypothesis.
Competing models make distinct predictions under partial perturbation. Additive or threshold-linear models predict graded compensation when two components are strong, whereas conjunctive multiplicative models predict supra-additive failure under dual partial reductions. Hierarchical gating models predict ordered dominance of specific components, whereas the present framework predicts symmetric veto effects irrespective of component identity. These distinctions can be tested empirically using factorial perturbation designs.
Falsifiability
The framework is refutable in well-defined ways. Evidence that would falsify the model includes:
• Archetype falsification: Robust lordosis expression under physiological conditions despite complete disruption of the VMH–PAG circuit.
• Drive falsification: Robust lordosis expression under physiological conditions in the absence of neurohumoral priming.
• Context falsification: Robust lordosis expression under physiological conditions in the absence of appropriate somatosensory context.
• Threshold-field falsification: Failure of manipulations of Φ (e.g., dopaminergic facilitation, serotonergic activation, or stress-axis engagement) to shift the threshold at which the product
yields expression.
Importantly, experimental paradigms involving supernormal sensory convergence or elevated neuromodulatory gain are treated as boundary conditions rather than falsifications, provided they operate through scaling of C or Φ. The model would be invalidated only if behavioral expression were shown to violate conjunctive necessity without such compensatory mechanisms.
By specifying these criteria explicitly, the ARCH × Φ framework moves beyond descriptive synthesis to a testable theoretical proposal, inviting direct experimental validation, quantitative comparison with additive alternatives, and principled revision.
5. Conclusion
The present analysis demonstrates that lordosis in the female rat provides a uniquely well-characterized system for examining how behavioral expression emerges through the convergence of multiple necessary factors. Reframing decades of empirical findings within the ARCH × Φ framework clarifies that neural circuitry, neurohumoral drive, and contextual sensory input are each indispensable under physiological conditions: reduction of any single component below threshold abolishes expression, whereas their joint alignment above threshold yields a reliable, stereotyped reflex. Incorporation of Φ as a modulatory field further accounts for how arousal, neuromodulatory tone, stress, and developmental transitions rescale the effective threshold for expression without altering the identity of the required components.
By reanalyzing classic dose–response data from Hardy and DeBold within this framework, the present work also shows that thresholded multiplicative models quantitatively outperform additive alternatives in capturing lordosis expression, reinforcing the view of lordosis as a threshold-governed state transition rather than a linear causal chain.
Viewed in this light, the present work advances a conjunctive convergence for behavioral expression which occurs when all requisite conditions align above threshold and fails when any one is absent or subthreshold. Although developed here in the context of lordosis, this formulation provides a formal template for behaviors in which convergence defines the boundary between latent potential and expressed action.
In doing so, the framework returns to Lewin’s original vision of a field theory of behavior—one in which behavior arises from the interaction of internal and external determinants rather than from either alone. The ARCH × Φ model extends this vision by specifying how neural architecture, neurohumoral drive, contextual input, and arousal must jointly interact to cross a behavioral threshold.
The value of this proposal lies in making explicit what has long remained implicit in behavioral science: behavior is governed not by additive sufficiency, but by conjunctive, threshold-dependent probabilities. By formalizing this logic, the ARCH × Φ framework generates falsifiable predictions, invites direct experimental tests, and offers a principled route toward unifying fragmented findings across motivated behaviors. The present synthesis therefore aims not to close debate, but to provide a formal structure within which future empirical work can refine, validate, or revise the convergence model.
The ARCH × Φ framework extends Lewin’s original insight26 by specifying how neural architecture, neurohumoral drive, contextual input, and arousal must jointly converge to cross a behavioral threshold, thereby transforming a qualitative principle into a formally testable execution rule. As Sapolsky has emphasized, biology is not governed by single causes but by probabilities—a perspective captured here by treating behavioral expression as a thresholded state transition rather than a linear causal chain.27
AI disclosure
Portions of this manuscript, including text drafting, organization, tables, diagrams and language refinement, were assisted by OpenAI’s GPT-5. The AI was used to improve clarity, style, and structure, but all conceptual content, interpretation of findings, and final revisions were developed and approved by the author. The author assumes full responsibility for the accuracy, integrity, and originality of the work.


Comments on this article Comments (0)