Density but not climate affects the population growth rate of guanacos (<i>Lama guanicoe</i>) (Artiodactyla, Camelidae)

María Zubillaga; Oscar Skewes; Nicolás Soto; Jorge E Rabinovich

doi:10.12688/f1000research.2-210.v2

Home Browse Density but not climate affects the population growth rate of guanacos...

ALL Metrics

Views

Downloads

Get PDF

Get XML

Export

▬

✚

Research Article

Negative/null result

Revised

Density but not climate affects the population growth rate of guanacos (Lama guanicoe) (Artiodactyla, Camelidae)

[version 2; peer review: 2 approved, 1 approved with reservations]

María Zubillaga¹, Oscar Skewes², Nicolás Soto³, Jorge E Rabinovich¹

PUBLISHED 28 May 2014

Author details Author details

¹ Centro de Estudios Parasitológicos y de Vectores (CEPAVE, CONICET-CCT-La Plata, UNLP), Universidad Nacional de La Plata, La Plata, Argentina
² Universidad de Concepción, Chillán, Chile
³ Servicio Agrícola Ganadero (SAG), XII Región, Chile

OPEN PEER REVIEW

REVIEWER STATUS

Abstract

We analyzed the effects of population density and climatic variables on the rate of population growth in the guanaco (Lama guanicoe), a wild camelid species in South America. We used a time series of 36 years (1977-2012) of population sampling in Tierra del Fuego, Chile. Individuals were grouped in three age-classes: newborns, juveniles, and adults; for each year a female population transition matrix was constructed, and the population growth rate (λ) was estimated for each year as the matrix highest positive eigenvalue. We applied a regression analysis with finite population growth rate (λ) as dependent variable, and total guanaco population, sheep population, annual mean precipitation, and winter mean temperature as independent variables, with and without time lags. The effect of population size was statistically significant, but the effects of the sheep population and the climatic variables on guanaco population growth rate were not statistically significant.

Keywords

Camelidae, climatic variables, density effects, guanaco, population regulation, population growth rate

Corresponding author: María Zubillaga

Competing interests: No competing interests were disclosed.

Grant information: The author(s) declared that no grants were involved in supporting this work.

Copyright: © 2014 Zubillaga M et al. This is an open access article distributed under the terms of the Creative Commons Attribution License, which permits unrestricted use, distribution, and reproduction in any medium, provided the original work is properly cited. Data associated with the article are available under the terms of the Creative Commons Zero "No rights reserved" data waiver (CC0 1.0 Public domain dedication).

How to cite: Zubillaga M, Skewes O, Soto N and Rabinovich JE. Density but not climate affects the population growth rate of guanacos (Lama guanicoe) (Artiodactyla, Camelidae) [version 2; peer review: 2 approved, 1 approved with reservations]. F1000Research 2014, 2:210 (https://doi.org/10.12688/f1000research.2-210.v2) First published: 09 Oct 2013, 2:210 (https://doi.org/10.12688/f1000research.2-210.v1) Latest published: 18 Sep 2014, 2:210 (https://doi.org/10.12688/f1000research.2-210.v3)

Revised Amendments from Version 1

We evaluated the comments of both referees (Dr. Baldi and Dr. Acebes) and considered them to be very useful. Following the reviewers’ suggestions we:

1) Improved the description and justification of the methodology used with respect to the guanaco sampling. In relation to the estimation of the guanaco population size we specified the use of the method proposed by Leopold, and we developed the necessary assumptions for this method to be valid. Brief comments about the surveyed area were also included to support the sampling methodology. Some questions related to the population sampling with the Distance method were not considered because we didn’t use that method.

2) Re-processed the regressions incorporating the sheep population as a new independent variable of the guanaco population growth rate (l); so our new analysis now has 6 independent variables: sheep population, guanaco population size, winter temperature, winter temperature with a lag of 1 year, annual precipitation and annual precipitation with a lag of 4 years. Our main results didn’t change and it was confirmed that only the guanaco population size seems to have an effect on the population growth rate (l).

3) Complied with Dr. Acebes suggestion to use the Akaike measure of goodness of fit and so we changed the software used in the analysis (from Statistica to language R).

As a consequence of these changes in the analysis, Table 1 and Table S1 (now referred to as Data set 1) were modified.

Lastly, owing to these changes and corrections some citation were removed and others were incorporated.

See the authors' detailed response to the review by Pablo Acebes
See the authors' detailed response to the review by Ricardo Baldi

Introduction

In order to understand population dynamics and optimize the management of wildlife populations it is important to identify how populations are affected by environmental factors and their own density, particularly in species living in extreme environments. Mechanisms that regulate populations of the guanacos (Lama guanicoe) are poorly known; this species was heavily exploited in the Patagonian steppe, and its numbers and distribution have diminished significantly during the last century because of grazing conflicts with a sheep-based society, and overhunting (the guanaco’s historical distribution has been reduced by 75% in Chile and Peru, and by 60% in Argentina)¹. The guanaco is in the Least Concern IUCN Red List category (http://www.iucnredlist.org/, downloaded on 11 September 2013) but it has been included in Appendix II of CITES 2013 (http://www.cites.org/eng/app/2013/E-Appendices-2013-06-12.pdf).

No population of any species can grow indefinitely, and population checks based upon different processes restrict population size and/or geographic distribution; these processes are either density-stabilizing or density-limiting². The former are of a biotic nature and depend on the interaction between individuals of the same or different species, while the latter are independent of population size. Stabilization results from density-dependence, with a regulatory effect that varies in intensity with the size or density of the population itself, however, not all density-dependent factors are density-stabilizing. The density-limiting factors can also be considered density-responsive because the per capita amount or availability of resources decreases as the population density increases. Thus, these two types of factors (density-stabilizing and density-limiting) rarely act independently: the density-limiting factors (generally of a physical and/or climatic nature), may determine the level at which populations become stabilized by the density-dependent processes, but they do not have a stabilizing capacity per se; for this reason many wildlife population dynamic and management models include the effects of climatic variables (e.g., Dennis & Otten, 2000; Colchero et al., 2009)^3,4.

The guanaco is one of the two extant wild South American camelids, and ranges from Northern Peru through Chile, and across Patagonia to southern Argentina and Chile, reaching Tierra del Fuego. It is found from sea level to nearly 4500 m on the Andes mountain range, and occupies a wide variety of habitats from hardpan deserts to scrublands to grasslands⁵.

Although there are several studies on the population regulation processes in mammals in general^6,7, and in ungulates in particular^8,11, there are very few studies in wild South American camelids that analyze population growth regulation. There are several studies dealing with population dynamics of vicuña (Vicugna vicugna)^12–14 and guanacos^15–17; however none of them considered the effect of density, livestock and climate on population growth rate.

Thus, our purpose in this work was to test the hypothesis that population density, sheep stock, and climatic variables, affect the growth rate of the guanaco population from the island of Tierra del Fuego, Chile.

Materials and methods

Study area

We analyzed the guanaco population of the “Cameron” ranch (-53.9 S, -69.3 W), with an area of the 2000 km² located in the Southern region of the Tierra del Fuego island, Chile. The altitude range is 0–300 m above sea level, and the ranch is a mosaic of steppe with fragments of forest; the latter is a deciduous forest (Nothofagus spp) while the steppe is composed of meadows, peats and prairies. The forested area is about 8.8% of the total study area, with some degree of forest clearance that offers adequate visibility for guanaco sampling. The guanaco is the dominant wild herbivore, while sheep are the dominant domestic species; densities of the latter have fluctuated in the last decades between 11 and 23 sheep/km²¹⁸. In contrast to the mainland, the puma (Puma concolor), the main predator of guanacos, is absent on the island; since 1977 guanaco hunting has been controlled by the Chilean National Forest Corporation (CONAF, according to its Spanish acronym) and the Chilean Agricultural and Livestock Service (SAG, according to its Spanish acronym).

The climate of the Tierra del Fuego island is characterized by an average annual precipitation of 200–400 mm, while in the forested areas the average precipitation fluctuates between 400–600 mm per year¹⁹. The average annual temperature is 6.5°C and the average winter temperature is 2.2°C.

Guanaco population sampling

Guanacos were counted for 34 consecutive years between 1977 and 2012 (except in 1986 and 1996), using the transect method with an undefined band width, from 1977 to 1995, and with a fixed width band from 1996 to 2012 (the latter with a maximum of 500 m to each side of the transect)^20–22. The sampling methodology was changed by expert recommendation made in 1995²³; in 2000 the fixed and the undefined band width methods were applied simultaneously, we tested both results and found no significant statistical difference between them. The sampling period was carried out in the autumn and lasted approximately 7 days between 10:30 and 19:00 h, with two observers in two 4×4 vehicles going over the main, secondary and local roads at speeds slower than 40 km/h. Despite randomly selected transects being recommended²⁴, preexisting roads were used because according to Soto (2010)¹⁸ the existing system of roads is an adequate sample of the area. Each road was covered only once, and in addition to individual guanaco counts, the following were recorded: weather conditions, time, distance (km) from the starting point, GPS coordinates, observation distance from the transect (m) to guanacos, an estimate of the angle to the animal’s position, and – when the animals were observed in groups – the number of individuals, the type of social group, and its structure (sex, and the age class: newborn, juvenile and adult). Observation distances were made by naked eye. The road network and all geo-referenced observations were processed with the Arc View 9.3 Geographical Information System (SIG), and transferred using program Map Source^®. The cartography was kindly provided by the Chilean Agricultural and Livestock Service (SAG).

The population size was estimated as given in Soto¹⁸ which was based on the King method modified by Leopold (1933)²⁵ described by Raedeke (1978)¹⁹, given by:

N = \frac{A * n}{2 * y * x} (1)

where N is the total population to be estimated, A is the total study area surface, n is the total number of animals counted, x is the total transect distance covered (m) rounded to one meter, and y is the average of the perpendicular distance (m) from the transect to the animals counted (the factor of 2 is included to consider that there is one band to each side of the transect). The variance (S²) was estimated by (2), with p = n/N, and used to estimate the 95% upper and lower confidence intervals.

S^{2} = \frac{n}{p2} * \frac{1 - p + n}{n + 2} (2)

Raedeke (1978)¹⁹ claims that the Leopold method is valid when the following conditions are satisfied: (1) the road systems must be an adequate sampling of the study area, (2) the network road must be randomly distributed, and (3) the animals included in the sampling must be randomly distributed in relation to the observer’s route and he considers that in the south of the Tierra del Fuego Island these assumptions are fulfilled. Soto 2010¹⁸ compared population estimations by the Leopold and Distance methods and found that the value of the means estimate by Leopold methods fall within the confidence intervals estimated by Distance; additionally, as all sampling periods used the same methodology whatever bias might exist in the estimation of the mean abundance using the Leopold method, the relative changes among years (and thus the temporal trend) will be adequately represented; thus, we conclude that the Leopold’s method seems adequate for our purposes¹⁸.

The area effectively surveyed in each sampling period was around 420 km² (about 20%, of the area under study).

Climatic variables

We evaluated the possible impact of two climatic variables on guanaco population growth rate: average annual precipitation (mm/year) and winter temperature (as the average of the temperatures of June, July and August, in °C). These climatic variables were selected because some studies suggested that they have an influence on guanaco demographic parameters: Rey et al. 2012²⁶ observed that after a severe drought the proportion of guanaco yearlings/females decreased significantly, and Sarno et al. 1999¹⁷ detected a negative effect of winter snowfall on guanaco juvenile survival; because we had insufficient snowfall data we used the winter temperature as a proxy for winter snowfall. We used the 25 years (1977–2002) precipitation and temperature time series of the CRU TS 2.1 database, compiled by the Tyndall Centre, Climatic Research Unit, School of Environmental Sciences of the University of East Anglia, United Kingdom (http://www.cru.uea.ac.uk/cru/data/hrg.htm). As the CRU TS 2.1 data ended in 2002, we completed that time series for 2003 to 2012 from the closest meteorological station to the Cameron ranch: Punta Arenas (Chile); this data was downloaded from the Internet site of the Meteorological Service of Chile (http://www.meteochile.gob.cl/).

Sheep population

The livestock effect was evaluated by considering the sheep population, based on time series data obtained from Soto (personal communication). Only eight years of data were available (1980, 1985, 1990, 1995, 2000, 2005, 2008 and 2011); as the sheep population change between years was relatively smooth, we interpolated linearly between two consecutive data points to generate a complete time series of 36 years.

Guanaco population analysis

We estimated the finite rate of increase (λ) as a measure of population growth rate for each of the 36 years of the guanaco data (population estimates were not available for years 1986 and 1996, and were linearly interpolated). To estimate λ we developed a three age-class (newborns, juveniles and adults) female-only matrix model, and estimated the matrix parameters by fitting the model predictions to the field total population estimates; we summed the three age classes and multiplied the result by two (guanacos have an approximately 50% sex-ratio). The fit was carried out in an Excel^® spreadsheet using the Solver tool, and the sum of squares (SSQ) as goodness of fit criterion (details can be found in Rabinovich and Zubillaga, 2012²⁷). This process resulted in a set of 36 population age-class structured matrices, and from each matrix we calculated the largest positive eigenvalue²⁸ as an estimate of λ, using the PopTools add-in, an Excel program developed by Greg Hood (http://www.cse.csiro.au/poptools/).

Population analysis

To test our hypothesis, we used a multiple regression analysis to check the relationship between the population growth rate (λ) as a dependent variable and guanaco population size (in natural logs), sheep population size (in natural logs), and climatic variables (annual mean precipitation in mm/year, and winter mean temperature in °C) as independent variables. In the case of the climatic variables we also evaluated the effects of various time lags (T), with T = 1 to 7 years for precipitation, and T = 1 year for winter temperature; the lags were applied by averaging the previous T lagged years, as suggested by Shaw et al. (2012)¹³ for the vicuña population (these lagged variables were used in the regression analyses in addition to the non-lagged precipitation and winter temperature variables). The inclusion of time lags is convenient because it may detect possible cumulative climatic effects on ungulate population growth rates as has been observed in, for example, deer and moose²⁹ and in vicuñas¹³. The multiple regression was carried out using the statistical package “lm” of the RStudio software (Version 0.97.449 – ©2009–2012 RStudio, Inc.). Since for multiple regression analysis it is necessary to check that there is no collinearity (significant correlations among the predictor variables), we carried out a correlation analysis between independent variables, and used a p value < 0.05 to determine statistical significance. We used the Akaike index (AIC) as a goodness of fit criterion.

Results

Data set 1 shows for each of the 36 years of guanaco sampling all the variables (dependent and independent) used in the regression analysis.

Year	Guanaco population	95% lower limit CI	95% upper limit CI	Sheep population	Lambda	P	Av winter temp
1977	5372	5176	5568	45000	1.155	319.8	1.57
1978	5744	5541	5947	45000	1.159	358.5	2.5
1979	6940	6337	7543	45000	1.161	346.4	3
1980	6693	6128	7258	45000	1.159	333.4	2.13
1981	8297	7707	8887	44600	1.158	399	2.67
1982	12334	11539	13129	44200	1.155	320.8	1.5
1983	10670	9969	11371	43800	1.155	285.5	2.87
1984	19078	18964	19192	43400	1.121	319	1.03
1985	11219	10501	11937	43000	1.105	341.6	3.1
1986	11771	11031	12510	42600	1.093	388.8	2.3
1987	12323	11562	13084	42200	1.084	344.9	2.37
1988	13027	12265	13789	41800	1.081	306.4	2.6
1989	14094	13253	14935	41400	1.08	398.7	2.7
1990	14604	13775	15433	41000	1.082	517.8	2.47
1991	17775	17155	18395	38000	1.053	383.2	1.73
1992	20774	20219	21329	35000	1.004	327.1	1.3
1993	16410	15560	17260	32000	1.039	370	2.47
1994	17626	16716	18536	29000	1.066	457.9	2.23
1995	21445	20153	22737	26000	1.057	389.1	0.37
1996	21111	19752	22470	27800	1.084	404.3	2.97
1997	20777	19351	22203	29600	1.14	408	2.03
1998	28978	27749	30207	31400	1.085	455.8	3.77
1999	27809	26518	29100	33200	1.114	300.9	2.27
2000	28935	27446	30424	35000	1.154	441.3	2.07
2001	38841	37366	40316	35400	1.031	349.1	2.1
2002	38363	36810	39916	35800	1.037	397.5	1.7
2003	32273	30818	33728	36200	1.156	437.6	3.57
2004	43128	41089	45166	36600	1.176	363.5	3.47
2005	58597	56134	61060	37000	0.932	374.7	2.13
2006	52456	49820	55092	32000	0.901	411.4	2.83
2007	33125	31360	34890	27000	1.192	383.9	2.83
2008	61334	58546	64123	22000	1.067	352.2	2.13
2009	60488	57672	63304	29667	0.84	353.1	3.26
2010	44773	42537	47010	37333	1.153	319.1	2.1
2011	56973	54410	59537	45000	1.07	391.6	2.46

Dataset 1.Guanaco population abundance, sheep population abundance, estimated population annual rate of growth, average annual precipitation, and average winter temperature of the Cameron ranch, Tierra del Fuego.

Guanaco population abundance (individuals), lower and upper limits of the 95% confidence intervals (CI), sheep population abundance (individuals), estimated population annual rate of growth (lambda), average annual precipitation (P; mm/year), and average winter temperature (celsius). Guanaco population values were not available for years 1986 and 1996, and were linearly interpolated; sheep population values were only available for years 1980, 1985, 1990, 1995, 2000, 2005, 2008 and 2011; other values were linearly interpolated.

Correlation analysis between the climatic variables showed a statistically significant correlation (p < 0.05) only among the precipitation variables for all the 1 to 7 year lags (but not with non-lagged precipitation), while the correlation results between all other independent climatic variables were not statistically significant. Due to the statistically significant correlation among the lagged precipitations we carried out seven independent regression analyses, all of them with the same independent and dependent variables, except the independent variables of lagged-precipitation, which were used in each regression run with a different lag value. We observed that the regression with precipitation lag T = 3 was the only one, aside from total guanaco population size, that had the intercept statistically significant. In all case the multiple regression analysis indicated that the total population (LnNtot) was the only statistically significant variable (AIC = -81.599 p < 0.0514 and F = 2.414) (Table 1).

Table 1. Results of multiple regression analysis between the population growth rate (λ) as dependent variable, and (in log scale) total guanaco population (LnNtot), sheep population (LnSheep), annual mean precipitation (Annual Precip), mean precipitation with lags of 3 years (Precip (T = 3)), winter mean temperature (Winter temp.), and winter mean temperature with 1 year of lag (Winter temp (T = 1)) as independent variables.

The results show the regression coefficients (e Estimate), their standard errors (Std.Error) and t-test values (t value), with their probability value (Pr(>|t|)).

	Estimate	Std. Error	t value	Pr(>ǀtǀ)
Intercept	1.8840	0.8682	2.1700	0.0383
LnNtot	-0.0492	0.0220	-2.2370	0.0331
LnSheep	-0.0272	0.0654	-0.4150	0.6809
Annual Precip	-0.0001	0.0002	-0.3580	0.7228
Winter temp	0.0173	0.0191	0.9030	0.3738
Precip (T = 3)	-0.0003	0.0005	-0.5590	0.5803
Winter temp (T = 1)	0.0309	0.0182	1.6980	0.1002

We also carried out a simple regression analysis using λ as the dependent variable and only the guanaco population size (in natural logs, LnNtot) as an independent variable, in order to compare this result with the full model (guanaco population, sheep population and climatic variables as independent variables). Table 2 shows the result of this second regression analysis, which was highly significant (AIC = -87.847, p < 0.0018, and F = 11.48,) and the resulting regression equation was λ = 1.6373 – 0.0552 (±0.0163) LnNtot.

Table 2. Results of the simple regression analysis between the population growth rate (λ) as dependent variable, and (in log scale) total guanaco population (LnNtot).

Interpretation of the statistical parameters as in Table 1.

	Estimate	Std. Error	t value	Pr(>ǀtǀ)
Intercept	1.6373	0.1624	10.082	9.45E-12
LnNtot	-0.0552	0.0163	-3.388	0.00179

The negative slope of the regression equation is an indication of a density-dependent process, since when the population increases the per capita population growth rate decreases (Figure 1). The intercept of the regression line at λ = 1 (population at equilibrium) results in a population size of 103,000 guanacos (51 guanaco/km²), which can be considered as an estimate of the carrying capacity of the Cameron ranch for this guanaco population.

Figure 1. Effect of the guanaco population size on guanaco’s finite population growth rate (λ).

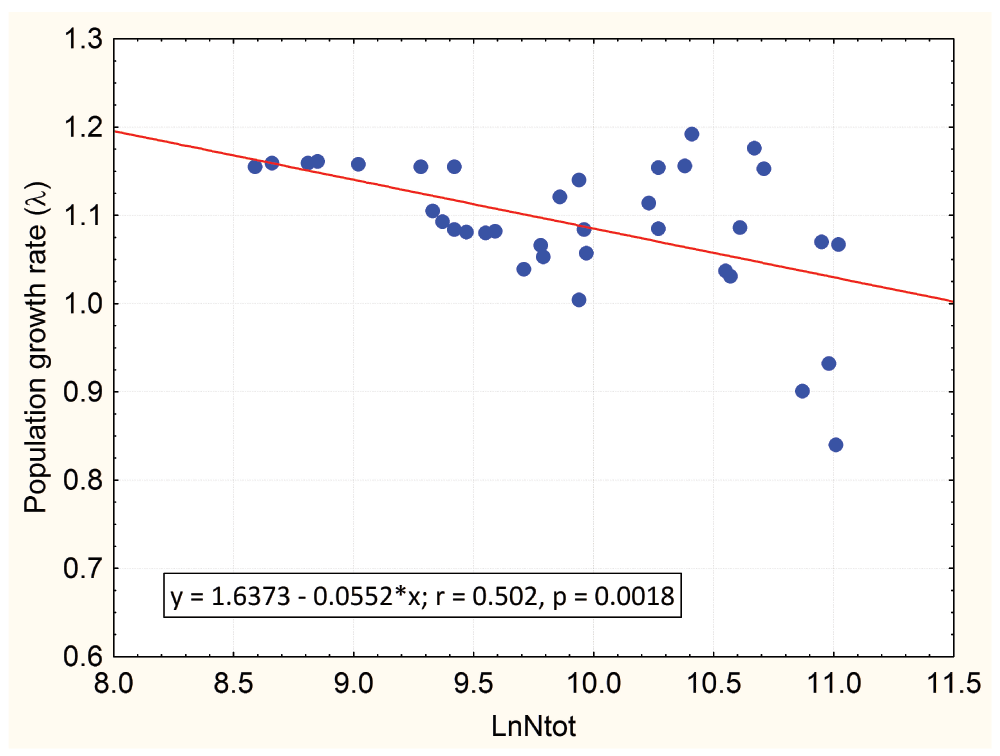
On the x-axis the guanaco population from the Cameron ranch (Tierra del Fuego, Chile) was transformed to a natural logarithmic scale. The values of λ represent the finite population growth rate (on a per year time unit).

Discussion

We were not able to confirm the expected effect of either climatic variables or sheep population on the population rate of growth (λ) in the guanaco population of the Cameron ranch. We expected an effect of climatic variables because Sarno et al. (1999)¹⁷ found a relationship between winter weather and guanaco yearling’s survival, and Rey et al. (2012)²⁶ recorded the effects of a drought on guanaco fecundity. Thus we anticipated that as winter temperature and/or annual precipitation decrease, the guanaco population growth rate might also decrease, as shown by Mech et al. 1987²⁹ with deer and moose. They also used a simple linear regression, and found that as winter snow accumulation increased, annual percentage change in population numbers decreased. With respect to sheep population, we also expected to find some type of relationship because this domestic herbivore is considered a competitor of the guanaco³⁰ for food and water. Our negative results are even more surprising because in the last 10–12 years of the time-series data the guanaco population fluctuated remarkably, suggesting some extraneous factor in addition to between population density, maybe climatic variables. It is well known that environmental effects are more important when the population size is near the carrying capacity, particularly in large mammals characterized by low reproductive rates, long life-spans, and populations that are resource-limited (features typical of species referred to as the “K-selected” species)³¹. The difference between our results and those of Sarno et al. (1999)¹⁷ may reflect that these authors used the average winter snowfall while we considered average winter temperature.

The results of the guanaco population sampling suggest a certain trend in the population size, with a more or less exponential growth in the first few years, becoming more variable as the population grows, with more marked fluctuations during the last 10–12 years; this may imply that the population is becoming stabilized, possibly approaching its carrying capacity. On the other hand, the sampling results of those last 10–12 years show abrupt “jumps” in some years (for example 2004–2005) that may be the consequence of the mobility of guanacos from the Cameron ranch to neighboring sites and vice versa; since the transect sampling does not identify individuals the effects of possible local displacements could not be considered.

On the other hand the lack of effects of the sheep population size on the finite population growth rate (λ) in this guanaco population conforms well with a recent study³² in Southern Chile that found that the potential competition between guanaco and sheep is low.

In contrast to our results, a study by Taper & Gogan (2002)³³ on the Yellowstone elk population, with weather variables included as covariates within a dynamic model, found that spring precipitation had a positive regression coefficient.

Contrary to what was expected based on the literature of ungulate population dynamics, weather variables do not seem to influence the density-dependent population growth rate of the Cameron ranch guanaco population. Our aim was to carry out a preliminary analysis that would help identify some of the regulatory processes in this guanaco population and so we used a simple multiple regression analysis as a first step in that direction. However, we note that in order to test the effects of climatic variables on population regulation of large ungulates such as the guanaco, the use of a population dynamic model would be recommended. A population dynamic model would better account for the interaction between density-dependent processes and weather variables than a simple multiple regression between the latter and guanaco population growth rate.

Data availability

F1000Research: Dataset 1. Guanaco population abundance, sheep population abundance, estimated population annual rate of growth, average annual precipitation, and average winter temperature of the Cameron ranch, Tierra del Fuego, 10.5256/f1000research.2375.d27483

Author contributions

MZ and JER conceived the study. NS and OS sampled and estimated the population size. MZ designed the analysis. MZ and JER were responsible for all writing phases of the manuscript. All authors were involved in the revision of the draft manuscript and have agreed to publish the article.

Competing interests

No competing interests were disclosed.

Grant information

The author(s) declared that no grants were involved in supporting this work.

Acknowledgements

We are grateful for the help provided by the Public Service of the Regional Government of the XII Region of Magallanes and Chilean Antarctica (Project: “Productive and Sustainable Management of the Guanaco in Tierra del Fuego Island, Phases II and III”) under an agreement with the University of Concepción, Chile, 1999).

Faculty Opinions recommended

References

1. Franklin WL, Bas MF, Bonacic CF, et al.: Striving to manage Patagonia guanacos for sustained use in the grazing agroecosystems of southern Chile. Wildl Soc Bull. 1997; 25(1): 65–73. Reference Source
2. Case TJ: An illustrated guide to Theoretical Ecology. Oxford, University Press. 2000; 449. Reference Source
3. Dennis B, Otten M: Joint effects of density dependence and rainfall on abundance of san joaquin kit fox. J Wildl Manage. 2000; 64(2): 388–400. Publisher Full Text
4. Colchero F, Medellin RA, Clark JS, et al.: Predicting population survival under future climate change: density dependence, drought and extraction in an insular bighorn sheep. J Anim Ecol. 2009; 78(3): 666–673. PubMed Abstract | Publisher Full Text
5. Franklin WL, Johnson WE: Hand Capture of Newborn Open-Habitat Ungulates: The South American Guanaco. Wildl Soc Bull. 1994; 22(2): 253–259. Reference Source
6. Ostfeld RS, Canham CD, Pugh SR: Intrinsic Density-Dependent Regulation of Vole populations. Nature. 1993; 366(6452): 259–261. PubMed Abstract | Publisher Full Text
7. Bateman AW, Ozgul A, Coulson T, et al.: Density dependence in group dynamics of a highly social mongoose, Suricata suricatta. J Anim Ecol. 2012; 81(3): 628–639. PubMed Abstract | Publisher Full Text
8. Koons DN, Terletzky P, Adler PB, et al.: Climate and density-dependent drivers of recruitment in plains bison. J Mammal. 2012; 93(2): 475–481. Publisher Full Text
9. Bardsen BJ, Tveraa T: Density-dependence vs. density-independence - linking reproductive allocation to population abundance and vegetation greenness. J Anim Ecol. 2012; 81(2): 364–376. PubMed Abstract | Publisher Full Text
10. Serrano E, Angibault JM, Cargnelutti B, et al.: Density dependence of developmental instability in a dimorphic ungulate. Biol Lett. 2008; 4(5): 512–514. PubMed Abstract | Publisher Full Text | Free Full Text
11. Stewart KM, Bowyer RT, Ruess RW, et al.: Herbivore Optimization by North American Elk: Consequences for Theory and Management. Wildl Monogr. 2006; 167(1): 1–24. Publisher Full Text
12. Rabinovich JE, Hernández MJ, Cajal JL: A simulation model for the management of vicuña populations. Ecol Model. 1985; 30(3–4): 275–295. Publisher Full Text
13. Shaw AK, Galaz JL, Marquet PA: Population dynamics of the vicuña (Vicugna vicugna): density-dependence, rainfall, and spatial distribution. J Mammal. 2012; 93(3): 658–666. Publisher Full Text
14. Bonacic C, Macdonald DW, Galaz J, et al.: Density Dependence in the camelid Vicugna vicugna: the Recovery of a Protected Population in Chile. Oryx. 2002; 36(2): 118–125. Publisher Full Text
15. Sarno RJ, Franklin WL: Population Density and Annual Variation in Birth Mass of Guanacos in Southern Chile. J Mammal. 1999; 80(4): 1158–1162. Publisher Full Text
16. Sarno RJ, Franklin WL: Maternal expenditure in the polygynous and monomorphic guanaco: suckling behavior, reproductive effort, yearly variation, and influence on juvenile survival. Behav Ecol. 1999; 10(1): 41–47. Publisher Full Text
17. Sarno RJ, Clark WR, Bank MS, et al.: Juvenile guanaco survival: management and conservation implications. J Appl Ecol. 1999; 36(6): 937–945. Publisher Full Text
18. Soto VN: Distribución y Abundancia de la Población de Guanacos (Lama guanicoe, Muller 1776) en el Área Agropecuaria de Tierra del Fuego (Chile) y su Relación de Carga Animal con la Ganadería Ovina. Tesis de Estudios Avanzados (Dea). Universidad Internacional de Andalucía - Universidad de Córdoba. 2010.
19. Raedeke KJ: El guanaco de Magallanes, Chile. Su distribución y Biología. Corporación Nacional Forestal Publicación Técnica N° 4, Ministerio de Agricultura Chile. 1978; 364. Reference Source
20. Tellería Jorge JL: Manual para el censo de los Vertebrados terrestres. Editorial Raíces., Madrid, España. 1986; 278. Reference Source
21. Davis D, Winstead R: Estimación de tamaños de poblaciones de vida silvestre. In: H.S. Mosby, R.H. Giles Jr. y S.D. Schemnitz (Eds). Manual de técnicas de gestión de vida silvestre. The Widlife Society, Bethesda, Maryland. 1987; 233–258.
22. Caughley G: Analysis of vertebrate populations. A Wiley-Interscience publication. John Wiley & Sons Ltd. 1980; 234. Reference Source
23. Duran Ríos JC: Informe Final Proyecto "Manejo Productivo y sustentable del guanaco en isla Tierra del Fuego. XII Región"- (Año 1). CONAF-FNDR, Región de Magallanes y Antártica Chilena. Santiago, Chile. 1995; 178.
24. Eberhardt LL: Transect methods for population studies. J Wildl Manage. 1978; 42(1): 1–31. Publisher Full Text
25. Leopold A: Game management. Charles Scribner and sons, New York. 1933; 481. Reference Source
26. Rey A, Novaro A, Sahores M, et al.: Demographic effects of live shearing on a guanaco population. Small Ruminant Res. 2012; 107(2): 92–100. Publisher Full Text
27. Rabinovich JE, Zubillaga M: Informe Final del proyecto: "Modelo de manejo de poblaciones de guanacos para la Provincia del Chubut". 2012. Reference Source
28. Caswell H: Matrix population models: construction, analysis, and interpretation. 2nd edn. Sinauer Associates. Sunderland, Massachusetts. 2001; 722. Reference Source
29. Mech LD, McRoberts RE, Peterson RO, et al.: Relationship of Deer and Moose Populations to Previous Winters' Snow. J Anim Ecol. 1987; 56(2): 615–627. Publisher Full Text
30. Baldi R, Pelliza A, Elston D, et al.: High Potential for Competition Between Guanacos and Sheep In Patagonia. J Wildl Manage. 2004; 68(4): 924–938. Publisher Full Text
31. Fowler CW: Density Dependence as Related to Life History Strategy. Ecology. 1981; 62(3): 602–610. Publisher Full Text
32. Iranzo EC, Traba J, Acebes P, et al.: Niche segregation between wild and domestic herbivores in Chilean Patagonia. PLoS One. 2013; 8(3): e59326. PubMed Abstract | Publisher Full Text | Free Full Text
33. Taper ML, Gogan PJP: The Northern Yellowstone Elk: Density Dependence and Climatic Conditions. J Wildl Manage. 2002; 66(1): 106–122. Publisher Full Text

Comments on this article Comments (0)

Version 3

VERSION 3 PUBLISHED 09 Oct 2013

Author details Author details

Competing interests

No competing interests were disclosed.

Grant information

The author(s) declared that no grants were involved in supporting this work.

Article Versions (3)

version 3

Revised

Published: 18 Sep 2014, 2:210

https://doi.org/10.12688/f1000research.2-210.v3

version 2

Revised

Published: 28 May 2014, 2:210

https://doi.org/10.12688/f1000research.2-210.v2

version 1

Published: 09 Oct 2013, 2:210

https://doi.org/10.12688/f1000research.2-210.v1

© 2014 Zubillaga M et al. This is an open access article distributed under the terms of the Creative Commons Attribution License, which permits unrestricted use, distribution, and reproduction in any medium, provided the original work is properly cited. Data associated with the article are available under the terms of the Creative Commons Zero "No rights reserved" data waiver (CC0 1.0 Public domain dedication).

Download

Export To

metrics

	Views	Downloads
F1000Research	-	-
PubMed Central Data from PMC are received and updated monthly.	-	-

Citations

SEE MORE DETAILS

CITE

how to cite this article

Zubillaga M, Skewes O, Soto N and Rabinovich JE. Density but not climate affects the population growth rate of guanacos (Lama guanicoe) (Artiodactyla, Camelidae) [version 2; peer review: 2 approved, 1 approved with reservations]. F1000Research 2014, 2:210 (https://doi.org/10.12688/f1000research.2-210.v2)

NOTE: If applicable, it is important to ensure the information in square brackets after the title is included in all citations of this article.

track

receive updates on this article

Track an article to receive email alerts on any updates to this article.

Open Peer Review

Current Reviewer Status: ?

Key to Reviewer Statuses VIEW HIDE

ApprovedThe paper is scientifically sound in its current form and only minor, if any, improvements are suggested

Approved with reservations A number of small changes, sometimes more significant revisions are required to address specific details and improve the papers academic merit.

Not approvedFundamental flaws in the paper seriously undermine the findings and conclusions

Version 2

VERSION 2

PUBLISHED 28 May 2014

Revised

Views

Reviewer Report 21 Aug 2014

Pablo Acebes, Department of Ecology, Autonomous University of Madrid, Madrid, Spain

Approved

https://doi.org/10.5256/f1000research.4501.r5906

The authors have improved the ms from their first submitted version. Please see the comments below to further improve the article:

First paragraph (introduction): please put guanaco in the singular.
Guanaco population sampling section: please replace ‘SIG’ with ‘GIS’.
Guanaco population sampling section:

CITE

Report a concern

Respond or Comment

Views

Reviewer Report 04 Aug 2014

Gary Luck, Institute for Land, Water, and Society, Charles Sturt University, Albury, Australia

Approved

https://doi.org/10.5256/f1000research.4501.r2049

CITE

Report a concern

Respond or Comment

Version 1

VERSION 1

PUBLISHED 09 Oct 2013

Views

Reviewer Report 19 Dec 2013

Pablo Acebes, Department of Ecology, Autonomous University of Madrid, Madrid, Spain

Approved with Reservations

https://doi.org/10.5256/f1000research.2588.r2847

The authors explore the population dynamics of a long-term monitored guanaco population (36 years) in the Chilean Tierra del Fuego, trying to discern if the process is governed by population size and/or environmental (climatic) variables, assuming that guanaco growth rate follows a density-dependent process. Although the topic is very interesting, the authors have room to improve the manuscript. Below the authors will find major and minor comments.

Major comments
The manuscript is classified as a “Research article” when indeed it seems a “Short note”. It would greatly benefit from deeper and more detailed explanations of:

The theory of ungulate population dynamics, driven by density-dependent and density-independent processes; please expand this topic in the introduction and discuss more deeply your results considering the theoretical framework (see comments below).
The census methodology (see comments below).
Statistical modeling (see comments below).

Ungulate populations are regulated via endogenous forces (density-dependent processes), and exogenous forces (density-independent): weather and predation. Weather determines the primary production, i.e. the resource (forage) availability, which in turn determines the carrying capacity. On the other hand weather, through extreme conditions (e.g. severe winter climate), modulates population dynamics (starvation, survival). Predation is considered an important force which shapes population dynamics as well. In addition, poaching or overhunting act as predation, and competition with other ungulates is another important exogenous force. With this framework authors should justify:

The background supporting the study, as it currently is a bit poor, in my view. The authors should explain more in detail, for example, which are the differences between the density-stabilizing and the density-limiting processes, or the evidence of including climatic variables when modelling population growth rate trends.
The use of these climatic variables: the average annual precipitation and winter temperature. Without any justification, authors could have also included others variables in the models, as climatic variables do not account for the pattern described, but this doesn’t necessarily mean that climate hasn’t got any effect on the guanaco population growth rate. Moreover authors should explain if these two climatic variables are selected as indicators of primary production and harsh weather conditions.
As authors stated in introduction, guanaco populations have undergone overhunting (poaching) and competition with sheep, these being two of the major forces of their dramatic decline in the last century. For that reason, it is quite surprising that no variables related to livestock were included in the modelling procedure. The population has increased a lot in the studied period (x8) and just climate and/or density-dependent process do not explain alone such increase in my view. Therefore authors should consider including livestock effects, its influence on resource availability along the studied period and the mentioned overhunting, as this could really explain the detected trend.

The guanaco sampling method has changed during the studied period (different band widths). Besides, were the transects chosen based on the topography and vegetation cover of the ranch to ensure that all areas were visible to census-takers along their transects? I am not sure if that could be a source of error, but authors should discuss this point. Moreover, I recommend authors to re-analyze their data using the DISTANCE program (Buckland et al., 2004) to estimate population size over the period, as the analyses performed by this package seems much more robust that the one employed by authors. If they do so, authors could also include topographic variables in the models to see whether the resulting models change. The reason is that the authors do not explain if guanacos occur in both biomes (steppe and forest), because if that was true, detection of guanacos was completely different in both ecosystems. Therefore the band width of 500 or 1000m is not valid for forests.

Regarding the population size estimated along the 36 years (Supplementary table), important (huge) differences are found, for example between 2004 and 2005 or between 2006 and 2007, or between 2007 and 2008. My concern is if such “jumps” could be related to the census surveyed. Please discuss this point.
The analytical approach employed by the authors doesn’t seem appropriate in my view, as they also recognize in the discussion, and that could be the reason for not finding any climatic variable significant in the model:

The authors use a stepwise regression when other approaches such as logistic regressions, Ricker or Beverton–Holt models could give more suitable results. Please explain or justify your decision.
The selection of the best model among the candidates should be done by Akaike’s information.

Minor comments

Refer to climatic variables or climatic effects, instead of climatic covariables.
Explain more in detail Corani & Gatto’s studies.
Please remove information related to metabolic studies between guanacos and sheep (1st paragraph of study area section).
Please add Nothofagus spp among the brackets after deciduous forest (study area section) if it is the case.
Give more information about livestock ranching, density, and size and the relation of livestock rangers with guanacos along the studied period (study area section).
Are the guanacos found both in the steppe and the forest biomes?
Please re-write the paragraph related to guanaco sampling through transect method in the consecutive periods (it is not clear enough).
Please remove information related to binoculars and GPS brands (did the authors use the same gadgets across 36 years?).
Explain the interest of using time lags (T) as covariables in the model.
Please add the Statistica version employed.
Please move explanations of the analyses perform from results to material & methods section.

Competing Interests: No competing interests were disclosed.

I confirm that I have read this submission and believe that I have an appropriate level of expertise to confirm that it is of an acceptable scientific standard, however I have significant reservations, as outlined above.

CITE

Report a concern

Author Response 14 May 2014

Maria Zubillaga, Centro de Estudios Parasitológicos y de Vectores (CEPAVE), Universidad Nacional de La Plata, La Plata, Argentina

14 May 2014

Author Response
- "The background supporting the study, as it currently is a bit poor, in my view. The authors should explain more in detail, for example, which are the differences between the
... Continue reading
"The background supporting the study, as it currently is a bit poor, in my view. The authors should explain more in detail, for example, which are the differences between the density-stabilizing and the density-limiting processes, or the evidence of including climatic variables when modelling population growth rate trends."

After the following paragraph that was already in the original text:
“No population of any species can grow indefinitely, and population checks based upon different processes restrict population size and/or geographic distribution; these processes are either density-stabilizing or density-limiting”

We added the following paragraph explaining the differences between the density-stabilizing and the density-limiting processes.

“The former are of a biotic nature and depends on the interaction between individuals of the same or different species, while the latter are independent of population size. Stabilization results from density-dependence, with a regulatory effect that varies in intensity with the size or density of the population itself, however, not all density-dependent factors are density-stabilizing. The density-limiting factors can also be considered density-responsive because the per capita amount or availability of resources decreases as the population density increases. Thus, these two types of factors (density-stabilizing and density-limiting) rarely act independently: the density-limiting factors (generally of a physical and/or climatic nature), may determine the level at which populations become stabilized by the density-dependent processes, but they do not have a stabilizing capacity per se; for this reason many wildlife population dynamic and management models include the effects of climatic variables (e.g., Dennis & Otten, 2000; Colchero et al., 2009)^3,4”.

"The use of these climatic variables: the average annual precipitation and winter temperature. Without any justification, authors could have also included others variables in the models, as climatic variables do not account for the pattern described, but this doesn’t necessarily mean that climate hasn’t got any effect on the guanaco population growth rate. Moreover authors should explain if these two climatic variables are selected as indicators of primary production and harsh weather conditions."

To explain and justify the use of these climatic variables the paragraph below was incorporated in the section “Climatic variables”:
“These climatic variables were selected because some studies suggested that they have influence on guanaco demographic parameters: Rey et al. 2012²⁶ observed that after a severe drought the proportion guanaco yearlings/female decreased significantly, and Sarno et al. 1999¹⁷ detected a negative effect of winter snowfall on guanaco juvenile survival; because we had insufficient snowfall data we used the winter temperature as a proxy for winter snowfall.”

"As authors stated in introduction, guanaco populations have undergone overhunting (poaching) and competition with sheep, these being two of the major forces of their dramatic decline in the last century. For that reason, it is quite surprising that no variables related to livestock were included in the modelling procedure. The population has increased a lot in the studied period (x8) and just climate and/or density-dependent process do not explain alone such increase in my view. Therefore authors should consider including livestock effects, its influence on resource availability along the studied period and the mentioned overhunting, as this could really explain the detected trend."

In relation with the “poaching” the following paragraph was incorporated in section “Study area” to justify why this variable was not considered in our study:

“In contrast to the continent, the puma (Puma concolor), the main predator of guanacos, is absent in the island; since 1977 the guanaco hunting has been controlled by Chilean National Forest Corporation (CONAF, according to its Spanish acronym) and the Chilean Agricultural and Livestock Service (SAG, according to its Spanish acronym).”

In relation to the suggestion to incorporate livestock in the analysis, we re-analyzed our multiple regression incorporating the variable livestock as sheep population. We re-processed the regressions incorporating the sheep population as a new independent variable as a possible predictor of the guanaco population growth rate (l); so our new analysis increased from 5 to 6 independent variables: sheep population, guanaco population size, winter temperature, winter temperature with a lag of 1 year, annual precipitation, annual precipitation with a lag of 3 years. Our main results didn’t change and it was confirmed that only the guanaco population size seems to have an effect on the population growth rate (l). These changes can be found in the “Methods” and in the “Results” sections.

“The guanaco sampling method has changed during the studied period (different band widths). Besides, were the transects chosen based on the topography and vegetation cover of the ranch to ensure that all areas were visible to census-takers along their transects? I am not sure if that could be a source of error, but authors should discuss this point.”

In the Section “Guanaco population sampling” we added the following paragraphs where we explain the motive of the change and justify the transects chosen:

“The sampling methodology was changed by an expert recommendation made in 1995 ²³; as in year 2000 the fixed and the undefined band width methods were applied simultaneously, we tested both results and found no significant statistical difference between them.”
“Despite randomly selected transects are recommended²⁴, preexisting roads were used because according to Soto (2010)¹⁸ the existing system of roads is an adequate sample of the area.”

“Moreover, I recommend authors to re-analyze their data using the DISTANCE program (Buckland et al., 2004) to estimate population size over the period, as the analyses performed by this package seems much more robust that the one employed by authors. If they do so, authors could also include topographic variables in the models to see whether the resulting models change. The reason is that the authors do not explain if guanacos occur in both biomes (steppe and forest), because if that was true, detection of guanacos was completely different in both ecosystems. Therefore the band width of 500 or 1000m is not valid for forests.”

In the Section “Guanaco population sampling” the following paragraphs was incorporated to justify the methodology used:

“Raedeke (1978)¹⁹ claims that the Leopold method is valid when the following conditions are satisfied: (1) the road systems must be an adequate sampling of the study area, (2) the network road must be randomly distributed, and (3) the animals included in the sampling must be randomly distributed in relation to the observer’s route; and he considers that in the south of the Tierra del Fuego Island these assumptions are fulfilled. Soto 2010¹⁸ compared population estimations by the Leopold and Distance methods and found that the value of the means estimate by Leopold methods fall within the confidence intervals estimated by Distance; additionally, as all sampling periods used the same methodology whatever bias might exist in the estimation of the mean abundance using the Leopold method, the relative changes among years (and thus the temporal trend) will be adequately represented; thus, we conclude that the Leopold’s method seems adequate for our purposes¹⁸.”

In relation to the forest and the sampling methodology, as the area occupied by forests is low and it has some degree of intervention, the visibility of the guanaco is adequate, hence we considered that the forest is a minor component and that does not affect the efficiency of the sampling procedure. In the section “Study area” the next paragraph was incorporated:

“The forested area is about 8.8% of the total study area, with different degrees of forest clearance that offers adequate visibility for guanaco sampling.”

“Regarding the population size estimated along the 36 years (Supplementary table), important (huge) differences are found, for example between 2004 and 2005 or between 2006 and 2007, or between 2007 and 2008. My concern is if such “jumps” could be related to the census surveyed. Please discuss this point.”

In the “Discussion” section we added the following discussion as required by the reviewer:
“The results of the guanaco population sampling suggest a certain trend in the population size, with a sort of exponential growth in the first few years, becoming more variable as the population grows, with more marked fluctuations during the last 10-12 years; this may imply that the population is becoming stabilized, possibly approaching its carrying capacity. On the other hand, the sampling results of those last 10-12 years show abrupt “jumps” in some years (for example 2004-2005) that may be the consequence of the mobility of guanacos from the Cameron ranch to neighboring sites and vice versa; since the transect sampling does not identify individuals the effects of possible local displacements could not be considered.”

“The authors used a stepwise regression when other approaches such as logistic regressions, Ricker or Beverton-Holt models could give more suitable results. Please explain or justify your decision.”

Our goal was to carry out a preliminary analysis that would guide us in the study of the population regulation process in the guanaco. As there are studies in ungulate that have used simple multiple regression analysis and obtained good/satisfactory results, we considered that it was of interest to test this technique as a first step in such an analysis.
In the manuscript the following paragraph was incorporated in the “Discussion” section to justify our decision:

"Contrary to what was expected based on the bibliography of ungulate’s population dynamics, weather variables do not seem to influence the density-dependent population growth rate process of the guanaco population of the Cameron ranch. Our aim was to carry out a preliminary analysis that would help identify some of the regulation processes in guanaco population; so we used a simple multiple regression analysis as a first step in that direction; nevertheless, our conclusion is that in order to test the effects of climatic variables on population regulation of large ungulates as the guanaco, the use of a population dynamic model would be recommended, for they seem to account better for the interaction between density-dependent processes and weather variables than a simple regression between the latter and guanaco population growth rate.”

“The selection of the best model among the candidates should be done by Akaike’s information”

This suggestion was considered and the respective Akaike’s values were calculated.

Minor comments:
“Refer to climatic variables or climatic effects, instead of climatic covariables.”

The recommendation was applied.

“Explain more in detail Corani & Gatto’s studies.”

With the previous changes we realize that the citation of Corani and Gatto (2007) is not necessary any more. Mainly because the essence of that paper is the proposal of a methodology that is not strictly relevant to our work. The phrase with this citation was deleted.

“Please remove information related to metabolic studies between guanacos and sheep (1st paragraph of study area section).”

The suggestion was carried out.

“Please add Nothofagus spp among the brackets after deciduous forest (study area section) if it is the case.”

This information is already incorporated.

“Give more information about livestock ranching, density, and size and the relation of livestock rangers with guanacos along the studied period (study area section).”

This information was already incorporate in the section “Sheep population”

“Are the guanacos found both in the steppe and the forest biomes?”

Yes, the guanacos use both biomes, but they mostly use the open habitat (i.e. steppes and meadows).

“Please re-write the paragraph related to guanaco sampling through transect method in the consecutive periods (it is not clear enough).”

The paragraph was improved.

“Please remove information related to binoculars and GPS brands (did the authors use the same gadgets across 36 years?).”

The recommendation was carried out.

“Explain the interest of using time lags (T) as covariables in the model.”

The next paragraph was incorporated in section “Population analysis”:

“The inclusion of time lags is convenient because it may detect possible cumulative climatic effects on ungulate population growth rates as it was observed in, e.g., deer and moose ²⁹ and in vicuñas¹³”.

“Please add the Statistica version employed.”

The Statistica tools was replaced by language R (Version 0.97.449 – ©2009-2012 RStudio, Inc.) to obtain the value of Akaike and satisfy the item 3.2 (see above).

“Please move explanations of the analyses perform from results to material & methods section.”

The recommendation was carried out.
"The background supporting the study, as it currently is a bit poor, in my view. The authors should explain more in detail, for example, which are the differences between the density-stabilizing and the density-limiting processes, or the evidence of including climatic variables when modelling population growth rate trends."

After the following paragraph that was already in the original text:
“No population of any species can grow indefinitely, and population checks based upon different processes restrict population size and/or geographic distribution; these processes are either density-stabilizing or density-limiting”

We added the following paragraph explaining the differences between the density-stabilizing and the density-limiting processes.

“The former are of a biotic nature and depends on the interaction between individuals of the same or different species, while the latter are independent of population size. Stabilization results from density-dependence, with a regulatory effect that varies in intensity with the size or density of the population itself, however, not all density-dependent factors are density-stabilizing. The density-limiting factors can also be considered density-responsive because the per capita amount or availability of resources decreases as the population density increases. Thus, these two types of factors (density-stabilizing and density-limiting) rarely act independently: the density-limiting factors (generally of a physical and/or climatic nature), may determine the level at which populations become stabilized by the density-dependent processes, but they do not have a stabilizing capacity per se; for this reason many wildlife population dynamic and management models include the effects of climatic variables (e.g., Dennis & Otten, 2000; Colchero et al., 2009)^3,4”.

"The use of these climatic variables: the average annual precipitation and winter temperature. Without any justification, authors could have also included others variables in the models, as climatic variables do not account for the pattern described, but this doesn’t necessarily mean that climate hasn’t got any effect on the guanaco population growth rate. Moreover authors should explain if these two climatic variables are selected as indicators of primary production and harsh weather conditions."

To explain and justify the use of these climatic variables the paragraph below was incorporated in the section “Climatic variables”:
“These climatic variables were selected because some studies suggested that they have influence on guanaco demographic parameters: Rey et al. 2012²⁶ observed that after a severe drought the proportion guanaco yearlings/female decreased significantly, and Sarno et al. 1999¹⁷ detected a negative effect of winter snowfall on guanaco juvenile survival; because we had insufficient snowfall data we used the winter temperature as a proxy for winter snowfall.”

"As authors stated in introduction, guanaco populations have undergone overhunting (poaching) and competition with sheep, these being two of the major forces of their dramatic decline in the last century. For that reason, it is quite surprising that no variables related to livestock were included in the modelling procedure. The population has increased a lot in the studied period (x8) and just climate and/or density-dependent process do not explain alone such increase in my view. Therefore authors should consider including livestock effects, its influence on resource availability along the studied period and the mentioned overhunting, as this could really explain the detected trend."

In relation with the “poaching” the following paragraph was incorporated in section “Study area” to justify why this variable was not considered in our study:

“In contrast to the continent, the puma (Puma concolor), the main predator of guanacos, is absent in the island; since 1977 the guanaco hunting has been controlled by Chilean National Forest Corporation (CONAF, according to its Spanish acronym) and the Chilean Agricultural and Livestock Service (SAG, according to its Spanish acronym).”

In relation to the suggestion to incorporate livestock in the analysis, we re-analyzed our multiple regression incorporating the variable livestock as sheep population. We re-processed the regressions incorporating the sheep population as a new independent variable as a possible predictor of the guanaco population growth rate (l); so our new analysis increased from 5 to 6 independent variables: sheep population, guanaco population size, winter temperature, winter temperature with a lag of 1 year, annual precipitation, annual precipitation with a lag of 3 years. Our main results didn’t change and it was confirmed that only the guanaco population size seems to have an effect on the population growth rate (l). These changes can be found in the “Methods” and in the “Results” sections.

“The guanaco sampling method has changed during the studied period (different band widths). Besides, were the transects chosen based on the topography and vegetation cover of the ranch to ensure that all areas were visible to census-takers along their transects? I am not sure if that could be a source of error, but authors should discuss this point.”

In the Section “Guanaco population sampling” we added the following paragraphs where we explain the motive of the change and justify the transects chosen:

“The sampling methodology was changed by an expert recommendation made in 1995 ²³; as in year 2000 the fixed and the undefined band width methods were applied simultaneously, we tested both results and found no significant statistical difference between them.”
“Despite randomly selected transects are recommended²⁴, preexisting roads were used because according to Soto (2010)¹⁸ the existing system of roads is an adequate sample of the area.”

“Moreover, I recommend authors to re-analyze their data using the DISTANCE program (Buckland et al., 2004) to estimate population size over the period, as the analyses performed by this package seems much more robust that the one employed by authors. If they do so, authors could also include topographic variables in the models to see whether the resulting models change. The reason is that the authors do not explain if guanacos occur in both biomes (steppe and forest), because if that was true, detection of guanacos was completely different in both ecosystems. Therefore the band width of 500 or 1000m is not valid for forests.”

In the Section “Guanaco population sampling” the following paragraphs was incorporated to justify the methodology used:

“Raedeke (1978)¹⁹ claims that the Leopold method is valid when the following conditions are satisfied: (1) the road systems must be an adequate sampling of the study area, (2) the network road must be randomly distributed, and (3) the animals included in the sampling must be randomly distributed in relation to the observer’s route; and he considers that in the south of the Tierra del Fuego Island these assumptions are fulfilled. Soto 2010¹⁸ compared population estimations by the Leopold and Distance methods and found that the value of the means estimate by Leopold methods fall within the confidence intervals estimated by Distance; additionally, as all sampling periods used the same methodology whatever bias might exist in the estimation of the mean abundance using the Leopold method, the relative changes among years (and thus the temporal trend) will be adequately represented; thus, we conclude that the Leopold’s method seems adequate for our purposes¹⁸.”

In relation to the forest and the sampling methodology, as the area occupied by forests is low and it has some degree of intervention, the visibility of the guanaco is adequate, hence we considered that the forest is a minor component and that does not affect the efficiency of the sampling procedure. In the section “Study area” the next paragraph was incorporated:

“The forested area is about 8.8% of the total study area, with different degrees of forest clearance that offers adequate visibility for guanaco sampling.”

“Regarding the population size estimated along the 36 years (Supplementary table), important (huge) differences are found, for example between 2004 and 2005 or between 2006 and 2007, or between 2007 and 2008. My concern is if such “jumps” could be related to the census surveyed. Please discuss this point.”

In the “Discussion” section we added the following discussion as required by the reviewer:
“The results of the guanaco population sampling suggest a certain trend in the population size, with a sort of exponential growth in the first few years, becoming more variable as the population grows, with more marked fluctuations during the last 10-12 years; this may imply that the population is becoming stabilized, possibly approaching its carrying capacity. On the other hand, the sampling results of those last 10-12 years show abrupt “jumps” in some years (for example 2004-2005) that may be the consequence of the mobility of guanacos from the Cameron ranch to neighboring sites and vice versa; since the transect sampling does not identify individuals the effects of possible local displacements could not be considered.”

“The authors used a stepwise regression when other approaches such as logistic regressions, Ricker or Beverton-Holt models could give more suitable results. Please explain or justify your decision.”

Our goal was to carry out a preliminary analysis that would guide us in the study of the population regulation process in the guanaco. As there are studies in ungulate that have used simple multiple regression analysis and obtained good/satisfactory results, we considered that it was of interest to test this technique as a first step in such an analysis.
In the manuscript the following paragraph was incorporated in the “Discussion” section to justify our decision:

"Contrary to what was expected based on the bibliography of ungulate’s population dynamics, weather variables do not seem to influence the density-dependent population growth rate process of the guanaco population of the Cameron ranch. Our aim was to carry out a preliminary analysis that would help identify some of the regulation processes in guanaco population; so we used a simple multiple regression analysis as a first step in that direction; nevertheless, our conclusion is that in order to test the effects of climatic variables on population regulation of large ungulates as the guanaco, the use of a population dynamic model would be recommended, for they seem to account better for the interaction between density-dependent processes and weather variables than a simple regression between the latter and guanaco population growth rate.”

“The selection of the best model among the candidates should be done by Akaike’s information”

This suggestion was considered and the respective Akaike’s values were calculated.

Minor comments:
“Refer to climatic variables or climatic effects, instead of climatic covariables.”

The recommendation was applied.

“Explain more in detail Corani & Gatto’s studies.”

With the previous changes we realize that the citation of Corani and Gatto (2007) is not necessary any more. Mainly because the essence of that paper is the proposal of a methodology that is not strictly relevant to our work. The phrase with this citation was deleted.

“Please remove information related to metabolic studies between guanacos and sheep (1st paragraph of study area section).”

The suggestion was carried out.

“Please add Nothofagus spp among the brackets after deciduous forest (study area section) if it is the case.”

This information is already incorporated.

“Give more information about livestock ranching, density, and size and the relation of livestock rangers with guanacos along the studied period (study area section).”

This information was already incorporate in the section “Sheep population”

“Are the guanacos found both in the steppe and the forest biomes?”

Yes, the guanacos use both biomes, but they mostly use the open habitat (i.e. steppes and meadows).

“Please re-write the paragraph related to guanaco sampling through transect method in the consecutive periods (it is not clear enough).”

The paragraph was improved.

“Please remove information related to binoculars and GPS brands (did the authors use the same gadgets across 36 years?).”

The recommendation was carried out.

“Explain the interest of using time lags (T) as covariables in the model.”

The next paragraph was incorporated in section “Population analysis”:

“The inclusion of time lags is convenient because it may detect possible cumulative climatic effects on ungulate population growth rates as it was observed in, e.g., deer and moose ²⁹ and in vicuñas¹³”.

“Please add the Statistica version employed.”

The Statistica tools was replaced by language R (Version 0.97.449 – ©2009-2012 RStudio, Inc.) to obtain the value of Akaike and satisfy the item 3.2 (see above).

“Please move explanations of the analyses perform from results to material & methods section.”

The recommendation was carried out.
Competing Interests: No competing interests Close
Report a concern
Respond or Comment

COMMENTS ON THIS REPORT

Author Response 14 May 2014

Maria Zubillaga, Centro de Estudios Parasitológicos y de Vectores (CEPAVE), Universidad Nacional de La Plata, La Plata, Argentina

14 May 2014

Author Response
- "The background supporting the study, as it currently is a bit poor, in my view. The authors should explain more in detail, for example, which are the differences between the
... Continue reading
"The background supporting the study, as it currently is a bit poor, in my view. The authors should explain more in detail, for example, which are the differences between the density-stabilizing and the density-limiting processes, or the evidence of including climatic variables when modelling population growth rate trends."

After the following paragraph that was already in the original text:
“No population of any species can grow indefinitely, and population checks based upon different processes restrict population size and/or geographic distribution; these processes are either density-stabilizing or density-limiting”

We added the following paragraph explaining the differences between the density-stabilizing and the density-limiting processes.

“The former are of a biotic nature and depends on the interaction between individuals of the same or different species, while the latter are independent of population size. Stabilization results from density-dependence, with a regulatory effect that varies in intensity with the size or density of the population itself, however, not all density-dependent factors are density-stabilizing. The density-limiting factors can also be considered density-responsive because the per capita amount or availability of resources decreases as the population density increases. Thus, these two types of factors (density-stabilizing and density-limiting) rarely act independently: the density-limiting factors (generally of a physical and/or climatic nature), may determine the level at which populations become stabilized by the density-dependent processes, but they do not have a stabilizing capacity per se; for this reason many wildlife population dynamic and management models include the effects of climatic variables (e.g., Dennis & Otten, 2000; Colchero et al., 2009)^3,4”.

"The use of these climatic variables: the average annual precipitation and winter temperature. Without any justification, authors could have also included others variables in the models, as climatic variables do not account for the pattern described, but this doesn’t necessarily mean that climate hasn’t got any effect on the guanaco population growth rate. Moreover authors should explain if these two climatic variables are selected as indicators of primary production and harsh weather conditions."

To explain and justify the use of these climatic variables the paragraph below was incorporated in the section “Climatic variables”:
“These climatic variables were selected because some studies suggested that they have influence on guanaco demographic parameters: Rey et al. 2012²⁶ observed that after a severe drought the proportion guanaco yearlings/female decreased significantly, and Sarno et al. 1999¹⁷ detected a negative effect of winter snowfall on guanaco juvenile survival; because we had insufficient snowfall data we used the winter temperature as a proxy for winter snowfall.”

"As authors stated in introduction, guanaco populations have undergone overhunting (poaching) and competition with sheep, these being two of the major forces of their dramatic decline in the last century. For that reason, it is quite surprising that no variables related to livestock were included in the modelling procedure. The population has increased a lot in the studied period (x8) and just climate and/or density-dependent process do not explain alone such increase in my view. Therefore authors should consider including livestock effects, its influence on resource availability along the studied period and the mentioned overhunting, as this could really explain the detected trend."

In relation with the “poaching” the following paragraph was incorporated in section “Study area” to justify why this variable was not considered in our study:

“In contrast to the continent, the puma (Puma concolor), the main predator of guanacos, is absent in the island; since 1977 the guanaco hunting has been controlled by Chilean National Forest Corporation (CONAF, according to its Spanish acronym) and the Chilean Agricultural and Livestock Service (SAG, according to its Spanish acronym).”

In relation to the suggestion to incorporate livestock in the analysis, we re-analyzed our multiple regression incorporating the variable livestock as sheep population. We re-processed the regressions incorporating the sheep population as a new independent variable as a possible predictor of the guanaco population growth rate (l); so our new analysis increased from 5 to 6 independent variables: sheep population, guanaco population size, winter temperature, winter temperature with a lag of 1 year, annual precipitation, annual precipitation with a lag of 3 years. Our main results didn’t change and it was confirmed that only the guanaco population size seems to have an effect on the population growth rate (l). These changes can be found in the “Methods” and in the “Results” sections.

“The guanaco sampling method has changed during the studied period (different band widths). Besides, were the transects chosen based on the topography and vegetation cover of the ranch to ensure that all areas were visible to census-takers along their transects? I am not sure if that could be a source of error, but authors should discuss this point.”

In the Section “Guanaco population sampling” we added the following paragraphs where we explain the motive of the change and justify the transects chosen:

“The sampling methodology was changed by an expert recommendation made in 1995 ²³; as in year 2000 the fixed and the undefined band width methods were applied simultaneously, we tested both results and found no significant statistical difference between them.”
“Despite randomly selected transects are recommended²⁴, preexisting roads were used because according to Soto (2010)¹⁸ the existing system of roads is an adequate sample of the area.”

“Moreover, I recommend authors to re-analyze their data using the DISTANCE program (Buckland et al., 2004) to estimate population size over the period, as the analyses performed by this package seems much more robust that the one employed by authors. If they do so, authors could also include topographic variables in the models to see whether the resulting models change. The reason is that the authors do not explain if guanacos occur in both biomes (steppe and forest), because if that was true, detection of guanacos was completely different in both ecosystems. Therefore the band width of 500 or 1000m is not valid for forests.”

In the Section “Guanaco population sampling” the following paragraphs was incorporated to justify the methodology used:

“Raedeke (1978)¹⁹ claims that the Leopold method is valid when the following conditions are satisfied: (1) the road systems must be an adequate sampling of the study area, (2) the network road must be randomly distributed, and (3) the animals included in the sampling must be randomly distributed in relation to the observer’s route; and he considers that in the south of the Tierra del Fuego Island these assumptions are fulfilled. Soto 2010¹⁸ compared population estimations by the Leopold and Distance methods and found that the value of the means estimate by Leopold methods fall within the confidence intervals estimated by Distance; additionally, as all sampling periods used the same methodology whatever bias might exist in the estimation of the mean abundance using the Leopold method, the relative changes among years (and thus the temporal trend) will be adequately represented; thus, we conclude that the Leopold’s method seems adequate for our purposes¹⁸.”

In relation to the forest and the sampling methodology, as the area occupied by forests is low and it has some degree of intervention, the visibility of the guanaco is adequate, hence we considered that the forest is a minor component and that does not affect the efficiency of the sampling procedure. In the section “Study area” the next paragraph was incorporated:

“The forested area is about 8.8% of the total study area, with different degrees of forest clearance that offers adequate visibility for guanaco sampling.”

“Regarding the population size estimated along the 36 years (Supplementary table), important (huge) differences are found, for example between 2004 and 2005 or between 2006 and 2007, or between 2007 and 2008. My concern is if such “jumps” could be related to the census surveyed. Please discuss this point.”

In the “Discussion” section we added the following discussion as required by the reviewer:
“The results of the guanaco population sampling suggest a certain trend in the population size, with a sort of exponential growth in the first few years, becoming more variable as the population grows, with more marked fluctuations during the last 10-12 years; this may imply that the population is becoming stabilized, possibly approaching its carrying capacity. On the other hand, the sampling results of those last 10-12 years show abrupt “jumps” in some years (for example 2004-2005) that may be the consequence of the mobility of guanacos from the Cameron ranch to neighboring sites and vice versa; since the transect sampling does not identify individuals the effects of possible local displacements could not be considered.”

“The authors used a stepwise regression when other approaches such as logistic regressions, Ricker or Beverton-Holt models could give more suitable results. Please explain or justify your decision.”

Our goal was to carry out a preliminary analysis that would guide us in the study of the population regulation process in the guanaco. As there are studies in ungulate that have used simple multiple regression analysis and obtained good/satisfactory results, we considered that it was of interest to test this technique as a first step in such an analysis.
In the manuscript the following paragraph was incorporated in the “Discussion” section to justify our decision:

"Contrary to what was expected based on the bibliography of ungulate’s population dynamics, weather variables do not seem to influence the density-dependent population growth rate process of the guanaco population of the Cameron ranch. Our aim was to carry out a preliminary analysis that would help identify some of the regulation processes in guanaco population; so we used a simple multiple regression analysis as a first step in that direction; nevertheless, our conclusion is that in order to test the effects of climatic variables on population regulation of large ungulates as the guanaco, the use of a population dynamic model would be recommended, for they seem to account better for the interaction between density-dependent processes and weather variables than a simple regression between the latter and guanaco population growth rate.”

“The selection of the best model among the candidates should be done by Akaike’s information”

This suggestion was considered and the respective Akaike’s values were calculated.

Minor comments:
“Refer to climatic variables or climatic effects, instead of climatic covariables.”

The recommendation was applied.

“Explain more in detail Corani & Gatto’s studies.”

With the previous changes we realize that the citation of Corani and Gatto (2007) is not necessary any more. Mainly because the essence of that paper is the proposal of a methodology that is not strictly relevant to our work. The phrase with this citation was deleted.

“Please remove information related to metabolic studies between guanacos and sheep (1st paragraph of study area section).”

The suggestion was carried out.

“Please add Nothofagus spp among the brackets after deciduous forest (study area section) if it is the case.”

This information is already incorporated.

“Give more information about livestock ranching, density, and size and the relation of livestock rangers with guanacos along the studied period (study area section).”

This information was already incorporate in the section “Sheep population”

“Are the guanacos found both in the steppe and the forest biomes?”

Yes, the guanacos use both biomes, but they mostly use the open habitat (i.e. steppes and meadows).

“Please re-write the paragraph related to guanaco sampling through transect method in the consecutive periods (it is not clear enough).”

The paragraph was improved.

“Please remove information related to binoculars and GPS brands (did the authors use the same gadgets across 36 years?).”

The recommendation was carried out.

“Explain the interest of using time lags (T) as covariables in the model.”

The next paragraph was incorporated in section “Population analysis”:

“The inclusion of time lags is convenient because it may detect possible cumulative climatic effects on ungulate population growth rates as it was observed in, e.g., deer and moose ²⁹ and in vicuñas¹³”.

“Please add the Statistica version employed.”

The Statistica tools was replaced by language R (Version 0.97.449 – ©2009-2012 RStudio, Inc.) to obtain the value of Akaike and satisfy the item 3.2 (see above).

“Please move explanations of the analyses perform from results to material & methods section.”

The recommendation was carried out.
"The background supporting the study, as it currently is a bit poor, in my view. The authors should explain more in detail, for example, which are the differences between the density-stabilizing and the density-limiting processes, or the evidence of including climatic variables when modelling population growth rate trends."

After the following paragraph that was already in the original text:
“No population of any species can grow indefinitely, and population checks based upon different processes restrict population size and/or geographic distribution; these processes are either density-stabilizing or density-limiting”

We added the following paragraph explaining the differences between the density-stabilizing and the density-limiting processes.

“The former are of a biotic nature and depends on the interaction between individuals of the same or different species, while the latter are independent of population size. Stabilization results from density-dependence, with a regulatory effect that varies in intensity with the size or density of the population itself, however, not all density-dependent factors are density-stabilizing. The density-limiting factors can also be considered density-responsive because the per capita amount or availability of resources decreases as the population density increases. Thus, these two types of factors (density-stabilizing and density-limiting) rarely act independently: the density-limiting factors (generally of a physical and/or climatic nature), may determine the level at which populations become stabilized by the density-dependent processes, but they do not have a stabilizing capacity per se; for this reason many wildlife population dynamic and management models include the effects of climatic variables (e.g., Dennis & Otten, 2000; Colchero et al., 2009)^3,4”.

"The use of these climatic variables: the average annual precipitation and winter temperature. Without any justification, authors could have also included others variables in the models, as climatic variables do not account for the pattern described, but this doesn’t necessarily mean that climate hasn’t got any effect on the guanaco population growth rate. Moreover authors should explain if these two climatic variables are selected as indicators of primary production and harsh weather conditions."

To explain and justify the use of these climatic variables the paragraph below was incorporated in the section “Climatic variables”:
“These climatic variables were selected because some studies suggested that they have influence on guanaco demographic parameters: Rey et al. 2012²⁶ observed that after a severe drought the proportion guanaco yearlings/female decreased significantly, and Sarno et al. 1999¹⁷ detected a negative effect of winter snowfall on guanaco juvenile survival; because we had insufficient snowfall data we used the winter temperature as a proxy for winter snowfall.”

"As authors stated in introduction, guanaco populations have undergone overhunting (poaching) and competition with sheep, these being two of the major forces of their dramatic decline in the last century. For that reason, it is quite surprising that no variables related to livestock were included in the modelling procedure. The population has increased a lot in the studied period (x8) and just climate and/or density-dependent process do not explain alone such increase in my view. Therefore authors should consider including livestock effects, its influence on resource availability along the studied period and the mentioned overhunting, as this could really explain the detected trend."

In relation with the “poaching” the following paragraph was incorporated in section “Study area” to justify why this variable was not considered in our study:

“In contrast to the continent, the puma (Puma concolor), the main predator of guanacos, is absent in the island; since 1977 the guanaco hunting has been controlled by Chilean National Forest Corporation (CONAF, according to its Spanish acronym) and the Chilean Agricultural and Livestock Service (SAG, according to its Spanish acronym).”

In relation to the suggestion to incorporate livestock in the analysis, we re-analyzed our multiple regression incorporating the variable livestock as sheep population. We re-processed the regressions incorporating the sheep population as a new independent variable as a possible predictor of the guanaco population growth rate (l); so our new analysis increased from 5 to 6 independent variables: sheep population, guanaco population size, winter temperature, winter temperature with a lag of 1 year, annual precipitation, annual precipitation with a lag of 3 years. Our main results didn’t change and it was confirmed that only the guanaco population size seems to have an effect on the population growth rate (l). These changes can be found in the “Methods” and in the “Results” sections.

“The guanaco sampling method has changed during the studied period (different band widths). Besides, were the transects chosen based on the topography and vegetation cover of the ranch to ensure that all areas were visible to census-takers along their transects? I am not sure if that could be a source of error, but authors should discuss this point.”

In the Section “Guanaco population sampling” we added the following paragraphs where we explain the motive of the change and justify the transects chosen:

“The sampling methodology was changed by an expert recommendation made in 1995 ²³; as in year 2000 the fixed and the undefined band width methods were applied simultaneously, we tested both results and found no significant statistical difference between them.”
“Despite randomly selected transects are recommended²⁴, preexisting roads were used because according to Soto (2010)¹⁸ the existing system of roads is an adequate sample of the area.”

“Moreover, I recommend authors to re-analyze their data using the DISTANCE program (Buckland et al., 2004) to estimate population size over the period, as the analyses performed by this package seems much more robust that the one employed by authors. If they do so, authors could also include topographic variables in the models to see whether the resulting models change. The reason is that the authors do not explain if guanacos occur in both biomes (steppe and forest), because if that was true, detection of guanacos was completely different in both ecosystems. Therefore the band width of 500 or 1000m is not valid for forests.”

In the Section “Guanaco population sampling” the following paragraphs was incorporated to justify the methodology used:

“Raedeke (1978)¹⁹ claims that the Leopold method is valid when the following conditions are satisfied: (1) the road systems must be an adequate sampling of the study area, (2) the network road must be randomly distributed, and (3) the animals included in the sampling must be randomly distributed in relation to the observer’s route; and he considers that in the south of the Tierra del Fuego Island these assumptions are fulfilled. Soto 2010¹⁸ compared population estimations by the Leopold and Distance methods and found that the value of the means estimate by Leopold methods fall within the confidence intervals estimated by Distance; additionally, as all sampling periods used the same methodology whatever bias might exist in the estimation of the mean abundance using the Leopold method, the relative changes among years (and thus the temporal trend) will be adequately represented; thus, we conclude that the Leopold’s method seems adequate for our purposes¹⁸.”

In relation to the forest and the sampling methodology, as the area occupied by forests is low and it has some degree of intervention, the visibility of the guanaco is adequate, hence we considered that the forest is a minor component and that does not affect the efficiency of the sampling procedure. In the section “Study area” the next paragraph was incorporated:

“The forested area is about 8.8% of the total study area, with different degrees of forest clearance that offers adequate visibility for guanaco sampling.”

“Regarding the population size estimated along the 36 years (Supplementary table), important (huge) differences are found, for example between 2004 and 2005 or between 2006 and 2007, or between 2007 and 2008. My concern is if such “jumps” could be related to the census surveyed. Please discuss this point.”

In the “Discussion” section we added the following discussion as required by the reviewer:
“The results of the guanaco population sampling suggest a certain trend in the population size, with a sort of exponential growth in the first few years, becoming more variable as the population grows, with more marked fluctuations during the last 10-12 years; this may imply that the population is becoming stabilized, possibly approaching its carrying capacity. On the other hand, the sampling results of those last 10-12 years show abrupt “jumps” in some years (for example 2004-2005) that may be the consequence of the mobility of guanacos from the Cameron ranch to neighboring sites and vice versa; since the transect sampling does not identify individuals the effects of possible local displacements could not be considered.”

“The authors used a stepwise regression when other approaches such as logistic regressions, Ricker or Beverton-Holt models could give more suitable results. Please explain or justify your decision.”

Our goal was to carry out a preliminary analysis that would guide us in the study of the population regulation process in the guanaco. As there are studies in ungulate that have used simple multiple regression analysis and obtained good/satisfactory results, we considered that it was of interest to test this technique as a first step in such an analysis.
In the manuscript the following paragraph was incorporated in the “Discussion” section to justify our decision:

"Contrary to what was expected based on the bibliography of ungulate’s population dynamics, weather variables do not seem to influence the density-dependent population growth rate process of the guanaco population of the Cameron ranch. Our aim was to carry out a preliminary analysis that would help identify some of the regulation processes in guanaco population; so we used a simple multiple regression analysis as a first step in that direction; nevertheless, our conclusion is that in order to test the effects of climatic variables on population regulation of large ungulates as the guanaco, the use of a population dynamic model would be recommended, for they seem to account better for the interaction between density-dependent processes and weather variables than a simple regression between the latter and guanaco population growth rate.”

“The selection of the best model among the candidates should be done by Akaike’s information”

This suggestion was considered and the respective Akaike’s values were calculated.

Minor comments:
“Refer to climatic variables or climatic effects, instead of climatic covariables.”

The recommendation was applied.

“Explain more in detail Corani & Gatto’s studies.”

With the previous changes we realize that the citation of Corani and Gatto (2007) is not necessary any more. Mainly because the essence of that paper is the proposal of a methodology that is not strictly relevant to our work. The phrase with this citation was deleted.

“Please remove information related to metabolic studies between guanacos and sheep (1st paragraph of study area section).”

The suggestion was carried out.

“Please add Nothofagus spp among the brackets after deciduous forest (study area section) if it is the case.”

This information is already incorporated.

“Give more information about livestock ranching, density, and size and the relation of livestock rangers with guanacos along the studied period (study area section).”

This information was already incorporate in the section “Sheep population”

“Are the guanacos found both in the steppe and the forest biomes?”

Yes, the guanacos use both biomes, but they mostly use the open habitat (i.e. steppes and meadows).

“Please re-write the paragraph related to guanaco sampling through transect method in the consecutive periods (it is not clear enough).”

The paragraph was improved.

“Please remove information related to binoculars and GPS brands (did the authors use the same gadgets across 36 years?).”

The recommendation was carried out.

“Explain the interest of using time lags (T) as covariables in the model.”

The next paragraph was incorporated in section “Population analysis”:

“The inclusion of time lags is convenient because it may detect possible cumulative climatic effects on ungulate population growth rates as it was observed in, e.g., deer and moose ²⁹ and in vicuñas¹³”.

“Please add the Statistica version employed.”

The Statistica tools was replaced by language R (Version 0.97.449 – ©2009-2012 RStudio, Inc.) to obtain the value of Akaike and satisfy the item 3.2 (see above).

“Please move explanations of the analyses perform from results to material & methods section.”

The recommendation was carried out.
Competing Interests: No competing interests Close
Report a concern

Views

Reviewer Report 20 Nov 2013

Ricardo Baldi, Terrestrial Ecology Research Unit, Centro Nacional Patagónico, Puerto Madyrn, Argentina

Approved with Reservations

https://doi.org/10.5256/f1000research.2588.r2048

The authors hypothesized that population density and climatic variables affect the growth rate of the population of guanacos in the study area. However, as it is detailed under the “Study area” subsection, the domestic sheep share the area with the guanaco and substantial changes in stocking rate have been reported for the ranch during the study period. It is known that sheep and guanacos select similar diets across different parts of the range they share, and usually sheep presence and abundance explain a substantial amount of variation in the abundance of guanacos, included the study area comprising the Estancia Cameron as described by Raedeke (1979). In his work, Raedeke described that sheep are managed “rotationally” around the property, taken seasonally to different areas in winter and summer, and this makes guanacos move seasonally to the forest habitat. Therefore, it would be expected that variations in sheep abundance, not only seasonally but in total numbers through time, could affect the estimates of guanaco abundance. In my opinion, this is a major issue in the design of this work. Also, as explained below, the survey design of this work could play a key role in the quality of the estimates obtained, which is reflected also in the interpretation of results. All of these do not mean that density dependent processes are not likely to occur, but to my understanding it is not possible to rule out other processes to be conclusive.

Guanaco population sampling

The surveys were conducted at a 2,000 km² ranch where the habitat is a mosaic of steppe and forest biomes. The authors indicate that they surveyed guanacos using the “transect method with a variable width” from 1977 to 2000. Is this the distance sampling? If so, it is based on measuring the perpendicular distance from the transect to the object. Also, it is says that the surveying methodology was changed to “fixed width band” in 2001 and subsequent years. Some comments and questions on these issues regarding survey design are:

Were both the steppe and forest habitats surveyed using the same methodology? Transect lines to observe individuals and make direct counts are commonly used in open habitats, but not in the forest. However if this was not the case, the authors need to account for the variation in the probability of detection as it is expected to vary significantly between such contrasting habitat types.
There was a change in the surveying method, which also brings the point of detection probability. While the line transect method assumes that the probability of detecting objects on the line (distance=0) is p=1, and as objects are far from the line the probability of detection follows a certain declining function, the main assumption of the strip transect method is that the probability of detecting objects within the strip is 1 (i.e. no objects are left undetected). This variation in the probability of detection according to the methodology applied during each period must be discussed. Also, the ways that the density estimates were obtained are unclear and must be specified (i.e. distance sampling, other calculation methods).
Regarding the estimate of population size, several considerations can be made about the extrapolation of absolute densities to population numbers. First, the spatial pattern of the transects surveyed could be determinant of biased estimates, if the objects are not randomly distributed in relation to the survey line (i.e. if the transect follows a geographic feature in such a way the animals are either attracted or deterred). Perhaps the transects are located across certain areas – for example the steppe – but not the forest and thus the estimate could be biased towards the density calculated for the surveyed portion of the total area. This is especially important at the time of extrapolate densities to obtain population size numbers, as densities are strictly valid for the areas effectively surveyed while traveling along the transect lines. In any case, it would be useful to provide the distribution of surveyed lines across the area. The second point I find relevant to discuss regarding survey design is the proportion of the area effectively surveyed. How many km² were comprised by the lines and strips surveyed? Again, the extrapolation of densities to population size at a larger scale must account for possible limitations related to the survey design and effort invested.

Results and discussion

Major fluctuations of the guanaco population occurred during the last 10-12 years analyzed, as can be found in the additional data file provided, and also pointed out by the authors. But this variation could well be due to the changes in methodology at the time of the population surveys. As said above, it is necessary to provide detailed information on the type of survey conducted, the differences with the previous method and the way the density estimates were obtained. It would be informative if the authors provide the errors associated with the population estimates.

As proposed above, sheep densities could be affecting guanaco population trends, but the design of the work does not allow accounting for this factor. In my opinion, sheep densities must be included as an explanatory variable as there is evidence they affect guanaco numbers. Also, as the authors concluded that in this study the guanaco populations was near carrying capacity, and this must be common to both guanacos and sheep, thus sheep must be considered in the analysis as its density was markedly variable during the study period. Another factor that should be considered at the time of the discussion is the possibility of guanacos moving from the surveyed surroundings or even from Cameron to neighboring sites, as they may respond to changes in the spatial availability of resources by occupying different sites. In summary, the marked fluctuations in population size require the examination and discussion of other possible factors before concluding that density dependent processes would drive population trends.

Competing Interests: No competing interests were disclosed.

CITE

Report a concern

Author Response 14 May 2014

Maria Zubillaga, Centro de Estudios Parasitológicos y de Vectores (CEPAVE), Universidad Nacional de La Plata, La Plata, Argentina

14 May 2014

Author Response
- "The authors hypothesized that population density and climatic variables affect the growth rate of the population of guanacos in the study area. However, as it is detailed under the “Study
... Continue reading
"The authors hypothesized that population density and climatic variables affect the growth rate of the population of guanacos in the study area. However, as it is detailed under the “Study area” subsection, the domestic sheep share the area with the guanaco and substantial changes in stocking rate have been reported for the ranch during the study period. It is known that sheep and guanacos select similar diets across different parts of the range they share, and usually sheep presence and abundance explain a substantial amount of variation in the abundance of guanacos, included the study area comprising the Estancia Cameron as described by Raedeke (1979). In his work, Raedeke described that sheep are managed “rotationally” around the property, taken seasonally to different areas in winter and summer, and this makes guanacos move seasonally to the forest habitat. Therefore, it would be expected that variations in sheep abundance, not only seasonally but in total numbers through time, could affect the estimates of guanaco abundance. In my opinion, this is a major issue in the design of this work. Also, as explained below, the survey design of this work could play a key role in the quality of the estimates obtained, which is reflected also in the interpretation of results. All of these do not mean that density dependent processes are not likely to occur, but to my understanding it is not possible to rule out other processes to be conclusive."

In relation to the suggestion to incorporate livestock in the analysis, we re-analyzed our regression incorporating the variable livestock as sheep population; we re-processed the regressions incorporating the sheep population as a new independent variable of the guanaco population growth rate (l); so our new analysis increased from 5 to 6 independent variables: sheep population, guanaco population size, winter temperature, winter temperature with a lag of 1 year, annual precipitation, annual precipitation with a lag of 3 years. Our main results didn’t change and it was confirmed that only the guanaco population size seems to have an effect on the population growth rate (l). These changes can be found in the “Methods” and in the “Results” paragraphs.

"The surveys were conducted at a 2,000 km² ranch where the habitat is a mosaic of steppe and forest biomes. The authors indicate that they surveyed guanacos using the “transect method with a variable width” from 1977 to 2000. Is this the distance sampling? If so, it is based on measuring the perpendicular distance from the transect to the object."

No, the sampling methodology did not use the program Distance. The citations of Buckland et al. (1993 and 2001) were removed to avoid possible misinterpretations with the sampling methodology used.The method used to estimate the population size was the King method modified by Leopold (1933) as described in Raedeke (1978). In the manuscript it was explained and justified this method with the following paragraph:

“Raedeke (1978)¹⁹ claims that the Leopold method is valid when the following conditions are satisfied: (1) the road systems must be an adequate sampling of the study area, (2) the network road must be randomly distributed, and (3) the animals included in the sampling must be randomly distributed in relation to the observer’s route; and he considers that in the south of the Tierra del Fuego Island these assumptions are fulfilled. Soto 2010¹⁸ compared population estimations by the Leopold and Distance methods and found that the value of the means estimate by Leopold methods fall within the confidence intervals estimated by Distance; additionally, as all sampling periods used the same methodology whatever bias might exist in the estimation of the mean abundance using the Leopold method, the relative changes among years (and thus the temporal trend) will be adequately represented; thus, we conclude that the Leopold’s method seems adequate for our purposes¹⁸. The area effectively surveyed in each sampling period was around 420 km² (about 20%, of the area under study).”
"Also, it is says that the surveying methodology was changed to “fixed width band” in 2001 and subsequent years. Some comments and questions on these issues regarding survey design are:
Were both the steppe and forest habitats surveyed using the same methodology? Transect lines to observe individuals and make direct counts are commonly used in open habitats, but not in the forest. However if this was not the case, the authors need to account for the variation in the probability of detection as it is expected to vary significantly between such contrasting habitat types."

We corrected in the manuscript the years where the change in band width occurred: variable band width from 1977 to 1995, and with a fixed width band (with a maximum of 500 m to each side of the transect) from 1996 to 2012.

The area occupied by forest is low and it has some degree of intervention, the visibility of the guanaco is adequate, hence we considered that the forest is a minor component and it does not affect the efficiency of sampling. In the section “Study area” the following paragraph was incorporated:
"The forested area is about 8.8% of the total study area, with different degrees of forest clearance that offers adequate visibility for guanaco sampling.”

"There was a change in the surveying method, which also brings the point of detection probability. While the line transect method assumes that the probability of detecting objects on the line (distance=0) is p=1, and as objects are far from the line the probability of detection follows a certain declining function, the main assumption of the strip transect method is that the probability of detecting objects within the strip is 1 (i.e. no objects are left undetected). This variation in the probability of detection according to the methodology applied during each period must be discussed. Also, the ways that the density estimates were obtained are unclear and must be specified (i.e. distance sampling, other calculation methods)."

We improved this section and the next paragraph was incorporate to explain this change. The population size was estimated by King method modified by Leopold (1933) as described by Raedeke (1978), which was also clarified in the manuscript.
"The sampling methodology was changed by an expert recommendation made in 1995 ²³; as in year 2000 the fixed and the undefined band width methods were applied simultaneously, we tested both results and found no significant statistical difference between them.”

"Regarding the estimate of population size, several considerations can be made about the extrapolation of absolute densities to population numbers. First, the spatial pattern of the transects surveyed could be determinant of biased estimates, if the objects are not randomly distributed in relation to the survey line (i.e. if the transect follows a geographic feature in such a way the animals are either attracted or deterred). Perhaps the transects are located across certain areas – for example the steppe – but not the forest and thus the estimate could be biased towards the density calculated for the surveyed portion of the total area. This is especially important at the time of extrapolate densities to obtain population size numbers, as densities are strictly valid for the areas effectively surveyed while traveling along the transect lines. In any case, it would be useful to provide the distribution of surveyed lines across the area. The second point I find relevant to discuss regarding survey design is the proportion of the area effectively surveyed. How many km² were comprised by the lines and strips surveyed? Again, the extrapolation of densities to population size at a larger scale must account for possible limitations related to the survey design and effort invested."

Although the transects are not randomly distributed, the preexisting roads can be considered as an adequate sample of the area. This comment was incorporate in the manuscript.

"Despite randomly selected transects are recommended²⁴, preexisting roads were used because according to Soto (2010)¹⁸ the existing system of roads is an adequate sample of the area.”
The second point was considered and the area effectively surveyed was estimated. In the “Guanaco population sampling” section the following paragraph was incorporated:
"The area effectively surveyed in each sampling period was around 420 km² (about 20%, of the area under study).”

"Major fluctuations of the guanaco population occurred during the last 10-12 years analyzed, as can be found in the additional data file provided, and also pointed out by the authors. But this variation could well be due to the changes in methodology at the time of the population surveys. As said above, it is necessary to provide detailed information on the type of survey conducted, the differences with the previous method and the way the density estimates were obtained. It would be informative if the authors provide the errors associated with the population estimates."

The errors associated with the population estimates are given in Table S1 where the lower and upper limits of the 95% confidence intervals (CI) are shown.

"As proposed above, sheep densities could be affecting guanaco population trends, but the design of the work does not allow accounting for this factor. In my opinion, sheep densities must be included as an explanatory variable as there is evidence they affect guanaco numbers. Also, as the authors concluded that in this study the guanaco populations was near carrying capacity, and this must be common to both guanacos and sheep, thus sheep must be considered in the analysis as its density was markedly variable during the study period. Another factor that should be considered at the time of the discussion is the possibility of guanacos moving from the surveyed surroundings or even from Cameron to neighboring sites, as they may respond to changes in the spatial availability of resources by occupying different sites. In summary, the marked fluctuations in population size require the examination and discussion of other possible factors before concluding that density dependent processes would drive population trends."

This factor (sheep population) has been incorporated, and the corresponding analysis was carried out; see in the “Materials and methods” section “Sheep Population” and the section “Results”. In the “Discussion” section the following paragraph was included where we recognized the possibility of guanaco moving as possible source of error in the sampling:
“The results of the guanaco population sampling suggest a certain trend in the population size, with a sort of exponential growth in the first few years, becoming more variable as the population grows, with more marked fluctuations during the last 10-12 years; this may imply that the population is becoming stabilized, possibly approaching its carrying capacity. On the other hand, the sampling results of those last 10-12 years show abrupt “jumps” in some years (for example 2004-2005) that may be the consequence of the mobility of guanacos from the Cameron ranch to neighboring sites and vice versa; since the transect sampling does not identify individuals the effects of possible local displacements could not be considered.”
"The authors hypothesized that population density and climatic variables affect the growth rate of the population of guanacos in the study area. However, as it is detailed under the “Study area” subsection, the domestic sheep share the area with the guanaco and substantial changes in stocking rate have been reported for the ranch during the study period. It is known that sheep and guanacos select similar diets across different parts of the range they share, and usually sheep presence and abundance explain a substantial amount of variation in the abundance of guanacos, included the study area comprising the Estancia Cameron as described by Raedeke (1979). In his work, Raedeke described that sheep are managed “rotationally” around the property, taken seasonally to different areas in winter and summer, and this makes guanacos move seasonally to the forest habitat. Therefore, it would be expected that variations in sheep abundance, not only seasonally but in total numbers through time, could affect the estimates of guanaco abundance. In my opinion, this is a major issue in the design of this work. Also, as explained below, the survey design of this work could play a key role in the quality of the estimates obtained, which is reflected also in the interpretation of results. All of these do not mean that density dependent processes are not likely to occur, but to my understanding it is not possible to rule out other processes to be conclusive."

In relation to the suggestion to incorporate livestock in the analysis, we re-analyzed our regression incorporating the variable livestock as sheep population; we re-processed the regressions incorporating the sheep population as a new independent variable of the guanaco population growth rate (l); so our new analysis increased from 5 to 6 independent variables: sheep population, guanaco population size, winter temperature, winter temperature with a lag of 1 year, annual precipitation, annual precipitation with a lag of 3 years. Our main results didn’t change and it was confirmed that only the guanaco population size seems to have an effect on the population growth rate (l). These changes can be found in the “Methods” and in the “Results” paragraphs.

"The surveys were conducted at a 2,000 km² ranch where the habitat is a mosaic of steppe and forest biomes. The authors indicate that they surveyed guanacos using the “transect method with a variable width” from 1977 to 2000. Is this the distance sampling? If so, it is based on measuring the perpendicular distance from the transect to the object."

No, the sampling methodology did not use the program Distance. The citations of Buckland et al. (1993 and 2001) were removed to avoid possible misinterpretations with the sampling methodology used.The method used to estimate the population size was the King method modified by Leopold (1933) as described in Raedeke (1978). In the manuscript it was explained and justified this method with the following paragraph:

“Raedeke (1978)¹⁹ claims that the Leopold method is valid when the following conditions are satisfied: (1) the road systems must be an adequate sampling of the study area, (2) the network road must be randomly distributed, and (3) the animals included in the sampling must be randomly distributed in relation to the observer’s route; and he considers that in the south of the Tierra del Fuego Island these assumptions are fulfilled. Soto 2010¹⁸ compared population estimations by the Leopold and Distance methods and found that the value of the means estimate by Leopold methods fall within the confidence intervals estimated by Distance; additionally, as all sampling periods used the same methodology whatever bias might exist in the estimation of the mean abundance using the Leopold method, the relative changes among years (and thus the temporal trend) will be adequately represented; thus, we conclude that the Leopold’s method seems adequate for our purposes¹⁸. The area effectively surveyed in each sampling period was around 420 km² (about 20%, of the area under study).”
"Also, it is says that the surveying methodology was changed to “fixed width band” in 2001 and subsequent years. Some comments and questions on these issues regarding survey design are:
Were both the steppe and forest habitats surveyed using the same methodology? Transect lines to observe individuals and make direct counts are commonly used in open habitats, but not in the forest. However if this was not the case, the authors need to account for the variation in the probability of detection as it is expected to vary significantly between such contrasting habitat types."

We corrected in the manuscript the years where the change in band width occurred: variable band width from 1977 to 1995, and with a fixed width band (with a maximum of 500 m to each side of the transect) from 1996 to 2012.

The area occupied by forest is low and it has some degree of intervention, the visibility of the guanaco is adequate, hence we considered that the forest is a minor component and it does not affect the efficiency of sampling. In the section “Study area” the following paragraph was incorporated:
"The forested area is about 8.8% of the total study area, with different degrees of forest clearance that offers adequate visibility for guanaco sampling.”

"There was a change in the surveying method, which also brings the point of detection probability. While the line transect method assumes that the probability of detecting objects on the line (distance=0) is p=1, and as objects are far from the line the probability of detection follows a certain declining function, the main assumption of the strip transect method is that the probability of detecting objects within the strip is 1 (i.e. no objects are left undetected). This variation in the probability of detection according to the methodology applied during each period must be discussed. Also, the ways that the density estimates were obtained are unclear and must be specified (i.e. distance sampling, other calculation methods)."

We improved this section and the next paragraph was incorporate to explain this change. The population size was estimated by King method modified by Leopold (1933) as described by Raedeke (1978), which was also clarified in the manuscript.
"The sampling methodology was changed by an expert recommendation made in 1995 ²³; as in year 2000 the fixed and the undefined band width methods were applied simultaneously, we tested both results and found no significant statistical difference between them.”

"Regarding the estimate of population size, several considerations can be made about the extrapolation of absolute densities to population numbers. First, the spatial pattern of the transects surveyed could be determinant of biased estimates, if the objects are not randomly distributed in relation to the survey line (i.e. if the transect follows a geographic feature in such a way the animals are either attracted or deterred). Perhaps the transects are located across certain areas – for example the steppe – but not the forest and thus the estimate could be biased towards the density calculated for the surveyed portion of the total area. This is especially important at the time of extrapolate densities to obtain population size numbers, as densities are strictly valid for the areas effectively surveyed while traveling along the transect lines. In any case, it would be useful to provide the distribution of surveyed lines across the area. The second point I find relevant to discuss regarding survey design is the proportion of the area effectively surveyed. How many km² were comprised by the lines and strips surveyed? Again, the extrapolation of densities to population size at a larger scale must account for possible limitations related to the survey design and effort invested."

Although the transects are not randomly distributed, the preexisting roads can be considered as an adequate sample of the area. This comment was incorporate in the manuscript.

"Despite randomly selected transects are recommended²⁴, preexisting roads were used because according to Soto (2010)¹⁸ the existing system of roads is an adequate sample of the area.”
The second point was considered and the area effectively surveyed was estimated. In the “Guanaco population sampling” section the following paragraph was incorporated:
"The area effectively surveyed in each sampling period was around 420 km² (about 20%, of the area under study).”

"Major fluctuations of the guanaco population occurred during the last 10-12 years analyzed, as can be found in the additional data file provided, and also pointed out by the authors. But this variation could well be due to the changes in methodology at the time of the population surveys. As said above, it is necessary to provide detailed information on the type of survey conducted, the differences with the previous method and the way the density estimates were obtained. It would be informative if the authors provide the errors associated with the population estimates."

The errors associated with the population estimates are given in Table S1 where the lower and upper limits of the 95% confidence intervals (CI) are shown.

"As proposed above, sheep densities could be affecting guanaco population trends, but the design of the work does not allow accounting for this factor. In my opinion, sheep densities must be included as an explanatory variable as there is evidence they affect guanaco numbers. Also, as the authors concluded that in this study the guanaco populations was near carrying capacity, and this must be common to both guanacos and sheep, thus sheep must be considered in the analysis as its density was markedly variable during the study period. Another factor that should be considered at the time of the discussion is the possibility of guanacos moving from the surveyed surroundings or even from Cameron to neighboring sites, as they may respond to changes in the spatial availability of resources by occupying different sites. In summary, the marked fluctuations in population size require the examination and discussion of other possible factors before concluding that density dependent processes would drive population trends."

This factor (sheep population) has been incorporated, and the corresponding analysis was carried out; see in the “Materials and methods” section “Sheep Population” and the section “Results”. In the “Discussion” section the following paragraph was included where we recognized the possibility of guanaco moving as possible source of error in the sampling:
“The results of the guanaco population sampling suggest a certain trend in the population size, with a sort of exponential growth in the first few years, becoming more variable as the population grows, with more marked fluctuations during the last 10-12 years; this may imply that the population is becoming stabilized, possibly approaching its carrying capacity. On the other hand, the sampling results of those last 10-12 years show abrupt “jumps” in some years (for example 2004-2005) that may be the consequence of the mobility of guanacos from the Cameron ranch to neighboring sites and vice versa; since the transect sampling does not identify individuals the effects of possible local displacements could not be considered.”
Competing Interests: None Close
Report a concern
Respond or Comment

COMMENTS ON THIS REPORT

Author Response 14 May 2014

Maria Zubillaga, Centro de Estudios Parasitológicos y de Vectores (CEPAVE), Universidad Nacional de La Plata, La Plata, Argentina

14 May 2014

Author Response
- "The authors hypothesized that population density and climatic variables affect the growth rate of the population of guanacos in the study area. However, as it is detailed under the “Study
... Continue reading
"The authors hypothesized that population density and climatic variables affect the growth rate of the population of guanacos in the study area. However, as it is detailed under the “Study area” subsection, the domestic sheep share the area with the guanaco and substantial changes in stocking rate have been reported for the ranch during the study period. It is known that sheep and guanacos select similar diets across different parts of the range they share, and usually sheep presence and abundance explain a substantial amount of variation in the abundance of guanacos, included the study area comprising the Estancia Cameron as described by Raedeke (1979). In his work, Raedeke described that sheep are managed “rotationally” around the property, taken seasonally to different areas in winter and summer, and this makes guanacos move seasonally to the forest habitat. Therefore, it would be expected that variations in sheep abundance, not only seasonally but in total numbers through time, could affect the estimates of guanaco abundance. In my opinion, this is a major issue in the design of this work. Also, as explained below, the survey design of this work could play a key role in the quality of the estimates obtained, which is reflected also in the interpretation of results. All of these do not mean that density dependent processes are not likely to occur, but to my understanding it is not possible to rule out other processes to be conclusive."

In relation to the suggestion to incorporate livestock in the analysis, we re-analyzed our regression incorporating the variable livestock as sheep population; we re-processed the regressions incorporating the sheep population as a new independent variable of the guanaco population growth rate (l); so our new analysis increased from 5 to 6 independent variables: sheep population, guanaco population size, winter temperature, winter temperature with a lag of 1 year, annual precipitation, annual precipitation with a lag of 3 years. Our main results didn’t change and it was confirmed that only the guanaco population size seems to have an effect on the population growth rate (l). These changes can be found in the “Methods” and in the “Results” paragraphs.

"The surveys were conducted at a 2,000 km² ranch where the habitat is a mosaic of steppe and forest biomes. The authors indicate that they surveyed guanacos using the “transect method with a variable width” from 1977 to 2000. Is this the distance sampling? If so, it is based on measuring the perpendicular distance from the transect to the object."

No, the sampling methodology did not use the program Distance. The citations of Buckland et al. (1993 and 2001) were removed to avoid possible misinterpretations with the sampling methodology used.The method used to estimate the population size was the King method modified by Leopold (1933) as described in Raedeke (1978). In the manuscript it was explained and justified this method with the following paragraph:

“Raedeke (1978)¹⁹ claims that the Leopold method is valid when the following conditions are satisfied: (1) the road systems must be an adequate sampling of the study area, (2) the network road must be randomly distributed, and (3) the animals included in the sampling must be randomly distributed in relation to the observer’s route; and he considers that in the south of the Tierra del Fuego Island these assumptions are fulfilled. Soto 2010¹⁸ compared population estimations by the Leopold and Distance methods and found that the value of the means estimate by Leopold methods fall within the confidence intervals estimated by Distance; additionally, as all sampling periods used the same methodology whatever bias might exist in the estimation of the mean abundance using the Leopold method, the relative changes among years (and thus the temporal trend) will be adequately represented; thus, we conclude that the Leopold’s method seems adequate for our purposes¹⁸. The area effectively surveyed in each sampling period was around 420 km² (about 20%, of the area under study).”
"Also, it is says that the surveying methodology was changed to “fixed width band” in 2001 and subsequent years. Some comments and questions on these issues regarding survey design are:
Were both the steppe and forest habitats surveyed using the same methodology? Transect lines to observe individuals and make direct counts are commonly used in open habitats, but not in the forest. However if this was not the case, the authors need to account for the variation in the probability of detection as it is expected to vary significantly between such contrasting habitat types."

We corrected in the manuscript the years where the change in band width occurred: variable band width from 1977 to 1995, and with a fixed width band (with a maximum of 500 m to each side of the transect) from 1996 to 2012.

The area occupied by forest is low and it has some degree of intervention, the visibility of the guanaco is adequate, hence we considered that the forest is a minor component and it does not affect the efficiency of sampling. In the section “Study area” the following paragraph was incorporated:
"The forested area is about 8.8% of the total study area, with different degrees of forest clearance that offers adequate visibility for guanaco sampling.”

"There was a change in the surveying method, which also brings the point of detection probability. While the line transect method assumes that the probability of detecting objects on the line (distance=0) is p=1, and as objects are far from the line the probability of detection follows a certain declining function, the main assumption of the strip transect method is that the probability of detecting objects within the strip is 1 (i.e. no objects are left undetected). This variation in the probability of detection according to the methodology applied during each period must be discussed. Also, the ways that the density estimates were obtained are unclear and must be specified (i.e. distance sampling, other calculation methods)."

We improved this section and the next paragraph was incorporate to explain this change. The population size was estimated by King method modified by Leopold (1933) as described by Raedeke (1978), which was also clarified in the manuscript.
"The sampling methodology was changed by an expert recommendation made in 1995 ²³; as in year 2000 the fixed and the undefined band width methods were applied simultaneously, we tested both results and found no significant statistical difference between them.”

"Regarding the estimate of population size, several considerations can be made about the extrapolation of absolute densities to population numbers. First, the spatial pattern of the transects surveyed could be determinant of biased estimates, if the objects are not randomly distributed in relation to the survey line (i.e. if the transect follows a geographic feature in such a way the animals are either attracted or deterred). Perhaps the transects are located across certain areas – for example the steppe – but not the forest and thus the estimate could be biased towards the density calculated for the surveyed portion of the total area. This is especially important at the time of extrapolate densities to obtain population size numbers, as densities are strictly valid for the areas effectively surveyed while traveling along the transect lines. In any case, it would be useful to provide the distribution of surveyed lines across the area. The second point I find relevant to discuss regarding survey design is the proportion of the area effectively surveyed. How many km² were comprised by the lines and strips surveyed? Again, the extrapolation of densities to population size at a larger scale must account for possible limitations related to the survey design and effort invested."

Although the transects are not randomly distributed, the preexisting roads can be considered as an adequate sample of the area. This comment was incorporate in the manuscript.

"Despite randomly selected transects are recommended²⁴, preexisting roads were used because according to Soto (2010)¹⁸ the existing system of roads is an adequate sample of the area.”
The second point was considered and the area effectively surveyed was estimated. In the “Guanaco population sampling” section the following paragraph was incorporated:
"The area effectively surveyed in each sampling period was around 420 km² (about 20%, of the area under study).”

"Major fluctuations of the guanaco population occurred during the last 10-12 years analyzed, as can be found in the additional data file provided, and also pointed out by the authors. But this variation could well be due to the changes in methodology at the time of the population surveys. As said above, it is necessary to provide detailed information on the type of survey conducted, the differences with the previous method and the way the density estimates were obtained. It would be informative if the authors provide the errors associated with the population estimates."

The errors associated with the population estimates are given in Table S1 where the lower and upper limits of the 95% confidence intervals (CI) are shown.

"As proposed above, sheep densities could be affecting guanaco population trends, but the design of the work does not allow accounting for this factor. In my opinion, sheep densities must be included as an explanatory variable as there is evidence they affect guanaco numbers. Also, as the authors concluded that in this study the guanaco populations was near carrying capacity, and this must be common to both guanacos and sheep, thus sheep must be considered in the analysis as its density was markedly variable during the study period. Another factor that should be considered at the time of the discussion is the possibility of guanacos moving from the surveyed surroundings or even from Cameron to neighboring sites, as they may respond to changes in the spatial availability of resources by occupying different sites. In summary, the marked fluctuations in population size require the examination and discussion of other possible factors before concluding that density dependent processes would drive population trends."

This factor (sheep population) has been incorporated, and the corresponding analysis was carried out; see in the “Materials and methods” section “Sheep Population” and the section “Results”. In the “Discussion” section the following paragraph was included where we recognized the possibility of guanaco moving as possible source of error in the sampling:
“The results of the guanaco population sampling suggest a certain trend in the population size, with a sort of exponential growth in the first few years, becoming more variable as the population grows, with more marked fluctuations during the last 10-12 years; this may imply that the population is becoming stabilized, possibly approaching its carrying capacity. On the other hand, the sampling results of those last 10-12 years show abrupt “jumps” in some years (for example 2004-2005) that may be the consequence of the mobility of guanacos from the Cameron ranch to neighboring sites and vice versa; since the transect sampling does not identify individuals the effects of possible local displacements could not be considered.”
"The authors hypothesized that population density and climatic variables affect the growth rate of the population of guanacos in the study area. However, as it is detailed under the “Study area” subsection, the domestic sheep share the area with the guanaco and substantial changes in stocking rate have been reported for the ranch during the study period. It is known that sheep and guanacos select similar diets across different parts of the range they share, and usually sheep presence and abundance explain a substantial amount of variation in the abundance of guanacos, included the study area comprising the Estancia Cameron as described by Raedeke (1979). In his work, Raedeke described that sheep are managed “rotationally” around the property, taken seasonally to different areas in winter and summer, and this makes guanacos move seasonally to the forest habitat. Therefore, it would be expected that variations in sheep abundance, not only seasonally but in total numbers through time, could affect the estimates of guanaco abundance. In my opinion, this is a major issue in the design of this work. Also, as explained below, the survey design of this work could play a key role in the quality of the estimates obtained, which is reflected also in the interpretation of results. All of these do not mean that density dependent processes are not likely to occur, but to my understanding it is not possible to rule out other processes to be conclusive."

In relation to the suggestion to incorporate livestock in the analysis, we re-analyzed our regression incorporating the variable livestock as sheep population; we re-processed the regressions incorporating the sheep population as a new independent variable of the guanaco population growth rate (l); so our new analysis increased from 5 to 6 independent variables: sheep population, guanaco population size, winter temperature, winter temperature with a lag of 1 year, annual precipitation, annual precipitation with a lag of 3 years. Our main results didn’t change and it was confirmed that only the guanaco population size seems to have an effect on the population growth rate (l). These changes can be found in the “Methods” and in the “Results” paragraphs.

"The surveys were conducted at a 2,000 km² ranch where the habitat is a mosaic of steppe and forest biomes. The authors indicate that they surveyed guanacos using the “transect method with a variable width” from 1977 to 2000. Is this the distance sampling? If so, it is based on measuring the perpendicular distance from the transect to the object."

No, the sampling methodology did not use the program Distance. The citations of Buckland et al. (1993 and 2001) were removed to avoid possible misinterpretations with the sampling methodology used.The method used to estimate the population size was the King method modified by Leopold (1933) as described in Raedeke (1978). In the manuscript it was explained and justified this method with the following paragraph:

“Raedeke (1978)¹⁹ claims that the Leopold method is valid when the following conditions are satisfied: (1) the road systems must be an adequate sampling of the study area, (2) the network road must be randomly distributed, and (3) the animals included in the sampling must be randomly distributed in relation to the observer’s route; and he considers that in the south of the Tierra del Fuego Island these assumptions are fulfilled. Soto 2010¹⁸ compared population estimations by the Leopold and Distance methods and found that the value of the means estimate by Leopold methods fall within the confidence intervals estimated by Distance; additionally, as all sampling periods used the same methodology whatever bias might exist in the estimation of the mean abundance using the Leopold method, the relative changes among years (and thus the temporal trend) will be adequately represented; thus, we conclude that the Leopold’s method seems adequate for our purposes¹⁸. The area effectively surveyed in each sampling period was around 420 km² (about 20%, of the area under study).”
"Also, it is says that the surveying methodology was changed to “fixed width band” in 2001 and subsequent years. Some comments and questions on these issues regarding survey design are:
Were both the steppe and forest habitats surveyed using the same methodology? Transect lines to observe individuals and make direct counts are commonly used in open habitats, but not in the forest. However if this was not the case, the authors need to account for the variation in the probability of detection as it is expected to vary significantly between such contrasting habitat types."

We corrected in the manuscript the years where the change in band width occurred: variable band width from 1977 to 1995, and with a fixed width band (with a maximum of 500 m to each side of the transect) from 1996 to 2012.

The area occupied by forest is low and it has some degree of intervention, the visibility of the guanaco is adequate, hence we considered that the forest is a minor component and it does not affect the efficiency of sampling. In the section “Study area” the following paragraph was incorporated:
"The forested area is about 8.8% of the total study area, with different degrees of forest clearance that offers adequate visibility for guanaco sampling.”

"There was a change in the surveying method, which also brings the point of detection probability. While the line transect method assumes that the probability of detecting objects on the line (distance=0) is p=1, and as objects are far from the line the probability of detection follows a certain declining function, the main assumption of the strip transect method is that the probability of detecting objects within the strip is 1 (i.e. no objects are left undetected). This variation in the probability of detection according to the methodology applied during each period must be discussed. Also, the ways that the density estimates were obtained are unclear and must be specified (i.e. distance sampling, other calculation methods)."

We improved this section and the next paragraph was incorporate to explain this change. The population size was estimated by King method modified by Leopold (1933) as described by Raedeke (1978), which was also clarified in the manuscript.
"The sampling methodology was changed by an expert recommendation made in 1995 ²³; as in year 2000 the fixed and the undefined band width methods were applied simultaneously, we tested both results and found no significant statistical difference between them.”

"Regarding the estimate of population size, several considerations can be made about the extrapolation of absolute densities to population numbers. First, the spatial pattern of the transects surveyed could be determinant of biased estimates, if the objects are not randomly distributed in relation to the survey line (i.e. if the transect follows a geographic feature in such a way the animals are either attracted or deterred). Perhaps the transects are located across certain areas – for example the steppe – but not the forest and thus the estimate could be biased towards the density calculated for the surveyed portion of the total area. This is especially important at the time of extrapolate densities to obtain population size numbers, as densities are strictly valid for the areas effectively surveyed while traveling along the transect lines. In any case, it would be useful to provide the distribution of surveyed lines across the area. The second point I find relevant to discuss regarding survey design is the proportion of the area effectively surveyed. How many km² were comprised by the lines and strips surveyed? Again, the extrapolation of densities to population size at a larger scale must account for possible limitations related to the survey design and effort invested."

Although the transects are not randomly distributed, the preexisting roads can be considered as an adequate sample of the area. This comment was incorporate in the manuscript.

"Despite randomly selected transects are recommended²⁴, preexisting roads were used because according to Soto (2010)¹⁸ the existing system of roads is an adequate sample of the area.”
The second point was considered and the area effectively surveyed was estimated. In the “Guanaco population sampling” section the following paragraph was incorporated:
"The area effectively surveyed in each sampling period was around 420 km² (about 20%, of the area under study).”

"Major fluctuations of the guanaco population occurred during the last 10-12 years analyzed, as can be found in the additional data file provided, and also pointed out by the authors. But this variation could well be due to the changes in methodology at the time of the population surveys. As said above, it is necessary to provide detailed information on the type of survey conducted, the differences with the previous method and the way the density estimates were obtained. It would be informative if the authors provide the errors associated with the population estimates."

The errors associated with the population estimates are given in Table S1 where the lower and upper limits of the 95% confidence intervals (CI) are shown.

"As proposed above, sheep densities could be affecting guanaco population trends, but the design of the work does not allow accounting for this factor. In my opinion, sheep densities must be included as an explanatory variable as there is evidence they affect guanaco numbers. Also, as the authors concluded that in this study the guanaco populations was near carrying capacity, and this must be common to both guanacos and sheep, thus sheep must be considered in the analysis as its density was markedly variable during the study period. Another factor that should be considered at the time of the discussion is the possibility of guanacos moving from the surveyed surroundings or even from Cameron to neighboring sites, as they may respond to changes in the spatial availability of resources by occupying different sites. In summary, the marked fluctuations in population size require the examination and discussion of other possible factors before concluding that density dependent processes would drive population trends."

This factor (sheep population) has been incorporated, and the corresponding analysis was carried out; see in the “Materials and methods” section “Sheep Population” and the section “Results”. In the “Discussion” section the following paragraph was included where we recognized the possibility of guanaco moving as possible source of error in the sampling:
“The results of the guanaco population sampling suggest a certain trend in the population size, with a sort of exponential growth in the first few years, becoming more variable as the population grows, with more marked fluctuations during the last 10-12 years; this may imply that the population is becoming stabilized, possibly approaching its carrying capacity. On the other hand, the sampling results of those last 10-12 years show abrupt “jumps” in some years (for example 2004-2005) that may be the consequence of the mobility of guanacos from the Cameron ranch to neighboring sites and vice versa; since the transect sampling does not identify individuals the effects of possible local displacements could not be considered.”
Competing Interests: None Close
Report a concern

Comments on this article Comments (0)

Version 3

VERSION 3 PUBLISHED 09 Oct 2013

Open Peer Review

Reviewer Status

Reviewer Reports

	Invited Reviewers
	1	2	3
Version 3 (revision) 18 Sep 14
Version 2 (revision) 28 May 14		read	read
Version 1 09 Oct 13	read	read

Ricardo Baldi, Centro Nacional Patagónico, Puerto Madyrn, Argentina
Pablo Acebes, Autonomous University of Madrid, Madrid, Spain
Gary Luck, Charles Sturt University, Albury, Australia

Comments on this article

All Comments(0)

Add a comment

Browse by related subjects

Back to all reports

Reviewer Report

15 Views

21 Aug 2014 | for Version 2

Pablo Acebes, Department of Ecology, Autonomous University of Madrid, Madrid, Spain

15 Views Cite this report Responses(0)

Approved

The authors have improved the ms from their first submitted version. Please see the comments below to further improve the article:

First paragraph (introduction): please put guanaco in the singular.
Guanaco population sampling section: please replace ‘SIG’ with ‘GIS’.
Guanaco population sampling section: please remove ‘surface’ in “A is the total study area surface”.
Results: part of the results is a justification of the analyses carried out and should be placed in Material and Methods.
Discussion: in my view one of the most important results is the absence of negative effects of sheep on guanaco population growth rate that indeed has been cited as one of the major drivers of guanaco population decline particularly in Patagonia in the 20 century. For that reason I think authors should discuss this important result more deeply.

Competing Interests

No competing interests were disclosed.

I confirm that I have read this submission and believe that I have an appropriate level of expertise to confirm that it is of an acceptable scientific standard.

Respond to this report

Responses (0)

Back to all reports

Reviewer Report

10 Views

04 Aug 2014 | for Version 2

Gary Luck, Institute for Land, Water, and Society, Charles Sturt University, Albury, Australia

10 Views Cite this report Responses(0)

Approved

I have cross checked the comments from the two original referees with the responses from the authors and consider that the authors have adequately addressed all comments. The study has various limitations, such as a limited set of predictor variables, lack of the use of a sampling technique (e.g. Distance sampling) that accounts for differences in detectability, and application of a simple regression analysis. The authors have adequately addressed each of these major issues in their response to referees - though readers should be aware of these limitations when interpreting the results of the study.

Competing Interests

No competing interests were disclosed.

I confirm that I have read this submission and believe that I have an appropriate level of expertise to confirm that it is of an acceptable scientific standard.

Respond to this report

Responses (0)

Back to all reports

Reviewer Report

36 Views

19 Dec 2013 | for Version 1

Pablo Acebes, Department of Ecology, Autonomous University of Madrid, Madrid, Spain

36 Views Cite this report Responses(1)

Approved With Reservations

The theory of ungulate population dynamics, driven by density-dependent and density-independent processes; please expand this topic in the introduction and discuss more deeply your results considering the theoretical framework (see comments below).
The census methodology (see comments below).
Statistical modeling (see comments below).

The background supporting the study, as it currently is a bit poor, in my view. The authors should explain more in detail, for example, which are the differences between the density-stabilizing and the density-limiting processes, or the evidence of including climatic variables when modelling population growth rate trends.
The use of these climatic variables: the average annual precipitation and winter temperature. Without any justification, authors could have also included others variables in the models, as climatic variables do not account for the pattern described, but this doesn’t necessarily mean that climate hasn’t got any effect on the guanaco population growth rate. Moreover authors should explain if these two climatic variables are selected as indicators of primary production and harsh weather conditions.
As authors stated in introduction, guanaco populations have undergone overhunting (poaching) and competition with sheep, these being two of the major forces of their dramatic decline in the last century. For that reason, it is quite surprising that no variables related to livestock were included in the modelling procedure. The population has increased a lot in the studied period (x8) and just climate and/or density-dependent process do not explain alone such increase in my view. Therefore authors should consider including livestock effects, its influence on resource availability along the studied period and the mentioned overhunting, as this could really explain the detected trend.

The authors use a stepwise regression when other approaches such as logistic regressions, Ricker or Beverton–Holt models could give more suitable results. Please explain or justify your decision.
The selection of the best model among the candidates should be done by Akaike’s information.

Minor comments

Refer to climatic variables or climatic effects, instead of climatic covariables.
Explain more in detail Corani & Gatto’s studies.
Please remove information related to metabolic studies between guanacos and sheep (1st paragraph of study area section).
Please add Nothofagus spp among the brackets after deciduous forest (study area section) if it is the case.
Give more information about livestock ranching, density, and size and the relation of livestock rangers with guanacos along the studied period (study area section).
Are the guanacos found both in the steppe and the forest biomes?
Please re-write the paragraph related to guanaco sampling through transect method in the consecutive periods (it is not clear enough).
Please remove information related to binoculars and GPS brands (did the authors use the same gadgets across 36 years?).
Explain the interest of using time lags (T) as covariables in the model.
Please add the Statistica version employed.
Please move explanations of the analyses perform from results to material & methods section.

Competing Interests

No competing interests were disclosed.

Respond to this report

Responses (1)

Author Response

14 May 2014

Maria Zubillaga, Centro de Estudios Parasitológicos y de Vectores (CEPAVE), Universidad Nacional de La Plata, La Plata, Argentina

"The background supporting the study, as it currently is a bit poor, in my view. The authors should explain more in detail, for example, which are the differences between the density-stabilizing and the density-limiting processes, or the evidence of including climatic variables when modelling population growth rate trends."

After the following paragraph that was already in the original text:

“No population of any species can grow indefinitely, and population checks based upon different processes restrict population size and/or geographic distribution; these processes are either density-stabilizing or density-limiting”

We added the following paragraph explaining the differences between the density-stabilizing and the density-limiting processes.

“The former are of a biotic nature and depends on the interaction between individuals of the same or different species, while the latter are independent of population size. Stabilization results from density-dependence, with a regulatory effect that varies in intensity with the size or density of the population itself, however, not all density-dependent factors are density-stabilizing. The density-limiting factors can also be considered density-responsive because the per capita amount or availability of resources decreases as the population density increases. Thus, these two types of factors (density-stabilizing and density-limiting) rarely act independently: the density-limiting factors (generally of a physical and/or climatic nature), may determine the level at which populations become stabilized by the density-dependent processes, but they do not have a stabilizing capacity per se; for this reason many wildlife population dynamic and management models include the effects of climatic variables (e.g., Dennis & Otten, 2000; Colchero et al., 2009)^3,4”.

"The use of these climatic variables: the average annual precipitation and winter temperature. Without any justification, authors could have also included others variables in the models, as climatic variables do not account for the pattern described, but this doesn’t necessarily mean that climate hasn’t got any effect on the guanaco population growth rate. Moreover authors should explain if these two climatic variables are selected as indicators of primary production and harsh weather conditions."

To explain and justify the use of these climatic variables the paragraph below was incorporated in the section “Climatic variables”:

“These climatic variables were selected because some studies suggested that they have influence on guanaco demographic parameters: Rey et al. 2012²⁶ observed that after a severe drought the proportion guanaco yearlings/female decreased significantly, and Sarno et al. 1999¹⁷ detected a negative effect of winter snowfall on guanaco juvenile survival; because we had insufficient snowfall data we used the winter temperature as a proxy for winter snowfall.”

"As authors stated in introduction, guanaco populations have undergone overhunting (poaching) and competition with sheep, these being two of the major forces of their dramatic decline in the last century. For that reason, it is quite surprising that no variables related to livestock were included in the modelling procedure. The population has increased a lot in the studied period (x8) and just climate and/or density-dependent process do not explain alone such increase in my view. Therefore authors should consider including livestock effects, its influence on resource availability along the studied period and the mentioned overhunting, as this could really explain the detected trend."

In relation with the “poaching” the following paragraph was incorporated in section “Study area” to justify why this variable was not considered in our study:

“In contrast to the continent, the puma (Puma concolor), the main predator of guanacos, is absent in the island; since 1977 the guanaco hunting has been controlled by Chilean National Forest Corporation (CONAF, according to its Spanish acronym) and the Chilean Agricultural and Livestock Service (SAG, according to its Spanish acronym).”

In relation to the suggestion to incorporate livestock in the analysis, we re-analyzed our multiple regression incorporating the variable livestock as sheep population. We re-processed the regressions incorporating the sheep population as a new independent variable as a possible predictor of the guanaco population growth rate (l); so our new analysis increased from 5 to 6 independent variables: sheep population, guanaco population size, winter temperature, winter temperature with a lag of 1 year, annual precipitation, annual precipitation with a lag of 3 years. Our main results didn’t change and it was confirmed that only the guanaco population size seems to have an effect on the population growth rate (l). These changes can be found in the “Methods” and in the “Results” sections.
“The guanaco sampling method has changed during the studied period (different band widths). Besides, were the transects chosen based on the topography and vegetation cover of the ranch to ensure that all areas were visible to census-takers along their transects? I am not sure if that could be a source of error, but authors should discuss this point.”

In the Section “Guanaco population sampling” we added the following paragraphs where we explain the motive of the change and justify the transects chosen:

“The sampling methodology was changed by an expert recommendation made in 1995 ²³; as in year 2000 the fixed and the undefined band width methods were applied simultaneously, we tested both results and found no significant statistical difference between them.”
“Despite randomly selected transects are recommended²⁴, preexisting roads were used because according to Soto (2010)¹⁸ the existing system of roads is an adequate sample of the area.”

“Moreover, I recommend authors to re-analyze their data using the DISTANCE program (Buckland et al., 2004) to estimate population size over the period, as the analyses performed by this package seems much more robust that the one employed by authors. If they do so, authors could also include topographic variables in the models to see whether the resulting models change. The reason is that the authors do not explain if guanacos occur in both biomes (steppe and forest), because if that was true, detection of guanacos was completely different in both ecosystems. Therefore the band width of 500 or 1000m is not valid for forests.”

In the Section “Guanaco population sampling” the following paragraphs was incorporated to justify the methodology used:

“Raedeke (1978)¹⁹ claims that the Leopold method is valid when the following conditions are satisfied: (1) the road systems must be an adequate sampling of the study area, (2) the network road must be randomly distributed, and (3) the animals included in the sampling must be randomly distributed in relation to the observer’s route; and he considers that in the south of the Tierra del Fuego Island these assumptions are fulfilled. Soto 2010¹⁸ compared population estimations by the Leopold and Distance methods and found that the value of the means estimate by Leopold methods fall within the confidence intervals estimated by Distance; additionally, as all sampling periods used the same methodology whatever bias might exist in the estimation of the mean abundance using the Leopold method, the relative changes among years (and thus the temporal trend) will be adequately represented; thus, we conclude that the Leopold’s method seems adequate for our purposes¹⁸.”

In relation to the forest and the sampling methodology, as the area occupied by forests is low and it has some degree of intervention, the visibility of the guanaco is adequate, hence we considered that the forest is a minor component and that does not affect the efficiency of the sampling procedure. In the section “Study area” the next paragraph was incorporated:

“The forested area is about 8.8% of the total study area, with different degrees of forest clearance that offers adequate visibility for guanaco sampling.”

“Regarding the population size estimated along the 36 years (Supplementary table), important (huge) differences are found, for example between 2004 and 2005 or between 2006 and 2007, or between 2007 and 2008. My concern is if such “jumps” could be related to the census surveyed. Please discuss this point.”

In the “Discussion” section we added the following discussion as required by the reviewer:
“The results of the guanaco population sampling suggest a certain trend in the population size, with a sort of exponential growth in the first few years, becoming more variable as the population grows, with more marked fluctuations during the last 10-12 years; this may imply that the population is becoming stabilized, possibly approaching its carrying capacity. On the other hand, the sampling results of those last 10-12 years show abrupt “jumps” in some years (for example 2004-2005) that may be the consequence of the mobility of guanacos from the Cameron ranch to neighboring sites and vice versa; since the transect sampling does not identify individuals the effects of possible local displacements could not be considered.”
“The authors used a stepwise regression when other approaches such as logistic regressions, Ricker or Beverton-Holt models could give more suitable results. Please explain or justify your decision.”

Our goal was to carry out a preliminary analysis that would guide us in the study of the population regulation process in the guanaco. As there are studies in ungulate that have used simple multiple regression analysis and obtained good/satisfactory results, we considered that it was of interest to test this technique as a first step in such an analysis.
In the manuscript the following paragraph was incorporated in the “Discussion” section to justify our decision:

"Contrary to what was expected based on the bibliography of ungulate’s population dynamics, weather variables do not seem to influence the density-dependent population growth rate process of the guanaco population of the Cameron ranch. Our aim was to carry out a preliminary analysis that would help identify some of the regulation processes in guanaco population; so we used a simple multiple regression analysis as a first step in that direction; nevertheless, our conclusion is that in order to test the effects of climatic variables on population regulation of large ungulates as the guanaco, the use of a population dynamic model would be recommended, for they seem to account better for the interaction between density-dependent processes and weather variables than a simple regression between the latter and guanaco population growth rate.”
“The selection of the best model among the candidates should be done by Akaike’s information”

This suggestion was considered and the respective Akaike’s values were calculated.

Minor comments:

“Refer to climatic variables or climatic effects, instead of climatic covariables.”

The recommendation was applied.
“Explain more in detail Corani & Gatto’s studies.”

With the previous changes we realize that the citation of Corani and Gatto (2007) is not necessary any more. Mainly because the essence of that paper is the proposal of a methodology that is not strictly relevant to our work. The phrase with this citation was deleted.
“Please remove information related to metabolic studies between guanacos and sheep (1st paragraph of study area section).”

The suggestion was carried out.
“Please add Nothofagus spp among the brackets after deciduous forest (study area section) if it is the case.”

This information is already incorporated.
“Give more information about livestock ranching, density, and size and the relation of livestock rangers with guanacos along the studied period (study area section).”

This information was already incorporate in the section “Sheep population”
“Are the guanacos found both in the steppe and the forest biomes?”

Yes, the guanacos use both biomes, but they mostly use the open habitat (i.e. steppes and meadows).
“Please re-write the paragraph related to guanaco sampling through transect method in the consecutive periods (it is not clear enough).”

The paragraph was improved.
“Please remove information related to binoculars and GPS brands (did the authors use the same gadgets across 36 years?).”

The recommendation was carried out.
“Explain the interest of using time lags (T) as covariables in the model.”

The next paragraph was incorporated in section “Population analysis”:

“The inclusion of time lags is convenient because it may detect possible cumulative climatic effects on ungulate population growth rates as it was observed in, e.g., deer and moose ²⁹ and in vicuñas¹³”.
“Please add the Statistica version employed.”

The Statistica tools was replaced by language R (Version 0.97.449 – ©2009-2012 RStudio, Inc.) to obtain the value of Akaike and satisfy the item 3.2 (see above).
“Please move explanations of the analyses perform from results to material & methods section.”

The recommendation was carried out.

View more View less

Competing Interests

No competing interests

Back to all reports

Reviewer Report

25 Views

20 Nov 2013 | for Version 1

Ricardo Baldi, Terrestrial Ecology Research Unit, Centro Nacional Patagónico, Puerto Madyrn, Argentina

25 Views Cite this report Responses(1)

Approved With Reservations

Were both the steppe and forest habitats surveyed using the same methodology? Transect lines to observe individuals and make direct counts are commonly used in open habitats, but not in the forest. However if this was not the case, the authors need to account for the variation in the probability of detection as it is expected to vary significantly between such contrasting habitat types.
There was a change in the surveying method, which also brings the point of detection probability. While the line transect method assumes that the probability of detecting objects on the line (distance=0) is p=1, and as objects are far from the line the probability of detection follows a certain declining function, the main assumption of the strip transect method is that the probability of detecting objects within the strip is 1 (i.e. no objects are left undetected). This variation in the probability of detection according to the methodology applied during each period must be discussed. Also, the ways that the density estimates were obtained are unclear and must be specified (i.e. distance sampling, other calculation methods).
Regarding the estimate of population size, several considerations can be made about the extrapolation of absolute densities to population numbers. First, the spatial pattern of the transects surveyed could be determinant of biased estimates, if the objects are not randomly distributed in relation to the survey line (i.e. if the transect follows a geographic feature in such a way the animals are either attracted or deterred). Perhaps the transects are located across certain areas – for example the steppe – but not the forest and thus the estimate could be biased towards the density calculated for the surveyed portion of the total area. This is especially important at the time of extrapolate densities to obtain population size numbers, as densities are strictly valid for the areas effectively surveyed while traveling along the transect lines. In any case, it would be useful to provide the distribution of surveyed lines across the area. The second point I find relevant to discuss regarding survey design is the proportion of the area effectively surveyed. How many km² were comprised by the lines and strips surveyed? Again, the extrapolation of densities to population size at a larger scale must account for possible limitations related to the survey design and effort invested.

Competing Interests

No competing interests were disclosed.

Respond to this report

Responses (1)

Author Response

14 May 2014

Maria Zubillaga, Centro de Estudios Parasitológicos y de Vectores (CEPAVE), Universidad Nacional de La Plata, La Plata, Argentina

"The authors hypothesized that population density and climatic variables affect the growth rate of the population of guanacos in the study area. However, as it is detailed under the “Study area” subsection, the domestic sheep share the area with the guanaco and substantial changes in stocking rate have been reported for the ranch during the study period. It is known that sheep and guanacos select similar diets across different parts of the range they share, and usually sheep presence and abundance explain a substantial amount of variation in the abundance of guanacos, included the study area comprising the Estancia Cameron as described by Raedeke (1979). In his work, Raedeke described that sheep are managed “rotationally” around the property, taken seasonally to different areas in winter and summer, and this makes guanacos move seasonally to the forest habitat. Therefore, it would be expected that variations in sheep abundance, not only seasonally but in total numbers through time, could affect the estimates of guanaco abundance. In my opinion, this is a major issue in the design of this work. Also, as explained below, the survey design of this work could play a key role in the quality of the estimates obtained, which is reflected also in the interpretation of results. All of these do not mean that density dependent processes are not likely to occur, but to my understanding it is not possible to rule out other processes to be conclusive."

In relation to the suggestion to incorporate livestock in the analysis, we re-analyzed our regression incorporating the variable livestock as sheep population; we re-processed the regressions incorporating the sheep population as a new independent variable of the guanaco population growth rate (l); so our new analysis increased from 5 to 6 independent variables: sheep population, guanaco population size, winter temperature, winter temperature with a lag of 1 year, annual precipitation, annual precipitation with a lag of 3 years. Our main results didn’t change and it was confirmed that only the guanaco population size seems to have an effect on the population growth rate (l). These changes can be found in the “Methods” and in the “Results” paragraphs.
"The surveys were conducted at a 2,000 km² ranch where the habitat is a mosaic of steppe and forest biomes. The authors indicate that they surveyed guanacos using the “transect method with a variable width” from 1977 to 2000. Is this the distance sampling? If so, it is based on measuring the perpendicular distance from the transect to the object."

No, the sampling methodology did not use the program Distance. The citations of Buckland et al. (1993 and 2001) were removed to avoid possible misinterpretations with the sampling methodology used.The method used to estimate the population size was the King method modified by Leopold (1933) as described in Raedeke (1978). In the manuscript it was explained and justified this method with the following paragraph:

“Raedeke (1978)¹⁹ claims that the Leopold method is valid when the following conditions are satisfied: (1) the road systems must be an adequate sampling of the study area, (2) the network road must be randomly distributed, and (3) the animals included in the sampling must be randomly distributed in relation to the observer’s route; and he considers that in the south of the Tierra del Fuego Island these assumptions are fulfilled. Soto 2010¹⁸ compared population estimations by the Leopold and Distance methods and found that the value of the means estimate by Leopold methods fall within the confidence intervals estimated by Distance; additionally, as all sampling periods used the same methodology whatever bias might exist in the estimation of the mean abundance using the Leopold method, the relative changes among years (and thus the temporal trend) will be adequately represented; thus, we conclude that the Leopold’s method seems adequate for our purposes¹⁸. The area effectively surveyed in each sampling period was around 420 km² (about 20%, of the area under study).”

"Also, it is says that the surveying methodology was changed to “fixed width band” in 2001 and subsequent years. Some comments and questions on these issues regarding survey design are:

Were both the steppe and forest habitats surveyed using the same methodology? Transect lines to observe individuals and make direct counts are commonly used in open habitats, but not in the forest. However if this was not the case, the authors need to account for the variation in the probability of detection as it is expected to vary significantly between such contrasting habitat types."

We corrected in the manuscript the years where the change in band width occurred: variable band width from 1977 to 1995, and with a fixed width band (with a maximum of 500 m to each side of the transect) from 1996 to 2012.

The area occupied by forest is low and it has some degree of intervention, the visibility of the guanaco is adequate, hence we considered that the forest is a minor component and it does not affect the efficiency of sampling. In the section “Study area” the following paragraph was incorporated:

"The forested area is about 8.8% of the total study area, with different degrees of forest clearance that offers adequate visibility for guanaco sampling.”

"There was a change in the surveying method, which also brings the point of detection probability. While the line transect method assumes that the probability of detecting objects on the line (distance=0) is p=1, and as objects are far from the line the probability of detection follows a certain declining function, the main assumption of the strip transect method is that the probability of detecting objects within the strip is 1 (i.e. no objects are left undetected). This variation in the probability of detection according to the methodology applied during each period must be discussed. Also, the ways that the density estimates were obtained are unclear and must be specified (i.e. distance sampling, other calculation methods)."

We improved this section and the next paragraph was incorporate to explain this change. The population size was estimated by King method modified by Leopold (1933) as described by Raedeke (1978), which was also clarified in the manuscript.

"The sampling methodology was changed by an expert recommendation made in 1995 ²³; as in year 2000 the fixed and the undefined band width methods were applied simultaneously, we tested both results and found no significant statistical difference between them.”

"Regarding the estimate of population size, several considerations can be made about the extrapolation of absolute densities to population numbers. First, the spatial pattern of the transects surveyed could be determinant of biased estimates, if the objects are not randomly distributed in relation to the survey line (i.e. if the transect follows a geographic feature in such a way the animals are either attracted or deterred). Perhaps the transects are located across certain areas – for example the steppe – but not the forest and thus the estimate could be biased towards the density calculated for the surveyed portion of the total area. This is especially important at the time of extrapolate densities to obtain population size numbers, as densities are strictly valid for the areas effectively surveyed while traveling along the transect lines. In any case, it would be useful to provide the distribution of surveyed lines across the area. The second point I find relevant to discuss regarding survey design is the proportion of the area effectively surveyed. How many km² were comprised by the lines and strips surveyed? Again, the extrapolation of densities to population size at a larger scale must account for possible limitations related to the survey design and effort invested."

Although the transects are not randomly distributed, the preexisting roads can be considered as an adequate sample of the area. This comment was incorporate in the manuscript.

"Despite randomly selected transects are recommended²⁴, preexisting roads were used because according to Soto (2010)¹⁸ the existing system of roads is an adequate sample of the area.”

The second point was considered and the area effectively surveyed was estimated. In the “Guanaco population sampling” section the following paragraph was incorporated:

"The area effectively surveyed in each sampling period was around 420 km² (about 20%, of the area under study).”

"Major fluctuations of the guanaco population occurred during the last 10-12 years analyzed, as can be found in the additional data file provided, and also pointed out by the authors. But this variation could well be due to the changes in methodology at the time of the population surveys. As said above, it is necessary to provide detailed information on the type of survey conducted, the differences with the previous method and the way the density estimates were obtained. It would be informative if the authors provide the errors associated with the population estimates."

The errors associated with the population estimates are given in Table S1 where the lower and upper limits of the 95% confidence intervals (CI) are shown.
"As proposed above, sheep densities could be affecting guanaco population trends, but the design of the work does not allow accounting for this factor. In my opinion, sheep densities must be included as an explanatory variable as there is evidence they affect guanaco numbers. Also, as the authors concluded that in this study the guanaco populations was near carrying capacity, and this must be common to both guanacos and sheep, thus sheep must be considered in the analysis as its density was markedly variable during the study period. Another factor that should be considered at the time of the discussion is the possibility of guanacos moving from the surveyed surroundings or even from Cameron to neighboring sites, as they may respond to changes in the spatial availability of resources by occupying different sites. In summary, the marked fluctuations in population size require the examination and discussion of other possible factors before concluding that density dependent processes would drive population trends."

This factor (sheep population) has been incorporated, and the corresponding analysis was carried out; see in the “Materials and methods” section “Sheep Population” and the section “Results”. In the “Discussion” section the following paragraph was included where we recognized the possibility of guanaco moving as possible source of error in the sampling:

“The results of the guanaco population sampling suggest a certain trend in the population size, with a sort of exponential growth in the first few years, becoming more variable as the population grows, with more marked fluctuations during the last 10-12 years; this may imply that the population is becoming stabilized, possibly approaching its carrying capacity. On the other hand, the sampling results of those last 10-12 years show abrupt “jumps” in some years (for example 2004-2005) that may be the consequence of the mobility of guanacos from the Cameron ranch to neighboring sites and vice versa; since the transect sampling does not identify individuals the effects of possible local displacements could not be considered.”

View more View less

Competing Interests

None

Alongside their report, reviewers assign a status to the article:

Approved - the paper is scientifically sound in its current form and only minor, if any, improvements are suggested

Approved with reservations - A number of small changes, sometimes more significant revisions are required to address specific details and improve the papers academic merit.

Not approved - fundamental flaws in the paper seriously undermine the findings and conclusions

$cdnUrl/2375/ff0e5fd1-cc0a-495d-aae7-a3e2092e317d_Guanaco_abundance_V2.csv Guanaco population abundance, sheep population abundance, estimated population annual rate of growth, average annual precipitation, and average winter temperature of the Cameron ranch, Tierra del Fuego Guanaco population abundance (individuals), lower and upper limits of the 95% confidence intervals (CI), sheep population abundance (individuals), estimated population annual rate of growth (lambda), average annual precipitation (P; mm/year), and average winter temperature (celsius). Guanaco population values were not available for years 1986 and 1996, and were linearly interpolated; sheep population values were only available for years 1980, 1985, 1990, 1995, 2000, 2005, 2008 and 2011; other values were linearly interpolated.

Data has been updated in following columns: sheep population [ranges of changed values are only for years: 1981-1984; 1986-1989; 1991- 1994; 1996-1999; 2001-2004; 2006-2007, 2009-2010]; data of winter temperature (Av winter temp); annual precipitation (P) [ranges of changed values are only for years: 2003-2011]. 0,1,4,6,7 5 1

Click here to access the data.

Downloaded data do not display as expected? Download the data (1.71KB)

[1] 1. Franklin WL, Bas MF, Bonacic CF, et al.: Striving to manage Patagonia guanacos for sustained use in the grazing agroecosystems of southern Chile. Wildl Soc Bull. 1997; 25(1): 65–73. Reference Source

[2] 2. Case TJ: An illustrated guide to Theoretical Ecology. Oxford, University Press. 2000; 449. Reference Source

[3] 3. Dennis B, Otten M: Joint effects of density dependence and rainfall on abundance of san joaquin kit fox. J Wildl Manage. 2000; 64(2): 388–400. Publisher Full Text

[4] 4. Colchero F, Medellin RA, Clark JS, et al.: Predicting population survival under future climate change: density dependence, drought and extraction in an insular bighorn sheep. J Anim Ecol. 2009; 78(3): 666–673. PubMed Abstract | Publisher Full Text

[5] 5. Franklin WL, Johnson WE: Hand Capture of Newborn Open-Habitat Ungulates: The South American Guanaco. Wildl Soc Bull. 1994; 22(2): 253–259. Reference Source

[6] 6. Ostfeld RS, Canham CD, Pugh SR: Intrinsic Density-Dependent Regulation of Vole populations. Nature. 1993; 366(6452): 259–261. PubMed Abstract | Publisher Full Text

[7] 7. Bateman AW, Ozgul A, Coulson T, et al.: Density dependence in group dynamics of a highly social mongoose, Suricata suricatta. J Anim Ecol. 2012; 81(3): 628–639. PubMed Abstract | Publisher Full Text

[8] 8. Koons DN, Terletzky P, Adler PB, et al.: Climate and density-dependent drivers of recruitment in plains bison. J Mammal. 2012; 93(2): 475–481. Publisher Full Text

[9] 9. Bardsen BJ, Tveraa T: Density-dependence vs. density-independence - linking reproductive allocation to population abundance and vegetation greenness. J Anim Ecol. 2012; 81(2): 364–376. PubMed Abstract | Publisher Full Text

[10] 10. Serrano E, Angibault JM, Cargnelutti B, et al.: Density dependence of developmental instability in a dimorphic ungulate. Biol Lett. 2008; 4(5): 512–514. PubMed Abstract | Publisher Full Text | Free Full Text

[11] 11. Stewart KM, Bowyer RT, Ruess RW, et al.: Herbivore Optimization by North American Elk: Consequences for Theory and Management. Wildl Monogr. 2006; 167(1): 1–24. Publisher Full Text

[12] 12. Rabinovich JE, Hernández MJ, Cajal JL: A simulation model for the management of vicuña populations. Ecol Model. 1985; 30(3–4): 275–295. Publisher Full Text

[13] 13. Shaw AK, Galaz JL, Marquet PA: Population dynamics of the vicuña (Vicugna vicugna): density-dependence, rainfall, and spatial distribution. J Mammal. 2012; 93(3): 658–666. Publisher Full Text

[14] 14. Bonacic C, Macdonald DW, Galaz J, et al.: Density Dependence in the camelid Vicugna vicugna: the Recovery of a Protected Population in Chile. Oryx. 2002; 36(2): 118–125. Publisher Full Text

[15] 15. Sarno RJ, Franklin WL: Population Density and Annual Variation in Birth Mass of Guanacos in Southern Chile. J Mammal. 1999; 80(4): 1158–1162. Publisher Full Text

[16] 16. Sarno RJ, Franklin WL: Maternal expenditure in the polygynous and monomorphic guanaco: suckling behavior, reproductive effort, yearly variation, and influence on juvenile survival. Behav Ecol. 1999; 10(1): 41–47. Publisher Full Text

[17] 17. Sarno RJ, Clark WR, Bank MS, et al.: Juvenile guanaco survival: management and conservation implications. J Appl Ecol. 1999; 36(6): 937–945. Publisher Full Text

[18] 18. Soto VN: Distribución y Abundancia de la Población de Guanacos (Lama guanicoe, Muller 1776) en el Área Agropecuaria de Tierra del Fuego (Chile) y su Relación de Carga Animal con la Ganadería Ovina. Tesis de Estudios Avanzados (Dea). Universidad Internacional de Andalucía - Universidad de Córdoba. 2010.

[19] 19. Raedeke KJ: El guanaco de Magallanes, Chile. Su distribución y Biología. Corporación Nacional Forestal Publicación Técnica N° 4, Ministerio de Agricultura Chile. 1978; 364. Reference Source

[20] 20. Tellería Jorge JL: Manual para el censo de los Vertebrados terrestres. Editorial Raíces., Madrid, España. 1986; 278. Reference Source

[21] 21. Davis D, Winstead R: Estimación de tamaños de poblaciones de vida silvestre. In: H.S. Mosby, R.H. Giles Jr. y S.D. Schemnitz (Eds). Manual de técnicas de gestión de vida silvestre. The Widlife Society, Bethesda, Maryland. 1987; 233–258.

[22] 22. Caughley G: Analysis of vertebrate populations. A Wiley-Interscience publication. John Wiley & Sons Ltd. 1980; 234. Reference Source

[23] 23. Duran Ríos JC: Informe Final Proyecto "Manejo Productivo y sustentable del guanaco en isla Tierra del Fuego. XII Región"- (Año 1). CONAF-FNDR, Región de Magallanes y Antártica Chilena. Santiago, Chile. 1995; 178.

[24] 24. Eberhardt LL: Transect methods for population studies. J Wildl Manage. 1978; 42(1): 1–31. Publisher Full Text

[25] 25. Leopold A: Game management. Charles Scribner and sons, New York. 1933; 481. Reference Source

[26] 26. Rey A, Novaro A, Sahores M, et al.: Demographic effects of live shearing on a guanaco population. Small Ruminant Res. 2012; 107(2): 92–100. Publisher Full Text

[27] 27. Rabinovich JE, Zubillaga M: Informe Final del proyecto: "Modelo de manejo de poblaciones de guanacos para la Provincia del Chubut". 2012. Reference Source

[28] 28. Caswell H: Matrix population models: construction, analysis, and interpretation. 2nd edn. Sinauer Associates. Sunderland, Massachusetts. 2001; 722. Reference Source

[29] 29. Mech LD, McRoberts RE, Peterson RO, et al.: Relationship of Deer and Moose Populations to Previous Winters' Snow. J Anim Ecol. 1987; 56(2): 615–627. Publisher Full Text

[30] 30. Baldi R, Pelliza A, Elston D, et al.: High Potential for Competition Between Guanacos and Sheep In Patagonia. J Wildl Manage. 2004; 68(4): 924–938. Publisher Full Text

[31] 31. Fowler CW: Density Dependence as Related to Life History Strategy. Ecology. 1981; 62(3): 602–610. Publisher Full Text

[32] 32. Iranzo EC, Traba J, Acebes P, et al.: Niche segregation between wild and domestic herbivores in Chilean Patagonia. PLoS One. 2013; 8(3): e59326. PubMed Abstract | Publisher Full Text | Free Full Text

[33] 33. Taper ML, Gogan PJP: The Northern Yellowstone Elk: Density Dependence and Climatic Conditions. J Wildl Manage. 2002; 66(1): 106–122. Publisher Full Text

Density but not climate affects the population growth rate of guanacos (Lama guanicoe) (Artiodactyla, Camelidae)

Abstract

Keywords

Revised Amendments from Version 1

Introduction

Materials and methods

Study area

Guanaco population sampling

Climatic variables

Sheep population

Guanaco population analysis

Population analysis

Results

Table 2. Results of the simple regression analysis between the population growth rate (λ) as dependent variable, and (in log scale) total guanaco population (LnNtot).

Figure 1. Effect of the guanaco population size on guanaco’s finite population growth rate (λ).

Discussion

Data availability

Author contributions

Competing interests

Grant information

Acknowledgements

References

Comments on this article Comments (0)

Open Peer Review

Comments on this article Comments (0)

Open Peer Review

Reviewer Status

Reviewer Reports

Comments on this article

Browse by related subjects

The problem

How to fix it

Competing Interests Policy

Stay Updated