Keywords
Sequence alignment algorithms, hydrophobicity scale, protein homologs, TMATCH
Sequence alignment algorithms, hydrophobicity scale, protein homologs, TMATCH
Manuscript revision two added considerable material owing to reviewer inputs. One reviewer noted the importance of the 8 property class scales and requested further evidence. The 8 property class scales discussion was expanded. Support for the property classes came from Multi-Linear Regression correlation coefficient analysis with many scales, such as the scales in table 11, with attendant manuscript discussion. Three of the property classes came from 49 AA scales from our AA property database and an ANOPA analysis (1D, 2D and 3D), which was cross correlated through an analysis of the same 49 AA properties with both Principle Components Analysis (PCA) and non-metric Multi-Dimensional Scaling (nmMDS). The 3D ANOPA analysis showed that the relation vector recovers hydrophobicity as the dominant underlying factor behind the set of 49 amino-acid property vector scales. The MLR analysis consisted of 157 of the most reliable/apt amino-acid property scales in our database as the Y vectors and the 8 property class scales as the X vectors. Of 157 scales, 145 scales (92.4 percent) were found to be statistically significant (P <= 5%), Figures 6-16, 18 and tables 4-9 have been added and discussed in the revised manuscript. The 49 amino-acid property scales are summarized as:
See the authors' detailed response to the review by Ana Jerončić
See the authors' detailed response to the review by Charles Carter
An understanding of the properties and functions of a protein or a nucleic acid often begins with a search of the sequence against databases of proteins (or nucleic acids) with known properties or functions. The fundamental assumption is that sequence leads to structure which in turn leads to an understanding of the function. Search algorithms have improved and continue to improve. Yet, with proteins in particular, it remains difficult to detect remote homologies in the so called twilight zone where proteins have low percent sequence identities starting around 20–25 % and descending to around 10–15%. We describe a hydrophobicity scale that is proving to be an excellent measure of sequence relatedness. A robust estimate of the hydrophobicity based sequence identity can be calculated directly from a global alignment score, which may be directly used in database searches.
Proteins with low sequence identities, possessing statistically insignificant similarities by conventional measures, but having similar secondary/tertiary structures, which would not be identified as statistically significant by other methods such as FASTA and Smith-Waterman can be identified as homologous using a new alignment algorithm (manuscript in preparation) through the enhanced information content of our hydrophobicity proclivity scale.
Hydrophobicity scales (also often called metrics) as understood in the literature are generally divided into four categories, derived from
Experimental physio-chemical data
Log of a partition coefficient derived from protein structure (e.g. Fraction amino-acids inside vs. outside, fraction amino-acids in contact with water vs. completely buried, etc.)
Amino-acid mutation/substitution rates and
Participation rates/probabilities of occurrence in folded protein secondary structure
There are a large number and myriad types of scales that appear in the literature starting from the 1960’s through to the present with a fair amount of variation amongst these scales. The correlation between some of the hydrophobicity scales can be best understood as that derived from the energy of interaction between amino-acids and water or the energetics of partition of amino-acids from water as the reference state and some other environment such as a non-polar solvent or the interior of a folded protein. Hydrophobicity can thus be joined within a single, unified, conceptual framework1,2
Our hydrophobic index is the result of an extensive mining of the literature about proteins and amino acid scales/metrics in different environments. Almost all hydrophobicity scales reflect in some way a measure of the energetics of transfer of an amino-acid (or proteins) from one solvent environment (water) to another (folded protein or multiple protein assembly). During our data mining and analysis, three hydrophobicity metrics emerged as the most appropriate since we could relate those scales to multiple fundamental properties of the 20 natural amino acids using multi-variate statistical procedures, thermodynamics and biophysical chemistry considerations2–4. Hydrophobicity scales reflect different physical properties of amino-acids, such as metrics derived from aminoacid partitioning patterns (e.g. from the hydrophobic core to the exterior of proteins) or log of partition ratios between water and organic solvents. We found, as widely suggested in the literature, that the free energy of transfer from water to octanol turns out to be a good proxy for the hydrophobic core environment of folded proteins.
Our hydrophobicity proclivity scale was deployed as part of a new protein alignment algorithm TMATCH5,6, which is our adaptation of the Needleman-Wunsch dynamic programming alignment algorithm that uses TMATCH has adapted the Needleman-Wunsch fundamental dynamic programming alignment algorithm. In TMATCH, the local alignment score reinforces favorable diagonal sequences that are paired with fixed gap opening penalties. The TMATCH algorithm is especially designed to take advantage of the extra information available within our hydrophobicity scale to detect homologies, as opposed to the probabilities derived from raw percent identities.
Low sequence identities, possessing statistically insignificant local alignment similarities using methods such as FASTA and BLAST and using conventional percent identity measures, but having similar secondary/tertiary structures, can be identified using our TMATCH algorithm and our amino-acid hydrophobicity proclivity scale.
The TMATCH5,6 algorithm uses a fixed gap penalty and therefore abandons the notion of an affine gap penalty (based upon a linear weighting function), which is problematical as there is no deep, underlying theoretical construct for choosing a specific affine gap penalty function, which derives from statistical theory and/or from protein function/structure. The TMATCH algorithm uses the fact that local pair-wise sequences of high homology result in diagonal (upper left to lower right) traces in dotmatrix/dot-plot algorithm. When these local pairwise diagonal traces exist in the optimal/near-optimal alignment catchment basin, which is defined as an area about the dot-matrix major diagonal, they will contribute to and be included within the global/near global alignment traces within the dot-plot/dot-matrix.
TMATCH5,6 captures these dot-plot/dot-matrix algorithmic properties by introducing the notion of score “rewards” for favorable (e.g. local alignment score optimization) cell-cell diagonal transitions and score “punishments” for unfavorable cell-cell diagonal transitions. Fixed gap penalties are assessed for horizontal or vertical cell-cell transitions. Pairwise comparisons of amino-acids in the alignment are done with hydrophobicity proclivity scale. In addition to the diagonal score for a given table cell, the traditional dynamic programing score algorithm is used for calculating entry from the left or above subject to the fixed gap opening penalty.
The similarity calculated for two aligned proteins are based upon the percent hydrophobic fuzzy match similarity of two protein sequences being aligned. The average number of pair-wise fuzzy matches in the alignment allow for the computation of a statistical relationship test without having to actually extract the alignments, thereby saving the associated computational overhead.
As an alignment search algorithm, we have carefully benchmarked the TMATCH5,6 algorithm performance against several protein families and achieved very good results as compared to FASTA, BLAST and PSI BLAST. Specifically, we have worked with Glutathione proteins, G proteins, Rhodopsin proteins, Tryptophan like Serine proteases and DNA Polymerase B enzymes. The latter two protein families are especially challenging due to having low percent sequence identities, yet highly conserved tertiary structures. For the DNA Polymerase B and Tryptophan like Serine Protease families, we have seeded the protein sequence cohorts with proteins that are not within the families, but will come somewhat close to these two families with normal alignment algorithms and/or cause alignment algorithms to have pathological behaviors. The TMATCH search alignment algorithm did very well in these trials.
Our primary and starting premise was to look for clustering, single/multiple linear patterns or non-linear patterns between all amino-acid scales within our database as seen in the scatter plot of any two-given amino-acid scales. Extensive cross correlation with the primary and derived (from primary properties or experimental scales) metrics was done using regression modelling in order to recover the best and most meaningful hydrophobicity metrics. Through this extensive analysis, we were able to identify patterns and arrive at metrics describing amino acid properties. We derived a number of additional metrics by differentiating metrics that were intrinsic as opposed to extrinsic, as understood in thermodynamics.
Along the way, we found that multiple linear series occurring in scatter plots between many pairs of aminoacid properties, which was a striking pattern. Many of these multi-family linear series ranged between clearly discernible to very high quality; the latter end of the range being what we concentrated on. We also cross checked to see if sister AA property scales in the same class such as hydrophobicity resulted in similar patterns, such as which we see in Figure 1 and Figure 2 and in Table 2. Once the linear/non-linear (single and multi-family) patterns were found a detailed review of these patterns were made to find underlying physico-chemical and biological reasons for these patterns as well as statistical generalizations. The most relevant scatter plots were selected based upon their quality (visual and linear/non-linear regression) and explanatory power for protein structure and function, and reliability/specificity for protein alignments.
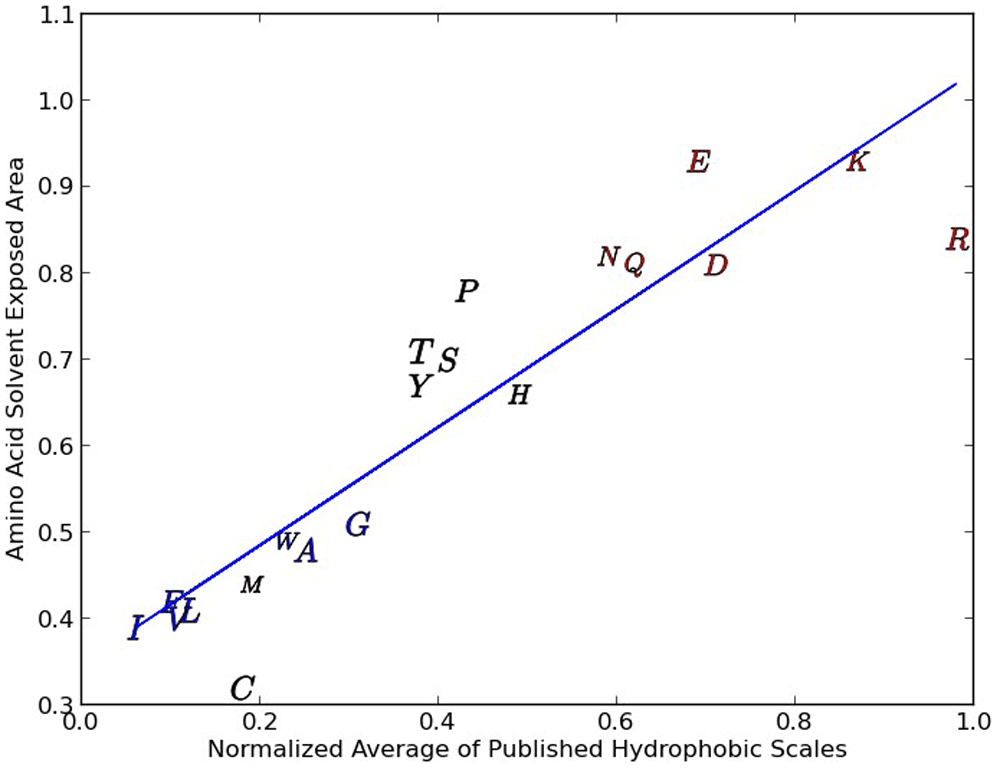
Note that the Y scatter tends to go up with polar and ionic amino acids.
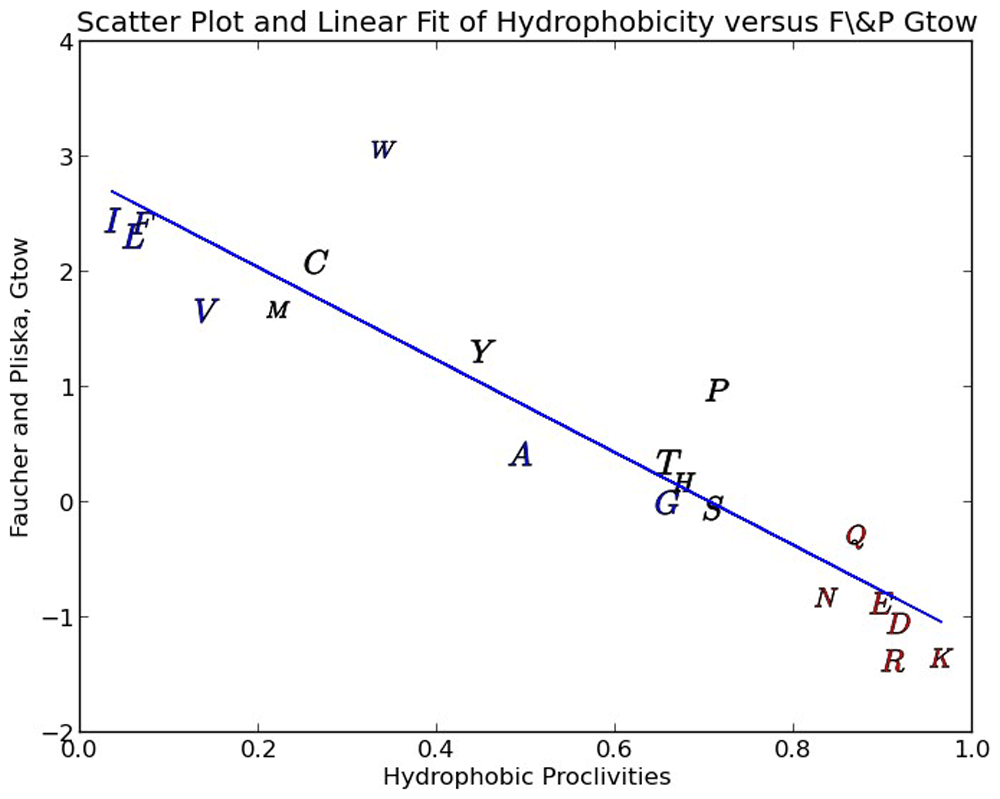
Tryptophan and Proline diverge from the regression line and this can be explained by the ring structure of the secondary group being relatively wide, which impacts the surface tension of the corresponding aqueous clathrate and the stearic packing effects of these two residues in a folded protein.
We relied on several different sources for our analysis. For data on amino-acid surface areas, we used Rose et al.7. Amino acid mass information was obtained using the AAINDEX accession number #FASG7601018,9. Amino acid volume data was obtained from Creighton10. Amino acid absolute entropy of formation was from the AAINDEX database using accession number #HUTJ7001028,9 We arrived at our hydrophobicity scale after exhaustive analysis which included numerous scatter plots and the running of a number of multiple regressions. The question we were trying to answer was - What was the best hydrophobicity scale, or combination of scales, that best represented the role of the different amino acids in proteins?
We started by first collecting many hydrophobicity indices and physico-chemical indices from the literature and scatter plotted/regressed the hydrophobicity indices against each other, and the harvested physico-chemical properties and their derived intrinsic properties of amino acids. For example when a hydrophobic scale is plotted against the ratio of the surface area per specific volume (volume/molecular weight) for each amino acid we get a scatter plot with a distinct pattern. In such a scatter plot, we can identify one or more sets of clusters/linear clusters of amino acids, each set of which is considered to be a "property class".
We were able to find three hydrophobicity scales that were the most robust from the regression cross correlation study. The hydrophobicity proclivity scale that we report in the present paper are the normalized average of three normalized scales2–4
We created a normalized average of the three key hydrophobicity scales (The index i=1 is from Tang2, index i=2 is from Neumaier3 and the index i=3 is from the average of the collected scales in Juretic4). This normalized average of three scales provides a reasonably unbiased estimate of the "true" average hydrophobicity relationship amongst the 20 amino-acids (index j, from 1 to 20)
The hydrophobicity scale as calculated using Equation 2 using the scales published 2–4 has a number of interesting relationships with key physico-chemical properties of the amino-acids in proteins. For example, this normalized average of these three best hydrophobicity metrics possesses statistically significant linear correlation with many other reliable hydrophobicity metrics derived from multiple literature hydrophobicity scales.
We selected 49 different amino acid properties from a large data set of more than several hundred properties on the Japanese genome net AAINDEX database and from other literature sources. Our objective was to span a wide range of properties that could be used to model the most important underlying central tendencies of the amino acid properties when they are in different proteins and in different contexts. We were interested in determining how we could reduce the rather large number of studies of amino acids in different environments into a core set of properties/values that could best represent all 20 natural amino acids. Our goals for selecting amino-acid property scales from the AAINDEX database was to obtain a balance of molecular properties, statistical properties describing average secondary structure proclivities and average amino-acid fraction compositions, experimentally measured HPLC retention times, and experimentally measured amino-acid bulk properties. Twelve of the amino acid property scales were selected to represent measures of average amino-acid fractional burial in folded proteins and/or most popular/widely used literature hydrophobicity scales. The 49 AA properties are represented by:
2 sequence frequency scales
6 secondary structure propensity scales
8 hydrophobicity scales
4 free energy scales (in water, protein folding/unfolding)n-Octanol to water (Gtow) scale
8 HPLC retention time scales
4 probabilities of an AA inside a folded protein core or on the outside
7 molecular property scales
10 physical (experimentally measured) property scales
There were approximately 175 primary amino-acid property scales of particular interest harvested from the literature to represent the broad range of physico-chemical properties to be found in the literature. We down selected for 49 amino-acid scales used for the multi-variate analysis (PCA, nmMDS, ANOPA) portion of our study, of which around 25 were derivative scales prepared from ratios of fundamental molecular properties such as volume and mass, which would represent intrinsic versus extrinsic scales in the thermodynamical sense. About another 10–15 scales represent averages of literature reported amino-acid property scales. Note that the scales selected represent a very wide range of amino-acid properties including secondary structure statistical propensity scales, fundamental molecular properties like surface area/mass/volume, bulk properties such as index of refraction/melting point/pK-C, HPLC retention times, free energy in water, solvent/water partitioning, average fraction occurring in proteins, average amino-acid burial in proteins/amino-acid exposure with water in folded proteins, hydrophobicity scales, NMR parameters, Rf parameters, several literature Principal Component Analysis/Factor Analysis parametric scales and other miscellaneous property scales.
The analytical method we used for this data is called the analysis of patterns (ANOPA). In some ways, the ANOPA analysis process resembles “factor analysis.”
ANOPA is a pattern projection method. The ANOPA procedure projects n-space pattern point/vectors into a 3-dimensional object which is a cylinder. The axis of the cylinder, called a relation vector, is formed from the pattern point centroid (averages of each AA property for all points) to an out-group average point (averages of each AA property for a pair of selected points). The out-group pair are selected on the basis of a histogram of the pattern point Euclidean distances from the pattern point centroid. Two pattern point distances are calculated with respect to the relation vector from a projection of each point onto the relation vector yielding the distance along the relation vector and the distance from the relation vector. The angle of rotation of each pattern point projection about the relation vector is calculated. Thus, a cylindrical coordinate system is formed which is then converted into rectilinear coordinates. The X prime and Y prime rectilinear coordinates are formed from each pattern point’s pattern projection distance times the cosine and sine respectively of the pattern projection angle of rotation. The Z prime coordinate is simply the pattern projection intersection distance along the relation vector.
We confirmed the results of the ANOPA analysis through a Principal Component Analysis (PCA) analysis of the same 49 amino-acid property scales and calculation of correlation coefficients between the 3 axes of each of the PCA analysis and ANOPA analysis. To even add more confidence to confirm the ANOPA findings we also run a nonmetric Multiple Dimensional Scaling (nmMDS) analysis on the same 49 amino-acid property scales. These latter two analysis were conducted with the software package PAleontology STatistics - PAST11,12. The ANOPA calculations were performed in the Microsoft Excel 2010 package with the established ANOPA equations13 and cross checked with a de novo Python software implementation.
The correlation coefficients, simple linear regressions and the Multi-Linear Regression (MLR) analysis were computed using the statistics functions and statistics data package of the Microsoft Excel 2010 package. There are two statistical tests run on the MLR regressions involving the Property Class (PC) scales (for example Table 3). The first is the F test that comes with the stock standard Microsoft Excel 2010 statistics package MLR add in software. The second statistical test used is a Students T test, where the T statistic is a standard transform of the correlation coefficient that possesses a Students T distribution with the null hypothesis that R =0 and there is no statistically significant relationship. The correlation coefficient T test number of degrees of freedom (20) is reduced by 2 for each X variable coefficient in the regression and by 1 for the Y axis intercept.
Where N=20 for the number of amino-acids. The conservative degrees of freedom for the 8 Property Class scales (described in the results section and found in Table 3) are calculated as 20 less the loss of degrees of freedoms for the MLR regression, where the degrees of freedom are 20 less two times eight (average and standard deviation for each PC) and less 1 for the regression intercept, or d f = 20–(2*8 + 1). The critical value of the T (df =3) statistic is 2.3604, yielding a P value of 4.968%, which we round to the customary statistically significant Alpha tail area P =5%. Correspondingly, the minimum R2 to have statistical significance in the present study is 0.65, which is a correlation coefficient R =0.8062.
The argument we present herein is not that the MLR regression is superior to that of the binary regression, because of higher correlation coefficients, although possibly that may be true, but rather that the amino-acid property class MLR represents more information because more properties represent more of the behaviors of amino-acids in a larger series of contexts and behaviors in real proteins. Our argument also contends that by having a MLR with the 8 property class scales (Table 3), for example, reflects more contexts because the amino-acids partition into sub-sets and that these different context sub-sets join to determine amino-acid behavior in protein folding, interactions with water, interactions with membranes, secondary structure and electronic behaviors associated with AA-AA interactions. Moreover, we argue that within any given regression that the higher the correlation coefficient, the stronger the evidence for the superiority of a given hydrophobicity scale within that regression criterion. Top performance of a hydrophobicity scale within several regression relationship criterion’s based upon different property information leads to a performance/robustness conclusion based upon the consilience of the evidence. We also note that the practice of encoding of attribute, qualitative or state data as integers for the purposes of statistical analysis is widespread and fruitfully used in engineering and science, especially within the enterprise of taxonomy in Biology.
We use the coefficient of determination (R2) rather than the correlation coefficient because it is a much more conservative statistic than the correlation coefficient (R) and can meaningfully be interpreted as the percent linearity between the dependent variable and the X independent variable(s) used in the regression. Concerns might be raised concerning two points regarding the property class MLR, which are the possibility of inter-correlation between X variables and the loss of degrees of freedom in the regression statistics (over-fitting). We deal with these concerns in several fashions. First off, we calculate a T test significance only for the regression itself and not for any individual X variable regression coefficient since the Y variable regression performance itself is what is being measured (see for example Table 11). Secondly, we introduce a correlation coefficient T test as described above. Thirdly, we establish general and specific regression observations as verified over many regressions.
We allow for some dimensionality reduction due to inter-X pair correlation as long as the dimensionality reduction (i.e. percent reduction in the number of states with discrete variables) is not large and new information is being brought forth between each pair of X variables. Property class two partitions into two linear subgroups on the basis of polar and non-polar amino-acids. Property class four partitions into 4 linear subgroups on the basis of size, relative amounts of non-polar area and the presence/absence of a relatively strong or weak polar group. While property class 4 does reflect the polar/non-polar distinction to some extent, it does not reflect a strong and clear partition of AA by polarity or non-polarity, therefore new information is introduced by the addition of property class 4. Property classes 2 and 4 are highly correlated by classical measures and have a Kendall tau coefficient of 0.82 and a Pearson correlation coefficient of 0.86. We note that there are 2*4 =8 possible combinations of states between property classes 2 and 4, but in fact there are actually 5 states formed thereby giving a dimensionality reduction of 1-5/8 =37.5%, which we consider to be an acceptable price for the new information. Where there is no new information adduced by inclusion of a X variable we find that the magnitude of the correlation coefficients are reduced and even more significantly reduced by the squaring process to get the coefficient of determination. Furthermore, we demand that any set of property class vectors produce large significant coefficient of determinations with many disparate AA property scales in our database. The latter criterion produces a very, very high degree of statistical confidence that the collection of property class scales can serve as a highly robust basis set for MLR vector regressions that can evaluate the robustness/significance of many individual AA property scales. There are no other statistically significant inter-property class correlations (see Table 9).
Another key point is that the MLR X’s are not single variables, but rather are column vectors with each column vector having values for each amino-acid. In this context, we equate the concept of a scale with the concept of a column vector. Having made this distinction, the concept of a Multi-Linear Regression (MLR) is still valid and simply represents a broader mathematical context. Our use of the MLR methodology with the 8 property class scales (Table 3) we develop is to evaluate a correlation relationship as whole entity, so the entire MLR correlation is what is used/important, and the statistical significance of individual variable regression coefficients is not meaningful in our context as we do not seek to assess the statistical significance of individual vectors. If the MLR method was being used to fit a variable for the purpose of extrapolating new Y values with scale values outside of the basis set, such as with new amino-acids, then the statistical significance of individual variable coefficients would be germane.
When doing AA property scale pair scatter plots between each property scale selected for our database we often find clustering behavior which indicates that the amino-acids are partitioning into distinct sub-sets and each amino-acid can be assigned a numerical value for the ordinal number of the sub-set into which it partitions. The clustering relationships uncovered for any particular pair of two AA property scales is generally driven by molecular geometry, secondary group geometry, numbers and types of atoms/inter-atomic bonding in the secondary group, molecular size, molecular mass, molecular volume, molecular surface area and entropy distribution about the molecule. No given pair of AA property scale relationships represents the full range of these molecular properties and the nature of the interaction with water and cellular membranes.
The key point though is that there are distinct sets and sub-sets, which when numerically encoded can jointly describe each amino-acid as a row vector of some dimensionality M. We have found through extensive analysis that M=8 is a very good size. Within each property pair scatter-plot where clustering occurs, we can have different patterns such as unstructured clusters, multiple quasi-parallel linear clusters or multiple linear clusters that intersect at some point (often at Glycine or Alanine). Karplus15 noted this pattern, although not as extensively as what we report. Generally, there is a geometric ordering that allows the assignment of a meaningful ordinal number. To reiterate, a property class scale (column vector) represents a relationship between property scales and the values assigned within the scale to each amino acid are their respective sub-set/cluster ordinal number. Property class scales assembled in this way can be used as one of the basis set vectors to be used to evaluate the performance and reliability of any individual amino-acid property scale.
We report herein a recast of the ANOPA linear algebra vector equations13 in the as implemented form. The ANOPA equations are cast in a quasi-software convention. We need to note that the three property class vectors defined using the 3D ANOPA coordinate system planes represents the correlation based dimensionality reduction from a pattern space of dimension 49 to a pattern space of dimension 3.
Pattern vectors (points), N objects (row vectors, amino-acids), M properties (dimensions)
Resulting object property array/table O(M,N)
Table Row index –> i =1-N (can imply column vector of results)
Table Column index –> j =1-M (can imply row vector of results)
Vector without an index implies the vector as a whole entity
Vector norm of any vector G is symbolized by |G|
Normalized object table No(i,j) = Range[j=1-M] - >((O(i,j)-MIN(O(i,j))/(MAX(O(i,j))-MIN(O(i,j)))
Group Centroid/Average Ca(j) =(Sum [i =1-N] - >No(i,j))/N
Dimension Delta2 Dd(i,j) =Range[i =1-N] - >(Range[j=1-M] ->(No(i,j)-Ca( j))2)
Distance of object pattern points to group centroid A0(i) =(Sum[j =1-M] ->Dd(i,j))0.5
Select two objects (amino-acids a + b) –> No(a,j) and No(b,j) to calculate an outgroup average per the selection rules from the histogram of pattern point A0(i) distances to the pattern set centroid
A0(i) distances to centroid Oa(j) =(No(a,j)+No(b,j))/2
Out group to centroid delta U0(j) =(Oa(j)-Ca(j))
Normalized dist along relation vector T0(i) = (Sum[j =1-M] ->(No(i,j)-Ca(j))*U0(j)/|U 0|2)
Origin projection T0 type distance Ot = (Sum[j =1- M] ->(0-Ca(j))*U0(j)/|U0|2)
Origin projection reference vector Ur(j) = (Ot*U0(j)+Ca(J))
Pattern point dist from relation vector D2(i) = (Sum[j =1-M] ->(Ca(j)-No(i,j)+T0(i)*U0(j)2 )0.5)
Cosine of pattern projection vector to relation vector with origin ref vector Ct(i) =(Sum[j =1-m] - >((Ca(i)-No(i,j)+T0(i)*U0(i))*Ur(j)/(|Ur|*D2(I))))
Angle of rotation about relation vector Ar(i) =ARC- COS(Ct(i))
Distance along relation vector Z’(i) =To(i)*|U0|
Rectalinear X from D2 and Ar: X’(i) =D2(i)*COS(Ar(i))
Rectalinear Y from D2 and Ar: Y’(i) =D2(I)*SIN(Ar(i))
Hydrophobicity scales are typically derived from a measure of the probability that a particular residue will be buried in the core of the protein, away from water. What confounds these calculations is the fact that in most proteins, many of the hydrophobic residues are still exposed to the water (solvent). It is often not clear on how to treat residues that have properties intermediate between hard core hydrophobic and polar residues. The size of the residues and difference between alkyl and aromatic residues also pose some difficulty in the calculation of a hydrophobicity scale. Calculations involving cysteine residues add additional complexity in that some of those residues may be involved in providing proteins structural stability through formation of disulfide bonds. Thus, calculation of contributions to any hydrophobicity index through analysis of where specific residues are in a given protein has been complicated and contributed to the scatter we see in the data.
We demonstrate this scatter (in this case level sensitivity) by examining the normalized average of several popular hydrophobicity scales16–21 versus the probability of an amino-acid solvent-exposed area (SEA)22,23 greater than 30 square Angtroms (shown in Figure 1) A good contrasting example scale has been published in 1 and is derived from an analysis of 28 literature hydrophobicity metrics, which when compared with our normalized average of three hydrophobicity scales that forms our hydrophobicity proclivity scale, possesses a strong linear relationship (R2 =0.959) illustrating a relationship with relatively little data scatter.
Figure 1 shows that there is indeed a relationship between the average of five hydrophobicity scales described above and whether or not a particular amino acid is within a protein core or exposed on the surface. We see one tight grouping of amino acids in the figure (I, F, V, L, M, W, A and G) and two loose groupings that include P, T, S, Y, H and N, Q, E, D, K and R. The group at the top right (N, Q, E, D, K and R) include amino acids that are ionic/strongly polar and the central group of amino acids are of intermediate polarity. The tight group of amino acids are primarily amino acids with hydrophobic residues. As we go from the very hydrophobic group to the less hydrophobic group (from the lower left to the top right) the scatter goes up. This scatter is indicative of the increase in water amino acid interaction and of the difficulty of accurately calculating the contribution of any particular residue.
In Figure 2 we show a scatter plot of our amino-acid hydrophobicity proclivities against the popular Fauchere & Pliska free energy of amino-acid transfer from n-Octanol to water (Gtow) scale15,24. It is common in the literature to see n-Octanol used as a proxy for the typical hydrophobic core of folded globular proteins, consequently the Gtow scale has been widely used as a measure of hydrophobicity. As can be seen in Figure 2 the correlation is quite good at 85.9 % linearity (coefficient of determination). The regression of these two scales is used to derive a fitted (calibrated) free energy of transfer and reported in Table 1 and used in our new alignment algorithm. Since Gtow reflects a delta G (energy) of transfer, hydrophobic proclivities can also be seen to relate directly to energy (Table 1).
These property class vectors can serve as a set of basis vectors for a large swath of amino-acid physico-chemical properties. MLR regressions were conducted with 157 of the most reliable/apt amino-acid property scales in our database as the Y vectors and the 8 property class scales as the X vectors. Of 157 scales, 145 scales (92.4 percent) were found to be statistically significant (P less than or equal to 5 percent) for both the regression F test and the T test (methods section) at the same time; a very rigorous test indeed. The threshold of statistical significance for the coefficient of determination is 68 percent.
The reasonableness of our hydrophobicity scale is also demonstrated by examining the relationship between our scale and the mean residue depth (dpx) defined as the distance between the interior of a protein amino-acid and the nearest water molecule in the aqueous shell surrounding the protein25,26. In Figure 3 we show that there is a strong relationship (97 % linearity) between the dpx metric and our hydrophobic proclivities. The dpx metric is a straight forward geometrical description of the local protein interior and can be expected to provide similar information to the solvent accessible area and buried surface area metrics. The dpx depth and hydrophobic proclivities correlate with amino-acid/protein properties such as average protein domain size, secondary structure, protein stability, free energy of formation of protein complexes, major literature amino-acid hydrophobicity scales, residue conservation, post-translational modifications like phosphorylation, and hydrogen/deuterium amide proton exchange rates15,25,26.
Consider Figure 4 where our normalized average hydrophobicity index is scatter plotted against the area per specific volume of each amino acid (shown using their alphabetical representations).
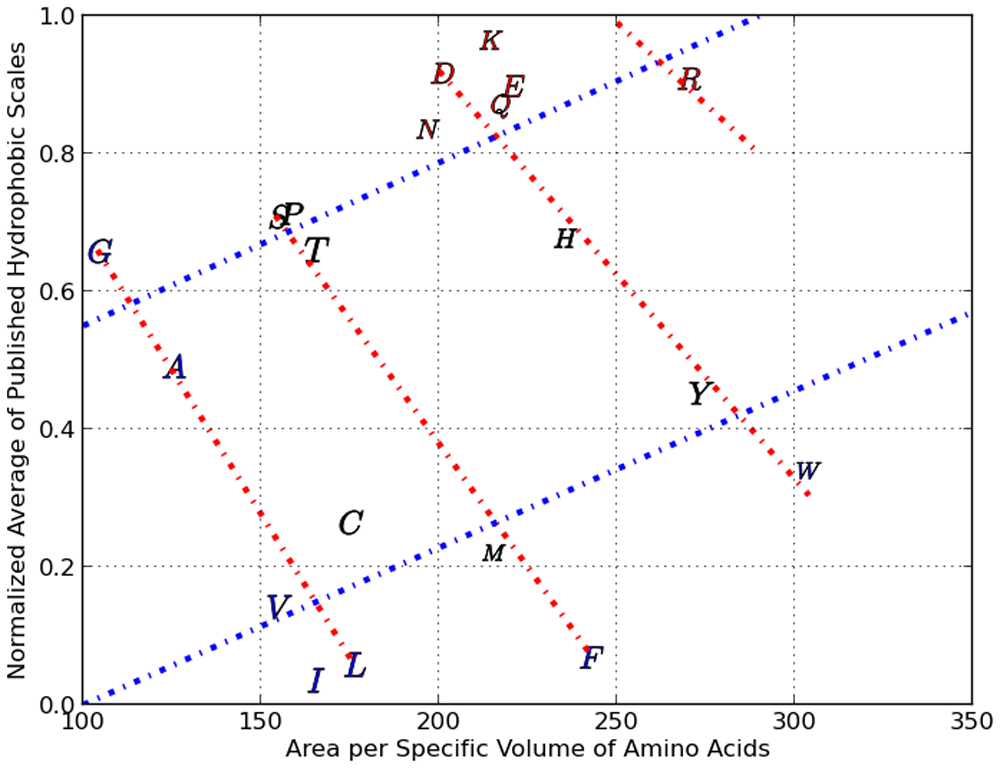
There are two Property Classes illustrated here with 4 red and 2 blue lines with each line assigned an ordinal number relative to zero within its property class.
We can clearly see cross-hatched patterns where for example the amino acids G, A, C, V, I and L are on a straight line (starting from the top left to bottom right). Moving right, we see that S, P, T, M and F are on a straight line (nearly parallel to the line formed by G,A,C,V and I). Continuing further right, we see a third line which crosses several amino acids, followed by an outlier, amino acid R. This series of four lines form what we call Property Class 1. We assign a numerical value of 0 to the line through G,A,C,V and I and a value of 1 to the next line and so on. In the same Figure 4 we can see the formation of Property Class 2 which contains only two linear clusters ranging from the lower left to the upper right. One of the Class two series consists of V, I, l, C, M, P, Y and W, with the other series made up of the rest of the amino acids. We arrived at Property Class 3 and Property Class 4 by scatter plotting our normalized average hydrophobicity index against specific absolute entropy (and this is shown in Figure 5) The four property classes we identified respectively in the scatter plots shown as Figure 4 and Figure 5, along with the respective X axes physico-chemical property, correlated very highly (as multiple linear regression factors) with our normalized average of three robust hydrophobic indices (shown as avg 3H) having an R squared >95 %. Property class #5 reflects a scatter plot between the delta G of burial of AA secondary groups15 (as Y) and the number of atoms in the respective secondary group10, which resulted in 5 linear series. Each of the linear series numbers (0 through 4) for each AA forms the basis of property class #5. The multiple linear regression of the delta G of secondary group burial with number of secondary group atoms and property class #5 resulted in an R2 of 98.1%. Property classes #6, #7 and #8 were derived from 49 fundamental amino-acid properties and derived scales that are based upon an analysis with Analysis of Patterns (ANOPA)13. Together PC #1 to #8 represents eight X vectors in the multiple linear regression reported in the third column of Table 2 and the statistical F test and T test for this column can be seen in Table 11 (which includes a couple more amino-acid property scales).
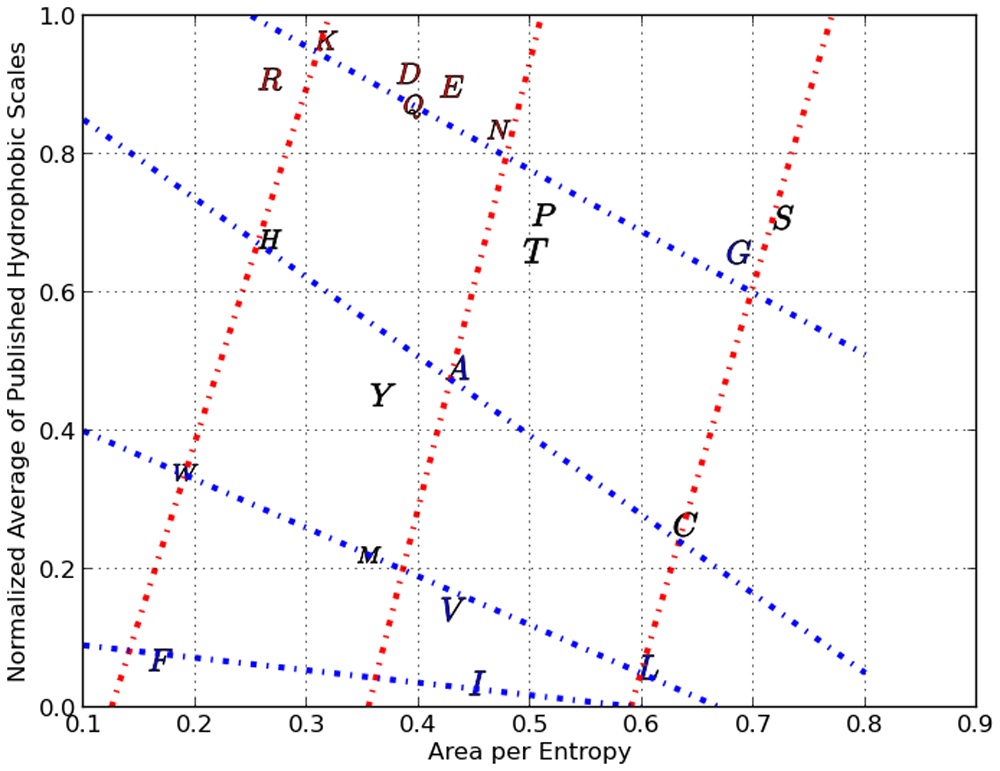
There are two Property Classes illustrated here with 4 blue and 3 red lines with each line assigned an ordinal number relative to zero within its property class.
Additionally, the 8 property class vectors can serve as a set of basis vectors for a large swath of amino-acid physicochemical properties. MLR regressions were conducted with 157 of the most reliable/apt amino-acid property scales in our database as the Y vectors and the 8 property class scales as the X vectors. Of 157 scales, 145 scales (92.4 percent) were found to be statistically significant (P less than or equal to 5%) for both the regression F test and the T test (methods section) at the same time; a very rigorous test indeed. The threshold of statistical significance (alpha P =5%) for the coefficient of determination is 68 percent.
In Table 2 we summarize the performance of several of the hydrophobicity scales published in the literature. The hydrophobicity scales shown as rows are compared with four important quality metrics that are either amino acid physico-chemical properties or derived from such properties. The quality of inter scale regressions are shown as R2. The performance of each row scale can be observed relative to the other row scales within each of the four columns, where the higher the R2 the better the performance of the row scale with regards to the column scale. There are 13 rows in Table 2 representing 11 hydrophobicity scales, one solvent exposed area scale and one delta G of transfer from water to an organic solvent (Octanol).
Of the 11 hydrophobicity scales in Table 2, 7 are popular scales in practice, three are the constituent scales of our hydrophobicity proclivity scale and our hydrophobicity proclivity scale. These row choices in Table 2 are to illustrate a close relationship between AA hydrophobicity and the transfer of an amino acid to an organic solvent (n-Octanol, Table 1 column 2), used as a proxy for the internal environment of a folded protein, as well as to compare AA hydrophobicity with an AA Solvent Exposed Area scale (column 1) also representing a folded protein environment. The high R2 between the row dG of transfer to Octanol and the first column AA Solvent Exposed Area (SEA) scale in Table 2 illustrates the aptness of comparing the dG of AA burial in protein "solvent" to a solvent-solvent transfer model between water as the reference state and an organic solvent as the transfered or final state. In Table 2, the inclusion of the row SEA is to illustrate the high R2 with the first column SEA illustrating the consistency of folded protein behaviour in SEA scales derived from different data sets. With the Rose AA percent buried row hydrophobicity scale7, similar lessons can be gleaned as with the row Octanol and SEA scales, as the Rose scale represents the environment of a folded protein. The very high R2 between these three row scales and the last two column regression scales in Table 2 illustrate a strong justification for including these row scales, as protein folding is thereby strongly linked with other physicochemical properties of amino-acids, as reflected by these two columns. We describe the regression X variables in the 4 columns of Table 2) below.
We can see that the correlation between our hydrophobicity scale (shown as avg 3H in Table 2) and the Moelbert average amino-acid solvent Accessible Surface Area (ASA) within proteins has an R2 =84.7%. The ASA is the average area of each amino acid exposed to water in the globular proteins. When our hydrophobicity proclivity scale approaches 1 (i.e. hydrophilic) the ASA goes up as would be expected, with the converse being true as our hydrophobicity scale approaches 0 (i.e. hydrophobic) the ASA goes down27.
The amino-acid Accessible Surface Area (ASA) has long been suggested as a reasonably accurate proxy for hydrophobicity15,22,27 as is also seen in a related scale, the Solvent Exposed Area > 30 square angstroms22,23. The amino-acid property classes are vector sets of clusters/linear families of curves in multiple linear regression relationships between two (or more) amino-acid physico-chemical properties. The first two columns (ASA and Gtow) represent paired variable linear regressions and the third column (Property Classes #1 to #8, Table 3) and fourth column (Property Class #1 to #4, AA area/specific volume10 and specific absolute entropy8,9) represent multiple linear regressions.
The R2 in the first two columns of Table 2 represent linear regression results between the Y (row) vectors and the X (column) vectors. The R2 in the last two columns of Table 2 derive from multiple linear regressions, where the independent (X) variables are vectors of amino-acid property Classes (PC) and/or amino-acid physico-chemical properties, and each row parameter is the dependent variable, respectively. Again, the Property Classes can be thought of as distinct subsets of amino-acids representing multiple linear series/clusters (within scatter plots or multiple linear regressions) of amino-acids in reference regressions associated with X variable vectors from some key physico-chemical metrics plotted against the hydrophobicity proclivity vector scale.
In Table 2, we see that the F and P Gtow scale performs as well (i.e. high R2) as the best of the hydrophobicity scales within columns 1, 2 and 4, thus, further justifying our selection of the Gtow scale as our baseline standard for a free energy of transfer from an aqueous solvent environment to a non-aqueous solvent. The SEA > 30 A2 does as well as the popular hydrophobicity scales in Table 2 and has good correlation with the F and P Gtow scale in column two and thereby establishes a direct link between the F and P Gtow scale and the free energy of burial of aminoacids in proteins and providing strong evidence justifying a solvent-solvent transfer model for protein folding.
The Tang Q and Neumeier X scales are the top performing individual hydrophobicity scales as seen in the first two column results, followed on average by the Rose scale. The Juretic Avg scale generally performs as well as the five popular hydrophobicity scales in columns one and two, but more importantly it performs better than any other single hydrophobicity scale except for the Tang Q and Neumeirer X scales in columns three and four. Since we consider columns three and four to be a more rigorous test for a robust, high performance hydrophobicity scale, we see the justification for selecting the Tang Q, Neumeirer X and Juretic Avg as the scales from which to prepare our hydrophobicity proclivity (3H) scale. Our hydrophobicity proclivity scale performs basically as well as the best individual hydrophobicity scales in columns one and two, but it is the top performer in columns three and four. No other hydrophobicity scale that we evaluated on average performed as well (i.e. magnitude of R2) in regression comparisons with amino-acid physico-chemical properties as our hydrophobicity proclivity scale. In Table 2 column three is the 8 sets of numbers (vectors), dubbed as property classes and are eight X vectors (Table 3) in the multiple linear regression relationships with the R2 shown in the third column. These eight property class vectors can form multi-linear regression fits with very high R2 with a large number of the physico-chemical properties of the of the 20 amino-acids in our accumulated AA physico-chemical property database, thereby serving as proxy’s for these properties. In Table 2 column four, we see four property class vectors (#1-#4) and two AA physicochemical property vector scales (surface area/specific volume, specific absolute entropy); column four is included to illustrate the method of construction of the eight Property Class (PC) vectors represented by column 3.
Strong relationships exist between some of our aminoacid property database and the Wolfenden free energy (delta G) of transfers between vapor-water, vapor-cyclohexane and cyclohexane-water. This experimental system using dG of transfers of amino-acid secondary group analogs was devised to eliminate the confounding effect of water content within the organic solvent and to eliminate the effect of the amino-acid backbone, such that only the contributions of the secondary group analog dG free energies of transfer could be calculated. The dG of transfer of vapor-water is strongly correlated to several hydrophobicity scales, drawing a link with the rest of the cognate literature, and the amount of polar area in the respective amino-acids (Table 10). This latter correlation is an important insight into the energetic distinction between polar/non-polar surface area as part of the hydrophobicity phenomenon. The dG of AA secondary group analog transfer between cyclohexane-water also strongly correlates to several hydrophobicity scales, but also correlates to average amino-acid exposed (to water) surface area in folded proteins (Table 10). Also notice the strong relationship between dG of transfer of AA secondary groups between vapor-water and cyclohexane—water in scatter-plot Figure 17. The dG of AA secondary group analog transfer between vapor and cyclohexane is strongly related to amino-acid property scales related to the size, bulk, mass and polarizability of the amino-acid secondary groups (Table 10).
The data discussed above is from our database and joint papers by Dr Richard Wolfenden, Dr Charles Carter and/or Dr. Anna Radzicka28–33. The joint papers omit the data for Proline. The dG of transfer approach using classical physical chemistry procedures relating the vapor phase, Cyclohexane and water is unique in the literature. The data estimates for Proline are based upon multiple AA property regressions, because the data is not covered in original work for several reasons. First off, the secondary group of 3 methylene Carbons forms a 5 membered ring between the alpha Carbon and the amino group attached to the alpha Carbon. Secondarily, Proline is not technically an amino-acid, so the structural difference impacts its interaction energy with water and Cyclohexane. Thirdly, the actual preparation of a Proline analog is not without difficulty. Several estimates of key Proline values were undertaken through regression modeling. Without Proline in the data, the regression R2 estimates don’t change very much from the regressions with and without the estimated Proline data values.
Plot Figure 6 is the A0 distances histogram, which represents the distances from the centroid average to each pattern vector/point. This 1D ANOPA analysis is independent of any input to the calculations and is used as the first step in the algorithmic selection of the best pair of pattern points (objects) to select for the out group average for the 2D and 3D ANOPA analysis. We see four putative sub-populations (perhaps non-random correlation sub-structures) representing correlation based clustering. The ANOPA algorithm seeks to find pairs of pattern points from either the right hand side sub-population distribution tail (first pass) or the left hand side sub-population distribution tail (second pass, if needed) that represent an out group choice that is generally congruent in number and size of the 1D ANOPA histogram sub-populations, which in this case is 4, with the 2D ANOPA sub-population clusters in Figure 7. The green line represents the selection of the amino-acids Leucine and Isoleucine on the right tail of the 3rd sub-population. The Sub-populations are processed from right to left in the iterative search for the best two amino-acids to form the out group average.
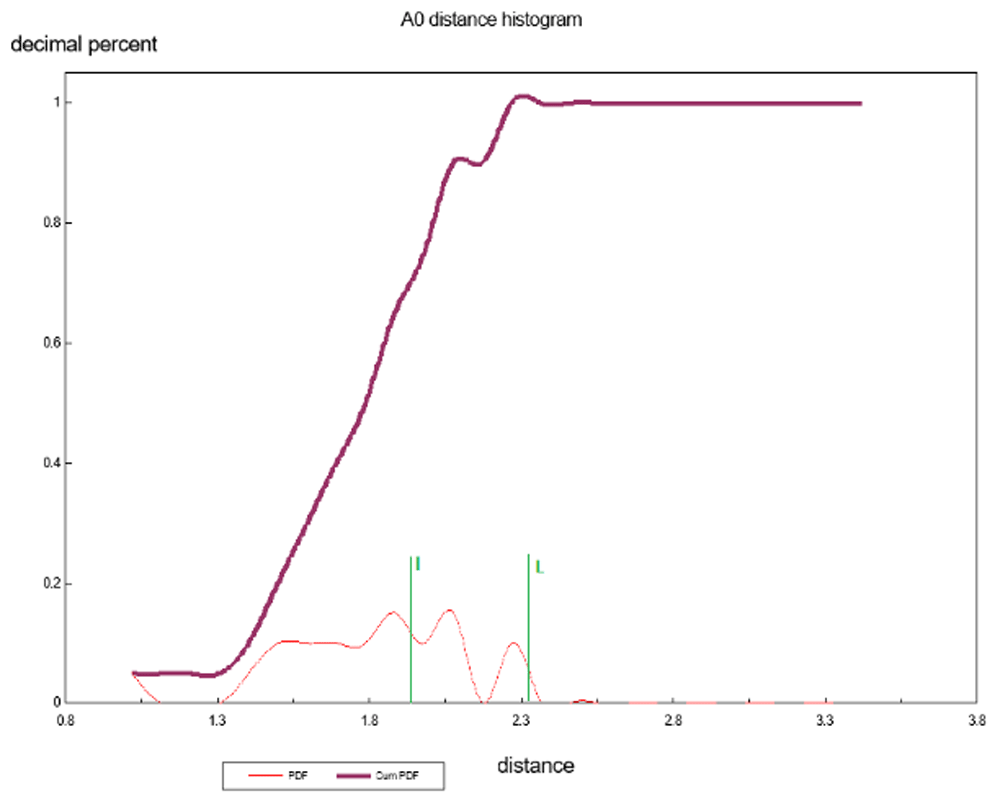
There are 4 population clusters and a single value as shown and this structure is consistent with the structure of the 2D ANOPA sub-population analysis.
With (I, L) chosen for the out group, the 2D ANOPA (T0, d2) scatter plot Figure 7 reveals 4 clusters (defined by oval circumscribing) and a singleton point. This pattern in the 2D ANOPA scatter plot is consistent with the number and size of sub-populations in the 1D ANOPA histogram analyses. T0 are the normalized parametric distances along the relation vector/line, where the out group average is normalized to 1. The d2 distances are the pattern point distances from the relation vector/line. The clusters in the 2D ANOPA scatter plot Figure 7 are resolving by hydrophobicity, polarity, charge, degree of secondary group SP2 hybridization and secondary group size. The 3D ANOPA plot is in Figure 11.
Each distinct pair of the 3D ANOPA coordinates forms one of the 3 coordinate planes in Plot Figure 8. These 3 pairs of coordinates for each amino-acid effectively provides a projection of the 3D structure onto each of the three coordinate planes. In this plot there are 4 distinct clusters of amino-acids numbered 0–3. Scatter plots and correlation analysis between Z’ and a number of hydrophobicity scales show a very strong linear/curvilinear correlation, which is not surprising given that many of the 49 AA property scales are either hydrophobicity scales or strongly correlate with hydrophobicity scales, like reversed phase HPLC retention times. Reverse phase HPLC retention times represent the interaction between an AA and a water/non-polar surface where a clathrate structure forms. Correlation analysis with the y’ coordinates with their corresponding d2 scales are very linear (R2 =97.27%); the later representing the amino-acid distances from the relation vector. The Y’ coordinate represents the relative amount of polar area and aliphatic vs. aromatic/SP2 hybridization area. See Table 6 and Table 4.
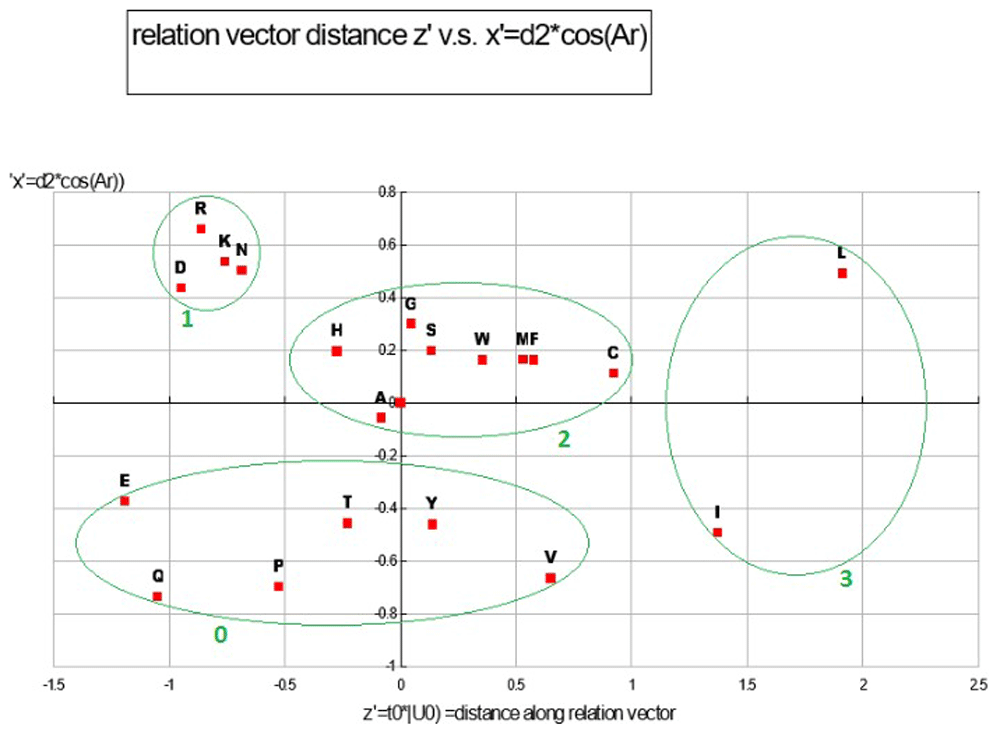
This plot represents a property class with 4 clusters of amino-acids each assigned an ordinal number relative to zero.
We see that the ANOPA X’ is reflective of protein secondary structure propensities, which interestingly have some bearing on HPLC retention times. The reflection of secondary structure by the X’ ordinate may be because the information reflected by the X’ ordinate is related to Van Der Waals dispersion forces and the secondary group induction effects that modulate the pk-C of the amino-acid Carboxilic acid groups, both effects of which can be related to the fraction of non-polar surface area and/or polar surface area.
Within each of the 4 clusters that we see in Plot Figure 9, the most polar/charged secondary group is located toward the top with the progression moving to the lesser polar/degree of charge, possessing more hydrophobic area, on the lower end. The AA size and amount of hydrophobic surface area is a large part of what drives these clusters, with there being a difference in the hydrophobicity of Carbons in different hybridization states with a SP3 (aliphatic) hybridized Carbon more hydrophobic than a Carbon in a SP2 (aromatic) hybridization state. Sulfur atoms act more like hydrophobic area in amino-acids compared to what can be seen in band 2 above with Nitrogen or Oxygen atoms, although not as strongly hydrophobic as Carbons in a SP3 configuration. The hydrophobicity of an amino-acid is in direct relation to the total amount of hydrophobic surface area and the relative area partitioning between aliphatic Carbon, aromatic Carbon and Sulfur. The X’ coordinates also have a reasonably strong linear relationship to secondary structure revealed in scatter plots against metrics sensitive to secondary structure, such as a metric derived from our hydrophobicity proclivity scale, a beta sheet configuration proclivity scale, and a double bend proclivity scale (2*H-B-DB), which has good performance compared to the secondary structure of proteins of known secondary structure (unpublished results). When a plot of the primary sequence ordinal numbers against a running average of size 3 of the 2*H-B-DB metric goes above 0 (especially above 0.5) an alpha helix is indicated and when the running average of 3 of this metric goes below zero (especially below -0.15) a beta sheet is indicated. This metric is symmetric about zero and has a nice sinusoidal shape in regions of intercalating and alternating alpha helices and beta sheets or intercalating and alternating alpha helices. See Table 4 and Table 5.
The Y’ ANOPA ordinate is strongly related to a couple of HPLC scales and a couple of ANOPA process related distances. The Y’ ordinate has a relationship with PCA ordinate II and nmMDS ordinate II. Through these latter two relation- ships the ANOPA Y’ ordinate has a relationship with size and surface area, which are reflected as links with some of the hydrophobicity metrics.
The Z’ ANOPA ordinate is shown below to be strongly related to a number of hydrophobicity metrics and amino-acid folded protein burying/water exposure propensities.
Statistically significant correlations are in bold face and weaker, non-trivial correlations in italics. Each pair of columns represent an ANOPA axis that is correlated with the respective PCA or nmMDS axes. Each pair of columns represent a linear correlation and a curvi-linear correlation, with the latter typically being higher. The correlations are expressed as R2, which is more conservative statistic. With one exception, each ANOPA ordinate only corresponds with one PCA or nmMDS ordinate. The regressions from which the R2 derive are from a simple linear regression (plain R2) and an unconstrained sixth order polynomial curvi-linear regression (O(6) Poly R2).
The Z’,Y’ Plot Figure 10 has the hydrophobicity related Z’ ordinate as the X-axis and the Y’ ordinate picks up something of a non-linear/curvi-linear component involving the relative amounts of polar surface area, with the relative fraction of dipole vs. ionic surface area, with non-polar surface area and with the aliphatic vs. aromatic area fractions. We can see the former effect in the main sequence of group #1, in the relative placement of group #0/group #4 and in the placement of Tyrosine above Phenylalanine in group 4. See Table 5 and Table 6.
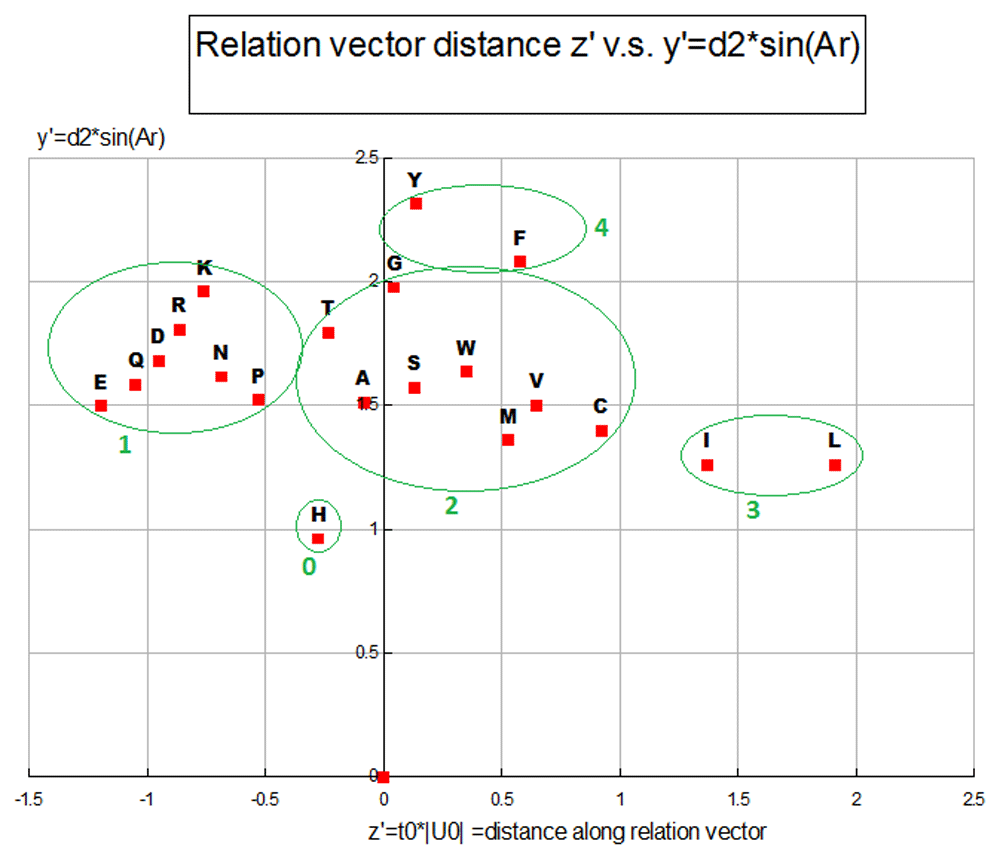
This plot represents a property class with 5 clusters of amino-acids each assigned an ordinal number relative to zero.
In the three 3D ANOPA Plots (Figure 12 and Figure 13 and Figure 14) we see the relation vector, ensemble average to the out-group average L,I, and its reflection, with a total line segment between the –out-group average to the +out-group average oriented along the Z’ (Z prime) axis.
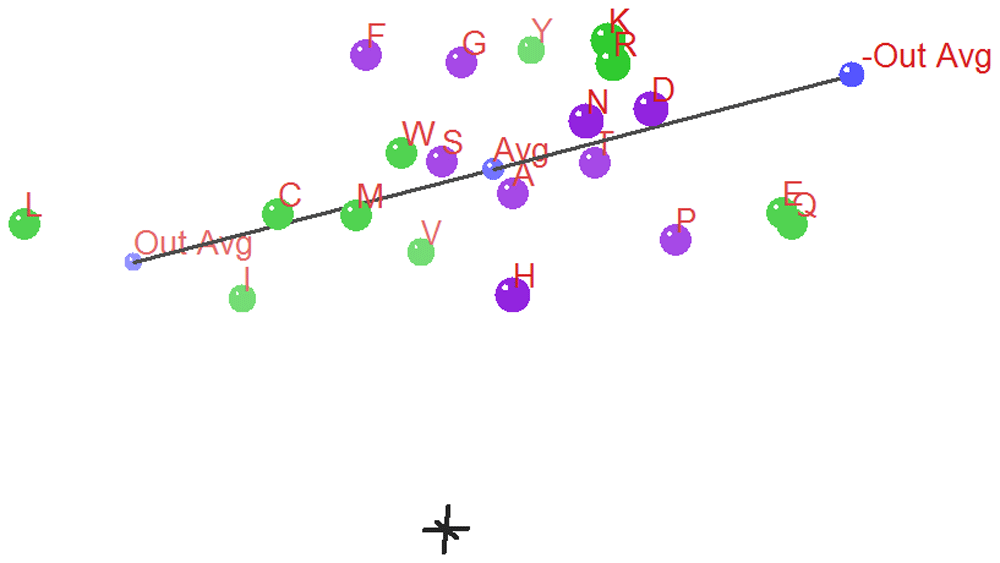
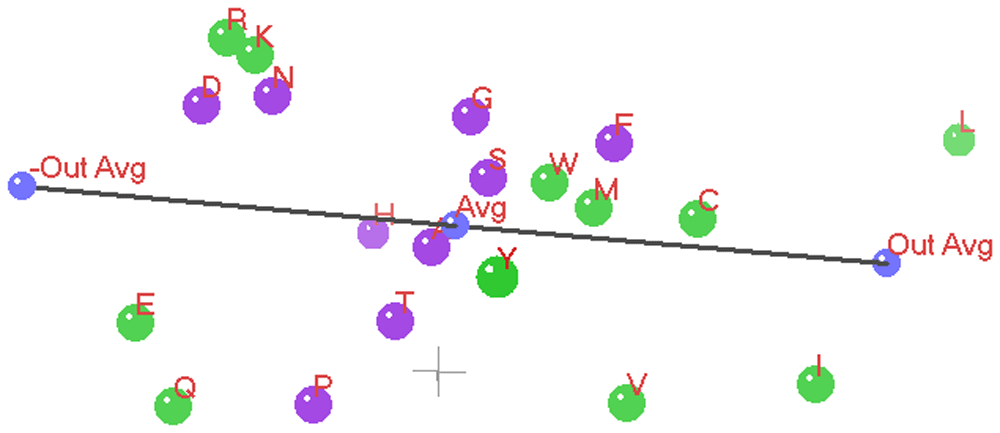

The Z’ axis is primarily related to hydrophobicity. In the background in gray is the 0,0,0 origin marked by a small (X,Y,Z) coordinate axes. The 3D ANOPA procedure calculates the amino-acid pattern point projection distances along the relation vector, the pattern point distances from the relation vector and the angle of rotation about the relation vector. In recent work by Dr. Charles Carter and Dr. Richard Wolfenden28–33, they have found that their hydrophobicity measures/scales partition into two parts reflecting the amino-acid assignments to the two types/classes of amino-acid tRNA Synthetase (aaRS) enzymes that charge the tRNA’s with their matching amino-acids. The Carter/Wolfenden work shows that the anti-codon loop of tRNA’s reflect the hydrophobicity dual partitioning as does their newly discovered and more primitive tRNA stem code. The amino-acids have been color coded green or purple depending upon which of the two aaRS’s their matching tRNA’s map to. We can see that the purple points cluster together and are sandwiched between the green points, where the purple points represent amino-acids of either moderate hydrophobicity/size and the smaller polar amino-acids Aspartic acid and Asparagine. These last two 3D ANOPA views give more perspective on the placement of amino-acids with respect to hydrophobicity and by whether or not they partition according to their class I or class II aaRS enzymes.
What we see in the ANOPA (Z’, Y’), (Z’,X’) and (X’,Y’) Plots (Figure 8, Figure 9 and Figure 10) are the relationship between each amino-acid and the cavity it creates in water. The creation of a cavity in water creates a clathrate shell of waters with a surface tension. There is a pressure-volume work energy cost for creating the cavity in water and a surface tension-area work energy cost in opening of the cavity in water. We also see that there is an offsetting free energy cost that mitigates the aqueous cavity opening cost that derives from the attraction (wetting force) of the aqueous clathrate shell to the surface of the amino-acid. We have non-polar surface area (aliphatic, aromatic/PI resonance network) interacting through Van Der Waals and induced dipole interactions. We also have dipole, hydrogen bonding, and ionic interactions between amino-acid surfaces with the aqueous clathrate shells. The surfaces of amino-acids are partitioned up to have some subset of these interactions with the aqueous clathrate shells. Table 4, Table 5 and Table 6 are the summary results of a correlation study of the ANOPA X’, Y’ and Z’ versus correlated/highly correlated scales from our amino-acid property database.
The correlation between the Z’ axis and hydrophobicity proclivity scale means that the there is a strong justification for this H-index being a preferred hydrophobicity scale. Many of the amino-acid properties within the 49 AA property scales used for the ANOPA analysis are either hydrophobicity scales or are scales partially to strongly related to the factors underlying hydrophobicity.
We have used the rules of ANOPA to look at choices of amino-acids from the outer and inner sub-population tails in the 1D ANOPA A0 distance histogram plot Figure 6. The deliberate selection of a number of amino-acid properties related directly or indirectly strongly suggested that a pair of large surface area aliphatic residues would be an optimal choice as it was found through the ANOPA 2D and 3D analysis and other subsidiary analysis.
We can cross check the ANOPA analysis through a Principal Component Analysis (PCA) analysis of the same 49 amino-acid property scales and by calculation of correlation coefficients between the 3 axes of each of the PCA analysis (3D scatter-plot Figure 15) and ANOPA analysis. To even add more grist for the mill to confirm the ANOPA findings we can also run a non-metric Multiple Dimensional Scaling (nmMDS) analysis (3D scatter-plot Figure 16) on the same 49 amino-acid property scales. We see the results in the two coefficient of determination (R2) Table 7 and Table 8, where we find that there are good to excellent correlations between the three analysis. A strong correlation between multi-variate classification procedure ordinate scales are reflected in bold fonts and weaker, but non-trivial, relationships are reflected in non-bold, italic font. The inter-ordinate axis correlated relationships are measured by the coefficient of determination (R2), both linear correlation and curvi-linear correlation with polynomials of order 6 – O(6). Generally speaking, there is good correlation amongst the three coordinate systems as seen in the ANOPA vs. nmMDS/PCA Table 7 and in the nmMDS vs. PCA Table 8. Where there is a strong linear correlation there is also a strong curvi-linear correlation, with the latter correlation scoring higher. In these two tables, with the exception of the ambiguous ANOPA Y’ scale relationships with the nmMDS Axis II and III scales, the rest of the relationships have singularly strong paired relationships, whereas the other paired relationships are weak, if not zero (independent). In plot (Figure 18) it can be seen that there is a fast roll off of the PCA Eigenvalues/variances, with the first three principal components representing 68% of the pattern point variation. ANOPA suffers no such loss of information.
There is only one strong and statistically significant match between each of the 3 PCA and 3 nmMDS axes, which provides strong evidence to conclude that these two analysis are essentially telling the same story and reinforcing the comparison between these two multi-variate analytical methods and ANOPA. The regressions from which the R2 derive are from a simple linear regression (plain R2) and an unconstrained sixth order polynomial curvi-linear regression (O(6) Poly R2).
Since the PC values are discrete, ordinal values that encode sub-set membership and the fact that due to the nature of the amino-acids there are going to be some sub-set memberships that overlap, we can expect to see some inter-scale correlation. An inter-scale correlation would have to exceed 0.806 to be statistically significant and there is only one pair of scales that meet this condition. For reasons discussed in the method section, the apparent correlation does not reflect a significant loss of dimensionality and there is a different informational content reflected by each scale. The MLR regressions will servo/weight each PC scale to effectively include/exclude the scale from being related/utilized in the establishment of a MLR regression correlation used to judge the quality of relationship of various amino-acid property/attribute scales.
These statistically significant relationships provide us with more insight into the meanings of both the Wolfenden-Carter dG scales and the database metrics reported in this table. The v>wa scale is the dG of vapor to water. The c>wb scale is the dG of Cyclohexane to water. The vap - chx scale is the dG of transfer of vapor to Cyclohexane. The transfer dG’s of Cyclohexane to water and vapor to water are strongly correlated. The transfer dG of vapor to water is strongly related to hydrophobicity and polar surface area. The transfer dG of Cyclohexane to water is strongly related to surface area and proclivity to have more than 30 square angstroms in contact with water in folded proteins. The dG of transfer from vapor to Cyclohexane is strongly correlated to molecular size and asymmetry. The regressions from which the R2 derive are from a simple linear regression (plain R2) and an unconstrained sixth order polynomial curvi-linear regression (O(6) Poly R2).
A few relevant rows have been added for additional correlation purposes. Generally speaking, the T test is more conservative than the Excel 2010 regression package F test.

X = dG vapor to water (#235) vs. Y =dG Cyclohexane to water (#236) plot.
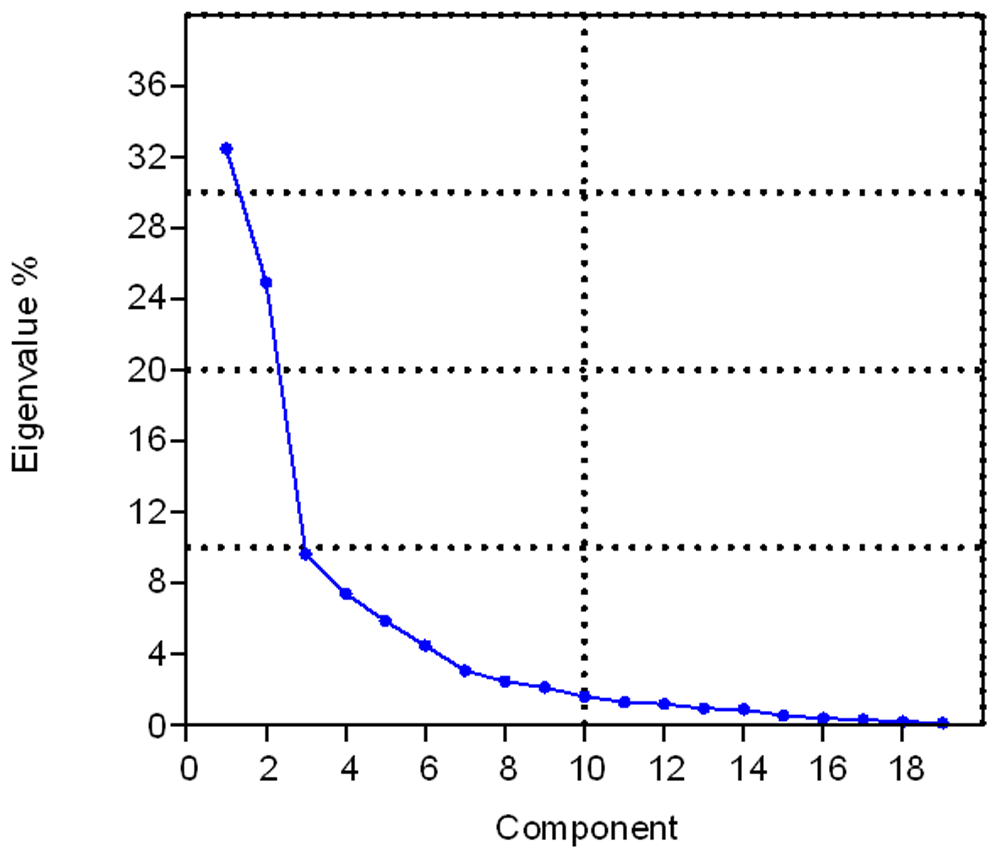
The first 3 Principal Components represent about 67% of the data variation.
From this perspective of the 3D nmMDS plot Figure 16, we see that Alanine (A) is the far apex past the ensemble average, from which the point cloud fans out in moving toward the viewer, somewhat akin to a cone. The points position themselves according to hydrophobicity/polarity, alkyl vs. aromatic surface area and size. The amino-acids L,I,V,C are located off to one side as in the 3D ANOPA analysis.
Generally, we see the same clusters of amino-acids in the PCA 3D plot as we do in the nmMDS plot, such as K,R,D, V,I, F,W and P,T,Y. Broadly speaking, the amino-acid points position themselves according to hydrophobicity/polarity, alkyl vs. aromatic surface area and size similar to the nmMDS analysis. The amino-acids L,I,V,C are located off to one side as in the 3D ANOPA analysis.
We point out the excellent linear relationship between our hydrophobicity proclivity scale and the dpx average residue depth (from water) scale in Figure 5 of the manuscript. The dpx scale is derived from a suite of proteins with actual solved folded structures, hence dpx is in effect a protein structural description of hydrophobicity where the deeper on average that a residue is buried, the more hydrophobic it is. Contrast the dpx concept with the ideas of average solvent exposed area, average buried area, percent buried, etc. When the relationships in Figure 3–Figure 5 (with supporting literature) are taken together, the hydrophobicity potential driving protein folding is suggested to be the traditional solvent-solvent partitioning model of protein folding where amino-acids partition between aqueous exposure and burial within the hydrophobic core of folded proteins. We believe that this traditional model of the primary driving force for globular protein folding is apt, but needs some updates and modifications that we develop in detail within the forthcoming manuscript - Hydrophobicity revisited: A Molecular Story34. We are suggesting in the present manuscript that aqueous clathrates form about the hydrophobic areas of amino-acids in an unfolded state (a structural feature) and hydrophobic surface area on folded proteins possess a surface tension like a gas bubble in water. We are also suggesting that the physics driving the initial stages of protein folding is the same physics as the coalescing/condensing of bubbles of non-polar gaseous species or of fine hydrophobic liquid droplet dispersion’s in water. We expand upon this hypothesis in the forthcoming manuscript.
The great organizing principle embodied within the hydrophobicity proclivities (and implied by dpx), is that of a neo solvent-solvent partitioning effect, where the energetics of the solvent shell waters are the dominant effect in the energy balance. As with clathrates (ordered aqueous shells), which form spontaneously with hydrophobic molecules, there is a solvent shell of ordered waters that form spontaneously around solvated globular proteins. However, there is a confounding factor in trying to obtain an accurate hydrophobicity proclivity in that even the most hydrophobic protein will have some average solvent exposed area, so it is reasonable to postulate that there is some functional reason for exposure of some grease to the solvent. The presence of hydrophobic surface area causes an aqueous clathrate shell to form at that point perhaps effectively becoming part of the folded structure of the folded protein, possibly as a retaining structural element operating through surface tension and putting the interior of the globular protein under pressure. The importance of amino-acid hydrophobicity to the structure and function of globular proteins is critical to the function and survival of cells, a reality that is even reflected in the very structure of the standard genetic code.
The amino-acid codons are arranged/coded in such a way as to reflect the underlying hydrophobicity of the respective amino-acids. A careful analysis reveals that the genetic code has a built in redundancy through amino-acid hydrophobicity (in addition to codon redundancy) such that point mutations in a codon that yield a different codon tend to result in an amino-acid with similar hydrophobicity. It has been shown that the underlying amino-acid codon structure has a direct relationship with high quality hydrophobicity scales that are published in the literature35.
Our aim in developing a single hydrophobicity scale for the purposes of protein alignments was to try to develop a scale which reliably represented the central (average) hydrophobic tendency as a robust first order effect that allows simple, but meaningful paired comparison of aminoacids for homology relationships. Adding additional variables/properties would in our opinion detract from our goals of simplicity of calculation and utilization of what we believe is the primary first order effects/mechanics driving the initial stages of protein folding.
The derivative variables concept used in this paper refers primarily to ratios of molecular properties or directly measurable bulk properties of amino-acids. In this way, we derive normalized intrinsic thermodynamical properties versus extrinsic/bulk properties. For example, we find that the ratio of amino-acid surface areas to their volume has a strong relationship to hydrophobicity. Other derivative variables that we have used could be exemplified by estimating the water cavity volume/surface area using amino-acid volume and surface areas and some assumptions about the geometry of the aqueous cavity.
A legitimate question about the hydrophobic proclivity scale we have described is why our scale is superior to alignment score matrices such as PAM (Point Accepted Mutation)36, BLOSUM (BLOCK Substitution Matrix)37 or Gonnet38 that continue to be used for multiple protein alignments and database search alignments.
There are indeed several practical and theoretical problems with the use of these log odds score matrices for the alignment of divergent protein sequences. For example, BLAST and several of the major multi-sequence alignment programs like Clustal W use particular BLOSUM matrices as the default. BLAST uses BLOSUM62 as the default. Quotes from select papers have been summarized below to more clearly illustrate these problems.
The substitution matrices used by the alignment programs are generally log of Bayesian probabilities for two aminoacids I and J of the form:
The probability of occurrence of the 20 primary aminoacids is not the same throughout the domain/kingdoms of life, so this mathematical formulation can cause issues for identifying and aligning homologous proteins from distantly related organisms.
Superimposed on the log of Bayesian probabilities formalism are evolutionary models derived from Markov stochastic process evolutionary models (PAM), which implies apriori knowledge of the evolutionary amino-acid substitution rates. Necessarily, if one chooses PAM or BLOSUM, one must choose one of the series of matrices that one believes is appropriate for the approximate evolutionary distance between any two protein sequences under analysis. Obviously, this practice can cause an undue restriction if the evolutionary distance is too great within the protein dataset being aligned. The only assumption that we make with hydrophobicity and our new alignment algorithm5,6 is that nature will strongly tend to substitute similar amino-acids in order to preserve the overall function and structure of homologous proteins, and that it is possible to define a hydrophobicity distance to define a fuzzy match between any two amino-acids, which is recognized as a “similarity match.”
We summarize the salient points regarding alignment matrices with quotes from four select literature articles below.
1. “The most common substitution matrices currently used (BLOSUM and PAM) are based on protein sequences with average amino acid distributions, thus they do not represent a fully accurate substitution model for proteins characterized by a biased amino acid composition"39
2. “We have investigated patterns of amino acid substitution among homologous sequences from the three Domains of life and our results show that no single amino acid matrix is optimal for any of the datasets"40
3. “Many phylogenetic inference methods are based on Markov models of sequence evolution. These are usually expressed in terms of a matrix (Q) of instantaneous rates of change but some models of amino acid replacement, most notably the PAM model of Dayhoff and colleagues, were originally published only in terms of time-dependent probability matrices (P(t)). Previously published methods for deriving Q have used eigen-decomposition of an approximation to P(t). We show that the commonly used value of t is too large to ensure convergence of the estimates of elements of Q. We describe two simpler alternative methods for deriving Q from information such as that published by Dayhoff and colleagues"41.
4. These authors note another interesting problem with the residue substitutions rates use in the Q matrix: “Because different local regions such as binding surfaces and the protein interior core experience different selection pressures due to functional or stability constraints, we use our method to estimate the substitution rates of local regions. Our results show that the substitution rates are very different for residues in the buried core and residues on the solvent-exposed surfaces"42.
Tomii et al.9 essentially conclude that in the "evolutionary" limit, alignment/mutation matricies reflect the hydrophobcity and amino-acid secondary group size. For example, when the correlation coefficient between a hydrophobicity scale and a amino-acid secondary group size, and the PAM matricies are plotted against the PAM distance, the correlation coefficient monotonically increases from 0.58 at a PAM near zero, to a PAM distance of 200 where the correlation corefficient reaches an asymtotic limit of about 0.739
The amount of information available to an alignment algorithm is essential to its ability to find matching proteins, especially matches with remote homologies where the percentage identity has dropped off to around 20–25 %. In this study we have sought to find an optimal, central tendency hydrophobicity scale that would reflect the real properties of amino-acids within the context of folded proteins. We contend that hydrophobic proclivities transcend mere statistical trends and reflect the functional necessities of globular proteins by amino acid properties according to a solvent-solvent (water interior of a folded protein) partitioning model. Within this model the primary driving force is that of water-water attractions that exceed water-amino acid attractions. Hydrophobicity is not a force that repels amino acids from water, but rather that water molecules attract each other more. When hydrophobic amino acids are exposed to water, clathrate shells spontaneously form at those areas, creating an anchored aqueous patch of ordered water molecules with surface tension. Thus, the preferred hydrophobicity scale of hydrophobic proclivities as we have described here provides significant new information to alignment algorithms and in particular our TMATCH algorithm (described elsewhere)5,6, optimized to work with our hydrophobicity proclivity scale.
There are some issues in using water/non-polar solvent partitioning ratios as proxies for hydrophobicity, primarily regarding the standardization of water concentration within a non-polar solvent (miscible with water), particularly when that solvent is capable of hydrogen bonding. Uncontrolled or variable amounts of water dragged into the organic solvent phase by solutes in solvent/water solute partition experiments can cause significant variation within the calculated Gibbs free energies of transfer of the solute from one phase to the other. We also point out that solvent/water solute concentration ratios, used to calculate free energy of transfers from water to a non-polar phase, as a hydrophobicity measure relevant to protein folding, suffers from a systemic error if the organic solvent is incapable of hydrogen bonding, which is not the case within the hydrophobic “solvent like” core of folded globular proteins. Our hydrophobicity proclivity scale has no units, but rather is a normalized proclivity. We show in Figure 4 of the manuscript that our hydrophobicity proclivity scale is directly relatable to free energy of solvent-solvent transfer using a popular dGow (water to n-octanol) scale. We also point out that characterizing the amino-acid secondary groups alone does not treat the important contribution to the free energetic’s of folding by peptide bonds, such as is accounted for by some researchers by treating the 20 amino-acids as guests in the center of tri-peptides in octanol to water free energy studies.
There is a large profusion of hydrophobicity scales in the literature, which pose many difficulties in trying to numerically reflect the wide range of amino-acid behaviors, as well as the difficulties inherent in trying to define hydrophobicity as an experimentally measurable concept related to the driving forces of protein folding. We have relied upon other experimentally measured amino-acid properties to cross check our hydrophobicity proclivity scale using methods such as Multiple Linear Regression (Table 3). For example, we can draw a good linear correlation between certain hydrophobicity scales, such as our hydrophobicity proclivity scale, and amino-acid reverse phase (C18 column) HPLC retention times; to which we point out that other researchers have drawn similar conclusions. We believe that the difficulties of using water to non-polar solvent dG of transfer have been largely mitigated and obviated through the analytical procedures reported in this paper.
In the final analysis, we are showing that a robust, high performance hydrophobicity scale enshrines much more information that can be captured within substitutional rate matrices, particularly for remote homologous proteins were the assumption of constant aminoacid substitutional rates become invalid for various reasons. Our TMATCH5,6 algorithm is structured to leverage the extra information inherent in our hydrophobicity proclivity scale to reflect a global alignment capturing the secondary and super-secondary structure which lead to tertiary structure. The TMATCH5,6 algorithm transition weighting scheme automatically tends to capture areas of high local hydrophobic similarity, despite low having low percent identity, like would be captured in a dot plot algorithm.
DC arrived at the hydrophobicity index several years ago after an exhaustive look at the literature and through extensive regression analysis of several published values of amino acid properties in proteins and how they may contribute to the structure of proteins in solution. This paper is the result of a long collaborative effort with KC whose interests were also in understanding protein structure and search algorithms in bioinformatics.
We (DC and KKC) appreciate our discussions about proteins and their solution structure with Dr. Joseph Ng (Department of Biological Sciences) and Dr. John Shriver (Department of Chemistry) of University of Alabama in Huntsville.
| Views | Downloads | |
|---|---|---|
| F1000Research | - | - |
|
PubMed Central
Data from PMC are received and updated monthly.
|
- | - |
Is the work clearly and accurately presented and does it cite the current literature?
Partly
Is the study design appropriate and is the work technically sound?
Partly
Are sufficient details of methods and analysis provided to allow replication by others?
Yes
If applicable, is the statistical analysis and its interpretation appropriate?
I cannot comment. A qualified statistician is required.
Are all the source data underlying the results available to ensure full reproducibility?
No source data required
Are the conclusions drawn adequately supported by the results?
Partly
Competing Interests: No competing interests were disclosed.
Reviewer Expertise: Molecular dynamic simulations, transcriptomics
Competing Interests: No competing interests were disclosed.
References
1. Wolfenden R, Lewis CA, Yuan Y, Carter CW: Temperature dependence of amino acid hydrophobicities.Proc Natl Acad Sci U S A. 2015; 112 (24): 7484-8 PubMed Abstract | Publisher Full TextCompeting Interests: No competing interests were disclosed.
Alongside their report, reviewers assign a status to the article:
| Invited Reviewers | |||
|---|---|---|---|
| 1 | 2 | 3 | |
|
Version 2 (revision) 15 Oct 20 |
read | ||
|
Version 1 21 Oct 15 |
read | read | |
Provide sufficient details of any financial or non-financial competing interests to enable users to assess whether your comments might lead a reasonable person to question your impartiality. Consider the following examples, but note that this is not an exhaustive list:
Sign up for content alerts and receive a weekly or monthly email with all newly published articles
Already registered? Sign in
The email address should be the one you originally registered with F1000.
You registered with F1000 via Google, so we cannot reset your password.
To sign in, please click here.
If you still need help with your Google account password, please click here.
You registered with F1000 via Facebook, so we cannot reset your password.
To sign in, please click here.
If you still need help with your Facebook account password, please click here.
If your email address is registered with us, we will email you instructions to reset your password.
If you think you should have received this email but it has not arrived, please check your spam filters and/or contact for further assistance.
https://chemrxiv.org/authors/David_Cavanaugh/8853095
https://chemrxiv.org/authors/David_Cavanaugh/8853095