How to put plant root uptake into a soil water flow model

Xuejun Dong

doi:10.12688/f1000research.7686.2

Home Browse How to put plant root uptake into a soil water flow model

ALL Metrics

Views

Downloads

Get PDF

Get XML

Export

▬

✚

Method Article

Revised

How to put plant root uptake into a soil water flow model

[version 2; peer review: 2 approved, 1 approved with reservations]

Xuejun Dong^1,2

PUBLISHED 08 Aug 2022

Author details Author details

¹ North Dakota State University, Central Grassland Research Extension Center, Streeter, USA
² Texas A&M AgriLife Research, Uvalde, USA

Xuejun Dong
Roles: Conceptualization, Methodology, Writing – Original Draft Preparation, Writing – Review & Editing

OPEN PEER REVIEW

REVIEWER STATUS

This article is included in the Agriculture, Food and Nutrition gateway.

This article is included in the Plant Science gateway.

Abstract

The need for improved crop water use efficiency calls for flexible modeling platforms to implement new ideas in plant root uptake and its regulation mechanisms. This paper documents the details of modifying a soil infiltration and redistribution model to include (a) dynamic root growth, (b) non-uniform root distribution and water uptake, (c) the effect of water stress on plant water uptake, and (d) soil evaporation. The paper also demonstrates strategies of using the modified model to simulate soil water dynamics and plant transpiration considering different sensitivity of plants to soil dryness and different mechanisms of root water uptake. In particular, the flexibility of simulating various degrees of compensated uptake (whereby plants tend to maintain potential transpiration under mild water stress) is emphasized. The paper also describes how to estimate unknown root distribution and rooting depth parameters by the use of a simulation-based searching method. The full documentation of the computer code will allow further applications and new development.

Keywords

Computer simulation, Richards’ equation, Root growth, Soil water balance, Transpiration, Uptake compensation, Water stress

Corresponding author: Xuejun Dong

Competing interests: No competing interests were disclosed.

Grant information: This paper is part of North Dakota Agricultural Experiment Station project ND6149 and Texas A&M AgriLife Research Hatch project TEX09574, both funded by the USDA NIFA.
The funders had no role in study design, data collection and analysis, decision to publish, or preparation of the manuscript.

Copyright: © 2022 Dong X. This is an open access article distributed under the terms of the Creative Commons Attribution License, which permits unrestricted use, distribution, and reproduction in any medium, provided the original work is properly cited.

How to cite: Dong X. How to put plant root uptake into a soil water flow model [version 2; peer review: 2 approved, 1 approved with reservations]. F1000Research 2022, 5:43 (https://doi.org/10.12688/f1000research.7686.2) First published: 08 Jan 2016, 5:43 (https://doi.org/10.12688/f1000research.7686.1) Latest published: 08 Aug 2022, 5:43 (https://doi.org/10.12688/f1000research.7686.2)

Revised Amendments from Version 1

The major differences between this version of the article and the previously published version are reflected in (1) an update of Figure, (2) the addition of a sink term for root water uptake in all governing equations, including a further discussion of the contents related to the sink term, and (3) minor changes to correct a few typos and update on literature citations.

See the author's detailed response to the review by Hirotaka Saito
See the author's detailed response to the review by Jun Fan
See the author's detailed response to the review by Brijesh K Yadav

Introduction

Increased biomass and yield of agricultural crops hinges on improved efficiency of root water uptake^1,2. Biophysical mechanisms responsible for the improved uptake efficiency in turn rely on linkages between plant physiological processes and the physics of soil water movement; the development of the latter has been well illustrated in 3,4 and 5. Research literature in this and closely related areas has been profound in past decades, though roughly two categories of approach can be identified: one that is mechanistic and one that is phenomenological in nature. The mechanistic approach has improved our understanding of the soil-root interactions by identifying major resistances and driving forces of water flow from soil to roots^3,4, as well as the scale-dependent interactions and geometry among soil organisms responsible for water and nutrient uptake^6,7. Yet effective mechanistic modeling needs a large amount of empirical data support, which can not always be met due to various factors constraining research activities. On the other hand, an intuitive, phenomenological approach can be implemented with less empirical data support. Examples of this latter approach may include constraining root water uptake capacity by soil water potential⁸, by root length distribution^9–11, and through additional modifications of the root uptake sensitivity to local soil water potential and root density^12–16, which allows compensated uptake to maintain potential transpiration^17,18.

One of the major goals of agronomic management for increased water use efficiency is to channel water loss through transpiration¹⁹. This to some extent can be aided by the compensated root uptake, which has been implemented in software such as HYDRUS (http://www.pc-progress.com/en/Default.aspx?hydrus-1d) through the use of a threshold root uptake adaptation factor, whereby reduced water uptake in water-stressed parts of the root zone is fully compensated for by increased uptake in other soil regions where water is available²⁰.

However, root water uptake compensation has been implemented in different studies using different models, which naturally calls for the flexibility of implementation of various forms of the compensation mechanism in root uptake studies. The first objective of this paper is to show that this flexibility can be obtained by using a water flow model extended from an original model as described in 5. This extended model was used in generating numerical solutions of water flow problems in 16.

The second objective of this paper is to provide a tool for quantifying plant water uptake under conditions where information of root depth and distribution pattern is not known. This is relevant to agricultural applications as fine root information remains difficult to obtain despite the progress made in advanced underground sensing²¹. We take advantage of inverse modeling, similar to 22 and 10, to find optimal solutions of unknown root parameters based on good measurement of soil water content, which can be obtained through the use of various soil moisture sensors. Despite excellent documentation of the methods for solving the soil water flow equations relevant to agricultural water management^3,5, the author has not seen a paper documenting the details of how to put the root uptake component into a soil water flow model, as well as providing the details of a search-based optimization procedure for root parameter estimation. This article provides a further documentation of the methods as used in 16, with the focus of highlighting details related to the computer implementation of the numerical methods.

Methods

Implementation

The one dimensional Richards equation of soil water flow in a vegetated soil in the vertical direction can be written as

c \frac{\partial h}{\partial t} = \frac{\partial}{\partial z} [K \frac{\partial h}{\partial z}] - \frac{\partial K}{\partial z} - S (z, t), (1)

where h is water pressure head / soil matric potential (m), t is time (s), z space (m, positive downward and soil surface as zero), K hydraulic conductivity (m/s), and $c = \frac{\partial θ}{\partial h}$ soil water capacity, and S(z,t) the rate of plant root water uptake at location and time. The reason why there is a negative sign in Equation 1 is that, when we take the space derivative for the gravity potential head z, namely, in ∂z/∂z, the value in the numerator changes in the opposite direction as that in the denominator: gravity head always decreases downwards but our chosen space z increases downwards.

Equation 1 can be solved using the implicit finite difference method as described by 5. Here is a summary of key points with a few intuitive comments. Let’s for now assume surface fluxes as precipitation, irrigation, or surface evaporation. As Equation 1 considers soil water dynamics both in space (vertical axis) and time, we need to properly discretize the equation considering both space and time, in order to solve it numerically. Here we let all h’s that take space derivatives be approximated using values at the old (t) or the new time (t +1), but let K’s be approximated in old time (t). All other variables not taking partial derivatives are to be approximated in the old time. Assume the vertical axis is equally divided by Δz, to approximate Equation 1 at z = z_i and t_n+1 = t_n+Δt, we have the following formula to use:

\frac{c_{i, t} (h_{i}^{*} - h_{i, t})}{Δ t} = \frac{K_{i + 0.5, t} (h_{i + 1}^{*} - h_{i}^{*})}{{(Δ z)}^{2}} - \frac{K_{i - 0.5, t} (h_{i}^{*} - h_{i - 1}^{*})}{{(Δ z)}^{2}} - \frac{(K_{i + 0.5, t} - K_{i - 0.5, t})}{Δ z} - S_{i, t}, (2)

where S_i,t refers to the root water uptake occurring at the ith block at current time t. In 16, S_i,t was calculated as

S_{i, t} = \frac{α (h_{i, t}) T_{t} (β + 1) {(1 - z_{i} / L_{t})}^{β}}{86400000 L_{t}}, (3)

where α(h_i,t) (dimensionless) is the reduction factor of root uptake as a function of soil water potential at location i and time t, T_t and L_t are potential transpiration (mm/day) and root depth (m) at time t, z_i is the vertical coordinate (m), and β is an empirical factor determining vertical distribution of root length density according to 12. The factor of 86400000 was used to ensure the unit of S_i,t is second^-1 (there are 86400 seconds in one day and one meter is equivalent to 1000 mm).

In Equation 2, soil matric potential at the new time (t+1) is indicated using a star as superscript. One interesting aspect of Equation 2 is that the space index for K is shifted to the upper edge of each of the blocks, while the index of h or θ is located at the center of the blocks (Figure 1). This is the characteristic of the block-centered finite difference scheme and it will enable the calculation of fluxes between two adjacent soil layers, or blocks, as seen in the right sub-figure of Figure 1, which is based on Figure 5–13 of Warrick’s book (on page 195). In Figure 1, we reinforce the idea that, similar to the situation of conductivity, K, the index for flux density also is located at the edge of the blocks. Intuitively, this makes sense, because in the head-based equation of soil water flow, K and J have the same unit (both are in m/s). As a result, we can compare the magnitude of K and J directly. For example, if the water conductivity of the surface soil is similar to the rate of precipitation, we can roughly say that all the rainwater would have time to fully infiltrate into the soil before ponding on the soil surface.

Figure 1. Block-centered finite difference scheme for numerical solution of 1-D Richards equation with plant root water uptake.

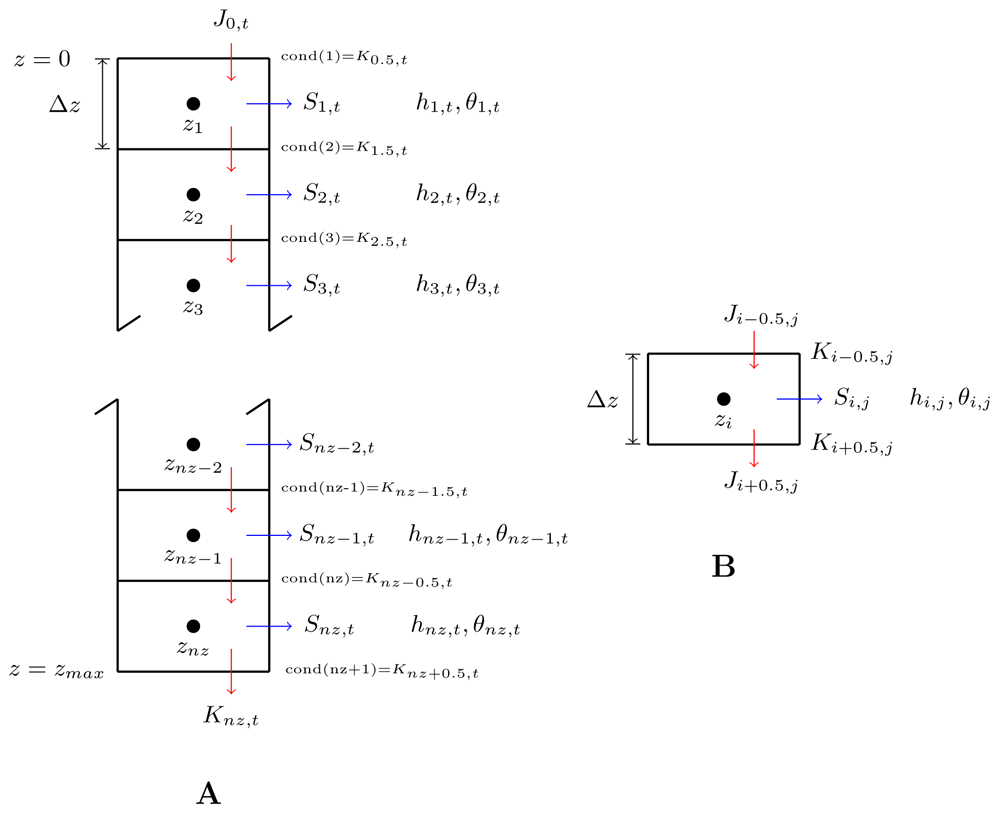
(A). A profile of soil of z_max m deep is vertically divided into nz layers, each of which is Δz m thick. Each layer is considered as one block in the finite difference scheme and its center is marked by a solid black dot. Pressure heads (h) and water content (θ) of each of the blocks are indexed at the center while water conductivities (cond() or K) and fluxes (J)-shown as downward red arrows, which in reality may also go upward- are indexed at the top and bottom edges. The blue arrows indicate the fluxes of root water uptake, if any, from different blocks. Note for variables with two subscripts, the first one indicates the space coordinate while the second one the time coordinate. B. Highlight of one internal block. Modified based on Figure 5–13 of 5.

The terms of Equation 2 can be collected to form a tridiagonal system of linear equations, with the water potentials for the new time (starred) arranged at the left side and those for the old time on the right side of the equation. Then, terms for different space segments can be collected to form the following equation:

A_{i} h_{i - 1}^{*} + B_{i} h_{i}^{*} + C_{i} h_{i + 1}^{*} = D_{i}, i = 1, \dots, n z, (4)

which can be written in matrix form as

[\begin{array}{l} B_{1} & C_{1} & 0 & \dots & 0 & 0 & 0 \\ A_{2} & B_{2} & C_{2} & \dots & 0 & 0 & 0 \\ ⋮ & ⋮ & ⋮ & ⋱ & ⋮ & ⋮ & ⋮ \\ 0 & 0 & 0 & \dots & A_{n z - 1} & B_{n z - 1} & C_{n z - 1} \\ 0 & 0 & 0 & \dots & 0 & A_{n z} & B_{n z} \end{array}] \times [\begin{array}{l} h_{1}^{*} \\ h_{2}^{*} \\ ⋮ \\ h_{n z - 1}^{*} \\ h_{n z}^{*} \end{array}] = [\begin{array}{l} D_{1} \\ D_{2} \\ ⋮ \\ D_{n z - 1} \\ D_{n z} . \end{array}] (5)

Equation 5 is called tridiagonal because, for the coefficients of the nz by nz square matrix, the elements are all zero except for those located along the three main diagonals. From Equation 5, we can see that A₁ = C_nz = 0. Actually, values of the coefficients on the left side of Equation 5 should be determined considering the boundary conditions at the soil surface and at the bottom of the root zone. Equation 5 can be solved numerically using the Thomas algorithm (summarized in Table 5–6 of 5, page 191).

The complete coefficients of the tridiagonal system of the Richards’ equation without a root water uptake sink were summarized in Table 5–7 of 5 (page 194). When the root uptake is considered, as in Equation 2, it turns out that only the D_i terms for various upper boundary conditions need to be changed, while other terms (i.e., A_i, B_i, and C_i) remain the same as in Table 5–7 of 5. Specifically, the D_i terms for different nodes (or blocks as shown in Figure 1) with root water uptake are shown below:

For internal nodes (i=2, …, nz–1):

D_{i} = \frac{c_{i, t} h_{i, t}}{Δ t} - \frac{(K_{i + 0.5, t} - K_{i - 0.5, t})}{Δ z} - S_{i, t} . (6)

For upper node with J(0,t):

D_{1} = \frac{c_{1, t} h_{1, t}}{Δ t} - \frac{(J (0, t) - K_{1.5, t})}{Δ z} - S_{1, t} . (7)

For upper node with h(0,t):

D_{1} = \frac{c_{1, t} h_{1, t}}{Δ t} - \frac{(K_{1.5, t} - K_{0.5, t})}{Δ z} + \frac{K_{0.5, t} h (0, t)}{{(Δ z)}^{2}} - S_{1, t} . (8)

For lower node with unit hydraulic gradient:

D_{n z} = \frac{c_{n z, t} h_{n z, t}}{Δ t} - \frac{(K_{n z, t} - K_{n z - 0.5, t})}{Δ z} - S_{n z, t} . (9)

After pressure heads for the new time (h^*’s) are computed using the Thomas algorithm, the flux of water between each pair of two neighboring blocks can be computed. However, to update the water content of the ith block, the following equation is used:

θ_{i}^{*} \approx θ_{i, t} - \frac{Δ t (J_{i + 0.5}^{*} - J_{i - 0.5}^{*})}{Δ z} - Δ t S_{i, t}, i = 1, \dots, n z . (10)

To meet the requirement of mass balance, the water content of the ith block at the new time ( $θ_{i}^{*}$ ) is caused by (1) the original water content at the previous time step (θ_i,t), (2) the contribution from the adjacent upper block $(+ \frac{Δ t}{Δ z} J_{i - 0.5}^{*})$ during the time step from the old time to the new time, (3) the contribution from the adjacent lower block $(− \frac{Δ t}{Δ z} J_{i + 0.5}^{*})$ , and (4) the contribution due to plant water extraction (–ΔtS_i,t). So, the water balance requires that

\begin{array}{l} θ_{i}^{*} \approx θ_{i, t} + \frac{Δ t}{Δ z} J_{i - 0.5}^{*} - \frac{Δ t}{Δ z} J_{i + 0.5}^{*} - Δ t S_{i, t} \\ = θ_{i, t} - \frac{Δ t (J_{i + 0.5}^{*} - J_{i - 0.5}^{*})}{Δ z} - Δ t S_{i, t}, \end{array} (11)

where i =1, …, nz. To understand why some terms are positive and others are negative in Equation 11, we need to keep in mind (1) the mass conservation of the ith block (see Figure 1B), and (2) our choice of the vertical axis (downwards positive). For example, if the flux across the lower edge of the ith block is upward in direction, i.e., $J_{i + 0.5}^{*}$ is negative (because the upward direction is against our positive z axis), then the corresponding term in Equation 11 becomes positive. This is reasonable because an upward flux from the lower edge will add water to the ith block (again, see Figure 1B). Finally, the reason why there is a Δt in the sink term is that by multiplying S_i,t with Δt, we get a soil water content (since the unit of S_i,t is T^–1).

Detailed solution procedures of the above model “Austere-Layered" (hereafter referred to as AL.f) are provided in 5. Here in order to let this soil water flow model simulate root uptake, the following new components have been added: (a) dynamic root growth, (b) non-uniform root distribution and water uptake, (c) effect of water stress on plant water uptake, and (d) soil evaporation. Following Warrick’s original model, the extended model (ALS.f) was also programmed using Fortran 77. See https://zenodo.org/record/42663. To facilitate further development, variables (array variables and non-array variables) used in the original program AL.f, as well the extended program ALS.f, are listed in 23 (in four tables). The subroutine SINK() in ALS.f encapsulates various options for root uptake mechanisms. Similar to some other external subroutines, such as THOMAS(), variables inside the subroutine are local, so that they are not listed in the tables of 23. In the following we document major changes made to the program ALS.f:

Modeling water flow in variably saturated soil

The model AL.f was modified to include the flux update scheme proposed by 24 and was applied in program a2&3.for of 5. The main idea is summarized in the following (variables referred to are included in ALS.f):

• Assume we use the flux upper boundary condition (B_TYPE= 2). At each new time step, the old hydraulic conductivities and soil water capacities are used to find the needed coefficients for solving the tridiagonal system of equations. However, the surface flux is temporarily not considered (C2=0). Then, these coefficients are provided to the Thomas subroutine to find the updated pressure head (HSTAR). The trial soil water content at the new time (THETA) is found using the newly computed conductivities based on values of HSTAR as well as the surface flux.
• The trial value of THETA is accepted only if the soil water content at a depth interval, or that for intervals immediately adjacent to this current depth interval, is unsaturated. In such a case, the soil water retention curve is used to update the new pressure head H based on the trial value of THETA.
• Otherwise, the trial value of THETA is rejected, the value of HSTAR is accepted as the updated value for H, and the updated THETA is computed from the soil water retention curve based on HSTAR.

Testing different ending soil water potentials for optimal root uptake

Detailed information regarding the root uptake sink term is included in 23. In particular, Equation 1 of 23 illustrates the importance of four water pressure heads for root uptake: h₁ marks the anaerobiosis point; h₄ the pressure head at permanent wilting point, and h₂ and h₃ marks the range of pressure head for optimal root uptake (see Figure 3 of reference 16). Here we refer to h₃ as the ending water potential for optimal uptake, because root uptake starts to reduce when the soil water potential becomes lower than this point. As different plants might have different sensitivity to a mild water stress, it is useful to test the model’s sensitivity to h₃.

Following 14 and 25, h₃ may be assumed as $h_{3}^{1} = - 11 m$ for a slow transpiration of $T_{p}^{1} = 1 {mm day}^{- 1}$ and $h_{3}^{2} = - 5 m$ for a fast transpiration of $T_{p}^{2} = 5 {mm day}^{- 1} .$ We tested two more possibilities of the h₃ values, namely, $(h_{3}^{1}, h_{3}^{2}) = (- 14, - 8) m,$ and $(h_{3}^{1}, h_{3}^{2}) = (- 16, - 10),$ for $(T_{p}^{1}, T_{p}^{2}) = (1, 5) mm {day}^{- 1} .$ We also assumed that h₃ changed in a linear fashion for intermediate transpiration rates between $T_{p}^{1} = 1$ and $T_{p}^{2} = 5 {mm day}^{- 1}),$ using different $h_{3}^{1}$ and $h_{3}^{2}$ values:

h_{3} = a T_{p} + h_{3}^{1} - a T_{p}^{1}, (12)

where $a = (h_{3}^{1} - h_{3}^{2}) / (T_{p}^{1} - T_{p}^{2}) .$ This change is reflected in the new subroutine HTHREE, as shown in ALS.f. This (Equation 12) is another form of Equation 2 of 23 but with variable $h_{3}^{1}$ and $h_{3}^{2}$ , as shown in Equation 6 of 16.

Testing different functions for root water uptake

The extended program ALS.f also allows for testing different root uptake functions with or without compensation mechanisms, such as those demonstrated in 14,15,26. In particular, in subroutine SINK(), the model of 12 is used when ICPS= 1; a function of 9 is used when ICPS= 3; and the compensation function of 14 (in combination with Wu’s function) is used when ICPS= 2. The normalized root density function (L_nrd) of 9 has four parameters:

L_{n r d} (z_{r}) = R_{1} + R_{2} z_{r} + R_{3} z_{r}^{2} + R_{4} z_{r}^{3}, (13)

where z_r = z/Z_r(t) is the normalized root density at time t with Z_r(t) the maximum rooting depth (m) at time t. The coefficients R₁ through R₄ represent experimentally fitted values for wheat, with R₁ = 2.21, R₂ = -3.72, R₃ = 3.46, and R₄ = -1.87 according to 9. The compensation function of 14 and 15 at time t has the following form:

S_{i} = \frac{α_{i}^{2} L_{n r d, i}^{λ} T_{p}}{Δ z_{i} \sum_{i = 1}^{n} α_{i} L_{n r d, i}^{λ}}, (14)

where S_i is the actual water uptake from ith soil depth increment, α_i is the reduction function for this ith depth increment, L_nrd,i the normalized root density function for the ith depth increment, Δz_i the thickness (m) of the ith depth increment, and λ is a fitting parameter varying from 0.01 to 2.0 according to 14.

Details of simulation-based searching program

In order to cope with situations in which the information of rooting depth and root distribution pattern is unknown, the program ALS.f was converted into a subroutine and is callable by a searching main program, ALSS.f, which is available at https://zenodo.org/record/42702. This conversion was quite straight forward in Fortran 77 in that we only did three things: (a) we deleted parameters BETA and ZRMAX from the parameter listing; (b) we converted the program ALS.f from a main program to a subroutine using 2 input dummy variables BETA and ZRMAX and 7 output dummy variables; and (c) we let this subroutine be called multiple times using different values of true BETA and true ZRMAX from arrays BETAS() and ZRMAX() within the main program unit and made sure that only the values of selected 7 variables were returned to the main program but all the other information from within the subroutine ALS() is lost after each run.

Operation

The provided two Fortran programs, ALS.f and ALSS.f, can be run using one of the freely available compilers, such as g95 (http://www.g95.org/), gFortran under mingw-w64 (https://www.mingw-w64.org/), or gFortran under Cygwin (https://www.cygwin.com/), the latter of which mimics Unix commands on a Windows computer.

To run ALS.f and ALSS.f, the following input information is needed (see 23):

• Soil physical properties and in particular soil water retention curve and saturated hydraulic conductivity. The exact format of data structure is shown in the supplementary data file ALS.DAT, which follows the template provided by 5. A method for predicting soil water retention curves based on easily measured soil texture and bulk density data is illustrated in 27.
• Initial soil water content profile. This must be provided and put to exact format as shown in supplementary data file INITF.DAT, following the template provided by 5. The measured soil water content must be interpolated so that every depth increment of soil has a water content value in it. One method of data interpolation is outlined in 16 using routines provided in 28 and 29.
• Measured terminating soil water content. This can be the measured soil water content on last day of simulation and must be entered in the format as shown in TERMF.DAT of 23. No interpolation is needed for this file.
• Daily weather data. Daily evapo-transpiration rate, daily average air temperature, daily rainfall, relative humidity, as well as leaf area index, must be entered in data file WEA2.DAT in the order as shown in the data file. Daily leaf area index can be interpolated based on field measured values, as shown in 16.

There are four output files from ALS.f²³:

• OUTS.DAT – Mirrors output from AL.f of 5.
• OUTS2.DAT – Daily soil water potential and water contents for interested soil depths.
• INFS.DAT – Mirrors output from AL.f of 5.
• WUE.DAT – Summary of daily cumulative water loss.

There are seven output files from ALSS.f. They provide the following information based on particular realization of combinations of root distribution shape factor BETAS and the maximum rooting depth ZRMAXS²³:

• ARD.DAT – Average relative discrepancy between measured and simulated soil water content throughout the simulation period.
• C_AEVA.DAT – Cumulative soil evaporation throughout the simulation period.
• C_ATRA.DAT – Cumulative transpiration throughout the simulation period.
• WBELOW.DAT – Amount of water to deep drainage out of the specified root zone. This was inherited from AL.f
• WADD.DAT – Amount of water added to the system. This was also inherited from AL.f
• BIGI.DAT – Cumulative infiltration. This was also inherited from AL.f
• PCTDIF.DAT – Percent difference in water balance, defined in 5 as (BIGI-WADD)/WADD*100.

The main difference between the output files of ALS.f and those of ALSS.f is that the outputs from the former are a summary of water balance from the simulation of soil water balance based on one set of root parameters (rooting depth and shape factors), while those from the latter (ALSS.f) contain the simulation outcomes using many sets of root parameters (see next section for further details).

Use cases

Programs ALS.f and ALSS.f in their current forms were customized to simulate the soil water dynamics for 111 days from May 14 to September 1, 2009 in a mixed-grass prairie ecosystem¹⁶. The model was also applied to simulate soil water dynamics of a same grassland under long-term heavy grazing by cattle³⁰. This is reflected both in the programs and the input data files. To use the model in other locations and other durations, appropriate changes must be made both in a few parameters of the programs and input data files. The two potential uses of the programs are outlined in the following:

• If root distribution parameter BETA and maximum rooting depth ZRMAX are known, then program ALS.f may be used to simulate soil water dynamics with root uptake. Make sure to provide updated values for the major parameter values, such as JMATUR (Julian day number of growth maturity), JTHAW (Julian day number of growth initiation), BETA, and ZRMAX.
• If root distribution parameter BETA and maximum rooting depth ZRMAX are unknown, then it is recommended to first use ALSS.f to find the optimal values for BETA and ZRMAX before using ALS.f to simulate soil water dynamics. Before running ALSS.f, three things must be done:
- 1. Check to see if the current value of h₃ (see Equation 1 of 23) is correct by changing, if necessary, the value of parameter IHTH (current default value is set to 1, meaning $(h_{3}^{1}, h_{3}^{2}) = (- 11, - 5)) .$ See the preamble of subroutine SINK() for two other options.
- 2. Check to see if the parameter of ICPSN is correctly specified. Currently, the default value is 1, meaning to use Ojha’s compensation function. Setting the value of ICPSN to 2 will switch to Li-Yadav’s compensation function, and a value of 3 will invoke Wu’s uptake function (without compensation).
- 3. Check the nested DO LOOPs structure to adjust the admissible values for index variable II (currently it is set to have 16 different values for BETA) and JJ (currently it is set to have 22 different values for ZRMAX). At the same time, the following lines in the main program of ALSS.f must be changed to be compatible with the range of index values in the nested DO LOOPS.
```
BETAS(1)=0.5
DO I=1,15
  BETAS(I+1)=BETAS(I)+0.25
END DO

ZRMAXS(1)=0.75
DO I=1,21
  ZRMAXS(I+1)=ZRMAXS(I)+0.05
END DO
```
• Finally, it is recommended to put both the program files and the required input data files in the same folder before running the programs.

Summary

While plant root water uptake has been implemented in commercial software packages, very few researchers have found the time to document important details of how root uptake can be included in a soil water flow model. This paper tries to fill this knowledge gap by using a simple computer program aided with sample input data sets. Specifically, we modified and extended a soil water flow model of 5 to include plant root water uptake capability. We showed that the extended program has the flexibility of considering different sensitivity of root uptake, as well as different water uptake mechanisms. We also modified the model to search for optimal root parameters based on measured soil water content data. This is relevant for new application in that field data of root development usually is expensive and sometimes difficult to obtain, and the utilization of a searching-based modeling approach will help to identify root parameters for improved water balance characterization, which in turn may help to identify ways to improve crop water use efficiency under field conditions. No menu-driven user interface is provided but the author believes that, under some circumstances of knowledge discovery, it is more efficient to work directly with a well-structured computer program, such as the one described in this paper, than relying on a packaged one.

Data availability

Underlying data

No data are associated with this article

Extended data

Three supplemental data files available from: https://doi.org/10.5281/zenodo.6958793

- Supplementary material 1. Definition of variables used in the computer programs ALS.f.

This file contains four tables documenting the variables used in AL.f (Supplementary Tables 1 and 3) and those added in ALS.f (Supplementary Tables 2 and 4).

- Supplementary material 2. More details about the root uptake term.

This file documents details of the water uptake term as used in the extended Fortran program ALS.f. It is useful for those who are curious about how the water extraction term is specified in the model

- Supplementary material 3. Data files for ALS.f and ALSS.f.

This includes (a) four input data files common to ALS.f and ALSS.f, (b) four Output files from ALS.f (OUTS.DAT, OUTS2.DAT, INFS.DAT, WUE.DAT), (c) seven output files from ALSS.f (ARD.DAT, C_AEVA.DAT, C_ATRA.DAT, WBELOW.DAT, WADD.DAT, BIGI.DAT, PCTDIF.DAT).

Data are available under the terms of the Creative Commons Attribution 4.0 International license (CC-BY 4.0).

Software availability

ALS.f is available from: https://zenodo.org/record/42663

ALSS.f is available from: https://zenodo.org/record/42702

ALS.f archived source code as at the time of publication: http://dx.doi.org/10.5281/zenodo.42663³¹

ALSS.f archived source code as at the time of publication: http://dx.doi.org/10.5281/zenodo.42702³²

License: Academic free license ("AFL") v.3.0 http://opensource.org/licenses/afl-3.0.php

Acknowledgments

The author thanks Bob Patton, Paul and Anne Nyren and Lyle Prunty at North Dakota State University for fruitful collaboration leading to this paper.

Faculty Opinions recommended

References

1. Campbell GS, Diaz R: Simplified soil-water balance models to predict crop transpiration. In F. R. Bidinger and C. Johansen, editors, Drought research priorities for the dryland tropics. International Crops Institute for the Semi-Arid Tropics, Parancheru, A. P. 502 324, India, 1988; 15–26. Reference Source
2. Passioura JB, Angus JF: Improving productivity of crops in water-limited environments. In D. L. Sparks, editor, Advances in Agronomy. Elsevier Science, USA, 2010; 106: 37–75. Publisher Full Text
3. Campbell GS: Soil Physics with Basic: Transport Models for Soil–Plant Systems. Developments in Soil Science 14. Elsevier, New York, 1985. Reference Source
4. Hopmans JW, Bristow KL: Current capabilities and future needs of root water and nutrient uptake modeling. In D. L. Sparks, editor, Advances in Agronomy. Elsevier Science, USA, 2002; 77: 103–183. Publisher Full Text
5. Warrick AW: Soil Water Dynamics. Oxford University Press, 2003. Reference Source
6. Roose T, Schnepf A: Mathematical models of plant-soil interaction. Philos Trans A Math Phys Eng Sci. 2008; 366(1885): 4597–4611. PubMed Abstract | Publisher Full Text
7. Leitner D, Schnepf A, Klepsch S, et al.: Comparison of nutrient uptake between three-dimensional simulation and an averaged root system model. Plant Biosystem. 2010; 144(2): 443–447. Publisher Full Text
8. Feddes RA, Kowalik PJ, Zaradny H: Simulation of field water use and crop yield. Center for Agricultural Publishing and Documentation, Wageningen, The Netherlands, 1978. Reference Source
9. Wu J, Zhang R, Gui S: Modeling soil water movement with water uptake by roots. Plant Soil. 1999; 215(1): 7–17. Publisher Full Text
10. Zuo Q, Zhang R: Estimating root-water-uptake using an inverse method. Soil Sci. 2002; 167(9): 561–571. Publisher Full Text
11. Zuo Q, Jie F, Zhang R, et al.: A generalized function of wheat’s root length density distributions. Vadose Zone J. 2004; 3: 271–277. Reference Source
12. Ojha CS, Rai AK: Nonlinear root water uptake model. J Irrig Drain Eng. 1996; 122(4): 198–201. Publisher Full Text
13. Adiku SG, Rose CW, Braddock RD, et al.: On the simulation of root water extraction: examination of a minimum energy hypothesis. Soil Sci. 2000; 165(3): 226–236. Publisher Full Text
14. Li KY, De Jong R, Boisvert JB: An exponential root water uptake model with water stress compensation. J Hydrol. 2001; 252(1–4): 189–204. Publisher Full Text
15. Yadav BK, Mathur S, Siebel MA: Soil moisture dynamics modeling considering the root compensation mechanism for water uptake by plants. J Hydrol Eng. 2009; 14(9): 913–922. Publisher Full Text
16. Dong X, Patton BD, Nyren AC, et al.: Quantifying root water extraction by rangeland plants through soil water modeling. Plant Soil. 2010; 335(1): 181–198. Publisher Full Text
17. Heinen M: Compensation in root water uptake models combined with three-dimensional root length density distribution. Vadose Zone J. 2014; 13(2). Publisher Full Text
18. Verma P, Loheide SP, Eamus D, et al.: Root water compensation sustains transpiration rates in an Australian woodland. Adv Water Resour. 2014; 74: 91–101. Publisher Full Text
19. Bodner G, Nakhforoosh A, Kaul HP: Management of crop water under drought: A review. Agron Sustain Dev. 2015; 35(2): 401–442. Publisher Full Text
20. Simunek J, Hopmans JW: Modeling compensated root water and nutrient uptake. Ecol Model. 2009; 220(4): 505–521. Publisher Full Text
21. Jayawickreme DH, Jobbágy EG, Jackson RB: Geophysical subsurface imaging for ecological applications. New Phytol. 2014; 201(4): 1170–1175. PubMed Abstract | Publisher Full Text
22. Musters PA, Bouten W: A method for identifying optimum strategies of measuring soil water contents for calibrating a root water uptake model. J hydrol. 2000; 227(1–4): 273–286. Publisher Full Text
23. Dong X: Supplemental data for “How to put plant root uptake into a soil water flow model”. Zenodo. 2022. http://www.doi.org/10.5281/zenodo.6958793
24. Kirkland MR, Hills RG, Wierenga PJ: Algorithms for solving Richards’ equation for variably saturated soils. Water Resour Res. 1992; 28(8): 2049–2058. Publisher Full Text
25. Yang D, Zhang T, Zhang K, et al.: An easily implemented agro-hydrological procedure with dynamic root simulation for water transfer in the crop-soil system: validation and application. J Hydrol. 2009; 370(1–4): 177–190. Publisher Full Text
26. Lai CT, Katul G: The dynamic role of root-water uptake in coupling potential to actual transpiration. Adv Water Resour. 2000; 23(4): 427–439. Publisher Full Text
27. Dong X, Patton BD: Predicting soil water retention curves based on particle-size distribution using a Minitab macro. Afr J Soil Sci. 2015; 3(1): 079–085. Reference Source
28. Doughty S: Solve It: Computer Aided Mathematics for Science and Engineering. Gulf Publishing Company, 1995. Reference Source
29. Hanna OT, Sandall OC: Computational Methods in Chemical Engineering. Prentice Hall PTR, 1995. Reference Source
30. Dong X, Patton BD, Nyren PE: Responses of plant root and soil microbial respiration to seasonal rain events in a mixed-grass prairie under different grazing intensities. In G.-S. Zhou, editor, International Symposium on Adaptation of Terrestrial Ecosystems to Climate Change and Future Earth. Hubei Hotel, Beijing, China, Institute of Botany, Chinese Academy of Sciences, 2013; 148–158. Reference Source
31. Dong X: A plant root water uptake model. Zenodo. 2015. http://www.doi.org/10.5281/zenodo.42663
32. Dong X: A program for searching optimal root parameters in plant water uptake modeling. Zenodo. 2015. http://www.doi.org/10.5281/zenodo.42702

Comments on this article Comments (0)

Version 2

VERSION 2 PUBLISHED 08 Jan 2016

Author details Author details

¹ North Dakota State University, Central Grassland Research Extension Center, Streeter, USA
² Texas A&M AgriLife Research, Uvalde, USA

Xuejun Dong
Roles: Conceptualization, Methodology, Writing – Original Draft Preparation, Writing – Review & Editing

Competing interests

No competing interests were disclosed.

Grant information

This paper is part of North Dakota Agricultural Experiment Station project ND6149 and Texas A&M AgriLife Research Hatch project TEX09574, both funded by the USDA NIFA.
The funders had no role in study design, data collection and analysis, decision to publish, or preparation of the manuscript.

Article Versions (2)

version 2

Revised

Published: 08 Aug 2022, 5:43

https://doi.org/10.12688/f1000research.7686.2

version 1

Published: 08 Jan 2016, 5:43

https://doi.org/10.12688/f1000research.7686.1

© 2022 Dong X. This is an open access article distributed under the terms of the Creative Commons Attribution License, which permits unrestricted use, distribution, and reproduction in any medium, provided the original work is properly cited.

Download

Export To

metrics

	Views	Downloads
F1000Research	-	-
PubMed Central Data from PMC are received and updated monthly.	-	-

Citations

SEE MORE DETAILS

CITE

how to cite this article

Dong X. How to put plant root uptake into a soil water flow model [version 2; peer review: 2 approved, 1 approved with reservations]. F1000Research 2022, 5:43 (https://doi.org/10.12688/f1000research.7686.2)

NOTE: If applicable, it is important to ensure the information in square brackets after the title is included in all citations of this article.

track

receive updates on this article

Track an article to receive email alerts on any updates to this article.

Open Peer Review

Current Reviewer Status: ?

Key to Reviewer Statuses VIEW HIDE

ApprovedThe paper is scientifically sound in its current form and only minor, if any, improvements are suggested

Approved with reservations A number of small changes, sometimes more significant revisions are required to address specific details and improve the papers academic merit.

Not approvedFundamental flaws in the paper seriously undermine the findings and conclusions

Version 1

VERSION 1

PUBLISHED 08 Jan 2016

Views

Reviewer Report 11 Nov 2016

Hirotaka Saito, Graduate School of Agriculture, Tokyo University of Agriculture and Technology, Fuchu, Japan

Approved

https://doi.org/10.5256/f1000research.8276.r16853

CITE

Report a concern

Author Response 07 Sep 2022

Xuejun Dong, North Dakota State University, Central Grassland Research Extension Center, Streeter, USA

07 Sep 2022

Author Response

Thanks for the encouraging comments; your suggestions are accepted. I inspected references #14 and #15 and made corrections about the source of Eqn (14). In this case, I think both ... Continue reading Thanks for the encouraging comments; your suggestions are accepted. I inspected references #14 and #15 and made corrections about the source of Eqn (14). In this case, I think both #14 and #15 should be acknowledged, since they provide different insights to the same problem.
I added the sink term to all governing equations. Also, a clear figure has been provided to replace the blurred Figure 1 in the previous submission.
Thanks for the encouraging comments; your suggestions are accepted. I inspected references #14 and #15 and made corrections about the source of Eqn (14). In this case, I think both #14 and #15 should be acknowledged, since they provide different insights to the same problem.
I added the sink term to all governing equations. Also, a clear figure has been provided to replace the blurred Figure 1 in the previous submission.
Competing Interests: No competing interests were disclosed. Close
Report a concern
Respond or Comment

COMMENTS ON THIS REPORT

Author Response 07 Sep 2022

Xuejun Dong, North Dakota State University, Central Grassland Research Extension Center, Streeter, USA

07 Sep 2022

Author Response

Thanks for the encouraging comments; your suggestions are accepted. I inspected references #14 and #15 and made corrections about the source of Eqn (14). In this case, I think both ... Continue reading Thanks for the encouraging comments; your suggestions are accepted. I inspected references #14 and #15 and made corrections about the source of Eqn (14). In this case, I think both #14 and #15 should be acknowledged, since they provide different insights to the same problem.
I added the sink term to all governing equations. Also, a clear figure has been provided to replace the blurred Figure 1 in the previous submission.
Thanks for the encouraging comments; your suggestions are accepted. I inspected references #14 and #15 and made corrections about the source of Eqn (14). In this case, I think both #14 and #15 should be acknowledged, since they provide different insights to the same problem.
I added the sink term to all governing equations. Also, a clear figure has been provided to replace the blurred Figure 1 in the previous submission.
Competing Interests: No competing interests were disclosed. Close
Report a concern

Views

Reviewer Report 24 Oct 2016

Jun Fan, Institute of Soil and Water Conservation, Northwest A&F University, Yangling, China

Approved with Reservations

https://doi.org/10.5256/f1000research.8276.r11894

CITE

Report a concern

Author Response 07 Sep 2022

Xuejun Dong, North Dakota State University, Central Grassland Research Extension Center, Streeter, USA

07 Sep 2022

Author Response

Thanks for the insightful comments! Yes, I agree it is not a typical research paper, but one documenting methodical details of a previously published paper. The dynamics of root and ... Continue reading Thanks for the insightful comments! Yes, I agree it is not a typical research paper, but one documenting methodical details of a previously published paper. The dynamics of root and LAI growth are considered in the model, although not in a mechanistic manner in which the growth of roots and leaves are dynamically linked to the local weather and soil water availability. Again, the focus is on describing in detail the computer implementation procedure, along with explanation of important concepts, but lacks a direct comparison with other published models. As noted above, I hope the further comparisons can be achieved in future work.
Thanks for the insightful comments! Yes, I agree it is not a typical research paper, but one documenting methodical details of a previously published paper. The dynamics of root and LAI growth are considered in the model, although not in a mechanistic manner in which the growth of roots and leaves are dynamically linked to the local weather and soil water availability. Again, the focus is on describing in detail the computer implementation procedure, along with explanation of important concepts, but lacks a direct comparison with other published models. As noted above, I hope the further comparisons can be achieved in future work.
Competing Interests: No competing interests were disclosed. Close
Report a concern
Respond or Comment

COMMENTS ON THIS REPORT

Author Response 07 Sep 2022

Xuejun Dong, North Dakota State University, Central Grassland Research Extension Center, Streeter, USA

07 Sep 2022

Author Response

Thanks for the insightful comments! Yes, I agree it is not a typical research paper, but one documenting methodical details of a previously published paper. The dynamics of root and ... Continue reading Thanks for the insightful comments! Yes, I agree it is not a typical research paper, but one documenting methodical details of a previously published paper. The dynamics of root and LAI growth are considered in the model, although not in a mechanistic manner in which the growth of roots and leaves are dynamically linked to the local weather and soil water availability. Again, the focus is on describing in detail the computer implementation procedure, along with explanation of important concepts, but lacks a direct comparison with other published models. As noted above, I hope the further comparisons can be achieved in future work.
Thanks for the insightful comments! Yes, I agree it is not a typical research paper, but one documenting methodical details of a previously published paper. The dynamics of root and LAI growth are considered in the model, although not in a mechanistic manner in which the growth of roots and leaves are dynamically linked to the local weather and soil water availability. Again, the focus is on describing in detail the computer implementation procedure, along with explanation of important concepts, but lacks a direct comparison with other published models. As noted above, I hope the further comparisons can be achieved in future work.
Competing Interests: No competing interests were disclosed. Close
Report a concern

Views

Reviewer Report 04 Feb 2016

Brijesh K Yadav, Department of Hydrology, Indian Institute of Technology Roorkee, Roorkee, India

Approved

https://doi.org/10.5256/f1000research.8276.r11896

CITE

Report a concern

Author Response 07 Sep 2022

Xuejun Dong, North Dakota State University, Central Grassland Research Extension Center, Streeter, USA

07 Sep 2022

Author Response

Thank you for the interesting comments! This paper attempts to provide a further documentation to an earlier paper by Dong et al. (Plant and Soil, 335:181-198, 2010). The focus is ... Continue reading Thank you for the interesting comments! This paper attempts to provide a further documentation to an earlier paper by Dong et al. (Plant and Soil, 335:181-198, 2010). The focus is on providing details on computer implementation of the model. For completeness, several supplemental files, data sets, and computer code, are provided. I understand it can be difficult for the reader to switch back and forth between the main paper and the supplemental files. But I hope this way of presentation will save space and avoid repeating published material. For examples of how the choices of model parameters influence the results, one can refer to the paper of Dong et al. (2010), in which a number of scenarios of varying soil physical and root parameters are discussed in detail. Also, one may refer to the conference paper by Dong at al (2013), in which the same model was applied to simulate soil water flow in a heavily grazed pasture (cited in the paper). In this paper, a direct comparison of this model against some other models is not done. I leave it for a future effort.

Yes, I have included a sink term for all major equations. Also, some further discussions on the sink terms are provided. Finally, Figure 1 has been re-drawn.
Thank you for the interesting comments! This paper attempts to provide a further documentation to an earlier paper by Dong et al. (Plant and Soil, 335:181-198, 2010). The focus is on providing details on computer implementation of the model. For completeness, several supplemental files, data sets, and computer code, are provided. I understand it can be difficult for the reader to switch back and forth between the main paper and the supplemental files. But I hope this way of presentation will save space and avoid repeating published material. For examples of how the choices of model parameters influence the results, one can refer to the paper of Dong et al. (2010), in which a number of scenarios of varying soil physical and root parameters are discussed in detail. Also, one may refer to the conference paper by Dong at al (2013), in which the same model was applied to simulate soil water flow in a heavily grazed pasture (cited in the paper). In this paper, a direct comparison of this model against some other models is not done. I leave it for a future effort.

Yes, I have included a sink term for all major equations. Also, some further discussions on the sink terms are provided. Finally, Figure 1 has been re-drawn.
Competing Interests: No competing interests were disclosed. Close
Report a concern
Respond or Comment

COMMENTS ON THIS REPORT

Author Response 07 Sep 2022

Xuejun Dong, North Dakota State University, Central Grassland Research Extension Center, Streeter, USA

07 Sep 2022

Author Response

Thank you for the interesting comments! This paper attempts to provide a further documentation to an earlier paper by Dong et al. (Plant and Soil, 335:181-198, 2010). The focus is ... Continue reading Thank you for the interesting comments! This paper attempts to provide a further documentation to an earlier paper by Dong et al. (Plant and Soil, 335:181-198, 2010). The focus is on providing details on computer implementation of the model. For completeness, several supplemental files, data sets, and computer code, are provided. I understand it can be difficult for the reader to switch back and forth between the main paper and the supplemental files. But I hope this way of presentation will save space and avoid repeating published material. For examples of how the choices of model parameters influence the results, one can refer to the paper of Dong et al. (2010), in which a number of scenarios of varying soil physical and root parameters are discussed in detail. Also, one may refer to the conference paper by Dong at al (2013), in which the same model was applied to simulate soil water flow in a heavily grazed pasture (cited in the paper). In this paper, a direct comparison of this model against some other models is not done. I leave it for a future effort.

Yes, I have included a sink term for all major equations. Also, some further discussions on the sink terms are provided. Finally, Figure 1 has been re-drawn.
Thank you for the interesting comments! This paper attempts to provide a further documentation to an earlier paper by Dong et al. (Plant and Soil, 335:181-198, 2010). The focus is on providing details on computer implementation of the model. For completeness, several supplemental files, data sets, and computer code, are provided. I understand it can be difficult for the reader to switch back and forth between the main paper and the supplemental files. But I hope this way of presentation will save space and avoid repeating published material. For examples of how the choices of model parameters influence the results, one can refer to the paper of Dong et al. (2010), in which a number of scenarios of varying soil physical and root parameters are discussed in detail. Also, one may refer to the conference paper by Dong at al (2013), in which the same model was applied to simulate soil water flow in a heavily grazed pasture (cited in the paper). In this paper, a direct comparison of this model against some other models is not done. I leave it for a future effort.

Yes, I have included a sink term for all major equations. Also, some further discussions on the sink terms are provided. Finally, Figure 1 has been re-drawn.
Competing Interests: No competing interests were disclosed. Close
Report a concern

Comments on this article Comments (0)

Version 2

VERSION 2 PUBLISHED 08 Jan 2016

Open Peer Review

Reviewer Status

Reviewer Reports

	Invited Reviewers
	1	2	3
Version 2 (revision) 08 Aug 22
Version 1 08 Jan 16	read	read	read

Brijesh K Yadav, Indian Institute of Technology Roorkee, Roorkee, India
Jun Fan, Northwest A&F University, Yangling, China
Hirotaka Saito, Tokyo University of Agriculture and Technology, Fuchu, Japan

Comments on this article

All Comments(0)

Add a comment

Browse by related subjects

Back to all reports

Reviewer Report

22 Views

11 Nov 2016 | for Version 1

Hirotaka Saito, Graduate School of Agriculture, Tokyo University of Agriculture and Technology, Fuchu, Japan

22 Views Cite this report Responses(1)

Approved

The article entitled "How to put plant root uptake into a soil water flow model" by Dong is in general well written and technically sound. However when I read this manuscript, I just found it a bit difficult to read as most relevant information such as Feddes function was in a supplemental file. There were no examples in the manuscript either. In my opinion, if the author is providing a tool to evaluate root water uptake, several examples (more than one) need to be included in the manuscript; for example how the choice the model affect soil water dynamics. This fact really makes it difficult to evaluate the manuscript.

There should be a sink term, S, that is used to account for root water uptake in Eq (1).
Figure 1 needs to be upgraded. They get blurred.

Competing Interests

No competing interests were disclosed.

I confirm that I have read this submission and believe that I have an appropriate level of expertise to confirm that it is of an acceptable scientific standard.

Respond to this report

Responses (1)

Back to all reports

Reviewer Report

23 Views

24 Oct 2016 | for Version 1

Jun Fan, Institute of Soil and Water Conservation, Northwest A&F University, Yangling, China

23 Views Cite this report Responses(1)

Approved With Reservations

It is an interesting topic and the text is well written but it is requested some program experience. It is a technical report not fully a scientific paper. It gave sufficient detail information about this model and also some relative programs. If a plant root uptake model with plant growth process which can report LAI or other parameters for ET calculation was put to Soil water flow model, this is more useful. If some cases can be tested and compared with other models, it will make user to use it easily. I fully agreed that it can be published as so far and give more opportunities to test it.

Competing Interests

No competing interests were disclosed.

I confirm that I have read this submission and believe that I have an appropriate level of expertise to confirm that it is of an acceptable scientific standard, however I have significant reservations, as outlined above.

Respond to this report

Responses (1)

Author Response

07 Sep 2022

Xuejun Dong, North Dakota State University, Central Grassland Research Extension Center, Streeter, USA

Thanks for the insightful comments! Yes, I agree it is not a typical research paper, but one documenting methodical details of a previously published paper. The dynamics of root and LAI growth are considered in the model, although not in a mechanistic manner in which the growth of roots and leaves are dynamically linked to the local weather and soil water availability. Again, the focus is on describing in detail the computer implementation procedure, along with explanation of important concepts, but lacks a direct comparison with other published models. As noted above, I hope the further comparisons can be achieved in future work.

View more View less

Competing Interests

No competing interests were disclosed.

Back to all reports

Reviewer Report

40 Views

04 Feb 2016 | for Version 1

Brijesh K Yadav, Department of Hydrology, Indian Institute of Technology Roorkee, Roorkee, India

40 Views Cite this report Responses(1)

Approved

The text is nicely written and I have few minor comments as described below.

Some references order is not cited correctly. For example the compensation function in equation 7 is proposed by "15" instead of the cited reference is number "14". Similaraly the rest of the citation numbers needs to be corrected.

The author has shown the moisture flow equation (Eqn 1) without the sink term. Since the focus of this article is on plant root uptake, so sink term should be included in all the governing equations along with their discrete form.

The figure 1 can be improved to make it more readable.

Competing Interests

No competing interests were disclosed.

I confirm that I have read this submission and believe that I have an appropriate level of expertise to confirm that it is of an acceptable scientific standard.

Respond to this report

Responses (1)

Author Response

07 Sep 2022

Xuejun Dong, North Dakota State University, Central Grassland Research Extension Center, Streeter, USA

Thank you for the interesting comments! This paper attempts to provide a further documentation to an earlier paper by Dong et al. (Plant and Soil, 335:181-198, 2010). The focus is on providing details on computer implementation of the model. For completeness, several supplemental files, data sets, and computer code, are provided. I understand it can be difficult for the reader to switch back and forth between the main paper and the supplemental files. But I hope this way of presentation will save space and avoid repeating published material. For examples of how the choices of model parameters influence the results, one can refer to the paper of Dong et al. (2010), in which a number of scenarios of varying soil physical and root parameters are discussed in detail. Also, one may refer to the conference paper by Dong at al (2013), in which the same model was applied to simulate soil water flow in a heavily grazed pasture (cited in the paper). In this paper, a direct comparison of this model against some other models is not done. I leave it for a future effort.

Yes, I have included a sink term for all major equations. Also, some further discussions on the sink terms are provided. Finally, Figure 1 has been re-drawn.

View more View less

Competing Interests

No competing interests were disclosed.

Alongside their report, reviewers assign a status to the article:

Approved - the paper is scientifically sound in its current form and only minor, if any, improvements are suggested

Approved with reservations - A number of small changes, sometimes more significant revisions are required to address specific details and improve the papers academic merit.

Not approved - fundamental flaws in the paper seriously undermine the findings and conclusions

[1] 1. Campbell GS, Diaz R: Simplified soil-water balance models to predict crop transpiration. In F. R. Bidinger and C. Johansen, editors, Drought research priorities for the dryland tropics. International Crops Institute for the Semi-Arid Tropics, Parancheru, A. P. 502 324, India, 1988; 15–26. Reference Source

[2] 2. Passioura JB, Angus JF: Improving productivity of crops in water-limited environments. In D. L. Sparks, editor, Advances in Agronomy. Elsevier Science, USA, 2010; 106: 37–75. Publisher Full Text

[3] 3. Campbell GS: Soil Physics with Basic: Transport Models for Soil–Plant Systems. Developments in Soil Science 14. Elsevier, New York, 1985. Reference Source

[4] 4. Hopmans JW, Bristow KL: Current capabilities and future needs of root water and nutrient uptake modeling. In D. L. Sparks, editor, Advances in Agronomy. Elsevier Science, USA, 2002; 77: 103–183. Publisher Full Text

[5] 5. Warrick AW: Soil Water Dynamics. Oxford University Press, 2003. Reference Source

[6] 6. Roose T, Schnepf A: Mathematical models of plant-soil interaction. Philos Trans A Math Phys Eng Sci. 2008; 366(1885): 4597–4611. PubMed Abstract | Publisher Full Text

[7] 7. Leitner D, Schnepf A, Klepsch S, et al.: Comparison of nutrient uptake between three-dimensional simulation and an averaged root system model. Plant Biosystem. 2010; 144(2): 443–447. Publisher Full Text

[8] 8. Feddes RA, Kowalik PJ, Zaradny H: Simulation of field water use and crop yield. Center for Agricultural Publishing and Documentation, Wageningen, The Netherlands, 1978. Reference Source

[9] 9. Wu J, Zhang R, Gui S: Modeling soil water movement with water uptake by roots. Plant Soil. 1999; 215(1): 7–17. Publisher Full Text

[10] 10. Zuo Q, Zhang R: Estimating root-water-uptake using an inverse method. Soil Sci. 2002; 167(9): 561–571. Publisher Full Text

[11] 11. Zuo Q, Jie F, Zhang R, et al.: A generalized function of wheat’s root length density distributions. Vadose Zone J. 2004; 3: 271–277. Reference Source

[12] 12. Ojha CS, Rai AK: Nonlinear root water uptake model. J Irrig Drain Eng. 1996; 122(4): 198–201. Publisher Full Text

[13] 13. Adiku SG, Rose CW, Braddock RD, et al.: On the simulation of root water extraction: examination of a minimum energy hypothesis. Soil Sci. 2000; 165(3): 226–236. Publisher Full Text

[14] 14. Li KY, De Jong R, Boisvert JB: An exponential root water uptake model with water stress compensation. J Hydrol. 2001; 252(1–4): 189–204. Publisher Full Text

[15] 15. Yadav BK, Mathur S, Siebel MA: Soil moisture dynamics modeling considering the root compensation mechanism for water uptake by plants. J Hydrol Eng. 2009; 14(9): 913–922. Publisher Full Text

[16] 16. Dong X, Patton BD, Nyren AC, et al.: Quantifying root water extraction by rangeland plants through soil water modeling. Plant Soil. 2010; 335(1): 181–198. Publisher Full Text

[17] 17. Heinen M: Compensation in root water uptake models combined with three-dimensional root length density distribution. Vadose Zone J. 2014; 13(2). Publisher Full Text

[18] 18. Verma P, Loheide SP, Eamus D, et al.: Root water compensation sustains transpiration rates in an Australian woodland. Adv Water Resour. 2014; 74: 91–101. Publisher Full Text

[19] 19. Bodner G, Nakhforoosh A, Kaul HP: Management of crop water under drought: A review. Agron Sustain Dev. 2015; 35(2): 401–442. Publisher Full Text

[20] 20. Simunek J, Hopmans JW: Modeling compensated root water and nutrient uptake. Ecol Model. 2009; 220(4): 505–521. Publisher Full Text

[21] 21. Jayawickreme DH, Jobbágy EG, Jackson RB: Geophysical subsurface imaging for ecological applications. New Phytol. 2014; 201(4): 1170–1175. PubMed Abstract | Publisher Full Text

[22] 22. Musters PA, Bouten W: A method for identifying optimum strategies of measuring soil water contents for calibrating a root water uptake model. J hydrol. 2000; 227(1–4): 273–286. Publisher Full Text

[23] 23. Dong X: Supplemental data for “How to put plant root uptake into a soil water flow model”. Zenodo. 2022. http://www.doi.org/10.5281/zenodo.6958793

[24] 24. Kirkland MR, Hills RG, Wierenga PJ: Algorithms for solving Richards’ equation for variably saturated soils. Water Resour Res. 1992; 28(8): 2049–2058. Publisher Full Text

[25] 25. Yang D, Zhang T, Zhang K, et al.: An easily implemented agro-hydrological procedure with dynamic root simulation for water transfer in the crop-soil system: validation and application. J Hydrol. 2009; 370(1–4): 177–190. Publisher Full Text

[26] 26. Lai CT, Katul G: The dynamic role of root-water uptake in coupling potential to actual transpiration. Adv Water Resour. 2000; 23(4): 427–439. Publisher Full Text

[27] 27. Dong X, Patton BD: Predicting soil water retention curves based on particle-size distribution using a Minitab macro. Afr J Soil Sci. 2015; 3(1): 079–085. Reference Source

[28] 28. Doughty S: Solve It: Computer Aided Mathematics for Science and Engineering. Gulf Publishing Company, 1995. Reference Source

[29] 29. Hanna OT, Sandall OC: Computational Methods in Chemical Engineering. Prentice Hall PTR, 1995. Reference Source

[30] 30. Dong X, Patton BD, Nyren PE: Responses of plant root and soil microbial respiration to seasonal rain events in a mixed-grass prairie under different grazing intensities. In G.-S. Zhou, editor, International Symposium on Adaptation of Terrestrial Ecosystems to Climate Change and Future Earth. Hubei Hotel, Beijing, China, Institute of Botany, Chinese Academy of Sciences, 2013; 148–158. Reference Source

[31] 31. Dong X: A plant root water uptake model. Zenodo. 2015. http://www.doi.org/10.5281/zenodo.42663

[32] 32. Dong X: A program for searching optimal root parameters in plant water uptake modeling. Zenodo. 2015. http://www.doi.org/10.5281/zenodo.42702

How to put plant root uptake into a soil water flow model

Abstract

Keywords

Revised Amendments from Version 1

Introduction

Methods

Implementation

Figure 1. Block-centered finite difference scheme for numerical solution of 1-D Richards equation with plant root water uptake.

Modeling water flow in variably saturated soil

Testing different ending soil water potentials for optimal root uptake

Testing different functions for root water uptake

Details of simulation-based searching program

Operation

Use cases

Summary

Data availability

Underlying data

Extended data

Software availability

Acknowledgments

References

Comments on this article Comments (0)

Open Peer Review

Comments on this article Comments (0)

Open Peer Review

Reviewer Status

Reviewer Reports

Comments on this article

Browse by related subjects

Competing Interests Policy

Stay Updated