Keywords
antibody, network, thermodynamics, binding, entropy, energy landscape
antibody, network, thermodynamics, binding, entropy, energy landscape
Theoretical backgrounds have been revised in accordance with the reviewers' suggestions. Figure 1 is significantly changed to comply with the reviewers’ suggestions, and only minor modifications have been made to the remaining figures. Theory now explains the different contribution of enthalpy and entropy changes to binding, reflecting the flexibility of antibodies at different stages of maturation.
See the author's detailed response to the review by Jordan D. Dimitrov
See the author's detailed response to the review by Jonghoon Kang
Blood is a massive and critically important extracellular space of multicellular organisms. It is a fluid tissue with cellular, macro- and small molecular components that perfuses the whole multicellular organism, being in direct contact with vascular endothelial cells and blood cells. Its components are potentially derived from any cell of the organism via secretion and leakage (Anderson & Anderson, 2002). Such a hugely diverse molecular pool needs to be regulated with respect to the quality and quantity of its components. One of the mechanisms of regulation is the generation of antibodies by the humoral adaptive immune system (Prechl, 2017a; Prechl, 2017b). Considering the diversity of antibodies and the diversity of molecular targets, the interaction landscape of the humoral immune system is presumably the most diverse in an organism. In this opinion article, I approach antibody homeostasis from the thermodynamic point of view, depicting antibody-antigen interactions in a novel energy landscape model. The currently used funnel energy landscape model is suitable for the description of folding and binding of one or a few molecules, but it would require landscapes of intractable sizes to depict a whole system, like adaptive immunity. I introduce the fountain energy landscape, a projection of the multidimensional binding landscape of antibodies to the dimensions of entropic penalty and energy of molecular interactions, to accommodate the vast range of interactions of antibodies.
Molecular interactions can be described by examining structural, kinetic and thermodynamic properties of the binding. Structural approaches aim to define the relative spatial positions of the constituting atoms of the interacting partners in the bound and unbound forms of a molecule. The advantage of the structural approach is the high resolution visual rendering of molecular structure that helps human perception. Systematic analysis of protein structures gives insight into the evolution of protein complexes and the dynamics of assembly and disassembly (Marsh & Teichmann, 2015). Structural information can reveal networks of protein interactions (Kiel et al., 2008). Kinetic studies follow temporal changes of association and dissociation of interacting partners. These observations are easily applicable to a simple system with a few components only, but it is difficult to describe complex systems and crowded molecular environments (Schreiber et al., 2009; Zheng & Wang, 2015). Thermodynamics examines the changes in free energy that accompany a binding event; providing statistical descriptions of enthalpic and entropic components of the interaction. Energy landscape theory resolves some shortcomings and integrates these approaches by assuming the presence of many different conformations that converge to thermodynamically stable forms -- the route taken to obtain this conformation dictating the kinetics of the events (Bryngelson et al., 1995). The intramolecular interactions of proteins lead to the emergence of the functional protein conformation, a process called folding. The energy landscape of folding is assumed to be funnel shaped, the stable form of the protein being at the bottom of the funnel with the lowest free energy state (Finkelstein et al., 2017; Wolynes, 2015).
The process of folding is obviously strongly dependent not only on general physical parameters, such as temperature and pressure, but on the quality and quantity of molecules present in the system. Water is the solvent of life and interactions with water molecules (Fogarty & Laage, 2014) are of key importance in all molecular interactions associated with life. The concentration of hydrogen ions (pH), cations and anions and small molecules modulate interactions (Lecerf et al., 2017). Macromolecules influence interactions not only by taking part in the interactions, but also by the excluded volume effect, restricting diffusional freedom (Zhou et al., 2008). A detailed definition of the binding environment is therefore indispensable for a realistic depiction of the binding energy landscape. Defining the antibody binding landscape in blood would therefore at least require a complete list of all constituents of blood, better involving abundance of each molecule.
Antibodies are globular glycoproteins secreted into the blood and other biological fluids by plasma cells (Nutt et al., 2015), descendants of B cells that had been stimulated by antigen. B cells are thus raised in an antigenic environment, the function of the immune system being the selection and propagation of B cells, which can respond to the antigenic environment. The essence of humoral immunity is therefore the definition and control of this antigenic environment by regulating molecular interactions via generation of antibodies with defined concentrations, affinity to target and effector functions. Antibodies are actually a family of oligomeric proteins, with distinct constant regions that qualify them into classes and subclasses, and with distinct variable domains that determine their binding specificity (Schroeder & Cavacini, 2010). While most of us think of antibodies as molecules with a well-defined specificity, in fact the majority of the circulating antibodies (especially of the IgM class) is not monospecific (specific to one target), but rather poly-specific and cross-reactive (Kaveri et al., 2012; Seigneurin et al., 1988). Any comprehensive systems approach to describe antibody function therefore must account for the presence of both highly specific and poly-specific antibodies. Our quantitative model of antibody homeostasis accordingly attempts to provide a unified framework for the complete humoral adaptive immune system (Prechl, 2017b). Thermodynamically this translates to the generation of a binding energy landscape suitable for maintaining molecular integrity of the host organism.
The funnel energy landscape is a theoretical approach used for the depiction of conformational entropy and free energy levels of one particular molecule (Bryngelson et al., 1995). Besides the description of intramolecular binding (folding) it can also be applied for the interpretation of homo- or hetero-specific binding, such as aggregation or ligand binding (Zheng & Wang, 2015). If we tried to describe antibody binding by the binding funnel energy landscape, we would face two interconnected problems, one deriving from antibody heterogeneity and the other from target heterogeneity. Antibody variable domains constitute the most diverse repertoire of all the proteins present in the organism, estimates being in the range of 109–1011 different primary structures at any particular time of sampling, the hard upper limit being the number of B cells in a human body, around 1012 cells (Bianconi et al., 2013). Even if the tertiary structures show orders of magnitude of lower diversity, we still face an immense variability. On the other side, poly-specific antibodies bind to a multitude of targets, with limits to the number of known targets being posited only by experimentation. A combination of these two factors implies that the binding funnel approach would not allow a clearly comprehensible yet thorough description of antibody-antigen binding. To resolve this issue, here I develop the concept of a binding fountain energy landscape model.
A system under observation can be described thermodynamically by the transfer of heat, work and matter between the system and its surroundings. According to the first law of thermodynamics any form of energy transfer between systems is accompanied by an equal change of energy transferred in the opposite direction (Figure 1A). In our approach to the description of energy landscape we shall consider our system under observation, blood, as an open system. For each antibody that enters this system (transfer of matter) we shall follow the changes in enthalpy and entropy until equilibrium is reached, accompanied by the release of energy in the form of heat from the system. We shall neglect thermodynamic properties attributable to binding valency (number of binding sites) and isotype, in order to focus our attention to properties of the antigen binding site, denoted as Fv.
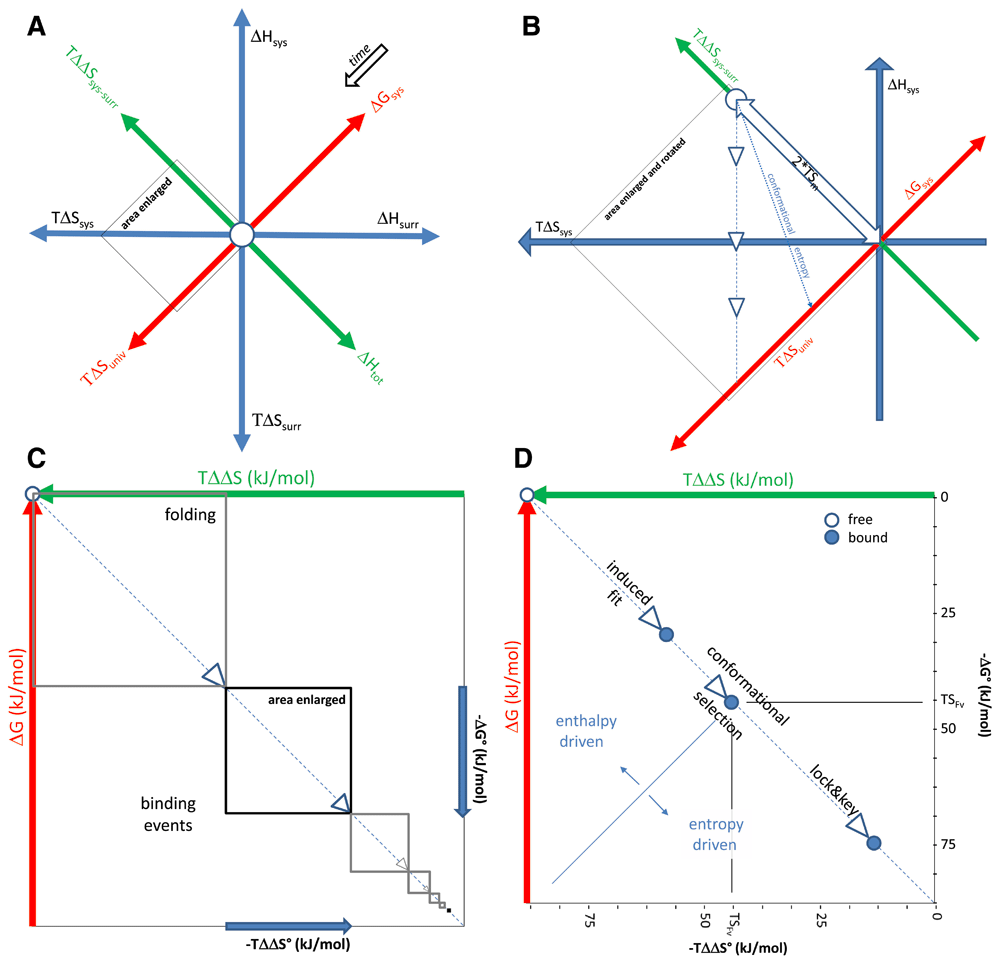
(A) A system (sys) under observation can change its energy content at the expense of its surroundings (surr). Whichever direction it moves in these thermodynamic dimensions, there will always be gain and loss. (B) Adding matter to the system is at the expense of the surroundings, causing an entropic imbalance twice the energy TSm of matter, equivalent to the total change in enthalpy Htot. For this energy to be converted into entropy of the universe (univ), the system will release heat, lowering enthalpy of the system. Equilibrium conditions represent states of the system when maximum amount of heat is released, these conditions identify the pathway of evolution of the molecule introduced into the system, shown here with a dashed line and white arrowheads. Total conversion of the matter into heat would lead to maximal TΔSuniv increase and total loss of entropy of the matter, which is conformational entropy in our case, represented by dotted line. (C) The molecule introduced into the system interacts with solvent and other molecules, these events are distinct interaction units of folding and binding, respectively. (D) Within such an interaction unit, the ratio of energies contributing to binding changes gradually, increase of solvent entropy overtaking dominance from decrease of conformational entropy. The range of free energy changes associated with antibody binding are shown.
We can plot the properties of the system using dimensions of enthalpy and entropy. Using these dimensions changes to Gibb’s free energy G of the system are defined by
ΔGsys=ΔHsys-TΔSsys 1)
where H stands for enthalpy, T for thermodynamic temperature and S for entropy. ΔG is linearly related to ΔH and TΔS as plotted in Figure 1. According to the second law of thermodynamics the sum of the entropies of interacting thermodynamic systems increases. This increase of entropy of the universe ΔSuniv identifies the arrow of time. Natural processes are proceeding in the direction so as to decrease the free energy of the system (Figure 1), which is related to the entropy of the universe as
-TΔSuniv=ΔGsys 2)
We can also identify a dimension ΔE that is orthogonal to G, defined by
ΔE= ΔHsys+TΔSsys 3)
where E stands for the dimension orthogonal to G. Dividing by T we obtain
ΔE/T=ΔHsys/T+ΔSsys 4)
Since the entropy of the surroundings changes according to
ΔSsurr= -ΔHsys/T 5)
we can substitute its negative value in equation 3
ΔE/T= -ΔSsurr+ΔSsys 6)
Now multiplying both sides by T we get
ΔE=T(ΔSsys-ΔSsurr)=TΔΔSsys-surr 7)
Thus, the dimension orthogonal to G represents the difference between the entropy change of the system and the entropy change of the surroundings. We shall call it entropy imbalance. When this dimension has zero value then entropy changes within the system and outside are identical. When work (W) is done on the system the change to TΔSuniv is described by
TΔSuniv=W-ΔHsys+TΔSsys 8)
with the system moving along a pathway of equilibrium conditions (England, 2015). Rearranging the equation, we obtain
W=ΔH-TΔSsys-TΔSuniv 9)
While work drives a gradual change, if matter (characterized by TSm) is taken from the surroundings (-TΔSsurr) into the system (TΔSsys) we observe a sudden change, with TΔSuniv being zero at the start of the ensuing processes
TΔSsys-TΔSsurr=ΔH-TΔSsys-TΔSuniv 10)
as indicated by the white arrow in Figure 1B. For the entropy of the universe to increase, this energy created by moving matter into the system must be used to increase the entropy of the universe. As equation 8 suggests this requires the balanced decrease of ΔHsys and increase of TΔSsys.
How the system returns this energy to the surroundings basically defines a pathway of equilibrium conditions determined by the interaction of the system with the matter added to it. The pathway of equilibrium conditions is described by
W-ΔHsys+TΔSsys≥kBTlnK 11)
when work is done on the system (England, 2015). In our case the work needs to be replaced by the entropy imbalance caused by the transfer of matter into the system
2*TSm-ΔHsys+TΔSsys=kBTlnK 12)
showing the relationship between the maximum TΔSuniv and TSm (Figure 1B). Introducing a protein into a system will initiate a sequence of events whereby the protein searches for the lowest possible free energy state. This will involve folding and binding events (Figure 1C). Proteins evolve to interact with other molecules constituting the living system, so folding is followed by interactions further decreasing ΔGsys, this may involve multiple binding events. Folding and binding therefore shows a continuity and within such an interaction unit the forces driving the events and therefore the nature of the interactions show a similar pattern (Figure 1D). The size of these units will depend on the properties of the protein: intrinsically disordered proteins would possess relatively small folding units, whereas proteins with very specific ligand binding ability may fold in larger units.
First in each interaction unit the surface of the protein available for binding searches the structural space of the system, engaging in enthalpy driven interactions. A particular sequence tests its potential conformations against the system, reaching equilibrium when the best fitting target is found. When the contribution of enthalpy and entropy to the binding energy is equal, binding can be driven by the presence of targets that stabilize a particular conformation. Further evolution of the protein should be driven by the target itself, the improving fit achieved by replacing amino acids so as to maximize fit. Optimization of specific binding is mediated by searching the sequence space of the molecule against a selected target molecule of the system, replacing amino acids and selecting the best fitting structure. This second half of the pathway will be driven by entropy maximization (Figure 1D), with increasing hydrophobic effect contribution as more solvent is excluded from the binding site.
During these interactions different entropic components contribute to TΔSsys
ΔSsys=ΔSconf+ΔSsolv+ΔSr,t 13)
where ΔSconf stands for conformational, ΔSsolv for solvation and ΔSr,t for translational and rotational entropy change. The decrease in ΔSsys along the pathway is brought about by the decrease in conformational, translational and rotational entropy of the introduced molecule - in our case the antibody. In practical terms it means that interactions with other molecules dissolved in the system will decrease the freedom of the antibody molecule to change its conformation and move around in the solvent. This decrease is represented by the dotted line in Figure 1B and D. Loss of conformational entropy is itself associated with the number of atoms at the binding interface and the buried surface area (Marillet et al., 2017). Experimental evidence suggests that reversible binding is characterized by a range of energies, limits observed both for maximal and minimal values, which are dependent on the magnitude of the interacting surface, whether characterized by the number of atoms or by buried surface area (Brooijmans et al., 2002; Smith et al., 2012). However, as the “fit” of the binding evolves the contribution of solvent entropy, also called hydrophobic effect, to ΔSsys surpasses this negative contribution. Considering the relationship of TΔSsys and the entropic penalty of binding - contributed by ΔSconf and ΔSr,t - the pathway of equilibrium conditions is divided into two parts. The point separating these two parts is identified by TSFv on the entropic imbalance and free energy axes, representing the range of energy changes associated with the evolution of fit of the Fv part of the antibody. Thus, when half of the entropy imbalance is compensated for and half of the maximal free energy decrease occurs the nature of binding changes (Figure 1B,D).
In the first region of the pathway binding is driven by enthalpy-entropy compensation, enthalpy being the main contributor to binding energy. Forces contributing to non-covalent binding induce the fit of the molecule to the target at an entropic cost (Figure 1C). Fluctuations in free energy level may reverse this process, allowing the molecule to move between different conformer states. This is a region where binding is truly reversible, meaning that reactions may proceed “backwards” without changing the composition of the system.
Where negative and positive contributions from entropy cancel out binding may be mediated solely by non-covalent binding forces triggering a conformational change. This suggests that the antibody molecule “clicks” to its target by selecting from multiple thermodynamically equivalent conformations the one optimal for binding. This state corresponds to the molten globule phase of protein folding.
Further decrease in conformational entropy will increase the buried surface area, excluding ever more water molecules from the binding site. Binding here will be dominated by hydrophobic effects, leading to entropy driven reversible binding. If -ΔGsys within an interaction unit reaches energies of covalent bond formation irreversible binding, chemical events take place.
In order to visualize the conformational component of the binding landscape let us spin our two-dimensional plot around the free energy axis at TΔΔSsys-surr = 2*TSm to obtain a three dimensional surface (Figure 2). Just like the funnel energy landscape, this surface should be a hypersurface: a surface that incorporates the multiple dimensions of possible arrangements of atoms of the binding molecules (Bryngelson et al., 1995; Liu et al., 2012). Native unbound antibody molecules entering our landscape will move down along a path, searching for equilibrium while interacting with their targets with an increasing binding energy. A binding path ends when the antibody finds equilibrium conditions in its lowest state of energy, corresponding to binding to a target with the highest affinity. Where this point is located depends both on the antibody and the nature of its target (conformation and physico-chemical characteristics). The hypersurface of binding events in the space of conformation, entropic imbalance and free energy generated by this approach we shall call a binding fountain energy landscape.
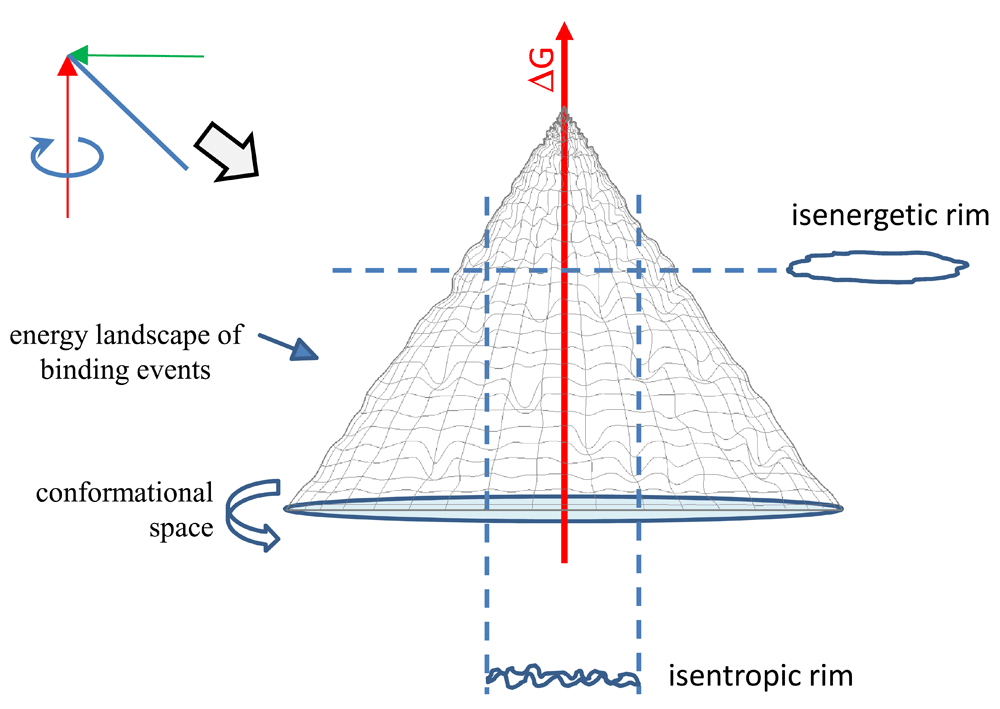
(A) By spinning the former representation in Figure 1 around the anchored axis we obtain a conical surface. This surface represents binding events of different interacting molecules of the system in equilibrium. Thermodynamically defined subsets of binding events in the binding fountain can be obtained by looking at events in the isenergetic or isentropic rim.
While the conical surface of equilibrium binding events is a theoretical surface, we can obtain descriptors of real binding events by looking at subsets of events of the interaction space. By cutting the binding fountain horizontally at a given ΔG value we obtain the isenergetic rim (Figure 2B). The isenergetic rim is the distribution of ΔS of binding events with identical ΔG. Thus, its shows the range of entropic imbalances that give rise to binding at the given ΔG in our system of study. By cutting the skirt of the surface at a given ΔS value, we obtain the isentropic rim (Figure 2B). The isentropic rim is the collection of binding events with identical TΔΔSsys-surr and a range of corresponding ΔG values. Thus, its ΔG distribution shows the range of free energy changes that give rise to binding at the given TΔΔSsys-surr in our system of study.
We have so far worked out an energy landscape interpretation tool, which helps map all the binding events that occur in a molecularly complex environment, such as blood. We assumed that antibodies secreted into the blood gain their native unbound conformations then engage in binding events of various energies until they reach their specific target. The path leading towards thermodynamic equilibrium can be rugged, caused by less specific contacts, or smooth, with few intermediate binding states (Figure 3A). It is important to note, however, that blood is the most heterogenous biological fluid, comprising potentially all molecules found in the organism (Anderson & Anderson, 2002). Besides a huge number of secreted molecules, any leakage from tissues, debris of cell death and foreign molecules may be present in blood. This vast molecular diversity generates a binding site diversity that we may assume to approach a randomized structural space, representing all potential variants of an antibody binding site covering up to 3000 Å2 (Marillet et al., 2017). Such a diverse binding space should approach a power law distribution of binding partners, with decay of partners as we increase binding energy or affinity (Figure 3B) (Zheng & Wang, 2015). A rugged start is therefore expected for all antibodies, with the path smoothing out depending on the paratope properties and the content of the binding landscape. As we approach higher energy and lower entropic imbalance regions the epitope “sharpens”, as Irun Cohen termed (Cohen & Young, 1991) the gradually increasing affinity of antibodies (Figure 3C), inserting the antibody with ever higher atomic precision into the system. This sharpening involves both a gradually increasing buried surface area and better fitting surfaces and various combinations of these components. It is also apparent that sectors of conformational space contain structurally related binding sites, since sharpening reveals more details of epitopes that appear identical at lower resolution (Figure 3D), later maturing into distinct conformational entities. This relationship also reflects the clonal relationship of antibodies going through affinity maturation, gaining sharper but constrained vision of targets by improving their fit (Kang et al., 2015).
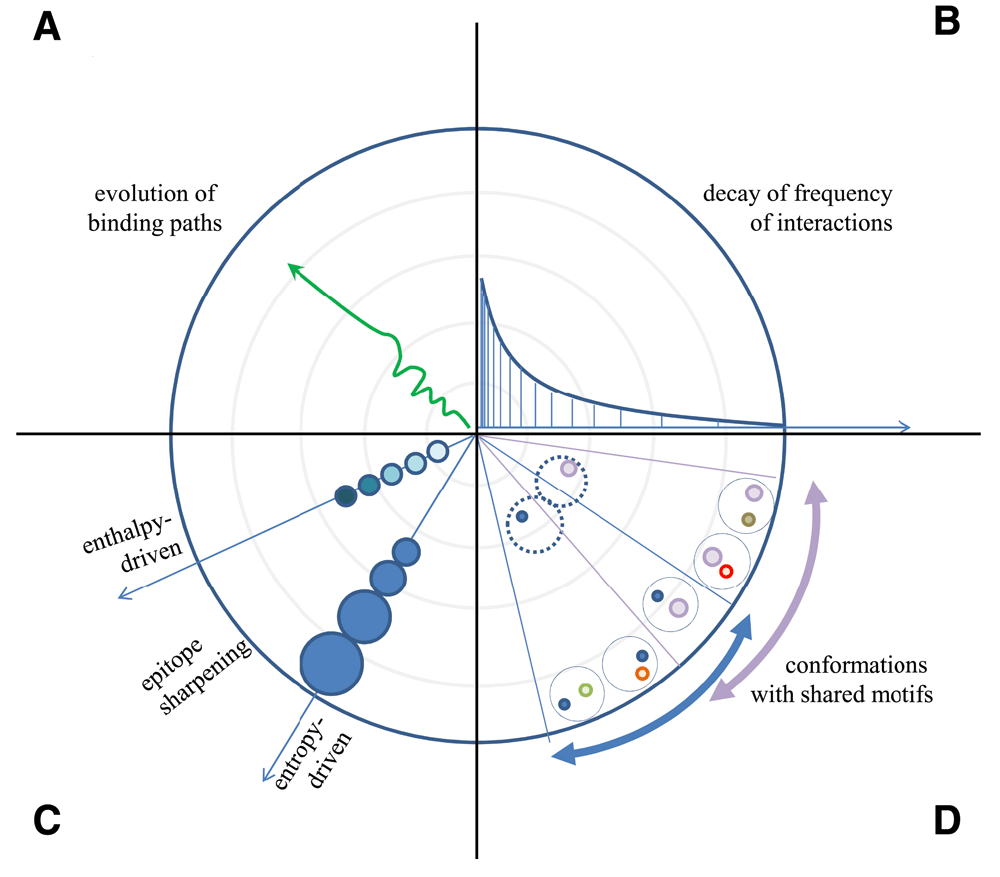
(A) Sequential binding of an evolving antibody appears as a path with more or less rugged track. (B) The frequency of interactions decreases by power law decay as we approach high energy binding with high entropic penalty. (C) The nature of contact accounting for binding changes by improved fit with stronger binding forces and by increased buried interface area. (D) Conformations of binding surfaces share common origin with identical structural motifs closer to the “source” of the fountain, the region of low energy interactions.
The binding landscape is the set of all potential interactions in a given fluid with given constituents, each interaction being positioned according to the entropic imbalance, conformation and free energy decrease. In the binding fountain representation we can trace the fate of a particular evolving antibody in time as a binding path or display several different antibodies at an imaginary thermodynamic equilibrium (Figure 4A). Owing to the fact that blood is a highly heterogenous fluid with a vast diversity of potential binding sites, the frequency of low energy interactions is very high. At the tip of the fountain, antibodies are “surfing” along the ripples of low affinity interactions. Moving down the surface they encounter interaction partners with gradually improved fit, spending more and more time in an interaction, until the target with best fit, that is highest free energy decrease and largest entropic penalty, is found (Figure 4A).
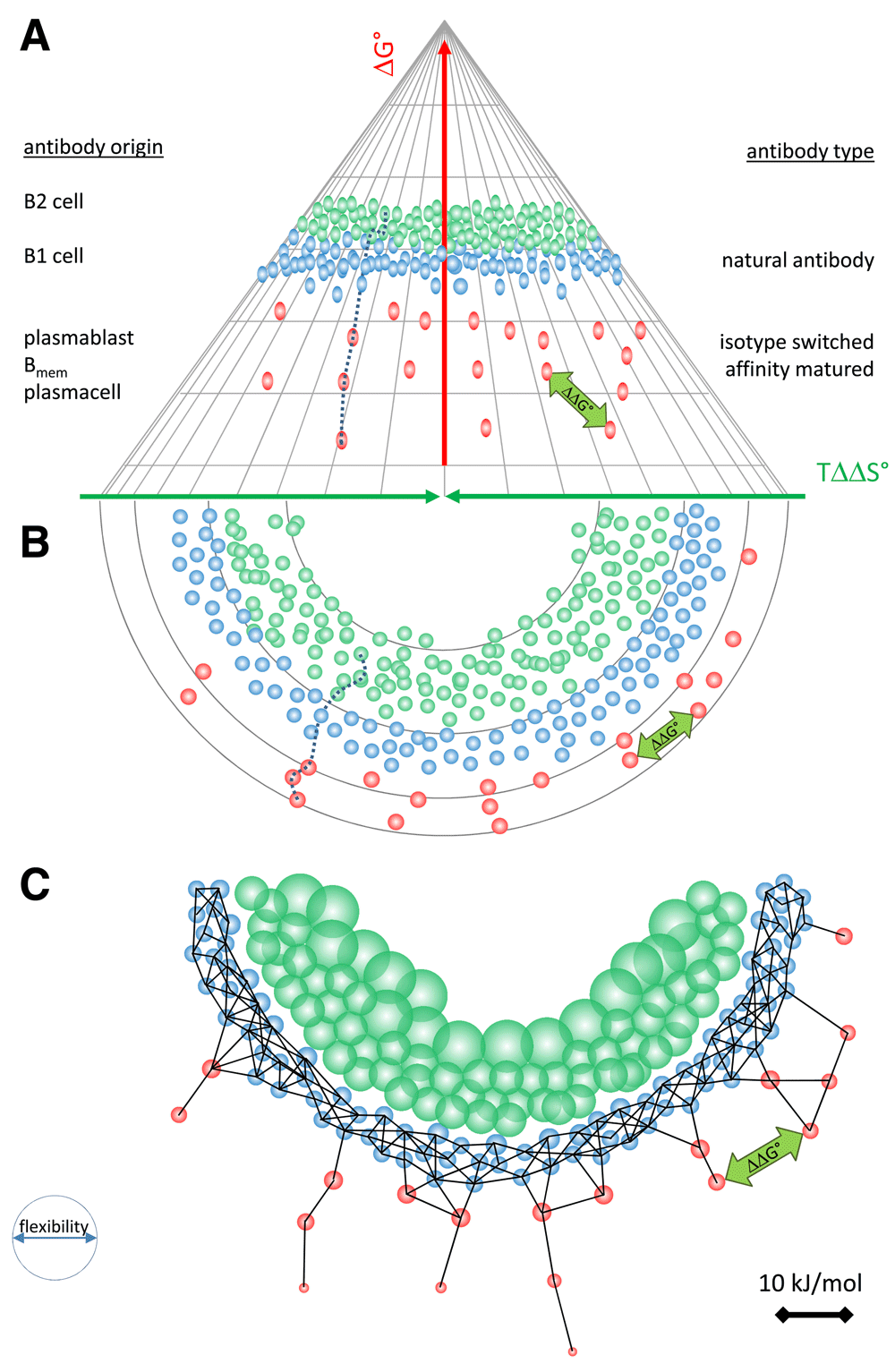
(A) Side view and (B) top view of the antibody binding fountain energy landscape. An antibody evolves down a binding path, shown by the dotted line. Antibodies may function as B-cell antigen receptors or be secreted by various cells as shown. Under standard state conditions natural antibodies (blue beads) and affinity matured thymus dependent antibodies (red beads) are arranged according to their conformation, entropic imbalance and free energy level. The distance between any two binding events can be expressed as ΔΔG, which represents the cross-reactivity of the two antibodies concerned. (C) We can further project these events into an interaction space where a network is formed based on distance and flexibility. Linkage for secreted antibodies is shown.
Interactions in the blood cannot reach thermodynamic equilibrium; molecules are continuously entering and leaving this compartment. On the other hand, due to the constant turbulent mixing, the distribution of molecules is constantly approaching homogeneity. Thus, we may display antibodies at an imaginary equilibrium where their position reflects their potential energy minimum in the system. This is where actually target antigen-bound antibody molecules are accumulating (Figure 4A,B). Under standard conditions free enrgy and equilibrium constants are related according to
ΔG°= -RTlnKA 14)
Registering the position of all the copies of a given antibody species should show a distribution of bound forms determined not only by ΔG°, but also by the availability of the target molecules, which is antigen concentration [Ag]. Under non-equilibrium conditions the energy landscape changes
ΔG= -RTlnKA+RTlnQ = RTln(Q/KA) 15)
where Q is the reaction quotient [AbAg]/([Ab]*[Ag]). Adding either free antibody or free antigen to the system will decrease Q, resulting in a decrease of ΔG. This will appear as a depression in the corresponding position of the landscape.
The disappearance of the target ([Ag]≈ 0 M) will lead to the disappearance of the low energy position in the landscape. As a consequence, the antibody will accumulate in the interaction with the next available energy level, albeit the ratio of bound to free form will be lower as dictated by the higher KD value. Alternatively, the antibody can search the neighboring conformational space along the isenergetic rim for a binding site with similar ΔG°. High concentrations of the target ([Ag]>>KD) will deplete antibody resulting in the potential overflow of related antibodies from the neighboring conformational space. The distance ΔΔG° between any two interactions has three components: a free energy component, a conformational component and an entropic penalty component. These components are perceptible from the side view, top view and both views of the binding fountain, respectively (Figure 4A,B).
We can also incorporate a physico-chemical property such as flexibility into the landscape. Flexibility, the ability to undergo thermally induced structural fluctuations is related to conformational entropy. To appreciate these factors we can project the interactions of a binding fountain into a space where the distance of the interactions is defined by ΔΔG and the flexibility of antibody is displayed as the diameter of the node of representing an antibody (Figure 4C). Please note that natural antibodies “jump” conformational space because of their ability to move between conformers. This appears as longer edges in the network. This representation also explains the ability of the humoral immune system to react with any conformation: the overlapping nodes of BCRs from a continuum in the conformational space represented by isentropic rim in this part of the landscape. This visualization is similar to the recently described network representation of antibody-antigen interactions (Prechl, 2017b).
The adaptive immune system responds to an antigenic stimulus by the production of antibodies reacting with the eliciting antigen. In our binding landscape an antigenic stimulus appears as an impression on the hypersurface representing antibody interactions, the position of the impression being determined by the conformation of fitting antibodies. The fact that an antigen can stimulate the humoral immune system implies that secreted antibodies that could efficiently bind to the antigen are not present. The antigen therefore binds to the membrane antibodies (B-cell receptors, BCR) of specific B cells (Figure 5). If BCR engagement reaches a threshold the affected B cells proliferate, differentiate and secrete antibodies (Prechl, 2017a). Depending on the nature of the antigen, the route of entry into the host, the presence of costimulatory signals, the ensuing response can proceed basically in two distinct ways. A thymus independent (TI) response will result in the generation of antibodies with binding properties identical to the parental B cell, since there is no affinity maturation. The structure of the binding site does not change, conformation, entropic imbalance and ΔG° of binding will be identical to the original interaction (Figure 5A). These interactions take place in regions with moderate conformational entropy loss and high interaction frequency, meaning that of the huge repertoire of BCRs several will respond. B1 cells are frequently involved in TI responses, which is also supported by our landscape theory. First, the BCR has the unique property of possessing multiple conformations with similar or identical ΔG°. This may explain the strong tonic signaling that keeps these cells in a cycling activated form. Second, typical TI antigens are huge molecules with repetitive motifs, which enhances conformational selection of the binding site once the antigen is captured by any site. The response appears as a standing wave, the appearance of antigen showing as the development of the impression, the response of antibody secretion as the disappearance of the impression as free antigen is replaced by bound antigen and immune complexes are removed. This kind of response seems suited for keeping concentrations of target molecules stable. We can think of the response as a closely knit elastic net that regains its original shape after applying pressure to a point (Figure 5A).
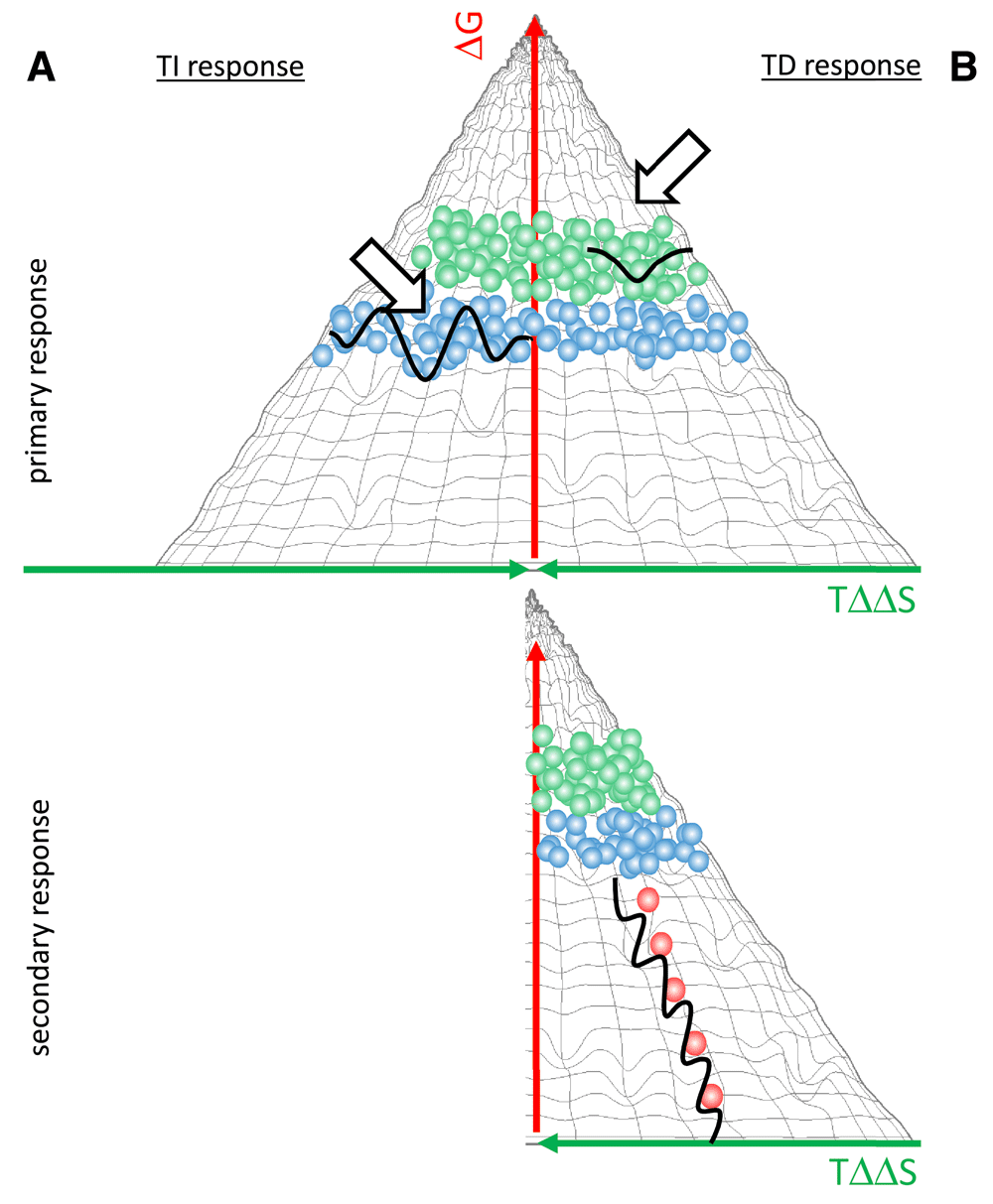
(A) Thymus-independent responses are characterized by antibodies of lower affinity. A closely knit network of antibody forming cells responds as an elastic net. There is no secondary response for TI immunity (B) Primary thymus-dependent responses are characterized by the expansion and antibody secretion of B2 cells. Germinal center reactions allow the evolution of antibodies with increasing affinity. This corresponds to a wave of interactions sweeping down the slope of the fountain.
Thymus dependent (TD) responses will involve the affinity maturation of the antibody binding site, the sequential generation of antibodies with increasing affinity. The primary response consists of the proliferation and antibody secretion by the group of naïve B2 cells that recognize the antigen. Antigen specific B2 cells also enter germinal centers where rounds of somatic hypermutation and affinity selection evolve binders. As the binding site matures, the entropic imbalance and ΔG° decreases. The interactions will take place at different positions of the binding landscape (Figure 5B). The response appears as a propagating wave sweeping down the slope of the binding fountain energy landscape. This wave is taking along the antigen, resulting in the efficient elimination of antigenic molecules.
It is important to note the relative identity of binding partners in this landscape: an antibody can bind to antigens but can also be the target of another antibody. The unique binding site of an antibody, the paratope that determines idiotype (identity as a binder), is itself part of the binding landscape. This can be especially important for antibodies with high intrinsic specificity rate (Zheng & Wang, 2015) that are eager to bind and reach their conformation with lowest energy level. I suggest that in the absence of antigen these high affinity binders could be refrained from non-specific binding by engaging their binding sites in lower affinity interactions.
Blood carries potentially all the molecules expressed in the host, along with those originating from the environment. To ensure that all these molecules find their intended binding partners a regulated binding landscape evolved: the clonal immune system. The appearance of clonally diversifying immunity in vertebrates is considered a major transition in the evolution of life: it is a system capable of evolving proteins with controlled affinity against any target molecule within the lifetime of an organism (Müller et al., 2018). It is therefore interesting to compare protein evolution in various scales of time. A nascent protein molecule evolves by attaining a conformation best fitting the energy landscape available for the protein: folding takes place in a matter of seconds (Finkelstein et al., 2017). The protein world evolved during the billions of years life on Earth, predating the appearance of cellular life (Caetano-Anollés et al., 2009). Tracing the evolution of a given protein in these timeframes also shows stages of degeneracy > evolution of domains > specificity. The evolution of antibodies shows a similar pattern: promiscuous binding of flexible antibody forms utilized as B-cell receptors scanning the complete conformational space, a selected repertoire of antibodies that change conformation to fit onto the target, and an evolved repertoire of rigid high-affinity binders that perfectly match target conformation. The clonal humoral immune system generates a regulated binding landscape by constantly sampling the molecular environment via a huge repertoire of B-cell receptors and by the generation of antibodies with a wide range of specificities and affinities. To allow the thermodynamic representation of this multitude of interactions, it is shown here that this landscape can be visualized as a binding fountain, in an analogy with the folding funnel energy landscape. The binding fountain landscape is an anchored conformation landscape with the entropic imbalance of binding anchoring the axis of free energy. Binding sites form a surface, which represents binding events in thermodynamically equilibrium. This landscape can be further projected into a multidimensional space of the antibody-antigen interaction network. This systemic perception and interpretation of antibody function is expected to help reveal how the immune system actually functions as a whole, a thermodynamic network of interactions, taking us closer to the systems level understanding of adaptive humoral immunity.
| Views | Downloads | |
|---|---|---|
| F1000Research | - | - |
|
PubMed Central
Data from PMC are received and updated monthly.
|
- | - |
References
1. Roussel M.R.: A life scientist's guide to physical chemistry. Cambridge University Press.2012.Competing Interests: No competing interests were disclosed.
Reviewer Expertise: Thermodynamics, immunology, kinetics
Is the topic of the opinion article discussed accurately in the context of the current literature?
Partly
Are all factual statements correct and adequately supported by citations?
Partly
Are arguments sufficiently supported by evidence from the published literature?
Partly
Are the conclusions drawn balanced and justified on the basis of the presented arguments?
Partly
Competing Interests: No competing interests were disclosed.
Reviewer Expertise: Thermodynamics, immunology, kinetics
Is the topic of the opinion article discussed accurately in the context of the current literature?
Yes
Are all factual statements correct and adequately supported by citations?
Yes
Are arguments sufficiently supported by evidence from the published literature?
Yes
Are the conclusions drawn balanced and justified on the basis of the presented arguments?
Yes
Competing Interests: No competing interests were disclosed.
Alongside their report, reviewers assign a status to the article:
| Invited Reviewers | ||
|---|---|---|
| 1 | 2 | |
|
Version 2 (revision) 15 Feb 18 |
read | |
|
Version 1 11 Sep 17 |
read | read |
Provide sufficient details of any financial or non-financial competing interests to enable users to assess whether your comments might lead a reasonable person to question your impartiality. Consider the following examples, but note that this is not an exhaustive list:
Sign up for content alerts and receive a weekly or monthly email with all newly published articles
Already registered? Sign in
The email address should be the one you originally registered with F1000.
You registered with F1000 via Google, so we cannot reset your password.
To sign in, please click here.
If you still need help with your Google account password, please click here.
You registered with F1000 via Facebook, so we cannot reset your password.
To sign in, please click here.
If you still need help with your Facebook account password, please click here.
If your email address is registered with us, we will email you instructions to reset your password.
If you think you should have received this email but it has not arrived, please check your spam filters and/or contact for further assistance.
Comments on this article Comments (0)